1 Introduction

Multiphase flows which appear in some of the thermal converters attracted many researchers in the recent papers. The identification of flow patterns in minichannels depends on the experimental and identification technique [1,2,3,4,5] used. Due to the changing dynamics of phenomena occurring during two-phase flow, nonlinear methods of data analysis were implemented in this field. Such algorithms as Hurst and Lyapunov exponents [6], correlation dimension or Kolmogorov entropy [7, 8] have been successfully used to classify flow patterns and analyse flow parameters oscillations. What is more, other complexity measures including Lempel–Ziv measure and recurrence quantification analysis (RQA) were applied to identify the main flow patterns and characterise the nonlinear dynamics of the flow [4, 5, 9, 10]. Despite all the research which has been undertaken, there is still a need of introducing methods of analysis over different timescales due to various frequencies of flow patterns occurrence. Recently developed algorithms—multiscale entropy (MSE) and composite multiscale entropy (CMSE), seem to be promising tools as they have already been applied to complex time series including: noise and real vibration data [11], laser Doppler flowmetry signals [12], laser speckle contrast images [13], human gait dynamics [14] or river flow time series [15]. In comparison with MSE, the CMSE algorithm reduces the variance of the estimated entropy values and in this way it can be used for shorter time series (less than 750 data points). Both algorithms are based on preparing a coarse-grained time series which characterises the system dynamics over different timescales and then calculating sample entropy (SampE). The SampE represents the regularity level of coarse-grained time series and is calculated in MSE and CMSE algorithms for each timescale factor [11]. In several papers, results obtained from multiscale entropy algorithms have been further analysed using artificial neural networks, complex networks and classifiers [11, 16,17,18].

The aim of the paper is to examine whether a signal gathered from a single detector (in this case an image representing a part of the video frame) may provide information about flow pattern in a minichannel. In order to verify this hypothesis, we performed multiscale analysis of air–water–glycerol flow focusing on changes in phase distribution during patterns transformation from fairly elongated bubbles (slug flow) into various sized air bubbles. Namely, we propose a method of two-phase flow image analysis using composite multiscale entropy (CMSE). In order to classify analysed flows, the complexity index (CI) and the support vector machine (SVM) classifier have been applied.

2 Experimental set-up and data characteristics

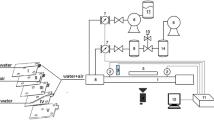
To differentiate various flow patterns, we adopt composite multiscale entropy (CMSE) applied to images recorded with a high-speed camera—Phantom v.1610 with the speed of 5000 fps. In the experiment, two-phase flow patterns in a circular minichannel (3 mm × 3 mm x 60 mm) have been taken under consideration. The flow consisted of two phases, liquid phase: water–glycerol solution (solution’s concentration: 45%) and air phase. The experimental schema is shown in Fig. 1. A pump (4—Fig. 1) generated compressed air which passed through an air tank (5—Fig. 1) and a valve (6—Fig. 1). Next, it was directed into the constant-pressure air tank (5—Fig. 1), a flow meter (8—Fig. 1) and a special micro-bubble generator (1—Fig. 1). A water tank (7—Fig. 1) was also a part of the set-up. The two-phase flow patterns were recorded using the Phantom v. 1610 high-speed camera (2—Fig. 1). The light (3—Fig. 1) was directed onto the minichannel (9—Fig. 1).

Fig. 1
figure 1

The experimental schema: 1—a special micro-bubble generator [8], 2—Phantom v. 1610 high-speed camera, 3—lightning system, 4—pumps, 5—constant-pressure air tanks, 6—a valve, 7—a water tank, 8—flow meters, 9—minichannel

Full size image

3 Method of data analysis

Using our experimental set-up (Fig. 1), two-phase flows of water–glycerol and air with different flow rates were studied systematically. The particular flow cases recorded through a transparent channel are illustrated by photographs in Fig. 2. For such ranges of air and water–glycerol flow rates, we observed in response various patters. In the limit of large fluid flow rate, the flow is fairly irregular with many small bubbles, while small fluid flow favours larger-sized bubbles. The bubbles merge to larger size with an increase in air flow rate with visible transition to slugs for low enough water flow rates. Interestingly, for a moderate level of air rate and low flow rate of fluid the flow can be more regular showing periodic distribution of flow phase densities.

Fig. 2
figure 2

The analysed two-phase flows with different air and water–glycerol rates

Full size image

Furthermore, to perform automatic identification of the flows, the gathered two-phase flow video frames (ten frames for each observed flow) have been converted into pixel matrices (64 pixels x 1280 pixels). First, a central part of the frame was extracted (24 pixels x 800 pixels). The pixels from the mentioned part of the frame were summed in each column, and this way, a one-dimensional time series was obtained, x = {x1, x2, …, xn}.

Next, we defined new variables due to the changing light conditions during the experiment and the following algorithm minimising the related errors:

$$ x_{n - 1}^{{\prime }} = \frac{{x_{n - 1} - x_{n} }}{{x_{n - 1} }}. $$
(1)

This new variable will be used in the next steps of analysis and denoted as x for notation simplicity.

Two-phase flow parameters, dynamics and patterns vary one from another, thus assessing the regularity of each flow is useful. One of the most common regularity coefficients is the sample entropy (SampE). It is frequently used to improve understanding of the nonlinear response of various dynamical systems [19,20,21]. This quantity gives information of the conditional probability that two similar series with m subsequent data points will remain similar if one more subsequent point is added. The similarity is estimated using a coarse-grained procedure which is based on a Heaviside step function with the parameter r which is the threshold concerning distance between samples. The r threshold defines the condition of distance between samples where the distance is shorter than r. If the particular number of neighbouring sequences, m, fulfils this requirement, then 1 is added to nn coefficient, and if one more sample does not change this condition, then 1 is also added to nd coefficient. Such coefficients are calculated through each scale factor τ of the time series. The sample entropy is defined as follows:

$$ {\text{SampE}} = - \log \frac{{n_{d} }}{{n_{n} }}. $$
(2)

Nevertheless, it is not applicable for determining the regularity of long-term structures; thus, the multiscale entropy (MSE) [22, 23] and also the composite multiscale entropy (CMSE) [11] were defined. The composite multiscale entropy using images was applied to the one-dimensional time series x. In order to use the CMSE, a coarse-grained series from original time series was formed. Two basic steps of the algorithm were as follows: (1) forming multiple coarse-grained time series for all scale factors τ = 50; (2) computing sample entropy for all coarse-grained time series for m = 2 and deriving the CMSE value which is the mean of τ sample entropy values. The coarse-grained time series is defined as:

$$ y_{k,p}^{\left( \tau \right)} = \frac{1}{\tau }\mathop \sum \limits_{{i = \left( {p - 1} \right)*\tau + k}}^{p*\tau + k - 1} x_{i,} \quad 1 \le p \le \frac{N}{\tau }, 1 \le k \le \tau, $$
(3)

where N—the length of each examined time series, x, τ—scale factor, k—number of the coarse-grained series for each τ and p—length of each coarse-grained time series. A coarse-grained time series for scale factor τ = 2 is prepared according to the scheme presented in Fig. 3. The CMSE algorithm is characterised by several parameters: τ—scale factor, m—embedded dimension which states that two similar sequences of m subsequent points will still be similar when one more consecutive point is considered, N—number of points of the one-dimensional time series, r—maximum norm of the distance between samples and σ—standard deviation of each coarse-grained time series.

Fig. 3
figure 3

The procedure of coarse-grained time-series preparation. The original time series consisting of the x elements is characterised by the starting sampling time step. The transformed effected series yk,p (τ) are related to the effective scale τ where the elements are averages of τ consecutive neighbours of the original elements. Composite procedure takes into account various choices of neighbours as illustrated for τ = 2

Full size image

The CMSE values for each of the considered flow are calculated according to the following formula:

$$ {\text{CMSE}}\left( {x,\tau , m, r} \right) = \frac{1}{\tau }\mathop \sum \limits_{k = 1}^{\tau } {\text{SampE}}\left( {y_{k}^{\left( \tau \right)} , m, r} \right). $$
(4)

In this paper, the CMSE values were calculated for numerous scale factors, τ ϵ {1,2,3, …, 50}, and the obtained values for each flow were averaged for ten extracted frames of the flow. In the next step, the complexity index (CI) which is the integral of the CMSE curve was calculated for each averaged CMSE function. The CI enables quantifying the integrated complexity of the data across multiple scales.

4 Flow pattern characteristics

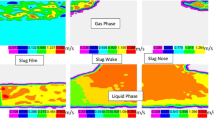
The obtained CMSE curves for all 56 observed flows presented in Fig. 2 varied one from another. Figure 4d shows three representative CMSE curves with complexity index values shown in the figure’s legend obtained for image signals (Fig. 4a–c).

Fig. 4
figure 4

Input one-dimensional time series and example frames of the registered flow patterns (a, b, c) and CMSE functions and CI values obtained for them (d). The CMSE curves obtained for mentioned flows with the following air (qa) and water–glycerol (qw) rates: a qa = 0.07 ln/min, qw = 32.66 kg/h, b qa = 0.199 ln/min, qw = 16.15 kg/h, c qa = 0.328 ln/min and qw = 43.44 kg/h. In the flows, such patterns were observed: a bubbles, b slugs, c minibubbles as concluded from Fig. 2

Full size image

One can observe a hyperbolic-like shape in Fig. 4d for minibubbles flow (Fig. 4c) with a monotonic decrease. These data are related to white noise stochastic distribution of fairly small bubbles inclusions. Note that the mixture of the diameters and positions of bubbles varies as well. On the other hand, in CMSE shape of bubbles flow (Fig. 4a) we observe minimum at scale τ = 3 and maximum around 8 (Fig. 4d). The minimum signals the formation of more correlated (periodic) flow of the larger bubbles which are separated by roughly constant fluid spaces. Additionally, the period of such a modulated distribution is close to 3. For smaller and larger scales, this self-organisation phenomenon is blurred. The situation in case of slug flow (Fig. 4b) is different as instead of minimum we observe more flat distribution informing about the presence of flow correlations but also the absence of characteristic distances (Fig. 4d).

For all observed flows, the CI values were in the following range: 4.24 ÷ 15.33. On the basis of calculations and visual observation, a table consisting of CI values for each flow and a class of flow patterns {I, II, III, IV} which was determined for each flow was prepared. In the next step, the data were analysed by WEKA (Waikato Environment for Knowledge Analysis) software [24]. The LibSVM classification was performed on the mentioned table. Based on several iterations of classification tests, the validation of the prepared table was conducted. Finally, the results table consisted of 16 flows of class I with the CI in the range of 4.24 ÷ 8.70, 15 flows of class II with the CI in the range of 10.01 ÷ 11.87, 10 flows of class III with the CI in the range of 12.00 ÷ 13.86 and 15 flows of class IV with the CI in the range of 14.00 ÷ 15.33. The percentage of correctly classified instances was equal to 96.43%. The total number of instances (flows) was 56.

Consequently, Fig. 5 presents four distinguished flow classes according to CI value and SVM classification: Class I presents slugs flow; class II presents short slugs and cap bubbles flow; class III presents bubbles and minibubbles flow; and class IV presents minibubbles and dispersed bubbles flow. According to the performed analysis, a flow pattern map for all analysed flows was obtained and is shown in Fig. 6. This map indicates that flows from class I (slugs flow) were clearly distinguished from all other flows. For better clarity, five particular regions of pattern’s classification results are separated with bold lines (Fig. 6). The middle region represents the least stable patterns as all identified flow classes mix in this area. One can also see that bubbles and minibubbles flows (III) and minibubbles and dispersed bubbles flows (IV) share neighbouring places on the flow pattern map. Two ‘corners’ of the map present areas which were clearly separated—left, upper ‘corner’ shows flows from class II (short slugs and cap bubbles flow) and right, lower ‘corner’ flows from class IV (minibubbles and dispersed bubbles flow).

Fig. 5
figure 5

Flows classes versus CI values according to SVM classification grouped for the cases from Fig. 2

Full size image
Fig. 6
figure 6

Flow pattern map obtained based on CI value and SVM classification procedure: I—slugs flow, II—short slug and cap bubbles flow, III—bubbles and minibubbles flow, IV—minibubbles and dispersed bubbles flow. The bold lines distinguish regions with clearly classified patterns from those which identified pattern mix

Full size image

Figure 7 shows CMSE functions for example flows from particular classes denoted as (a)–(l) as defined in Table 1.

Fig. 7
figure 7

CMSE functions of example flows characterised in Table 1: a example flows from class I, b example flows from class II, c example flows from class III, d example flows from class IV. The cases (a–l) as defined in Table 1

Full size image
Table 1 Characterisation of example flow from particular classes presented in Fig. 7 including CI values and flow rates
Full size table

The particular cases presented in Fig. 7 are grouped into classes (I)–(IV). The classification is based on the obtained parameters of CI for the example flows presented in Fig. 7.

The standard deviation (SD) of CI value was calculated using CMSE functions obtained for ten subsequent frames of each flow calculated for all scale factors. Interestingly, basing on this parameter we can classify the flows into four classes: slugs (I), large and intermediate bubbles (II and III) with self-organisation tendency and finally the most stochastic flow with small bubbles (IV).

5 Conclusions

In our studies of multiphase flow in a minichannel, we used the composite multiscale entropy and complexity index to classify the flow. The curves of CMSE for slugs flows (class I) have a flat distribution informing about the presence of flow correlations but also the absence of characteristic distances as in many cases slugs were moving one after another with no gaps. As far as class II—short slugs and bubbles flow and class III—bubbles and minibubbles flow are concerned, the CMSE shapes reach minimum for low scales and maximum couple points further. This fact indicates that in these flows, bubbles and short slugs were separated by fluid flow. Finally, the CMSE curves for minibubbles and dispersed bubbles flow (class IV) have a hyperbolic shape as fairly small bubbles resemble white noise stochastic distribution. The CI for identified classes was the higher, the more instabilities of the flow and small-sized patterns were observed.

A further classification of the flows was based on SVM algorithm applied in WEKA software. The percentage of correctly classified instances was high and equal to 96.43%. According to the obtained flow pattern map, flows from class I (slugs flow) were clearly distinguished from all other flows. The particular regions of pattern’s classification consist of a.o. the middle region which presents the least stable area as all of the identified flow classes are mixed there. It forms a sort of a temporary pattern area between slugs and minibubbles. One can see that the errors in classification may have been caused by two very similar classes of flow—class III and class IV. Both classes include minibubbles patterns which fluctuate and move during an observed flow. What is more, only ten subsequent frames were taken into account; thus, some instabilities observed in this short part of the video strongly influenced the results of the classification.

We succeeded to identify the particular flow patterns by analysing images obtained from a ‘single detector’—in this case a part of the video frame of the flow. In the analysis, flows with changing air and fluid flow rates based on CI values using SVM classification were identified. We can conclude that it is possible to gather information about the flow using a single detector situated in a particular position of the minichannel. Additionally, it can be stated that CMSE was able to indicate a formation of flows with periodic tendency to the particular phase distributions. We assume that for channels with bigger size and with uniform lighting conditions, other algorithms such as multivariate multiscale entropy algorithms may be beneficial.