The 50th anniversary of the coupled channels Born approximation (CCBA) and the coupled reaction channels (CRC) theories of nucleon transfer reactions (a unique interplay between theory, experiment and computer technology, conducted during the most tumultuous period in modern American society)

Abstract

Nucleon transfer reactions have played a fundamental role in understanding the single-particle components, shell structure and collective properties of atomic nuclei. The conventional distorted wave Born approximation (DWBA) envisioned the nucleon transfer reaction as a one-step process, which proceeds directly from the ground state of the target nucleus to a state of the residual nucleus. The coupled channels Born approximation (CCBA) and coupled reaction channels (CRC) theories evolved because a number of nucleon transfer reaction cross sections could not be reconciled within the DWBA. These coupled channels models revealed that, in addition to the “one-step” process of the DWBA, “multi-step” nucleon transfer processes involving accessary pathways can participate in populating the final nuclear state. In the CCBA, the auxiliary pathways involved inelastic excitations of the target and/or residual nucleus, whereas, in the CRC, the pathways included sequential nucleon transfer passing through nuclear states of an intermediate partition. Coherent addition of contributions from one-step and multi-step nucleon transfer processes resulted in dramatic alterations in reaction cross sections, which were experimentally confirmed. The CCBA and CRC linked the structure of the nuclei participating in a reaction to modalities of nucleon transfer arising during the relative motion between the interacting ions. These complementary theories inexorably changed physicists’ interpretations of nucleon transfer reactions and, in doing so, heralded in the new field of direct heavy-ion reactions.

1 Overview: “Nature loves to hide”, Heraclitus of Ephesus (fifth century B.C.)

Nucleon transfer reactions have profoundly helped in determining the underlying structure of atomic nuclei. The data acquired from these experiments, however, have provided the most meaningful information about nuclei when interpreted through a quantum mechanical description of the relative motion between the colliding ions and in calculating the matrix elements characterizing the various transitions between nuclear states assumed to be involved in the reaction. The distorted wave Born approximation (DWBA) was the most widely used theory of nucleon transfer reactions in the 1960s and into the 70s. It viewed the nucleon transfer reaction as a one-step process, which proceeded directly from the ground state of the target nucleus (the initial state) to a state of the residual nucleus (the final state).

The coupled channels Born approximation (CCBA) and the coupled reaction channels (CRC) theories evolved because, by the late 1960s, an increasing number of nucleon transfer reaction cross sections could not be reconciled within the DWBA. These complimentary theories went beyond the DWBA by demonstrating that, in addition to the “one-step” (direct) nucleon transfer process, “multi-step” (indirect) nucleon transfer processes involving a variety of auxiliary pathways could participate in reaching the final nuclear state. Flux through these supplementary pathways was shown to depend critically on the structure of the nuclear states participating in the reaction. In the CCBA, the additional pathways contained inelastic excitations of the target and/or residual nucleus. In the CRC, the supplementary pathways involved sequential nucleon transfer through nuclear states of an intermediate partition. Quantal interference between contributions arising from one-step and multi-step nucleon transfer processes was found to give rise to dramatic alterations in reaction cross sections, which ultimately became signatures by which these complementary processes were experimentally confirmed. The CCBA and CRC, for the first time, linked the detailed structure of the nuclear states participating in a reaction to various modalities of nucleon transfer that can arise during the relative motion between the collision partners. These theories redefined the field of nuclear reaction physics by dramatically changing the way researchers described nucleon transfer reactions.

On the 50th anniversary of the CCBA and CRC, we present the intriguing story about how these far-reaching theories emerged, the individuals involved in the original research, the methodologies employed, the bold theoretical predictions made along with their subsequent experimental verifications and the unprecedented success these models enjoyed during the 1970s, resulting in a grande miraculum decennium. This narrative is our attempt to recount important contributions in nuclear reaction physics that led to the CCBA and CRC theories becoming powerful tools for deconstructing nucleon transfer reactions and for extracting information about the structure of the interacting nuclei. Moreover, these coupled channels formulations consisted of a computational framework that proved to be applicable across the nuclear landscape.

In this account, we trace the evolution of the CCBA and CRC models, which originally were devised to describe light-ion-induced nucleon transfer reactions, and delineate why and how these quantum mechanical formulations were subsequently modified to become essential tools for understanding heavy-ion nucleon transfer reactions. At the Lawrence Berkeley National Laboratory (LBL) in Berkeley, California, a collaboration between R. J. Ascuitto and N. K. Glendenning led to a comprehensive CCBA theory of nucleon transfer reactions; and the CCBA calculations of Ascuitto, Glendenning and B. Sorensen confirmed, for the first time, the presence and importance of multi-step two-neutron transfer processes participating in (p, t) reactions involving rare-earth deformed nuclei. We also assess the insightful computer simulation studies of Ascuitto and Vaagen, while at the Niels Bohr Institute (NBI) and the Nordic Institute for Theoretical Physics (NORDITA), in Copenhagen, Denmark, which unequivocally demonstrated that heavy-ion-induced nucleon transfer reactions, despite the near-classical conditions for their relative motion, required a full quantum mechanical description to fully understand experimental reaction cross sections. Of paramount importance in portraying the evolution of the CCBA, we acknowledge the ground-breaking experiments performed by K. A. Erb and a small group of outstanding graduate students at the Wright Nuclear Structure Laboratory (WNSL), at Yale University. Their research confirmed far-reaching predictions of the CCBA, which ultimately established it as the most successful and prolific theory of nucleon transfer reactions.

In terms of the CRC, we present early calculations of Ascuitto, Glendenning and Sorensen, at LBL, which revealed the importance of sequential two-neutron transfer processes contributing to proton inelastic excitation of neutron-pairing vibrational states in even-even nuclei; the calculations of J. Bang and colleagues, at NBI, that demonstrated the crucial role played by sequential one-neutron transfer processes in (t, p) reactions involving light nuclei; and the subsequent contributions of T. Tamura, T. Udagawa and coworkers, at the University of Texas, in Austin, Texas, which convincingly showed the need to include sequential one-neutron transfer processes when calculating heavy-ion-induced two-neutron transfer reaction cross sections in shell-structured nuclei.

This narrative, however, is not only about particularly important accomplishments in nuclear reaction physics. It also sheds light on how the turbulent conditions that existed in American society during the Vietnam War era impaired research in nuclear reaction physics, and significantly impeded academic activities in general, in the USA. In a sense, this account provides a microcosm of the deleterious relationship that emerged between science, society and the Federal Government in the late 1960s and 70s. In this presentation, we draw on personal experiences involving the volatile anti-Vietnam War riots in Berkeley, the Kent State massacre at Kent State University in Ohio, the protesting students’ takeover of the Courant Institute of Mathematical Sciences at New York University (NYU) and the sobering Moratorium March in Washington, D.C. Our story centers around the plight of a few aspiring nuclear physicists who, despite concerns about a lack of jobs in physics, elected to remain at Yale’s WNSL as graduate students and junior faculty with the goal of completing heavy-ion nucleon transfer reactions designed to confirm or refute far-reaching implications of the newly proposed CCBA and CRC theories. Their remarkable resolve played a major role in revitalizing research in nucleon transfer reactions, and, in doing so, helped launch the new field of heavy-ion reaction physics in the 1970s.

In this manuscript, for simplicity, we present the various coupled channels equations for nucleon transfer reactions in a symbolic form, i.e., by not explicitly expressing the relative motion wavefunctions in terms of their angular and radial components. In actual calculations, however, the relative motion wavefunctions are usually expanded in terms of spherical harmonics, since the angular integrations can be performed in closed form. What then remains is a set of coupled equations in the radial coordinate, which must be solved on a computer. Additionally, some quantum numbers and vector couplings employed to describe nuclear states are not included. Our goal is to present the coupled channels equations in a form that would be more suitable for a diverse group of readers, especially for those with only a modest knowledge of quantum mechanics and/or nuclear physics.

Lastly, this account of the original coupled channels descriptions of nucleon transfer reactions sheds light on a remarkable inflection point in the history of nuclear reaction physics, through its dialogue, the authors personal experiences and a unique collection of figures which chronologically reveal the unprecedented successes of the CCBA and CRC models achieved in the 1970s.

1.1 The DWBA

During the 1960s, the DWBA, as pioneered at the Oak Ridge National Laboratory (ORNL) in Oak Ridge, Tennessee, became the most useful theory of nucleon transfer reactions. The reaction was viewed as caused by a weak interaction that induces a one-step (direct) nucleon transfer process to occur between two channels, i.e., from the ground state of the target nucleus (initial channel) to a state of the residual nucleus (final channel). The wavefunctions describing the relative motion between the interacting ions were determined by an optical model potential, whose parameters were usually chosen to describe elastic scattering in the incoming and outgoing channels. The DWBA was largely valid when the transfer reaction could be treated as a perturbation on the elastic scattering. However, coupling between the elastic channel and inelastic scattering and/or nucleon transfer channels can sometimes be strong. Under these circumstances, it was known how to incorporate, at least in a formal way, coupling between the elastic channel and other open channels through alterations in the parameters of the optical model potentials. Nevertheless, as this report will demonstrate, only an explicit coupled channels approach provided an adequate representation of these reactions, since it incorporated inelastic scattering and/or nucleon transfer on an equal footing with elastic scattering.

By the late 60s, however, an increasing number of nucleon transfer reactions could not be understood within the context of the DWBA. Consequently, some researchers began questioning basic tenets of the DWBA. Ascuitto, a graduate student at Rensselaer Polytechnic Institute (RPI), in Troy, New York, was awarded a postdoctoral fellowship at LBL in the Division of Nuclear Chemistry. At RPI, his research entailed assessing the importance of inelastic scattering in two-nucleon transfer reactions involving 2s-1d shell deformed nuclei, using a second-order plane wave Born approximation. Glendenning was the director of the nuclear theory group at LBL, and was an established researcher. At the time, he was involved in determining the shapes of deformed rare earth nuclei by analyzing alpha particle inelastic scattering data. Since the two investigators shared common interests, they readily began a productive collaboration, which ultimately led to a comprehensive description of nucleon transfer reactions that included effects from inelastic scattering and sequential nucleon transfer.

At this point in time, however, America had fallen into the depths of despair, as the two most influential proponents of peace-in-Vietnam were silenced forever. As the war in South East Asia escalated, Berkeley, the home of LBL, emerged as the epicenter for the anti-Vietnam War Movement. The Vietnam Day March, the People’s Park Riot (bloody Thursday), Cal-students’ violent anti-Vietnam War demonstrations, Sheriff’s deputies beating and shooting protestors along Telegraph Avenue, police using tear gas and chemical Mace to disperse crowds, a firebombing on the University of California’s campus, and widespread experimentation with mind-altering drugs had transformed the Bohemian town of Berkeley into a veritable civil war zone. The protesting and rioting became a narcotic for many of the student demonstrators. No community in America had a richer involvement in antiestablishment activities than Berkeley, or, as some called it, Berserkley. Ultimately, 2700 National Guard troops carrying loaded rifles with drawn bayonets were required to restore a modicum of order. Lawrence Berkeley National Laboratory became surrounded by social chaos. Consequently, for Ascuitto, and likely other fellows conducting research at LBL, it was becoming increasingly more difficult to concentrate on their work, as life outside of the laboratory presented an ever-growing challenge.

1.2 The CCBA and CRC

When the situation in Berkeley became intolerable, Ascuitto would often escape to the tranquility of Angel Island in San Francisco Bay to conduct non-computer aspects of his research. There, working at an old wooden table near the highest point on the island, he constructed a readily calculable CCBA model that employed an intuitive approach, the so-called source term method, to fully incorporate multi-step nucleon transfer processes into a workable theory of nucleon transfer reactions. In this formulation, a system of homogeneous coupled Schrodinger equations, containing optical model potentials to describe the relative motion between the incoming particle and the target nucleus, was used to incorporate inelastic excitations of the target nucleus. Likewise, a similar system of coupled equations was used to include inelastic excitations of the residual nucleus. However, the latter set of coupled equations needed to be inhomogeneous, i.e., source terms were required on the right side of these equations, to account for nucleon transfer between the initial and final partitions. The aim of this approach was to numerically solve the two systems of coupled equations and determine the S-matrix elements for the overall reaction by directly imposing the physical asymptotic boundary conditions on the partial wave solutions.

After nearly a year of conducting research in an unsettling Berkeley environment, Ascuitto and Glendenning managed to introduce the CCBA as a generalized theory of nucleon transfer reactions. Their unique formulation of the CCBA explicitly included inelastic excitations of the target nucleus followed by nucleon transfer (s) and/or nucleon transfer (s) followed by inelastic excitations of the residual nucleus. Additionally, the CCBA employed a quantum mechanical treatment of the matrix elements characterizing the various inelastic scattering and nucleon transfer transitions between nuclear states assumed to be involved in the reaction. The inelastic scattering transitions were treated to all orders, but the intrinsically weaker nucleon transfer transitions to first order. The CCBA represented a major leap in our understanding of light-ion-induced nucleon transfer reactions, and subsequently became essential for interpreting many aspects of heavy-ion-induced nucleon transfer reactions.

Fig. 1

Spatial coordinates for a nucleon transfer reaction A (a, b) B, a = b + x and B = A + x

At the time, the traditional practice in nuclear reaction physics was that theorists and experimentalists worked separately, and seldom did the twain meet. The CCBA and CRC, however, changed that practice, as nuclear structure and reaction dynamics became inextricably connected. Nuclear physicists stopped thinking of nucleon transfer reactions as involving an incoming nuclide (or nucleon) elastically scattering off a featureless target nucleus and occasionally transferring one, or a few nucleons, thereby leading to the residual nucleus. The CCBA and CRC led researchers to realize that in a nucleon transfer reaction, “as the incoming nuclide (or nucleon) comes into close proximity to the target nucleus, their mutual interaction can induce a variety of inelastic excitations involving vibrations or rotations of the target nucleus, and likewise for the corresponding outgoing nucleon (or nuclide) and the residual nucleus, while exchanging nucleons as a unit, or sequentially. The CCBA model initially inspired many young theorists and experimentalists to explore new avenues in nuclear reaction physics, and computer scientists around the world to compose general purpose computer programs to numerically solve the more complex, newly proposed coupled channels Schrodinger equations required to describe nucleon transfer reactions.

Early successes of the CCBA and CRC were generating renewed interest in studying light-ion-induced nucleon transfer reactions. Unfortunately, for young nuclear physicists in the USA, the breakthroughs provided by the newly proposed coupled channels theories were of little consolation, as society was crumbling around them. Student antiwar protests were increasing and becoming a disruptive force in America. University campuses were evolving into harbingers for anti-government activities. To make matters worse, the Johnson Administration ostensibly abolished draft deferments for most graduate students. Consequently, the number of physics students working in university laboratories was rapidly declining. A contributing factor was that many young physicists were concerned their research would be applied toward destructive ends, as exemplified by the discovery of Agent Orange and Napalm, rather than helping to solve society’s most urgent problems.

1.3 Why not heavy-ion-induced nucleon transfer reactions

The Department of Energy (DOE) and the National Science Foundation (NSF) unfortunately responded to the bleak economic conditions in the USA during the Vietnam War era by further reducing support for academic nuclear physics research and by steadfastly shutting down many university-based particle accelerators. In these pre-Nuclear Science Advisory Committee (NSAC) days, the federal funding agencies in the USA began pressuring the remaining functioning nuclear physics laboratories to shift accelerator-based research to the new field of heavy-ion physics. Fortuitously, this questionable funding strategy provided a unique opportunity for Ascuitto and Glendenning, and subsequently Ascuitto and Vaagen, to further showcase the CCBA and CRC theories, by modifying them to accommodate heavy-ion-induced nucleon transfer reactions.

Two institutional collaborations, “Yale’s WNSL and NBI/NORDITA” and “WNSL and Brookhaven National Laboratory (BNL)”, provided opportunities for physics graduate students to study heavy-ion reactions. WNSL and NBI/NORDITA contributed theoretical support and the WNSL and BNL collaboration possessed the upgraded accelerators and particle detection facilities required to perform the high-resolution experiments needed to study heavy-ion reactions. Embarking on this research was important, since the CCBA and CRC models employed “quantum mechanical” descriptions of heavy-ion reactions, whereas “semiclassical models” were typically being used to interpret heavy-ion scattering experiments. Competition between the two theoretical approaches was mounting. However, reproducing experimental outcomes would be the final arbitrator.

Although there was a burgeoning interest in studying heavy-ion reactions, it was unclear if, or in what manner, they could be utilized to investigate nuclear structure, or help in delineating how the recently proposed multi-step nucleon transfer processes might be manifested in experimental cross sections. Ascuitto (on leave from Yale University) was at NBI and Vaagen (from the University of Bergen, in Norway) was at NORDITA. They would embark on a fruitful collaboration. Advancements in the computer industry allowed these two young investigators to perform computer-simulations of a variety of heavy-ion reactions. Despite the “near-classical” conditions for the relative motion between colliding heavy ions, i.e., large partial wave angular momenta, short de Broglie wavelengths, and a strong Coulomb interaction, their quantum mechanical calculations revealed that, as heavy ions undergo grazing collisions, there is strong loss of flux (absorption) from the elastic channel. The duo believed a well-demarcated region of strong absorption would require a quantum mechanical approach for nucleon transfer reactions, since it would provide a substrate for wave diffraction and interference phenomena.

1.4 “The only trustworthy bridge between man and Nature is the experiment”

After about a year in Copenhagen, Ascuitto, now accompanied by Vaagen, returned to Yale’s WNSL. Their goal was to employ the CCBA to computationally simulate a heavy-ion nucleon transfer reaction that would definitively demonstrate the presence and importance of multi-step nucleon transfer pathways. After considerable deliberation, they settled on a reaction involving deformed tungsten (W) nuclei, i.e., ¹⁸⁶W (¹²C, ¹⁴C) ¹⁸⁴W, at a bombarding energy of 70 MeV. In these W nuclei, both the nuclear and Coulomb interactions are strong, which would contribute to enhanced inelastic excitations. The CCBA calculations included all inelastic and two-neutron transfer transitions connecting the 0⁺, 2⁺ and 4⁺ members of the ground state rotational bands of ¹⁸⁶W and ¹⁸⁴W. In the Copenhagen spirit, the intrinsic states of these deformed nuclei were described as a Bardeen–Cooper–Schrieffer (BCS) vacuum for quasiparticles. The neutron wavefunctions (orbitals) from which the intrinsic states were constructed corresponded to eigenfunctions of a Woods–Saxon potential having a shape defined by the deformation characteristics of the W nuclear surfaces.

The CCBA calculations for the proposed reaction indeed revealed “unmistakable departures” from semiclassical (bell-shaped) angular distributions. The angular distribution for the 0⁺ ground state of ¹⁸⁴W (the superconducting two-neutron transfer transition) was “unimodal”, i.e., bell-shaped and peaked at an angle corresponding to a classical grazing collision, consistent with the expected “one-step” two-neutron transfer process. However, the angular distribution for the 2⁺ and 4⁺ excited states of ¹⁸⁴W were “bimodal”, i.e., each angular distribution contained two bell-shaped components with separate peaks and a well-defined local minimum residing between the peaks. This dramatic bimodal pattern indicated that two types of two-neutron transfer processes were populating the excited states, i.e., one-step (direct) two-neutron transfer competing with multi-step (indirect) two-neutron transfer. Such bimodal angular distributions, as observed for the 2⁺ and 4⁺ excited states of ¹⁸⁴W, had not previously been reported and could not be explained by any semiclassical model, or the DWBA. This bimodal feature was shown to arise from quantal interference between coherent contributions from the two distinctly different modes of nucleon transfer. If indeed these predicted angular distributions proved to be correct, one surely would need to employ a quantum mechanical coupled channels description of heavy-ion nucleon transfer reactions involving collective nuclei.

The American–Norwegian tandem confidently presented their findings at an invited talk at the International Conference on Reactions between Complex Nuclei in Nashville, Tennessee, in 1974. Several months later, the predicted bimodal angular distributions for the 2⁺ and 4⁺ excited states of ¹⁸⁴W were fully confirmed experimentally by a WNSL/BNL team headed by K. A. Erb of Yale University. Nature finally revealed its answer to a decade old question regarding the presence of multi-step nucleon transfer processes. The results appeared as a rapid publication in Phys. Rev. Lett, in 1974. These dramatic results showed that one could understand heavy-ion nucleon transfer reactions in detail not previously attained in nuclear reaction physics. It is ironic that the additional calculations required to include multi-step nucleon transfer processes, so often considered an undesirable complexity by much of the nuclear physics community, would yield simple and readily interpretable signatures in angular distributions.

1.5 The CRC was gaining popularity

By 1970, it had already been shown at LBL and NBI that sequential neutron transfer processes can be important in several light-ion-induced nucleon transfer reactions. However, these CRC models had not been extended to include heavy-ion reactions. The experimental group at Argonne National Laboratory (ANL) conducted a series of elegant heavy-ion two-neutron (n) transfer reactions in shell-structured nuclei. They showed that the conventional DWBA, which assumes the two neutrons to be transferred simultaneously, i.e., as a unit (n₁ + n₂), markedly underestimated the absolute cross sections for the reactions. To address this long-standing problem, T. Tamura, T. Udagawa and coworkers, at the University of Texas in Austin, employed a second-order DWBA to calculate the “sequential two-neutron transfer process”, i.e., n₁ followed by n₂. In 1976, D. H. Feng, T. Udagawa and T. Tamura analyzed a reaction previously reported by ANL, namely ⁴⁸Ca (¹⁸O, ¹⁶O) ⁵⁰Ca. Their calculations revealed that the simultaneous and sequential two-neutron transfer processes yielded similar angular distributions with comparable-size cross sections. The “coherent addition” of contributions from both modes of neutron transfer was found to reproduce the experimental cross sections! Quantum effects once again prevailed.

1.6 The timing was perfect

The CCBA and CRC came along at precisely the right time to complement an improved understanding of nuclear structure, and to benefit from advancements in the computer industry. In the 1960s, information gleaned from nucleon transfer reactions depended critically on the conventional DWBA to help interpret experimental data. In a sense, theory was driven by the experimental data. Alternatively, and perhaps more gratifying, would be to have a theory that predicted certain unexpected results which ultimately could be confirmed through experimentation. Such was the case with the CCBA in the 1970s. The CCBA and later the CRC fostered an unprecedented collegiality between theorists and experimentalists, as researchers began communicating in a common language, which resulted in shared rewards.

The coupled channels approach is still the foundation for interpreting many direct nuclear reactions half a century later, especially when multi-step nucleon transfer processes must be considered. This multichannel approach has also emerged as an important tool in Atomic and Molecular Physics, Nuclear Engineering, Nuclear Astrophysics, Radiation Physics and Computer Science. However, for the higher bombarding energies utilized in nucleon transfer reactions today, many reaction channels are open and nucleon continuum states can become important. Thus, the traditional practice of employing distorted wavefunctions governed by optical model potentials to describe the relative motion between interacting ions may no longer be completely suitable, especially for reactions involving nuclei at the limits of stability. Likewise, under the extreme kinematic conditions encountered when halo nuclei with exotic structures emerge near nuclear drip lines, some of the standard approximations for understanding reactions may be invalid. Nevertheless, for nuclear reactions involving light and medium mass ions, the 1970s proved to be a remarkably productive period for theoreticians, experimentalists, postdoctoral fellows and graduate students conducting research in nuclear reaction physics at universities and national laboratories worldwide.

1.7 Conclusions

This manuscript traces the contributions of a small group of nuclear physicists stationed largely at Yale, whose work ultimately led to the development, and confirmation, of the CCBA and CRC theories of heavy-ion-induced nucleon transfer reactions. This story, however, cannot be fully portrayed without shedding light on the obstacles these initial investigators had to overcome, both at LBL and WNSL, in order to successfully conduct research during the most turbulent period in American society. From a historical perspective, our narrative about the evolution of the CCBA and CRC provides a unique glimpse into the deleterious relationship that developed between the Federal Government, society and science in America during the Vietnam War era. Anti-Vietnam War riots ensued on many university campuses, since students felt betrayed by their government for not being truthful about the war. Although we have limited our scientific discourse mainly to ground-breaking advancements in nuclear reaction physics in the 1960s and 70s, we made selections that may be biased because of our involvement in this field. Nevertheless, over the years, other authors have covered complementary topics in considerable detail. We do apologize to the many excellent nuclear physicists whose work remained outside the scope of this presentation, which is intended to focus on the evolution of the CCBA and CRC models, on the 50th anniversary of their conception.

In this narrative, we disclose how these coupled channels theories became powerful tools for delineating the interplay between nuclear structure and reaction dynamics. Although most heavy-ion nucleon transfer reactions occur under “near-classical conditions”, Ascuitto and Vaagen using the CCBA unequivocally demonstrated that a wave-mechanical picture is required, at least in the region where the nuclear interaction is important, to accurately account for reactions involving collective nuclei. In the 1970s, the CCBA’s remarkable success revealed how the structure of the nuclear states participating in a reaction governs the types of nucleon transfer processes that can occur during the relative motion of the colliding ions. Despite the additional complexity of CCBA and CRC calculations, these theories ultimately provided cogent interpretations of a myriad of reaction cross sections, and, in doing so, undeniably changed the way physicists interpreted nucleon transfer reactions. Our narrative about the evolution of the CCBA and CRC descriptions of nucleon transfer reactions reveals that the key to finding the solution to a complex problem can be hidden in the journey.

2 Background: “Study the past if you would define the future”, Confucius (fifth century B.C.)

The study of nuclear reactions effectively began with the development of particle accelerators in ~ 1930. These instruments permitted the creation of a variety of particle beams and allowed researchers to conduct nuclear reaction experiments in a laboratory under controlled conditions. Accelerators were pioneered by J. D. Cockroft and E. T. S. Walton, at the University of Cambridge, in Cambridge, UK, and E. O. Lawrence, at the University of California, Berkeley. In 1932, Cockroft and Walton used electrostatic acceleration to develop a particle accelerator that produced the first transmutation of an element (lithium) into another element (helium), with the reaction ¹H + ⁷Li → ⁴He + ⁴He + energy. The reaction also provided the first experimental verification of Einstein’s famous formula E = mc². Cockroft and Walton shared the Nobel Prize in Physics in 1951 for their work. In 1929, Lawrence, working in a makeshift laboratory at the University of California, Berkeley, was inspired by a paper written by a Norwegian engineer Rolf Wideroe, on the acceleration of positive ions. Information gleaned from Wideroe’s apparatus, led Lawrence to construct a circular particle accelerator, which became known as the cyclotron. Although the prototype looked more like a Rube Goldberg machine, it confirmed Lawrence’s proposal. He received the Nobel Prize in Physics in 1939 for the invention. In the late 1920s, an American Rhodes Scholar, R. J. Van de Graaff, while working on his PhD thesis at Oxford University, in Oxford, England, became intrigued with an idea put forth by Ernest Rutherford, that accelerating particles to very high speeds could be used as a means of disintegrating nuclei. After returning to the USA in 1929, while working at Princeton’s Palmer Physics Laboratory, Van de Graaff constructed an “electrostatic accelerator”, which ultimately was capable of generating a terminal voltage of ~ 1.5 MeV. A variation of the Van de Graaff accelerator, the “tandem-accelerator”, could produce voltages twice as high. Tandem accelerators were subsequently employed to study a variety of nucleon transfer reactions. During the 1960s and 70s, modified tandem accelerators became the most important instruments for investigating direct nuclear reactions. M. Mladjenovic’s excellent book on the early years of nuclear physics provides a comprehensive review of particle accelerators [47].

In 1935, several intriguing experiments were performed by Lawrence, E. M. McMillan and R. L. Thornton using the newly upgraded cyclotron at the University of California, Berkeley. They showed that when relatively heavy elements are bombarded with low energy (up to ~ 3.6 MeV) deuterons, a reaction takes place which results in proton emission and conversion of the target nucleus into an isotope of mass number one-unit greater [41]. The reaction may be represented as follows: ²D + ^AX → ¹H + ^(A+1)X. It was referred to as a transmutation, but later became known as a “stripping” reaction. The cross section for the reaction was found to increase uniformly with deuteron bombarding energy, but the increase was far less rapid than what would have been predicted from Gamow’s penetration factor for transmission of a charged particle through the Coulomb barrier of the target nucleus.

2.1 An early theory of a nucleon transfer reaction

Concurrently in 1935, J. R. Oppenheimer and M. Phillips introduced a reaction mechanism to explain transmutation experiments [50]. They proposed, due to the large radius and small dissociation energy of the deuteron, that, as the deuteron approaches the surface of the target nucleus, the proton is repelled by the electrostatic field of the target nucleus and the neutron is captured by the attractive interaction with the target nucleus. This process did not require the deuteron to penetrate the Coulomb barrier. The theory was applicable when the binding energy of the captured neutron in the residual nucleus is greater than the separation energy of the deuteron (2.2 MeV). The calculated cross section’s dependence on deuteron energy was found to be in good agreement with the experimental data. This was the first theory of a nucleon transfer reaction.

World War II followed, which greatly reduced investigative activity in pure science, as most research was directed toward projects relevant to the war. After the war, however, there was a rapid expansion in basic research as a result of work done during the war in electronics, instrumentation, nuclear physics, etc. Federal funding became available at an unprecedented level. Thus, there was further development of the Cockcroft–Walton accelerator, Lawrence’s cyclotron and the Van de Graaff accelerator, as they became the primary instruments used to study nuclear structure, compound nucleus formation and direct nuclear reactions.

2.2 The concept of a direct nucleon transfer reaction

By 1950, it became apparent that, in contrast to the compound nucleus reaction in which the emitted particles are distributed isotopically in angle, certain higher bombarding energy reactions, (d, p), often exhibited angular distributions of the outgoing particles that were forward peaked. A student, S. T. Butler, on a scholarship from the Australian National University and working on a PhD at the University of Birmingham, Birmingham, England, recognized that a distinctly different reaction mechanism would be required to explain these forward peaked cross sections. He envisioned (d, p) reactions as arising from a grazing collision between the projectile and target nucleus. Consequently, these reactions would involve higher partial wave angular momenta (larger impact parameters), compared to reactions leading to compound nucleus formation.

Butler further proposed that the forward peaked angular distributions would be indicative of a “stripping-type” reaction, in which the neutron of the deuteron is captured by the target nucleus, while the outgoing proton carries off the balance of momentum and energy. Since the binding energy of the deuteron is small, the momentum (p) of the outgoing proton (p_p) would be comparable to that of the incoming deuteron (p_d). Consequently, the angular distribution of the outgoing proton would preferentially be peaked in the forward direction (i.e., small scattering angles). Butler showed that these kinematic conditions become possible if the reaction proceeds as a direct transition, i.e., from the ground state of the target nucleus to a state of the residual nucleus. Such a direct nucleon transfer process would be of short duration ~ 10⁻²² s, approximately the transit time of the projectile, compared to the survival time for the compound nuclear state, which was a million times longer at ~ 10⁻¹⁶ s.

In 1950, Butler presented a quantum mechanical formulation of nucleon stripping reactions [23], which permitted a qualitative interpretation of many experimental angular distributions. His calculations revealed that, for (d, p) reactions, the angular distribution of the outgoing particle possessed a pronounced maximum at an angle for which qR_N ~ lc, where q is the linear momentum delivered to the target nucleus, R_N is approximately the nuclear radius and lc is the orbital angular momentum transferred to the target nucleus. As lc increases, the maximum was shown to move to larger angles and decrease in amplitude quite rapidly. Thus, the position of the maximum in the angular distribution provided lc, which in turn determined the parity of the final nuclear state, if the parity of the initial nuclear state was known. (Similarly, information about the spin of the final nuclear state could be obtained.) It was quickly realized that, if the target nucleus’ ground state features are known, properties of the residual nucleus’ state could be deduced. The concept of a direct nucleon transfer reaction emerged and became a powerful tool in the emerging field of nuclear spectroscopy.

The early work of Butler opened the door for more precise calculations by physicists from around the world. The plane wave Born approximation (PWBA) became the theory of choice, since it readily followed from well-known quantum mechanical principles [25]. However, there were two fundamental shortcomings of the PWBA description of the transition amplitude for a nucleon transfer reaction. First, in Born approximation calculations, it was assumed that nucleon transfer occurs only at the surface of the target nucleus (R_N). At smaller distances, it was felt the projectile likely penetrated the nucleus and contributed to compound nucleus formation. Thus, contributions to the transition amplitude from the interior of the target nucleus (R < R_N) were rejected. Second, the PWBA described the relative motion by straight-line trajectories, as the Coulomb and nuclear interactions were neglected. It would be through the subsequent discovery of the optical model potential that the wavefunctions describing the relative motion between the incoming particle and the target nucleus, and the outgoing particle and the residual nucleus, would be adequately represented in the Born approximation.

2.3 The optical model potential

In the 1950s, the optical model potential was conceived. It proved to be one of the most important contributions to the field of nuclear reaction physics, both from an experimental and theoretical standpoint. In 1958, H. Feshbach at the Massachusetts Institute of Technology, in Cambridge published the seminal work on this subject, in which he provided a theoretical justification for the optical model potential [30]. Since the optical model potential ultimately played a fundamental role in understanding direct nuclear reactions during the 1960s and 70s, we review pertinent early work on this subject.

The prevailing thought in the early 50s was that an incoming nucleon upon entering the target nucleus would undergo a cascade of collisions with resident nucleons until most of its energy was distributed among them, thereby reaching thermal equilibrium to form the compound nucleus state. However, Feshbach, C. E. Porter and V. Weisskopf in two important papers raised concerns about the validity of the assumption that, “an incident particle immediately upon entering a nucleus would give rise to compound nucleus formation”. They justified their concerns by employing a quantum mechanical model to describe the scattering of neutrons impinging on a target nucleus [31, 32]. In analogy to the shell model, the target nucleus was replaced with an attractive potential well. However, the potential well was provided with an imaginary component to simulate absorption of incident neutrons entering the nucleus. Using wave mechanics, they demonstrated that for certain values of the imaginary part of the potential, the incoming neutron wave can penetrate the potential, be attenuated, but not completely absorbed. The neutron wave could then emerge to interfere with the incident waves. This quantum mechanical feature suggested that the neutron upon entering a nucleus could move along its boundary, escape and contribute to the scattering process. Their finding led to the so-called “cloudy crystal ball” model of the nucleus, which was a precursor to the “optical model potential”.

The optical model potential was initially introduced for the purpose of describing elastic scattering of nucleons from nuclei. The fundamental assumption of the optical model potential is that the interactions between a nucleon (or nucleons of a light ion) and the nucleons of the target nucleus can be represented by an average central potential that depends only on the relative coordinate between the incoming particle and the target nucleus. In a sense, the optical model potential complemented the shell model potential, by including unbound states. If the optical model potential were purely real-valued, it could produce elastic scattering. However, at the bombarding energies utilized to study nuclear reactions, inelastic scattering and other reaction channels are open. Thus, some flux would be removed from the elastic channel. If the optical model potential were complex-valued, it would have the effect of absorbing particles from the incident beam, which could account for nonelastic processes. Subsequent analyses of elastic scattering data confirmed that optical model potentials indeed needed to be complex-valued, with a negative imaginary part, to accurately describe differential cross sections.

Over the years, a standard optical model potential evolved. The Woods–Saxon form of the optical model potential (U) was most commonly employed [67]. This potential, in its standard form, was typically parameterized as follows:

$$ U\left( R \right) \, = \, Vo/ \, [1 \, + \, \exp \, (R \, - \, R_{{\mathbf{v}}} )/a_{{\mathbf{v}}} ] \, + \, i \, Wo/ \, [{1 } + {\text{ exp }}(R \, - \, R_{{\mathbf{w}}} )/a_{{\mathbf{w}}} ], $$

(1)

where V_o is the potential well depth (~ 50 MeV) and a_v is a diffuseness parameter related to the rate of falloff of the radial distribution. R_v is a nuclear radius parameter, which is expressed as R_v = r_vA^1/3, where r_v is ~ 1.25 fm and A is the mass number. Similarly, for the complex component of the optical model potential. R is the relative coordinate. In the case of charged particles, a Coulomb potential must be included which is taken as a uniform distribution of charge for R < R_c, and zero for R > R_c. Generally, optical model potential parameters chosen to describe elastic scattering data vary smoothly with energy and nuclear size. However, when inelastic scattering and/or nucleon transfer channels are strongly coupled to the elastic channel, these processes need to be explicitly included in scattering calculations. An optical model potential has also been used to describe the scattering between two nuclei, as the distance (R) between their centers approaches the sum of their radii. Now, the nucleus radius parameters are usually taken as R_o = r_o (A₁^1/3 + A₂^1/3). However, it would not be reasonable to assume that the effective interaction between two nuclei can be described solely in terms of a potential acting between their centers, when the colliding nuclei overlap appreciably.

2.4 The distorted wave Born approximation (DWBA)

In the early 1960s, there was a significant increase in the number of particle accelerators and spectrographs. Thus, there was great interest in studying direct nuclear reactions initiated by a variety of new ions. Moreover, it became possible to accelerate monoenergetic beams of these particles in say Van de Graaff accelerators to energies high enough to adequately populate low-lying energy states of nuclei. Although the parameterized optical model potential was originally introduced to describe elastic scattering cross sections, it was also subsequently employed to determine wavefunctions depicting the relative motion between colliding ions. These wavefunctions, which are “distorted from plane waves”, were then employed in transition amplitudes to calculate cross sections for many direct nuclear reactions. Hence, the plane wave Born approximation (PWBA) was replaced by the so-called distorted wave Born approximation (DWBA). The DWBA, as advocated by G. R. Satchler and colleagues at ORNL, became the most widely used theory for analyzing nuclear reactions [56]. The primary assumptions underlying the DWBA are that: (1) the transfer process takes place directly from the ground state of the target nucleus (entrance channel-α) to the final state of the residual nucleus (exit channel-β), as proposed by Butler nearly a decade earlier, (2) the optical model potential adequately describes the wavefunctions for the relative motion between the interacting ions, in the region where nucleon transfer takes place and (3) the transfer process is sufficiently weak so that it can be treated in lowest order, i.e., as a perturbation on the elastic scattering.

Consider a stripping-type reaction, A (a, b) B, in which a nucleon or a cluster (x) is transferred from an incoming particle (a) to the target nucleus (A) resulting in an outgoing particle (b) and the residual nucleus (B), where a = b + x and B = A + x. For this simplified case, the DWBA transition amplitude (T_βα), connecting the entrance channel (α) of the (a + A) partition to the exit channel (β) of the (b + B) partition, is most commonly expressed as follows:

$$ T_{\beta \alpha } = < \chi_{\beta }^{\left( - \right)} ({\mathbf{R}}_{\beta } )(\Phi_{\beta } \left( {{\mathbf{b}}, \, {\mathbf{B}}} \right), \, [V_{\beta } - U_{\beta } ],\Phi_{\alpha } \left( {{\mathbf{a}}, \, {\mathbf{A}}} \right))\chi_{\alpha }^{\left( + \right)} ({\mathbf{R}}_{\alpha } ) > . $$

(2)

The bracket  <…> denotes the integration is carried out over position coordinates. Figure 1 shows a typical coordinate system of vectors used to describe such a reaction.

The channel vector R_α is between (a) and (A) and R_β is between (b) and (B). The internal vector r₁ is between (x) and (b) composing (a) and the internal vector R₁ is between (x) and (A) composing (B). The distorted wavefunction χ_α⁽⁺⁾(R_α), which describes the relative motion between (a) and (A), is determined by an optical model potential in channel α, namely U_α. Likewise, the distorted wavefunction χ_β⁽⁻⁾ (R_β), which describes the relative motion between (b) and (B), is determined by an optical model potential in channel β, namely U_β. The superscript (+) indicates outgoing spherical waves and (−) incoming spherical waves, at infinity. The channel state functions, Φ_α and Φ_β, are denoted symbolically and simply taken as $\Phi_{\alpha } \left( {{\mathbf{a}}, \, {\mathbf{A}}} \right) = [\varphi ({\mathbf{a}})\varphi_{\alpha } ({\mathbf{A}})]$ and $\Phi_{\beta } \left( {{\mathbf{b}}, \, {\mathbf{B}}} \right) = [\varphi ({\mathbf{b}})\varphi_{\beta } ({\mathbf{B}})]$. The nuclear state function φ(a) depends on intrinsic coordinates (η_b and η_x) and the internal vector r₁, and φ_α(A) on (η_A). Similarly, φ(b) depends on (η_b), and φ_β(B) on (η_A and η_x) and the internal vector R₁.

The quantity V_β is an effective interaction between (b) and (B), and [V_β–U_β] represents the post (β) form of the nucleon transfer interaction. One may also use [V_α–U_α] in Eq. (2), which represents the prior (α) form of the nucleon transfer interaction. Formally, if the interaction terms [V_β–U_β] and [V_α–U_α] are treated exactly in Eq. (2), they yield the same transition amplitude, the so-called post (β)-prior (α) symmetry. The nucleon transfer interaction terms are usually approximated as follows: [V_α–U_α] = VxA + [VbA–U_α] or ~ VxA and [V_β–U_β] = Vbx + [VbA–U_β] or ~ Vbx. The matrix elements of [VbA–U_α] and [VbA–U_β] are usually neglected because the mass of A is about the same as that of B, with both being considerably greater than (x).

The bracketed term (…) in Eq. (2) involves integration over the intrinsic coordinates, (η_b, η_x, and η_A) of the core nuclei (b), (x) and (A), and the internal vectors r₁ and R₁.

It is prudent to transform the coordinates (r₁ and R₁) into (R_α and R_β), since the distorted wavefunctions, χ_α⁽⁺⁾(R_α) and χ_β⁽⁻⁾(R_β), are numerical solutions to Schrodinger equations at specific points. This transformation of the coordinate vectors yields a Jacobian (J), which relates the differential volume elements between the two system of vectors, i.e., dr₁dR₁ = J dR_αdR_β, where J = [aB/x (B + b)]³. The DWBA transition amplitude in the coordinate representation can then be determined using (R_α and R_β), namely:

$$ T_{\beta \alpha } = J\iint {{\text{d}}{\mathbf{R}}_{\alpha } {\text{d}}{\mathbf{R}}_{\beta } }\chi_{\beta }^{( - )*} ({\mathbf{R}}_{\beta } )\user2{\mathcal{F}}_{\beta \alpha } ({\mathbf{R}}_{\beta } ,{\mathbf{R}}_{\alpha } )\chi_{\alpha }^{( + )} ({\mathbf{R}}_{\alpha } ), $$

(3a)

where

$$ \user2{\mathcal{F}}_{\beta \alpha } ({\mathbf{R}}_{\beta } ,{\mathbf{R}}_{\alpha } ) = (\Phi_{\beta } ({\mathbf{b}},{\mathbf{B}}),V_{bx} ,\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}})), $$

(3b)

which is called the “form factor”. The form factor is a function of the channel coordinates (R_α and R_β). It characterizes the transfer of (x) from its nuclear state in φ(a) in channel (α) to its nuclear state in φ_β(B) in channel (β). The post-representation of the nucleon transfer interaction Vbx has been employed. The outer brackets (…) on the right side of Eq. (3b) involve integration over the intrinsic coordinates (η_b, η_x and η_A). The resultant DWBA transition amplitude involves a six-dimensional integral, which can be simplified in some cases.

2.5 The “no-recoil” approximation

In the early 1970s, the no-recoil approximation was primarily used to evaluate form factors characterizing nucleon transfer between nuclear states. In this case, the channel coordinates (Fig. 1), which are given by,

$$ {\mathbf{R}}_{\alpha } = {\mathbf{R}} + (x/a){\mathbf{r}}_{1} $$

(4a)

$$ {\mathbf{R}}_{\beta } = {\mathbf{R}} - (x/B){\mathbf{R}}_{1} = (A/B){\mathbf{R}} - (x/B){\mathbf{r}}_{1} , $$

(4b)

were approximated by dropping the terms (x/a) and (x/B), which often are small. These are referred to as recoil terms, since the centers of mass of the cores are shifted (by recoil) due to the transfer of (x). In the no-recoil approximation, the DWBA transition amplitude can most easily be evaluated by reverting back to the coordinates (r₁ and R₁). Since, in this simple example, the cores (A) and (b) are assumed to be inert, the integration over intrinsic coordinates yields:

$$ (\Phi_{\beta } ({\mathbf{b}},{\mathbf{B}}),V_{bx} ,\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}})) = \varphi_{\beta } ({\mathbf{R}}_{1} )^{*}V_{bx} (r_{1} )\varphi_{\alpha } ({\mathbf{r}}_{1} ), $$

(5)

where the wavefunction φ_β (R₁) describes the motion of (x) in the residual nucleus (B) and the wavefunction φ_α (r₁) the motion of (x) in the projectile (a). Dropping the terms (x/a) and (x/B) from the arguments of the distorted wavefunctions, the no-recoil approximation of the transition amplitude reduces to:

$$ T_{\beta \alpha } = \int {{\text{d}}{\mathbf{R}}\chi_{\beta }^{( - )*} (A/B\,{\mathbf{R}})\user2{\mathcal{F}}_{\beta \alpha } ({\mathbf{R}})} \chi_{\alpha }^{( + )} ({\mathbf{R}}), $$

(6)

where in this case, the form factor describing the transfer of (x) is given by:

$$ {\user2{\mathcal{F}}}_{\beta \alpha } ({\mathbf{R}}) = \int {{\text{d}}{\mathbf{r}}_{{1}} \varphi_{\beta } } ({\mathbf{R}} + {\mathbf{r}}_{{1}} )^{*} {\text{Vbx}} ({\text{r}}_{{1}} )\varphi_{\alpha } ({\mathbf{r}}_{{1}} ). $$

(7)

A number of the quantities displayed in this Background section are utilized in the Story section and are described in the Appendix sections.

The no-recoil form factor ${\user2{\mathcal{F}}}_{\beta \alpha } ({\mathbf{R}})$ proved invaluable for studying the influence of nuclear structure in light-ion and subsequently in heavy-ion-induced one- and two-nucleon transfer reactions for two reasons: (1) it specifies the “magnitude and phase” of the amplitude characterizing the transfer process, given that (x) in the residual nuclear state of (B) is correlated in space and spin in the same way as it was correlated in the projectile (a) and (2) the form factor’s magnitude near, and its falloff beyond, the nuclear surface indicates the likelihood of (x) being transferred at R. Thus, it was important to treat the form factor correctly in its tail region. Also, the calculation of the form factor was greatly simplified.

2.6 Recoil effects

The no-recoil approximation had little effect on light-ion-induced nucleon transfer calculations. However, the situation in heavy-ion reactions was quite different [16, 27, 48]. As these studies pointed out, for heavy-ion reactions the larger size of the projectiles in conjunction with the smaller wavelengths associated with their relative motion can render the no-recoil approximation less reliable. The lowest order correction from recoil entails retaining the term (x/a) in χ_α⁽⁺⁾ (R + (x/a)r₁) to first order. Assuming B ~ A and B >> a, the entrance channel distorted wavefunction can be expanded as follows:

$$ \chi_{\alpha }^{\left( + \right)} ({\mathbf{R}}_{\alpha } ) \, \sim [{1} + \, (x/a){\mathbf{r}}_{{1}} \cdot \nabla ]\chi_{\alpha }^{\left( + \right)} ({\mathbf{R}}) \sim [{1} + i(x/a){\mathbf{r}}_{{1}} \cdot {\mathbf{K}}_{\alpha } \left( R \right)]\chi_{\alpha }^{\left( + \right)} ({\mathbf{R}}), $$

(8)

where the gradient has been evaluated in the WKB approximation, and K_α (R) is the local wave number near the distance of closest approach for a grazing collision. Note, whereas the no-recoil form factor involves a “scalar” interaction, Vbx (r₁), the first-order recoil correction term is a “vector” interaction, Vbx (r₁) r₁, which must be taken in scalar product with (x/a) K_α (R). The lowest order correction from recoil was found to profoundly alter the angular momentum selections rules for certain heavy-ion nucleon transfer reactions.

For the transition amplitude in Eq. (2), consider the transferred cluster (x) to be in an initial state with angular momentum j_a = l_a + s_x in nucleus (a), and in a final state with j_B = l_B + s_x in nucleus (B), where (x) has spin s_x. It also follows that the transferred orbital angular momentum L is given by L = l_a–l_B. In the no-recoil approximation, the form factor in Eq. 7 is a function of one variable, and thus a term with angular momentum L must contain $Y_{L}^{M} \left( {{\hat{\mathbf{R}}}} \right)$, and hence have a parity change of (−)^L. These are called “natural parity” transitions. Recoil effects, however, allow “unnatural parity” transitions with L such that parity change becomes (−)^L+1. Perhaps, the most dramatic example of the importance of recoil effects was for the reaction ¹³C (¹²C, ¹³C) ¹²C, at a bombarding energy of 78 MeV [26]. The selection rule for this transfer allows L = 0 and 1. The no-recoil approximation yields only L = 0 transfer; whereas, the recoil term includes L = 1 transfer. In quantum mechanics, the coherent addition of both the L = 0 and L = 1 contributions is required, and indeed, this mechanical wave feature beautifully reproduced the experimental angular distribution.

One of the long-standing tenets of the DWBA was that the shape of an angular distribution for say a stripping reaction is largely determined by the orbital angular momentum (l_c) delivered to the target nucleus during nucleon transfer. This relationship was originally realized by Butler in the 1950s. Classically, for any l_c value greater than zero, the projectile will be able to interact with the target nucleus to produce nucleon exchange only for scattering angles beyond a certain minimum value. This minimum angle is determined, in lowest order, only by the size of the target nucleus’ radius, the magnitude of l_c and the bombarding energy. However, this signature feature of the DWBA ultimately proved to be an important clue to its inadequacy. By the late 1960s, although the DWBA had been successful in describing cross sections for many nuclear reactions, there were an increasing number of cases for which the conventional DWBA proved to be inadequate. Also, as particle accelerators improved in design and data acquisition became more precise, one needed to account for more subtle and sophisticated phenomena.

2.7 Beyond the DWBA

In the mid-60s, S. K. Penny and Satchler had introduced a generalization of the DWBA which included inelastic excitations [51]. In analogy to Eq. (2), an extended transition amplitude was taken as:

$$ T_{\beta \alpha } = \sum \limits_{\alpha ^{\prime}\beta ^{\prime}} < \chi_{\beta ^{\prime}}^{\beta ( - )} ({\mathbf{R}}_{\beta } )(\Phi_{\beta ^{\prime}} \left( {{\mathbf{b}}, \, {\mathbf{B}}} \right),[V_{\beta ^{\prime}} - U_{\beta ^{\prime}} ],\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}}, \, {\mathbf{A}}} \right))\chi_{\alpha ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) > . $$

(9)

The summation includes nuclear states assumed to be strongly excited by inelastic scattering in the target and residual nucleus. The distorted wavefunctions, $\chi_{\alpha ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\alpha } )$, which describe the relative motion between (a) and (A) in channel $\alpha ^{\prime}$, are now governed by a generalized optical model potential, $U_{\alpha ^{\prime}}$, which can induce inelastic excitations in the initial partition. Similarly, the distorted wavefunctions, $\chi_{\beta ^{\prime}}^{\beta ( - )} ({\mathbf{R}}_{\beta } )$, which describe the relative motion between (b) and (B) in channel $\beta ^{\prime}$, are now determined by a generalized optical model potential, $U_{\beta ^{\prime}}$, which can induce inelastic excitations in the final partition. The term $[V_{\beta ^{\prime}} - U_{\beta ^{\prime}}]$ represents the post-form of the nucleon transfer interaction. Although Eq. (9) was an algebraically straight-forward extension of the DWBA transition amplitude, no numerical calculations were reported. In this formulation, however, as the number of nuclear states included in the coupled channels equations for inelastic scattering increases, the calculated associated nucleon transfer transition amplitudes rapidly become excessive.

In a landmark paper in 1965, T. Tamura at ORNL demonstrated the importance of employing coupled channels calculations to describe inelastic scattering in collective nuclei [62]. At the time, this was the first large-scale computer calculation performed for a nuclear reaction, which was an important achievement. In 1966, a few calculations, performed under highly limited conditions, included some effects of inelastic scattering on nucleon transfer reactions [37, 39, 42]. However, incorporating inelastic scattering into a comprehensive theory of nucleon transfer reactions evidently was a complex problem, and not well understood. Thus, the problem remained unaddressed for the remainder of the decade.

3 A 15-year journey for researchers and a nation: “Do not go where the path might lead, go instead where there is no path and leave a trail”, Ralph Waldo Emerson

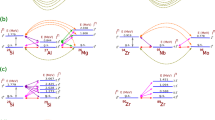
The story about the evolution of the coupled channels Born approximation (CCBA) theory of nucleon transfer reactions begins in the mid-1960s with an American graduate student, R. J. Ascuitto, in the Physics Department of Rensselaer Polytechnic Institute (RPI) in Troy New York, the oldest technological research university in the English-speaking world. He was faced with the daunting task of finding a research topic for his PhD thesis. After a few unproductive months, he ran across an article on two-nucleon transfer reactions that aroused his curiosity. He was interested in quantum mechanical descriptions of inelastic scattering and had some knowledge about the structure of 2s–1d shell deformed nuclei. Since electromagnetic transition rates are enhanced in these collective nuclei, he assumed inelastic excitations likewise would be strong and might influence nucleon transfer reactions. Thus, he began investigating the effects of combining inelastic scattering and two-nucleon transfer reactions involving light deformed nuclei. The focus of the study was to assess the importance of a two-step two-nucleon transfer process involving an intermediate inelastic excitation. A schematic representation of such a reaction is provided in Fig. 2. The reaction could proceed by the usual one-step nucleon transfer process (α to β′), i.e., from the ground state (α) of the target nucleus (A) to an excited state (β′) of the residual nucleus (B), straight arrow. The reaction, however, can also progress by a two-step nucleon transfer process (α to α′ to β′), i.e., an inelastic excitation from the ground state (α) to an excited state (α′) of the target nucleus (A), wavy arrow, followed by nucleon transfer from the excited state (α′) to the excited state (β′) of the residual nucleus (B), straight arrow. Likewise, for (α to β to β′).

Fig. 2

Representation of transitions that can participate in a nucleon transfer reaction, A (a, b) B. The channels α and α′ designate the ground state and an excited state of the target nucleus (A), respectively. The channels β and β′ indicate the ground state and an excited state of the residual nucleus (B), respectively. Transitions involving nucleon transfer are represented by unidirectional straight arrows, e.g., α to β, α to β′ or α′ to β′. Transitions involving inelastic excitation (and deexcitation) are represented by bidirectional wavy arrows, e.g., between α and α′ or between β and β′. The one-step (direct) nucleon transfer process populating the excited state β′ of the residual nucleus (B) entails the α to β′ transition only (DWBA). The two-step (indirect) nucleon transfer processes populating the excited state β′ of the residual nucleus (B) entail the α to α′ inelastic scattering transition followed by the α′ to β′ nucleon transfer transition, and the α to β nucleon transfer transition followed by the β to β′ inelastic scattering transition. As the figure illustrates, the inelastic scattering transitions are treated to all orders (bidirectional arrows), whereas the nucleon transfers transitions are treated to first order (unidirectional arrows)

He employed a second-order plane wave Born approximation to calculate the two-step two-nucleon transfer process. The interaction inducing inelastic excitations was taken as the spatial derivative of a nuclear potential that reflected the deformed shape of the target and/or residual nucleus. The intrinsic states of the deformed nuclei were described by a determinant of Nilsson orbitals. About six months later, preliminary calculations for a modeled ³¹P (³He, p) ³³S reaction indicated that the two-step (indirect) two-nucleon transfer process yielded a cross section of comparable magnitude to that of the one-step (direct) two-nucleon transfer process. At lunch one day, Ascuitto happened to show his calculations to Professor Jack Davidson a nuclear theorist in the Physics Department at RPI. Two months later, he received a letter from Norman K. Glendenning offering him a postdoctoral fellowship in the Nuclear Chemistry Division of Lawrence Berkeley National Laboratory (LBL).

3.1 Lawrence Berkeley National Laboratory (LBL) was an oasis of hope

Berkeley California was a relatively small town. It was, and still is, home to the University of California, one of the finest institutions of higher education in the world. Despite its apparent tranquility, by the mid-1960s, Berkeley had evolved into a hotbed for anti-Vietnam War activities. Many of the students’ antiwar protests erupted into conflicts with armed police dressed in full riot gear. Tear gas and occasionally chemical Mace were deployed to control crowds, which occasionally left a memorable haze over the Cal campus. Berkeley provided the perfect environment for nurturing the so-called counterculture movement, which fostered a hippie lifestyle, the use of marijuana, free love and unabashed psychedelic drug experimentation. Telegraph Ave, once a prominent street lined with specialty shops, boutiques and cafes, degraded into what some called, “the largest freak show on earth”.

Lawrence Berkeley National Laboratory, nestled in the beautiful Berkeley hills above the sprawling university campus, became a refuge for young scientists. Despite the ongoing unrest in Berkeley, LBL generally provided a supportive environment for a young researcher in nuclear physics. The Nuclear Chemistry Division encouraged creative and independent thinking, and facilitated exchange of ideas between the various scientists through weekly conferences. At times, however, for a young American researcher, LBL became a difficult place to work. Interacting with a number of research fellows from other countries proved to be a challenge. They vehemently opposed the US’ involvement in the Vietnam War and became quite vocal in expressing their views about it. Arguments often ensued, and it became increasingly difficult for Ascuitto to defend America’s position in South East Asia. Although far from ideal, leaving the laboratory and working elsewhere for several days at a time was his most productive option.

The incessant debating among fellows at LBL about the war, and the ongoing student unrest on the Cal campus, caused a senior researcher at the laboratory to suggest Ascuitto take time off and visit Angel Island in San Francisco Bay, stating, “that place can have a therapeutic effect” (Fig. 3). Indeed, the ferry trip from Fisherman’s Wharf in San Francisco to the island was wonderfully relaxing. Upon stepping off the ferry, one is awe struck by the fog lifting off the cold waters of the Bay, and the fragrance of eucalyptus trees scattered along the shoreline of the island. This was in sharp contrast to the smell of vinegar from tear gas that occasionally permeated the streets of Berkeley. He worked at a small wooden picnic table with two benches located near the highest point on the Island (Mount Livermore). This location provided a cool breeze off the bay waters and a magnificent view of the Bay Bridge, Treasure Island and the glistening Golden Gate Bridge.

Fig. 3

Ferry entrance to Angel Island in San Francisco Bay

After several trips to the Island, it became apparent to Ascuitto that a realistic theory describing the interplay between inelastic scattering and nucleon transfer would require a full quantum mechanical treatment of the reaction, and that plane waves would be insufficient to describe the relative motion between the colliding ions. Moreover, it was imperative, given the recent advancements in computers, that a proposed model of nucleon transfer reactions should be realistic enough to permit detailed analysis of experimental data, and hopefully to even have reliable predictive powers. Fortunately, Ascuitto knew mathematical techniques for numerically solving second-order differential equations and had sufficient experience (but far from being an aficionado) with the new FORTRAN IV language to construct the much-needed computer programs that would ultimately be required to perform the desired calculations.

3.2 A CCBA theory was formulated, and there were early successes

Collective inelastic scattering cross sections are typically an order of magnitude larger than nucleon transfer cross sections. Thus, there are two situations in which inelastic excitations should be included in calculations of nucleon transfer reactions. First, if in the reaction A (a, b) B, where say a = b + x, the configuration of the nucleons composing (A) remains essentially the same for the final state in the residual nucleus (B), i.e., B = A + x, then the usual DWBA may be valid. However, if the state of motion of the core nucleons in (B) is different from (A), i.e., B = A′ + x, then inclusion of inelastic scattering that can create such a difference becomes essential. Second, and less obvious, is when inelastic excitations are so strong as to produce significant deexcitation back into the elastic channel. In this circumstance, the usual one-channel optical model potential may not provide a good representation of the relative motion wavefunctions in the vicinity of the nuclear surface, where nucleon transfer takes place.

The CCBA theory was constructed as an extension of a coupled channels description of inelastic scattering. In its original formulation, a set of homogeneous coupled channels Schrodinger equations, containing a generalized optical model potential, was employed to describe the relative motion and inelastic excitations among retained nuclear states for the initial (a + A) partition of the nucleons, i.e., for channels associated with the incoming nucleon, or nuclide (a), interacting with the target nucleus (A). Likewise, a similar set of coupled channels Schrodinger equations was used to describe the relative motion and inelastic excitations among retained nuclear states for the final (b + B) partition of the nucleons, i.e., for channels associated with the outgoing nuclide (b), or nucleon, interacting with the residual nucleus (B). However, the latter set of coupled equations needed to be inhomogeneous, i.e., source terms were required on the right side of these equations to account for exchange of the nucleon (s) between nuclear states associated with the initial partition and final partition. Since the nucleon transfer process was included to first order, this formulation was referred to as a coupled channels Born approximation, and hence the acronym CCBA. The coupled channels equations describing inelastic scattering effects on nucleon transfer reactions are summarized in symbolic form below, see also Appendix 1.

For the (a + A) partition, with channels α (incoming) and α′, α′′…, the coupled channels equations describing the inelastic scattering between (a) and (A) are given by:

$$ (T_{\alpha ^{\prime}} + U_{\alpha ^{\prime}} - E_{\alpha ^{\prime}} )\chi_{\alpha ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) + \sum\limits_{\alpha ^{\prime\prime}} {U_{\alpha ^{\prime}\alpha ^{\prime\prime}} } \chi_{\alpha ^{\prime\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) = \, 0, $$

(10a)

where the summation is over α″ ≠ α′. Here T_α′ is the kinetic energy operator describing the relative motion between (a) and (A) for channel α′. The term U_α′ denotes the diagonal matrix element of a generalized optical model potential (U) in channel α′, i.e.,

$$ U_{\alpha ^{\prime}} = U_{\alpha ^{\prime}\alpha ^{\prime}} = (\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right),U,\Phi_{\alpha ^{\prime}} ({\mathbf{a}},{\mathbf{A}})), $$

(10b)

where $\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right)$ is a channel state function. The term U_α′α″, in Eq. (10a), is a non-diagonal matrix element of U. It describes an inelastic transition from the nuclear state α″ to α′ of (A), with

$$ U_{\alpha ^{\prime}\alpha ^{\prime\prime}} = (\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right),U,\Phi_{\alpha ^{\prime\prime}} ({\mathbf{a}},{\mathbf{A}})). $$

(10c)

The channel state functions, $\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right)$, are specified in Appendix 1. For simplicity, they are defined simply as:

$$ \Phi_{\alpha ^{\prime}} ({\mathbf{a}},{\mathbf{A}}) = [\varphi \left( {\mathbf{a}} \right)\varphi_{\alpha ^{\prime}} \left( {\mathbf{A}} \right)],\;{\text{with corresponding channel energy}}\,E_{\alpha ^{\prime}} , $$

(10d)

where φ(a) and φ_α′(A) are nuclear state functions for (a) and (A), respectively. Originally, it was assumed that a nuclide (a) remains unexcited, although this condition can easily be relaxed. The generalized optical model potential depends on the relative coordinate R_α and nuclear coordinates of A, and thus, it can induce inelastic excitations in (A). The distorted wavefunctions χ describe the relative motion between (a) and (A) in the various channels of the (a + A) partition.

For the (b + B) partition with channels β, β′, β″… one obtains analogous coupled channels equations. However, these equations are inhomogeneous, i.e., they contain source terms (ρ), namely

$$ (T_{\beta ^{\prime}} + U_{\beta ^{\prime}} - E_{\beta ^{\prime}} )\chi_{\beta ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) + \sum\limits_{\beta ^{\prime\prime}} {U_{\beta ^{\prime}\beta ^{\prime\prime}} } \chi_{\beta ^{\prime\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) = \rho_{\beta ^{\prime}}^{\alpha } ({\mathbf{R}}_{\beta } ). $$

(11a)

The source terms ρ on the right side of Eq. (11a) describe nucleon transfer between nuclear states in channels (α, α′,…) of the (a + A) partition and those in channels (β, β′, …) of the (b + B) partition. They are given by:

$$ \rho_{\beta ^{\prime}}^{\alpha } ({\mathbf{R}}_{\beta } ) = - \sum \limits_{\alpha ^{\prime}} < (\Phi_{\beta ^{\prime}} \left( {{\mathbf{b}},{\mathbf{B}}} \right),[V_{\beta ^{\prime}} - U_{\beta ^{\prime}} ],\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right))\chi_{\alpha ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) > , $$

(11b)

where the integrations within  <…> are carried out over all coordinates except the relative coordinate R_β. Here V_β′ is an effective interaction between (b) and (B) in channel β′. See the original formulation of these equations in Appendix 1.

The aim of this formulation was to solve the coupled channels equations by imposing the physical asymptotic boundary conditions on the distorted wavefunctions for the channels, and thereby directly determining the S-matrix elements for the reaction. These boundary conditions are that the entrance channel (α), which represents the incoming nucleon (or nuclide) and the target nucleus in its ground state, has incoming and outgoing spherical waves, consistent with the incident beam and a scattered wave in channel (α). For all other channels of both partitions, there are only outgoing spherical waves. The source term method proved to be conceptually more intuitive and computationally more efficient than what would have been achieved using a more traditional approach which involves calculating the multitude of nucleon transfer transition amplitudes.

In the mid-60s, computer technology was growing at an unprecedented rate, which laid the foundation for remarkable innovations in the industry. Computer hardware had progressed from vacuum tubes to solid-state devices such as transistors and integrated circuits. The Dynamic Random-Access Memory (DRAM) chip was invented, which vastly increased the storage capacity of computers. The supercomputer became a reality, which soon allowed nuclear physicists to tackle problems barely envisioned a decade earlier. Unfortunately, in many cases, pencil and paper were soon replaced by punch cards. LBL housed a Control Data Corporation (CDC) 6600 computer. The CDC 6600 had been upgraded to become the world’s fastest scientific computer, although by today's standards it likely would be considered painfully slow. Nevertheless, within about a 1-year period of time, Ascuitto went from using a Wang desktop calculator, with minimal degrees of programming ability, and a small IBM computer at RPI to having access to a CDC 6600 at LBL!

3.3 In 1968, the Vietnam War was at its peak and America was embroiled in crisis

During that infamous year, America was on a path of self-destruction. On April 4th, Dr. M. L. King Jr. was assassinated by a white supremacist at the Lorraine Motel in Memphis, which widened the racial divide and escalated rioting on many university campuses. R. F. Kennedy, who was running for President of the USA, was fatally shot as he departed the Ambassador Hotel in Los Angeles seven weeks later, at the age of 42. Kennedy was the acknowledged leader of the anti-Vietnam War movement. An embattled President L. B. Johnson, who was bedeviled by the war, declined to run for reelection, and R. M. Nixon won the presidency with only 43.4 percent of the popular vote, due to the third-party pro-segregationist candidate G. C. Wallace. Television brought the full horrors of the Tet offensive in Vietnam to 56 million American families, which sent shock waves across the home front. The Tet offensive by North Vietnamese troops galvanized Americans’ opposition to the war. It proved the war’s end was nowhere in sight, and that the US military likely could not win a conventional war in jungles 10,000 miles away. The aftershock of these events registered around the world.

3.4 The CCBA’s first test (two ground-breaking experiments)

By 1969, Berkeley became the New Left’s west coast headquarters, and a bloody war zone. Despite the chaos surrounding LBL, Ascuitto and Glendenning, working in the Nuclear Chemistry Division, managed to publish an important article in Physical Review on inelastic scattering processes in nucleon transfer reactions [2]. The Abstract to the article red:

It must certainly be true for some levels in all nuclei, and all levels in some nuclei, that the usual treatment of particle-transfer reactions, which neglects inelastic effects, is invalid. Here a practical method for taking these effects into account is described. The method is discussed in terms of the (d, p) reaction, but it has a much broader application.

Over the next decade, the authors’ speculation proved to be correct. Soon thereafter, they extended the CCBA, for say (t, p) reactions, to accommodate microscopic descriptions of collective nuclei, by incorporating calculated matrix elements for the two-neutron transfer operators [d^† d^†]_J and the inelastic excitation operators [d^† $\overline {d}$]_J into the coupled channels formalism [3, 4].

Ascuitto was ecstatic that his desire to become a physicist was materializing. As a youngster, he became fascinated with physics after seeing Alan B. Shepard on television, becoming the first American to travel into outer space, by completing a suborbital flight aboard Freedom 7. Nevertheless, Ascuitto was conflicted over the manuscript being published. By the grace of God, he was provided with an opportunity to pursue a career in physics. However, he was constantly haunted by the memory of 17 of his High School classmates, Army draftees in basic training for Vietnam, who perished in a plane crash on a deserted field in South Carolina. They never had a chance at a career. On November 15, 1969, Ascuitto participated in the Moratorium March in Washington, D.C., the largest anti-Vietnam War protest (Fig. 4). It was estimated that at least 500,000 individuals gathered to demand withdrawal of American troops from South East Asia. At the Moratorium March, he carried a large poster with the names of his friends, some of whom died in the jungles of Vietnam and others in that fatal plane crash in South Carolina. At one point, a large group of participants in the march, led by Pete Seeger, began singing John Lennon’s new song “Give Peace a Chance”. The diverse crowd singing in unison, young and old, waving the “V-peace sign”, left one overwhelmed. At that point, saddened, Ascuitto gazed into the crowd and asked, “It is time to leave the United States”?

Fig. 4

The Moratorium March to end the War in Vietnam took place on November 15, 1969 in Washington D.C. Five hundred thousand people rallied together for the cause of peace. Led by Coretta Scott King, the group marched down Pennsylvania Avenue to the White House, and was peaceful. Note the United States Capital building in the background

Two ground-breaking experiments would be performed. These important experiments would become the first challenge for the new CCBA theory. The first experiment was conducted at the University of Minnesota, in Minneapolis. It involved the ¹⁷⁶Yb (p, p′) ¹⁷⁶Yb inelastic scattering reaction and the associated ¹⁷⁶Yb (p, t) ¹⁷⁴Yb two-neutron transfer reaction, at a bombarding energy of 19 MeV. The no-recoil CCBA calculations included all inelastic scattering and two-neutron transfer transitions between the 0⁺, 2⁺, 4⁺ and 6⁺ members of the ground state rotational band of ¹⁷⁶Yb and ¹⁷⁴Yb. Thus, for each of the four states in ¹⁷⁴Yb, there is a two-neutron transfer transition from each of the four states of ¹⁷⁶Yb, i.e., a total of 16 two-neutron transfer transitions. In the DWBA, there would be only a single two-neutron transfer transition, directly from the ground state of ¹⁷⁶Yb to a state of ¹⁷⁴Yb, i.e., a total of 4 two-neutron transfer transitions. The deformation parameters β₂, β₄ and β₆ characterizing the Yb nuclear surfaces, required for the optical model potential and the Coulomb interaction, were determined from α-particle inelastic scattering experiments. The intrinsic nuclear state of the ground state rotational band was taken as a BCS vacuum constructed from valence neutron states (orbitals) determined using a deformed Woods–Saxon nuclear potential. Figure 5a shows that the coupled channels calculations yielded an excellent description of the proton inelastic scattering reaction. Likewise, Fig. 5b shows the CCBA calculations provided an equally accurate representation of both the angular distributions and relative magnitudes of the experimental cross sections for the corresponding two-neutron transfer reaction. In contrast, the DWBA calculations poorly described the experimental data. Data are from Oothoudt et al. [49]. The CCBA calculations were performed at LBL by Ascuitto et al. [5,6,7].

Fig. 5

a Coupled channels calculations of differential cross sections for proton inelastic scattering populating the 0⁺, 2⁺ and 4⁺ members of the ground state rotational band of ¹⁷⁶Yb, at a bombarding energy of 19 MeV. The calculations are based on nuclear surface deformation parameters obtained from analysis of α-particle inelastic scattering data. b CCBA calculations of differential cross sections for the complimentary ¹⁷⁶Yb (p, t) ¹⁷⁴Yb reaction populating the 0⁺, 2⁺, 4⁺ and 6⁺ members of the ground state rotational band of ¹⁷⁴Yb. CCBA calculations included all inelastic scattering and two-neutron transfer transitions connecting the 0⁺, 2⁺, 4⁺ and 6⁺ states of ¹⁷⁶Yb and those of ¹⁷⁴Yb, calculations were by Ascuitto et al. [7]. The DWBA calculations bore little relationship to the experimental data and thus are not shown. Data are from Oothoudt et al. [49]

The second experiment, was conducted at Yale University’s Wright Nuclear Structure Laboratory (WNSL), in New Haven, Connecticut. It involved the ¹⁸⁶W (p, d) ¹⁸⁵W reaction, at a bombarding energy of 18 MeV. An enormous spectrograph, capable of particle detection with energy resolution (ΔE/E) of better than 0.05%, allowed simultaneous detection of outgoing particles at 23 different angles ranging from 0° to 172.5° degrees. The no-recoil CCBA calculations included all inelastic scattering and one-neutron transfer transitions between the 0⁺, 2⁺ and 4⁺ members of the ground state rotational band of ¹⁸⁶W, and the 3/2⁻, 5/2⁻, 7/2⁻, 9/2⁻ members of the 3/2⁻ [512] ground state rotational band of ¹⁸⁵W interconnected with the 1/2⁻_, 3/2⁻, 5/2⁻, 7/2⁻, 9/2⁻ members of the 1/2⁻ [510] first excited state rotational band of ¹⁸⁵W. Thus, for each of the nine states in ¹⁸⁵W, there is a one-neutron transfer transition from each of the three states of ¹⁸⁶W, i.e., a total of 27 one-neutron transfer transitions. In the DWBA, there would be a single one-neutron transfer transition, directly from the ground state of ¹⁸⁶W to a state of ¹⁸⁵W, i.e., a total of 9 one-neutron transfer transitions. The deformation parameters β₂ and β₄ characterizing the W surfaces, for the optical model potential and the Coulomb interaction, were determined from α-particle inelastic scattering experiments. The intrinsic nuclear states of the rotational bands were constructed from neutron states (orbitals) using a deformed Woods–Saxon nuclear potential. At the time, and even by today’s standards, these were large-scale CCBA calculations, which successfully described one- and two-neutron transfer reactions in rare-earth deformed nuclei.

Figure 6 shows representative CCBA angular distributions for the ¹⁸⁶W (p, d) ¹⁸⁵W reaction. Three of the angular distributions would correspond to angular momentum transfer of l = 1, if the reaction were viewed as involving only a direct transition from the ground state of ¹⁸⁶W to the 3/2⁻ (0 keV), 1/2⁻ (24 keV) or 3/2⁻ (94 keV) states of ¹⁸⁵W. The three angular distributions, however, were “distinctly different”, and each was correctly reproduced by the CCBA. In contrast, the DWBA calculations predicted the three angular distributions to be essentially identical, clearly inconsistent with the data. Moreover, the cross sections for the 3/2⁻ (0 keV) and 9/2⁻ (302 keV) final states of ¹⁸⁵W were grossly underestimated by the DWBA, while both were well-reproduced by the CCBA. Data are from R. J. Ascuitto, C. H. King and L. J. McVay at WNSL; and the CCBA calculations were performed by Ascuitto and King at the Courant Institute of Mathematical Sciences at New York University (NYU) [10].

Fig. 6

CCBA and DWBA calculations of differential cross sections for the ¹⁸⁶ W (p, d) ¹⁸⁵ W reaction populating representative members of the interconnected 3/2 ⁻ [ 512] ground state and 1/2 ⁻ [510] first excited state rotational bands of ¹⁸⁵ W, at a bombarding energy of 18 MeV. CCBA calculations included all inelastic scattering and one-neutron transfer transitions connecting the 0⁺, 2⁺ and 4⁺ members of the ground state rotational band of ¹⁸⁶ W and the nine states of the interconnected bands of ¹⁸⁵ W. Data and calculations are from Ascuitto et al. [10]. Note the “different” angular distributions for the 1/2⁻, 3/2⁻ and 3/2⁻ states. In the DWBA, they would be considered to involve only l = 1 transitions, and thus were predicted to be essentially identical in shape

Figure 7a compares CCBA angular distributions corresponding to two-neutron transfer pathways for the ¹⁷⁶Yb (p, t) ¹⁷⁴Yb reaction populating the 2⁺ state of ¹⁷⁴Yb. The direct two-neutron transfer process and the indirect two-neutron transfer processes yielded cross sections of comparable magnitude, but had very different angular distributions. Figure 7b compares CCBA angular distributions corresponding to one-neutron transfer pathways for the ¹⁸⁶W (p, d) ¹⁸⁵W reaction populating the 1/2⁻ state of ¹⁸⁵W. The direct one-neutron transfer process and the combined indirect one-nucleon transfer processes yielded cross sections of comparable magnitude, but again had very different angular distributions. For these (p, t) and (p, d) reactions, only the coherent addition (quantal counting) of the amplitudes characterizing contributions from the various neutron transfer pathways brought about agreement with the experimental data. The CCBA had burst on the scene in the most emphatic way possible. Analyses of nuclear transfer reactions would be forever changed.

Fig. 7

a CCBA calculations of differential cross sections populating the 2⁺ state of ¹⁷⁴Yb, corresponding to separate two-neutron transfer pathways for the ¹⁷⁶Yb (p, t) ¹⁷⁴Yb reaction, at a bombarding energy of 19 MeV. The differential cross sections for the direct and indirect two-neutron transfer processes (involving intermediate inelastic scattering) are comparable in magnitude, but each is “different” in shape. Only the coherent addition of contributions from all the two-neutron transfer pathways leading to the 2⁺ state reproduced the experimental data in Fig. 5 [7]. b CCBA calculations of differential cross sections populating the 1/2⁻ state of ¹⁸⁵W, corresponding to separate one-neutron transfer pathways for the ¹⁸⁶W (p, d) ¹⁸⁵W reaction, at a bombarding energy of 18 MeV. The differential cross sections for the direct and indirect one-neutron transfer processes (involving intermediate inelastic scattering) are comparable in magnitude, but “different” in shape. Only the coherent addition of contributions from all the one-neutron transfer pathways leading to the 1/2⁻ state reproduced the experimental data in Fig. 6 [10]

Looking back, it may seem obvious that the DWBA would not adequately describe nucleon transfer reactions involving nuclei in which inelastic excitations are strong. However, at the time, the DWBA was a cherished entity and the most widely used theory of nucleon transfer reactions. Moreover, the newly proposed CCBA was viewed with caution by many established researchers, as they considered it more of a mathematical accomplishment rather than a true theory of nucleon transfer reactions. Unfortunately, at the time, the soundness of the underlying physics contained in the CCBA was not fully appreciated. The CCBA’s unique ability to integrate nuclear structure and reaction dynamics was an important contribution, and testified to the robustness of the new model. Moreover, the CCBA’s success provided confidence in the numerical techniques employed to solve the large system of coupled inhomogeneous, complex-valued second-order differential equations needed to describe these reactions. This result was significant since calculations of such complexity had not previously been reported. The CCBA ushered in a new era in the study of light-ion-induced nucleon transfer reactions. However, additional confirmatory experiments would be required, as, “extraordinary claims require extraordinary evidence”, Carl Sagan.

Subsequently, coupled channels calculations were employed to describe charge exchange reactions. V. A. Madsen, M. J. Stomp, V. R. Brown, et al. showed that coupled channels calculations are essential for understanding the systematics of charge exchange reactions in collective nuclei [46]. As a follow-up, C. Wong, V. R. Brown, V. R. Madsen and S. M. Grimes at Lawrence Livermore Laboratory, in Livermore, California, studied (p, n) reactions to ground and excited state analogs in samarium isotopes at bombarding energies of 20, 24.5 and 26 MeV [66]. These researchers showed that multi-step charge exchange processes, involving intermediate inelastic excitations, played a vital role in understanding these reactions.

3.5 Early CRC models were formulated

By 1969, coupled reaction channels (CRC) models were evolving. Although it is certainly true that most collective inelastic scattering cross sections are considerably larger than those for nucleon transfer cross sections, there are some nucleon transfer reactions that are strong. In these situations, strong coupling between elastic scattering, inelastic scattering and nucleon transfer channels could be important. At LBL, Ascuitto developed a CRC model for reactions involving “two partitions” of the nucleons, that permitted including contributions from nucleon transfer channels back into elastic and inelastic scattering channels. A generalization of the CCBA was utilized to derive the required coupled channels equations. For the reaction A (a, b) B, the coupled channels equations were found to be as follows:

For the (a + A) partition with channels α (incoming) and α′, α″,… one obtains:

$$ (T_{\alpha ^{\prime}} + U_{\alpha ^{\prime}} - E_{\alpha ^{\prime}} )\chi_{\alpha ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) + \sum \limits_{\alpha ^{\prime\prime}} U_{\alpha ^{\prime}\alpha ^{\prime\prime}} \chi_{\alpha ^{\prime\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) = \, \mathop {\rho_{\alpha ^{\prime}} ({\mathbf{R}}_{\alpha } )}\limits_{{({\text{source terms}})}} . $$

(12a)

For the (b + B) partition with channels β, β′, β″…, the coupled channels equations are:

$$ (T_{\beta ^{\prime}} + U_{\beta ^{\prime}} - E_{\beta ^{\prime}} )\chi_{\beta ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) + \sum\limits_{\beta ^{\prime\prime}} {U_{\beta ^{\prime}\beta ^{\prime\prime}} } \chi_{\beta ^{\prime\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) = \mathop {\rho_{\beta ^{\prime}} ({\mathbf{R}}_{\beta } )}\limits_{{({\text{source terms}})}} . $$

(12b)

The source term ρ_α′(R_α) on the right side of Eq. (12a), which describes nucleon transfer from the (b + B) partition back into the (a + A) partition, is presented differently than in Eq. (11b):

$$ \rho_{\alpha ^{\prime}} ({\mathbf{R}}_{\alpha } ) = - \sum \limits_{\beta ^{\prime\prime}} (\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right),[V_{\alpha ^{\prime}} - U_{\alpha ^{\prime}} ],\Phi_{\beta ^{\prime\prime}} \left( {{\mathbf{b}},{\mathbf{B}}} \right))\chi_{\beta ^{\prime\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\beta } ). $$

(12c)

The source term ρ_β′(R_β) on the right side of Eq. (12b), which describes nucleon transfer from the (a + A) partition into the (b + B) partition, likewise is given by:

$$ \rho_{\beta ^{\prime}} ({\mathbf{R}}_{\beta } ) = - \sum \limits_{\alpha ^{\prime\prime}} (\Phi_{\beta ^{\prime}} \left( {{\mathbf{b}},{\mathbf{B}}} \right) ,[V_{\beta ^{\prime}} - U_{\beta ^{\prime}} ],\Phi_{\alpha ^{\prime\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right))\chi_{\alpha ^{\prime\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ). $$

(12d)

In this approach, the state function for the entire system was not represented as an expansion in terms of the nuclear states of the two mass partitions, which would lead to non-orthogonality terms. An alternative approach for the two-partition problem which includes the non-orthogonality terms associated with nuclear states of different partitions is provided in Appendix 2. Some prefer additional outer brackets < … > in Eqs. 12c and 12d.

At LBL, Ascuitto, Glendenning and Sorenson used the new CRC model, in a zero-range nucleon transfer approximation, to study the ⁴⁸Ca (p, p′) ⁴⁸Ca* inelastic scattering reaction leading to the well-known 0⁺ neutron-pairing vibrational state at 5.45 MeV in ⁴⁸Ca, at a bombarding energy of 12 MeV [6] (Fig. 8a). The direct inelastic scattering transition (p, p′) to the 0⁺ pairing vibrational state is hindered. However, they found the sequential two-neutron transfer process, (p, t) followed by (t′, p′), to be strong. Sequential two-neutron transfer was determined to be the major process contributing to the experimental inelastic scattering cross section. Concurrently, at NBI, J. Bang and S. Wollesen employed a second-order DWBA, in a zero-range nucleon transfer approximation, to study the ¹⁰B (t, p) ¹²B two-neutron transfer reaction, at a bombarding energy of 10 MeV [17] (Fig. 8b). They found the sequential one-neutron transfer process, (t, d) followed by (d′, p′), to be strong. Sequential one-neutron transfer was determined to be the major process contributing to the experimental two-neutron transfer cross section. These two early CRC calculations were instrumental in bringing attention to the nuclear physics community of the importance of sequential nucleon transfer processes, which set the stage for numerous experiments and theoretical calculations describing such reactions.

Fig. 8

Schematic representation of: a a sequential two-neutron transfer process, (p, t) followed by (t, p), contributing to a proton inelastic scattering (p, p′) reaction and b a sequential one-neutron transfer process, (t, d) followed by (d, p), contributing to a two-neutron transfer (t, p) reaction

By the mid-70s, CRC-type calculations by researchers from around the world were revealing a myriad of nucleon transfer processes, as dictated by the underlying structure of the nuclear states involved in the reactions. These studies opened-up a fascinating area for research quite apart from the practical value of more accurately determining properties of nuclear states. Many theoretical and experimental papers began appearing from various centers on the subject. To mention a few, R. S. Mackintosh, at LBL, used coupled channels calculations to study the interplay between the ²⁴Mg (p, p′) and ²⁴Mg (p, d) reactions. He found that the angular distributions for inelastic proton scattering were significantly altered by the strongly coupled neutron pickup (p, d) reaction, to the extent that extracted deformation parameters for ²⁴Mg were markedly altered [44, 45]. At the University of Texas in Austin, W. R. Croker, T. Udagawa and H. H. Wolter used second-order DWBA calculations to study the ⁸⁸Sr (h, t) ⁸⁸Y reaction. Angular distributions corresponding to the 4⁻, 5⁻ and the 2⁺–3⁺ doublet states of ⁸⁸Y could not be explained by the conventional DWBA. However, the second-order DWBA calculations, which included the sequential one-nucleon transfer processes, (h, α) followed by (α′, t) and (h, d) followed by (d′, t), provided a good representation of the shapes and relative magnitudes of the experimental angular distributions [24]. At the University of Tokyo, H. Segawa, K. I. Kubo and A. Arima used a combination of CCBA and second-order DWBA calculations to understand the ¹⁸O (p, t) ¹⁶O* reaction populating the 2⁻ unnatural parity state at 8.87 MeV of ¹⁶O [58]. The direct two-neutron transfer transition leading to the 2⁻ state is essentially forbidden. However, these investigators showed that a combination of: (1) a two-step two-nucleon transfer process involving proton inelastic excitation of the 2⁺ excited state of ¹⁸ O followed by two-neutron pickup (p, t) and (2) a sequential one-nucleon transfer processes (p, d) followed by (d′, t) involving the 5/2⁻, 1/2⁻, 3/2⁻ and 3/2⁺ intermediate states of ¹⁷O are important. Collectively, they provided a good representation of the experimental angular distribution for the 2⁻ state. For these different experiments, in the spirit of quantum mechanics, only the coherent addition of contributions from the various nucleon transfer processes reproduced the experimental cross sections.

3.6 The Vietnam War was having a deleterious impact on academic physics in America

Despite the early successes of the CCBA and CRC models for understanding light-ion-induced nucleon transfer reactions, it became evident to young researchers in the field, and to many Americans in general, that the USA was embroiled in two wars, one in South East Asia and the other on university campuses at home. Many students believed the political problems brewing in the USA would likely never be solved in the halls of the U.S. congress. Thus, the more rebellious individuals’ ultimate goal was to convert university campuses into bunkers for organizing protests against the federal government. To lend credence to their approach, the Johnson Administration essentially abolished draft deferments for male graduate students, which obviously would impact academic research. The draft had become the subject of intense controversy between the White House, Congress and Educators across America. It was estimated that Johnson’s new policy would reduce graduate school enrollment by ~ 50%. Less prestigious schools were hit hardest since top schools would simply dig deeper to fill their student body. Unfortunately, at the time, Harvard University President N. M. Pusey’s response to stopping deferments for male graduate students was, “we shall be left with the lame, the halt, the blind and the female”!

Moreover, many Americans believed all citizens should share responsibilities equally, and physicists should be drafted along with everyone else. Perhaps the most thoughtful account by a scientist being drafted was provided by Robert Laughlin, who in 1998 was awarded the Nobel prize in physics. In his autobiography for the Nobel Foundation, he wrote, “despite misgivings about the Vietnam War and despite recognizing that not being able to do physics for two years could harm his intended career, he did not evade the draft”.

During the late 1960s and early 70s, the number of physics graduate students and fellows working in university laboratories significantly decreased in part due to the abolishment of draft deferments, and because researchers were uneasy about future employment opportunities in physics. Consequently, many university laboratories were left shorthanded, and academic research suffered enormously. Additionally, many aspiring young physicists were concerned their work might be applied toward destructive ends. Perhaps the most publicized example was the defoliant “Agent Orange”. This substance was discovered by a graduate student while conducting research in plant physiology at the University of Illinois. It was developed to enhance the flowering of soybeans. However, it ultimately became a highly destructive chemical weapon used against Vietnam, Laos and Cambodia. It has been estimated that the US military spread 11 million gallons of Agent Orange over 25% of South Vietnam. Perhaps the most horrific weapon discovered was “Napalm”. It was invented in a Harvard University secret research laboratory in Cambridge Massachusetts. It was an incendiary mixture of a gelling agent and a volatile petrochemical. It could cause death by burns and/or asphyxiation. On March 4, 1969, hundreds of faculty and student scientists stopped their research at the Massachusetts Institute of Technology (MIT), and many other institutions, to examine the involvement of academic science in the Vietnam War effort. Regrettably, the movement was largely symbolic. Nevertheless, the event did reinforce the belief that the scientific community had a moral obligation to promote science as a tool to benefit a peaceful world.

3.7 Bloody Thursday in Berkeley

On May 15th, 1969, a group of 30,000 of Berkeley’s 100,000 residents marched to protest the closing of People’s Park. The People’s Park was a gathering place for students, hippies and street people. It was an impromptu garden on a small (250 ft × 450 ft) plot of land purchased by the University of California, Berkeley. The peoples’ intention was to maintain the park as a recreation area for the community. The University wanted it closed. As the situation escalated, police suddenly started beating students with clubs and finally opened fire on the crowd with bird and buck shot. Several individuals were killed. One hundred and twenty-eight were admitted to hospitals for shot gun wounds, head trauma and other serious injuries. In retaliation, a group of about 6000 students and other street protestors began marching onto the Berkeley campus. Ascuitto happened to be on campus that day and shockingly witnessed desks and chairs being thrown out of classroom windows and off roof tops, while he was confronting aggressive rioters. Suddenly, directly in front of him, a police car was set ablaze. Eventually, the crowd was doused with tear gas delivered from a military helicopter. Berkeley became a war zone. Governor Ronald Reagan’s Chief of Staff, Edwin Meese III, called on the county to urgently send reserves. Nearly 800 officers responded. For some of us working at LBL, it was becoming increasingly more difficult to concentrate on research, given the volatile and at times dangerous situation in Berkeley. On one occasion, while Ascuitto and his daughter were in a car, suddenly they were surrounded by a group of angry antiwar protestors. The protestors began rocking the car and banging on the windows. Shortly, everyone was engulfed by tear gas. Ascuitto and his daughter narrowly managed to escape, although they subsequently required medical attention. Such was Berkeley, and such was America.

Ascuitto’s fellowship at LBL was concluding and he desperately needed to find a job. In the late 60s and throughout the 70s, positions in nuclear physics at academic centers and laboratories in the USA were almost non-existent. These were tough years. An overpopulation of physics PhDs after WWII, the tremendous cost of the Vietnam War, the successful conclusion of NASA's Apollo Program and severe federal cutbacks in R&D created the worst job shortage for physicists the USA had ever experienced. Fortunately, Ascuitto received a phone call from D. Allan Bromley, the legendary Director of WNSL at Yale University. The conversation was brief. Bromley simply stated, “Hello Bob. Would you like a position in the Physics Department of Yale University”? Ascuitto paused, and after thinking about war-torn Berkeley, colleagues that wound up teaching physics in high schools and small colleges, and those simply jobless, he accepted the position. It was the only job offer he received.

3.8 Yale was déjà vu

By May of 1970, Ascuitto was at Yale; however, it felt more like Berkeley. At one point, in New Haven, Connecticut there were police everywhere in full riot gear, buildings were boarded up and signs read, “End the War, Stop the Bloodshed, and Napalm on the Cops”. Other signs read, “Black Panthers Forever and free Bobby and Ericka”. The Black Panther Party, well-known in the Bay Area of California, was now on the East Coast. It was a revolutionary organization that ostensibly fought to end oppression of African Americans and to stop the Vietnam War. It was formed in Oakland California by Huey Newton and Bobby Seale in 1966. The group was identified by its distinctive black outfits and by carrying guns in public to defend against police brutality. Authorities in Connecticut had arrested Bobby Seale (national party chairman) and Ericka Huggins (founder of the New Haven Chapter of the Black Panther Party). They were charged with being involved in the murder of a member of the Black Panther Party in Connecticut. New Haven was in complete turmoil. Finally, after a protracted and highly visible trial, the jury ended in a deadlock, and charges were dismissed. Welcome to New Haven, Connecticut!

3.9 Kent State became seared into America’s consciousness

On May 4th, 1970, a tragic event unfolded at Kent State University in Kent, Ohio. At a large student protest over the bombing of neutral Cambodia by the US Military, 28 members of the Ohio National Guard opened fire on hundreds of unarmed protestors. Four students were killed, and many others suffered serious injuries. The shootings came to symbolize the deep political and social divisions in America during the Vietnam War era. Anti-war protests at university campuses spread rapidly after the Kent State incident, radicalizing more and more students. All told, 30 ROTC buildings subsequently went up in flames across the USA. A nationwide student strike ensued, which forced many colleges, universities and research laboratories to close.

Ascuitto and several of his graduate students experienced a serious repercussion following the Kent State massacre. The nuclear reaction group at Yale’s WNSL was conducting one of its trips to the Courant Institute of Mathematical Sciences at New York University (NYU), in New York City, to perform coupled channels calculations. The Computer Center at the Courant Institute housed a CDC 6600 computer similar to the one at LBL. Upon arriving at the Institute, the director was found sitting on the sidewalk openly weeping, as thick smoke bellowed out of broken windows. New York University students in conjunction with the Transcendental Students Group had taken over the Institute in opposition to NYU’s connection to the Atomic Energy Commission, and in revenge for the Kent State incident. As the Yale group entered the Institute, smoke reeked with the unmistakable odor of marijuana. Protestors were actively engaged in attempting to demolish the mainframe of the computer. Instinctively, they kicked open the door to the file room. Much of its contents was reduced to ashes. Valuable magnetic tapes containing much of the Yale group’s computer programs were destroyed. Nearly a year’s work would be lost. On the drive back to Yale, not a single word was uttered. At one point, someone flipped on the radio. Ironically, it was Joan Baez with that unforgettable soprano voice singing, “We shall overcome”. Somehow, what transpired that fateful day seemed less painful.

3.10 “At least I’m sure it may be so in Denmark”. William Shakespeare, Hamlet Act I, Sc 5

As the only nuclear theorist at Yale, with a heavy teaching load, a woefully inadequate computer facility, the Courant Institute’s computer center not fully operational after the NYU students’ takeover, and America’s escalating involvement in the Vietnam War, Ascuitto concluded he needed time out of the USA. Fortunately, he was awarded a one-year NATO fellowship to study abroad. In helping decide where to spend the sabbatical year, he contacted an old friend Bent Sorensen now at NBI. Sorensen had spent a year at LBL and collaborated with Ascuitto on several papers related to nuclear structure and nucleon transfer reactions. Sorensen suggested he conduct the NATO fellowship at NBI. Ascuitto happily agreed, and, in September of 1973, it was off to Copenhagen! From a scientific perspective, NBI was the Mecca for nuclear physics. The Institute was founded by Niels Bohr in 1921 as the Institute for Theoretical Physics of the University of Copenhagen. Most of its original funding came from the Carlsberg brewery and the Rockefeller Foundation. The Institute officially became the Niels Bohr Institute in 1965.

Soon after arriving at NBI, Ascuitto was asked to share an office with Vaagen, a graduate student from the University of Bergen, in Bergen, Norway. Vaagen was working at NORDITA as a NORDITA stipendiate in nuclear physics. NORDITA was established as the Nordisk Institut for Teoretisk Atomfysik in 1957 by Niels Bohr and the Swedish physicist Torsten Gustafson. A branch of NORDITA was located adjacent to NBI. What evolved at NBI/NORDITA was a highly productive working relationship and a life-long friendship between the young American and Norwegian researchers.

By this time, the CCBA had successfully explained a variety of light-ion-induced one-and two-neutron transfer reactions. It appeared that if the structure of the nuclear states involved in a nucleon transfer reaction was known, the CCBA could accurately describe the experimental cross sections. Consequently, due to the success of the CCBA, enthusiasm for conducting additional experimental research involving light-ion-induced nucleon transfer reactions was waning, especially since many smaller particle accelerators in the USA were systematically being shut down.

Federal funding agencies in the USA began exerting considerable pressure on the remaining academic nuclear physics laboratories to shift focus of accelerator-based research to the new field of heavy-ion physics. Thus, it seemed prudent for Ascuitto and Vaagen to investigate if the CCBA could be modified to accommodate reactions involving heavy-ion projectiles. Heavy-ion reactions typically involve high partial wave angular momenta, short de Broglie wavelengths and a strong Coulomb interaction during the relative motion between the colliding ions. Given these features, researchers began using semiclassical models to study heavy-ion scattering. In the early 1970s, R.A. Broglia, S. Landowne and A. Winther, at NBI, published an insightful paper in Phys. Lett on semiclassical formulations of heavy-ion nuclear reactions. They employed the Wentzel–Kramers–Brillouin (WKB) approximation to describe the relative motion between the interacting heavy ions [21], see also [22]. At the time, however, Ascuitto and Vaagen had concerns that the WKB might not adequately account for loss of flux (absorption) in the elastic scattering channel, the dominant channel in a heavy-ion reaction. If such an absorption process is weak, it likely would not significantly distort classical trajectories. However, if the absorption is strong, it might dramatically alter the behavior of the semiclassical scattered waves. Therefore, they pursued a full quantum mechanical treatment of heavy-ion-induced nucleon transfer reactions.

Ascuitto and Vaagen initially evaluated an important quantal effect, namely loss of flux during elastic scattering between heavy ions. They calculated absorption coefficients (η), as a function of incoming partial wave angular momenta (l_in), using optical model potentials that reproduced heavy-ion elastic scattering data. The absorption coefficients were defined as $\eta_{l\textbf{\textit{in}}} = | 1-\text{S}_{l\textbf{\textit{in}}} |^{\bf 2}$, where S_lin is the magnitude of the S-matrix elements for elastic scattering. Since the de Broglie wavelength for the relative motion is short, determining a region of strong absorption in l_in-space would reflect its distribution in R-space. The η_lin values were found to decrease dramatically, from unity (complete partial wave absorption) to zero (partial wave scattering), over a “narrow” range of l_in values. The l_in value with η_lin ~ 0.5 corresponds to a grazing collision. Their results indicated that, when colliding heavy ions come into close proximity, there can be significant loss of flux in the elastic channel. Moreover, the sharp decline of η_lin signified that the absorption process possessed a well-defined edge or boundary, which would provide a substrate for creating a variety of wave diffraction and interference phenomena.

3.11 In 1973, the American Physical Society Meeting in Washington D.C, was dedicated to New Directions in Nuclear Physics

The American–Norwegian tandem was invited to present their rationale for employing a quantum mechanical description of heavy-ion nucleon transfer reactions. Their approach assumed a typical direct heavy-ion reaction arises from a grazing collision, in which there is little overlap of matter between the two nuclei. Consequently, nucleon exchange would take place over a narrow band of incoming partial wave angular momenta (or impact parameters). In this restricted region of R-space, they postulated that significant loss of flux in the elastic channel, in conjunction with the interplay between the attractive nuclear interaction and the strong diffractive repulsive Coulomb field, would drastically modify semiclassical trajectories participating in heavy-ion nucleon transfer reactions.

At the Washington meeting, Ascuitto and Vaagen presented no-recoil CCBA calculations, which modeled a two-neutron stripping reaction involving vibrational nuclei (tin-Sn), e.g., the ¹¹⁶Sn (¹⁸O, ¹⁶O) ¹¹⁸Sn reaction populating the 0⁺ ground state and the collective 2⁺ excited state of ¹¹⁸Sn, at a bombarding energy of 100 MeV. In this simulation study, they focused on an S-matrix characterization of the reaction. Since the de Broglie wavelength for the relative motion between the interacting heavy ions is short compared to nuclear dimensions, there is a close correspondence between incoming partial wave angular momentum (l_in) and impact parameter. They displayed plots of the absolute magnitude of the S-matrix elements as a function of l_in for the various two-neutron transfer pathways (Fig. 9a). At the time, the S-matrix was thought to yield information only about the amplitudes of the outgoing waves at large distances. However, their calculations revealed that plots of the magnitude of the S-matrix elements versus l_in can provide important clues as to the nature of the nucleon transfer mechanism near the nuclear surface.

Fig. 9

a The absolute value of S-matrix elements vs. incoming partial wave angular momenta (L_in) for: a inelastic scattering, a one-step (direct) two-neutron transfer process, and two-step (indirect) two-neutron transfer processes, for the modeled ¹¹⁶Sn (¹⁸O, ¹⁶O) ¹¹⁸Sn reaction, at a bombarding energy of 100 MeV. For heavy-ion-induced reactions, the de Broglie wavelength for the relative motion is short and thus the S-matrix elements vary smoothly with respect to L_in values (or impact parameters). The structure of the S-matrix element plots with respect to L_in depends on the nature of the reaction mechanism. b The corresponding CCBA calculations of differential cross sections for the modeled two-neutron transfer reaction. Shown are the differential cross sections for individual two-neutron transfer pathways corresponding to: the one-step process (dashed arrow) and two-step processes (solid arrows), leading to the collection 2⁺ vibrational state of ¹¹⁸Sn

For the direct two-neutron transfer process, the S-matrix element plot is bell-shaped. The peak in the plot is at l_in ~ 57, which corresponds to the classical grazing angle for the collision. The full width at half-maximum has Δl_in ~ 11. The sudden decrease on the low side of the peak corresponds to the rapid onset of strong absorption. The slow falloff beyond the peak reflects the tail of the two-neutron transfer form factor, which decays exponentially in accordance with the two-neutron binding energy in both the projectile (¹⁸O) and residual nucleus (¹¹⁸Sn).

For the inelastic scattering (0⁺ to 2⁺) process, the S-matrix element plot is biphasic; the proximal peak reflects the attractive nuclear potential; whereas, the distal peak the repulsive Coulomb interaction. The local minimum reflects the destructive interference between the two opposing interactions at l_in ~ 60. The falloff with increasing l_in decreases slowly due to the long-range of the Coulomb interaction. As would be anticipated, for the two-step two-neutron transfer process, the S-matrix element plot is similar in shape to that for inelastic scattering, since the two-step process encompasses inelastic excitation and two-neutron transfer. However, the falloff with increasing l_in is much “faster” than for inelastic scattering or direct two-neutron transfer alone, consistent with the two-step process being more localized to the nuclear surface in R-space. The peak is at l_in ~ 54, with Δl_in ~ 6. Consequently, the distribution in l-space is narrower for the two-step compared to the one-step two-neutron transfer process. The narrower l window for two-step transfer is reflected by an increase in width (Δθ) of the corresponding angular distribution around the grazing peak, since Δl_in Δθ ~ 1, consistent with the uncertainty relationship. Figure 9b shows the associated angular distributions corresponding to the S-matrix plots.

3.12 Spatial localization of a two-step, two-nucleon transfer process involving an intermediate inelastic excitation, which represents a conditional not disjointed process

At the Washington meeting, Ascuitto and Vaagen also presented a simulation study elucidating spatial characteristics of a heavy-ion-induced, two-step, two-nucleon transfer process. For simplicity, they considered a reaction, A (a, b) B, in which an incoming ion (a) initiates an inelastic excitation of the target nucleus (A), from its ground state (α) to an excited state (α′), followed by two-nucleon transfer from the excited state (α′) to a state (β') of the residual nucleus (B), i.e., (α to α′ to β′). Both the inelastic excitation and two-nucleon transfer transitions were assumed to be “unidirectional”, i.e., no back couplings. A similar pathway would involve (α to β to β′), see Fig. 2. In this limit, the coupled channels equations simplify considerably, namely

$$ (T_{\alpha } + U_{\alpha } - E_{\alpha } )\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) = 0\, \left( {\text{elastic scattering}} \right), $$

(13a)

$$ \begin{aligned} (T_{\alpha ^{\prime}} + U_{\alpha ^{\prime}} - E_{\alpha ^{\prime}} )\chi_{\alpha ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) = - (\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right),& [V_{\alpha ^{\prime}} - {\text{U}}_{\alpha ^{\prime}} ], \Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}))\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha} ), \\& ({\text{inelastic excitation}},\,\alpha \,\,{\text{to}}\,\,\alpha ^{\prime}) \\ \end{aligned} $$

(13b)

and

$$ \begin{aligned} (T_{\beta ^{\prime}} + U_{\beta ^{\prime}} - E_{\beta ^{\prime}} )\chi_{\beta ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) = - (\Phi_{\beta ^{\prime}} \left( {{\mathbf{b}},{\mathbf{B}}} \right), & [V_{\beta ^{\prime}} - {\text{U}}_{\beta ^{\prime}} ],\Phi_{\alpha ^{\prime}} ({\mathbf{a}},{\mathbf{A}}))\chi_{\alpha ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\alpha} ). \\ & ({\text{nucleon transfer}},\,\alpha ^{\prime}\,\,{\text{to}}\,\,\beta ^{\prime}) \\ \end{aligned} $$

(13c)

For these equations, T is the usual kinetic energy operator describing the relative motion between the interacting ions. The nuclear (intrinsic) Hamiltonian (${\user2{\mathcal{H}}}$) satisfies ${\user2{\mathcal{H}}}_{\delta } \Phi_{\delta } = \varepsilon_{\delta } \Phi_{\delta },$ with channel state function, $\Phi_{\delta }$, and channel energy, $E_{\delta } = E - \varepsilon_{\delta }$. The term V_δ is an effective interaction between (a) and (A) or (b) and (B) and $U_{\delta } = (\Phi_{\delta } ,V_{\delta } ,\Phi_{\delta } )$ is taken as an optical model potential, with (δ = α, α′ or β′).

The solutions to Eqs. (13b) and (13c) can be determined using successive approximations. In the zeroth-order approximation, one obtains the distorted wavefunction $\chi_{{{\mathbf{0}}\alpha }}^{\alpha ( + )}$, with $\chi_{{{\mathbf{0}}\alpha ^{\prime}}}^{\alpha ( + )}$ and $\chi_{{{\mathbf{0}}\beta ^{\prime}}}^{\alpha ( + )}$ being zero, as the incident wave is only in channel α. In the first-order approximation, $\chi_{{{\mathbf{1}}\alpha ^{\prime}}}^{\alpha ( + )}$ describes the one-step inelastic scattering process (α to α′) and $\chi_{{{\mathbf{1}}\beta ^{\prime}}}^{\alpha ( + )}$ a one-step, two-nucleon transfer process (α to β′). In the second-order approximation, a component of $\chi_{{{\mathbf{2}}\beta ^{\prime}}}^{\alpha ( + )}$ describes the two-step, two-nucleon transfer process (α to α′ to β′), which symbolically can be written as follows:

$$ \begin{aligned} \chi_{{{\mathbf{2}}\beta ^{\prime}}}^{\alpha \left( + \right)} ({\mathbf{R}}_{\beta } ) & = G_{\beta ^{\prime}}^{\left( + \right)} (\Phi_{\beta ^{\prime}} \left( {{\mathbf{b}},{\mathbf{B}}} \right),[V_{\beta ^{\prime}} - U_{\beta ^{\prime}} ],\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right)) \\ & \quad \times G_{\alpha ^{\prime}}^{\left( + \right)} (\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right),[V_{\alpha ^{\prime}} - U_{\alpha ^{\prime}} ],\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right))\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ), \\ \end{aligned} $$

(14)

where G is the Green’s function operator. In its spatial representation, and for large R_β, is

$$ G_{\beta ^{\prime}}^{\left( + \right)} ({\mathbf{R}}_{\beta ^{\prime}} ,{\mathbf{R}}^{\prime}_{\beta ^{\prime}} ) \to \exp (ik_{\beta ^{\prime}} R_{\beta ^{\prime}} )/R_{\beta ^{\prime}} \left\{ {(m_{\beta ^{\prime}} /2\pi \hbar^{2} )\chi_{\beta ^{\prime}}^{\alpha \left( - \right)*} ({\mathbf{R}}^{\prime}_{\beta ^{\prime}} }) \right\}. $$

(15)

Thus, the corresponding two-step, two-nucleon transfer transition amplitude, i.e., the second-order DWBA, becomes:

$$ \begin{aligned} T_{\beta ^{\prime}\alpha ^{\prime}\alpha } & = < \chi_{\beta ^{\prime}}^{\alpha \left( - \right)} ({\mathbf{R}}_{\beta } )(\Phi_{\beta ^{\prime}} \left( {{\mathbf{b}},{\mathbf{B}}} \right), \, [V_{\beta ^{\prime}} - U_{\beta ^{\prime}} ],\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right)) \\ & \quad \times G_{\alpha ^{\prime}}^{\left( + \right)} (\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right), \, [V_{\alpha ^{\prime}} - U_{\alpha ^{\prime}} ],\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right))\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) > , \\ \end{aligned} $$

(16)

see Appendix 3. Of course, to calculate the Green’s function and thus the transition amplitude requires computing distorted wavefunctions describing the relative motion in the three channels, which satisfy:

$$ (T_{\delta } + U_{\delta } - E_{\delta } )\chi_{\delta } ({\mathbf{R}}_{\delta } ) = 0,\quad {\text{ with}}\,\,(\delta = \alpha ,\alpha ^{\prime}\,\,\,{\text{or}}\,\,\beta ^{\prime}). $$

(17)

The transition amplitude T_β′α′α for the two-step, two-nucleon transfer process is best calculated using the coordinate space representation, namely

$$ \begin{aligned} & \quad \quad \quad \,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad ({\text{depends on}}\,{\mathbf{R}}_{\beta } \,\,{\text{and}}\,\,{\mathbf{R}}_{\alpha ^{\prime}} ) \\ T_{\beta ^{\prime}\alpha ^{\prime}\alpha } & = \int {{\text{d}}{\mathbf{R}}_{\beta } } \int {{\text{d}}{\mathbf{R}}_{\alpha } } \{ \chi_{\beta ^{\prime}}^{\left( - \right)*} ({\mathbf{R}}_{\beta } )\int {{\text{d}}{\mathbf{R}}_{\alpha ^{\prime}} } \int {{\text{d}}{\mathbf{R}}^{\prime}_{\alpha ^{\prime}} } (\Phi_{\beta ^{\prime}} \left( {{\mathbf{b}}, \, {\mathbf{B}}} \right),[V_{\beta ^{\prime}} - U_{\beta ^{\prime}} ],\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}}, \, {\mathbf{A}}} \right)) \\ & \quad \times < {\mathbf{R}}_{\alpha ^{\prime}} ,G_{\alpha ^{\prime}}^{\left( + \right)} ,{\mathbf{R}}^{\prime}_{\alpha ^{\prime}} > (\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right), \, [V_{\alpha ^{\prime}} - U_{\alpha ^{\prime}} ],\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right))\} \chi_{\alpha }^{\left( + \right)} ({\mathbf{R}}_{\alpha } ), \\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad ({\text{depends on}}\,\,{\mathbf{R}}^{\prime}_{\alpha ^{\prime}} \,\,{\text{and}}\,\,{\mathbf{R}}_{\alpha } ) \\ \end{aligned} $$

(18)

where ${<}{\textbf{R}}_{\alpha ^{\prime}} ,{\text{G}}_{\alpha ^{\prime}}^{\left( + \right)} ,{\textbf{R}}^{\prime}_{\alpha ^{\prime}} {>}$ is the spatial representation of the Green’s function, which is provided in Appendix 1. If one replaces the distorted wavefunctions by their WKB equivalents, integrates over the nonlocality coordinate $({\mathbf{R}}_{\alpha ^{\prime}} - {\mathbf{R}}^{\prime}_{\alpha ^{\prime}} )$, and uses an adiabatic, local energy approximation, ${<} {\mathbf{R}}_{\alpha ^{\prime}} ,{\text{G}}_{\alpha ^{\prime}}^{\left( + \right)} ,{\mathbf{R}}^{\prime}_{\alpha ^{\prime}} {>}$ reduces to a delta function, i.e., $\delta ({\mathbf{R}}_{\alpha ^{\prime}} - {\mathbf{R}}^{\prime}_{\alpha ^{\prime}} )/E_{\alpha ^{\prime}} (R_{{\text{o}}} )$, where E_α′ is a local energy averaged over a surface specified by R_o, in channel (α′)_.

The transition amplitude then reduces to:

$$ T_{\beta ^{\prime}\alpha ^{\prime}\alpha } = { 1}/E_{\alpha ^{\prime}} ({R}_{{\text{o}}} )\int {{\text{d}}{\mathbf{R}}_{\beta } } \int {{\text{d}}{\mathbf{R}}_{\alpha } } \chi_{\beta ^{\prime}}^{\left( - \right)*} ({\mathbf{R}}_{\beta } ){\user2{\mathcal{F}}}_{\beta ^{\prime}\alpha ^{\prime}\alpha } ({\mathbf{R}}_{\beta } ,{\mathbf{R}}_{\alpha } )\chi_{\alpha }^{\left( + \right)} ({\mathbf{R}}_{\alpha } ), $$

(19)

for which a generalized form factor ${\user2{\mathcal{F}}}_{\beta ^{\prime}\alpha ^{\prime}\alpha }$ can be defined as follows:

$$ \begin{aligned} & \quad \quad \quad \,\quad \quad \quad ({\text{depends on}}\,{\mathbf{R}}_{\beta } \,\,{\text{and}}\,\,{\mathbf{R}}_{\alpha ^{\prime}} ) \\ {\user2{\mathcal{F}}}_{\beta ^{\prime}\alpha ^{\prime}\alpha } ({\mathbf{R}}_{\beta } ,{\mathbf{R}}_{\alpha } ) & = \int {{\text{d}}{\mathbf{R}}_{\alpha ^{\prime}} } (\Phi_{\beta ^{\prime}} \left( {{\mathbf{b}}, \, {\mathbf{B}}} \right),[V_{\beta ^{\prime}} - U_{\beta ^{\prime}} ],\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}}, \, {\mathbf{A}}} \right)) \\ & \quad \times (\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right), \, [V_{\alpha ^{\prime}} - U_{\alpha ^{\prime}} ],\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right)) \\ & \quad \quad \quad \quad \quad ({\text{depends on}}\,\,{\mathbf{R}}_{\alpha ^{\prime}} \,\,{\text{and}}\,\,{\mathbf{R}}_{\alpha } ) \\ \end{aligned} $$

(20)

In the no-recoil limit, the transition amplitude can be further reduced, since R_α ~ R_β = R. Each of the bracketed terms (.…) in Eq. (20) contains a form factor. For the inelastic excitation (α to α′), the form factor has a component of the interaction localized to the nuclear surface that involves the derivative with respect to R of the nuclear potential and the long-range Coulomb interaction, i.e.,

$$ \begin{aligned} {\user2{\mathcal{F}}}_{{{\varvec{inel}}}} \left( R \right) & = - \beta_{N} R_{{\text{o}}} \,\delta V/\delta R \, + \beta_{{\text{c}}} 3e^{{\mathbf{2}}} Z_{1} Z_{{\mathbf{2}}} R_{{\text{c}}}^{{\text{L}}} /\left( {\left( {2L + \, 1} \right) \, R^{(L + 1)} } \right),\,\,\, R > R_{{\text{c}}} , \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,({\text{nuclear}})\quad \quad \quad \quad ({\text{Coulomb}}) \\ \end{aligned} $$

(21)

where β_N and β_c are parameters characterizing a vibrating or deformed nuclear surface. For two-nucleon transfer, the form factor decays exponentially as,

$$ {\user2{\mathcal{F}}}_{{{\varvec{tran}}}} \left( R \right)\sim {\text{exp }}\left[ { - \, \left( {4mB/\hbar^{2} } \right) \, R} \right], \, \,\,\,{\text{for large}}\; \, R, $$

(22)

where B is the binding energy of the two-nucleon cluster. Since the two form factors in Eqs. (21) and (22) appear conjointly in the integrand of Eq. (20), their “magnitude and phase”, near the region of nucleon exchange are critically important in determining the nature of any interference, i.e., constructive or destructive, between the one-step and two-step two-nucleon transfer process. Furthermore, the conjoined form factor for the two-step two-nucleon transfer process decreases more rapidly with increasing R than the form factor for inelastic excitation or direct two-nucleon transfer alone. Such an enhanced spatial localization of the two-step process was already evident in the S-matrix element plots vs. incoming partial wave angular momenta and can profoundly affect the angular distribution of the outgoing particles for the reaction.

3.13 Recapitulation (modification of the conventional DWBA)

In Ascuitto and Glendenning’s original paper on the CCBA in 1969 [2], they emphasized that, in addition to multi-step nucleon transfer processes, when inelastic excitations are strong “deexcitation” back into the elastic channel can become important. On this basis alone, the DWBA may fail, since the usual one-channel optical model potential may not adequately account for flux lost in the incoming and/or outgoing channels, or provide a good representation of the relative motion wavefunctions in the vicinity of the nuclear surface where direct reactions take place, see also Ascuitto and E. A. Seglie (Ascuitto 1984). The conventional DWBA, which employed an empirical optical model potential for both the entrance and exit channels, was successful in reproducing many direct inelastic scattering cross sections in the 1960s. However, by the mid-70s, as experiments became more sophisticated, a number of inelastic scattering reactions were reported in which the DWBA failed to describe the angular distribution associated with an excited nuclear state, even when the state was weakly coupled to the elastic channel. This situation, however, tended to occur when the weakly excited nuclear state was in proximity to another nuclear state “strongly” coupled to the elastic channel.

An example was the ⁴⁰Ca (¹⁶O, ¹⁶O) ⁴⁰Ca* reaction, at a bombarding energy of 60 MeV, reported by K. E. Rehm, W. Henning, J. R. Erskine and D. G. Kovar, at Argonne National Laboratory [55]. The collective 3⁻ state at 3.74 MeV in ⁴⁰Ca was found to be strongly excited by inelastic scattering; whereas, the 5⁻ state at 4.49 MeV was only weakly excited. Additionally, shell model calculations revealed the 3⁻ state was not coupled to the 5⁻ state. Coupled channels calculation yielded a good representation of the angular distribution for both the 3⁻ and 5⁻ states. Surprisingly, however, when the conventional DWBA was employed to describe the more-weakly excited 5⁻ state, it failed to reproduce the angular distribution. What was going on? One would have expected the DWBA to adequately represent the angular distribution for the 5⁻ state.

A simplified model was introduced to shed light on this unexpected result [12]. Ascuitto et al. carried out a coupled channels calculation of inelastic scattering which contained three channels, α, β and γ. The incoming channel, α, contained the incident beam and the 0⁺ ground state of ⁴⁰Ca. The outgoing channels β and γ contained the 3⁻ and 5⁻ excited states of ⁴⁰Ca, respectively. A generalized optical model potential (U) was used in the coupled channels calculation for the inelastic scattering reaction. It was assumed that the diagonal matrix elements of U satisfy U_αα = U_ββ = U_γγ = U_o, where U_o was referred to as a “bare” optical model potential. The non-diagonal matrix elements of U gave rise to the inelastic transitions. For the α to β transition (excitation) and β to α transition (deexcitation), U_βα and U_αβ were taken as equal in magnitude and strong. For the α to γ transition, U_γα was taken as weak; and for the β to γ transition, U_γβ was taken to be zero, i.e., no coupling between the 3⁻ and 5⁻ states. Under these conditions, the coupled channels equations describing the relative motion wavefunctions χ decouple and simplify:

$$ (T_{\alpha } + U_{{\text{o}}} - E_{\alpha } )\chi_{\alpha }^{( + )} = - U_{\alpha \beta } \chi_{\beta }^{( + )} \,\,\,\,\, {\text{deexcitation}} $$

(23a)

$$ (T_{\beta } + U_{{\text{o}}} - E_{\beta } )\chi_{\beta }^{( + )} = - U_{\beta \alpha } \chi_{\alpha }^{( + )} \,\,\,\,\, {\text{excitation}} $$

(23b)

$$ (T_{\gamma } + U_{{\text{o}}} - E_{\gamma } )\chi_{\gamma }^{( + )} = - U_{\gamma \alpha } \chi_{\alpha }^{( + )} \,\,\,\,\, {\text{excitation}} $$

(23c)

The parameters for U_o were determined by requiring that the “coupled channels” calculation reproduces the experimental elastic scattering data. The transition amplitude corresponding to Eq. (23c) can be obtained using the source term method, see Appendix 1.

The corresponding transition amplitude (T) for direct excitation of the 5⁻ state, γ, in this system of equations, becomes:

$$ T_{\gamma \alpha } = < \chi_{{\gamma ,{\text{o}}}}^{\left( - \right)} , \, U_{\gamma \alpha } ,\chi_{{\alpha ,{\text{ cc}}}}^{\left( + \right)} > , $$

(24)

where $\chi_{{\alpha ,{\text{ cc}}}}^{\left( + \right)}$ is the relative motion wavefunction for the incoming channel α, which is obtained by solving the coupled Eqs. (23a) and (23b). $\chi_{{\gamma ,{\text{o}}}}^{\left( - \right)}$ is the distorted wavefunction for the outgoing channel γ, which now is determined by the “bare” optical model U_o, i.e., $\chi_{{\gamma ,{\text{o}}}}^{\left( - \right)}$ satisfies:

$$ (T_{\gamma } + U_{{\text{o}}}^{\left( - \right)} - E_{\gamma } )\chi_{{\gamma ,{\text{ o}}}}^{\left( - \right)} = 0. $$

(25)

Since U_γβ is zero, the only strong coupling for the system is between the α and β channels, i.e., between the 0⁺ ground state and the collective 3⁻ excited state of ⁴⁰Ca.

These investigators then replaced χ_α,cc⁽⁺⁾ in Eq. (24) with the relative motion wavefunction χ_α,DW⁽⁺⁾, which satisfies the equation to,

$$ (T_{\alpha } + {\user2{\mathcal{U}}} - E_{\alpha } )\chi_{{\alpha ,{\text{ DW}}}}^{\left( + \right)} = 0. $$

(26)

In Eq. (26), in the spirit of the DWBA, the parameters of the one-channel optical model potential ${\user2{\mathcal{U}}}$ were adjusted to fit the experimental elastic scattering cross section. In doing so, it was assumed that ${\user2{\mathcal{U}}}$ would account for absorption of flux in the elastic channel arising as a consequence of strong coupling between the α and β channels. This formulation led to a modified DWBA transition amplitude, namely

$$ T_{\gamma \alpha } = < \chi_{{\gamma ,{\text{ o}}}}^{\left( - \right)} ,U_{\gamma \alpha } ,\chi_{{\alpha ,{\text{ DW}}}}^{\left( + \right)} > , $$

(27)

where the entrance channel distorted wavefunction, χ_α,DW, is generated, as usual, by a one-channel optical model potential ${\user2{\mathcal{U}}}$, which describes the experimental elastic scattering data for the reaction.

The exit channel distorted wavefunction, $\chi_{{\gamma ,{\text{ o}}}}^{\left( - \right)}$, however, is not determined by ${\user2{\mathcal{U}}}$, but by the “bare” optical model potential U_o, i.e., the potential that reproduces the elastic scattering data only within the context of the coupled channels calculation. This modification of the conventional DWBA transition amplitude, i.e., with complementary but different optical model potentials for the incoming and outgoing channels, yielded an excellent description of the angular distribution for the 5⁻ state of ⁴⁰Ca. In this case, the modified form of the DWBA, Eq. (27), adequately compensated for the strong inelastic excitation (and deexcitation) between the 0⁺ ground state and the 3⁻ excited state of ⁴⁰Ca. This finding led to an important area of heavy-ion reaction research, in which experiments were performed and formulations were developed to study effects of strong coupling between the elastic channel and other reaction channels on the optical model potential. See also important discussions by [40, 65].

The concept of a modified DWBA, Eq. (27), had important implications for strong coupling in nucleon transfer reactions. Ascuitto and Seglie, while at WNSL, considered a stripping reaction, A (a, b) B with a = b + x and B = A + x, which consisted of an entrance channel (α) in partition (a + A) strongly coupled via nucleon transfer of (x) to an exit channel (β) in partition (b + B). The conventional DWBA invariably would employ an empirical optical model potential (${\user2{\mathcal{U}}}$) that fits the elastic scattering data for both the entrance and exit channels. The empirical optical model potential for the entrance channel would reflect feedback from the (β) to the (α) channel. However, the empirical optical model potential for the exit channel would reflect feedback from the (α) to the (β) channel. Employing both these optical model potentials in a DWBA transition amplitude would be tantamount to double-counting the influence of the nucleon transfer process on the relative motion between the colliding ions. Thus, by taking ${\user2{\mathcal{U}}}$ for both the entrance and exit channels, partial waves grazing the nuclear surface would likely be absorbed too strongly, which could adversely impact calculated angular distributions, particularly at forward angles. In this case, the corresponding modified DWBA for a strongly coupled nucleon transfer process is diagrammatically depicted in Fig. 10.

Fig. 10

A schematic representation of strong coupling in a nucleon transfer reaction. Note, when described as a DWBA transition amplitude, the incoming empirical elastic scattering optical model potential (${\user2{\mathcal{U}}}$) and the outgoing bare optical model potential (U_o) are different

3.14 The duo returned to WNSL

As their fellowship year at NBI/NORDITA was concluding, the duo needed to make a decision about future employment. Should they go to WNSL, or separate and seek positions elsewhere? Moreover, Ascuitto was still highly conflicted over the US military involvement in South East Asia, and the friends he lost due to the War. Fortunately, on January 27, 1973, representatives of the USA, North and South Vietnam and the Vietcong signed a peace treaty in Paris, purportedly ending US' military involvement in the Vietnam War. In actuality, the Paris Accords provided President Nixon with a means of saving face politically, by beginning the withdrawal of US troops. Nevertheless, it was not until April 30, 1975, that the last Americans were airlifted out of South Vietnam, as Saigon fell to communist forces. Many Americans finally achieved some inner peace over the war. Still, the Vietnam War was the most unpopular foreign war in US history and cost 58,000 American lives, and 3–4 million Vietnamese were killed.

In reality, in order to continue research in nuclear reaction physics, Ascuitto and Vaagen reluctantly needed to return to WNSL, since it had a heavy-ion accelerator and the job market in academic nuclear physics was essentially non-existent in America. Wright Nuclear Structure Laboratory was the brainchild of Professor D. Allan Bromley. His desire was to transform Yale University into a world leader in experimental nuclear physics. He believed the best way to achieve this goal would be to have a state-of-the-art particle accelerator on campus. Bromley, as Director of the newly established laboratory, initiated the design of the first MP (Emperor) Tandem Van de Graaff electrostatic accelerator. Construction began in 1964, and the Arthur Williams Wright Nuclear Structure Laboratory (WNSL) was dedicated in 1966. Under Bromley’s leadership, WNSL rose to become the premier university experimental nuclear physics research center in the world, and was widely recognized as the “birthplace of heavy-ion nuclear physics”.

Graduate students, post-docs and junior faculty from around the world flocked to WNSL for training in experimental nuclear physics. Early ground-breaking experiments at the laboratory led to the discovery of nuclear molecules, nuclear compressibility, the spectroscopic structure of light ions and isobaric analogue states. In 1973, however, WNSL’s tandem particle accelerator required an upgrade of the charging system and in tube design, which amounted to significant down time. Bromley was acutely aware of theoretical research that potentially could advance their experimental nuclear reaction physics program. He also realized that the two young theorists returning from NBI/NORDITA to WNSL were making important contributions to the rapidly growing field of heavy-ion nucleon transfer reactions. Thus, Bromley envisioned that at WNSL, the combination of a revitalized accelerator in conjunction with the theorists’ newly developed CCBA and CRC models could help usher in a new era in heavy-ion reaction physics.

At WNSL, a close collaboration soon evolved between the newly arrived theorists and the experimental group headed by K. A. Erb. Erb was an outstanding young nuclear physicist, an accomplished administrator and a compassionate mentor of graduate students. The WNSL’s nuclear reaction group’s research in heavy-ion reactions came to fruition when CCBA calculations began revealing remarkably strong coupling between inelastic scattering and nucleon transfer channels especially in collective nuclei. More importantly, quantal coherence effects arising from interference between direct and indirect nucleon transfer processes were found to produce striking alterations in angular distributions.

Despite early successes of the CCBA in describing a variety of light-ion-induced nucleon transfer reactions, many experienced researchers remained skeptical about needing to perform full quantum mechanical calculations for heavy-ion reactions. Their main reservation was that in a wave-mechanical analysis of these reactions, it might be necessary to determine contributions from many (perhaps hundreds of) partial waves to adequately describe the cross sections, as was the case in Coulomb excitation. This would make the computation time inordinately long and numerical accuracy might be compromised. However, Ascuitto and Vaagen, and earlier Ascuitto and Glendenning, pointed out a flaw in that argument. They advocated that at the bombarding energies being utilized, nucleon transfer reactions between medium-mass nuclei would in fact involve a relatively “narrow” band of partial wave angular momenta (l), or impact parameters [b = (l + 1/2)/k], because of strong absorption as the nuclei come into close proximity and the exponential decay of nucleon transfer form factors.

At low angular momenta (small impact parameters) flux would be lost primarily to more complicated open channels and compound nucleus formation, as represented by the imaginary part of the optical model potential. At high angular momenta (large impact parameters), for one-step nucleon transfer, the form factor for the process decreased exponentially with respect to increasing distance beyond the nuclear surface. Furthermore, as already discussed, for two-step nucleon transfer processes (with intermediate inelastic excitations) the overall form factor is governed essentially by the “product” of an inelastic scattering form factor and a nucleon transfer form factor and thus would decay even faster. Consequently, the number of partial wave angular momenta required to calculate cross sections would not be excessive.

Therefore, Ascuitto and Vaagen, and earlier Ascuitto and Glendenning [8], contended that “heavy-ion nucleon transfer reactions would converge relatively rapidly with respect to increasing partial wave angular momenta, even at bombarding energies near the Coulomb barrier when Coulomb excitation is important”. Moreover, the ratio of indirect to direct nucleon transfer processes was found to increase as the Q-value of the reaction departs from optimal value. The findings of these investigators made a quantum mechanical computations of heavy-ion nucleon transfer reactions not only feasible, but essential, which led investigators around the world to confidently modify computer codes to accommodate these reactions.

3.15 Heavy-ion two-neutron transfer reactions involving vibrational nuclei (CCBA’s intimate dependence on nuclear structure)

Ascuitto and Vaagen’s CCBA simulation studies of heavy-ion-induced nucleon transfer reactions presented at the American Physical Society Meeting in Washington D. C. in 1973, also addressed the importance of including the structure of the target and residual nucleus. They employed no-recoil CCBA calculations to model the inverse reactions, ¹²⁰Sn (¹⁸O,¹⁶O) ¹²²Sn and ¹²²Sn (¹⁶O,¹⁸O) ¹²⁰Sn. The coupled channels calculations included the 0⁺ ground state and collective 2⁺ excited state of both the target and residual nucleus. The 0⁺ ground state (vacuum state) for the vibrational nuclei was constructed using five active neutron states distributed around the Fermi level, namely (g_7/2, 2d_5/2, 3s_1/2, h_11/2, 2d_3/2). The neutrons were assumed to interact through a pairing interaction, chosen to reproduce average nuclear properties for the Sn mass region. The collective 2⁺ state was taken as a superposition of two quasiparticles [1].

In 1973, Ascuitto and Glendenning had predicted that for heavy-ion two-neutron transfer reactions involving vibrational nuclei, the stripping and inverse pickup reactions would yield distinctly different angular distributions for the collective 2⁺ [9]. This result followed since, in the two-quasiparticle approximation of the 2⁺ state, the parentage amplitude for two-neutron transfer connecting the 0⁺ ground state of the target nucleus to the collective 2⁺ state of the residual nucleus is “opposite” in sign for the stripping, compared to the pickup, reaction. In contrast, the amplitudes characterizing intermediate inelastic excitations connecting the 0⁺ ground state to the collective 2⁺ state in the target and residual nucleus carry the same sign (Fig. 11). Consequently, for the stripping reaction, say ¹²⁰Sn (¹⁸O,¹⁶O) ¹²²Sn, the sign of the parentage amplitude for the one-step two-neutron transfer is “(+)” and for the two-step two-neutron transfers they are net “(−)”, i.e., (6) × (4) and (1) × (5) (Fig. 11). However, for the inverse pickup reaction, ¹²²Sn (¹⁶O,¹⁸O) ¹²⁰Sn, the sign of the parentage amplitude for the one-step two-neutron transfer is “(−)” and for the two-step two-neutron transfers are net “(−)”, i.e., (5) × (4) and (1) × (6). Therefore, one-step two-neutron transfer would interfere destructively with two-step two-neutron transfer for the stripping, and conversely constructively for the pickup, reactions. In 1975, this quantal interference effect was confirmed experimentally by D. K. Scott, et al., at LBL [57].

Fig. 11

Parentage amplitudes characterizing pathways leading to the collective 2⁺ states in vibrational nuclei. Parentage amplitudes are based on a quasiparticle random phase approximation; in this case the Y’s are small. The sign of the amplitude for the direct two-neutron transfer transition in a stripping reaction is positive (+), whereas, for the inverse pickup reaction it is negative (−) [8, 9]

In 1977, a pair of elegant two-neutron transfer reactions involving vibrational nuclei were reported by Bond et al. [19]. These experiments contrasted the angular distributions for the stripping and inverse pickup reactions involving Germanium (Ge) nuclei, namely ⁷⁴Ge (¹⁸O,¹⁶O) ⁷⁶Ge, at a bombarding energy of 75 MeV and ⁷⁶Ge (¹⁶O,¹⁸O)⁷⁴Ge, at a bombarding energy of 77.66 MeV. These heavy-ion reactions provided conclusive evidence for dramatic differences in the angular distributions for the 2⁺ vibrational state, between the stripping and pickup reactions (Fig. 12a, b) [19]. The experimental confirmation of the prediction of Ascuitto and Glendenning for heavy-ion two-neutron transfer reactions involving vibrational nuclei was important, as it provided confidence in the CCBA as an accurate theory when the structure of the target and residual nuclei is well defined.

Fig. 12

Experimental data and CCBA calculations of differential cross sections for the ⁷⁴Ge (¹⁸O, ¹⁶O) ⁷⁶Ge and the ⁷⁶Ge (¹⁶O, ¹⁸O) ⁷⁴Ge “inverse” two-neutron transfer reactions populating the 0⁺ ground state and the collective 2⁺ excited state in the residual nuclei, at bombarding energies of 75 MeV and 77.66 MeV, respectively. Data and calculations are from Bond, Korner, Lemaire, Pisano and Thorn [19]. Destructive interference between one-step (direct) and two-step (indirect) two-neutron transfer processes for the stripping reaction is present, as evidenced by the prominent dip in the angular distribution for the 2⁺ state of ⁷⁶Ge. This destructive interference pattern for the stripping reaction was previously predicted for vibrational nuclei [8, 9]

Ascuitto and Vaagen went further by demonstrating that the two-step, two-neutron transfer process in vibrational nuclei, involving an intermediate inelastic excitation, is more localized to the nuclear surface than the corresponding direct two-neutron transfer process. For bombarding energies moderately above the Coulomb barrier, their CCBA calculations indicated that the angular distribution for the two-step, two-neutron transfer process, is “more forward peaked, oscillatory and of greater width” compared to the direct two-neutron transfer alone (DWBA). In 1976, these findings were corroborated by R. J. Ascuitto, J. S. Vaagen, D. J. Pisano, C. E. Thorn, J. R. Lein and G. Loyhoiden with the ¹²⁴Te (¹²C, ¹⁴C) ¹²²Te reaction, at a bombarding energy of 70 MeV (Fig. 13) [14]. Verification of these alterations in the angular distribution for the two-step process was significant, since, despite the near-classical conditions for the relative motion, the distinct features in the angular distribution represented quantum phenomena. The oscillations in the angular distribution, particularly for the collective 2⁺ state, reflected the localization in l-space for the two-step process, as was evident in the earlier plots of the S-matrix elements vs. incoming partial wave angular momenta. In R-space, such heavy-ion transfer reactions occur essentially in a ring, bounded on the inner side by strong absorption and on the outer side by the exponential decay of the bound state neutron wavefunctions. Consequently, the forward oscillations in the angular distributions arise from interference of diffracted waves originating from opposite sides of the nucleus. By complementarity between angular momentum and scattering angle, the width of the angular distribution around the classical grazing angle satisfies Δl Δθ ~ 1.

Fig. 13

Experimental data and CCBA and DWBA calculations of differential cross sections for the ¹²⁴Te (¹²C, ¹⁴C) ¹²²Te two-neutron transfer reaction populating a the 0⁺ ground state and b the collective 2⁺ excited state of ¹²²Te, at a bombarding energy of 70 MeV. The DWBA predicted bell-shaped angular distributions for both the 0⁺ ground state and 2⁺ excited state, which was in marked contrast to the experimental data. The 2⁺ state was “forward-peaked, oscillatory and with increased width” as previously predicted for vibrational nuclei [8, 9]. Also shown is the importance of Coulomb excitation. Data and calculations and from Ascuitto et al. [14]

3.16 “A proposed experiment is a question which science asks of nature and the measurement is the recording of nature’s answer” Max Plank

Surprisingly, despite successes of the CCBA in describing light-ion-induced reactions, a substantial number of established nuclear physicists were dubious about needing to perform such complex computer calculations to describe, semiclassical heavy-ion reactions. Their reticence in accepting the CCBA was, in part, due to computer technophobia and/or the misguided belief that the coupled channels formulations were more of a mathematical rather than a physics accomplishment. The undeniable truth was that the coupled channels calculations describing light-ion-induced reactions involving deformed nuclei, e.g., inelastic scattering, (p, t), (p, d) and (p, n) reactions, occurred because these theories comprehensively integrated nuclear structure and reaction dynamics.

Consequently, Ascuitto and Vaagen were determined to employ the CCBA to simulate an experiment that would unequivocally reveal the existence of multi-step nucleon transfer processes in heavy-ion reactions. This matter was urgent, since several nuclear theory and computer science groups in the USA, Japan and Europe, with superior computational facilities, were gearing up to perform CCBA calculations, using a multiple transition amplitudes approach. At Yale, however, the computer facility on campus remained problematic. The Courant Institute of Mathematical Sciences’ computer center at NYU was still not fully accessible to outside users after being ravaged by antiwar protestors. Nevertheless, it was realized that the Courant Institute’s CDC 6600 computer could be accessed using a specialized telephone transmission line at Yale’s Computer Center in New Haven. After several months of bureaucratic negotiations, a communication system was finally installed. It was far from ideal, but it worked. The system had long turnaround times, slow printouts, and was available only a few nights a week for 2–3 h. Nevertheless, in spite of these shortcomings, the transmission line provided a means of performing judiciously selected calculations. In the end, however, intuition not computer technology would help Ascuitto and Vaagen prevail in the race.

The two investigators focused on the (¹²C, ¹⁴C) reaction in rare-earth deformed (rotational) nuclei to ascertain which nuclei might best demonstrate the presence of these elusive indirect nucleon transfer processes. Adiabatic Bohr–Mottelson nuclear state functions were employed, which consisted of a rotational wavefunction ($\user2{\mathcal{D}}$) corresponding to an axially symmetric nucleus, and an intrinsic nuclear wavefunction (χ), i.e.,

$$ \Phi_{M}^{J} (A) \, = [\left( {2J \, + \, 1} \right)/8\pi^{2} ]^{1/2} {\user2{\mathcal{D}}}_{M}^{J} (\Omega )\chi (A^{\prime}), $$

(29)

where Ω represents standard orientation angles (φ, θ, ψ). In analogy to their previous work in spherical (vibrational) nuclei, a BCS vacuum was employed to describe the intrinsic state χ(A′), which was constructed using 20–30 valence neutron wavefunctions (orbitals) distributed around the Fermi level. The neutron orbitals were taken as eigenfunctions of a deformed Woods–Saxon potential having a shape defined by the deformation characteristics of the target and residual nucleus. The neutrons were coupled through a standard pairing interaction, chosen to reproduce average nuclear properties for the mass region. The intrinsic two-neutron transfer form factors were determined using Bang-inspired Sturmian methods, which insured the individual neutron wavefunctions decay in accordance with appropriate binding energies, see their subsequent work [64].

Their preliminary calculations, based on the characteristics of neutron states around the Fermi level, revealed that the J = 2 component of the intrinsic two-neutron transfer form factor became markedly reduced; whereas, the J = 4 component was enhanced, in tungsten (W) nuclei. Consequently, the angular distribution for the 2⁺ member of the ground state rotational band in the residual nucleus should be significantly different from that of the 4⁺ member of the band, in a background of indirect two-neutron transfer processes. In the DWBA, these two angular distributions were predicted to be essentially identical and purely bell-shaped. Given these findings, Ascuitto and Vaagen settled on the reaction ¹⁸⁶W (¹²C, ¹⁴C) ¹⁸⁴W, at a bombarding energy of 70 MeV. Obviously, in these deformed nuclei, both the nuclear and Coulomb interactions are strong, and thus inelastic excitations in ¹⁸⁶W and ¹⁸⁴W would be enhanced.

It was mid-May in 1974. Ascuitto and Vaagen were at the Yale computer center transmitting information to the NYU CDC 6600 system that was required to perform the CCBA calculations for their proposed reaction. This study included the 0⁺, 2⁺ and 4⁺ members of the ground state rotational bands of ¹⁸⁶W and ¹⁸⁴W. The shapes of the generalized Woods–Saxon optical model potentials for the coupled channels equations were defined through two nuclear surface deformation parameters, i.e., β₂ and β₄, determined from alpha particle inelastic scattering. Several hours later, the printer began cranking out the results of the calculations. Indeed, the 2⁺ angular distribution was significantly different from the 4⁺ distribution! Ascuitto smiled and uttered to Vaagen, “Nature is not winning this one”. For the two investigators, it was a magical moment.

The angular distribution for the 0⁺ ground state of ¹⁸⁴W was “unimodal”, i.e., bell-shaped with a peak at ~ 65°, which is the classical scattering angle for a grazing collision between ¹²C and ¹⁸⁶W at 70 MeV. This angular distribution is characteristic of a predominately “one-step” two-neutron pickup process, as anticipated for the superconducting transition. Conversely, the angular distribution for the 2⁺ and 4⁺ excited states of ¹⁸⁴W were “bimodal”, i.e., they contained two superimposed bell-shaped angular distributions with separate peaks and a local minimum separating the peaks. This bimodal pattern indicated that two distinctly different modalities of two-neutron transfer were involved in populating the excited states.

The angular distribution for the 2⁺ state of ¹⁸⁴W was found to be populated predominately by “two-step” processes, i.e., an inelastic excitation of the 2⁺ state of ¹⁸⁶W followed by two-neutron transfer from the 2⁺ state of ¹⁸⁶W to the 2⁺ state of ¹⁸⁴W, and the inverse process. Moreover, in the angular distribution for the 2⁺ state, the height of the proximal peak was “considerably less” than that for the distal peak. This decrease in cross section at forward angles arose from destructive interference between nuclear and Coulomb excitation (~ 1/R³) during the intermediate inelastic excitations. In contrast, the angular distribution for the 4⁺ state of ¹⁸⁴W stemmed mainly from destructive interference between “one-step” and “two-step” processes; i.e., (1) two-neutron transfer from the 0⁺ ground state of ¹⁸⁶W to the 4⁺ state of ¹⁸⁴W and (2) an inelastic excitation of the 4⁺ state of ¹⁸⁶W followed by two-neutron transfer leading to the 4⁺ state of ¹⁸⁴W, and the inverse process. Now, the height of the proximal peak was comparable to that for the distal peak, since destructive interference from Coulomb excitation (~ 1/R⁵) which is less important at forward angles.

At the International Conference on Reactions between Complex Nuclei held June 10th–14th, in 1974, in Nashville, Tennessee, the duo shared their CCBA calculations for the proposed ¹⁸⁶W (¹²C, ¹⁴C) ¹⁸⁴W reaction with a huge audience of nuclear physicists from around the world [11]. In their invited talk, they revealed distinctively different angular distributions for the 2⁺ and 4⁺ states of ¹⁸⁴W, which resulted from competition between one-step and multi-step two-neutron transfer processes. If these uniquely non-classical features could be experimentally verified, it would profoundly impact interpretations of heavy-ion nucleon transfer reactions. At the conclusion of their presentation, a distinguished scientist in the audience stood up and emphatically asked, “is it really necessary to perform such complex calculations in order to understand seemingly simple angular distributions”. Ascuitto responded with, “physics is simple only for the ONE, and the answer to your question is YES”.

3.17 Collegiality prevailed

A brief digression is in order concerning the ¹⁸⁶W (¹²C,¹⁴C) ¹⁸⁴W reaction. The group at WSNL was fully prepared to perform the proposed experiment. The detection apparatus was set up and the targets were constructed. Shortly thereafter, however, Karl Erb, the leader of the experimental group, was notified that the accelerator was malfunctioning and would not be available. What next! Erb contacted a colleague of his at BNL, J.J. Kolata, to inquired if the experiment could be performed there. BNL housed a Tandem Van de Graaff electrostatic accelerator, similar to the one at WNSL. The BNL accelerator provided well-controlled, high-quality beams, which was required to perform accurate heavy-ion reaction experiments. Fortunately, the accelerator at BNL was not in use over the ensuing weekend. Consequently, the experiment would be undertaken at BNL by the WNSL group in conjunction with Kolata. Ironically, being just across the Long Island Sound, in some respects BNL was in competition with WNSL. Nevertheless, although never proven, the team apparently was given the go ahead to proceed with the experiment at BNL!

Prior to the WNSL group leaving for BNL, Ascuitto and Vaagen provided them with their CCBA calculations of the angular distributions for the ¹⁸⁶W (¹²C,¹⁴C) ¹⁸⁴W reaction. If their prediction of the outcome of the experiment was correct, both WNSL and BNL would be elated. However, if the prediction of anomalous 2⁺ and 4⁺ angular distributions was incorrect, the duo would be highly embarrassed, since their preliminary calculations were highly publicized at the International Conference on Reactions between Complex Nuclei in Nashville. On Monday morning, Erb presented their experimental results. He had a smile on his face. The experiment strikingly confirmed the predicted bimodal angular distributions for the 2⁺ and 4⁺ states of ¹⁸⁴W (Fig. 14) [28]. It appeared that one could now understand heavy-ion two-neutron transfer reactions in detail not previously attained. This remarkable success of the CCBA reminded one of the hit-song performed by the Monkees in 1967, titled “I’m a Believer”, written by Neil Diamond. A half decade of work paid off! Finally, the nuclear physics community acknowledged the full ramifications of the CCBA. Most analyses of heavy ion reactions had to change.

Fig. 14

a CCBA calculations of differential cross sections for the ¹⁸⁶W (¹²C, ¹⁴C) ¹⁸⁴W two-neutron transfer reaction populating the 0⁺, 2⁺ and 4⁺ members of the ground state rotational band of ¹⁸⁴W, at a bombarding energy of 70 MeV. Note the angular distributions for the 2⁺ and 4⁺ states of ¹⁸⁴W are bimodal, as previously predicted by Ascuitto and Vaagen at the International Conference on Reactions between Complex Nuclei in Nashville, Tennessee, in [11]. b Shows the intrinsic J = 4 no-recoil two-neutron transfer form factor which is negative in the tail region. c demonstrates that the two-step process, inelastic excitation (+) followed by two-neutron transfer (+), interferes destructively with the one-step two-neutron transfer process (−). Data are from Erb et al. [28]

In 1976, at the European Conference on Nuclear Physics with Heavy Ions, in Caen, France, a major portion of the talks centered around one-step and multi-step nucleon transfer processes in heavy-ion nucleon transfer reactions. In an invited talk, Hanson and Garrett [36] acknowledged that, given the CCBA findings of Ascuitto and Vaagen on nucleon transfer reactions in vibrational and rotational nuclei, there would be difficulties in attempting to extract information about collective nuclei using the conventional DWBA. R. Bock in his conference summary [18] raised concerns about computer availability to routinely perform CCBA calculations, but expressed confidence in the CCBA theory by proclaiming, “the beauty of the interference patterns in angular distributions and their clear relation to changing nuclear structure is evident”. Low [43] presented a comprehensive description of various nucleon exchange mechanisms involved in heavy-ion nucleon transfer reactions. By analyzing a variety of reactions, Low concluded that “the CCBA’s inclusion of inelastic excitations largely explained the wide variety of different angular distributions being observed in heavy-ion nucleon transfer reactions”.

3.18 Nucleon-collective core coupling

The CCBA was finally gaining universal support as an accurate theory of heavy-ion two-neutron transfer reactions. Thus, the WNSL/BNL collaboration embarked on an investigation of a one-proton transfer reaction in which a valence proton is weakly coupled to a collective core. In 1978, G. B. Sherwood, K. A. Erb, D. L. Hanson et al., studied the ⁴⁸Ti (¹⁶O, ¹⁵N) ⁴⁹V reaction, at a bombarding energy of 50 MeV. They employed full-recoil CCBA calculations, which included all one-proton transfer transitions between the 0⁺ ground state and collective 2⁺ excited state of ⁴⁸Ti and the 7/2⁻ ground state and the collective 9/2⁻ and 11/2⁻ excited states of ⁴⁹ V. The ground state of ⁴⁹V was taken as a f_7/2 proton coupled to the ground state of ⁴⁸Ti. The 9/2⁻ and 11/2⁻ excited states of ⁴⁹V were assumed to be composed of the f_7/2 proton coupled to the collective 2⁺ excited state of ⁴⁸Ti, with perhaps small single-particle admixtures. A generalized optical model potential was used to describe inelastic excitations of ⁴⁸Ti.

The CCBA calculations provided a good representation of the experimental angular distributions (Fig. 15). The angular distribution for the 7/2⁻ ground state of ⁴⁹V was bell-shaped, typical of a “one-step” one-proton transfer process, i.e., ⁴⁸Ti (0⁺) (¹⁶O,¹⁵N) ⁴⁹V (7/2⁻). In contrast, the angular distributions for the 9/2⁻ and 11/2⁻ excited states of ⁴⁹V were distinctly different. For the 9/2⁻ state of ⁴⁹V, the angular distribution was forward peaked with an increased width, consistent with dominate “two-step” one-proton transfer processes involving intermediate inelastic excitations of ⁴⁸Ti, i.e., ⁴⁸Ti (0⁺) (¹⁶O, ¹⁶O') ⁴⁸Ti (2⁺) followed by ⁴⁸Ti (2⁺) (¹⁶O,¹⁵N) ⁴⁹V (9/2⁻) and ⁴⁸Ti (0⁺) (¹⁶O,¹⁵N) ⁴⁹V (7/2⁻) followed by ⁴⁹V (7/2⁻) (¹⁵N, ¹⁵N')⁴⁹V (9/2⁻). For the 11/2⁻ excited state of ⁴⁹V, the angular distribution was forward peaked and exhibited a “dramatic dip” near the classical grazing angle. This angular distribution was largely governed by destructive interference between a one-step one-proton transfer process and two-step one-proton transfer processes. A one-step proton transfer process connecting the ground state of ⁴⁸Ti to the 11/2⁻ excited state of ⁴⁹V resulted from a small single-particle admixture in the wavefunction for the 11/2⁻ state. Remarkably, an admixture of less than 2% of the h_11/2 spectroscopic strength was found to produce the prominent minimum in the angular distribution [59]. Coherent contributions from both direct and indirect nucleon transfer processes described the measured angular distributions. This reaction demonstrated the exquisite sensitivity of the CCBA to details in the structure of the nuclear states participating in a reaction.

Fig. 15

Experimental data and CCBA calculations of differential cross sections for the ⁴⁸Ti (¹⁶O, ¹⁵N) ⁴⁹V one-proton transfer reaction populating the 7/2⁻ ground state and the 11/2⁻ and 9/2⁻ collective excited states of ⁴⁹V, at a bombarding energy of 50 MeV [59]. CCBA calculations have the same overall normalizations for all states

3.19 The CRC and the sequential two-neutron transfer process

By the mid-70s, conventional DWBA calculations of heavy-ion-induced two-neutron transfer reactions in shell-structured nuclei were found to significantly underestimate absolute reaction cross sections. The shape of the angular distributions, however, were generally in agreement with the data. The standard approach in these calculations was to consider the two neutrons (n) to be transferred simultaneously, i.e., as a unit (n₁ + n₂). Investigators began speculating if important physics was missing. A question remained, namely “what if the two neutrons could, or are, transferred sequentially”, i.e., n₁ followed by n₂. Moreover, if the angular distributions for the two processes are similar, it would be difficult to distinguish between them, or to know whether one or both processes were occurring. If the transition amplitude for the simultaneous transfer process is T₁; then the corresponding cross section is determined by ${\vert T_{\textbf{1}} \vert}^{\textbf{2}}$. If the transition amplitude for the sequential transfer process is T₂, then the corresponding cross section is determined by ${\vert T_{\textbf{2}} \vert}^{\textbf{2}}$. In a quantal description, however, the transition amplitude including both processes would involve the coherent addition of T₁ and T₂, and the net cross section for the reaction would be determined by ${\vert T_{\textbf{1}}+T_{\textbf{2}} \vert}^{\textbf{2}}$.

In 1975, Gotz et al. at NBI, using a semiclassical model of a two-nucleon transfer reaction, revealed that cross sections for simultaneous and sequential two-nucleon transfer can be comparable in magnitude [35]. The same year, Kammuri, using a second-order DWBA and no-recoil, likewise found that cross sections for simultaneous and sequential two-nucleon transfer to be similar in magnitude. He also found angular distributions for the two processes to be similar, particularly for zero angular momentum transfer [38]. One year later, Feng, Udagawa and Tamura, employing a second-order DWBA, studied the ⁴⁸Ca (¹⁸O,¹⁶O) ⁵⁰Ca reaction, at a bombarding energy of 50 MeV [29]. Their calculations, which included full-recoil effects, revealed that the simultaneous and sequential two-neutron transfer processes indeed have similar angular distributions with comparable cross sections (Fig. 16) [29]. Thus, including both processes increased the absolute magnitude of the cross section by ~ four-fold, consistent with the experimental data! These were important findings, as they helped resolve the persistent problem of underestimating heavy-ion two-neutron transfer cross sections, and again revealed the importance of a coupled channels approach and quantum counting in calculating the reaction cross sections.

Fig. 16

Second-order DWBA calculations of differential cross sections for the ⁴⁰Ca (¹⁸O, ¹⁶O) ⁵⁰Ca two-neutron transfer reaction populating the 0⁺ ground state of ⁵⁰Ca, at a bombarding energy of 50 MeV, by Feng et al. [29]. Data are from Petersen et al. [52]. a σ₁ corresponds to the simultaneous (n₁ + n₂) two-neutron transfer process using a standard shell model wavefunction; σ₂ corresponds to the sequential (n₁ followed by n₂) two-neutron transfer process using the standard shell model wavefunction; σ₁' corresponds to the simultaneous (n₁ + n₂) two-neutron transfer process but with an extended shell model wavefunction; and σ₄ corresponds to the coherent addition of the simultaneous (σ₁') and sequential (σ₂) two-neutron transfer process. For this ground state (0⁺)-to-ground state (0⁺) transition both processes have similar (bell-shaped) angular distributions. b) Second-order DWBA calculations of differential cross sections for the ⁴⁰Ca (¹⁸O, ¹⁶O) ⁵⁰Ca two-neutron transfer reaction populating both the 0⁺ ground state and 2⁺ excited states of ⁵⁰Ca, by Takemasa and Yoshida [61]. The dashed line corresponds to the simultaneous two-neutron transfer process, the dot-dashed line to the sequential one neutron transfer process, and the solid line the coherent addition of contributions from both processes. Note both processes have similar angular distributions. Data are from Petersen et al. [52]. c Schematic representation of the sequential and simultaneous two-neutron transfer processes

3.20 Decomposition of the sequential two-nucleon transfer process

In the early CRC calculations, nucleon transfer transitions were considered to be unidirectional, which is a good approximation for most reactions involving low-lying nuclear states in shell-structured nuclei. The net transition amplitude (T), connecting the incoming channel α to the outgoing channel β, can be determined by a perturbative method, recall Appendix 3. The second-order approximation to the coupled channels equations contains in part the transition amplitude T_βγα, in which the two nucleons are transferred sequentially, i.e., one after the other. It represents an indirect transition from α to γ to β, with γ being a channel corresponding to an intermediate partition (c + C). The two-step transition amplitude can be represented as follows, see Appendix 3:

$$ \begin{aligned} T_{\beta \gamma \alpha } & = \,< \chi_{\beta }^{( - )} ({\mathbf{R}}_{\beta } )(\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right),[V_{\beta } - \, U_{\beta } ],\Phi_{\gamma } \left( {{\mathbf{c}},{\mathbf{C}}} \right))G_{\gamma }^{( + )} \\ & \quad \times (\Phi_{\gamma } \left( {{\mathbf{c}},{\mathbf{C}}} \right), \, [V_{\alpha } - \, U_{\alpha } ],\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right))\chi_{\alpha }^{( + )} ({\mathbf{R}}_{\alpha } ) > . \\ \end{aligned} $$

(30)

The transition amplitude contains the prior (α)–post (β) forms of the nucleon transfer interaction, which eliminates non-orthogonality terms arising from nuclear state functions of the different partitions. G_γ⁽⁺⁾ is the Green’s function operator in the intermediate channel γ. In the coordinate representation, the second-order Born approximation transition amplitude may be written as follows:

$$ T_{\beta \gamma \alpha } = \iint { {\text{d}}{\mathbf{R}}_{\beta } {\text{d}}{\mathbf{R}}_{\alpha } } \chi_{\beta }^{\left( - \right)*} ({\mathbf{R}}_{\beta } ){\user2{\mathcal{F}}}({\mathbf{R}}_{\beta } ,{\mathbf{R}}_{\alpha } )\chi_{\alpha }^{\left( + \right)} ({\mathbf{R}}_{\alpha } ), $$

(31)

where an effective form factor ${\user2{\mathcal{F}}}$ can be defined as follows:

$$ \begin{aligned} &\,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad ({\text{depends on}}\,{\mathbf{R}}_{\beta } \,\,{\text{and}}\,\,{\mathbf{R}}_{\gamma } ) \\ {\user2{\mathcal{F}}}({\mathbf{R}}_{\beta } ,{\mathbf{R}}_{\alpha } ) & = \iint { {\text{d}}{\mathbf{R}}_{\gamma } {\text{d}}{\mathbf{R}}^{\prime}_{\gamma } }\left( {\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right),\left[ {V_{\beta } - U_{\beta } } \right],\Phi_{\gamma } \left( {{\mathbf{c}},{\mathbf{C}}} \right)} \right) G_{\gamma }^{( + )} ({\mathbf{R}}_{\gamma } ,{\mathbf{R}}^{\prime}_{\gamma } ) \\ & \quad \times (\Phi_{\gamma } \left( {{\mathbf{c}},{\mathbf{C}}} \right), \, \left[ {V_{\alpha } - U_{\alpha } } \right],\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right)). \\ &\quad \quad \quad \quad ({\text{depends on}}\,\,{\mathbf{R}}^{\prime}_{\gamma } \,\,\,\,\,{\text{and}}\,\,\,\,{\mathbf{R}}_{\alpha } ) \\ \end{aligned} $$

(32)

An intuitively useful result follows if one evaluates the Green’s function in an adiabatic, local energy approximation. Under this condition, $G_{\gamma }^{( + )} ({\mathbf{R}}_{\gamma } ,{\mathbf{R}}^{\prime}_{\gamma } )$ reduces to − δ(R′_γ–R_γ)/ < E_γ (R_o) > , where E_γ is the local channel energy averaged over a surface specified by R_o. Then, ${\user2{\mathcal{F}}}$ becomes:

$$ \begin{aligned} & \qquad\qquad \quad \quad \quad \quad \quad \quad \quad \quad \quad ({\text{depends on}}\,{\mathbf{R}}_{\beta } \,\,{\text{and}}\,\,{\mathbf{R}}_{\gamma } ) \\ {\user2{\mathcal{F}}}({\mathbf{R}}_{\beta } ,{\mathbf{R}}_{\alpha } ) & = - 1/ < E_{\gamma } (R_{{\text{o}}} ) > \int {{\text{d}}{\mathbf{R}}_{\gamma } } \left( {\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right),\left[ {V_{\beta } - U_{\beta } } \right],\Phi_{\gamma } \left( {{\mathbf{c}},{\mathbf{C}}} \right)} \right) \\ & \quad \times (\Phi_{\gamma } \left( {{\mathbf{c}},{\mathbf{C}}} \right), \, \left[ {V_{\alpha } - U_{\alpha } } \right],\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right)), \\ & \quad \quad \quad \quad ({\text{depends on}}\,\,{\mathbf{R}}_{\gamma } \,\,\,\,\,{\text{and}}\,\,\,\,{\mathbf{R}}_{\alpha } ) \\ \end{aligned} $$

(33)

which is governed by the “product of two form factors”, one characterizing the first nucleon transfer (α to γ) and the other the second nucleon transfer (γ to β).

For pedagogical purposes, it is useful to consider the no-recoil limit, where the channel coordinates become proportional but with identical directions, i.e., R_α ~ R_β ~ R_γ = R. The effective form factor then reduces to,

$$ \begin{aligned} {\user2{\mathcal{F}}}({\mathbf{R}}) & = - {1}/ < E_{{{\varvec{\upgamma}}}} (R_{{\text{o}}} ) > (\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right),[V_{\beta } - \, U_{\beta } ],\Phi_{\gamma } \left( {{\mathbf{c}},{\mathbf{C}}} \right)) \, \\ & \quad \times \left( {\Phi_{\gamma } \left( {{\mathbf{c}},{\mathbf{C}}} \right),[V_{\alpha } - U_{\alpha } ],\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right)} \right). \\ \end{aligned} $$

(34)

[13].

As an example, let us consider a two-nucleon stripping reaction involving monopole transfer, i.e.,

$$ a[b + \psi \left( {{\mathbf{r}}_{{1}} ,{\mathbf{r}}_{{2}} } \right)_{0} ] + A \to b + B[A + \psi \left( {{\mathbf{R}}_{{1}} ,{\mathbf{R}}_{{2}} } \right)_{0} ]. $$

(35)

The form factor for the simultaneous nucleon transfer process using the prior interaction V (R₁) becomes,

$$ {2}\iint {{\text{d}}{\mathbf{r}}_{{1}} {\text{d}}{\mathbf{r}}_{{2}} }\psi *\left( {{\mathbf{R}}_{{1}} ,{\mathbf{R}}_{{2}} } \right)_{0} V\left( {R_{1} } \right)\psi \left( {{\mathbf{r}}_{{1}} ,{\mathbf{r}}_{{2}} } \right)_{0} . $$

(36)

From Eq. (34), the corresponding effective form factor for the sequential nucleon transfer process involves the prior V (R₁)–post V (r₂), interaction, namely

$$ - {2}/ {<} E_{{\gamma}} (R_{{\text{o}}} ) {>} \iint {{\text{d}}{\mathbf{r}}_{{1}} {\text{d}}{\mathbf{r}}_{{2}} }\psi *\left( {{\mathbf{R}}_{{\mathbf{1}}} ,{\mathbf{R}}_{{\mathbf{2}}} } \right)_{0} V\left( {r_{{2}} } \right)V\left( {R_{1} } \right)\psi \left( {{\mathbf{r}}_{{1}} ,{\mathbf{r}}_{{2}} } \right)_{0} . $$

(37)

This expression can be further simplified by replacing V (r₂) with an average value (V_o), since the nuclear separation (R) is contained in V(R₁), i.e., R₁ = R + r₁. Hence, one obtains

$$ - {2}V_{{\text{o}}} / {<} E_{\gamma } (R_{{\text{o}}} ) {>} \iint {{\text{d}}{\mathbf{r}}_{{1}} {\text{d}}{\mathbf{r}}_{{2}} }\psi *\left( {{\mathbf{R}}_{{1}} ,{\mathbf{R}}_{{2}} } \right)_{0} V\left( {R_{{1}} } \right)\psi \left( {{\mathbf{r}}_{{1}} ,{\mathbf{r}}_{{2}} } \right)_{0} , $$

(38)

which is essentially the same, to within a multiplicative factor, to the form factor for simultaneous nucleon transfer. Thus, if one neglects specific nucleon configurations or matching conditions, the angular distribution for the two-step sequential nucleon transfer process can be expected to be similar to that for the one-step simultaneous nucleon transfer process, especially if the angular momentum transfer is zero. In contrast, the two-step two-nucleon transfer process, involving an intermediate inelastic excitation, typically has an angular distribution characteristically different from that for the one-step two-nucleon transfer process alone, as the effective form factor for that case suggests. It was by this difference in the form factors that permitted fruitful studies of the interplay between nuclear structure, inelastic excitations and nucleon transfer processes, which profoundly influenced interpretations of many nucleon transfer reactions involving collective nuclei.

3.21 Reflections

During the decade of the 70s, the WNSL/BNL collaboration was the most active experimental program studying heavy-ion nucleon transfer reactions. Erb directed a small group of graduate students at Yale that conducted a series of innovative experiments, both at WNSL and BNL. These studies firmly established the CCBA as the most influential theory of light-ion and heavy-ion-induced one- and two-nucleon transfer reactions involving collective nuclei. The group enthusiastically undertook challenging experiments, and found creative ways to perform the large-scale computer calculations required to analyze experimental data. The amazing productivity of these individuals helped sustain WNSL’s landmark tandem Van de Graaff particle accelerator during the 70s that formed the heart of the laboratory, and, in doing so, helped ignite the new field of direct heavy-ion reactions.

Each member of the team at WNSL, as with many young nuclear physics researchers across the USA, felt a palpable presence associated with working in a dysfunctional society during the late 1960s and the 70s. Moreover, these individuals came to the harsh realization that job opportunities in academic physics were scarce and many needed to rethink their careers. The massive economic drain imposed by the Vietnam War contributed to skyrocketing Federal deficits and deteriorating economic conditions at home. These events took a severe toll on the job market for physicists, perhaps the worst ever. Consequently, the highly productive WNSL nuclear reaction group had to disband. Fortunately, most of these dedicated individuals went on to have distinguished and rewarding careers in applied research, computer technology, defense analysis, medicine and government service.

Ascuitto went on to receive a M.D. degree from Yale University Medical School, and ultimately specialized in Pediatric Cardiology. He became the Suzanne S. Schaefer Professor of Pediatric Cardiology and held the Edward G. Schlieder-LA Regents Educational Foundational Chair in Pediatric Cardiology, while serving as Director of Pediatric Cardiology and was Adjunct Professorship in Theoretical Physics, at Tulane University, New Orleans, Louisiana. He became an international leader in the field of cardiac metabolism, and a pioneer in the use of computational fluid dynamics to assess blood flow behavior associated with surgical repairs of congenital heart disease. Vaagen advanced to become Professor of Theoretical Subatomic Physics at the University of Bergen, Bergen, Norway. His research involved delineating the structure of light nuclei, determining properties of halo nuclei and identifying quantal features of exotic nuclei near nuclear drip lines. He became co-founder, and served as Coordinator, of the Russian-Nordic-British Theory Collaboration. Glendenning continued to make important contributions in theoretical nuclear physics. After the 1970s, he concentrated on astrophysics, with a focus on quark and hadronic matter in neutron stars. He authored several popular science books, which became outstanding references for researchers in nuclear structure and astrophysics. Glendenning received the Alexander von Humboldt award for Senior U.S. Scientists in 1994, for outstanding research in nuclear physics and astrophysics. Erb headed up the experimental heavy-ion reaction group at WNSL. He played an essential role in implementing experiments that ultimately confirmed the CCBA theory of nucleon transfer reactions involving heavy-ion projectiles. He ultimately became the Director of the Office of Polar Programs at NSF and Director of the U.S. Antarctic Program. Erb received the President Senior Executive Service Meritorious award in 1998 and 2003 and the President’s Distinguished Service award in 2006.

Tamura remained a leader in the field of nuclear reaction physics. He received the Argonne Universities Association Distinguished Scientist Award in 1972 and the Alexander von Humboldt award for Senior U.S. Scientists in 1981. Udagawa enjoyed a prolific career in theoretical nuclear physics. In 2009, the Emperor of Japan bestowed on Udagawa the Order of the Sacred Treasure for his contributions to fostering USA and Japan relations. Tamura and Udagawa enjoyed a highly productive collaboration. They, along with their colleagues at the Center for Nuclear Studies at the University of Texas in Austin, went on to make important contributions in nuclear reaction physics. Many of their graduate students and postdoctoral fellows ultimately became highly respected researchers in the field of nuclear reactions.

Lastly, this manuscript is dedicated to the memory of D. A. Bromley, Director of WNSL (1963–1989), at Yale University. Bromley foresaw in the late 1960s the importance of coupled channels models of nucleon transfer reactions, and realized the critical role these theories might play in supporting the new field of heavy-ion reaction physics in the 70s. He graciously provided research support for young physicists from around the world, and helped the nuclear reaction group at Yale to implement the ground-breaking experiments required to verify the accuracy of the CCBA and CRC theories. After a brilliant career in nuclear physics, Bromley became the Director and Assistant to the President of the United States for Science and Technology at the Executive Office of the President (1989–1993). He was awarded the National Medal of Science in 1988 by President Ronald W. Reagan for seminal work on nuclear molecules and in the development of tandem accelerators and semiconductor detectors for charged particles. Bromley fathered the field of precision heavy-ion physics.

In conclusion, despite the extensive effort required to establish the CCBA and CRC theories of nucleon transfer reactions, during the volatile late 1960s and 70s in America, and the catalyst these computational models provided on the evolving field of heavy-ion-induced direct nuclear reactions, a generation of academic nuclear physicists was lost largely as a consequence of the Vietnam War. Regrettably, the Vietnam War left many young scientists in America with distrust and cynicism about their country’s leaders. To this day, many of those who opposed and/or participated in the Vietnam conflict still question the US’ rational for entering what proved to be an immoral war, which ultimately profoundly impacted academic physics.

Appendices

Appendix 1: The original CCBA formulation for two partitions of the nucleons

During a particularly volatile period, at the height of Vietnam War protests in Berkeley, Ascuitto retreated to Angel Island in San Francisco Bay to escape the chaos. His plan was to reevaluate the problem of incorporating inelastic scattering into nucleon transfer reactions. He considered a simplified reaction, A (a, b) B, involving two partitions of the nucleons, i.e., (a + A) and (b + B). He assumed no inelastic excitations and only a single nucleon transfer between an initial channel (α), i.e., containing an incoming ion (a) and the target nucleus (A) in its ground state, and a final channel (β), i.e., containing the outgoing ion (b) and the residual nucleus (B) in its final state.

The Schrodinger equation for the system is given by:

$$ \left( {H \, - \, E} \right)\Psi = \, 0, $$

(39)

where Ψ is the state function for the system, H the Hamiltonian and E the energy. The Hamiltonian may be written as follows:

$$ H = {\user2{\mathcal{H}}} + \, T \, + \, U \, + \, \left( {V \, - \, U} \right), $$

(40)

where ${\user2{\mathcal{H}}}$ is the nuclear (intrinsic) Hamiltonian and T the kinetic energy operator describing the relative motion between (a) and (A) or (b) and (B). V an effective interaction between the reaction partners, i.e., let V_α be between (a) and (A) and V_β between (b) and (B). An optical model potential (U), which depends only on the relative coordinate, was added and subtracted in Eq. (40). Equations (39) and (40) can then be rearranged as follows:

$$ ({\user2{\mathcal{H}}} + T + U - E)\Psi = - \left( {V - U} \right)\Psi . $$

(41)

For the incoming channel (α) of the (a + A) partition, the intrinsic Hamiltonian is defined as:

$$ {\user2{\mathcal{H}}}_{\alpha } = h\left( a \right) + H_{\alpha} \left( A \right), $$

(42)

where the Schrodinger equations for the nuclear wavefunctions satisfy [h(a) − ε_a] φ(a) = 0 and [H_α(A) − ε_α] φ_α(A) = 0. The channel state function, Φ_α(a, A), was defined simply in terms of the nuclear wavefunctions for (a) and (A) as follows:

$$ \Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}) = [\varphi \left( {\mathbf{a}} \right)\varphi_{\alpha } \left( {\mathbf{A}} \right)], $$

(43)

where

$$ ({\user2{\mathcal{H}}}_{\alpha } - E_{\alpha } )\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}) = 0,\quad {\text{ with channel energy}}\;E_{\alpha } = E - (\varepsilon_{{\text{a}}} + \varepsilon_{\alpha } ). $$

(44)

Multiplying Eq. (41) from the left with Φ_α(a, A)* and integrating over intrinsic coordinates yields:

$$ (T_{\alpha } + U_{\alpha } - E_{\alpha } )(\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}),\Psi ) = - (\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}),[V_{\alpha } - U_{\alpha } ],\Psi ). $$

(45)

where $U_{\alpha } = (\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}),V_{\alpha } ,\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}))$ is taken as an optical model potential in channel α.

For the outgoing channel (β), of the (b + B) partition, one similarly obtains:

$$ (T_{\beta } + U_{\beta } - E_{\beta } )(\Phi_{\beta } ({\mathbf{b}},{\mathbf{B}}),\Psi ) = - (\Phi_{\beta } ({\mathbf{b}},{\mathbf{B}}),[V_{\beta } - U_{\beta } ],\Psi ). $$

(46)

Equations (45) and (46) describe the proposed reaction. To obtain a workable solution, however, requires knowing the state function Ψ for the system which is not attainable. Consequently, Ψ must be approximated in some fashion. Since one is interested in a reaction involving only two partitions, i.e., (a + A) and (b + B), it is logical to represent Ψ in term of nuclear wavefunctions corresponding to the initial (incoming) channel α, and the final (outgoing) channel β.

The left side of Eq. (45) describes the relative motion in the (α) channel. Thus, in lowest order, Ψ on the left side of Eq. (45) was approximated by:

$$ \Psi \approx \Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}})\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ), $$

(47)

where $\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } )$ is the distorted wavefunction describing the relative motion between (a) and (A) in channel (α). The superscript α on χ denotes the incoming channel (α) and the (+) outgoing scattered waves. The right side of Eq. (45) contains nucleon transfer from the (β) back into the (α) channel. Hence, in this matrix element, Ψ on the right side of Eq. (45) was approximated by:

$$ \Psi \approx \Phi_{\beta } ({\mathbf{b}},{\mathbf{B}})\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ), $$

(48)

where $\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } )$ is the distorted wavefunction describing the relative motion between (b) and (B). Equation (45) then becomes:

$$ (T_{\alpha } + U_{\alpha } - E_{\alpha } )\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) = - (\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}),[V_{\alpha } - U_{\alpha } ],\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right))\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ). $$

(49)

Similarly, the left side of Eq. (46) describes the relative motion in the (β) channel. Remaining in lowest order, Ψ on the left side of Eq. (46) was approximated by:

$$ \Psi \approx \Phi_{\beta } ({\mathbf{b}},{\mathbf{B}})\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ), $$

(50)

where $\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } )$ is the distorted wavefunction describing the relative motion between (b) and (B) in channel (β). The right side of Eq. (46) contains nucleon transfer from (α) into the (β) channel. Hence, in this matrix element, Ψ on the right side of Eq. (46) was approximated by:

$$ \Psi \approx \Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}})\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ), $$

(51)

where $\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } )$ is the distorted wavefunction describing the relative motion between (a) and (A). Equation (46) then becomes:

$$ (T_{\beta } + U_{\beta } - E_{\beta } )\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) = - (\Phi_{\beta } ({\mathbf{b}},{\mathbf{B}}),[V_{\beta } - U_{\beta } ],\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right))\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ). $$

(52)

Therefore, the coupled equations describing the reaction in lowest order become:

$$ (T_{\alpha } + U_{\alpha } - E_{\alpha } )\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) = - (\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}),[V_{\alpha } - U_{\alpha } ],\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right))\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ). $$

(53a)

$$ (T_{\beta } + U_{\beta } - E_{\beta } )\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) = - (\Phi_{\beta } ({\mathbf{b}},{\mathbf{B}}),[V_{\beta } - U_{\beta } ],\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right))\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ). $$

(53b)

In the original formulation, nucleon transfer from the (β) back into the (α) channel in Eq. (53a) was neglected. This followed since nucleon transfer from (α) to (β) is usually weak. Consequently, the second-order transition from (β) back into (α) would be even weaker. Therefore, the coupled channels equations reduced to the simplified form:

$$ (T_{\alpha } + U_{\alpha } - E_{\alpha } )\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) = 0. $$

(54a)

$$ (T_{\beta } + U_{\beta } - E_{\beta } )\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) = - \rho_{\beta \alpha } ({\mathbf{R}}_{\beta } ), $$

(54b)

where ρ, the so-called source term, was taken as:

$$ \rho_{\beta \alpha } ({\mathbf{R}}_{\beta } ) = < (\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right),[V_{\beta } - U_{\beta } ],\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}))\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) > . $$

(54c)

The integrations in the source term of Eq. (54c) are carried out over all coordinates except R_β. Here [V_β–U_β] is the interaction that gives rise to nucleon transfer between (α) and (β). The matrix element $(\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right),[V_{\beta } - U_{\beta } ],\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}))$, when integrated over intrinsic coordinates, remains a function of the two channel coordinates R_α and R_β. The coupled channels equations simplify greatly in the no-recoil approximation, since R_α becomes proportional to R_β. The parameters of the optical model potential (U_α) in Eq. (54a) are usually chosen to describe the elastic scattering data between (a) and (A). The merits and possible faults of this assumption are discussed in the Story section.

The boundary conditions for these equations are that the incoming channel (α) has incoming and outgoing spherical waves, consistent with a plane wave representing the incident beam, and a scattered wave. In contrast, the outgoing channel (β) has only outgoing spherical waves. Specifically:

$$ \begin{aligned} \chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) & \to {\text{exp }}(i{\mathbf{R}}_{\alpha } \cdot {\mathbf{k}}_{\alpha } ) + {\text{exp }}(iR_{\alpha } k_{\alpha } )/R_{\alpha } {\user2{\mathcal{F}}}_{\alpha \alpha } (\Theta ), \\ R_{\alpha } & \to \infty \\ \end{aligned} $$

(55a)

$$ \begin{aligned} \chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) & \to {\text{exp }}(iR_{\beta } k_{\beta } )/R_{\beta } {\user2{\mathcal{F}}}_{\beta \alpha } (\Theta ) \\ R_{\beta } & \to \infty \\ \end{aligned} $$

(55b)

where the ${\user2{\mathcal{F}}}_{{\text{s}}}$ are the reaction amplitudes. The differential cross section for the (α to β) reaction is directly related to the magnitude of the ${\user2{\mathcal{F}}}_{{\text{s}}}$ squared.

Equation (54b) can be solved using the Green’s function method. The distorted wave Green's function (G) satisfies the equation:

$$ (T_{\beta } + \, U_{\beta } - \, E_{\beta } )G_{\beta }^{\left( + \right)} ({\mathbf{R}}_{\beta } ,{\mathbf{R}}^{\prime}_{\beta } ) \, = \delta ({\mathbf{R}}_{\beta } - {\mathbf{R}}^{\prime}_{\beta } ). $$

(56)

The solution to the inhomogeneous Eq. (54b) is then given by:

$$ \chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) = - \int {{\text{d}}{\mathbf{R}}^{\prime}_{\beta } } G_{\beta }^{\left( + \right)} ({\mathbf{R}}_{\beta } ,{\mathbf{R}}^{\prime}_{\beta } ) < (\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right), \, [V_{\beta } - U_{\beta } ],\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right))\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) > . $$

(57)

The Green’s function does not possess a closed form because of the optical model potential U.

However, the two independent solutions of the homogeneous portion of Eq. (54b), needed to construct G_β⁽⁺⁾, can be numerically solved on a computer. This is best accomplished by using partial wave (l) expansions of the wave functions (χ) in terms of spherical harmonics $Y_{l}^{m } (\hat{{{\mathbf{R}}}})$. The first independent radial solution F_l is regular at the origin and has outgoing spherical waves at infinity. The distorted wavefunction $\chi_{\beta }^{\alpha ( + )}$ satisfying the homogeneous portion of Eq. (54b), in its partial wave expansion, is given by:

$$ \begin{gathered} \chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) \, = {4}\pi \sum\limits_{{\varvec{l}}} {i^{l} F_{l} } (R_{\beta } ,k_{\beta } )/(R_{\beta } k_{\beta } )\sum\limits_{{\varvec{m}}} {[Y_{l}^{m } } (\hat{{\mathbf{R}}}_{\beta } )Y_{l}^{m*} (\hat{{\mathbf{k}}}_{\beta})]. \hfill \\ \hfill \\ \end{gathered} $$

(58)

The quantity (k_β) is the usual wave number. If U is zero, and in the absence of the Coulomb potential, χ reduces to a plane wave. When the Coulomb potential is present, an additional phase factor, exp (iσ_l), is required in Eq. (58). The second independent radial solution H_l ⁽⁺⁾ is irregular at the origin and has outgoing spherical waves at infinity.

The standard distorted wave Green's function in spherical coordinates is then given by:

$$ \begin{aligned} G_{\beta } ^{\left( + \right)} ({\mathbf{R}}_{\beta } ,{\mathbf{R}}^{\prime}_{\beta } ) & = ({2}m_{\beta } /\hbar^{{\mathbf{2}}} )({1}/R_{\beta } R^{\prime}_{\beta } k_{\beta } )\sum\limits_{{\varvec{l}}} {F_{{\varvec{l}}} } (R_{\beta } < )H_{{\varvec{l}}} ^{\left( + \right)} (R_{\beta } > ) \\ & \quad \times \sum\limits_{{\varvec{m}}} {[Y_{l}^{m } ({\hat{\mathbf{R}}}_{\beta } )Y_{l} ^{m*} ({\hat{\mathbf{R}}}^{\prime}_{\beta } )]} \\ \end{aligned} $$

(59)

where Yl^m is a spherical harmonic, and R_β < is the lesser of (R_β, R′_β). For large R_β, H_l⁽⁺⁾ (R_β) approaches the outgoing spherical wave exp i(R_β k_β − lπ/2) at infinity. Hence,

$$ G_{\beta }^{( + )} ({\mathbf{R}}_{\beta } ,{\mathbf{R}}^{\prime}_{\beta } ) \to {\text{exp }}(iR_{\beta } k_{\beta } )/R_{\beta } \{ (m_{\beta } /{2}\pi \hbar^{{2}} )\chi_{\beta }^{\alpha ( - )*} ({\mathbf{R}}^{\prime}_{\beta } )\} $$

(60)

where,

$$ \chi_{\beta }^{\alpha ( - )*} ({\mathbf{R}}^{\prime}_{\beta } ) = {4}\pi \sum\limits_{{\varvec{l}}} {i^{ - l} } F_{l} (R^{\prime}_{\beta } , \, k_{\beta } )/(R^{\prime}_{\beta } k_{\beta } ) \sum\limits_{{\varvec{m}}} {Y_{l} ^{m*} (\hat{{{\mathbf{R}}^{\prime} }}_{\beta })Y_{l}^{m} \left( {\hat{{{\mathbf{k}}^{\prime} }}}_{\beta } \right)} . $$

(61)

Here k′_β, has the magnitude of k_β, but is in the direction of R_β. The distorted wavefunction χ⁽⁻⁾ has incoming spherical waves; whereas, χ⁽⁺⁾ and $\chi^{( - )*}$ have outgoing spherical waves at infinity. For large R_β, in Eq. (57),

$$ \begin{aligned} \chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) & \to {\text{exp }}(iR_{\beta } k_{\beta } ) /{\text{R}}_{\beta } \{ - {\mathcal{K}} \\ & \quad \times < \chi_{\beta }^{\alpha ( - )} ({\mathbf{R}}_{\beta } )(\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right),[V_{\beta } - U_{\beta } ],\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right))\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) > \} . \\ \end{aligned} $$

(62)

The quantity in brackets {…} in Eq. (62) is the reaction amplitude ${\user2{\mathcal{F}}}_{\beta \alpha }$. It is, to within the multiplicative factor, ${\user2{\mathcal{K}}} = (m_{\beta } /2\pi \hbar^{2} )$, the DWBA transition amplitude for the nucleon transfer reaction. As a computational check, Ascuitto found Eqs. (54a), (54b) and (54c) to yield precisely the same magnitude and differential cross section as the traditional DWBA, as they should.

The Eqs. (54a) and (54b) served as a template. It then followed directly that for channels (α, α′, α″…) of the (a + A) partition and channels (β, β′, β″…) of the (b + B) partition, the coupled channels equations describing inelastic scattering in conjunction with nucleon transfer become:

$$ (T_{\alpha ^{\prime}} + U_{\alpha ^{\prime}} - E_{\alpha ^{\prime}} )\chi_{\alpha ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) + \sum \limits_{\alpha ^{\prime\prime}} U_{\alpha ^{\prime}\alpha ^{\prime\prime}} \chi_{\alpha ^{\prime\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) = 0 $$

(63a)

$$ (T_{\beta ^{\prime}} + U_{\beta ^{\prime}} - E_{\beta ^{\prime}} )\chi_{\beta ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) + \sum \limits_{\beta ^{\prime\prime}} U_{\beta ^{\prime}\beta ^{\prime\prime}} \chi_{\beta ^{\prime\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) = - \rho_{\beta ^{\prime}} ({\mathbf{R}}_{\beta } ) $$

(63b)

with the source terms given by,

$$ \rho_{\beta ^{\prime}} ({\mathbf{R}}_{\beta } ) = \sum \limits_{\alpha ^{\prime}} < (\Phi_{\beta ^{\prime}} \left( {{\mathbf{b}},{\mathbf{B}}} \right),[V_{\beta ^{\prime}} - U_{\beta ^{\prime}} ],\Phi_{\alpha ^{\prime}} \left( {{\mathbf{a}},{\mathbf{A}}} \right))\chi_{\alpha ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) > . $$

(63c)

The optical model potential (U) now depends on nuclear coordinates as well as the relative coordinate and hence the non-diagonal matrix elements of U, e.g., U_α′α″ and U_β′β″, describe inelastic transitions. The boundary conditions on the distorted wavefunctions are given by:

$$ \begin{aligned} \chi_{\alpha ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) & \to \delta_{\alpha ^{\prime}\alpha } {\text{exp }}(i\mathbf{k}_{\alpha } \cdot {\mathbf{R}}_{\alpha } ) + {\text{exp }}(ik_{\alpha ^{\prime}} R_{\alpha } )/R_{\alpha } {\mathcal{F}}_{\alpha ^{\prime}\alpha } (\Theta ), \\ R_{\alpha } & \to \infty \\ \end{aligned} $$

(64a)

$$ \begin{aligned} \chi_{\beta ^{\prime}}^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) & \to {\text{exp }}(ik_{\beta ^{\prime}} R_{\beta } )/R_{\beta } {\mathcal{F}}_{\beta ^{\prime}\alpha } (\Theta ), \\ R_{\beta } & \to \infty \\ \end{aligned} $$

(64b)

Again, the ${\user2{\mathcal{F}}}_{{\beta ^{\prime}\alpha {\text{s}}}}$ are the corresponding reaction amplitudes.

In practical calculations, the CCBA (and CRC) equations can be simplified by employing partial wave expansions of the relative motion wavefunctions. This is accomplished by introducing channel state functions corresponding to total angular momentum (I), namely Φ^I, as follows:

$$ \Phi_{{{\text{C}}_{{\text{a}}} }}^{I} (\hat{{\mathbf{R}}}_{{\text{a}}} ,{\mathbf{a}},{\mathbf{A}}) = [[{\text{Y}}_{la} (\hat{{\mathbf{R}}}_{{\text{a}}} ),\varphi_{{\alpha {\text{a}}}} \left( {\mathbf{a}} \right)_{{{\text{ja}}}} ]_{{{\text{Ja}},}} \varphi_{{\alpha {\text{A}}}} \left( {\mathbf{A}} \right)_{{{\text{JA}}}} ]^{I} , $$

(65)

where I = Ja + J_A = la + ja + J_A and C_a represents the quantum numbers (l_α, α_a j_a, α_AJ_A), and the brackets [..,..] indicate angular momentum coupling. The state function $\Psi^{I( + )}$ corresponding to the equation for the (a + A) partition, namely

$$ (T_{{{\text{a}},{\text{A}}}} + V_{{{\text{a}},{\text{A}}}} + h\left( a \right) + H\left( A \right) - E)\Psi = 0, $$

(66)

is expanded as follows,

$$ \Psi_{{{\text{C}}_{{\text{a}}} }}^{I( + )} = {1}/R_{{\text{a}}} \sum \limits_{{\text{C}}^{\prime}_{{\text{a}}} } {\mathcal{U}}_{{{\text{C}^{\prime}}_{{\text{a}}} }}^{I} (R_{{\text{a}}} )\Phi_{{{\text{C}^{\prime}}_{{\text{a}}} }}^{I} (\hat{\mathbf{R}}_{{\text{a}}} ,{\mathbf{a}},{\mathbf{A}}), $$

(67)

which has an incident wave in channel C_a. In the usual fashion, the homogeneous coupled channels equations assume the form:

$$ [T_{{{\text{C}}_{{\text{a}}} }} + V_{{{\text{C}}_{{\text{a}}} ,{\text{C}}_{{\text{a}}} }}^{I} (R_{{\text{a}}} ) - E_{{{\text{C}}_{{\text{a}}} }} ]{\mathcal{U}}_{{{\text{C}}_{{\text{a}}} }}^{I} ({R}_{{\text{a}}} ) + \sum \limits_{{\text{C}}^{\prime}_{{\text{a}}} } V_{{{\text{C}}_{{\text{a}}} ,{\text{C}^{\prime}}_{{\text{a}}} }}^{I} (R_{{\text{a}}} ){\mathcal{U}}_{{{\text{C}^{\prime}}_{{\text{a}}} }}^{I} (R_{{\text{a}}} ) = 0, $$

(68)

with $E_{\text{C}_{\text{a}}}$ = E − Eα_a − Eα_A, subject to the physical boundary condition,

$$ {\mathcal{U}}_{{{\text{C}^{\prime}}_{{\text{a}}} }}^{I} (R_{{\text{a}}} ) \to \delta_{{{\text{C}^{\prime}}_{{\text{a}}} ,{\text{C}}_{{\text{a}}} }} I_{la} (R_{{\text{a}}} ) - (v_{{\text{a}}} /v^{\prime}_{{\text{a}}} )^{{{1}/{2}}} S_{{{\text{C}^{\prime}}_{{\text{a}}} ,{\text{C}}_{{\text{a}}} }}^{I} O_{{l^{\prime}_{{\text{a}}} }} (R_{{\text{a}}} ). $$

(69)

Likewise, the inhomogeneous coupled channels equations for the (b + B) partition become:

$$ [T_{{{\text{C}}_{{\text{b}}} }} + V_{{{\text{C}}_{{\text{b}}} ,{\text{C}}_{{\text{b}}} }}^{I} (R_{{\text{b}}} ) - E_{{{\text{C}}_{{\text{b}}} }} ]{\mathcal{U}}_{{{\text{C}}_{b} }}^{I} ({R}_{{\text{b}}} ) + \sum \limits_{{\text{C}}^{\prime}_{{\text{b}}} } V_{{{\text{C}}_{{\text{b}}} ,{\text{C}^{\prime}}_{{\text{b}}} }}^{I} (R_{{\text{b}}} ){\mathcal{U}}_{{{\text{C}^{\prime}}_{{\text{b}}} }}^{I} (R_{{\text{b}}} ) = - \rho_{{{\text{C}}_{{\text{b}}} }}^{I} (R_{{\text{b}}} ), $$

(70)

where the source term ρ is given by:

$$ \rho_{{{\text{C}}_{{\text{b}}} }}^{I} (R_{{\text{b}}} ) = R_{{\text{b}}} \sum \limits_{{\text{C}}^{\prime}_{{\text{a}}} } < \Phi_{{{\text{C}}_{{\text{b}}} }}^{I} (\hat{{{\mathbf{R}}}}_{{\text{b}}} ,{\mathbf{b}},{\mathbf{B}}),{\mathcal{V}},\Phi_{{{\text{C}}^{\prime}_{{\text{a}}} }}^{I} (\hat{{{\mathbf{R}}}}_{{\text{a}}} ,{\mathbf{a}},{\mathbf{A}}){\mathcal{U}}_{{{\text{C}}^{\prime}_{{\text{a}}} }}^{I} (R_{{\text{a}}} )/R_{{\text{a}}} > , $$

(71)

where ${\user2{\mathcal{V}}}$ is the transfer interaction. The physical boundary condition is that the channels C_b have only outgoing waves:

$$ {\mathcal{U}}_{{{\text{C}}_{{\text{b}}} }}^{{\text{I}}} (R_{{\text{b}}} ) \to - (v_{{\text{a}}} /v_{{\text{b}}} )^{1/2} S_{{{\text{C}}_{{\text{b}}} ,{\text{C}}_{{\text{a}}} }}^{{\text{I}}} O_{l_{\text{b}}} (R_{{\text{b}}} ). $$

(72)

Here, I represent incoming and O outgoing spherical waves at infinity, and S are the values of the S-matrix elements, from which the cross sections can be calculated.

Appendix 2: A CRC formalism for two partitions of the nucleons (strong coupling in nucleon transfer)

Several investigators in the late 60s considered strong coupling in nucleon transfer reactions under limited conditions [53, 54, 60]. It is useful to consider a simplified nucleon transfer reaction of the type A (a, b) B, which exhibits strong coupling between two channels, i.e., the incoming channel α of the (a + A) partition and the outgoing channel β of the (b + B) partition. The Schrodinger equation is given by:

$$ (H - E)\Psi = 0, $$

(73)

where Ψ is the state function for the system, H is the Hamiltonian and E the energy. For this example, Ψ was usually represented as follows:

$$ \Psi = \Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}})\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) + \Phi_{\beta } ({\mathbf{b}},{\mathbf{B}})\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ). $$

(74)

Clearly, the channel state functions, Φ, are not orthogonal, as they are eigenfunctions of different Hamiltonians. Nevertheless, incorporating Eqs. (73) and (74) leads to:

$$ \left( {H - E} \right)\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}})\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) + \left( {H - E} \right)\Phi_{\beta } ({\mathbf{b}},{\mathbf{B}})\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) = \, 0. $$

(75)

The Hamiltonian (H) may be partitioned in the usual fashion as follows:

$$ H = {\user2{\mathcal{H}}}_{\alpha } + T_{\alpha } + V_{\alpha } = {\user2{\mathcal{H}}}_{\beta } + T_{\beta } + V_{\beta } , $$

(76)

where ${\user2{\mathcal{H}}}$ is the nuclear (intrinsic) Hamiltonian and T is the kinetic energy operator describing the relative motion between (a) and (A) in channel α or between (b) and (B) in channel β. V_α is an effective interaction between (a) and (A) and V_β between (b) and (B). Multiplying Eq. (75) from the left with $\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right)^*$ and integrating over intrinsic coordinates yields:

$$ (T_{\alpha } + U_{\alpha } - E_{\alpha } )\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) = - (\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right),[H - E],\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right))\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) , $$

(77)

where $U_{\alpha } = (\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right),V_{\alpha } ,\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right))$ is taken as an optical model potential in channel (α). On the right side of Eq. (77), we can replace [H–E] with $[T_{\beta } + U_{\beta } - E_{\beta } ] + [V_{\beta } - U_{\beta } ]$, where $U_{\beta } = (\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right),V_{\beta } ,\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right))$ is an optical model potential in channel (β). Equation (77) then becomes:

$$ \begin{aligned} (T_{\alpha } + U_{\alpha } - E_{\alpha } )\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) & = - \{ (\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right),[V_{\beta } - \, U_{\beta } ],\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right))\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) \\ & \quad + (\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right),\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right))[T_{\beta } + U_{\beta } - E_{\beta } ]\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } )\} . \\ \end{aligned} $$

(78)

Multiplying Eq. (75) from the left with $\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right)^*$ and integrating over intrinsic coordinates, yields the complimentary equation:

$$ (T_{\beta } + U_{\beta } - E_{\beta } )\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) = - (\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right),[H - E],\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right))\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) . $$

(79)

On the right side of Eq. (79), we can replace (H–E) with $[T_{\alpha } + U_{\alpha } - E_{\alpha } ] + [V_{\alpha } - U_{\alpha } ]$. Equation (79) then becomes:

$$ \begin{aligned} (T_{\beta } + U_{\beta } - E_{\beta } )\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) & = - \{ (\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right),[V_{\alpha } - \, U_{\alpha } ],\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right))\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) \\ & \quad + (\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right),\Phi_{\alpha } \left( {{\mathbf{a}}, \, {\mathbf{A}}} \right))[T_{\alpha } + U_{\alpha } - E_{\alpha } ]\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } )\} . \\ \end{aligned} $$

(80)

The first term on the right side of Eqs. (78) and (80) contains a standard nucleon transfer matrix element connecting the (β) channel to the (α) channel and the (α) channel to the (β) channel, respectively. The second term on the right side of Eqs. (78) and (80) arises due to non-orthogonality of the channel state functions corresponding to the different partitions. The terms $\left( {\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right),\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right) } \right)$ and $\left( {\Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right),\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right) } \right)$ are similar in form to the usual nuclear state function overlaps required to calculate nucleon transfer form factors. There is also a dynamic component to the non-orthogonality terms, namely $[T_{\beta } + U_{\beta } - E_{\beta } ]\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } )$ in Eq. (78) and $[T_{\alpha } + U_{\alpha } - E_{\alpha } ]\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } )$ in Eq. (80). Note, if the nucleon transfer transitions are unidirectional, i.e., elastic scattering dominates, the dynamic portion of the non-orthogonality terms will be negligible. In the 70s, the non-orthogonal terms were mostly neglected, and it was never really established how they might contribute to an understanding of the interplay between nuclear structure and reaction dynamics, see also [15, 24, 43].

Appendix 3: A CRC formalism for three partitions of the nucleons (the second-order DWBA)

The group at LBL and NBI originally, and others by the mid-1970s, introduced CRC models involving nucleon transfer reactions. For a reaction of the type, A (a, c) C followed by C (c, b) B, the state function for the system, Ψ, was expanded in terms of channel state functions of the three partitions, namely:

$$ \Psi = \Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right)\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) + \Phi_{\gamma } \left( {{\mathbf{c}},{\mathbf{C}}} \right)\chi_{\gamma }^{\alpha ( + )} ({\mathbf{R}}_{\gamma } ) + \Phi_{\beta } \left( {{\mathbf{b}},{\mathbf{B}}} \right)\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ), $$

(81)

where α represents the incoming channel in the (a + A) partition, γ is the intermediate channel in the (c + C) partition, and β is the outgoing channel in the (b + B) partition. If the reaction involves sequential transfer of two neutrons, n₁ and n₂, Φ_γ (c, C) must maintain anti-symmetry between n₁ and n₂, i.e., there is no definite order to the transfer of the neutrons. Using our standard approach, one obtains:

$$ \begin{aligned} & \left( {H - E} \right)\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}})\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) + \left( {H - E} \right)\Phi_{\gamma } ({\mathbf{c}},{\mathbf{C}})\chi_{\gamma }^{\alpha ( + )} ({\mathbf{R}}_{\gamma } ) \\ & \quad + \left( {H - E} \right)\Phi_{\beta } ({\mathbf{b}},{\mathbf{B}})\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } ) = \, 0, \\ \end{aligned} $$

(82)

where H is the Hamiltonian and E the energy of the system.

The Hamiltonian (H) may be partitioned as usual:

$$ H = {\mathcal{H}}_{\alpha } + T_{\alpha } + V_{\alpha } = {\mathcal{H}}_{\gamma } + T_{\gamma } + V_{\gamma } = {\mathcal{H}}_{\beta } + T_{\beta } + V_{\beta } , $$

(83)

where ${\user2{\mathcal{H}}}$ is the nuclear (intrinsic) Hamiltonian and T is the kinetic energy operator describing the relative motion between (a) and (A) in channel α, between (c) and (C) in channel γ and between (b) and (B) in channel β. V_α is an effective interaction between (a) and (A), V_γ between (c) and (C) and V_β between (b) and (B). Multiplying Eq. (82) from the left with Φ_α(a, A)^*, and integrating over intrinsic coordinates, yields:

$$ \begin{aligned} (T_{\alpha } + \, U_{\alpha } - E_{\alpha } )\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) & = - \{ (\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}),\left( {H - E} \right),\Phi_{\gamma } \left( {{\mathbf{c}},{\mathbf{C}}} \right))\chi_{\gamma }^{\alpha ( + )} ({\mathbf{R}}_{\gamma } ) \\ & \quad + (\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}),\left( {H - \, E} \right),\Phi_{\beta } ({\mathbf{b}},{\mathbf{B}}))\chi_{\beta }^{\alpha ( + )} ({\mathbf{R}}_{\beta } )\} , \\ \end{aligned} $$

(84)

where $U_{\alpha } = (\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}),V_{\alpha } ,\Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}))$ is taken as an optical model potential in channel α.

Likewise, there are equations similar to (84) for (γ) in terms of (α) and (β), and for (β) in terms of (α) and (γ).

When the right side of these equations is small and/or nucleon transfer transitions are considered unidirectional, the system of equations can be formally solved by successive approximations.

In the zeroth-order approximation, one obtains:

$$ (T_{\alpha } + \, U_{\alpha } - E_{\alpha } )\chi_{0\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) = 0, $$

(85)

where $\chi_{0\gamma }^{\alpha ( + )}$ and $\chi_{0\beta }^{\alpha ( + )}$ are zero, since only channel (α) contains the incident beam. In the first-order approximation, one obtains the transition amplitude for the one-step (direct) nucleon transfer process, (α) to (β), which is essentially the conventional DWBA transition amplitude,

$$ T_{\beta \alpha } = - < \chi_{\beta }^{\alpha ( - )} ({\mathbf{R}}_{\beta } )(\Phi_{\beta } ({\mathbf{b}},{\mathbf{B}}), \, \left( {H - E} \right),\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right))\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) > . $$

(86)

When H operates to the right, (H–E) becomes [V_α–U_α]. When H operates to the left, (H–E) becomes [V_β–U_β]. If everything is done properly, the two forms of the transition amplitude should yield the same result.

In the second-order approximation, one obtains a transition amplitude which contains the two-step (successive) nucleon transfer process, (α) to (γ) to (β). It is referred to as the second-order DWBA transition amplitude and is given by:

$$ \begin{aligned} T_{\beta \gamma \alpha } & = < \chi_{\beta }^{\alpha ( - )} ({\mathbf{R}}_{\beta } )(\Phi_{\beta } ({\mathbf{b}},{\mathbf{B}}), \, \left( {H - E} \right),\Phi_{\gamma } \left( {{\mathbf{c}},{\mathbf{C}}} \right))G_{\gamma }^{( + )} \\ & \quad \times (\Phi_{\gamma } \left( {{\mathbf{c}},{\mathbf{C}}} \right), \, \left( {H - E} \right),\Phi_{\alpha } \left( {{\mathbf{a}},{\mathbf{A}}} \right))\chi_{\alpha }^{\alpha ( + )} ({\mathbf{R}}_{\alpha } ) > . \\ \end{aligned} $$

(87)

When, for the (α) to (γ) transition in Eq. (87), H operates to the right, (H–E) becomes [V_α–U_α]. When, for the (γ) to (β) transition in Eq. (87), H operates to the left, (H–E) becomes [V_β–U_β]. This yields the so-called prior (α)–post (β) forms of the nucleon transfer interactions in the transition amplitude, which eliminates the non-orthogonality terms. Here G_γ⁽⁺⁾ is the Green’s function operator in channel (γ). Its representation in coordinate space $< {\mathbf{R}}_{\gamma } ,G_{\gamma }^{( + )} ,{\mathbf{R}}^{\prime}_{\gamma } >$ is given in Appendix 1. Finally, to calculate T_βγα one must additionally solve the equations for the distorted wavefunctions in the various channels, namely

$$ (T_{\delta } + U_{\delta }^{{\left( { + , \, - } \right)}} - E_{\delta } )\chi_{\delta }^{{\left( { + , \, - \, } \right)}} ({\mathbf{R}}_{\delta } ) = \, 0, \, \,\,\,\,\,\,\,{\text{with}}\,\,\, \, (\delta = \gamma ,\beta ), $$

(88)

in addition to Eq. (85). Lastly, consider the important sequential transfer of two neutrons, i.e., (a + A) leading to (b + B), via the intermediate channel (c + C), with a = b + 2n, c = b + n and C = A + n, and B = A + 2n. The channel state functions are then given by:

$$ \begin{aligned} & \Phi_{\alpha } ({\mathbf{a}},{\mathbf{A}}) = [\varphi_{{\text{a}}} \left( {{\mathbf{b}}, \, {\mathbf{n}}_{{\mathbf{1}}} , \, {\mathbf{n}}_{{\mathbf{2}}} } \right)\varphi_{{\text{A}}} \left( {\mathbf{A}} \right)],\Phi_{\beta } ({\mathbf{b}},{\mathbf{B}}) = [\varphi_{{\text{b}}} \left( {\mathbf{b}} \right)\varphi_{{\text{B}}} ({\mathbf{A}},{\mathbf{n}}_{{\mathbf{1}}} , \, {\mathbf{n}}_{{\mathbf{2}}} )],\,\,\,{\text{and}} \\ & \Phi_{\gamma } ({\mathbf{c}},{\mathbf{C}}) = {1}/\surd {2 }[\varphi_{{\text{c}}} ({\mathbf{b}}, \, {\mathbf{n}}_{{\mathbf{2}}} )\varphi_{{\text{C}}} ({\mathbf{A}},{\mathbf{n}}_{{\mathbf{1}}} ) - \varphi_{{\text{c}}} ({\mathbf{b}}, \, {\mathbf{n}}_{{\mathbf{1}}} )\varphi_{{\text{C}}} ({\mathbf{A}},{\mathbf{n}}_{{\mathbf{2}}} )]. \\ \end{aligned} $$

(89)