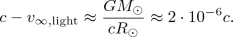Henry Cavendish and the effect of gravity on propagation of light: a postscript

Abstract

This paper is devoted to two hitherto unpublished original documents by Henry Cavendish (1731–1810) which provide insight into his calculations of the deflection of light by isolated celestial bodies. Together with a transcription of these documents, we comment on their contents in the present-day language of physics. Moreover, we compare them with a paper by Johann Georg von Soldner (1776–1833) on the same subject.

1 Introduction

The history of ideas about the deflection of light by the gravitational attraction of celestial bodies goes back to the times of Isaac Newton (1642–1726). In fact, in his book Opticks [18] he, in 1704, asks the question (3rd Book, Query No. 1):

Do not Bodies act upon Light at a distance, and by their action bend its Rays, and is not this action (caeteris paribus) strongest at the least distance?

Another of his queries even gives us an idea of how Newton imagined light itself (Query No. 29):

Are not the Rays of Light very small Bodies emitted from shining Substances?

However, the first published calculation of this kind of light deflection goes back to the German astronomer and geodesist Johann Georg von Soldner (1776–1833) [25]. There is a huge body of literature on pre-relativistic approaches to light deflection where, inevitably, the work of Soldner is mentioned and discussed in detail. Here we only cite [3,4,5, 7, 19, 27,28,29,30] and, from the point of view of physics teaching [12].

Only in more recent times, the English physicist and chemist Henry Cavendish (1731–1810) is mentioned in this respect. Cavendish is most well known for his discovery of the chemical element hydrogen and the torsion-balance experiment named after him, that made him, loosely speaking, “the man who weighed the Earth.” More about Cavendish’s life and work can be found in [8, 13, 14, 22].

In 1921, indeed, the Astronomer Royal of those days, Sir Frank Watson Dyson, compiled, on invitation by the editor of Cavendish’s Scientific Papers, Sir Edward Thorpe, four excerpts from Cavendish’s astronomical manuscripts for publication in the second volume [26]. Among them is “an isolated scrap on the bending of a ray of light by gravitation, which is of interest, as the possibility of the bending of a ray of light by a gravitational field is at present engaging attention, though Cavendish was working on a corpuscular theory.” Dyson’s even shorter excerpt from Cavendish’s undated note, which is very short anyway, reads as follows [26, p. 437]:

(4) To find the bending of a ray of light which passes near the surface of any body by the attraction of that body.

Let s be the centre of body and a a point of surface. Let the velocity of body revolving in a circle at a distance ${\overline{as}}$ from the body be to the velocity of light as 1 : u, then will the sine of half bending of the ray be equal to $\frac{1}{1 + u^2}$.

Dyson, who played a decisive role in, and announced the results of, the expeditions that, in 1919, confirmed the deflection of starlight at the limb of the Sun, added in brackets: “[This deflection is half the amount given by Einstein’s law of gravitation.]” And he also speculated that Cavendish could have been inspired by the above-mentioned Newton’s “Query No. 1”. For more about Dyson’s role in the solar-eclipse expeditions and biographical details, the interested reader is referred to the recent book by Kennefick [9].

It is very likely that an immediate source of inspiration for Cavendish was the letter written to him by Reverend John Michell (1724–1793) on May 26, 1783. In particular, Michell thought that it was possible to determine the mass of a star by measuring the diminution of the speed of light as a consequence of the gravitational attraction of that star on the light corpuscles emanating from it. He arrived at the conclusion that stars with the same average density as the Sun, but a size 500 times larger, remain invisible for far-away observers because the escape velocity at the surface of such stars exceeds the velocity of light. Michell called them “dark stars.”

The date of this letter gives many authors reason to believe that Cavendish’s undated note could have been written in 1783/84. As a matter of fact, we read:

In fact, Henry Cavendish (1731–1810) appears to have come to essentially the same result as von Soldner in an unpublished manuscript of about 1784, inspired by John Michell’s paper of the previous year on the escape of light from a massive body. [11, p. 120, footnote 10]

One of the earliest calculations of the deflection of light from a distant source by a foreground gravitational field is due to Henry Cavendish around 1784. Unfortunately, the only evidence that he did such a calculation is on an isolated scrap of paper. [20, p. 4]

Presumably stimulated by the correspondence with his friend Michell, Henry Cavendish calculated, around 1784, the deflection of light by a body, assuming the corpuscular theory of light and Newton’s law of gravitation. He did not publish his calculation, but stated the result on an isolated scrap of paper. [23, p.1]

The only evidence we have that he did the calculation at all was a single item found early in this century among his papers, which were in the possession of the Duke of Devonshire, during a project to complete the compilation and publication of his oeuvre. [30]

In this respect, only Jungnickel and McCormmach claim that Cavendish’s note could have been written no earlier than in 1804. They argue that the piece of paper Cavendish wrote on contained watermarks which were not in use before that year:

Cavendish continued to hold to the particle theory of light after Thomas Young introduced the wave theory of light in 1800: in or after 1804 Cavendish calculated the gravitational bending of light passing near the surface of a body such as the limb of a star or the edge of a hair. $^{152}$ $\dots$ $^{152}$ Sci. Pap. 2:437. The calculation is undated, but an inspection of the watermark on the paper shows that it could not have been earlier than 1804. [8, p. 414]

Cavendish’s manuscripts are still in the possession of the Duke of Devonshire today, saved in private collections in Chatsworth House (England). The authors of the present paper are very grateful to the assistant archivist of Chatsworth House, Mr. Aidan Haley, as well as the photo librarian, Mrs. Diane Naylor, for providing us with a copy of the complete Cavendish note on light deflection (see Fig. 1). Specifically, we found it interesting that in the second part of this note, not published by Dyson, in addition to a brief explanation of the result, there was also a reference to another page called by Cavendish “A.5”. Also this page was kindly made available to us (see Fig. 2). From the content of this page, it becomes evident in detail how Cavendish arrived at his result about the deflection of light.

Our paper is focused on the transcription and explanation of these two documents. It is organized as follows: Sect. 2 is a postscript of the complete Cavendish note on the “isolated scrap of paper.” In Sect. 3, we accomplish the same for the page A.5. Although we want to adhere to the original version as much as possible, we nevertheless use present-day notations and physical concepts, even if these were not available in the days of Cavendish and Newton. In this way, we want to make it easier for the reader to follow Cavendish’s reasoning.

Section 4 is then devoted to Cavendish’s result, its presentation in today’s formal language as well as to a comparison with Soldner’s derivation.

Furthermore, “Appendix A” contains the transcription of the manuscripts shown in Figs. 1 and 2. We, of course, retain Cavendish’s notation but, at the same time, we indicate where points, lines or angles are meant. For the sake of better understanding, we add the two branches of the hyperbola to the first figure of Cavendish’s page A.5 and the light-deflecting celestial body to the second.

Finally, we compile in “Appendix B” all those characteristics of a hyperbola which Cavendish made use of and which are required for an understanding of this paper.

2 An “Isolated Scrap of Paper”

In the first part of his note which was included in the Scientific Papers [26] by Dyson, Cavendish communicated his result: The deflection angle $\delta$ is implicitly given by

$$\begin{aligned} \sin \frac{\delta }{2} = \frac{1}{1 + u^2}, \end{aligned}$$

(1)

where u denotes the ratio

$$\begin{aligned} u = \frac{c}{v_{\mathrm {circ}}(R)} \end{aligned}$$

(2)

of the velocity c of light to the velocity $v_{\mathrm {circ}}$ on a circular orbit at the distance $R = \overline{\mathrm {F_1V_1}}$ from the centre $\mathrm {F}_1$ of the light-deflecting body (see Fig. 4).

Fig. 1

The complete “isolated scrap of paper” of which an abridged version was reprinted in the Scientific Papers [26]. (The Devonshire Collections, Chatsworth, Henry Cavendish Group VIII/53, “Collection of papers on comets”)

In the second, unpublished part of the note (see Fig. 1 and transcription), Cavendish presented a short explanation of this result and referred to page A.5 for a more detailed one. The main result of this page A.5 is the velocity $v(r_1)$ that any body can have at an arbitrary point $\mathrm {P}$ of a hyperbola due to the gravitational attraction of a celestial body. In terms of the velocity on a circle with radius $r_1$, $v_\mathrm {circ} (r_1)$, this velocity is given by (for derivation see Sect. 3, Lemma 1)

$$\begin{aligned} \left[ \frac{v(r_1)}{v_{\mathrm {circ}}(r_1)} \right] ^2 = \frac{r_1 + 2a}{a}. \end{aligned}$$

From this it follows, for $r_1 \gg a$, that the ratio of the velocity at an infinitely large distance on the hyperbola, $v_{\infty }$, to the velocity $v_{\mathrm {circ}}(R)$ on a circle with radius R is (see Sect. 3, Lemma 2)

$$\begin{aligned} \frac{v_{\infty }}{v_{\mathrm {circ}}(R)} = \sqrt{\frac{R}{a}} \equiv u. \end{aligned}$$

(3)

This is the original definition of the quantity u. At his page A.5, Cavendish did not explicitly refer to light. However, having been an advocate of Newton’s theory according to which light was composed of corpuscles, he was able to transfer his result to the particles of light provided that for them the equivalence of inertia and gravity was supposed to be valid as well. In that case, the mass of those particles did not matter and optics was nothing but an application of (celestial) mechanics to light.

Thus, the ratio (2) becomes a special case of Eq. (3), and what is called “velocity of light” by Cavendish is the velocity of the particles of light at infinity: $v_{\infty ,\mathrm {light}} = c$. Furthermore, this makes clear that, according to Newtonian celestial mechanics, the orbits of the particles of light must be hyperbolas as long as their deflection is due to “normal” celestial bodies. (Michell’s “dark stars” were not known to exist.)

Among the many characteristics of the hyperbola, Cavendish made use of $\overline{\mathrm {V_1Q}} = \overline{\mathrm {F_1C}} = e$ and the fact that the impact parameter fulfils $\overline{\mathrm {F_1N}} = \overline{\mathrm {CQ}} = b$ (and therefore $\overline{\mathrm {CN}} = a$; see Sect. 3, Lemma 2). For the deflection angle $\delta$, we get from the triangles $\triangle \mathrm {CQV}_1$ and $\triangle \mathrm {CF_1N}$ of Fig. 4 the expression

$$\begin{aligned} \sin \frac{\delta }{2} = \frac{\overline{\mathrm {CV}_1}}{\overline{\mathrm {V_1Q}}} = \frac{\overline{\mathrm {CN}}}{\overline{\mathrm {F_1C}}} = \frac{a}{e} \end{aligned}$$

and, by means of $e = a + R$ and the definition (3) of u,

$$\begin{aligned} \sin \frac{\delta }{2} = \frac{1}{1 + \dfrac{R}{a}} = \frac{1}{1 + u^2}. \end{aligned}$$

For particles of light, this is nothing but the deflection angle (1) with u given by the ratio (2).

3 The page “A.5”

The page A.5 comprises the calculations which, among other things, lead to the result about the deflection of light as it was communicated on the “isolated scrap of paper” (see Fig. 2 and transcription).

Fig. 2

Cavendish’s page “A.5,” where he calculates the velocity of a body in an arbitrary point of a hyperbola. (The Devonshire Collections, Chatsworth, Henry Cavendish Group VIII/53, “Collection of papers on comets”)

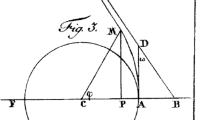
To begin with, Cavendish defined his notation for points and lines in the figures of that page. In what follows we refer to the present-day notation of Figs. 3 and 4. Among the characteristics of the hyperbola, Cavendish mentions first that the bisector of the angle has the direction of the orbit in $\mathrm {P}$, that is the direction of the tangent $\overline{\mathrm {PT}}$ to the hyperbola in $\mathrm {P}$. Moreover, he defined the symbol v as the ratio of two velocities, namely the velocity at the point $\mathrm {P}$ on the hyperbola to the velocity on a circle of radius $r_1 = \overline{\mathrm {F_1P}}$.

3.1 Lemma 1

In Lemma 1, Cavendish calculated the velocity that a body had in an arbitrary point of its hyperbolic orbit, due to the attractive gravitational force of a celestial body with its centre in the focus $\mathrm {F}_1$. This calculation consisted of a geometrical and a physical part.

Fig. 3

The geometry of the hyperbola (I). The meaning of the symbols is as follows. $\mathrm {P}$: any point on a branch of a hyperbola, $\mathrm {F}_1$ and $\mathrm {F}_2$: foci, $\mathrm {V}_1$ and $\mathrm {V}_2$: vertices, $r_1 = \overline{\mathrm {F_1P}}$ and $r_2 = \overline{\mathrm {F_2P}}$: lengths of the focal radii, $a = \overline{\mathrm {V_1C}}$: semi-transverse axis, $e = \overline{\mathrm {F_1C}}$: linear eccentricity, $\overline{\mathrm {PT}}$: tangent to the hyperbola in $\mathrm {P}$, $\frac{1}{2}{\mathcal {L}}$: semi-latus rectum

The geometrical part started with the law of cosines in the triangle $\triangle \mathrm {F_1PF}_2$. We have

$$\begin{aligned} r_1^2 - 2(r_1 \cos \gamma )r_2 + r_2^2 = (2e)^2. \end{aligned}$$

The projection of the focal radius $r_1$ onto $r_2$ is $p = \overline{\mathrm {PK}} = r_1 \cos \gamma$. This yields, together with Eq. (B.3) (see “Appendix B”),

$$\begin{aligned} r_1^2 - 2pr_2 + r_2^2 = 4a^2 + 4b^2. \end{aligned}$$

Now we replace $b^2$ by the latus rectum ${\mathcal {L}}$ (parameter of the hyperbola) and $a^2$ by $4a^2 = \left( r_2 -r_1 \right) ^2$, making use of Eqs.  (B.4) and (B.1), respectively, to get

$$\begin{aligned} r_1^2 - 2pr_2 + r_2^2 = \left( r_2^2 - 2r_1r_2 + r_1^2 \right) + 2{\mathcal {L}} a. \end{aligned}$$

This reduces to

$$\begin{aligned} {\mathcal {L}} a = r_2 \left( r_1 - p \right) . \end{aligned}$$

Making use again of the definition (B.1) in order to express $r_2$ by $r_1$ and applying the relation $1 - \cos \gamma = 2\sin ^2 \frac{\gamma }{2}$, we end up with

$$\begin{aligned} {\mathcal {L}} a = \left( r_1 + 2a \right) \cdot 2r_1 \sin ^2 \frac{\gamma }{2}. \end{aligned}$$

(4)

As Cavendish communicated without comments, the physical part of this lemma is expressed by

$$\begin{aligned} {\mathcal {L}} = 2r_1\left[ \frac{v(r_1)}{v_{\mathrm {circ}}(r_1)} \right] ^2 \sin ^2 \frac{\gamma }{2}. \end{aligned}$$

(5)

Here we designated by the symbol v the velocity itself and not, like Cavendish, the ratio of two velocities. We derive this connection between the geometry and the physics of the motion on a hyperbola in present-day language.

The Newtonian attractive force of gravitation,

$$\begin{aligned} \mathbf {F} = -G \frac{Mm}{r^2} \cdot \frac{\mathbf {r}}{r}, \end{aligned}$$

(6)

is a central force in the narrower sense, for its direction $\left( -\frac{\mathbf {r}}{r} \right)$ is purely radial and also its modulus depends on the radial coordinate r only. Force fields of this kind fulfil the conservation laws of energy and angular momentum $\mathbf {P}$. In Eq. (6), M is the mass of the central body. This body we may consider at rest as long as we do not deal with a genuine two-body problem. The universal, Newtonian gravitational constant is designated by G. Its modern value is $G = 6{.}67384 \cdot 10^{-11} \frac{ \mathrm {m}^3}{\mathrm {kg}\cdot \mathrm {s}^2}$.

The term “Newtonian” says no more than “this is the gravitational constant of Newton’s theory of gravitation.” In particular, it does not say that it is named after Newton because he might have introduced this constant into his theory or even knew its value. He did not. As Hecht pointed out recently [6], confirming [8], it was about a lifetime after Cavendish that Boys [1] and Poynting [21] introduced the constant G, thus completing Eq. (6). Already the title of Boys’ paper indicates that the name “Newtonian” was attached to G at the very first moment of its implementation. Today, this name is in common use not only in countless scientific papers but also in physics textbooks of which we, at random, cite [10, 16, 24].¹

It belongs to the standard repertoire of any introduction to classical mechanics to solve the problem of motion for the force field (6). Expressed by the polar coordinates r and $\varphi$ of Fig. 3, the shape of the orbit is given by

$$\begin{aligned} r(\varphi ) = \frac{ \dfrac{|\mathbf {P}|^2}{GMm^2}}{1 + \varepsilon \cos \varphi }. \end{aligned}$$

A comparison with Eq. (B.5) of “Appendix B” reveals that this is a hyperbola for $\varepsilon > 1$. In particular, we infer the relation

$$\begin{aligned} {\mathcal {L}} = 2\cdot r\left( \frac{\pi }{2} \right) = 2\frac{ |\mathbf {P}|^2}{GMm^2}, \end{aligned}$$

according to which the latus rectum is the geometrical representative of angular momentum.

By its very definition, the modulus of the angular momentum is (vector product)

According to Fig. 3, and making use of the above-mentioned characteristic of the hyperbola, namely that the bisector of the angle has the direction of $\mathbf {v}$, we get and therefore

$$\begin{aligned} {\mathcal {L}} = \frac{2}{GM} r_1^2 v^2 \sin ^2 \frac{\gamma }{2}. \end{aligned}$$

Replacing the constant GM by the velocity on a circular orbit,

$$\begin{aligned} v_{\mathrm {circ}}(r_1) = \sqrt{ \frac{GM}{r_1}}, \end{aligned}$$

(7)

we eventually reproduce Cavendish’s formula (5).

The notion of “angular momentum” was available neither at Cavendish’s time nor when Newton, one hundred years before, wrote his Principia. But we may assume without a doubt that Cavendish was very familiar with Newton’s book [8]. We read [17, Book 1, Section 3: Proposition 16, Theorem 8, Corollary 9]:

$\dots$ it follows $\dots$ that the velocity of a body revolving in a conic will have the same ratio to the velocity of a body revolving in a circle at the same distance that a mean proportional between that common distance and half of the principal latus rectum of the conic has to the perpendicular dropped from the common focus to the tangent of the conic.

This, translated into formulas (the “mean proportional” is nothing but the geometric mean value), is

$$\begin{aligned} \frac{v(r_1)}{v_{\mathrm {circ}}} = \frac{ \sqrt{r_1 \cdot \frac{1}{2} {\mathcal {L}}}}{d}, \end{aligned}$$

where $d = r_1 \sin \frac{\gamma }{2}$ is the length of the perpendicular $\overline{\mathrm {F_1L}}$ from the focus $\mathrm {F}_1$ onto the tangent $\overline{\mathrm {PT}}$ (see Fig. 3). Solving for ${\mathcal {L}}$ yields Eq. (5) again.

In a last step, we bring together the geometrical and physical parts of Cavendish’s derivation. From Eqs. (4) and (5), we obtain

$$\begin{aligned} \left[ \frac{v(r_1)}{v_{\mathrm {circ}}(r_1)} \right] ^2 = \frac{r_1 + 2a}{a}. \end{aligned}$$

(8)

3.2 Lemma 2

Lemma 2 again consists of a geometrical and a physical part.

The geometrical part starts with a characteristic of the hyperbola which was, at least to Cavendish, fundamental (“by nature of the hyperbola”): If $\overline{\mathrm {V_1Q}} \parallel g_2$, then $\overline{\mathrm {V_1Q}} = \overline{\mathrm {F_1C}} = e$ (see Fig. 4 and “Appendix B”). Given that, we get $\overline{\mathrm {CQ}} = b$, because in the triangle $\triangle \mathrm {V_1CQ}$, we have $\overline{\mathrm {V_1C}} = a$ and $e^2 = a^2 + b^2$. The rectangular triangles $\triangle \mathrm {V_1CQ}$ and $\triangle \mathrm {F_1NC}$ not only have their hypotenuses in common but also the adjoining interior angles ( and ); both triangles are congruent. Consequently, $\overline{\mathrm {F_1N}} = \overline{\mathrm {CQ}} = b$ and $\overline{\mathrm {CN}} = \overline{\mathrm {V_1C}} = a$. The dimension of the impact parameter is the same as that of the semi-conjugate axis, that is b.

Furthermore, if $\overline{\mathrm {G_1G_2}} \parallel \overline{\mathrm {F_1F_2}}$, we have

$$\begin{aligned} \frac{ \frac{1}{2} \overline{\mathrm {G_1G_2}}}{\overline{\mathrm {CG_2}}} = \frac{\overline{\mathrm {CN}}}{\overline{\mathrm {F_1C}}} = \frac{\overline{\mathrm {V_1C}}}{\overline{\mathrm {F_1C}}} = \frac{a}{e}, \end{aligned}$$

which is immediately evident from the triangles $\triangle \mathrm {G_2CH}$ and $\triangle \mathrm {F_1CN}$.

The physical part of this lemma once more deals with ratios of velocities. For $r_1 \gg a$, that is “at infinity,” the main result (8) of Lemma 1 turns into

$$\begin{aligned} \frac{v_{\infty }}{v_{\mathrm {circ}}(r_1)} = \sqrt{ \frac{r_1}{a}}. \end{aligned}$$

(The distance designated x by Cavendish must not be confused with the x coordinate in Figs. 3 and 4.)

For the sake of comparison, Cavendish invoked the velocity on a circle of radius $\overline{\mathrm {F_1N}} = b$ to obtain (cf. Eq. (7))

$$\begin{aligned} \frac{v_{\infty }}{v_{\mathrm {circ}}(b)} = \frac{v_{\infty }}{v_{\mathrm {circ}}(r_1)} \cdot \frac{v_{\mathrm {circ}}(r_1)}{v_{\mathrm {circ}}(b)} = \sqrt{ \frac{r_1}{a}} \cdot \sqrt{ \frac{b}{r_1}} = \sqrt{ \frac{b}{a}}. \end{aligned}$$

This ratio may be formed for other circular orbits as well. For a circle of radius $\overline{\mathrm {F_1V}_1} = R$, we regain the ratio (3).

Fig. 4

The geometry of the hyperbola (II). The meaning of the symbols is as follows. $g_1$ and $g_2$: asymptotes, $\delta$: angle of intersection of the asymptotes, b: semi-conjugate axis and impact parameter, hatched: gravitating celestial body of radius R. It is $\overline{\mathrm {V_1Q}} \parallel g_2$ and $\overline{\mathrm {G_1G}_2} \parallel \overline{\mathrm {F_1F}_2}$

4 Deflection of light: Cavendish and Soldner

In this section, we put Cavendish’s work into context with that of his contemporary Soldner. We cited the extensive literature about Soldner’s paper [25] already in Sect. 1.

In Newton’s theory of light corpuscles, the particles get accelerated by a celestial body while approaching it. The main result of Cavendish’s page A.5, that is the ratio (8) of velocities, yields, together with the velocity (7) on a circular orbit,

$$\begin{aligned} v^2(r_1) = GM \left( \frac{2}{r_1} + \frac{1}{a} \right) . \end{aligned}$$

As $r_1 \rightarrow \infty$, it follows $v^2_{\infty } = \dfrac{GM}{a}$ and therefore

$$\begin{aligned} v^2(r_1) = v^2_{\infty } + 2 \frac{GM}{r_1}. \end{aligned}$$

(9)

This is nothing but the law of conservation of energy, a concept that was available neither to Cavendish nor to Newton.

With Cavendish’s choice $v_{\infty ,\mathrm {light}} = c$, Eq. (9), when applied to light, turns into

$$\begin{aligned} v_{\mathrm {light}}^2(r_1) = c^2 + 2 \frac{GM}{r_1}. \end{aligned}$$

Making explicit use of Eq. (7), formula (1) becomes

$$\begin{aligned} \sin \frac{\delta }{2} = \frac{1}{1 + \dfrac{c^2 R}{GM}} = \frac{GM}{c^2 R} \frac{1}{1 + \dfrac{GM}{c^2 R}}. \end{aligned}$$

(10)

In order to reproduce this formula, Will wrote [30]: “It is interesting to try to reproduce Cavendish’s answer (in the absence of his own detailed calculations) $\dots$ The simplest explanation is that Cavendish assumed that the speed of light was c $\dots$ at infinity.” It follows without doubt from the second part of the “isolated scrap of paper” that Cavendish has chosen just this initial condition for the deflection of light. Therefore, Will’s “simplest explanation” is correct.

The quantity $\frac{GM}{c^2}$ has the dimension of length and is a geometric measure for the strength of the gravitational field of a body with mass M. It appears, with a factor 2, in Einstein’s theory of gravitation as well, where it is named “Schwarzschild radius.” If we calculate this measure for the Sun, making use of our present-day knowledge of the universal gravitational constant G, and relate it to its radius $R_{\odot }$, we get

$$\begin{aligned} \frac{GM_{\odot }}{c^2 R_{\odot }} \approx 2 \cdot 10^{-6} \ll 1. \end{aligned}$$

(11)

In view of the smallness of this value, we may assume $\sin \frac{\delta }{2} \approx \frac{\delta }{2}$, and Eq. (10) becomes, in the leading order of this quantity,

$$\begin{aligned} \delta \approx 2\,\frac{GM}{c^2 R}. \end{aligned}$$

(12)

This is the formula for the deflection of light as it is presented in modern scientific literature on Newtonian light deflection. For the deflection of light at the limb of the Sun, we get the deflection angle $\delta \approx 0{.}84''$. As Dyson noticed [26], the angle $\delta$ turned out to be twice as large in Einstein’s theory.

Cavendish did not make further comments on light deflection beyond his result (1). In particular, he did not evaluate the angle $\delta$ numerically. At least, he would not have been able to do this in the same way as we did when we simply substituted the numerical values of G, $M_\odot$, and $R_\odot$ into formula (12). The constant G, as a universal constant of Nature, can be found neither in Cavendish’s paper [2] nor in Newton’s Principia [17].

However, in all formulas describing the deflection of light, the constant G permanently appears in combination with the mass M of the light-deflecting celestial body. The product GM may be understood as a specific, “individual,” gravitational constant characterizing the gravitational field of the mass M. Hence, the quantity that matters is GM, not G. We may take for granted that also Cavendish and Soldner were aware of this.

In his above-mentioned paper, Cavendish was mainly interested in measuring the average density of the Earth. To that end, he determined the attractive force that the Earth exerts on small lead balls, that is, their weight. The radius of the Earth given, this amounts to measuring the specific gravitational constant GM of the Earth. In order to extract the mass of the Earth from the combination GM, Cavendish had to perform a second measurement, that is, the attractive force between larger lead spheres and the smaller ones. For that measurement, he used the torsion-balance named after him, that, by the way, goes back to Michell too [8]. He arrived at the result that the mean density if the Earth was 5.448 that of water.

From a today’s point of view, Cavendish had everything at his disposal that was necessary to calculate explicitly the deflection of light. But it might well be that for him, being a physicist and chemist, it was not obvious to ask for the numerical value of $\delta$ and its observability.

What is even more because of its universality, he could have calculated the Newtonian gravitational constant G from his data. However, we have to be cautious not to project the knowledge we have today back onto the past when people were used to work with proportions and ratios instead of equations like (6). The first who completed this equation by formally introducing G, and, at the same time, measured the value of G using an apparatus of Cavendish type, were Poynting [21] and Boys [1] in the early 1890s.

Soldner, in 1801, based his calculation on the following assumption [25] (English translation taken from [7]): “From A let a light ray go $\dots$ horizontally, with a velocity such that it goes the distance v in one second.” In our Fig. 3, this point A corresponds to the point $V_1$ on the surface of the light-deflecting celestial body. Soldner’s result for the deflection angle $\delta$, expressed by his symbol v for the velocity of light, is

$$\begin{aligned} \tan \frac{\delta }{2} = \frac{2 g_{\mathrm {Soldner}}}{v(R) \sqrt{v^2(R) - 4 g_{\mathrm {Soldner}}}}, \end{aligned}$$

(13)

which is equivalent to

$$\begin{aligned} \sin \frac{\delta }{2} = \frac{2 g_{\mathrm {Soldner}}}{v^2(R) - 2 g_{\mathrm {Soldner}}}. \end{aligned}$$

By means of the replacement rule

$$\begin{aligned} 2\, g_{\mathrm {Soldner}} \longrightarrow \frac{GM}{R} = gR, \end{aligned}$$

this turns into

$$\begin{aligned} \sin \frac{\delta }{2} = \frac{GM}{v^2(R) \cdot R}\cdot \frac{1}{1 - \dfrac{GM}{v^2(R) \cdot R}}. \end{aligned}$$

(14)

In this replacement rule, g is the gravitational acceleration at the surface of the light-deflecting celestial body (surface gravity). As Treder and Jackisch [27] pointed out, the factor 2 is due to the definition of g, and acceleration in general, in Soldner’s days. (Within the scope of this paper, it is not necessary to review the still ongoing debate on the “factor-2 problem” in Soldner’s paper, including confusion that arised from printing errors. See references cited in the Introduction.)

From Soldner’s paper, we cannot unequivocally identify the point of the orbit where his velocity of light, v, is supposed to have the value c. Two possibilities have been discussed in the literature:

• 1. It seems most natural to interpret Soldner’s above-mentioned quotation in such a way that he put $v(R) = c$ as an initial condition. This point of view was adopted by Will [30]. In that case, Eq. (14) becomes, in contrast to Eq. (10),

  $$\begin{aligned} \sin \frac{\delta }{2} = \frac{GM}{c^2 R} \frac{1}{1 - \dfrac{GM}{c^2 R}}. \end{aligned}$$

  Thus, Soldner and Cavendish arrived at different results which, however, coincide with the deflection angle (12) in the leading order of a series expansion in terms of the small quantity $\frac{GM}{c^2 R}$. Soldner’s initial condition, $v(R) = c$, leads to the consequence that the velocity of light at an infinitely great distance is, according to Eq. (9),

  $$\begin{aligned} v_{\infty ,\mathrm {light}} = c \,\sqrt{1 - 2\frac{GM}{c^2 R}}. \end{aligned}$$

  At infinity, where the light comes from, and where the gravitational attraction of isolated celestial bodies does not exist anymore, all particles of light should have the same velocity irrespective of the mass and the size of the light-deflecting body they are going to encounter later on their orbit. When reversing the light path, Soldner should have reset the velocity of light to $v_{\infty ,\mathrm {light}} = c$. However, even though this shortcoming is noteworthy as a matter of principle, we don’t have reason to overestimate it. From the point of view of measurement it is insignificant, even more if we take into account the accuracy with which the velocity of light had been determined in those days. Indeed, because of (11), we get for the Sun (see also [30])

  

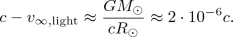
  We have direct evidence from his paper that Soldner was well aware of how small the quantity $\frac{GM}{c^2 R}$ was, that is nothing but one half of the deflection angle. He realized that the more realistic problem to be solved was that of the propagation of light emanating from a star at a finite distance from the Sun. This light gets deflected by the Sun with a mass different from that of the source and is detected by an observer at a finite distance. Neither Cavendish nor Soldner solved this problem, but Soldner, assuming “that the light ray comes from an infinitely great distance”, argued that it would not make much difference. We read [25] (English translation in [7]: “As this maximum value [of the deflection angle for the Earth – note added by the authors] is quite unobservable, it would be superfluous to go further; or to determine $\dots$ by how much it becomes smaller when the distance of the star from which the light ray comes is assumed to be finite and corresponding to a given magnitude.” Indeed, we can show that about 70 per cent of the deflection of light take place in the interval $-R \le y \le R$ of Fig. 4.

• 2. It is, perhaps, a consideration like this that prompted Treder and Jackisch to add to their paper [27] the following footnote: “Soldner’s $\dots$ speed of light at infinity is $v_{\infty } = c$ $\dots$ and at finite distances $v > c$”. In that case, Eq. (9) yields

  $$\begin{aligned} v(R) = c \,\sqrt{1 + 2\frac{GM}{c^2 R}}. \end{aligned}$$

  This, when inserted into Eq. (14), is in complete agreement with Cavendish’s result (10), of course. However, as already said above, we do not find an explicit reference to this assumption in Soldner’s paper [25].

For Soldner, having been trained as an astronomer, it must have been almost a matter of course to calculate the numerical value of the deflection angle and to speculate about its observability.

In order to calculate the deflection of light by the Earth, he took the data for the radius of the Earth and the acceleration of its gravity from Laplace [15].

For the Sun, Soldner did not present the values of the corresponding quantities. But he knew, for sure, that the “astronomical key” to determining the specific gravitational constant, $GM_\odot$, was the planetary motion, in particular Kepler’s Third Law

$$\begin{aligned} \frac{T^2}{a^3} = \frac{4\pi ^2}{GM}. \end{aligned}$$

(15)

Here T is the orbital period of a companion (planet) that is orbiting its central body (the Sun) in an ellipse with semi-major axis a. This law was expressed by Gauss, in 1809, as the constant²

$$\begin{aligned} k_\mathrm {Gauss} = \sqrt{GM} = 2\pi \frac{a^{3/2}}{T}. \end{aligned}$$

Thus, the simplest solution to determine $GM_\odot$ would be to substitute into Kepler’s Third Law the data for the Earth’s orbit. However, a careful reading of Soldner’s paper [25] reveals that he refers, consistent with his deflection formula (13), to the surface gravity of the Sun which incorporates also the Sun’s radius: “If one substitutes $\dots$ the acceleration of gravity on the surface of the sun, and one takes the radius of that body for unity $\dots$ .” If only the distance of the Earth from the Sun, that is, the Sun’s parallax, is known, it is easy to determine the radius of the Sun, in units of length, from its angular diameter in the sky. These data Soldner might have taken from Laplace again.

But what about the gravitational acceleration at the surface of the Sun? Soldner tells us nothing about that in his paper. So, we present one conceivable method to express the unknown gravitational acceleration at the surface of the Sun by that at the surface of the Earth. To our mind, this method is in the spirit of Soldner’s times, but we, of course, do not claim, because of lack of information, that Soldner followed exactly this line of reasoning.

We may reasonably assume that he, like Cavendish, was familiar with Newton’s Principia. There we read [17, Book 3; Proposition 8, Theorem 8, Corollary 1]:

For the weights of equal bodies revolving in circles around planets are (by book 1, prop. 4, corol. 2) as the diameters of the circles directly and the squares of the periodic times inversely, and weights at the surfaces of the planets or at any other distances from the center are greater or smaller (by the same proposition) as the inverse squares of the distances.

Indeed, the gravitational acceleration of a celestial body at distance r is, according to Newton’s law (6),

$$\begin{aligned} g(r) = \frac{GM}{r^2} \propto \frac{1}{r^2}. \end{aligned}$$

(16)

Replacing GM by means of Kepler’s Third Law (15) for a circular orbit of radius r, we get

$$\begin{aligned} g(r) = 4\pi ^2 \frac{r}{T^2} \propto \frac{r}{T^2}. \end{aligned}$$

If and designate the distance of the Earth from the Sun and its orbital period, respectively, we get for the surface of the Sun

and, correspondingly, for the Moon as the companion of the Earth

As mentioned above, the gravitational acceleration at the surface of the Earth (its surface gravity) was known to Soldner. Thus, we finally arrive at the sought-after expression

for the surface gravity of the Sun in terms of that of the Earth. Substituting all values for radii R, distances r and periods T as they were known at Soldner’s times, we obtain from (12) and (16)

for the deflection angle at the solar limb.

5 Final comments

The essential parts of this paper are Sects. 2 and 3 where we analyze the two documents from Cavendish’s unpublished papers shown in Figs. 1 and 2.

The first part of the “isolated scrap of paper” has already been published in Cavendish’s Scientific Papers [26]. From the hitherto unpublished second part, we learn that Cavendish assumed the “correct” initial condition for the deflection of light, that is $v_{\infty ,\mathrm {light}} = c$.

At his page A.5 that we, by permission, publish for the first time, Cavendish calculated the orbital velocity at an arbitrary point of the hyperbola without making reference to light. He arrives at the result (8). Basically, in the language of present-day physics, he applied the method of angular-momentum conservation. The structure of this page as well as the predominantly geometrical way of reasoning remind us of Newton’s Principia as an archetype. Indeed, theorems and lemmata are formulated first and serve as the basis for applications and examples afterwards.

In particular, the two documents are linked up by Newton’s theory of light corpuscles. This theory allows for transferring the result (8) to the particles of light. Therefore, what is written down on the “isolated scrap of paper” is nothing but an application of hyperbolic motion. In this way, we can understand at last why the “isolated scrap of paper” was included in Cavendish’s “Collection of Papers on Comets.” In fact, also some comets move in hyperbolic orbits, of course having individual velocities $v_{\infty } > 0$. Usually we are merely not interested in the deflection angle of their orbits.

If those authors, cited in the Introduction, are right who conjecture that Cavendish’s undated notes are an immediate reaction to Michell’s letter, we certainly can consider Cavendish a precursor of Soldner.

However, we must not forget the objection made by Jungnickel and McCormmach [8] that Cavendish could not have published his notes earlier than in 1804. In that case, it is worth mentioning that Cavendish adhered to the idea of light corpuscles even though Thomas Young performed and published his famous experiments on the wave nature of light also in the first decade of the 19th century. Then, Cavendish cannot be considered a precursor of Soldner anymore. Instead, the question is legitimate as to whether he refused to publish his notes because Soldner already published his calculations, including a numerical value of light deflection. This is, however, very unlikely because biographers consistently report that is was a characteristic trait of Cavendish to be, for complex reasons, very reluctant and not much interested to publish his results (see, for example, [8]). As far as we know, there are, at least, no documents to prove that Cavendish was acquainted with Soldner’s publication.

We hope that our paper will have an impact on the historiography of the pre-relativistic theories of light deflection in general, and Cavendish’s contribution in particular, at least in so far as the matter of whether and how Cavendish did his calculations is settled.

Appendices

Appendix

A. Transcription of documents

1.1 A.1. Transcription of the “Isolated Scrap of Paper”

To find the bending of a ray of light which passes near the surface of any body by the attraction of that body

Let s (2nd fig. of A5) be [the] center of [the] body and a a point of [its] surface. Let the veloc[ity] of [the] body revolving in [a] circle at dist[ance] ${\overline{as}}$ from [the] body be to [the] vel[ocity] [of] light as 1 : u, then will [the] sine [of] $\frac{1}{2}$ [of the] bending of the ray be equal to

$$\begin{aligned} \frac{1}{1 + u^2}. \end{aligned}$$

For take ${\overline{ac}} : {\overline{as}}$ as $1 : u^2$ and, with focus s, vertex a and center c, draw the hyperb[ola] $ea \varepsilon$ and let ${\overline{gcf}}$ and ${\overline{cm}}$ be the asymptotes and ${\overline{cb}}$ the sem[i] conj[ugate] axis, then ${\overline{ab}} = {\overline{cs}}$ and ${\overline{sn}} = {\overline{cb}}$ and, by A5, [the] vel[ocity] of the body at infin[ite] dist[ance] in this hyperb[ola] will be to [the] vel[ocity] in [a] circle at a as

$$\begin{aligned} \sqrt{\frac{{\overline{as}}}{{\overline{ac}}}} : 1 \end{aligned}$$

as it be by supp[osition], and the sine of $\frac{1}{2}$ [of the] bending of [the] ray or

1.2 A.2. Transcription of page “A.5”

The calculation in A.3 considered more accurately.

Let s and h be [the] foci, c [the] center, ${\overline{cd}}$ and ${\overline{cb}}$ the semiaxes, p [a] point on [the] curve and let ${\overline{sp}} = a$, ${\overline{cd}} = d$, let ${\overline{pt}}$ bisect and conseq[uently] be parallel to path and let and [the] vel[ocity] at p be to that in [a] circle at [the] same dist[ance] as v : 1.

Lem[ma 1]) Let a, d and v signify [the] same things as in P[age] 1, then in [a] hyperbola,

$$\begin{aligned} v^2 = \frac{2d + a}{d}. \end{aligned}$$

For let the letters in [the] fig[ure] signify [the] same things with regard to [the] hyperb[ola] as in fig[ure] 1 with regard to the ellipse. Then³

$$\begin{aligned} {\overline{sp}}\,^2 - 2\, {\overline{pk}} \cdot {\overline{ph}} + {\overline{ph}}\,^2 = {\overline{sh}}\,^2 = 4\,{\overline{bc}}^2 + 4\,{\overline{dc}}^2 = 2 {\mathcal {L}} \cdot {\overline{dc}} + {\overline{ph}}\,^2 - 2\, {\overline{sp}} \cdot {\overline{ph}} + {\overline{sp}}\,^2 \end{aligned}$$

therefore

therefore

$$\begin{aligned} v^2 = \frac{a + 2d}{d}. \end{aligned}$$

Lem[ma] 2) Let ed be an hyperb[ola], c the center, s [the] focus, ${\overline{ad}}$ the princip[al] axis, ${\overline{cb}}$ [the] semiconj[ugate] [axis], ${\overline{fg}}$ and ${\overline{cm}}$ the asymptotes, ${\overline{sn}}$ a perpend[icular] to ${\overline{fg}}$. Then by nature of [the] hyperb[ola] ${\overline{fg}}$ is parallel to ${\overline{ab}}$ and ${\overline{ab}} = {\overline{sc}}$, therefore ${\overline{ns}} = {\overline{cb}}$ and ${\overline{cn}} = {\overline{ac}}$ and, if ${\overline{gm}}$ is parallel to ${\overline{ds}}$, ${\overline{gm}} : {\overline{cg}}$ is as $2 {\overline{ac}} : {\overline{cs}}$.

Now [the] vel[ocity] at infin[ite] dist[ance] x is to [the] vel[ocity] in [a] circle at that dist[ance] as $\sqrt{\frac{x}{d}} : 1$ and therefore is to [the] vel[ocity] in [a] circle at dist[ance] ${\overline{sn}}$ as

$$\begin{aligned} \sqrt{\frac{x}{d}} : \sqrt{\frac{x}{{\overline{sn}}}} \quad \text {as} \quad \sqrt{\frac{{\overline{sn}}}{d}} : 1. \end{aligned}$$

B. The geometry of the hyperbola

In this “Appendix,” we compile those of the many characteristics of an hyperbola which are necessary for an understanding of Cavendish’s calculations and which were mentioned by himself. Moreover, even though this material can be found in every mathematics textbook dealing with conic sections so that the majority of the readers is supposed to be familiar with it, we have to introduce the notation used throughout this paper in order to make it a self-consistent reading. We refer to Figs. 3 and 4 which correspond, with a few minor additions, to the two figures at Cavendish’s page A.5.

The hyperbola is the locus of all points in a plane for which the difference of the distances from two fixed points is constant. These two points $\mathrm {F}_1$ and $\mathrm {F}_2$ are named foci. The distance of the foci from the centre $\mathrm {C}$ of the line $\overline{\mathrm {F_1F}_2}$ is the linear eccentricity, $e = \overline{\mathrm {CF}_1} = \overline{\mathrm {CF}_2}$.

Translated into formulas, the definition of the hyperbola reads

$$\begin{aligned} r_1 - r_2 = \pm 2a, \end{aligned}$$

(B.1)

with $r_1 = \overline{\mathrm {F_1P}}$ and $r_2 = \overline{\mathrm {F_2P}}$, and $2a > 0$ being a characteristic constant. With the coordinates x and y of an arbitrary point $\mathrm {P}$ on the hyperbola, this turns into what is called the standard form

$$\begin{aligned} \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \end{aligned}$$

(B.2)

of the equation of the hyperbola. Here we defined

$$\begin{aligned} b = \sqrt{e^2 - a^2}. \end{aligned}$$

(B.3)

From $y = 0$, we immediately infer the graphic meaning of the constant a: It is the distance of the two vertices $\mathrm {V}_1$ and $\mathrm {V}_2$ from each other, which is called transverse axis, $2a = \overline{\mathrm {V_1V}_2}$.

The standard form of the equation of the hyperbola yields, together with Eq. (B.3), the ordinate

$$\begin{aligned} \frac{1}{2} {\mathcal {L}} \equiv |y(\pm e)| = \frac{b^2}{a} \end{aligned}$$

(B.4)

that corresponds to the abscissa $x = \pm e$ of the foci. The quantity ${\mathcal {L}}$ is called parameter of the hyperbola or latus rectum. It is the length of the chord across the hyperbola that is perpendicular to the transverse axis and contains one focal point.

The tangent $\overline{\mathrm {PT}}$ of the hyperbola at point P bisects the angle of the two focal radii $\overline{\mathrm {F_1P}}$ and $\overline{\mathrm {F_2P}}$. So we have

For large coordinates x, the hyperbola approaches the two straight lines

$$\begin{aligned} y = \pm \frac{b}{a} x \end{aligned}$$

through the origin which are named asymptotes $g_1$ and $g_2$. For the abscissa $x = \pm a$ of the vertices $\mathrm {V}_1$ and $\mathrm {V}_2$ we immediately obtain $y = \pm b$. Consequently, the quantity b is the ordinate of the vertices of the hyperbola, measured at its asymptotes. It is called semi-conjugate axis.

The shortest distance $\overline{\mathrm {F_1N}}$ of the asymptote $g_2$ from the focus $F_1$, which for reasons of symmetry is also the distance of both asymptotes from the two foci, is called impact parameter. It is $\overline{\mathrm {F_1N}} = b$ and, because of Eq. (B.3), $\overline{\mathrm {CN}} = a$.

The line parallel to an asymptote through a vertex (in Fig. 4, the line $\overline{\mathrm {V_1Q}}$ parallel to $g_2$ through $\mathrm {V}_1$) intersects the ordinate axis at the point $\mathrm {Q}$ whose distance from the centre $\mathrm {C}$ is $\overline{\mathrm {CQ}} = b$. Therefore, it is $\overline{\mathrm {V_1Q}} = e$ because of Eq. (B.3); the two triangles $\triangle \mathrm {F_1NC}$ and $\triangle \mathrm {V_1CQ}$ are congruent.

The angle $\delta$ of intersection of the asymptotes $g_1$ and $g_2$ is that angle with its vertex in C, about which we have to rotate the asymptote $g_2$ in order to make it coincide with $g_1$. This angle of intersection of the asymptotes is nothing but the deflection angle of a light ray coming from infinity. Since $g_2$ goes parallel to $\overline{\mathrm {V_1Q}}$, the angle with its vertex at $\mathrm {Q}$ is again $\frac{\delta }{2}$, and from the rectangular triangle $\triangle \mathrm {CQV}_1$ we infer

$$\begin{aligned} \sin \frac{\delta }{2} = \frac{a}{e}. \end{aligned}$$

If we shift the origin of the coordinate system to the focus $\mathrm {F}_1$ and introduce the polar coordinates r und $\varphi$ (see Fig. 3), the standard form (B.2) of the equation of the hyperbola transforms into the polar equation,

$$\begin{aligned} r = \frac{ \frac{1}{2}{\mathcal {L}}}{1 + \varepsilon \cos \varphi }, \end{aligned}$$

(B.5)

which is sometimes called focal equation. The quantity $\varepsilon = \frac{e}{a} > 1$ is the numerical eccentricity of the hyperbola.