1 Introduction

The need for high-precision atomic spectroscopic data for astrophysical purposes has increased over the last few years [1,2,3,4,5,6]. Though theoretical data is available, in general, no existing theoretical framework is as accurate as is required for the detailed spectroscopic analysis of wavelengths, energy levels or transition probabilities of low charge states of complex elements [7]. Atomic data, especially for rare earths like neodymium, is either old and not updated [8], or unavailable. Even the NIST database [9], which is one of the most used repositories for atomic data in the world, has almost no record of doubly ionised neodymium spectral lines, though recent works are available [10], and for singly ionised neodymium lines, the data is compiled from Albertson et. al. of 1942 [11] and Meggers et. al. of 1975 [12] and transition probability values from Hartog et. al. of 2003 [13]. Thus producing accurate atomic data of low charge states of rare-earths like doubly ionised neodymium in a controlled environment like a laboratory is of critical need for astrophysicists and for confirming theoretical findings [14,15,16].

In this paper, we have investigated the suitability of our new in-house hollow-cathode lamp as a light source to measure accurate transition probabilities of Nd III. To do this we have checked the stability of the spectral emission and the discharge characteristics of the newly built hollow-cathode lamp.

Fig. 1
figure 1

Schematic diagram of the experimental setup

Full size image

1.1 Measurement of transition probabilities

Transition probabilities refer to Einstein’s A coefficients [17]. Each electron in the upper energy level (u) of an excited atom spontaneously decays to a lower energy level (l) with the emission of radiation. The irradiance of this transition is measured in our laboratory. The measured irradiances have to be intensity calibrated, taking into account the spectral response of the experimental setup (optics, diffraction grating, and detector). To obtain this response function, we use different standard calibration lamps, namely deuterium for the UV spectral region and tungsten for the visible region (more details can be found in [18]). The intensity calibrated irradiance (\(I_{ul}\)) is proportional to the transition probability (\(A_{ul}\)) and the upper energy level population (\(N_u\)) and inversely proportional to the wavelength of the emitted light (\(\lambda _{ul}\)).

$$\begin{aligned} I_{ul} = \frac{MN_uA_{ul}}{\lambda _{ul}} \end{aligned}$$
(1)

where M is a geometrical constant.

Depending on the selection rule of the electronic transition in an atom, several lower levels (i) are possible for an electron in an upper energy level to decay into. According to [19], the branching fraction is expressed as

$$\begin{aligned} BF_{ul}=\frac{A_{ul}}{\Sigma _i A_{ui}} \end{aligned}$$
(2)

From eqs. 1 and 2, we can express branching fraction as,

$$\begin{aligned} BF_{ul}=\frac{\lambda _{ul}I_{ul}}{\Sigma _i I_{ui}\lambda _{ui}} \end{aligned}$$
(3)

The radiative lifetime (\(\mathrm {\tau _u}\)) of an atomic level u is related to the sum of transition probabilities from that upper energy u to all the possible lower energy levels i through the following equation [20]:

$$\begin{aligned} \tau _u=\frac{1}{\Sigma _i A_{ui}} \end{aligned}$$
(4)

Therefore from Eqs. 2 and 4, we can express the transition probability as the ratio of two quantities that can be measured in a laboratory:

$$\begin{aligned} A_{ul}=\frac{BF_{ul}}{\tau _u} \end{aligned}$$
(5)

Using these irradiances, we calculate branching fractions and combine them with theoretically calculated or experimentally measured lifetimes to obtain transition probabilities.

2 Experimental setup

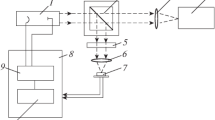
Our experimental setup is shown in Fig. 1. We use a hollow-cathode lamp with a cathode insert made of neodymium as a radiative plasma source. The lamp is operated with a DC power supply and a constant flow of argon as the carrier gas. In addition, the lamp is water-cooled to prevent damage by overheating while operating and to reduce the Doppler width of lines. The setup can be divided into two parts: the plasma source, and the setup used for recording the spectra.

The plasma source comprises hollow-cathode lamp, a gas and vacuum system, and a power supply unit, and the spectra are recorded with a 1.5m Jobin-Yvon diffraction grating spectrometer and a CMOS detector. Plain mirror M1 is placed at the back of the lamp as shown in Fig. 1 to reconstruct the self-absorbed spectra as discussed in [18], and when self-absorbed lines are not present or measured, it is kept in the position as shown by the dotted lines. Flap F1 is placed in the position shown to prevent light from reaching the spectrometer when we want to measure the background signal. Otherwise, it is kept in the position as shown by the dotted lines. The motor controlling the movements of M1, F1, and the spectrometer grating are connected to the Agilent A/D converter, with the help of a general purpose interface bus (GPIB) connected to the computer. The pinholes P1 and P2 are used to make sure that the beam of light reaching the spectrometer is from the central, hottest part of the plasma which has the highest concentration of cathode ions. The diameter of pinholes in P1 and P2 ranges from 0.6 mm to 11 mm but we normally use 3 mm. Concave mirror M3 focuses the light coming from M2 at the entrance slit of the spectrometer which is at the focal plane of M3.

2.1 Plasma source

Plasma sources can be classified based on electron density and electron temperature, which are related to the degree of ionisation of the species in the plasma. Hollow-cathode lamps are widely used as a reliable source for accurately measuring atomic parameters from the VUV (vacuum ultraviolet) to the IR (infrared) and for technological applications (like deposition of thin films [21]). For example, when paired with a Fourier transform spectrometer, they are used to measure oscillator strengths and/or branching fractions [22, 23] and hyperfine structure for neutral and singly ionised iron group elements and up to doubly ionised species for heavier elements due to their different ionisation energy. When paired with a diffraction grating spectrometer like ours, they are used to measure oscillator strengths [24] and population density [25]. When laser-induced fluorescence technique is used, they are used to measure hyperfine structure [26], population density [27] and lifetimes of neutral [28] and singly ionised [29] species.

2.1.1 Choice of carrier gas

A noble gas with well-known spectra is usually used as a carrier gas in a hollow-cathode lamp due to its nonreactive nature [30]. The gas used depends on the size and mass of the cathode ions to be sputtered. Usually, for the spectroscopic study of Nd, either argon or neon is used [10, 13, 31].

Sputtering yield (Y) is the statistical probability of the number of atoms sputtered from a target when a gas ion strikes it [32]. Sputtering yield depends on the initial kinetic energy (E) of the moving noble gas ion in eV, the atomic mass of cathode atoms (\(m_{\textrm{c}}\)), the atomic mass of the moving noble gas ions (\(m_{\textrm{n}}\)) in atomic mass units and the surface binding energy of the target atoms (\(U\mathrm {_{sb}}\)). The following semi-empirical expression, also known as Bohdansky’s equation [33], approximates the sputtering yield:

$$\begin{aligned} Y= (6.4*10^{-3})m_\textrm{c}\gamma ^{5/3}E^{0.25} (1-\frac{E_\textrm{th}}{E})^{3.5} \end{aligned}$$
(6)

with \(\mathrm {\gamma }\) defined as:

$$\begin{aligned} \gamma =\frac{4m_\textrm{c}m_\textrm{n}}{ (m_\textrm{c}+m_\textrm{n})^2} \end{aligned}$$

where \(E_\textrm{th}\) is the threshold energy for sputtering and is defined as the projectile energy at which the sputtering yield is zero [34]. It can be expressed as follows [32]:

$$\begin{aligned} E_\textrm{th}=\frac{U_\textrm{sb}}{\gamma (1-\gamma )}\;\;\;\;\;\;; \;\;\; \textrm{for}\;\; \frac{m_\textrm{n}}{m_\textrm{c}}<0.3 \nonumber \\ E_\textrm{th}=8U_\textrm{sb} (\frac{m_\textrm{n}}{m_\textrm{c}})^{2/5};\;\;\; \textrm{for}\;\;\frac{m_\textrm{n}}{m_\textrm{c}}>0.3 \end{aligned}$$
(7)
Fig. 2
figure 2

Dependence of sputtering yield Y on the atomic mass of the noble gas, \(m_\textrm{n}\), for E=100 eV, \(U_\textrm{sb}\)=4.3 eV (for neutral neodymium atoms), \(m_\textrm{c}\)=144.42

Full size image

Figure 2, shows the dependence of sputtering yield on the atomic mass of the noble gas. As can be seen, the sputtering yield of krypton is maximum. However, the recombination energy also has to be considered as it is responsible for the excitation of the sputtered ions. Direct excitation of the singly ionised sputtered ions may occur for levels situated within +5000 \(\mathrm {cm^{-1}}\) and -10,000 \(\mathrm {cm^{-1}}\) of the recombination energy of the noble gas [35] as shown in Eq. (14). Though argon has a sputtering yield of Y=0.85, its recombination energy is higher than that of krypton or xenon and its atomic mass is half of that of krypton, which makes it easier for it to gain more kinetic energy for sputtering. All these factors and the affordable price per liter of argon, makes it the best choice as a carrier gas for the study of doubly ionised neodymium.

Fig. 3
figure 3

Schematic diagram of the hollow cathode lamp

Full size image

2.1.2 Plasma production in a hollow-cathode lamp

Electrons, released from the cathode surface due to thermionic emission gain kinetic energy proportional to the mean free path travelled in the electric field and transfer this to the noble gas atoms through collisions. So, depending on the kinetic energy, either an excited atom of Ar is produced (collisional excitation [18]) as shown in Eq. (8) (where \(\mathrm {Ar^*}\) is excited neutral argon), an excited atom of Ar is de-excited (collisional de-excitation [18])) as shown in Eq. (9) or a singly ionised argon is produced (collisional ionisation [18])) as shown in Eq. (10).

$$\begin{aligned}{} & {} Ar+e^-\xrightarrow {}Ar^*+e^- \end{aligned}$$
(8)
$$\begin{aligned}{} & {} Ar^*+e^-\xrightarrow {}Ar+e^-+ \textrm{photon} \end{aligned}$$
(9)
$$\begin{aligned}{} & {} Ar+e^-\xrightarrow {}Ar^++2e^- \end{aligned}$$
(10)

Depending on their kinetic energy, the pair of electrons in Eq. (10) collide with another atom of argon repeating one of the above-mentioned processes, which results in a chain reaction. The kinetic energy of the argon ions is responsible for sputtering the metal atoms from the bulk (\(\mathrm {Nd_{cathode}}\)) into the plasma and ionising it by collisional ionisation as shown in Eq. (11). The electron released due to ionising the metal atom is absorbed by the positively charged argon ion, releasing recombination energy \(E_\mathrm {{rec}}\) by a process called radiative recombination. This energy excites the metal ion to a higher energy level as shown in Eq. (13).

$$\begin{aligned}{} & {} Ar^{+*}+Nd_{cathode}\xrightarrow {}Ar^++Nd^++e^- \end{aligned}$$
(11)
$$\begin{aligned}{} & {} Ar^++e^-\xrightarrow {}Ar+E_\mathrm {{rec}} \end{aligned}$$
(12)
$$\begin{aligned}{} & {} Nd^+\xrightarrow {E_\mathrm {{rec}}}Nd^{+*}+\Delta E \end{aligned}$$
(13)

where \(\Delta E\) is the difference between the recombination energy of the argon ion and the energy of the excited energy level of Nd. According to [35], the reaction shown in Eq. (13) is more likely to take place if relation 14 is satisfied.

$$\begin{aligned} -5000\;\mathrm {cm^{-1}}<\Delta E<10000\;\mathrm {cm^{-1}} \end{aligned}$$
(14)

Once the metal ion is sputtered in the plasma, it collides and interacts with electrons and other argon ions resulting in further excitation and/or ionisation of the atoms.

2.1.3 Structure of hollow-cathode lamp

Figure 3 shows the schematic structure of the hollow-cathode lamp used in our laboratory. Our hollow-cathode lamp is an adaptation of the one used in the Fourier Transform Spectroscopy laboratory at Imperial College London [30], the design of which was kindly shared with us by Prof. Pickering. It consists of two anodes, made of stainless steel, to achieve a symmetrical discharge and one cathode which contains an exchangeable cylinder of the desired metal. The body of the lamp is made of transparent glass to see the colour of the plasma produced and to act as insulators between the anodes and cathode.

The elongated structure of the anode increases the overall length of the lamp, which separates the window from the cathode preventing the deposition of the sputtered cathode ions on the glass window. Moreover, the gas flow direction, being away from the front window, keeps this window clean, helping to prevent a decrease in its transmittance from metal deposition.

2.1.4 Vacuum system

A constant supply of carrier gas at an optimum pressure is maintained inside the lamp with a gas and vacuum system. The gas is first led into a mixer area. A multichannel mass flow controller (MKS Type 1179A Mass-Flo Controller) with four channels controls gas fluxes. Two channels control gas flux between \(\mathrm {10^3\;}\)-\(\mathrm {10^5\;mm^3/min}\) and the other two channels allow for much finer flow control between 10 -\(\mathrm {10^3\;mm^3/min}\). This allows the introduction of up to 4 gases simultaneously in controlled quantities. A needle valve is used at the outlet pipe to regulate the pressure. When the lamp operates, the pressure inside it is recorded using a Balzers APG manometer.

2.1.5 Power supply unit

Fig. 4
figure 4

Schematic diagram of the power supply of the lamp

Full size image

Figure 4 shows the schematic diagram of the power supply unit used. We use the fug-elektronik gmbh 8200 rosenheim as a DC power supply. The maximum current and voltage reach 1 A and 2 kV respectively. Two adjustable ballast resistor units are connected in series with the current supply to the anode and cathode of the lamp as shown in Fig. 4. These ballast resistors result in potential drop allowing higher current to be supplied to the lamp with lesser potential difference across its electrode. The black boxes shown in Fig. 4 are HS 100R resistors each of 100 \(\Omega \). The equivalent resistance leading to the anode from the power supply can be either 100 \(\Omega \) (if point B is connected to D), 200 \(\Omega \) (if point C is connected to D), or 800 \(\Omega \), and the equivalent resistance leading to the power supply from the cathode can be either 250 \(\Omega \) (if H is connected to E), 100 \(\Omega \) (if G is connected to E) or 0 (if E is connected to F). Thus the equivalent resistance of the whole circuit in Fig. 4 is the sum of the resistance of the lamp and the ballast resistor unit before the lamp.

We have used several resistors of 100 \(\Omega \) in parallel to achieve equivalent resistances that could be achieved by using fewer units in series to prevent the resistors from damage due to overheating.

2.2 The monochromator

The radiation from the lamp is first focused at the entrance slit of a 1.5 m Czerny-Turner type Jobin-Yvon spectrometer with a reflective diffraction grating of 2400 lines/mm, a spectral range of 200 nm to 800 nm, and a resolving power of 150000 at 450 nm. The width of the entrance slit range from 10 \(\mu \)m to 1500 \(\mu \)m. Depending on the orientation of the diffraction grating, a particular wavelength, referred to as the syntony wavelength is incident in the centre of the CMOS camera and the wavelength range in one frame of the detector varies from 3.5 nm at 200 nm to 1.4 nm at 800 nm.

Mirrors M2 and M3 in Fig. 1, used to focus the light beam at the entrance slit of the monochromator, are aligned carefully so that the entirety of the diffraction grating is illuminated to exploit its maximum resolving power. Theoretically, the main problem of a grating spectrometer is the interference of second and first-order wavelengths in the spectra. To prevent this, we use optical filters to band limit the detected radiation. The time required to change the syntony from 200 nm to 800 nm is around 14 min and the integration time to capture and save a spectrum is less than 1 s.

2.3 Choice of detector

The detector needed to record spectra with enough resolving power to observe the spectral lines of interest depends on the intrinsic width of the spectral lines we want to measure. Line width can be classified as follows:

  • Intrinsic Width (\(w_\mathrm {{intrin}}\)): This is the width introduced by the light source. It is due to several broadening mechanisms such as natural broadening, doppler broadening, broadening due to the interaction of neighboring particles, pressure broadening, etc [36]. The main broadening mechanism in a hollow cathode lamp is Doppler broadening [36].

  • Instrumental Width (\(w_\mathrm {{instru}}\)): With our experimental setup, line width broadening can be caused only by the monochromator (\(w_\mathrm {{mono}}\)) discussed above and the detector (\(w_\mathrm {{detector}}\)).

    $$\begin{aligned} w_\textrm{instru}\le w_\mathrm {{mono}}+w_\mathrm {{detector}} \end{aligned}$$
    (15)

The spectral lines in a crowded spectrum (e.g. Nd III) must be resolved to accurately measure transition probabilities. For this, the instrumental width (\(w_\mathrm {{instru}}\)) should be less than the intrinsic line width \(w_\mathrm {{intrin}}\) [36]. The value of \(w_\mathrm {{intrin}}\) for Nd III line at 508.53 nm reported in [10] is approximately 4 pm. Since the monochromator has already been chosen, the minimum value of \(w_\mathrm {{mono}}\) cannot be reduced. Thus we have to choose the camera in such a way so that the following condition is fulfilled.

$$\begin{aligned} w_\mathrm {{intrin}}>w_\mathrm {{instru}} \end{aligned}$$
(16)

A test was performed to measure \(w_\mathrm {{mono}}\) introduced by the 1.5m Jobin-Yvon spectrometer and the guiding optical elements. For this, a laser source of 543.5 nm was used in place of the lamp, and the final result was observed using a Photo-multiplier tube (PMT) placed at the exit slit of the monochromator. The width of the laser line was measured to be 4 pm when the entrance slit of the monochromator was 10 \(\mu \)m. Since theoretically, a laser has a negligibly small line width, the measured value corresponds to the width introduced by our monochromator \(w_\mathrm {{mono}}\)(=4 pm). The same line was recorded with three different detectors, listed in Table 1, instead of the PMT to measure the total instrumental width \(w_\mathrm {{instru}}\) introduced by the monochromator-detector pair.

Table 1 Instrumental line width introduced by the combination of monochromator-detector for different types of detectors
Full size table

After a thorough search of the latest cameras available on the market, it was found that the CMOS PCO edge 4.26 UV camera meets Eq. (16). This detector has a pixel size of 6.5 \(\mu \)m*6.5 \(\mu \)m and the monochromator-detector pair produces an instrumental line width of about 4 pm. We have acquired this detector and will use it to measure the transition probabilities. Figure 5 shows a Fe+Ar spectrum obtained by adding the irradiance falling on the vertical strip of 2048 pixels of the image (2048*2048 pixels) taken by this camera.

Fig. 5
figure 5

Example of a spectrum of Fe + Ar as recorded by the CMOS PCO edge 4.26 UV camera

Full size image

3 Results and discussion

At the moment, the main objective of our laboratory is to measure transition probabilities of doubly ionised neodymium. However, to carry out tests and characterise the newly built hollow cathode lamp, we have used an iron cathode due to its well-known spectral data available in [9]. Before turning the lamp on, the vacuum and the gas system were turned on to keep the argon flow in the lamp. The pressure inside the lamp was maintained at 90 to 100 Pa. When the lamp was turned on with a current of 200 mA, the pressure increased immediately to around 150 Pa but is stabilised after about five minutes at around 115 Pa. The plasma in the lamp was purple due to the presence of argon and changed to white at a pressure below 110 Pa and a current of more than 0.7 A due to the presence of iron in the plasma. Every time the current was increased, the pressure in the lamp increased immediately and stabilised to a lower value after four to five minutes. Thus the pressure was different for different input currents.

It is important to have a deep understanding of the lamp to consider all the possible sources of uncertainties in our upcoming spectroscopic studies. For this reason, we have performed different tests to characterise our hollow cathode lamp.

3.1 Voltage current characteristic

Due to the lower concentration of cathode ions in the plasma, a hollow cathode discharge can be considered as an electric discharge of the carrier gas. In general, a gas discharge is characterised by plotting the voltage between the electrodes versus the current. As mentioned in [37], a gas discharge characteristic can be classified depending on the value of the applied current: Townsend discharge (\(10^{-10}-10^{-6}\) A), normal glow discharge (\(10^{-3}-10^{-1}\) A), abnormal glow discharge (\(10^{-1}-1\) A), and arc discharge (\(\mathrm {>10}\) A).

According to [38], low-pressure glow discharges exhibit better spectroscopic properties than arc discharges and it is clear from [10, 13] that if the input current is as low as in normal glow discharge (\(10^{-3}-10^{-1}\) A), it is not possible to obtain Nd spectral lines because it is not possible to sputter neodymium atoms from the cathode. Therefore we need to operate our lamp in the abnormal glow discharge region and the plot of the voltage across the lamp and the applied current should be a straight line with a positive slope.

First, we need to calculate the voltage across the lamp (\(V_\textrm{L}\)) using Eq. (17). The value of the ballast resistors (R) (showed in Fig. 4) was set to 200 \(\Omega \), the current in the circuit (I) and the voltage applied across the whole circuit (V) were displayed on the DC source.

$$\begin{aligned} V_L=V-I*R \end{aligned}$$
(17)

Then \(V_L\) was plotted against I at different gas pressures inside the lamp as shown in Fig. 6. We chose a range from 0.02 A to 0.5 A for I and the pressure was varied from 120 Pa to 200 Pa. We chose these ranges of current and pressure as it was best suited for the lamp to produce the spectra we required. The Fe+Ar discharge was stable in this pressure range and the lines of interest could be identified and observed easily. At a current below 0.02 A the lamp did not turn on and above 0.5 A in the chosen pressure range, the lamp became unstable and started pulsing. Even though abnormal glow discharge occurs within the range of \(10^{-1}-1\)A, it was observed that the linearity in the gas discharge curve is maintained from 0.02 A.

Fig. 6
figure 6

V-I characteristic of the hollow-cathode lamp using an iron cathode and argon as a carrier gas

Full size image

Since the voltage-current curves in Fig. 6 are linear with a positive slope, it can be concluded that the hollow-cathode lamp is operating in the abnormal glow region where the resistance of the lamp remains constant for a given pressure. The resistance of the lamp can be obtained from the slope of the best-fit straight line for the voltage-current characteristics. It was observed that the resistance of the lamp reduced with an increase in pressure. This is due to the increase in the number of charged particles in the form of argon ions in the plasma with an increase in pressure.

3.2 Plasma stability

In our laboratory, we will measure transition probabilities using the branching fraction method [39]. This requires the measurement of irradiances of all transitions from one upper energy level. We are limited to measuring transitions from those upper energy levels that have transitions within the measurable spectral range. If the plasma in the lamp changes its characteristics during the time the spectrometer measures all the spectral lines related to the upper energy level, then the uncertainty in the measurement would increase considerably.

Fig. 7
figure 7

Evolution of the irradiances of the Ar II lines at 349.1 nm, 423.7 nm [40], and 611.5 nm [41] over time

Full size image

To ensure that the plasma in the hollow-cathode lamp is stable, we have recorded the irradiances of three Ar II lines with OMA EG &G 1455R-512HQ detector every 14 min for almost two hours as shown in Fig. 7. We have chosen the Ar II lines at 349.1 nm, 423.7 nm [40], and 611.5 nm [41]. These lines are among the strongest Ar lines from 200 to 800 nm according to [9]. Moreover, the fact that these lines are spread over a spectral range of 262 nm, ensures the stability of the lamp over that same spectral range. It can be observed from Fig. 7 that the first data point of the curve is smaller than all others for all the lines and that the irradiance seems to stabilise. This suggests that we must wait at least 15 min for the lamp and the detector to stabilise before taking measurements. The irradiance of the lines remains well within 10% from the average. This proves that the plasma remains stable and that we can perform reproducible measurements of atomic parameters using our setup for almost two hours.

4 Conclusion

In this work, we have characterised a newly built hollow cathode lamp by measuring its voltage-current characteristics and stability with time. We conclude that our lamp is in the abnormal glow region and it remains stable for at least two hours. We have also measured the instrumental spectral line width introduced by our setup. We conclude that to resolve spectral lines in a very crowded spectrum such as that of neodymium, we need to match the instrumental width introduced by our setup to the intrinsic width of those lines. To achieve this we have conducted a study with different detectors and a state-of-the-art CMOS camera that introduces a width smaller than the one introduced by our monochromator, thus upgrading our laboratory to measure transition probabilities of rare-earth elements.

Measurement of transition probabilities is a complex experimental task but the knowledge acquired in this work has led to a better understanding of experimental setup and will help us to measure accurate transition probabilities by reducing experimental uncertainties as much as possible.