1 Introduction

Praseodymium has one of the richest spectra of all the elements. The main part of the spectrum is located in the visible green region what causes a great interest in the lighting industry [1]. Astrophysicists are also interested in studying the structure of the praseodymium line, because notably strong spectral lines of this element are commonly observed in the spectra of the cooler chemically peculiar (CP) stars. These stars are distinguished by strong overabundances of lanthanides compared to solar system values. Many CP stars possess sufficiently strong and uniform magnetic fields to distinctly resolve numerous atomic lines into Zeeman’s \(\pi \)- and \(\sigma \)- components.

Belonging to the lanthanide group, praseodymium features a single stable isotope, \(^{141}\)Pr, with a nuclear spin of \(I=5/2\). The ground state of Pr I is \(4f^36s^2 \ ^4I_{9/2}\). Recently discovered energy levels of praseodymium remain without designation. The quantum number J of known levels varies between 1/2 and 21/2.

As all odd isotopes, the spectral lines of praseodymium show hyperfine structure. The hyperfine (hf) splitting of levels of praseodymium is of the order of 10\(^{-3}\) to 1 cm\(^{-1}\). The magnetic dipole moment and electric quadrupole moment of the nucleus are: \(\mu _I = 4.2754(5) \mu _N\) and \(Q = -0.0059\) barns, respectively [2].

Numerous researchers have investigated the hyperfine spectra of praseodymium. The electron ground state has been meticulously examined using atomic beam magnetic resonance techniques [3, 4]. Childs and Goodman [5] studied the hf structure of low lying levels of Pr I utilizing high-resolution laser-radio-frequency double-resonance techniques on an atomic beam. In these papers, the authors discovered new levels and corrected some earlier assignments. A large number of spectral lines of Pr have been investigated by Blaise et al. [6] and Ginibre [7, 8]. Ginibre’s experimental work was based on the analysis of high-resolution Fourier transform (FT) spectra in the IR and visible ranges, resulting in the discovery of numerous new levels. In recent years, the Guthöhrlein group [9] and Furmann et al. [10] explored praseodymium spectra with the help of laser spectroscopy uncovering new levels and classifying a large number of spectral lines. Investigations of the Pr spectrum, using FT spectroscopy or laser spectroscopy, were performed in Graz (in the group of L.W.) since 2010 [11]. Beside determination of the hf constants, the main focus of this work was the discovery of previously unknown energy levels, in order to enable explanation of unclassified spectral lines in FT spectra. Most recent results were published in 2021 (ref. [12] and references therein). Further work is in progress.

The initial observation of the Zeeman effect of the ground state of Pr I was reported in [13]. Subsequently, the Zeeman effect of all levels within the \(^4\)I ground multiplet of Pr I was reported in [14] and reinvestigated by the use of atomic beam magnetic resonance methods in [15]. Landé \(g_J\)- factors for 40 levels spanning the range 8350–28400 cm\(^{-1}\) were outlined in [7] and verified by theoretical analysis. These data cited in [7] have been obtained by Camus and Fred at Argonne National Laboratory by the use of a Paschen–Runge spectrograph. Additionally, a study of the Zeeman structure of 6 lines in the wavelength range of 649.572–669.351 nm conducted in 2016 was described in [16].

Experimental Landé \(g_J\) factors are crucial spectroscopic parameters. They are helpful in determining the designation of atomic levels, provide information about configuration mixing and can be used for a calibration of the magnitude of a magnetic field.

The laser spectroscopy results presented in the current paper concern the Zeeman structure of praseodymium lines in the wavelength range between 566.0 and 651.7 nm. The methods of laser absorption spectroscopy enable precise studies of the atomic structure. The problem arises where the spectrum is very complex and it is impossible to separate the individual components of the structure. In such a situation, it is necessary to use a computer program that simulates the shape of the spectrum. These programs require the use of line profile models and theoretically predictable intensity ratios of the components of the structure. An additional difficulty in interpreting the spectra of complex atoms is the saturation effect induced at high power densities of the exciting laser light. Although reducing laser power may mitigate saturation effects, it often amplifies experimental noise. Due to saturation, stronger components, characterized by larger transition probabilities, may exhibit relatively lower intensities compared to weaker components.

In the years 2017–2018, we carried out very extensive measurements of the hyperfine structure and the Zeeman effect of praseodymium lines using the LIF technique. Results of these studies were published in two papers [17, 18]. At that time, however, we did not have a computer program that could take into account the saturation effect. So, we were unable to interpret many of the spectra previously recorded. Also, many observations of the Zeeman structure were analyzed only for one direction of polarization of the incident light, either \(\pi \) or \(\sigma \). Now, with an improved computer program at our disposal, we were able to re-analyze previously recorded spectra. Thanks to this, we obtained new spectroscopic data and were also able to increase the precision of previously reported results, which include observations of both the \(\pi \) and \(\sigma \) components.

2 The saturation effect in the Zeeman spectra recorded using the LIF technique

Fig. 1
figure 1

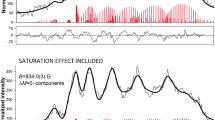
The Zeeman-hf structures (\(\pi \) and \(\sigma \) patterns) of the 596.0933 nm line. Thin lines are experimental contours, and thick lines are computer-fitted structures. The upper figures in both sets \(\Delta M = \pm 1\) and \(\Delta M = 0\) present the plot of the computer best fit obtained considering the saturation effect

Full size image
Fig. 2
figure 2

The Zeeman-hf structures (\(\pi \) and \(\sigma \) patterns) of the 620.4306 nm line. Thin lines are experimental contours, and thick lines are computer-fitted structures. The upper figures in both sets \(\Delta M = \pm 1\) and \(\Delta M = 0\) present the plot of the computer best fit obtained considering the saturation effect

Full size image

At sufficiently large laser intensities, the optical pumping rate on an absorbing transition becomes larger than the relaxation rates. This results in a noticeable decrease of the population of the absorbing levels. The phenomenon of saturation was described in the well-known monograph [19]. Numerous papers are related to the effect of saturation and experiments with optical pumping (see e.g. [20,21,22,23]). Some works (see [24, 25]) focus specifically on the influence of saturation on the recording of Zeeman or hfs spectra using laser absorption spectroscopy. The saturation effect causes distortions in the shape of the recorded spectra in relation to predictions, which take into account the theoretical ratios of transition probabilities between the individual components. In paper [24], a difference was noted in the hfs spectra recorded using Fourier transform emission and laser optogalvanic spectroscopy. The differences in the spectra were reduced by introducing the saturation parameter into the intensity formula for the hfs components.

In our recent two papers [26, 27] basing on the theoretical description of the saturation effect from the monograph [19], we presented a method that allows to take this effect into account in the analysis of the recorded LIF spectra. This method involves taking into account the saturation effect in the population of states by modifying the theoretical transition probabilities according to the expression:

$$\begin{aligned} A^{sat} _{MM'} \sim \frac{A_{MM'}}{1+A_{MM'}/A_{S}} \end{aligned}$$
(1)

Here \(A_{MM'}\) is the unsaturated transition rate of the Zeeman transition \(M\rightarrow M'\), directly proportional to the intensity of radiation, and \(A_S\) is the saturation rate. The \(A_{MM'}\) rate for a given direction of observation and polarization can be calculated from appropriate theoretical formulas. The \(A_{S}\) has the same constant value for all components of the Zeeman structure and can be determined as a fitting parameter. The method described above has been successfully used by us in the analysis of the spectra of vanadium and niobium [28, 29].

Formula (1) results from the theory assuming that we are dealing with a two-level atomic system in a state of thermodynamic equilibrium. In addition, it is also obvious that we will obtain a correct fit using this formula only if we can assume that the \(A_S\) parameter remains constant throughout the entire scan—in other words, there is no fluctuation in laser power. Equation (1) shows that the influence of the saturation effect on the intensity of the Zeeman component depends on the ratio \(A_{MM'}/A_S\), and because \(A_S\) has the same constant value for all components of the structure the stronger \(M \rightarrow M'\) components have relatively lower intensity in relation to weaker components.

3 Experiment

Our experimental setup was detailed in our previous papers [17, 18]. The source of free Pr atoms was a hollow cathode discharge lamp filled with argon used as a buffer gas. Using the discharge, we can excite atoms, by laser light, not only from their ground, but also from higher excited states.

Our laser system consisted of a cw frequency—doubled Nd: YAG laser and a tunable ring dye laser. We used Rhodamine 6 G, Kiton Red and DCM dyes, which allowed us to achieve a range of 560–650 nm. The power of our dye laser could reach 800mW. Upon excitation of atoms by laser light, several fluorescence lines emanate from the upper excited atomic state. The most convenient for observation line, often the strongest, is selected by the use of monochromator. The investigated lines are enumerated in Table 1 with their corresponding wavelengths of the LIF signal presented in the last column. By scanning the laser light wavelength across the line pattern, slight variations in the population of the upper state occur, consequently altering the intensity of the induced fluorescence light. These fluctuations in the LIF signal mirror the structure of the observed atomic line.

Table 1 Atomic lines of Pr I investigated in our study
Full size table

To enhance the signal-to-noise ratio and eliminate background radiation emitted by the Pr-Ar plasma discharge, we employed a phase-sensitive detection method.

The discharge region is enveloped by a container containing liquid nitrogen, utilized to cool the hollow cathode lamp. This cooling mechanism serves to stabilize the discharge and reduce the Doppler width approximately 40–50 % of the spectral lines up to several hundred MHz. To investigate the Zeeman effect, we placed a permanent magnet directly within the cooling liquid, thereby generating a magnetic field of approximately 800 G in the observation region. The magnetic field was meticulously calibrated, achieving an accuracy below 1%, by observing the Zeeman structure of two argon lines: at 586.031 nm in the green-red region and 638.4717 nm in the red region, respectively.

The Zeeman patterns of praseodymium lines were recorded for two states of linear polarization of the exciting laser light in order to obtain the \(\pi \)- and \(\sigma \)- components, separately. We used a half-wave plate and a Glan prism polarizer in order to change the polarization direction of the exciting laser light. The measuring sequence was as follows: in the first step we observed the hf structure of a selected atomic line looking for optimal conditions for observation. In the next step, the permanent magnet was placed in the container with liquid nitrogen and the magnetic field value was measured with the help of Ar lines. Such a measurement was repeated each time when the state of linear polarization of the entering laser light was changed. We noticed that the magnetic field value was slightly different in measurements with different polarization of the laser light. This small effect (less than 5 % ) can be explained by the fact that the laser beam passes the region of magnetic field through different paths determined by setting the optical system (\(\lambda /2\)-plate, Glan polarizer and lenses) and that the magnetic field in the observation region is slightly inhomogeneous, probably because of the field edge effect. We took into account this effect in the analysis of the spectra considering different magnetic field values for different polarizations. In the next step, we switched the laser wavelength to the Pr line under investigation and recorded its Zeeman pattern.

4 Computer analysis of recorded spectra

To conduct computer simulations of the recorded spectra, we used a computer program, the description of which can be found in the paper [30]. This program has been modified to take into account the saturation effect described by formula (1), see Figs. 1, 2.

For computer simulations, it is necessary to know the hf constants related to the lower and upper state of the observed transition. For all spectral lines in the present investigation, the hyperfine structure constants of the upper and lower levels were known. These data are presented in Table 2. For most of the observed lines, Lande \(g_J\) factors of the lower energy levels ( \(g_J^{low}\)) of the transition were also known. These data can be found in the NIST database. In our previous computer analysis, in order to limit the number of free parameters as much as possible, we used a two-step procedure. In the first step, the \(g_J^{low}\) values were used as fixed parameters when we were looking for the \(g_J^{up}\) values. In the second step, after determining the value of \(g_J^{up}\), this value was treated as a fixed parameter to find an improved value of \(g_J\) for the lower level. With this method of fitting, the determined values of \(g_J^{low}\) cannot be very different compared to the values presented in the NIST database.

Table 2 Values of atomic structure parameters used as input data in the fitting procedure
Full size table

In the currently performed computer analysis, both Lande coefficients \(g_J\) of the upper and lower levels were treated as free fitting parameters. With this method of data processing, we were able to confirm the reliability of the data presented in the NIST database. On the other hand, in several cases this method increased the measurement uncertainty associated with determining the value of \(g_J^{up}\). The results of currently performed simulations are presented in Table 3. Three columns present, one after the other: values from the NIST database, then our previous results presented in [17, 18], and the last column shows the results of the current investigation.

Table 3 Results—Lande factor values
Full size table

The results of the currently performed measurements are presented in the table along with their measurement uncertainties, which result from the statistical distribution of results of measurements carried out in various laboratory conditions for slightly variable values of magnetic fields and for the \(\pi \) and \(\sigma \) polarizations. Statistical errors were also corrected by the Student’s t-distribution coefficients.

5 Conclusion

A computer program, which takes into account the saturation effect, was used to analyze the Zeeman spectra of Pr lines. Using this program, we were able to analyze spectra that we had previously excluded from the analysis due to the large discrepancy between the recorded spectral contour and computer simulations. The spectra of four lines of praseodymium, which were previously rejected, this time were successfully analyzed; we have determined 3 new values of \(g_J\). We also re-analyzed the Zeeman spectra for four other lines. This analysis was successfully performed for both the \(\pi \) and \(\sigma \) components, which improved the overall precision of the previously determined \(g_J\) values. The current analysis also allowed for the verification of previously published data on the values of the hyperfine structure constants A and B.