1 Introduction

Neptunium (Np), with atomic number Z = 93 is the first transuranic actinide. In the environment, only one of the twenty-five isotopes of \(^{219-244}\)Np known at present, is found in trace amounts, namely \(^{237}\)Np (t\(_{1/2} = 2.1\times 10^{6}\) y), being created as decay products from transmutation reactions in uranium ores. However, the main source of Np isotope contamination, found today on earth and specifically in the biosphere, is fallout from nuclear weapon testing. An estimated total of about three tons of \(^{237}\)Np has been released globally into the environment by above-ground nuclear explosions [1]. Historically, the element Np was synthesized for the first time by McMillan and Abelson in 1940 via the reaction chain

$$\begin{aligned} ^{238}_{ 92}\text {U} \xrightarrow [\text {}]{{(n,\gamma )}}\; ^{239}_{ 92}\text {U} \xrightarrow [\text {23 min}]{{\beta ^-}}\; ^{239}_{ 93}\text {Np}, \end{aligned}$$
(1)

with \(^{239}\)Np (t\(_{1/2}\) = 2.356 d) decaying subsequently into \(^{239}\)Pu [2]. The long-lived isotope \(^{237}\)Np was produced one year later by Wahl and Seaborg using the reaction

$$\begin{aligned} ^{238}_{ 92}\text {U} \xrightarrow [\text {}]{{(n,2n)}}\; ^{237}_{ 92}\text {U} \xrightarrow [\text {6.75 d}]{{\beta ^-}}\; ^{237}_{ 93}\text {Np}, \end{aligned}$$
(2)

which involves bombardment of \(^{238}\)U with fast neutrons [3]. Today, Np is generated steadily and in macroscopic amounts within the nuclear fuel cycle with one ton of nuclear-spent fuel containing typically 500 g of \(^{237}\)Np, corresponding to typical production rates of \(\sim \)10 kg in each conventional pressurized water reactor per year [4]. Subject to the chemical conditions within the repositories and the geological characteristics of the surrounding environment, neptunium can exist in four different oxidation states, +III to +VI, with Np(V) species exhibiting the highest mobility [5]. Thus Np represents a major hazard in the final disposal of nuclear waste due to the high radiotoxicity and the long half-life of the isotope \(^{237}\)Np.

As a consequence, the ultra-trace analysis of Np in environmental samples is of high relevance, in particular regarding the closure and reliable sealing of long-term repositories for nuclear waste [6]. The necessary development of efficient and selective non-radiometric determination methods for Np based on the implementation of laser ionization into mass spectrometry requires the development of efficient, easy-to-implement ionization schemes and detailed atomic spectroscopy [7]. Currently, existing ionization schemes of Np are applying sequential three- or two-step excitation induced by dye lasers [8] or require three Ti:sapphire lasers [6].

In this work, novel two-step excitation schemes in the spectral range of Ti:sapphire lasers, which turn out to be far more reliable and easier to operate than dye lasers, were investigated regarding their suitability for Np ultra-trace analysis. This reduces the complexity and susceptibility to errors of the technique in particular regarding studies on multiple isotopes or even elements. However, a reduction in the number of excitation steps involved may also negatively affect sensitivity as well as selectivity of the process, which must be examined before application.

In 1977, Fred et al. [9] measured 6069 lines of Np in the range between 4000 and 40,000 cm\(^{-1}\) with the Argonne 9 m Pashen-Runge spectrograph. They classified 130 even- and 329 odd-parity energy levels. A few years later Worden et al. [10] added 27 odd- and 37 even-parity energy levels in the range of 33,000 to 37,000 cm\(^{-1}\) to that data set. They also determined the ionization potential (IP) as 50,536(4) cm\(^{-1}\) from a dedicated study of the Rydberg series involving ionization in a pulsed electric field. Delayed application of intermittent electric field 5 \(\mu \)s after the populating laser pulse permitted decay of shorter-lived valence states that beforehand obscured the Rydberg series identification. The most recent value of the IP of Np was reported by Köhler et al. to be 50,535(2) cm\(^{-1}\) [11]. It was derived using three-step resonance ionization and applying the saddle-point model, which involves the ionization of highly excited atoms in a static electric field. This approach is much easier to realize and analyze without relying on the assignment of individual Rydberg series within an overwhelming multitude of other levels but has a similar precision in complex spectra to one of the Rydberg series investigations. More recently this model was also utilized by Studer et al. [12] and by Kneip et al. [13] for studies on the IP of Pm and Cm, respectively, in a rather similar context as reported here.

In this work, the investigation of the atomic structure of neptunium within the energy region around the first IP is presented. The studies include the search for strong auto-ionizing states (AI), which were addressed from three different odd-parity intermediate energy levels. As part of the process to identify efficient ionization schemes, a detailed examination of the first excited states (FES) was undertaken, focusing on line profiles and including the measurement of atomic level lifetimes. Due to the complexity of the Np spectra and the absence of easily assignable Rydberg series, a re-determination of the IP was accomplished using the electric field ionization method analogous to [12, 13].

2 Experimental setup

Fig. 1
figure 1

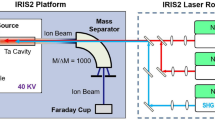
Illustration of the RISIKO mass separator with ion trajectory highlighted in green and laser beams in blue and violet. The FI-LIST is an optional part and has been used only for the ionization potential measurements. Details on RISIKO specifications can be found in reference [14], and FI-LIST in [15]

Full size image

Our study employs resonance ionization spectroscopy (RIS) as a technique known for its remarkable sensitivity regarding the examination of minuscule sample amounts. Applying the stepwise photoionization process with well-tuned pulsed laser radiation also offers inherent selectivity for a specific element or even isotope. A 10 \(\mu \)L sample containing approximately \(4 \times 10^{13}\) atoms of \(^{237}\)Np in dilute nitric acid solution was dripped onto a \(4\times 4\) mm\(^2\) zirconium carrier foil with a thickness of 25 \(\upmu \)m and subsequently evaporated slowly to dryness under an infrared lamp. Accordingly, a sample containing about \(2\times 10^{13}\) atoms of \(^{237}\)Np and \(2\times 10^{13}\) atoms of \(^{239}\)Pu was prepared to test the schemes’ element selectivity. The foil was folded and placed in the hot cavity atomizer of the Mainz University RISIKO mass separator and laser ion source facility, as sketched in Fig. 1. The atomizer is a 35 mm long tantalum tube with a 2.5 mm inner diameter and can be resistively heated up to about 1700 \(^{\circ }\textrm{C}\) [14]. The ions created in the source unit are extracted and the resulting ion beam is shaped by ion optics and mass separated in a \(60^{\circ }\) sector field magnet. Ions passing a separation slit downstream of the magnet are quantitatively counted by a special channel electron multiplier (MagneTOF) detector, which ensured high detection efficiency at a very low background.

Fig. 2
figure 2

Measured AI spectra above the ionization potential excited from three different first excited states: 25,075.15 \(\, \text {cm}^{-1} \) (\(J = 13/2\)) (blue graph in a), 25,342.48 \(\, \text {cm}^{-1} \) (\(J = 11/2\)) (green graph in b) and 25,277.64 \(\, \text {cm}^{-1} \) (\(J = 9/2\)) (orange in c) as well as a spectrum obtained by only one laser without additional first excitation step (d). For simple identification of resonances not stemming from the chosen FES, the latter spectrum was relocated by the energy of the respective FES and inserted in dark red color as an upper trace into each AI spectrum, as explained in the caption of Fig. 6. AI resonances studied in detail in this work are highlighted by pale red boxes

Full size image

Laser ionization is normally carried out within the atomizer tube to ensure the highest efficiency in spectroscopic studies. The spectral resolution of this arrangement is limited to a few GHz linewidth by the Doppler broadening, occurring within the atomic vapor. Different ancillary devices have been developed to overcome such limitations. Based upon the Laser Ion Source Trap (LIST) [16], which comprises two electrodes, a radiofrequency quadrupole (RFQ) structure, and an exit plate, providing full suppression of background ions stemming from surface ionization on the hot cavity walls, the perpendicular illuminated version PI-LIST [17, 18] has been set up. By the transverse introduction of laser radiation with respect to the atom beam effusing from the atomizer cavity, high resolution is obtained for studies on hyperfine structures and isotope shifts. A further upgrade is the field ionization version, i.e., the FI-LIST [15], specifically designed for precise adjustment of an external electric field, which is needed for the determination of the ionization potential via the saddle-point model. FI-LIST is formed as a unit consisting of three electrodes in front of the regular LIST RFQ structure. At the first electrode, which is located at a distance of 0.5 mm from the cavity exit, a low negative potential is applied to repel electrons created inside the hot cavity atomizer. A second electrode following immediately has two purposes: One is to repel surface-ionized ions by a positive potential, and the second is to create a well-defined homogeneous electric field toward the third electrode, which is set on a similar but negative potential. These two electrodes are separated by exactly 10 mm distance, and the interaction region for laser radiation with the effusing atomic beam is arranged precisely in the center point of the arrangement. Created ions are directed through electrode three to enter the guiding field of the RFQ structure, which also acts as a protective shield against any influences or disturbances from the high acceleration voltage of the mass spectrometer. A detailed characterization and discussion of the performance of this FI-LIST unit can be found in [15].

Optical transitions of a two-step excitation scheme in the spectrum of the Np atom are induced by using two tunable, pulsed Ti:sapphire lasers pumped by 15 W each of a commercial, frequency-doubled Nd:YAG laser at 532.0nm with 10 kHz repetition rate. Two specific Z-shape resonator geometry types of such tunable lasers were used. These are the so-called standard Ti:sapphire of the Mainz University design, which operates with a typical pulse length of 50 ns, a spectral linewidth of 5 GHz, and up to 4 W average output power [19], but does not permit continuous long-range wavelength scans. The grating-tuned Ti:sapphire laser allows mode-hope-free tuning in the entire accessible spectral range with an output power of up to 2 W and a spectral linewidth of 2–5 GHz [20]. The tuning range of both laser types is 700–1000 nm and can be extended to 350–500 nm by a resonator-internal frequency doubling process within a beta barium borate (BBO) crystal. The fundamental frequency of each laser was measured by a commercial wavemeter (High Finesse WS6-600), with a precision of 600 MHz or 20% of the laser linewidth. Laser beams enter the RISIKO mass separator either anti-collinearly to the ion beam through the dipole magnet, or alternatively, when using the FI-LIST, both lasers are introduced into the interaction region in transversal geometry (see Fig. 1).

3 Ionization schemes

Fig. 3
figure 3

Two-step excitation schemes investigated in Np. The top part is the comparison of the relative efficiencies between the different schemes. The ion counts of AI starting from the first excited states at 25,342.48 \(\, \text {cm}^{-1} \) and 25,277.64 \(\, \text {cm}^{-1} \) are magnified 10 times to visualize the shape of their profiles. The electron configurations are taken from [21] and the IP value from [11]

Full size image

Starting from the even-parity ground state \(5f^{4}6d7s^{2}\) \(^6L\) (\(J = 11/2\)), three different FES at 25,075.15 \(\, \text {cm}^{-1} \) (\(J = 13/2\)) (blue in Figs. 2, 3, 4, 5), 25,342.48 \(\, \text {cm}^{-1} \) (\(J = 11/2\)) (green) and 25,277.64 \(\, \text {cm}^{-1} \) (\(J = 9/2\)) (orange), were chosen for investigation of two-step excitation schemes. Unfortunately, configuration assignments of all three first excited levels are not available. To identify suitable ionization schemes into low-lying autoionizing levels, the grating-tuned laser was scanned by about 800 \(\, \text {cm}^{-1} \) just above the IP for all three cases as shown in the upper part of Fig. 2. During the scanning process of the second laser, a population of alternative FES occurs on occasion. Via a two-photon one-color 1 + 1’ excitation including non-resonant ionization, this leads to extra peaks in the spectra, which would be incorrectly assigned and must be removed. These artifacts in the ionization spectra can be easily detected by scanning the examined range using only one laser, as presented in the lowest trace of Fig. 2. Relocating this spectrum must be done by properly replacing the overall energy value. In the case of excitation with two lasers, the first-step energy is added to the scanning laser energy. In single laser excitation via 1 + 1’ by just twice the second step energy gives the proper peak location and discloses these contributions for easy removal, as shown in Fig. 2 by the individual upper traces given in dark red color in each spectrum. Remarkably, 1 + 1’ scan revealed a very strong two-step one-color scheme at \(2\times 25{,}551.93 \, \text {cm}^{-1} = 51{,}103.86 \, \text {cm}^{-1} \) (pink in Figs. 2, 3), which quasi resonantly populates an AI level at 51,103.7 \(\, \text {cm}^{-1} \), found later on through two different two-step excitation schemes. In Fig. 2, the AI states marked with pale red boxes were chosen as second excited steps. These candidates were selected either according to their strength or favorable wavelength concerning the emission range of the laser. Corresponding seven investigated ionization schemes are illustrated in Fig. 3. The resonance curves and the relative efficiencies of the schemes, obtained from the ion counts measured under identical atomizer and laser power conditions, are given in the upper part of Fig. 3. In addition, a reference one-color 1 + 1’ scheme was employed to subsequently adjust the data for any significant experimental variations not caused by the lasers. A list of the level positions of the five newly reported AI resonances of even parity is given in Table 1, even though no precise angular momenta or assignments can be given.

Table 1 Energy levels and possible J of the investigated AI resonances presented in Fig. 3; three of them were found to be the same state
Full size table

The most efficient scheme turned out to be the one starting at FES 25,075.15 \(\, \text {cm}^{-1} \) with \(J = 13/2\), for which an efficient first-step excitation is expected by the angular momentum change of \(\mathrm {\Delta } J = +1\). This is seemingly combined with an efficient ionization channel in the second step. The scheme is approximately two times more efficient than the one-color 1 + 1’ scheme and about ten times more efficient than the other schemes investigated. Two schemes, i.e., the one with a FES with \(J = 13/2\) (blue in Figs. 3–5) and a FES with \(J = 9/2\) and an AI at 50,909.41 \(\, \text {cm}^{-1} \) (orange) were explicitly proven not to be affected by an intentional plutonium admixture; when the sample with a similar amount of Np and Pu was tested, the Pu, which is much more volatile than Np or U and thus causes more background, was fully suppressed. This verification makes them perfect candidates for fundamental studies of lowest-abundance short-lived isotopes of Np as well as for trace analysis. In both cases, the occurrence of a large surplus of the neighboring elements, e.g., U or Pu must be considered. From the scans of four different first excitation steps, as presented in Fig. 4, we derive that excitations into the four intermediate levels show experimental linewidths of maximum 1.3 \(\, \text {cm}^{-1} \) for the J=13/2 transition, values around 1 \(\, \text {cm}^{-1} \) for the two J=11/2 transitions, down to 0.5 \(\, \text {cm}^{-1} \) for the J=9/2 transition (FWHM). Aside from a small contribution from saturation broadening, caused by a possibly slightly too high laser power chosen for one or the other of these strong transitions, this finding is ascribed to a particularly large hyperfine structure (HFS) in the excited state for J=13/2. As will be discussed in detail in a forthcoming paper [22], where we have studied this effect in the two ground-state transitions at 398.80 nm and 395.61 nm using high-resolution spectroscopy. The overall width of the HFS in the first one to the \(J = 13/2\) intermediate level amounts to more than 1 \(\, \text {cm}^{-1} \), while the most significantly narrower peak of the transition to the \(J = 9/2\) level is caused by a HFS of less than 0.5 \(\, \text {cm}^{-1} \), fully explaining the values obtained here. The experimentally determined energies of all four FES are in full agreement with the literature values from Blaise et al. [23].

Fig. 4
figure 4

Line profiles of the four first excited steps into energy levels at 25,075.15 \(\, \text {cm}^{-1} \) (\(J = 13/2\)), 25,551.93 \(\, \text {cm}^{-1} \) (\(J = 11/2\)), 25,342.48 \(\, \text {cm}^{-1} \) (\(J = 11/2\)) and 25,277.64 \(\, \text {cm}^{-1} \) (\(J = 9/2\))

Full size image

Lifetimes of the FES were assessed by measuring the decay of the FES population. This was achieved by introducing a well-controlled delay between the second-step laser and the first-step laser and recording the decrease in the ion signal as a function of delay time. The corresponding temporal decay of the population in the excited state is plotted against this difference between the laser pulse settings in Fig. 5. After a start sequence, representing the rapid growth and decline of the laser pulse, it follows the expected exponential. It is important to note that, correspondingly, this method for determining lifetimes is not suitable for lifetimes significantly shorter than the laser-pulse duration (\(\approx \) 50 ns). On the other hand, lifetimes longer than approx 3 \(\mathrm {\mu s}\) are also inaccessible, due to the mean free path of the atoms in the source, which affects and falsifies the result [24]. Consequently, we were unable to determine the very short lifetime for the FES at 25,075.15 \(\, \text {cm}^{-1} \) (Fig. 5), where we only give an upper limit. The lifetimes of the FES at 25,342.48 \(\, \text {cm}^{-1} \) and 25,277.64 \(\, \text {cm}^{-1} \) were determined to be 230(12) ns and 173(9) ns, respectively. These values represent the averages obtained from measurements conducted with two distinct laser power levels of 100 mW and \(\approx \) 370 mW of the first step laser to avoid any possible influences caused by saturation.

Fig. 5
figure 5

Lifetime measurements for the first excited levels at: a 25,075.15 \(\, \text {cm}^{-1} \) (\(J = 13/2\)), b 25,342.48 \(\, \text {cm}^{-1} \) (\(J = 11/2\)), and c) 25,277.64 \(\, \text {cm}^{-1} \) (\(J = 9/2\)) measured with a laser power of 100 mW. The ion signal was recorded three times for each excited state to enhance statistics and later fitted with an exponential function. Additional details are provided in the text

Full size image
Fig. 6
figure 6

Spectra of neutral neptunium acquired by scanning the second-step laser just below the IP for the three distinct FES at 25,075.15 \(\, \text {cm}^{-1} \) (\(J = 13/2\)) (blue graph in a), 25,342.48 \(\, \text {cm}^{-1} \) (\(J = 11/2\)) (green graph in b) and 25,277.64 \(\, \text {cm}^{-1} \) (\(J = 9/2\)) (orange graph in c). The lowest trace is a scan of a single laser (d), which is also indicated in dark red color as an upper trace in each spectrum beginning from different FES. The proper relocation of its energetic position as provided within the plots is achieved by dividing the scan width of the \(1 + 1'\) excitation by two and adding the individual first-step energy of the respective two-step excitation. This eases the determination of artifacts in the scans. Notably, there is no noticeable presence of a Rydberg series in these spectra

Full size image

4 Ionization potential

The first attempt to determine the ionization potential of Np applied in this work involved measurements of ionization spectra in a range of about 350 \(\, \text {cm}^{-1} \) below the ionization potential in search of Rydberg series, which could give the IP as a convergence limit. The collected data are given in Fig. 6 in a similar way as the scans above the IP in Fig. 2, but using logarithmic intensity scaling to account for the appearance of weak peaks and structures, which might relate to Rydberg series. All the spectra show numerous resonances within a very rich and heavily complex structure of three orders of magnitude dynamical range; however, no evident pattern that could be assigned to a Rydberg series to deliver the IP was observed. In addition, by using only the scanning laser without first-step excitation, it was verified, that the majority of peaks observed relate to artifacts, caused by alternative first-step excitations with subsequent non-resonant ionization. Furthermore, correlations between remaining peaks, which could have been used for assignment of the angular momentum J, were only found in few case. Thus, no further analysis of the positions, widths, and intensities of these structures has been performed.

As a consequence, an alternative method was worked out and the IP was determined using the saddle point model, as extensively discussed by Littman et al. [25]. This approach utilizes the ionization of highly excited states just below the expected IP within a static electric field. For that purpose, the FI-LIST was installed at RISIKO, modifying the conventional laser ion source [15]. In an external field, ionization appears at a threshold \(W_s\) described by

$$\begin{aligned} W_{s} = \text {IP} - 2\sqrt{\frac{Z_{\text {eff}}e^{3}F}{4\pi \epsilon _{0}}} \end{aligned}$$
(3)
Fig. 7
figure 7

Scans of the second-step laser under different conditions. The top (red) trace represents the laser scan taken without any electric field. The middle (violet) trace is the scan with a detuned first excitation step, revealing parasitic resonances. The lower traces (blue scans) represent the laser scans conducted at different electric fields F, with the corresponding electric field value indicated on the right side. The green dashes denote the peaks chosen for the detailed field scans

Full size image

where the effective charge of the atomic core is \(Z_\text {eff}\), and the external field strength is F. Equation 3 can be simplified for highly excited states, by assuming \(Z_\text {eff} = 1\), resulting in \(W_{s} = \text {IP} - 6.12 \mathrm { (V \cdot cm)}^{-1/2} \cdot \sqrt{F}\). Hence, the IP can be determined through the precise measurement of a suitable number of field ionization thresholds \(W_{s}\) and extrapolation to zero-field conditions.

The scheme via the FES at 25,075.15 \(\, \text {cm}^{-1} \) with \(J = 13/2\) was used for the field ionization measurements, as it delivered a significantly higher count rate compared to any other scheme investigated. An overview of the second-step laser scans performed in a range of about 120 \(\, \text {cm}^{-1} \) below up to slightly above the IP under various electric field strengths is depicted in Fig. 7, in linear y-scaling. The a) trace is obtained without any electric field. There, the ionization was induced by non-resonant processes, e.g., by black body radiation, collisions or non-resonant photons. It compares well to the relevant part of the similar spectrum shown in blue in Fig 6, measured with the conventional laser ion source but exhibits somewhat reduced line intensities. For this reason, the scan was accordingly recorded at a higher atomizer temperature to increase the signal-to-background ratio. The b) trace represents resonances induced only by the second laser, which appear as artifacts in the a) spectrum too. Importantly, these resonances remain unaffected by the presence of an electric field because their excitation energy actually exceeds the IP. The c) to g) traces, given in blue color, show scans performed under different electric fields. It is evident that a higher electric field results in a shift of the ionization threshold toward lower energies. Structures lying above the ionization threshold are preserved independent of the field strengths, showing no significant influence of Stark splittings or shifts. This behavior was similarly observed in the early spectroscopic studies on actinides by Köhler and colleagues [8, 11]. The same behavior was also observed in Pm [12] and it suggests the absence of strong Rydberg peaks in the spectra, which would be influenced significantly by electric fields due to their high polarizability, as observed similarly, e.g., in Yb [15].

Fig. 8
figure 8

Electric field ionization thresholds obtained by scanning electrode two—a trace and electrode three, b trace for the energy level at 50,474.22 \(\, \text {cm}^{-1} \). For more information see the text

Full size image

For the investigations on the IP, we explicitly studied 12 peaks marked with green lines (see Fig. 7) in the range from 50,454 \(\, \text {cm}^{-1} \) to 50,526 \(\, \text {cm}^{-1} \) within electric fields between 2 and 184 V/cm strength. This region is significantly closer to zero field conditions and thus the IP than the one used in the studies by Köhler et al. [11], where they had to use electric field strengths as high as 60 to 340 V/cm for proper operation conditions of the used TOF mass spectrometer. This proximity to zero field reduces influences from improper systematic field determination and error contributions from an extrapolation over a wide range. As it was impossible to scan the field via addressing both electrodes involved, i.e., electrodes two and three (see Fig. 1), of the FI-LIST structure at the same time but in opposite directions, two different scans were carried out for each resonance marked in Fig. 7. Either electrode two was scanned with electrode three set onto the central value of the desired range but with opposite polarity or vice versa. An illustration for the two voltage scans for the energy level at 50,474.22 \(\, \text {cm}^{-1} \) is provided in Fig. 8. The data shown in Fig. 8a correspond to the scan using electrode two, while Fig. 8b shows the scan of electrode three, showing the good agreement among the obtained curves. In none of the twelve cases, any significant discrepancy outside the errors was observed except for a difference in the background level. This is ascribed to the background arising from electron-impact ionization, which was specifically induced by the field settings when scanning electrode two and could not be suppressed fully in the measurements. It was addressed by conducting additional measurements with detuned lasers. This allowed us to subtract any disturbing trend of this background from the data.

Fig. 9
figure 9

Extracted ionization thresholds as a function of the square root of the electric field. The thresholds are represented by orange and red points, depending on whether the electrode two or three was scanned, respectively. The blue line corresponds to the fitted curve for all presented data. The insets display an enlarged view of the deviation between the data points and the fitted line, with a magnification factor of 20x for regions 1–3, and 25x for the others

Full size image

The measured ionization thresholds can be precisely reproduced by a sigmoid function S(F), effectively capturing the convolution of the expected step function with the Gaussian profile of the peak shape

$$\begin{aligned} S(F) = A_{0} + {\frac{A_{1}}{1+e^{-k(F-F_{T})}}}, \end{aligned}$$
(4)

with an offset \(A_{0}\), amplitude \(A_{1}\), exponential coefficient k determining the width, and turning point \(F_{T}\). The latter is identified as the ionization threshold for the corresponding excitation energy, following the detailed discussion and arguments given e.g. in [12]. In order to determine the IP, the parameters of \(W_{s}\) were evaluated as a function of \(\sqrt{F}\), as presented in Fig. 9. The data points given in orange and red correspond to the scans conducted with variations of electrode two and electrode three, respectively. As pointed out above and visualized in the inlays of Fig. 9, individual data points from both scans are in perfect agreement and confirm the expected linear trend. A fit according to Eq. 3 resulted in

$$\begin{aligned} W_{s}^{F}= & {} 50{,}535.54(15) \, \text {cm}^{-1} \nonumber \\{} & {} \quad - 6.029(9) \mathrm {(Vcm)}^{-1/2} \cdot \sqrt{F}. \end{aligned}$$
(5)

That indicates an IP of 50,535.54(15) \(\, \text {cm}^{-1} \), which is in excellent agreement with the literature value of 50,535(2) \(\, \text {cm}^{-1} \) [11]. The line slope is slightly smaller than the value of 6.12 (V cm)\(^{-1/2}\) expected from the saddle point model, which was also previously reported and explained when characterizing the FI-LIST [15]. This fact has already been discussed in the literature, notably in references [12, 26]. It could be attributed to determining the separation distance between the electrodes defining the electric field incorrectly by about 0.1 mm. An alternative explanation attributes the finding to the Stark effect, which is not considered in the simplified saddle point model. Regardless of the origin, it is important to note that the electrode spacing solely affects the slope of the line and does not modify the y-axis intersection, which represents the IP. For all examined voltage configurations, simulations using the SIMION code [27] were performed within a ±2 mm range from the central interaction point of the ionization region for consideration of a possible misalignment of one or both lasers or possible field disturbance by geometric effects. In all cases, the deviation between simulated electric field strength and nominal is well below 1%. It just starts to deviate for the lowest values of around 4 V/cm. Corresponding corrections are included in the presented data and errors.

5 Conclusion and outlook

Extensive studies in the atomic spectrum of neutral neptunium were carried out by two-step laser resonance ionization spectroscopy to search (i) for Rydberg and auto-ionizing levels, (ii) to determine efficient excitation schemes for fundamental investigations and trace analytics, and (iii) for a re-determination of the ionization potential. Three first-step transitions to different—J intermediate levels were investigated including the determination of their lifetimes. Scans below and above the IP were performed. Below the IP an especially rich and strongly fissured structure was found, which prevented the identification of the Rydberg series or any useful analysis of individual level positions. Based on the three first excitation steps, seven reasonably efficient ionization schemes leading above the IP, which are connected to different auto-ionizing resonances of even parity were identified and characterized. Some schemes were tested for the relative suppression of Pu and were found to be good candidates for ultra-trace analysis as well as for fundamental studies of lowest-abundance short-lived Np isotopes, i.e., regarding isotope shift or hyperfine structure measurements. The different first excitation steps were investigated in more detail by determination of their lifetimes and the line profiles.

To re-determine the IP of neptunium, the electric field ionization method based on the saddle point model was employed, yielding a value of 50,535.54(15) \(\, \text {cm}^{-1} \). This result is in excellent agreement with the current literature value of 50,535(2) \(\, \text {cm}^{-1} \) derived by Köhler et al. [11], and represents an improvement in precision by more than an order of magnitude. The good agreement confirms the former measurements by Köhler et al. and proves that the newly developed FI-LIST source unit is a well-suited tool for IP measurements of complex and rare elements. Its application at on-line and off-line radioactive ion beam facilities, e.g., ISOLDE at CERN, and ISAC at TRIUMF, is foreseen for further IP investigation on other exotic atomic species. For future experiments, a reduction of background stemming from electron impact ionization is planned by establishing a fixed electron repeller potential relative to electrode two, for instance, setting \(\mid \)U\({1}\) \(\mid \) = U2—offset, for which the optimal offset value still needs to be determined. Additionally, we could easily implement a time-gated data acquisition relative to the laser pulse, furthermore significantly reducing background from continuous surface ionization or dark counts of the detector [18]. When employing this method, it is crucial to account for ions reaching the detector earlier at higher electric fields.