Abstract
The electronic state spectroscopy of 2(5H)-thiophenone, C4H4OS, has been investigated by high-resolution vacuum ultraviolet photoabsorption in the 3.76–10.69 eV energy range using synchrotron radiation, together with novel quantum chemical calculations performed at the equation of motion coupled cluster singles and doubles (EOM-CCSD) level of theory. The major electronic transitions have been assigned to valence and Rydberg character, with relevant C=O, C=C and C–C stretching vibrations across the entire absorption spectrum. Photolysis lifetimes in the Earth’s atmosphere (0–50 km altitude) have been estimated from the absolute photoabsorption cross-sections, indicating that solar photolysis can be expected to be a strong sink mechanism.
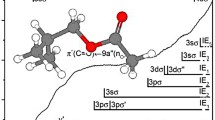
Graphical abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this contribution, we continue investigating the electronic state spectroscopy of five-membered sulphur-containing ring compounds and derivatives, with specific attention given here to 2(5H)-thiophenone, C4H4OS. We have recently considered the lowest-lying valence, mixed valence-Rydberg and Rydberg states of thiophene (C4H4S) [1], due to its role in solid-state material properties as well as in the development of novel of π-conjugated materials, while the two isomeric chlorinated derivatives 2-chlorothiophene and 3-chlorothiophene, C4H3ClS [2], have shown relevance as key selected elements for the development of new optoelectronic materials [3, 4]. 2(5H)-thiophenone is relevant in biological and pharmaceutical applications (e.g. treatment of common heart and cancer diseases) [5] (and references therein); however, its main role is closely related to the production of synthetic targets and intermediates [6].
Other studies that have relevance to the current work include valence shell photoelectron studies on the lowest-lying ionic states [7] and Fourier transform infrared spectroscopy in a low-temperature inert matrix [8]. Experiments on photoinduced ring-opening reactions with internal conversion and intersystem crossing [9] and with ultrafast transient infrared spectroscopy [10] have also been reported. Moreover, the electronic structure and geometry of the neutral molecule 2(5H)-thiophenone molecule have been investigated by theoretical methods [9,10,11,12].
A thorough literature survey reveals no previous detailed information on the low-lying electronic states of C4H4OS in the 3.76–10.69 eV energy range, so we provide for the first time a detailed analysis of the electronic excitation of 2(5H)-thiophenone, by joint high-resolution vacuum ultraviolet (VUV) photoabsorption measurements with state-of-the-art theoretical calculations at the equation of motion coupled cluster singles and doubles (EOM-CCSD) level of theory. In the next section, we present a summary of the structure and properties of 2(5H)-thiophenone. A brief discussion of the experimental details and the computational methods employed in the calculations are given in Sect. 3. Section 4 is devoted to the results and discussion, and the absolute photoabsorption cross sections are used to calculate photolysis rates from 0 to 50 km altitude in the Earth’s atmosphere. Finally, some conclusions that can be drawn from this study are given in Sect. 5.
2 Structure and properties of 2(5H)-thiophenone
The 2(5H)-thiophenone molecule, (C4H4OS), has CS symmetry (A′ and A″) in its electronic ground state, which has calculated valence electronic configuration as: … (10a′)2 (11a′)2 (12a′)2 (13a′)2 (14a′)2 (15a′)2 (16a′)2 (2a″)2 (17a′)2 (18a′)2 (19a′)2 (3a″)2 (20a′)2 (21a′)2 (4a″)2 (5a″)2, while the ordering of (4a″) and (21a′) is reversed to that defined in Chin et al. [7]. The character of the ground-state MOs (Supplementary Information (SI)) reveals that the highest occupied molecular orbital (HOMO), 5a″, is the S 3p lone pair \(\left( {n_{{\text{S}}} } \right)\) out of the molecular plane, while (HOMO-1), 4a″, is mainly π(C=C). The third highest occupied molecular orbital (HOMO-2), 21a′, is the O 2p lone pair orbital \(\left( {\overline{n}_{{\text{O}}} } \right)\) in the molecular plane with some σ(CS) bonding character. The VUV photoabsorption spectrum in Figs. 1, 2, 3, 4 and 5 shows features that are due to electronic excitations from the ground-state molecule to molecular orbitals of valence and Rydberg characters. To help with such assignments, we list in Table 1 the major calculated vertical excitation energies and oscillator strengths.
The available infrared absorption data of Breda et al. [8] on the fundamental vibrational modes of 2(5H)-thiophenone have been used to help assigning the photoabsorption features. From the vibrational energies (and frequencies) in the ground electronic state, these have been assigned to 0.213 eV (1713.9 cm–1) for C2=O6 stretching, \(v_{4}^{\prime } \left( {a^{\prime } } \right)\), 0.200 eV (1615.4 cm–1) for C3=C4 stretching, \(v_{5}^{\prime } \left( {a^{\prime } } \right)\) and 0.078 eV (629.8 cm–1) for S1–C2 stretching/C2=O6 in-plane bending/C5–S1 stretching, \(v_{14}^{\prime } \left( {a^{\prime } } \right)\) (see the atom numbering in Fig. 1); note that the vibrational modes numbering is based on decreasing energy from the data of Breda et al. [8]. The vibrational structure notation of a given mode (X) assigned in the spectrum is adopted as \(X_{m}^{n}\), with m and n the initial and final vibrational states, respectively. However, when the \(0_{0}^{0}\) transition is not discernible, we use the notation \(X^{n}\) instead.
The four lowest experimental vertical (v)/adiabatic (ad) ionisation energies that have been used to calculate the quantum defects associated with transitions to Rydberg orbitals are taken from the photoelectron work of Chin and co-workers [7] to be 9.63 eV \(\left( {5a^{\prime \prime } } \right)^{ - 1}\), 10.58 eV \(\left( {4a^{\prime\prime}} \right)^{ - 1}\), 9.76 eV \(\left( {21a^{\prime } } \right)^{ - 1}\) and 12.25 eV \(\left( {20a^{\prime } } \right)^{ - 1}\).
3 Methodology
3.1 Experiment
A full description of the experimental apparatus used to obtain the high-resolution VUV photoabsorption spectrum of 2(5H)-thiophenone (Fig. 1) has been reported before [13, 14]. Briefly, the AU-UV beam line utilises synchrotron radiation produced by the ASTRID2 storage ring (Aarhus University, Denmark), and was used to perform the photoabsorption experiments. High-resolution (better than 0.08 nm) VUV radiation is passes through an absorption gas cell that is filled with vapour of 2(5H)-thiophenone. The absorption cell is enclosed by transmission windows (MgF2), with the transmitted light detected by a photomultiplier tube (PMT). The absolute pressure of the gas sample in the cell is monitored by a capacitance manometer (Chell CDG100D), while saturation effects are avoided by recording the absorption data in small regions using a pressure in the range 0.043–0.28 mbar according to the local cross-section. This methodology guarantees to have attenuations of 50% or less. The 2(5H)-thiophenone absolute photoabsorption cross-section values σ, in Figs. 1, 2, 3, 4 and 5 (1 Mb ≡ 10–18 cm2), were obtained using the well-known Beer–Lambert attenuation law \(I_{t} = I_{0} e^{{\left( { - N\sigma l} \right)}}\), where It is the light intensity transmitted through the gas sample, Io is that through the evacuated cell, N is the molecular number density of C4H4OS, and l is the absorption path length (15.5 cm). Note that background scans were also recorded with the empty gas cell. For each absorption spectrum recorded, the synchrotron beam current was monitored.
The accuracy of the VUV absorption cross-section data is obtained by recording the different sections of the spectrum in 5 or 10 nm sections, with an overlap of 10 points between the adjoining sections. ASTRID 2 operates in a “top-up” mode, which guarantees a quasi-constant light intensity as a function of time, thus compensating for beam decay in the storage ring. The small variations in beam current (and therefore light intensity) of up to 2–3% are removed by normalising the data to the beam current in the storage ring. Such a procedure allows an accuracy in photoabsorption cross-sections obtained to within ± 5%. The comprehensive assignments in the different absorption regions are listed in Tables 2, 3, 4 and 5.
The liquid sample of 2(5H)-thiophenone was purchased from Sigma-Aldrich, with a stated purity of 98%. The sample was degassed through repeated freeze–pump–thaw cycles before use.
3.2 Theoretical methods
Quantum chemical calculations were performed in the optimised geometry of 2(5H)-thiophenone (Fig. SI1), at the CCSD level of calculation with the aug-cc-pVTZ basis set from Dunning et al. [15, 16] for H, C and O. For the S atom, the modified aug-cc-p(V + d)Z from Dunning et al. [15] was employed. For the description of Rydberg excited states, the basis set was augmented at the mass centre of the molecule by a set (6s6p4d) of diffuse orbitals, taken from [16]. The excited electronic states were obtained for the ground-state optimised molecular geometry, employing the EOM-CCSD method [17] and the aug-cc-pV(T + d)Z + R basis set (Tables 1 and SI1), using the MOLPRO 2019.1 code [18, 19]. The nature of each excitation was assessed by visual inspection of the natural orbitals for each transition and the average value < r2 > of the electronic cloud. The calculated vertical excitation energies of the lowest singlet states (S1–S7) at different levels of theory have also been obtained and compared to previous results too (see Table SI2). Similarly, the calculated vertical ionisation energies (CCSD geometry with the aug-cc-pV(T + d)Z basis set) using several methods are compared with the available experimental values shown in Table SI3.
4 Results and discussion
The room-temperature VUV photoabsorption spectrum of 2(5H)-thiophenone is shown in Fig. 1 in the photon energy range of 3.76–10.69 eV. To help interpreting the spectrum, our EOM-CCSD calculations are summarised in Table 1, while complete calculated vertical excitation energies are given in Table SI1 of the Supplementary Information. The spectroscopic assignments for the different bands are detailed in Tables 2, 3, 4 and 5 together with the calculated vertical excitation energies of the singlet states (S1–S7) and the lowest-lying ionic states (Tables SI2 and SI3). The lowest-lying electronic excitation results are assigned to valence and Rydberg (see Sect. 4.4), the latter converging to the lowest-lying ionic states, (5a″)–1 \(\tilde{X}^{2} A^{\prime \prime }\), (4a″)–1 \(\tilde{A}^{2} A^{\prime \prime }\), (21a′)–1 \(\tilde{B}^{2} A^{\prime }\) and (20a′)–1 \(\tilde{C}^{2} A^{\prime }\). The EOM-CCSD results in Table 1 are compared with the experimental data, where a reasonably good level of agreement is obtained (a few tenths of 1 eV). The different spectral sections (Figs. 2, 3, 4, 5) show fine structures that have been assigned to C2=O6 stretching, C3=C4 stretching and S1–C2 stretching/C2=O6 in-plane bending/C5–S1 stretching modes. The broadness of the photoabsorption bands above 7.0 eV, albeit the fine structure superimposed on these, is mostly due to the overlap of different Rydberg electronic states. As a consequence of such contributions (vibronic excitations in valence and Rydberg states), the different sections of the absorption spectrum (Figs. 2, 3, 4, 5) do not contain the complete set of assignments, which otherwise would manifest particularly congested, but are listed in detail in Tables 2, 3, 4 and 5. The normal mode description of vibrations is relevant throughout the entire photoabsorption spectrum with special attention to the lowest-lying excitations, with the possibility of Fermi resonances.
The main electronic excitations are assigned to the promotion of an electron from the \(n_{{\text{S}}}\) (HOMO), πCC (HOMO-1) and in-plane oxygen lone pair \(\overline{n}_{{\text{O}}}\) (HOMO-2) to the lowest unoccupied molecular orbitals (Tables 1 and SI1, Fig. SI2). The following sections present a comprehensive description of the electronic state spectroscopy of 2(5H)-thiophenone in the different photoabsorption regions with the help of the quantum chemical calculations.
4.1 Electronic excitations in the energy range 3.7–7.0 eV
Figure 2a depicts a broad spectral feature with weak vibrational features that are assigned in Table 2. The photoabsorption cross-section in this region has a maximum at 4.787 eV with a value of 5.94 Mb, and the calculations suggest this transition to be due to \(\pi_{{{\text{CC}}}}^{*} + \pi_{{{\text{CO}}}}^{*} \left( {6a^{\prime \prime } } \right) \leftarrow n_{{\text{S}}} \left( {5a^{\prime \prime } } \right), \left( {2\;^{1} A^{\prime } \leftarrow \tilde{X}\;^{1} A^{\prime } } \right)\) with an oscillator strength of 0.05785 (Table 1). However, another less intense electronic transition at 4.028 eV, fL ≈ 0.0004, (Fig. 2b) is due to promotion of an electron from the HOMO-2 (21a′) to the LUMO (6a″), \(\pi_{{{\text{CC}}}}^{*} + \pi_{{{\text{CO}}}}^{*} \left( {6a^{\prime \prime } } \right) \leftarrow \overline{n}_{{\text{O}}} \left( {21a^{\prime } } \right), \left( {1\;^{1} A^{\prime \prime } \leftarrow \tilde{X}\;A^{\prime } } \right)\). The rather low-intensity of the band is related to poor overlap between the in-plane \(\overline{n}_{{\text{O}}} \left( {21a^{\prime } } \right)\) and the out-of-plane LUMO (6a″). Note that similar behaviour has recently been noted in the lowest-lying absorption band of formic acid [20]. The calculations in Table 1 reveal that the electronic transitions from the ground state to \(1\;^{1} A^{\prime \prime }\) and \(2\;^{1} A^{\prime }\) show antibonding \(\pi_{{{\text{CO}}}}^{*}\) and \(\pi_{{{\text{CC}}}}^{*}\) characters (Fig. SI2). Investigations of the photoinduced processes at 257 nm (4.644 eV) [9, 10] of such absorption band have reported prompt ring-opening (< 1 ps) from the characteristic antisymmetric ketene stretching mode, yet \(\sim\)60% of the photoexcited molecules find their way back to the parent S0 state vibrationally excited [10]. This seems to be in line with the experimental evidence of the present absorption band. It is interesting to note that cuts along the RC–S ring-opening coordinate, involving the ground and the first 1A′ and 1A″ states, exhibit strong vibrational coupling between the states that can be promoted by normal modes of a″ symmetry, allowing the excited system to return to the ground state [10]. Although from the assignments no a″ vibrational modes have been noted, we cannot discard the possibility of their relevance to the absorption band.
The 2(5H)-thiophenone absorption band in the photon energy range of 3.7–4.5 eV shows extensive vibrational features. Analysis of these features in Fig. 2b reveals contributions of the C2=O6 stretching, \(v_{4}^{\prime } \left( {a^{\prime } } \right)\), C3=C4 stretching, \(v_{5}^{\prime } \left( {a^{\prime } } \right)\) S1–C2 stretching/C2=O6 in-plane bending/C5–S1 stretching, \(v_{14}^{\prime } \left( {a^{\prime } } \right)\) modes, with the average vibrational spacing being 0.210, 0.190 and 0.072 eV, respectively (Table 2), although the origin of the band is not discernible. Further analysis of Fig. 2b also reveals a change in the slope of the band at \(\sim\) 4.1 eV. This can suggest the presence of another underlying state contributing to the spectrum. Xie et al. [9] calculated vertical excitation energies of the three lowest triplet states (T1–T3) at different levels of theory, with T1 at \(\sim\) 4.12 eV (95 kcal mol−1). While such a forbidden transition is typically indiscernible in experimental photoabsorption spectrum, the low intensity of the band (< 0.2 Mb) may be related in some way to a contribution of this nature.
The next electronic transition has its \(0_{0}^{0}\) origin at 5.75(6) eV (Table 3) and the maximum of the absorption band peaks at 6.344 eV with a cross-section of 23.21 Mb. The calculations in Table 1 assign the electronic transition to promotion of an electron from the HOMO-1 (4a″) to the LUMO (7a″), \(\pi_{{{\text{CC}}}}^{*} + \pi_{{{\text{CO}}}}^{*} \left( {6a^{\prime \prime } } \right) \leftarrow \pi_{{{\text{CC}}}} \left( {4a^{\prime \prime } } \right),\left( {3\;^{1} A^{\prime } \leftarrow \tilde{X}\;^{1} A^{\prime } } \right)\), with an oscillator strength of 0.14547. Although the major transitions predicted in the calculations for this energy region are valence in character, two Rydberg states are also tentatively assigned in Table 5, at 6.344 eV (4sσ ← 5a″) and 6.37(1) eV (4sσ ← 21a′), which will be discussed in Sect. 4.4. Nevertheless, analysis of the 5.5–7.0 eV energy region shows that the C2=O6 stretching, \(v_{4}^{\prime } \left( {a^{\prime } } \right)\), C3=C4 stretching, \(v_{5}^{\prime } \left( {a^{\prime } } \right)\) and S1–C2 stretching/C2=O6 in-plane bending/C5–S1 stretching, \(v_{14}^{\prime } \left( {a^{\prime } } \right)\) modes are active, with average vibrational spacing of 0.209, 0.183 and 0.065 eV, respectively (Table 3). On the higher energy side of the band (above 6.5 eV, see Fig. 3), at 6.93(0) eV a broad feature with a cross-section value of 14.73 Mb is assigned to the \(\pi_{{{\text{CC}}}}^{*} + \pi_{{{\text{CO}}}}^{*} \left( {22a^{\prime } } \right) \leftarrow \overline{n}_{{\text{O}}} \left( {21a^{\prime } } \right)\), \(\left( {4\;^{1} A^{\prime } \leftarrow \tilde{X}\;^{1} A^{\prime } } \right)\) transition (Table 1).
Table SI2 shows the calculated vertical excitation energies at different levels of theory compared with previous work and the present experimental data. The level of agreement between the experimental data for the singlet states S1 (4.028 eV) and S2 (4.787 eV) is very good with MS-CASPT2/cc-pVDZ [9] and ADC(2)/aug-cc-pV(T + d)Z + R, while S3 (6.344 eV) is better described by CASPT2/SA3-CAS(10,8)/6-31G*/MM [11]. Due to the closeness between the calculated S4 and S5 states, from the experiment we can only discern the latter (6.930 eV) which is reasonably obtained at the RS2C/SA-CAS(6,15)/aug-cc-pV(T + d)Z + R level of theory from multi-reference calculations. Table SI2 emphasises the fact that the calculated lowest-lying vertical transition energies are very method and basis set dependent.
4.2 Electronic excitations in the energy range 7.0–8.5 eV
The next electronic transition has its \(0_{0}^{0}\) origin at 7.315 eV, has a maximum intensity of 52.46 Mb at 7.827 eV, and is assigned to a transition from the electronic ground state to Rydberg orbitals, \(3d\sigma \left( {a^{\prime } } \right) \leftarrow \overline{n}_{{\text{O}}} \left( {21a^{\prime } } \right) + 3d\pi \left( {a^{\prime \prime } } \right) \leftarrow n_{{\text{S}}} \left( {5a^{\prime \prime } } \right),\left( {9\;^{1} A^{\prime } \leftarrow \tilde{X}\;^{1} A^{\prime } } \right)\), and with a calculated electronic radial spatial extent (144) indicative of such character (Table 1). The transition is mainly accompanied by excitation of C2=O6 stretching, \(v_{4}^{\prime } \left( {a^{\prime } } \right)\) (spacing 0.244 eV) with a few quanta of C3=C4 stretching, \(v_{5}^{\prime } \left( {a^{\prime } } \right)\) (spacing 0.195 eV) and S1–C2 stretching/C2=O6 in-plane bending/C5–S1 stretching, \(v_{14}^{\prime } \left( {a^{\prime } } \right)\) (spacing 0.061 eV) modes. Another Rydberg state excitation at 7.827 eV is assigned to (4pσ ← 4a″), though this is more thoroughly discussed in Sect. 4.4. This absorption band is shown in detail in Fig. 4 with the assignments of the spectral features in Table 3. The absorption features above about 8 eV are also broad and can be due to the contribution of the mixing character with other Rydberg \(\left( {5a^{\prime \prime } } \right)^{ - 1}\) and \(\left( {21a^{\prime } } \right)^{ - 1}\) series, also showing relevant vibrational structure discussed in more detail below and listed in Table 4.
From the calculated vertical excitation energies in Table SI2 for the singlet excited state S7, the RS2C/SA-CAS(6,15)/aug-cc-pV(T + d)Z + R level of theory from multi-reference calculations gives a better agreement with the experiment (to within 0.2 eV), while EOM-CCSD/aug-cc-pV(T + d)Z + R (7.022 eV) and ADC(2)/aug-cc-pV(T + d)Z + R (7.064 eV) underestimate it by 10%.
4.3 Electronic excitations in the energy range of 8.5–10.7 eV
This band of the photoabsorption spectrum is dominated by a large number of spectral features that are assigned to members of the different Rydberg transitions converging to the (5a″)–1 \(\tilde{X}\;^{2} A^{\prime \prime }\), (4a″)–1 \(\tilde{A}\;^{2} A^{\prime \prime }\), (21a′)–1 \(\tilde{B}\;^{2} A^{\prime }\) and (20a′)–1 \(\tilde{C}\;^{2} A^{\prime }\) ionic states of 2(5H)-thiophenone (discussed in detail below). The features contributing to the absorption spectrum result from the overlap of the different Rydberg electronic states and the different vibrational modes contributing to the spectrum (Table 4), thus yielding rather broad features as well as to augment others, which otherwise would not manifest so intensely (Fig. 5). The calculations in Table 1 (and Table SI1) do not predict any valence excitations in this photon energy region, despite the background contribution to the absorption spectrum. Note that in this region, and especially above 9.5 eV, photoionisation to the (5a″)–1, (4a″)–1 and (21a′)–1 states may contribute to the spectrum and so reducing the observable features within this region.
4.4 Rydberg series
The photoabsorption spectrum of 2(5H)-thiophenone show features reminiscent of Rydberg character (Figs. 3, 4, 5) across the majority of the bands, with the experimental energies, assignments and quantum defects in Table 5. Table SI3 lists the calculated valence and outer valence vertical ionisation energies (IEs) for 2(5H)-thiophenone at the EOM-CCSD/aug-cc-pV(T + d)Z, together with other different levels of theory, and compares with the experimental photoelectron data [7]. A close inspection of these values reveals that all the theoretical methods agree reasonably well with each other to within 0.1–0.3 eV; P3+ seems to be the more accurate, while those provided by the Koopmans’ theorem are larger, which is due to electron correlations and relaxation being neglected. The P3+ and EOMIP-CCSD [21] results are very close to each other, while the EOMIP-CC3 method [22] tends to overestimate by as much as 6% the experimental data. The geometry of the 2(5H)-thiophenone was kept at CS symmetry, in the optimised ground state geometry, as indicated in Fig. S1.
Each absorption feature in the spectrum has been tested with the well-known Rydberg formula: \(E_{n} = IE - \frac{R}{{\left( {n - \delta } \right)^{2} }}\), where IE is the ionisation energy, n is the principal quantum number of the Rydberg orbital of energy En, R is the Rydberg constant (13.61 eV), and δ is the quantum defect resulting from the penetration of the Rydberg orbital into the core. From the work of Robin, we find that for sulphur, the expected range of value for the different quantum defects are: 1.9 < δ < 2.0 for ns, 1.4 < δ < 1.8 for np, and 0.1 < δ < 0.5 for nd [23]. We are not aware of any previous detailed assignments of the Rydberg features as those carried out here.
The first member (n = 4) of the lowest-lying Rydberg transition at 6.344 eV is assigned to the \(\left( {4s\sigma \leftarrow \left( {5a^{\prime\prime}} \right)} \right)\) excitation, with a quantum defect δ = 1.96 (Table 5). In Sect. 4.1 (see Fig. 3), we have noted that the absorption band that may contain a contribution of the 4sσ member is mostly due to a valence character rather than Rydberg. Table 5 lists other members of the Rydberg \(ns\sigma\) series up to n = 10, whereas the features at 8.14(6), 9.100, 9.253 and 9.350 eV (n = 5sσ, 7sσ, 8sσ and 9sσ) have also been assigned to the contribution of other Rydberg members 3dσ′(21a′)–1, 6pπ(21a′)–1, 6dσ′(5a″)–1/5pσ(4a″)–1, and 7dσ(5a″)–1, respectively. The rather high value of the quantum defects for the 9 s and 10 s members are attributed to the influence of the other closest-lying Rydberg states.
The first members of the two np (npσ ← 5a″) and (npπ ← 5a″) series are connected with absorption features at 6.93(0) and 7.54(2) eV (δ = 1.75 and 1.45, respectively) (Table 5). The mixed valence character of these transitions, in particular for the lowest absorption features (Sect. 4.2), can be related to the relatively high values of the quantum defects. The 6pσ and 7pπ features at 8.847 and 9.18(4) eV can also be assigned to 3dσ(4a″)–1 and 5dσ′(21a′)–1. Our assignments also report the presence of two nd (ndσ ← 5a″) and (ndσ′ ← 5a″) series, with the n = 3 features at 7.90(2) and 8.06(7) eV (δ = 0.19 and 0.05) (Table 5). The features at 8.698 (4dσ) and 9.05(7) eV (5dσ) are also assigned to 5pπ(21a′)–1 and 5sσ(4a″)–1. It is relevant to note that higher-lying members of the \(nd\) Rydberg series up to n = 7 have been assigned in the photoabsorption spectrum. However, due to the rather low intensity of the absorption features, we have attempted no further assignment of n > 7 members of the Rydberg series.
The Rydberg series converging to the ionic electronic first excited state, listed in Table 5, have been assigned to the \(\left( {ns\sigma ,np\sigma ,np\pi ,nd\sigma ,nd\sigma^{\prime } \leftarrow 4a^{\prime \prime } } \right)\) transitions. The first members in Table 5 of the \(ns\sigma ,np\sigma ,np\pi ,nd\sigma\) and \(nd\sigma^{\prime }\) series have been obtained for features at 7.51(0) eV (δ = 1.89), 7.827 eV (δ = 1.78), 8.51(8) eV (δ = 1.43), 8.84(7) eV (δ = 0.20) and 8.98(4) eV (δ = 0.08), respectively. Absorption features at 7.51(0) and 9.96(3) eV can also contribute to 4pπ(21a′)–1 and 5dσ(4a″)–1.
The next set of Rydberg series converging to the ionic electronic second excited state have been assigned to the \(\left( {ns\sigma ,np\sigma ,np\pi ,nd\sigma ,nd\sigma^{\prime } \leftarrow 21a^{\prime } } \right)\) transitions. Table 5 lists the first members of the \(ns\sigma ,np\sigma ,np\pi ,nd\sigma\) and \(nd\sigma^{\prime }\) series at 6.37(1) eV (δ = 2.00), 7.42(4) eV (δ = 1.59), 7.51(0) eV (δ = 1.54), 7.99(9) eV (δ = 0.22) and 8.14(6) eV (δ = 0.10), respectively. The feature at 9.54(8) eV assigned to n = 10sσ is also due to a Rydberg transition to 4pσ(20a′)−1.
Finally, the Rydberg series converging to the ionic electronic third excited state have been assigned to the \(\left( {ns\sigma ,np\sigma ,np\pi ,nd\sigma \leftarrow 20a^{\prime } } \right)\) transitions. The first members of the \(ns\sigma ,np\sigma ,np\pi\) and \(nd\sigma\) series in Table 5 are associated with features at 8.89(1) eV (δ = 1.99), 9.45(8) eV (δ = 1.76), 10.19(6) eV (δ = 1.43) and 10.50(7) eV (δ = 0.21), respectively. For members of the Rydberg series n > 4, no tentative assignments have been performed because their energy positions lie outside the photon energy range investigated in the present experiments.
Vibrational excitation involving some of the Rydberg series converging to the \(\left( {5a^{\prime \prime } } \right)^{ - 1}\), \(\left( {4a^{\prime \prime } } \right)^{ - 1}\), \(\left( {21a^{\prime } } \right)^{ - 1}\) and \(\left( {20a^{\prime } } \right)^{ - 1}\) states is assigned in Tables 3 and 4, and not included in Fig. 5 to avoid congestion. The fine structure has been assigned to the C2=O6 stretching, \(v_{4}^{\prime } \left( {a^{\prime } } \right)\), the C3=C4 stretching, \(v_{5}^{\prime } \left( {a^{\prime } } \right)\) and the S1–C2 stretching/C2=O6 in-plane bending/C5–S1 stretching, \(v_{14}^{\prime } \left( {a^{\prime } } \right)\) modes. Combination bands of these modes have also been assigned.
4.5 Absolute photoabsorption cross sections and atmospheric photolysis
The absolute cross-section values listed in Table 1 are related to the most prominent electronic transitions. A comprehensive literature survey reveals no previous studies to compare with the ultraviolet photoabsorption data in the wavelength region of 116–330 nm (3.76–10.69 eV) covered in the present work. Photolysis rates of 2(5H)-thiophenone in the Earth’s atmosphere, from 0 km altitude up to 50 km (the limit of the stratopause), can be estimated by combining the high-resolution VUV absolute photoabsorption cross-sections and the solar actinic flux distribution [24]. To obtain such information and thus the local lifetime of a given molecular compound emitted to the atmosphere under sunlit conditions [16], we use a well-established methodology with details thoroughly described in Reference [25]. The quantum yield for dissociation is assumed to be unity due to lack of any information in the literature. Computed photolysis lifetimes of less than 1 sunlit day were calculated at altitudes above ground level, thus indicating that 2(5H)-thiophenone can be efficiently broken up by UV absorption at those altitudes. We are not aware of any complete study of the gas-phase kinetics for 2(5H)-thiophenone reactions with ·OH radicals or any other radical relevant within the Earth’s atmosphere (e.g. Cl, NO3, O3) to assess the role of such processes as the main sink mechanism.
5 Conclusions
We have reported for the first time a comprehensive study of the electronic state spectroscopy of 2(5H)-thiophenone in the 3.76–10.69 eV photon energy range. The absolute values of the present measured high-resolution cross sections have been assigned to valence and Rydberg transitions, with the help of quantum chemical calculations, the latter providing vertical excitation energies and oscillator strengths. The joint experimental and theoretical methodology has allowed the assignment of the fine structure in the spectrum, which is due to the contributions of C2=O6 stretching, \(v_{4}^{\prime } \left( {a^{\prime } } \right)\), C3=C4 stretching, \(v_{5}^{\prime } \left( {a^{\prime } } \right)\), and S1–C2 stretching/C2=O6 in-plane bending/C5–S1 stretching, \(v_{14}^{\prime } \left( {a^{\prime } } \right)\) modes. The photolysis lifetimes of 2(5H)-thiophenone were also obtained for the Earth’s atmosphere, from 0 km up to 50 km (the limit of the stratopause), demonstrating that solar photolysis is expected to be a strong sink if no other relevant gas-phase reactions with ·OH and other radicals present in the Earth’s atmosphere (e.g. Cl, NO3, O3) prevail.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The VUV spectrum will be uploaded to Softcon and the MPI-Mainz UV/Vis spectral Atlas (https://www.uv-vis-spectral-atlas-mainz.org/uvvis/)].
References
D.B. Jones, M. Mendes, P. Limão-Vieira, F.F. Silva, N.C. Jones, S.V. Hoffmann, M.J. Brunger, J. Chem. Phys. 150, 064303 (2019)
F.V.S. Oliveira, A.S. Barbosa, N.C. Jones, S.V. Hoffmann, P. Limão-Vieira, J. Quant. Spectrosc. Radiat. Transf. 296, 108443 (2023)
N.L. Campbell, W.L. Duffy, G.I. Thomas, J.H. Wild, S.M. Kelly, K. Bartle, M. O’Neill, V. Minter, R.P. Tuffin, J. Mater. Chem. 12, 2706 (2002)
M. Romanini, P. Negrier, M. Barrio, D. Mondieig, P. Serra, M.J. Zuriaga, R. Macovez, J.L. Tamarit, Cryst. Growth Des. 19, 6405 (2019)
J.D. Coyle, Chem. Rev. 78, 97 (1978)
N.B. Carter, A.E. Nadany, J.B. Sweeney, J. Chem. Soc. Perkin Trans. 1, 2324 (2002)
W.S. Chin, Z.P. Xu, C.Y. Mok, H.H. Huang, H. Mutoh, S. Masuda, J. Electron Spectrosc. Relat. Phenom. 88–91, 97 (1998)
S. Breda, I. Reva, R. Fausto, J. Mol. Struct. 887, 75 (2008)
B. Bin Xie, B.L. Liu, X.F. Tang, D. Tang, L. Shen, W.H. Fang, Phys. Chem. Chem. Phys. 23, 9867 (2021)
D. Murdock, S.J. Harris, J. Luke, M.P. Grubb, A.J. Orr-Ewing, M.N.R. Ashfold, Phys. Chem. Chem. Phys. 16, 21271 (2014)
B. Bin Xie, W.H. Fang, ChemPhotoChem 3, 897 (2019)
G.M.J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J.E. Deustua, D.G. Fedorov, J.R. Gour, A.O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S.S. Leang, H. Li, W. Li, J.J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B.Q. Pham, P. Piecuch, D. Poole, S.R. Pruitt, A.P. Rendell, L.B. Roskop, K. Ruedenberg, T. Sattasathuchana, M.W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J.L. Galvez Vallejo, B. Westheimer, M. Włoch, P. Xu, F. Zahariev, M.S. Gordon, J. Chem. Phys. 152, 154102 (2020)
S. Eden, P. Limão-Vieira, S.V. Hoffmann, N.J. Mason, Chem. Phys. 323, 313 (2006)
M.H. Palmer, T. Ridley, S.V. Hoffmann, N.C. Jones, M. Coreno, M. De Simone, C. Grazioli, M. Biczysko, A. Baiardi, P. Limão-Vieira, J. Chem. Phys. 142, 134302 (2015)
J. Dunning, K.A. Peterson, A.K. Wilson, J. Chem. Phys. 114, 9244 (2001)
D. Duflot, S. V. Hoffmann, N. C. Jones, and P. Limão-Vieira, in Radiation Bioanalysis Spectroscopic Techniques and Theoretical Methods, ed. by A. S. Pereira, P. Tavares, and P. Limão-Vieira (Springer, 2019), pp. 43–81
C. Hampel, K.A. Peterson, H.J. Werner, Chem. Phys. Lett. 190, 1 (1992)
H.J. Werner, P.J. Knowles, G. Knizia, F.R. Manby, M. Schütz, WIREs Comput. Mol. Sci. 2, 242 (2012)
H.-J. Werner, P. J. Knowles, et al, (2019). MOLPRO, version, a package of ab initio programs. https://www.molpro.net
P.A.S. Randi, D.F. Pastega, M.H.F. Bettega, N.C. Jones, S.V. Hoffmann, S. Eden, A. Souza Barbosa, P. Limão-Vieira, Spectrochim. Acta Part A 289, 122237 (2023)
J.F. Stanton, J. Gauss, J. Chem. Phys. 101, 8938 (1994)
J.F. Stanton, J. Gauss, J. Chem. Phys. 111, 8785 (1999)
M.B. Robin, Higher Excited States of Polyatomic Molecules, vol. III (Academic Press, 1985)
Chemical Kinetics and Photochemical Data for Use in Stratospheric Modelling, Evaluation Number 12, NASA, Jet Propulsion Laboratory, JPL, Publication 97–4, January 15 (1997).
P. Limão-Vieira, S. Eden, P.A. Kendall, N.J. Mason, S.V. Hoffmann, Chem. Phys. Lett. 364, 535 (2002)
Acknowledgements
SK acknowledges the Portuguese National Funding Agency (FCT) through PD/BD/142831/2018 and COVID/BD/152673/2022, and together with PLV the research grant CEFITEC (UIDB/00068/2020). This work was also supported by Radiation Biology and Biophysics Doctoral Training Programme (RaBBiT, PD/00193/2012); UCIBIO (UIDB/04378/2020). D.D. thanks the support from the CaPPA Project (Chemical and Physical Properties of the Atmosphere) funded by the French National Research Agency (ANR) through the PIA (Programme d’Investissement d’Avenir) under Contract No. ANR-10-LABX-005; the Région Hauts de France and the Ministère de l’Enseignement Supérieur et de la Recherche (CPER ECRIN) and the European Fund for Regional Economic Development for their financial support. This work was performed using HPC resources from GENCI-TGCC (Grant No. 2022-A0110801859) and the Centre de Ressources Informatiques (CRI) of the Université de Lille. The authors wish to acknowledge the beam time at the ISA synchrotron, Aarhus University, Denmark. The research leading to this work has been supported by the Project CALIPSOplus under the Grant Agreement 730872 from the EU Framework Programme for Research and Innovation HORIZON 2020. GG acknowledges the Spanish Ministerio de Ciencia e Innovación (Project No. PID2019-104727RB-C21) and the EURAMET’s Project 21GRD02 BIOSPHERE. This contribution is also based upon work from the COST Action CA18212-Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology).
Funding
Open access funding provided by FCT|FCCN (b-on).
Author information
Authors and Affiliations
Contributions
S.K. and N.C.J. performed the experimental measurements. D.D. performed the quantum chemistry calculations. S.K., N.C.J., S.V.H. and P.L.V. analysed the data. P.L.V. and G.G. conceptualised and supervised the project. P.L.V. and D.D. wrote the manuscript.
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
We dedicate this contribution to the memory of the late Professor Michael Brunger with whom we have had a fruitful and loyal scientific cooperation for almost two decades.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kumar, S., Duflot, D., Jones, N.C. et al. The electronic structure of 2(5H)-thiophenone investigated by vacuum ultraviolet synchrotron radiation and theoretical calculations. Eur. Phys. J. D 77, 202 (2023). https://doi.org/10.1140/epjd/s10053-023-00771-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjd/s10053-023-00771-w