1 Introduction

The gravitational collapse, particularly the final stage of a sufficiently massive collapsing star, remains a formidable challenge in theoretical astrophysics. Most stellar entities, including stars, white dwarfs, and neutron stars, result from the gravitational collapse process. For stars with masses exceeding Chandrasekhar’s limit of \(1.4 M_\odot \), possess gravitational collapse driven by degeneracy pressure. The pressures exerted by electrons or neutrons are insufficient to counterbalance gravity, resulting in an ongoing gravitational collapse [1]. It is widely theorized that the collapse of such massive stars eventually leads to the formation of a space-time singularity [2]. However, the inquiry into the eventual outcomes of such massive stars as they deplete their nuclear fuel-essentially, the possible culmination of prolonged gravitational collapse-has been a crucial problems in astronomy and astrophysics for decades. Addressing this question necessitates an investigation into the dynamical collapse scenarios of stars within the framework of gravitational theories such as Einstein’s general theory of relativity.

In general relativity (GR), the nonlinearity of Einstein’s field equations (EFE) complicates the quest for precise solutions to collapse phenomena when considering equations of state (EoS) and radiation transport properties of fluids. It is evident that once collapsing fluids become enveloped by an event horizon, collapse towards the central singularity becomes inevitable. Thus, understanding the application of the EoS up to the point of horizon formation is imperative. In massive stars, nuclear fusion prevents the counteraction of gravitational collapse by thermal pressure, leading to the collapse into a spacetime singularity [3, 4]. According to Penrose’s Cosmic Censorship Conjecture (CCC), the resulting spacetime singularity from gravitational collapse should be obscured behind the event horizon, suggesting that a black hole (BH) is the only conceivable endpoint of collapse [4]. Various models concerning the gravitational collapse of matter have been developed, some of which lead to the formation of a naked singularity (NS)-the strong cosmic censorship conjecture [5].

Currently, theoretical astrophysicists are confronted with difficulties in comprehending the ultimate outcome of a massive star’s collapse. The inquiry into the fate of massive stars as they deplete their nuclear fuel has long been a pivotal challenge in astrophysics. Consequently, our ongoing research could unveil novel astrophysical phenomena beyond black holes and naked singularities, guiding future investigations. Exploring the dynamics of stellar collapse scenarios from different aspects is imperative for gaining insight into the potential outcomes of gravitational collapse. At this juncture, it is crucial to recall that the Oppenheimer–Snyder model (OS) [6] serves as the foundational framework concerning the inexorable progression of black hole (BH) development in terms of solutions. The OS collapse scenario represented a highly idealized examination, wherein they initiated the investigation of gravitational collapse employing dust fluids. The most comprehensive collapse model encompasses a spherically symmetric self-gravitating sphere, wherein the stellar interior incorporates factors such as pressure, shear, heat flux, etc. Numerous scholars have explored gravitational collapse considering perfect fluid, anisotropy, and dissipation (refer to [7,8,9] and additional references). Subsequently, the current inquiry delves into significant configurations of homogeneous gravitational collapse with a perfect fluid sphere, elucidating their thorough analysis.

In the field of General Relativity (GR), it is commonly understood that the dynamics of collapsing fluids can be characterized by various factors including the four-velocity vectors, shear tensor, vorticity tensor (which is absent in our scenario), and the expansion scalar (\(\Theta \)). This scalar quantity, \(\Theta \), denotes the rate of change in the volume of fluid elements and plays a crucial role in understanding collapsing configurations. Recent investigations by authors [10, 11] have delved into a novel category of inhomogeneous gravitational collapse featuring a uniform expansion scalar. This framework potentially illuminates the dynamics of collapsing stellar systems and bears significant astrophysical implications. Additionally, the authors have explored the astrophysical consequences of perpetual homogeneous gravitational collapse with a rational parameterization of the expansion scalar [12].

The formulation of Einstein’s field equations (EFE) has enabled theoretical physicists to propose various models elucidating high-gravity astrophysical phenomena such as quasars, black holes, and other extraordinarily dense entities stemming from gravitational collapse. However, the pool of exact solutions to EFEs remains relatively sparse, particularly in capturing the realistic dynamics of gravitational collapse. Hence, the aim of our present study is to investigate the homogeneous collapse of perfect-fluid distributions from a fresh perspective and, by incorporating appropriate boundary conditions, to derive exact solutions of the EFEs and discuss the singularity analysis. Given that the homogeneous gravitational collapse scenario necessitates a uniform expansion scalar \(\Theta = \Theta (t)\), our approach endeavors to attain solutions to the field equations in a model-agnostic manner. Since the massive stars possess continual gravitational collapse leading to space-time singularity as its end state. Therefore for our present investigation, we consider a massive star namely \(\beta \) Canis Majoris and will discuss the gravitational collapse and its singularity analysis. \(\beta \) Canis Majoris is among the most massive and luminous stars in the Galaxy, residing in the southern constellation of Canis Major at an approximate distance of 500 light-years from the Sun. This star has a mass of about 13 times that of the Sun and a radius approximately 9.7 times larger than the Sun’s radius.

The paper is organised as follows: In Sect. 2, the basic equations for a gravitational collapsing system are discussed in the background of the FLRW (Friedmann–Leimatre–Robertson–Walker) spacetime metric with perfect fluid distributions and considered the Schwarzschild metric as an exterior space-time. In Sect. 3, we have introduced the novel parameterization of the expansion scalar \(\Theta \) describing the gravitational collapsing configuration. The exact solutions of EFEs and the dynamics of models are discussed in Sect. 4. In Sect. 5, we discuss the singularity analysis of a collapsing system’s apparent horizon and the phenomenon of an eternal collapsing system. In Sect. 6, we discuss the energy conditions for the model together with their graphical representations. The stability analysis via the Herrera approach for our model is described in Sect. 7. The last Sect. 8 contains the discussion and concluding remarks.

2 General formalism for the gravitational collapsing system

The Friedmann–Leimatre–Robertson–Walker (FLRW) metric is a form of spherically symmetric space-time, and the study of FLRW solutions has always been a central topic in relativistic cosmology and in this sense, a great deal of attention is paid to the investigation of collapsing phenomena ([13,14,15,16,17,18] and references therein). Since the dynamics of a generic collapse is very complicated and tools to address such a problem in gravitational theory are still under development. Thus, it is useful to work with a simple collapse scenario as of a homogeneous fluid distribution. Thus, for the gravitational collapsing system, here we consider that the space-time inside the stellar system is homogeneous and isotropic, which is described by the FLRW metric

$$\begin{aligned} ds_{-}^{2}=-dt^{2}+a^{2}(t)dr^{2}+R^{2} d\Omega ^{2} \end{aligned}$$
(1)

wherein \(d\Omega ^{2}=d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}\) is the metric on unit 2-sphere, a(t) is the scale the factor and \(R=R(t,r)\) is the geometrical radius of the collapsing star given by,

$$\begin{aligned} R(t,r)=r a(t) \end{aligned}$$
(2)

where the coordinates are taken as \(x^{i}=(t,r,\theta ,\phi )\), \(i=0,1,2,3\) and the fluid 4-velocity vector \(V^{i}\) satisfy \(V^{i}V_{i}=-1\), where \(V^{i}=(1,0,0,0)\). The energy-momentum tensor for the perfect fluid distribution is given by,

$$\begin{aligned} T_{j}^{i}=diag(\rho ,p,p,p) \end{aligned}$$
(3)

where \(\rho \) and p are the energy density and pressure respectively.

The expansion-scalar

$$\begin{aligned} \Theta =V_{;i}^{i}=3\frac{\dot{R}}{R} \end{aligned}$$
(4)

where dot (.) denotes the derivative with respect to t.

The Einstein’s field equations

$$\begin{aligned} R_{j}^{i}-\frac{1}{2}R\delta _{j}^{i}=\textsf{x}T_{j}^{i} \end{aligned}$$
(5)

for the present system yields the following two independent equations (where \(\textsf{x}=\frac{8\pi G}{c^{4}}\) )

$$\begin{aligned} & \textsf{x}\rho -\frac{1}{3}\Theta ^{2}=0 \end{aligned}$$
(6)
$$\begin{aligned} & \textsf{x}p+\frac{1}{3}\Theta ^{2}+\frac{2}{3}\dot{\Theta }=0 \end{aligned}$$
(7)

The mass-function m(t, r) of the collapsing star at any moment (t, r) is described by [19].

$$\begin{aligned} m(t,r)=\frac{1}{2}R\left( 1+R_{,i}R_{,j}g^{ij}\right) =\frac{1}{18}\Theta ^{2}R^{3} \end{aligned}$$
(8)

where (,) denotes the partial differentiation. Also in view of Eqs. (6)–(7) and (8), we have

$$\begin{aligned} \dot{m}=-\frac{1}{2}\textsf{x}p\dot{R}R^{2} \end{aligned}$$
(9)

2.1 The junction condition and the Kretschmann curvature

In general relativity, Jebsen–Birkhoff’s theorem states that the Schwarzschild solution is the exact solution of vacuum Einstein field equations describing the gravitational fields exterior to a spherically symmetric star. Since the theorem’s applicability is local, it can be used as a boundary condition for any stellar system. In our present studies, we consider the geometry of the exterior region of a star to be described by the Schwarzschild metric

$$\begin{aligned} ds^{2}_{+} = -\left( 1-\frac{2M}{\xi }\right) dT^{2} + \frac{d\xi ^{2}}{\left( 1- \frac{2M}{\xi }\right) } + \xi ^{2} d\Omega ^{2} \end{aligned}$$
(10)

where M represents the Newtonian mass of a star (called Schwarzschild mass) and the coordinate of exterior space-time is \((T, \xi , \theta ,\phi )\).

The boundary hyper-surface \(\Sigma \) separates the stellar system into the interior \((ds^{2}_{-})\) and the exterior \((ds^{2}_{+})\) spacetime manifolds. The matching of interior metric (1) to the exterior Schwarzschild metric (10) on the hyper-surface \(\Sigma \) yield the boundary condition [20].

$$\begin{aligned} m\left( t,r\right) \overset{\Sigma }{=}\ M \end{aligned}$$
(11)

The Eq. (11) is the well-known boundary condition given by Santos [20] which shows that the mass-function m(t, r) must be equal to the Schwarzschild mass M on \(\Sigma \).

The singularities are the points in space-time where the normal smoothness of manifold structures breaks down. In other words, these are the points where the energy density or the curvature quantities, such as the scalar polynomials constructed out of the metric tensor and the Riemann tensor, diverge. One example of such a quantity is the Kretschmann scalar curvature (KS), which is sometimes called the Riemann tensor squared [21].

$$\begin{aligned} \mathcal {K}=R_{i j k \delta } R^{i j k \delta } \end{aligned}$$
(12)

For the metric(1), it gives

$$\begin{aligned} \mathcal {K}=\dfrac{12\left( \dot{a}^{4}+a^{2}\ddot{a}^{2}\right) }{a^{4}} \end{aligned}$$
(13)

3 \(\Theta \)-parametrization

The system of differential equations (7)–(8) includes only two independent equations involving three unknowns: a(t), p(t), and \(\rho (t)\). Consequently, an additional constraint is needed to fully determine the solution of the Einstein field equations (EFEs). It is well known that the EFEs alone do not completely determine the solution due to an extra degree of freedom, which is typically resolved by using an equation of state that relates p and \(\rho \). Numerous researchers [22,23,24] have extensively studied the phenomenon of gravitational collapse using an equation of state. These investigations aim to elucidate the end stage of collapse, distinguishing between the formation of black holes and naked singularities. Several studies have employed shear-free parameterization to analyze singularities in gravitational collapse [25,26,27,28]. Gundlach and Martin and Garcia [29] explored the use of power law parameterization for charge in the context of gravitational collapse, demonstrating that in the critical limit, black holes are primarily influenced by the charge with the rate of decay. Herrera et al. [30] discussed the expansion-free (\(\Theta = 0\)) spherically symmetric collapse, examining its generation of cavity evolutions and refuting the occurrence of singularities. Recently, authors have investigated various expansion scalar parameterizations to solve the field equations describing the eternal collapse of stellar systems [12, 31]. Indeed, a critical analysis of solutions in general relativity (or in modified gravity theories) often focuses on the parameterization of physical and kinematical parameters used by theoretical physicists.

In this paper, we introduce some parametrization schemes for the kinematical variable – the expansion scalar \(\Theta \). The rationale for introducing these specific parametrization methods is as follows:

In the study of cosmological models, the Hubble parameter (\(H = \frac{\dot{R}}{R}\)) quantifies the expansion rate of the universe, where R represents the scale factor and denotes the radius of the universe. Current observations indicate that the universe is expanding and accelerating over time, implying that H should be consistently positive (\(H > 0\)) throughout the universe’s evolution. In the context of stellar evolution, such as in a star, the nuclear fusion processes occurring in the core lead to a loss of equilibrium, causing the star to collapse under its own gravity [5]. During this collapse, the internal thermal pressure, generated by nuclear reactions of hydrogen (H) or helium (He) molecules, decreases, allowing the gravitational pressure to dominate. Consequently, the collapse rate of the star increases, drawing matter inward towards the center of gravity. According to general relativity, two types of motion (velocities) occur in a collapsing system: \(\frac{\dot{R}}{R}\), which measures the variation of the radius R per unit proper time, and \(\dot{(\delta l)}\), the variation of the infinitesimal proper radial distance \(\delta l\) between two neighboring fluid particles per unit of proper time.

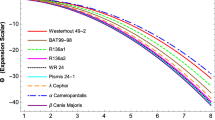
The expansion scalar \(\Theta \) is defined as the rate of change of elementary fluid particles, indicating the collapsing rate of the fluid distribution in a stellar system. Critical analyses show that in collapsing configurations, \(|\Theta |\) increases over time t. During the collapse process, \(\Theta < 0\), where the negative sign convention represents the motion of collapsing fluids toward the center of the star, with \(\Theta = 3\frac{\dot{R}}{R}<0\) for collapsing configurations. Therefore, \(\Theta \) can be considered as a function of t to accurately describe its behavior and the collapsing configuration (as illustrated in Fig. 1). Recently, the authors [11, 12] have utilized the parametrization of \(\Theta \) to solve the field equations for collapsing systems.

We have considered parameterization of \(\Theta \) as an exponential and power law function of t as follows

$$\begin{aligned} \Theta = {\left\{ \begin{array}{ll} -e^{\alpha t}, & \alpha \ge 0 \\ -t^k, & k \ge 0 \end{array}\right. } \end{aligned}$$
(14)

where \(\alpha \) and k are model parameters.

4 Exact solutions and the physical viability of homogeneous gravitational collapse

The Eq. (14) is the additional constraint, that has been used for the solution of EFEs (6)–(7). By using Eq. (4) into (14) and integrating, we have for \(\Theta =-e^{\alpha t}\) that

$$\begin{aligned} a(t)=C_{1}e^{-\frac{{e^{t\alpha }}}{3\alpha }} \end{aligned}$$
(15)

where \(C_{1}\) is an integrating constant. In order to determine the value of \(C_1\), we use the boundary condition (11) on \(\Sigma \) at \(r = r_0\).

Table 1 The values of scale factor (a), density (\(\rho \)) and pressure (p) for both models
Full size table
Table 2 The values of Kretschmann curvature (\(\mathcal {K}\)) and collapsing acceleration (\(\frac{\ddot{a}}{a}\)) for both models
Full size table
Table 3 The values of mass (m) and rate of change in mass (\(\dot{m}\)) for both models
Full size table

Assuming that the star begins to collapse at moment \((t, r) = (t_0, r_0)\) which is the initial boundary condition for the system. Thus, in view of Eqs. (8) and (15), Eq. (11) gives

$$\begin{aligned} r_{0}^{3}C_{1}^{3}e^{2\alpha t_{0}-\frac{1}{\alpha }e^{\alpha t_{0}}}=18M \end{aligned}$$
(16)

which is an equation in \(C_{1}\), therefore we obtain

$$\begin{aligned} C_{1}=\left( \frac{18M}{r_{0}^{3}}\right) ^{\frac{1}{3}}e^{\frac{1}{3}\left( \frac{1}{\alpha }e^{\alpha t}-2\alpha t_{0}\right) } \end{aligned}$$
(17)

Now substituting the value of \(C_{1}\) into Eq. (15) we obtain

$$\begin{aligned} a(t)=\left( \frac{18M}{r_{0}^{3}}\right) ^{\frac{1}{3}}e^{-\frac{1}{3\alpha } \left( e^{\alpha t}-e^{\alpha t_{0}}+2\alpha ^{2}t_{0}\right) } \end{aligned}$$
(18)

In view of Eqs. (14) and (18) we obtain from Eqs. (6)–(7) that

$$\begin{aligned} \textsf{x}\rho= & \frac{1}{3}e^{2\alpha t} \end{aligned}$$
(19)
$$\begin{aligned} \textsf{x}p= & \frac{1}{3}e^{\alpha t}\left( -e^{\alpha t}+2\alpha \right) \end{aligned}$$
(20)

Also from Eqs. (8)–(9), (13) and (18) we obtained the collapsing mass (m), rate of change of mass (\(\dot{m}\)), the Kretschmann curvature (\(\mathcal {K}\)) and the collapsing acceleration (\(\frac{\ddot{a}}{a}\))

$$\begin{aligned} m(t,r)= & M\left( \frac{r}{r_{0}}\right) ^{3}e^{\frac{1}{\alpha }\left[ 2\alpha ^{2}\left( t-t_{0}\right) -e^{\alpha t}+e^{\alpha t_{0}}\right] } \end{aligned}$$
(21)
$$\begin{aligned} \dot{m}= & M{\left( \frac{r}{r_{0}}\right) }^{3}\left( 2\alpha -e^{\alpha t}\right) e^{\frac{-e^{\alpha t}+2\alpha ^{2}(t-t_0)+e^{\alpha t_0 }}{\alpha }} \end{aligned}$$
(22)
$$\begin{aligned} \mathcal {K}= & \frac{4}{27} e^{2 \alpha t }\left( 2 e^{2 \alpha t } - 6 \alpha e^{ \alpha t} + 9 \alpha ^2 \right) \end{aligned}$$
(23)
$$\begin{aligned} \frac{\ddot{a}}{a}= & \frac{1}{9} e^{\alpha t} (e^{\alpha t} - 3 \alpha ) \end{aligned}$$
(24)

Similarly, for the power law parametrization \(\Theta = -t^k \), we have obtained the values of geometrical and physical quantities which are summarized in Tables 1, 2 and 3. It can be observe from (19), (23) and Tables 1 and 2 that \(\rho \rightarrow \infty \), \(\mathcal {K} \rightarrow \infty \) as \(t \rightarrow \infty \) i.e., the collapse time is \(t = t_s = \infty \).

It can be seen from Eqs. (18)–(24) that all the quantities, namely \(a, p, \rho , m, \mathcal {K}\) and \(\frac{\ddot{a}}{a}\) are obtained in terms of stellar mass M. Therefore, the model is applicable to the study of astrophysical stellar objects whose masses and radii are known. For the physical viability and graphical representation of the models, we have chosen the massive star \(\beta \)-Canis Majoris [32, 33] with mass= \(13.5 \pm 0.5 M_\odot \) and radius = \(9.7 \pm 1.3 R_\odot \). For this data set, the values of the model parameters are found to be \(\alpha =0.662\) and \(k=2.153\). For the sake of calculation, we have considered the geometrized units as (\(G = c = 1, M_\odot =1 = R_\odot =1, r_0 =1.0\) and \(t_0 =1.0\)). The dynamical behaviour of our collapsing model is shown by the graphical representations in Figs. 1, 2, 3, 4, 5, 6 and 7.

Fig. 1
figure 1

a Variation of expansion scalar \(\Theta \). b Variation of scalar factor a(t) for massive stars \(\beta \)-Canis Majoris for both models given in Table 1. Here negative sign of \(\Theta \) represents the collapsing configuration (motion of fluid towards the centre of system)

Full size image
Fig. 2
figure 2

a Evolution of energy density \(\rho \). b Evolution of Kretschmann curvature \(\mathcal {K}\) for massive stars \(\beta \)-Canis Majoris for both models given in Tables 1 and 2

Full size image
Fig. 3
figure 3

a Evolution of pressure p. b Evolution of collapsing acceleration \(\frac{\ddot{a}}{a}\) for massive stars \(\beta \)-Canis Majoris for both models given in Tables 1 and 2. Here negative sign of p represents the collapsing configuration (direction of pressure towards the centre of system)

Full size image
Fig. 4
figure 4

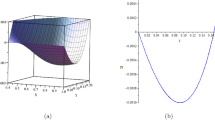
a Variation of the mass m w.r.t t and r for model: \(\Theta = -e^{\alpha t}\). b Variation of the mass m w.r.t t and r for model: \(\Theta = -t^{k}\) for massive stars \(\beta \)-Canis Majoris given in Table 3

Full size image
Fig. 5
figure 5

a Rate of change in mass \(\dot{m}\) for model: \(\Theta = -e^{\alpha t}\). b Rate of change in mass \(\dot{m}\) for model: \(\Theta = -t^{k}\) for massive stars \(\beta \)-Canis Majoris given in Table 3

Full size image

5 Singularity analysis: apparent horizon and eternal collapse

5.1 Formation of an apparent horizon

The possible end state of gravitational collapse, resulting in either a black hole (BH) or a neutron star (NS), is determined by the formation of trapped surfaces in space-time as the collapse advances. Initially, during the onset of gravitational collapse, no regions of space-time are trapped. However, as it reaches critical high densities, trapped surfaces emerge, leading to the development of an apparent-horizon region [34, 35]. The singularity may be causally connected to or isolated from the outside universe, depending on the sequence in which trapped surfaces form as the collapse progresses. It has been observed that the apparent horizon generally forms between the time of singularity formation and when it intersects with the outer Schwarzschild event horizon [36].

In the black hole (BH) scenario, the apparent horizon forms before the singularity occurs. As the singularity forms, the event horizon in the external space-time fully encompasses the final stages of the collapse [37, 38]. In the naked singularity (NS) scenario, the apparent horizon forms after the singularity has formed. The apparent horizon then moves outward to intersect with the event horizon at the boundary, occurring later than the singularity formation.

For the FLRW space-time metric (1), the apparent horizon is defined by

$$\begin{aligned} R_{,i} R_{,j} g^{ij} = \left( r \dot{a}\right) ^2 - 1 = 0 \end{aligned}$$
(25)

where the comma (,) denotes the partial derivatives and \(R = r a\).

This study focuses on singularity formation resulting from the gravitational collapse of a star, we assume that the star is initially untrapped at (t, r) = \((t_{0},r_{0})\). Then

$$\begin{aligned} R_{,i} R_{,j} g^{ij}|_{(t_{0},r_{0})} = \left( r_{0}^2 \dot{a}^2(t_{0}) \right) - 1 < 0 \end{aligned}$$
(26)

Further, let us assume at the moment \((t,r) = (t_{AH},r_{AH})\) the whole star collapses inside the apparent-horizon, then it follows from Eq. (25) that

$$\begin{aligned} \dot{R}^2(t_{AH},r_{AH})-1= r^2_{AH} \dot{a}^2(t_{AH})-1 = 0 \end{aligned}$$
(27)

In case of \(\Theta = -e^{\alpha t}\), by using Eq. (18) into (27) we obtain the time formation of apparent horizon

$$\begin{aligned} t_{AH} & = \frac{1}{6\alpha ^2} \Bigg [-2e^{\alpha t_{0}}+4\alpha ^2 t_0 + 3\alpha Log \left( \frac{(\frac{3}{2})^{\frac{2}{3}}r_0^2}{M^{\frac{3}{2}} r_{AH}^2}\right) \nonumber \\ & \quad \ - 6\alpha \mathcal {W(X)} \Bigg ] \end{aligned}$$
(28)

where \(\mathcal {X}= -\frac{1}{(18\,M)^{\frac{1}{3}}} \left( \frac{r_0^2}{\alpha r_{AH}^2} \right) e^{-\frac{1}{3\alpha }e^{\alpha t_0}+\frac{2}{3} \alpha t_0} \) and \(\mathcal {W}\) denotes the Lambert W-functionFootnote 1 defined by the equation \(\mathcal {W(X)} e^{\mathcal {X}}=\mathcal {X}\) (see [39] for more details). For \(\mathcal {X} \ge -\frac{1}{e} = -0.3679\), \(\mathcal {W(X)}\) gives the real values. Here we can see that the value of \(\mathcal {X}\) depends on \(\alpha \) and M. For example- stellar mass \(M = 13.5 M_\odot \), \(\alpha =0.662\), we get the value of \(\mathcal {X} = -1.1275 \times 10^{-7}\), where \(M_\odot = 1.989 \times 10^{30} Kg\) is the Solar mass. Thus, we see that Eq. (28) gives the finite real value of \(t_{AH}\) (time formation of apparent horizonFootnote 2)

The geometrical radius of apparent-horizon surface is

$$\begin{aligned} R_{AH} = r_{AH} a(t_{AH}) = (18M)^{\frac{1}{3}} \frac{r_{AH}}{r_0} e^{{\frac{ 1}{3 \alpha }( e^{\alpha t_0} - e^{\alpha t_{AH}} -2\alpha ^2 t_0)}}\nonumber \\ \end{aligned}$$
(29)

The total contribution of a collapsing star to the mass of apparent-horizon region is

$$\begin{aligned} M_{AH}= & m|_{(t_{AH},r_{AH})}\nonumber \\= & \left( \frac{9 M}{4}\right) ^{\frac{1}{3}} \frac{r_{AH}}{r_0} e^{\frac{-1}{6 \alpha } \left( \mathcal {M} (\frac{12}{M})^{ \frac{1}{3}} \frac{r_{AH}}{r_0} +4 \alpha ^2 t_0 -2e^{\alpha t_0}\right) } \end{aligned}$$
(30)

where \(\mathcal {M} = e^{ \frac{2}{3} \alpha t_0 - \frac{1}{3\alpha } e^{\alpha t_0} } -\mathcal {W(X)}\)

Analogously, for the second case \(\Theta = -t^k\), we obtained the value of \(t_{AH}\), \(R_{AH}\) and \(M_{AH}\) which are summarized in Table 4.

5.2 Occurance of eternal collapse phenamenon

The formation of a space-time singularity, marked by the divergence of the curvature \(\mathcal {K}\) and the energy density \(\rho \), typically results from the gravitational collapse (GC) of stellar systems. Assuming the star begins to collapse at time \(t=t_{0}\) under condition (26), where it is not initially trapped, we observe from Tables 1, 2 and Fig. 2a, b that \(\rho \rightarrow \infty \) and \(\mathcal {K} \rightarrow \infty \) as \(t = t_{s} \rightarrow \infty \). In other words, the energy density and Kretschmann curvature diverge at an infinite commoving time, indicating that the star collapses indefinitely to reach the space-time singularity. Moreover, Table 4 demonstrates that apparent horizons form at a finite comoving time \(t_{AH}\), significantly earlier than the collapse time \(t_{s} \rightarrow \infty \). Consequently, the singularity is not naked, as an apparent horizon has already formed by the time \(t_{AH}\) (see Table 4). Table 3 also indicates that the mass vanishes at the collapse time \(t_{s}\). Since regular black holes form during gravitational collapse with a finite mass in a finite collapse time, rather than with \(m \rightarrow 0\) and \(t_{s} \rightarrow \infty \) which does not occur in our case. Additionally, the continuous increase in acceleration, depicted in Fig. 3b, indicates the accelerating phase of gravitational collapse. Hence, we conclude that a homogeneous gravitating system collapses over an infinite comoving time to reach the singular stage, and may thus be termed an “Eternal Collapsing Object (ECO)” [40, 41].

Table 4 Apparent horizon: time (\(t_{AH}\)), surface radius (\(R_{AH}\)) and mass (\(M_{AH}\)) for both models
Full size table

6 Energy conditions

In gravitational theories, energy conditions are used to extract insights from general relativity without relying on a specific equation of state (EoS) for the stress-energy tensor, owing to the largely unknown properties of stellar interiors [42]. Typically, the stress-energy tensor exhibits a linear relationship between \(\rho \) and p under certain constraints. This section outlines the essential energy conditions required to ensure the physical viability of the model.

6.1 Weak energy condition (WEC)

For the interior fluid distribution of the stellar system and a physically acceptable model of gravitational collapse, the weak energy condition (WEC) must be satisfied. The WEC stipulates that the energy density, as measured by any time-like observer, must be non-negative (\(\rho \ge 0\)) and that the pressure should not dominate the energy density to an excessive extent (\(\rho + p \ge 0\)). Our collapsing models meet these criteria, as demonstrated in Fig. 6.

6.2 Null energy condition (NEC)

For a gravitational collapse model to be physically viable, it must adhere to the null energy condition, which requires \(\rho + p \ge 0\). As demonstrated in Fig. 6, our model satisfies this condition.

6.3 Strong energy condition (SEC)

According to the strong energy condition (SEC), \(\rho + p \ge 0\) and \(\rho + |3p| \ge 0\). Our model satisfies the SEC, as demonstrated in Fig. 7.

Fig. 6
figure 6

a Nature of WEC. b Nature of NEC for massive stars \(\beta \)-Canis Majoris

Full size image
Fig. 7
figure 7

a Nature of SEC. b The stability criteria: speed of sound for massive stars \(\beta \)-Canis Majoris

Full size image

7 Stability analysis

Herrera’s cracking method [43] offers a valuable approach for assessing the stability of stellar models, particularly regarding the fluid distribution in self-gravitating and compact stellar objects. This technique is used to determine whether a collapsing fluid configuration remains stable. For a stellar model to be deemed physically acceptable, the speed of sound must adhere to causality conditions: \(0< V_s^2 < 1\). This means that the speed of sound within the star must be less than the speed of light c, here we assumed \(c = 1\) and \(V_s\) represents the speed of sound propagation within the system.

$$\begin{aligned} V^2_{s}= |\frac{dp}{d\rho }|= {\left\{ \begin{array}{ll} 1-\alpha e^{-\alpha t}, & \text{ for } \text{ model }: \Theta = -e^{\alpha t} \\ 1-(k-1)t^{-(k+1)}, & \text{ for } \text{ model }: \Theta = -t^k \end{array}\right. }\nonumber \\ \end{aligned}$$
(31)

It can be observed from Eq. (31) that \(V_s^2 <1 \) throughout collapsing evolution for the massive stars \(\beta \)-Canis Majoris as shown in Fig. 7.

8 Discussion and concluding remarks

The aim of this research is to undertake a thorough examination of \(\Theta \)-parametrization and to explore novel aspects of the uniform gravitational collapse phase within stellar systems. Investigating exact solutions and the emergence of singularities holds significant importance in the realm of general relativity, even within contemporary contexts. While numerous exact solutions exist, only a handful yield physically meaningful outcomes, often within highly constrained scenarios. Consequently, our study focuses on gravitational collapse and conducts a comprehensive analysis of singularity formation within the framework of homogeneous and isotropic FLRW geometry. We introduce two parameterizations of \(\Theta \) as time-dependent functions, namely, exponential (\(-e^{\alpha t}\)) and power law (\(-t^{k}\)), which accurately depict the collapsing dynamics of the stellar system (as depicted in Fig. 1a). Furthermore, we apply boundary conditions to explicitly derive exact solutions in terms of stellar mass (M).

A systematic discussion is presented, assuming the parameterization (14) and obtaining the exact solutions in explicit form (as shown in Tables 1 and 2). We have also discussed the collapsing mass (m) and (\(\dot{m}\)) during the collapsing configuration, as can be seen in Table 3. It is observed that the scale factor a is decreasing whereas the pressure \(p(<0)\), density \(\rho \), and Kretschman curvature k are continuously increasing during the collapsing process (as shown in Figs. 1, 2, and 3). Also, from Eq. (24) and Table 2, we have shown that our models represent an accelerating phase of collapse (as shown in Fig. 3b), and hence, with the ever-increasing Kretschmann curvature and density, which tend to extend physical space-time to an infinite extent, the collapse of sufficiently massive objects may continue forever. In Sect. 5, the formation of the apparent horizon is discussed, and it turns out that the apparent horizon develops before the singularity formation \(t_{AH}<t_{s}\) (see Table 4). We have also obtained the geometric radius \(R_{AH}\) and finite mass \(M_{AH}\) of the apparent-horizon surface, which are summarised in Table 4. From Table 3, we see that the mass m(t, r) decreases during such a collapsing configuration (as shown in Fig. 4). The ECO is a massive and continuing collapse that tries to attain the singular state in an infinite time, and its mass would be \(m\rightarrow 0\) as \(t_{s}\rightarrow \infty \). It can be seen that \(\dot{m}\) continuously decreases, which shows the loss of mass with time, as shown in Fig. 5.

To draw a definitive conclusion about singularity formation, we analyzed the final state of the collapse process by comparing the times of singularity formation (\(t_{s}\)) and apparent horizon formation (\(t_{AH}\)). Both the Kretschmann curvature and energy density appear to diverge as \(t= t_{s} \rightarrow \infty \), indicating that singularity formation results from gravitational collapse over an infinite time scale. Consequently, it is possible that gravitational collapse could lead to either quasi-stable ultra-compact configurations or ongoing collapse scenarios, depending on the unknown high-density behavior and potential phase transitions of the collapsing matter under such conditions. Therefore, more massive and compact collapsing objects are considered as Eternal Collapsing Objects (ECOs). This Eternal Collapsing Object (ECO) can be considered “a mathematical black hole that never achieves a finite equilibrium state.” In this context, continued gravitational collapse should lead to an eternal state rather than singularities, resulting in objects that are eternally collapsing or contracting rather than forming regular space-time singularities [40, 41]. Although in the present paper, we have considered \(\beta \) Canis Majoris as an example of a massive star to discuss the nature of singularity during gravitational collapse, our model can also be applied to other massive stars of masses \(\ge 1.4 M_\odot \). Our model here presents very physically realistic stellar systems because the obtained solutions with all the physical and geometrical parameters are in terms of the mass M of the star, and hence it may be explored towards astrophysically more stars. The advantage of our model, however, is that we have presented here a fully consistent general relativistic model to describe the collapsing scenarios of stellar objects of known mass and radius. In 2014, Vaz [44] introduced a new aspect of black holes, describing them as non-singular quantum objects which are not covered by an event horizon. He suggested that the ultimate state of a collapsing star could be a fundamentally quantum object-an extremely compact dark star-supported by quantum gravity rather than degeneracy pressure, similar to how ordinary atoms are stabilized by quantum mechanics. Recently, Corda [45] analyzed the mass and energy spectra of Vaz’s quantum shell using a Schrödinger-like approach, further reinforcing Vaz’s conclusion that the final outcome of gravitational collapse may not be a space-time singularity enveloped by a horizon, rather represents a quantum object with a dark surface.

Our models are subjected to the stability criteria and satisfy the energy conditions (Figs. 6, 7). Additionally, it should be noted that our models have supported the conclusions of Misner [46], who claimed that even though we are well aware of the possibility of general relativity failing as we approach the ultra-high-density region, we should still consider the predictions of general relativity in this regime since they may provide some evidence as to what to expect from a more general theory of gravity that performs in this regime.

As expected, in a general study as presented here, a great deal of questions remain. Thus, before ending, we would like to present a partial list of issues that should be addressed in future investigations:

  • Eternal collapse phenomenon: Does the collapse happen for an infinite comoving time due to the specific parametrization of the expansion scalar \(\Theta \) made in this work?

  • Does the inhomogeneous gravitational collapsing system deny the eternal collapse phenomenon or not?

  • What would be the possible end state of homogeneous gravitational collapse with such \(\Theta \)-parameterizations when explored in modified gravity theories f(R), f(R, T), Gauss–Bonnet, Scalar field, etc.?

  • Using astrophysical data on stars’ masses M and radii R to discuss the numerical model of collapsing stars?

  • Since our model describes physically realisable stellar structures without resorting to exotic matter distributions such as dark energy and dark matter. Does such exotic matter distribution change such a possible end state of collapse?

  • Looking to future studies, it would be of interest to relax the conditions defining a perfect fluid to incorporate anisotropic stresses, shear, and dissipation in the stellar interior.