Quantum instability of the Cauchy horizon in a charged de-Sitter spacetime with dark matter

Abstract

The strong cosmic censorship conjecture (SCCC) requires that spacetime cannot be extended beyond the Cauchy horizon. This ensures the predictability of spacetime. In this paper, we investigate the SCCC for a spherically symmetric charged de-Sitter black hole surrounded by dark matter using classical and quantum scalar fields. At the classical level, we analyze the behavior of scalar waves near the Cauchy horizon using the method developed by Hintz and Vasy. We find a relationship between the Sobolev regularity of scalar waves and the spectral gap of quasinormal modes. In the nearly extremal region, this may lead to a violation of the SCCC. At the quantum level, we first provide a proof of the renormalizability of the quantum scalar field in dark-matter black holes. Using numerical methods, we then demonstrate that the renormalized quantum stress-energy tensor for any Hadamard state exhibits quadratic divergence near the Cauchy horizon in the nearly extremal region. The quadratic divergence of the renormalized quantum stress-energy tensor is sufficient to convert the Cauchy horizon into a singularity. Thus, the SCCC is preserved by quantum effects. Since the quadratic divergence is more singular than the behavior of classical scalar field perturbations near the Cauchy horizon, it means there is a region where physics is dominated by quantum effects. We study the influence of dark matter on quantum effects in this region and we find there is a monotonic relationship between the dark matter and the strength of quantum effects. The numerical results show that the quantum effects will become stronger as dark matter increases.

1 Introduction

In general relativity, the future evolution of the metric and matter fields can be predicted by specifying the initial data on a spacelike hypersurface, also known as a Cauchy surface. More precisely, the values of the metric and matter fields are uniquely determined within the domain of dependence of the Cauchy surface. When a Cauchy horizon appears, spacetime can extend into the region beyond the Cauchy horizon, where the metric or matter fields become unpredictable. To address this issue, Penrose proposed the strong cosmic censorship conjecture (SCCC), which requires that all spacetimes be globally hyperbolic, meaning no extendable Cauchy horizons exist [1].

It is well known that asymptotically flat and de Sitter RN black holes have Cauchy horizons. In the asymptotically flat case, it has been proven that the Cauchy horizon would be converted into a singularity by the blue-shift effect [2,3,4]. However, the situation changes dramatically for a cosmological constant $\Lambda >0$. In [5], the behavior of linear scalar waves near the Cauchy horizon of an RNdS black hole has been studied using microlocal analysis. They found that the solution $\phi$ of the Klein–Gordon equation $\nabla _{a}\nabla ^{a}\phi -m^2\phi =0$ with smooth initial data has Sobolev regularity $H^{1/2+\alpha /{\kappa _{1}}-0^+}$ near the Cauchy horizon. Here, $\kappa _{1}$ is the surface gravity of the Cauchy horizon, and $\alpha$ is the spectral gap which is given by

$$\begin{aligned} \alpha =\text {inf}\{-\text {Im}(\omega _{nlm})\}, \end{aligned}$$

(1.1)

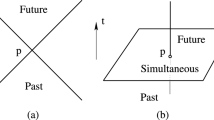
where $\omega _{nlm}$ is the quasinormal modes of region I in Fig. 1. If $\alpha /{\kappa _{1}}>1/2$, it means the singular behavior of scalar waves is sufficiently weak near the Cauchy horizon such that spacetime can be extended beyond the Cauchy horizon. The values of $\alpha /{\kappa _{1}}$ for massless scalar fields in the RNdS black hole have been analyzed in [6]. They found $\alpha /{\kappa _{1}}>1/2$ in the near extremal regime. Therefore, the SCCC is violated under classical linear scalar perturbations.

In order to restore SCCC in RNdS spacetime, the quantum effect near the Cauchy horizon has been studied in [7]. They studied a real Klein–Gordon quantum field in RNdS spacetime. For technical convenience, a Unruh state has been constructed in RNdS spacetime by the bulk to boundary correspondence and it is shown to be Hadamard. Here, the definition of Hadamard state is given in Sect. 4 and it plays an important role in quantum field theory in curved spacetime. Indeed, any physically reasonable state should be Hadamard. Therefore, it is natural to focus on Hadamard states. The behavior of the renormalized quantum stress energy tensor $\langle T_{uv}\rangle _{rem,\Psi }$ near the Cauchy horizon for an arbitrary Hadamard state $\Psi$ has been studied in [7]. It has been proven that the leading divergence term of $\langle T_{VV}\rangle _{rem,\Psi }$ is given by

$$\begin{aligned} \langle T_{VV}\rangle _{rem,\Psi }\sim C\vert V_{-}\vert ^{-2},\quad \text {as}\quad V_{-}\rightarrow 0^{-}, \end{aligned}$$

(1.2)

where $V_{-}$ is the affine parameter of null geodesic transverse to the Cauchy horizon. Here C is independent of the state. Due to practical limitations, $C\ne 0$ was only verified for a small number of black hole parameters. Using a semi-analytic method, $C\ne 0$ has been verified for various values of scalar field masses and spacetime parameters in [8]. Using the divergence behavior $C\vert V_{-}\vert ^{-2}$, it has been shown that this singular behavior would convert the Cauchy horizon into a singularity [7]. Therefore, the SCCC is restored by the quantum effect. In this situation, it is natural to compare the divergence behaviors of classical and quantum stress energy tensors. Using Sobolev regularity $H^{1/2+\alpha /{\kappa _{1}}-0^+}$, the divergence behavior of the classical stress energy tensor has been studied in [7] and it is given by

$$\begin{aligned} T_{VV}\sim C\vert V_{-}\vert ^{-2+2\beta },\quad \text {as}\quad V_{-}\rightarrow 0^{-}, \end{aligned}$$

(1.3)

where $\beta >1/2$. In the usual case, one may regard the quantum effect as a small modification compared to the classical effect. However, the situation changes dramatically near the Cauchy horizon. The quantum effects dominate the physics near the Cauchy horizon.

The existence of dark matter and dark energy has been verified by various experiments and observations [9]. However, all the experiments and observations imply the existence of dark matter from indirect findings, and the compositions of dark matter are still unknown. Many theories have been proposed to describe dark matter. The perfect fluid dark matter (PFDM) is one of the candidates for dark matter [10]. In this model, dark matter behaves as a perfect fluid and black hole solutions surrounded by PFDM have been obtained [11, 12]. It is interesting to study the influence of PFDM on the behaviors of classical and quantum scalar field near the Cauchy horizon. For one thing, the behaviors of classical or quantum scalar field will determine whether the SCCC is violated at the classical or quantum level. For another thing, as discussed in the previous paragraph, there is a region where physics is dominated by quantum effects in RNdS spacetime. Recently, the quantum effects in this region has received widespread attention. The geodesic deviation effects in this region has been studied in [7]. For charged quantum fields, it turns out that the Cauchy horizon can be charged or discharged [13]. For rotating black hole, there exists a quantum twisting effect [14] in this region. It is natural to ask whether there exists such a region where dark matter appears. If there exists such a region, we will study the influence of PFDM on the quantum effects in this region.

Fig. 1

The Penrose diagram of a charged de Sitter black hole surrounded by perfect fluid dark matter

In this paper, we investigate the SCCC for a spherically symmetric charged de Sitter black hole surrounded by perfect fluid dark matter at classical and quantum levels and we study the influence of PFDM on the quantum effects in the region where physics is dominated by quantum effects instead of classical effects. The paper is organized as follows. In Sect. 2, we present the geometry of a charged de Sitter black hole surrounded by perfect fluid dark matter. In Sect. 3, we use the method developed by Hintz and Vasy [5] to analyze scalar waves near the Cauchy horizon. In Sect. 4, we review the algebraic formulation of quantum field theory [7, 15, 16]. We construct a Unruh state in region $\text {I}\cup \text {II}\cup \text {III}$ of Fig. 1 and show it is a Hadamard state. In Sect. 5, we investigate the validity of the SCCC at both classical and quantum levels. At the classical level, according to numerical results of the spectral gap [17], we find that the SCCC can be violated in the nearly extremal region. At the quantum level, we calculate the renormalized quantum stress energy tensor for an arbitrary Hadamard state using the method developed in [7]. We find $C\ne 0$ in (1.2) and the SCCC is restored by the divergence behavior $C\vert V_{-}\vert ^{-2}$ of the renormalized quantum stress energy tensor. We find the behavior of quantum scalar field is more singular than the behavior of classical scalar field near the Cauchy horizon and thus, there exist a region where physics is dominated by quantum effects. We study the influence of PFDM on the quantum effects in this region. we find there is a monotonic relationship between the dark matter and the strength of quantum effects. It turns out that the quantum effects will become stronger as dark matter increases. In Sect. 6, we give our conclusions.

2 Charged black hole in perfect fluid dark matter

In this section, we study a charged de-Sitter black hole surrounded by perfect fluid dark matter. The corresponding action can be written as [18,19,20]

$$\begin{aligned} S=\frac{1}{16\pi }\int d^4x\sqrt{-g}\left( R-2\Lambda -F^{ab}F_{ab}+\mathcal {L}_\text {DM}\right) , \end{aligned}$$

(2.1)

where $\Lambda >0$ is the cosmological constant, $F_{ab}$ is the electromagnetic tensor field and $\mathcal {L}_{DM}$ is the dark matter Lagrangian density. By varying the action, the field equation is given by

$$\begin{aligned} \begin{aligned} R_{ab}-\frac{1}{2}Rg_{ab}+\Lambda g_{ab}&=T^\text {EM}_{ab}+T^\text {DM}_{ab},\\ \nabla _{a}F^{ab}&=0, \end{aligned}\end{aligned}$$

(2.2)

where $T^{EM}_{ab}$ is the energy–momentum tensor of electromagnetic field and $T^{DM}_{ab}$ is the energy–momentum tensor of dark matter. Following [18,19,20], the solution of a charged de Sitter black hole surrounded by perfect fluid dark matter is given by (Fig. 2)

$$\begin{aligned} \begin{aligned} ds^2&=-f(r)dt^2+\frac{1}{f(r)}dr^2+r^2d\mathbb {S}^2, \\ A_{a}&=-\frac{Q}{r}dt_{a}, \end{aligned} \end{aligned}$$

(2.3)

where $A_{a}$ is the electric four potential and

$$\begin{aligned} f(r)=1-\frac{2M}{r}+\frac{Q^2}{r^2}+\frac{b}{r}\ln \left( \frac{r}{\vert b \vert }\right) -\frac{\Lambda r^2}{3}. \end{aligned}$$

(2.4)

Here M is the mass of black hole, Q is the charge of black hole and $b>0$ is the parameter describing the perfect fluid dark matter. The stress energy–momentum tensor of the perfect fluid dark matter is given by

$$\begin{aligned} T^{\mu }_{ \nu }=\text {diag}\left( \frac{b}{r^3},\frac{b}{r^3},-\frac{b}{2r^3},-\frac{b}{2r^3}\right) . \end{aligned}$$

(2.5)

In this paper, we consider parameters of spacetime in a physical region where f(r) has 3 simple positive roots $0<r_{1}<r_{2}<r_{3}$, corresponding to Cauchy horizon, event horizon and cosmological horizon. The Penrose diagram is drawn in Fig. 1.

Now, we review the coordinate systems introduced in [7, 32]. By choosing integration constant, the tortoise coordinate near $r_2$ takes form

$$\begin{aligned} r_{*}=\frac{1}{\vert f'(r_2)\vert }\text {log}(\vert r-r_2\vert )+C+O(\vert r-r_2\vert ). \end{aligned}$$

(2.6)

Then $r_*$ tends to $-\infty$ near $r=r_2$ and tends to $\infty$ near $r=r_{1/3}$. Now, the Kruskal coordinates in region I are given by

$$\begin{aligned} U:=-e^{-\kappa _2u},\quad V_{c}:=-e^{-\kappa _3v}, \end{aligned}$$

(2.7)

where $u=t-r_{*}$, $v=t+r_{*}$ and $\kappa _{2/3}$ are surface gravities corresponding to $r_{2/3}$. Now, we can extend U smoothly from $(-\infty ,0)$ to $(-\infty ,\infty )$, then U crosses the event horizon $H^R$ into region II. Similarly, we can extend $V_{c}$ smoothly from $(-\infty ,0)$ to $(-\infty ,\infty )$, then $V_{c}$ crosses the cosmological horizon $H^L_C$ into region III. Using tortoise coordinate, in region $\text {II}\cup \text {III}$, U and $V_c$ take the same form (2.7) as in region I. Similarly, we define another Kruskal coordinates in region II

$$\begin{aligned} U_{-}:=-e^{\kappa _1u},\quad V_{-}:=-e^{-\kappa _1v}. \end{aligned}$$

(2.8)

Here $u=t-r_{*}$, $v=t+r_{*}$ and $\kappa _1$ is the surface gravity corresponding to $r_{1}$. We extend $V_{-}$ smoothly from $(-\infty ,0)$ to $(-\infty ,\infty )$, then $V_{-}$ crosses the Cauchy horizon $CH^R$.

3 Wave behavior near the Cauchy horizon

In order to investigate the validity of SCCC in a charged de Sitter spacetime surrounded by dark matter, we need to study SCCC at both classical and quantum level. The first step is to use the method developed by Hintz and Vasy [5] to analyze scalar waves. This result will play an important role in SCCC at both classical and quantum level. At classical level, the behavior of scalar waves near the Cauchy horizon has been studied by Hintz and Vasy [5] in RNdS spacetime. According to theorem 1.1 of [5], the solutions of Klein–Gordon equation with smooth initial data have Sobolev regularity $H^{1/2+\alpha /\kappa _{1}-0^{+}}$ near the Cauchy horizon, where $\kappa _{1}$ is the surface gravity of the Cauchy horizon. Here $\alpha$ is the spectral gap and it is given by the relation $\alpha =\text {inf}\{\text {Im}\omega _{nlm}\}$, where $\omega _{nlm}$ are quasinormal modes of region I in Fig. 1. This gives the relation between Sobolev regularity of scalar waves perturbations and spectral gap of quasinormal modes. At quantum level, in order to study the behaviors of quantum energy momentum tensor near the Cauchy horizon for any Hadamard state, following the strategy of [7], we need to decompose quantum energy momentum tensor into several parts, see (5.1) and the Sobolev regularity of scalar waves near the Cauchy horizon controls the behavior of the first term on the right side of the Eq. (5.1). Furthermore, the decay property of scalar waves in [5] has been used to prove Unruh state is Hadamard in RNds spacetime [7]. From the above discussion, we see the behaviors of scalar waves obtained in [5] play an important role in SCCC. Therefore, in this section, we use the method developed by Hintz and Vasy [5] to analyze scalar waves in a charged de-Sitter spacetime surrounded by perfect fluid dark matter. Following [5], the first step is to introduce a new coordinate system and modify spacetime behind the Cauchy horizon, see Fig. 3. This new coordinate system will cover region $\Omega ^{0}$ in Fig. 4. Now, we recall from [5] this new coordinate system. Roughly speaking, this new coordinate system behaves like (u, r) or (v, r) coordinates near $r_j$ and behaves like (t, r) away from $r_j$. To be more specific, we take coordinate transformations

$$\begin{aligned} dt_{j}=dt-s_j[f^{-1}+c_j(r)]dr \end{aligned}$$

(3.1)

near $r_j$, where $c_j(r)$ are smooth functions and $s_j=-\text {sgn}f'(r_j)$. Then the metric takes form

$$\begin{aligned} ds^2= & -fdt^2_{j}-2s_{j}(1+fc_{j})dt_{j}dr\nonumber \\ & -(2c_{j}+fc^2_{j})dr^2+r^2d\mathbb {S}^2. \end{aligned}$$

(3.2)

We first consider coordinate transformations (3.1) near $r_3$ in region $r_2<r<r_3$. We take $j=3$ and metric takes form (3.2). The coordinate singularity near $r_3$ has been removed and we can extend this coordinate system $(t_3,r)$ to $r>r_3$. Now, the coordinate system ($t_3,r$) covers region $(r_2,\infty )$. Taking $c_3=-f^{-1}$ in $(r_2+2\delta ,r_3-2\delta )\cup (r_3+2\delta ,\infty )$, we find metric takes form (2.3) there. Similarly, we take coordinate transformations (3.1) near $r_2$ with $j=2$. We can extend this coordinate system $(t_2,r)$ to $r<r_2$ and it covers region $(r_1,r_3)$. Taking $c_2=-f^{-1}$ in $(r_1+2\delta ,r_2-2\delta )\cup (r_2+2\delta ,r_3-2\delta )$, it is easy to see metric takes form (2.3) there. For technical convenience, we modify f to a smooth function $f_{*}$ by requiring $f_{*}\equiv f$ in $[r_1-2\delta ,\infty )$ and $f_{*}$ has a single root $r_0$ in $(0,r_1)$, see Fig. 2. By taking coordinate transformations (3.1) near $r_1$ with $j=1$, we find coordinate system ($t_1,r$) covers region $(r_0,r_2)$. Taking $c_1=-f^{-1}$ in $(r_0+2\delta ,r_1-2\delta )\cup (r_1+2\delta ,r_2-2\delta )$, metric takes form (2.3) with f replaced by $f_{*}$. Finally, we take coordinate transformations (3.1) near $r_0$ with $j=0$, $s_0=-\text {sgn}f_{*}'(r_0)$ and $c_0(r)\in C^{\infty }$. This coordinate system $(t_0,r)$ covers region $(0,r_2)$. Taking $c_0=-f^{-1}$ in $(0,r_0-2\delta )\cup (r_0+2\delta ,r_1-2\delta )$, metric takes form (2.3) with f replaced by $f_{*}$.

Now, we glue these coordinate systems ($t_j,r$) together. Firstly, we focus on $(t_2,r)$ and $(t_3,r)$. It is easy to see $dt_2=dt=dt_3$ in $(r_2+2\delta ,r_3-2\delta )$ and we can arrange $t_2=t_3$ there. We define coordinate system ($t_{23},r$) by requiring $t_{23}\equiv t_2$ for $r\in (r_1,r_2+2\delta ]$ and $t_{23}\equiv t_3$ for $r\in (r_2+2\delta ,\infty )$. Similarly, we have $dt_1=dt=dt_{23}$ in $(r_1+2\delta ,r_2-2\delta )$ and we can arrange $t_1=t_{23}$ there. We define coordinate system ($t_{13},r$) by requiring $t_{13}\equiv t_1$ for $r\in (r_0,r_1+2\delta ]$ and $t_{13}\equiv t_{23}$ for $r\in (r_1+2\delta ,\infty )$. Finally, we can arrange $t_{13}=t_0$ in $(r_0+2\delta ,r_1-2\delta )$ and we obtain $t_{*}$ by requiring $t_{*}\equiv t_0$ for $r\in (0,r_0+2\delta ]$ and $t_{*}\equiv t_{13}$ for $r\in (r_0+2\delta ,\infty )$. Therefore, we define a coordinate system $(t_{*},r,\theta ,\phi )$ covers region $0<r<\infty$.

Fig. 2

$f_*$ is the modification of f behind Cauchy horizon. f is denoted by solid line. The dash dot line denotes the difference between f and $f_*$

Fig. 3

The Penrose diagram for spacetime with the modified metric function $f_*$. The singularity in region IV has been removed

In summary, we modify the spacetime behind the Cauchy horizon and define a coordinate system $(t_{*},r,\theta ,\phi )$ which has been introduced in [5] with a slightly difference choosing of $c_j$. The modified metric takes form

$$\begin{aligned} ds^2= & -f_{*}dt^2_{*}+f^{-1}_{*}dr^2+r^2d\mathbb {S}^2, \quad r\in [r_{j}+2\delta ,r_{j+1}-2\delta ] \end{aligned}$$

(3.3)

$$\begin{aligned} ds^2= & -f_{*}dt_{*}^2-2s_j(1+f_{*}c_{j})dt_{*}dr\nonumber \\ & -(2c_{j}+f^{*}c_{j}^2)dr^2+r^2d\mathbb {S}^2,\quad \vert r-r_{j}\vert \le 2\delta . \end{aligned}$$

(3.4)

From now on, we focus on the region $M^{0}=\{r_{0}-4\delta<r<r_{3}+4\delta \}$. For technical convenience, we introduce the boundary defining function $\tau =e^{-t_{*}}$ and add boundary $\tau =0$ to $M^{0}$ by defining

$$\begin{aligned} M=\left( M^{0}\sqcup [0,1)_{\tau }\times (r_{0}-4\delta ,r_{3}+4\delta )\times \mathbb {S}^2\right) /\sim , \end{aligned}$$

(3.5)

where we identify $(\tau ,r,\theta ,\phi ) \in (0,1)\times (r_{0}-4\delta ,r_{3}+4\delta )\times \mathbb {S}^2$ with $(t_{*}=-\text {log}\tau ,r,\omega )\in M^{0}$.

For technical convenience, we require $dt_{*}$ is timelike in a neighborhood of $(r_0,r_1)\cup (r_2,r_3)$. If $r\in (r_0+2\delta -r_1-2\delta )\cup (r_2+2\delta ,r_3-2\delta )$, it is easy to see $dt_{*}$ is timelike. If $\vert r-r_{j}\vert \le 2\delta$, using metric form (3.4), we need $g^{ab}dt_{*a}dt_{*b}=c_j(2+fc_j)<0$. Firstly, we consider the neighborhood of $(r_2,r_3)$. If $r\in (r_2,r_3)$, we have $f>0$ and we choose $c_{2/3}\in (-2f^{-1},0)$. If $r>r_3$ or $r<r_2$, the timelike condition is equivalent to $c_j<0$. We have already set $c_2=-f^{-1}>0$ for $r\in (r_1+2\delta ,r_2-2\delta )$ and $c_3=-f^{-1}>0$ for $r\in (r_3+2\delta ,\infty )$. We choose $c_2<0$ for $r\in (r_2-2\delta ',r_2)$ and $c_3<0$ for $r\in (r_3,r_3+2\delta ')$, where $0<\delta '<\delta$. Then $dt_{*}$ is timelike in $(r_2-2\delta ',r_3+2\delta ')$. Similarly, we choose $c_{0/1}\in (-2f^{-1},0)$ for $r\in (r_0,r_1)$, $c_0<0$ for $r\in (r_0-2\delta ',r_0)$ and $c_1<0$ for $r\in (r_1,r_1+2\delta ')$. Then $dt_{*}$ is timelike in $(r_0-2\delta ',r_1+2\delta ')$.

Following [5], we define several spacelike hypersurfaces

$$\begin{aligned} H_{I,0}= & \left\{ t_{*}\ge t_{*,0}, r=r_{0}-2\delta '\right\} ,\nonumber \\ H_{F}= & \left\{ t_{*}=t_{*,0},r_{0}-2\delta '\le r \le r_{1}+2\delta '\right\} ,\nonumber \\ H_{F,2}= & \left\{ \epsilon t_{*}+r=r_2-2\delta ', r_{1}+2\delta '\le r \le r_{2}-2\delta '\right\} , \nonumber \\ H_{I}= & \left\{ t_{*}=0, r_{2}-2\delta '\le r \le r_{3}+2\delta '\right\} ,\nonumber \\ H_{F,3}= & \left\{ t_{*}\ge 0,r=r_{3}+2\delta '\right\} , \end{aligned}$$

(3.6)

where $\epsilon$ is a small positive constant to be determined later and $t_{*,0}=\epsilon ^{-1}(r_2-r_1-4\delta ')$. Using results in previous paragraph, $H_{I}$ and $H_{F}$ are spacelike hypersurfaces. Using $g^{ab}dr_{a}dr_{b}=f<0$, $H_{I,0}$ and $H_{F,3}$ are spacelike hypersurfaces. Now, we consider hypersurface $H_{F,2}$ and we have $g^{ab}(\epsilon dt_{*a}+dr_{a})(\epsilon dt_{*b}+dr_{b})=(2c_j+fc_j^2)\epsilon ^2-2s_j(1+fc_j)\epsilon +f=-(1-\epsilon c_js_j)(2s_j\epsilon -f(1-\epsilon s_jc_j))$. We require $1-\epsilon c_2s_2>0$ and $2s_j\epsilon -f(1-\epsilon s_jc_j)>0$. Since $f<0$ and $f<\text {max}\{f(r_1+2\delta '),f(r_2-2\delta ')\}<0$ in $(r_1+2\delta ',r_2-2\delta ')$, we only need to take $\epsilon$ small enough. Then we conclude $H_{F,2}$ is a spacelike hypersurface. These hypersurfaces bound a region of interest $\Omega ^{0}$, which is submanifold of $M^{0}$ with corner see Fig. 4. We can add boundary to $\Omega ^{0}$ by the same process as $M^{0}$ and we denote it by $\Omega$, see Fig. 5. The boundaries we added are $X=\partial M$ and $Y=\partial M \cap \Omega$.

Fig. 4

The Penrose diagram for $\Omega ^{0}$ which is bounded by hypersurfaces defined in (3.6)

Fig. 5

$\Omega$ is obtained by adding boundary to $\Omega ^{0}$. The boundary $\partial \Omega$ corresponds to blowing up $i^{+}$

In this paper, we consider solutions of Klein–Gordon equation with smooth initial data posed on $H_{I}$. For any u satisfies Klein–Gordon equation with compact smooth initial value, according to Theorem 4.7 of [21], one can always find a smooth function with compact support such that $u=Ef$, where E is propagator of Klein–Gordon equation. It is also obvious from Theorem 4.7 of [21], we can choose the support of f in $\Omega ^{0}\cap \{r>r_1\}$. Furthermore, u can be written as $u=E^{+}f-E^{-}f$ and only the retarded part $v:=E^{+}f$ contributes to the wave behavior near the Cauchy horizon and $i^{+}$. Therefore, we consider the forward problem $\nabla _{a}\nabla ^{a}v-m^2v=f$ with vanishing initial data on $H_{I}$.

The next step is to study global behavior of the null-geodesic flow. Before doing this, we briefly discuss the motivation. For a distribution solution u of Klein–Gordon equation, we want to study the singularity behavior of u and this can be described by the wave front set [22] which is a subset of $T^{*}M\setminus 0$, where 0 denotes the zero section. The wave front set (WF) is defined as follow: for a distribution u in $R^{n}$, we say $(x_{0},\xi _0) \notin \text {WF}(u)$ if and only if there exists $\chi _{0}\in C^\infty _{0}(R^n)$ with $\chi _{0}(x_{0})\ne 0$ and a open conic neighborhood $\Gamma$ of $\xi _{0}$ such that for all $N>0$ there is a constant $C_N$ satisfies

$$\begin{aligned} \vert \widehat{\chi _{0}u}(\xi )\vert \le C_N(1+\vert \xi \vert ^2)^{-N}, \forall \xi \in \Gamma , \end{aligned}$$

(3.7)

where $\widehat{\chi _{0}u}$ is the Fourier transform of $\chi _{0}u$. Here $C^\infty _{0}(R^n)$ denote smooth functions with compact support. As a result of microlocalized elliptic regularity theorem, the wave front set of u is contained in the characteristic set $\Sigma$ and its behaviors are controlled by the propagation of singularities theorem [22]. This means the points of $\text {WF}(u)$ propagate along the bicharacteristic strips of Klein–Gordon operator. The bicharacteristic strips are curves on characteristic set $\Sigma$ which are generated by the Hamiltonian flow, where the Hamiltonian is the principal symbol of Klein–Gordon operator. In local coordinates the Hamiltonian vector fields can be written as

$$\begin{aligned} H_{P}=\sum _{j=1}^n\frac{\partial P}{\partial \xi _j}\frac{\partial }{\partial x_j}-\frac{\partial P}{\partial x_j}\frac{\partial }{\partial \xi _j}. \end{aligned}$$

(3.8)

In this case, the principal symbol P of Klein–Gordon operator is $-g^{ab}k_ak_b$ and the characteristic set is $\{(x,k_a)\in ^bT^*M\setminus 0:g^{ab}k_ak_b=0\}$. The index b denote the cotangent bundle for manifold with boundary. It is obvious that the Hamiltonian flow $H_{p}$ is null-geodesic flow. Therefore, the singular part propagates along null geodesics in characteristic set. In fact, the wave front set mentioned above only describes the part which are singular and we need to know the degree of singularity. Therefore, we consider wave front set $\text {WF}^{s,r}$ which corresponds to weight Sobolev space $H^{s,\alpha }:=\tau ^\alpha H^s_b(M)$. The principal symbol, characteristic set and bicharacteristic strips can be defined similarly in the b-setting [23]. Furthermore, the propagation of singularities theorem is still valid [23]. Therefore, the points in $\text {WF}^{s,r}$ propagate along the null-geodesic flow in the characteristic set.

Now, we study the global behavior of the null-geodesic flow in $^bT_{\Omega }M$. From the Penrose diagram, we can choose a smooth future point timelike vector field $F^{a}$ in $\Omega$. Then we can split characteristic set $\Sigma$ into two connected components

$$\begin{aligned} \Sigma =\Sigma _{+}+\Sigma _{-}, \Sigma _{\pm }=\left\{ (x,k_a)\in \Sigma _{\pm }: \pm g^{ab}k_aF_b>0\right\} .\nonumber \\ \end{aligned}$$

(3.9)

According to [23], there are several important behaviors of the null-geodesic flow. Roughly speaking, we may have nontrapping curves, radial points and trapped sets.

Following [5], we first analyze the Hamiltonian flow $H_{p}$ near horizon and we will see it corresponds to radial points. We define

$$\begin{aligned} L_{j}:= ^bN^{*}\left( Y\cap \left\{ r=r_{j}\right\} \right) . \end{aligned}$$

(3.10)

To study the the Hamiltonian flow $H_{p}$ near $L_{j}$, it is convenient to set $c_j=0$ and indeed we go back to the $v-r$ or $u-r$ coordinates. Then metric takes form

$$\begin{aligned} ds^2=-f_{*}dt_{j0}^2-2s_{j}dt_{j0}dr+r^2d\mathbb {S}^2. , \end{aligned}$$

(3.11)

where $dt_{j0}$ are obtained by setting $c_j=0$ in (3.1). In this coordinate, the b-covectors can be written as

$$\begin{aligned} \sigma \frac{d\tau _{j0}}{\tau _{j0}}+\xi dr +\eta d\omega , \end{aligned}$$

(3.12)

where $\tau _{j0}=e^{-t_{j0}}$. Using metric form (3.11), the principal symbol P is given by

$$\begin{aligned} P=-2s_j\sigma -f_{*}\xi ^2-r^{-2}\eta ^a\eta _a. \end{aligned}$$

(3.13)

Due to the conic property of wave front set, we can define a fiber radially compactified cotangent bundle $^b\overline{T}^{*}M$ with $\partial ^b \overline{T}^{*}M \simeq (T^{*}M\setminus 0)/R^{+}$ [23]. In this setting, the wave front set is a subset of $\partial ^b \overline{T}^{*}M$ and we should consider the rescaled Hamilton vector field $H_{R,P}=\rho H_{P}$, where $\rho$ is a boundary defining function on $^b\overline{T}^{*}M$ satisfies $\rho =0$ and $d\rho \ne 0$ on $\partial ^b \overline{T}^{*}M$. We can choose $\rho =1/{\vert \xi \vert }$ and introduce rescaled coordinates [5] $\widehat{\eta }=\eta \rho$, $\widehat{\sigma }=\sigma \rho$ near $\partial L_{j}$. According to [23], we say a submanifold L of $\partial ^b \overline{T}^{*}M$ which is invariant under rescaled Hamilton flow is a source or sink if it satisfies

$$\begin{aligned} \pm H_{R,P} \rho _{L}=\beta \rho _{L}+F_2+F_3, \end{aligned}$$

(3.14)

where $+$ corresponds to a source, − corresponds to a sink, $\rho _{L}$ is a quadratic defining function of L, $\beta \ge 0$, $F_2\ge 0$ and $F_3$ vanishes cubically at L. Following [5], $\partial L_{j}$ is a source if $s_{j}\text {sign}(\xi )=1$ or a sink if $s_{j}\text {sign}(\xi )=-1$ for Hamiltonian flow within $\partial ^b \overline{T}^{*}_XM$ with $\beta =2\vert f_*'(r_{j})\vert$, $F_2=0$ and $\rho _{L}=\vert \widehat{\eta }\vert ^2+\vert \widehat{\sigma }\vert ^2$.

Now, we study the trapped set in region $r_2<r<r_3$. In this region, the metric takes form (2.3) and $\zeta \in ^bT^*M$ can be written as $\zeta =\sigma d\tau /\tau +\xi dr+\eta d\omega$. For $\zeta \in \Sigma$, we need $H_Pr=0$ and $H^2_Pr=0$. We have $H_Pr=-2f\xi$ and this leads to $\xi =0$. Using $\xi =0$ and $g^{ab}\zeta _a\zeta _b=0$, we find $H^2_Pr=-2r^2f^{-1}(r^{-2}f)'$. Now we have

$$\begin{aligned} (r^{-2}f)'=r^{-5}\left( -4Q^2+(b+6M-2r)r-3br\ln \frac{r}{b}\right) ,\nonumber \\ \end{aligned}$$

(3.15)

so we need to study the zero points of $g(r)=-4Q^2+(b+6M-2r)r-3br\ln (r/b)$ in $(r_2,r_3)$. We will prove there is only one zero point of g(r) in $(r_2,r_3)$. The strategy is to prove g(r) has odd number zero points in $(r_2,r_3)$ and g(r) has at most two zero points in $(0,\infty )$. Combining these two conditions, we conclude g(r) has only one zero point $r_P$ in $(r_2,r_3)$. At this time, this zero point $r_P$ may correspond to a degenerate point, i.e. $g'(r_P)=0$. However, this corresponds to a zero measure set in parameter space of spacetime and we will omit it for technology convenience. Now, we first prove g(r) has odd number zero points in $(r_2,r_3)$. It is easy to see $f(r_2)=0=f(r_3)$ and $r^{-2}f(r)>0$ in region $r_{2}< r < r_{3}$, so the zero points number of $(r^{-2}f)'$ or g(r) should be an odd number. Next, we consider the zero points of g(r) in $(0,\infty )$. We find $g(r)\rightarrow -4Q^2<0$ as $r\rightarrow 0^{+}$ and $g(r)\rightarrow -2r^2<0$ as $r\rightarrow \infty$. We consider the zero points of $g'(r)=6M-2b-4r-3b\ln (r/b)$. It is easy to see $g'(r)$ has one zero point $r_{zero}$. Using $g'(r)\rightarrow -3b\ln (r/b)>0$ as $r\rightarrow 0^{+}$, g(r) is a monotonically increasing function in $(0,r_{zero})$ and g(r) is a monotonically decreasing function in $(r_{zero},\infty )$. Therefore, g(r) has two, one or zero roots corresponding to $g(r_{zero})>0$, $g(r_{zero})=0$ or $g(r_{zero})<0$. Therefore, g(r) has at most two roots. Combining g(r) has at most two zero points in $0<r<\infty$ and g(r) has odd number zero points in $r_2<r<r_3$, we conclude g(r) has one zero point $r_{P}$ in $(r_2,r_3)$. So we have the trapped set

$$\begin{aligned} \widetilde{\Gamma }=\{(\tau ,r,\omega ;\sigma ,\xi ,\eta )\in \Sigma :r=r_P,\xi =0\}. \end{aligned}$$

(3.16)

Similarly, by choosing $f_{*}$, there is only one root $r_{P*}$ in $r_{0}<r<r_{1}$. We have the trapped set

$$\begin{aligned} \widetilde{\Gamma }_{*}=\{(\tau ,r,\omega ;\sigma ,\xi ,\eta )\in \Sigma :r=r_{P*},\xi =0\}. \end{aligned}$$

(3.17)

Now, we study the global behavior of null-geodesic flow in $^bT^*\Omega$. The Hamiltonian vector fields $H_{p}$ tangent to the boundary $\tau =0$, so we can investigate the interior $^bT^*\Omega ^{0}$ and boundary $^bT^*Y$ regions separately. For convenience, we set

$$\begin{aligned} L_{j}^{\pm }:=L_{j}\cap \Sigma _{\pm }, \quad \Gamma :=\widetilde{\Gamma }\cap \{\tau =0\}, \quad \Gamma ^{\pm }_*:=\Gamma _{*}\cap \Sigma _{\pm }.\nonumber \\ \end{aligned}$$

(3.18)

Following [5], we begin by studying the global behavior of null-geodesic flow in $^bT^*\Omega ^{0}\cap \Sigma _{-}$. We first consider bicharacteristic curves in $\Sigma _{-}$. If we project a bicharacteristic curve $\gamma$ in $\Sigma _{-}$ to base manifold, it corresponds to a future-pointing null geodesic $\widetilde{\gamma }$ [16]. Using Penrose diagram and footnote 71 of [24], in the backward direction, $\gamma$ either crosses $H_{I}\cup H_{I,0}$ or tends to $L_{0}^{-}\cup L_{1}^{-}\cup \Gamma ^{-}_*$ and in the forward direction, $\gamma$ either crosses $H_{F}\cup H_{F,2}\cup H_{F,3}$ or tends to $L_{2}^{-}\cup L_{3}^{-} \cup \Gamma ^{-}$. Similarly, for $\gamma \in \Sigma _{+}$, in the forward direction, $\gamma$ either crosses $H_{I}\cup H_{I,0}$ or tends to $L_{0}^{+}\cup L_{1}^{+}\cup \Gamma ^{+}_*$ and in the backward direction, $H_{F}\cup H_{F,2}\cup H_{F,3}$ or tends to $L_{2}^{+}\cup L_{3}^{+} \cup \Gamma ^{+}$.

Now, we study the global behavior of null-geodesic flow in $^bT^*Y\cap \Sigma _{-}$. Firstly, $\gamma$ may lie in $L_{j}^{-}\cup \Gamma ^{-}\cup \Gamma ^{-}_{*}$. If $\gamma \notin L_{j}^{-}\cup \Gamma ^{-}\cup \Gamma ^{-}_{*}$, using the formula (3.8) of Hamiltonian vector fields and metric form (3.3) and (3.4) in the corresponding regions, we can analysis the sign of $H_Pr$. Combining the source/sink properties at $L_{j}$ and footnote 71 of [24], following [5], in the backward direction, $\gamma$ either crosses $H_{I,0}$ or tends to $L_2^{-}\cup L_3^{-}\cup \Gamma ^{-}\cup \Gamma ^{-}_*$ and in the forward direction, $\gamma$ either crosses $H_{F,3}$ or tends to $L_0^{-}\cup L_1^{-}\cup \Gamma ^{-}\cup \Gamma ^{-}_*$. Similarly, for $\gamma \in \Sigma _{+}$, in the forward direction, $\gamma$ either crosses $H_{I,0}$ or tends to $L_2^{+}\cup L_3^{+}\cup \Gamma ^{+}\cup \Gamma ^{+}_*$ and in the backward direction, $\gamma$ either crosses $H_{F,3}$ or tends to $L_0^{+}\cup L_1^{+}\cup \Gamma ^{+}\cup \Gamma ^{+}_*$.

Now, following [5], we study the global regularity of forward solution to $\nabla ^{a}\nabla _{a}u-m^2u=f$. Firstly, we define the weighted Sobolev space $H^{s,\alpha }_b(M)$ where s(r) is a smooth function of r and $H^{s,\alpha }(M):=\tau ^\alpha H^s_b(M)$. Due to the discussion after (3.6), we consider the wave behaviors of retarded solutions $u=E^{+}f$ with f supported in $\Omega ^{0} \cap \left\{ r>r_1\right\}$. Using $\text {supp}u\subset J^{+}(\text {supp}f)$, if we restrict u to $\Omega$, we find the restriction $\tilde{u}$ is supported at $H_{I}\cup H_{I,0}$ and extendible at $H_{F}\cup H_{F,2}\cup H_{F,3}$. So we restrict $H^{s,\alpha }_b(M)$ to $\Omega$ and we consider weighted Sobolev space $H^{s,r}_{b,\text {fw}}(\Omega )$ with those supported/extendible properties at corresponding boundaries. By duality, we define weighted Sobolev space $H^{s,r}_{b,\text {bw}}(\Omega )$ which is supported at $H_{F}\cup H_{F,2}\cup H_{F,3}$ and extendible at $H_{I}\cup H_{I,0}$. To avoid the trapped set estimates on $\Gamma _{*}$ and radial points estimates on $L_{0}$, following [5], we choose a complex absorption operator $\mathcal {Q}\in \Psi ^2_b(M)$ which is elliptic in $\{t>t_{*,0}+1,r_0-\delta<r<r_1-\delta \}$. We require the principal symbol $\sigma \left( Q\right)$ satisfies ${\mp }\sigma \left( Q\right) \ge 0$ on $\Sigma _{\pm }$. Now we consider the modified operator $\mathcal {P}:=\nabla _{a}\nabla ^{a}-m^2-iQ$. Due to the sign of $\sigma \left( Q\right)$, we can propagate the regularity in the backward/forward direction on $\Sigma {\pm }$.

In order to use high/low regularity estimates on $L_{j}$, we need forward/backward order functions for weight $\alpha$ [5]. The forward order function s(r) for weight $\alpha$ satisfies s(r) is constant for $r<r_1+\delta ''\cup r>r_1+2\delta ''$, $s(r)<1/2+\beta _1\alpha$ for $r<r_1+\delta ''$, $s(r)>1/2+\text {max}(\beta _2\alpha ,\beta _3\alpha )$ for $r>r_1+2\delta ''$ and $s'(r)\ge 0$, where $\delta ''$ is a small positive constant. Similarly, the backward order function s(r) for weight $\alpha$ satisfies s(r) is constant for $r<r_1+\delta ''\cup r>r_1+2\delta ''$, $s(r)>1/2+\beta _1\alpha$ for $r<r_1+\delta ''$, $s(r)<1/2+\text {max}(\beta _2\alpha ,\beta _3\alpha )$ for $r>r_1+2\delta ''$ and $s'(r)\le 0$. Now, combining radial points estimates, propagation of singularities estimates, elliptic estimates and normally hyperbolic trapping estimates, following Proposition 2.9 of [5], we have the following estimates.

Supposing s and $s_{0}$ are forward order functions for the weight $\alpha <0$ with $s_{0}<s$, we have

$$\begin{aligned} \Vert u \Vert _{H^{s,\alpha }_{b,\text {fw}}(\Omega )}\le C\left( \Vert \mathcal {P}u\Vert _{H^{s-1,\alpha }_{b,\text {fw}}(\Omega )}+\Vert u \Vert _{H^{s_0,\alpha }_{b,\text {fw}}(\Omega )}\right) . \end{aligned}$$

(3.19)

By duality, supposing $s'$ and $s'_{0}$ are backward order functions for the weight $-\alpha$ with $s'_{0}<s'$, we have

$$\begin{aligned} \Vert u \Vert _{H^{s',-\alpha }_{b,\text {bw}}(\Omega )}\le C\left( \Vert \mathcal {P^*}u\Vert _{H^{s'-1,-\alpha }_{b,\text {bw}}(\Omega )}+\Vert u \Vert _{H^{s'_0,-\alpha }_{b,\text {bw}}(\Omega )}\right) .\nonumber \\ \end{aligned}$$

(3.20)

The proof in Proposition 2.9 of [5] is valid in our case and we only need to check the trapping estimates in [25]. We need to check the conditions above Theorem 3.2 of [25]. It is not difficult to see most of the conditions are met and we only need to check whether $\{\phi _{+},\phi _{-}\}>0$ on trapped set $\Gamma$, see (3.4) of [25]. According to the discussion in Sect. 3 of [25], trapping of rescaled hamiltonian vector field within $^bS^{*}_{X}M$ is equivalent to normal hyperbolicity of semiclassical Hamilton vector field. This is equivalent to consider Hamilton vector field with $\sigma =\pm 1$ in $T^{*}X$. Following [26], we consider the linearization of the Hamilton flow near trapped set $\Gamma$. We have $H_{P}(r-r_{P})=-2f\xi$ and $H_P\xi =f^{-2}f'\sigma ^2-2r^{-3}|\eta |^2=f^{-2}f'\sigma ^2-2*f^{-1}\sigma ^2=f^{-2}r^2(r^{-2}f)'$, where we use $\sigma =\pm 1$ and $f^{-1}\sigma ^2=r^{-2}|\eta |^2$ on $\Sigma$. We have

$$\begin{aligned} & H_{P} \left( \begin{array}{cc} r-r_P \\ \xi \end{array} \right) \nonumber \\ & \quad =\left( \begin{array}{cc} 0 & -2f(r_P) \\ f^{-2}(r_P)r_{P}^2(r^{-2}f)''(r_P) & 0 \end{array} \right) \left( \begin{array}{cc} r-r_P \\ \xi \end{array} \right) .\nonumber \\ \end{aligned}$$

(3.21)

The eigenvalues are $\lambda _{\pm }=\pm (-2f^{-1}(r_P)r_{P}^2(r^{-2}f)''(r_P))^{1/2}$. As in Proposition 2.1 of [26], we denote $\beta =\pm (r^2/f-\alpha ^2)^{1/2}$. We have $\beta ''_{\alpha \alpha }={\mp }(r_P^2/f(r_P))^{-1/2}$, $\beta ''_{\theta \theta }={\mp }(r_P^2/f(r_P))^{1/2}$ and $\beta ''_{\alpha \theta }=0$, so it is nondegeneracy. Then, the arguments in Sect. 2 of [26] go through unchanged and this gives normally hyperbolic trapping.

Now, following [5], to prove $\mathcal {P}$ is a Fredholm operator, one need to prove it satisfies Fredholm estimates [23] which can be written as

$$\begin{aligned} \begin{aligned} \Vert u \Vert _{\mathcal {X}}&\le C\left( \Vert \mathcal {P}u\Vert _{\mathcal {Y}}+\Vert u \Vert _{\mathcal {\tilde{X}}}\right) ,\\ \Vert v \Vert _{\mathcal {Y^*}}&\le C\left( \Vert \mathcal {P^*}u\Vert _{\mathcal {X^*}}+\Vert u \Vert _{\mathcal {\tilde{Z}}}\right) , \end{aligned}\end{aligned}$$

(3.22)

where the inclusion maps $\mathcal {X}\rightarrow \mathcal {\tilde{X}}$ and $\mathcal {Y^*}\rightarrow \mathcal {\tilde{Z}}$ are compact. If $\mathcal {P}$ satisfies Fredholm estimates, one may prove $\mathcal {P}:X_{\mathcal {P}}\rightarrow \mathcal {Y}$ is a Fredholm operator where $X_{\mathcal {P}}=\left\{ u\in \mathcal {X}:\mathcal {P}u\in \mathcal {Y}\right\}$. In our case, we have $X_{\mathcal {P}}=\left\{ u\in H^{s,\alpha }_{b,\text {fw}}(\Omega ):\mathcal {P}u\in H^{s-1,\alpha }_{b,\text {fw}}(\Omega )\right\}$ and $\mathcal {Y}=H^{s-1,\alpha }_{b,\text {fw}}(\Omega )$. Comparing with (3.19), we find $H^{s,\alpha }_{b,\text {fw}}(\Omega ) \rightarrow H^{s_{0},\alpha }_{b,\text {fw}}(\Omega )$ is not compact. Therefore, we need to consider the normal operator and its Mellin transformation [23]. The Mellin transformation in $\tau$ is given by

$$\begin{aligned} \hat{u}(\sigma ,.)=\int _{0}^{\infty }\tau ^{-i\sigma }u(\tau ,.)\frac{d\tau }{\tau }. \end{aligned}$$

(3.23)

We can Mellin transform $H^{s,\alpha }_{b}([0,\infty )_{\tau }\times X)$ and restrict $\text {Im}\sigma =-\alpha$, then we have an isomorphism

$$\begin{aligned} H^{s,\alpha }_{b}([0,\infty )_{\tau }\times X)\cong L^2(\{\text {Im}\sigma =-\alpha \},H^{s,-s}_{\langle |\sigma |\rangle ^{-1}}(X)),\nonumber \\ \end{aligned}$$

(3.24)

where $H^{s,w}_h(X)=h^{-w}H^{s}_{h}(X)$, $H^{s}_{h}$ is the semiclassical Sobolev space, $X=\partial M$ and $\langle |\sigma |\rangle =(1+|\sigma |^2)^{1/2}$. The normal operator $N(\mathcal {P})$ is defined by freezing coefficients of $\mathcal {P}$ at boundary and normal operator family $\hat{\mathcal {P}}(\sigma )$ is given by conjugating $N(\mathcal {P})$ by Mellin transformation. We first consider $\sigma$ is finite number and $\hat{\mathcal {P}}(\sigma )$ can be regarded as an element of $\text {Diff}^2(X)$. According to the support properties of $H^{s,\alpha }_{b,\text {fw}}$, we consider Sobolev space $H^{s}_{\text {fw}}(Y)$ on $Y=\partial \Omega \cap X$, which is supported at $r_{0}-2\delta '$ and extendible at $r_3+2\delta '$. Similarly, we have the semiclassical Sobolev space $H^{s}_{h,\text {fw/bw}}(Y)=H^{s,-s}_h(Y)=h^{s}H^{s}_{h}(Y)$ which is supported/extendible at $r_{0}-2\delta '$ and extendible/supported at $r_3+2\delta '$. Now, $\hat{\mathcal {P}}(\sigma )$ is elliptic in $\{r_0<r<r_1\} \cup \{r_2<r<r_3\}$ and we can use elliptic estimate here. The Hamilton vector field of $\hat{\mathcal {P}}(\sigma )$ in $T^*X$ is identified with the Hamilton vector field of Klein–Gordon in $^b{T}_{X}^{*}M$ with $\sigma =0$. Therefore, $L_j$ are still radial points and we want to use radial estimates there. In this case, according to [24], we need to check whether $s>1/2-\beta '_{j}\text {Im}\sigma$ or $s<1/2-\beta '_{j}\text {Im}\sigma$. It is easy to see $\beta '_{j}=\beta _{j}$ and according to Mellin transformation, we consider $\text {Im}\sigma =-\alpha$. Therefore, it is equivalent to check whether $s>1/2+\beta _{j}\alpha$ or $s<1/2+\beta _{j}\alpha$. For s in (3.19), it is a forward order function for weight $\alpha$, so we use high regularity radial estimate near $L_{2}\cup L_{3}$ and low regularity radial estimate near $L_{1}$. Finally, one can use same method as in Proposition 2.9 of [5] to give estimates near $r_0-2\delta$ and $r_3+2\delta$. Then, we have

$$\begin{aligned} \Vert v \Vert _{H^{s}_{\text {fw}}(Y)} \le C(\sigma )\left( \Vert \hat{\mathcal {P}}(\sigma )v\Vert _{H^{s-1}_{\text {fw}}(Y)}+ \Vert v \Vert _{H^{s_0}_{\text {fw}}(Y)} \right) , \end{aligned}$$

(3.25)

where s and $s_{0}$ are forward order functions of weight $-\text {Im}\sigma$ with $s_0<s$. The dual estimate is given by

$$\begin{aligned} \Vert v \Vert _{H^{s'}_{\text {bw}}(Y)} \le C(\bar{\sigma })\left( \Vert \hat{\mathcal {P}}^{*}(\bar{\sigma })v\Vert _{H^{s'-1}_{\text {bw}}(Y)}+ \Vert v \Vert _{H^{s'_0}_{\text {bw}}(Y)} \right) ,\nonumber \\ \end{aligned}$$

(3.26)

where $s'$ and $s'_{0}$ are backward order functions of weight $\text {Im}\sigma$ with $s'_0<s'$. This gives the Fredholm property of $\hat{\mathcal {P}}(\sigma )$ for $\sigma$ in any compact region.

Now, we consider $\vert \text {Re}\sigma \vert \rightarrow \infty$ with $\vert \text {Im}\sigma \vert <C$. To capture the behavior of $\vert \text {Re}\sigma \vert \rightarrow \infty$, it is nature to use semiclassical analysis [23]. Thus, we consider the semiclassical operator

$$\begin{aligned} \mathcal {P}_{h,z}:=h^2\hat{\mathcal {P}}(z/h), \end{aligned}$$

(3.27)

where $h=(1+|\sigma |^2)^{-1/2}$ and $z=h\sigma$. In semiclassical case, the elliptic set and wave front set are subsets of $\bar{T}^{*}X$, where $\bar{T}^{*}X$ fiber-radially compactified of $T^{*}X$. The interior of $\bar{T}^{*}X$ is $T^{*}X$ and the boundary $\partial \bar{T}^{*}X$ is defined by

$$\begin{aligned} \partial \bar{T}^{*}X\simeq (T^{*}X{\setminus } 0)/R^{+}. \end{aligned}$$

(3.28)

Similarly, we study the behavior of Hamiltonian vector field of semiclassical principal symbol of $\mathcal {P}_{h,z}$. Using $\vert \text {Re}\sigma \vert \rightarrow \infty$ with $\vert \text {Im}\sigma \vert <C$, we have $z=\pm 1+O(h)$ and Hamiltonian vector field of semiclassical principal symbol $P_{h,z}$ with $z=\pm 1$ in $T^{*}X$ is equivalent to the Hamiltonian vector field with $\sigma =\pm 1$ in $T^{*}X$. Therefore, we only need consider the behavior of Hamiltonian vector field with $\sigma =\pm 1$. To include the boundary $\partial \bar{T}^{*}X$, we consider the rescaled Hamiltonian vector field with $\sigma =\pm 1$ in $\bar{T}^{*}X$. Similarly to Proposition 2.9 of [5], one may use semiclassical radial points estimates near $L_j$, semiclassical trapped estimates near trapped set, semiclassical estimates of propagator of singularity near $\{r=r_3+2\delta \}\cup \{r=r_0-2\delta \}$ and semiclassical elliptic estimates. Then, following Proposition 2.10 of [5], we have

$$\begin{aligned} \Vert v \Vert _{H^{s}_{h,\text {fw}}(Y)} \le C\left( \Vert h^{-2}\mathcal {P}_{h,z}v\Vert _{H^{s-1}_{h,\text {fw}}(Y)}+ \Vert v \Vert _{H^{s_0}_{h,\text {fw}}(Y)} \right) ,\nonumber \\ \end{aligned}$$

(3.29)

where $h^{-1}\text {Im}z\in [c_1,c_2]$ with $0<c_1<c_2$. Here s and $s_0<s$ are forward order functions for any weight $\alpha \in [-c_2,-c_1]$. The dual estimates is given by

$$\begin{aligned} \Vert v \Vert _{H^{s'}_{h,\text {bw}}(Y)} \le C\left( \Vert h^{-2}\mathcal {P^*}_{h,z}v\Vert _{H^{s'-1}_{h,\text {bw}}(Y)}+ \Vert v \Vert _{H^{s'_0}_{h,\text {bw}}(Y)} \right) , \nonumber \\ \end{aligned}$$

(3.30)

where $s'$ and $s'_0<s'$ are backward order functions for any weight $\alpha \in [c_1,c_2]$. This gives the Fredholm property of $\hat{\mathcal {P}}(\sigma )$ for $\vert \text {Re}\sigma \vert \rightarrow \infty$ with $\text {Im}\sigma \in [c_1,c_2]$. Combining (3.25), (3.26), (3.29) and (3.30), $\hat{\mathcal {P}}(\sigma ): \mathcal {X}^{s}_{\langle |\sigma |\rangle ^{-1},\text {fw}}\rightarrow H^{s-1}_{\langle |\sigma |\rangle ^{-1},\text {fw}}(Y)$ is a Fredholm operator for $\text {Im}\sigma \in [c_1,c_2]$, where $\mathcal {X}^{s}_{\langle |\sigma |\rangle ^{-1},\text {fw}}=\{u\in H^{s}_{\langle |\sigma |\rangle ^{-1},\text {fw}}(Y)\, \hat{\mathcal {P}}(\sigma )u\in H^{s-1}_{\langle |\sigma |\rangle ^{-1},\text {fw}}(Y)\}$. For $h\rightarrow 0$ or $\vert \text {Re}\sigma \vert \rightarrow \infty$ equivalently, the second terms on the right hand of (3.29) and (3.30) can be absorbed into the left hand sides. Therefore, $\mathcal {P}_{h,z}$ is invertible for $z=\pm 1+O(h)$, $h^{-1}\text {Im}z \in [c_1,c_2]$ and $h\rightarrow 0$. Using (3.27), $\hat{\mathcal {P}}(\sigma )$ is invertible for $\vert \text {Re}\sigma \vert \rightarrow \infty$ and $\text {Im}\sigma \in [c_1,c_2]$. Then, by analytic Fredholm theory, $\sigma \mapsto \hat{\mathcal {P}}^{-1}(\sigma )$ is a meromorphic family of operators with poles of finite rank. Therefore, $\hat{\mathcal {P}}(\sigma )^{-1}$ has only finite poles in $\text {Im}\sigma \in [c_1,c_2]$. One may choose $c_1<-\alpha <c_2$ such that $\hat{\mathcal {P}}(\sigma )^{-1}$ is invertible on the line $\text {Im}\sigma =-\alpha$. For $\vert \text {Re}\sigma \vert \rightarrow \infty$ and $\text {Im}\sigma =-\alpha$, we have

$$\begin{aligned} \Vert v \Vert _{H^{s}_{h,\text {fw}}(Y)} \le C\Vert \hat{\mathcal {P}}(\sigma )v\Vert _{H^{s-1}_{h,\text {fw}}(Y)}. \end{aligned}$$

(3.31)

According to radial point estimates in [24], the second term on the right hand of (3.25) can be replaced by the residual term $\Vert v \Vert _{H^{-N}_{\text {fw}}(Y)}$ for $\forall N\in R$. Then, for $\text {Re}\sigma$ in any compact region and $\text {Im}\sigma =-\alpha$, as a result of Sect. 4.3 of [27], we have

$$\begin{aligned} \Vert v \Vert _{H^{s}_{\text {fw}}(Y)} \le C\Vert \hat{\mathcal {P}}(\sigma )v\Vert _{H^{s-1}_{\text {fw}}(Y)}. \end{aligned}$$

(3.32)

In view of the isomorphism in Mellin transformation (3.24), we have

$$\begin{aligned} \Vert u \Vert _{H^{s,\alpha }_{b,\text {fw}}(([0,\infty )_{\tau }\times Y))} \le C\Vert N(\mathcal {P})u\Vert _{H^{s-1,\alpha }_{b,\text {fw}}(([0,\infty )_{\tau }\times Y))}. \nonumber \\ \end{aligned}$$

(3.33)

Here s is a forward order function for weight $\alpha <0$. u is supported at $[0,\infty )_{\tau }\times (Y\cap \{r=r_0-2\delta \})$ and extendible at $[0,\infty )_{\tau }\times (Y\cap \{r=r_3+2\delta \})$. We can identify the points in $\Omega$ with points in $[0,\infty )_{\tau }\times Y$ by boundary defining function $\tau$. Then, the $H^{s,\alpha }_{b,\text {fw}}(\Omega )$ norm is equivalent to the corresponding restriction norm of $H^{s,\alpha }_{b,\text {fw}}(([0,\infty )_{\tau }\times Y))$.

Following [5], for technical convenience, we strengthen the conditions on forward order functions $s_0$ and s for the weight $\alpha$ in (3.19) by requiring $s-1>s_0$. Similarly, we strengthen the conditions on backward order functions $s'_0$ and $s'$ for the weight $-\alpha$ in (3.20) by requiring $s'-1>s'_0$. From the Fredholm estimates (3.22) and (3.22), we require $H^{s'-1,-\alpha }_{b,\text {bw}}(\Omega )$ to be the dual space of $H^{s,\alpha }_{b,\text {fw}}(\Omega )$ and this corresponds to $s'=1-s$. In order to use (3.33) and its dual estimate, we need $\hat{\mathcal {P}}(\sigma )^{-1}$ is invertible on the line $\text {Im}\sigma =-\alpha$ and $\hat{\mathcal {P}^{*}}(\sigma )^{-1}$ is invertible on the line $\text {Im}\sigma =\alpha$. Using $\hat{\mathcal {P}^{*}}(\sigma )=\hat{\mathcal {P}}(\bar{\sigma })^{*}$, these two conditions are equivalent. Now, we turn to the second term on the right hand of (3.25). As shown in [5], the second term on the right hand of (3.22) can be rewritten as

$$\begin{aligned} \Vert u \Vert _{H^{s_0,\alpha }_{b,\text {fw}}(\Omega )}\le \Vert (1-\chi ) u\Vert _{H^{s_0,\alpha }_{b,\text {fw}}(\Omega )}+\Vert \chi u\Vert _{H^{s_0,\alpha }_{b,\text {fw}}(\Omega )},\nonumber \\ \end{aligned}$$

(3.34)

where $\chi \in C^{\infty }(\Omega )$, $\chi =1$ near Y and $\chi$ is supported in a small collar neighborhood of Y. The first term on the right hand supported away from boundary, the weight $\alpha$ can be replaced by $\alpha -1$. We apply (3.33) to the second term and using the identity $N(\mathcal {P})\chi =-\chi (\mathcal {P}-N(\mathcal {P}))+\chi \mathcal {P}+[N(\mathcal {P}),\chi ]$. Using the supported property of $\chi$, (3.19) can be written as

$$\begin{aligned} \Vert u \Vert _{H^{s,\alpha }_{b,\text {fw}}(\Omega )}\le C\left( \Vert \mathcal {P}u\Vert _{H^{s-1,\alpha }_{b,\text {fw}}(\Omega )}+\Vert u \Vert _{H^{s_0+1,\alpha -1}_{b,\text {fw}}(\Omega )}\right) .\nonumber \\ \end{aligned}$$

(3.35)

Similarly, the dual estimate can be written as

$$\begin{aligned} \Vert u \Vert _{H^{s',-\alpha }_{b,\text {bw}}(\Omega )}\le C\left( \Vert \mathcal {P^*}u\Vert _{H^{s'-1,-\alpha }_{b,\text {bw}}(\Omega )}+\Vert u \Vert _{H^{s_0'+1,-\alpha -1}_{b,\text {bw}}(\Omega )}\right) .\nonumber \\ \end{aligned}$$

(3.36)

As a result of enhanced conditions $s-1>s_0$ and $s'-1>s'_0$, the inclusion map $H^{s,\alpha }_{b,\text {fw}}(\Omega )\rightarrow H^{s_0+1,\alpha -1}_{b,\text {fw}}(\Omega )$ and $H^{s',-\alpha }_{b,\text {bw}}(\Omega )\rightarrow H^{s'_0+1,-\alpha -1}_{b,\text {bw}}(\Omega )$ are compact. Taking $s'=1-s$, $\mathcal {P}: \mathcal {X}^{s,\alpha }\rightarrow H^{s-1,\alpha }_{b,\text {fw}}(\Omega )$ is a Fredholm operator, where

$$\begin{aligned} \mathcal {X}^{s,\alpha }=\{u\in H^{s,\alpha }_{b,\text {fw}}(\Omega ): \mathcal {P}u\in H^{s-1,\alpha }_{b,\text {fw}}(\Omega ) \} \end{aligned}$$

(3.37)

In the above calculations, we use the enhanced conditions $s-1>s_0$ and $s'-1>s'_0$ and takes $s'=1-s$. So, $s>3/2+\text {max}(\beta _2\alpha ,\beta _3\alpha )$ for $r>r_1+2\delta ''$ and $s'>3/2-\beta _1\alpha$ for $r<r_1+\delta ''$. By taking $s'=1-s$, we have $s(r)<-1/2+\beta _1\alpha$ for $r<r_1+\delta ''$ and this weaken the regularity of u near the Cauchy horizon. Using Theorem 2.13 of [5], we can remove the condition $s(r)<-1/2+\beta _1\alpha$ for $r<r_1+\delta ''$ and the regularity of u near the Cauchy horizon is $s(r)<1/2+\beta _1\alpha$ again.

As in [24], in order to improve the regularity of $\alpha$ by shifting contour of inverse Mellin-transformation, we need to study the resonances of $\hat{\mathcal {P}}(\sigma )$ and residual term of $\hat{\mathcal {P}}(\sigma )^{-1}$. A resonant state u for a resonance $\sigma$ is defined by $u\in \text {Ker}_{H^s_{\text {fw}}}\hat{\mathcal {P}}(\sigma )$. When $m=0$, we can follow Lemma 2.14 of [5]. When $m\ne 0$, we may find some certain values of $(M,Q,b,\Lambda )$ which have resonances (also called quasinormal modes) in region $\{r_2<r<r_3\}$ with $\text {Im}\sigma >0$. However, these corresponds to unstable spacetimes and we exclude these unphysical parameters.

Now, we can prove every resonant state u with $\text {Im}\sigma >0$ is supported in $\{r_0\le r\le r_1\}$. For $m=0$, we can follow the proof in Lemma 2.14 of [5]. It is not difficulty to see the conditions in [28] are satisfied in our case. So, for every resonant state u with $\text {Im}\sigma >0$, we have $u\equiv 0$ in $\{r_2<r<r_3\}$. Using radial points estimates near $r=r_{2,3}$ and footnote 58 of [24], we have $u\equiv 0$ for $\vert r-r_{2/3}\vert <\delta '''$. Therefore, u is supported at $r=r_0-2\delta$, $r=r_2$ and $r=r_3$. By energy estimates [29], we find $u\equiv 0$ in $\{r_0-2\delta \le r<r_0\}\cup \{r_1<r\le r_2\}\cup \{r_3\le r<r_3+2\delta \}$. For $m\ne 0$, by the discussion in the preceding paragraph, we have $u\equiv 0$ in $\{r_2<r<r_3\}$. Similarly, we have $u\equiv 0$ in $\{r_0-2\delta \le r<r_0\}\cup \{r_1<r\le r_2\}\cup \{r_3\le r<r_3+2\delta \}$. Next, we consider resonant states with $\text {Im}\sigma =0$. For $m=0$, according to Sect. 3 of [28], there is only one resonance $\sigma =0$ for $r_2<r<r_3$ and the corresponding resonant states are constant in $r_2<r<r_3$. For a resonant state $u=C$ in $r_2<r<r_3$, we can apply the above discussion to $u-C$ and we find $u=C$ in $r>r_1$. For $m>0$, we first consider the resonances in $r_2<r<r_3$ and it is equivalent to studying the quasi-normal modes in $r_2<r<r_3$. The solutions of Klein–Gordon operator can be written in a general from [7]

$$\begin{aligned} & \psi _{\omega lm}(t,r,\theta ,\phi )\nonumber \\ & \quad =(2\pi )^{-\frac{3}{2}}(2\vert \omega \vert )^{-\frac{1}{2}}r^{-1}R_{\omega l}(r)Y_{lm}(\theta ,\phi )e^{-i\omega t}. \end{aligned}$$

(3.38)

The radial equation is given by

$$\begin{aligned} -\frac{d^2R_{\omega l}}{dr_{*}^2}+(V_{l}-\omega ^2)R_{\omega l}=0, \end{aligned}$$

(3.39)

where

$$\begin{aligned} V_{l}(r)=f(r)\left( \frac{l(l+1)}{r^2}+\frac{f'(r)}{r}+m^2\right) . \end{aligned}$$

(3.40)

Following [7], we consider the Wronskian

$$\begin{aligned} W(r_{*})=\overline{R}_{\omega l}\frac{dR_{\omega l}}{dr_{*}}-R_{\omega l}\frac{d\overline{R}_{\omega l}}{dr_{*}}. \end{aligned}$$

(3.41)

When $\text {Im}\omega =0$, using radial equation (3.39), we find $dW(r_{*})/dr_{*}=0$. Taking outgoing conditions near $r=r_{2/3}$ into Wronskian $W(r_{*})$, we have $\omega =0$. Then, we can use the method in [30] to show $\psi _{\omega lm}(t,r,\theta ,\phi )=0$. Therefore, for $m>0$ and $\text {Im}\sigma =0$, there are no quasi-normal modes in $r_2<r<r_3$. The above discussions show the resonant states are supported in $r\le r_1$.

Now, we study the structure of resonances. Near a resonance $\sigma _{0}$, the Laurent expansion of $\hat{\mathcal {P}}(\sigma )^{-1}$ can be written as

$$\begin{aligned} \frac{A_{k}}{(\sigma -\sigma _{0})^k}+\frac{A_{k-1}}{(\sigma -\sigma _{0})^{k-1}}+\cdots +\frac{A_{1}}{(\sigma -\sigma _{0})}+A_{0}. \end{aligned}$$

(3.42)

We are interested in the region $\{r>r_1\}$ and we denote R the restriction of distributions on Y to $\{r>r_1\}$. We study $R\circ \hat{\mathcal {P}}(\sigma )^{-1}$. Following Lemma 8.3 of [31], for $\text {Im}\sigma >0$, the range of $A_k(k>0)$ are supported in $r\le r_1$. For $\text {Im}\sigma =0$ and $m>0$, similarly, the range of $A_k (k>0)$ are supported in $r\le r_1$. For $\text {Im}\sigma =0$ and $m=0$, according to [28], if resonance $\sigma _{0}\ne 0$, the same method shows the range of $A_k(k>0)$ are supported in $r\le r_1$. If resonance $\sigma _{0}=0$ and $m=0$, following Lemma 2.14 of [5], the order of the pole $\sigma =0$ is equal to 1. Using Lemma 8.3 of [31], we have $\hat{\mathcal {P}}(0)A_1=0$ and this corresponds to constant functions in $r>r_1$.

Now, we consider the solvability of $\mathcal {P}u=f$. Following Lemma 2.15 and Corollary 2.16 of [5], by modifying $f\in H^{s-1,\alpha }_{b,\text {fw}}(\Omega )$ in $r<r_1$, there always exists $u\in H^{s,\alpha }_{b,\text {fw}}(\Omega )$ such that $\mathcal {P}u=f'$, where $f'$ is the modified source. If $f\in H^{s-1,\alpha }_{b,\text {fw}}(\Omega )$ supported in $r>r_1$, using $f-f'$ supported in $r<r_1$, there always exists $u\in H^{s,\alpha }_{b,\text {fw}}(\Omega )$ such that $\mathcal {P}u=f$ in $r>r_1$ and the restriction of u to $r>r_1$ is unique.

Now, following Proposition 2.17 of [5], we consider the regularity of u which is a forward solution of $\nabla _{a}\nabla ^{a}u-m^2u=f$ in $r>r_1$, where f is a smooth function with compact support and f is supported in $\Omega ^{0}\cap \{r>r_1\}$. Using the solvability of u, there exists $u\in H^{\tilde{s},\tilde{\alpha }}_{b,\text {fw}}(\Omega )$ such that $\nabla _{a}\nabla ^{a}u-m^2u=f$ in $r>r_1$, where $\tilde{\alpha }<0$, $\hat{\mathcal {P}}(\sigma )$ is invertible on $\text {Im}\sigma =-\tilde{\alpha }$, $\tilde{s}(r)>3/2+\text {max}(\beta _2\tilde{\alpha },\beta _3\tilde{\alpha })$ and $\tilde{s}$ is a forward order function for weight $\tilde{\alpha }<0$. First, we improve the weight $\tilde{\alpha }$. The complex absorption operator is not dilation-invariant, so we choose a cutoff function $\chi '\equiv 1$ near $\tau =0$ and $\chi '$ supported in dilation-invariant region of complex absorption operator. We have $\mathcal {P}(\chi 'u)=f_1:=\chi 'f'+[\mathcal {P},\chi ']u$, where $f'$ is the modified source introduced in previous paragraph. Taking Mellin transformation and using the invertibility of $\hat{\mathcal {P}}(\sigma )$ on $\text {Im}\sigma =-\tilde{\alpha }$, we have $\widehat{\chi 'u}(\sigma )$=$\widehat{\mathcal {P}}^{-1}(\sigma )\widehat{f_1}(\sigma )$. Now, by taking inverse Mellin transformation, we have

$$\begin{aligned} \chi 'u=\frac{1}{2\pi }\int _{\text {Im}\sigma =-\tilde{\alpha }}\tau ^{i\sigma }\widehat{\mathcal {P}}^{-1}(\sigma )\widehat{f_1}(\sigma )d\sigma . \end{aligned}$$

(3.43)

Now, we shift contour by Cauchy’s theorem and boundaries at infinity give no contribution by high energy estimate. Indeed, following [5], we have high energy estimate $\Vert v \Vert _{H^{\tilde{s}-1}_{h,\text {fw}}(Y)} \le C\Vert \mathcal {P}_{\sigma }v\Vert _{H^{\tilde{s}}_{h,\text {fw}}(Y)}$ for $\text {Im}\sigma >-\gamma _{0}$, where $\gamma _{0}=f(r_P)\lambda _{+}/4$. Now, we shift contour to $\text {Im}\sigma =-\alpha$ such that the contour does not contain any resonances for $r_2<r<r_3$ with $\text {Im}\sigma <0$. Computing the inverse Mellin transformation and multiplying a cutoff function $\chi$ supported in $\chi '\equiv 1$, we have

$$\begin{aligned} \chi u(\tau ,x)=\sum _{i,j}\tau ^{i\sigma _{i}}\vert \text {log}\tau \vert ^{j}a_{i,j}(x)\chi (\tau )+u', \end{aligned}$$

(3.44)

where the first term on the right hand corresponds to residual terms and second term on the right hand corresponds integral on $\text {Im}\sigma =-\alpha$. Now, we have $u'\in H^{\tilde{s},\alpha }_{b,\text {fw}}(\Omega )$. We can improve the regularity of $u'$ and we have $u'\in H^{s,\alpha }_{b,\text {fw}}(\Omega )$, where s is the forward order function for weight $\alpha$. Using $f'\in C^{\infty }(\Omega ^{0})$, we have $u'\in C^{\infty }$ for $r>r_1$ and $u'\in H^{1/2+\alpha \beta _1-0^{+},\alpha }_{b}$ near $r=r_1$. Following enlarged domain argument in Proposition 2.17 of [5] and restricting residual terms to $r>r_1$, we have

$$\begin{aligned} u=C+u', \end{aligned}$$

(3.45)

where $u'\in C^{\infty }$ for $r>r_1$, $u'\in H^{1/2+\alpha \beta _1-0^{+},\alpha }_{b}$ near $r=r_1$, C is a constant for $m=0$ and $C=0$ for $m\ne 0$.

In summary, if u is a solution of Klein Gordon equation $\nabla _{a}\nabla ^{a}u-m^2u=0$ with smooth initial data on $H_I$, then u takes form (3.45). This gives the singular behaviors of u near Cauchy horizon.

4 Quantum fields on curved spacetime and Hadamard states

In this section, we first briefly review the algebraic formulation of quantum theory given in [7, 15, 16]. Then following [7], we construct Unruh state and comparison state as Hadamard states in corresponding regions.

Now, we set up the quantum theory in a globally hyperbolic spacetime $(M,g_{ab})$. A spacetime is globally hyperbolic if it has a hypersurface $\Sigma$ such that each inextensible causal curve intersects $\Sigma$ at exactly one point. This hypersurface $\Sigma$ is called Cauchy surface. In a globally hyperbolic spacetime $(M,g_{ab})$, the Klein–Gordon wave operator $P=\nabla _{a}\nabla ^{a}-m^2$ has a unique retarded/advanced Green’s function $E^{\pm }$ such that $E\in \mathcal {D}'(M\times M)$, $P\circ E^{\pm }=E^{\pm }\circ P=I_{id}$ and $\text {supp}E^{\pm }\subset \{(x,y),x\in J^{\pm }(y)\}$, where $D'(M\times M)$ denotes distributions on $M\times M$ [21]. The propagator E is given by $E:=E^{+}-E^{-}$. Following [7], we define an $*$-algebra $\mathfrak {A}(M,g_{ab})$ generated by $\hat{\phi }(f)$ and a unit $\textbf{1}$, where f is a complex-valued smooth function with compact support and $\hat{\phi }$ is an operator-valued distribution which satisfies

$$\begin{aligned} 1. & \hat{\phi }(c_1f_1+c_2f_2) =c_1\hat{\phi }(f_1)+c_2\hat{\phi }(f_2)\quad \text {for all}\quad c_1,c_2\in \mathbb {C}, \end{aligned}$$

(4.1)

$$\begin{aligned} 2. & \hat{\phi }((\nabla _{a}\nabla ^{a}-m^2)f)=0, \end{aligned}$$

(4.2)

$$\begin{aligned} 3. & \hat{\phi }(f)^{*}=\hat{\phi }(\bar{f}), \end{aligned}$$

(4.3)

$$\begin{aligned} 4. & [\hat{\phi }(f_1),\hat{\phi }(f_2)]=iE(f_1,f_2)1. \end{aligned}$$

(4.4)

Then we can define states corresponding to algebra $\mathfrak {A}(M,g_{ab})$. A state is a linear map $\omega$: $\mathfrak {A}(M,g_{ab})\rightarrow \mathbb {C}$ satisfies $\omega (\textbf{1})=1$ and $\omega (a^{*}a)\ge 0$ for all $a\in \mathfrak {A}(M,g_{ab})$. Since the algebra generated by $\hat{\phi }(f)$ and a unit $\textbf{1}$, a state can be determined uniquely by its n-points functions

$$\begin{aligned} \omega _{n}(x_1,\ldots ,x_n):=\omega (\hat{\phi }(x_1)\cdots \hat{\phi }(x_n)). \end{aligned}$$

(4.5)

In this paper, we consider quasifree states which have vanishing odd n-point functions and even n-point functions are determined by two-point function. Therefore, a quasifree state is determined uniquely by its two-point function $\omega _{2}(x_1,x_2)$. Since the algebra satisfies (4.1)-(4.4), the two-point function $\omega _{2}(x,x')$ satisfies

$$\begin{aligned} 1. & (\nabla _{a}\nabla ^{a}-m^2)\omega _{2}(x,x')=(\nabla _{a'}\nabla ^{a'}-m^2)\omega _{2}(x,x')=0, \end{aligned}$$

(4.6)

$$\begin{aligned} 2. & \omega _{2}(x,x')-\omega _{2}(x',x)=iE(x,x'), \end{aligned}$$

(4.7)

$$\begin{aligned} 3. & \int \int \omega _{2}(x,x')\bar{f}(x)f(x')dg(x)dg(x')\ge 0. \end{aligned}$$

(4.8)

A physical state must satisfy Hadamard condition which determines the singular behavior of two-point function $\omega _2(x_1,x_2)$ when $x_1$ is close to $x_2$. More precisely, we focus on the convex normal neighborhood $U\subset M$ which is an open set such that for any two points $x_1$ and $x_2$ in U, they can be connected by a unique geodesic contained in U. Therefore, the signed squared geodesic distance $\sigma (x_1,x_2)$ can be determined uniquely when $x_1$ and $x_2$ in U. Now, we introduce Hadamard condition: for $(x_1,x_2)\in U\times U$, where U is a convex normal neighborhood, the two-point function $\omega _2(x_1,x_2)$ for state $\omega$ can be written as [7, 15]

$$\begin{aligned} & \omega _2(x_1,x_2)=\lim _{\epsilon \rightarrow 0^{+}}\frac{1}{4\pi ^2}\nonumber \\ & \quad \times \left( \frac{\Delta ^{\frac{1}{2}}(x_1,x_2)}{\sigma +i\epsilon T}+V(x_1,x_2)\text {log}(\sigma +i\epsilon T)+W_{\omega }(x_1,x_2)\right) ,\nonumber \\ \end{aligned}$$

(4.9)

where $\Delta$ is the Van Vleck–Morette determinant, V is determined by Hadamard recursion relation [33], $C^{\infty }(U\times U)\ni W_{\omega }$ depends on state $\omega$, $T=T(x_1)-T(x_2)$, T(x) is a time function on U and $\epsilon \rightarrow 0^{+}$ in distribution sense. The singular terms are determined by local geometry and the explicit expressions are given in [34]. An important motivation to study Hadamard states is that vacuum and thermal states in flat spacetime are Hadamard states [35]. In this paper, we focus on the behavior of energy momentum tensor and this corresponds to $x_1=x_2$. Due to the singular behavior at $x_1=x_2$, using the point-splitting scheme, the renormalized energy momentum tensor $\left\langle T_{uv}\right\rangle _{ren}$ is defined by

$$\begin{aligned} \left\langle T_{uv}\right\rangle _{ren}(x)=\lim _{x\rightarrow x'}(\left\langle T_{uv}(x,x')\right\rangle -C_{uv}(x,x')), \end{aligned}$$

(4.10)

where $C_{uv}(x,x')$ is the counter term. In fact, there are some ambiguities on counter term $C_{uv}(x,x')$ [36, 37] and the difference $C_{uv}(x,x')-C'_{uv}(x,x')$ of two counter terms are linear combinations of geometry terms which are smooth near the Cauchy horizon. We are interested in the divergent behaviors of energy momentum tensor near the Cauchy horizon, so the ambiguities on counter terms won’t affect our result.

Now, we need to construct Hadamard states and the existence of Hadamard states has been established in [38,39,40,41,42, 47] by several methods. In this paper, following [41,42,43], we construct Hadamard states by bulk to boundary correspondence and this method gives a positive frequency modes interpretation on boundary null surfaces. Following [42, 44], we consider the bulk region $\text {N}=\text {I}\cup \text {II}\cup \text {III}$ in Fig. 1 and the corresponding null boundary surfaces are $H=H^{L}\cup H^{-}$ and $H_{c}=H^{-}_{c}\cup H_{c}^{R}$. We first define positive frequency modes $\psi ^{U,\text {in/up}}_{\omega lm}$ ($\omega \ge 0$) which are solutions of Klein–Gordon equation. Exploiting the spherical symmetry, the solutions can be written as

$$\begin{aligned} & \psi ^{U,\text {in/up}}_{\omega lm}(t,r,\theta ,\varphi )\nonumber \\ & \quad =(2\pi )^{-\frac{3}{2}}(2\omega )^{-\frac{1}{2}}r^{-1}Y_{lm}(\theta ,\varphi )\Psi _{\omega l}^{U,\text {in/up}}(t,r). \end{aligned}$$

(4.11)

We impose initial conditions of $\psi ^{U,\text {in/up}}_{\omega lm}$ on null boundary surfaces $H\cup H_{c}$

$$\begin{aligned} \Psi _{\omega l}^{U,\text {in}}=\left\{ \begin{array}{lr} e^{-i\omega V_{c}}, & H_c\\ 0, & H\\ \end{array}\right. ,\quad \Psi _{\omega l}^{U,\text {up}}=\left\{ \begin{array}{lr} 0, & H_c\\ e^{-i\omega U}, & H\\ \end{array}\right. , \end{aligned}$$

(4.12)

where $U,V_c$ are Kruskal coordinates given in Sect. 2. Now, we define Unruh state in region $\text {N}$. Using positive frequency modes, we can decompose quantum field operator as follow:

$$\begin{aligned} \hat{\phi }=\int ^{\infty }_{0}d\omega \sum _{X,l,m}\left( \psi ^{U,X}_{\omega lm}a^{X}_{\omega lm}+\psi ^{U,X*}_{\omega lm}a^{X\dagger }_{\omega lm}\right) , \end{aligned}$$

(4.13)

where $X\in \{{\text {up},\text {in}}\}$, $a^{X}_{\omega lm}$ is the annihilation operator and $a^{X\dagger }_{\omega lm}$ is the creation operator. The Unruh vacuum state $\vert 0\rangle _{U}$ is defined by

$$\begin{aligned} a^{X}_{\omega lm}\vert 0\rangle _{U}=0. \end{aligned}$$

(4.14)

As discussed above, we can also define Unruh state in region $\text {N}$ by giving its n-point functions. By the property of quasifree states, this is equivalent to giving its 2-point function. Following [7, 41, 42], the 2-point function of Unruh state is given by

$$\begin{aligned} & \langle \hat{\phi }(f_1)\hat{\phi }(f_2)\rangle _U=-\frac{r^2_2}{\pi }\int _{\mathbb {R}}\int _{\mathbb {R}}\int _{S^2} \nonumber \\ & \quad \times \frac{Ef_1\vert _{H}(U_{1},\Omega )Ef_2\vert _{H}(U_{2},\Omega )}{(U_{1}-U_2-i0^{+})^2}d^2\Omega dU_{1}dU_{2}\nonumber \\ & \quad -\frac{r^2_3}{\pi }\int _{\mathbb {R}}\int _{\mathbb {R}}\int _{S^2} \frac{Ef_1\vert _{H_{c}}(V_{c},\Omega )Ef_2\vert _{H_{c}}(V'_{c},\Omega )}{(V_{c}-V'_{c}-i0^{+})^2}d^2\Omega dV_{c}dV'_{c}.\nonumber \\ \end{aligned}$$

(4.15)

First, we need to prove the integrals in (4.15) are convergence. Exploiting $\text {supp}E^{\pm }\subset \{(x,y),x\in J^{\pm }(y)\}$, we have $Ef\vert _{H}$ is supported in $(-\infty ,U_{0})\times \Omega$, where $U_0$ depends on f and a similar conclusion can be found for $H_{c}$. Therefore, we need to study the asymptotic behavior of Ef near $i^{-}$. Combining the the result of wave decay (3.45) and Sobolev embedding theorem, following theorem 4.4 of [7], the wave behavior of Ef near $i^{-}$ is given by

$$\begin{aligned} \vert \partial ^{m}Ef(t_{*},r,\theta ,\phi )\vert \le C e^{\alpha t_{*}} \vert f\vert _{C^{l}(\text {N})}, \end{aligned}$$

(4.16)

where $(t_{*},r,\theta ,\phi )$ is introduced in Sect. 3, $\partial ^{m}$ is a derivative in $(t_{*},r,\theta ,\phi )$ with $m>0$ and l depends on m. We have $e^{\alpha t_{*}}\sim \vert U\vert ^{-\alpha /\kappa _{2}}$ on H as $U\rightarrow -\infty$ and $e^{\alpha t_{*}}\sim \vert V_c\vert ^{-\alpha /\kappa _{3}}$ on $H_{c}$ as $V_c\rightarrow -\infty$. With these asymptotic behaviors of Ef near $i^{-}$, following the proposition IV.1 of [45], the integrals in (4.15) are convergence.

Now we need to check the state conditions (4.6), (4.7) and (4.8). Since

$$\begin{aligned} (\nabla _{a}\nabla ^{a}-m^2)E(x,x')=(\nabla _{a'}\nabla ^{a'}-m^2)E(x,x')=0,\nonumber \\ \end{aligned}$$

(4.17)

the field equation condition (4.6) is satisfied. Using the formula [22]

$$\begin{aligned} \frac{1}{(x+i0^{+})^{k}}-\frac{1}{(x-i0^{+})^{k}}=2\pi i(-1)^{k}\frac{\delta ^{(k-1)}}{(k-1)!}, \end{aligned}$$

(4.18)

we have

$$\begin{aligned} & \langle \hat{\phi }(f_1)\hat{\phi }(f_2)\rangle _U- \langle \hat{\phi }(f_2)\hat{\phi }(f_1)\rangle _U \nonumber \\ & \quad =ir^2_2\int _{\mathbb {R}}\int _{S^2}(Ef_1\vert _{H}\partial _UEf_2\vert _{H} \nonumber \\ & \qquad -Ef_2\vert _{H}\partial _UEf_1\vert _{H})dUd^2\Omega \nonumber \\ & \qquad + ir^2_3\int _{\mathbb {R}}\int _{S^2}(Ef_1\vert _{H_{c}}\partial _{V_c}Ef_2\vert _{H_{c}} \nonumber \\ & \qquad -Ef_2\vert _{H_{c}}\partial _{V_c}Ef_1\vert _{H_{c}})dV_cd^2\Omega . \end{aligned}$$

(4.19)

Using the asymptotic behaviors of Ef near $i^{-}$, it is easy to see the integrals are convergence. For any solution $\phi =Ef_1$ of Klein–Gordon equation and smooth function $f_2$ with compact support, the Lemma 3.2.1 of [46] states

$$\begin{aligned} \int _{\text {N}}f_{2}Ef_{1} d^4g(x)=\int _{\Sigma }n^{a}(Ef_1\nabla _{a}Ef_2-Ef_2\nabla _{a}Ef_1)d\Sigma ,\nonumber \\ \end{aligned}$$

(4.20)

where $\Sigma$ is the Cauchy surface of $\text {N}$ and $n^{a}$ is the future pointing normal unit vector. Since $Ef_1$ and $Ef_2$ are solutions of Klein–Gordon equation, the integral in (4.20) is $\Sigma$-independent by Gauss law. Following discussion in Section 2.4 of [42] or Section 4 of [7], by considering a series of $\Sigma _{n}$ and taking the limit, the integral in $\Sigma _{n}$ is equal to integral on $H\cup H_{c}$. Therefore, the commutator condition (4.7) is satisfied. According to Proposition 3.2 of [42], we have

$$\begin{aligned} \langle \hat{\phi }(\bar{f})\hat{\phi }(f)\rangle _U= & \int _{\mathbb {R}_+}\int _{S^2}\overline{\hat{\psi _H}(k,\Omega )}\hat{\psi _H}(k,\Omega )2kr_2^2dkd^2\Omega \nonumber \\ & +\int _{\mathbb {R}_+}\int _{S^2}\overline{\hat{\psi _c}(k,\Omega )}\hat{\psi _c}(k,\Omega )2kr_3^2dkd^2\Omega ,\nonumber \\ \end{aligned}$$

(4.21)

where $\hat{\psi _H}$ is the U-Fourier–Plancherel transformation of $Ef\vert _{H}$ and $\hat{\psi _c}$ is the $V_c$-Fourier–Plancherel transformation of $Ef\vert _{H_{c}}$. It is easy to see the positive condition (4.8) is satisfied.

We now show the two-point function of Unruh state (4.15) satisfies the Hadamard condition (4.9). As shown in [16], the Hadamard condition is equivalent to the following wave front set condition on two-point function $\omega _2(x_1,x_2)$

$$\begin{aligned} WF(\omega _2)= & \{(x_1,x_2,\xi _1,\xi _2)\in T^{*}(M\times M)\backslash \{0\} \vert \nonumber \\ & \times (x_1,\xi _1)\sim (x_2,-\xi _2),\xi _1\triangleright 0\}, \end{aligned}$$

(4.22)

where $\{0\}$ denotes the null section of $T^{*}(M\times M)$ and $\triangleright$ means $\xi _1$ is future directed. Here $(x_1,\xi _1)\sim (x_2,-\xi _2)$ means that there is a null geodesic $\gamma$ connecting $x_1$ and $x_2$ such that $\xi _1$ and $-\xi _2$ are cotangent vectors of $\gamma$ respectively at $x_1$ and $x_2$. Here we use the Fourier–Plancherel transformation to define wave front set and it gives an extra minus sign comparing with usual Fourier transformation. More precisely, the Fourier–Plancherel transformation is given by $\mathcal {F}(u)(k)=\int e^{ikx}u(x)dx$.

Now, we demonstrate the Unruh state is Hadamard. Indeed, our situation is very similar to [40, 42, 45] and the methods developed in these papers are sufficient to prove Hadamard condition in our case. Therefore, we will briefly discuss the strategy of proof. We want to show two inclusions $\subset$ and $\supset$ valid. We first consider the inclusion $\subset$. In Sect. 3, we investigate the bicharacteristic strips of Klein–Gordon operator and we have trapped set in region I. In this case, following [42], we restrict Unruh state to region I. Then, the two-point function of Unruh state can be written as

$$\begin{aligned} \langle \hat{\phi }(f_1)\hat{\phi }(f_2)\rangle _U=\omega _{2H}(f_{1},f_{2})+\omega _{2H_{c}}(f_{1},f_{2}), \end{aligned}$$

(4.23)

where $f_{1}$ and $f_{2}$ are smooth functions with compact supports in region $\text {I}$. Here $\omega _{2H}(f_{1},f_{2})$ is the first term on the right hand of (4.15) and $\omega _{2H_{c}}(f_{1},f_{2})$ is the second term on the right hand of (4.15). We define a continuous one-parametric group $\beta ^{X}_{t}$ generated by killing vector field $\partial _t$ by requiring

$$\begin{aligned} \beta ^{X}_{\tau }f(t,r,\theta ,\varphi )=f(t-\tau ,r,\theta ,\varphi ), \end{aligned}$$

(4.24)

where f is a smooth function with compact support in region $\text {I}$. Following Lemma V.3 of [45], we have $\omega _{2H}$ is KMS like at inverse temperature $2\pi /\kappa _{2}$ and $\omega _{2H_{c}}$ is KMS like at inverse temperature $2\pi /\kappa _{3}$. Two-point function $\omega _{2X}(x_1,x_2)$ is KMS like [42] at inverse temperature $\beta _{H}$ if

$$\begin{aligned} & \int _{\mathbb {R}}\hat{f}(t)\omega _{2X}(h_1,\beta ^{X}_{t}h_2)dt\nonumber \\ & \quad =\int _{\mathbb {R}}\hat{f}(t+i\beta _{H})\omega _{2X}(\beta ^{X}_{t}h_2,h_1)dt, \end{aligned}$$

(4.25)

for every $f\in C^{\infty }_{0}(R,R)$. Here $h_1$ and $h_2$ are smooth functions with compact supports in region $\text {I}$. Then we can follow the proof of Theorem 5.1 of [35] to show the restriction of Unruh state to region I satisfies the Hadamard condition (4.22). Now, we need to consider the wave front set of Unruh two-point function $\omega _{2}(x_1,x_2)$ with either $x_1$, either $x_2$ or both in N/I. Fortunately, according to Lemma V.1 of [45], we only need to consider the diagonal part of the primed wavefront set

$$\begin{aligned} \Delta _{T^{*}_{N\times N}}=\{(x,k;x,k)\in T^{*}{(\text {N}\times \text {N})}\}, \end{aligned}$$

(4.26)

where k is null. Then we need to show

$$\begin{aligned} \text {WF}'(\omega _{2})\cap \Delta _{T^{*}_{\text {N}\times \text {N}}}\subset \mathbb {N}^{+}\times \mathbb {N}^{+}, \end{aligned}$$

(4.27)

where $\mathbb {N}^{+}$ is the forward pointing null cones

$$\begin{aligned} \mathbb {N}^{+}=\{(x,k)\in T^{*}N\setminus 0:g^{ab}k_{a}k_{b}=0,k\triangleright 0\}. \end{aligned}$$

(4.28)

Here the primed wavefront set of $\omega _{2}(x_1,x_2)$ is defined by

$$\begin{aligned} \text {WF}'(\omega _{2})=\{(x_1,\xi _1;x_2,\xi _2)\vert (x_1,\xi _1;x_2,-\xi _2)\in \text {WF}(\omega _{2})\}.\nonumber \\ \end{aligned}$$

(4.29)

Following [41, 42], we consider $\omega _{2}(f_k,f_k)$, where $f_{k}(x):=f(x)e^{ikx}$. Using the wave behavior (3.45), then Proposition V.5 goes through in our case and it verifies Unruh state satisfies the Hadamard condition (4.22) in N/I. The inclusion $\subset$ has been proved. Following Theorem 4.2 of [7], we have the inclusion $\supset$. Therefore, we have the Unruh state is Hadamard in N.

In order to simplify calculations of renormalization, following [7], we introduce the comparison state in region $\text {II}\cup \text {IV}$ of Fig. 3. Now, the corresponding hypersurfaces are $CH=CH^{+}\cup CH^{L}$ and $\tilde{H}^R$. We define the comparison state as a vacuum state by imposing positive frequency modes $\psi ^{C,\text {in/up}}_{\omega lm}$ $(\omega \ge 0)$ to corresponding hypersurfaces. Similarly, the positive frequency modes $\psi ^{C,\text {in/up}}_{\omega lm}$ can be written as

$$\begin{aligned} & \psi ^{C,\text {in/up}}_{\omega lm}(t,r,\theta ,\varphi )\nonumber \\ & \quad =(2\pi )^{-\frac{3}{2}}(2\omega )^{-\frac{1}{2}}r^{-1}Y_{lm}(\theta ,\varphi )\Psi _{\omega l}^{C,\text {in/up}}(t,r). \end{aligned}$$

(4.30)

We impose initial conditions of $\psi ^{C,\text {in/up}}_{\omega lm}$ on null boundary surfaces $CH\cup \tilde{H}^R$

$$\begin{aligned} \Psi _{\omega l}^{C,\text {in}}=\left\{ \begin{array}{lr} e^{-i\omega V_{-}}, & CH\\ 0, & \tilde{H}^R\\ \end{array}\right. ,\quad \Psi _{\omega l}^{C,\text {up}}=\left\{ \begin{array}{lr} 0, & CH\\ \ e^{-i\omega u}, & \tilde{H}^R\\ \end{array}\right. .\nonumber \\ \end{aligned}$$

(4.31)

Here $V_{-}$ is defined in Sect. 2 and $u:=t-r_{*}$. The spacetime structure of region IV is similar to region I. By applying the discussion in Sect. 3 to region IV, we obtain similar wave behaviors. Similarly, the comparison state satisfies the Hadamard condition (4.9).

5 Strong cosmic censorship and quantum effects near the Cauchy horizon

In this section, we begin by investigating the validity of SCCC using classical and quantum scalar fields. During the process of studying the SCCC, we find the quantum effects are stronger than classical effects near the Cauchy horizon and thus, there is a region where physics is dominated by quantum effects. To explore the impact of dark matter on physics in this region, we study the influence of dark matter on quantum effects.

Now, we study the validity of SCCC. As shown in Sect. 3, the classical scalar field has Sobolev regularity $H^{1/2+\alpha \beta _1-0^{+}}_{b}$, where $\beta _{1}=\kappa _{1}^{-1}$. Here $\alpha$ is the the spectral gap and it is given by $\alpha =\text {inf}\{-\text {Im}(\omega _{nlm})\}$, where $\omega _{nlm}$ are quasinormal modes of region I in Fig. 1. If $\alpha \beta _1>1/2$, the metric can be extended as a weak solution across the Cauchy horizon. The values of $\alpha \beta _1$ has been studied in [17] and there exist a region where $\alpha \beta _1>1/2$. This implies the SCCC can be violated at classical level. The current question is whether quantum effect can restore SCCC. Therefore, we need to study the divergence of quantum stress energy tensor near Cauchy horizon. In order to restore SCCC, we need to show the divergence is strong enough to convert the Cauchy horizon into a singularity for all Hadamard states. The problem is that we can’t traverse all Hadamard states. This has been solved in [7] by decomposing the stress energy tensor into several parts and verifying the leading divergence term is state independent. Following this strategy, the renormalized quantum stress energy tensor for an arbitrary Hadamard state $\Psi$ can be written as

$$\begin{aligned} \langle T_{uv}\rangle _{\Psi }-C_{uv}= & (\langle T_{uv}\rangle _{\Psi }-\langle T_{uv}\rangle _{U})+(\langle T_{uv}\rangle _{U}\nonumber \\ & -\langle T_{uv}\rangle _{C})+(\langle T_{uv}\rangle _{C}-C_{uv}), \end{aligned}$$

(5.1)

where $C_{uv}$ is the counter term, U denote the Unruh state and C denote the comparison state. Now, we study the first term on the right hand of (5.1). Using wave behavior (3.45), following Proposition 5.1 of [7], we have

$$\begin{aligned} \langle T_{V_{-}V_{-}}\rangle _{\Psi }-\langle T_{V_{-}V_{-}}\rangle _{U}\sim \vert V_{-}\vert ^{-2+2\alpha \beta _{1}} \quad \text {as}\quad V_{-}\rightarrow 0^{-},\nonumber \\ \end{aligned}$$

(5.2)

where $\alpha \beta _{1}>1/2$. This term behaves like classical stress energy tensor near the Cauchy horizon. The last term on the right hand of (5.1) is smooth near the Cauchy horizon. Finally, we consider the divergence of second term on the right hand of (5.1). Using $\partial v/\partial V_{-}=-(\kappa _{1}V_{-})^{-1}$, we have $T_{V_{-}V_{-}}=(\kappa _{1}V_{-})^{-2}T_{vv}$. We study the limiting behavior of $(\langle T_{vv}\rangle _{U}-\langle T_{vv}\rangle _{C})$ as $V_{-}\rightarrow 0^{-}$. If $(\langle T_{vv}\rangle _{U}-\langle T_{vv}\rangle _{C})$ blows up as $V\rightarrow 0^{-}$, then the divergence of $(\langle T_{V_{-}V_{-}}\rangle _{U}-\langle T_{V_{-}V_{-}}\rangle _{C})$ is stronger than $1/\vert V_{-}\vert ^{2}$. If $(\langle T_{vv}\rangle _{U}-\langle T_{vv}\rangle _{C})$ as $V\rightarrow 0^{-}$ tends to a nonzero constant, then the divergence of $(\langle T_{V_{-}V_{-}}\rangle _{U}-\langle T_{V_{-}V_{-}}\rangle _{C})$ is proportional to $1/\vert V_{-}\vert ^{2}$. In these two cases, according to the discussion in Sect. I of [7], the singular behaviors of $\langle T_{V_{-}V_{-}}\rangle _{\Psi }$ are strong enough to convert the Cauchy horizon into a singularity. If $(\langle T_{vv}\rangle _{U}-\langle T_{vv}\rangle _{C})$ as $V\rightarrow 0^{-}$ tends to 0, then we need to analyze how it tends to 0. For example, it may tends to 0 as $1/v^{m}$ or $V^n_{-}$. In this situation, the valid of SCCC can be analyzed case by case.

Now, we turn to the calculation of $(\langle T_{vv}\rangle _{U}-\langle T_{vv}\rangle _{C})$. We first focus on $\langle T_{vv}\rangle _{U}$. We need to solve positive frequency modes $\psi ^{U,\text {in/up}}_{\omega lm}$ with initial data on $H\cup H_{c}$. We are interested in the value of $\psi ^{U,\text {in/up}}_{\omega lm}$ near the Cauchy horizon and it is determined by the initial data on $H^{L}\cup H^{R}$. Following [7, 32], the initial data on $H\cup H_{c}$ can be translated to the initial data on $H^{L}\cup H^{R}$. For technical convenience, following [7, 48], we introduce Boulware modes $\psi ^{{B,\text {I/II}},\text {in/up}}_{\omega lm}$. Exploiting the spherical symmetry, $\psi ^{{B,\text {I/II}},\text {in/up}}_{\omega lm}$ can be written as

$$\begin{aligned} & \psi ^{{B,\text {I/II}},\text {in/up}}_{\omega lm}(t,r,\theta ,\varphi )\nonumber \\ & \quad =(2\pi )^{-\frac{3}{2}}(2\omega )^{-\frac{1}{2}}r^{-1} Y_{lm}(\theta ,\varphi )\Psi _{\omega l}^{{B,\text {I/II},\text {in/up}}}(t,r). \end{aligned}$$

(5.3)

In region I, the initial data of Boulware modes are given by

$$\begin{aligned} \Psi _{\omega l}^{B,\text {I},\text {in}}=\left\{ \begin{array}{lr} e^{-i\omega v}, & H^{-}_c\\ \ 0, & \tilde{H}^-\\ \end{array}\right. ,\quad \Psi _{\omega l}^{B,\text {I},\text {up}}=\left\{ \begin{array}{lr} 0, & H^{-}_c\\ \ e^{-i\omega u}, & \tilde{H}^-\\ \end{array}\right. .\nonumber \\ \end{aligned}$$

(5.4)

Similarly, in region II, the initial data of Boulware modes are given by

$$\begin{aligned} \Psi _{\omega l}^{B,\text {II},\text {in}}=\left\{ \begin{array}{lr} e^{-i\omega v}, & H^R\\ \ 0, & \tilde{H}^L\\ \end{array}\right. ,\quad \Psi _{\omega l}^{B,\text {II},\text {up}}=\left\{ \begin{array}{lr} 0, & H^R\\ \ e^{-i\omega u}, & \tilde{H}^L\\ \end{array}\right. .\nonumber \\ \end{aligned}$$

(5.5)

For technical convenience, we define $\psi ^{{B,\text {II}},\text {out}}_{\omega lm}$ by requiring

$$\begin{aligned} \Psi _{\omega l}^{B,\text {II},\text {out}}=\left\{ \begin{array}{lr} e^{-i\omega v}, & CH^L\\ \ 0, & CH^R\\ \end{array}\right. ,\quad \end{aligned}$$

(5.6)

Using t-invariant in region I and II, $\Psi ^{{B,\text {I/II}},\text {in/up}}_{\omega l}$ can be decomposed as $\Psi ^{{B,\text {I/II}},\text {in/up}}_{\omega l}=e^{-i\omega t}R^{{B,\text {I/II}},\text {in/up}}_{\omega l}$. In region I, the initial data in (5.4) are translated to asymptotic condition

$$\begin{aligned} \begin{aligned} R_{\omega l}^{B,\text {I},\text {in}}&=\left\{ \begin{array}{lr} e^{-i\omega r_{*}}+\rho ^{\text {I},\text {in}}_{\omega l}e^{i\omega r_{*}}, & r_{*}\rightarrow \infty ,\\ \ \tau ^{\text {I},\text {in}}_{\omega l}e^{-i\omega r_{*}}, & r_{*}\rightarrow -\infty ,\\ \end{array}\right. \\ R_{\omega l}^{B,\text {I},\text {up}}&=\left\{ \begin{array}{lr} e^{i\omega r_{*}}+\rho ^{\text {I},\text {up}}_{\omega l}e^{-i\omega r_{*}}, & r_{*}\rightarrow -\infty ,\\ \ \tau ^{\text {I},\text {up}}_{\omega l}e^{i\omega r_{*}}, & r_{*}\rightarrow \infty .\\ \end{array}\right. \end{aligned}\end{aligned}$$

(5.7)

Here $\tau ^{\text {I},\text {X}}_{\omega l}$ and $\rho ^{\text {I},\text {X}}_{\omega l}$ are reflection and transmission coefficients and they satisfy

$$\begin{aligned} \vert \tau ^{\text {I},\text {X}}_{\omega l}\vert ^2+\vert \rho ^{\text {I},\text {X}}_{\omega l}\vert ^2=1. \end{aligned}$$

(5.8)

Similarly, in region II, the initial data in (5.5) are translated to asymptotic condition

$$\begin{aligned} \begin{aligned} R_{\omega l}^{B,\text {II},\text {in}}&=\left\{ \begin{array}{lr} \tau ^{\text {II},\text {in}}_{\omega l}e^{-i\omega r_{*}}+\rho ^{\text {II},\text {in}}_{\omega l}e^{i\omega r_{*}}, & r_{*}\rightarrow \infty ,\\ \ e^{-i\omega r_{*}}, & r_{*}\rightarrow -\infty ,\\ \end{array}\right. \\ R_{\omega l}^{B,\text {II},\text {up}}&=\left\{ \begin{array}{lr} \tau ^{\text {II},\text {up}}_{\omega l}e^{i\omega r_{*}}+\rho ^{\text {II},\text {up}}_{\omega l}e^{-i\omega r_{*}}, & r_{*}\rightarrow \infty ,\\ \ e^{i\omega r_{*}}, & r_{*}\rightarrow -\infty .\\ \end{array}\right. \end{aligned}\end{aligned}$$

(5.9)

The coefficients $\tau ^{\text {II},\text {X}}_{\omega l}$ and $\rho ^{\text {II},\text {X}}_{\omega l}$ satisfy

$$\begin{aligned} \vert \tau ^{\text {II},\text {X}}_{\omega l}\vert ^2-\vert \rho ^{\text {II},\text {X}}_{\omega l}\vert ^2=1. \end{aligned}$$

(5.10)

Now, we can translate the initial data on $H\cup H_{c}$ to the initial data on $H^{L}\cup H^{R}$. The Boulware mode $\psi ^{{B,\text {I},\text {in}}}_{\omega lm}$ can be translated to the initial data $\tau ^{\text {I},\text {in}}_{\omega l}\psi ^{{B,\text {II}},\text {up}}_{\omega lm}$ on $H^{R}$. Similarly, the Boulware mode $\psi ^{{B,\text {I}},\text {up}}_{\omega lm}$ can be translated to the initial data $\rho ^{\text {I},\text {up}}_{\omega l}\psi ^{{B,\text {II}},\text {up}}_{\omega lm}$ on $H^{R}$. In order to exploiting the initial data of comparison state, we restriction the Boulware modes in region II to $CH^L$. We have $\psi ^{{B,\text {II}},\text {in}}_{\omega lm}\vert _{CH^L}=\tau ^{\text {II},\text {in}}_{\omega l}\psi ^{{B,\text {II}},\text {out}}_{\omega lm}$ and $\psi ^{{B,\text {II}},\text {up}}_{\omega lm}\vert _{CH^L}=\rho ^{\text {II},\text {up}}_{\omega l}\psi ^{{B,\text {II}},\text {out}}_{\omega lm}$. Now, we consider mode-sum expression for $(\langle T_{vv}\rangle _{U}-\langle T_{vv}\rangle _{C})$ which can be written as

$$\begin{aligned} \langle T_{vv}\rangle _{U}-\langle T_{vv}\rangle _{C}= & \int ^{\infty }_0d\omega \sum _{X,l,m}(\overline{\partial _v\psi ^{U,\text {X}}_{\omega lm}}\partial _v\psi ^{U,\text {X}}_{\omega lm}\nonumber \\ & -\overline{\partial _v\psi ^{C,\text {X}}_{\omega lm}}\partial _v\psi ^{C,\text {X}}_{\omega lm}). \end{aligned}$$

(5.11)

Using Fourier transform $e^{-i\omega U}=\int \alpha _{\omega \omega '}e^{-i\omega u}d\omega '$, we can replace Unruh modes by Boulware modes. Here the explicit expression of $\alpha _{\omega \omega '}$ is given in [32]. As discussed above, we can use the initial data on $H^{L}\cup H^{R}$ to giving the expression of $\overline{\partial _v\psi ^{U,\text {X}}_{\omega lm}}\partial _v\psi ^{U,\text {X}}_{\omega lm}$ near $CH^L$ ($U\rightarrow \infty$). Similarly, we can use the initial data on $CH^{L}$ to giving the expression of $\overline{\partial _v\psi ^{C,\text {X}}_{\omega lm}}\partial _v\psi ^{C,\text {X}}_{\omega lm}$ near $CH^L$. The explicit expression has been obtained in [7] and it is given by

$$\begin{aligned} \langle T_{vv}\rangle _{U}-\langle T_{vv}\rangle _{C}=\frac{1}{16\pi ^3r^2_1}\sum _l\frac{2l+1}{4\pi }\int ^{\infty }_0d\omega \omega n_l(\omega ),\nonumber \\ \end{aligned}$$

(5.12)

where $n_l(\omega )$ can be written as

$$\begin{aligned} n_l(\omega )= & \vert \tau ^{\text {I},\text {in}}_{\omega l}\vert ^2\vert \tau ^{\text {II},\text {in}}_{\omega l}\vert ^2\text {coth}\frac{\pi \omega }{\kappa _{3}}\nonumber \\ & +\left( \vert \rho ^{\text {I},\text {up}}_{\omega l}\vert ^2 \vert \tau ^{\text {II},\text {in}}_{\omega l}\vert ^2+\vert \rho ^{\text {II},\text {up}}_{\omega l}\vert ^2\right) \text {coth}\frac{\pi \omega }{\kappa _{2}}\nonumber \\ & +2\text {csch}\frac{\pi \omega }{\kappa _{2}}\text {Re}\left( \rho ^{\text {I},\text {up}}_{\omega l}\tau ^{\text {II},\text {in}}_{\omega l}\overline{\rho ^{\text {II},\text {up}}_{\omega l}}\right) -\text {coth}\frac{\pi \omega }{\kappa _{1}}.\nonumber \\ \end{aligned}$$

(5.13)

Using t invariant, the value of $\langle T_{vv}\rangle _{U}-\langle T_{vv}\rangle _{C}$ on $CH^{L}$ equals to the value on $CH^{R}$. Therefore, we need to study the value of the integral on the right hand of (5.12).

Fig. 6

Numerical results for $\omega n_l(\omega )M$ as a function of $\omega M$ for different values of l and b/M with $\Lambda M^2=0.02$, $b/M=0.25$, and $Q/Q_{\text {max}}=0.97$

Fig. 7

Numerical results for $\tilde{C}M^4$ as a function of $Q/Q_\text {max}$ at a fixed $\Lambda M^2=0.02$ with $b/M=0.25$ (left panel) and $b/M=0.5$ (right panel)

Fig. 8

Numerical results for $\tilde{C}M^4$ as a function of $Q/Q_\text {max}$ for $\Lambda M^2=0.02$ with different values of b/M

Now, we study the validity of the SCCC at the quantum level. Combining the results of the wave behavior in Sect. 3 and the numerical results in [17], SCCC may be violated in the near-extremal region under classical scalar field perturbations. Therefore, we need to study the behavior of the quantum stress-energy tensor in the near-extremal region. According to the above discussion, the leading divergence of the quantum stress-energy tensor near the Cauchy horizon is described by Eq. (5.12). For convenience, we define

$$\begin{aligned} \tilde{C}:=\frac{1}{16\pi ^3r^2_1}\sum _l\frac{2l+1}{4\pi }\int ^{\infty }_0d\omega \omega n_l(\omega ). \end{aligned}$$

(5.14)

The explicit form of $n_l$ is given in Eq. (5.13), which depends on the transmission and reflection coefficients. We need to solve the radial equation (3.39) with boundary conditions (5.7) and (5.9). By directly numerically integrating the radial equation (3.39) with boundary conditions (5.7) and (5.9), we can obtain the transmission and reflection coefficients. Substituting the transmission and reflection coefficients into Eq. (5.13), we obtain the value of $n_l$. As an example, we plot $\omega n_l(\omega )M$ as a function of $\omega M$ for massless scalar fields with $\Lambda M^2=0.02$ and $Q/Q_{\text {Max}}=0.97$, with b/M taking values of 0.25 and 0.5, and $l=0,1,2$ in Fig. 6. Here, $Q_{\text {max}}$ corresponds to the charge of an extremal black hole. From Fig. 6, we can see that $\omega n_l(\omega )M$ decays quickly enough with increasing $\omega M$ to ensure that the integral in Eq. (5.14) is convergent. Comparing $\omega n_l(\omega )M$ for different values of l, we find that $\omega n_l(\omega )M$ decreases rapidly as l increases. Therefore, the summation over l in Eq. (5.14) is convergent. Now, we study the behavior of $\tilde{C}$. Figure 7 shows the behavior of $M^4\tilde{C}$ as a function of $Q/Q_{\text {max}}$ for massless scalar fields with fixed $\Lambda M^2=0.02$ and b/M taking values of 0.25 and 0.5. We see that in the region where SCCC is violated under classical perturbations, $\tilde{C}\ne 0$, and as $Q/Q_{\text {max}}\rightarrow 1$ (corresponding to an extremal black hole), $\tilde{C}$ tends to 0. Therefore, SCCC can be restored under these spacetime parameters. To study the impact of dark matter on SCCC, Fig. 8 shows the behavior of $M^4\tilde{C}$ as a function of $Q/Q_{\text {max}}$ for massless scalar fields with $\Lambda M^2=0.02$ and different dark matter parameters. Since the dark matter parameter b should be a small value in practice, we study the behavior of $\tilde{C}$ in more detail for $b/M<0.2$ in the left panel of Fig. 8. From Fig. 8, we can see that $\tilde{C}$ is generally non-zero. Therefore, quantum effects save SCCC.

From the above discussion, in the near-extremal region, we find the $V_{-}V_{-}$-component of classical stress-energy tensor has a behavior not more singular than $\vert V_{-}\vert ^{-2+2\alpha /{\kappa _{1}}}$ and the quantum stress-energy tensor has a quadratic divergence $\tilde{C}\vert V_{-}\vert ^{-2}$. It turns out that the quantum stress-energy tensor grows faster than the classical stress-energy tensor near the Cauchy horizon. Thus, there is a region where physics is dominated by quantum effects. It is interesting to study the influence of PFDM on the quantum effects in this region. The strength of quantum effects is given by $\tilde{C}\vert V_{-}\vert ^{-2}$ and $\tilde{C}$ depends on the parameters of spacetime. In the near-extremal region, the values of $\tilde{C}$ has been studied in Fig. 8. When $Q/Q_{\text {max}}$ is fixed, $\tilde{C}$ increases as b increases. It corresponds to that the dark matter will enhance the quantum effects. In our case, the $V_{-}V_{-}$-component of quantum stress-energy tensor plays an important role in the geodesic deviation equation [7]. Thus, in this region, the geodesics will suffer a stronger crushing ($\tilde{C}>0$) or stretching ($\tilde{C}<0$) effect due to the dark matter.

6 Conclusions

In this paper, we investigate the validity of SCCC for a spherically charged de-Sitter black hole surrounded by PFDM by considering classical and quantum scalar fields. At the classical level, we analyze scalar waves near the Cauchy horizon using the method developed by Hintz and Vasy [5]. We find that the scalar waves have Sobolev regularity $H^{1/2+\alpha /{\kappa _{1}}-0^+}$ near the Cauchy horizon. According to the numerical results in [17], we find that SCCC can be violated in the nearly extremal region where $\alpha /{\kappa _{1}}>1/2$. At the quantum level, we study the VV-component of the renormalized quantum stress-energy tensor for an arbitrary Hadamard state near the Cauchy horizon. We find that the leading divergent term is $\tilde{C}\vert V_{-}\vert ^{-2}$, where $\tilde{C}$ is state-independent and $\tilde{C}$ equals to the right-hand side of (5.12). According to the numerical results for $\tilde{C}$, we find $\tilde{C}\ne 0$ in general. The quadratic divergence of the renormalized quantum stress-energy tensor is singular enough to convert the Cauchy horizon into a singularity. Thus, SCCC is preserved by quantum effects. Using Sobolev regularity (3.45) and Proposition 5.1 of [7], we find that the singular behavior of classical scalar field perturbations is $\vert V_{-}\vert ^{-2+2\alpha /{\kappa _{1}}}$, where $\alpha /{\kappa _{1}}>1/2$. Comparing the classical and quantum stress-energy tensors, we find that the divergence behavior of the quantum stress-energy tensor is more singular than the behavior of classical scalar field perturbations near the Cauchy horizon. This means quantum effects are stronger than classical effects and there is a region where physics is dominated by quantum effects. We study the influence of PFDM on the quantum effects in this region and we find the dark matter will enhance the quantum effects. For example, the geodesics will suffer a stronger crushing ($\tilde{C}>0$) or stretching ($\tilde{C}<0$) effect due to the dark matter. Thus, it appears that the dark matter plays an important role in quantum effects.