Searching for beyond the Standard Model physics using the improved description of ¹⁰⁰Mo $2\nu \beta \beta$ decay spectral shape with CUPID-Mo

Abstract

The current experiments searching for neutrinoless double-$\beta$ ($0\nu \beta \beta$) decay also collect large statistics of Standard Model allowed two-neutrino double-$\beta$ ($2\nu \beta \beta$) decay events. These can be used to search for Beyond Standard Model (BSM) physics via $2\nu \beta \beta$ decay spectral distortions. ¹⁰⁰Mo has a natural advantage due to its relatively short half-life, allowing higher $2\nu \beta \beta$ decay statistics at equal exposures compared to the other isotopes. We demonstrate the potential of the dual read-out bolometric technique exploiting a ¹⁰⁰Mo exposure of 1.47 kg $\times$ years, acquired in the CUPID-Mo experiment at the Modane underground laboratory (France). We set limits on $0\nu \beta \beta$ decays with the emission of one or more Majorons, on $2\nu \beta \beta$ decay with Lorentz violation, and $2\nu \beta \beta$ decay with a sterile neutrino emission. In this analysis, we investigate the systematic uncertainty induced by modeling the $2\nu \beta \beta$ decay spectral shape parameterized through an improved model, an effect never considered before. This work motivates searches for BSM processes in the upcoming CUPID experiment, which will collect the largest amount of $2\nu \beta \beta$ decay events among the next-generation experiments.

1 Introduction

Neutrinoless double-$\beta$ ($0\nu \beta \beta$) decay is a hypothetical nuclear decay not allowed by the Standard Model (SM). The potential observation of $0\nu \beta \beta$ decay would demonstrate the violation of the $B-L$ symmetry of the SM. Moreover, it would also prove the Majorana nature of neutrinos, offering crucial insights into the fundamental symmetries governing particle interactions. Beyond the primary focus on $0\nu \beta \beta$ decay, the pursuit of large masses, extended data collection periods, and appropriate $\beta \beta$ isotopes in $0\nu \beta \beta$ experiments lead to a high collection of events from two-neutrino double-$\beta$ ($2\nu \beta \beta$) decay [1,2,3,4,5,6,7,8]. $2\nu \beta \beta$ decay is a second-order weak process occurring in the same $0\nu \beta \beta$ decay sources. It is particularly interesting for its relevance in the search for Beyond Standard Model (BSM) processes. Indeed, many theories predict the existence of exotic double-$\beta$ decays, called this way because they are characterized by a continuum energy distribution of the two emitted electrons similar to the $2\nu \beta \beta$ one (Fig. 1) [9]. These include the emission of new exotic particles such as scalar bosons known as “Majorons” or massive sterile neutrinos. Additionally, there is the possibility of observing violations of fundamental symmetries like the Lorentz invariance. Recently, other BSM cases have been investigated, like the potential effect of right-handed leptonic currents in $2\nu \beta \beta$ [10] and the neutrino self-interactions [11].

Majorons are massless Nambu–Goldstone bosons resulting from the spontaneous $B-L$ symmetry breaking in the low-energy regime [12, 13] and could play a role in the $0\nu \beta \beta$ decay coupling to the Majorana neutrinos [14]. Despite many theories being disfavored by the accurate measurements of the width of the Z boson decay [15], currently, different models predict the emission of one or two [16] Majorons in the $0\nu \beta \beta$ decay, these are denoted as

$$\begin{aligned} (A, Z) \rightarrow (A, Z+2)+2 e^{-}+\chi _{0} \quad (\beta \beta \chi _{0}), \end{aligned}$$

(1)

or

$$\begin{aligned} (A, Z) \rightarrow (A, Z+2)+2 e^{-}+2\chi _{0} \quad (\beta \beta \chi _{0}\chi _{0}). \end{aligned}$$

(2)

In these models, the Majoron carries a non-zero lepton number [17] or it is a component of a massive gauge boson [18] or a “bulk” field [19]. Recently, schemes with massive Majoron-like particles have become popular since they could play the role of dark matter [20,21,22,23]. The signature of these decays can be distinguished from the SM $2\nu \beta \beta$ one thanks to the different spectral index n, which determines the position of the maximum intensity in the two emitted electrons’ energy spectrum. In particular, the differential decay rate is proportional to

$$\begin{aligned} \frac{d \Gamma }{d T} \propto \left( Q_{\beta \beta }-T\right) ^{n}, \end{aligned}$$

(3)

where T is the total kinetic energy of the two electrons emitted, and $Q_{\beta \beta }$ is the Q-value. The value of the spectral index is $n = 5$ for the SM $2\nu \beta \beta$ decay, while for the Majoron-emitting modes, it can be $n= 1,2,3$, or 7 (left panel Fig. 1).

Fig. 1

Standard Model $2\nu \beta \beta$ decay (black) compared with different exotic double-$\beta$ decay spectra. Left panel: comparison of different Majoron-emitting modes with spectral indexes $n = 1,2,3$, and 7. Central panel: Lorentz-violating $2\nu \beta \beta$ decay represented in the case of pure LV $2\nu \beta \beta$ decay (dashed line) and summed to the SM $2\nu \beta \beta$ one with an arbitrary value of |$\dot{a}_{o f}^{(3)}$ | (pink solid line). Right panel: $2\nu \beta \beta$ decay with sterile neutrino emission ($\nu N \beta \beta$) for $m_N$ = 0.5 MeV (blue) and 1.5 MeV (green) in case of pure $\nu N \beta \beta$ decay (dotted lines) and mixed with the SM $2\nu \beta \beta$ one assuming $\sin ^2 \theta = 0.1$ (blue and green solid lines)

Some BSM theories involve a Lorentz invariance violation (LV) and the CPT (Charge-Parity-Time reversal) symmetry violation terms in the Lagrangian. These theories have been developed in the Standard Model Extension (SME) framework, in such a way that the SM gauge invariance is preserved [24, 25]. The neutrino sector was extensively studied in the SME framework [26,27,28] and the majority of these effects are experimentally investigated through neutrino oscillations and time-of-flight measurements [29]. Nevertheless, four operators equally change all neutrino energies and have no impact on oscillations, which can be studied through weak decays [30, 31] and are the so-called countershaded operators, labeled as “oscillation free” (of). The interaction of these operators with neutrinos modifies their four-momentum in a way that

$$\begin{aligned} q^{\alpha }=(\omega , \textbf{q}) \longrightarrow q^{\alpha }=\left( \omega , \textbf{q}+\textbf{a}_{o f}^{(3)}-\dot{a}_{o f}^{(3)} \hat{\textbf{q}}\right) , \end{aligned}$$

(4)

where $\textbf{a}_{o f}^{(3)}$ encodes all the 3 directional of components while $\dot{a}_{o f}^{(3)}$ represents the anisotropic one [30, 31]. This results in a perturbation of the $2\nu \beta \beta$ decay rate, which can be written as the sum of two components

$$\begin{aligned} \Gamma =\Gamma _{SM}+ 10 \dot{a}_{o f}^{(3)} \Gamma _{LV}, \end{aligned}$$

(5)

where $\Gamma _{SM}$ is the SM $2\nu \beta \beta$ decay rate and $\Gamma _{LV}$ is the perturbation induced by the Lorentz violation. The energy distribution of the two electrons emitted in the LV $2\nu \beta \beta$ decay is shifted to higher energies compared to the SM $2\nu \beta \beta$ decay (central panel Fig. 1).

In the past years, some BSM theories have hypothesized the existence of a sterile neutrino N with a mass $m_N$ at accessible energies [32,33,34,35,36,37,38]. The sterile neutrino can also be considered a candidate for dark matter [39]. Experimentally, the parameter of interest is the active-sterile mixing strength $\sin ^2 \theta$, which determines the mixing angle between the electron neutrino flavor and the sterile one. The existence of a sterile neutrino with a mass $m_N < Q_{\beta \beta }$ can induce an effect on the $2\nu \beta \beta$ decay spectral shape [40, 41], implying the emission of one sterile neutrino in the decay

$$\begin{aligned} (A, Z) \rightarrow (A, Z+2)+2 e^{-}+\bar{\nu }+N \quad (\nu N \beta \beta ), \end{aligned}$$

(6)

while the emission of two sterile neutrinos is considered negligible. The $0\nu \beta \beta$ experiments are sensitive to the sterile neutrino mass range from 0.1 MeV up to 3 MeV (depending on $Q_{\beta \beta }$) due to kinematical conditions. This region is particularly interesting due to the relative weakness of the actual constraints coming from single $\beta$-decay experiments, $\sin \theta \sim$ 10$^{-3}$–10$^{-2}$ [42,43,44,45,46]. The effect on the total decay rate is given by

$$\begin{aligned} \Gamma = \cos ^4 \theta \Gamma _{SM}+2 \cos ^2 \theta \sin ^2 \theta \Gamma _{\nu N}, \end{aligned}$$

(7)

where the first term $\Gamma _{SM}$ accounts for the SM $2\nu \beta \beta$ decay and the second term $\Gamma _{\nu N}$ represents the $\nu N \beta \beta$ decay [40, 41]. The energy spectrum in the case of pure $\nu N \beta \beta$ decay events is characterized by a shift in the Q-value determined by the mass $m_N$ of the sterile state and a smaller Phase Space Factor (PSF) compared to $2\nu \beta \beta$ decay (right panel Fig. 1).

In this framework, scintillating cryogenic calorimeters are one of the most promising technologies for $0\nu \beta \beta$ decay searches [47, 48] and the study of $2\nu \beta \beta$ decay spectral shape [6, 8]. These detectors offer outstanding capabilities in terms of energy resolution, radiopurity, background rejection, detection efficiency, and mass scalability [47,48,49,50]. CUPID-Mo exploits this technology to demonstrate the performances and the experimental feasibility of a mid-scale experiment with $\textrm{Li}_2\textrm{MoO}_4$-based bolometers. In this paper, we present the results of the search for exotic double-$\beta$ decays of ¹⁰⁰Mo exploiting the full data taking of the CUPID-Mo experiment. This analysis relies on the background model which provides a detailed description of the background sources releasing energy in the CUPID-Mo detector [8, 50]. Differently from the previous analyses, CUPID-Mo is the first experiment to account for the systematic uncertainties of the $2\nu \beta \beta$ decay spectral shape, parameterized through the improved $2\nu \beta \beta$ decay description [51, 52], in the search for exotic double-$\beta$ decays. The promising results obtained in this analysis motivate the interest in investigating the CUPID potential in the search for new physics processes involving distortion of the $2\nu \beta \beta$ decay spectral shape. CUPID is a next-generation ton-scale experiment aiming to reach unprecedented sensitivities on $0\nu \beta \beta$ decay of ¹⁰⁰Mo using Li$_{2}$ $^{100}$MoO$_4$ cryogenic calorimeters [53]. After one year of data taking, the ¹⁰⁰Mo exposure in CUPID will be about 150 times higher than the CUPID-Mo, providing impressive statistics on the SM $2\nu \beta \beta$ decay. Finally, with this work we analyze the main limits in searching for these BSM processes with cryogenic calorimeters and propose possible solutions to overcome these problems in future searches with CUPID.

2 Experimental setup

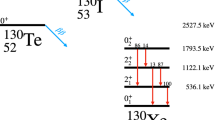
CUPID-Mo is an experiment at Laboratoire Souterrain de Modane (LSM) in France aiming to search for $0\nu \beta \beta$ decay of ¹⁰⁰Mo. It was installed in the EDELWEISS cryostat [54], optimized for low background measurements. The detector acquired data at a stable temperature of $\sim$20 mK from March 2019 to June 2020, for a total ¹⁰⁰Mo exposure of 1.47 kg $\times$ years. The experiment is made up of 20 cryogenic calorimeters consisting of Li$_{2}$ $^{100}$MoO$_4$ crystals produced from molybdenum enriched in ¹⁰⁰Mo to $\sim$97% and read-out by Neutron Transmutation Doped (NTD) Ge thermistors. Each crystal has a cylindrical shape and an average weight of 210 g. $\textrm{Li}_2\textrm{MoO}_4$-based bolometers are among the best detectors in this field due to the excellent energy resolution (7.7 ± 0.4 keV FWHM at 3034 keV [47, 55]) and the intrinsic radio-purity [50]. Moreover, these scintillating crystals permit the identification of the $\alpha$ background from the $\beta /\gamma$ interactions [47]. To detect the scintillation light and allow particle identification, thin Ge wafers, which also operate as cryogenic calorimeters, are positioned between Li$_{2}$ $^{100}$MoO$_4$ crystals along the tower. These Light Detectors (LDs) are also read out with NTD Ge thermistors and coated with a $\sim$70 nm layer of SiO$_2$ to increase the light collection. In this setup, each Li$_{2}$ $^{100}$MoO$_4$ crystal faces the top and the bottom with LDs, as an exception for the crystals on the top floor which face only one LD. A cylindrical copper holder and polytetrafluoroethylene pieces constitute the supporting structure for each crystal and the adjacent LDs. In addition, a reflective foil (3 M Vikuiti™) surrounds each Li$_{2}$ $^{100}$MoO$_4$ crystal to increase the light collection. The detector set-up consists of 20 bolometers arranged in five towers, four modules for each tower. These are suspended using stainless steel springs to reduce the vibrational noise. More details on the detector structure are in Ref. [56]. The cryogenic set-up is composed of five copper screens corresponding to the different thermal stages (300 K, 100 K, 50 K, 1 K, and 10 mK). Two lead shields aim to screen the detector from the environmental $\gamma$ radioactivity, an internal 14 cm thick Roman lead shield installed at the 1 K stage and a 20 cm thick external lead shield [57]. In the same way, two 10 cm and 55 cm thick polyethylene shields (internal and external, respectively) are installed to shield against environmental neutrons [56]. Finally, the entire setup is surrounded by plastic scintillators acting as muon veto.

3 Experimental data

Experimental data are acquired as a continuum time stream and digitized with a sampling frequency of 500 Hz both for Li$_{2}$ $^{100}$MoO$_4$ detectors and LDs. The data are divided into twelve datasets, where each dataset corresponds to about 1 month of data taking and is sub-divided into a series of runs. Each run is characterized by a period of $\sim$24 h of stable data taking. At the beginning and the end of each dataset, specific calibration runs are acquired by deploying a ²³²Th/²³⁸U source in the vicinity of the detector array. The characteristic $\gamma$-lines of ²³²Th and ²³⁸U produce several peaks in Li$_{2}$ $^{100}$MoO$_4$ crystals enabling the calibration of all the detectors. The light detectors cannot be calibrated with the ²³²Th/²³⁸U sources since $\gamma$-rays are not fully contained in the LD volume. For this reason, specific runs are acquired by using an intense ⁶⁰Co source, able to stimulate the production of fluorescence ¹⁰⁰Mo X-rays at $\sim$17 keV used to calibrate LDs. Without calibration sources, each detector has an average trigger rate of about 14 mHz [50].

Experimental data are acquired and processed with C++ based software packages developed by previous bolometric experiments [56, 58]. All the triggered events are acquired in a 3-seconds time window (1 s of pre-trigger). Each Li$_{2}$ $^{100}$MoO$_4$ detector is associated with its adjacent LD(s). First, we apply a series of cuts aiming to remove periods of detector instabilities and not-optimized data takings. We reconstruct the pulse amplitudes using an optimal filter [59]. This method allows the production of a new pulse with the maximum signal-to-noise ratio by selectively weighting the frequency components of the signal and suppressing those that are more affected by noise. Then, the filtered waveforms are corrected in order to remove the amplitude’s dependence on the initial detector temperature. For more details on the data processing see Ref. [47]. The detectors’ energy scale is determined through calibration runs, which provide the calibration function parameters calculated using the $\gamma$-ray peaks produced by the ²³²Th/²³⁸U sources. A quadratic function with a zero intercept is used to calibrate the $\beta /\gamma$ energy region. The $\alpha$ events appear in the background spectrum in a high energy range that spans from 4 to 10 MeV. Due to the different detector responses to $\gamma$-rays and $\alpha$-particles, the $\alpha$ spectrum shows a mis-calibration of about 8%. In this case, we use the ²¹⁰Po $\alpha$-peak to re-calibrate the $\alpha$ region. Given the granularity of the detector, the information about the timing of each event with respect to the other detectors is extremely useful for studying the topology of radioactive decays, as explained in the next section. In order to do that, we tag each event occurring in a ±10 ms time window with other detectors. The variable describing the number of channels that triggered a pulse in the same time window is called multiplicity.

4 Data selection

The data selection for the source spectra employed in the background model fit (explained in Sec. 6) is based on particle identification and time-coincidence criteria. The $\alpha$ identification relies on the scintillation light detected by the adjacent LD(s) coupled to each Li$_{2}$ $^{100}$MoO$_4$ crystal [47].

Following the approach used in other bolometric experiments [6, 60], we select the following spectra:

• $\mathcal {M}_{1\alpha }$: $\alpha$ events with multiplicity = 1 and an energy in the 3 to 10 MeV range.

• $\mathcal {M}_{1\beta /\gamma }$: $\beta /\gamma$ events with multiplicity = 1 and an energy in the 0.1 to 4 MeV range.

• $\mathcal {M}_2$: the sum of energies released in two crystals coincident in time (multiplicity = 2) within the 0.2–4 MeV range.

To select a clean data sample, we apply a series of quality cuts based on pulse shape and light yield. Details on the data selection and efficiency evaluation can be found in Refs. [47, 50]. The resulting efficiencies from the cuts applied in CUPID-Mo data are $\varepsilon _1 = (88.9 \pm 1.1)$% for $\mathcal {M}_{1\beta /\gamma }$, $\varepsilon _2 = (83.3 \pm 2.5)$% for $\mathcal {M}_2$, and $\varepsilon _3 = (94.7 \pm 1.0)$% for $\mathcal {M}_{1\alpha }$.

5 Monte Carlo simulations

We reproduce the signature of the background sources by producing a series of Monte Carlo simulations. For this purpose, we employ the version 10.04 of Geant4 [61]. The geometry implemented in simulations faithfully reproduces the experimental structure from small detector components to cryostat vessels and radiation shields (see Ref. [50] for more details). We generate radioactive decays in the experiment components using both Decay0 [62] and Geant4 (G4RadioactiveDecay library). Particle propagation through the experimental geometry employs the Livermore low-energy physics models [63].

We use the detector response model to reproduce the simulated spectra with the measured data. We model the energy resolution with a Gaussian shape where the mean is the energy deposited in the simulation and the standard deviation is derived from the experimental data. Pulses falling below the energy threshold of <40 keV are excluded, and the multiplicity is reproduced within a ±10 ms time window. We parameterize the scintillation light energy measured by the LD as a second-order polynomial of Li$_{2}$ $^{100}$MoO$_4$ detectors energy to reconstruct light signals in data. The LD energy resolution is modeled as a Gaussian with a standard deviation depending on the energy deposited in the corresponding Li$_{2}$ $^{100}$MoO$_4$ crystal. This approach ensures faithful replication of the light yield cuts in the simulations as observed in the experimental data. Data selection efficiencies are also taken into account in the simulations by generating a random number r for each event uniformly distributed between 0 and 1.

6 Background model

In our previous work, we conducted a thorough background model analysis utilizing a Markov Chain Monte Carlo (MCMC) Bayesian fit sampling the joint posterior probability density function (p.d.f.) of the model parameters utilizing the JAGS software [50, 64]. Experimental data for each bin b and energy $E_b$ are modeled as a linear combination $f(E_b; \vec {N})$ of the background sources weighted by a set of scaling factors called normalization parameters $\vec {N}$. We consider as likelihood function the product of Poisson distributions

$$\begin{aligned} \mathcal {L} \big ({\text {data}}|\vec {N}\big ) = \prod _{i}^{3} \prod _{b}^{N_{\text {bins}}} {\text {Pois}}\big (n_{i,b} \mid f_{i} \big (E_b; \vec {N}\big )\big ) \end{aligned}$$

(8)

where $n_{i,b}$ is the experimental number of counts for each bin in the i-th spectrum. The joint posterior p.d.f. has the form

$$\begin{aligned} p\big (\vec {N}|{\text {data}}\big ) \propto \mathcal {L} \big ({\text {data}}|\vec {N}\big ) \times \pi (\vec {N}), \end{aligned}$$

(9)

where $\pi (\vec {N})$ represents a set of the prior distributions [50]. With a Bayesian fit, we can model the uncertainties of various background sources and include them directly in the fit by choosing a specific prior p.d.f. for each contribution.

In the list of background components utilized in the fit, we included ²³²Th and ²³⁸U contaminations in all detector and cryostat components. We account for the breaks in the secular equilibrium of ²³²Th and ²³⁸U sources by producing separate simulations of their sub-chains. Specifically, in the ²³²Th chain, break points occur at ²²⁸Ra and ²²⁸Th, while in the ²³⁸U chain, break points are ²³⁴U, ²³⁰Th, ²²⁶Ra, and ²¹⁰Pb. Additionally, we consider other contributions, such as ⁴⁰K contamination in the springs and the outermost cryogenic thermal shield, ⁶⁰Co from cosmogenic activation in all copper components, and ⁴⁰K, ⁸⁷Rb and ⁹⁰Sr/⁹⁰Y in crystals. Decays are generated within the bulk of components and on the surface for nearby elements, following an exponential density profile $e^{-x/\lambda }$, where $\lambda$ is a variable depth parameter (for most of the surface contaminants $\lambda$ = 10 nm, see Ref. [50] for details). Initially, the $2\nu \beta \beta$ decay of ¹⁰⁰Mo was simulated in the background model under the Single-State Dominance (SSD) hypothesis, utilizing exact Dirac electron wave functions [65]. Subsequently, we incorporated an improved description [51, 52] of the $2\nu \beta \beta$ decay into the fit, with marginalization over the theoretical uncertainty of the spectral shape [8]. The fit also includes the $2\nu \beta \beta$ decay of ¹⁰⁰Mo to ¹⁰⁰Ru 0$_1^+$ excited state, pile-up produced by $2\nu \beta \beta$ decay events occurring in the same crystal, and random coincidences between two crystals.

Finally, a total of 67 sources are included in the fit. We modeled all the priors as non-negative uniform p.d.fs. The only informative priors are set for the $2\nu \beta \beta$ decay from ¹⁰⁰Mo to ¹⁰⁰Ru 0$_1^+$ excited state (with a half-life of $T_{1/2}=(6.7 \pm 0.5) \times 10^{20}$ years [66]), the stainless steel springs contamination (from screening measurements), the accidental coincidences, determined from the rate of single events, and the $2\nu \beta \beta$ decay pile-up, estimated with the calibration runs (see Ref. [50] for details). Variable binning is employed for the three spectra to ensure sufficient counts in each bin, thereby minimizing the impact of statistical fluctuations. A minimum bin size of 15 keV is chosen for $\mathcal {M}_{1\beta /\gamma }$ and $\mathcal {M}_2$, while a 20 keV minimum bin size is used for $\mathcal {M}_{1\alpha }$. The minimum number of counts in each bin is 50 for $\mathcal {M}_{1\beta /\gamma }$ and 30 for $\mathcal {M}_2$ and $\mathcal {M}_{1\alpha }$. Additionally, each peak is selected to be fully contained within one bin to mitigate the systematic effects of the detector response on the results.

7 BSM analysis

The search for exotic double-$\beta$ decays is performed by individually incorporating the new physics spectra into the background model fit. Each MCMC sample reconstructs the joint posterior p.d.f. of the normalization parameters. The normalization parameter $N_j$ of the j-th BSM process is directly related to the decay rate through the formula

$$\begin{aligned} \Gamma _j = \dfrac{N^{j}_{MC} \cdot N_{j}}{T \cdot \varepsilon \cdot N_{\beta \beta }}. \end{aligned}$$

(10)

Here, $N^{j}_{MC}$ denotes the total number of decays generated in the simulation, $N_{\beta \beta }$ is the total number of ¹⁰⁰Mo atoms, T is the experiment lifetime and $\varepsilon$ is the efficiency. In our case, the efficiency has been included in the simulations and, therefore, already accounted into the normalization parameter. The value of the product $T \cdot N_{\beta \beta }$ in CUPID-Mo corresponds to $(99.7 \pm 0.2)\times 10^{23}$ ¹⁰⁰Mo nuclei $\times$ y.

All new physics spectra in this analysis are simulated using exact Dirac wave functions with finite nuclear size and electron screening [67]. We use the SSD approximation for all the BSM spectra since the difference with their corresponding higher-state dominance (HSD) approximated spectrum in the total number of events is negligible compared to the systematic uncertainties of the model. We define as reference fit the configuration of sources described above. We consider two possible scenarios: the “standard” background model fit, as described in Ref. [50], which uses the SSD hypothesis for ¹⁰⁰Mo $2\nu \beta \beta$ decay, and the Improved Model (IM) fit, detailed in Ref. [8], which utilizes the improved description for the ¹⁰⁰Mo $2\nu \beta \beta$ decay spectral shape [51, 52]. Previous analyses from many experiments in this field use either the SSD or the HSD approximation to model the $2\nu \beta \beta$ decay spectral shape [5, 7, 68,69,70,71,72,73]. For the first time in the search for exotic double-$\beta$ decays, the uncertainties of the SM $2\nu \beta \beta$ decay spectral shape are marginalized in the fit using an extended model to describe the $2\nu \beta \beta$ spectral shape [51, 52]. Following the improved description, the $2\nu \beta \beta$ decay rate or, more specifically, the PSF can be decomposed as

$$\begin{aligned} G^{2 \nu } & = G_{0}^{2 \nu } + \xi _{31}^{2 \nu } G_{2}^{2 \nu } + \frac{1}{3}\left( \xi _{31}^{2 \nu }\right) ^{2} G_{22}^{2 \nu } + \left[ \frac{1}{3}\left( \xi _{31}^{2 \nu }\right) ^{2}\right. \nonumber \\ & \quad \left. + \xi _{51}^{2 \nu }\right] G_{4}^{2 \nu }, \end{aligned}$$

(11)

where $G_{0}, G_{2}, G_{22}$ and $G_{4}$ are the PSFs for different terms in the Taylor expansion of the lepton energies and $\xi _{31}$, $\xi _{51}$ are parameters depending on the ratios of the Gamow-Teller Nuclear Matrix Elements (NMEs). For ¹⁰⁰Mo, the values of the PSFs are $G_{0}$ = 3.303 $\times$ $10^{-18}$ year$^{-1}$, $G_{2}$ = 1.509 $\times$ $10^{-18}$ year$^{-1}$, $G_{22}$ = 4.320 $\times$ $10^{-19}$ year$^{-1}$, and $G_{4}$ = 1.986 $\times$ $10^{-19}$ year$^{-1}$ [51]. In the IM fit, the four spectra corresponding to $G_{0}, G_{2}, G_{22}$, and $G_{4}$ are simulated using exact Dirac wave functions with finite nuclear size and electron screening [67], and they are included in the fit separately. To accurately describe the $2\nu \beta \beta$ decay spectral shape, the fit model is modified to marginalize over the $\xi$ parameters. Since $\xi _{31}$ and $\xi _{51}$ are strongly anti-correlated, a Gaussian prior is placed on the ratio $\xi _{31}/\xi _{51}$ with a mean equal to the SSD prediction and a conservative 5% uncertainty [8]. This choice relies on the nuclear structure calculations, where the value of $\xi _{31}/\xi _{51}$ can be reliably obtained [51, 74]. Within the SSD hypothesis, the value of the ratio is 0.367 [51]. For more details on the IM fit, see Ref. [8].

We perform a series of additional fits to assess the systematic uncertainties. These are listed as follows:

• The dominant contribution at low energies comes from ²³²Th and ²³⁸U contaminations in cryostat components. However, the signatures of these sources in close (10 mK) and far (300 K) components are almost degenerate, leading to a possible mis-modeling. To estimate the uncertainty related to the source location, we alternatively remove the 300 K and 10 mK sources from the fit.

• In the background model fit, the decay chain ⁹⁰Sr/⁹⁰Y is included. Both these isotopes decay through pure $\beta$-decays, producing a featureless spectrum correlating with the $2\nu \beta \beta$ decay and BSM components. In the background model fit we measure a ⁹⁰Sr/⁹⁰Y activity of $179^{+36}_{-32}$ $\mu$Bq/kg. However, the presence of ⁹⁰Sr/⁹⁰Y is still uncertain since other unexplained contributions at low energies can induce its convergence. This systematic test involves removing this contribution from the fit.

• In the reference fit, some contributions present a posterior p.d.f. converging to a value compatible with zero or show an exponential shape flattened to zero. The minimal model is a fit performed by removing these contributions.

• As described above, we use a minimum bin size of 15 keV on $\mathcal {M}_{1\beta /\gamma }$, nevertheless, we consider also different values for the binning (1, 2, and 20 keV).

• Two fits are performed varying the energy scale by ±1 keV to account for a possible energy bias.

  Table 1 ¹⁰⁰Mo values of the PSF G and NME for different Majoron-emitting decays. The values of G are taken from Ref. [76]. For the Majoron mode with n = 1, the NME values are taken from Ref. [77]. For the other modes, the NMEs have been calculated in the framework of the interacting boson model [78]. For the Majoron mode n = 2, no calculations for the PSF and the NME are available

  Fig. 2

  

  Upper limits at 90% CI on the decay rate of different Majoron-emitting decays with the SSD approximation for $2\nu \beta \beta$ decay (green) and the improved description implemented in the fit (orange). The solid color corresponds to the limit obtained from the reference while the shaded one indicates the systematic uncertainty. The percentage difference between the results using the SSD and the IM fits (with the systematics) is highlighted in the orange column. The shaded gray columns show the limit obtained by NEMO-3 using the SSD assumption [7, 70]

• The theoretical uncertainties on the $2\nu \beta \beta$ decay Bremsstrahlung cross-section may affect the accuracy of MC simulations on the $2\nu \beta \beta$ decay spectrum. In order to assess this uncertainty, we perform the fit with alternative $2\nu \beta \beta$ decay spectra obtained by varying the Bremsstrahlung cross-section by ±10% [75].

The uncertainties on the efficiency (1.2%) and the ¹⁰⁰Mo enrichment (0.2%) are directly marginalized in the posterior p.d.fs. with Gaussian priors. In the following sections, the way to extract the physical parameters for the different BSM processes and their results are described.

8 Results

Even though the search for all the exotic double-$\beta$ decays is conducted with the same fitting procedure, the way to extract a limit on the physical parameters is significantly different. Majoron-emitting decays do not interfere with the SM $2\nu \beta \beta$ decay which is just considered an independent process. In this case, the SM $2\nu \beta \beta$ decay acts as a background. Conversely, the existence of $\nu N \beta \beta$ decay tends to suppress the SM $2\nu \beta \beta$ decay rate by a factor $\cos ^4 \theta$. The Lorentz-violating $2\nu \beta \beta$ decay also interferes with the SM $2\nu \beta \beta$ decay rate by introducing an additional term on the PSF. In the last two scenarios, increasing the sample size of $2\nu \beta \beta$ decay events will result in lower statistical uncertainties. This will make it more sensitive to deviations [9]. ¹⁰⁰Mo is one of the best nuclides among the $2\nu \beta \beta$ decay emitters to detect Lorentz-violating $2\nu \beta \beta$ decay and sterile neutrino emissions because of its relatively short half-life.

Table 2 Lower limits on the half-life at 90% CI and upper limits on the neutrino-Majoron coupling constant for different Majoron-emitting modes are shown both for SSD and IM fits, including systematics

8.1 Majoron-emitting decays

In this study, we performed the analysis of four different Majoron-emitting modes, corresponding to $n = 1,2,3$, and 7. The parameter of interest is the decay rate $\Gamma _{0 \nu M}$ of the different processes, which can be easily converted into a limit on the neutrino-Majoron coupling $g_{ee}^{M}$ through the formula

$$\begin{aligned} \Gamma _{0 \nu M} = G_{0 \nu M} \left| \left\langle g_{ee}^{M} \right\rangle \right| ^{2 m} \left| M_{0 \nu M}\right| ^{2}, \end{aligned}$$

(12)

where $G_{0 \nu M}$ and $\left| M_{0 \nu M}\right|$ are PSFs and NMEs for the Majoron-emitting modes, while m is the number of Majorons emitted. The ¹⁰⁰Mo values of $G_{0 \nu M}$ and $\left| M_{0 \nu M}\right|$ for different Majoron-emitting modes are summarized in Table 1. No evidence of signal was found for any of the decays mentioned above setting 90% Credible Interval (CI) limits on their half-lives by integrating the posterior p.d.f. on the corresponding decay rates. We performed the aforementioned systematic tests to determine the systematic uncertainty. For $n = 1, 2$, and 3, the systematics with a greater impact on the results are +10% Bremsstrahlung, –1 keV energy scale, and ⁹⁰Sr/⁹⁰Y. In the Majoron mode $n = 7$, where the signature exhibits a spectrum shifted at lower energies compared to the SM $2\nu \beta \beta$ decay (see Fig. 1), the situation is inverted, with dominant effects from –10% Bremsstrahlung, +1 keV energy scale, and source location. These tests demonstrate that uncertainties in modeling the low-energy part of the $\mathcal {M}_{1\beta /\gamma }$ spectrum limit the sensitivity for exotic double-$\beta$ decay searches. In a conservative approach, we quote as the final limit the least stringent including systematics. The same systematic checks are performed in the IM fit. The uncertainty on the $2\nu \beta \beta$ decay spectral shape, parameterized in the improved description, significantly reduces the sensitivity for Majoron-emitting decays, as depicted in Fig. 2. This effect is more pronounced in Majoron modes with $n < 5$, where the signal relies mostly on the high-energy side of the $2\nu \beta \beta$ decay spectrum. We report the limits on half-lives and neutrino-Majoron coupling constants obtained in this analysis for SSD and IM in Table 2. Only results with the SSD fit can be directly compared with the other experiments, where the same assumption on the $2\nu \beta \beta$ decay spectral shape was made. In the SSD assumption, the obtained limits are less stringent with factors of 1.8 for n = 1, 1.7 for n = 2, 2 for n = 3, and 5.4 for n = 7 compared to NEMO-3 [7, 70]. However, the ¹⁰⁰Mo exposure available in CUPID-Mo ($\sim$1.5 kg $\times$ years) is 22 times less than the NEMO-3 exposure ($\sim$34 kg $\times$ years), demonstrating the high sensitivity of the dual readout bolometric technique for these searches.

8.2 Lorentz-violating $2\nu \beta \beta$ decay

The violation of Lorentz and CPT symmetries introduces a perturbation in the SM-$2\nu \beta \beta$ spectrum. By adding the LV spectrum in the background model, the measured decay rate of the LV perturbation $\Gamma _{LV}^m$ and the SM $2\nu \beta \beta$ decay $\Gamma _{SM}^m$ can be evaluated from the normalization parameters. Since the countershaded operator ($\dot{a}_{o f}^{(3)}$) can assume negative values, under-fluctuations for the LV component are allowed in the fit. The ratio of the decay rates is directly proportional to $\dot{a}_{o f}^{(3)}$ through

$$\begin{aligned} \dfrac{\Gamma _{LV}^m}{\Gamma _{SM}^m} = \dot{a}_{o f}^{(3)} \cdot 10 \cdot \dfrac{\delta G_{LV}}{G_{SM}}, \end{aligned}$$

(13)

where the NMEs cancel out, $\delta G_{LV}$ is the PSF of the Lorentz perturbation, and $G_{SM}$ is the SM $2\nu \beta \beta$ decay PSF. Finally, the countershaded operator can be calculated from

$$\begin{aligned} \dot{a}_{o f}^{(3)} = C \cdot \dfrac{\Gamma _{LV}^m}{\Gamma _{SM}^m}, \end{aligned}$$

(14)

where C is a constant value. In this case, the collection of high $2\nu \beta \beta$ decay statistics plays an important role in constraining possible Lorentz-violating effects. In both the SSD and the IM fit, the posterior p.d.f. converges within a range compatible with zero, setting a double-sided limit at 90% CI on the negative and positive values of the $\dot{a}_{o f}^{(3)}$ parameter. We set the limits by taking into account the strong anti-correlation of the LV $2\nu \beta \beta$ decay component with the SM one by calculating the $\dfrac{\Gamma _{LV}^m}{\Gamma _{SM}^m}$ ratio for each MCMC sampling. In the SSD fit, the value of the factor C is calculated from the values of the PSFs in the SSD assumption, $C = (299.0$ ± 0.2) $\times$ $10^{-6}$ GeV$^{-1}$ [67], where the error comes mostly from the uncertainty on the ¹⁰⁰Mo $Q_{\beta \beta }$ and it is calculated as in Ref. [79]. In the IM fit, the PSF of SM $2\nu \beta \beta$ decay is explicitly calculated from the $\xi$ parameters.

The systematic checks listed above are performed on both the SSD and the IM fits, showing dominant effects for Bremsstrahlung, energy scale, and ⁹⁰Sr/⁹⁰Y. A summary of the results is represented in Fig. 3. The final limits including systematic in the SSD fit are

$$\begin{aligned} -8.1\times 10^{-6}< \dot{a}_{o f}^{(3)} < 2.2\times 10^{-6}, \end{aligned}$$

while in the IM fit

$$\begin{aligned} -6.5\times 10^{-6}< \dot{a}_{o f}^{(3)} < 2.5\times 10^{-5}. \end{aligned}$$

The strong anti-correlation between the LV spectrum and the $\xi$ parameters leads to a large broadening of the $\dot{a}_{o f}^{(3)}$ posterior, thus a weaker limit. The most stringent limit on the LV $2\nu \beta \beta$ decay of ¹⁰⁰Mo has been set by NEMO-3 [7], corresponding to $(-4.2<\dot{a}_{o f}^{(3)}<3.5) \times 10^{-7}$ (Fig. 3), assuming the single state dominance for the $2\nu \beta \beta$ decay. In our case, the SSD fit prefers negative values of the $\dot{a}_{o f}^{(3)}$ parameter, producing a stronger limit on the positive values than the negative ones. Contrarily, in the IM fit the $\dot{a}_{o f}^{(3)}$ converges at positive values.

Fig. 3

Top: double-sided limits at 90% CI on the Lorentz-violating countershaded operator with the SSD approximation for $2\nu \beta \beta$ decay (green) and the improved description implemented in the fit (orange). The solid color corresponds to the limit obtained from the reference fit, while the shaded one shows the effect of systematics. Bottom: current limits on the Lorentz-violating countershaded operator for different double-$\beta$ decay emitters at 90% CL obtained assuming either SSD or HSD approximations [5, 7, 68, 80, 81]. For ⁸²Se and ¹¹⁶Cd only positive limits are provided

Table 3 Upper limits on the active-sterile mixing strength $\sin ^2 \theta$ for different values of sterile neutrino masses $m_N$ [67]

Fig. 4

Limits on the active-sterile mixing strength $\sin ^2 \theta$ as a function of the sterile neutrino mass $m_N$. The blue region represents the region excluded by the GERDA including systematics, covering the $m_N$ range 0.1–0.9 MeV [68]. The green region is excluded by CUPID-Mo assuming the improved model to describe the $2\nu \beta \beta$ decay spectral shape and including systematics. The green dashed line shows the limit obtained from the reference IM fit. The red lines represent the limits obtained using the SSD assumption with and without systematics (solid and dashed lines, respectively)

8.3 Sterile neutrino emissions

We investigated a mass range for sterile neutrino masses $m_N$ from 0.5 to 1.5 MeV, with 0.1 MeV steps. The active-sterile mixing strength can be calculated for different sterile neutrino masses as [40, 41]

$$\begin{aligned} \sin ^2 \theta = \frac{G_{SM}}{2 G_{\nu N}} \cdot \dfrac{\Gamma _{\nu N}^m}{\Gamma _{SM}^m}, \end{aligned}$$

(15)

where $G_{\nu N}$ is the PSF of the sterile neutrino spectrum, calculated for each sterile neutrino mass considered [67]. The same considerations on $G_{SM}$ done in the previous section are also valid in this case. No signal evidence is found for any of the considered masses, setting a 90% CI limit on $\sin ^2 \theta$. We identified as dominant systematic effects − 10% Bremsstrahlung, + 1 keV energy scale, and minimal model. The same systematics are performed in the IM fit. All the obtained limits are summarized in Table 3 and Fig. 4. For sterile neutrino masses lower than 1.2 MeV, the $\nu N \beta \beta$ decay component starts correlating with the $2\nu \beta \beta$ one, and this effect is amplified when the $2\nu \beta \beta$ decay shape is described with the IM. In particular, for low values of $m_N$ the shape of $\nu N \beta \beta$ decay spectrum becomes more similar to the SM component. In the framework of $0\nu \beta \beta$ experiments, GERDA set limits on $\sin ^2 \theta$, spanning a range for sterile neutrino masses from 0.1 to 0.9 MeV, as reported in Fig. 4. Nevertheless, existing bounds on the active-sterile mixing strength from $\beta$-decay and solar neutrino experiments [42,43,44,45,46] have already excluded this region of the parameter space, setting limits on $\sin \theta$ in the range 10$^{-3}$–10$^{-2}$ [42,43,44,45,46].

Fig. 5

Exotic double-$\beta$ decay spectra compared to the experimental data with a number of counts corresponding to the 90% CI limit obtained in the SSD fit. The LV $2\nu \beta \beta$ decay spectrum represents only the limit on the positive side. The black dots correspond to the experimental data, the gray spectrum is the background reconstructed by the background model while the blue spectrum represents the SM $2\nu \beta \beta$ decay

9 Conclusions and outlook

We presented the results of the searches for exotic double-$\beta$ decays with CUPID-Mo. The analysis exploited the precise spectral shape reconstruction provided by the background model. No signal evidence has been found for any of the BSM processes investigated, setting a 90% CI limit on the corresponding new physics parameter. For the first time, the theoretical uncertainties of the $2\nu \beta \beta$ decay spectral shape, parameterized through the improved model description [51], have been taken into account in this type of search. This work demonstrated that uncertainties on the $2\nu \beta \beta$ decay shape induce a significant reduction in sensitivity for all the processes investigated, requiring better theoretical constraints, higher statistics, and precise background reconstruction at low energies in the next-generation experiments. A parallel analysis was performed using a fixed spectral shape for the $2\nu \beta \beta$ decay (single-state dominance) to compare the results with those of other experiments. The limits at 90% CI on the experimental data are represented in Fig. 5. CUPID-Mo set stringent constraints on the neutrino-Majoron coupling and the Lorenz-violating countershaded operator, despite the relatively small exposure ($\sim$ 1.5 kg $\times$ years), the limits are only a factor 2–10 less stringent than NEMO-3 ones ($\sim$ 34 kg $\times$ years) [7, 70]. The search for $\nu N \beta \beta$ decay has been performed for the first time using cryogenic calorimeters. Exploiting the high Q-value of ¹⁰⁰Mo, CUPID-Mo data allowed constraining the active-sterile mixing strength for higher values of $m_N$ compared to GERDA. Nevertheless, that region of the parameter space was already excluded by $\beta$-decay and solar neutrino experiments [42,43,44,45,46]. The results of CUPID-Mo demonstrate the potential of the bolometric technique for exotic double-$\beta$ decay searches. These promising results motivate the interest in investigating these BSM processes in the next-generation CUPID experiment. This study extensively analyzed the main limitations in sensitivity. In particular, the theoretical uncertainties on the $2\nu \beta \beta$ decay spectral shape, the uncertainty on the presence of pure $\beta$-emitters in crystals, and the small statistics are the primary limiting factors. In the future, improvements in NME calculations can further constrain the $\xi$ parameters of the $2\nu \beta \beta$ decay improved description. For the next-generation CUPID experiment, the possibility of measuring the ⁹⁰Sr and ⁴⁰K concentration in $\textrm{Li}_2\textrm{MoO}_4$ crystals with a sensitivity $\lesssim 10^{-20}$ g/g will be extremely helpful in overcoming the problem of pure $\beta$-decays.