Topological charges via Barrow entropy of black hole in metric-affine gravity

Abstract

This paper examines distinct ensembles such as canonical, mixed, and grand canonical ensembles of recently postulated black hole which is considered to be an ideal solution of metric-affine gravity utilizing the Duan’s $\phi$-mapping theory. In the scenario, charged and uncharged topological characteristics associated to thermodynamic stability criteria are explored. In contrast to the canonical ensemble, which is always possesses the constant electric and magnetic charges, but mixed ensemble possesses the constant potentials (both magnetic and electric). Also, grand canonical ensemble maintains the constant electric and magnetic potentials for both charges. Initially, we find the topological classes connected via critical points in all of the aforementioned ensembles.

1 Introduction

The thermodynamical structure of a black hole (BH) not only in the framework of general relativity (GR) but also in the modified theories of gravity is one of the most fascinating and advance research topic [1]. The renowned four laws of BH mechanics are put into practice to analyze the thermal parameters and conduct of BHs [2, 3]. According to the Hawking–Page phase transition [4], which establishes an explicit connection between thermodynamics and gravity, and this was a significant discovery in this field. Hawking and Page investigated the potential of a phase transition for Anti-de Sitter spacetime involving thermal radiation of BH, and through this framework of AdS/CFT correspondence, these transitions are analogous to phase transitions such as confinement or de-confinement [5, 6]. This study reveals to the phase transition for both small and large charged BHs in AdS space which is extremely comparable with the phase transition of van der Waal fluid. Subsequently, there has been a pursuit to understand the underlying microstructure of a BH by using various approaches.

Investigating BH topology is one way to explore the thermodynamic features of BHs in the context of extended phase space. In this direction, numerous research efforts to describe the topological charges and their families of BH in modified theories of gravity. To provide further clarity, in [7], stationary BHs are considered. The topological classes are calculated in Kerr and Kerr–Newman BHs respectively. Furthermore, they calculate the AdS case and the singly-rotating BH in higher dimensions. [7, 8]. In addition to analyzing topological charges in general relativity, some scientists utilize these classifications in modified gravity theories, such as Lovelock gravity and Gauss–Bonnet gravity [9, 10]. In such cases, the topological charges are completely distinct, which opens up a new perspective on how GR and modified gravity differ from one another. In the case of a free energy phase transition, one can consider a conventional ensemble computation of distinct BH states with varied radii at a constant Hawking temperature. We substitute the ensemble temperature T with the Hawking temperature of BH, thus transforming the free energy into a continuous function corresponding to the BH radius. To be more precise, the free energy can be obtained in both off-shell regions, which define the steady Einstein field equation while the on-shell regions comply with the equation. The thermodynamic viability of various on-shell BHs at a given temperature can be resplendently visualized using the Gibbs free energy. Local minima or maxima of the Gibbs free energy demonstrates the local or global stability, respectively, while the worldwide minimum indicates the globally stable BH. Recent study indicates free energy seems not only helpful for BH topological thermodynamics but also provides a crucial role in understanding the dynamics associated with the BH phase transition [11,12,13]. A well known relation can be written as

$$\begin{aligned} P=-\frac{\Lambda }{8 \pi G}, \end{aligned}$$

(1)

where, gravitational constant is presented by G. In the context of thermodynamics, there exists a relationship between the thermodynamic volume, denoted as V, and the thermodynamic pressure, denoted as P. When considering the first law of BH thermodynamics, this relationship leads to a modified formulation:

$$\begin{aligned} d M=~\sum _i Y_i d x^i+T d S+V d P, \end{aligned}$$

(2)

where S is the entropy, $Y_i d x^i$ is the i-th chemical potential term, and T is the Hawking temperature. In this scenario, we study the criticality of BHs involves the adoption of thermodynamic topology. Inaugurated in [14,15,16,17], this novel technique, current $\phi$-mapping (Duan’s topological) theory is utilized to investigate the thermodynamics of a BH through critical points. As a result, this analysis is specified with various topological classes are determined and characterized through conventional critical points. A summary of the essential mathematical steps is provided below. The temperature T of a BH is computed in the form of state parameter P, entropy S and other thermodynamic amounts as

$$\begin{aligned} T=T\left( S, P, x^i\right) , \end{aligned}$$

(3)

where $x^i$ describes the various thermodynamic parameters. Then, the state parameter is eradicated by employing $\left( \partial _S T\right) _{P x^i}=$ 0, and a novel potential $\Phi$, referred as Duan’s potential is developed as

$$\begin{aligned} \Phi =\bigg (\sin \theta \bigg )^{-1} T\left( S, x^i\right) . \end{aligned}$$

(4)

From the above equation, the expression “($\big (\sin \theta \big )^{-1}$”)” is used to establish the connection. In Duan’s $\phi$-mapping theory [16, 17], a two-dimensional vector $\phi =\left( \phi ^S,\phi ^\theta \right)$ is stated as

$$\begin{aligned} \phi ^\theta =\left( \partial _\theta \Phi \right) _{S, x^i}, \quad and \quad \phi ^S=\left( \partial _S \Phi \right) _{\theta , x^i}. \end{aligned}$$

(5)

The fact that $\theta$ exists in the vector field $\phi$ indicates that $\theta =\pi /2$ is the vector field’s consistent zero point. The following formula may be utilized to determine the critical points. Additionally, $j^\mu$, the topological charge, remains unchanged, indicating that $\phi ^a\left( x^i\right) =0$. The resulting structure verifies the presence of some topological current, where $\Sigma$ is similar for a particular parameter area, which is given as

$$\begin{aligned} Q=\int _{\Sigma } j^0 d^2 x=\sum _{i=1}^N w_i.=\sum _{i=1}^N \beta _i n_i. \end{aligned}$$

(6)

Here, the topological current density, the winding number of the i-th zero point of $\phi$, and the Hope index are denoted by the variables $j^0,~w_i$, and $\beta _i$, respectively. Novel points of criticality as well as typical critical point are given respectively, for critical points having topological classes $-\,1$ and $+\,1$. The total of various categories related to every critical point determines the overall topological class for a BH. In [14], the topological investigation in thermodynamics was studied of numerous BHs [19,20,21,22,23,24].

An other way to discuss topology for BH thermodynamics has also been investigated in [25]. In this approach, BH models are considered deficient in thermodynamic parameter spaces. The shortcomings are subsequently investigated in relation to their winding numbers. It has been determined that the thermal stability of agreeing with BH solution is correlated with the value of the winding number deficiencies. Therefore, various BH models are categorized according to their topological charge, that is now referred to as the total of all the winding charges. The generating free energy F is introduced at the beginning of the study and is described as follows

$$\begin{aligned} \mathcal {F}=-S~\left( \tau \right) ^{-1}+E, \end{aligned}$$

(7)

where S and E are the entropy and potential energy, while $\tau$ represents an amount that has the dimensions of time. A vector field $\phi$ is expressed via F in the following way

$$\begin{aligned} \phi =\left( \partial _{r_{+}}\mathcal {F},-\cot \Theta \csc \Theta \right) . \end{aligned}$$

(8)

The vector $\phi$ has a zero point at $\Theta =\pi /2$. In order to obtain unit vector, given formulation can be employed as

$$\begin{aligned} n^a=\frac{\phi ^a}{\Vert \phi \Vert }, \quad \phi ^1=\phi ^r and \quad \phi ^2=\phi ^{\Theta }. \end{aligned}$$

(9)

Here, $(a=1,2)$, and the zero points of $n^1$ are determined according to a particular value of $\tau$. For every one of the aforementioned zero points, the winding numbers (charges) can be obtained. By adding up all of the distinct winding numbers associated with each BH charge, one can find the topological number for a BH. So, various topological defects have been addressed in [25]; also this concept has been extended to a variety of BHs in [7, 26,27,28,29,30,31,32,33,34,35]. Thus, one can express the topological class as

$$\begin{aligned} Q=\left( 2 \pi \right) ^{-1}~\Omega =\frac{1}{2 \pi } \oint _C \epsilon _{a b} n^a \partial _i n^b d x^i. \end{aligned}$$

(10)

Here, we parameterize the closed curves $C_1$ and $C_2$ by the angle $\vartheta \in (0,2 \pi )$ as

$$\begin{aligned} \left\{ \begin{array}{l} r=a \cos \vartheta +r_0, \\ \theta =b \sin \vartheta +\frac{\pi }{2}. \end{array}\right. \end{aligned}$$

(11)

We select $\left( a, b, r_0\right)$ for $C_1$, and $C_2$. Then we calculate $\Omega$ along $C_1$ and $C_2$. Finding an approach that takes into account the non-metricity tensor (NMT) and the topological charge in the context of metric-affine gravity. This modification allows an extensive examination regarding the entropy of the entire solution and parameters like $\kappa _{\textrm{s}}$, $\kappa _{\textrm{sh}}$, and $\kappa _{\textrm{d}}$ are related to the spin, shear, and dilation charges through the first law of BH thermodynamics. Therefore, the cosmological consideration and the contribution to the gravitational waves (spectrum) of considered model and some other important features to be studied.

Our objective in this study is to expand the exploration of BH topological charges within the context of metric-affine gravity. This paper is structured as follows. In Sect. 2, we provide a concise overview of our intriguing class of BHs in the context of metric-affine gravity with Barrow entropy. In Sect. 3, we discuss the topology of BHs in metric-affine gravity thermodynamics within the canonical ensemble. In Sect. 4, we introduce a BH solution as topological thermodynamic defects in the canonical ensemble. In Sect. 5, we explore thermodynamics in the mixed canonical ensemble. In Sect. 6, we present a BH solution as topological thermodynamic defects in the mixed ensemble. In Sect. 7, we examine BH grand canonical ensembles (GCE). In Sect. 8, we introduce a BH solution as topological thermodynamic defects in GCE. Finally, we offer some concluding remarks.

2 A brief description of BH within metric-affine gravity and Barrow entropy

GR is a well-defined theory that investigates gravitational interactions including matter characteristics utilizing space-time geometry as well as the energy-momentum tensor. From both the geometrical and physical perspectives, we consider the Lorentzian metric tensor $g_{\mu \nu }$ to analysis the smooth manifold that is employed to construct the Levi-Civita affine connection $\Gamma ^\lambda _{\mu \nu }$. A traceless NMT must be taken into consideration in the gravitational action, which is caused by metric affine gravity to provide the biggest family of BH solutions in the context of dynamical torsion with nonmetricity. As a geometrical structure to GR, a second order parity-preserving action providing a dynamical traceless NMT is given as [36,37,38,39,40]

$$\begin{aligned} S= & \int d^4 x \sqrt{-g}\left\{ \mathcal {L}_{\textrm{m}}+\frac{1}{16 \pi }\left[ -R+2 f_1 \tilde{R}_{(\lambda \rho ) \mu \nu } \tilde{R}^{(\lambda \rho ) \mu \nu }\nonumber \right. \right. \\ & \left. \left. +2 f_2\left( \hat{R}_{(\mu \nu )}-\tilde{R}_{(\mu \nu )}\right) \left( \hat{R}^{(\mu \nu )}-\tilde{R}^{(\mu \nu )}\right) \right] \right\} , \end{aligned}$$

(12)

where $\tilde{R}^{(\lambda \rho ) \mu \nu }$, $\tilde{R}_{(\mu \nu )}$ and $\quad \hat{R}_{\mu \nu }$ are the affine-connected forms of Riemann, Ricci and co-Ricci tensors. Further, three independent traces of this tensor leads to $\tilde{R}_{\mu \nu }=\tilde{R}^\lambda _{\mu \lambda \nu }$, . In order to determine the largest family of BH solutions with dynamical torsion and nonmetricity in metric-affine gravity, we must consider a propagating traceless nonmetricity tensor in the gravitational action of metric-affine gravity. Here, R denotes the Ricci scalar, $\mathcal {L}_{\textrm{m}}$ represents the matter Lagrangian, g describes determinant of metric tensor and $f_1$, $f_2$ stand for Lagrangian coefficients. This metric function can be modified to consideration such as cosmological constant with Coulomb electromagnetic fields, electric charge ($q_e$) as well as magnetic charge ($q_m$), which are separated from torsion [41,42,43]. Therefore, the hyper momentum provides its suitable separation into shear, spin and dilation currents [39, 40, 44,45,46]. People have also done interesting works in this direction. Moreover, the model’s effective gravitational action generalized on the basis of these characteristics. The spherically symmetric static spacetime’s parameterization approach is [42, 47,48,49,50] follows as

$$\begin{aligned} ds^2=-\Psi (r)dt^2+\Psi ^{-1}(r)dr^2 +r^2d\theta ^2+r^2\sin ^2\theta d\phi ^2.\nonumber \\ \end{aligned}$$

(13)

In the emission process, to compare with the typical case of GR, a matter currents connected to nonmetricity and torsion in general energy classes will potentially influence this efficiency and spectrum. Intriguingly, a perturbative explanation of the energy-momentum tensor within vacuum change of quantum field associated to the torsion and NMT of the solution is provided in order to investigate the dissipation assessed on its event horizon; this would also involve additional modifications to the GR system [50, 51]. The metric function (Reissner–Nordstrom–de Sitter-like) can be described as [40]

$$\begin{aligned} \Psi (r)= & 1-\frac{2 m}{r}+\frac{d_1 \kappa _{\textrm{s}}^2-4 e_1 \kappa _{\textrm{d}}^2-2 f_1 \kappa _{\textrm{sh}}^2+q_{\textrm{e}}^2+q_{\textrm{m}}^2}{r^2}\nonumber \\ & +\frac{\Lambda }{3} r^2, \end{aligned}$$

(14)

Here, $\kappa _{\textrm{d}}$, $\kappa _{\textrm{s}}$ and $\kappa _{\textrm{sh}}$ represent the dilation charges, spin and shear, respectively. The most extensive family-charged BH models are derived in metric affine gravity with real constants $e_1$ and $d_1$. In Ref. [53], Barrow studied the features that quantum-gravitational efforts could supply an impenetrable, revising the BH real horizon region and fractal structure on the BH surface. As a result, a new BH entropy associated follows as

$$\begin{aligned} S_{B}=\bigg (\frac{A}{A_{0}}\bigg )^{1+\frac{\Delta }{2}}. \end{aligned}$$

(15)

Here, $A_{0}$ represents the Planck area; at this stage, A is the ordinary horizon area. Besides, it is associated with Tsallis entropy (nonextensive) execution [54]; this entropy is unique from the quantum corrected entropy [55] with logarithmic. This supply is a most straightforward analysis for distinctive values of $\Delta$. One can expressed the well-known formula as Bekenstein-Hawking entropy with $\Delta =0$; so that we have the maximal twisting in this case.

3 Topology of BH in metric-affine gravity thermodynamics in canonical ensemble

We obtain the BH’s mass parameter M with entropy $S_B$ as

$$\begin{aligned} m= & \frac{1}{6} \left( \!\pi ^{-\frac{\Delta }{2}-1} {S_B}\right) ^{-\frac{1}{\Delta +2}} \left( -8 \pi P \left( \pi ^{-\frac{\Delta }{2}-1} {S_B}\right) ^{\frac{4}{\Delta +2}}+3 q_{\epsilon }^2\nonumber \right. \\ & \left. + 3 q_{m}^2+3 \left( \pi ^{-\frac{\Delta }{2}-1} {S_B}\right) ^{\frac{2}{\Delta +2}}-3D \right) . \end{aligned}$$

(16)

where D is defined in the Appendix section. We expressed the temperature in terms of pressure, horizon radius (where $r_h$ represents the radius of the horizon), electric and magnetic charges as

$$\begin{aligned} T=-\frac{\pi ^{-\frac{\Delta }{2}-1} {r_h}^{-\Delta -3} \left( 8 \pi P {r_h}^4 +q_{\epsilon }^2+q_{m}^2-{r_h}^2-D\right) }{2 (\Delta +2)}.\nonumber \\ \end{aligned}$$

(17)

Use of condition $\frac{\partial T}{\partial S}=0$, leads to pressure expression as

$$\begin{aligned} P=\frac{-3 d_{1}\kappa _{s} ^2+D\Delta +6 f_1 \kappa _{sh} ^2-\left( (\Delta +3) q_{\epsilon }^2\right) -(\Delta +3) q_{m}^2+\Delta {r_h}^2+{r_h}^2+12 \kappa _{d}^2 \epsilon _1 }{8 \pi (\Delta -1) {r_h}^4}. \end{aligned}$$

(18)

Plugging P in Eq. (17), one can expressed the T yields follows as

$$\begin{aligned} T=-\frac{\pi ^{-\frac{\Delta }{2}-1} r_h^{-\Delta -3} \left( -2 d_{1}\kappa _{s} ^2+ 4 f_1 \kappa _{sh} ^2-2 q_{\epsilon }^2-2 q_{m}^2+r_h^2+8 \kappa _{d}^2 \epsilon _1 \right) }{\Delta ^2+\Delta -2}.\nonumber \\ \end{aligned}$$

(19)

Now, we may utilize the technique that designed in the introduction to examine a space parameter and obtain the vector field’s zero points. Accordingly, the zero points are precisely analogous to the on-shell BH solution. The topological charge could be obtained via $\Phi$-mapping and topological current theory. $\Phi$ is referred as the thermodynamic function and it is defined as

$$\begin{aligned} \begin{aligned} \Phi&=\frac{1}{\sin \theta } T \\&=-\frac{\pi ^{-\frac{\Delta }{2}-1} \csc (\theta ) r_h^{-\Delta -3} \left( -2 d_{1} \kappa _s^2+4 f_1 \kappa _{sh} ^2-2 q_{\epsilon }^2-2 q_{m}^2+r_h^2+8 \kappa _{d}^2 \epsilon _1 \right) }{\Delta ^2+\Delta -2}, \end{aligned} \end{aligned}$$

(20)

Fig. 1

Normalized vector field n in $r_h/r_0$ against $\theta$ for BH within canonical ensemble. The dot exhibits the critical point

Figure 1 shows the vector plot of n in a $r_h$ vs $\theta$ plane for BH in metric-affine gravity. For this plot, the dot signifies the critical point (CP1). In order to determine the critical point, one cane define $\theta =\pi /2$ in Eq. (14) then set its value to zero. In this way, the location of the point (critical) is at $(r_h, \theta ) \simeq (3.40,\pi /2)$ for $q_{\epsilon }=1$, $q_{m}=1,~d_1=0.5,~f_1=2.5,~\epsilon _1=0.4,~\kappa _s=1.2,~\kappa _d=0.5$ and $\kappa _{sh}=0.02$ respectively. The vector fields $\phi =\left( \phi ^{r_h}, \phi ^\theta \right)$ possess the following vector components:

$$\begin{aligned} \phi ^{r_{h}}= & \left( \frac{\partial \Phi }{\partial r_{h}}\right) _{q_{e, q_m, \theta }}\end{aligned}$$

(21)

$$\begin{aligned}= & \frac{\pi ^{-\frac{\Delta }{2}-1} \csc (\theta ) {r_h}^{-\Delta -4} \left( A-2 (\Delta +3) q_{\epsilon }^2-2 (\Delta +3) q_{m}^2+\Delta {r_h}^2+{r_h}^2+24 \kappa _{d}^2 \epsilon _1 \right) }{\Delta ^2+\Delta -2}. \end{aligned}$$

(22)

Here A is defined in the Appendix section and

$$\begin{aligned} \phi ^\theta =\left( \frac{\partial \Phi }{\partial \theta }\right) _{q_e, q_m, r_{+}}= \frac{\pi ^{-\frac{\Delta }{2}-1} \csc (\theta ) \cot (\theta ) {r_h}^{-\Delta -3} \left( -2 d_{1} \kappa _{s} ^2+4 f_1 \kappa _{sh} ^2-2 q_{\epsilon }^2-2 q_{m}^2+{r_h}^2+8 \kappa _{d}^2 \epsilon _1 \right) }{\Delta ^2+\Delta -2}. \end{aligned}$$

(23)

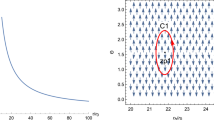
We depict the isobaric curves encircling the critical point in Fig. 2 to determine how it behaves. The critical point is indicated by a black dot in the phase structure. Through the red curve, one can discern the $P = P_c$ isobaric curve. Additional paths for $P > P_c$ and $P < P_c$ are located above and below the red curve, respectively. In Fig. 2, it can be seen that when $P < P_c$, there exists an unstable region between the large and small BH phases. This region is characterized by a negative slope section in the phase structure. The components of the normalized vector expressed are

$$\begin{aligned} \frac{\phi ^{r_h}}{\Vert \phi \Vert }=\frac{\pi ^{-\frac{\Delta }{2}-1} \csc (\theta ) {r_h}^{-\Delta -4} \left( A-2 (\Delta +3) q_{\epsilon }^2-2 (\Delta +3) q_{m}^2+\Delta {r_h}^2+{r_h}^2+24 \kappa _{d}^2 \epsilon _1 \right) }{ \bigg [{\pi ^{-\Delta -2} \csc ^2(\theta ) {r_h}^{-2 (\Delta +4)} \left( \left( A-2 (\Delta +3) q_{\epsilon }^2-2 (\Delta +3) q_{m}^2+\Delta {r_h}^2+{r_h}^2+24 \kappa _{d}^2 \epsilon _1 \right) ^2+{r_h}^2 \cot ^2(\theta ) B^2\right) }\bigg ]^{\frac{1}{2}}}.\nonumber \\ \end{aligned}$$

(24)

Here B is defined in the Appendix, and

$$\begin{aligned} \frac{\phi ^\theta }{\Vert \phi \Vert }=\frac{\pi ^{-\frac{\Delta }{2}-1} \csc (\theta ) \cot (\theta ) {r_h}^{-\Delta -3} \left( B \right) }{ \bigg [{\pi ^{-\Delta -2} \csc ^2(\theta ) {r_h}^{-2 (\Delta +4)} \left( \left( A-2 (\Delta +3) q_{\epsilon }^2-2 (\Delta +3) q_{m}^2+\Delta {r_h}^2+{r_h}^2+24 \kappa _{d}^2 \epsilon _1 \right) ^2+{r_h}^2 \cot ^2(\theta ) B^2\right) }\bigg ]^{\frac{1}{2}}}.\nonumber \\ \end{aligned}$$

(25)

Fig. 2

Plot of T vs $r_h$ plane for BH in canonical ensemble for different values of state parameter P. The dot represents the critical point

Fig. 3

Plot of $\Omega$ against $\vartheta$ for the contours $C_1$ and $C_2$

The normalized vector $n=\left( \frac{\phi ^{r_h}}{\Vert \phi \Vert }, \frac{\phi ^\theta }{\Vert \phi \Vert }\right)$ is plotted in Fig. 1. This figure displays the vector plot of n in a $r_{h}$ against $\vartheta$ plane for BH. One can obtained the critical points as

$$\begin{aligned} P_c= & \frac{1}{96 \pi \left( D- q_{\epsilon }^2-q_{m}^2 \right) }, r_c=\sqrt{6} \sqrt{ q_{\epsilon }^2+q_{m}^2-D },\nonumber \\ T_c= & \frac{1}{3 \sqrt{6} \pi \sqrt{ q_{\epsilon }^2+q_{m}^2-D}}. \end{aligned}$$

(26)

Figure 3 shows the topological charge with $(a,~b,~r_0)= (0.15,~0.39,3.08)$ for $C_1$ and $(a,b,r_0)=(0.18,0.42,3.1)$ for $C_2$ whenever Q leads to $\frac{1}{2 \pi } \Omega (2 \pi )$. The curve that is blue represents $C_1$, while the red curve is for $C_2$ respectively. The topological charge for the critical point bounded by the contour $C_1$ is calculated to be $Q_{C_ 1}=-1$ for fixed values of $q_{\epsilon }=0.4,~q_{m}=1,~d_1=0.5,~\Delta =0.6,~f_1=2.5,~\epsilon _1=0.4,~\kappa _s=1.2,~\kappa _d=0.5$ and $\kappa _{sh}=0.02$ respectively. The contour ${C}_2$ relates to having zero topological charge because it excludes any critical point. As a result, $Q=-1$ signifies the overall topological charge, while for $C_1$, the function $\Omega (\theta )$ drops non-linearly until it approaches to $-2 \pi$ at $\vartheta =2 \pi$ whereas $\Omega (\vartheta )$ for $C_2$ turns zero at $\vartheta =2 \pi$.

4 Topological thermodynamic shortcomings in canonical ensemble as a BH solution

The on-shell BHs are precisely related to the extremal points of the Gibbs free energy. One may get a general idea of the thermodynamic equilibrium of various on-shell BHs at a specific temperature by employing the Gibbs free energy. In particular, the global lowest point denotes a globally steady BH, whereas the local maximum or minimum point on the Gibbs free energy represents the local unstable and stable BHs. Now, we delve into examining the BH solution in canonical ensemble by considering it as thermodynamic defects with topological significance. With the help of entropy and mass of the BH from (15), (12) in (7), The generalized free energy is calculated as

$$\begin{aligned} F=\frac{2 \Delta \left( q_{\epsilon }^2+q_{m}^2-D \right) }{3 (\Delta -1) r_h}- \frac{\pi ^{\frac{\Delta }{2}+1} {r_h}^{\Delta +2}}{\tau }+\frac{(\Delta -2) {r_h}}{3 (\Delta -1)}.\nonumber \\ \end{aligned}$$

(27)

The vector field components are calculated as (8)

$$\begin{aligned} \phi ^{r_h}=\frac{1}{3} \left( C+\frac{\Delta -2}{\Delta -1}-\frac{3 \pi ^{\frac{\Delta }{2}+1} (\Delta +2) {r_h}^{\Delta +1}}{\tau }\right) , \end{aligned}$$

(28)

here C is defined in the Appendix, and second component as

$$\begin{aligned} \phi ^{\theta } =- \csc (\theta ) \cot (\theta ). \end{aligned}$$

(29)

Fig. 4

Plot of unit vector field n in $r_h/r_0$ vs $\theta$ plane for BH in defects in canonical ensemble with $\tau =150$. The dot represents the critical point

Fig. 5

Plot of unit vector field n in $r_h/r_0$ vs $\theta$ plane for BH in defects in canonical ensemble with $\tau =200$. The dot represents the critical point

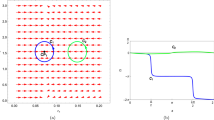
By changing $\Theta =\pi / 2$ to zero and substituting it into the expression for $n^1$, these unit vectors determined to identify the zero points. For example, substituting $q_m / r_0=1$, $q_e / r_0=1$ and $\tau / r_0=150$, one can derive the zero point $\left( Z P_1\right)$ in Fig. 4 placed at $\left( r_{h} / r_0, \Theta \right) =(9.5, \pi / 2)$. In this case, the size of a void surrounding the BH dictates the arbitrary length scale $r_h$. Conversely, at $\left( r_{h} / r_0, \Theta \right) =(0.45, \pi / 2)$ in Fig. 5, we got the ZP2 zero point with a lower pressure value at the critical pressure $P_c$ and fixed $\tau / r_0=200$. In the same way, Fig. 6 displays the unit vector representations with the zero point along with winding numbers $-\,1$ and $+\,1$, respectively. The prescription outlined in the previous section is used to determine the winding number or topological charge associated with the critical sites, which are $Z P_3, Z P_4$ in Fig. 6. The result is $w=+\,1$. These are shown in Fig. 6. The corresponding unit vectors are

$$\begin{aligned} n^1=\frac{C+\frac{\Delta -2}{\Delta -1}-\frac{3 \pi ^{\frac{\Delta }{2}+1} (\Delta +2) {r_h}^{\Delta +1}}{\tau }}{3 \sqrt{\frac{1}{9} \left( C+\frac{\Delta -2}{\Delta -1}- \frac{3 \pi ^{\frac{\Delta }{2}+1} (\Delta +2) {r_h}^{\Delta +1}}{\tau }\right) ^2+\cot ^2(\theta ) \csc ^2(\theta )}},\nonumber \\ \end{aligned}$$

(30)

and

$$\begin{aligned} n^2=-\frac{\cot (\theta ) \csc (\theta )}{\sqrt{\frac{1}{9} \left( C+\frac{\Delta -2}{\Delta -1}- \frac{3 \pi ^{\frac{\Delta }{2}+1} (\Delta +2) {r_h}^{\Delta +1}}{\tau }\right) ^2+\cot ^2(\theta ) \csc ^2(\theta )}}.\nonumber \\ \end{aligned}$$

(31)

One can the obtain the analytic expression for $\tau$ by setting $\phi ^{r_h}=0$ and corresponding to zero points follows as

$$\begin{aligned} \tau =\frac{3 \pi ^{\frac{\Delta }{2}+1} \left( \Delta ^2+\Delta -2\right) {r_h}^{\Delta +3}}{(\Delta -2) {r_h}^2-2 \Delta \left( d_{1}\kappa _{s} ^2-2 f_1 \kappa _{sh} ^2+q_{\epsilon }^2+q_{m}^2-4 \kappa _{d}^2 \epsilon _1 \right) }.\nonumber \\ \end{aligned}$$

(32)

Fig. 6

Plot of the unit vector field n in $r_h/r_0$ vs $\theta$ plane for BH in defects in canonical ensemble with $\tau =150$. The dot represents the critical point

Fig. 7

The zero points of $\phi ^{r_h}$ in $r_h$ vs $\tau$ plane for BH in defects in canonical ensemble for pressure less than the critical pressure $P_c$

For $q_{\epsilon }=1,~q_{m}=1,~d_1=0.5,~f_1=2.5,~\epsilon _1=0.4,~\kappa _s=1.2,~\kappa _d=0.5,~\kappa _{sh}=0.2$ and $P=0.1$, we plot $r_h=r_0$ vs $\tau =r_0$ depicted in Fig. 7. The plot illustrates two branches of the BH in the areas where $\tau < \tau _a$ represents the red line and $\tau > \tau _a$ shows the blue dashed line. Here, we observe the behavior in canonical and mixed ensembles. A stable BH region is demonstrated by the later branch, whereas the former branch shows an unstable BH zone. Any zero point in the stable along with unstable region has winding numbers $w = -\,1$ and $w = +\,1$ respectively.

5 BH in mixed ensemble

In this scenario, the electric potential $\phi _ e$ as well as magnetic charge $q_m$ persist constant. The electric potential is expressed as $\phi _{e}$

$$\begin{aligned} \phi _e=\frac{q_{\epsilon }}{r_h}. \end{aligned}$$

(33)

The mass and temperature become

$$\begin{aligned} m=\frac{3 d_{1}\kappa _{s} ^2-6 f_1 \kappa _{sh} ^2-8 \pi P {r_h}^4+3 q_{m}^2+3 {r_h}^2 {\phi _e}^2+3 {r_h}^2- 12 \kappa _{d}^2 \epsilon _1 }{6 {r_h}},\nonumber \\ \end{aligned}$$

(34)

Our intent is to study the link between the critical point and topological charge in more detail. We have determined that the maximum point of the spindle curve is represented by a critical point associated to negative topological charge. First law could be employed to indicate a first-order phase transition line in the $T-r_h$ plane that is close to that point. While for a critical point associated with positive topological class, it represents a minimum point of the spinodal curve. The authors infer that a first-order phase transition can emerge from a traditional critical point linked with a topological charge of $-\,1$, whereas the presence of a new critical point associated with a topological charge of $+\,1$ may not necessarily show the proximity of a first-order phase transition. The modified temperature can be written as

$$\begin{aligned} T=\frac{\pi ^{-\frac{\Delta }{2}-1} {r_h}^{-\Delta -3} \left( D-8 \pi P {r_h}^4-q_{m}^2+{r_h}^2 \left( {\phi _e}^2+1\right) \right) }{2 (\Delta +2)}.\nonumber \\ \end{aligned}$$

(35)

Thermodynamics function as

$$\begin{aligned} \phi= & \frac{T}{\sin (\theta )}\nonumber \\= & -\frac{\pi ^{-\frac{\Delta }{2}-1} \csc (\theta ) {r_h}^{-\Delta -3} \left( 8 \pi P {r_h}^4+q_{m}^2-{r_h}^2 \left( {\phi _e}^2+1\right) -D \right) }{2 (\Delta +2)}.\nonumber \\ \end{aligned}$$

(36)

The vector fields $\phi =\left( \phi ^{r_h}, \phi ^\theta \right)$ have the following vector components are

$$\begin{aligned} \phi ^{r_h}=\frac{\pi ^{-\frac{\Delta }{2}-1} \csc (\theta ) {r_h}^{-\Delta -4} \left( -(\Delta +3)D+8 \pi (\Delta -1) P {r_h}^4+(\Delta +3) q_{m}^2-(\Delta +1) {r_h}^2 \left( {\phi _e}^2+1\right) \right) }{2 (\Delta +2)}. \end{aligned}$$

(37)

Here D is defined in the Appendix section and $\phi ^{\theta }$ as

$$\begin{aligned} \phi ^{\theta }=\frac{\pi ^{-\frac{\Delta }{2}-1} \cot (\theta ) \csc (\theta ) {r_h}^{-\Delta -3} \left( 8 \pi P {r_h}^4+q_{m}^2-{r_h}^2 \left( {\phi _e}^2+1\right) -D \right) }{2 (\Delta +2)}. \end{aligned}$$

(38)

Fig. 8

Normalized vector field n in $r_h/r_0$ against $\theta$ for BH in mixed ensemble. The dot shows the critical point

Fig. 9

Isobaric curves of BH in mixed ensemble. For $P= P_c$, the red curve represents the isobaric curve. The dot exhibits the critical point

The pressure value is determined under the critical pressure $P_c$. Maintaining the same combination of pressure and charge that corresponds to $r_h /r_0$, we can find a zero point $ZP_1$ placed at $\left( r_{h} / r_0, \Theta \right) =(1.8, \pi / 2)$ in Fig. 8 for fixed values of $q_{\epsilon }=1,~q_{m}=1,~d_1=0.5,~\Delta =0.9,~f_1=0.5,~\epsilon _1=0.4,~\kappa _s=1.2,~\kappa _d=0.5,~P=0.005,~\kappa _{sh}=0.02$ and $\phi =0.03$ respectively. We depict the isobaric curves surrounding the critical point in Fig. 9 to determine its nature. A dot indicates where the phase structure’s critical point occurs. The red curve represents the isobaric curve for $P = P_c$. The red curves are the location of the alternative trajectories for $P > P_c$ and $P < P_c$, respectively, which are located above and below them. The big and small BH phases are identified for $P < P_c$ by the regions (unstable and stable) that are the slope sections of the phase structure by two extremal points that correspond to each isobaric curve, as can be seen in Fig. 9. The components of the normalized vector $\phi$ are

$$\begin{aligned} \frac{\phi ^{r_h}}{\Vert \phi \Vert }= \frac{\pi ^{-\frac{\Delta }{2}-1} \csc (\theta ) {r_h}^{-\Delta -4} E}{ \sqrt{{\pi ^{-\Delta -2} \csc ^2(\theta ) {r_h}^{-2 (\Delta +4)} \left( E^2+{r_h}^2 \cot ^2(\theta ) \left( +8 \pi P {r_h}^4+q_{m}^2-{r_h}^2 \left( {\phi _e}^2+1\right) -D\right) ^2\right) }}}, \end{aligned}$$

(39)

Here E is defined in Appendix, and

$$\begin{aligned} \frac{\phi ^\theta }{\Vert \phi \Vert }=\frac{\pi ^{-\frac{\Delta }{2}-1} \cot (\theta ) \csc (\theta ) {r_h}^{-\Delta -3} \left( +8 \pi P {r_h}^4+q_{m}^2-{r_h}^2 \left( {\phi _e}^2+1\right) -D \right) }{ \sqrt{{\pi ^{-\Delta -2} \csc ^2(\theta ) {r_h}^{-2 (\Delta +4)} \left( E^2+{r_h}^2 \cot ^2(\theta ) \left( 8 \pi P {r_h}^4+q_{m}^2-{r_h}^2 \left( {\phi _e}^2+1\right) -D \right) ^2\right) }}}. \end{aligned}$$

(40)

Corresponding critical points are

$$\begin{aligned} P_c= & -\frac{\left( {\phi _e}^2-1\right) ^2}{96 \pi \left( q_{m}^2-D \right) }, \quad r_c=\frac{\sqrt{6} \sqrt{D-q_{m}^2 }}{\sqrt{{\phi _e}^2-1}},\nonumber \\ T_c= & -\frac{\left( {\phi _e}^2-1\right) ^{3/2}}{3 \sqrt{6} \pi \sqrt{D-q_{m}^2 }}. \end{aligned}$$

(41)

A similar process as we discussed earlier, Fig. 10 shows the topological charge with $(a,~b,~r_0)= (~0.19,~0.06,~9.08)$ for $C_1$ and $(a,b,r_0)=(0.33,0.2,8.1)$ for $C_2$ respectively. $C_1$ and $C_2$ are depicted by the blue and red curves, respectively. It has been noticed that the topological charge for the critical point bounded by the contour $C_1$ is $Q_{C_1}=-1$ for fixed values of $q_{\epsilon }=1,~q_{m}=1,~d_1=0.5,~\Delta =0.2,~f_1=0.5,~\epsilon _1=0.4,~\kappa _s=1.2,~\kappa _d=0.5,~\tau =150$ and $\kappa _{sh}=0.02$ respectively. Zero topological charge is connected to contour ${C}_2$ because it doesn’t have any critical point. Consequently, $Q=-1$ represents the overall topological charge. Moreover, the function $\Omega (\theta )$ for $C_1$ falls non-linearly until it reaches a value $-2 \pi$ at $\vartheta =2 \pi$. Besides that, $\Omega (\vartheta )$ for $C_2$ turns into zero at $\vartheta =2 \pi$.

Fig. 10

Plot of the $\Omega$ against $\vartheta$ plot for the contour C

6 BH solution as topological thermodynamic flaws in mixed ensemble

In this section, we now explore the BH in metric affine gravity with mixed ensemble. Usually, we begin by referring to the generalized free energy potential as

$$\begin{aligned} F=m-q_{\epsilon } {\phi _e}-\frac{S}{\tau }. \end{aligned}$$

(42)

In this case, modified mass can be calculated as

$$\begin{aligned} m=\frac{3 d_{1}\kappa _{s} ^2-6 f_1 \kappa _{sh} ^2-8 \pi P {r_h}^4+3 q_{m}^2+3 {r_h}^2 {\phi _e}^2+ 3 {r_h}^2-12 \kappa _{d}^2 \epsilon _1 }{6 {r_h}}.\nonumber \\ \end{aligned}$$

(43)

From (8), generalized free energy potential can be obtained as

$$\begin{aligned} F= & \frac{ d_{1}\kappa _{s} ^2-2 f_1 \kappa _{sh} ^2-2 q {r_h} {\phi _e}+q_{m}^2+{r_h}^2 \left( {\phi _e}^2+ 1\right) -4 \kappa _{d}^2 \epsilon _1 }{2 {r_h}}\nonumber \\ & -\frac{4}{3} \pi P {r_h}^3-\frac{\pi ^{\frac{\Delta }{2}+1} \left( {r_h}^2\right) ^{\frac{\Delta }{2}+1}}{\tau }. \end{aligned}$$

(44)

This can be written the form of potential as

$$\begin{aligned} \phi ^{{r_h}}= & \frac{- d_{1}\kappa _{s} ^2+2 f_1 \kappa _{sh} ^2-q_{m}^2+{r_h}^2 \left( {\phi _e}^2+1\right) + 4 \kappa _{d}^2 \epsilon _1 }{2 {r_h}^2}\nonumber \\ & -4 \pi P {r_h}^2-\frac{\pi ^{\frac{\Delta }{2}+1} (\Delta +2) \left( {r_h}\right) ^{\Delta +1}}{\tau }, \end{aligned}$$

(45)

and

$$\begin{aligned} \phi ^{\theta }=-\cot (\theta ) \csc (\theta ). \end{aligned}$$

(46)

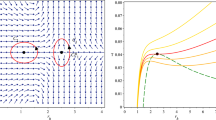
We take $q_{\epsilon }=1,~q_{m}=1,~d_1=0.5,~\Delta =0.8,~f_1=0.5,~\epsilon _1=0.4,~\kappa _s=1.2,~\kappa _d=0.5,~\tau =25,~P=0.05$ and $\kappa _{sh}=0.2$ with $r_h$ an arbitrary positive constant, so the only zero point in $\theta - r_h$ plane at $(r_h/r_0, \theta ) = (0.83, \pi /2)$. From Fig. 11, the boundary of a particular area is determined by the loop that surrounds the zero point, which also generates the winding number of point P. This is due to the presence of a single defect, and a result in a global topological number is $w = -1$ for the BH solution in metric affine gravity. In Fig. 12, taking $\tau =25$, the two intersection points can be seen in $\theta - r_h$ plane at $(r_h/r_0, \theta ) = (-2, \pi /2)$ and $(r_h/r_0, \theta ) = (0.95, \pi /2)$ respectively. In general, with greater $\tau$, more than one critical points are coincide. These critical points are the part of the annihilation points simply can be check. The winding numbers of the two zero points are $w_1 = -1$ and also $w_2 = 1$ respectively. Therefore, $w = w_1 + w_2 = 0$ represents the global topological number for BH. The corresponding unit vectors are

$$\begin{aligned} n^{1}=\frac{(D-q_{m}^2+{r_h}^2 \left( {\phi _e}^2+1\right) )/2 {r_h}^2-4 \pi P {r_h}^2- (\pi ^{\frac{\Delta }{2}+1} (\Delta +2) \left( {r_h}\right) ^{\Delta +1})/\tau }{\left( \left( (q_{m}^2-{r_h}^2 \left( {\phi _e}^2+1\right) -D)/{2 {r_h}^2}+4 \pi P {r_h}^2+(\pi ^{\frac{\Delta }{2}+1} (\Delta +2) \left( {r_h}\right) ^{\Delta +1})/\tau \right) ^2+\cot ^2(\theta ) \csc ^2(\theta )\right) ^{\frac{1}{2}}}, \end{aligned}$$

(47)

and

$$\begin{aligned} n^{2}=-\frac{\cot (\theta ) \csc (\theta )}{\left( \left( (q_{m}^2-{r_h}^2 \left( {\phi _e}^2+1\right) -D)/{2 {r_h}^2}+4 \pi P {r_h}^2+(\pi ^{\frac{\Delta }{2}+1} (\Delta +2) \left( {r_h}\right) ^{\Delta +1})/\tau \right) ^2+\cot ^2(\theta ) \csc ^2(\theta )\right) ^{\frac{1}{2}}}. \end{aligned}$$

(48)

One can obtain the analytic expression for $\tau$ by setting $\phi ^{r_h}=0$ follows as

$$\begin{aligned} \tau =-\frac{2 \pi ^{\frac{\Delta }{2}+1} (\Delta +2) \left( {r_h}\right) ^{\Delta +3}}{ d_{1} \kappa _{s} ^2-2 f_1 \kappa _{sh} ^2+8 \pi P {r_h}^4+q_{m}^2-{r_h}^2 \left( \phi e^2+1\right) -4 \kappa _{d}^2 \epsilon _1 }.\nonumber \\ \end{aligned}$$

(49)

Fig. 11

Plot of the unit vector field n in $r_h/r_0$ vs $\theta$ plane for BH in canonical ensemble with $\tau =25$. The dot represents the critical point

Fig. 12

Plot of unit vector field n in $r_h/r_0$ vs $\theta$ plane for BH in canonical ensemble with $\tau =30$. The dot represents the critical point

A graph shows the relationship between $r_h$ and $\tau$ for specific parameters in metric affine gravity is presented in Fig. 13. It is evident there exist no solution for $\tau > \tau _c$ and this tend to be two distinct regions of BH such as small and large respectively. In addition, these findings are also resemblance of spherically symmetric BH in Einstein–Gauss–Bonnet theory.  From Eq. (49), we investigate the BH stability associated to the states. Hence, a BH has large radius is easily demonstrated to be stable (positive free energy), while a BH with small radius becomes unstable (negative free energy).

The parameterized form is given in Eq. (10). We calculated these curves as $(a,b,r_0)= (0.11,0.14,1.45)$ for $C_1$ and $(a,b,r_0)=(0.92,0.29,2.95)$ for $C_2$ respectively. The results are given in Fig. 14 with fixed parameters $q_{\epsilon }=1,~q_{m}=1,~d_1=0.5,~\Delta =0.8,~f_1=0.5,~\epsilon _1=0.4,~\kappa _s=0.2,~\kappa _d=0.5,~\tau =25,~P=0.05$ and $\kappa _{sh}=0.02$ respectively. It is quite easy to notice that the topological charge for complete closed curves is $Q=0$ for $C_2$ and $Q=-1$ for $C_1$.

7 BH in GCE

In the GCE, both the magnetic potential $\phi _m$ and electric potential $\phi _e$ are held fixed $\phi _e=\frac{q_{\epsilon }}{r_h}$ and $\phi _m=\frac{q_m}{r_h}$ respectively. The mass function can be expressed as

$$\begin{aligned} m=\frac{3 \left( d_{1}\kappa _{s} ^2-2 f_1 \kappa _{sh} ^2-4 \kappa _{d}^2 \epsilon _1 \right) -8 \pi P {r_h}^4+3 {r_h}^2 \left( {\phi _e}^2+{\phi _m}^2+1\right) }{6 {r_h}}.\nonumber \\ \end{aligned}$$

(50)

And modified temperature takes the following form

$$\begin{aligned} T=\frac{\pi ^{-\frac{\Delta }{2}-1} {r_h}^{-\Delta -3} \left( D-8 \pi P {r_h}^4+{r_h}^2 \left( {\phi _e}^2+{\phi _m}^2\!+\!1\right) \right) }{2 (\Delta +2)}\nonumber \\ \end{aligned}$$

(51)

Now, we further move to study the topology of BH thermodynamics in GCE. As a result, unique topological classes are employed to specify the critical points in the thermal analysis, and those classes offer the framework for both new and classical critical points. The thermodynamics function $\phi =\frac{1}{\sin \theta } T\left( S, x^i\right)$, therefore calculated as

$$\begin{aligned} \phi = \frac{\pi ^{-1-\frac{\Delta }{2}} \csc (\theta ) {r_h}^{-\Delta -3} \left( D-8 \pi P {r_h}^4+{r_h}^2 \left( {\phi _e}^2+{\phi _m}^2+1\right) \right) }{2 (\Delta +2)}.\nonumber \\ \end{aligned}$$

(52)

The vector fields $\phi =\left( \phi ^{r_h}, \phi ^\theta \right)$ contain the following vector components:

$$\begin{aligned} \phi ^{r_h}= \frac{\pi ^{-\frac{\Delta }{2}-1} \csc (\theta ) {r_h}^{-\Delta -4} \left( -(\Delta +3)D+8 \pi (\Delta -1) P {r_h}^4-(\Delta +1) {r_h}^2 \left( {\phi _e}^2+{\phi _m}^2+1\right) \right) }{2 (\Delta +2)}, \end{aligned}$$

(53)

and

$$\begin{aligned} \phi ^{\theta }=-\frac{\pi ^{-\frac{\Delta }{2}-1} \cot (\theta ) \csc (\theta ) {r_h}^{-\Delta -3} \left( D-8 \pi P {r_h}^4+{r_h}^2 \left( {\phi _e}^2+{\phi _m}^2+1\right) \right) }{2 (\Delta +2)}. \end{aligned}$$

(54)

Again we adopt the similar process, the unit vectors are drawn and examined the zero points by substituting $\Theta =\pi / 2$ in $n^1$ and comparing it to zero. For example, setting $q_e =1, q_m=1$ and $\tau / r_0=150$, we can find the one zero point $\left( Z P_1\right)$ in Fig. 15 is located at $\left( r_{h} / r_0, \Theta \right) =(-0.16, \pi / 2)$. Here, $r_h$ represents an arbitrary length scale and its value depends on the extent to which a cavity around the BH. In Fig. 16, we find out zero point $ZP_2$ at $\left( r_{h} / r_0, \Theta \right) =(0.16, \pi / 2)$ where the pressure configuration associated with $\tau / r_0=200$, we observed that, the pressure value is taken below the critical pressure $P_c$ it has a same charge. After normalization, the vector $\phi$ has the following components are

$$\begin{aligned} \frac{\phi ^{r_h}}{\Vert \phi \Vert }= \frac{\pi ^{-\frac{\Delta }{2}-1} (\theta ) {r_h}^{-\Delta -4} Y}{\bigg [{\pi ^{-\Delta -2}(\theta ) {r_h}^{-2 (\Delta +4)} \left( Y^2+{r_h}^2 \cot ^2(\theta ) \left( D-8 \pi P {r_h}^4+{r_h}^2 \left( {\phi _e}^2+{\phi _m}^2+1\right) \right) ^2\right) }\bigg ]^{\frac{1}{2}}}, \end{aligned}$$

(55)

and

$$\begin{aligned} \frac{\phi ^\theta }{\Vert \phi \Vert }=\frac{\pi ^{-\frac{\Delta }{2}-1} \cot (\theta ) \csc (\theta ) {r_h}^{-\Delta -3} \left( 8\pi P {r_h}^4-{r_h}^2 \left( {\phi _e}^2+{\phi _m}^2+1\right) -D \right) }{\bigg [{\pi ^{-\Delta -2} \csc ^2(\theta ) {r_h}^{-2 (\Delta +4)} \left( F^2+{r_h}^2 \cot ^2(\theta )\left( D-8 \pi P {r_h}^4+{r_h}^2\left( {\phi _e}^2+{\phi _m}^2+1\right) \right) ^2\right) }\bigg ]^{\frac{1}{2}}}. \end{aligned}$$

(56)

Here Y is defined in Appendix. The illustration of the unit vectors along with the zero points is exhibited in Fig. 17. The critical points $Z P_3$ and $Z P_4$ are located in Fig. 17, the topological charge associating to these zero points are derived from the following instruction, which is discussed in the prior section.

8 Topological thermodynamic defects as BH solutions in GCE

In order to determine the BH as a topological defect in thermodynamics, we may utilize the generic free energy potential in the following manner

$$\begin{aligned} F=m-q_{\epsilon } {\phi _{e}}- S (\tau )^{-1}-q_m{\phi _{m}} \end{aligned}$$

(57)

From (8), the vector components can be expressed as

$$\begin{aligned} \phi ^{r_h}= & \frac{ D-r_h^2 \left( {\phi _e}^2+{\phi _m}^2-1\right) }{2 r_h^2}-4 \pi P r_h^2\nonumber \\ & -\frac{\pi ^{\frac{\Delta }{2}+1} (\Delta +2) \left( r_h\right) ^{\Delta +1}}{\tau } \end{aligned}$$

(58)

and

$$\begin{aligned} \phi ^{\theta }=-\cot (\theta ) \csc (\theta ) \end{aligned}$$

(59)

In this case, only one charge is permitted, which is a standard one. When the BH is over charged, the associated horizon connected to this charge is disappear. However, for critical points, one can anticipate the existence of a pair formation or annihilation because of the invariant total topological charge. In Fig. 18, we show that, the two branches of critical points connected to their slopes, such as $C_1$ and $C_2$, with fixed parameters $q_{\epsilon }=1,~q_{m}=1,~d_1=0.5,~\Delta =0.8,~f_1=0.5,~\epsilon _1=0.4,~\kappa _s=0.2,~\kappa _d=0.5,~\tau =25,~P=0.05$ and $\kappa _{sh}=0.02$ respectively. One can see that the slops are emerge at $\tau \approx 15.70$. Thus, spacetime encounters a topological transition from a BH to a naked singularity. One can obtained the corresponding unit vectors are

$$\begin{aligned} n^{1}=\frac{-({r_h}^2 \left( {\phi _e}^2+{\phi _m}^2-1\right) -D)/{2 {r_h}^2}-4 \pi P {r_h}^2-(\pi ^{\frac{\Delta }{2}+1} (\Delta +2) \left( {r_h}\right) ^{\Delta +1})/{\tau }}{\bigg [\left( ({r_h}^2 \left( {\phi _e}^2+{\phi _m}^2-1\right) -D)/{2 {r_h}^2}+4 \pi P {r_h}^2+(\pi ^{\frac{\Delta }{2}+1} (\Delta +2) \left( {r_h}\right) ^{\Delta +1})/{\tau }\right) ^2+\cot ^2(\theta ) \csc ^2(\theta )\bigg ]^{\frac{1}{2}}}, \end{aligned}$$

(60)

and

$$\begin{aligned} n^{2}=-\frac{\cot (\theta ) \csc (\theta )}{\bigg [\left( ({r_h}^2 \left( {\phi _e}^2+{\phi _m}^2-1\right) -D)/{2 {r_h}^2}+4 \pi P {r_h}^2+(\pi ^{\frac{\Delta }{2}+1} (\Delta +2) \left( {r_h}\right) ^{\Delta +1})/{\tau }\right) ^2+\cot ^2(\theta ) \csc ^2(\theta )\bigg ]^{\frac{1}{2}}}. \end{aligned}$$

(61)

Fig. 13

The zero points of $\phi ^{r_h}$ in $\tau =r_0$ vs $r_h=r_0$ plane for BH in canonical ensemble for pressure less than the critical pressure $P_c$

Fig. 14

Plot of the $\Omega$ against $\vartheta$ plot for the contour C

Fig. 15

Plot of the normalized vector field n in $r_h/r_0$ vs $\theta$ plane for BH in GCE. The dot represents the critical point

Fig. 16

Plot unit vector field n in $r_h/r_0$ vs $\theta$ plane for BH in GCE with $\tau =150$. The dot represents the critical point

Fig. 17

Plot of unit vector field n in $r_h/r_0$ vs $\theta$ plane for BH in GCE with $\tau =200$. The dot exhibits the critical point

Fig. 18

The zero points of $\phi ^{r_h}$ in $\tau$ vs $r_h$ plane for BH in GCE for P less than $P_c$

Fig. 19

The zero points of $\phi ^{r_h}$ in $\tau$ vs $r_0$ plane for BH in GCE for P less than $P_c$

Fig. 20

Plot of the $\Omega$ against $\vartheta$ plot for the contour C

It is important to discuss a relation $r_h - \tau$, we deduced this relation of the BH at event horizon in Eq. (62). Here, we will show the distinct winding numbers with numerous values of P with fixed parameters $q_{\epsilon }=1,~q_{m}=1,~d_1=0.5,~\Delta =0.8,~f_1=0.5,~\epsilon _1=0.4,~\kappa _s=0.2,~\kappa _d=0.5, \tau =25$ and $\kappa _{sh}=0.02$ respectively, we exhibit the on-shell solution curve on $r_h - \tau$ plane as shown in Fig. 19. By setting $\phi ^{r_h}=0$, one may formulate an analytical equation for $\tau$ linking to zero point as

$$\begin{aligned} \tau =\frac{2 \pi ^{\frac{\Delta }{2}+1} (\Delta +2) \left( {r_h}\right) ^{\Delta +3}}{D-8 \pi P {r_h}^4- {r_h}^2 \left( {\phi _e}^2+{\phi _m}^2-1\right) }. \end{aligned}$$

(62)

Finally, we extract the relation of $\Omega$ with respect to $\vartheta$. This outcome is plotted in Fig. 20. It is quite easy to notice from the figure that $Q=-1$ for $C_1$ and $Q=1$ for $C_2$ respectively. Hence, we verify that the naked singularity possesses a charge of $Q=0$, consistent with predictions. In this view, the same process was discussed to revolving the boson star without event horizon through contrasting it in Ref. [56]. Consequently, they are part of the identical topological class.

9 Conclusion

In this paper, we have deduced a BH in metric-affine gravity and examined the topology thermodynamics in the existence of Barrow entropy, and discussed the three various ensembles: canonical, mixed and GC ensembles by using the theory of Duan’s topological current $\phi$- mapping. In detail, we have thoroughly investigated the topological charges and obtained the analytically expressions for thermodynamical quantities like Hawking temperature, pressure and free energy connected to BH in metric-affine gravity to provides the stability of a system. We considered the BH in metric affine gravity as topological defects, and examined the local and global stability through thermodynamic topological analysis. According to our computations, the total topological class in both canonical and mixed ensembles was $-\,1$, and 0, these values remained constant as per modification of the others thermodynamic parameters.

The total topological charge (class) in the GCE has been determined to be either equal to 0 (when $\phi _e^2 + \phi _m^2 < 1$) or 1 (when $\phi _e^2 + \phi _m^2 > 1$) with fixed values of the electric as well as magnetic potentials respectively. Also, we have acquired the there exist an annihilation point (when $\phi _e^2 + \phi _m^2> 1$) or a single generation point (when $\phi _e^2 + \phi _m^2 < 1$) in this analysis. We have studied an other important technique for explore the BH thermodynamics’ topological features. In this process, the $\Omega$ curve is an effective method to acquire topological information regarding thermodynamic systems. We observed that the function $\phi$ which is connected to the topological charge for every zero point, i.e., critical points and add up the whole contributions (parts), this provides a overall topological class for the thermodynamic system. So, this outcome is examined in Fig. 20. It is quite easy to deduce from the figure where $Q=-1$ for $C_1$ and $Q=1$ for $C_2$ respectively. Thus, we verified that $Q = 0$ corresponds to the naked singularity. In addition, we compared these results with recently published article in Ref. [56].

It is an interesting and exciting phenomenon to study the topological charge of the BH solutions in the modified theory of gravities, and also investigate the relation between the horizon topology and topological charges. There are numerous issues that meet the criteria for further research. The examination of the BH in the framework of metric affine gravity aligns with existing findings in the literature, and this study offers valuable insights for future research endeavors.

Appendix

Some calculations are defined here

$$\begin{aligned} A= & 2\Delta D-6 d_{1}\kappa _{s} ^2+12 f_1 \kappa _{sh} ^2, \end{aligned}$$

(63)

$$\begin{aligned} B= & 2D-2 q_{\epsilon }^2-2 q_{m}^2+{r_h}^2, \end{aligned}$$

(64)

$$\begin{aligned} C= & -\frac{2 \Delta \left( q_{\epsilon }^2+q_{m}^2-D \right) }{(\Delta -1) {r_h}^2},\end{aligned}$$

(65)

$$\begin{aligned} E= & -(\Delta +3)D+8 \pi (\Delta -1) P {r_h}^4\nonumber \\ & +(\Delta +3) q_{m}^2-(\Delta +1) {r_h}^2{\phi _e}^2+1, \end{aligned}$$

(66)

$$\begin{aligned} Y= & -(\Delta +3) D+8 \pi (\Delta -1) P {r_h}^4\nonumber \\ & -(\Delta +1) {r_h}^2 \left( {\phi _e}^2+{\phi _m}^2+1\right) , \end{aligned}$$

(67)

where $D=-d_{1}\kappa _{s} ^2+2 f_1 \kappa _{sh} ^2+4 \kappa _{d}^2 \epsilon _1$.