1 Introduction

Since the discovery of an accelerated expansion phase of our Universe at the late epoch [1, 2], two approaches are proposed to explain this mysterious phenomenon, please see Refs. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] for comprehensive reviews but not for a complete list. Among these two approaches, one is the dark energy as new energy component with negative pressure, the other is modified gravity theory at large scales. Both of them can provide almost the same background evolution of our Universe [18,19,20], but the formation of the large scale structure might be different. Therefore it is deserved to discriminate the dark energy from the modified gravity at the background and perturbation levels. One more interesting question is how one can propose the possible form of modified gravity which can mimic not only the background evolution but also the large scale structure formation of our Universe. Usually, the gravity action is determined by considering some Noether symmetries and to be ghost-free, then the proposed form is confronted by cosmic observations. As results, the proposed gravity action will be excluded or not. On the contrary, one can reverse the above process and takes the observational data points as a starting point. This is the topic of model-independent reconstruction of modified gravity.

In the literatures, many forms of modified gravity are proposed [10,11,12,13,14,15,16,17, 21], but we will mainly focus on the f(T) and f(R) gravity as workhorses to present a viable methodology to reconstruct the modified gravity at the background and perturbation levels in this work. For the f(T) gravity, see Refs. [21, 22] for reviews, and model-independent f(T) forms were reconstructed via Gaussian process from the observed Hubble data points [23,24,25] at the background level. Here, we would like warning the reader that the f(T) gravity suffers the superluminal propagation and Cauchy problems as pointed out in Refs. [26, 27]. This is mainly due to the strong coupling which could hide the degrees of freedom under physically relevant background [28, 29]. The strong coupling problems seem to be ubiquitous in the f(T) theory, but this does not preclude performing the linear perturbations without encountering any apparent inconsistencies [30]. For the f(R) gravity, see Refs. [10,11,12,13,14,15,16,17] for reviews, a reconstruction from the expansion history can be found in Refs. [31, 32] for examples. But the reconstruction of f(R) gravity in a model-independent way directly from cosmic observations is still not reported in the literatures.

This paper is structured as follows. In Sect. 2, we present the key equations that will be used to reconstruct the f(T) and f(R) gravity at the background and linear order perturbation levels respectively. In Sects. 3 and 4, the reconstructed results are presented for the f(T) and f(R) gravity respectively. Section 5 is the conclusion.

2 f(T) and f(R) gravity and methodology

For a spatially flat Friedmann–Lemaître–Robertson–Walker (FLRW) metric

$$\begin{aligned} ds^2=-c^2dt^2+a^2(t)\, \delta _{ij} dx^i dx^j, \end{aligned}$$
(1)

where c is the speed of light and a(t) is the scale factor. The Friedmann equations of f(T) cosmology are given by [21]

$$\begin{aligned} H^2= & \frac{8\pi G_{\textrm{N}}}{3}\rho _m - \frac{f}{6} + \frac{Tf_T}{3}, \end{aligned}$$
(2)
$$\begin{aligned} {\dot{H}}= & -\frac{4\pi G_{\textrm{N}}(\rho _m+P_m)}{1+f_{T}+2Tf_{TT}}, \end{aligned}$$
(3)

where \(H\equiv {\dot{a}}/a\) is the Hubble parameter and the dot denoting derivative with respect to the cosmic time t, \(\rho _m\) and \(P_m\) are respectively the energy density and pressure of the matter fluid. Additionally, in the above equations \(f_{T}\equiv \partial f/\partial T\), \(f_{TT}\equiv \partial ^{2} f/\partial T^{2}\), where the torsion scalar T can be written in the following form in FLRW geometry

$$\begin{aligned} T=6H^2. \end{aligned}$$
(4)

For the f(R) gravity, the Friedmann equations are written as [12]

$$\begin{aligned} 3FH^2= & (FR-f)/2-3H{\dot{F}}+8\pi G_{\textrm{N}}\rho _m, \end{aligned}$$
(5)
$$\begin{aligned} -2F{\dot{H}}= & {\ddot{F}}-H{\dot{F}}+8\pi G_{\textrm{N}}(\rho _m+P_m), \end{aligned}$$
(6)

where \(F\equiv \partial f/\partial R\) and R is the Ricci scalar

$$\begin{aligned} R=6(2H^2+{\dot{H}}), \end{aligned}$$
(7)

which can also be rewritten in terms of the decelerated parameter \(q(z)=-1+(1+z)H'/H\) as

$$\begin{aligned} R=6H^2\left[ 1-q(z)\right] , \end{aligned}$$
(8)

here the prime denotes the derivative with respect to the redshift \(z=1/a-1\).

We will mainly use the Eqs. (2) and (5) to reconstruct the form of f(T) and f(R) with the addition of the growth rate equation for a modified gravity

$$\begin{aligned} (1+z)f'_{\delta }-f^2_{\delta }+\left[ (1+z)\frac{H'}{H}-2\right] f_{\delta }+\frac{3\mu }{2}\varOmega _m(z)=0, \end{aligned}$$
(9)

where \(\varOmega _{m}(z)=H^2_0\varOmega _{m}(1+z)^{3}/H^2\) is the dimensionless dark matter energy density, and the general function \(\mu \)

$$\begin{aligned} \mu =\frac{G_{\textrm{eff}}}{G_{\textrm{N}}}, \end{aligned}$$
(10)

effectively corresponds to a modification to the Newtonian constant \(G_{\textrm{N}}\) and characterizes MG theory at the linear matter density perturbation level. In GR, \(\mu \equiv 1\) is respected.

For the f(T) gravity, \(\mu \) is written as [33]

$$\begin{aligned} \mu =\frac{1}{1+f_{T}}. \end{aligned}$$
(11)

For the f(R) gravity, \(\mu \) is given by [12]

$$\begin{aligned} \mu =\frac{1}{F}\frac{4+3M^2a^2/k^2}{3(1+M^2a^2/k^2)}, \end{aligned}$$
(12)

where \(M^2=R(1/m-1)/3\) and \(m=Rf_{,RR}/f_{,R}\). Here \(F\equiv f_{,R}>0\) and \(f_{,RR}>0\) are required to avoid the appearance of ghosts and a tachyonic instability respectively [12].

Thus once one has the growth rate \(f_{\delta }(z)\), which can be reconstructed from the redshift space distortion (RSD) measurements \(f\sigma _8(z)\) [34,35,36], one obtains \(\mu \) via

$$\begin{aligned} \mu =\frac{2}{3\varOmega _m(z)} \left\{ -(1+z)f'_{\delta }+f^2_{\delta } +\left[ 2 - (1+z) \frac{H'}{H} \right] f_{\delta } \right\} , \end{aligned}$$
(13)

and consequently the function \(f_T\) and \(F\equiv f_R\) at the linear matter density perturbation level. Here we have to emphasize that the \(\mu \) varies only with respect to the redshift z in this work, it is mainly due to the scale-dependence is outside the range probed by large scale structure surveys within the linear perturbation theory.

It would be convenient to summarize the key equations that will be used for reconstruction as follows. For f(T) gravity at the linear perturbation level, from Eq. (2), one has

$$\begin{aligned} f(T)=6H^2\left[ \varOmega _{m}(z) -3+\frac{2}{\mu (z)} \right] , \end{aligned}$$
(14)

where the relation \(f_T=1/\mu -1\) and the definition of torsion \(T=6H^2\) are used. And at the background level, one also has another form by relating the values of f at \(z_{i+1}\) and \(z_{i}\) via Eq. (2) [23,24,25]

$$\begin{aligned} & f(z_{i+1}) - f(z_{i}) \nonumber \\ & \quad = 3(z_{i+1} - z_{i})H^{2}(z_{i})\frac{T^{\prime } (z_{i})}{T(z_{i})} \Bigg [1 - \varOmega _{m}(z_{i}) + \frac{f(z_{i})}{6H^{2}(z_{i})} \Bigg ], \nonumber \\ & \quad = 6 (z_{i+1} - z_{i}) H^2(z_{i})\frac{H^{\prime } (z_{i})}{H(z_{i})}\Bigg [ 1 - \varOmega _{m}(z_{i}) + \frac{f(z_{i})}{6H^{2}(z_{i})} \Bigg ],\nonumber \\ \end{aligned}$$
(15)

where \(f|_{z=0}=-6H^2_0(1-\varOmega _{m0})\) as initial condition will be adopted, the subscript ‘0’ indicates the present value of the corresponding quantity. This is equivalently to take \(\mu =1\) at present, i.e. the GR case. For f(R) gravity, from Eq. (5), one has

$$\begin{aligned} f(R)=6H^2\left[ \varOmega _{m}(z)-\frac{q(z)}{\mu (z)}-(1+z)\frac{\mu '(z)}{\mu ^2(z)} \right] , \end{aligned}$$
(16)

where the relation \(F\equiv f_R=1/\mu \) is used after omitting the scale k dependence. Here we should mention that f(R) cannot be reconstructed only at the background level via Eq. (5) because of the existence of an extra degree of freedom \({\dot{F}}=(1+z)H\mu '/\mu ^2\). For dealing with this situation, the growth rate function Eq. (9) is required as an extra equation to give \({\dot{F}}\).

Starting from the definition of the growth rate

$$\begin{aligned} f_{\delta }\equiv \frac{d\ln \delta }{d\ln a} =-(1+z)\,\frac{\delta ^\prime }{\delta }, \end{aligned}$$
(17)

where \(\delta (z)\equiv \delta \rho _m/\rho _m\) is the linear matter density contrast. One has the first order derivative of \(f_{\delta }(z)\) with respect to the redshift z

$$\begin{aligned} f'_{\delta }=-\frac{\delta ^\prime (z)/\delta _0}{\delta (z)/\delta _0}-(1+z)\left[ \frac{\delta ''(z)/\delta _0}{\delta (z)/\delta _0} - \frac{(\delta '(z)/\delta _0)^2}{(\delta (z)/\delta _0)^2}\right] , \end{aligned}$$
(18)

where

$$\begin{aligned} \frac{\delta ^\prime (z)}{\delta _0}= & -\frac{1}{\sigma _{8,\,0}}\frac{f\sigma _8(z)}{1+z}\,, \end{aligned}$$
(19)
$$\begin{aligned} \frac{\delta (z)}{\delta _0}= & 1-\frac{1}{\sigma _{8,\,0}} \int _0^z \frac{f\sigma _8({\tilde{z}})}{1+{\tilde{z}}}\,d{\tilde{z}}, \end{aligned}$$
(20)
$$\begin{aligned} \frac{\delta ''(z)}{\delta _0}\equiv & \left[ \frac{\delta ^\prime (z)}{\delta _0}\right] '= \frac{1}{\sigma _{8,\,0}}\frac{f\sigma _8(z)}{(1+z)^2}- \frac{1}{\sigma _{8,\,0}}\frac{[f\sigma _8(z)]'}{1+z}. \end{aligned}$$
(21)

and \(\sigma _8(z)=\sigma _8(z=0)\delta (z)/\delta (z=0)=\sigma _{8,0}\delta (z)/\delta _0\) for the perturbation within spheres of radius \(8h^{-1}\)Mpc. Therefore, one can reconstruct the relevant functions \(f_{\delta }\), \(f'_{\delta }\) and \(f''_{\delta }\) by using the observed \(f\sigma _{8,{\textrm{obs}}}\) data via Gaussian processes. For the 63 \(f\sigma _{8,\,obs}\) data points, please see Table A1 in Ref. [37] and references therein for example. The Planck 2018 results \(\sigma _{8,0}=0.8111\pm 0.0060\) [38, 39] is adopted in this work.

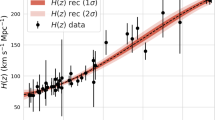
In order to reconstruct the Hubble parameter H(z) and \(H'(z)\) we use the the distance moduli from Pantheon+ SNe Ia samples [40, 41] and the observational Hubble data points from the cosmic chronometers (CC) and from clustering measurements (BAO), see Tables A2 and A3 in Ref. [37] and references therein for examples.

For the data-driven and model-independent reconstruction, we resort to Gaussian process [42, 43], which was used extensively in cosmology study in the last few years [43,44,45,46,47,48,49,50,51,52,53,54,55,56]. The Gaussian process can reconstruct the function f(x) from data points \(f(x_i)\pm \sigma _i\) via a point-to-point Gaussian distribution [42, 43], without assuming a specific parameterized form. Finally, the modified factor \(\mu \) can be obtained in a completely data-driven and model-independent way. For the technical details, please see Refs. [36, 56].

3 Reconstructing f(T)

In this section, we will present the reconstructed f(T) at the background and linear perturbation levels based on the Eqs. (15) and (14) respectively. After implementing Gaussian process, the reconstructed evolutions of H(z), \(H'(z)\) and \(\varOmega _{m}(z)\equiv 8\pi G_{\textrm{N}}\rho _m/3H^2=\varOmega _{m0}(1+z)^3/E^2(z)\) versus to the redshift z are plotted in Fig. 1, where \(E\equiv H/H_0\) is the dimensionless Hubble parameter and the corresponding quantities for the spatially flat \(\varLambda \)CDM cosmology are plotted as black dashed lines for comparison. The \(\varLambda \)CDM cosmology is taken as \(H^2(z)=H^2_0[\varOmega _{m0}(1+z)^3+\varOmega _{\varLambda 0}]\) with \(\varOmega _{m0}=0.334\) (\(\varOmega _{\varLambda 0}=1-\varOmega _{m0}\)) from SH0ES [57] for consistence. From the \(\varOmega _{m}(z)\) panel of Fig. 1, one can find a crossover of \(\varOmega _{m}=1\) line at high redshifts \(z>2.0\). In theory this excess would be unreasonable, but at the data points side it just means lower derived H(z) values at \(z>2.0\) as comparison to the \(\varLambda \)CDM cosmology predictions. It may also imply that a spatially flat \(\varLambda \)CDM cosmology deviates from cosmic observations at high redshifts in \(1\sigma \) region as shown also in the Hubble diagram of Fig. 1. Here we would like warning the reader that this deviation strongly depends on the derived Hubble parameter H(z) values which are suppressed at high redshifts comparing to \(\varLambda \)CDM cosmology predictions. Of course, there might be other reasons such as an unusual dark matter containing in our Universe (but we still assume a usual pressureless matter when one derive the \(\varOmega _{m}(z)\)), and a negative energy density of dark energy at high redshifts,  et al. . To confirm this high redshift deviation, more observed H(z) values at high redshifts are required.

Fig. 1
figure 1

The reconstructed evolutions of H(z), \(H'(z)\) and \(\varOmega _{m}(z)\) with respect to the redshift z in \(1\sigma \) shadow regions are plotted from the top to bottom. The black dashed lines denote the corresponding quantities predicted from the spatially flat \(\varLambda \)CDM cosmology: \(H^2(z)=H^2_0[\varOmega _{m0}(1+z)^3+\varOmega _{\varLambda 0}]\) with \(\varOmega _{m0}=0.334\) (\(\varOmega _{\varLambda 0}=1-\varOmega _{m0}\)) from SH0ES

Full size image

In Fig. 2, we show the reconstructed torsion T and f(T) versus to the redshift z, and f(T) versus to T with \(1\sigma \) regions from the top panel to the bottom panel respectively, where the red and blue ones correspond to reconstructed results from the background and linear perturbation levels respectively. As for comparison, the \(\varLambda \)CDM cosmology case is also plotted as thin green lines. It can seen that the reconstructed f(T) forms from the background and linear perturbation levels cannot match well in \(1\sigma \) regions. And significant evolutions for f(T) versus to the redshift z and the torsion T in the case of the linear perturbation levels. It might imply the possible tension between background and linear perturbation within \(1\sigma \) regions. Meanwhile, the reconstructed results would be lack of predictions due to sparse data points at high redshifts. Thus in this situation, the currently available observed data points are not good enough to provide a viable form of f(T). We will see that it is the same in the f(R) gravity case. Since the reconstructed curves of f(T) with respect to T has already obtained, one can try to fit the curves using a polynomial function of the form \(y(x,{\textbf {w}})=\sum ^{M}_{j=0}w_j x^j\). With the observation of the variations of the f(T) with respect to T at the background and linear order perturbation levels, one can choose the second order and third order fitting respectively for introducing the minimum free model parameters as possible. Thus at the background level, one obtains the fitting polynomial as \(f(T)\approx \xi ^{BG}_0 T_0+\xi ^{BG}_1 T_0 (T/T_0)+\xi ^{BG}_2 T_0 (T/T_0)^2\) with \(\xi ^{BG}_0=-0.63,\xi ^{BG}_1=-0.0056,\xi ^{BG}_2=-0.0089\). Similarly up to the third order in the linear order perturbation case, the fitting polynomial \(f(T)\approx \xi ^{PE}_0 T_0+\xi ^{PE}_1 T_0 (T/T_0)+\xi ^{PE}_2 T_0 (T/T_0)^2+\xi ^{PE}_3 T_0 (T/T_0)^3\) is chosen where \(\xi ^{PE}_0=-9.46,\xi ^{PE}_1=10.21,\xi ^{PE}_2=-2.45, \xi ^{PE}_3=0.16\) are obtained. The fitting polynomials are also shown in bottom panel of Fig. 2.

Fig. 2
figure 2

Top panel: The reconstructed torsion T and f(T) within \(1\sigma \) versus to the redshift z at the background and linear perturbation levels. Bottom panel: The reconstructed f(T) versus to the torsion T within \(1\sigma \) region at the background and linear perturbation levels. The thick grey and black lines are obtained from the polynomial fitting results

Full size image

4 Reconstructing f(R)

Repeating the similar process as done in the Sect. 3 but based on the Eq. (16), we show the reconstructed Ricci scalar R and f(R) versus the redshift z, and f(R) versus to the Ricci scalar R with \(1\sigma \) regions from the top panel to the bottom panel respectively, where the GR, Hu-Sawicki and Starobinsky f(R) gravity models with proper model parameters are also plotted for comparisons. From the top panel of Fig. 3, one can find that the reconstructed f(R) crosses the zero boundary from the positive values to the negative ones around \(z\sim 0.75\). This transition will change the signature of the gravity action and make it to be instability and existence of ghost. Before the transition, the reconstructed f(R) is very close to the GR case, where the observed Hubble data points is relative dense. This line segment corresponds to the little bump at the left begging of f(R) line in the bottom panel of Fig. 3. Beyond this bump for the reconstructed f(R), one can see a significant departure from GR in 1\(\sigma \) regions. It can also be seen that the Hu-Sawicki and Starobinsky f(R) gravity with the proper model parameters can match GR very well. It might also imply the possible tension between background and linear perturbation within \(1\sigma \) regions. Meanwhile, the reconstructed results would be lack of predictions due to sparse data points at high redshifts as the same situation in f(T) gravity case. The reconstructed form of f(R) from the perturbation with currently available data points might be only viable at small values of R, i.e the little bump part at the left begging of f(R) line in the bottom panel of Fig. 3. Beyond that the tachyonic instability and ghosts appear. It implies the limitation of the currently available data points to reconstruct f(R) from linear matter perturbation side. The same as f(T) case, one can fit the reconstructed evolution f(R) curves by a polynomial up to the third order of R in the form \(f(R)\approx \xi _0 R_0+\xi _1 R_0 (R/R_0)+\xi _2 R_0 (R/R_0)^2+\xi _3 R_0 (R/R_0)^3\) with \(\xi _0=45.58 \xi _1=-57.38, \xi _2=17.53 \xi _3=-1.51\). The fitting polynomial is also shown in bottom panel of Fig. 3.

Fig. 3
figure 3

Top panel: The reconstructed Ricci scalar R and f(R) within \(1\sigma \) region versus to the redshift z at the background and linear perturbation levels. Bottom panel: The reconstructed f(R) versus to the Ricci scalar R within \(1\sigma \) region at the background and linear perturbation levels. Where the GR, Hu-Sawicki and Starobinsky f(R) gravity models are also plotted for comparison. The thick black lines are obtained from the polynomial fitting results

Full size image

5 Conclusion and discussion

In this paper, the f(T) and f(R) gravity are directly reconstructed from the cosmic observations at the background and linear matter perturbation levels respectively in a model independent way, where the possible polynomial forms are given by fitting the reconstructed curves. For the f(T) gravity, the form of f(T) can be reconstructed from both the background and perturbation levels, and a departure in \(1\sigma \) regions is found in these two approaches. It might imply the existence of tension between the background and perturbation levels. But for the f(R) gravity, one cannot only reconstruct the possible f(R) form at the background levels due to the existence of an extra degree for freedom \({\dot{F}}\), which will be solved by the addition of the growth rate function. For requiring \(f_{,R}>0\) and \(f_{,RR}>0\) to avoid a tachyonic instability and be ghosts free in theory, the reconstructed form of f(R) might be viable in the redshift range of \(z<0.75\). But we have to point out that the reconstructed results would be lack of predictions due to sparse data points at high redshifts. We hope the future cosmic observations will fill this gap.