New properties of elastic pp and $p\bar{p}$ scattering at high energies

Abstract

Data-driving determination of the new properties of elastic scattering at small angles on the basis on all existing experimental data for $d\sigma /dt$ of pp and $p\bar{p}$ at $\sqrt{s} \ge 540$ GeV allows us to obtain the main characteristics of the nonstandard terms of the elastic scattering amplitude. The energy dependence of the oscillation term and the term with an extremely large slope is determined. It was shown that part of the oscillation term has a different sign for pp and $p\bar{p}$ reactions; hence, it is part of the Odderon amplitude. The period of the oscillation term agrees with the scaling properties predicted by the Auberson–Kinoshita–Martin (AKM) theorem. The high quality quantitative description of all data at $\sqrt{s} \ge 540$ GeV in the framework of the high energy general structure (HEGS) model supports such a phenomenon which can be connected with peripheral hadron interaction.

1 Introduction

Now many physical researchers concentrate on the search for new physics beyond the Standard Model. However, there are such problems as confinement, hadron interaction at larger distances, non-perturbative hadron structure (parton distribution functions (PDFs), generalized parton distributions (GPDs) and others) that should be explored in the framework of the Standard Model. These problems are connected with the hadron interaction at high and super-high energies and with the problem of energy dependence of the scattering amplitude and total cross sections. This reflects a tight connection of the main properties of elastic hadron scattering with the first principles of quantum field theory [1, 2] and the concept of the scattering amplitude as a unified analytic function of its kinematic variables [3].

Researches into the structure of the elastic hadron scattering amplitude at superhigh energies and small momentum transfer, t, outline a connection between experimental knowledge and the fundamental asymptotic theorems, which are based on the first principles. This connection provides information about hadron interaction at large distances where the perturbative QCD does not work [4], which gives the premise for a new theory to be developed.

For example, it was shown [5] that if the Pomeranchuk theorem was broken and the scattering amplitude grew to the maximal possible extent but did not break the Froissart boundary, many zeros in the scattering amplitude should be present in the nearest domain of $t \rightarrow 0$ in the limit $s \rightarrow \infty$. The search for some oscillations in elastic scattering at small t has a long story. For example, in [6], using the complex Regge poles, it was shown that the peripheral contributions of inelastic diffraction processes lead to the appearence in elastic cross sections of large and small periodical structures on transfer momenta. In [7], a bump structure was obtained at small t. Many attempts were made to research oscillations in the differential cross sections (for example [8]). Really, with increasing energy some new effects [9] in differential cross sections can be discovered at small t [10].

In the papers [11, 12], it was shown that AKM oscillations with scaling properties could exist in high-precision experimental data of the UA4/2 Collaboration. This was confirmed now in [13]. An attempt to find such oscillations with high frequency in the new experimental data, obtained by the ATLAS Collaboration, show practically zero result. However, the picture can be more complicated and especially it concerns an energy dependence of such a periodical structure.

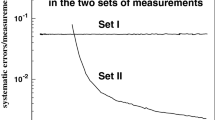
There are many models that describe the elastic scattering at different energies. Two large reviews [14, 15] present some of them. Note, the most famous models [16,17,18]. Some comparisons of our model with others are presented in [19]. One of the important differences of our approach from other consists in the different method of the calculations of $\chi ^2$, which shows the difference between the experimental data and model calculations (see Appendix C). Also, in most part the model examines a large amount of experimental data, including the data on the diffraction dip-bump structure and large momentum transfers. However, they do not take into account the Coulomb-hadron interference region (CNI), (for example, model [20] with 43 fitted parameters). On the contrary, some models take into account the CNI region but do not take into account the diffraction dip-bump structure as, for example, the TOTEM Collaboration and [21]. This leads to the construction of an artificial scattering amplitude, that does not work at more large momentum transfer.

Now we examine some peculiarities of the scattering amplitude assuming the existence of the potential of hadron-hadron interactions at large distance and carry out a new high accuracy treatment of all experimental data at $\sqrt{s} \ge 540$ GeV.

The new data obtained at the large hadron collider (LHC) by the TOTEM and ATLAS Collaborations made it possible to accurately analyse our model assumptions. Of course, to analyze new data more accurately in order to find some new peculiarity in hadron elastic scattering, one needs to have a simple model as a background which, with a few free parameters, gives a good description of specific properties such as the form and energy dependence of the diffraction minimum-maximum and description of the Coulomb-hadron region of experimental data. The high energy generalized structure (HEGS) model [19, 22] was chosen for our analysis (see Appendices A and B). The model is based on the general quantum field theory principles (analyticity, unitarity, etc.) and takes into account the basic information on the structure of a nucleon as a compound system and the hadron structure at large distances through the generalized parton distribution function [23,24,25,26]. The obtained GPDs [27, 28] allow one to simultaneously calculate the electromagnetic and gravitomagnetic form factors from one form of GPDs. The HEGS model uses both these form factors without any free parameters, which provides the hard structure of the model. In the framework of the model, a good quantitative description of the pp and $p\bar{p}$ was obtained [19] (3416 experimental points were included in the analysis in the energy region 9.8 GeV $\le \sqrt{s} \le 8.$ TeV and in the region of momentum transfer $0.000375 \le |t| \le 15$ GeV$^2$). The experimental data are included in 92 separate sets of 32 experiments [29, 30]. The whole Coulomb-hadron interference region, where the experimental errors are remarkably small, was included in our data analysis. As a result, it was obtained for the number of experimental data $N=3416$ $\sum _{i=1}^{N} \chi _{i}^{2}/N=1.28$ with only 8 fitting parameters.

Table 1 Sets of $\frac{d\sigma }{dt}$ ($k_i$ -additional normalization coefficient)

The high precision experimental data obtained by the TOTEM and ATLAS Collaboration at $\sqrt{s} = 7 - 13$ TeV show a significant deviation from the standard exponential behavior at small momentum transfer [49], as first observed by the TOTEM Collaboration [35, 39, 50, 51]. Regardless of the concrete model, some tension between the data of the TOTEM and ATLAS Collaborations is observed, which is reflected in the definition of the sizes of the total cross sections. The usual practice of taking into account the fitting procedure of the experimental errors in quadrature of statistical and systematical errors does not remove this tension but only decreases the value of $\chi ^2$. As a result, in some papers the analysis was carried out for the TOTEM and ATLAS data separately, for example [52]. In contrast, our strategy in all our model analysis is vastly different (see Appendix C). In the standard fit, the statistical errors are taken into account. Since an uncertainty of luminosity gives the main contribution to the systematic errors, it is taken into account in the form of an additional normalization coefficient, which is equal for all data of one set. As a result, all data of all sets of different experimental Collaborations are taken into account simultaneously.

Using our model for the analysis of the new data of the TOTEM Collaboration at $\sqrt{s}=13$ TeV shows the existence of new peculiarities in the differential cross section at small angles. It was shown that the differential cross section has some small oscillatory behavior [53]. This effect was confirmed independently of a concrete model by the statistically based method [53, 54] also at a high confidence level (see Appendix D). Earlier, the oscillation behavior of the differential cross section was observed in the data of the UA4/2 Collaboration at the SPS accelerator at $\sqrt{s}= 541$ GeV [12] and at low energies [55].

Further careful analysis also showed the existence in the scattering amplitude of the term with an extremely large slope [56]. In the work [56], the analysis of both sets of the TOTEM data at 13 TeV was carried out with additional normalization equal to unity and taking into account only statistical errors in experimental data.

Fig. 1

The differential cross sections are calculated in the framework of the HEGS model with the additional terms for pp scattering at $\sqrt{s} = 13$ TeV (upper line and data) and for $p\bar{p}$ scattering at $\sqrt{s} = 541$ GeV (lower line and data)

Fig. 2

The differential cross sections are calculated in the framework of the HEGS model with the additional terms (anomalous and oscillation) at $\sqrt{s} = 13$ TeV (upper line and data) multiplied by 10; at $\sqrt{s} = 7$ TeV and at $\sqrt{s} = 2.76$ TeV [40] divided by 10 (lower curve and data)

Both effects have been confirmed in the analysis of all sets of the experimental data obtained at the LHC [57]. However, to study the properties of the new effects in elastic scattering, one should include in the analysis the experimental data for proton-antiproton scattering and essentially extend the energy region.

Fig. 3

The $d\sigma /dt$ of elastic pp scattering (calculated in the model with Odderon contribution and two additional terms) for pp scattering at 2.76 TeV (the data of the TOTEM Collaboration - squares) are compared with the calculations and data for $p\bar{p}$ at $\sqrt{s}=1.8$ TeV ( triangles down) and at $\sqrt{s}=546$ GeV (dashed line and diamond and circles)

2 s and t dependence of new peculiarities in elastic scattering

In this work, all high energy data of pp and $p\bar{p}$ scattering are included in the analysis. Especially, this is important in view of a wide discussion [58] of the comparison of the Odderon contributions to $p\bar{p}$ scattering of the D0 experiment at $\sqrt{s} = 1.96$ TeV [41] and to pp scattering of the TOTEM experiment at $\sqrt{s} = 2.76$ TeV [40]. Also, the high precision data of the UA4/2 Collaboration related to $p\bar{p}$ scattering should be taken into account. Hence, let us include in our analysis all experimental data at $\sqrt{s} \ge 540$ GeV (see Table 1).

As was found from an analysis of the TOTEM data at 13 TeV, there exists an additional anomalous term in the scattering amplitude with an essentially larger slope than the standard term [56]. Usually, some terms with a large slope are related to the second Reggions. However, in all models the second Regge terms (like $f_0, \rho , \omega ...$) show a decrease in their contributions with energy, like $1/s^{1/2}$. As a result of our analysis, the form of an additional anomalous term was determined as

$$\begin{aligned} f_{an}(t)= & {} i h_{an} \ln {(\hat{s}/s_{0})}/k \nonumber \\{} & {} \times \exp [-\alpha _{an} (|t|+(2t)^2/t_{n})\ln {(\hat{s}/s_{0})}] \ F_{em}^2(t); \end{aligned}$$

(1)

where $h_{an}$ is the constant determining the size of the anomalous term with a large slope - $\alpha _{an}$; $F_{em}(t)$ is the electromagnetic form factor, which was determined from the GPDs [28], and $\ k=\ln (13000^2 \ \textrm{GeV}^{2}/s_{0}) \$ is introduced for normalization of $h_{an}$ at 13 TeV, $t_{n}=1$ GeV$^2$-normalization factor (see Appendix B for definitions of $\hat{s}$ and $s_{0}$). Such a form adds only two additional fitting parameters, and this term is supposed to grow with energy of order $\ln {(\hat{s}/s_{0})}$. The term has a large imaginary part and a small real part determined by the complex $\hat{s}$. Note that for analysis of the basic properties of elastic scattering, the experimental data are usually taken in a narrow region of momentum transfer. This can lead to a bad description if we take a wider region. Now all terms of our scattering amplitude are used in all regions of the available experimental data.

Now let us try to find the form of an additional oscillation contribution to the basic elastic scattering amplitude (see Appendix B). Our fitting procedure takes the oscillatory function

$$\begin{aligned} f_{osc}(t)= & {} i h_{osc} (1 \pm i) \ln {(\hat{s}/s_{0})}/k J_{1}(\tau )/\tau \ A^{2}(t), \nonumber \\ \tau= & {} \pi \ (\phi _{0}-t)/t_{0}; \end{aligned}$$

(2)

here $J_{1}(\tau )$ is the Bessel function of the first order; $t_{0}=1/[a_{p}/(\ln {(\hat{s}/s_{0})}/k)]$, where $a_{p}=17.15$ GeV$^{-2}$ is the fitting parameter, that leads to AKM scaling on $\ln {(\hat{s}/s_0)}$; A(t) is gravitomagnetic form factor, which was determined from the GPDs [28] and $h_{osc}$ is the constant that determines the amplitude of the oscillatory term with the period determined by $\tau$. This form has only a few additional fitting parameters and allows one to represent a wide range of possible oscillation functions. For simplicity, the phase $\phi _{0}$ is taken as zero for pp and small value for $p\bar{p}$ scattering. Inclusion in the fitting procedure of the data of $p\bar{p}$ elastic scattering shows that the part of oscillation function changes its sign for the crossing reactions. As a result, the plus sign is related with pp and minus with $p\bar{p}$ elastic scattering. Hence, this part is the crossing-odd amplitude, which has the same simple form for pp and $p\bar{p}$ scattering only with different sign. Of course, it’s analytical properties require further researches.

The wider energy region used in this analysis allows one to reveal the logarithmic energy dependence of the oscillation term. Let us compare the constant (size) of the oscillation function of three independent analyses (only 13 TeV, all LHC data, all data above 500 GeV): $h_{osc}^{a}=0.350\pm 0.014 \ \textrm{GeV}^{-2}; \ h_{osc}^{b}=0.370\pm 0.013 \ \textrm{GeV}^{-2}; h_{osc}^{c}=0.270\pm 0.007 \ \textrm{GeV}^{-2}$. The size of $h_{osc}$ is smaller in the last case; however, the error is decreased. Perhaps, this reflects a more complicated form of energy dependence, for example, we can not determine the power of $\ln (s)$ exactly and take it as unity. In future, we intend to study this problem using an essentially wider energy interval up to $\sqrt{s}=3.6$ GeV, where some oscillation was also observed in $p\bar{p}$ scattering [55]. Note, despite the logarithmic growth of the oscillation term, its relative contribution decreases as the main scattering amplitude grows as $\ln ^{2}(s)$.

Fig. 4

$R_{\mathrm th}$ of Eq. 3 (the solid thick line) and $R_{\mathrm exper.}$ of Eq. 4 of the TOTEM data at $\sqrt{(}s)=13$ TeV (the dashed line)

Fig. 5

$R_{\mathrm th}$ of Eq. 3 (the solid thick line) and $R_{\mathrm exper.}$ of Eq. (4) (the triangles up) at $\sqrt{(}s)=13$ TeV (ATLAS data)

After the fitting procedure, with the modern version of FUMILY [59, 60], we obtain $\chi ^2/dof =1.23$ (remember that we used only statistical errors). The total number of experimental points of 24 sets equals 1288 and the sum of $\sum \chi ^2 = 1568$. If we remove the oscillatory function, then $\sum \chi ^2 = 4344$ increases significantly. If we make a new fit without $f_{osc}$, then $\sum \chi ^2 = 2512$ decreases but remains large. However, the basic parameters change slightly (see second column below);

Our model calculations for the differential cross sections are represented in Figs. 1, 2 and 3. It can be seen that the model gives a beautiful description of the differential cross section especially at LHC energies in both the Coulomb-hadron interference region and the region of the diffraction dip for all energies. A phenomenological form of the scattering amplitude determined for small t can lead to very different differential cross sections at larger t. This effect is especially prominent when it is connected with the differential cross section at 13 TeV, as the diffraction minimum is located at a non-large t. An important point of obtaining a good description of the available experimental data in a wide region of energies and momentum transfer is that two additional specifical functions are used in the model in the whole region of Mandelstam’s variables.

As a result, two parameters of the additional term of Eq. (1) are well defined $h_{an}=2.10 \pm 0.05 \ \textrm{GeV}^{-2}; \ \ \ \alpha _{an} =0.51 \pm 0.03 \ \textrm{GeV}^{-2}$. The sizes of constant $h_{an}$ obtained in our three different studies can be compared for 3 different studies (first analysis [56] include only 13 TeV experimental data; the second analysis [57] taken into account all data on elastic scattering obtained at LHC; third case (present analysis) taken into account all data above 500 GeV, including proton-antiproton data). If it is an artifact, presented only at 13 TeV experiments, the size of $h_{an}$ has to be decreased when we include more and more experimental data. However we have for these 3 studies: $h_{an}^{a}=1.70\pm 0.05 \ \textrm{GeV}^{-2}$; $h_{an}^{b}=1.54 \pm 0.08 \ \textrm{GeV}^{-2}$; $h_{an}^{c}=2.10 \pm 0.05 \ \textrm{GeV}^{-2}$. The maximum value was obtained in the last case when we used the experimental data in a wider region of s and t, including the data of crossing reaction.

To see the oscillations in the differential cross sections, let us determine two values – one is purely theoretical

$$\begin{aligned} R_{\mathrm th}(t) = \frac{d\sigma /dt_{\mathrm th0+osc}}{d\sigma /dt_{\mathrm th0}}-1, \end{aligned}$$

(3)

and other with experimental data

$$\begin{aligned} R_{\mathrm exper.}(t)= \frac{d\sigma /dt_{exper.}}{d\sigma /dt_{th0}}-1. \end{aligned}$$

(4)

Here $d\sigma /dt_{th0}$ is the model calculation without the oscillation part and $d\sigma /dt_{\mathrm th0+osc}$ is the model calculation with the oscillation part. The corresponding values are calculated from our fit of all data and can be derived from every separate set of experimental data.

Fig. 6

$R_{\mathrm th}$ (the solid thick line) and $R_{\mathrm exper.}$(the short dash line and squares) are the TOTEM data at $\sqrt{(}s)=7$ TeV

Fig. 7

$R_{\mathrm th}$ (the solid thick line) and $R_{\mathrm exper.}$(the solid line, the data of the UA4/2 Collaboration and dashed line, the data of UA4 Collaboration) at $\sqrt{(}s)=541$ GeV and $\sqrt{(}s)=546$ GeV

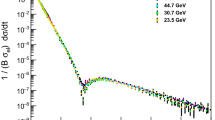
For two sets of the TOTEM and ATLAS data at 13 TeV the values $R_{\mathrm th}(t)$ and $R_{\mathrm exper.}(t)$ are presented in Figs. 4 and 5. We can see that $R_{\mathrm th}$ is similar to the value $R_{\mathrm exper.}$. The oscillation contribution is small; however, the noise of the background decreases with t and does not damp the oscillation part. In Fig. 6, these values are presented for experimental data obtained at $\sqrt{s}=7$ TeV.

Fig. 8

The different form of the peripheral potentials are compared. The modified Gaussian form of the potential $h_{gs}\exp [\alpha _{gs}r^2]/(1 + r/r_{0})$ ( dashed line), the calculation of our anomalous term in the r-representation Eq. (5) (the solid line); for comparison, the r-representation of the standard exponential behavior in the q-representation (thin solid line) and exponential behavior in r-representation $h_{e}\exp [b_{e} r]/(1 + r/r_{0})$ (dotted line) are also shown

The corresponding values calculated from the fit of two sets of the UA4 and UA4/2 data at 541 GeV are presented in Fig. 7. At small t, there is a large noise; however, the oscillation contributions can be seen. Such a periodical structure has a sufficiently long period, especially compared to the periodical structure with high frequency analysed in the previous work [12, 13]. Our analysis of high frequency oscillations shows that they can occur at 13 GeV with a small amplitude, which means an essential decrease compared to the oscillations at 541 GeV. The stability of such amplitude is determined with a large error $h_{osc}= 0.014 \pm 0.012$ GeV$^{-2}$.

Fig. 9

The oscillation term Eq. (2) in the r-representation Eq. 6 (solid line) is compared with the Gaussian form $h_{g} \exp [b_{g} r^2]$ (dashed line)

Fig. 10

The imaginary (long dashed line) and real (short dashed line) parts of the main (without oscillation term) elastic hadron scattering amplitude at 13 TeV

In Fig. 8, different forms of peripheral potentials are compared. The dotted line represents the modified exponential form of the potential $h_{e}\exp [b_{e} r]/(1 + r/r_{0})$, the solid line shows the calculation of our anomalous term in the r-representation

$$\begin{aligned} V_{an}(r)=\int q \ dq \sin (q r)/r \exp [-\alpha _{an} (q^2+(2q^2)^2/q^{2}_{0} ) ]. \nonumber \\ \end{aligned}$$

(5)

It is compared with the modified Gaussian form of the potential (dashed line) $h_{gs}\exp [\alpha _{gs}r^2]/(1 + r/r_{0})$, where $h_{gs}$ is a constant providing the same size as our $V_{an}(r)$ (Eq. 5) and $r_{0}$ is a selectable interaction radius. Obviously, the last form well reproduces our anomalous term in the r-representation. For comparison, the r-representation of the standard exponential behavior in the q-representation (thin solid line) is also shown.

The oscillation term, Eq. (2), in the r-representation is presented in Fig. 9 (solid thick line)

$$\begin{aligned} V_{osc}(r) = \int q \ dq \sin (q r)/r J_{1}[\tau ]/\tau , \end{aligned}$$

(6)

where $J_{1}[\tau ]/\tau$ is determined by Eq. (2). It is compared with the Gaussian form $h_{g} \exp [b_{g} r^2]$ (dashed line) where $h_{g}$ is a constant, providing the same size as our $V_{osc}(r)$ (Eq. 6) and $b_g$ is the fitting Gaussian radius. Of course, it does not reproduce small oscillations. Oscillations will appear in the q-representation if we cut the potential at a large distance.

3 Some other possible origins of periodic structure

The structure of the differential cross sections of elastic scattering has a complicated form that is dependent on s and t (see, for example, [61]). First the diffractive properties of elastic scattering are represented in the dip-bump structure that reflects the eikonalization of the Born scattering amplitude with the s and t dependence of its real and imaginary part. Of course, a periodic structure can be determined by the zeros of the real and imaginary parts of the scattering amplitude. Thus, the diffraction minimum is determined by the zero of the imaginary part. The dispersion relations require that the real part of the amplitude has zero at small momentum transfer. However, the s and t dependence essentially differs from the periodic structure presented in the paper. The corresponding real and imaginary parts of the elastic scattering amplitude at 13 TeV are shown in Fig. 10.

Fig. 11

The comparison of $\varDelta _{R}^{th}(s,t)$, Eq. (7) (solid line), of elastic pp scattering at 13 TeV and $|Re(f_{osc})| + |Im(f_{osc})|$ of the oscillation function of Eq. (2) (dashed line)

There is an additional zero at some value of t where the real part of the Coulomb amplitude (which has the negative sign) equals in absolute value the real part of the hadronic amplitude. Let us determine the value $\varDelta _{R}$ that is dependent on the size of the real part of the scattering amplitude

$$\begin{aligned} \varDelta _{R}^{th}(s,t)=(ReF_C(t)+ReF_h(s,t))^2. \end{aligned}$$

(7)

Obviously, it gives the minimum at one point of $t_{min}$ where the real part of the Coulomb amplitude is opposite to the real part of the scattering amplitude. the real part of the scattering amplitude. Let us compare this value with our periodic structure, see Fig. 11. It is obvious that the t dependence is very different for the examined values.

4 Conclusion

The existence of the new effects in high energy elastic pp and $p\bar{p}$ scattering is revealed by using the data-driving method for the first time at a quantitative level. Using the HEGS model based on the GPDs allows us to describe at a quantitative level all experimental data on pp and $p\bar{p}$ elastic scattering above $\sqrt{s} = 540$ GeV with taking into account only statistical errors. However, only the presence in the model of two anomalous terms, determined by the interaction in the peripheral region allows us to obtain a sufficiently small $\chi ^2$. These additional terms affect the value of the total cross sections and parameter $\rho (s,t)$ - ratio of the real to imaginary part of the elastic scattering amplitude. As a result, we have obtained at $\sqrt{s} =13$ TeV $\sigma _{tot} = 110.4 \pm 0.4$ mb and $\rho (t=0) =0.106 \pm 0.005$.

The phenomenon of oscillations of the elastic scattering amplitude gives us important information about the behavior of the hadron interaction potential at large distances. Earlier, the existence of such oscillations in experimental data at $\sqrt{s}=13$ TeV was shown at the statistical level by three methods: (a) the method of statistically independent selection; (b) the comparison of the $\chi ^2$ without oscillation ($\sum \chi ^2 =1140$) and with oscillation ($\sum \chi ^2 = 515$); (c) the comparison of $R_{th}$ and $R_{exp}$. All three methods show the presence of a periodical structure. Data-driving method shows the existence of such a periodical structure in both crossing symmetric reactions of pp and $p\bar{p}$ elastic scattering. It is very important that the oscillation term has the crossing odd properties. Hence, probably, it is part of the Odderon amplitude. Our analysis shows the logarithmic growth of a term like this.

The corresponding hadron potential has no simple exponential behavior. Our calculations show that it has a modified Gaussian form with probably a cut at large distances. This may be due to the glueball states of the gluon. In such a form, the gluon can be distributed at large distances above the confinement level. These new effects are very important in searching for new physics in the framework of the Standard Model, for example, checking up the dispersion relations, analyticity and crossing symmetry of the scattering amplitude. This should be especially considered when determining the total cross sections, the ratio of the elastic to the total cross sections, and the energy dependence of $\rho (s,t)$ (the ratio of the real to the imaginary part of the elastic scattering amplitude).

These results allow us to make some predictions for hadron interactions at essentially larger energies at future colliders and at ultra-high energies of cosmic rays. These effects are likely to exist also in experimental data at essentially smaller energies [62] but they might have a more complicated form (with two different periods, for example). Also, these effects impact our description of spin-dependent hadron interactions at low energies (including the energy of NICA project).

Appendices

Appendix A: Eikonalization of the scattering amplitude

The total elastic amplitude in general gets five helicity contributions, but at high energy it is sufficient to keep only spin-non-flip hadron amplitudes. The final elastic hadron scattering amplitude is obtained after the unitarization of the Born term. So, first, we have to calculate the eikonal phase

$$\begin{aligned} \chi (s,b) \ = -\frac{1}{2 \pi } \ \int \ d^2 q \ e^{i \textbf{b} \cdot \textbf{q} } \ F^\textrm{Born}_{h}\left( s,q^2\right) \, \end{aligned}$$

(8)

and then obtain the hadron scattering amplitude

$$\begin{aligned} F_{h}(s,t)= & {} i s \int \ b \ J_{0}(b q) \varGamma (s,b) \ db \end{aligned}$$

(9)

$$\begin{aligned} \textrm{with } \ \ \varGamma (s,b)= & {} 1- \exp [\chi (s,b)]. \end{aligned}$$

(10)

Numerical integration allows one to calculate an additional term in both the direct and eikonal approach.

Appendix B: High energy generalized structure model

As a basis, we take our HEGS model [19, 22] that quantitatively describes, with only a few parameters, the differential cross section of pp and $p\bar{p}$ from $\sqrt{s} =9$ GeV up to 13 TeV, including the Coulomb-hadron interference region and the high-|t| region up to $|t|=15$ GeV$^2$ and quantitatively well describes the energy dependence of the form of the diffraction minimum [61]. However, to avoid possible problems connected with the low-energy region, we consider here only the asymptotic variant of the model [63]. The total elastic amplitude in general receives five helicity contributions, but at high energy it is enough to write it as $F(s,t) = F^{h}(s,t)+F^\textrm{em}(s,t) e^{i\varphi (s,t)}$ , where $F^{h}(s,t)$ comes from the strong interactions, $F^\textrm{em}(s,t)$ from the electromagnetic interactions and $\varphi (s,t)$ is the relative phase between the electromagnetic and strong interactions [64,65,66]. The Born term of the elastic hadron amplitude at large energy can be written as a sum of two pomeron and odderon contributions,

$$\begin{aligned} F_{\mathbb {P} }(s,t)= & {} \hat{s}^{\epsilon _0}\left( C_{\mathbb {P}} F_1^2(t) \ \hat{s}^{\alpha ' \ t} + C'_{\mathbb {P}} A^2(t) \ \hat{s}^{\alpha ' t\over 4} \right) , \end{aligned}$$

(11)

$$\begin{aligned} F_{\mathbb {O} }(s,t)= & {} i \hat{s}^{\epsilon _0+{\alpha ' t\over 4}} \left( \pm C'_{\mathbb {O}} t/(1-r_{\mathbb {O} }^{2} t ) \right) A^2(t). \end{aligned}$$

(12)

Finally, the Born amplitude is $F_{Born}(s,t) = F_{\mathbb {P} }(s,t) + F_{\mathbb {O} }(s,t)$. The simultaneously fitting procedure of all 24 sets lead to the value of the parameters: $C_{\mathbb {P}}=3.30 \pm 0.02$ GeV$^{-2}$, $C'_{\mathbb {P}}=1.39\pm 0.02$ GeV$^{-2}$, $C'_{\mathbb {O}}=-0.56\pm 0.03$ GeV$^{-2}$, $r_{\mathbb {O}}^2 = 4.9\pm 1.4$ GeV$^{-2}$. The sizes and the energy and momentum transfer dependence of the real part of the elastic scattering amplitude $Re F(s,t)_{B}$ are determined by the complex energy $\hat{s}=s exp(-i\pi /2)$. Hence, the model does not introduce some special functions or assumptions for $Re F_{B}(s,t)$. All terms are supposed to have the same intercept $\alpha _0=1+\epsilon _0=1.11$, and the pomeron slope is fixed at $\alpha '=0.24$ GeV$^{-2}$. The model takes into account two hadron form factors $F_1(t)$ and A(t), which correspond to the charge and matter distributions [28]. Both form factors are calculated as the first and second moments of the same GPDs. Taking into account the Mandelstam region of the analyticity of the scattering amplitude for the $2 \rightarrow 2$ scattering process with identical mass $s+u+t=4 m_{p}^2$ one takes the normalized energy variable s in complex form $\hat{s}/s_{0}$ with

$s_{0}=4 m_{p}^{2}$, where $m_{p}$ is the mass of the proton.

In the present model, a small additional term is introduced into the slope, which reflects some possible small nonlinear properties of the intercept. As a result, the slope of the amplitude in the form $\hat{s}^{\alpha ' t} = exp^{B(s,t) t}$ is taken as

$$B(s,t) \ = \alpha ^{\prime } \ln (\hat{s}/s_{0}) (1 -k_1 t/(\ln (\hat{s}/s_0))/k e^{k_2 \ln (\hat{s}/s_{0}) t}).$$

This form leads to the standard form of the slope as $t \rightarrow 0$ and $t \rightarrow \infty$. Note that our additional term at large energies has a similar form as an additional term to the slope coming from the $\pi$ loop examined in Ref. [67] and recently in Ref. [49].

Appendix C: Fitting procedure

There are two essentially different ways of including statistical and systematic uncertainties in the fitting procedure [68]. The first one, mostly used in connection with the differential cross sections (for example [15, 18]), takes into account statistical and systematic errors in quadrature form: $\sigma _{i(tot)}^2 = \sigma _{i(stat)}^2+ \sigma _{i(syst)}^2$ and

$$\begin{aligned} \chi ^{2}= \sum _{i=1}^{n} \frac{ ( \hat{E}_{i} - F_{i}(\textbf{a}) )^2 }{\sigma _{i(tot)}^{2}}, \end{aligned}$$

(13)

with a standard definitions: $\hat{E}_{i}$ - experimental data and $F_{i}(\textbf{a})$ - model calculations with parameters $\textbf{a}$.

The second method accounts for the basic property of systematic uncertainties, i.e. the fact that these errors have the same sign and size in proportion to the effect in one set of experimental data and possibly have a different sign and size in another set. To account for these properties, extra normalization coefficients $k_{j} = 1 \pm \sigma _{j}$ for the measured data are introduced in the fit. This method is often used by research collaborations to extract, for example, the parton distribution functions of nucleons [69, 70] and nuclei [71] in high energy accelerator experiments, or in astroparticle physics [72]. In this case, $\sigma _{i(tot)}^2 = \sigma _{i(stat)}^2$ and the systematic uncertainty are taken into account as an additional normalization coefficient, $k_j$, and the size of $\sigma _j$ is assumed to have a standard systematic error,

$$\begin{aligned} \chi ^{2} = \sum _{j=1}^{m} \left\{ \sum _{i=1}^{n} \frac{ ( k_{j} \hat{E}_{ij} - F_{ij} )^2 }{ \sigma ^{2}_{ij(st.)} } + \frac{(1-k_j)^2}{\sigma ^{2}_{j}} \right\} . \end{aligned}$$

(14)

In the first case, the “quadrature form” of the experimental uncertainty gives a wide corridor in which different forms of the theoretical amplitude can exist. In the second case, the “corridor of the possibility” is essentially narrow, and it restricts different forms of theoretical amplitudes [68].

Appendix D: Statistical method

The usual method of minimization $\chi ^2$ in this situation often works poorly. On the one hand, we should define a certain model for part of the scattering amplitude having zeros in the domain of small t. However, this model may slightly differ from a real physical picture. On the other hand, the effect is rather small and gives an insignificant change in the sum of $\chi ^2$. Therefore, in this work let us apply first another method, namely, the method of comparing of two statistically independent choices, for example [54]. If we have two statistically independent choices $x^{'}_{n_1}$ and $x^{''}_{n_2}$ of values of the quantity X distributed around a definite value of A with the standard error equal to 1, we can try to find the difference between $x^{'}_{n_1}$ and $x^{''}_{n_2}$. For that we can compare the arithmetic mean of these choices $\varDelta X = (x^{'}_1 + x^{'}_2 +... x^{'}_{n1})/n_1 - (x^{''}_1 + x^{''}_2 +... x^{''}_{n2})/n_2 = \overline{x^{'}_{n_1}} - \overline{x^{''}_{n_2}}.$ The standard deviation for that case will be $\delta _{\overline{x}} = [1/n_1 +1/n_2]^{1/2}$. And if $\varDelta X / \delta _{\overline{x}}$ is larger than 3, we can say that the difference between these two choices has the $99\%$ probability.