1 Introduction

Deep inelastic scattering (DIS) processes play a unique role in developing the theoretical understanding of the high energy interaction in QCD. Indeed, the main ideas of Colour Glass Condensate(CGC)/saturation approach (see Ref. [1] for a review): the saturation of the dipole density and the new dimensional scale (\(Q_s\)), which increases with energy, have become the common language for discussing the high energy scattering in QCD. All these ideas are rooted in the theoretical description of DIS [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18].

We are going to discuss the multiplicity distribution of the produced gluons in DIS. The multiplicity distributions and especially the entropy of produced gluons have become a hot subject during the past several years [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37] and we hope that this paper will look at these problems at different angle. However, before discussing the multiplicity distribution it looks reasonable to summarize our theoretical achievements in DIS.

First and most importantly is that the scattering amplitude of the colourless dipole with the size \(x_{01}\) which determines the DIS cross section, satisfies the Balitsky–Kovchegov (BK) non-linear equation [38, 39]:

$$\begin{aligned} \frac{\partial N_{01}}{\partial Y}{} & {} =\,\bar{\alpha }_S\int \frac{d^2\,x_{02}}{2 \pi } \frac{ x^2_{01}}{x^2_{02}\,x^2_{12}}\,\nonumber \\{} & {} \quad \times \Big \{ N_{02} + N_{12} - N_{02}N_{12} - N_{01}\Big \} \end{aligned}$$
(1)

where \(N_{ik}=N\left( Y, \varvec{x}_{ik},\varvec{b}\right) \) is the scattering amplitude of the dipoles with size \(x_{ik}\) and with rapidity Y at the impact parameter \(\varvec{b}\).

It has been shown that Eq. (1) leads to a new dimensional scale: saturation momentum [10] which has the following Y dependence [10, 40,41,42,43]:

$$\begin{aligned} Q^2_s\left( Y, b\right) \,\,=\,\,Q^2_s\left( Y=Y_0, b\right) \,e^{\bar{\alpha }_S\,\kappa \,Y\,-\,\,\frac{3}{2\,\gamma _{cr}} \ln Y } \end{aligned}$$
(2)

where \(Y_0\) is the initial value of rapidity and \(\kappa \) and \(\gamma _{cr}\) are determined by the following equationsFootnote 1:

$$\begin{aligned}{} & {} \kappa \,\,\equiv \,\, \frac{\chi \left( \gamma _{cr}\right) }{1 - \gamma _{cr}}\,\,=\,\, - \frac{d \chi \left( \gamma _{cr}\right) }{d \gamma _{cr}}~~~\,\,\,\nonumber \\{} & {} \quad \hbox {and}\,\,\,~~~\chi \left( \gamma \right) \,=\,\,2\,\psi \left( 1 \right) \,-\,\psi \left( \gamma \right) \,-\,\psi \left( 1 - \gamma \right) \end{aligned}$$
(3)

In Refs. [40, 41] (see also Re, [42, 43]) it is shown that in the vicinity of the saturation scale the scattering amplitude takes the following form:

$$\begin{aligned} N_{01}\left( z\right) \,\,\,=\,\,\,\hbox {Const} \left( x^2_{10}\,Q^2_s\left( Y\right) \right) ^{\bar{\gamma }} \end{aligned}$$
(4)

with \(\bar{\gamma }= 1 - \gamma _{cr}\). In Eq. (4) we introduce a new variable z, which is equal to:

$$\begin{aligned} z\,\,= & {} \,\,\ln \left( x^2_{01}\,Q^2_s\left( Y, b\right) \right) \,\,\,\nonumber \\= & {} \,\,\,\,\bar{\alpha }_S\,\kappa \,\left( Y\,-\,Y_A\right) \,\,+\,\,\xi \end{aligned}$$
(5)

where \(\xi = \ln x^2_{01}\). Note that we neglected the term \(\frac{3}{2\,\gamma _{cr}} \ln Y\) in Eq. (2).

It turns out that inside the saturation region: \(x^2_{01}\,Q^2_s\left( Y\right) \,>\,1\) the scattering amplitude shows the geometric scaling behaviour, being a function of one variable \(x^2_{01}\,Q^2_s\left( Y\right) \):

$$\begin{aligned} N_{01}\left( Y,x_{01},b\right) = N\left( x^2_{01}\,Q^2_s\left( Y,b\right) \right) \end{aligned}$$
(6)

It is instructive to note, that this behaviour has been proven on general theoretical grounds [45] and has been seen in the experimental data on DIS [46,47,48].

Finally, in Refs. [49,50,51] the solution to Eq. (1) was found deep into saturation region for \(z \,\gg \,1\) which has the following form:

$$\begin{aligned} N_{01}\left( z\right) \,\,\,=\,\,1\,\,\,-\,\,\,\hbox {Const}\,\exp \Big ( - \frac{z^2}{2\,\kappa }\Big ) \end{aligned}$$
(7)

where \(\textrm{Const} \) is a smooth function of z.

We have defined the saturation region as \( x^2_{10}\,Q^2_s\left( Y,b\right) \,>\,1\). However, in Refs. [52, 53] it has been noted that actually for very large \(x_{10} \) the non-linear corrections become small and we have to solve linear BFKL equation. This feature can be seen directly from the eigenfunction of this equation. Indeed, the eigenfunction has the following form [7, 8]

$$\begin{aligned}{} & {} \phi _\gamma \left( \varvec{r}, \varvec{R}, \varvec{b}\right) \,\,\,\nonumber \\{} & {} \quad =\,\,\,\left( \frac{ r^2\,R^2}{\left( \varvec{b} + \frac{1}{2}(\varvec{r} - \varvec{R})\right) ^2\,\left( \varvec{b} - \frac{1}{2}(\varvec{r} - \varvec{R})\right) ^2}\right) ^\gamma \xrightarrow {b\,\gg \,r,rR}\,\,\nonumber \\{} & {} \qquad \times \left( \frac{ R^2\,r^2}{b^4}\right) ^\gamma \,\,\equiv \,\,e^{\gamma \,\xi }~~\hbox {with}\,\,0 \,<\,Re\gamma \,<\,1 \end{aligned}$$
(8)

for any kernel which satisfies the conformal symmetry. In Eq. (8) R is the size of the initial dipole at \(Y=0\) while \(r\equiv x_{10}\) is the size of the dipole with rapidity Y.

One can see that for \(r=x_{10} \,>\,min[R, b]\), \(\phi _\gamma \) starts to be small and the non-linear term in the BK equation could be neglected. In this paper we wish to discuss the DIS for \(Q^2 \ge 1 \,\mathrm{{GeV}}^2\) and in the region of small x. In other words we consider \(x_{10} < R\), where R is the radius of a hadron. Bearing this in mind we can replace Eq. (8) by the following one:

$$\begin{aligned} \phi _\gamma \left( \varvec{r}, \varvec{R}, \varvec{b}\right) \,\,\,= & {} \,\,\,\left( \frac{ r^2\,R^2}{\left( \varvec{b} - \frac{1}{2}\varvec{R}\right) ^2\,\left( \varvec{b} + \frac{1}{2}\varvec{R})\right) ^2}\right) ^\gamma \nonumber \\= & {} \left( r^2 Q_s\left( Y=0, b, R\right) \right) ^\gamma \end{aligned}$$
(9)

Therefore, we can absorb all impact parameter dependence in the dependence of the saturation scale on b.

The main goal is to find the multiplicity distributions and the entropy of produced gluons in the kinematical region of Eq. (7). In other words, we wish to decipher the saturated amplitude in terms of produced gluons. Fortunately, the equations for the cross section of production of n gluons have been derived in the framework of CGC (see Ref. [54]). The next section is a brief review of the results of Ref. [54]. In this section we emphasize the two main ingredients on which the derivation of the equations is based: the AGK cutting rules [55, 56] and the BFKL equation [2,3,4,5,6], which gives the production of gluons in a particular kinematic region typical for leading log(1/x) approximation of perturbative QCD.

In Sect. 3 we discuss solutions to the equations for the total cross section \( \sigma _{tot}\), for the cross section of diffraction production \(\sigma _{sd}\) and the cross section for productions of n gluons \(\sigma _n\). We show that both the total cross section and the cross section of the diffraction production reaches the unitarity limit: \(\sigma _{tot}(b) = 2\) and \(\sigma _{sd} = 1\), while \(\sigma _n \) are small and proportional to \(\,\frac{1}{\bar{n}(z)} \exp \left( - n/\bar{n}(z)\right) \) with \(\bar{n}(z) \,\,\propto \,\, \exp \Big ( \frac{z^2}{2\,\kappa }\Big )\). In Sect. 4 we estimate the value of the entropy of produced gluons. In conclusions we summarize our results and discussed related problems.

2 Generating functional for multipartical production processes

2.1 Generating functional for the scattering amplitude

The scattering amplitude, given by BK equation (see Eq. (1)), can be viewed as a sum of the “fan” BFKL Pomeron diagrams [10,11,12,13,14, 57,58,59,60,61,62,63,64,65,66,67,68] (see Fig. 1). The value of the triple Pomeron vertex is determined by the non-linear term of the BK equation. However, it has been shown in Refs. [12,13,14] that the BK equation has a quite different interpretation in which the BFKL kernel

Fig. 1
figure 1

a The fan diagrams in the BFKL Pomeron calculus that describe the BK equation (see Eq. (1)). b The unitarity constraints for the exchange of the BFKL Pomeron: the structure of the cut Pomeron. This constraints determines the cut Pomerons that are shown in Fig. 2 by the wavvy lines which are crossed by the dashed ones

Full size image
$$\begin{aligned} \frac{ \bar{\alpha }_S}{2\,\pi } K\left( x_{01}|x_{02},x_{12}\right) \,\,=\,\,\frac{ \bar{\alpha }_S}{2\,\pi } \frac{ x^2_{01}}{x^2_{02}\,x^2_{12}} \end{aligned}$$
(10)

gives the probability for decay of one dipole with size \(x_{10}\) to two dipoles with sizes \(x_{02}\) and \(x_{12}\).

The simplest and the most transparent technique to incorporate this decay is the generating functional which allows us to reduce the calculation of the high energy elastic amplitude to consideration of a Markov process. The generating functional is defined as [12,13,14, 69,70,71]

$$\begin{aligned} Z_0\left( Y;\{u\} \right) \,\,\equiv \,\,\sum _{n=1}\,\int \,\, P_n\left( Y; r_1, \dots ,r_n \right) \,\,\prod ^{n}_{i=1}\,u(r_i) d^2r_i \nonumber \\ \end{aligned}$$
(11)

where \(u(r_i)\) is an arbitrary function of \(r_i\) and \(b_i\). \(P_n\) is the probability density to find n dipoles with sizes \(r_1,\dots ,r_n\) at rapidity Y.Footnote 2 For functional of Eq. (11) we have two obvious conditions:

$$\begin{aligned}{} & {} \hbox {initial conditions:} \quad Y =0 \,\, P_n\,=\,0\,\, \hbox {for\,\,\,} n \,>\,1\,\, \nonumber \\{} & {} \quad \hbox {and}\,\, P_1 = \delta ( \varvec{r} \,-\,\varvec{r}_1)\delta (\varvec{b} - \varvec{b}_1);Z_0\left( Y =0;\{u\}\right) \,\,=\,\,u(r)\,; \nonumber \\ \end{aligned}$$
(12a)
$$\begin{aligned}{} & {} \hbox {boundary conditions:} \quad u =1\,\, Z_0\left( Y;\{u\}\right) |_{u=1}\,\,=\,\,1; \end{aligned}$$
(12b)

Equation (12b) follows from the physical meaning of \(P_n\) and represents the conservation of the total probability, while Eq. (12a) indicates that we are considering the interaction of one dipole with the target.

The Markov process can be described as the following equation for the generating functional:

$$\begin{aligned} \frac{d Z_0\left( Y;\{u\} \right) }{d Y}= & {} \,\frac{\bar{\alpha }_S}{2 \pi }\,\int \,\,d^2 r \;d^2 r' \,K\left( r | r', |\varvec{r} - \varvec{r'}|\right) \left\{ \,-u(r)\,\right. \nonumber \\{} & {} \left. +\, u(r')\,u(|\varvec{r'} - \varvec{r}|)\right\} \,\frac{\delta }{\delta u(r)} \,\, Z_0\left( Y;\{ u\} \right) \nonumber \\ \end{aligned}$$
(13)

Two terms of this equation has simple meaning of increase of the probability to find n-dipoles due to decay of one dipole to two dipoles (birth terms, the second term in Eq. (13)) and of decrease of the probability since one of n-dipoles can decay (death term, the first term in Eq. (13))

Equation (13) is general and can be used for arbitrary initial condition. In the case of Eq. (12a) it can be rewritten as the non-linear equation. Equation (13) being a linear equation with only first derivative has a general solution of the form \(Z_0\left( Y-y;\{u\}\right) \equiv Z_0\left( \{u(Y-y)\} \right) \). Inserting this solution and using the initial condition of Eq. (12a) we obtain the non-linear equation

$$\begin{aligned} \frac{d Z_0\left( Y;\{u\}\right) }{d Y}= & {} \frac{\bar{\alpha }_S}{2 \pi }\int d^2 r' \,K\left( r| r', | \varvec{r} - \varvec{r'}|\right) \nonumber \\{} & {} \times \left\{ Z_0\left( Y,\{u\}\right) - Z^2_0\left( Y,\{u\}\right) \right\} \end{aligned}$$
(14)

It is easy to see that Eq. (14) can be re-written as the Balitsky–Kovchegov equation [38, 39] for the scattering amplitude (see for example Ref. [1]).

2.2 AGK cutting rules and generating functional for the production of gluons

Based on this probability interpretation of the sum of “fan” diagrams in Ref. [54] an attempt was made to develop the probability approach for the production of the gluon using the AGK cutting rules [55, 56]. It is worthwhile mentioning that such kind of approach was successfully applied for interactions of two BFKL cascades in the simple case with zero transverse dimension [69, 70, 72]. The AGK cutting rules use that the BFKL Pomeron [2,3,4,5,6] gives the cross section of produced gluons in the specific kinematic region typical for leading log(1/x) approximation of perturbative QCD. These cutting rules allow us to expand the contribution of the exchange of n BFKL Pomerons as a definite sum of the final states with the average number of produced gluon \( k \Delta Y\), where \(k\, \le \, n\) and \(\Delta \,Y \) is the mean multiplicity for one BFKL Pomeron exchange. Actually, the AGK cutting rules introduce three different triple Pomeron vertices (see Fig. 2).

Fig. 2
figure 2

Three vertices for gluon production accordingly to AGK cutting rules for fan diagrams in the BFKL Pomeron calculus. The wavy lines denote the BFKL Pomerons. The wavy lines crossed by the dashed ones show the cut Pomerons

Full size image

The structure of the production processes is determined by the s-channel unitarity constraints for the BFKL Pomeron:

$$\begin{aligned} 2 N^{BFKL}\left( Y; r, b \right) \,\,=\,\, G^{BFKL}_{in}\left( Y;r,b\right) \end{aligned}$$
(15)

where \(N^{BFKL}\left( Y; r, b \right) \) is the contribution to the scattering amplitude by the BFKL Pomeron \( G^{BFKL}_{in}\left( Y;r,b\right) \) is the cross section of produced gluons, which was actually calculated in Ref. [2,3,4,5,6] and which is shown in Fig. 1b. In framework of the AGK cutting rules it is called the cut Pomeron which is shown in Fig. 2 by the wavy lines which are crossed by the dashed ones.

In Ref. [54] it is introduced a generalization of Eq. (11):

$$\begin{aligned}{} & {} Z \left( Y;\{u\},\{v\}\right) \nonumber \\{} & {} \quad \equiv \,\,\sum ^{\infty }_{n=0,m=0}\,\int \,\, P^m_n\left( y; r_1, \dots ,r_n; r_1,\dots , r_m \right) \,\,\nonumber \\{} & {} \qquad \times \prod ^{n}_{i=1}\,u(r_i) \prod ^{m}_{k=1}\,v(r_k) d^2r_i\,d^2r_k \end{aligned}$$
(16)

where \(P^m_n\) is the probability to find (i) n dipoles in the wave function of the fast dipole, which interact with the target at time \(\tau =0\); and (ii) m dipoles which can be detected at \(\tau =\infty \). In other words, \(P^m_n\) is the probability to have n dipoles with sizes \(r_1, \dots , r_n\) at \(\tau = 0 \) at rapidity Y, which do not survive until \(\tau =\infty \) and cannot be measured, while the dipoles with sizes \( r_1, \dots , r_m\) reach \(\tau = \infty \) and can be caught by detectors.

The initial conditions of Eq. (12a) has to be replaced by

$$\begin{aligned} Z\left( Y =0;\{u\}, \{v\}\right) \,\,=\,\,v(r) \end{aligned}$$
(17)

and we have two boundary conditions:

$$\begin{aligned}{} & {} (1)~~Z \left( Y;\{u\},\{v\}\right) |_{u=1,v=1} \,\,=\,\,1; ~~~~~\nonumber \\{} & {} \quad (2) ~~Z\left( Y; \{u\},\{ v \}\right) |_{v=2u-1} =2 \;Z_0\left( Y; \{u \}\right) \,\,-1; \end{aligned}$$
(18)

The first one comes from the conservation of probabilities while the second stems from the s-channel unitarity:

$$\begin{aligned} 2 N\left( Y, r, b\right) \,\,=\,\,\sigma _{sd}\left( Y, r,b\right) \,\,+\,\,\sigma _{in} \left( Y, r, b\right) \end{aligned}$$
(19)

where \(\sigma _{sd}\) and \(\sigma _{in}\) are the single diffraction and inelastic cross sections at fixed impact parameter b.

In Ref. [54] the AGK cutting rules for the ”fan” diagrams were reduced to the following linear equation for \( Z \left( Y;\{u\},\{\zeta = 2\,u - v\}\right) \):

$$\begin{aligned}{} & {} \frac{\partial \tilde{Z} \left( Y;\{u\},\{\zeta \}\right) }{\partial Y}\,\,=\,\,\frac{\bar{\alpha }_S}{2 \pi }\,\int \,d^2 r_2 \,K\left( r_{10}| r_{12}, r_{02}\right) \nonumber \\{} & {} \quad \times \left\{ \left( u(r_{12})\,u(r_{02})\,-\,u(r_{10}) \right) \frac{\delta \tilde{Z} \left( y;\{u\},\{\zeta \}\right) }{\delta u(r_{10})}\,\,\right. \nonumber \\{} & {} \quad \left. +\,\,\left( \zeta (r_{12})\,\zeta (r_{02})\,-\,\zeta (r_{10}) \right) \,\frac{\delta \tilde{Z} \left( y;\{u\},\{\zeta \}\right) }{\delta \zeta (r_{10})}\right\} \end{aligned}$$
(20)

Each term in Eq. (20) has the same transparent probabilistic interpretation as in Eq. (13).

2.3 The master equation for \(\sigma _n\)

Equation (20) can be used for an arbitrary initial condition. For DIS scattering the initial condition of Eq. (17) results in the non-linear equation. This equation takes the most elegant form for the generating functional which is defined as

$$\begin{aligned}{} & {} M\left( Y-Y_0; r,b\right) \nonumber \\{} & {} \quad = \,\, 1\,\,\,-\,\, Z\left( Y-Y_0; \{u\},\{ v\} \right) \nonumber \\{} & {} \quad =\,\sum ^{\infty }_{n=1,m=0}\,\,\frac{ (-1)^{n + m + 1}}{n!\,m!}\,\,\nonumber \\{} & {} \qquad \times \Bigg \{\int \,\prod ^n_{i =1}\,\,d^2r_i\,\int \,\prod ^m_{k =1}\,\,d^2r_k\,\gamma (r_i)\,\gamma _{in}(r_k) \nonumber \\{} & {} \qquad \times \frac{\delta }{\delta u(r_i) } \,\,\frac{\delta }{\delta v(r_k) }\Bigg \} \,Z\left( Y-Y_0); \{u\},\{v\}\right) \Big |_{u(r)=1, v(r)=1}\nonumber \\ \end{aligned}$$
(21)

where \(u(r) = 1 - \gamma (r)\) and \(v(r) = 1 - \gamma _{in}(r)\).

For \(M\left( Y; r,b\right) \) the non-linear equation is obtained from Eq. (20) in Ref. [54]:

$$\begin{aligned}{} & {} \frac{\partial M(Y;r_{10},b)}{\partial Y}\nonumber \\{} & {} \quad = \,\,\frac{\bar{\alpha }_S}{2 \pi }\,\int \,d^2 r_2 \,K\left( r_{10}| r_{12}, r_{02}\right) \left\{ M(Y;r_{12},b)\,\right. \nonumber \\{} & {} \qquad \left. +\, M(Y;r_{20},b)\,- \,M(Y;r_{10},b)\,\right. \nonumber \\{} & {} \qquad \left. + M(Y;r_{12},b)M(Y;r_{20},b) \,\right. \nonumber \\{} & {} \qquad -\,2\,M(Y;r_{12},b)N(Y;r_{20},b) \nonumber \\{} & {} \qquad \left. -\,2\, N(Y;r_{12},b) M(Y;r_{20},b) \,\right. \nonumber \\{} & {} \qquad \left. +\, 2 N(Y;r_{12},b) N(Y;r_{20},b) \right\} \end{aligned}$$
(22)

The first check of this equation: \(M(y;r_{10},b)\) for \(\gamma _{in}=0\) gives the cross section of diffraction production \(M(y;r_{10}, b)|_{\gamma _{in}=0} = \sigma _{sd}\). This equation coincides with the equation for the diffraction production of Ref. [73].

If we want to find a cross section with the k-produced gluons in dipole nucleus (or proton) interaction we need to calculate

$$\begin{aligned} \sigma _k\left( Y,r; b \right) \,\,\,= & {} \,\,\frac{1}{k!}\,\int \,\,\, d^2 r_i \,d^2 b_i\prod ^k_{i = 1}\,\gamma _{in}(r_i)\nonumber \\{} & {} \times \left( \frac{\delta }{\delta \gamma _{in}(r_i)}\,M \left( Y;\{\gamma \},\{\gamma _{in} \}\right) \right) \Big |_{\gamma _{in}=0} \end{aligned}$$
(23)

where \(\gamma (r)\) is the low energy elastic amplitude and \(\gamma _{in}(r) = 2 \gamma (r)\) at low energy (\(Y_0\)).

2.4 Solutions for Pomeron calculus in zero transverse dimension

For the Pomeron calculus in zero transverse dimension Eqs. (20) and (22) were solved in Ref. [72]. The solutions for the generating functions take the forms:

$$\begin{aligned} Z_0\left( Y, u\right)= & {} \,\frac{u e^{ - \Delta \,Y}}{ 1 - u \left( 1 \,-\,e^{ - \Delta \,Y} \right) }; \end{aligned}$$
(24a)
$$\begin{aligned} Z\left( Y, u, v \right)= & {} \frac{2u e^{ - \Delta \,Y}}{ 1 - u \left( 1 \,-\,e^{ - \Delta \,Y} \right) } \,\nonumber \\{} & {} -\,\frac{(2u -v) e^{ - \Delta \,Y}}{ 1 - (2u -v)\left( 1 \,-\,e^{ - \Delta \,Y} \right) }; \end{aligned}$$
(24b)

where \(\Delta \) is the intercept of the BFKL Pomeron. From Eq. (23) we obtain:

$$\begin{aligned} \sigma _k\,\,=\,\,\frac{e^{ \Delta \,Y }\,\left( e^{ \Delta \,Y}\,-\,1 \right) ^{k-1}}{\left( 1 - 2\,\gamma \left( e^{ \Delta \,Y}\,-\,1 \right) \right) ^{k+1}}\,\gamma _{in}^k \end{aligned}$$
(25)

where \(\gamma \) and \(\gamma _{in}\) are the scattering amplitude and [production cross section of two dipoles at low energy. From Eq. (15) \(\gamma _{in} = 2 \gamma \).

Using Eq. (24a) we can calculate the scattering amplitude, which has the following form:

$$\begin{aligned} N\left( Y\right) \,\,=\,\,\frac{\gamma }{1 - (1 - \gamma )\left( 1\,\,-\,\,e^{ -\Delta \,Y }\right) }\,\,=\,\, \frac{\tilde{\gamma } e^{ \Delta \,Y } }{\tilde{\gamma } e^{ \Delta \,Y }\, -\,1} \nonumber \\ \end{aligned}$$
(26)

where \(\tilde{\gamma } = \gamma /(1 - \gamma )\).

Considering \(e^{ \Delta \,Y } \) as Pomeron Green’s function and using the AGK cutting rules for the scattering amplitude of Eq. (26) we reproduce at large values of Y the same \(\sigma _k\) which follow from Eq. (25). We believe that this observation is a strong argument for that our probabilistic treatment of gluon production is correct.

3 The cross sections of gluon production deep in the saturation region

The main goal of this paper is to find \(\sigma _k\) solving Eq. (22) in the kinematic region where we have the scattering amplitude of Eq. (7). In other words, we are looking for the solutions for the scattering amplitude of the dipole with size \(r \equiv r_{01}\) and rapidity Y in the kinematic region where \(r^2 Q^2_s(Y, b)\,\,\gg \,\,1\).

3.1 The total cross section

The total cross section can be obtained considering \(M\left( Y, r, b\right) \) for \(\gamma _{in}(r_i) = 2 \gamma (r_i)\). From the unitarity constraints of Eq. (19) we expect that in our kinematic region \(\sigma _{tot}\left( Y, r,b\right) \) approaches the unitarity limit of \(\sigma _{tot} \rightarrow 2\). Introducing \(\sigma _{tot}\left( Y, r,b\right) \,\,=\,\,2\,\,-\,\,\Delta _{tot}\left( Y, r,b\right) \) and \(N \left( Y, r,b\right) \,\,=\,\,1\,\,-\,\,\Delta _0\left( Y, r, b\right) \), we can rewrite Eq. (22) in the following form. neglecting the contribution of \(\Delta _{in}^2\) or/and \(\Delta _0^2\):

$$\begin{aligned}{} & {} \frac{\partial \Delta _{tot} (Y;r_{01},b)}{\partial Y} \,\,\nonumber \\{} & {} \quad =\,\, \frac{\bar{\alpha }_S}{2 \pi } \,\, \int \limits _ {{\begin{array}{l} r_{02} \,\gg \,1/Q_s(Y)\\ r_{12}\,\gg \,1/Q_s(Y) \end{array}}}\, d^2 r_2 \,K\left( r_{01}| r_{12}, r_{02}\right) \left( \Delta _{tot} (Y;r_{02},b) \right. \nonumber \\{} & {} \quad \left. +\,\, \Delta _{tot} (Y;r_{12},b)\,\, -\, \,\Delta _{tot} (Y;r_{01},b)\right) \nonumber \\{} & {} \quad -\,2\,\frac{\bar{\alpha }_S}{2 \pi }\,\,\,\,\, \int \limits _ {{\begin{array}{l} r_{02} \,\gg \,1/Q_s(Y)\\ r_{12}\,\gg \,1/Q_s(Y) \end{array}}} \,\,\,\,\,\,\,\,\,\,\,\,\,d^2 r_2\,K\left( r_{01}| r_{12}, r_{02}\right) \nonumber \\{} & {} \quad \left( \Delta _{0} (Y;r_{02},b),\,+\,\, \Delta _{0} (Y;r_{12},b) \right) \end{aligned}$$
(27)

One can see that Eq. (27) has solution: \( \Delta _{tot} (Y;r_{01},b)\,=\,2\, \Delta _{0} (Y;r_{01},b)\). Indeed, substituting this solution into Eq. (27) we obtain the equation for \(\Delta _{0} (Y;r_{01},b)\):

$$\begin{aligned}{} & {} \frac{\partial \Delta _{0} (Y;r_{01},b)}{\partial Y} \,\,\nonumber \\{} & {} \quad =\,\, -\,\left( \frac{\bar{\alpha }_S}{2 \pi } \,\,\,\,\, \int \limits _{{\begin{array}{l} r_{02} \,\gg \,1/Q_s(Y)\\ r_{12}\,\gg \,1/Q_s(Y) \end{array}}} \,\,\,\,\,\,\,\,\,\,\,\,\,d^2 r_2 \,K\left( r_{01}| r_{12}, r_{02}\right) \right) \nonumber \\{} & {} \quad \Delta _{0} (Y;r_{01},b)\,\, =\,\,- z\,\,\Delta _{0} (Y;r_{01},b) \end{aligned}$$
(28)

which is the equation for \(\Delta _0\), that has been discussed in Ref. [49,50,51], and from which follows the asymptotic behaviour of Eq. (7).

3.2 The diffraction production

As we have discussed the master equation (see Eq. (22)) coincides with the equation of Ref. [73], which has been derived in a quite different way than it is done here. For the cross section of diffraction production we need to consider \(M(Y;r_{10},b) \) of Eq. (21) at \(\gamma _{in}\left( r\right) =0\). From Eq. (19) we expect that \(\sigma _{in}(Y; r_{10},b)\) approaches 1 at high energies. Bearing this in mind we introduce \(\sigma _{sd}\left( Y, r,b\right) \,\,=\,\,1\,\,-\,\,\Delta _{sd}\left( Y, r,b\right) \) and \(N \left( Y, r,b\right) \,\,=\,\,1\,\,-\,\,\Delta _0\left( Y, r, b\right) \). Plugging these expressions in Eq. (22) we see that

$$\begin{aligned}{} & {} \frac{\partial \Delta _{sd} (Y;r_{01},b)}{\partial Y} \,\,\nonumber \\{} & {} \quad =\,\, -\,\left( \frac{\bar{\alpha }_S}{2 \pi } \,\,\, \int \limits _ {{\begin{array}{l} r_{02} \,\gg \,1/Q_s(Y)\\ r_{12}\,\gg \,1/Q_s(Y) \end{array}}} \,\,\,d^2 r_2 \,K\left( r_{01}| r_{12}, r_{02}\right) \right) \nonumber \\{} & {} \qquad \,\Delta _{sd} (Y;r_{01},b)=\,\,- z\,\,\Delta _{sd} (Y;r_{01},b).\,\,\nonumber \\ \end{aligned}$$
(29)

In the variable z of Eq. (5) Eq. (29) takes the form:

$$\begin{aligned} \kappa \frac{d\Delta _{sd} (z)}{d \,z}=-z\Delta _{sd} (z) \end{aligned}$$
(30)

with the solution:

$$\begin{aligned} \Delta _{sd} (z) \,\,=\,\,C(z)\exp \left( - \frac{z^2}{ 2\,\kappa }\right) \end{aligned}$$
(31)

where \(\kappa \) is given by Eq. (3) and C(z) is a smooth function of z. Therefore, \(\sigma _{sd}\left( Y, r,b\right) \) at large values of Y has the form of Eq. (7) and shows the geometric scaling behaviour as it has been discussed in Ref. [73].

It is instructive to note that \(\sigma _{tot}\left( Y, r,b\right) \,\,=\,\,2\,\,-\,\,\Delta _{in}\left( Y, r,b\right) \) and \(\sigma _{sd}\left( Y, r,b\right) \,\,=\,\,1\,\,-\,\,\Delta _{sd}\left( Y, r,b\right) \) are the solutions of the same equation. We believe that this observation is the important check that the main ideas of Ref. [54], which result in deriving Eq. (22), are correct.

3.3 \(\sigma _1\left( Y, r,b\right) \)

Using Eq. (23) we can obtain the equations for \(\sigma _k\) from the master equation by differentiating this equation. First taking \(\frac{\delta }{\delta \gamma _{in}(r_i) }\) from both parts of Eq. (22) and putting \( \gamma _{in}(r_i) = 0\) we obtain the following equation for \(\sigma _1\left( Y, r,b\right) \):

$$\begin{aligned} \frac{\partial \sigma _1 (Y;r_{01},b)}{\partial Y}= & {} \,\, \frac{\bar{\alpha }_S}{2 \pi } \,\,\,\,\, \int \limits _ {{\begin{array}{l} r_{02} \,\gg \,1/Q_s(Y)\\ r_{12}\,\gg \,1/Q_s(Y) \end{array}}}\nonumber \\{} & {} \times d^2 r_2 \,K\left( r_{01}| r_{12}, r_{02}\right) \Bigg \{ \sigma _1\left( Y,r_{02},b\right) \,\nonumber \\{} & {} +\,\sigma _1\left( Y,r_{12},b\right) \,-\,\sigma _1\left( Y,r_{01},b\right) \,\,\nonumber \\{} & {} +\,\,\sigma _1\left( Y,r_{02},b\right) \,\sigma _{sd} \left( Y,r_{02},b\right) \, \nonumber \\{} & {} +\, \sigma _1\left( Y,r_{12},b\right) \,\sigma _{sd}\left( Y,r_{02},b\right) \nonumber \\ \,{} & {} -\,2\,\sigma _1\left( Y,r_{02},b\right) \,N \left( Y,r_{02},b\right) \,\nonumber \\{} & {} -\,2\, \sigma _1\left( Y,r_{12},b\right) \,N\left( Y,r_{02},b\right) \Bigg \} \end{aligned}$$
(32)

The high energy asymptotic behaviour we get from Eq. (32) substituting \(\sigma _{sd}\left( Y,r_{i,i+1},b\right) \,=\,1 - \Delta _{sd}\left( z\right) \) and \(N \left( Y, r,b\right) \,\,=\,\,1\,\,-\,\,\Delta _0\left( Y, r, b\right) \), Eq. (32) takes the following form:

$$\begin{aligned}{} & {} \frac{\partial \sigma _1 (Y;r_{01},b)}{\partial Y} \,\,\nonumber \\{} & {} \quad =\,\,-\, \left( \frac{\bar{\alpha }_S}{2 \pi } \,\,\, \int \limits _ {{\begin{array}{l} r_{02} \,\gg \,1/Q_s(Y)\\ r_{12}\,\gg \,1/Q_s(Y) \end{array}}}\! d^2 r_2 \,K\left( r_{01}| r_{12}, r_{02}\right) \right) \nonumber \\{} & {} \quad \times \Bigg \{ \,\sigma _1\left( Y,r_{01},b\right) \,-\,\,\sigma _1\left( Y,r_{02},b\right) \,\Delta _{in} \left( Y,r_{02},b\right) \,\nonumber \\{} & {} \quad -\,\, \sigma _1\left( Y,r_{12},b\right) \,\Delta _{in}\left( Y,r_{02},b\right) \Bigg \} =\,\,- z\,\sigma _1\left( Y,r_{01},b\right) \nonumber \\ \end{aligned}$$
(33)

where \( \Delta _{in}\left( Y,r_{0i},b\right) = 2 \Delta _{0}\left( Y,r_{0i},b\right) \,-\,\Delta _{sd}\left( Y,r_{0i},b\right) \). The total inelastic cross section has the form: \( \sigma _{in} = 1 - \Delta _{in}\left( Y,r_{0i},b\right) \) and the above equation for \(\Delta _{in}\) follows from the unitarity constraints (see Eq. (19)).

Neglecting the second and the third terms in the curly bracket one can see that the geometric scaling solution of Eq. (33) has the same form as Eq. (30) for \( \Delta _{sd} (z) \). Hence

$$\begin{aligned} \kappa \frac{d\, \sigma _{1} (z)}{d \,z} \,\,= & {} \,\,- z\,\, \sigma _{1} (z)~~~\hbox {with the solution}~~~\nonumber \\ \sigma _1 (z) \,\,= & {} \,\,C(z)\exp \left( - \frac{z^2}{ 2\,\kappa }\right) \end{aligned}$$
(34)

We will discuss below the influence of the neglected terms on the solution of Eq. (34)

It turns out that it is convenient to discuss the solutions in the momentum representation, where Eq. (34) takes the form of convolution. Adding and subtracting the gluon reggeization term in the momentum representation we obtain the following equation for the geometric scaling solution:

$$\begin{aligned}{} & {} \kappa \frac{d \, \sigma _{1} ({\tilde{z}})}{d \,{\tilde{z}}} \,\,=\,\,\,\, \int \frac{d^2 k'_T}{(2 \pi )^2} K\left( \varvec{k}_T,\varvec{k}'_T\right) \,\,\nonumber \\{} & {} \quad \sigma _1\left( {\tilde{z}}' \right) \,\,\,-\,\,{\tilde{z}}\,\sigma _1\left( {\tilde{z}}\right) \,\,+\,\, \Delta _{in}\left( {\tilde{z}}\right) \sigma _1\left( {\tilde{z}}\right) \end{aligned}$$
(35)

where \(K\left( \varvec{k}_T,\varvec{k}'_T\right) \) is the BFKL kernel in momentum representation:

$$\begin{aligned}{} & {} K\left( \varvec{k}_T,\varvec{k}'_T\right) \,\,\sigma _1\left( Y, \varvec{k}'_T, b \right) \,\nonumber \\{} & {} \quad =\,\frac{1}{\left( \varvec{k}_T - \varvec{k}'_T\right) ^2} \,\,\,\sigma _1\left( Y, \varvec{k}'_T, b \right) \nonumber \\{} & {} \qquad -\,\,\frac{k^2_T}{\left( \varvec{k}_T - \varvec{k}'_T\right) ^2\,\left( \left( \varvec{k}_T - \varvec{k}'_T\right) ^2\,+\,k'^2_T\right) }\,\,\sigma _1\left( Y, \varvec{k}_T, b \right) \nonumber \\ \end{aligned}$$
(36)

\({\tilde{z}}\) is a new scaling variable:

$$\begin{aligned} {\tilde{z}}\,\,\,=\,\,\kappa \,\bar{\alpha }_S\,Y \,\,-\,\,\ln k^2_T\,\,=\,\,\ln \left( \frac{Q^2_s\left( Y, b\right) }{k^2_T}\right) \end{aligned}$$
(37)

Using the Mellin transform:

$$\begin{aligned} \sigma _1\left( {\tilde{z}}, b \right) \,\,=\,\,\int \limits ^{\epsilon + i \infty }_{\epsilon - i \infty } \frac{d \gamma }{2\,\pi \,i} e^{ \gamma \,{\tilde{z}}} \,\sigma _1\left( \gamma , b\right) \end{aligned}$$
(38)

we can rewrite Eq. (35) in the form:

$$\begin{aligned} \left( \kappa \,\gamma \,\,-\,\,\chi \left( \gamma \right) \right) \sigma _1\left( \gamma , b\right) =\frac{ d \sigma _1\left( \gamma , b\right) }{d\,\,\gamma } \end{aligned}$$
(39)

with the solution

$$\begin{aligned} \sigma _1\left( \gamma , b\right) \,\,=\,\,\sigma ^{init}_{1} \left( b\right) \exp \left( \frac{1}{2}\kappa \,\gamma ^2 \,\,+\,\int ^\gamma _{\frac{1}{2}} \chi \left( \gamma '\right) d \gamma '\right) \nonumber \\ \end{aligned}$$
(40)

where \(\sigma ^{init}_1\) has to be found from the initial conditions. Plugging Eq. (40) into Eq. (38) we can take the integral over \(\gamma \) using the method of steepest decent. The equation for the saddle point takes the form:

$$\begin{aligned} {\tilde{z}}+ \kappa \gamma _{SP} \,+\, \chi \left( \gamma _{SP}\right) =0 \end{aligned}$$
(41)

Since \(\chi \left( \gamma _{SP}\right) \sim \ln \gamma _{SP}\) the value of \(\gamma _{SP} = -{\tilde{z}}/\kappa \). Hence

$$\begin{aligned} \sigma _1\left( {\tilde{z}}\right) \,\,=\,\,C\left( {\tilde{z}}\right) e^{ - \frac{{\tilde{z}}^2}{2\,\kappa }} \end{aligned}$$
(42)

with \(C\left( {\tilde{z}}\right) \) being a smooth function of \({\tilde{z}}\). Therefore, at large values of Y the solutions in coordinate and momentum representations have the same form in z and \({\tilde{z}}\), respectively. The last term in Eq. (35) leads to replacement of \({\tilde{z}}\rightarrow {\tilde{z}}- \int \limits ^{\infty }_0 d{\tilde{z}}' \,\Delta _{in}\left( {\tilde{z}}\right) \) in Eq. (42). One can see this solving the simplified equation:

$$\begin{aligned} \kappa \frac{d \, \sigma _{1} ({\tilde{z}})}{d \,{\tilde{z}}} =-\,\,{\tilde{z}}\,\sigma _1\left( {\tilde{z}}\right) \,\,+\,\, \Delta _{in}\left( {\tilde{z}}\right) \sigma _1\left( {\tilde{z}}\right) \end{aligned}$$
(43)

with the solution:

$$\begin{aligned} \sigma _1\left( {\tilde{z}}\right)= & {} \textrm{C} \exp \left( - \frac{{\tilde{z}}^2}{2\,\kappa } + \frac{1}{\kappa }\int ^{{\tilde{z}}}_0 d {\tilde{z}}' \,\Delta _{in}\left( {\tilde{z}}'\right) \right) \nonumber \\= & {} \textrm{C} \exp \left( - \frac{{\tilde{z}}^2}{2\,\kappa } + \frac{1}{\kappa } \int ^{\infty }_0 d {\tilde{z}}' \,\Delta _{in}\left( {\tilde{z}}'\right) - \underbrace{ \frac{1}{\kappa }\int ^{\infty }_{{\tilde{z}}} d {\tilde{z}}' \,\Delta _{in}\left( {\tilde{z}}'\right) }_{\ll 1}\right) \nonumber \\= & {} \mathrm{C'}\exp \left( - \frac{\left( {\tilde{z}}- \int ^{\infty }_{{\tilde{z}}} d {\tilde{z}}' \,\Delta _{in}\left( {\tilde{z}}'\right) \right) ^2}{2\,\kappa }\right) \end{aligned}$$
(44)

3.4 \(\sigma _2\left( Y, r,b\right) \)

Applying \(\frac{1}{2}\frac{\delta }{\delta \gamma _{in}(r_1)}\,\frac{\delta }{\delta \gamma _{in}(r_2) }\) to the both parts of the master equation we obtain:

$$\begin{aligned} \frac{\partial \sigma _2 (Y;r_{01},b)}{\partial Y}= & {} \frac{\bar{\alpha }_S}{2 \pi } \int \limits _ {{\begin{array}{l} r_{02} \,\gg \,1/Q_s(Y)\\ r_{12}\,\gg \,1/Q_s(Y) \end{array}}} d^2 r_2 \,K\left( r_{01}| r_{12}, r_{02}\right) \nonumber \\{} & {} \times \Bigg \{ \sigma _2\left( Y,r_{02},b\right) \nonumber \\{} & {} +\sigma _2\left( Y,r_{12},b\right) \,-\,\sigma _2\left( Y,r_{01},b\right) \,\,\nonumber \\{} & {} +\,\,\sigma _2\left( Y,r_{02},b\right) \,\sigma _{sd} \left( Y,r_{02},b\right) \,\nonumber \\{} & {} +\,\sigma _1\left( Y,r_{12},b\right) \,\nonumber \\{} & {} \times \sigma _{1}\left( Y,r_{02},b\right) \,+\,\sigma _2\left( Y,r_{12},b\right) \,\nonumber \\ {}{} & {} \qquad \sigma _{sd}\left( Y,r_{02},b\right) \nonumber \\{} & {} -\,2\,\sigma _2\left( Y,r_{02},b\right) \,N \left( Y,r_{02},b\right) \,\nonumber \\{} & {} -\,2\sigma _2\left( Y,r_{12},b\right) \,N\left( Y,r_{02},b\right) \Bigg \} \end{aligned}$$
(45)

Replacing at large Y \(\sigma _{sd}\left( Y, r,b\right) \,\,=\,\,1\,\,-\,\,\Delta _{sd}\left( Y, r,b\right) \) and \(N \left( Y, r,b\right) \,\,=\,\,1\,\,-\,\,\Delta _0\left( Y, r, b\right) \) we reduce Eq. (33) to the form:

$$\begin{aligned}&\frac{\partial \sigma _2 (Y;r_{01},b)}{\partial Y} \,\,\nonumber \\&\quad =\,\,-\, \left( \frac{\bar{\alpha }_S}{2 \pi } \, \int \limits _ {{\begin{array}{l} r_{02} \,\gg \,1/Q_s(Y)\\ r_{12}\,\gg \,1/Q_s(Y) \end{array}}}\!\! d^2 r_2 \,K\left( r_{01}| r_{12}, r_{02}\right) \right) \sigma _2\left( Y,r_{01},b\right) \nonumber \\&\quad +\,\, \frac{\bar{\alpha }_S}{2 \pi } \,\,\,\,\, \int \limits _ {{\begin{array}{l} r_{02} \,\gg \,1/Q_s(Y)\\ r_{12}\,\gg \,1/Q_s(Y) \end{array}}} d^2 r_2 \,K\left( r_{01}| r_{12}, r_{02}\right) \,\nonumber \\&\quad \times \Big \{ \,\sigma _1\left( Y, r_{02},b\right) \, \sigma _1\left( Y, r_{12},b\right) \nonumber \\&\quad + \,\sigma _2\left( Y,r_{02},b\right) \left( 2\,\Delta _0\left( Y, r_{12}, b\right) \,-\,\Delta _{sd}\left( Y, r_{12}, b\right) \right) \,\,\nonumber \\&\quad +\,\, \sigma _2\left( Y,r_{12},b\right) \left( 2\,\Delta _0\left( Y, r_{02}, b\right) \,-\,\Delta _{sd}\left( Y, r_{02}, b\right) \right) \nonumber \\ \end{aligned}$$
(46)

In momentum representation in the region with the geometric scaling behaviour Eq. (46) takes the form:

$$\begin{aligned} \kappa \frac{d \,\sigma _2\left( {\tilde{z}}\right) }{d\,{\tilde{z}}}\,\,= & {} \,\, - {\tilde{z}}\,\sigma _2\left( {\tilde{z}}\right) \,\,+\,\,2\,\left( \,\underbrace{ 2\,\Delta _0\left( {\tilde{z}}\right) \,-\,\Delta _{sd}\left( {\tilde{z}}\right) }_{ \Delta _{in}\left( {\tilde{z}}\right) } \right) \nonumber \\{} & {} \times \sigma _2\left( {\tilde{z}}\right) \,+ \,\,\sigma ^2_1\left( {\tilde{z}}\right) \end{aligned}$$
(47)

where \(\Delta _{in}\left( {\tilde{z}}\right) \) is the moment representation of \(\Delta _{in}\left( z\right) \) with \(\sigma _{in}\left( z \right) = 1 - \Delta _{in}\left( z\right) \).

The general solution to Eq. (47) is a sum of the solution to homogeneous part of the equation and the particular solution of the non-homogeneous one. The homogeneous solution has the form:

$$\begin{aligned} \sigma _2\left( {\tilde{z}}\right) \,\,=\,\,\sigma _1\left( {\tilde{z}}\right) \exp \left( - 2\int \limits ^{\infty }_{{\tilde{z}}} \Delta _{in}\left( {\tilde{z}}'\right) d {\tilde{z}}'\right) \end{aligned}$$
(48)

where \(\sigma _1\left( {\tilde{z}}\right) \) is given by Eq. (42).

We can find the initial conditions for \(\sigma _n\) by assuming that for \({\tilde{z}}\,<\,0\) only the BFKL Pomeron exchange contribute to \(\sigma _1\), while all \(\sigma _k =0\) in this kinematic region. In other words, we assume that we can neglect the “fan” BFKL Pomeron diagrams dealing only with the BFKL Pomeron exchange for \({\tilde{z}}< 0\). For this initial conditions the solution to Eq. (47) can be written as:

$$\begin{aligned} \sigma _2\left( {\tilde{z}}\right) \,\,\,=\,\,\sigma _1\left( {\tilde{z}}\right) \exp \left( - 2\int \limits ^{\infty }_{{\tilde{z}}} \Delta _{in}\left( {\tilde{z}}'\right) d {\tilde{z}}'\right) \int \limits ^{{\tilde{z}}}_0 \sigma _1\left( {\tilde{z}}'\right) \frac{d {\tilde{z}}'}{\kappa }, \nonumber \\ \end{aligned}$$
(49)

if we neglect the contributions of the order of \(\sigma _1^3\).

3.5 \(\sigma _3\left( Y, r,b\right) \) and \(\sigma _k \left( Y, r,b\right) \)

Using Eq. (23) we obtain for \(\sigma _3(Y;r_{01},b)\):

$$\begin{aligned}{} & {} \frac{\partial \sigma _3 (Y;r_{01},b)}{\partial Y} = \,\, \nonumber \\{} & {} \quad \frac{\bar{\alpha }_S}{2 \pi } \,\,\,\,\, \int \limits _ {{\begin{array}{l} r_{02} \,\gg \,1/Q_s(Y)\\ r_{12}\,\gg \,1/Q_s(Y) \end{array}}} d^2 r_2 \,K\left( r_{01}| r_{12}, r_{02}\right) \nonumber \\{} & {} \qquad \times \Bigg \{ \sigma _3\left( Y,r_{02},b\right) \,+\,\sigma _3\left( Y,r_{12},b\right) \,-\,\sigma _3\left( Y,r_{01},b\right) \,\,\nonumber \\{} & {} \qquad +\,\,\sigma _3\left( Y,r_{02},b\right) \,\sigma _{sd} \left( Y,r_{02},b\right) \, \,\nonumber \\{} & {} \qquad +\,\sigma _3\left( Y,r_{12},b\right) \,\sigma _{sd}\left( Y,r_{02},b\right) \nonumber \\{} & {} \qquad + \sigma _2\left( Y,r_{02},b\right) \,\sigma _{1}\left( Y,r_{12},b\right) \,\,\nonumber \\{} & {} \qquad +\,\,\, \sigma _2\left( Y,r_{12},b\right) \,\sigma _{1}\left( Y,r_{02},b\right) \nonumber \\{} & {} \qquad -\,2\, \sigma _3\left( Y,r_{02},b\right) \,N \left( Y,r_{02},b\right) \nonumber \\{} & {} \qquad -\,2\, \sigma _3\left( Y,r_{12},b\right) \,N\left( Y,r_{02},b\right) \Bigg \} \end{aligned}$$
(50)

Using the asymptotic expansion for \(\sigma _{sd}\) and N we obtain for the solutions with geometric scaling behaviour:

$$\begin{aligned} \kappa \frac{d \,\sigma _3\left( {\tilde{z}}\right) }{d\,{\tilde{z}}}= & {} - {\tilde{z}}\,\sigma _3\left( {\tilde{z}}\right) +\,\,2\,\Delta _{in}\left( {\tilde{z}}\right) \sigma _3\left( {\tilde{z}}\right) \,+ \,\,2\sigma _2\left( {\tilde{z}}\right) \,\sigma _1\left( {\tilde{z}}\right) \end{aligned}$$
(51)

The solution to Eq. (51) has the form:

$$\begin{aligned} \sigma _3\left( {\tilde{z}}\right) \,\,\,= & {} \,\,\sigma _1\left( {\tilde{z}}\right) \exp \left( - 2\int \limits ^{\infty }_{{\tilde{z}}} \Delta _{in}\left( {\tilde{z}}'\right) d {\tilde{z}}'\right) \Bigg (\int \limits ^{{\tilde{z}}}_0 \sigma _1\left( {\tilde{z}}'\right) \ \frac{d {\tilde{z}}'}{\kappa }\Bigg )^2 \end{aligned}$$
(52)

The general equation for \(\sigma _k\left( Y, r,b\right) \) reads as follows:

$$\begin{aligned}{} & {} \frac{\partial \sigma _k(Y;r_{01},b)}{\partial Y} \nonumber \\{} & {} \quad = \frac{\bar{\alpha }_S}{2 \pi } \,\,\,\,\, \int \limits _ {{\begin{array}{l} r_{02} \,\gg \,1/Q_s(Y)\\ r_{12}\,\gg \,1/Q_s(Y) \end{array}}} \,\,\,\,\,\,\,\,\,\,\,\,\,d^2 r_2 \,K\left( r_{01}| r_{12}, r_{02}\right) \nonumber \\{} & {} \qquad \times \Bigg \{ \sigma _k\left( Y,r_{02},b\right) \,+\,\sigma _k\left( Y,r_{12},b\right) \,-\,\sigma _k\left( Y,r_{01},b\right) \,\,\nonumber \\{} & {} \qquad +\,\,\sigma _k\left( Y,r_{02},b\right) \,\sigma _{sd} \left( Y,r_{02},b\right) \,\nonumber \\{} & {} \qquad \,+\,\sigma _k\left( Y,r_{12},b\right) \,\sigma _{sd}\left( Y,r_{02},b\right) \nonumber \\{} & {} \qquad +\sum _{j=1}^{k-1} \sigma _{k - j}\left( Y,r_{02},b\right) \,\sigma _{j}\left( Y,r_{12},b\right) \nonumber \\{} & {} \qquad -\,2\, \sigma _k\left( Y,r_{02},b\right) \,N \left( Y,r_{02},b\right) \nonumber \\{} & {} \qquad -\,2\,\sigma _k\left( Y,r_{12},b\right) \,N\left( Y,r_{02},b\right) \Bigg \} \end{aligned}$$
(53)

We can check that solution to Eq. (53) has the following form:

$$\begin{aligned} \sigma _k\left( {\tilde{z}}\right)= & {} \sigma _1\left( {\tilde{z}}\right) \exp \left( - 2\int \limits ^{\infty }_{{\tilde{z}}} \Delta _{in}\left( {\tilde{z}}'\right) d {\tilde{z}}'\right) \nonumber \\{} & {} \times \Bigg (\int \limits ^{{\tilde{z}}}_0 \sigma _1\left( {\tilde{z}}'\right) \ \frac{d {\tilde{z}}'}{\kappa }\Bigg )^{k-1} \end{aligned}$$
(54)

Note that in term \( \sum _{j=1}^{k-1} \sigma _{k - j}\left( Y,r_{02},b\right) \,\sigma _{j}\left( Y,r_{12},b\right) \) in Eq. (53) we can replace the factor \(\exp \left( - 2\int \limits ^{\infty }_{{\tilde{z}}} \Delta _{in}\left( {\tilde{z}}'\right) d {\tilde{z}}'\right) = 1\) keeping accuracy of the order of \(\sigma ^k_1\).

In Eq. (54) we have two smooth functions that have to be determined from the initial conditions: C(z) of Eq. (42) and function \(D\left( {\tilde{z}}\right) \) in the expression for \(2 \Delta _{in}\left( {\tilde{z}}\right) = D({\tilde{z}})\exp \left( - \frac{{\tilde{z}}^2}{2\,\kappa }\right) \). We believe that the only condition that we need is

$$\begin{aligned} \int \limits ^{\infty }_0 C\left( {\tilde{z}}'\right) \,\frac{d {\tilde{z}}'}{\kappa }\,=\,\,1 \end{aligned}$$
(55)

In this case the unitary constraints of Eq. (19) or/and Eq. (27):

$$\begin{aligned} \sigma _{in}\left( {\tilde{z}}\right) \,\,=\,\,\sum ^{\infty }_{k=1} \,\sigma _k\left( {\tilde{z}}\right) \,\,\propto \,\,{\tilde{z}}\end{aligned}$$
(56)

which provides that \(\sigma _{in}\left( z \right) \) in the coordinate representation reaches the unitarity limit \(\sigma _{in}\left( z \right) = 1\). The sum itself has the form:

$$\begin{aligned} \sigma _{in}\left( {\tilde{z}}\right) \,\,=\,\,\frac{ e^{ - {\tilde{z}}^2/2 \kappa }C\left( {\tilde{z}}\right) \exp \left( - \int \limits ^\infty _{{\tilde{z}}} D\left( {\tilde{z}}'\right) e^{ - {\tilde{z}}'^2/2 \kappa }\frac{d {\tilde{z}}'}{\kappa }\right) }{ \int \limits ^\infty _{{\tilde{z}}} C\left( {\tilde{z}}'\right) e^{ - {\tilde{z}}'^2/2 \kappa }\frac{d {\tilde{z}}'}{\kappa }} \nonumber \\ \end{aligned}$$
(57)

while

$$\begin{aligned}{} & {} \sigma _k\left( {\tilde{z}}\right) \,\,\nonumber \\{} & {} \quad =\,\,e^{ - {\tilde{z}}^2/2 \kappa }C\left( {\tilde{z}}\right) \exp \left( - \int \limits ^\infty _{{\tilde{z}}} D\left( {\tilde{z}}'\right) e^{ - {\tilde{z}}'^2/2 \kappa }\frac{d {\tilde{z}}'}{\kappa }\right) \nonumber \\{} & {} \qquad \times \left( 1\,\,-\,\, \int \limits ^\infty _{{\tilde{z}}} C\left( {\tilde{z}}'\right) e^{ - {\tilde{z}}'^2/2 \kappa }\frac{d {\tilde{z}}'}{\kappa } \right) ^{k-1} \end{aligned}$$
(58)

Neglecting \( \int \limits ^\infty _{{\tilde{z}}} D\left( {\tilde{z}}'\right) e^{ - {\tilde{z}}'^2/2 \kappa }\frac{d {\tilde{z}}'}{\kappa } \,\sim e^{ - {\tilde{z}}'2/2 \kappa } \,\ll \,1\) and denoting \(\int \limits ^\infty _{{\tilde{z}}} C\left( {\tilde{z}}'\right) e^{ - {\tilde{z}}'^2/2 \kappa }\frac{d {\tilde{z}}'}{\kappa } \) by \(1/\bar{n}\left( {\tilde{z}}\right) \) we see that

$$\begin{aligned}{} & {} \sigma _k\left( {\tilde{z}}\right) \,\,=\,\,e^{ - {\tilde{z}}^2/2 \kappa }C\left( {\tilde{z}}\right) \left( 1\,\,-\,\, \frac{1}{\bar{n}\left( {\tilde{z}}\right) } \right) ^{k-1}\nonumber \\{} & {} \quad \times \xrightarrow {\bar{n}\left( {\tilde{z}}\right) \,\,\gg \,\,1} e^{ - {\tilde{z}}^2/2 \kappa }C\left( {\tilde{z}}\right) \exp \Big ( - \frac{k-1}{\bar{n}\left( {\tilde{z}}\right) }\Big ) \end{aligned}$$
(59)

Equation (59) as well as all equations in this paper, are written at fixed impact parameter b. Hence we need to integrate \( \sigma _k \left( {\tilde{z}}\right) \) over b to obtain the cross section of produced k-gluons. The b-dependence enters our formulae through the saturation momentum (see Eq. (5), Eq. (9) and Eq. (37). In perturbative QCD the variable \(\xi \) in Eq. (5) is determined by the form of the eigenfunction for the BFKL equation (see Eq. (8)). However, it has been shown [74,75,76,77] that the typical b that contribute in the integrals for cross sections turn out to be of the order of \(r e^{\lambda Y}\) and they lead to the violation of the Froissart theorem [78, 79]. Therefore, we need to introduce the non-perturbative corrections at large b. Equation (59) is written in the convenient form to introduce such corrections to the saturation momentum: \(Q^2_s\left( Y,b\right) = Q^2_s\left( Y,b=0\right) \exp \left( - \mu \,b\right) \)., where \(\mu \) is a new non-perturbative parameter. The multiplicity \(\bar{n}\left( {\tilde{z}}\right) \) takes the form

$$\begin{aligned}{} & {} \bar{n}\left( {\tilde{z}}(b)\right) \nonumber \\{} & {} \quad = \Bigg (\frac{C\left( \infty \right) }{{\tilde{z}}(b=0) - \mu \,b}\exp \left( - \frac{\left( {\tilde{z}}(b=0) - \mu b\right) ^2}{2 \kappa }\right) \Bigg )^{-1}\,\,\,\nonumber \\{} & {} \quad = \,\,\frac{1}{\mathcal{A}}\, \exp \left( \frac{\left( {\tilde{z}}(b=0) - \mu b\right) ^2}{2 \kappa }\right) \end{aligned}$$
(60)

where \(\mathcal{A} \) is a smooth function of \({\tilde{z}}\).

Fig. 3
figure 3

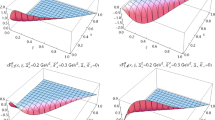
\(\sigma _k\left( {\tilde{z}},b\right) \) in Eq. (62) versus \(t = {\tilde{z}}(b=0) - \mu \,b\) at different values of k. \(\kappa =4.88, \mathcal{A} = 2\)

Full size image

The region of integration over b is \( 0< b < {\tilde{z}}(b=0)\) since for larger b the scattering amplitude is small and cannot be treated in our approach. Introducing a new variable \(t = {\tilde{z}}(b=0) - \mu \,b\) one can see that for the integral has a maximum at \( t_{SP} =\sqrt{2 \,\kappa \,\ln \left( \mathcal{A} (k-1)\right) } \) (see Fig. 3). Therefore, for for \(t_{SP} \,\le {\tilde{z}}(b=0)\) the main contribution is determined by the saddle point contribution which gives

$$\begin{aligned} \sigma _k= & {} \frac{t_{SP} (2\,\pi )^{3/2} \kappa }{e\,\mu ^2} \frac{1}{k - 1} \frac{1}{t_{SP}} \,\Big ({\tilde{z}}(b=0) - t_{SP}\Big )\nonumber \\= & {} \frac{ (2\,\pi )^{3/2} \kappa }{e\,\mu ^2} \frac{1}{(k-1) }\Bigg ({\tilde{z}}(b=0) -\sqrt{2 \,\kappa \,\ln \left( \mathcal{A} (k-1)\right) }\Bigg ) \nonumber \\ \end{aligned}$$
(61)

These \(\sigma _k\) mildly depend on \({\tilde{z}}(b=0)\) for all \(k-1 \le \,\bar{n}\left( {\tilde{z}}(b=0)\right) \). For larger k the main contributions stem from \(b \rightarrow 0\). Estimating the slope at b=0 by the method of steepest decent we obtain for \(k-1 \,> \,\bar{n}\left( {\tilde{z}}(b=0)\right) \):

$$\begin{aligned}{} & {} \sigma _k\left( {\tilde{z}}(b = 0),t=0\right) \, =\,\,\,\int \limits _{0< b < {\tilde{z}}(b=0)} \sigma _k \left( {\tilde{z}}(b)\right) d^2 b\,\,\nonumber \\{} & {} \quad =\,\,\frac{2\,\pi }{\mu ^2}\,\, \frac{\kappa ^2}{{\tilde{z}}(b=0)\,\,\bar{n}\left( {\tilde{z}}(b=0)\right) } \frac{\bar{n}^2\left( {\tilde{z}}(b=0)\right) }{(k-1)^2}\,\, \nonumber \\{} & {} \qquad \times \exp \Big ( - \frac{k - 1}{\bar{n}\left( {\tilde{z}}(b=0)\right) }\Big ) \end{aligned}$$
(62)

The notation indicates that the cross section is calculated for the forward scattering.

Using Eqs. (61) and (62) we can estimate the value of the total inelastic cross section:

$$\begin{aligned}&\sigma _{in}\left( {\tilde{z}}(b = 0),t=0\right) = \sum _{k=1}^{\infty } \sigma _k\left( {\tilde{z}}(b = 0) \right) \,\,\nonumber \\&\quad =\int \limits ^{\bar{n}\left( {\tilde{z}}(b=0)\right) }_1 d k \sigma _k\left( Eq.~(61)\right) + \int \limits _{\bar{n}\left( {\tilde{z}}(b=0)\right) }^{\infty } d k\sigma _k\left( Eq.~(62) \right) \nonumber \\&\quad = \frac{(2\,\pi )^{3/2}}{3\,e\,\mu ^2}{\tilde{z}}^3(b=0) +\frac{2\,\pi }{\mu ^2} \frac{\kappa ^2}{{\tilde{z}}(b=0)} \end{aligned}$$
(63)

From Eq. (63) one can see that the main contribution to the total inelastic cross section comes from \(k-1 \le \,\bar{n}\left( {\tilde{z}}(b=0)\right) \).

Hence, the probability to emit k gluons at large \({\tilde{z}}\) is equal to

$$\begin{aligned} p_k,&=\frac{\sigma _k\left( {\tilde{z}}(b = 0) \right) }{ \sigma _{in}\left( {\tilde{z}}(b = 0),t=0\right) }\,\,\nonumber \\&= \left\{ \begin{array}{l}\,\,\frac{ 2\, \kappa }{{\tilde{z}}^3(b=0) } \frac{\Big ({\tilde{z}}(b=0) -\sqrt{2\,\kappa \,\ln (k-1)} \Big ) }{(k-1) } ~ \hbox {for}\,\,\,k-1 \le \bar{n} \, \left( {\tilde{z}}(b=0)\right) ;\\ \\ \,\, \frac{2\,e\,\kappa ^2}{{\tilde{z}}^4(b=0)} \frac{1}{\bar{n}\left( {\tilde{z}}(b=0)\right) } \frac{\bar{n}^2\left( {\tilde{z}}(b=0)\right) }{(k-1)^2}\\ \quad \exp \Big ( - \frac{k - 1}{\bar{n}\left( {\tilde{z}}(b=0)\right) }\Big )\,\,\,\,\,\hbox {for}\,\,\, k-1 > \bar{n}\left( {\tilde{z}}(b=0)\right) ;\\ \end{array} \right. \end{aligned}$$
(64)

It is worthwhile mentioning that the probabilities \(p_k\) do not depend on the value of the typical non-perturbative \(b = 1/\mu \) since this dependence cancels in the ratio \(p_k = \sigma _k/\sigma _{in}\) (compare Eqs. (61),  (62) and  (63)). Note that \(\sigma _n \propto \,1/\mu ^2\). However, \(p_k\) depends on the way how we introduce the non-perturbative impact parameter dependence. We wish to recall that our way of taking into account the non-perturbative corrections is in accord with the Froissart theorem [78, 79] for scattering amplitude.

4 Entropy of produced gluons

From Eq. (64) we can find the value of von Neumann entropy of produced gluons:

$$\begin{aligned} S_E&=- \sum _{k=1}^{\infty } p_k \ln p_k=\!\int \limits ^{\bar{n}\left( {\tilde{z}}(b=0)\right) }_1\!\! dk \,p_k \ln p_k+\! \int \limits _{\bar{n}\left( {\tilde{z}}(b=0)\right) }^{\infty }\!\! dk p_k \ln p_k \end{aligned}$$
(65)

From Eq. (64) one can see that (i) the largest contribution stems from the first sum in Eq. (65), since the second term is suppressed as \(1/{\tilde{z}}^4(b=0)\) (see Eq. (63)); and (ii) in \(\ln p_k\) we can restrict ourselves by the term: \( - \ln (k-1)\). All other contributions are smaller. Taking the integral we obtain for large values of \({\tilde{z}}(b=0)\):

$$\begin{aligned} S_E\,\,=\,\,0.3\,\frac{{\tilde{z}}^2(b=0)}{2\,\kappa }\,\, \end{aligned}$$
(66)

In Eq. (66) we see two strange results. First, \(S_E \propto \frac{{\tilde{z}}^2(b=0)}{2\,\kappa }\). At large Y \(\frac{{\tilde{z}}^2(b=0)}{2\,\kappa }\) can be written as \(S_E \propto \frac{1}{2}{\tilde{z}}\,\bar{\alpha }_S\,Y\) which is in two times smaller the entropy for the BFKL cascade estimated in Ref. [23]. However, it turns out that actually extra \(\frac{1}{2}\) stems from our assumption about geometric scaling behaviour of the cross sections. In Ref. [23] as well as in Ref. [80], it is assumed that the cross sections are functions of Y and \({\tilde{z}}\) but not only \({\tilde{z}}\). Coming back to Eq. (33) one can see that for \(\sigma _1\left( Y, {\tilde{z}}\right) \) we obtain the solution: \(\sigma _1\left( Y, {\tilde{z}}\right) \propto \exp \left( -\,\bar{\alpha }_SY {\tilde{z}}\right) \) and \(\bar{n}\left( {\tilde{z}}(b=0)\right) \propto \,\,\exp \left( \bar{\alpha }_SY {\tilde{z}}\right) \). Finally, \(S_E \propto \alpha _SY {\tilde{z}}\) in agreement with Ref. [23]. Second, factor 0.3 in Eq. (66) stems from the integration over b. Indeed, if we estimate the entropy at fixed b using Eq. (59), we obtain \(S_E\,\,=\,\frac{{\tilde{z}}^2(b)}{2\,\kappa }\). Therefore, we can state that non -perturbative corrections that determine the large b behaviour of the saturation momentum, lead to a decrease of the entropy if we believe in estimate of Refs. [23, 80] for the entropy of the BFKL cascade at the moment of interaction with the target.

5 Conclusions

In this paper we found the multiplicity distributions for produced gluons based on the equations derived in Ref. [54]. These equations follow from the generating functional approach to Color Glass Condensate effective theory and from AGK cutting rules [55, 56]. AGK cutting rules allow us to use the principal property of the BFKL Pomeron: it gives the cross section of produced gluons in the particular kinematic region of leading log(1/x) approximation of perturbative QCD.

We solve the equations in the deep saturation region where the scattering amplitude has the form of Eq. (7). It turns out that the multiplicity distribution for \(k-1 \,<\, \bar{n} \propto \exp \left( z^2/2 \kappa \right) \) is proportional to \((1/(k-1))\Big (z- \sqrt{2\,\kappa \,\ln (k-1)}\Big )\). In this equation \(\bar{n} \propto \exp \left( z^2/2 \kappa \right) \) is the average number of produced gluons with \(z = \kappa \,\bar{\alpha }_SY - \ln Q^2\) where \(Q^2\) is the virtuality of the photon and \(Y = \ln (1/x)\). For \(k-1 \,\ge \, \bar{n} \propto \exp \left( z^2/2 \kappa \right) \) the multiplicity distribution almost reproduces the KNO scaling behaviour with the average number of gluons \( \bar{n} \propto \exp \left( z^2/2 \kappa \right) \). The value of \(\kappa \) is given by Eq. (3). The KNO function \(\Psi \left( \frac{k}{\bar{n}}\right) = \exp \left( -\,k/\bar{n}\right) \).

We estimated the value of the entropy of produced gluons which has been a subject of hot recent discussions [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. We obtain \(S_E= 0.3 \,\frac{z^2}{2 \kappa } \). First factor \( \frac{z^2}{2 \kappa } \) is twice smaller the entropy of the BFKL cascade estimated in Ref. [23] (see also Ref. [80]).Footnote 3

As we have discussed in the previous section, we believe that this difference stems from our assumption that all cross sections should have geometric scaling behaviour. Second, factor 0.3 in the equation for the entropy stems from the non-perturbative corrections, which provide the correct behaviour of the saturation momentum at large b. Therefore, we claim that the non-perturbative corrections can decrease the entropy if we believe in the estimates of Refs. [23, 80] for the entropy of the BFKL cascade. This is the most interesting result of the paper and we have to admit that we have two problems for future: (i) how coefficient 0.3 depends on the form of non-perturbative dependence of the scattering amplitude on the impact parameter; and (ii) how the running of QCD coupling could influence this coefficient.Footnote 4 The running QCD coupling needs a special investigation since it has not been introduced even in the equation for the diffraction production, which has been for long time on the market. However, in this paper we consider DIS processes in the kinematic region where the scattering amplitude has a geometric scaling behaviour. Since such behaviour preserves for running QCD coupling [1] we expect that all effects of running \(\bar{\alpha }_S\) can be absorbed in the Y dependence of the saturation scale, which differs from Eq. (2) (see Ref. [1]). The new expression for the saturation scale will change the expression for \(\tilde{z}\left( b = 0\right) \) but will not affect the integration over nonperturbative region of b.

As far as the form of non-perturbative b dependence is concerned, we wish to recall that our b dependence is in agreement with the Froissart theorem [78, 79]. We plan to consider the scattering with the nuclear target for which we know the non-perturbative impact parameter dependence (see, for example, Ref. [1]).

We would like to stress that we deliberately calculated the entropy of the produced dipoles, which can be measured and has been measured in DIS [81]: we evaluated the cross sections for n produced dipoles, estimate the probability to produce n dipoles (\(p_n\)) and determine the entropy \(S_E= - \sum _n p_n \ln p_n\). It should be noted that the entropy at fixed impact parameter is equal to \( S_E\,\,=\,\,\ln \left( \bar{n}\left( z\right) \right) = \frac{z(b)^2}{2\,\kappa }\) and coincides with the entropy of the parton cascade estimated in Refs. [23, 80]. Our results can be trusted at large values of z and it is difficult to compare it with the experimental data of Ref. [81], since it turns out that for all x in this paper \(z \le 1\) with the saturation momentum from Ref. [82].

It should be stressed that we consider DIS in the region of large z where the scattering amplitude has the geometric scaling behaviour. It means that we can discuss DIS with proton at small x, but we have to be very careful with DIS on nuclear target. Indeed, for the nuclear target the geometric scaling behaviour is valid only in the limited region even at large z [83,84,85]. In the vast part of the saturation region we do not expect the geometric scaling behaviour for the cross section of produced gluons and have to solve the equation for \(\sigma _k\) with the initial conditions:

$$\begin{aligned} \sigma _k\left( \xi , Y=Y_A\right) = \frac{1}{k!}\Omega ^k\left( Y_A,r,b\right) \exp |\left( - \,\Omega \left( Y_A,r,b\right) \right) \nonumber \\ \end{aligned}$$
(67)

where \(\Omega \left( Y_A,r,b\right) = \sigma _{\hbox { dipole-proton}} \left( Y_A,r\right) \,T_A\left( b\right) \). \(\sigma _{\hbox { dipole-proton}} \left( Y_A,r\right) = 2 \int d^2 b N_0\left( Y_A,r]\right) \) and \(N_0\) is the initial condition for the scattering amplitude of the dipole with the proton. \(Y_A = \ln A^{1/3}\) and A is the number of the nucleons in a nucleus. \(T_A\) is the optical width of nucleus, which gives the number of nucleons at given value of impact parameter b. To find the multiplicity distribution for DIS with nucleus naturally is our next problem to solve.