1 Introduction

Lorentzian wormholes (WHs) act as tunnel-like structure connecting two distinct domains of the same universe or different universes. WHs were first theorized in 1916 by Flamm [1] after the immediate discovery of Schwarzschild solution. Almost twenty years later, this idea was further developed by Einstein and Rosen [2] joining the two same Schwarzschild geometries at their horizons. This mathematical representation is called Einstein–Rosen bridge. However, the breakthrough came after the seminal work by Morris and Thorne [3]. Within the context of general relativity (GR), they developed WH solution for static and spherically symmetric spacetime. The salient features of their model is that the spacetime does not have any event horizon and possesses a stress-energy tensor which violates the null energy condition (NEC) according to the need of the geometrical structure [3]. Such violation of matter is called ‘exotic matter’ and necessary for WH geometry to maintain their mouths opened. Moreover, the WH processed a minimal surface area satisfying a flare-out condition. Moreover, Morris et al. [4] have also shown the possibility of transforming WHs into time machines. More information about WH solutions can be found in [5, 6].

For the sake of traversable WHs, the inevitable consequence is the presence of exotic matter for the existence of the stable configuration [3, 6]. within the GR context the exotic matter means the violation of the null energy condition (NEC) at least in a throat neighborhood of the WH. This is a basic difficulty in WH geometry, which can be minimized by finding conditions on it [7]. Further, Nandi et al. [8] have improved this procedure by knowing the exact amount of exotic matter in a given spacetime. It was shown in [7] that the exotic matter can be concentrated on the throat of the WH, by cutting and pasting two manifolds to obtain a new geodesically complete manifold. This new procedure is known as thin-shell WHs and need less exotic matter. Following this work Poisson and Visser [9] studied the stability of the configuration under linear perturbations. Later, thin-shell WHs have been widely discussed in Refs. [10,11,12,13].

Thus a central aspect of WH physics is related to minimized/evacuate the exotic matter. Concerning this many attempts have been taken for the last three decades. On the other hand, sustainable WH solutions have been found with phantom energy EoS in Refs. [14,15,16]. The linearized stability analysis of phantom WHs were investigated in [17]. The main reason for the consideration is that the violation of NEC is a natural consequence in the phantom regime, and also the energy density increases with time. In this spirit, WHs supported by generalized Chaplygin gas [18,19,20], polytropic phantom energy [21], varying cosmological constant [22] and ghost scalar fields [23] have been studied in detail. In Ref. [24] evolving WH solution supported by phantom energy EoS was found within GR context.

Any attempt to construct WHs requires the exotic matter in Einstein gravity. Several attempts have been made to alleviate the problem or justify them in a legitimate way. Leaving aside the GR, alternative theories of gravity have received much attention in competition with GR. Naturally, some authors have investigated WH solution in modified gravity. A few related examples of these alternatives theories are third-order Lovelock gravity [25, 26], f(Q) gravity [27,28,29], hybrid metric-Palatini gravity [30, 31] and extended theories of gravity [32, 33]. In recent times, WH solutions have also been found in scalar-tensor theories [34,35,36], Einstein–Cartan gravity [37, 38], braneworld gravity [39,40,41], higher order gravity [42, 43], higher-dimensional cosmological WHs [44], Einstein–Gauss–Bonnet theory [45,46,47]. Traversable WH solutions were further examined in f(R, T) gravity [48,49,50] with R being the Ricci scalar of a spacetime and trace of the matter stress-energy tensor T. Apart from these studies, authors in [51, 52] have showed that one may construct WH structure satisfying the NEC for normal matter threading the WH throat. In the same spirit, WHs have also been found in f(R, T) gravity without resorting to exotic matter [53,54,55].

Thus, it is always interesting to explore WH geometries in modified gravity theories in hope of finding solutions without exotic matter. In this regard, we construct models that admit the traversable WH geometries in framework of Rastall–Rainbow (R–R) gravity theory [56]. Motivated by the important effect of two distinct theories, namely, the Rastall theory [57] and the gravity’s rainbow [58], R–R gravity theory was proposed by Mota et al. [56]. This new theory has been tested in the strong-field regime. In the astrophysics context, Mota et al. [56] have studied neutron stars (NSs) assuming relativistic equations of state (EoS) of nuclear matter. They obtained stable NSs with maximum mass as high as \(M \sim 2 M_{\odot }\), but the radii are a bit too large. Same gravity theory has been considered for anisotropic stars in [59]. In [60, 61], authors have obtained stable quark stars (QSs) showing the effect of R–R parameters on the mass-radius relations. Indeed, the charged gravastars solution has recently been undertaken by [62]. In particular, WH geometry has also been explored in Ref. [63] for different kinds of EoS and showed the effect of R–R parameters on it. Given the general nature of f(R) gravity [64] and its equivalence to scale-dependent gravity, it is reasonable to inquire whether Rainbow gravity is itself a special case of one of these proposals. In the case of f(R) theory the Einstein–Hilbert action is modified by replacing the Ricci scalar R with a function of R and this construction successfully deals with the accelerated expansion of the universe problem without appealing to dark energy. The action is modified not the metric. Scale-dependent gravity uses ideas from quantum gravity and speculates that the coupling ’constants’ are in fact variables. The form of the metric is not affected. On the other hand in Rainbow gravity [56, 58], the main idea is that the metrics are affected by energy scales. For these reasons we infer that Rainbow gravity is distinct from both f(R) gravity as well as scale dependent gravity. Calzada et al. [65] recently proved that every f(R) gravity can be represented as a scale dependent gravity at the level of the action and at the level of the field equations. However, the converse is false and this is demonstrated through counterexamples.

Motivated by the ongoing prosperity of R–R gravity theory, the present article aims to explore the possible existence of WHs in the dark matter halo. Our findings concur with the recently reported results in [66] to corroborate the findings of WHs in galactic halos due to the dark matter density profiles. Beside that we have also shown the effect of R–R parameters on the geometric structure of WH solutions.

The paper is organised as follows: Sect. 2 is devoted to review the basic properties of R–R gravity theory, focusing on the development of static spherically symmetric WH configuration. In Sect. 3, we show that the galactic halo possesses the necessary properties in support for the existence of traversable WHs, due to the dark matter density profiles. In the same spirit the energy conditions are tested for the whole WH spacetime. The Sect. 4 is devoted to the summary and discussion.

2 Rastall–Rainbow gravity and the structural equation for wormhole

The R–R gravity theory has been proposed by Mota et al [56] as a combination of two modified theories, namely, the Rastall theory [57] and the Rainbow theory [58]. Below, we will discuss both theories separately and its combination also.

2.1 Rainbow theory

Doubly (or deformed) special relativity (DSR) was proposed as a combination of the modified dispersion relations (MDR) with the special relativity by Amelino-Camelia [67]. The DSR is characterized by the velocity of light c and the Planck energy \(E_p\). Further, generalization of DSR to the curved spacetime leads to a new theory called as rainbow gravity (or gravity’s rainbow) [58]. An important aspect in the formulation of gravity’s rainbow is a modified energy-momentum dispersion relation, and such modification is usually written as

$$\begin{aligned} E^{2} \Xi (x)^{2} - p^{2}\Sigma (x)^{2} = m^{2}, \end{aligned}$$
(1)

in which \(x = E/E_{p}\) represents the dimensionless energy ratio between the Planck energy \(E_{p}\) and \(E_{p}\) is the maximum energy for a test particle of mass m. Here, the correction terms \(\Xi (x)\) and \(\Sigma (x)\) are the so called rainbow functions, and responsible for the modification of the energy-momentum dispersion relation in the high-energy limit. However, in the IR limit, \(x = E/E_{p} \rightarrow 0\), which implies

$$\begin{aligned} \lim _{x\rightarrow 0} \Xi (x)=1, \quad \lim _{x \rightarrow 0} \Sigma (x)=1, \end{aligned}$$
(2)

and we recover the standard energy-momentum dispersion relation. Now, the energy dependent metric can be written in the following form [58]

$$\begin{aligned} g^{\mu \nu }(x)=\eta ^{ab} e_{a}^{\mu }(x)\otimes e_{b}^{\nu }(x), \end{aligned}$$
(3)

where \(\eta ^{ab}\) is the Minkowski metric. The energy-dependent vierbein fields \(e_{a}^{\mu }(x)\) are related to the energy-independent ones by considering a transformation implemented by

$$\begin{aligned} e_{0}^{\mu }(x)=\frac{1}{\Xi (x)} \widetilde{e}_{0}^{\mu }, \quad e_{k}^{\mu }(x)=\frac{1}{\Sigma (x)} \widetilde{e}_{k}^{\mu }. \end{aligned}$$
(4)

the index runs from \(k = (1, 2, 3)\) represents the spatial coordinates. Finally, the spherically symmetric line element of gravity’s rainbow is given as [58]

$$\begin{aligned} ds^{2}= & {} -\frac{e^{2\Phi (r)}}{\Xi ^{2}(x)} dt^{2}+ \frac{dr^2}{\Sigma ^{2}(x) \left( 1-\frac{b(r)}{r}\right) }+\frac{r^{2}}{\Sigma ^{2}(x)}(d\theta ^{2}\nonumber \\{} & {} \quad +\sin {\theta }^{2}d\phi ^{2}), \end{aligned}$$
(5)

where the functions \(\Phi (r)\) and b(r) depend on the radial coordinate r. One may also observe that the spherical coordinate (r, t, \(\theta \) and \(\phi \)) are independent of the energy of the probe particles. Since, Eq. (5) represents a WH spacetime having the following features: (i) a minimal surface area called the throat of the WH with the condition \(b(r_0)= r_0\); (ii) the throat connects two asymptotically flat regions of the spacetime; and (iii) the redshift function \(\Phi (r)\) must be finite in the entire spacetime to avoid the presence of event horizons. Furthermore, the shape function b(r) should satisfy the condition \(b^{\prime }(r_0) < 1\) at the WHs throat with the flaring-out condition \(\frac{b(r)-rb^{\prime }(r)}{b^2(r)}>0\) [3]. We should also assume that \(1-b(r)/r > 0\) for the region out of the throat. In the next section, we consider the Rastall gravity to an energy dependent Rastall gravity theory by absorbing the the energy metric and examine the effect of rainbow functions onto it.

2.2 Rastall theory

In 1972, Rastall gravity theory has been proposed as a phenomenological extension of General Relativity (GR) by Rastall [57]. According to his proposal the usual conservation law on the energy-momentum tensor does not hold in curved spacetime and replaced by the relation

$$\begin{aligned} T_{\, \, \mu ;\nu }^{\nu }=\bar{\lambda }R_{,\mu }, \end{aligned}$$
(6)

Here, the covariant derivative of stress-energy tensor is proportional to the Ricci scalar and \(\bar{\lambda }\) is an undetermined constant. One can write the Eq. (6) in more convenient form

$$\begin{aligned} \left( T_{\, \, \mu }^{\nu }-\bar{\lambda }\delta _{\, \,\mu }^{\nu }R\right) _{;\, \nu } =0. \end{aligned}$$
(7)

As a result, there exists a curvature-matter coupling, which can recast the field equation as follows

$$\begin{aligned} R^{\nu }_{\, \, \mu }-\frac{1}{2}\delta _{\, \,\mu }^{\nu }R= 8\pi G\left( T_{\, \, \mu }^{\nu }-\bar{\lambda }\delta _{\, \,\mu }^{\nu }R\right) . \end{aligned}$$
(8)

With the help of Eq. (8), the field equation of Rastall theory takes the final form where the stress-energy tensor stays on the right side, i.e.,

$$\begin{aligned} R^{\nu }_{\, \, \mu }-\frac{\lambda }{2}\delta _{\, \,\mu }^{\nu }R= 8\pi G T_{\, \, \mu }^{\nu }, \end{aligned}$$
(9)

where \(\bar{\lambda } = \frac{1 - \lambda }{16 \pi G}\) and \(\lambda \) is a Rastall free parameter that includes a nonminimal curvature-matter coupling. Interestingly, we re-obtain the standard general relativistic equation of motion when \(\bar{\lambda } = 0\) (or \(\lambda = 1\)).

2.3 Rastall–Rainbow theory

Following the above discussion, authors in [56] have pointed out that one can construct another modified gravity theory, called Rastall–Rainbow (R–R ) gravity by combining both theories in a specified manner. Thus, using the definition given by Eq. (9), we can write the modified Einstein’s field equations as a combine effect of Rainbow and Rastall gravity, under a single formalism

$$\begin{aligned} G_{\mu }{}^{\nu }(x) \equiv R_{\mu }{}^{\nu }(x) - \frac{\eta }{2}\delta _{\mu }{}^{\nu }(x)R(x) = k(x) T_{\mu }{}^{\nu }(x) , \end{aligned}$$
(10)

where \(k(x) = 8 \pi G(x)\) and G(x) represents the energy-dependent gravitational constant. As a result, we get an energy dependent field equations in R–R gravity theory. Following the argument given in [56] that the R–R theory leads to an interplay between gravity, high-energy physics and quantum theory.

Since we are searching for the WH solutions analytically, thus we assume an anisotropic stress-energy tensor of the form

$$\begin{aligned} T_{\mu \nu }=(\rho +p_t)u_\mu u_\nu + p_t g_{\mu \nu }-(p_{t}-p_{r}) \chi _{\mu }\chi _{\nu }, \end{aligned}$$
(11)

where \(u^\mu \) is the fluid 4-velocity of matter field, \(\chi _{\mu }\) is the unit radial vector so that \(\chi _{\mu } \chi ^{\mu } = 1\) and \(g_{\mu \nu }\) is the metric tensor. Here, \(\rho = \rho (r)\) represents the energy density, while \(p_r = p_r(r)\) and \(p_t = p_t (r)\) are two pressure components along the radial and transverse direction, respectively.

Rearranging the Eq. (10) in its covariant form, we can cast the usual Einstein tensor in the left side, with an effective energy-momentum tensor on the right-hand side, as follows

$$\begin{aligned} G_{\mu \nu }=R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R=8\pi G\tau _{\mu \nu }, \end{aligned}$$
(12)

where

$$\begin{aligned} \tau _{\mu \nu }=T_{\mu \nu }-\frac{(1-\lambda )}{2(1 - 2\lambda )}g_{\mu \nu }T. \end{aligned}$$
(13)

Finally, starting from (5) and (12), we get the components of the energy-momentum tensor for R–R gravity in the following forms (throughout this study, we assume \(G(x)=1\))

$$\begin{aligned}{} & {} \frac{b^{\prime }}{r^{2}} \!=\! 8\pi \bar{\rho }, \end{aligned}$$
(14)
$$\begin{aligned}{} & {} 2\left( 1\!-\!\frac{b}{r}\right) \frac{\Phi ^{\prime }}{r}\!-\!\frac{b}{r^{3}} \!=\! 8\pi \bar{p}_{r}, \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \left( 1\!-\!\frac{b}{r}\right) \left[ \Phi ^{\prime \prime }\!+\!\Phi ^{\prime 2}\!-\!\frac{b^{\prime }r\!-\!b}{2r(r\!-\!b)}\Phi ^{\prime }\!-\!\frac{b^{\prime }r\!-\!b}{2r^2(r\!-\!b)} \!+\!\frac{\Phi ^{\prime }}{r}\right] \!=\! 8\pi \bar{p}_{t}, \nonumber \\ \end{aligned}$$
(16)

where a prime denotes a derivative with respect to the radial coordinate r, and \(\bar{\rho }\) is the effective energy density with \(\bar{p}_{r}\) and \(\bar{p}_{t}\) are the effective pressure components, defined by

$$\begin{aligned} \bar{\rho }&= \frac{1}{\Sigma (x)^{2}}\left[ \alpha _{1}\rho +\alpha _{2}p_{r}+2\alpha _{2}p_{t}\right] , \end{aligned}$$
(17)
$$\begin{aligned} \bar{p}_{r}&= \frac{1}{\Sigma (x)^{2}}\left[ \alpha _{2}\rho +\alpha _{1}p_{r}-2\alpha _{2}p_{t}\right] , \end{aligned}$$
(18)
$$\begin{aligned} \bar{p}_{t}&= \frac{1}{\Sigma (x)^{2}}\left[ \alpha _{2}\rho -\alpha _{2}p_{r}+\alpha _{3}p_{t}\right] , \end{aligned}$$
(19)

with

$$\begin{aligned} \alpha _{1}=\frac{1-3\lambda }{2(1-2\lambda )}, \qquad \alpha _{2}=\frac{1-\lambda }{2(1-2\lambda )}, \qquad \alpha _{3}=-\frac{\lambda }{1-2\lambda }. \end{aligned}$$

In the following, we see that the equations (14–16) are different from the usual TOV equations for a static spherically symmetric anisotropic fluid, but one can recover this for \(\lambda =1\) and \(\Sigma =1\). Finally, we have three differential equations (14)−(16) having five unknown quantities, i.e., \(\Phi (r)\), b(r), \(\rho (r)\), \(p_r(r)\) and \(p_t(r)\), respectively. Form mathematical view point this is an undetermined system of equations. To overcome this challenge, researchers adopted different strategies elegantly. But, our current interest is to search for a stable traversable WH in dark matter galactic halos. Subsequent studies confirm our findings.

Fig. 1
figure 1

The plots displayed in this presentation illustrate b(r) and \(b(r)-b'(r) r\) using Eqs. (22), (25), and (28), respectively. The parameter values employed in the analysis are as follows: \(r_0 = 0.85\) and \(\lambda = 0.36\), \(\Sigma [x] = 0.6\), \(\rho _s = 0.003\), and \(R_s = 0.75\), 2.75, 0.30 in Planck units

Full size image

3 Commonly considered models for galactic dark matter halos

In the context of dark matter halos, several investigations have been conducted that propose the existence of galactic WHs [68,69,70]. These investigations primarily rely on rotation curves as their basis. It is worth noting that the concept of dark matter was initially proposed to explain the flat rotation curves observed in galaxies, based on measurements of the Oort constants [71] and studies of the masses of galaxy clusters [72, 73]. To account for these flat rotation curves, the Navarro-Frenk-White density profile function [74, 75] was proposed, which demonstrated improved agreement with certain dark matter halo simulations [76]. Typically, the WH throat is enclosed by distinct types of dark matter halos. The observed violation of energy conditions provides evidence for the existence of these dark halos. In this study, we aim to examine the effects and characteristics of various types of dark matter halos. Consequently, we explore embedded WH solutions that incorporate multiple diverse dark matter halo profiles in this section.

Fig. 2
figure 2

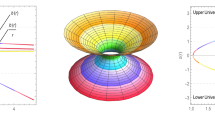
The plots presented here portray the embedding diagram (Top panel) and the embedded surface z(r) (Bottom panel) for the three analyzed DM models. The parameter values used in the analysis are as follows: \(r_0 = 0.85\) and \(\lambda = 0.36\), \(\Sigma [x] = 0.6\), \(\rho _s = 0.003\), and \(R_s = 0.75\) in Planck units

Full size image

3.1 The Navarro–Frenk–White (NFW) profile

The distribution of dark matter halo in the context of Cold Dark Matter (CDM) is commonly described by the NFW profile. The NFW profile was derived from N-body simulations [66, 74, 75, 77, 78] and can be expressed in the following form,

$$\begin{aligned} \rho \equiv \rho _{NFW}=\frac{\rho _s}{\frac{r}{R_s}\left( 1+\frac{r}{R_s}\right) ^2}. \end{aligned}$$
(20)

In the NFW profile, the parameter \(R_s\) represents the characteristic radius of the dark matter halo, while \(\rho _s\) corresponds to the density at the center of the halo (zero radius) in the universe. For the M87 galaxy, the values for the NFW profile parameters are as follows: \(\rho _s = 0.008\times 10^{7.5} M_{\odot }{\text {kpc}}^{-3}\) [79] and \(R_s = 130~kpc\) [66]. The NFW density profile provides an explanation for a wide range of models that exhibit extremely weak effects of particle collisions. This profile encompasses a vast family of models with such characteristics.

Now, utilizing Eqs. (14–16) and Eq. (20) specific to zero-tidal-force WHs, we derive the expression for the shape function as follows,

$$\begin{aligned} b(r) =\frac{8 \pi \rho _s R_s^3}{\lambda \Sigma [x]^2} \Bigg [\frac{R_s}{r+R_s}+ \log (r+R_s)\Bigg ] + \mathcal {C}_a, \end{aligned}$$
(21)

where \(\mathcal {C}_a\) is the integrating constant. This value can be determined by imposing the condition \(b(r_0) = r_0\), which leads to the following equation,

$$\begin{aligned} b(r)= & {} r_0 + \frac{8 \pi \rho _s R_s^3}{\lambda \Sigma [x]^2} \Bigg [\frac{R_s}{r+R_s}+ \log (r+R_s)\Bigg ] \nonumber \\{} & {} - \frac{8 \pi \rho _s R_s^3}{\lambda \Sigma [x]^2} \Bigg [\frac{R_s}{r_0+R_s}+ \log (r_0+R_s)\Bigg ]. \end{aligned}$$
(22)

The shape function is dependent on both parameters \(\lambda \) and \(\Sigma \), respectively. Thus, to fulfill the required conditions for a static WH solution, we examine a specific WH model with the throat located at \(r_0\) and \(b'(r_0) < 1\). This can be accomplished by assigning suitable values to the remaining parameters, namely \(\rho _s\), \(R_s\), \(\Sigma \), and \(\lambda \). By fixing these parameter values, we can generate plots of the shape function and the embedding diagram, obtained by rotating the WH configuration around the z-axis over a \(2\pi \) angle. These plots provide valuable insights into the existence and characteristics of the WH, (see the left panel of Figs. 1 and 2 to observe the plotted shape function and embedding diagram.)

Fig. 3
figure 3

The plots presented here illustrate the evolution of \(\rho \) for the three analyzed DM models. The parameter settings used for the analysis are as follows: \(r_0 = 0.85\), \(\rho _s = 0.003\), and \(R_s = 0.75\), 2.75, 0.30 in Planck units

Full size image

3.2 The Thomas–Fermi (TF) profile

In contrast to the Cold Dark Matter (CDM) model, the Bose–Einstein Condensation (BEC-DM) model demonstrates notable advantages in describing the small-scale behaviors of galaxies. In reality, within the inner regions of galaxies, particle interactions become exceedingly strong, resulting in a departure from a cold state. The density profile for the BEC-DM model can be effectively described by the Thomas–Fermi (TF) profile [80], which can be expressed as follows,

$$\begin{aligned} \rho \equiv \rho _{TF}=\rho _{s}\frac{\sin (\frac{\pi }{R_s} r)}{\frac{\pi }{R_s} r}, \end{aligned}$$
(23)

where \(\rho _{s}\) represents the center density of the BEC-DM halo and \(R_s\) corresponds to the radius at which pressure and density vanish. When compared to the NFW profile, the BEC-DM model predicts a notably lower density in the centers of galaxies. In the case of the Milky Way galaxy, the values for the BEC-DM parameters are \(\rho _s = 3.43\times 10^{7} M_{\odot }{\text {kpc}}^{-3}\) and \(R_s = 15.7\) kpc, as reported by Hou et al. [81] and Xu et al. [82].

Now, employing Eqs. (14) through (16) and Eq. (23) for zero-tidal-force WHs, we can determine the shape function as follows,

$$\begin{aligned} b(r)= & {} \frac{8 \rho _s R_s }{\lambda \Sigma [x]^2} \Bigg [\frac{R_s^2 \sin \left( \frac{\pi r}{R_s}\right) }{\pi ^2} -\frac{r R_s \cos \left( \frac{\pi r}{R_s}\right) }{\pi }\Bigg ] + \mathcal {C}_b,\nonumber \\ \end{aligned}$$
(24)

where \(\mathcal {C}_b\) is the integrating constant. We can determine its value by imposing the condition \(b(r_0) = r_0\), which leads to the following formula,

$$\begin{aligned} b(r)= & {} r_0 + \frac{8 \rho _s R_s }{\lambda \Sigma [x]^2} \Bigg [\frac{R_s^2 \sin \left( \frac{\pi r}{R_s}\right) }{\pi ^2}-\frac{r R_s \cos \left( \frac{\pi r}{R_s}\right) }{\pi }\Bigg ] \nonumber \\{} & {} - \frac{8 \rho _s R_s }{\lambda \Sigma [x]^2} \Bigg [\frac{R_s^2 \sin \left( \frac{\pi r_0}{R_s}\right) }{\pi ^2}-\frac{r_0 R_s \cos \left( \frac{\pi r_0}{R_s}\right) }{\pi }\Bigg ]. \end{aligned}$$
(25)

This second shape function is also dependent on both parameters \(\lambda \) and \(\Sigma \) and satisfies the necessary conditions for a static WH solution, specifically \(b'(r_0) < 1\) at \(r_0\). To achieve this, we can fix appropriate values for the remaining parameters, namely \(\rho _s\), \(R_s\), \(\Sigma \), and \(\lambda \). Subsequently, we can generate plots of the shape function and the embedding diagram by rotating the WH configuration around the z-axis over a \(2\pi \) angle. These plots offer valuable insights into the existence and characteristics of the WH (refer to the middle panel of Figs. 1 and 2 to observe the plotted shape function and embedding diagram).

Fig. 4
figure 4

The plots presented here illustrate the evolution of \(\rho +p_r\) for the three analyzed DM models. The parameter settings used for the analysis are as follows: \(r_0 = 0.85\), \(\rho _s = 0.003\), and \(R_s = 0.75\), 2.75, 0.30 in Planck units

Full size image

3.3 The pseudo isothermal (PI) profile

Apart from the CDM model and the BEC-DM model, there is another significant class of models associated with modified gravity theories called Modified Newtonian Dynamics (MOND) [83]. In the MOND model, the density profile is described by the PI profile, which can be expressed by the following formula,

$$\begin{aligned} \rho \equiv \rho _{PI}=\frac{\rho _s}{1+\left( \frac{r}{R_s}\right) ^2}. \end{aligned}$$
(26)

In this context, \(\rho _s\) represents the central density, while \(R_s\) represents the scale radius. For the ESO1200211 galaxy, the reported values for the parameters of the PI profile are \(\rho _s =0.0464 M_{\odot }{\text {pc}}^{-3}\) and \(R_s = 0.57\) kpc, as provided by Robles and Matos [84].

Now, using Eqs. (14)–(16) and Eq. (26) for zero-tidal-force WHs, we can calculate the shape function as follows,

$$\begin{aligned} b(r) =\frac{8 \pi \rho _s R_s^2 }{\lambda \Sigma [x]^2}\Bigg [r-R_s \tan ^{-1}\left( \frac{r}{R_s}\right) \Bigg ] +\mathcal {C}_c, \end{aligned}$$
(27)

where \(\mathcal {C}_c\) is the integrating constant. We can determine its value by imposing the condition \(b(r_0) = r_0\), which leads to,

$$\begin{aligned} b(r)= & {} r_0 + \frac{8 \pi \rho _s R_s^2 }{\lambda \Sigma [x]^2}\Bigg [r-R_s \tan ^{-1}\left( \frac{r}{R_s}\right) \Bigg ] \nonumber \\{} & {} - \frac{8 \pi \rho _s R_s^2 }{\lambda \Sigma [x]^2}\Bigg [r_0-R_s \tan ^{-1}\left( \frac{r_0}{R_s}\right) \Bigg ]. \end{aligned}$$
(28)

The third shape function considered in this context is determined by the parameters \(\lambda \) and \(\Sigma \). It satisfies the necessary conditions for a static WH solution, particularly ensuring that the derivative of the shape function with respect to the radial coordinate, denoted as \(b'(r_0)\), is less than 1 at \(r_0\). To achieve this, appropriate values for the remaining parameters, namely \(\rho _s\), \(R_s\), \(\Sigma \), and \(\lambda \), can be chosen. Subsequently, by rotating the WH configuration around the z-axis through a complete \(2\pi \) angle, we can generate plots illustrating the shape function and the embedding diagram. These plots provide valuable insights into the WH’s characteristics and existence (see the right panel of Figs. 1 and 2 for visual representations of the shape function and embedding diagram).

3.4 Energy conditions

In this section, we specifically focus on the ECs related to the matter content of the WH that are essential for achieving stability and traversability within dark matter galactic halos.

3.4.1 Energy conditions for NFW profile

Based on the preceding assumptions, the remaining two nonvanishing components of the gravity field equations can be expressed as follows,

$$\begin{aligned} p_r(r)&{=}&{-}\frac{ \rho _s R_s^3 }{ \lambda r^3 }\Bigg [\frac{r^2 ((\lambda {-}1) r_0{+}(\lambda {-}2) R_s){+}r R_s (r_0{-}R_s){+}r_0 R_s^2}{(r{+}R_s)^2 (r_0{+}R_s)}\nonumber \\{} & {} {+}\log (r{+}R_s){-}\log (r_0{+}R_s)\Bigg ] {-}\frac{r_0 \Sigma [x]^2}{8\pi r^3 }, \end{aligned}$$
(29)
$$\begin{aligned} p_t(r)&{=}&\frac{ \rho _s R_s^3 }{2\lambda }\Bigg [\frac{r^2 (r_0{-}2 \lambda (r_0{+}R_s)){+}r R_s (r_0{-}R_s)+r_0 R_s^2}{(r{+}R_s)^2 (r_0{+}R_s)}\nonumber \\{} & {} {+}\log (r{+}R_s){-}\log (r_0{+}R_s)\Bigg ]{+}\frac{r_0 \Sigma [x]^2}{16 \pi r^3}. \end{aligned}$$
(30)
Fig. 5
figure 5

The plots presented here illustrate the evolution of \(\rho +p_t\) for the three analyzed DM models. The parameter settings used for the analysis are as follows: \(r_0 = 0.85\), \(\rho _s = 0.003\), and \(R_s = 0.75\), 2.75, 0.30 in Planck units

Full size image

To analyze the ECs related to the matter content of the WH, we start by using the field equations (29)–(30) and considering the NFW density profile given by Eq. (20). In this analysis, we focus on the Null Energy Condition (NEC), which is defined by \(\rho +p_{r} \ge 0\) and \(\rho +p_{t} \ge 0\). The explicit expressions for the NEC can be obtained as follows,

$$\begin{aligned} \rho +p_r&{=}&\frac{\rho _s R_s^3 }{ \lambda r^3 }\Bigg [\frac{r (2 r{+}R_s)}{(r{+}R_s)^2}{-}\log (r{+}R_s){-}\frac{r_0}{r_0{+}R_s}{+}\log (r_0{+}R_s)\Bigg ]\nonumber \\{} & {} {-}\frac{r_0 \Sigma [x]^2}{8 \pi r^3 }, \end{aligned}$$
(31)
$$\begin{aligned} \rho {+} p_t&{=}&\frac{ \rho _s R_s^3 }{\lambda r^3}\Bigg [\frac{r (2 r{+}R_s)}{(r{+}R_s)^2}{-}\log (r{+}R_s){-}\frac{r_0}{r_0{+}R_s}{+}\log (r_0{+}R_s)\Bigg ]\nonumber \\{} & {} {-}\frac{r_0 \Sigma [x]^2}{8\pi r^3 }. \end{aligned}$$
(32)

3.4.2 Energy conditions for TF profile

Under the same assumptions as before, the remaining two nonvanishing components of the gravity field equations can be expressed as follows,

$$\begin{aligned} p_r(r)= & {} \frac{ \rho _s R_s}{ \pi ^3 \lambda r^3}\Bigg [-\left( \pi ^2 (\lambda -1) r^2+R_s^2\right) \sin \left( \frac{\pi r}{R_s}\right) \nonumber \\{} & {} +\pi r R_s \cos \left( \frac{\pi r}{R_s}\right) +R_s \left( R_s \sin \left( \frac{\pi r_0}{R_s}\right) \right. \nonumber \\{} & {} \left. -\pi r_0 \cos \left( \frac{\pi r_0}{R_s}\right) \right) \Bigg ]-\frac{ r_0 \Sigma [x]^2}{8 \pi r^3}, \end{aligned}$$
(33)
$$\begin{aligned} p_t(r)= & {} \Bigg [ \frac{ \rho _s R_s}{ \pi ^3 \lambda r^3}\Bigg [-\left( \pi ^2 (\lambda -1) r^2+R_s^2\right) \sin \left( \frac{\pi r}{R_s}\right) \nonumber \\{} & {} +\pi r R_s \cos \left( \frac{\pi r}{R_s}\right) +R_s \left( R_s \sin \left( \frac{\pi r_0}{R_s}\right) \right. \nonumber \\{} & {} \left. -\pi r_0 \cos \left( \frac{\pi r_0}{R_s}\right) \right) \Bigg ]-\frac{ r_0 \Sigma [x]^2}{ \pi r^3}\Bigg ]. \end{aligned}$$
(34)

To examine the ECs associated with the matter content of the WH, we start by employing the field equations (29)–(30) and considering the density profile given by the TF model, as described in Eq. (23). In this regard, we can derive the NEC for the TF model in the following manner,

$$\begin{aligned} \rho +p_r= & {} \frac{\rho _s R_s}{\pi ^3 \lambda r^3} \Bigg [(\pi r-R_s) (\pi r+R_s) \sin \left( \frac{\pi r}{R_s}\right) \nonumber \\{} & {} +\pi r R_s \cos \left( \frac{\pi r}{R_s}\right) +R_s \left( R_s \sin \left( \frac{\pi r_0}{R_s}\right) \right. \nonumber \\{} & {} \left. -\pi r_0 \cos \left( \frac{\pi r_0}{R_s}\right) \right) \Bigg ] -\frac{ r_0 \Sigma [x]^2}{8 \pi r^3}, \end{aligned}$$
(35)
$$\begin{aligned} \rho + p_t= & {} \frac{ \rho _s R_s}{2 \pi ^3 \lambda r^3} \Bigg [\left( \pi ^2 r^2+R_s^2\right) \sin \left( \frac{\pi r}{R_s}\right) \nonumber \\{} & {} -\pi r R_s \cos \left( \frac{\pi r}{R_s}\right) +R_s \left( \pi r_0 \cos \left( \frac{\pi r_0}{R_s}\right) \right. \nonumber \\{} & {} \left. -R_s \sin \left( \frac{\pi r_0}{R_s}\right) \right) \Bigg ]+ \frac{ r_0 \Sigma [x]^2}{16 \pi r^3}. \end{aligned}$$
(36)
Fig. 6
figure 6

The plots presented here illustrate the evolution of \(v_s^2\) for the three analyzed DM models. The parameter settings used for the analysis are as follows: \(r_0 = 0.85\), \(\rho _s = 0.003\), and \(R_s = 0.75\), 2.75, 0.30 in Planck units

Full size image

3.4.3 Energy conditions for PI profile

With the assumptions mentioned earlier, the remaining two nonvanishing components of the gravity field equations can be represented as follows,

$$\begin{aligned} p_r(r)= & {} \frac{ \rho _s R_s^2 }{ r^3\lambda \left( r^2+R_s^2\right) }\Bigg [-\lambda r^3+R_s \left( r^2+R_s^2\right) \nonumber \\{} & {} \left( \tan ^{-1}\left( \frac{r}{R_s}\right) -\tan ^{-1}\left( \frac{r_0}{R_s}\right) \right) \nonumber \\{} & {} +r^2 r_0-r R_s^2+r_0 R_s^2\Bigg ]-\frac{r_0 \Sigma [x]^2}{8 r^3\pi }, \end{aligned}$$
(37)
$$\begin{aligned} p_t(r)= & {} \frac{ \rho _s R_s^2}{2 r^3\lambda \left( r^2+R_s^2\right) } \Bigg [-2 (\lambda -1) r^3-R_s \left( r^2+R_s^2\right) \nonumber \\{} & {} \left( \tan ^{-1}\left( \frac{r}{R_s}\right) -\tan ^{-1}\left( \frac{r_0}{R_s}\right) \right) \nonumber \\{} & {} -r^2 r_0+r R_s^2-r_0 R_s^2\Bigg ]+\frac{r_0 \Sigma [x]^2}{16 \pi r^3 }\Bigg ].~~~~~~ \end{aligned}$$
(38)

By employing the field equations (29)–(30) and considering the density profile given by the PI model as described in Eq. (26), we can investigate the ECs associated with the matter content of the WH. Specifically, we focus on deriving the NEC for the PI model, which can be done in the following manner,

$$\begin{aligned} \rho +p_r= & {} \frac{ \rho _s R_s^2 }{ r^3\lambda \left( r^2+R_s^2\right) }\Bigg [R_s \left( r^2+R_s^2\right) \left( \tan ^{-1}\left( \frac{r}{R_s}\right) \right. \nonumber \\{} & {} \left. -\tan ^{-1}\left( \frac{r_0}{R_s}\right) \right) +r^2 r_0-r R_s^2+r_0 R_s^2\Bigg ]\nonumber \\{} & {} -\frac{r_0 \Sigma [x]^2}{8\pi r^3 }, \end{aligned}$$
(39)
$$\begin{aligned} \rho + p_t= & {} \frac{ \rho _s R_s^2 }{2 r^3\lambda \left( r^2+R_s^2\right) }\Bigg [-R_s \left( r^2+R_s^2\right) \left( \tan ^{-1}\left( \frac{r}{R_s}\right) \right. \nonumber \\{} & {} \left. -\tan ^{-1}\left( \frac{r_0}{R_s}\right) \right) +r^2 (2 r-r_0)+R_s^2 (r-r_0)\Bigg ]\nonumber \\{} & {} +\frac{r_0 \Sigma [x]^2}{16 \pi r^3 }.~~~~ \end{aligned}$$
(40)

3.5 Analyzing the three solutions and their stability

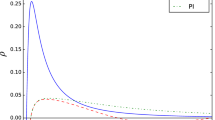
To begin our construction, we analyze the parameters separately, using values adopted in R–R gravity. We choose three values for \(\lambda =0.36,~1,~1.6\) and three values for \(\Sigma [x]=0.6,~1,~1.8\). These values are applied to the three examined dark matter models: the NWF profile, TF profile, and PI profile, respectively. The density profiles are investigated within the context of WH analyses, and their valid behavior is illustrated in Fig. 3 for the three models under consideration. Moreover, Fig. 3 demonstrates that in the vicinity of the WH throat, \(r_0=0.85\), the density remains positive in both the NFW and PI models. However, in the TF model, the density is positive at the throat but becomes negative at a certain distance. By considering specific values for the parameters: \(\lambda =0.36,~1,~1.6\), \(\Sigma [x]=0.6,~1,~1.8\), \(\rho _s=0.003\), and \(R_s=0.75\), as shown in Fig. 3, it can be confirmed that the density profiles exhibit the expected behavior and are consistent with the chosen parameter values. In Fig. 4, we present plots of \(\rho +p_r\) by using the following parameter values: \(r_0=0.85\), \(\lambda =0.36,~1,~1.6\), \(\Sigma [x]=0.6,~1,~1.8\), \(\rho _s=0.003\), and \(R_s=0.75\). We observe that \(\rho +p_r<0\) in all three cases. It is worth noting that when \(\lambda =1\) and \(\Sigma =1\), we obtain the GR solution for dark matter halo geometries. Subsequently, we plot \(\rho +p_t\) as shown in Fig. 5 with the same parameter sets. It is evident that \(\rho +p_t>0\) throughout the spacetime. This violation of the NEC arises due to the flaring-out condition. By employing the same analysis, we also determine the NEC of the WH solution at the throat. Consistently, we find that \(\rho +p_r<0\) and \(\rho +p_t>0\). We see in the vicinity of the WH throat, the NEC is violated. Upon examining the earlier analysis of the ECs, it is evident that the influence of different density profiles is quite similar. Although the three models considered are applied in distinct scenarios, they share certain properties in WH formation. This phenomenon is visually evident as some behaviors related to ECs practically coincide. In contrast, in scenarios involving very high densities and microscopic WHs, as anticipated, the model with the most significant deviation from GR prevails over the others.

Let us now turn our attention to the stability analysis of the static solutions described above, focusing on the adiabatic sound velocity denoted as \(v_s^2 = \frac{\partial {<p>}}{\partial {\rho }}\). Here, \(<p>\) represents the average pressure across the three spatial dimensions, specifically given by \(<p> = \frac{1}{3}(p_r + 2p_t)\). It is worth noting that this property holds true under the constraint \(0 \le v_s^2 < 1\).

By incorporating Eqs. (20), (23), and (26), along with Eqs. (29), (30), (33), (34), (37), and (38), we can calculate the explicit expressions for the adiabatic sound velocity corresponding to the three analyzed models using the following formula,

$$\begin{aligned} v_s^2 = \frac{d<p>}{dr} \left( \frac{d\rho }{dr}\right) ^{-1}. \end{aligned}$$
(41)

The adiabatic sound velocity plays a critical role in ensuring the stability of the solutions. It enables us to investigate the propagation of perturbations within the throat and verify the validity of our approximations for the ratio of the WH throat radius to the compactified space coordinate. Interestingly, the adiabatic sound velocity exhibits a distinct behavior with respect to the compactified space coordinate, as depicted in Fig. 6. Notably, within this compactified space, we observe that the flaring-out condition and stability conditions are simultaneously satisfied.

4 Concluding remarks

Our aim in this article is to find the possibility of having Lorentzian WHs in R–R gravity theory. The recently proposed R–R theory as a combination of the Rastall and rainbow theories has attracted a lot of interest in astrophysics and beyond. This theory may also be treated as a generalization of the Rastall gravity to an energy dependent Rastall theory. Here, our main motivation for considering WH solutions in dark matter halos around active galaxies. This was first pointed out in Ref. [69] that galactic halo would be a favourable location in existence of WHs. Thus, in order to obtain a complete description of WHs, we consider three different kinds of matter distribution within a halo (known as its ‘density profile’), such as (i) the Navarro–Frenk–White (NFW) profile, (ii) the Thomas–Fermi (TF) profile and (iii) the pseudo isothermal (PI) profile, respectively.

Next, using the field equations and density profiles, we obtain the shape function satisfying the necessary conditions to have WH solutions, see Figs. 1 and 2. Then, we investigate the energy conditions using those models under consideration. We see that the matter content WHs violate the NEC at the throat and it’s neighbourhood, as can be readily verified from Figs. 3, 4 and 5. Interestingly, the behaviour of ECs are almost similar in every cases under consideration. Finally, we examine the stable of the solution via adiabatic sound velocity. This requirement is also satisfied depending on the model parameters \(\lambda \) and \(\Sigma \), as shown in Fig. 6. The results illustrate that WHs could exists in galactic halo region, but needed more astrophysical datasets to confirm their possible existence.