The path to $\hbox {N}^3\hbox {LO}$ parton distributions

Abstract

We extend the existing leading (LO), next-to-leading (NLO), and next-to-next-to-leading order (NNLO) NNPDF4.0 sets of parton distribution functions (PDFs) to approximate next-to-next-to-next-to-leading order ($\hbox {aN}^3\hbox {LO}$). We construct an approximation to the $\hbox {N}^3\hbox {LO}$ splitting functions that includes all available partial information from both fixed-order computations and from small and large x resummation, and estimate the uncertainty on this approximation by varying the set of basis functions used to construct the approximation. We include known $\hbox {N}^3\hbox {LO}$ corrections to deep-inelastic scattering structure functions and extend the FONLL general-mass scheme to $\mathcal {O}\left( \alpha _s^3\right)$ accuracy. We determine a set of $\hbox {aN}^3\hbox {LO}$ PDFs by accounting both for the uncertainty on splitting functions due to the incomplete knowledge of $\hbox {N}^3\hbox {LO}$ terms, and to the uncertainty related to missing higher corrections (MHOU), estimated by scale variation, through a theory covariance matrix formalism. We assess the perturbative stability of the resulting PDFs, we study the impact of MHOUs on them, and we compare our results to the $\hbox {aN}^3\hbox {LO}$ PDFs from the MSHT group. We examine the phenomenological impact of $\hbox {aN}^3\hbox {LO}$ corrections on parton luminosities at the LHC, and give a first assessment of the impact of $\hbox {aN}^3\hbox {LO}$ PDFs on the Higgs and Drell–Yan total production cross-sections. We find that the $\hbox {aN}^3\hbox {LO}$ NNPDF4.0 PDFs are consistent within uncertainties with their NNLO counterparts, that they improve the description of the global dataset and the perturbative convergence of Higgs and Drell–Yan cross-sections, and that MHOUs on PDFs decrease substantially with the increase of perturbative order.

1 Introduction

Calculations of hard-scattering cross-sections at fourth perturbative order in the strong coupling, i.e. at next-to-next-to-next-to-leading order ($\hbox {N}^3\hbox {LO}$), have been available for a long time for massless deep-inelastic scattering (DIS) [1,2,3,4], and have more recently become available for a rapidly growing set of hadron collider processes. These include inclusive Higgs production in gluon-fusion [5, 6], bottom-fusion [7], in association with vector bosons [8], and in vector-boson-fusion [9], Higgs pair production [10], inclusive Drell–Yan production [11, 12], differential Higgs production [13,14,15,16,17], and differential Drell–Yan distributions [18, 19], see [20] for an overview.

In order to obtain predictions for hadronic observables with this accuracy, these partonic cross-sections must be combined with parton distribution functions (PDFs) determined at the same perturbative order. These, in turn, must be determined by comparing to experimental data theory predictions computed at the same accuracy. The main bottleneck in carrying out this programme is the lack of exact expressions for the $\hbox {N}^3\hbox {LO}$ splitting functions that govern the scale dependence of the PDFs: for these only partial information is available [21,22,23,24,25,26,27,28,29,30,31]. This information includes a set of integer N-Mellin moments, terms proportional to $n_f^k$ with $k\ge 1$, and the large- and small-x limits. By combining these partial results it is possible to attempt an approximate determination of the $\hbox {N}^3\hbox {LO}$ splitting functions [30, 32], as was successfully done in the past at NNLO [33].

At present a global PDF determination at $\hbox {N}^3\hbox {LO}$ must consequently be based on incomplete information: the approximate knowledge of splitting functions, and full knowledge of partonic cross-sections only for a subset of processes. A first attempt towards achieving this was recently made in Ref. [32], where the missing theoretical information on $\hbox {N}^3\hbox {LO}$ calculations was parametrized in terms of a set of nuisance parameters, which were determined together with the PDFs from a fit to experimental data.

Here we adopt a somewhat different strategy. Namely, we use a theory covariance matrix formalism in order to account for the missing perturbative information. It was shown in Ref. [34] that nuclear uncertainties can be included through a theory covariance matrix, and it was further shown in Refs. [35, 36] how such a theory covariance matrix can be constructed to account for missing higher-order uncertainties (MHOUs), estimated through renormalization and factorization scale variation. Here we will use the same formalism in order to also construct a theory covariance matrix for incomplete higher-order uncertainties (IHOUs), namely, those related to incomplete knowledge of the $\hbox {N}^3\hbox {LO}$ theory, specifically for the splitting functions and for the massive DIS coefficient functions. Equipped with such theory covariance matrices, we can perform a determination of PDFs at “approximate $\hbox {N}^3\hbox {LO}$” (hereafter denoted $\hbox {aN}^3\hbox {LO}$), in which the theory covariance matrix accounts both for incomplete knowledge of $\hbox {N}^3\hbox {LO}$ splitting functions and massive coefficient functions (IHOUs), and for missing $\hbox {N}^3\hbox {LO}$ corrections to the partonic cross-sections for hadronic processes (MHOUs).

We will thus present the $\hbox {aN}^3\hbox {LO}$ NNPDF4.0 PDF determination, to be added to the existing LO, NLO and NNLO sets [37], as well as the more recent NNPDF4.0 MHOU PDFs [38] that also include MHOUs in the PDF uncertainty. Besides using a different methodology to the MSHT20 study [32], here we are also able to include more recent exact results [28,29,30,31] that stabilize the $\hbox {N}^3\hbox {LO}$ splitting function parametrisation. Our construction is implemented in the open-source NNPDF framework [39]. Specifically, our $\hbox {aN}^3\hbox {LO}$ evolution is implemented in EKO [40] and the $\hbox {N}^3\hbox {LO}$ DIS coefficient functions, including the FONLL general-mass scheme, in YADISM [41]. With PDFs determined from the same global dataset and using the same methodology at four consecutive perturbative orders it is now possible to assess carefully perturbative stability and provide a reliable uncertainty estimation.

The outline of this paper is as follows. In Sect. 2 we construct an approximation to the $\hbox {N}^3\hbox {LO}$ splitting functions based on all known exact results and limits. We compare it with the MSHT approximation [32] as well as with the more recent approximation of Refs. [28,29,30]. In Sect. 3 we discuss available and approximate $\hbox {N}^3\hbox {LO}$ corrections to hard cross-sections: specifically, DIS coefficient functions, including a generalization to this order of the FONLL [42,43,44] method for the inclusion of heavy quark mass effects, and the Drell–Yan cross-section. In Sect. 4 we present the main results of this work, namely the $\hbox {aN}^3\hbox {LO}$ NNPDF4.0 PDF set, based on the results of Sects. 2 and 3. Perturbative convergence before and after the inclusion of MHOUs is discussed in detail, and results are compared to those of the MSHT group [32]. A first assessment of the impact of $\hbox {aN}^3\hbox {LO}$ PDFs on Drell–Yan and Higgs production is presented in Sect. 5. Finally, a summary and outlook on future developments are presented in Sect. 6. Expressions for the anomalous dimensions parametrized in Sects. 2.3, 2.4 are given in Appendix A.

2 Approximate $\hbox {N}^3\hbox {LO}$ evolution

We proceed to the construction and implementation of $\hbox {aN}^3\hbox {LO}$ evolution. We first describe our strategy to approximate the $\hbox {N}^3\hbox {LO}$ evolution equations, the way this is used to construct $\hbox {aN}^3\hbox {LO}$ anomalous dimensions and splitting functions, and to estimate the uncertainty in the approximation and its impact on theory predictions. We then use this strategy to construct an approximation in the nonsinglet sector, where accurate results have been available for a while [22], and benchmark it against these results. We then present our construction of $\hbox {aN}^3\hbox {LO}$ singlet splitting functions, examine our results, their uncertainties and their perturbative behavior, and also how they relate to NLL small-x resummation. We next describe our implementation of $\hbox {aN}^3\hbox {LO}$ evolution and study the impact of $\hbox {aN}^3\hbox {LO}$ on the perturbative evolution of PDFs. Finally, we compare our $\hbox {aN}^3\hbox {LO}$ singlet splitting functions to those of the MSHT group and to the recent results of [28,29,30].

2.1 Construction of the approximation

We write the QCD evolution equations as

$$\begin{aligned} \mu ^2 \frac{\partial f_i(x,\mu ^2)}{\partial \mu ^2} = \int \limits _{x}^{1} \frac{dz}{z} P_{ij} (x/z,a_s(\mu ^2)) f_j(z, \mu ^2), \end{aligned}$$

(2.1)

where $f_i(x,\mu ^2)$ is a vector of PDFs and, with $n_f$ active quark flavors, the $\left( 2n_f+1 \right) \times \left( 2n_f+1 \right)$ splitting function matrix $P_{ij}(x,a_s(\mu ^2))$ is expanded perturbatively as

$$\begin{aligned} P_{ij}(x,a_s(\mu ^2))= & {} a_s P_{ij}^{(0)}(x) + a_s^2 P_{ij}^{(1)}(x) + a_s^3 P_{ij}^{(2)}(x) \nonumber \\{} & {} + a_s^4 P_{ij}^{(3)}(x) + {\mathcal {O}}\left( a_s^5\right) . \end{aligned}$$

(2.2)

in powers of the strong coupling $a_s(\mu ^2) = \alpha _s(\mu ^2)/4\pi$.

Defining Mellin space PDFs $f_i(N,\mu ^2)$ (denoted in a slight abuse of notation by the same symbol as the x-space PDFs), and anomalous dimensions $\gamma _{ij}(N,a_s(\mu ^2))$ as minus the Mellin transforms of splitting functions,

$$\begin{aligned} f_i(N,\mu ^2)&= {\mathcal {M}}[f_i(x,\mu ^2)](N) \nonumber \\&= \int \limits _0^1 dx\,x^{N-1}f_i(x,\mu ^2) \end{aligned}$$

(2.3)

$$\begin{aligned} \gamma _{ij}(N,a_s(\mu ^2))&= {-}{\mathcal {M}}[P_{ij}(x,a_s(\mu ^2))](N) \nonumber \\&= - \int \limits _0^1 dx\,x^{N-1}P_{ij}(x,a_s(\mu ^2)) \end{aligned}$$

(2.4)

the evolution equations become

$$\begin{aligned} \mu ^2 \frac{\partial f_i(N,\mu ^2)}{\partial \mu ^2} = -\gamma _{ij} (N,a_s(\mu ^2)) f_j(N, \mu ^2), \end{aligned}$$

(2.5)

where the perturbative expansion of the anomalous dimensions is

$$\begin{aligned} \gamma _{ij}(N,a_s(\mu ^2))= & {} a_s \gamma _{ij}^{(0)}(N) + a_s^2 \gamma _{ij}^{(1)}(N)+ a_s^3 \gamma _{ij}^{(2)}(N) \nonumber \\{} & {} + a_s^4 \gamma _{ij}^{(3)}(N) + {\mathcal {O}}\left( a_s^5\right) . \end{aligned}$$

(2.6)

The $\left( 2n_f+1 \right) \times \left( 2n_f+1 \right)$ matrix of anomalous dimensions has seven independent entries (see e.g. [45]), driving the evolution of various PDF combinations as follows:

• All nonsinglet combinations

  $$\begin{aligned} q^{\pm }_{ij}&= q^\pm _i-{\bar{q}}^\pm _j, \end{aligned}$$

  (2.7)
  $$\begin{aligned} \quad q^\pm _i&=q_i\pm {{\bar{q}}}_i \end{aligned}$$

  (2.8)

  satisfy decoupled evolution equations with the same two anomalous dimension $\gamma _{\textrm{ns},\pm }$; note that the plus and minus variants of $\gamma _{\textrm{ns},\pm }$ start differing from each other already at NLO.

• The total valence combination

  $$\begin{aligned} V=\sum _{i=1}^{n_f} q^-_i \end{aligned}$$

  (2.9)

  satisfies a decoupled evolution equation with an anomalous dimension

  $$\begin{aligned} \gamma _{\textrm{ns,v}}= \gamma _\textrm{ns,s}+\gamma _{\textrm{ns},-} \, ; \end{aligned}$$

  (2.10)

  note that the flavor-independent “sea” contribution $\gamma _{\textrm{ns,s}}$ starts being nonzero only at NNLO.

• The singlet combination

  $$\begin{aligned} \Sigma = \sum _{i=1}^{n_f} q_i^+ \end{aligned}$$

  (2.11)

  mixes with the gluon

  $$\begin{aligned}{} & {} \mu ^2 \frac{\partial }{\partial \mu ^2} \begin{pmatrix} \Sigma (N,\mu ^2) \\ g(N,\mu ^2) \end{pmatrix} \nonumber \\{} & {} \quad = - \begin{pmatrix} \gamma _{qq}(N,a_s(\mu ^2)) &{} \gamma _{qg}(N,a_s(\mu ^2)) \\ \gamma _{gq}(N,a_s(\mu ^2)) &{} \gamma _{gg}(N,a_s(\mu ^2)) \\ \end{pmatrix}\nonumber \\{} & {} \qquad \times \begin{pmatrix} \Sigma (N,\mu ^2) \\ g (N,\mu ^2)\end{pmatrix}. \end{aligned}$$

  (2.12)

  The quark-quark entry of the anomalous dimension matrix can be further decomposed into nonsinglet and pure singlet contributions according to

  $$\begin{aligned} \gamma _{qq} = \gamma _{\textrm{ns},+} + \gamma _{{qq},\textrm{ps}}, \end{aligned}$$

  (2.13)

  where the pure singlet contribution $\gamma _{{qq},\textrm{ps}}$ starts at NLO.

There are thus seven independent contributions: three in the nonsinglet sector, $\gamma _{\textrm{ns},\pm }$ and $\gamma _{\textrm{ns,s}}$, and four in the singlet sector, $\gamma _{{qq},\textrm{ps}}$, $\gamma _{{qg}}$, $\gamma _{{gq}}$, and $\gamma _{{gg}}$. In turn, each of these anomalous dimensions can be expanded according to Eq. (2.6). Our goal is to determine an approximate expression for the corresponding seven $\gamma _{ij}^{(3)}(N)$ $\hbox {N}^3\hbox {LO}$ terms.

The information that can be exploited in order to achieve this goal comes from three different sources: (1) full analytic knowledge of contributions to the anomalous dimensions proportional to the highest powers of the number of flavors $n_f$; (2) large-x and small-x resummations provide all-order information on terms that are logarithmically enhanced by powers of $\ln (1-x)$ and $\ln x$ respectively; (3) analytic knowledge of a finite set of integer moments. We construct an approximation based on this information by first separating off the analytically known terms (1–2), then expanding the remainder on a set of basis functions and using the known moments to determine the expansion coefficients. Finally, we vary the set of basis functions in order to obtain an estimate of the uncertainties.

Schematically, we proceed as follows:

• 1. We include all terms in the expansion

  $$\begin{aligned} \gamma _{ij}^{(3)}(N){} & {} = \gamma _{ij}^{(3,0)}(N) + n_f \gamma _{ij}^{(3,1)}(N) \nonumber \\{} & {} \quad + n_f^2 \gamma _{ij}^{(3,2)}(N) + n_f^3 \gamma _{ij}^{(3,3)}(N), \end{aligned}$$

  (2.14)

  of the anomalous dimension in powers of $n_f$ that are fully or partially known analytically. We collectively denote such terms as $\gamma _{ij,n_f}^{(3)}(N)$.

• 2. We include all terms from large-x and small-x resummation, to the highest known logarithmic accuracy, including all known subleading power corrections in both limits. We denote these terms as $\gamma _{ij,N\rightarrow \infty }^{(3)}(N)$ and $\gamma _{ij,N\rightarrow 0}^{(3)}(N)$, $\gamma _{ij,N\rightarrow 1}^{(3)}(N)$ respectively. Possible double counting coming from the overlap of these terms with $\gamma _{ij,n_f}^{(3)}(N)$ is removed.

• 3. We write the approximate anomalous dimension matrix element $\gamma _{ij}^{(3)}(N)$ as the sum of the terms which are known exactly and a remainder ${\widetilde{\gamma }}_{ij}^{(3)}(N)$ according to

  $$\begin{aligned} \gamma _{ij}^{(3)}(N){} & {} = \gamma _{ij,n_f}^{(3)}(N) + \gamma _{ij,N\rightarrow \infty }^{(3)}(N) + \gamma _{ij,N\rightarrow 0}^{(3)}(N) \nonumber \\ {}{} & {} \quad + \gamma _{ij,N\rightarrow 1}^{(3)}(N) + {\widetilde{\gamma }}_{ij}^{(3)}(N). \end{aligned}$$

  (2.15)

  We determine the remainder as a linear combination of a set of $n^{ij}$ interpolating functions $G^{ij}_\ell (N)$ (kept fixed) and $H^{ij}_\ell (N)$ (to be varied)

  $$\begin{aligned} {\widetilde{\gamma }}_{ij}^{(3)}(N) = \sum _{\ell =1}^{n^{ij }-n_H} b^{ij}_\ell G^{ij}_\ell (N) +\sum _{\ell =1}^{n_H} b^{ij}_{n^{ij} -2+\ell } H^{ij}_{\ell }(N), \end{aligned}$$

  (2.16)

  with $n^{ij}$ equal to the number of known Mellin moments of $\gamma _{ij}^{(3)}(N)$. We determine the coefficients $b^{ij}_\ell$ by equating the evaluation of ${\widetilde{\gamma }}_{ij}^{(3)}(N)$ to the known moments of the splitting functions.

• 4. In the singlet sector, we take $n_H=2$ and we make ${\widetilde{N}}_{ij}$ different choices for the two functions $H^{ij}_\ell (N)$, by selecting them out of a list of distinct basis functions (see Sect. 2.4 below). Thereby, we obtain ${\widetilde{N}}_{ij}$ expressions for the remainder ${\widetilde{\gamma }}_{ij}^{(3)}(N)$ and accordingly for the $\hbox {N}^3\hbox {LO}$ anomalous dimension matrix element ${\gamma }_{ij}^{(3)}(N)$ through Eq. (2.15). These are used to construct the approximate anomalous dimension matrix and the uncertainty on it, in the way discussed in Sect. 2.2 below. In the nonsinglet sector instead, we take $n_H=0$, i.e. we take a unique answer as our approximation, and we neglect the uncertainty on it, for reasons to be discussed in greater detail at the end of Sect. 2.3.

2.2 The approximate anomalous dimension matrix and its uncertainty

The procedure described in Sect. 2.1 provides us with an ensemble of ${\widetilde{N}}_{ij}$ different approximations to the $\hbox {N}^3\hbox {LO}$ anomalous dimension, denoted $\gamma _{ij}^{(3),\,(k)}(N)$, $k=1,\dots {\widetilde{N}}_{ij}$ . Our best estimate for the approximate anomalous dimension is then their average

$$\begin{aligned} \gamma _{ij}^{(3)}(N)= \frac{1}{{\widetilde{N}}_{ij}}\sum _{k=1}^{{\widetilde{N}}_{ij}} \gamma _{ij}^{(3),\,(k)}(N). \end{aligned}$$

(2.17)

We include the uncertainty on the approximation, and the ensuing uncertainty on $\hbox {N}^3\hbox {LO}$ theory predictions, using the general formalism for the treatment of theory uncertainties developed in Refs. [34,35,36]. Namely, we consider the uncertainty on each anomalous dimension matrix element due to its incomplete knowledge as a source of uncertainty on theoretical predictions, uncorrelated from other sources of uncertainty, and neglecting possible correlations between our incomplete knowledge of each individual matrix element $\gamma _{ij}^{(3)}$. This uncertainty on the incomplete higher ($\hbox {N}^3\hbox {LO}$) order terms (incomplete higher order uncertainty, or IHOU) is then treated in the same way as the uncertainty due to missing higher order terms (missing higher order uncertainty, or MHOU).

Namely, we construct the shift of theory prediction for the m-th data point due to replacing the central anomalous dimension matrix element $\gamma _{ij}^{(3)}(N)$, Eq. (2.17), with each of the instances $\gamma _{ij}^{(3),\,(k)}(N)$, viewed as an independent nuisance parameter:

$$\begin{aligned} \Delta _m(ij,k)= T_{m}(ij,k) - {{\bar{T}}}_{m}, \end{aligned}$$

(2.18)

where ${{\bar{T}}}_{m}$ is the prediction for the m-th datapoint obtained using the best estimate Eq. (2.17) for the full anomalous dimension matrix, while $T_{m}(ij,k)$ is the prediction obtained when the the ij matrix element of our best estimate is replaced with the k-th instance $\gamma _{ij}^{(3),\,(k)}(N)$.

We then construct the covariance matrix over theory predictions for individual datapoints due to the IHOU on the ij $\hbox {N}^3\hbox {LO}$ matrix element as the covariance of the shifts $\Delta _m(ij,k)$ over all ${\widetilde{N}}_{ij}$ instances:

$$\begin{aligned} \text {cov}^{(ij)}_{mn} = \frac{1}{{\widetilde{N}}_{ij}-1} \sum _{k=1}^{{\widetilde{N}}_{ij} }\Delta _m(ij,k)\Delta _n(ij,k). \end{aligned}$$

(2.19)

We recall that we do not associate an IHOU to the nonsinglet anomalous dimensions and we assume conservatively that there is no correlation between the different singlet anomalous dimension matrix elements. Thus we can write the total contribution to the theory covariance matrix due to IHOU as

$$\begin{aligned} \text {cov}^\text {IHOU}_{mn} = \text {cov}^{(gg)}_{mn} +\text {cov}^{(gq)}_{mn} +\text {cov}^{(qg)}_{mn} +\text {cov}^{(qq)}_{mn}. \end{aligned}$$

(2.20)

The mean square uncertainty on the anomalous dimension matrix element itself is then determined, by viewing it as a pseudo-observable, as the variance

$$\begin{aligned} (\sigma _{ij}(N))^2= \frac{1}{{\widetilde{N}}_{ij}-1} \sum _{k=1}^{{\widetilde{N}}_{ij}} \left( \gamma _{ij}^{(3),\,(k)}(N)-\gamma _{ij}^{(3)}(N)\right) ^2.\nonumber \\ \end{aligned}$$

(2.21)

2.3 $\hbox {aN}^3\hbox {LO}$ anomalous dimensions: the nonsinglet sector

Information on the Mellin moments of nonsinglet anomalous dimensions is especially abundant, in that eight moments of $\gamma _{\textrm{ns},\pm }^{(3)}$ and nine moments of $\gamma _{\textrm{ns,s}}^{(3)}$ are known. An approximation based on this knowledge was given in Ref. [22]. More recently, further information on the small-x behavior of $\gamma _{\textrm{ns},\pm }^{(3)}$ was derived in Ref. [23]. While for $\gamma _{\textrm{ns},s}^{(3)}$ we directly rely on the approximation of Ref. [22], which already includes all the available information, we construct an approximation to $\gamma _{\textrm{ns},\pm }^{(3)}$ based on the procedure described in Sect. 2.1, in order to include also this more recent information, and also as a warm-up for the construction of our approximation to the singlet sector anomalous dimension that we present in the next section.

Contributions to $\gamma _{\textrm{ns},\pm }^{(3)}$ proportional to $n_f^2$ and $n_f^3$ are known exactly [21] (in particular the $n_f^3$ contributions to $\gamma _{\textrm{ns},\pm }^{(3)}$ coincide), while ${\mathcal {O}}( n_f^0)$ and ${\mathcal {O}}( n_f)$ terms¹ are known in the large-$N_c$ limit [22] and we include these in $\gamma _{\textrm{ns},\pm ,n_f}^{(3)}(N)$.

Small-x contributions to $\gamma _{\textrm{ns},\pm }$ are double logarithmic, i.e. of the form $a_s^{n+1} \ln ^{2n-k}(x)$, corresponding in Mellin space to poles of order $2n-k+1$ in $N=0$, i.e. $\frac{1}{N^{2n-k+1}}$, so at $\hbox {N}^3\hbox {LO}$ we have $n=3$ and thus

$$\begin{aligned} P_{\mathrm{ns,\,\pm }}^{(3)}(x) = \sum _{k=1}^{6} c^k_{\textrm{ns}, \,N\rightarrow 0} \ln ^k(1/x)+ O(x). \end{aligned}$$

(2.22)

The coefficients $c^k_{\textrm{ns},\,N\rightarrow 0}$ are known [23] exactly up to NNLL accuracy ($k=4,\,5,\,6)$, and approximately up to $\hbox {N}^6$LL ($k=1,\,2,\,3$). Hence, we let

$$\begin{aligned} \gamma _{\textrm{ns},\pm , \,N\rightarrow 0}^{(3)}(N)=\sum _{k=1}^{6} c^k_{\textrm{ns}, \,N\rightarrow 0} (-1)^k \frac{k!}{N^{k+1}}. \end{aligned}$$

(2.23)

Large-x logarithmic contributions in the $\overline{\textrm{MS}}$ scheme only appear in coefficient functions [47], and so the $x\rightarrow 1$ behaviour of splitting functions is provided by the cusp anomalous dimension $\sim \frac{1}{(1-x)_+}$, corresponding to a single $\ln (N)$ behavior in Mellin space as $N\rightarrow \infty$. This behavior is common to the pair of anomalous dimensions $\gamma _{\textrm{ns},\pm }^{(3)}(N)$. Furthermore, several subleading power corrections as $N\rightarrow \infty$ can also be determined and we set

$$\begin{aligned} \gamma _{\textrm{ns},\pm ,\,N\rightarrow \infty }^{(3)}(N) =A^{q}_4 S_1(N) + B_4^{q} + C_4^{q} \frac{S_1(N)}{N} + D_4^{q} \frac{1}{N} , \end{aligned}$$

(2.24)

where $S_1$ denotes the harmonic sum (see Eqs. A.18–A.19). The coefficient of the $\ln (N)$ term $A^{q}_4$, is the quark cusp anomalous dimension [24]. The constant coefficient $B^{q}$ is determined by the integral of the nonsinglet splitting function, which was originally computed in [22] in the large-$N_c$ limit and recently updated to the full color expansion [25] as a result of computing different $\hbox {N}^3\hbox {LO}$ cross-sections in the soft limit. The coefficients of the terms suppressed by 1/N in the large-N limit, $C^{q}$ and $D^{q}$, can be obtained directly from lower-order anomalous dimensions by exploiting large-x resummation techniques [21]. The explicit expressions of $\gamma _{\textrm{ns}\, \pm ,\,N\rightarrow \infty }^{(3)}(N)$ and $\gamma _{\textrm{ns}\, \pm ,\,N\rightarrow 0}^{(3)}(N)$ are given in Appendix A.

Table 1 The Mellin space interpolating functions $G^{\textrm{ns},\pm }_\ell (N)$ entering the parametrisation of the remainder term ${\widetilde{\gamma }}^{(3)}_{\textrm{ns}\, \pm }(N)$ for the nonsinglet anomalous dimension expansion of Eq. (2.16)

Fig. 1

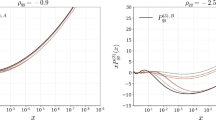
The $\hbox {aN}^3\hbox {LO}$ nonsinglet splitting functions $(1-x) P_{\textrm{ns},+}(x,\alpha _s)$ and $(1-x) P_{\textrm{ns},-}(x,\alpha _s)$, evaluated as a function of x for $n_f=4$ and $\alpha _s=0.2$ in our approximation compared to the previous approximation of Ref. [22] (denoted FHMRUVV), for which the approximation uncertainty, as estimated by its authors, is also displayed. For comparison, the (exact) NNLO result is also shown

The remainder terms, ${\widetilde{\gamma }}_{\mathrm{ns, \pm }}^{(3)}(N)$, are expanded over the set of eight functions $G^{\textrm{ns},\pm }_\ell (N)$ listed in Table 1. The coefficients $b^{\mathrm{ns,\pm }}_\ell$ (defined in Eq. (2.16)) are determined by imposing that the values of the eight moments given in Ref. [22] be reproduced. The set of functions $G^{\textrm{ns},\pm }_\ell (N)$ is chosen to adjust the overall constant ($\ell =1$), model the large-N behavior ($2\le \ell \le 5$) and model the small-N behavior ($\ell =6,7$), consistent with the general analytic structure of fixed order anomalous dimensions [48]. Specifically, the large-N functions are chosen as the logarithmically enhanced next-to-next-to-leading power terms ($\ln ^k(N)/N^2$, $\ell =2,3,4,5$) and the small-N functions are chosen as logarithmically enhanced subleading poles ($1/(N+1)^k$, $\ell =6,7$) and sub-subleading poles ($1/(N+2)$ or $1/(N+3)$, $\ell =8$). The last element, $\ell = 8$, is chosen at a fixed distance from the lowest known moment, $N=2$ for $\gamma _{\textrm{ns},+}^{(3)}(N)$ and $N=1$ for $\gamma _{\textrm{ns},-}^{(3)}(N)$.

In Fig. 1 we plot the resulting splitting functions $P_{\textrm{ns},\pm }^{(3)}(x)$, obtained by Mellin inversion of the anomalous dimension. We compare our approximation to the approximation of Ref. [22], for $\alpha _s=0.2$ and $n_f=4$, and also show the (exact) NNLO result for reference. Because the splitting function is a distribution at $x=1$ we plot $(1-x)P(x)$. The result of Ref. [22] also provides an estimate of the uncertainty related to the approximation, shown in the figure as a band, and we observe that this uncertainty is negligible except at very small x. As we include further constraints on the small-x behavior, the uncertainty on the approximation becomes negligible, as it can be checked by comparing results obtained by including increasingly more information in the construction of the approximation. Consequently, as mentioned in Sect. 2.1 above, we take $n_H=0$ in Eq. (2.16).

2.4 $\hbox {aN}^3\hbox {LO}$ anomalous dimensions: singlet sector

In order to determine the singlet-sector anomalous dimension matrix entering Eq. (2.12), we must determine $\gamma _{{qq},\textrm{ps}}$ that, together with the previously determined nonsinglet anomalous dimension, contributes to the qq entry, Eq. (2.13), and then also the three remaining matrix elements $\gamma _{{qg}}$, $\gamma _{{gq}}$, and $\gamma _{{gg}}$.

For all matrix elements, the leading large-$n_f$ ${\mathcal {O}}(n_f^3)$ contributions in Eq. (2.14) are known analytically [21], while for $\gamma _{{qq},\textrm{ps}}$ [49] and $\gamma _{{gq}}$ [31] the ${\mathcal {O}}(n_f^2)$ contributions are also known and we include all of them in $\gamma _{ij,n_f}^{(3)}(N)$.

Small-x contributions in the singlet sector include, on top of the double-logarithmic contributions $a_s^{n+1} \ln ^{2n-k}(x)$ that are present in the nonsinglet case, also single-logarithmic contributions $a_s^{n+1} \frac{1}{x} \ln ^{n}(x)$. In Mellin space, this means that on top of order $2n-k+1$ subleading poles in $N=0$, there are also leading poles in $N=1$ of order $n-k+1$, i.e. $\frac{1}{(N-1)^{n-k+1}}$. The leading-power single logarithmic contributions can be extracted from the leading [50,51,52,53,54] and next-to-leading [55,56,57,58,59] high-energy resummation at LLx [60] and NLLx [61,62,63] accuracy. This allows for a determination of the coefficients of the leading $\frac{1}{(N-1)^4}$ and next-to-leading $\frac{1}{(N-1)^3}$ contributions to $\gamma ^{(3)}_{gg}$ and of the next-to-leading $\frac{1}{(N-1)^3}$ contributions to $\gamma ^{(3)}_{qg}$. The remaining entries can be obtained from these by using the color-charge (or Casimir scaling) relation $\gamma _{iq}=\frac{C_F}{C_A}\gamma _{ig}$ [63, 64]. Hence, we set

$$\begin{aligned} \gamma _{gg,\,N\rightarrow 1}^{(3)}(N)&= c^4_{gg, \,N\rightarrow 1}\frac{1}{(N-1)^4}+c^3_{gg, \,N\rightarrow 1}\frac{1}{(N-1)^3}; \end{aligned}$$

(2.25)

$$\begin{aligned} \gamma _{qg,\,N\rightarrow 1}^{(3)}(N)&= c^3_{qg, \,N\rightarrow 1}\frac{1}{(N-1)^3}; \end{aligned}$$

(2.26)

$$\begin{aligned} \gamma _{iq,\,N\rightarrow 1}^{(3)}(N)&= \frac{C_F}{C_A} \gamma _{ig,\,N\rightarrow 1}^{(3)}(N),\quad i= q,\,g. \end{aligned}$$

(2.27)

Although only the leading pole of $\gamma _{gq}$ satisfies Eq. (2.27) exactly, at NNLO this relation is only violated at the sub-percent level [65], so this is likely to be an adequate approximation also at this order: this approximation is also adopted in Ref. [30]. An important observation is that both NLO and NNLO coefficients of the leading poles, $\frac{1}{(N-1)^2}$ and $\frac{1}{(N-1)^3}$ respectively, vanish accidentally. Hence, at $\hbox {N}^3\hbox {LO}$ the leading poles contribute for the first time beyond leading order. The subleading poles can be determined up to NNLL accuracy [23] and, thus, fix the coefficients of the $\frac{1}{N^7}$, $\frac{1}{N^6}$ and $\frac{1}{N^5}$ subleading poles for all entries of the singlet anomalous dimension matrix. All these contributions are included in $\gamma _{ij,N\rightarrow 1}^{(3)}(N)$ and $\gamma _{ij,N\rightarrow 0}^{(3)}(N)$.

In the singlet sector, large-x contributions whose Mellin transform is not suppressed in the large-N limit only appear in the diagonal qq and gg channels. In the quark channel these are already included, through Eq. (2.13) in $\gamma _{\textrm{ns},+,\,N\rightarrow \infty }^{(3)}(N)$, according to Eq. (2.24), while $\gamma ^{(3)}_{qq,\textrm{ps}}$ is suppressed in this limit. In the gluon-to-gluon channel they take the same form as in the nonsinglet and diagonal quark channel. Hence, we expand, as in Eq. (2.24),

$$\begin{aligned} \gamma _{gg,\,N\rightarrow \infty }^{(3)}(N) = A^{g}_4 S_1(N) + B^{g}_4 + C^{g}_4 \frac{S_1(N)}{N} + D^{g}_4 \frac{1}{N}. \end{aligned}$$

(2.28)

The coefficients $A^{g}_4$, $B^{g}_4$, $C^{g}_4$ and $D^{g}_4$ are the counterparts of those of Eq. (2.24): the gluon cusp anomalous dimension was determined in Ref. [24] and the constant in Ref. [25], while the $C^{g}_4$ and $D^{g}_4$ coefficients can be determined using results from Refs. [30, 66].

Off-diagonal qg and qg splitting functions have logarithmically enhanced next-to-leading power behavior at large-x:

$$\begin{aligned} P_{ij}^{(3)}(x) = \sum _{k=0}^{6} \sum _{l=0}^{\infty } c^{k,l}_{ij,\,N\rightarrow \infty } (1-x)^l \ln ^k(1-x). \end{aligned}$$

(2.29)

For $l=0$ the coefficients of the higher logs $k=4,5,6$ can be determined from $\hbox {N}^3\hbox {LO}$ coefficient functions, based on a conjecture [27, 67] on the large-x behavior of the physical evolution kernels that give the scale dependence of structure functions. The coefficient with the highest power $k=6$ cancels and thus we let

$$\begin{aligned} \gamma _{gq,\,N\rightarrow \infty }^{(3)}(N)&= \sum _{k=4}^5 c^{k,0}_{gq, \,N\rightarrow \infty } {\mathcal {M}}\left[ \ln ^k(1-x)\right] (N), \end{aligned}$$

(2.30)

$$\begin{aligned} \gamma _{qg,\,N\rightarrow \infty }^{(3)}(N)&= \sum _{k=4}^5 c^{k,0}_{qg, \,N\rightarrow \infty } {\mathcal {M}}\left[ \ln ^k(1-x)\right] (N) \nonumber \\&\quad {+} c^{k,1}_{qg, \,N\rightarrow \infty } {\mathcal {M}}\left[ (1{-}x)\ln ^k(1{-}x)\right] (N), \end{aligned}$$

(2.31)

where in $\gamma _{qg,\,N\rightarrow \infty }^{(3)}$ we have retained also the $l=1$ terms [29].

Finally, the pure singlet quark-to-quark splitting function starts at next-to-next-to-leading power as $x\rightarrow 1$, i.e. it behaves as $(1-x)\ln ^k(1-x)$, with $k\le 4$. The coefficients of the higher logs $k=3,4$ can be extracted by expanding the $x=1$ expressions from Refs. [27, 28]. Hence, we let

$$\begin{aligned} \gamma _{qq,\textrm{ps},\,N\rightarrow \infty }^{(3)}(N)= & {} \sum _{k=3}^4 \left[ c^{k,1}_{qq,\textrm{ps},\,N\rightarrow \infty } {\mathcal {M}}\left[ (1-x)\ln ^k(1-x)\right] (N) \right. \nonumber \\{} & {} \left. + c^{k,2}_{qq,\textrm{ps},\,N\rightarrow \infty } {\mathcal {M}}\left[ (1-x)^2\ln ^k(1-x)\right] (N)\right] \nonumber \\ \end{aligned}$$

(2.32)

Note that for the qq and qg entries we also include the (known) next-to-leading power contributions, while we do not include them for gq and gg because for these anomalous dimension matrix elements a significantly larger number of higher Mellin moments is known, hence there is no risk that the inclusion of these contributions could contaminate the intermediate x region where they are not necessarily dominant. The explicit expressions of $\gamma _{ij \,N\rightarrow \infty }^{(3)} (N)$, $\gamma _{ij \,N\rightarrow 0}^{(3)}(N)$ and $\gamma _{ij\,N\rightarrow 1}^{(3)}(N)$ are all given in Appendix A.

As discussed in Sect. 2.1, the remainder contribution ${\widetilde{\gamma }}_{ij}^{(3)}(N)$, Eq. (2.16), is determined by expanding each of its matrix elements over a set of $n^{ij}$ basis functions, where $n^{ij}$ is the number of known Mellin moments, and determining the expansion coefficients by demanding that the known moments be reproduced. Specifically, the known moments are the four moments computed in Ref. [26], the six additional moments for $\gamma _{qq,\textrm{ps}}$ and $\gamma _{qg}$ computed in Ref. [28] and Ref. [29] respectively, and the additional moment $N=10$ for $\gamma _{gg}$ and $\gamma _{gq}$ evaluated in Ref. [30]. These constraints automatically implement momentum conservation:

$$\begin{aligned} \begin{aligned} \gamma _{qg}(N=2) + \gamma _{gg}(N=2)&= 0, \\ \gamma _{qq}(N=2) + \gamma _{gq}(N=2)&= 0. \end{aligned} \end{aligned}$$

(2.33)

Table 2 The set of basis functions $G^{ij}_\ell (N)$ and $H^{ij}_\ell (N)$ used to parametrize the singlet sector remainder anomalous dimensions matrix elements ${\widetilde{\gamma }}_{ij}^{(3)}(N)$ according to Eq. (2.16)

The set of basis functions is chosen based on the idea of constructing an approximation that reproduces the singularity structure of the Mellin transform of the anomalous dimension viewed as analytic functions in N space [48], hence corresponding to the leading and subleading (i.e. rightmost) N-space poles with unknown coefficients as well as the leading unknown large-N behavior. As mentioned in Sect. 2.1, the uncertainty on the answer is then estimated by varying the set of basis functions, specifically by varying two out of the $n^{ij}$ basis functions. The way the basis functions are partitioned between the fixed functions $G^{ij}$ and the varying functions $H^{ij}$ is by always including in the fixed set the most leading unknown contributions, and in the $H^{ij}$ further subleading ones. The number of varying $H^{ij}$ is chosen to be larger when less exact information is known.

Specifically, the functions $G^{ij}$ are chosen as follows.

• 1. The function $G^{ij}_1(N)$ reproduces the leading unknown contribution in the large-N limit, i.e. the unknown term in Eq. (2.29) with highest k and lowest l.

• 2. The functions $G^{ij}_2(N)$ and $G^{ij}_3(N)$ reproduce the first two leading unknown contributions in the small-N limit, i.e. the unknown $\frac{1}{(N-1)^k}$ leading poles with highest and next-to-highest values of k, i.e. $k=2$ and $k=1$. For $\gamma _{qq,\textrm{ps}}$ and $\gamma _{qg}$ a subleading small-x pole with the same power and opposite sign is added to the leading pole with respectively $k=1,\,2$ and $k=1$, so as to leave unaffected the respective large-x leading power behavior Eqs. (2.31, 2.32).

• 3. For $\gamma _{qq,\textrm{ps}}$ and $\gamma _{qg}$, for which an additional five moments are known, the functions $G^{qj}_{4,\dots ,8}(N)$ reproduce subleading small- and large-N terms.

Note that a larger number of basis functions is chosen to describe the small-N poles rather than the large-N behavior because less exact information is available in the former case: so for instance only the leading pole Eq. (2.26) is known for $\gamma _{qg}^{(3)}(N)$, while the first two logarithmically enhanced large-N contributions to it Eq. (2.31) are known.

As mentioned, the functions $H^{ij}$ are chosen to reproduce further subleading contributions:

• 1. The functions $H^{gj}_1(N),H^{gj}_2(N)$ in the gluon sector, where only five moments are known exactly, are chosen to reproduce subleading small- and large-N terms, i.e. similar to $G^{qj}_{4,\dots ,8}(N)$.

• 2. The functions $H^{qg}_1(N),H^{qg}_2(N)$ are chosen as subleading and next-to-leading power large-x terms and the remaining unknown leading small-N pole.

• 3. The functions $H^{qq,\,\textrm{ps}}_1(N),H^{qq,\,\textrm{ps}}_2(N)$ are chosen as low-order polynomials, i.e., sub-subleading small-x poles.

Also as mentioned, the number of basis functions is greater for anomalous dimension matrix elements for which less exact information is available: 7 in the gluon sector (i.e. gg and gq), 6 for the qg entry and 4 for the pure singlet entry. For the gg entry two combinations are discarded as they lead to unstable (oscillating) results and we thus end up with ${\widetilde{N}}_{gg}=19$, ${\widetilde{N}}_{gq}=21$, ${\widetilde{N}}_{qg}=15$, and ${\widetilde{N}}_{qq}=6$ different parametrizations. The full set of basis functions $G^{ij}$ and $H^{ij}$ is listed in Table 2. We have checked that results are stable upon variation of these choices, so for instance including a larger number of $H^{ij}$ functions does not lead to significantly larger uncertainties.

Upon combining the exactly known contributions with the ${\widetilde{N}}_{ij}$ remainder terms according to Eq. (2.15) we end up with an ensemble of ${\widetilde{N}}_{ij}$ instances of $\gamma _{ij}^{(3),\,(k)}(N)$ for each singlet anomalous dimension matrix element and the final matrix elements $\gamma _{ij}^{(3)}(N)$ and their uncertainties $\sigma _{ij}(N)$ are computed using Eqs. (2.17) and (2.21) respectively.

2.5 Results: $\hbox {aN}^3\hbox {LO}$ splitting functions

Fig. 2

The nonsinglet splitting functions at LO, NLO, NNLO, and $\hbox {aN}^3\hbox {LO}$, normalized to the $\hbox {aN}^3\hbox {LO}$ central value and with a linear scale on the x axis. In each case we shown also the uncertainty due to missing higher orders (MHOU) estimated by scale variation according to Refs. [35, 36]

Fig. 3

The relative size of the uncertainty due to missing higher orders (MHOU) on the splitting functions of Fig. 2

Fig. 4

The singlet matrix of splitting functions $xP_{ij}$ at LO, NLO, NNLO and $\hbox {aN}^3\hbox {LO}$. From left to right and from top to bottom the gg, gq, qg and qq entries are shown. The MHOU estimated by scale variation is shown to all orders. At $\hbox {aN}^3\hbox {LO}$ the dark blue band corresponds to IHOU only, while the light blue band is the sum in quadrature of IHOU and MHOU

Fig. 5

Same as Fig. 4 with a linear scale on the x axis, and plotting $(1-x)x P_{ii}$ for diagonal entries

Fig. 6

Same as Fig. 3 for the singlet splitting function matrix elements. At NLO and NNLO we show the MHOU, while at $\hbox {aN}^3\hbox {LO}$ we also show the IHOU

Fig. 7

Comparison of the NLO, NNLO, and $\hbox {aN}^3\hbox {LO}$ splitting functions (same as in Fig. 4) to the small-x resummed NLO+NLL result of Ref. [68]. Only the IHOU on the $\hbox {aN}^3\hbox {LO}$ result is shown

We now present the $\hbox {aN}^3\hbox {LO}$ splitting functions constructed following the procedure described in Sects. 2.1–2.4. The nonsinglet result, already compared in Fig. 1 to the previous approximation of Ref. [22], is shown in Fig. 2 at the first four perturbative orders as a ratio to the $\hbox {aN}^3\hbox {LO}$ result. For each order we include the MHOU determined by scale variation according to Refs. [35, 36] and recall that there are no IHOU in the nonsinglet sector. As the nonsinglet splitting function are subdominant at small x we only show the plot with a linear scale in x. The relative size of the MHOU is shown in Fig. 3.

Inspecting Figs. 2 and 3 reveals good perturbative convergence² for all values of x. Specifically, the differences between two subsequent perturbative orders are reduced as the accuracy of the calculation increases, and, correspondingly, the MHOUs associated to factorization scale variations decrease with the perturbative accuracy. Indeed, the MHOU appears to reproduce well the observed behaviour of the higher orders, with overlapping uncertainty bands between subsequent orders except at LO at the smallest x values. Hence, the behavior of the perturbative series suggests that the MHOU estimate based on scale variation at $\hbox {N}^3\hbox {LO}$ is reliable.

Based on these results it is clear that in the nonsinglet sector the $\hbox {N}^3\hbox {LO}$ contribution to the splitting function is essentially negligible except at the smallest x values, as shown in Fig. 1. Consequently, for all practical purposes we can consider the current approximation to the nonsinglet anomalous dimension to be essentially exact, and with negligible MHOU.

The situation in the singlet sector is more challenging. The singlet matrix of splitting functions is shown in Figs. 4 and 5, respectively with a logarithmic or linear scale on the x axis. Because the diagonal splitting functions are distributions at $x=1$ in the linear scale plots we display $x(1-x)P_{ii}$. The corresponding relative size of the MHOU is shown in Fig. 6 for the first four perturbative orders, along with the IHOU on the $\hbox {aN}^3\hbox {LO}$ result, determined using Eq. (2.21).

A different behaviour is observed for the quark sector $P_{qi}$ and for the gluon sector $P_{gi}$. In the quark sector, the MHOU decreases with perturbative order for all x, but it remains sizable at $\hbox {aN}^3\hbox {LO}$ for essentially all x, of order 5% for $10^{-2}\lesssim x\lesssim 10^{-1}$. In the gluon sector instead for $x \gtrsim 0.03$ the MHOU is negligible, but at smaller x it grows rapidly, and in fact at very small x it becomes larger than the NLO MHOU. This is due to the presence of leading small-x logarithms, Eq. (2.25), which are absent at NLO. In fact the true gluon-sector MHOU at very small x is likely to be underestimated by scale variation, because while it generates the fourth-order leading pole present in the $\hbox {N}^4$LO (the fifth-order pole vanishes), it fails to generate the sixth-order pole known to be present in the $\hbox {N}^5$LO splitting function.

We now turn to the IHOU and find again contrasting behaviour in the different sectors. In the quark sector, thanks to the large number of known Mellin moments and the copious information on the large-x limit, the IHOU are significantly smaller than the MHOU, by about a factor three, and become negligible for $x\gtrsim 10^{-2}$. In the gluon sector instead the IHOU, while still essentially negligible for $x\gtrsim 0.1$, is larger than the MHOU except at very small $x\lesssim 10^{-4}$ where the MHOU dominates.

Consequently, for all matrix elements at large $x\gtrsim 0.1$ the behaviour of the singlet is similar to the behaviour of the nonsinglet: IHOU and MHOU are both negligible, meaning that $\hbox {aN}^3\hbox {LO}$ results are essentially exact, and the perturbative expansion has essentially converged, see Fig. 5. At smaller x, while the $\hbox {aN}^3\hbox {LO}$ and NNLO results agree within uncertainties, the uncertainties on the $\hbox {aN}^3\hbox {LO}$ are sizable, dominated by MHOUs in the quark channel and by IHOUs in the gluon channel.

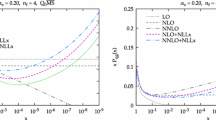
In the singlet sector the most dramatic impact of the $\hbox {aN}^3\hbox {LO}$ correction is at small x. It is thus interesting to compare the $\hbox {aN}^3\hbox {LO}$ singlet splitting functions with those obtained by the resummation of leading and next-to-leading order small-x logarithms of Ref. [68], namely the two highest powers of $\ln x$ contained in the $\hbox {N}^3\hbox {LO}$ result; this comparison is shown in Fig. 7. The agreement of all four entries $xP_{gg}$, $xP_{gq}$, $xP_{qg}$ and $xP_{qq}$ is remarkably good and well within the uncertainties in the two approaches. In particular the dip in $xP_{gg}$ at intermediate x at $\hbox {aN}^3\hbox {LO}$ (albeit with significant IHOU) is also a feature of the resummation. This is nontrivial, as the resummation includes only the asymptotic LLx and NLLx singularities at $N=1$, but none of the subleading results incorporated at $\hbox {aN}^3\hbox {LO}$. Instead, it uses a symmetrization which resums collinear and anti-collinear logarithms in the small-x expansion, and the effects of running coupling which change the nature of the small-x singularity (from a fourth order pole at $N=1$ in the fixed order $\hbox {N}^3\hbox {LO}$ result to a simple pole a little further to the right on the real axis).

That both the resummed and fixed order approaches converge to very similar results, at least in the range of x relevant for HERA and LHC, is very reassuring. It shows that in a global fit with current data, while NLLx resummation significantly improves the quality of a fixed order NNLO fit [69], the same improvement should also be seen by adding $\hbox {aN}^3\hbox {LO}$ corrections. Thus to find evidence for small-x resummation at $\hbox {aN}^3\hbox {LO}$, it will probably be necessary to go to yet smaller values of x, e.g. below $10^{-5}$, where the fixed order and resummed results will eventually diverge again.

2.6 Results: $\hbox {aN}^3\hbox {LO}$ evolution

The $\hbox {aN}^3\hbox {LO}$ anomalous dimensions discussed in the previous sections have been implemented in the Mellin-space open-source evolution code EKO [40] which enters the new pipeline [70] adopted by NNPDF in order to produce theory predictions used for PDF determination. The parametrization is expressed in terms of a basis of Mellin space functions which are numerically efficient to evaluate. In order to achieve full $\hbox {aN}^3\hbox {LO}$ accuracy, in addition to the anomalous dimensions, the four-loop running of the strong coupling constant $\alpha _s(Q)$ and the $\hbox {N}^3\hbox {LO}$ matching conditions dictating the transitions between schemes with different numbers of active quark flavor have also been implemented.

The $\hbox {N}^3\hbox {LO}$ matching conditions have been presented in Ref. [71] and subsequently computed analytically in Refs. [72,73,74,75,76,77,78,79,80,81]. The exception is the $a_{Hg}^{(3)}$ entry of the matching condition matrix, which is still unknown³ and which instead is parametrized using the first 5 known moments [71] and the LLx contribution as done in Ref. [83]. Also these matching conditions are implemented in EKO and thus it is possible to assess the impact of the inclusion of $\hbox {aN}^3\hbox {LO}$ terms on perturbative evolution.

In Fig. 8 we compare the result of evolving a fixed set of PDFs from $Q_0=1.65$ GeV up to $Q=100$ GeV at NLO, NNLO, and $\hbox {aN}^3\hbox {LO}$. We take as input the NNPDF4.0NNLO PDF set, and show results normalized to the $\hbox {aN}^3\hbox {LO}$ evolution. Results are shown for all the combinations that evolve differently, as discussed in Sect. 2.1, namely the singlet, gluon, total valence and nonsinglet ± combinations, with a logarithmic scale on the x axis for the singlet sector and a linear scale for the valence and nonsinglet combinations. The relative uncertainty on the gluon and singlet are shown in Fig. 9, with MHOU and IHOU separately displayed at $\hbox {N}^3\hbox {LO}$.

Fig. 8

Comparison of the result obtained evolving from $Q_0=1.65$ GeV to $Q=100$ GeV at NLO, NNLO, and $\hbox {aN}^3\hbox {LO}$ using NNPDF4.0 NNLO as fixed starting PDF. Results are shown as ratio to the $\hbox {aN}^3\hbox {LO}$ (from left to right and from top to bottom) for the gluon and singlet $\Sigma$, and for the V, $V_3$ and $T_3$ quark eigenstates of perturbative evolution (see Sect. 2.1). The total theory uncertainty is shown in all cases, i.e. the MHOU at NLO and NNLO, and the sum in quadrature of MHOU and IHOU at $\hbox {aN}^3\hbox {LO}$

In all cases the perturbative expansion appears to have converged everywhere, with almost no difference between NNLO and $\hbox {aN}^3\hbox {LO}$ except at small $x\lesssim 10^{-3}$, where singlet evolution is weaker at $\hbox {aN}^3\hbox {LO}$ than at NNLO due to the characteristic dip seen in the gluon sector splitting functions of Fig. 4. Because the gluon-driven small-x rise dominates small-x evolution this is a generic feature of all quark and gluon PDFs in this small-x region. It is interesting to observe that this is an all-order feature that persists upon small-x resummation, as already discussed at the end of Sect. 2.5 and seen in Fig. 7. In fact, the total theory uncertainty at $\hbox {aN}^3\hbox {LO}$ is at the sub-percent level for all $x\gtrsim 10^{-3}$. Hence, not only has the MHOU become negligible, but also the effect of IHOU on PDF evolution is only significant at small x.

Fig. 9

The relative size of the uncertainty on the gluon and singlet PDFs shown in Fig. 8. The MHOU is shown in all cases, and at $\hbox {aN}^3\hbox {LO}$ the IHOU is also shown

2.7 Comparison to other groups

We finally compare our approximation of the $\hbox {N}^3\hbox {LO}$ splitting functions to other recent results from Refs. [28,29,30, 32]. While the approach of Refs. [28,29,30] (FHMRUVV, henceforth) is very similar to our own, with differences only due to details of the choice of basis functions, a rather different approach is adopted in Ref. [32] (MSHT20, henceforth). There, the approximation is constructed from similar theoretical constraints (small-x, large-x coefficients and Mellin moments), but supplementing the parametrization with additional nuisance parameters, which control the uncertainties arising from unknown $\hbox {N}^3\hbox {LO}$ terms. However, these approximations are taken as a prior, and the nuisance parameters are fitted to the data along with the PDF parameters. The best-fit values of the parameters determine the posterior for the splitting function, and their uncertainties are interpreted as the final IHOU on it. A consequence of this procedure is that the posterior can reabsorb not only $\hbox {N}^3\hbox {LO}$ corrections, but any other missing contribution, of theoretical or experimental origin.

Fig. 10

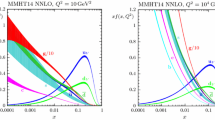
Same as Fig. 4, now comparing our $\hbox {aN}^3\hbox {LO}$ result to those of Ref. [32] (MSHT20) and Refs. [28,29,30] (FHMRUVV). In all cases the uncertainty band correspond to the IHOU as estimated by the various groups. For the MSHT20 results, we display both the prior and the posterior parametrizations (see text)

The comparison is presented in Fig. 10, for all the four singlet splitting functions. For the MSHT20 results both prior and posterior are displayed. It should be noticed that even though the uncertainty bands on the NNPDF4.0, DHMRUVV and MSHT20 prior are all obtained by varying the set of basis functions, they are found using somewhat different procedures, and their meaning is accordingly somewhat different. Indeed, for NNPDF4.0 the is constructed out of the covariance matrix according to Eq. (2.21). For FHMRUVV is instead the band between an upper and lower estimates which are representative of the envelope of all variations. Finally for the MSHT20 prior it is the variance of the probability distribution obtained assuming a multigaussian distribution of suitable nuisance parameters.

As expected, excellent agreement is found with the FHMRUVV result, for all splitting functions and for all x, especially for the $P_{qg}$ and $P_{qq}$ splitting functions, for which the highest number of Mellin moments is known. Good qualitative agreement is also found for $P_{gq}$ and $P_{gg}$, although at small x IHOUs are larger and consequently central values differ somewhat more, though still in agreement within uncertainties. Uncertainties are qualitatively similar, except at small x, where less exact information is available and both central values and uncertainties are less constrained. In this region the NNPDF4.0 is generally somewhat more conservative, possibly due to the fact that it is obtained by adding individual shifts in quadrature, rather than taking their envelope.

Coming now to MSHT20 results, good agreement is found with the prior, except for $P_{gq}$, for which MSHT20 shows a small-x dip accompanied by a large-x bump. The different small-x behaviour is likely due to the fact that MSHT20 do not enforce the color-charge relation Eq. (2.27) at NLLx, with the large-x bump then following from the constraints Eq. (2.33). Also, in the quark sector the MSHT20 prior has significantly larger IHOUs due to the fact that it does not include the more recent information on Mellin moments from Refs. [23, 28,29,30,31], which were not available at the time of the MSHT20 analysis [32]. At the level of posterior, however, significant differences appear also for $P_{gg}$, while persisting for $P_{gq}$. This means that the gluon evolution at $\hbox {aN}^3\hbox {LO}$ is being significantly modified by the data entering the global fit, and it is not fully determined by the perturbative computation. Further benchmarks of $\hbox {aN}^3\hbox {LO}$ splitting functions will be presented in Ref. [84].

3 $\hbox {N}^3\hbox {LO}$ partonic cross-sections

A PDF determination at $\hbox {N}^3\hbox {LO}$ requires, in addition to the splitting functions discussed in Sect. 2, hard cross-sections at the same perturbative order. Exact $\hbox {N}^3\hbox {LO}$ massless DIS coefficient functions have been known for several years [1,2,3,4, 85, 86], while massive coefficient functions are only available in various approximations [83, 87, 88]. For hadronic processes, $\hbox {N}^3\hbox {LO}$ results are available for inclusive Drell–Yan production for the total cross-section [8, 11, 12] as well as for rapidity [18] and transverse momentum distributions [19], though neither of these is publicly available.

We now describe the implementation of these corrections. First, we review available results on DIS coefficient functions and summarize the main features of the approximation that we will use for massive coefficient functions [87, 88]. Next we discuss how massless and massive DIS coefficient functions are combined to extend the FONLL general-mass variable-flavor number scheme to ${\mathcal {O}}\left( \alpha _s^3\right)$. Finally, we discuss $\hbox {N}^3\hbox {LO}$ corrections for hadronic processes and different options for their inclusion in PDF determination.

3.1 $\hbox {N}^3\hbox {LO}$ corrections to DIS structure functions

Fig. 11

Comparison of the exact NNLO massive gluon-initiated coefficient function $x C_{2,g}^{(2)}(\eta )$ to the approximation Eq. (3.3) from Ref. [87], plotted as a function of $\eta$, Eq. (3.5), for fixed $Q^2$. Results are shown for two different values of $Q^2$, one close to threshold $Q^2=2 m_h^2$ (left) and one at high scales $Q^2=16 m_h^2$ (right). The uncertainty on the approximate result is obtained by varying the interpolating functions $f_1(x)$ and $f_2(x)$ in Eq. (3.3)

Fig. 12

The approximate $\hbox {N}^3\hbox {LO}$ massive gluon (left) and quark singlet (right) coefficient functions as a function of $\eta$ for fixed $Q^2=2 m_h^2$. Our result based on the approximation of Ref. [87] is compared to the approximation of Ref. [83] (KLMV)

Fig. 13

Square root of the diagonal entries of the IHOU covariance matrix for the DIS datasets normalized to the experimental central value $D_i$. We show the IHOU before and after adding to the covariance matrix Eq. (2.20) that accounts for uncertainty on anomalous dimensions the extra component Eq. (3.6) due to the massive coefficient function. The experimental uncertainty is also shown for comparison

The DIS structure functions $F_i$ are evaluated from the convolution of PDFs and coefficient functions

$$\begin{aligned}&F_{i}(x,Q^2) = \sum _{k=1}^{n_f} C_{i,k}(x,\alpha _s) \otimes xq^+_k(x, Q^2) \nonumber \\&\qquad \qquad \qquad \quad + C_{i,g}(x,\alpha _s) \otimes xg(x, Q^2), \qquad i=\{2,L\},\nonumber \\&x F_3(x,Q^2) = \sum _{k=1}^{n_f} C_{3,k}(x,\alpha _s) \otimes xq^-_k(x, Q^2), \end{aligned}$$

(3.1)

with the coefficient functions evaluated in a perturbative QCD expansion

$$\begin{aligned} C_{i,k}(x,\alpha _s(Q^2)) = \sum _{n=0} \alpha _s^{n}(Q^2) C_{i,k}^{(n)}(x). \end{aligned}$$

(3.2)

Coefficient functions with all quarks assumed to be massless were evaluated at $\hbox {N}^3\hbox {LO}$ in [1, 2] for neutral-current charged-lepton scattering and recently independently benchmarked in [86]. The corresponding results for charged-current scattering were presented in [3, 4, 85].

For sufficiently low scale, some or all of the heavy quark masses cannot be neglected. Heavy quark contributions to structure functions may be treated in a decoupling scheme [89], in which heavy quarks do not contribute to the running of $\alpha _s$ and to PDF evolution, and coefficient functions acquire a dependence on the heavy quark mass $m_h$ [90]: $C_{i,k}=C_{i,k}(x,\alpha _s,m^2_h/Q^2)$ (massive coefficient functions, henceforth). The massive coefficient functions are known exactly up to NNLO for photon [91, 92], Z [93, 94] and W [95] exchange (for massless to massive transitions only) while at $\hbox {N}^3\hbox {LO}$ only partial results are available [83, 88, 96, 97] or in the $Q^2 \gg m_h^2$ limit [71, 72, 74, 75, 77, 98].

We adopt an approximation for the $\hbox {N}^3\hbox {LO}$ contribution $C_{i,k}^{(3)}(x,\alpha _s,m^2_h/Q^2)$ to massive coefficient functions for photon-induced DIS and neglect the axial-vector coupling of the Z boson, while we treat heavy quarks in the massless approximation for the W boson exchange. Such an approximation, based on known partial results, has been presented in Ref. [83], and recently revisited in Ref. [87]. The approaches of these references rely on the same known exact results, and differ in the details of the way they are combined and interpolated. Here we will follow Ref. [87], see also Ref. [88], to which we refer for further details. Exact results come from threshold resummation and high-energy resummation, and are further combined with the asymptotic large-$Q^2$ limit, thereby ensuring that the approximate massive coefficient function reproduces the exact massless result in the $Q^2/m_h^2\rightarrow \infty$ limit. In the approach of Refs. [87, 88] the massive coefficient functions are written as

$$\begin{aligned} C_{i,k}^{(3)}(x,m_h^2/Q^2){} & {} = C_{i,k}^{(3),\textrm{thr}}(x,m_h^2/Q^2) f_1(x) \nonumber \\{} & {} \quad + C_{i,k}^{(3),\textrm{asy}}(x,m_h^2/Q^2) f_2(x), \end{aligned}$$

(3.3)

where $C_{i,k}^{(3),\textrm{thr}}$ and $C_{i,k}^{(3),\textrm{asy}}$ correspond to the contributions coming from differently resummations, and $f_1(x)$ and $f_2(x)$ are two suitable matching functions.

For massive quarks the threshold limit is $x\rightarrow x_{\textrm{max}}$ with $x_{\textrm{max}} = \frac{Q^2}{4m_h^2 + Q^2}$ or $\beta \rightarrow 0$, with $\beta \equiv \sqrt{1- \frac{4m_h^2}{s}}$ and $s=Q^2\frac{1-x}{x}$ the center-of-mass energy of the partonic cross-section. In this limit, the coefficient function contains logarithmically enhanced terms of the form $\alpha _s^n \ln ^m\beta$ with $m\le 2n$ due to soft gluon emission, which are predicted by threshold resummation [99]. Further contributions of the form $\alpha _s^n \beta ^{-m}\ln ^l\beta$, with $m\le n$, arise from Coulomb exchange between the heavy quark and antiquark, and can also be resummed using non-relativistic QCD methods [100]. At $\hbox {N}^3\hbox {LO}$ all these contributions are known and can be extracted from available resummed results [83]; they are included in $C_{i,k}^{(3),\textrm{thr}}$.

In the high-energy limit, the coefficient function contains logarithmically enhanced terms of the form $\alpha _s^n \ln ^m x$ with $m\le n-2$, which are determined at all orders through small-x resummation at the LL level [97], from which the $\hbox {N}^3\hbox {LO}$ expansion can be extracted [83]. This result can be further improved [87, 88] by including a particular class of NLL terms related to NLL perturbative evolution and the running of the coupling. In the approach of Refs. [87, 88] the high-energy contributions are combined into $C_{i,k}^{(3),\textrm{asy}}$ with the asymptotic $Q^2 \gg m_h^2$ limit of the coefficient function in the decoupling scheme [71, 72, 74, 75, 77, 98], while subtracting overlap terms. This ensures that in the $Q^2 \gg m_h^2$ limit, the structure function, computed from $C_{i,k}^{(3),\textrm{asy}}$ combined with decoupling-scheme PDFs, coincides with the structure function computed in the limit in which the heavy quark mass is neglected and the heavy quark is treated as a massless parton. However, the asymptotic limit can only be determined approximately since in particular some of the matching conditions are not fully known.

The interpolating functions, used to combine the two contributions in Eq. (3.3), are chosen to satisfy the requirements

$$\begin{aligned} \begin{aligned} f_1(x) \xrightarrow [x \rightarrow 0]{} 0,&\quad f_1(x) \xrightarrow [x \rightarrow x_{\textrm{max}}]{} 1, \\ f_2(x) \xrightarrow [x \rightarrow 0]{} 1,&\quad f_1(x) \xrightarrow [x \rightarrow x_{\textrm{max}}]{} 0, \end{aligned} \end{aligned}$$

(3.4)

which ensure that the threshold contribution vanishes in the small-x limit and conversely. This guarantees that the approximation Eq. (3.3) is reliable in a broad kinematic range in the $(x,Q^2)$ plane: $C_{i,k}^{(3),\textrm{asy}}$ reproduces the massless limit for large $Q^2$ values and for all values of x, including the small-x limit, while $C_{i,k}^{(3),\textrm{thr}}$ describes the threshold limit, with x close to $x_{\textrm{max}}$. An uncertainty on the approximate coefficient function can be constructed varying the functional form of the interpolating functions, as well as that of terms which are not fully known. This includes the NLL small-x resummation and the matching functions that enter the asymptotic high $Q^2$ limit. This uncertainty vanishes in the $x\rightarrow x_{\textrm{max}}$ limit, for which the exact known limit is reproduced (with a fixed choice for the unknown constant $\beta$-independent terms), and becomes larger in the intermediate $\eta$ region. The interpolating functions and their uncertainties are optimized by using the same methodology at NNLO, where the full result is known. We refer to Ref. [87] for a detailed discussion of this construction.

This optimized approximation at NNLO is shown in Fig. 11, where we compare it to the exact result for the massive gluon-initiated coefficient function $x C_{2,g}^{(2)}(\eta )$, expressed in terms of the variable

$$\begin{aligned} \eta = \frac{Q^2(1-x)}{4m_h^2x}-1. \end{aligned}$$

(3.5)

Results are shown for two different values of the $Q^2/m_h^2$ ratio, close to threshold and at higher scales. Note that $\eta \rightarrow 0$ corresponds to $x\rightarrow x_{\textrm{max}}$ (threshold limit), while $\eta \rightarrow \infty$ corresponds to either $Q^2/m_h^2 \rightarrow \infty$ for fixed x (asymptotic limit), or $x\rightarrow 0$ for fixed $Q^2$ (high-energy limit). In this case the uncertainty band is obtained by varying the interpolating functions only.

The results found using the same procedure for the gluon and quark singlet coefficient functions at $\hbox {N}^3\hbox {LO}$ are displayed in Fig. 12, compared to the approximation of Ref. [83], each shown with the respective uncertainty estimate. Good agreement between the different approximations is found, especially for the dominant gluon coefficient function. The approximations agree in the asymptotic $\eta \rightarrow 0$ and $\eta \rightarrow \infty$ limits and in most of the $\eta$ range, but differ somewhat in the subasymptotic large $\eta$ region at fixed $Q^2$, which corresponds to the small x limit at fixed $Q^2$. These differences can be traced to the aforementioned inclusion in the procedure of Ref. [87, 88] of a particular class of NLL terms related.

The uncertainty involved in the approximation can be included as a further IHOU, alongside that discussed in Sect. 2.2, through an additional contribution to the theory covariance matrix. Namely, we define

$$\begin{aligned} \text {cov}^{C}_{mn} = \frac{1}{2} \left( \Delta _m(+)\Delta _n(+)+\Delta _m(-)\Delta _n(-)\right) . \end{aligned}$$

(3.6)

Here $\Delta _m(\pm )$ is the shift in the prediction for the m-th DIS data point obtained by replacing the central approximation to the massive coefficient function with the upper or lower edge of the uncertainty range determined in Ref. [87] and shown as an uncertainty band in Fig. 12. Note that unlike in Eq. (2.20), we divide by the number of independent variations, without decreasing it by one, because the central value is not the average of the variations, and thus is independent. The contribution Eq. (3.6) is then added to the IHOU covariance matrix as a further term on the right-hand side of Eq. (2.20).

The impact of this contribution to the IHOU is assessed in Fig. 13, where the square root of the diagonal component of the covariance matrix is shown for all the DIS data points in our dataset, comparing the IHOU before and after adding to Eq. (2.20) the extra component Eq. (3.6) due to the IHOU on the massive coefficient function. It is clear that the impact of IHOUs due to perturbative evolution is generally negligible, in agreement with the results discussed in Sect. 2.6 and shown in Fig. 8: IHOUs on splitting functions are only significant at small x, but available small-x data are at relatively low scale where the evolution length is small. The impact of IHOUs on massive coefficient functions is relevant for data on tagged bottom and charm structure functions, but otherwise moderate and only significant for structure function data close to the heavy quark production thresholds.

3.2 A general-mass variable flavor number scheme at $\hbox {N}^3\hbox {LO}$

Fig. 14

The charm structure function $F^{(c)}_{2}(x,Q^2,m_c^2)$ in the FONLL-E scheme, compared to the massive and massless scheme results (see text). Results are shown as a function of $Q^2$ for $x=2\times 10^{-4}$ (top left), $x=2\times 10^{-3}$ (top right), $x=2\times 10^{-2}$ (bottom left), and $x=2\times 10^{-1}$ (bottom right). The uncertainty shown on the FONLL and massive curves is the IHOU on the heavy quark coefficient functions Eq. (3.6)

Fig. 15

Same as Fig. 14, now comparing the FONLL-A (used at NLO ${\mathcal {O}}\left( \alpha _s\right)$), FONLL-C (used at NNLO ${\mathcal {O}}\left( \alpha _s^2\right)$), and FONLL-E (used at $\hbox {N}^3\hbox {LO}$ ${\mathcal {O}}\left( \alpha _s^3\right)$), all shown as a ratio to FONLL-E. The FONLL-E result includes the IHOU on the heavy quark coefficient functions Eq. (3.6)

The $\hbox {N}^3\hbox {LO}$ DIS coefficients functions described in the previous section enable the extension to ${\mathcal {O}}\left( \alpha _s^3\right)$ of the FONLL [101] general-mass variable flavor number scheme for DIS [42,43,44]. The goal of the FONLL strategy is results that are accurate and reliable for all values of $Q^2$ from the production threshold $Q^2 \sim m_h^2$ to the asymptotic limit $Q^2 \gg m_h^2$.

Assuming a single heavy quark, calculations performed in a decoupling scheme with $n_\ell$ light quarks retain the full dependence on the heavy quark mass and include the contribution of heavy quarks at a fixed perturbative order (massive scheme, henceforth). Calculations performed in a scheme in which the heavy quark is treated as massless (massless scheme, henceforth), and endowed with a PDF that satisfies perturbative matching conditions, resums logarithms of $Q^2/m_h^2$ to all orders through the running of the coupling and the evolution of PDFs, but does not include terms that are suppressed as powers of $\frac{m_h^2}{Q^2}$ and thus become relevant when . The FONLL prescription matches the two calculations by defining

$$\begin{aligned} F^{\textrm{FONLL}}_i{} & {} = F_{i}^{(n)}(x, Q^2,m_h^2) + F_{i}^{(n+1)}(x, Q) \nonumber \\{} & {} \quad - F_{i}^{(n,0)}(x, \ln (Q^2/m_h^2)), \qquad \ i = {2,L,3},\nonumber \\ \end{aligned}$$

(3.7)

where $F_{i}^{(n)}$ denotes the massive computation in which the $(n+1)$-th (heavy) flavor decouples, $F_{i}^{(n+1)}$ the one in which it is treated as massless, and $F_{i}^{(n,0)}$ is the asymptotic large-$Q^2$ limit of the massive scheme calculation, which depends only logarithmically on the heavy quark mass. This construction reduces to the decoupling calculation for $Q^2 \approx m_h^2$ and to the massless one for $Q^2 \gg m_h^2$.

The FONLL prescription of Eq. (3.7) was implemented in Ref. [42,43,44] for DIS to NNLO, by expressing all terms on the right-hand side in terms of $\alpha _s$ and PDFs all defined in the massless scheme. This has the advantage of providing an expression that can used with externally provided PDFs, that are typically available only in a single factorization scheme for each value of the scale Q.

However, the recent EKO code [40] allows, at any given scale, the coexistence of PDFs defined in schemes with a different number of massless flavors. Furthermore, the recent YADISM program [41] implements DIS coefficient functions corresponding to all three contributions on the right-hand side of Eq. (3.7). It is then possible to implement the FONLL prescription Eq. (3.7) by simply combining expressions computed in different schemes [102]. This formalism is especially advantageous at higher perturbative orders, where the analytic expressions relating PDFs in different scheme grow in complexity, and also above bottom threshold, where the iteration of Eq. (3.7) on charm and bottom heavy quarks leads to coexisting $n_f=3,\,4,\,5$ PDFs, while the method of Ref. [42,43,44] would require re-expressing the massive scheme PDFs into massless scheme PDFs twice.

In the FONLL method, Eq. (3.7), the first two terms on the right-hand side may be computed at different perturbative orders, provided one ensures that the third term correctly includes only their common contributions. In Ref. [42] some natural choices were discussed, based on the observation that in the massive scheme, the heavy quark contributes to the structure functions only at ${\mathcal {O}}\left( \alpha _s\right)$ and beyond, while in the massless scheme it already contributes at ${\mathcal {O}}\left( \alpha _s^0\right)$. Hence natural choices are to combine both the massive and massless contributions at ${\mathcal {O}}\left( \alpha _s\right)$ (FONLL-A), or else the massive contribution at ${\mathcal {O}}\left( \alpha _s^2\right)$ and the massless contribution at ${\mathcal {O}}\left( \alpha _s\right)$, i.e. both at second nontrivial order (FONLL-B). The corresponding two options at the next order are called FONLL-C and -D.

Here, we will consider FONLL-E, in which both the massless and massive contributions are determined at ${\mathcal {O}}\left( \alpha _s^3\right)$. The charm structure function $F^{(c)}_{2}(x,Q^2)$, computed in this scheme, is displayed in Fig. 14 as a function of $Q^2$ for four values of x (with $m_c=1.51$ GeV), and compared to the massive and massless scheme results, with the IHOU on the massive coefficient function shown for the first two cases. The structure functions are computed using the NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ PDF set (to be discussed in Sect. 4 below) which satisfies $\hbox {aN}^3\hbox {LO}$ evolution equations, as is necessary for consistency with the massless scheme result at high scale. It is clear that the FONLL results interpolate between the massive and massless calculations as the scale grows. The $Q^2$ value at which either of the massive or massless results dominate depend strongly on x. Except for the lowest $Q^2$ values, the IHOUs associated with the calculation remain moderate.

The perturbative convergence of the charm structure function is assessed in Fig. 15, where we compare the FONLL-A, FONLL-C and FONLL-E results, all shown as a ratio to FONLL-E, the latter also including the IHOU as in Fig. 14. Clearly, convergence is faster at higher scales due to asymptotic freedom, and it appears that the perturbative expansion has essentially converged for $Q^2\gtrsim 10$ $\hbox {GeV}^2$. On the other hand, the impact of $\hbox {aN}^3\hbox {LO}$ at low scale is sizable, up to 50% for small $Q^2$ and $x = 2\times 10^{-3}$. The IHOUs are correspondingly sizable at low scale, and in fact always larger than the difference between the NNLO and $\hbox {aN}^3\hbox {LO}$ results except at the highest x values and the lowest scales, implying that for the charm structure function $\hbox {aN}^3\hbox {LO}$ may be more accurate, but possibly not more precise than NNLO.

Fig. 16

Same as Fig. 15 for the inclusive structure function $F^{(\text {tot})}_{2}(x,Q^2)$. Note the different scale on the y axis

Fig. 17

Ratio of the total NC Drell–Yan cross-section as a function of the NNLO/NLO and $\hbox {N}^3\hbox {LO}$/NNLO calculations for the inclusive NC Drell–Yan cross-section in bins of $m_{\ell \ell }$, the invariant mass of the final-state dilepton pair, using the n3loxs code, integrated over all other kinematic variables. The $m_{\ell \ell }$ binning is chosen to be that of the ATLAS 7 TeV high-mass DY measurement [103]. The same PDF set is used in the numerator and denominator, namely NNPDF4.0 NNLO (for NNLO/NLO) and $\hbox {aN}^3\hbox {LO}$ (for $\hbox {N}^3\hbox {LO}$/NNLO). The vertical bands show the MHOU on the K-factors computed from scale variations

An analogous study of perturbative convergence of the inclusive structure function is shown in Fig. 16 (note the different scale on the y axis). Interestingly, the effect of the $\hbox {aN}^3\hbox {LO}$ corrections changes sign when going from $x=2\times 10^{-4}$ to larger values of x. In general, $\hbox {N}^3\hbox {LO}$ corrections are smaller at the inclusive level: specifically, $\hbox {aN}^3\hbox {LO}$ corrections to the inclusive structure function are below 2% for $\hbox {GeV}^{2}$, and at most of order 10% around the charm mass scale. The impact of the IHOUs on the heavy coefficient is further reduced due to the fact that charm contributes at most one quarter of the total structure function. Consequently, the $\hbox {aN}^3\hbox {LO}$ correction to the NNLO result is now larger than the IHOU in a significant kinematic region. This, together with the fact that $\hbox {aN}^3\hbox {LO}$ corrections are comparable or larger than typical experimental uncertainties on structure function data, motivates their inclusion in a global PDF determination.

3.3 $\hbox {N}^3\hbox {LO}$ corrections to hadronic processes

$\hbox {N}^3\hbox {LO}$ corrections to the total cross-section for inclusive neutral- (NC) and charged-current (CC) Drell–Yan production [11, 12] are available through the n3loxs public code [8], both for on-shell W and Z and as a function of the dilepton invariant mass $m_{\ell \ell }$. Differential distributions at the level of leptonic observables for the same processes have also been computed [18, 19], but are not publicly available. No $\hbox {N}^3\hbox {LO}$ calculations are available for other processes included in the NNPDF4.0 dataset.

The ratio of the NC total cross-section evaluated at two subsequent perturbative orders with a fixed set of PDFs, chosen as NNPDF4.0 NNLO when comparing NNLO to NLO results, and $\hbox {aN}^3\hbox {LO}$ when comparing $\hbox {N}^3\hbox {LO}$ to NNLO results, is shown in Fig. 17. Results are shown in the high-mass region, as a function of $m_{\ell \ell }$, with the same binning as the ATLAS 7 TeV measurement [103]. Perturbative convergence is apparent, with the $\hbox {N}^3\hbox {LO}$/NNLO ratio closer to unity and smoother than its NNLO/NLO counterpart: while NNLO corrections range between $+0.5\%$ and $+4\%$, at $\hbox {N}^3\hbox {LO}$ they are reduced to $-1.2\%$ and $+0.5\%$.

Total cross-section data are obtained by extrapolating measurements performed in a fiducial region. Whereas for NC Drell–Yan production in the central rapidity region and for dilepton invariant masses around the Z-peak, the $\hbox {N}^3\hbox {LO}$/NNLO cross-section ratio depends only mildly on the dilepton rapidity $y_{\ell \ell }$ [18, 19], it is unclear whether this is the case also off-peak or at very large and very small rapidities. Hence, the inclusion of $\hbox {N}^3\hbox {LO}$ corrections for hadronic processes is, at present, not fully reliable. We have consequently not included them in our default determination, but only in a dedicated variant, with the goal of assessing their impact.

The datasets for which $\hbox {N}^3\hbox {LO}$ corrections have been included in this variant are listed in Table 3. We include the high-mass NC cross-section, the Z rapidity distribution in the central rapidity region for on-shell Z-production, and the total W and Z cross-sections. For all these processes the $\hbox {N}^3\hbox {LO}$ cross-section is determined by multiplying the NNLO result by a K-factor determined using a fixed underlying PDF set, namely the $\hbox {aN}^3\hbox {LO}$ NNPDF4.0 PDF set to be discussed in Sect. 4 below. Specifically, for the rapidity distribution we take the same fixed K-factor as for the total cross-section. We do not include off-shell or double-differential rapidity distributions (specifically from CMS), off-forward rapidity distributions (specifically from LHCb) and low-mass total cross-sections, for all of which the approximation of assuming the K-factor to be independent of rapidity and/or amenable to fiducial extrapolation is even less reliable. The datasets are labeled as in Table 2.4 of Ref. [37].⁴

Despite the fact that we are not yet able to determine reliably $\hbox {N}^3\hbox {LO}$ corrections for currently available LHC measurements, we wish to include the full NNPDF4.0 dataset in our $\hbox {aN}^3\hbox {LO}$ PDF determination. To this purpose, we endow all data for which $\hbox {N}^3\hbox {LO}$ are not included with an extra uncertainty that accounts for the missing $\hbox {N}^3\hbox {LO}$ terms. This is estimated using the methodology of Refs. [35, 36], recently used in Ref. [38] to produce a variant of the NNPDF4.0 PDF sets that includes MHOUs.

Thus, when not including $\hbox {N}^3\hbox {LO}$ corrections to the hard cross-section, the theory prediction is evaluated by combining $\hbox {aN}^3\hbox {LO}$ evolution with the NNLO cross-sections. The prediction is then supplemented with a theory covariance matrix, computed varying the renormalization scale $\mu _R$ using a three-point prescription [35, 36]:

$$\begin{aligned} \text {cov}^{\textrm{NNLO}}_{mn} = \frac{1}{2} \left( \Delta _m(+)\Delta _n(+)+\Delta _m(-)\Delta _n(-)\right) , \end{aligned}$$

(3.8)

analogous to Eq. (3.6), but now with $\Delta _m(\pm )$ the shift in the prediction for the m-th data point obtained by replacing the coefficient functions with those obtained by performing upper or lower renormalization scale variation using the methodology of Ref. [36] (as implemented and discussed in Ref. [38], Eq. (2.9)). This MHOU covariance matrix is then added to the IHOU covariance matrix as a further term on the right-hand side of Eq. (2.20).

The impact of this uncertainty is shown in Fig. 18, where we show for all hadronic datasets the square root of the diagonal entries of the MHOU covariance matrix Eq. (3.8), compared to those of the IHOU covariance matrix Eq. (2.20), and to the experimental uncertainties, all normalized to the central theory prediction. The MHOU is generally larger than the IHOU, indicating that the missing $\hbox {N}^3\hbox {LO}$ terms in the hard cross-sections are larger than the IHOU uncertainty in $\hbox {N}^3\hbox {LO}$ perturbative evolution. The experimental uncertainties are generally larger still.

In addition to the NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ baseline PDF set obtained in this manner, we will also produce a NNPDF4.0 MHOU $\hbox {aN}^3\hbox {LO}$ set, in analogy to the NLO and NNLO MHOU sets recently presented in Ref. [38]. For this set, MHOUs on both perturbative evolution and on the hard matrix elements are included using the methodology of Refs. [35, 36] with a theory covariance matrix determined performing combined correlated renormalization and factorization scale variations with a 7-point prescription, as discussed in detail in Ref. [38]. In this case, we simply perform scale variation on the expressions at the order at which they are being computed, namely $\hbox {aN}^3\hbox {LO}$ for anomalous dimensions and DIS coefficient functions and NNLO for hadronic processes. The scale variation then is automatically larger and suitable deweights processes for which $\hbox {N}^3\hbox {LO}$ corrections are not available. The possibility of simultaneously including in a PDF determination processes for which theory predictions are only available at different perturbative orders is an advantage of the inclusion of MHOUs in the PDF determination, as already pointed out in Refs. [107, 108].

Fig. 18

Same as Fig. 13 now comparing the IHOU from Eq. (2.20) with the MHOU from Eq. (3.8) due to the missing $\hbox {N}^3\hbox {LO}$ correction to the matrix element. Results are shown for all hadronic data in the NNPDF4.0 dataset: specifically Drell–Yan (top) and top pair, single top, single-inclusive jet, prompt photon and dijet production (bottom)

Table 3 The LHC NC DY production datasets in NNPDF4.0 for which an $\hbox {N}^3\hbox {LO}$ K-factor has been included in a variant of the default $\hbox {aN}^3\hbox {LO}$ PDF determination (see Sect. 4). For each dataset we indicate the published references, the number of datapoints and the kinematic variables

4 NNPDF4.0 at $\hbox {aN}^3\hbox {LO}$

We now present the $\hbox {aN}^3\hbox {LO}$ NNPDF4.0 PDF sets. They have been obtained by using the dataset and methodology discussed in [37] and used for the construction of the LO, NLO, and NNLO NNPDF4.0 presented there, now extended to $\hbox {aN}^3\hbox {LO}$. The $\hbox {aN}^3\hbox {LO}$ results are obtained using the approximate $\hbox {N}^3\hbox {LO}$ splitting functions of Sect. 2, the exact massless and approximate massive $\hbox {N}^3\hbox {LO}$ coefficient functions of Sect. 3.1, and NNLO hadronic cross-sections supplemented by an extra uncertainty as per Sect. 3.3.

Theoretical predictions are obtained using the new theory pipeline of Ref. [70], which relies on the EKO evolution code [40] and on the YADISM DIS module [41]. As discussed in Sect. 3.2, this pipeline in particular includes a new FONLL implementation, that differs from the previous one by subleading terms. A further small difference in comparison to Ref. [37] is the correction of a few minor bugs in the data implementation. The overall impact of all these changes was assessed in Appendix A of Ref. [109], and was found to be very limited, so that the new and old implementations can be considered equivalent, and the PDF sets presented here can be considered the extension to $\hbox {aN}^3\hbox {LO}$ of the NNPDF4.0 PDF sets of Ref. [37].

In addition to the default NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ PDF determination, we also present an $\hbox {aN}^3\hbox {LO}$ PDF determination that includes MHOUs on all the theory predictions used in the PDF determination. This is constructed using the same methodology recently used to produce the NNPDF4.0MHOU NNLO PDF set in Ref. [38]. In order to be able to discuss perturbative convergence and the impact of MHOUs we will also present a NNPDF4.0MHOU NLO PDF set constructed using the same methodology, and exactly the same dataset as the default NNPDF4.0 NLO PDF set (which differs from the NNPDF4.0 NNLO dataset).

We finally construct two variants of the $\hbox {aN}^3\hbox {LO}$ PDF sets (both with and without MHOUs) with modified $\hbox {N}^3\hbox {LO}$ theory. In a first variant, we replace our own approximation to the $\hbox {N}^3\hbox {LO}$ anomalous dimensions, discussed in Sect. 2, with that of Refs. [28,29,30]. In the second variant, we will also include $\hbox {N}^3\hbox {LO}$ corrections for the processes listed in Table 3, as discussed in Sect. 3.3.

We first assess the fit quality, then present the PDFs and their uncertainties, and study perturbative convergence and the effect on it of the inclusion of MHOUs. We then specifically study the impact of $\hbox {aN}^3\hbox {LO}$ corrections on intrinsic charm. We then turn to the variants, and finally compare our results to the recent MSHT20 $\hbox {aN}^3\hbox {LO}$ PDFs.

4.1 Fit quality

Tables 4, 5, 6, 7 display the number of data points and the $\chi ^2$ per data point obtained in the NLO, NNLO, and $\hbox {aN}^3\hbox {LO}$ NNPDF4.0 fits with and without MHOUs. In Table 4 the datasets are grouped according to the process categorization used in Ref. [38]. Results for individual datasets are displayed in Table 5 (NC and CC DIS), in Table 6 (NC and CC DY), and in Table 7 (top pairs, single-inclusive jets, dijets, isolated photons, and single top). The naming of the datasets follows Ref. [37]. The value of the total $\chi ^2$ per data point is also shown as a function of the perturbative order in Fig. 19.

Table 4 The number of data points and the $\chi ^2$ per data point obtained in the NLO, NNLO, and $\hbox {aN}^3\hbox {LO}$ NNPDF4.0 fits without and with MHOUs, see text for details. The datasets are grouped according to the same process categorization as that used in Ref. [38]

Table 5 Same as Table 4 for DIS NC (top) and DIS CC (bottom) datasets

Table 6 Same as Table 4 for DY NC (top) and DY CC (bottom) datasets

Table 7 Same as Table 4 for (from top to bottom) top pair, single-inclusive jet, isolated photon and single top production datasets

The NLO and NNLO results without MHOUs are obtained using the NLO and NNLO NNPDF4.0 PDF sets [37]. The NNLO result with MHOUs is obtained using the NNPDF4.0MHOU NNLO set from Ref. [38], while, as already mentioned, the NNPDF4.0MHOU NLO presented here for the first time uses an identical methodology to NNPDF4.0MHOU NNLO [38], but the same dataset as NNPDF4.0 NLO [37]. Hence, the datasets with and without MHOU are always the same, but the NLO and NNLO datasets are not the same but rather follow Ref. [37]. The $\hbox {N}^3\hbox {LO}$ dataset is the same as NNLO. In all cases, the theoretical predictions entering the computation of the $\chi ^2$ are obtained with the new theory pipeline. The covariance matrix, whenever needed, is computed as described in Sect. 4.1 of Ref. [38]. The $\hbox {N}^3\hbox {LO}$ predictions are computed with the aforementioned $\hbox {aN}^3\hbox {LO}$ PDF sets. These are based on the same datasets and kinematic cuts as the NNPDF4.0 NNLO PDF sets, use the theoretical predictions discussed in Sects. 2, 3, and are supplemented with a IHOU covariance matrix as discussed in Sects. 2.2–3.1 and a MHOU for hadronic processes for which $\hbox {N}^3\hbox {LO}$ hard cross-sections are not available as discussed in Sect. 3.3.

Table 4 and Fig. 19 show that without MHOUs fit quality improves as the perturbative order increases. Note that this also happens when going from NNLO to $\hbox {N}^3\hbox {LO}$, despite the fact that $\hbox {N}^3\hbox {LO}$ corrections are only partially included, with hadronic matrix elements still computed at NNLO. This shows that the impact of $\hbox {N}^3\hbox {LO}$ corrections to evolution and DIS coefficient functions is significant enough to affect fit quality in a way that is qualitatively compatible with what one would expect when adding an extra perturbative order to the improvement already seen when going from NLO to NNLO.

On the other hand, when MHOUs are included, fit quality becomes independent of perturbative order within uncertainties (note that, with $N_{\textrm{dat}}=4462$, $\sigma _{\chi ^2}=0.03$). This suggests that the MHOU covariance matrix estimated through scale variation is correctly reproducing the observed shift between perturbative orders, i.e. the true MHOU. Note that if true this also means that at $\hbox {aN}^3\hbox {LO}$ the missing $\hbox {N}^3\hbox {LO}$ corrections to hadronic processes are correctly accounted for by the corresponding MHOU which is always included. Also, at $\hbox {aN}^3\hbox {LO}$ the fit quality is the same within uncertainties irrespective of whether MHOUs are included or not. This strongly suggests that inclusion of higher order terms in perturbative evolution and DIS coefficient function would not lead to further improvements, i.e. that in this respect, with experimental uncertainties, current methodology and current dataset the perturbative expansion has converged.

4.2 Parton distributions

We now examine the NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ parton distributions. We compare the NLO, NNLO and $\hbox {aN}^3\hbox {LO}$ NNPDF4.0 PDFs, obtained without and with inclusion of MHOUs, in Figs. 20, 21 and in Figs. 22, 23, respectively. Specifically, we show the up, antiup, down, antidown, strange, antistrange, charm and gluon PDFs at $Q=100$ GeV, normalized to the $\hbox {aN}^3\hbox {LO}$ result, as a function of x in logarithmic and linear scale. Error bands correspond to one sigma PDF uncertainties, which do (MHOU sets) or do not (no MHOU sets) include MHOUs on all theory predictions used in the fit. The PDF sets, with and without MHOUs, are the same used to compute the values of the $\chi ^2$ in Tables 4, 5, 6, 7.

The excellent perturbative convergence seen in the fit quality is also manifest at the level of PDFs. In particular, the NNLO PDFs are either very close to or indistinguishable from their $\hbox {aN}^3\hbox {LO}$ counterparts. Inclusion of MHOUs further improves the consistency between NNLO and $\hbox {aN}^3\hbox {LO}$ PDFs, which lie almost on top of each other. This means that the NNLO PDFs are made more accurate by the inclusion of MHOUs, and that the $\hbox {aN}^3\hbox {LO}$ PDFs have converged, in the sense discussed above. Exceptions to this stability are the charm and gluon PDFs, for which $\hbox {aN}^3\hbox {LO}$ corrections have a sizable impact. In the case of charm, they lead to an enhancement of the central value of about 4% for $x\sim 0.05$; in the case of gluon, to a suppression of about 2–3% for $x\sim 0.005$. In both cases, inclusion of MHOUs leads to an increase in PDF uncertainties by about 1–2%. This makes the NNLO and $\hbox {aN}^3\hbox {LO}$ charm PDFs with MHOUs compatible within uncertainties, and the NNLO and $\hbox {aN}^3\hbox {LO}$ gluon PDFs with MHOU almost compatible.

Fig. 19

The values of the total $\chi ^2$ per data point in the NNPDF4.0 NLO, NNLO, and $\hbox {aN}^3\hbox {LO}$ fits without and with MHOUs

Figure 24 presents a comparison similar to that of Figs. 20, 21, 22 for the gluon-gluon, gluon-quark, quark-quark, and quark-antiquark parton luminosities. These are shown integrated in rapidity as a function of the invariant mass of the final state $m_X$ for a center-of-mass energy $\sqrt{s}=14$ TeV. Their definition follows Eqs. (1)-(4) of Ref. [110].

As already observed for PDFs, perturbative convergence is excellent, and improves upon inclusion of MHOUs. The NNLO and $\hbox {aN}^3\hbox {LO}$ results are compatible within uncertainties for the gluon-quark, quark-quark, and quark-antiquark luminosities. Some differences are seen for the gluon-gluon luminosity, consistent with the differences seen in the gluon PDF. Specifically, the $\hbox {aN}^3\hbox {LO}$ corrections lead to a suppression of the gluon-gluon luminosity of 2–3% for $m_X\sim 100$ GeV. This effect is somewhat compensated by an increase in uncertainty of about 1% upon inclusion of MHOUs. Indeed, the NNLO and $\hbox {aN}^3\hbox {LO}$ gluon-gluon luminosities for $m_X\sim 100$ GeV differ by about $2.5\sigma$ without MHOU, but become almost compatible within uncertainties when MHOUs are included.

All in all, these results show that $\hbox {aN}^3\hbox {LO}$ corrections are generally small, except for the gluon PDF, and that at $\hbox {aN}^3\hbox {LO}$ the perturbative expansion has all but converged, with NNLO and $\hbox {aN}^3\hbox {LO}$ PDFs very close to each other, especially upon inclusion of MHOUs. They also show that MHOUs generally improve the accuracy of PDFs, though at $\hbox {aN}^3\hbox {LO}$ they have a very small impact. The phenomenological consequences of this state of affairs will be further discussed in Sect. 5.

4.3 PDF uncertainties

We now take a closer look at PDF uncertainties. In Fig. 25 we display one sigma uncertainties for the NNPDF4.0 NLO, NNLO, and $\hbox {aN}^3\hbox {LO}$ PDFs with and without MHOUs at $Q=100$ GeV. All uncertainties are normalized to the central value of the NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ PDF set with MHOUs. The NLO uncertainty is generally the largest of all in the absence of MHOUs, and for quark distributions the smallest once MHOUs are included. All other uncertainties, at NNLO and $\hbox {aN}^3\hbox {LO}$, with and without MHOUs, are quite similar to each other, especially for quark PDFs. The fact that upon inclusion of an extra source of uncertainty, namely the MHOU, PDF uncertainties are reduced (at NLO) or unchanged (at NNLO and $\hbox {aN}^3\hbox {LO}$) may look counter-intuitive. However, as already pointed out in Refs. [34, 38, 111], this can be understood to be a consequence of the increased compatibility of the data due to inclusion of MHOUs and of higher-order perturbative corrections.

Fig. 20

The NLO, NNLO and $\hbox {aN}^3\hbox {LO}$ NNPDF4.0 PDFs at $Q=100$ GeV. We display the up, antiup, down, antidown, strange, antistrange, charm and gluon PDFs normalized to the $\hbox {aN}^3\hbox {LO}$ result. Error bands correspond to one sigma PDF uncertainties, not including MHOUs on the theory predictions used in the fit

Fig. 21

Same as Fig. 20 in linear scale

Fig. 22

Same as Fig. 20 for NNPDF4.0MHOU PDF sets. Error bands correspond to one sigma PDF uncertainties also including MHOUs on the theory predictions used in the fit

Fig. 23

Same as Fig. 22 in linear scale

Fig. 24

The gluon-gluon, gluon-quark, quark-quark, and quark-antiquark parton luminosities as a function of $m_X$ at $\sqrt{s}=14$ TeV, computed with NLO, NNLO and $\hbox {aN}^3\hbox {LO}$ NNPDF4.0 PDFs without MHOUs (left) and with MHOUs (right), all shown as a ratio to the respective $\hbox {aN}^3\hbox {LO}$ results. Uncertainties are as in Figs. 20, 21, 22

Fig. 25

Relative one sigma uncertainties for the PDFs shown in Figs. 20, 21, 22. All uncertainties are normalized to the central value of the NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ set with MHOUs

Fig. 26

Same as Figs. 20, 21, 22, now comparing NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ PDFs without and with MHOUs

Fig. 27

Same as Fig. 24, now comparing NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ PDFs without and with MHOUs

Table 8 The $\phi$ uncertainty estimator for NNPDF4.0 PDFs at NLO, NNLO and $\hbox {aN}^3\hbox {LO}$ without and with MHOUs for the process categories as in Table 4

The impact of MHOUs on NLO and NNLO PDFs was extensively assessed in Ref. [38]. In a similar vein, here we focus on the impact of MHOUs on $\hbox {aN}^3\hbox {LO}$ PDFs. To this purpose, in Fig. 26 we compare the NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ PDFs with and without MHOUs. The related comparison for parton luminosities is presented in Fig. 27. Again, $\hbox {aN}^3\hbox {LO}$ PDFs and luminosities with and without MHOU are very compatible with each other. This evidence reinforces the expectation that perturbative corrections beyond $\hbox {N}^3\hbox {LO}$ will not alter PDFs significantly, at least with current data and methodology.

In analogy with Ref. [38], we also compare the $\phi$ estimator introduced in Ref. [112] (see Eq. (4.6) there). The estimator gives the ratio of the average correlated PDF uncertainty to the data uncertainty. As such, it provides an estimate of the consistency of the data: consistent data are combined by the underlying theory and lead to an uncertainty in the prediction which is smaller than that of the original data. The value of $\phi$ obtained in the NLO, NNLO, and $\hbox {aN}^3\hbox {LO}$ NNPDF4.0 fits with and without MHOUs (as in Table 4) is reported in Table 8. It is clear that $\phi$ converges to very similar values with the increase of the perturbative order and/or with inclusion of MHOUs for both the total dataset and for most of the data categories. This fact is further quantitative evidence of the excellent perturbative convergence of the PDF uncertainties.

4.4 Implications for intrinsic charm

The availability of the $\hbox {aN}^3\hbox {LO}$ PDFs discussed in Sects. 4.2, 4.3 allows us to revisit and consolidate our recent results on intrinsic charm. Specifically, based on the NNPDF4.0 NNLO PDF determination, we have found evidence for intrinsic charm [113] and an indication for a non-vanishing valence charm component [114]. In these analyses, the dominant source of theory uncertainty was estimated to come from the matching conditions that are used in order to obtain PDFs in a three-flavor charm decoupling scheme from high-scale data, while MHOUs were assumed to be subdominant. The uncertainty in the matching conditions was in turn estimated by comparing results obtained using NNLO matching and the best available $\hbox {aN}^3\hbox {LO}$ matching conditions, both applied to NNLO PDFs.

It is now possible to improve these results on three counts. First, we can now fully include MHOUs. Second, we can consistently combine $\hbox {aN}^3\hbox {LO}$ matching conditions and $\hbox {aN}^3\hbox {LO}$ PDFs, and perform a consistent comparison of NNLO and $\hbox {aN}^3\hbox {LO}$ results. Finally, knowledge of $\hbox {aN}^3\hbox {LO}$ matching conditions themselves is now improved thanks to recent results [81] that were not available at the time of the analysis of Ref. [113]. We will specifically discuss the determination of the total intrinsic charm component and we do not consider the valence component, because effects of MHOUs and of the flavor scheme transformation are already very small at NNLO [114].

Fig. 28

The total charm PDF, $xc^+(x,Q^2)$, in the 4FNS at $Q=1.65$ GeV (left) and 3FNS (right), as obtained from the NNPDF4.0 NLO, NNLO, and $\hbox {aN}^3\hbox {LO}$ fits without (top) and with (bottom) MHOUs. Error bands correspond to one sigma PDF uncertainties. Note that in the 3FNS the charm PDF does not depend on scale

Fig. 29

Same as Fig. 28, now comparing the total charm PDF in the 3FNS with and without MHOUs, respectively at NNLO (left) and $\hbox {aN}^3\hbox {LO}$ (right)

To this purpose, in Fig. 28 we show the total charm PDF, $xc^+(x,Q^2)$, in the 4FNS at $Q=1.65$ GeV and in the 3FNS, as obtained from using NNPDF4.0 NLO, NNLO and $\hbox {aN}^3\hbox {LO}$ without and with MHOUs. Note that in the 3FNS the charm PDF does not depend on scale. Error bands correspond to one sigma PDF uncertainties. The 4FNS results share the general features discussed in Sect. 4.2: the perturbative expansion converges nicely, with the $\hbox {aN}^3\hbox {LO}$ result very close to the NNLO. The convergence is further improved by the inclusion of MHOUs, which move the NNLO yet closer to the $\hbox {aN}^3\hbox {LO}$. The 3FNS result is especially remarkable: whereas the combination of $\hbox {aN}^3\hbox {LO}$ matching with NNLO PDFs, used in Ref. [113] to conservatively estimate MHOUs, was somewhat unstable, now results display complete stability, and in particular the NNLO and $\hbox {aN}^3\hbox {LO}$ results completely coincide.

In order to assess the impact of MHOUs more clearly, in Fig. 29 we compare the total charm PDF in the 3FNS with and without MHOUs, respectively at NNLO and $\hbox {aN}^3\hbox {LO}$. At NNLO MHOUs have a small but non-negligible impact on central values, with almost unchanged uncertainty, but at $\hbox {aN}^3\hbox {LO}$ they have essentially no impact, confirming the perturbative convergence of the result.

We thus proceed to a final re-assessment of the significance of intrinsic charm through the pull, defined as the central value divided by total uncertainty, using NNPDF4.0MHOU NNLO and $\hbox {aN}^3\hbox {LO}$ PDFs. We estimate the total uncertainty by adding in quadrature to the PDF uncertainty (which already includes the MHOU from the theory predictions used in the fit) a further theory uncertainty, taken equal to the difference between the central value at given perturbative order, and that at the previous perturbative order (so at NNLO from the difference to NLO, and so on). This now also includes the MHOU due to change in the matching from 4FNS to 3FNS, but also the shift in the 4FNS result that is in principle already accounted for by the MHOU. Also, it conservatively assumes that the shift between the current order and the next is equal to that from the previous order, rather than smaller. Results obtained with this conservative error estimate are shown in Fig. 30. It is clear that the significance of intrinsic charm is increased somewhat when going from NNLO to $\hbox {aN}^3\hbox {LO}$. It is now also somewhat increased already at NNLO in comparison to the result of Ref. [113], despite the more conservative uncertainty estimate, thanks to the increased accuracy of MHOU PDFs and the consistent and improved treatment of matching $\hbox {aN}^3\hbox {LO}$ conditions. Indeed, local significance at the peak is now more than three sigma for the default fit.

4.5 Dependence on the treatment of $\hbox {aN}^3\hbox {LO}$ corrections.

We now discuss two variants in the treatment of $\hbox {aN}^3\hbox {LO}$ corrections: a different approximation to perturbative evolution, and a different treatment of hadronic cross-sections.

Fig. 30

The pull (central value divided by total uncertainty) for the total charm PDF in the 3FNS obtained in the NNPDF4.0 NNLO and $\hbox {aN}^3\hbox {LO}$ fits with MHOUs

The $\hbox {aN}^3\hbox {LO}$ PDF sets presented in Sect. 4.2 are based on our approximation to the full set of $\hbox {N}^3\hbox {LO}$ splitting functions presented in Sect. 2. This approximation was compared in Sect. 2.7 to that recently presented in Refs. [22, 28,29,30] (FHMRUVV). In order to fully assess the impact of this different approximation to $\hbox {N}^3\hbox {LO}$ perturbative evolution we have repeated the $\hbox {aN}^3\hbox {LO}$ PDF determination, without and with MHOUs, but now using the FHMRUVV approximation to $\hbox {N}^3\hbox {LO}$ perturbative evolution, with everything else unchanged. PDFs obtained using the FHMRUVV approximation vs our own are compared in Fig. 31 without MHOUs and in Fig. 32 with MHOUs. PDFs are displayed at $Q=100$ GeV, normalized to the central value of our default result. Differences turn out to be completely negligible, as might have been expected given the good agreement at the level of splitting functions seen in Fig. 10.

As discussed in Sect. 3.3$\hbox {N}^3\hbox {LO}$ corrections to hadronic hard cross-sections are not included in our default $\hbox {aN}^3\hbox {LO}$ PDF determination. We can however assess the impact of the inclusion of all the publicly available corrections for all relevant data in the NNPDF4.0 dataset, listed in Table 3 and discussed in Sect. 3.3, using the methodology discussed in that Section. To this purpose, we have repeated the $\hbox {aN}^3\hbox {LO}$ PDF determination, with and without MHOUs, now with $\hbox {N}^3\hbox {LO}$ corrections for these datasets included. Note that for these processes NNLO corrections are currently already included through K-factors, hence this requires combining NNLO and $\hbox {N}^3\hbox {LO}$ K-factors, with ensuing loss of accuracy, which is one of the reasons why these corrections are not included in our default $\hbox {aN}^3\hbox {LO}$ determination. MHOUs on these $\hbox {N}^3\hbox {LO}$ predictions can be determined by scale variation as usual, given that renormalization scale variation at $\hbox {N}^3\hbox {LO}$ only requires knowledge of the NNLO result.

Fig. 31

Same as Fig. 20, now comparing the NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ PDFs and PDFs obtained using the FHMRUVV approximation to $\hbox {N}^3\hbox {LO}$ perturbative evolution

Fig. 32

Same as Fig. 31 for $\hbox {aN}^3\hbox {LO}$ PDF sets with MHOUs

Table 9 The number of data points and the $\chi ^2$ per data point for the datasets of Table 3 comparing the default fits (same as Table 6) to fits in which $\hbox {N}^3\hbox {LO}$ corrections are included following the methodology of Sect. 3.3, in both cases with and without MHOUs

The fit quality for the datasets of Table 3 both in the default determinations (with and without MHOU, same as Table 6) and after the inclusion of $\hbox {N}^3\hbox {LO}$ corrections (also with and without MHOU) is shown in Table 9. The ensuing PDFs are compared to the default NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ in Fig. 33 without MHOUs and in Fig. 34 with MHOUs. In both cases, PDFs are displayed at $Q=100$ GeV and are normalized to the central value of the corresponding default NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ set. The impact of these $\hbox {N}^3\hbox {LO}$ corrections on fit quality is very moderate, though in all cases but one (and in all cases with MHOUs) it leads to improved agreement. At the level of PDFs, however, the impact is only (barely) visible in the PDFs without MHOUs, and even in this case it only significantly impacts the strange and antistrange PDFs, for which it leads to an enhancement of 4–5% for $x\sim 0.1$, though well within the PDF uncertainty. Even this small effect is absent in the PDFs with MHOUs. We conclude that at present available $\hbox {N}^3\hbox {LO}$ corrections for hadronic processes have no effect on PDF determination. On the other hand, the improvement in fit quality is reassuring, and suggests that a more significant effect might be seen once $\hbox {N}^3\hbox {LO}$ corrections become available for a wider set of processes.

4.6 Comparison with MSHT20

We compare the NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ PDF set to the only other existing $\hbox {aN}^3\hbox {LO}$ PDF set, MSHT20 $\hbox {aN}^3\hbox {LO}$ [32]. As already discussed in Sect. 2.7, MSHT20 $\hbox {aN}^3\hbox {LO}$ PDFs are determined by fitting to the data the nuisance parameters that parametrize the IHOU uncertainty on a prior approximation to splitting functions. It follows that the ensuing central value is partly determined by the data, and the IHOU is entirely data-driven. When comparing NNPDF4.0 and MSHT20 $\hbox {aN}^3\hbox {LO}$ PDF sets it should of course be borne in mind that the sets already differ at NNLO due to differences in dataset and methodology. The NNLO MSHT20 and NNPDF4.0 PDF sets were compared in Fig. 21 and the corresponding parton luminosity in Fig. 60 of Ref. [37], while a detailed benchmarking was presented in Ref. [115].

The comparison of the $\hbox {aN}^3\hbox {LO}$ sets is presented in Fig. 35, where we show the NNPDF4.0 no MHOU set and the MSHT20 set recommended as baseline in Ref. [32] at $Q=100$ GeV, normalized to the NNPDF4.0 central value. All error bands are one sigma uncertainties. The dominant differences between the PDF sets are the same as already observed at NNLO, with the largest difference observed for the charm PDF, which is independently parametrized in NNPDF4.0, but not in MSHT20, where it is determined by perturbative matching conditions. However, the differences, while remaining qualitatively similar, are slightly reduced (by 1–2%) when moving from NNLO to $\hbox {aN}^3\hbox {LO}$. Exceptions are the charm and especially the gluon PDF, which differ more at $\hbox {aN}^3\hbox {LO}$. Specifically, the gluon PDF, while reasonably compatible for $x\lesssim 0.07$ at NNLO, disagrees at $\hbox {aN}^3\hbox {LO}$, with the MSHT20 result suppressed by 3–4% in the region $10^{-3}\lesssim x \lesssim 10^{-1}$, with a PDF uncertainty of 1-2%. This suppression of the MSHT20 gluon can likely be traced to the behavior of the $P_{gq}$ splitting function seen in Fig. 10.

Parton luminosities are compared in Fig. 36. Again the pattern is similar to that seen at NNLO, but now with a considerable suppression of the gluon-gluon and gluon-quark luminosities in the $M_X\sim 100$ GeV region that can be traced to the behavior of the gluon PDF seen in Fig. 35. The quark-quark luminosity remains similar in MSHT20 and NNPDF4.0 both at NNLO and $\hbox {aN}^3\hbox {LO}$. The impact of these effects on the computation of precision LHC cross-sections will be addressed in Sect. 5.

In order to understand better the comparative impact of $\hbox {aN}^3\hbox {LO}$ corrections, we compare for each set the NNLO and $\hbox {aN}^3\hbox {LO}$ luminosities. Results are shown in Fig. 37, normalized to the $\hbox {aN}^3\hbox {LO}$ result. The qualitative impact of the $\hbox {aN}^3\hbox {LO}$ corrections on either set is similar, but with a stronger $\hbox {aN}^3\hbox {LO}$ suppression of gluon luminosities for MSHT20. In particular the gluon-gluon luminosity is suppressed for $10^2\lesssim m_X\lesssim 10^3$ GeV by about 3% in NNPDF4.0 and 6% in MSHT20 and the gluon-quark luminosity is suppressed in the same region by about 1% in NNPDF4.0 and 3% in MSHT20. In the case of the gluon-gluon luminosity the differences between NNLO and $\hbox {aN}^3\hbox {LO}$ are larger than the respective PDF uncertainties (that do not include MHOUs in either case). As already mentioned in Sect. 2.7, a dedicated benchmark of $\hbox {aN}^3\hbox {LO}$ results is ongoing and will be presented in Ref. [84].

5 LHC phenomenology at $\hbox {aN}^3\hbox {LO}$ accuracy

We present a first assessment of the implications of $\hbox {aN}^3\hbox {LO}$ PDFs for LHC phenomenology, by looking at processes for which $\hbox {N}^3\hbox {LO}$ results are publicly available, namely the Drell–Yan and Higgs total inclusive cross-sections. We present predictions at NLO, NNLO, and $\hbox {aN}^3\hbox {LO}$ using both NNPDF4.0 and MSHT20 PDFs, consistently matching the perturbative order of the PDF and matrix element. At $\hbox {N}^3\hbox {LO}$ we also show results obtained with the currently common approximation of using NNLO PDFs with $\hbox {aN}^3\hbox {LO}$ matrix elements.

At each perturbative order, the uncertainty on the cross-section is determined by adding in quadrature the PDF uncertainty to the MHOU on the hard matrix element determined performing 7-point renormalization and factorization scale variation and taking the envelope of the results. This is the procedure that is most commonly used for the estimation of the total uncertainty on hadron collider processes, and we follow it here for ease of comparison with available results. In a more refined treatment, MHOUs on the hard cross-section can be included through a theory covariance matrix for the hard cross-section itself, like the MHOUs and IHOUs on the PDF. This would then make it possible to keep track of the correlation between these different sources of uncertainty [116,117,118].

Fig. 33

Same as Fig. 20, now comparing the NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ baseline PDF set without MHOUs to a variant obtained with inclusion of $\hbox {N}^3\hbox {LO}$ corrections for the hadronic processes of Table 3

Fig. 34

Same as Fig. 33 for $\hbox {aN}^3\hbox {LO}$ PDF sets with MHOUs

Fig. 35

Same as Fig. 20, now comparing the NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ baseline PDF set without MHOUs to the MSHT20 set recommended as baseline in Ref. [32]

Fig. 36

Same as Fig. 35 for parton luminosities as in Fig. 24

Fig. 37

Same as Fig. 36, now comparing $\hbox {aN}^3\hbox {LO}$ and NNLO parton luminosities, separately for the NNPDF4.0 (left) and MSHT20 (right) PDF sets, normalized to the $\hbox {aN}^3\hbox {LO}$ result

Here we plot results with a total uncertainty obtained combining these uncertainties in quadrature (both with and without MHOUs in the fit), and we also tabulate this total uncertainty (without MHOUs in the fit) along with the PDF uncertainty both with and without MHOUs. Also, in order to assess the impact of the use of $\hbox {aN}^3\hbox {LO}$ PDFs, we plot $\hbox {N}^3\hbox {LO}$ results obtained using NNLO and $\hbox {aN}^3\hbox {LO}$ PDFs, we tabulate the shift between the $\hbox {N}^3\hbox {LO}$ prediction obtained using NNLO and $\hbox {aN}^3\hbox {LO}$ PDFs, and we compare it to previous estimate of this expected shift based on the differences between NNLO and NLO PDFs. Indeed, predictions for processes computed at $\hbox {N}^3\hbox {LO}$ accuracy are commonly obtained using NNLO PDFs, with an extra uncertainty assigned to the result due to this mismatch in perturbative order between the PDF and the matrix element. A commonly used prescription in order to estimate this uncertainty [8, 119] is to take it equal to

$$\begin{aligned} \Delta ^{\textrm{app}}_{\textrm{NNLO}} \equiv \frac{1}{2}\left| \frac{\sigma ^{\textrm{NNLO}}_{\mathrm{NNLO-PDF}} - \sigma ^{\textrm{NNLO}}_{\mathrm{NLO-PDF}}}{\sigma ^{\textrm{NNLO}}_\mathrm{NNLO-PDF}}\right| , \end{aligned}$$

(5.1)

namely to assume that the same percentage shift, computed at one less perturbative order, would be twice as large. This prescription can now be compared to the exact result

$$\begin{aligned} \Delta ^{\textrm{exact}}_{\textrm{NNLO}} \equiv \left| \frac{\sigma ^{\mathrm{N^3LO}}_{\mathrm{N^3LO-PDF}} - \sigma ^\mathrm{N^3LO}_{\mathrm{NNLO-PDF}}}{\sigma ^{\mathrm{N^3LO}}_{\mathrm{N^3LO-PDF}}}\right| . \end{aligned}$$

(5.2)

5.1 Inclusive Drell–Yan production

We show results for inclusive charged-current and neutral-current gauge boson production cross-sections followed by their decays into the dilepton final state. Cross-sections are evaluated using the n3loxs code [8] for different ranges in the final-state dilepton invariant mass, $Q=m_{\ell \ell }$ for neutral-current and $Q=m_{\ell \nu }$ for charged-current scattering. Figure 38 displays the inclusive neutral-current Drell–Yan cross-section $pp\rightarrow \gamma ^*/Z \rightarrow \ell ^+\ell ^-$ and Figs. 39, 40 the charged-current cross-sections $pp\rightarrow W^\pm \rightarrow \ell ^\pm \nu _{\ell }$. We consider one low-mass bin ($30~\textrm{GeV}\le Q \le 60~\textrm{GeV}$), the mass peak bin ($60~\textrm{GeV}\le Q \le 120~\textrm{GeV}$), and two high-mass bins ($120~\textrm{GeV}\le Q \le 300~\textrm{GeV}$ and $2~\textrm{TeV}\le Q\le 3~\textrm{TeV}$), relevant for high-mass new physics searches [120]. In all cases, we compare the NLO, NNLO, and $\hbox {aN}^3\hbox {LO}$ predictions using NNPDF4.0 and MSHT20 PDFs determinations, with the same perturbative order in matrix element and PDFs, and also the $\hbox {aN}^3\hbox {LO}$ result with NNLO PDFs, and then we compare the $\hbox {aN}^3\hbox {LO}$ with NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ PDFs with and without MHOUs. The values of cross-sections and uncertainties are collected in Table 10.

Table 10 The $\hbox {N}^3\hbox {LO}$ cross-sections and uncertainties for the inclusive gauge boson production processes displayed in Figs. 38, 39, 40 and evaluated using the NNPDF4.0 and MSHT20 $\hbox {aN}^3\hbox {LO}$ PDFs. We show the percentage total theory uncertainty $\delta _{\textrm{th}}$, obtained adding in quadrature the 7-point scale variation MHOUs and the PDF uncertainty $\delta _{\textrm{PDF}}$ (not including MHOUs in the fit), which is also separately provided. In the case of NNPDF4.0 the value of $\delta _{\textrm{PDF}}$ with MHOUs in the fit is also listed. All uncertainties are expressed as percentage of the cross-section. We finally show the error $\Delta ^{\textrm{exact}}_{\textrm{NNLO}}$ Eq. (5.2) due to using NNLO PDFs at $\hbox {N}^3\hbox {LO}$, and the estimate of this error $\Delta ^{\textrm{app }}_\textrm{NNLO}$ Eq. (5.1), also expressed as a percentage

Fig. 38

The inclusive neutral-current Drell–Yan production cross-section, $pp\rightarrow \gamma ^*/Z \rightarrow \ell ^+\ell ^-$, for different ranges of the dilepton invariant mass $Q=m_{\ell \ell }$, from low to high invariant masses (top to bottom). Results are shown (left) comparing NLO, NNLO and $\hbox {aN}^3\hbox {LO}$ with matched perturbative order in the matrix element and PDF, and also at $\hbox {aN}^3\hbox {LO}$ with NNLO PDFs using NNPDF4.0 and MSHT20 PDFs and (right) at $\hbox {aN}^3\hbox {LO}$ with PDFs without and with MHOUs

In general we observe a good perturbative convergence, with predictions at two subsequent orders in agreement within uncertainties, and generally improved convergence upon including MHOUs on the PDF. Predictions based on NNPDF4.0 and MSHT20 are always consistent with each other within uncertainties. We can draw three main conclusions from Figs. 38, 39, 40 and Table 10. First, in many cases differences between the NNLO and $\hbox {N}^3\hbox {LO}$ predictions tend to be reduced when using consistently the appropriate PDFs at each order, rather than NNLO PDFs with $\hbox {N}^3\hbox {LO}$ matrix elements (though in some cases the results are unchanged). For instance, for the two lowest $m_{\ell \ell }$ bins for NC production $\hbox {aN}^3\hbox {LO}$ PDFs drive upwards the $\hbox {N}^3\hbox {LO}$ prediction, making it closer to the NNLO result. Second, the difference between PDFs with and without MHOUs, while moderate, remains non-negligible even at $\hbox {N}^3\hbox {LO}$, where it starts being comparable to the overall uncertainty, and thus it must be included in precision calculations. Third, the impact of using $\hbox {aN}^3\hbox {LO}$ instead of NNLO PDFs is actually smaller than the guess based on the estimate Eq. (5.1).

Fig. 39

Same as Fig. 38 for the inclusive charged-current Drell–Yan production cross-section, $pp\rightarrow W^+ \rightarrow \ell ^+\nu _{\ell }$

Fig. 40

Same as Fig. 38 for the inclusive charged-current Drell–Yan production cross-section, $pp\rightarrow W^- \rightarrow \ell ^-{\bar{\nu }}_{\ell }$

5.2 Inclusive Higgs production

We now consider Higgs production in gluon fusion, in associated production with vector bosons, and via vector-boson fusion (VBF). Predictions are obtained using the ggHiggs code [121] for gluon fusion, n3loxs for associate production, and proVBFH code [122] for VBF. Results are shown in Fig. 41 for gluon-fusion and VBF, and Fig. 42 for associate production with $W^+$ and Z (Table 11).

Here too we observe generally good perturbative convergence, even for gluon fusion, that notoriously has a very slowly converging expansion. Also in this case, there is generally better agreement between NNPDF4.0 and MSHT20 as the perturbative order increases, except for gluon fusion where the agreement is similar at all orders. Indeed, in all cases MSHT20 and NNPDF4.0 results agree within uncertainties at $\hbox {aN}^3\hbox {LO}$, while they do not at NLO for VBF, nor at NLO and NNLO for associated production. The impact of using $\hbox {aN}^3\hbox {LO}$ PDFs instead of NNLO PDFs at $\hbox {N}^3\hbox {LO}$ for NNPDF4.0 is very moderate for gluon fusion, somewhat more significant for associated production, and more significant for VBF, in which it is comparable to the PDF uncertainty. For MSHT20 instead a significant change from using $\hbox {aN}^3\hbox {LO}$ instead of NNLO PDFs is also observed for gluon fusion, where suppression of the cross-sections is seen when replacing NNLO with $\hbox {aN}^3\hbox {LO}$ PDFs. This follows from the behavior of the gluon luminosity seen in Fig. 37. The impact of MHOUs on the PDFs is generally quite small on the scale of the PDF uncertainty at all perturbative orders, and essentially absent for gluon fusion. For associated production it marginally improves perturbative convergence. Interestingly, for NNPDF4.0, for all Higgs production processes considered, and especially for gluon fusion, the estimate Eq. (5.1) is a substantial underestimate of the actual error which is made using NNLO PDFs at $\hbox {N}^3\hbox {LO}$. This follows from the fact that (see Fig. 24) for $m_X\sim 100$ GeV the NNLO gluon-gluon luminosity is actually closer to the NLO than to the $\hbox {aN}^3\hbox {LO}$, which in turn appears to be an accidental consequence of the behavior of the gluon PDF for $x\sim 10^{-2}$.

Table 11 Same as Table 10 for the Higgs production processes displayed in Figs. 41, 42

Fig. 41

Same as Fig. 38 for Higgs production in gluon-fusion and via vector-boson fusion

Fig. 42

Same as Fig. 38 for Higgs production in association with $W^+$ and Z gauge bosons: from top to bottom, Zh, $W^+h$, and $W^-h$

6 Summary and outlook

We have presented the first $\hbox {aN}^3\hbox {LO}$ PDF sets within the NNPDF framework, by constructing a full set of approximate $\hbox {N}^3\hbox {LO}$ splitting functions based on available partial results and known limits, approximate massive DIS coefficient functions, and extending to this order the FONLL general-mass scheme for DIS coefficient functions. We now summarize the new PDF sets that we are releasing, our main conclusions on their features, and our plans for future developments.

The NNPDF4.0 $\hbox {aN}^3\hbox {LO}$ PDF sets are available via the LHAPDF6 interface,

http://lhapdf.hepforge.org/  .

Specifically, we provide an $\hbox {aN}^3\hbox {LO}$ NNPDF4.0 set

NNPDF40_an3lo_as_01180

that supplements the LO, NLO and NNLO sets of Ref. [37].

We also provide NLO and $\hbox {aN}^3\hbox {LO}$ NNPDF4.0MHOU sets

NNPDF40_nlo_as_01180_mhou

NNPDF40_an3lo_as_01180_mhou

that supplement the NNLO NNPDF4.0MHOU PDF set of Ref. [38]. These sets include in the PDF uncertainty the MHOU on the processes used for PDF determination, but in all other respects (including the dataset) follow the default sets to which they can be directly compared.

For both $\hbox {aN}^3\hbox {LO}$ sets, we also release the corresponding sets including $\alpha _s$ variations,

NNPDF40_an3lo_as_01180_pdfas

NNPDF40_an3lo_as_01180_mhou_pdfas

in which replicas 101 and 102 correspond to fits with $\alpha _s(m_Z)=0.117$ and 0.119 respectively, in order to evaluate the combined PDF+$\alpha _s$ uncertainties following the prescription of [115, 123, 124].

All these sets are delivered as ensembles of $N_{\textrm{rep}}=100$ Monte Carlo replicas.

However, we also make available Hessian variants following [125, 126] and denoted

NNPDF40_an3lo_as_01180_hessian

NNPDF40_an3lo_as_01180_mhou_hessian

NNPDF40_an3lo_as_01180_pdfas_hessian

NNPDF40_an3lo_as_01180_mhou_pdfas_hessian

each set comprising $N_{\textrm{eig}}=50$ eigenvectors.

All these sets are also available on the NNPDF Collaboration website,

https://nnpdf.mi.infn.it/nnpdf4-0-n3lo/  .

where we also give the PDF sets discussed in Sect. 4.5 based on variant treatments of the $\hbox {aN}^3\hbox {LO}$ corrections. In addition to the LHAPDF grids themselves, all the results obtained in this work are reproducible by means of the open-source NNPDF code [39] and the related suite of theory tools.

We have provided a first assessment of these PDF sets by comparing them to their NLO and NNLO counterparts with and without MHOUs. Our main conclusions are the following

• For all PDFs good perturbative convergence is observed, with differences decreasing as the perturbative order increases, and the $\hbox {aN}^3\hbox {LO}$ result always compatible with the NNLO within uncertainties.

• For quark PDFs the difference between NNLO and $\hbox {aN}^3\hbox {LO}$ results is extremely small, suggesting that with current data and methodology the effect of yet higher orders is negligible.

• For the gluon PDF a more significant shift is observed between NNLO and $\hbox {N}^3\hbox {LO}$, thus making the inclusion of $\hbox {N}^3\hbox {LO}$ important for precision phenomenology.

• The inclusion of MHOUs improves perturbative convergence, mostly by shifting central values at each order towards the higher-order result, by an amount that decreases with increasing perturbative order.

• Upon inclusion of MHOUs the fit quality becomes all but independent of perturbative order, and PDF uncertainties generally decrease (or remain unchanged) due to the improved data compatibility.

• The effect of MHOUs at $\hbox {N}^3\hbox {LO}$ is very small for quarks but not negligible for the gluon PDF.

• Evidence for intrinsic charm is somewhat increased already at NNLO by the inclusion of MHOUs, and somewhat increased again when going from NNLO to $\hbox {N}^3\hbox {LO}$.

• The impact of $\hbox {N}^3\hbox {LO}$ corrections on the total cross-section for Higgs in gluon fusion is very small on the scale of the PDF uncertainty.

All in all, these results underline the importance of the inclusion of $\hbox {N}^3\hbox {LO}$ corrections and MHOUs for precision phenomenology at sub-percent accuracy.

Future NNPDF releases will include by default MHOUs, will be at all orders up to $\hbox {aN}^3\hbox {LO}$, and will include a photon PDF. Specifically, we aim to extend to $\hbox {aN}^3\hbox {LO}$ with MHOUs our recent construction of NNPDF4.0QED PDFs [109]. Indeed, $\hbox {aN}^3\hbox {LO}$ PDFs including a photon PDF (such as those recently released by MSHT20 [127]) will be a necessary ingredient for theory predictions based on state-of-the art QCD and electroweak (EW) corrections. In fact, we are working towards the consistent inclusion of combined $\hbox {QCD}\times \hbox {EW}$ corrections also in the theory predictions used for PDF determination.

Another important line of future development involves the all-order resummation of potentially large perturbative contributions in the large x and small x regions [69, 128]. This will involve matching resummed and fixed-order cross-sections and (at small x) perturbative evolution in the new streamlined NNPDF theory pipeline. Such resummed PDFs will be instrumental for precision phenomenology: specifically at small x, forward neutrino production at the LHC and scattering processes for high-energy astroparticle physics, and at large x, searches for new physics in high-mass final states at the LHC and future hadron colliders.

Explicit expressions of anomalous dimensions

We provide here explicit expressions for the $\gamma _{\textrm{ns}\, \pm ,\,N\rightarrow \infty }^{(3)}(N)$ and $\gamma _{\textrm{ns}\, \pm ,\,N\rightarrow 0}^{(3)}(N)$ anomalous dimension discussed in Sect. 2.3 and the $\gamma _{\textrm{ns}\, \pm ,\,N\rightarrow \infty }^{(3)}(N)$, $\gamma _{\textrm{ns}\, \pm ,\,N\rightarrow 0}^{(3)}(N)$ and $\gamma _{\textrm{ns}\, \pm ,\,N\rightarrow 1}^{(3)}(N)$ discussed in Sect. 2.4.

$\gamma _{\textrm{ns},\pm }^{(3)}(N)$:

$$\begin{aligned}&\gamma _{\textrm{ns},\pm , N\rightarrow 0}^{(3)}(N) \nonumber \\&\quad = -\frac{252.84}{N^7} + \frac{1580.25 -126.42 n_f}{N^6} \nonumber \\&\qquad +\frac{-5806.8 +752.198 n_f -18.963 n_f^2}{N^5} \nonumber \\&\qquad +\frac{14899.9 -2253.11 n_f +99.1605 n_f^2 -0.790123 n_f^3}{N^4} \nonumber \\&\qquad +\frac{- 28546.4 +5247.18 n_f -226.441 n_f^2 +2.89712 n_f^3}{N^3} \nonumber \\&\qquad +\frac{50759.7 -8769.15 n_f +395.605 n_f^2 -3.16049 n_f^3}{N^2}\end{aligned}$$

(A.1)

$$\begin{aligned}&\gamma _{\textrm{ns},\pm N\rightarrow \infty }^{(3)}(N) \nonumber \\&\quad = \left( +20702.4 -5171.92 n_f +195.577 n_f^2 \right. \nonumber \\&\qquad \left. +3.27234 n_f^3 \right) S_1(N) \nonumber \\&\qquad -23393.8+5550.04 n_f -193.855 n_f^2 -3.01498 n_f^3 \nonumber \\&\qquad + \left( 16950.9 - 2741.83 n_f + 26.6886 n_f^2 \right) \frac{S_1(N)}{N} \nonumber \\&\qquad +\frac{ +11126.6 -3248.4 n_f +180.432 n_f^2 + 0.526749 n_f^3 }{N} \end{aligned}$$

(A.2)

$\gamma _{gg}^{(3)}(N)$:

$$\begin{aligned}&\gamma _{gg,N\rightarrow 0}^{(3)}(N)\nonumber \\&\quad = \frac{- 103680 + 20005.9 n_f -568.889 n_f^2}{N^7} \nonumber \\&\qquad + \frac{- 17280 -19449.7 n_f +1725.63 n_f^2}{N^6} \nonumber \\&\qquad + \frac{- 627979 +80274.1 n_f -2196.54 n_f^2 + 4.74074 n_f^3}{N^5} \end{aligned}$$

(A.3)

$$\begin{aligned}&\gamma _{gg,N\rightarrow 1}^{(3)}(N) = -\frac{49851.7}{(N-1)^4} + \frac{213824 + 1992.77 n_f }{(N-1)^3} \end{aligned}$$

(A.4)

$$\begin{aligned}&\gamma _{gg,N\rightarrow \infty }^{(3)}(N) \nonumber \\&\quad = \left( +40880.3 -11714.2 n_f +440.049 n_f^2\right. \nonumber \\&\qquad \left. + 7.36278 n_f^3 \right) S_1(N) \nonumber \\&\qquad -68587.9 +18144 n_f -423.811 n_f^2 -0.906722 n_f^3 \nonumber \\&\qquad - \left( -85814.1+13880.5 n_f -135.111 n_f^2 \right) \frac{S_1(N)}{N} \nonumber \\&\qquad + \frac{- 54482.8 + 4341.13 n_f +21.3333n_f^2}{N} \end{aligned}$$

(A.5)

$\gamma _{gq}^{(3)}(N)$:

$$\begin{aligned}&\gamma _{gq,N\rightarrow 0}^{(3)}(N) \nonumber \\&\quad = \frac{- 37609.9 + 5309.63 n_f}{N^7} \nonumber \\&\qquad + \frac{ -35065.7 + 221.235 n_f}{N^6} \nonumber \\&\qquad + \frac{ -175455 + 9092.91 n_f + 778.535 n_f^2}{N^5}\end{aligned}$$

(A.6)

$$\begin{aligned}&\gamma _{gq,N\rightarrow 1}^{(3)}(N) = -\frac{22156.3}{(N-1)^4} + \frac{95032.9 + 885.674 n_f}{(N-1)^3} \end{aligned}$$

(A.7)

$$\begin{aligned}&\gamma _{gq,N\rightarrow \infty }^{(3)}(N) \nonumber \\&\quad = \left( -13.4431 +0.548697 n_f \right) L_{5,0}(N) \nonumber \\&\qquad + \left( -375.398 +34.4947 n_f -0.877915 n_f^2 \right) L_{4,0}(N) \end{aligned}$$

(A.8)

$\gamma _{qg}^{(3)}(N)$:

$$\begin{aligned}&\gamma _{qg,N\rightarrow 0}^{(3)}(N) \nonumber \\&\quad = \frac{14103.7 n_f -1991.11 n_f^2}{N^7} \nonumber \\&\qquad +\frac{2588.84 n_f +2069.33 n_f^2}{N^6} \nonumber \\&\qquad + \frac{68802.3 n_f -7229.38 n_f^2 -99.1605 n_f^3}{N^5} \end{aligned}$$

(A.9)

$$\begin{aligned}&\gamma _{qg,N\rightarrow 1}^{(3)}(N) = -\frac{7871.52 n_f}{(N-1)^3} \end{aligned}$$

(A.10)

$$\begin{aligned}&\gamma _{qg,N\rightarrow \infty }^{(3)}(N) \nonumber \\&\quad = \left( -1.85185 n_f +0.411523 n_f^2 \right) L_{5,0}(N) \nonumber \\&\qquad + \left( -35.6878 n_f +3.51166 n_f^2 + 0.0823045 n_f^3 \right) L_{4,0}(N) \nonumber \\&\qquad + \left( -2.88066 n_f -0.823045 n_f^2 \right) L_{5,1}(N) \nonumber \\&\qquad + \left( +40.5114 n_f -5.54184 n_f^2 -0.164609 n_f^3 \right) L_{4,1}(N) \end{aligned}$$

(A.11)

$\gamma _{qq,\textrm{ps}}^{(3)}(N)$:

$$\begin{aligned}&\gamma _{qq,\textrm{ps},N\rightarrow 0}^{(3)}(N) \nonumber \\&\quad = \frac{5404.44 n_f -568.889 n_f^2}{N^7} \nonumber \\&\qquad +\frac{3425.98 n_f +455.111 n_f^2}{N^6} \nonumber \\&\qquad +\frac{20515.2 n_f -1856.79 n_f^2 + 4.74074 n_f^3}{N^5} \end{aligned}$$

(A.12)

$$\begin{aligned}&\gamma _{qq,\textrm{ps},N\rightarrow 1}^{(3)}(N) = -\frac{3498.45 n_f}{(N-1)^3}, \end{aligned}$$

(A.13)

$$\begin{aligned}&\gamma _{qq,\textrm{ps},N\rightarrow \infty }^{(3)}(N) \nonumber \\&\quad = \left( +56.4609 n_f -3.6214 n_f^2 \right) L_{4,1}(N) \nonumber \\&\qquad + \left( +247.551 n_f -40.5597 n_f^2 + 1.58025 n_f^3 \right) L_{3,1}(N) \nonumber \\&\qquad +13.1687 n_f L_{4,2}(N) \nonumber \\&\qquad + \left( +199.111 n_f -13.6955 n_f^2 \right) L_{3,2}(N). \end{aligned}$$

(A.14)

The functions $L_{k,j}(N)$ are defined as the Mellin transform of $(1-x)^j\ln ^k(1-x)$:

$$\begin{aligned} L_{k,0}(N)&= {\mathcal {M}}\left[ \ln ^k(1-x)\right] (N) =(-1)^k k! \frac{S_{1_k, \dots , 1_1}(N)}{N} \end{aligned}$$

(A.15)

$$\begin{aligned} L_{k,1}(N)&= {\mathcal {M}}\left[ (1-x) \ln ^k(1-x)\right] \nonumber \\&= L_{k,0}(N) - L_{k,0}(N+1) \end{aligned}$$

(A.16)

$$\begin{aligned} L_{k,2}(N)&={\mathcal {M}}\left[ (1-x)^2 \ln ^k(1-x)\right] \nonumber \\&= L_{k,0}(N) - 2 L_{k,0}(N+1)+ L_{k,0}(N+2) \end{aligned}$$

(A.17)

with the multi-index harmonics of weight-k defined recursively as

$$\begin{aligned} S_{1_k,\dots ,1_1}(N) = \sum _{j=1}^{N} \frac{S_{1_{k-1}, \dots , 1_1}(j)}{j} \ \end{aligned}$$

(A.18)

and the termination condition

$$\begin{aligned} S_\emptyset = 1. \end{aligned}$$

(A.19)