1 Introduction

The Event Horizon Telescope (EHT) has recently made remarkable advancements by offering us a great platform to probe the nature of gravity under extreme conditions. The notable achievements are the unveiling images of the supermassive BH M87* [1,2,3] and the central BH in our Milky Way [4, 5]. These images feature dark central areas which represent the BH’s shadow caused by the intense gravitational bending of light near the BH [6,7,8]. The boundary of this shadow is determined by the unstable orbit of photons close to the BH, known as the photon sphere. The luminous rings seen in the images arise from outer photons orbits. Additionally, the ring-like structure in the image forms due to light rays which is influenced by the complex accretion flows that continuously illuminate the BH.

Bardeen explored the D-type shadow in Kerr BHs [7] and analyze the rotational influence of these BHs on light rays. This discovery sparked extensive research into BH shadows with numerous simulations and discussions of various BH shadows [9, 10]. These studies reveal that the properties of BH shadows are effected by the surrounding spacetime environment. Considerable attention has been given to BH shadows in different spacetime dimensions and under alternative gravity theories, including conformal gravity [11], Gauss–Bonnet theory [12, 13], Chern–Simons type theory [14], f(R) gravity [15], among others [16, 17]. Additionally, the shadows of naked singularities [18] and wormholes have been studied [19, 20]. The EHT has simulated images based on Kerr BHs within the framework of general relativity (GR). However, the EHT’s finite resolution leaves room for consideration of theories beyond GR. Consequently, there has been a significant amount of research using EHT’s shadow observations to test or place constraints on these modified theories of gravity [21,22,23,24].

The luminous ring-like structures seen in the images produced by the EHT are intimately linked to the radiation from accretion flow around BHs. The shape and characteristics of these accretion flows significantly influence the visual appearance of BHs. In real astrophysical environments, the accretion flows are complex and required general relativistic magnetohydrodynamic simulations to accurately depict BH images [25]. To understand the primary features of BH images and gravity in strong fields, simpler accretion structure models are often sufficient. For instance, Wald and colleagues introduced a basic model of disk around Schwarzschild BHs and categorized emissions based on the number of times light intersects the accretion disk: direct, lensed ring and photon ring correspond to \((n = 1)\), \((n = 2)\) and \((n = 3)\) respectively [26]. Their findings indicated that direct emissions are the main source of observed brightness in BH images, lensed ring emissions being less significant and photon ring emissions negligible. Various toy accretion disk models have been extensively studied [27, 28]. Another simplified model, spherical accretions has also garnered significant interest [29, 30]. In these models, the BH’s spacetime geometry predominantly determines the size and shape of the shadows. Additionally, accretion structures around BHs with unstable photon spheres show that such BHs could exhibit additional photon rings in their images with substantial contributions to overall brightness from both photon and lens ring emissions [31, 32]. Overall, the visual characteristics of BHs offer a potential path to differentiate between GR BHs and other compact objects or BH in alternative gravity theories [33,34,35,36,37,38,39,40].

The Joule–Thomson (JT) expansion is a key thermodynamic process that has garnered significant attention particularly in the context of van der Waals gases. This process is isenthalpic and allows for the observation of temperature changes as gas transitions from high to low pressure through a porous medium. Essentially, the JT expansion serves as a means to determine whether a gas undergoes heating or cooling. The point at which the JT coefficient equals zero is known as the inversion point, marking the transition between cooling and heating phases. In the realm of astrophysics, this concept has been applied to BHs, specifically viewing a BH’s mass as analogous to enthalpy [41]. The JT expansion in charged AdS BHs initially discussed [42], and further explorations have been extensively provided [43,44,45,46,47,48,49,50]. Detailed analysis have been performed on higher-dimensional charged AdS and Gauss–Bonnet AdS BHs [43, 44]. Additionally, the impact of rainbow gravity on the JT expansion of charged AdS BHs has been explored [51]. The JT expansion on Bardeen-AdS BH has been investigated [52, 53], while Born-Infeld AdS BHs have been studied [54].

In our study, we explore the JT expansion and visual characteristics which includes images of a BH within the context of Einstein-SU(N) non-linear sigma model (E-SU(N) NLSM). The NLSM stands as a crucial theoretical model with wide-rang applications, such as in the behavior of Goldstone-bosons [55], string theory [56], condensed matter physics [56], and super-gravity [57]. An example of its significance seen for \(N = 2\), which effectively describes the low-energy dynamics of pions in a \(3 + 1\) dimensional space [58]. The E-SU(N) NLSM posses angular defect, the angular defect refers to the deviation from the expected angular measurements due to the intense curvature of space-time. It is a feature that emerges from the solutions to Einstein’s field equations, particularly those that describe the space-time around a BH. When we move around a BH or try to measure the angles and distances in its vicinity, the intense gravitational field causes these measurements to differ significantly from what you would expect in a flat, non-curved space-time. This occurs because the trajectory of light or any object is distorted or curved due to the bending of space-time created by the mass of a BH. The angular defect becomes more pronounced near the event horizon of a BH where gravitational forces are most intense. This effect is vital in phenomena such as gravitational lensing where light bends around a BH.

The AdS/CFT correspondence is a significant duality in physics that links a form of string theory or supergravity in an AdS space (a spacetime characterized by a negative cosmological constant) to a conformal field theory (CFT) defined on the boundary of this space. This duality offers a holographic representation of gravity enabling the description of gravitational phenomena in a higher-dimensional AdS space through a quantum field theory without gravity on its lower-dimensional boundary. In AdS space, BHs manifest distinct thermodynamic properties that differ from those in flat or positively curved spaces. The negative cosmological constant enhances the stability of BH solutions and supports the existence of large stable BHs in thermal equilibrium which are pertinent in the AdS/CFT framework. Within this context, an angular defect often signifies a modification in the angular component of spacetime geometry which may result from various factors such as topological defects, brane configurations, or specific boundary conditions applied to the field theory. Such defects can modify both the local and global geometric characteristics of the AdS space and thus, the nature of BH solutions within it. The presence of an angular defect can significantly influence the thermodynamic behavior of BHs in AdS space by affecting their entropy, temperature and energy which are critical for the understanding of dual CFT. Since, AdS/CFT correspondence relates the thermodynamics of BHs in AdS space to the thermodynamics of a CFT on the boundary, an angular defect in the bulk geometry can lead to modifications in field theory. In the AdS/CFT framework, examining the effects of an angular defect on the thermodynamics of BHs yield how this defect modifies the bulk geometry and subsequently impacts the boundary field theory. Such analysis can reveal deep insights into the characteristics of the duality and how the dual CFT behaves, particularly regarding state counting, phase transitions, and correlation functions. Therefore, it’s intriguing to examine how the this model interacts with GR from a theoretical and practical standpoint. This interest has led to numerous studies on the Einstein-NLSM system [59,60,61,62]. A recent development in the considered model has been the discovery of BH solution [63]. Further research has been delved to study the impact of its coupling on the thermodynamical stability of BH [63]. Motivated form the given considerable importance of this model, we are interested to examine the visual properties which include images and heating and cooling phases of BHs within NLSM.

The paper organize as, in Sect. 2, we provide brief review of BHs in the E-SU(N) NLSM. In Sect. 2.1, we study JT expansion of BH in the E-SU(N) NLSM. In Sect. 3, we investigate the intensities and optical appearances of BH in the E-SU(N) NLSM. In Sect. 3.1, we discuss images of the BH in the E-SU(N) NLSM using static spherical accretions. Finally in Sect. 4, we summarize our results in conclusion.

2 Brief review of black holes in the E-SU(N) NLSM

The E-SU(N) NLSM provides a unique platform to explore the interplay between gravity and gauge theories. Gauge theories are fundamental in the standard model of particle physics and when combined with the geometrical nature of GR (as in the Einstein SU(N) model), offer a path towards understanding quantum gravity. The non-linear nature of the sigma model introduces complex dynamics that are not present in linear theories. This complexity can lead to new physical phenomena and a deeper understanding of non-linear dynamics in field theory and GR. The action describing the E-SU(N) NLSM in a four-dimensional spacetime (3+1) is characterized as follows [64]

$$\begin{aligned} I[g, U] = \int d^4x \sqrt{-g} \left[ R(2\kappa )^{-1} + \text {Tr}[L^\mu L_\mu ]\frac{K}{4} \right] , \end{aligned}$$
(1)

where \(L_\mu \) represents Cartan components

$$\begin{aligned} L_\mu =L^i_\mu t_i= \frac{1}{U}\partial _\mu U. \end{aligned}$$
(2)

All U(x) which belongs to SU(N), where N represents the flavor number, \(t_i\) are the generators of the SU(N) Lie algebra, K manifests coupling constant and for simplicity, we set \(c=\hbar =1\). In the model, Greek indices traverse the four dimensions of spacetime using positive signature and Latin indices are employed for dimensions within the internal space. The field equations can be obtained by varying the action, as illustrated in Eq. (1), w.r.t U and \(g_{\mu \nu }\) are expressed as

$$\begin{aligned} \nabla ^{\mu }L_\mu = 0,\end{aligned}$$
(3)
$$\begin{aligned} G_{\mu \nu }=\kappa T_{\mu _\nu }.\end{aligned}$$
(4)

In these equations, Einstein tensor symbolizes as \(G_{\mu \nu }\). \(\nabla ^{\mu }\) signifies the Levi Civita derivative, the energy-momentum tensor associated with the NLSM is \(T_{\mu _\nu }\). The formulation of \(T_{\mu _\nu }\) is as follows

$$\begin{aligned} T_{\mu \nu }= -\frac{K}{2} \text {Tr} \left( L_\mu L_\nu - \frac{1}{2} g_{\mu \nu } L^\alpha L_\alpha \right) . \end{aligned}$$
(5)

It is important to see that Eq. (3) is comprised of \(N^{2} -1\) NL, coupled differential equations of order two. For the matter field U, we set following Euler angle

$$\begin{aligned} U = e^{F_1(x^\mu ).T_3} e^{F_2(x^\mu ).T_2} e^{F_3(x^\mu ).T_3}, \end{aligned}$$
(6)

where \(T_{1}, T_{2}\) and \(T_{3}\) are matrices of Lie algebra SU(N). The metric for the spherically symmetric BH spacetime is given by

$$\begin{aligned} ds^2 = -f(r) dt^2 + \frac{1}{f(r)} dr^2 + r^2 d\theta ^2 + r^2 \sin ^2 \theta d\phi ^2. \end{aligned}$$
(7)

Accompanied by U as specified in Eq. (6), the \(F_{i}\) functions are characterized by the following specific form

$$\begin{aligned} F_1(x^\mu ) = -p\phi , \quad F_2(x^\mu ) = 2q\theta , \quad F_3(x^\mu ) = p\phi , \end{aligned}$$
(8)

where p, q are constants, the equations are solvable and lead to the following result

$$\begin{aligned} f(r) = 1 -2m r^{-1}-K\kappa a_{N} - \frac{1}{3}\Lambda r^2, \end{aligned}$$
(9)

where m is mass of BH and \(a_{N}\) is defined as

$$\begin{aligned} a_{N} = \frac{1}{6}(N^3 - N). \end{aligned}$$
(10)

Using \(a_{N}\), the metric function of the BH finally turns out to be

$$\begin{aligned} f (r) = -\frac{1}{6} K\kappa \left( N^3-N\right) -\frac{2 m}{r}-\frac{\Lambda r^2}{3}+1. \end{aligned}$$
(11)

This configuration effectively demonstrates pionic matter and an extension of the SU(N) BH [65, 66]. Additionally, this solution represent an asymptotically AdS version of the Barriola Vilenkin metric function [67], and transforms into the Schwarzschild-AdS BH for \(K = 0\). Notably, this solution simplifies to BH in the E-SU(2) using \(N = 2\), excluding Skyrme coupling [68]. Canfora et al., [69] studied the spherically symmetric BH solution in Einstein-Skyrme theory where Skyrme coupling \(\lambda \) gives an explicit contribution to f(r) of order \(\frac{1}{r^{2}}\). In comparison of this metric with charged AdS BH metric, one can see that Skyrme coupling contribute similar to electric charge in BH. The BHs exhibit an angular defect which is directly related to the value of N. It is widely recognized that angular defect influences the computation of mass and other thermodynamic properties of the system. Consequently, it is necessary to employ an extended thermodynamic formalism. The initial step in this formalism involves eliminating the angular defect from the metric function. This can be achieved by implementing following coordinate transformations

$$\begin{aligned} r=\tilde{r}(1-K\kappa a_{N})^{\frac{1}{2}},~t=\tilde{t}(1-K\kappa a_{N})^{\frac{-1}{2}} \end{aligned}$$
(12)

By implementing this modification, the metric described in Eqs. (7) and (9) assumes the following form

$$\begin{aligned} ds^2 = -F d\tilde{t}^2 + \frac{1}{F} d\tilde{r}^2 + (1-K\kappa a_{N}) \tilde{r}^2 (d\theta ^2 + \sin ^2 \theta d\phi ^2), \end{aligned}$$
(13)

where

$$\begin{aligned} F(\tilde{r}) = 1 - \frac{2\tilde{m}}{\tilde{r}} - \frac{\Lambda }{3} \tilde{r}^2, \end{aligned}$$
(14)

and \(\tilde{m}=\frac{m}{(1-K\kappa a_{N})\frac{3}{2}}\). In the updated coordinate system, the event horizon is situated at

$$\begin{aligned} \tilde{r}_+ =-\frac{\Lambda +(3\tilde{m}\Lambda ^2 + \sqrt{\Lambda ^3(9\tilde{m}^2\Lambda - 1)})^{\frac{3}{2}}}{\Lambda (3\tilde{m}\Lambda ^2 + \sqrt{\Lambda ^3(9\tilde{m}^2\Lambda - 1)})^{\frac{1}{3}}}. \end{aligned}$$
(15)
Fig. 1
figure 1

Plot of Hawking temperature versus horizon radius of BH within the framework of an E-SU(N) NLSM. We use different values of flavor number N with fixed other constants

Full size image

Following the approach outlined in Ref. [70], the computation becomes straightforward. By treating the cosmological constant as a bulk pressure and applying the standard counterterm method to obtain a finite Euclidean action, we can determine the mass, entropy, and temperature of the spherical BH solution. These quantities are expressed in terms of the event horizon radius as given in Eq. (15). The results are as follows

$$\begin{aligned} S = \pi (1 - K\kappa a_{N})\tilde{r}_+^2, \end{aligned}$$
(16)
$$\begin{aligned} T= \frac{1}{4\pi \tilde{r}_+} - \frac{\Lambda \tilde{r}_+}{4\pi }, \end{aligned}$$
(17)
$$\begin{aligned} M = (1 - K\kappa a_{N}) \tilde{m} = \frac{1}{6} (1 - K\kappa a_{N}) (3 -\Lambda \tilde{r}_+^2) \tilde{r}_+. \end{aligned}$$
(18)

2.1 Joule–Thomson expansion of black hole in the E-SU(N) NLSM

In this section, we discuss the widely recognized JT expansion, as detailed in references [43,44,45,46,47,48,49,50]. The expansion involves a gas moving from an area of higher pressure through a porous plug into a region of lower pressure, while maintaining constant enthalpy throughout the expansion. The variation in temperature relative to pressure during this process can be expressed as follows

$$\begin{aligned} \mu = \left( \frac{\partial T}{\partial P} \right) _H . \end{aligned}$$
(19)

In this context, \(\mu \) is referred to as the JT coefficient. By analyzing the sign of Eq. (19), it is feasible to ascertain whether the process will result in cooling or heating. During JT expansion, the temperature change can be either positive or negative. If the temperature change is positive (negative), then \(\mu \) is negative (positive), leading to the gas heating up (cooling down). Equation (19) can be reformulated in form of volume and heat capacity, utilizing the following first law

$$\begin{aligned} dU = - PdV+TdS , \end{aligned}$$
(20)

and \(H=PV+U\), the Eq. (20) turns out to be

$$\begin{aligned} dH = VdP +T dS. \end{aligned}$$
(21)

Given that \( dH = 0 \), Eq. (21) can be rewritten as follows

$$\begin{aligned} 0 = T \left( \frac{\partial S}{\partial P} \right) _H + V. \end{aligned}$$
(22)

As entropy is a state function, the differential \( dS \) can be represented as

$$\begin{aligned} dS = \left( \frac{\partial S}{\partial P} \right) _T dP + \left( \frac{\partial S}{\partial T} \right) _P dT. \end{aligned}$$

This can be restructured to yield the following expression

$$\begin{aligned} \left( \frac{\partial S}{\partial P} \right) _H = \left( \frac{\partial S}{\partial P} \right) _T + \left( \frac{\partial S}{\partial T} \right) _P \left( \frac{\partial T}{\partial P} \right) _H. \end{aligned}$$

By substituting this expression into Eq. (22), the following result can be derived

$$\begin{aligned} 0 = T \left( \left( \frac{\partial S}{\partial P} \right) _T + \left( \frac{\partial S}{\partial T} \right) _P \left( \frac{\partial T}{\partial P} \right) _H \right) + V. \end{aligned}$$
(23)

Utilizing the Maxwell relation

$$\begin{aligned} \left( \frac{\partial S}{\partial P} \right) _T = -\left( \frac{\partial V}{\partial T} \right) _P, \end{aligned}$$

and

$$\begin{aligned} C_P = T \left( \frac{\partial S}{\partial T} \right) _P, \end{aligned}$$

into Eq. (23) gives

$$\begin{aligned} -\left( \frac{\partial V}{\partial T} \right) _P T + \left( \frac{\partial T}{\partial P} \right) _H C_P + V =0. \end{aligned}$$

This can be further rearranged to yield the formula for the JT coefficient in the following manner [50]

$$\begin{aligned} \mu = \left( \frac{\partial T}{\partial P} \right) _H = \frac{1}{C_P} \left( T \left( \frac{\partial V}{\partial T} \right) _P - V \right) .\end{aligned}$$

\( \mu \)=0, yields inversion temperature which is given by

$$\begin{aligned} T_i = V \left[ \frac{\partial T}{\partial V} \right] _P. \end{aligned}$$

It determines the heating/cooling regions on the temperature-pressure plane.

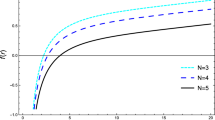
Figure 1 depicts the relationship between the Hawking temperature T and the horizon radius r of BH within the framework of an E-SU(N) NLSM. The graph contains four distinct curves, each corresponding to a different value of the flavor number \(N=2,3,4,5\). Each curve represents how the Hawking temperature changes with the BH’s horizon radius for a specific N. This variation indicates that the flavor number N, which is related to the internal configuration of the fields in the sigma model, significantly impacts the BH’s thermal properties. The Hawking temperature for each N shows a specific trend. The exact nature of this trend depends on the value of N but generally, the temperature seems to increase with increasing radius, which is a characteristic behavior of BHs in Hawking radiation theory. For smaller values of r, the temperature appears to rise sharply. This is indicative of the inverse relationship typically observed between the mass (and hence the radius) of a BH and its temperature. As BHs lose mass and shrink, their temperature increases, leading to faster Hawking radiation.

Fig. 2
figure 2

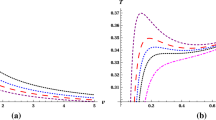
The graph depicts isenthalpic (shown in various colors) and inversion (illustrated in black) curves of a BH within the framework of an E-SU(N) NLSM in \(T-P\) plane. Each curves correspond to different values of \(m=0.5, 1, 1.5\) and 2 with fixed flavor number N. Different plots present different values of flavor number N

Full size image
Fig. 3
figure 3

The graph depicts isenthalpic (shown in various colors) and inversion (illustrated in black) curves of a BH within the framework of an E-SU(N) NLSM in \(T-P\) plane. Each curves correspond to different values of \(m=10, 20, 30\) and 40 with fixed flavor number N. Different plots present different values of flavor number N

Full size image
Fig. 4
figure 4

The graph depicts isenthalpic (shown in various colors) and inversion (illustrated in black) curves of a BH within the framework of an E-SU(N) NLSM in \(T-P\) plane. Each curves correspond to different values of \(m=10, 20, 30\) and 40 with fixed flavor number N. Different plots present higher values of flavor number \(N=20, 30, 40\) and 50

Full size image
Fig. 5
figure 5

The graph depicts isenthalpic (shown in various colors) and inversion (illustrated in black) curves of a BH within the framework of an E-SU(N) NLSM in \(T-P\) plane. Each curves correspond to different values of \(m=1, 1.5, 2, 2.5\) and 3 with \(N=0\)

Full size image

Figure 2: four plots represent the relationship between isenthalpic and inversion curves for BHs in the E-SU(N) NLSM, each corresponding to different flavor numbers \(N=2,3,4\) and 5. The graphs include four trajectories in each, representing BHs with different enthalpy values \(m=0.5,1,1.5\) and 2, with fixed values of other constants. Additionally, each graph features an inversion curve (black curve). The variation in the shape and position of the curves for different flavor numbers indicates that N significantly influences the thermodynamic properties of BHs. Higher flavor numbers tend to shift the curves, reflecting changes in temperature-pressure relationships. While all graphs maintain a similar qualitative pattern, quantitative differences are noticeable. As N increases, there is a noticeable shift in the curves, suggesting a dependency of thermodynamic properties on the flavor number. The shape and trajectory of the inversion curves vary with N. This implies that the maximum thermodynamic efficiency or peak behavior of these BHs is sensitive to changes in the underlying E-SU(N) NLSM parameters. For all values of N, increasing the enthalpy m shifts the curves, indicating that larger enthalpy BHs have distinct temperature-pressure characteristics compared to smaller ones within the same flavor number context. The important and interesting findings of our model is that above the inversion curves, isenthalpic curves exhibit positive slope which represents cooing phase. Below the inversion curves, these curves cease to exist, demonstrating that the BH does not transition into a heating phase. In Figs. 3 and 4, we used higher values of enthalpy and flavor number to compare the cooling and heating phases, we observe that increasing these parameters leads to high ranges of T and pressure P. However, even in these scenarios, heating phase does not occur.

In Fig. 5, we note a distinct behavior of isenthalpic curves when \(N=0\). In this case, the isenthalpic curves display both positive and negative slopes above and below the inversion curves, respectively. This pattern suggests phases of cooling and heating. Below the inversion curves, the isenthalpic curves indicate that the BH enters a heating phase. These findings are consistent with those reported in previous studies [43,44,45,46,47,48,49,50].

3 Analysis of intensities and optical appearances of black hole in the E-SU(N) NLSM

Each point where light rays intersect with the accretion disk results in energy extraction, significantly influencing the contributions of different emissions to the overall brightness. Due to substantial impact of flavor number N, it becomes crucial to investigate its effects on the visual perception of the BH in E-SU(N) NLSM. We assume the thin accretion disk emits isotropically in the rest frame of static worldlines. The specific intensity received by an observer, with emission frequency \(\nu _e\) is described by

$$\begin{aligned} I_o(\nu _o, r) = I_e(\nu _e, r)g^3, \end{aligned}$$
(24)

where \(g = \nu _o(\nu _e)^{-1} = (f(r))^{\frac{1}{2}}\) represents redshift factor, \(\nu _o\) is the frequency of observed light, and \(I_e(\nu _e, r)\) is intensity of accretion disk [71]. The total observed intensity \(I_{\text {obs}}(r)\), using \(I_o(r, \nu _o)\), turns out to be

$$\begin{aligned} I_{\text {obs}}(r)&= I_{\text {em}}(r) f(r)^2= \int I_e(\nu _e, r) g^4 d\nu _e \nonumber \\&=\int I_o(\nu _o, r) d\nu _o. \end{aligned}$$
(25)

In this context, we define \(I_{\text {em}}(r)\) as the aggregate emitted intensity, represented by \(I_{\text {em}}(r) = \int I_e(\nu _e, r)d\nu _e\). Considering that the reflected light ray can intersect disk multiple times, varying with the emission type, the overall intensity is therefore, the combined sum of intensities from each point of intersection, as indicated in [26].

$$\begin{aligned} I_{\text {obs}}(b) = \sum _{m}I_{\text {em}}(r) f(r)^2 \bigg |_{r=r_m(b)}. \end{aligned}$$
(26)

Here \(r_m(b)\) manifests transfer function representing the radial coordinate of the m-th intersection [28]. We study the visual characteristics of the considered BH by examining a particular simplified model for the accretion disk’s emission function. This function is characterized by a gradual decrease in intensity starting from the event horizon \(r_{h}\) as detailed in references [72, 73].

$$\begin{aligned} I_{\text {em}}(r) = {\left\{ \begin{array}{ll} \frac{I_o}{\pi } \left( \frac{\pi }{2} - \tan ^{-1}\frac{1}{\pi }(r + 1- r_{\text {isco}}) \right) \bigg / &{} \\ \left( \frac{\pi }{2} - \tan ^{-1}\left( \frac{r_h - r_{\text {isco}} + 1}{\pi }\right) \right) &{} r > r_h \\ 0 &{} r \le r_h, \end{array}\right. } \nonumber \\ \end{aligned}$$
(27)

where \(I_o\) represents the peak intensity and \(r_{isco}\) can be determined as [28]

$$\begin{aligned} r_{\text {isco}} = \frac{3f(r_{\text {isco}})f'(r_{\text {isco}})}{2f'(r_{\text {isco}})^2- f''(r_{\text {isco}})f(r_{\text {isco}})}. \end{aligned}$$
(28)
Fig. 6
figure 6

Plot of intensities emitted from the emission function versus impact parameter of BH in the E-SU(N) NLSM. Different curves are for different flavor number and fixed other constants

Full size image
Fig. 7
figure 7

Optical appearances of the BH in the E-SU(N) NLSM for selected parameters. Different plots corresponds to different values of flavor number

Full size image

Figures 6 and 7 display the intensities emitted from the emission function versus impact parameter for BHs in the E-SU(N) NLSM. Figure 6 features five curves, each corresponding to a different flavor number \(N=2, 3, 4, 5, 6\). For \(N = 6\), blue curve exhibits the highest peak, suggesting the strongest intensity at a specific impact parameter, followed by a gradual decrease. This indicates the most pronounced gravitational influence at this flavor number. The graph highlights the significant role of the flavor number in the E-SU(N) NLSM on the observed intensities around BHs. Higher flavor numbers tend to produce more intense gravitational effects, as indicated by the higher peaks in the corresponding curves while there is decrease in intensities from \(N=6\) to \(N=2\) at specific impact parameters. Moreover, the peak of \(I_{obs}\) for \(N=6\) shifts to smaller impact parameter value which suggests that it corresponds to smaller shadow region which can be observe in Fig. 7. We can observe the consistent behaviors of Fig. 6 in Fig. 7.

Fig. 8
figure 8

Plot of total observed intensities radiated from the static spherical accretion, as a function of impact parameter for BH in the E-SU(N) NLSM. Different curves are for different flavor number and fixed other constants

Full size image
Fig. 9
figure 9

Optical appearances of the BH in the E-SU(N) NLSM for selected parameters. Different plots corresponds to different values of flavor number

Full size image

3.1 Images of the black hole in the E-SU(N) NLSM using static spherical accretions

We explore the images of BH in the E-SU(N) NLSM surrounded by a static accretion. Typically, when particles are captured by a BH, they form a disk type flow around the BH, rotating with significant momentum. However, when the momentum is exceptionally low, the matter flows radially towards the BH, creating a symmetric and spherical accretion, as mentioned in [74]. For spherical and symmetry accretion, the values of \(I(\nu _o)\) perceived by an object at infinity \(r=\infty \) is calculated by integrating the specific emissivity along the photon path \(\gamma \), as detailed in [75]

$$\begin{aligned} I(\nu _o) = \int _{\gamma } g^3 j_e(\nu _e) dl_{\text {prop}}, \end{aligned}$$
(29)

where \(\nu _e\) and \(\nu _o\) are the emitted and observed photon frequencies, respectively. The red-shift g is define as \(g = \frac{\nu _o}{\nu _e} = \sqrt{f(r)}\). The emissivity represents as \(j_e(\nu _e)\) being the emitters rest-frame frequency, as stated in [75]. The infinitesimal proper length \(dl_{\text {prop}}\) is defined by

$$\begin{aligned} dl_{\text {prop}} = \sqrt{\frac{1}{f(r)} dr^2 + r^2 d\phi ^2} = \sqrt{\frac{1}{f(r)} + r^2 \left( \frac{d\phi }{dr} \right) ^2} dr, \end{aligned}$$
(30)

where \(\frac{d\phi }{dr}\). By further integrating Eq. (30), we derive the observed intensity as

$$\begin{aligned} I_{\text {obs}}&= \int _{\nu _o} I(\nu _o) d\nu _o = \int _{\nu _e} \int _{\gamma } g^4 j_e(\nu _e) dl_{\text {prop}} d\nu _e \nonumber \\ {}&= \int _{\gamma } \frac{f(r)^2}{r^2}\sqrt{\frac{1}{f(r)} + r^2 \left( \frac{d\phi }{dr} \right) ^2} dr. \end{aligned}$$
(31)

Figures 8 and 9 manifests the intensities emitted from a static and spherical accretion disk versus impact parameter for BHs in the E-SU(N) NLSM. It features five curves, each corresponding to a different flavor number \(N=2, 3, 4, 5\) and 6. The graph highlights the influence of the flavor number on the radiation intensity profile. Higher flavor numbers result in higher peaks, indicating stronger radiation intensities at specific impact parameters. We observe that higher flavor number corresponds to maximum peak with small impact parameter value which leads to smaller shadow regions as can be seen in Fig. 9.

4 Conclusion

In this manuscript, we have focused on the newly developed BHs within the E-SU(N) NLSM and studied JT expansion and observable features which include images of the BH. We have evaluated the JT coefficient along with inversion and isenthalpic curves to delve into the heating and cooling regions in the temperature-pressure plane of this model. Our research uncovered unique behaviors of these BHs diverging from previous findings. A notable aspect, we observed is the disappearance of inversion curves in the heating regions causing the BHs to remain in a cooling phase consistently. Furthermore, our research extended to analyze the effects of the flavor number N on the JT expansion of these BHs. We found that using higher values of enthalpy and flavor number N increases the range of isenthalpic and inversion curves yet the BHs continued to stay in the cooling phase.

We have also investigated the shadow and visual properties of these BHs, particularly in relation to their illumination under two theoretical static accretion models. We observed the significant role of flavor number on the observed intensities around BHs. The higher flavor number exhibited the higher peak suggested the high intensity at a specific impact parameter followed by a gradual decrease. Our analysis showed that higher flavor numbers correlated with increasing peaks in observed intensities which shift towards smaller impact parameters resulting in comparatively smaller images of the BHs which can be observed in Fig. 7.