Abstract
Measurements of quarkonia isolation in jets at the Large Hadron Collider (LHC) have been shown to disagree with fixed-order non-relativistic quantum chromodynamics (NRQCD) calculations, even at higher orders. Calculations using the fragmenting jet function formalism are able to better describe data but cannot provide full event-level predictions. In this work we provide an alternative model via NRQCD production of quarkonia in a timelike parton shower. We include this model in the Pythia 8 event generator and validate our parton-shower implementation against analytic forms of the relevant fragmentation functions. Finally, we make inclusive predictions of quarkonia production for the decay of the standard-model Higgs boson.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The production of quarkonia, flavourless mesons comprised of a heavy quark and its corresponding antiquark bound by the strong interaction, is still not fully understood in the context of hadron–hadron collisions, despite decades of study [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. For a complete review, see Ref. [22]. The reason for this is that our theory of the strong interaction, quantum chromodynamics (QCD), is best understood at large energy scales, whereas the dynamics of quarkonia production spans both large and small scales.
One of the first models of quarkonium production to make quantitative predictions was the colour-singlet model (CSM) [23,24,25,26,27], which factorises these perturbative and non-perturbative regimes. In the CSM, the production of the heavy quark/antiquark pair (\(Q \overline{Q} \)) is calculated using perturbative QCD, and these quarks are then bound non-perturbatively. In this second step, the constituents are assumed to be at rest in the quarkonium frame, and the colour and spin state of the \(Q \overline{Q} \) pair does not change during the binding. Comparisons of CSM predictions to Tevatron data [7, 8] demonstrated that the CSM, when calculated at leading fixed order, significantly underestimated the prompt production of \(\psi (1S)\) mesons, a  quarkonium state.Footnote 1
quarkonium state.Footnote 1
The initial fixed-order CSM predictions [27] for the Tevatron data lacked two important sources of \(\psi (1S)\) production: one, partonic fragmentation; and, two, feed-down from heavier quarkonium states such as the  \(\chi _{c}\) mesons. This first contribution can be significant in hadronic collisions because the rate for inclusive charm production is much larger than that calculated only from fixed-order processes such as \(q \overline{q} \rightarrow c \overline{c} \) and \(g g \rightarrow c \overline{c} \). Fragmentation functions [28,29,30,31,32] were derived for
\(\chi _{c}\) mesons. This first contribution can be significant in hadronic collisions because the rate for inclusive charm production is much larger than that calculated only from fixed-order processes such as \(q \overline{q} \rightarrow c \overline{c} \) and \(g g \rightarrow c \overline{c} \). Fragmentation functions [28,29,30,31,32] were derived for  , considering the simpler \(Z \rightarrow c \overline{c} \) process, and convolved with Tevatron jet cross-sections. This additional fragmentation contribution brought the CSM prediction into better agreement with data at high \(p_\text {T}\) of the \(\psi (1S)\), but the overall agreement with data was still poor. For feed-down contributions from the \(\chi _{c}\), predictions were made at fixed-order with the CSM [33,34,35]. These calculations contain a kinematic cut-off to regulate an infrared divergence, typically taken as the mass of the bound state. The quantitative CSM results are very sensitive to the exact choice of this cut-off. Even after accounting for feed-down, the CSM prediction still significantly disagrees with the Tevatron data.
, considering the simpler \(Z \rightarrow c \overline{c} \) process, and convolved with Tevatron jet cross-sections. This additional fragmentation contribution brought the CSM prediction into better agreement with data at high \(p_\text {T}\) of the \(\psi (1S)\), but the overall agreement with data was still poor. For feed-down contributions from the \(\chi _{c}\), predictions were made at fixed-order with the CSM [33,34,35]. These calculations contain a kinematic cut-off to regulate an infrared divergence, typically taken as the mass of the bound state. The quantitative CSM results are very sensitive to the exact choice of this cut-off. Even after accounting for feed-down, the CSM prediction still significantly disagrees with the Tevatron data.
With the realization that the CSM was inadequate to describe the data, non-relativistic QCD (NRQCD) theory [36,37,38,39] was developed. While NRQCD is similar to the CSM in that it factorises into a perturbative and non-perturbative component, it does not require the initial partonic state to have the same colour or quantum numbers as the final state, and allows, for example, the production of colour-octet states which then evolve into physical colour-singlet states.
Production rates for quarkonia at both the Tevatron and LHC are, in general, well described by NRQCD. However, NRQCD predicts \(\psi (1S)\) polarisation [40,41,42,43,44,45] that is not observed in LHC data [16,17,18]. Additionally, fixed-order NRQCD predicts relatively isolated \(\psi (1S)\) production, while LHC measurements demonstrate that \(\psi (1S)\) mesons are oftentimes produced in association with nearby particles. Recent developments in calculating quarkonium fragmentation functions promise to resolve these issues [46, 47]. However, a comprehensive approach for calculating these fragmentation functions is lacking. Here, we introduce an alternative approach of using the Pythia 48, [49,50,51] parton shower to calculate the production of quarkonia from fragmentation. The idea is inspired by an earlier study using the Ariadne program [52,53,54], but is implemented here with a complete and extensible set of quarkonia processes in the full Pythia 8 framework.
The remainder of this paper is organised as follows. In Sect. 2 we briefly review NRQCD, while in Sect. 3 we describe parton shower formalism. We then include NRQCD quarkonium fragmentation processes into the Pythia 8 parton-shower in Sect. 4. In Sect. 5, we present quantitative predictions using our approach, and finally, we provide conclusions in Sect. 6.
2 Non-relativistic quantum chromodynamics
Non-relativistic QCD is an effective field theory where a perturbative expansion is performed not only in the QCD coupling \(\alpha _s\), but also in the relative velocity between the two heavy quarks of the bound state. Including this relative velocity scale results in the expansion of the physical quarkonium state into non-physical Fock states. For a heavy quark state \(Q \overline{Q} \), the general Fock-state expansion is,

where v is the relative velocity between the constituent quark/antiquark, (1) in the superscript notates a colour-singlet state, and (8) in the superscript notates a colour-octet state. For a \(\psi (1S)\), this can be explicitly written as,

and for the \(\chi _{c}\) states as,

where J corresponds to 0, 1, and 2.
The heavy quarkonium cross-sections can then be factorised into short- and long-distance scales, which for initial partons \(a_1\) and \(a_2\) can be written as

where the  are perturbatively calculated partonic short-distance matrix elements (SDME) and
are perturbatively calculated partonic short-distance matrix elements (SDME) and  are empirically determined long-distance matrix elements (LDME). The sums are over the states of the Fock expansion of Eq. (1), where the indices correspond to the spin and colour quantum numbers, and an SDME and LDME must be provided for each term. For hadronic beams \(h_1\) and \(h_2\), the partonic cross-section is then convolved with the parton density functions (PDF) for the hadrons
are empirically determined long-distance matrix elements (LDME). The sums are over the states of the Fock expansion of Eq. (1), where the indices correspond to the spin and colour quantum numbers, and an SDME and LDME must be provided for each term. For hadronic beams \(h_1\) and \(h_2\), the partonic cross-section is then convolved with the parton density functions (PDF) for the hadrons

where the first two sums are over all possible partonic combinations \(a_i\) and \(a_j\). The PDFs for the two hadrons are given by \(f_1\) and \(f_2\), evaluated at the partonic energy scale \(\mu \) with corresponding momentum fractions \(x_1\) and \(x_2\).
For production of the \(\psi (1S)\) at the Large Hadron Collider (LHC), the fixed-order NRQCD partonic cross-section at leading order in \(\alpha _s\) is given by,

where the expansion in the relative quark/antiquark velocity is up to \(v^2\). Feed-down from \(\chi _{c}\) states contribute significantly to \(\psi (1S)\) production, with the partonic cross-sections given by

at leading order in \(\alpha _s\) and expanded up to v. In Pythia 8, a complete set of these \(2 \rightarrow 2\) unpolarised partonic cross-sections is available at fixed order in \(\alpha _s\), including for  states, where \(b \overline{b} \) configurations and arbitrary heavy radial excitations are also included, e.g. the \(\psi (2S)\) or \(\Upsilon (1S)\), but may need to be configured by the user. All of these partonic cross-sections are t-channel exchanges and diverge for low \(p_\text {T}\) of the quarkonium. These divergences are regularised either with a hard \(p_\text {T}\) cut-off or, in the case of multiple parton interactions in Pythia 8, a smooth damping factor.
states, where \(b \overline{b} \) configurations and arbitrary heavy radial excitations are also included, e.g. the \(\psi (2S)\) or \(\Upsilon (1S)\), but may need to be configured by the user. All of these partonic cross-sections are t-channel exchanges and diverge for low \(p_\text {T}\) of the quarkonium. These divergences are regularised either with a hard \(p_\text {T}\) cut-off or, in the case of multiple parton interactions in Pythia 8, a smooth damping factor.
The LDMEs of the \({\mathcal {O}}(1)\) leading colour-singlet Fock state, i.e. the Fock state with the same quantum numbers as the physical state, can be determined from the wave-function of the physical state at the origin. The LDMEs for the additional Fock states must be determined from fits to data, although velocity scaling rules can be used to relate these LDMEs. Typically, these fits are made to the differential quarkonium production cross-section with respect to the \(p_\text {T}\) of the quarkonium, as the colour-singlet contributions dominate at low \(p_\text {T}\), while the colour-octet contributions dominate at high \(p_\text {T}\). Using LDME fits from CDF, the differential cross-section in \(p_\text {T}\) of the \(\psi (1S)\) is described well at both the Tevatron [37, 55] and the LHC [56,57,58]. However, these NRQCD predictions are dominated by colour-octet contributions at high \(p_\text {T}\), which are typically transversely polarised, unlike colour-singlet contributions which are typically longitudinally polarised. This is in direct conflict with experimental results, which are primarily unpolarised across all \(p_\text {T}\) of the \(\psi (1S)\) [15,16,17,18, 59,60,61,62].
The relative isolation of quarkonia can also be measured experimentally, where a jet clustering algorithm such as anti-\(k_\text {T}\) can be used to group the quarkonium with surrounding activity, and observables such as \({p_\text {T}} (\text {quarkonium})/{p_\text {T}} (\text {jet})\) can be constructed. For fixed-order NRQCD predictions, quarkonia are expected to be relatively isolated for colour-singlet contributions. Even for fixed-order colour-octet contributions with a parton shower applied similar to that of Pythia 8, the quarkonia is still expected to be primarily isolated. However, measurements from both LHCb [19] and CMS [20, 21] do not show this isolation, and instead match distributions that are more consistent with production of the quarkonia from fragmentation rather than fixed-order calculations. In Refs. [47, 63], fragmenting jet functions (FJF) calculated via resummation, and similar to the fragmentation probabilities of Eq. (8) below, were used to model the LHCb data. However, these calculations are incomplete and do not include all sources of \(\psi (1S)\) production such as feed-down.
Until this work, Pythia 8 did not include NRQCD-based fragmentation contributions to quarkonium production. This contribution can be written, formally, as,

which is analogous to Eq. (5), but now uses the fixed-order partonic cross-section \(\,\text {d}{\hat{\sigma }}(a_i a_j \rightarrow a_k X)\) for parton \(a_i\) and \(a_j\) scattering to produce parton \(a_k\) inclusively, multiplied by the fragmentation probability  , which can be for either the sum of all Fock states or a specific Fock state. The precise definition of z varies within the literature, but generally all definitions reduce to the relative energy fraction carried by the emitted quarkonium in the high-energy limit.
, which can be for either the sum of all Fock states or a specific Fock state. The precise definition of z varies within the literature, but generally all definitions reduce to the relative energy fraction carried by the emitted quarkonium in the high-energy limit.
While this formalism can calculate quarkonium production from fragmentation, it cannot produce realistic event topologies that emulate events observed in experiments. Additionally, this type of calculation typically does not include competition between quarkonium states, i.e. the fragmentation probabilities do not simply factorize. In this work, we provide an alternative method that overcomes both of these shortcomings, by introducing quarkonium splittings into the Pythia 8 parton shower. This technique is formally equivalent to analytic resummation for inclusive observables, but provides more comprehensive results via a flexible Monte Carlo generator interface. To avoid double counting, this NRQCD parton shower should not be used together with fixed-order quarkonium processes without considering appropriate matching.Footnote 2
3 Parton showers
A complete description of the Pythia 8 parton shower is available in Ref. [64]. Here, a brief review is given, with a focus on the algorithmic procedure. Parton showers evolve partons produced from fixed-order calculations at high virtuality \(\mu _\text {max} \) to low virtuality \(\mu _\text {min} \) through a series of probabilistic parton emissions. While various parton showers differ in the choice of the evolution variable \(\mu \), it is illustrative to consider it as an energy-like scale. The probability for parton \(a_i\) to not radiate, i.e. \(a_i \rightarrow a_j a_k\), between virtualities \(\mu _1\) and \(\mu _2\) is given by,
where z is defined as \(E_j/E_i\), the fractional energy parton \(a_j\) takes from \(a_i\), and \(P_{i \rightarrow j k}\) is the splitting kernel for the process \(a_i \rightarrow a_j a_k\). A summation is performed over all available splitting kernels, e.g. for a gluon both the splittings \(g \rightarrow g g \) and \(g \rightarrow q \overline{q} \) would be summed, where the second splitting is over all kinematically available quark flavours.
 splitting is used for the \(\eta _c\), \({\psi }\), and \(\chi _{c}\) states
splitting is used for the \(\eta _c\), \({\psi }\), and \(\chi _{c}\) statesThe parton shower then proceeds through an iterative algorithm. For a given parton dipole with virtuality \(\mu _1\), a no-emission probability is uniformly sampled, \(\Delta _{i} (\mu _1,\mu _2) \in {\mathcal {U}}(0, 1)\), yielding an equation that can be solved for the emission scale \(\mu _2\). In practice, the integrands in Eq. (9) are complicated, and so the emission scale is calculated using an overestimate and rejection method called the veto algorithm. In this case, the summed integrands \(P_{i \rightarrow j k}\) of Eq. (9) are replaced by \(O_i\),
is valid for all \(\mu \) in the range \(\mu _2\) to \(\mu _1\), and all z in the range \(z_\text {min} \) to \(z_\text {max} \). If \(\alpha _s\) is evolved at first order, the new virtuality \(\mu _2\) can be calculated as
where \(b_0\) is the one-loop \(\beta \)-function coefficient [65], \((33 - 2n_f)/6\), and \(\Lambda \) is the scale from which \(\alpha _s\) is being evolved. If, instead, \(\alpha _s\) is fixed at one value, the new virtuality becomes,
After the virtuality \(\mu _2\) is determined according to Eq. (11) or Eq. (12), one of the quarkonium splittings \(a_i \rightarrow a_j a_k\) is chosen randomly with probability \(O_{i \rightarrow jk}/O_{i} \). A z is then randomly sampledFootnote 3 between \(z_\text {min} \) and \(z_\text {max} \). The splitting is accepted if,
where the right-hand side is a uniformly sampled random variable. If the splitting is rejected, then: the algorithm returns to Eq. (11) or Eq. (12); a new \(\mu _1\) is set as the old \(\mu _2\), \(\mu _2 \rightarrow \mu _1\), and a new \(\mu _2\) is selected; and the procedure continues as before. The parton shower continues until \(\mu _2\) drops below the minimum virtuality, \(\mu _\text {min} \). The virtuality variable \(\mu \) in Pythia 64 is defined as,
where \(\sqrt{s}\) is the centre-of-mass energy for the dipole, \(m_r\) is the mass of the radiating parton in the dipole, and z is a light-cone momentum fraction carried by the emitted parton.Footnote 4
4 Implementation
A full set of splitting kernels to complement the \(\psi (1S)\) and \(\chi _{c}\) fixed-order production implemented in Pythia 8, described in Sect. 2, were derived from fragmentation functions in the literature similar to those used in Eq. (8). The implemented splitting kernels, as well as their references, are given in Table 1. The full forms for all the implemented splitting kernels can be found in the references. We note that in comparison to Eq. (6) a number of splittings are missing, namely the gluon and heavy-quark initiated splittings to colour-octet states  ,
,  ,
,  , and
, and  . These gluon initiated splittings are omitted as they only enter at \(\alpha _s ^2\), while the
. These gluon initiated splittings are omitted as they only enter at \(\alpha _s ^2\), while the  splitting enters at order \(\alpha _s \). Similarly, the heavy-quark initiated splittings are omitted since they are suppressed by a factor of \(1/(N_c^2 - 1)^2\) with respect to their corresponding colour-singlet splittings [66].
splitting enters at order \(\alpha _s \). Similarly, the heavy-quark initiated splittings are omitted since they are suppressed by a factor of \(1/(N_c^2 - 1)^2\) with respect to their corresponding colour-singlet splittings [66].
To illustrate our procedure for including the NRQCD-based fragmentation functions in the Pythia 8 shower, we give the details for the  splitting. The splitting kernel is given as,
splitting. The splitting kernel is given as,

where the LDME
 depends upon the final physical state
depends upon the final physical state
 that this splitting kernel is being used to produce, e.g. the \(\psi (1S)\) as a
that this splitting kernel is being used to produce, e.g. the \(\psi (1S)\) as a
 state.
state.
This expression differs from that given in Ref. [30] for a number of reasons. First, the z convention used there is equivalent to \(1 - z\) in Pythia 8, and so a change of variables is made here. An additional factor of \(2\pi \) is also included to account for the \(1/(2\pi )\) in Eq. (9). There is already a factor of \(\alpha _s (\mu )\) in Eq. (9), so only one factor of \(\alpha _s\) is included, evaluated at the scale \(p_\text {T,evol}^{}\); in Ref. [30], both factors of \(\alpha _s\) are evaluated at a scale of \(3m_{Q}\). The choice for this scale is discussed in Sect. 5. Finally, the integration variable of Eq. (9) is \(\mu ^2 \equiv {p_\text {T,evol}^{2}} \), rather than s as provided in Ref. [30], so a Jacobian transforming from s to \(p_\text {T,evol}^{2}\) has been introduced:

Because there is already a factor of \(1/{p_\text {T,evol}^{2}} \) in Eq. (9), only the additional factor of \((s - m_{Q}^2)\) needs to be included, corresponding to the final line of Eq. (15). A similar conditioning must be done for all the splitting kernels of Table 1.
An overestimate must also be determined for Eq. (15). This can be determined analytically or numerically. For this splitting, we can factorise Eq. (15) into a z-independent component, and a z-dependent component f(z), given by,

A factor of \(1/(s - m_{Q}^2)^2\) is kept in the z-dependent component f(z) to ensure it remains dimensionless. The overestimate can then be written as,

where we have used the numerical knowledge that \(f(z) < 3/2\), and we use the parton shower cut-off to evaluate \(\alpha _s\). Since \((s - m_{Q}^2)\) must always be larger than  , we replace \((s - m_{Q}^2)\) with \(8m_{Q}^2\) in the numerator of the second term. Again, a similar procedure can be performed for the remaining splitting kernels of Table 1. For all the splitting kernels, we use the default recoil scheme in Pythia 8, which is based on dipole-style recoils.
, we replace \((s - m_{Q}^2)\) with \(8m_{Q}^2\) in the numerator of the second term. Again, a similar procedure can be performed for the remaining splitting kernels of Table 1. For all the splitting kernels, we use the default recoil scheme in Pythia 8, which is based on dipole-style recoils.
Some of the splitting kernels above deviate significantly enough from the example to warrant special mention. The  kernel is a \(1 \rightarrow 3\) splitting, rather than the normal \(1 \rightarrow 2\), and so the splitting kernel depends upon another kinematic variable, the digluon mass \(m_{g g}^{2}\), which must be sampled when generating the final-state kinematics. To handle these specific kinematics, a \(1 \rightarrow 2\) splitting is performed first, where the digluon is treated as a single massive parton. Later, this digluon object is decayed isotropically in its rest frame into the actual two final-state massless gluons. Another factor of \(\alpha _s\) enters into this splitting kernel, which is naturally evaluated at a scale of \(p_\text {T,evol}^{}\) with no choice given to the user. The
kernel is a \(1 \rightarrow 3\) splitting, rather than the normal \(1 \rightarrow 2\), and so the splitting kernel depends upon another kinematic variable, the digluon mass \(m_{g g}^{2}\), which must be sampled when generating the final-state kinematics. To handle these specific kinematics, a \(1 \rightarrow 2\) splitting is performed first, where the digluon is treated as a single massive parton. Later, this digluon object is decayed isotropically in its rest frame into the actual two final-state massless gluons. Another factor of \(\alpha _s\) enters into this splitting kernel, which is naturally evaluated at a scale of \(p_\text {T,evol}^{}\) with no choice given to the user. The  splitting kernel diverges rapidly as \({p_\text {T,evol}^{2}} \rightarrow 0\), and so a \(p_\text {T,evol}^{2}\)-dependent overestimate has been introduced to increase the sampling efficiency for this kernel. Finally, it should be noted that in a parton-shower context the splitting for the
splitting kernel diverges rapidly as \({p_\text {T,evol}^{2}} \rightarrow 0\), and so a \(p_\text {T,evol}^{2}\)-dependent overestimate has been introduced to increase the sampling efficiency for this kernel. Finally, it should be noted that in a parton-shower context the splitting for the
 Fock state must be treated specially as described in the following.
Fock state must be treated specially as described in the following.
There is one
 splitting, given by
splitting, given by  . This is unique because the splitting is \(1 \rightarrow 1\), rather than \(1 \rightarrow 2\), and arises from a delta function in the splitting kernel. Because the gluon has the same quantum numbers as the
. This is unique because the splitting is \(1 \rightarrow 1\), rather than \(1 \rightarrow 2\), and arises from a delta function in the splitting kernel. Because the gluon has the same quantum numbers as the
 , this splitting can be thought of as an off-shell gluon converting directly to a
, this splitting can be thought of as an off-shell gluon converting directly to a
 state when the virtuality of the gluon matches the corresponding quarkonium mass. The splitting kernel is then given by,
state when the virtuality of the gluon matches the corresponding quarkonium mass. The splitting kernel is then given by,

where \(\delta m\) is a small mass splitting, which for this work is set as \(0.01~\mathrm {\,Ge\hspace{-1.00006pt}V} \). The results of the parton shower are not sensitive to the choice of this mass splitting.
5 Results
The differential fragmentation probability from which the splitting kernel of Eq. (15) was derived can be integrated over s to determine the total fragmentation probability. From Ref. [30], this is

for \(\psi (1S)\) production from the  splitting at the lowest allowed scale of \(3m_{c}\). Here, z does not follow the same convention as Sects. 3 and 4, but rather is defined as
splitting at the lowest allowed scale of \(3m_{c}\). Here, z does not follow the same convention as Sects. 3 and 4, but rather is defined as  where \(\sqrt{s}\) is the centre-of-mass energy for the initial dipole. A comparison can be made directly between the parton-shower implementation of this work, and Eq. (20). This is done by producing a \(c \overline{c} \) dipole with a sufficiently high \(\sqrt{s}\) that mass effects are negligible. The Pythia 8 parton shower, with the inclusion of the individual quarkonium splitting kernels from Sect. 4 with no competition between the quarkonium splittings, is then run on this dipole. All QCD splittings are also switched off. The result can be seen in the left plot of Fig. 1, where the Pythia 8 result given by the blue histogram matches well with the analytic prediction of Eq. (20) corresponding to the dashed line. Similar agreement is also seen for the \(\eta _c\), shown in red.
where \(\sqrt{s}\) is the centre-of-mass energy for the initial dipole. A comparison can be made directly between the parton-shower implementation of this work, and Eq. (20). This is done by producing a \(c \overline{c} \) dipole with a sufficiently high \(\sqrt{s}\) that mass effects are negligible. The Pythia 8 parton shower, with the inclusion of the individual quarkonium splitting kernels from Sect. 4 with no competition between the quarkonium splittings, is then run on this dipole. All QCD splittings are also switched off. The result can be seen in the left plot of Fig. 1, where the Pythia 8 result given by the blue histogram matches well with the analytic prediction of Eq. (20) corresponding to the dashed line. Similar agreement is also seen for the \(\eta _c\), shown in red.
The DGLAP equations can be applied to Eq. (20) to numerically evolve the fragmentation probability from the scale of \(3m_{c}\) up to \(m_Z/2\). In Ref. [30] this is provided numericallyFootnote 5 for the \(\psi (1S)\) and \(\eta _c\), as given by the dashed blue and red lines, respectively, in the right plot of Fig. 1. The implementation of this work can be compared by showering a \(c \overline{c} \) dipole with \(\sqrt{s} = m_Z \), and keeping all QCD splittings switched on. The results are also given in the right plot of Fig. 1. It should be noted that for high z, where mass effects become negligible, the results match well. However, at low z the results differ significantly, because in Ref. [30] the masses of the \(\psi (1S)\) and \(\eta _c\) were not considered. Accounting for this mass can be seen clearly in the Pythia 8 result, where there are no quarkonia produced with \(z < 2m_{\psi (1S)}/m_Z \).
Analytic expressions similar to Eq. (20) are available in the literature for all the splittings of Table 1, evaluated at the lowest kinematically allowed scale. For heavy-quark radiators \(Q\), this scale is \(3m_{Q}\), while for gluon radiators \(g\), the scale is \(2m_{Q}\). In the left plot of Fig. 2 the fragmentation probabilities \(D_{g \rightarrow \psi (1S) ^{(1)}} (z, 2m_{c})\) and \(D_{g \rightarrow \eta _c ^{(1)}} (z, 2m_{c})\) for the colour singlet splittings  and
and  are given, respectively. There is good agreement between the parton-shower results and the analytic predictions. In the right plot of Fig. 2, comparisons between the parton-shower results and analytic predictions are given for \(D_{g \rightarrow \chi _{c 0} ^{(1)}} (z, 2m_{c})\), \(D_{g \rightarrow \chi _{c 1} ^{(1)}} (z, 2m_{c})\), and \(D_{g \rightarrow \chi _{c 2} ^{(1)}} (z, 2m_{c})\), corresponding to the splittings
are given, respectively. There is good agreement between the parton-shower results and the analytic predictions. In the right plot of Fig. 2, comparisons between the parton-shower results and analytic predictions are given for \(D_{g \rightarrow \chi _{c 0} ^{(1)}} (z, 2m_{c})\), \(D_{g \rightarrow \chi _{c 1} ^{(1)}} (z, 2m_{c})\), and \(D_{g \rightarrow \chi _{c 2} ^{(1)}} (z, 2m_{c})\), corresponding to the splittings  ,
,  , and
, and  , respectively. All three parton-shower results agree well with their corresponding analytic predictions.
, respectively. All three parton-shower results agree well with their corresponding analytic predictions.
The fragmentation probabilities, evaluated at the energy scale of \(3m_{c}\), for the production of the \(\chi _{c}\) from \(c\)-initiated splittings, are given in Fig. 3. On the left, the fragmentation probabilities \(D_{c \rightarrow \chi _{c J} ^{(1)}} (z, 3m_{c})\) are given for the colour-singlet splittings  . On the right, the fragmentation probabilities \(D_{c \rightarrow \chi _{c J} ^{(8)}} (z, 3m_{c})\) are given for the colour-octet splittings
. On the right, the fragmentation probabilities \(D_{c \rightarrow \chi _{c J} ^{(8)}} (z, 3m_{c})\) are given for the colour-octet splittings  . All six parton-shower results are in good agreement with the analytic predictions.
. All six parton-shower results are in good agreement with the analytic predictions.
Analytic predictions evolved up to the scale of \(m_Z \) are not available in the literature for any of the processes other than  and
and  for the \(\psi (1S)\) and \(\eta _c\), respectively. Consequently, we are not able to make comparisons similar to the right plot of Fig. 1. We instead provide results at the energy scale of \(m_Z/2\) in Fig. 4 for all the remaining splittings implemented in Pythia 8. The fragmentation probabilities for all the colour-singlet
for the \(\psi (1S)\) and \(\eta _c\), respectively. Consequently, we are not able to make comparisons similar to the right plot of Fig. 1. We instead provide results at the energy scale of \(m_Z/2\) in Fig. 4 for all the remaining splittings implemented in Pythia 8. The fragmentation probabilities for all the colour-singlet  splittings are given in the upper-left plot, while the equivalent fragmentation probabilities for the colour-octet
splittings are given in the upper-left plot, while the equivalent fragmentation probabilities for the colour-octet  splittings of the \(\chi _{c}\) states are given in the upper-right plot. The fragmentation probabilities for all the colour-singlet
splittings of the \(\chi _{c}\) states are given in the upper-right plot. The fragmentation probabilities for all the colour-singlet  splittings are given in the lower left, and the fragmentation probabilities for the colour-octet
splittings are given in the lower left, and the fragmentation probabilities for the colour-octet  splittings of Eq. (19) are given in the lower right.
splittings of Eq. (19) are given in the lower right.
There is some ambiguity in how colour-octet states should be treated in the parton shower after being produced, e.g. the
 states in the lower-right plot of Fig. 4. Because colour-octet states carry colour charge, they must undergo further QCD radiation before transitioning to their physical state, requiring the emission of one or more soft gluons. The default behaviour in Pythia 8, prior to this work, was to treat these states with twice the \(q \rightarrow q g \) splitting kernel,
states in the lower-right plot of Fig. 4. Because colour-octet states carry colour charge, they must undergo further QCD radiation before transitioning to their physical state, requiring the emission of one or more soft gluons. The default behaviour in Pythia 8, prior to this work, was to treat these states with twice the \(q \rightarrow q g \) splitting kernel,
i.e. the two heavy quarks of the quarkonium state would both be treated as radiators. However, in the case of the
 state, which is the only colour-octet state implemented here, it may be more appropriate to consider this colour-octet state as a massive gluon. The corresponding splitting kernel, derived from Ref. [69], is
state, which is the only colour-octet state implemented here, it may be more appropriate to consider this colour-octet state as a massive gluon. The corresponding splitting kernel, derived from Ref. [69], is
where the radiating gluon has mass \(m_g \) and the emitted gluon is massless. These splittings do not guarantee the gluon emission necessary to transition from an octet to singlet state, so the colour-octet states are required to have slightly larger masses than their corresponding physical states. They are then forced to transition to their physical states through the isotropic emission of a single soft gluon.
The difference between the two splittings of Eqs. (21) and (22) depends on when the gluon splitting producing the colour-octet state,  , occurs in the parton-shower evolution. Prior to this splitting, the gluon can continue to radiate, \(g \rightarrow g g \). Consequently, the second of the two splittings results in a transition much later in the parton-shower evolution, driven primarily by \(g \rightarrow g g \) splittings. The effects of these two different splitting kernels, as well as the pre-factor used for Eq. (21), can be explored by creating an initial dipole with a
, occurs in the parton-shower evolution. Prior to this splitting, the gluon can continue to radiate, \(g \rightarrow g g \). Consequently, the second of the two splittings results in a transition much later in the parton-shower evolution, driven primarily by \(g \rightarrow g g \) splittings. The effects of these two different splitting kernels, as well as the pre-factor used for Eq. (21), can be explored by creating an initial dipole with a  state at an \(\sqrt{s}\) of \(m_Z \), and evolving this downward to the parton shower cut-off scale. The results for this configuration are shown on the left of Fig. 5. The difference in the energy radiated away by the colour-octet state depending on the splitting kernel is sizeable. For the previous Pythia 8 default splitting of \(q \rightarrow q g \) with a pre-factor of 2, the colour-octet state remains relatively isolated. If the pre-factor is unphysically doubled again to a pre-factor of 4, the colour-octet state radiates significantly more, as expected. However, for the splitting \(g \rightarrow g g \), the colour-octet state radiates even more. In this work, this gluon splitting kernel has been used throughout, i.e. to produce the bottom-right plot of Fig. 4. It is also possible for colour-octet states to transition to other colour-octet states. For example, the splitting
state at an \(\sqrt{s}\) of \(m_Z \), and evolving this downward to the parton shower cut-off scale. The results for this configuration are shown on the left of Fig. 5. The difference in the energy radiated away by the colour-octet state depending on the splitting kernel is sizeable. For the previous Pythia 8 default splitting of \(q \rightarrow q g \) with a pre-factor of 2, the colour-octet state remains relatively isolated. If the pre-factor is unphysically doubled again to a pre-factor of 4, the colour-octet state radiates significantly more, as expected. However, for the splitting \(g \rightarrow g g \), the colour-octet state radiates even more. In this work, this gluon splitting kernel has been used throughout, i.e. to produce the bottom-right plot of Fig. 4. It is also possible for colour-octet states to transition to other colour-octet states. For example, the splitting  can occur at leading order. However, we expect that these transitions should provide a second-order effect to the gluon radiation of the initial
can occur at leading order. However, we expect that these transitions should provide a second-order effect to the gluon radiation of the initial  state, although future investigation is warranted.
state, although future investigation is warranted.
As mentioned in the discussion of Eq. (15), some choice needs to be made for the scale at which \(\alpha _s\) is evaluated. Given the diagrams for most quarkonium production, it is natural to choose the scale of the \(\alpha _s\) from Eq. (9) as \(p_\text {T,evol}^{}\), or whatever the virtuality of the parton shower is. However, the choice of scale for the remaining \(\alpha _s\) factors, e.g. the \(\alpha _s\) of Eq. (15), is not as clear. Here, we consider three different options for \(\mu \): the mass of the quarkonium m, the parton-shower virtuality \(p_\text {T,evol}^{}\), and the centre-of-mass of the dipole \(\sqrt{s}\). In the right plot of Fig. 5, the impact of this choice is shown for \(\psi (1S)\) production from a \(c \overline{c} \) dipole with \(\sqrt{s} = m_Z \), using only the  splitting kernel. The default choice of \(p_\text {T,evol}^{}\) is given in blue, and is identical to the corresponding blue curve in the right plot of Fig. 1. Switching to m provides a nearly identical result, while using \(\sqrt{s}\) significantly reduces the fragmentation probability, although the shape remains similar, as expected. It should be noted for the
splitting kernel. The default choice of \(p_\text {T,evol}^{}\) is given in blue, and is identical to the corresponding blue curve in the right plot of Fig. 1. Switching to m provides a nearly identical result, while using \(\sqrt{s}\) significantly reduces the fragmentation probability, although the shape remains similar, as expected. It should be noted for the  splitting, only one of the three factors of \(\alpha _s\) is effected by this scale choice, the other two are always evaluated at \(p_\text {T,evol}^{}\).
splitting, only one of the three factors of \(\alpha _s\) is effected by this scale choice, the other two are always evaluated at \(p_\text {T,evol}^{}\).
Up to this point, we have only considered parton-shower configurations where no competition is included between the various quarkonium splittings. This competition is critical when generating comprehensive quarkonium predictions. Because of this competition, the different fragmentation contributions do not simply factorize into independent pieces. To demonstrate the full flexibility of our implementation, we calculate the inclusive branching fractions for standard-model Higgs boson decays into quarkonia. When performing this calculation, all possible quarkonium splitting kernels are switched on with full competition, as well as all other possible splittings, i.e. QCD and electroweak. The results are given in Table 2, using the default LDMEs of Pythia 8 from Refs. [70,71,72]. Here, the branching fractions in the first set of columns are separated into quarkonium production from parton-shower feed-down and from non-quarkonium hadron decays, e.g. \(b\) hadrons. The second set of columns is production from the parton shower, separated by the splitting type. Here, \(X^{(8)}\) is any colour-octet production, \(g \rightarrow X^{(1)}\) is colour-singlet production from a gluon splitting, and \(Q \rightarrow X^{(1)}\) is colour-singlet production from heavy-quark splitting. The \(X^{(8)}\) column includes both production directly from a colour-octet state, and from feed-down that was produced by a colour-octet state. Conversely, the feed-down column includes production only from feed-down, but the feed-down may be produced by any mechanism.
For \(\psi (1S)\) states, production from non-quarkonium hadron decays dominates the branching fraction, while the parton-shower contribution is nearly two orders of magnitude smaller. This is similar for all the charmonium branching fractions. For bottomonium production there is no production from non-quarkonium hadron decays, as there are not sufficiently high-mass states. For the \(\eta _{b}\) and \(\Upsilon \), the primary production mechanism is colour-singlet production from \(b\) splittings, whereas for the \(\chi _{b}\) states, the primary production mechanism is from colour-octet splittings.
6 Conclusions
We have implemented a full-featured quarkonium parton shower in the Pythia 8 Monte Carlo event generator, available from version 8.310 onward. This parton shower can be used to model the LHC quarkonium isolation results, as well as explore the production of quarkonia in general. Our implementation includes all the relevant splitting kernels needed for the production of
 ,
,
 , and
, and
 states with arbitrary radial excitations and for \(Q \in c, b \). These splitting kernels have been validated against fragmentation probabilities available in the literature, whenever possible, and found to be in good agreement. We provide first predictions for a number of fragmentation probabilities evolved up to the energy scale of \(m_Z/2\). The framework is flexible, so that an arbitrary number of competing splitting kernels can be included. Various choices are available for the radiation of the colour-octet states, as well as a choice of scale for evaluating \(\alpha _s\). Finally, we provide comprehensive first predictions for the production of
states with arbitrary radial excitations and for \(Q \in c, b \). These splitting kernels have been validated against fragmentation probabilities available in the literature, whenever possible, and found to be in good agreement. We provide first predictions for a number of fragmentation probabilities evolved up to the energy scale of \(m_Z/2\). The framework is flexible, so that an arbitrary number of competing splitting kernels can be included. Various choices are available for the radiation of the colour-octet states, as well as a choice of scale for evaluating \(\alpha _s\). Finally, we provide comprehensive first predictions for the production of
 ,
,
 , and
, and
 states from decays of the standard-model Higgs boson. Future work includes developing a method to match these results from the parton shower with fixed-order predictions, including matrix-element corrections, and introducing additional splitting kernels, such as those needed for double-heavy meson and baryon production.
states from decays of the standard-model Higgs boson. Future work includes developing a method to match these results from the parton shower with fixed-order predictions, including matrix-element corrections, and introducing additional splitting kernels, such as those needed for double-heavy meson and baryon production.
Data availability
This manuscript has associated data in a data repository. [Author’s comment: The data can be reproduced using the open access software package, Pythia 8, which is available in the https://gitlab.com/Pythia8/releases repository.]
Notes
Here, spectroscopic notation is being used of the form
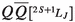 , where \(Q\) is the heavy flavour quark/antiquark pair, and S, L, J are the total spin, orbital, and total angular-momentum quantum numbers, respectively. For L, the orbitals S, P, and D correspond to orbital angular-momentum quantum numbers of 0, 1, and 2, respectively.
, where \(Q\) is the heavy flavour quark/antiquark pair, and S, L, J are the total spin, orbital, and total angular-momentum quantum numbers, respectively. For L, the orbitals S, P, and D correspond to orbital angular-momentum quantum numbers of 0, 1, and 2, respectively.Currently fixed-order quarkonium production is automatically switched off in the Pythia 8 multiparton interactions framework when the NRQCD shower is switched on. Future work is required to match this parton shower with fixed-order processes to ensure no double counting.
This sampling does not need to be uniform, and in many cases is not, as long as the appropriate transformation is applied after sampling.
This definition differs from the one used to construct the kinematics of the evolving system.
The results are only available in the published version of that paper, not the pre-print, and can be extracted from Fig. 2.
References
A.G. Clark et al., Electron pair production at the CERN ISR. Nucl. Phys. B 142, 29 (1978). https://doi.org/10.1016/0550-3213(78)90400-5
K. Ueno et al., Evidence for the \(\Upsilon ^{\prime \prime }\) and a search for new narrow resonances. Phys. Rev. Lett. 42, 486–489 (1979). https://doi.org/10.1103/PhysRevLett.42.486
C. Albajar et al., High transverse momentum \(J/\psi \) production at the CERN proton–anti-proton collider. Phys. Lett. B 200, 380–390 (1988). https://doi.org/10.1016/0370-2693(88)90792-7
C. Albajar et al., Low mass dimuon production at the CERN proton–anti-proton collider. Phys. Lett. B 209, 397–406 (1988). https://doi.org/10.1016/0370-2693(88)90969-0
C. Albajar et al., J/psi and psi-prime production at the CERN p anti-p collider. Phys. Lett. B 256, 112–120 (1991). https://doi.org/10.1016/0370-2693(91)90227-H
F. Abe et al., Production of \(J/\psi \) mesons from \(\chi _c\) meson decays in \(p{\bar{p}}\) collisions at \(\sqrt{s}=1.8\) TeV. Phys. Rev. Lett. 79, 578–583 (1997). https://doi.org/10.1103/PhysRevLett.79.578
D. Acosta et al., Measurement of the \(J/\psi \) meson and \(b-\)hadron production cross sections in \(p{\bar{p}}\) collisions at \(\sqrt{s} = 1960\) GeV. Phys. Rev. D 71, 032001 (2005). https://doi.org/10.1103/PhysRevD.71.032001. arXiv:hep-ex/0412071
S. Abachi et al., \(J/\psi \) production in \(p {\bar{p}}\) collisions at \(\sqrt{s}\) = 1.8-TeV. Phys. Lett. B 370, 239–248 (1996). https://doi.org/10.1016/0370-2693(96)00067-6
R. Aaij et al., Measurement of forward \(J/\psi \) production cross-sections in \(pp\) collisions at \(\sqrt{s}=13\) TeV. JHEP 10, 172 (2015) [Erratum: JHEP 05, 063 (2017)]. https://doi.org/10.1007/JHEP10(2015)172. arXiv:1509.00771 [hep-ex]
R. Aaij et al., Production of J/psi and Upsilon mesons in pp collisions at sqrt(s) = 8 TeV. JHEP 06, 064 (2013). https://doi.org/10.1007/JHEP06(2013)064. arXiv:1304.6977 [hep-ex]
R. Aaij et al., Measurement of \(J/\psi \) production in \(pp\) collisions at \(\sqrt{s}=2.76\) TeV. JHEP 02, 041 (2013). https://doi.org/10.1007/JHEP02(2013)041. arXiv:1212.1045 [hep-ex]
R. Aaij et al., Measurement of \(J/\psi \) production in \(pp\) collisions at \(\sqrt{s}=7~\rm {TeV}\). Eur. Phys. J. C 71, 1645 (2011). https://doi.org/10.1140/epjc/s10052-011-1645-y. arXiv:1103.0423 [hep-ex]
G. Aad et al., Measurement of the differential cross-sections of prompt and non-prompt production of \(J/\psi \) and \(\psi (2\rm S )\) in \(pp\) collisions at \(\sqrt{s} = 7\) and 8 TeV with the ATLAS detector. Eur. Phys. J. C 76(5), 283 (2016). https://doi.org/10.1140/epjc/s10052-016-4050-8. arXiv:1512.03657 [hep-ex]
V. Khachatryan et al., Measurement of J/\(\psi \) and \(\psi \)(2S) Prompt Double-Differential Cross Sections in pp Collisions at \(\sqrt{s}\)=7 TeV. Phys. Rev. Lett. 114(19), 191802 (2015). https://doi.org/10.1103/PhysRevLett.114.191802. arXiv:1502.04155 [hep-ex]
A. Abulencia et al., Polarization of \(J/\psi \) and \(\psi _{2S}\) mesons produced in \(p {\bar{p}}\) collisions at \(\sqrt{s}\) = 1.96-TeV. Phys. Rev. Lett. 99, 132001 (2007). https://doi.org/10.1103/PhysRevLett.99.132001. arXiv:0704.0638 [hep-ex]
R. Aaij et al., Measurement of \(J/\psi \) polarization in \(pp\) collisions at \(\sqrt{s}=7\) TeV. Eur. Phys. J. C 73(11), 2631 (2013). https://doi.org/10.1140/epjc/s10052-013-2631-3. arXiv:1307.6379 [hep-ex]
B. Abelev et al., \(J/\psi \) polarization in \(pp\) collisions at \(\sqrt{s}=7\) TeV. Phys. Rev. Lett. 108, 082001 (2012). https://doi.org/10.1103/PhysRevLett.108.082001. arXiv:1111.1630 [hep-ex]
S. Chatrchyan et al., Measurement of the prompt \(J/\psi \) and \(\psi \)(2S) polarizations in \(pp\) collisions at \(\sqrt{s}\) = 7 TeV. Phys. Lett. B 727, 381–402 (2013). https://doi.org/10.1016/j.physletb.2013.10.055. arXiv:1307.6070 [hep-ex]
R. Aaij et al., Study of J/\(\psi \) production in jets. Phys. Rev. Lett. 118(19), 192001 (2017). https://doi.org/10.1103/PhysRevLett.118.192001. arXiv:1701.05116 [hep-ex]
A.M. Sirunyan et al., Study of J/\(\psi \) meson production inside jets in pp collisions at \(\sqrt{s} =\) 8 TeV. Phys. Lett. B 804, 135409 (2020). https://doi.org/10.1016/j.physletb.2020.135409. arXiv:1910.01686 [hep-ex]
A. Tumasyan et al., Fragmentation of jets containing a prompt J\(/\psi \) meson in PbPb and pp collisions at \(\sqrt{s_{{\rm NN}}} =\) 5.02 TeV. Phys. Lett. B 825, 136842 (2022). https://doi.org/10.1016/j.physletb.2021.136842. arXiv:2106.13235 [hep-ex]
J.P. Lansberg, \(J/\psi \), \(\psi \) ’ and \(\Upsilon \) production at hadron colliders: A Review. Int. J. Mod. Phys. A 21, 3857–3916 (2006). https://doi.org/10.1142/S0217751X06033180. arXiv:hep-ph/0602091
C.H. Chang, Hadronic production of \(J/\psi \) associated with a gluon. Nucl. Phys. B 172, 425–434 (1980). https://doi.org/10.1016/0550-3213(80)90175-3
R. Baier, R. Ruckl, Hadronic production of J/psi and upsilon: transverse momentum distributions. Phys. Lett. B 102, 364–370 (1981). https://doi.org/10.1016/0370-2693(81)90636-5
R. Baier, R. Ruckl, Hadronic collisions: a quarkonium factory. Z. Phys. C 19, 251 (1983). https://doi.org/10.1007/BF01572254
F. Halzen, F. Herzog, E.W.N. Glover, A.D. Martin, The \(J/\psi \) as a trigger in \({\bar{p}} p\) collisions. Phys. Rev. D 30, 700 (1984). https://doi.org/10.1103/PhysRevD.30.700
E.W.N. Glover, A.D. Martin, W.J. Stirling, J/psi production at large transverse momentum at hadron colliders. Z. Phys. C 38, 473 (1988). https://doi.org/10.1007/BF01584398 [Erratum: Z. Phys. C 49, 526 (1991)]
E. Braaten, M.A. Doncheski, S. Fleming, M.L. Mangano, Fragmentation production of \(J/\psi \) and \(\psi ^\prime \) at the Tevatron. Phys. Lett. B 333, 548–554 (1994). https://doi.org/10.1016/0370-2693(94)90182-1. arXiv:hep-ph/9405407
E. Braaten, T.C. Yuan, Gluon fragmentation into heavy quarkonium. Phys. Rev. Lett. 71, 1673–1676 (1993). https://doi.org/10.1103/PhysRevLett.71.1673. arXiv:hep-ph/9303205
E. Braaten, Km. Cheung, T.C. Yuan, Z0 decay into charmonium via charm quark fragmentation. Phys. Rev. D 48, 4230–4235 (1993). https://doi.org/10.1103/PhysRevD.48.4230. arXiv:hep-ph/9302307
E. Braaten, T.C. Yuan, Gluon fragmentation into P wave heavy quarkonium. Phys. Rev. D 50, 3176–3180 (1994). https://doi.org/10.1103/PhysRevD.50.3176. arXiv:hep-ph/9403401
M. Cacciari, M. Greco, \(J/\psi \) production via fragmentation at the Tevatron. Phys. Rev. Lett. 73, 1586–1589 (1994). https://doi.org/10.1103/PhysRevLett.73.1586. arXiv:hep-ph/9405241
R. Barbieri, M. Caffo, E. Remiddi, Gluon jets from quarkonia. Nucl. Phys. B 162, 220–236 (1980). https://doi.org/10.1016/0550-3213(80)90261-8
R. Barbieri, M. Caffo, R. Gatto, E. Remiddi, Strong QCD corrections to p wave quarkonium decays. Phys. Lett. B 95, 93–95 (1980). https://doi.org/10.1016/0370-2693(80)90407-4
R. Barbieri, M. Caffo, R. Gatto, E. Remiddi, QCD corrections to p wave quarkonium decays. Nucl. Phys. B 192, 61–65 (1981). https://doi.org/10.1016/0550-3213(81)90192-9
G.T. Bodwin, E. Braaten, G.P. Lepage, Rigorous QCD analysis of inclusive annihilation and production of heavy quarkonium. Phys. Rev. D 51, 1125–1171 (1995) [Erratum: Phys. Rev. D 55, 5853 (1997)]. https://doi.org/10.1103/PhysRevD.55.5853. arXiv:hep-ph/9407339
E. Braaten, S. Fleming, Color octet fragmentation and the psi-prime surplus at the Tevatron. Phys. Rev. Lett. 74, 3327–3330 (1995). https://doi.org/10.1103/PhysRevLett.74.3327. arXiv:hep-ph/9411365
P.L. Cho, A.K. Leibovich, Color octet quarkonia production. Phys. Rev. D 53, 150–162 (1996). https://doi.org/10.1103/PhysRevD.53.150. arXiv:hep-ph/9505329
P.L. Cho, A.K. Leibovich, Color octet quarkonia production. 2. Phys. Rev. D 53, 6203–6217 (1996). https://doi.org/10.1103/PhysRevD.53.6203. arXiv:hep-ph/9511315
A.K. Leibovich, Psi-prime polarization due to color octet quarkonia production. Phys. Rev. D 56, 4412–4415 (1997). https://doi.org/10.1103/PhysRevD.56.4412. arXiv:hep-ph/9610381
E. Braaten, J. Lee, Polarization of \(\upsilon _{nS}\) at the Tevatron. Phys. Rev. D 63, 071501 (2001). https://doi.org/10.1103/PhysRevD.63.071501. arXiv:hep-ph/0012244
M. Beneke, M. Krämer, Direct \(J/\psi \) and \(\psi ^\prime \) polarization and cross-sections at the Tevatron. Phys. Rev. D 55, 5269–5272 (1997). https://doi.org/10.1103/PhysRevD.55.R5269. arXiv:hep-ph/9611218
E. Braaten, B.A. Kniehl, J. Lee, Polarization of prompt \(J/\psi \) at the Tevatron. Phys. Rev. D 62, 094005 (2000). https://doi.org/10.1103/PhysRevD.62.094005. arXiv:hep-ph/9911436
B. Gong, L.P. Wan, J.X. Wang, H.F. Zhang, Polarization for prompt J/\(\psi \) and \(\psi \)(2s) production at the Tevatron and LHC. Phys. Rev. Lett. 110(4), 042002 (2013). https://doi.org/10.1103/PhysRevLett.110.042002. arXiv:1205.6682 [hep-ph]
K.T. Chao, Y.Q. Ma, H.S. Shao, K. Wang, Y.J. Zhang, \(J/\psi \) polarization at hadron colliders in nonrelativistic QCD. Phys. Rev. Lett. 108, 242004 (2012). https://doi.org/10.1103/PhysRevLett.108.242004. arXiv:1201.2675 [hep-ph]
R. Bain, Y. Makris, T. Mehen, Transverse momentum dependent fragmenting jet functions with applications to quarkonium production. JHEP 11, 144 (2016). https://doi.org/10.1007/JHEP11(2016)144. arXiv:1610.06508 [hep-ph]
R. Bain, L. Dai, A. Leibovich, Y. Makris, T. Mehen, NRQCD confronts LHCb data on quarkonium production within jets. Phys. Rev. Lett. 119(3), 032002 (2017). https://doi.org/10.1103/PhysRevLett.119.032002. arXiv:1702.05525 [hep-ph]
T. Sjostrand, S. Mrenna, P.Z. Skands, PYTHIA 6.4 Physics and Manual. JHEP 05, 026 (2006). https://doi.org/10.1088/1126-6708/2006/05/026
T. Sjostrand, S. Mrenna, P.Z. Skands, A brief introduction to PYTHIA 8.1. Comput. Phys. Commun. 178, 852–867 (2008). https://doi.org/10.1016/j.cpc.2008.01.036
T. Sjöstrand, S. Ask, J.R. Christiansen, R. Corke, N. Desai, P. Ilten, S. Mrenna, S. Prestel, C.O. Rasmussen, P.Z. Skands, An introduction to PYTHIA 8.2. Comput. Phys. Commun. 191, 159–177 (2015). https://doi.org/10.1016/j.cpc.2015.01.024. arXiv:1410.3012 [hep-ph]
C. Bierlich et al., A comprehensive guide to the physics and usage of PYTHIA 8.3 (2022). https://doi.org/10.21468/SciPostPhysCodeb.8. arXiv:2203.11601 [hep-ph]
L. Lönnblad, ARIADNE version 4: a program for simulation of QCD cascades implementing the color dipole model. Comput. Phys. Commun. 71, 15–31 (1992). https://doi.org/10.1016/0010-4655(92)90068-A
P. Ernstrom, L. Lönnblad, Generating heavy quarkonia in a perturbative QCD cascade. Z. Phys. C 75, 51–56 (1997). https://doi.org/10.1007/s002880050446. arXiv:hep-ph/9606472
P. Ernstrom, L. Lönnblad, M. Vanttinen, Evolution effects in \(Z^0\) fragmentation into charmonium. Z. Phys. C 76, 515–521 (1997). https://doi.org/10.1007/s002880050574. arXiv:hep-ph/9612408
M. Cacciari, M. Greco, M.L. Mangano, A. Petrelli, Charmonium production at the Tevatron. Phys. Lett. B 356, 553–560 (1995). https://doi.org/10.1016/0370-2693(95)00868-L. arXiv:hep-ph/9505379
Y.Q. Ma, K. Wang, K.T. Chao, A complete NLO calculation of the \(J/\psi \) and \(\psi ^{\prime }\) production at hadron colliders. Phys. Rev. D 84, 114001 (2011). https://doi.org/10.1103/PhysRevD.84.114001. arXiv:1012.1030 [hep-ph]
B. Gong, X.Q. Li, J.X. Wang, QCD corrections to \(J/\psi \) production via color octet states at Tevatron and LHC. Phys. Lett. B 673, 197–200 (2009) [Erratum: Phys. Lett. B 693, 612-613 (2010)]. https://doi.org/10.1016/j.physletb.2009.02.026. arXiv:0805.4751 [hep-ph]
M. Butenschoen, B.A. Kniehl, Reconciling \(J/\psi \) production at HERA, RHIC, Tevatron, and LHC with NRQCD factorization at next-to-leading order. Phys. Rev. Lett. 106, 022003 (2011). https://doi.org/10.1103/PhysRevLett.106.022003. arXiv:1009.5662 [hep-ph]
M. Butenschoen, B.A. Kniehl, J/psi polarization at Tevatron and LHC: nonrelativistic-QCD factorization at the crossroads. Phys. Rev. Lett. 108, 172002 (2012). https://doi.org/10.1103/PhysRevLett.108.172002. arXiv:1201.1872 [hep-ph]
V.M. Abazov et al., Measurement of the polarization of the \(\Upsilon (1S)\) and \(\Upsilon (2S)\) states in \(p {\bar{p}}\) collisions at \(\sqrt{s}\) = 1.96-TeV. Phys. Rev. Lett. 101, 182004 (2008). https://doi.org/10.1103/PhysRevLett.101.182004. arXiv:0804.2799 [hep-ex]
S. Chatrchyan et al., Measurement of the \(Y(1S), Y(2S)\) and \(Y(3S)\) polarizations in \(pp\) collisions at \(\sqrt{s}=7\) TeV. Phys. Rev. Lett. 110(8), 081802 (2013). https://doi.org/10.1103/PhysRevLett.110.081802. arXiv:1209.2922 [hep-ex]
R. Aaij et al., Measurement of \(\psi (2S)\) polarisation in \(pp\) collisions at \(\sqrt{s}=7\) TeV. Eur. Phys. J. C 74(5), 2872 (2014). https://doi.org/10.1140/epjc/s10052-014-2872-9. arXiv:1403.1339 [hep-ex]
R. Bain, L. Dai, A. Hornig, A.K. Leibovich, Y. Makris, T. Mehen, Analytic and Monte Carlo studies of jets with heavy mesons and quarkonia. JHEP 06, 121 (2016). https://doi.org/10.1007/JHEP06(2016)121. arXiv:1603.06981 [hep-ph]
T. Sjostrand, P.Z. Skands, Transverse-momentum-ordered showers and interleaved multiple interactions. Eur. Phys. J. C 39, 129–154 (2005). https://doi.org/10.1140/epjc/s2004-02084-y. arXiv:hep-ph/0408302
P.A. Zyla et al., Review of particle physics. PTEP 2020(8), 083C01 (2020). https://doi.org/10.1093/ptep/ptaa104
Y.Q. Ma, J.W. Qiu, H. Zhang, Heavy quarkonium fragmentation functions from a heavy quark pair. I. \(S\) wave. Phys. Rev. D 89(9), 094029 (2014). https://doi.org/10.1103/PhysRevD.89.094029. arXiv:1311.7078 [hep-ph]
E. Braaten, T.C. Yuan, Gluon fragmentation into spin triplet S wave quarkonium. Phys. Rev. D 52, 6627–6629 (1995). https://doi.org/10.1103/PhysRevD.52.6627. arXiv:hep-ph/9507398
T.C. Yuan, Perturbative QCD fragmentation functions for production of P wave mesons with charm and beauty. Phys. Rev. D 50, 5664–5675 (1994). https://doi.org/10.1103/PhysRevD.50.5664. arXiv:hep-ph/9405348
R. Kleiss, R. Verheyen, Collinear electroweak radiation in antenna parton showers. Eur. Phys. J. C 80(10), 980 (2020). https://doi.org/10.1140/epjc/s10052-020-08510-w. arXiv:2002.09248 [hep-ph]
G. Altarelli, M.L. Mangano (eds.). 1999 CERN Workshop on standard model physics (and more) at the LHC, CERN, Geneva, Switzerland, 25-26 May: Proceedings, CERN Yellow Reports: Conference Proceedings (2000). https://doi.org/10.5170/CERN-2000-004
M. Bargiotti, V. Vagnoni, Heavy quarkonia sector in PYTHIA 6.324: Tuning, validation and perspectives at LHC(b) (2007)
F. Yuan, C.F. Qiao, K.T. Chao, \(D\) wave heavy quarkonium production in fixed target experiments. Phys. Rev. D 59, 014009 (1999). https://doi.org/10.1103/PhysRevD.59.014009. arXiv:hep-ph/9807329
Acknowledgements
We thank T. Sjöstrand who provided help working with the Pythia 8 parton shower and gave feedback on the manuscript, P. Skands who provided a thorough code review of our work, C. Bierlich for performing initial comparisons between the parton-shower and fixed-order calculations in Pythia 8, and the remainder of the Pythia 8 collaboration for their support of this work. We also thank V. Bertone, who provided code and explained QCD predictions of the evolution of charm fragmentation to charmonium, S. Prestel who provided initial impetus to the project, and J. Zupan and M. Whitehead who gave feedback on the manuscript. Finally, we thank S. Rous for providing us with the working name Leto for this project. SM is supported by the Fermi Research Alliance, LLC under Contract No. DE-AC02-07CH11359 with the U.S. Department of Energy, Office of Science, Office of High Energy Physics. PI is supported by NSF grants OAC-2103889 and NSF-PHY-2209769. NC and LL were supported by the MCnetITN3 H2020 Marie Curie Initial Training Network, contract 722104. In addition LL is supported by Swedish Research Council, contracts numbers 2016-03291 and 2020-04869.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Code availability
This manuscript has associated code/software in a data repository. [Author’s comment: The code used for this study is an open access software package, Pythia 8, which is available in the https://gitlab.com/Pythia8/releases repository.]
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cooke, N., Ilten, P., Lönnblad, L. et al. Non-relativistic quantum chromodynamics in parton showers. Eur. Phys. J. C 84, 432 (2024). https://doi.org/10.1140/epjc/s10052-024-12760-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-024-12760-3








 splitting with
splitting with  splitting
splitting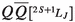 , where
, where