Towards higher-order calculations of quarkonia production with $k_T$-factorization: P-wave charmonia

Abstract

Inclusive P-wave charmonia production in hadronic collisions at high energies is discussed in the framework of non-relativistic QCD and $k_T$-factorization formalism. We present two consistent approaches to merge the usual leading order $k_T$-factorization calculations with tree-level next-to-leading order off-shell amplitudes. Using these prescriptions, we extracted long-distance matrix elements for $\chi _c$ mesons from a combined fit to available Tevatron and LHC data. In contrast to previous (leading order) calculations, our fits do not rule out the equalness of the color singlet wave functions of $\chi _{c1}$ and $\chi _{c2}$ states. The extracted values of long-distance matrix elements are employed to analyse the $\chi _c$ polarization data reported recently by the CMS Collaboration. Our predictions are in a reasonably good agreement with the Tevatron and LHC measurements within the theoretical and experimental uncertainties.

1 Introduction

Up to now, the production of heavy quarkonia (charmonia and bottomonia) in high energy hadronic collisions is under intense theoretical and experimental study [1,2,3]. It provides a sensitive tool probing Quantum Chromodynamics (QCD) in both perturbative and non-perturbative regimes, as the production mechanism involves both short and long distance interactions. A rigorous framework for the description of heavy quarkonia production is the non-relativistic QCD (NRQCD) [4,5,6], which is based on a double series expansion of perturbation theory in the strong coupling $\alpha _s$ and the relative velocity between the two constituent heavy quarks v. In this way, the perturbatively calculated cross sections for the short distance production of a heavy quark pair $Q\bar{Q}$ in an intermediate Fock state $^{2\,S + 1}L_J^{[a]}$ with spin S, orbital angular momentum L, total angular momentum J and color representation a (singlet, $a = 1$, or octet, $a = 8$) are accompanied with long distance matrix elements (LDMEs) which describe the subsequent non-perturbative transition of the intermediate $Q\bar{Q}$ pair into a physical meson via soft gluon radiation. Treating the soft transition probabilities as free parameters in the framework of collinear factorization approach at the next-to-leading order (NLO), a good description has been achieved for the charmonia ($J/\psi$, $\psi ^\prime$, $\chi _c$) and bottomonia ($\Upsilon$, $\chi _b$) transverse momentum distributions (see, for example [7,8,9,10,11,12,13] and [14,15,16,17,18,19], respectively). A possible solution to a long-standing problem known in the literature as the “Polarization Puzzle” [20,21,22] and the “Heavy Quark Spin Symmetry Puzzle” [23, 24] has been recently proposed [25], that could lead to a consensus on the mechanism of quarkonium formation.¹ Also, an approximate calculation of next-to-next-to-leading order including tree-level contributions to the color-singlet mechanism in the collinear scheme has become available [31, 32].

At high energies, a large piece of tree-level NLO + NNLO +$\cdots$ corrections to the perturbative production of heavy quark pairs can be efficiently taken into account in the framework of the $k_T$-factorization [33, 34] (or high energy factorization [35, 36]) approach. These corrections correspond to the diagrams with real gluon emissions in initial state, which dominate over other possible corrections at high energies. The $k_T$-factorization approach is based on the Balitsky–Fadin–Kuraev–Lipatov (BFKL) [37,38,39] or Ciafaloni–Catani–Fiorani–Marchesini (CCFM) [40,41,42,43] evolution equations for the gluon densities in the proton. The latter are known as the Transverse Momentum Dependent (TMD) or unintegrated gluon densities. This method can be considered as a convenient alternative to explicit high-order pQCD calculations. A detailed description and discussion of the $k_T$-factorization technique can be found in the review [44]. Nowadays, it has become a widely exploited tool and, being supplemented with the NRQCD formalism, has been successfully applied to the charmonia and bottomonia production at modern colliders (see for example [45,46,47,48,49,50] and references therein). A good agreement has been obtained with the LHC data, including the polarization observables for $J/\psi$, $\psi ^\prime$ and $\Upsilon (nS)$ mesons.

However, the $k_T$-factorization fits² to the experimental data require unequal values of the color singlet wave functions for P-wave states $\chi _{c1}$ and $\chi _{c2}$. The values [45, 47] extracted from the LHC measurements may differ from each other by a factor of 2–4 (see also [51]). Analogous results have been also found for some P-wave bottomonium states, namely, $\chi _{b1}(1P)$ and $\chi _{b2}(1P)$ mesons [50]. These results are at variance with the Heavy Quark Spin Symmetry (HQSS) relations [4,5,6], which are valid up to $\mathcal{O}(v^2)$ accuracy. According to the HQSS relations, the properties of states with different spin momentum S are identical, so that the transition probabilities involving the color singlet wave functions and color octet LDMEs can only differ by a factor representing the number of spin degrees of freedom. The situation awaits for an explanation.

On the one hand, one can argue [45, 47, 51] that treating the charmed quarks as spinless particles in the potential models might be an oversimplification (see [52, 53]), or that the radiative corrections to the wave functions may be large (as they are known to be for $J/\psi$ meson). But, on the other hand, the inconsistency may come from the fact that the up-to-now calculations [45,46,47,48,49,50,51] were only limited to the leading order in $\alpha _s$. Thus, one can hope that after taking into account additional higher-order contributions (not encoded in the CCFM-evolved TMD gluon densities) the HQSS relations could be restored. So, the main goal of the present study is to perform the NLO calculations in the $k_T$-factorization approach and to test the corresponding predictions at the Tevatron and LHC conditions.³

A well known difficulty in this kind of calculations is to properly avoid double counting. Indeed, the same gluon emission act can be accounted twice: as a part of the initial state radiation cascade (which is described as the evolution of TMD parton density) and as a part of the hard interaction process (which is described as an explicit NLO contribution). For more discussion see the review [44] and references therein. To avoid this double counting one has to properly match the LO and NLO off-shell amplitudes. Below we will adopt for our purposes a prescription which has been consistently applied to the c-jet production [54] and to the associated $W^\pm$ or Z and heavy quark production [55] at the LHC. Such calculations for heavy quarkonia will be performed for the first time.

The paper is organized as follows. In Sect. 2 we briefly describe our theoretical framework and basic steps of our calculation. In Sect. 3 we present the numerical results and discussion. Section 4 sums up our conclusions.

2 Theoretical framework

This section provides a brief review of the $k_T$-factorization formulas for P-wave charmonia production and a short description of the calculation steps.

Our method of calculations resembles the usual NLO* scheme, though there are two points of difference. First, the true leading order in the $k_T$-factorization approach is represented by $2\rightarrow 1$ subprocesses, while in the collinear pQCD the perturbation series starts from $2\rightarrow 2$ subprocesses. Accordingly, the $2\rightarrow 2$ subprocesses are regarded as next-to-leading in the $k_T$-factorization. Second, our calculations are restricted to tree-level approximation, but in a different way than the usual NLO*. The kinematic restrictions which reject virtual and infrared corrections arise in our approach from a double-counting-exclusion (DCE) condition, which separates the LO and NLO contributions (see below). For the sake of definiteness and clarity, we hereafter will refer to this scheme as to NLO$^\dag$.

2.1 Basic formulas

Fig. 1

Feynman diagrams which represent the $2 \rightarrow 1$ contributions to charmonia production

The true leading order (LO) contributions are represented by a number of off-shell (depending on the non-zero virtualities of incoming particles) $2\rightarrow 1$ gluon-gluon fusion subprocesses resulting in the production of a $c\bar{c}$ pair in the color singlet or color octet state. These processes are of $\mathcal{O}(\alpha _s^2)$ order, in contrast with the collinear QCD factorization where the perturbative expansion starts from the $2\rightarrow 2$ subprocesses. So, we have:

$$\begin{aligned} g^*(k_1)+g^*(k_2)\rightarrow c\bar{c}\left[ \, ^3P_J^{[1]},\, ^3S_1^{[8]},\ ^1P_1^{[8]}\right] (p), \end{aligned}$$

(1)

where the four-momenta of all particles are indicated in the parentheses. Corresponding Feynman diagrams are shown in Fig. 1. The color octet states further evolve into real mesons by non-perturbative QCD transitions: $c\bar{c}\rightarrow \chi _{cJ}+X$ with $J=0$, 1 or 2 where X may have quantum numbers of one or several gluons. The last contribution in (1) is formally suppressed by two extra powers of the relative charmed quark velocity v; it was, however, argued [12] that it could still be non-negligible and has to be taken into consideration. The calculation of $2 \rightarrow 1$ production amplitudes (1) is straightforward (see, for example [45,46,47] and references therein for more details). Here we only mention that the polarization tensor of incoming off-shell gluons is taken in the specific BFKL form [33,34,35,36]: $\sum \epsilon _i^\mu \epsilon _i^{*\nu } = k_{iT}^\mu k_{iT}^\nu /{\textbf{k}}_{iT}^2$, where $k_{iT}^2 = k_i^2 = - {\textbf{k}}_{iT}^2$ with $i = 1, 2$. This form is also known in the literature as Collins–Ellis–Gribov trick.

The next-to-leading order (NLO) is represented by the $\mathcal{O}(\alpha _s^3)$ subprocesses shown in Fig. 2:

$$\begin{aligned} g^*(k_1)+g^*(k_2)\rightarrow c\bar{c}\left[ \, ^3P_J^{[1]},\, ^3S_1^{[8]},\ ^1P_1^{[8]} \right] (p)+g(p_g). \nonumber \\ \end{aligned}$$

(2)

The evaluation of Feynman diagrams was partly described [56]. An essential point in doing the calculations is that the initial gluon off-shellness may violate gauge invariance. To solve this problem, we follow the technique [57,58,59]. First, we start with an extended set of diagrams where the off-shell gluon lines are considered as internal lines emitted by external quark fields, while the external quark fields are on-shell. Then, we apply the eikonal approximation for the emission of gluons, and this allows us to absorb the contributions from non-factorizable diagrams into factorizable ones, by means of modifying the expressions for three- and four-gluon couplings.⁴ Namely, the diagrams of the type $b'$ and $b''$ can be absorbed into the diagrams of the type b; the diagrams of the type $c'$ and $d'$ can be absorbed into the diagrams of the type c and d, respectively, and so on. The explicit expressions for the modified three- and four-gluon vertices $G_L$, $G_R$, $G_C$ and $G_4$ are presented [60]. So, for the gluons having the momenta $k_1$, $k_2$, $k_3$, $k_4$ and the respective colors a, b, c, d these vertices read:

$$\begin{aligned}{} & {} G_{abc}^{\mu \nu \lambda }(k_1,k_2,k_3) = g f_{abc}\left[ (k_2^\lambda - k_1^\lambda ) g^{\mu \nu } + (k_3^\mu - k_2^\mu ) g^{\nu \lambda } \right. \nonumber \\{} & {} \quad \left. + (k_1^\nu - k_3^\nu ) g^{\lambda \mu } \right] , \end{aligned}$$

(3)

$$\begin{aligned}{} & {} G_{L\,abc}^{\epsilon _1\nu \lambda }(k_1,k_2,k_3) = G_{abc}^{\epsilon _1\nu \lambda }(k_1,k_2,k_3) - g f_{abc} {\epsilon _1^\nu \epsilon _1^\lambda k_1^2 \over (\epsilon _1 k_3)}, \end{aligned}$$

(4)

$$\begin{aligned}{} & {} G_{R\,abc}^{\mu \epsilon _2\lambda }(k_1,k_2,k_3) = G_{abc}^{\mu \epsilon _2\lambda }(k_1,k_2,k_3) - g f_{abc} {\epsilon _2^\mu \epsilon _2^\lambda k_2^2 \over (\epsilon _2 k_3)}, \end{aligned}$$

(5)

$$\begin{aligned}{} & {} G_{C\,abc}^{\epsilon _1\epsilon _2\lambda }(k_1,k_2,k_3) = G_{abc}^{\epsilon _1\epsilon _2\lambda }(k_1,k_2,k_3)\nonumber \\{} & {} \quad + 2g f_{abc} \left[ {\epsilon _1^\lambda k_1^2 \over (\epsilon _1 k_2)} - {\epsilon _2^\lambda k_2^2 \over (\epsilon _2 k_1)} \right] , \end{aligned}$$

(6)

$$\begin{aligned}{} & {} G_{4\,abcd}^{\epsilon _1\epsilon _2\lambda \sigma }(k_1,k_2,k_3,k_4) = ig^2 f_{abr}f_{cdr}\left[ \epsilon _1^\sigma \epsilon _2^\lambda - \epsilon _1^\lambda \epsilon _2^\sigma \right] \nonumber \\{} & {} \quad + ig^2 f_{adr}f_{bcr}\nonumber \\{} & {} \quad \times \left[ \epsilon _1^\lambda \epsilon _2^\sigma - (\epsilon _1 \epsilon _2) g^{\lambda \sigma } -\frac{2k_2^2\epsilon _2^\sigma \epsilon _2^\lambda }{(\epsilon _2 k_3)(\epsilon _2 k_1)} - \frac{2k_1^2 \epsilon _1^\sigma \epsilon _1^\lambda }{(\epsilon _1 k_4)(\epsilon _1 k_2)}\right] \nonumber \\{} & {} \quad + ig^2 f_{acr}f_{dbr}\nonumber \\{} & {} \quad \times \left[ (\epsilon _1 \epsilon _2) g^{\lambda \sigma } - \epsilon _1^\sigma \epsilon _2^\lambda - \frac{2k_1^2 \epsilon _1^\sigma \epsilon _1^\lambda }{(\epsilon _1 k_3)(\epsilon _1 k_2)} - \frac{2k_2^2 \epsilon _2^\sigma \epsilon _2^\lambda }{(\epsilon _2 k_4)(\epsilon _2 k_1)}\right] ,\nonumber \\ \end{aligned}$$

(7)

where $f_{abc}$ are the SU(3) structure constants. The quantities

$$\begin{aligned} \epsilon _i^\mu = p_i^\mu x_i/|{\textbf{k}}_{iT}| \end{aligned}$$

(8)

play the role of incoming gluon polarization vectors; here $p_i^\mu$ are the initial proton momenta, $x_i$ are the gluon longitudinal momentum fractions and $k_{iT}$ are the (non-zero) gluon transverse momenta. The above effective vertices ensure the gauge invariance of the whole set of amplitudes despite the incoming gluons are off-shell.

Some of the diagrams can be interpreted in terms of gluon fragmentation: the diagram Fig. 2b refers to leading-order color-singlet fragmentation and the diagrams Fig. 2e, g, h represent color-octet fragmentation. These diagrams cannot be separated from all other diagrams for the reason of gauge invariance. However, if the interference between the ’fragmentation’ and ’non-fragmentation’ diagrams becomes small (which is the case at very large transverse momenta) the class of fragmentation diagrams can be considered separately, and the entire process can then be divided into hard scattering partonic subprocess and the so called single-parton fragmentation. Factorization of this kind [61,62,63,64,65,66,67,68,69,70,71] provides much convenience in simplifying the calculations and extending them to higher orders. The accuracy of the corresponding parton fragmentation function can be improved by including radiative corrections up to infinitely high order (by the means of evolution equation like DGLAP or BFKL).⁵

The limitations of single-parton fragmentation mechanism are connected to the fact that the interference between ’fragmentation’ and ’non-fragmentation’ diagrams may stay important up to rather large $p_T$. A dedicated study made for the charmed quark fragmentation [73, 74] shows that the fragmentation mechanism in its pure form becomes only valid not earlier than at $p_T\ge$ 40 GeV. However, these estimates do not promptly apply to gluons; the situation changes from process to process and every time requires a dedicated consideration.

Fig. 2

Feynman diagrams which represent the $2 \rightarrow 2$ contributions to charmonia production

The production amplitudes contain projection operators [75,76,77,78,79] which discriminate the spin-singlet and spin-triplet $c\bar{c}$ states:

$$\begin{aligned} \Pi _0= & {} {1\over (2m_c)^{3/2}} (\hat{p}_{\bar{c}} - m_c) \gamma _5 (\hat{p}_{c} + m_c), \nonumber \\ \Pi _1= & {} {1\over (2m_c)^{3/2}} (\hat{p}_{\bar{c}} - m_c) \hat{\epsilon }(S_z) (\hat{p}_{c} + m_c), \end{aligned}$$

(9)

where $m_c$ is the charmed quark mass, $p_c$ and $p_{\bar{c}}$ are the charmed quark and antiquark momenta, $p_{c} = p/2 + q$ and $p_{\bar{c}} = p/2 - q$. States with different projections of the spin momentum onto the z axis are represented by the polarization four-vector $\epsilon (S_z)$, and the relative momentum q of the quarks in a bound state is associated with the orbital angular momentum L. According to the general formalism [75,76,77,78,79], the terms showing no dependence on q are identified with the contributions to the $L = 0$ states while the terms linear in q are related to the $L = 1$ states with the polarization vector $\epsilon (L_z)$. The states with definite projections of the spin and orbital momenta $S_z$ and $L_z$ can be translated into states with definite total angular momentum $J_z$ (that is, the real mesonic states $\chi _{c0}$, $\chi _{c1}$, $\chi _{c2}$) through Clebsch–Gordan coefficients.

The analytical expressions for $2 \rightarrow 2$ off-shell matrix elements were obtained using the algebraic manipulation system form [80]. We have checked that in the on-shell limit we recover the well-known results [81].

To describe non-perturbative transitions of the color-octet $c\bar{c}$ pairs into real final state mesons we employ an approach [25] based on classical multipole radiation theory; the soft gluon emission amplitudes are taken identical to the ones describing real radiative transitions $\psi (2\,S)\rightarrow \chi _J+\gamma$ or $\chi _J\rightarrow J/\psi +\gamma$. This approach results in a good description of the available LHC data on charmonia and bottomonia polarizations (see [45,46,47,48,49,50] for more details).

According to the $k_T$-factorization prescription [33,34,35,36], the cross section of the considered processes is calculated as a convolution of the off-shell production amplitude $\bar{|\mathcal{A}|^2}$ and TMD gluon densities in a proton, $f_g(x, {\textbf{k}}_T^2, \mu ^2)$. Thus, the cross sections for the $2 \rightarrow 1$ and $2 \rightarrow 2$ subprocesses (1) and (2) can be written as:

$$\begin{aligned} \sigma _{2 \rightarrow 1}= & {} \int {2 \pi \over x_1 x_2 s F} f_g(x_1, {\textbf{k}}_{1T}^2, \mu ^2) f_g(x_2, {\textbf{k}}_{2T}^2, \mu ^2) \nonumber \\{} & {} \times |\mathcal{\bar{A}}|^2_{2 \rightarrow 1} \, d{\textbf{k}}_{1T}^2 d{\textbf{k}}_{2T}^2 dy {d\phi _1 \over 2\pi } {d\phi _2 \over 2\pi }, \end{aligned}$$

(10)

$$\begin{aligned} \sigma _{2 \rightarrow 2}= & {} \int {1 \over 8\pi (x_1 x_2 s) F} f_g(x_1, {\textbf{k}}_{1T}^2, \mu ^2) f_g(x_2, {\textbf{k}}_{2T}^2, \mu ^2)\nonumber \\{} & {} |\mathcal{\bar{A}}|^2_{2\rightarrow 2} d{\textbf{p}}_{T}^2 d{\textbf{k}}_{1T}^2 d{\textbf{k}}_{2T}^2 dy dy_g {d\phi _1 \over 2\pi } {d\phi _2 \over 2\pi }, \nonumber \\ \end{aligned}$$

(11)

where $\phi _1$ and $\phi _2$ are the azimuthal angles of the initial off-shell gluons, $p_T$ and y are the transverse momentum and rapidity of the produced $\chi _c$ meson, $y_g$ is the rapidity of the outgoing gluon, $\sqrt{s}$ is the pp center-of-mass energy, $\mu$ is the hard interaction scale and $F = 2\lambda ^{1/2}(\hat{s}, k_1^2, k_2^2)$ is the flux factor,⁶ where $\hat{s} = (k_1 + k_2)^2$ [83]. The necessary matching procedure for $2 \rightarrow 1$ and $2 \rightarrow 2$ contributions is discussed below.

2.2 TMD gluon densities in a proton

For the TMD gluon densities in a proton, we have tried two recent sets, referred to as LLM’2022 [84] and JH’2013 set 2 [85], and a rather old set A0 [86]. All these gluon densities are obtained from a numerical solution of the CCFM equation (at the leading logarithmic approximation, LLA) and are widely used in phenomenological applications (see, for example [87,88,89,90,91] and references therein). The parameters of (rather empirical) input distributions employed in the JH’2013 and A0 sets were derived from a fit to the HERA data on the proton structure functions $F_2(x, Q^2)$ and $F_2^c(x, Q^2)$ at small x. An analytical expression for the seed TMD gluon density in the very recent LLM’2022 set was suited to the best description of the LHC data on the charged hadron production at low transverse momenta $p_T \sim 1$ GeV in the framework of modified soft quark-gluon string model [92, 93], with taking into account the gluon saturation effects, which are important at low scales. Some phenomenological parameters were derived from the LHC and HERA data on several hard QCD processes (see [84] for more information). All these TMD gluon densities are available from the far-famed tmdlib package [94], which is a C$++$ library providing a framework and an interface to the different parametrizations.⁷

2.3 Numerical parameters

Following [96], we set the meson masses to $m(\chi _{c1}) = 3.51$ GeV, $m(\chi _{c2}) = 3.56$ GeV, $m(J/\psi ) = 3.096$ GeV and branching fractions $B(\chi _{c1} \rightarrow J/\psi + \gamma ) = 33.9$%, $B(\chi _{c2} \rightarrow J/\psi + \gamma ) = 19.2$% and $B(J/\psi \rightarrow \mu ^+\mu ^-) = 5.961$%. We use the one-loop expression for the QCD coupling $\alpha _s$ with $n_f = 4$ quark flavours at $\Lambda _\textrm{QCD} = 250$ MeV for A0 gluon density, and the two-loop expression for $\alpha _s$ with $n_f = 4$ and $\Lambda _\textrm{QCD} = 200$ MeV for LLM’2022 and JH’2013 set 2 densities. Our default choice for the renormalization scale $\mu _R$ is the transverse mass of the produced meson. The factorization scale $\mu _F$ was set to $\mu _F^2 = \hat{s} + {\textbf{Q}}_T^2$, where ${\textbf{Q}}_T$ is the net transverse momentum of the initial off-shell gluon pair. The choice of $\mu _R$ is rather standard for charmonia production, while the choice of $\mu _F$ is specific for CCFM evolution (see [40,41,42,43]). The definition of $\mu _F$ comes from the kinematics of gluon radiation or, more precisely, from the gluon angular ordering which is an inherent feature of CCFM evolution. The quantity $\hat{s}+{\textbf{Q}}_T^2$ describes the phase space available for the (angular ordered) gluon radiation; is sets the upper bound both for the emitted and exchanged transverse momentum. As it was mentioned above, the TMD gluon densities used in our present study were found as a numerical solution to the CCFM equation, where the initial (boundary) conditions were fitted to obtain the best description of the collider data. The entire fitting procedure was carried out based on the definition of $\mu _F$ given above. So, our choice was dictated by observing compatibility with the method of deriving the gluon density.

Using a different definition of $\mu _F$, a reasonable description of the data can also be achieved, but the parameters of the starting distribution would change significantly (see Table 1 in [86]). In fact, it means that varying $\mu _F$ requires just redoing the fit. We thus conclude that the definition of $\mu _F$ should be considered as an inherent part of the gluon distribution function, rather than free parameter subject to variations.⁸

2.4 Matching the $2 \rightarrow 1$ and $2 \rightarrow 2$ contributions

We now discuss the procedure for matching the $2\rightarrow 1$ and $2\rightarrow 2$ contributions, which is necessary to avoid the double counting mentioned above. The proper treatment is not an easy task since there is a lack of well established theoretical techniques. Our approach is mainly based on a prescription applied earlier [54, 55]. The main idea is to include the $2 \rightarrow 2$ contributions with certain limitations, so that to exclude the terms already taken into account as part of the CCFM evolution of gluon densities. Below we consider two possible matching scenarios.

2.4.1 Scenario A

This scenario is based on the notion that the emission of high-$p_T$ gluons is mainly due to hard parton interaction, while the emission of softer gluons can be included in the TMD gluon density. Within the proposed scheme, we sum together the $2\rightarrow 1$ and $2\rightarrow 2$ contributions, taking the $2\rightarrow 1$ subprocess without any restrictions, but put constraints on the CCFM evolution in the case of $2\rightarrow 2$ subprocess.

On the average, the transverse momenta of the gluons emitted during the evolution decrease from the hard interaction block to the proton. Assuming that the gluon emitted at the last evolution step compensates the whole transverse momentum of the gluon participating in the hard subprocess, we introduce a double-counting-exclusion (DCE) cut: $|{\textbf{p}}_{gT}| > \max (|{\textbf{k}}_{1T}|, |{\textbf{k}}_{2T}|)$. It excludes the terms generated by the CCFM evolution (explicitly presented in the $2 \rightarrow 1$ contributions) and ensures that hardest gluon emission in the $2 \rightarrow 2$ events comes from the hard matrix element. The evolution scale in the $2 \rightarrow 2$ subprocesses has to be shifted to the produced meson transverse mass, $\mu _F^2 \rightarrow m_T^2$, that corresponds to the standard evolution scale used in the $2 \rightarrow 1$ subprocesses. So, in this way the leading ($2 \rightarrow 1$) and next-to-leading ($2 \rightarrow 2$) contributions can be consistently summed together without double counting.

Fig. 3

Feynman diagrams for $\chi _c$ production via $^3P^{[1]}_J$ intermediate state in a $2\rightarrow 2$ subprocess (b), which is partially covered by a $2\rightarrow 1$ subprocess (a). The boxes represent multiple gluon emissions generated by the CCFM evolution

2.4.2 Scenario B

This scenario is based on the observation that only certain sets of $2 \rightarrow 2$ diagrams for some terms can contribute to the double counting. For example, the final state gluon emitted from the quark line is not taken into account in the terms generated by the CCFM evolution neither in $2 \rightarrow 2$ nor $2 \rightarrow 1$ subprocesses, see Figs. 1 and 2. It is clear that such contributions cannot be a source of double counting but nevertheless fall under the limitations of scenario A. Here we try more target restrictions mainly addressed to these diagrams. It could allow us to avoid the double counting without imposing significant restrictions for the rest ones.

Let us consider $^3P_J^{[1]}$ production mechanism. It is well known that taking the BFKL form for off-shell gluon polarization tensor sends to zero the contribution from non-factorizable $2 \rightarrow 2$ diagrams shown in Fig. 2. Only two of the remaining diagrams (namely, the diagrams of the type c and d) find themselves in the corresponding $2 \rightarrow 1$ terms supplemented with additional gluon emissions in the CCFM evolution cascade, see Fig. 3. To avoid relevant double counting one can limit the integration over the transverse momenta of the incoming off-shell gluons in the $2 \rightarrow 1$ subprocess from above with some value $k_T^\textrm{cut}$. At the same time, only the events with minimal gluon propagator $\sqrt{t} = \min \{ (k_1 - p_g)^2, (k_2 - p_g)^2 \}^{1/2}$ larger than the cut scale $k_T^\textrm{cut}$ are accepted when calculating the $2 \rightarrow 2$ contributions. The exact $k_T^\textrm{cut}$ value could be determined from the continuously merged $d\sigma _{2 \rightarrow 1}/dq_T$ and $d\sigma _{2 \rightarrow 2}/d \sqrt{t}$ distributions, where $q_T$ is the transverse momentum of any initial gluon in the $2 \rightarrow 1$ subprocess (see below). In this way one can also almost avoid the double counting region.⁹ So that, we propose the following merging scheme:

$$\begin{aligned} \circ&2\rightarrow 1&\left\{ \begin{aligned}&P = 1/2: k_{1T}< k^{cut }_{T},\ k_{2T} \; no cuts ; \\ {}&P = 1/2: k_{2T} < k^{cut }_{T},\ k_{1T} \; no cuts \end{aligned}\right. \nonumber \\ \circ&2\rightarrow 2&: \sqrt{t} > k^{cut }_{T} \end{aligned}$$

(12)

where the probabilities $P = 1/2$ are due to the symmetry of diagrams shown in Fig. 3.

Here we note that final state gluon, produced in the hard $2 \rightarrow 2$ subprocess, should resolve the charmed quark and antiquark before they form the intermediate Fock state. Therefore, it’s wavelength should be less than the typical transverse size of the latter. This requirement leads to a simple condition: $E_g^* > m_{c\bar{c}} v_c$, where $E_g^*$ is the emitted gluon energy (in the charmonium rest frame), $m_{c\bar{c}}$ is the mass of produced $c\bar{c}$ state and $v_c^2 \sim 0.23$ [4,5,6] is the relative velocity of the charmed quarks. Condition above preserve us from the collinear divergencies which originate when the final state gluon is emitted close to the charmed quark.¹⁰

Note also that the proposed scheme cannot be applied for intermediate $^3S_1^{[8]}$ state due to a presence of non-factorizable diagrams with two t-channel gluons (type e and f diagrams, Fig. 2). So, for this case we will exploit scenario A.

2.4.3 Determination of $k_T^\textrm{cut}$ and role of NLO$^\dag$ corrections

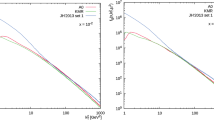
As it was mentioned above, a reasonable choice for $k_T^\textrm{cut}$, which is an essential part of scenario B, can be provided by the touch (meeting) point of the $d\sigma _{2 \rightarrow 1}/dq_T$ and $d\sigma _{2 \rightarrow 2}/d \sqrt{t}$ spectra. We perform these calculations in the rapidity region $|y(\chi _{cJ})| < 2.5$, which is close to the experimental conditions of the CMS and ATLAS Collaborations at the LHC. Our results for both color singlet states, $^3P^{[1]}_1$ and $^3P^{[1]}_2$, are shown in Fig. 4, where the dotted vertical line specifies the $k_{T}^\textrm{cut}$ value. So, for the selected phase space, the following values were obtained: $k_{T}^\textrm{cut} = 5.8\, (6.8)\,\textrm{GeV}$ for $^3P^{[1]}_1$ state and $k_{T}^\textrm{cut} = 0.7\, (0.9)\,\textrm{GeV}$ for $^3P^{[1]}_2$ state at $\sqrt{s} = 7\,(13)$ TeV. The difference in the $k_{T}^\textrm{cut}$ values for $^3P^{[1]}_1$ and $^3P^{[1]}_2$ states can be mainly attributed to the different behaviour of the corresponding production amplitudes at low transverse momenta.

It is important to note that the matched $2 \rightarrow 1$ and $2 \rightarrow 2$ cross sections very weakly depend on the exact $k_{T}^\textrm{cut}$ values. In fact, some reasonable variation in $k_{T}^\textrm{cut}$ by $\pm \,0.5$ GeV around its central value (pink bands in Fig. 4) results in a negligible difference in the LO $+$ NLO$^\dag$ predictions, as it will be demonstrated below. Thus, the uncertainties connected with the $k_{T}^\textrm{cut}$ choice are rather small and can be safely neglected in comparison with the ones coming, for example, from the standard scale variations.

Fig. 4

Matching the $d\sigma _{2\rightarrow 1}/dq_{T}$ and $d\sigma _{2\rightarrow 2}/d\sqrt{t}$ spectra for color singlet $^3P^{[1]}_1$ (right panel) and $^3P^{[2]}_1$ (left panel) in the central rapidity region $|y| < 2.5$ at $\sqrt{s} = 7$ and 13 TeV. The JH’2013 set 2 gluon density is used. Shaded pink bands represent a $\pm \,0.5$ GeV variation in the $k_T^\textrm{cut}$ values

Now we turn to a numerical comparison between the different merging scenarios and to a comparison of the LO $+$ NLO$^\dag$ predictions with the pure LO calculations. The $^3P^{[1]}_{J}$ and $^3S^{[8]}_{1}$ contributions are separately shown in Fig. 5 as functions of the produced $\chi _{cJ}$ meson transverse momentum for $\sqrt{s} = 7$ and 13 TeV. We find that the difference between the merging scenarios becomes well pronounced at large transverse momenta $p_T(\chi _{cJ})$, while both scenarios A and B lead to close results for $^3P^{[1]}_{J}$ spectra in the region of relatively low $p_{T}(\chi _{cJ}) < 20$ GeV. The difference observed at high $p_T(\chi _{cJ})$ can probably be attributed to the role of diagrams where gluons are emitted from the quark line. In the scenario A, such diagrams are suppressed by the DCE cut, while they are taken into account in the scenario B. The difference between the LO and LO $+$ NLO$^\dag$ predictions for the $^3P^{[1]}_{2}$ spectra in the scenario A is rather small.

Fig. 5

A comparison between the differential cross sections for $\chi _{c1}$ mesons produced in the $^3P^{[1]}_{1}$ channel (left panel), $\chi _{c2}$ mesons produced in the $^3P^{[1]}_2$ (right panel) and $^3S^{[8]}_1$ states (lower panel) in the central rapidity region $|y(\chi _{cJ})| < 2.5$ at $\sqrt{s} = 7$ and 13 TeV ($\times 100$) for merging scenarios A and B, and pure LO calculations. The shaded pink band represents the uncertainties coming from $k_{T}^\textrm{cut}$ variations indicated in Fig. 4. The LDMEs are taken from Table 1

3 Numerical results

In this section, we present the results of our calculations and perform a comparison with available Tevatron and LHC data. In contrast with previous calculations [45, 47], we preserve here the HQSS relations for the color singlet and color octet LDMEs:

$$\begin{aligned} \langle \mathcal {O}^{\chi _{cJ}}[^3P^{[1]}_{J}]\rangle= & {} 6N_c(2J+1)\,\frac{|\mathcal {R}^{'\chi _{c0}}(0)|^2}{4\pi }, \nonumber \\ \langle \mathcal {O}^{\chi _{cJ}}[^3S^{[8]}_1]\rangle= & {} (2J+1)\,\langle \mathcal {O}^{\chi _{c0}}[^3S^{[8]}_1]\rangle , \end{aligned}$$

(13)

where $|\mathcal {R}^{'\chi _{c0}}(0)|^2 = 0.075$ GeV$^5$ is the squared derivative of the $\chi _c$ color singlet wave function at the origin [52, 53]. The value of the color octet LDME, $\langle \mathcal {O}^{\chi _{c0}}[^3\,S^{[8]}_1]\rangle$, was extracted from a simultaneous best fit to the Tevatron and LHC data under the requirement that it should be positive. This requirement follows from the approach [25] used to describe the transitions of a color octet $c\bar{c}$ pair into a final state meson. We use the following data sets: ATLAS measurements of the $\chi _{c1}$ and $\chi _{c2}$ transverse momentum distributions at $\sqrt{s} = 7$ TeV [97] and CDF data on the $\chi _{c1} + \chi _{c2}$ combined spectra measured at $\sqrt{s} = 1.8$ TeV as functions of the $J/\psi$ transverse momentum after the radiative decay $\chi _c\rightarrow J/\psi +\gamma$ [98]. The results of our global fit and the corresponding ${\chi }^{2}/\mathrm{n.d.f.}$ values for different TMD gluon densities in a proton are collected in the Table 1. The LDMEs derived through the merging scenarios A and B differ from each other. However, for the A0 and LLM’2022 gluon distributions they more or less coincide within the fit uncertainties.

In both scenarios, the derived LDME values dramatically differ from the ones obtained in collinear calculations. So, for example, the value $\langle \mathcal {O}^{\chi _{c0}}[^3\,S^{[8]}_1]\rangle = 2.01 \cdot 10^{-3}$ GeV$^3$ was derived in the NLO NRQCD fit [13]. This is because collinear pQCD and $k_T$-factorization collect somewhat different contributions from higher order corrections (the so called large logarithms). Namely, the terms proportional to $\alpha _s^n \ln ^n(1/x)$ and $\alpha _s^n \ln ^n(\mu ^2/\Lambda _\textrm{QCD}^2)\ln ^n(1/x)$ (summed up to infinitely large n) are only present in the $k_T$-factorization, but not in collinear pQCD. The absolute normalization of these contributions is arbitrary (because of uncalculable LDME values) and so, the lack of certain contributions in collinear pQCD needs to be compensated by larger LDME’s. The difference between the fitted LDME’s indicates that the missed contributions are important.

Table 1 The fitted values of LDME’s $\langle \mathcal {O}^{\chi _{c0}}[^3\,S^{[8]}_1]\rangle /\textrm{GeV}^3$

Fig. 6

Differential cross sections for prompt $\chi _{c1}$ (upper panels) and $\chi _{c2}$ (lower panels) production in pp collisions at $\sqrt{s} = 7$ TeV as functions of the $\chi _{c}$ transverse momentum. The kinematic cuts are described in the text. The ATLAS data are taken from [97]

Fig. 7

Differential cross sections for prompt $\chi _{c1}$ (upper panels) and $\chi _{c2}$ (lower panels) production in pp collisions at $\sqrt{s} = 7$ TeV as functions of the decay $J/\psi$ transverse momentum. The kinematic cuts are described in the text. The ATLAS data are taken from [97]

Fig. 8

Differential cross section of prompt $\chi _{c}$ production in $p\bar{p}$ collisions at $\sqrt{s} = 1.8$ TeV as function of the decay $J/\psi$ transverse momentum. The kinematic cuts are described in the text. The CDF data are taken from [98]

Fig. 9

Different contributions to the $\chi _{c1}$ (upper panels) and $\chi _{c2}$ (lower panels) production cross sections in pp collisions at $\sqrt{s} = 7$ TeV. The JH’2013 set 2 gluon density is used. The kinematic cuts are described in the text. Blue shaded bands represent the uncertainties in the $\langle \mathcal {O} ^3\,S^{[8]}_1 \rangle$ determination (see Table 1). The ATLAS data are taken from [97]

Fig. 10

The ratio of the production rates $\sigma (\chi _{c2})/\sigma (\chi _{c1})$ calculated at $\sqrt{s} = 7$ TeV as function of the decay $J/\psi$ transverse momentum. The ATLAS and CMS data are taken from [97, 99]

The transverse momentum distributions of $\chi _c$ mesons obtained with the fitted LDMEs are shown in Figs. 6, 7 and 8. Individual contributions to the calculated cross sections from the considered production mechanisms are separately shown in Fig. 9. The shaded orange bands represent the estimated theoretical uncertainties for JH’2013 set 2 gluon density. The latter contain the uncertainties in the $\langle \mathcal {O} ^3S^{[8]}_1 \rangle$ determination (see Table 1) and scale uncertainties estimated by varying the renormalization scale within a factor of two, $\mu _R \rightarrow 2\mu _R$ and $\mu _R \rightarrow \mu _R/2$ through replacing the JH’2013 set 2 gluon with JH’2013 set 2$+$ or with JH’2013 set 2−, respectively (see [85] for more details). One can see that our predictions are in a reasonably good agreement with measured $\chi _c$ spectra within the theoretical and experimental uncertainties. However, we find that scenario B provides somewhat better description of the ATLAS data in comparison with scenario A, where contributions from the $^3S_1^{[8]}$ terms play more important role (see Fig. 9). In fact, scenario A leads to some underestimation of the measured $\chi _{c1}$ spectra and slight overestimation of the $\chi _{c2}$ data. This immediately results in an overestimation of the $\sigma (\chi _{c2})/\sigma (\chi _{c1})$ production rates, whereas the predictions of scenario B are more close to the data, as it is demonstrated in Fig. 10. The $\sigma (\chi _{c2})/\sigma (\chi _{c1})$ ratio is found to be sensitive to the TMD gluon density in a proton, and a reasonable description is achieved with JH’2013 set 2 gluon. The CDF measurements are described well by both merging scenarios, although the old A0 gluon distribution tends to overestimate the data in scenario A.

Additionally, in Figs. 6, 7, 8, 9 and 10 we show the results provided by the pure $2 \rightarrow 1$ calculations where the HQSS relations (13) are taken into account.¹¹ One can see that such calculations lead to an unsatisfactory description of the data.¹² In particular, the incorrect shapes of the $p_T$ distributions and noticeably overestimated $\chi _c$ relative production rates are observed, see Fig. 10. The inclusion of NLO$^\dag$ terms significantly improves the overall agreement with the data in both scenarios and also leads to a good description of the measured $\sigma (\chi _{c2})/\sigma (\chi _{c1})$ ratio in scenario B. Therefore, the previously stated violation of the HQSS relations for $\chi _c$ mesons [45, 47, 51] can be explained by the absence of higher-order corrections in the $\mathcal{O}(\alpha _s^2)$ off-shell amplitudes.

Next, the extracted LDMEs are employed to investigate the polarization of $\chi _{c1}$ and $\chi _{c2}$ mesons. We compare our predictions with the first results reported by the CMS Collaboration at $\sqrt{s} = 8$ TeV [100], which have established certain correlations between the polarization parameters $\lambda ^{\chi _{c1}}_{\theta }$ and $\lambda ^{\chi _{c2}}_{\theta }$. The data were collected in the $J/\psi$ rapidity range $|y^{J/\psi }| < 1.2$ for three subdivisions of $p_T$, namely, $8< p^{J/\psi }_{T} < 12$ GeV, $12< p^{J/\psi }_{T} < 18$ GeV and $18< p^{J/\psi }_{T} < 30$ GeV. The muon angular distribution is conventionally parametrized (in the $J/\psi$ helicity frame) as

$$\begin{aligned}{} & {} {d\sigma (J/\psi \rightarrow \mu \mu )\over d\cos \theta ^*\,d\phi ^*}\sim {1\over 3+\lambda _\theta } \nonumber \\{} & {} \quad \times \left( 1+\lambda _\theta \cos ^2\theta ^*+\lambda _\phi \sin ^2\theta ^*\cos 2\phi ^*\right. \nonumber \\{} & {} \quad \left. +\lambda _{\theta \phi }\sin 2\theta ^*\cos \phi ^* \right) , \end{aligned}$$

(14)

where $\theta ^*$ and $\phi ^*$ are the positive muon polar and azimuthal angles, so that the $\chi _{cJ}$ angular momentum is encoded in the polarization parameters $\lambda _\theta$, $\lambda _\phi$ and $\lambda _{\theta \phi }$. A simple correlation between the $\lambda _{\theta }^{\chi _{c1}}$ and $\lambda _{\theta }^{\chi _{c2}}$ parameters was determined in the CMS analysis [100]:

$$\begin{aligned} \lambda ^{\chi _{c2}}_{\theta }= & {} (-0.94 + 0.90\lambda ^{\chi _{c1}}_{\theta })\pm (0.51 + 0.05\lambda ^{\chi _{c1}}_{\theta }),\; \nonumber \\{} & {} 8< p^{J/\psi }_{T}< 12\; \textrm{GeV}, \nonumber \\ \lambda ^{\chi _{c2}}_{\theta }= & {} (-0.76 + 0.80\lambda ^{\chi _{c1}}_{\theta })\pm (0.26 + 0.05\lambda ^{\chi _{c1}}_{\theta }),\;\nonumber \\{} & {} 12< p^{J/\psi }_{T}< 18\; \textrm{GeV}, \nonumber \\ \lambda ^{\chi _{c2}}_{\theta }= & {} (-0.78 + 0.77\lambda ^{\chi _{c1}}_{\theta })\pm (0.26+0.06\lambda ^{\chi _{c1}}_{\theta }),\;\nonumber \\{} & {} 18< p^{J/\psi }_{T} < 30\; \textrm{GeV}. \end{aligned}$$

(15)

To evaluate these parameters, we collect the events simulated in the kinematic region defined by the CMS measurement [100] and generate the decay muon angular distributions according to the production and decay matrix elements. Then we can easily determine the polarization parameters $\lambda _{\theta }^{\chi _{c1}}$ and $\lambda _{\theta }^{\chi _{c2}}$ by applying a three-parametric fit based on (14). The results of our calculations are presented in Fig. 11 for both merging scenarios A and B. It can be noted that there is fairly good agreement with the expected values of $\lambda ^{\chi _{c2}}_{\theta }$ obtained at the fixed $\lambda ^{\chi _{c1}}_{\theta }$ from (15). However, there is some discrepancy between the results obtained in scenarios A and B. One can see that a better agreement with the CMS data is achieved within the scenario A. The latter can be addressed to a different role of the LO and NLO$^\dag$ terms in these two schemes. The $2 \rightarrow 2$ contribution provide lower polarization of the $^3P^{[1]}_{J}$ mesons as compared to the $2 \rightarrow 1$ contribution.

In the merging scenario B, the NLO$^\dag$ contributions are more important (see Fig. 5), thus leading to a decrease in the overall $\chi _c$ polarization. This effect is clearly seen in the behaviour of $\lambda ^{\chi _{c1}}_{\theta }$. The LO and NLO$^\dag$ contributions to the $^3S^{[8]}_1$ channel additionally suppress the $\chi _c$ polarization with increasing transverse momentum. Our predictions for the polarization parameters $\lambda ^{\chi _{c1}}_{\theta }$ and $\lambda ^{\chi _{c2}}_{\theta }$ are almost insensitive to the choice of TMD gluon densities.

Fig. 11

Polarization parameters $\lambda ^{\chi _{c1}}_{\theta }$ and $\lambda ^{\chi _{c2}}_{\theta }$ calculated at $\sqrt{s} = 8$ TeV in the rapidity region $|y^{J/\psi }| < 1.2$ for scenario A (left panel) and scenario B (right panel). “Experimental points” represent the $\lambda ^{\chi _{c2}}_{\theta }$ values obtained from the experimentally established relations (15)

Finally, we would like to reiterate that inclusion of NLO$^\dag$ terms in the $k_T$-factorization approach enables us to strictly adhere to the HQSS rules for both color singlet and color octet channels and describe simultaneously the available Tevatron and LHC data. Both the considered merging schemes provide a decent description of the data, although the present limitations in measuring the mesons transverse momenta do not allow us to make a choice in favor of one of the scenarios.

4 Conclusion

In the present paper we have considered inclusive P-wave charmonia production in proton-proton and proton–antiproton collisions at high energies in the $k_T$-factorization QCD approach beyond the standard leading-order approximation. For the first time we have included tree-level next-to-leading contributions to corresponding production cross sections and proposed two scenarios which consistently merge the $2 \rightarrow 1$ and $2 \rightarrow 2$ off-shell production amplitudes. We have introduced and discussed special conditions which are necessary to avoid the well-known double counting problem when calculating the higher-order corrections in the $k_T$-factorization approach.

Using several CCFM-evolved gluon densities in a proton, we have extracted long-distance matrix elements for $\chi _c$ mesons from a combined fit to available Tevatron and LHC data. In contrast to previous leading order $k_T$-factorization calculations, our fits do not conflict with equalizing the color-singlet wave functions for $\chi _{c1}$ and $\chi _{c2}$ states. The previously observed violation of the HQSS relations for $\chi _c$ mesons can be explained by the absence of higher-order corrections in the corresponding $\mathcal{O}(\alpha _s^2)$ off-shell production amplitudes. Taking into account the NLO$^*$ contributions provides a way to restore the HQSS relations and to improve an overall description of the data, especially the data on the relative production rate $\sigma (\chi _{c2})/\sigma (\chi _{c1})$. Moreover, this observable is found to be sensitive to the TMD gluon density in a proton and the best description is achieved with JH’2013 set 2 gluon. Our predictions are in a good agreement also with the first measurements of the $\chi _c$ polarization at the LHC reported recently by the CMS Collaboration.

As a concluding remark we mention that our study complements recent findings regarding the polarized amplitudes [101] and production rates [102] for the forward exclusive emission of light mesons in lepto-production at HERA and the forthcoming Electron-Ion Collider. The ratio $\sigma (\chi _{c2})/\sigma (\chi _{c1})$ serves as another well-promising observable in accessing the proton structure at small x.