Electron EDM and LFV decays in the light of Muon $(g-2)_\mu$ with U(2) flavor symmetry

Abstract

We study the interplay of New Physics (NP) among the lepton magnetic moment, the lepton flavor violation (LFV) and the electron electric dipole moment (EDM) in light of recent data of the muon $(g-2)_\mu$. The NP is discussed in the leptonic dipole operator with the U(2) flavor symmetry of the charged leptons, where possible CP violating phases of the three family space are taken into account. It is remarked that the third-family contributes significantly to the LFV decay, $\mu \rightarrow e\gamma$, and the electron EDM. The experimental upper-bound on $\mu \rightarrow e\gamma$ decay gives a severe constraint on the parameters of the flavor model. The predicted electron EDM is rather large due to the CP violating phases in the three family space. In addition, we also study $(g-2)_{e,\tau }$ of the electron and tauon, and EDMs of the muon and tauon as well as the $\tau \rightarrow e \gamma$ and $\tau \rightarrow \mu \gamma$ decays. The $\tau _R \rightarrow \mu _L \gamma$ decay is predicted to be close to the experimental upper-bound.

1 Introduction

The electric and magnetic dipole moments of the electron and the muon are low-energy probes of New Physics (NP) beyond the Standard Model (SM). Recently, the muon $(g-2)_\mu$ experiment at Fermilab reported a new measurement of the muon magnetic anomaly using data collected in 2019 (Run-2) and 2020 (Run-3) [1]. The improved analysis and run condition lead to more than a factor of two reduction in the systematic uncertainties, which is compared to the E989 experiment at Fermilab [2] and the previous BNL result [3]. This result indicates a $5.1\,\sigma$ discrepancy with the SM prediction by “Muon $g-2$ Theory Initiative” [4] (see also [5,6,7,8,9,10,11,12,13,14]).

However, there is a debatable point on the precise value of the SM prediction: the problem is the contribution of the hadronic vacuum polarization (HVP). The current situation is complicated. The CMD-3 collaboration [15] released results on the cross section that disagree at the $(2.5-5) \sigma$ level with all previous measurements, including those from the previous CMD-2 collaboration. The origin of this discrepancy is currently unknown. The BMW collaboration published the first complete lattice-QCD result with subpercent precision [16]. Their result is closer to the experimental average of the muon $(g-2)_\mu$ measurements, showing only a $1.7\sigma$ preference for NP in the muon $(g-2)_\mu$. Further studies are underway to clarify these theoretical differences. The white paper (the SM prediction) is expected to be updated including the HVP problem in 2024.

If the muon $(g-2)_\mu$ anomaly is due to NP, its effect could appear in other observables of the charged lepton sector. The interesting one is the electric dipole moments (EDM) of the electron. This year, the JILA group has reported a new upper-bound on the electron EDM, which is $|d_e|<4.1 \times 10^{-30} \mathrm e\, cm \,(90\%\, { confidence})$, by using the $\mathrm Hf\, F^+$ ions trapped by the rotating electric field [17]. It overcame the latest ACME collaboration result obtained in 2018 [18]. Precise measurements of the electron EDM will be rapidly updated in the future. The future sensitivity at ACME $\mathrm I\hspace{-1.13791pt}I\hspace{-1.13791pt}I$ is expected to be $|d_e|<0.3\times 10^{-30}\,\text {e\,cm}$ [19, 20]. In contrast, the present upper-bound of the muon [21] and tauon EDM’s [22,23,24] are not so tight.

The lepton flavor violation (LFV) is also possible NP phenomena of the charged leptons. The most severe constraint on LFV is the branching ratio of the $\mu \rightarrow e\gamma$ decay. The experimental bound is $\mathcal {B}({\mu ^+ \rightarrow e^+ \gamma }) < 4.2 \times 10^{-13}$ from the MEG experiment [25]. On the other hand, the current upper-bounds for $\mathcal {B}\,({\tau \rightarrow \mu \gamma })$ and $\mathcal {B}\,({\tau \rightarrow e \gamma })$ are $4.4~ \times ~ 10^{-8}$ and $3.3~ \times ~ 10^{-8}$ [26, 27], respectively.

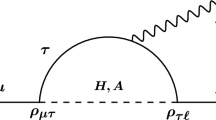
Comprehensive studies of the electric and magnetic dipole moments of leptons are given in the SM Effective Field Theory (SMEFT) [28,29,30] under the hypothesis of new degrees of freedom above the electroweak scale [31,32,33,34]. The phenomenological discussion of NP has presented taking into account the muon $(g-2)_\mu$ anomaly and the LFV bound in the SMEFT imposing $U(2)_{L_L} \otimes U(2)_{E_R}$ flavor symmetry [35], which is the maximally allowed subgroup of $U(3)_{L_L} \otimes U(3)_{E_R}$¹ acting only on the first two (light) families [38,39,40]. Since this flavor symmetry reduces the number of independent parameters of the flavor sector [41, 42], we can expect the interplay among possible NP evidence in the observables of different flavors, which is independent of the details of NP. Thus, the SMEFT with flavor symmetry can probe NP without discussing its dynamics in the flavor space.

We have already studied the interplay of NP among the muon $(g-2)_\mu$, the electron EDM and the $\mu \rightarrow e\gamma$ decay in the modular symmetry of flavors [43, 44], which is realized in the context of string effective field theory [45] (see also [46]). The results obtained are dependend on the modular weights of the charged leptons and the relevant discrete symmetry, considerably. Therefore, more general discussions are required to confirm the role of flavor symmetry in the NP search without depending on the details of the flavor model.

There are many possible discrete symmetries for the leptons flavor mixing [47,48,49,50,51,52,53,54,55,56,57]. Some of them are subgroups of continuous groups [50]. On the other hand, NP analysis of the SMEFT has been attractively performed by imposing the flavor symmetry of continuous group, especially U(2) [41, 42]. We also adopt the U(2) flavor symmetry for discussing the dipole operator of leptons to investigate NP [35]. In this paper, we present numerical discussions of the interplay of NP in light of recent data of the muon $(g-2)_\mu$ and the electron EDM by taking $U(2)_{L_L} \otimes U(2)_{E_R}$ flavor symmetry of the charged leptons. Since we discuss the electron EDM, we analyze NP in the three family space of $U(2)_{L_L} \otimes U(2)_{E_R}$ flavor symmetry, taking into account the possible CP violating phases. It is remarked that the third-family contributes significantly to the $\mu \rightarrow e\gamma$ decay and the electron EDM. In addition to the muon $(g-2)_\mu$ and the electron EDM, we also study $(g-2)_{e,\tau }$ of the electron and tauon, and EDMs of the muon and tauon as well as LFV processes $\tau \rightarrow e \gamma$ and $\tau \rightarrow \mu \gamma$.

The paper is organized as follows. In Sect. 2, we discuss the experimental constraints on the Wilson coefficients of the leptonic dipole operator. Section 3 presents our framework of the U(2) flavor model. Section 4 provides numerical discussions. The summary and discussion are devoted to Sect. 5. In Appendix A, the experimental constraints of the relevant Wilson coefficients of the leptonic dipole operator are presented. In Appendix B, the $3\times 3$ Yukawa matrices, $YY^\dagger$ and $Y^\dagger Y$, are given explicitly.

2 Constraints of Wilson coefficients of the dipole operator

2.1 Input experimental data

The combined result from the E989 experiment at Fermilab [1, 2] and the E821 experiment at BNL [3] on $a_\mu =(g-2)_\mu /2$, together with the SM prediction $a_\mu ^\textrm{SM}$ in [4], implies

$$\begin{aligned} \Delta a_\mu = a_\mu ^\textrm{Exp} - a_\mu ^\textrm{SM} = (249 \pm 49) \times 10^{-11}. \end{aligned}$$

(1)

We suppose that the contribution of NP appears in $\Delta a_\mu$.

However, the precise value of the SM prediction of HVP is still unclear. Further studies will clarify the theoretical differences. If $\Delta a_\mu$ is significantly lower, less than or of order $1\,\sigma$, one may obtain somewhat loose bound in phenomenological studies of NP [58]. In our study, we take a following reference value (the discrepancy of $5.1\,\sigma$ with the SM prediction) as the input in our numerical analysis:

$$\begin{aligned} \Delta a_\mu&= 249 \times 10^{-11}\,. \end{aligned}$$

(2)

We will comment on our result in the case that the discrepancy with the SM prediction is reduced in Sect. 5.

We also input the upper-bound of the electron EDM by the JILA group [17]:

$$\begin{aligned} |{d_e} |<4.1 \times 10^{-30} \, \mathrm e\,cm =6.3\times 10^{-14} \,TeV^{-1}\,. \end{aligned}$$

(3)

On the other hand, the upper-bound of the muon EDM is [21]:

$$\begin{aligned} |{d_\mu } |<1.8 \times 10^{-19} \, \mathrm e\,cm =2.76\times 10^{-3} \,TeV^{-1}\,. \end{aligned}$$

(4)

The tauon EDM can be evaluated through the measurement of CP-violating correlations in tauon-pair production such as $e^+e^-\rightarrow \tau ^+\tau ^-$ [22] (see also [23]). The present upper-bound on the tauon EDM $d_\tau$ is given as: [24]:

$$\begin{aligned}&-1.85\times 10^{-17}\mathrm{e\,cm}<\textrm{Re} \,d_\tau< 0.61\times 10^{-17}\mathrm{e\,cm},\ \nonumber \\&\quad -1.03\times 10^{-17}\mathrm{e\,cm}<\textrm{Im}\, d_\tau < 0.23\times 10^{-17}\mathrm{e\,cm}. \end{aligned}$$

(5)

Taking the bound of $\textrm{Re} \,d_\tau$, we have

$$\begin{aligned} |d_\tau |<1.85\times 10^{-17}\mathrm{e\,cm}=2.84\,\textrm{TeV}^{-1}\,. \end{aligned}$$

(6)

The experimental upper-bound for the branching ratio of $\mu \rightarrow e\gamma$ is [25]:

$$\begin{aligned} \mathcal {B}({\mu ^+ \rightarrow e^+ \gamma }) < 4.2 \times 10^{-13}\,. \end{aligned}$$

(7)

We also take account of the upper-bound for LFV comes from the branching ratios of $\tau \rightarrow \mu \gamma$ and $\tau \rightarrow e\gamma$ [26, 27]:

$$\begin{aligned} \mathcal {B}({\tau \rightarrow \mu \gamma })< 4.2 \times 10^{-8}\,,\quad \qquad \mathcal {B}({\tau \rightarrow e \gamma }) < 3.3 \times 10^{-8}\,. \end{aligned}$$

(8)

These input data are converted into the magnitudes of the Wilson coefficients of the leptonic dipole operator in the next subsection.

2.2 Wilson coefficients of the leptonic dipole operator

We make the assumption that NP is heavy and can be given by the SMEFT Lagrangian. Let us focus on the dipole operators of leptons and their Wilson coefficients at the weak scale as:

$$\begin{aligned}&\mathcal {O}_{\underset{LR}{e\gamma }} = \frac{v }{\sqrt{2}} {\overline{E}}_{L} \sigma ^{\mu \nu } E_{R} F_{\mu \nu }\,,\qquad \qquad \mathcal {C}_{\underset{LR}{e\gamma }}^\prime = \begin{pmatrix} \mathcal {C}_{\underset{ee}{e\gamma }}^\prime &{}\mathcal {C}_{\underset{e\mu }{e\gamma }}^\prime &{}\mathcal {C}_{\underset{e\tau }{e\gamma }}^\prime \\ \mathcal {C}_{\underset{\mu e}{e\gamma }}^\prime &{}\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime &{}\mathcal {C}_{\underset{\mu \tau }{e\gamma }}^\prime \\ \mathcal {C}_{\underset{\tau e}{e\gamma }}^\prime &{}\mathcal {C}_{\underset{\tau \mu }{e\gamma }}^\prime &{}\mathcal {C}_{\underset{\tau \tau }{e\gamma }}^\prime \\ \end{pmatrix} \,, \nonumber \\&\mathcal {O}_{\underset{RL}{e\gamma }} = \frac{v }{\sqrt{2}} {\overline{E}}_{R} \sigma ^{\mu \nu } E_{L} F_{\mu \nu }\,,\qquad \qquad \mathcal {C}_{\underset{RL}{e\gamma }}^\prime =\mathcal {C}_{\underset{LR}{e\gamma }}^{\prime \, \dagger } \,, \end{aligned}$$

(9)

where $E_L$ and $E_R$ denote three flavors of the left-handed and right-handed leptons, respectively, and v denotes the vacuum expectation value (VEV) of the Higgs field H. The prime of the Wilson coefficient indicates the flavor basis corresponding to the mass-eigenstate basis of the charged leptons. The relevant effective Lagrangian is written as:

$$\begin{aligned} \mathcal {L}_{\textrm{dipole}}= \frac{1}{\Lambda ^2}\,\left( \mathcal {C}_{\underset{LR}{e\gamma }}^\prime \mathcal {O}_{\underset{LR}{e\gamma }} +\mathcal {C}_{\underset{RL}{e\gamma }}^\prime \mathcal {O}_{\underset{RL}{e\gamma }} \right) \,, \end{aligned}$$

(10)

where $\Lambda$ is a certain mass scale of NP in the effective theory. Here the Wilson coefficient is understood to be evaluated at the weak scale (we neglect the small effect of running below the weak scale).²

Inputting the value in Eq. (2), the Wilson coefficient is obtained as [35] (see Appendix A):

$$\begin{aligned} \frac{1}{\Lambda ^2}\text {Re}\ [\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime ] = 1.0 \times 10^{-5} \, \textrm{TeV}^{-2} \,. \end{aligned}$$

(11)

The LFV process $\mu \rightarrow e \gamma$ gives us more severe constraint for the Wilson coefficient by the experimental data in Eq. (7). The upper-bound is obtained [35] (see Appendix A):

$$\begin{aligned} \frac{1}{\Lambda ^2}|\mathcal {C}_{\underset{e\mu (\mu e)}{e\gamma }}^\prime | < 2.1 \times 10^{-10} \, \textrm{TeV}^{-2} \, . \end{aligned}$$

(12)

Taking into account Eqs. (11) and (12), one has the ratio [35]:

$$\begin{aligned} \left| \frac{ \mathcal {C}_{\underset{e\mu (\mu e)}{e\gamma }}^\prime }{ \mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime }\right| < 2.1\times 10^{-5}\,. \end{aligned}$$

(13)

Thus, the magnitude of $\mathcal {C}_{\underset{e\mu (\mu e)}{e\gamma }}^\prime$ is much suppressed compared with $\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime$. This gives the severe constraint for parameters of the flavor model.

The $\tau \rightarrow \mu \gamma$ process also gives us another constraint for the Wilson coefficient by the experimental data in Eq. (8). The upper-bounds are obtained as seen in Appendix A:

$$\begin{aligned}&\frac{1}{\Lambda ^2}|\mathcal {C}_{\underset{\mu \tau (\tau \mu )}{e\gamma }}^\prime |< 2.65 \times 10^{-6} \, \textrm{TeV}^{-2} \,, \nonumber \\&\frac{1}{\Lambda ^2}|\mathcal {C}_{\underset{e\tau (\tau e)}{e\gamma }}^\prime | < 2.35 \times 10^{-6} \, \textrm{TeV}^{-2} . \end{aligned}$$

(14)

The electron EDM, $d_e$ is defined in the operator:

$$\begin{aligned} \mathcal {O}_{\textrm{edm}} = -\frac{i}{2}\,d_e(\mu ) \, {\overline{e}} \sigma ^{\mu \nu } \gamma _5 e F_{\mu \nu }\,, \end{aligned}$$

(15)

where $d_e=d_e(\mu =m_e)$. Therefore, the electron EDM is extracted from the effective Lagrangian

$$\begin{aligned} \mathcal {L}_{\textrm{EDM}}= \frac{1}{\Lambda ^2}\mathcal {C}_{\underset{ee}{e\gamma }}^\prime \mathcal {O}_{\underset{LR}{e\gamma }} + \mathrm h.c. = \frac{1}{\Lambda ^2}\mathcal {C}_{\underset{ee}{e\gamma }}^\prime \frac{v }{\sqrt{2}} {\overline{e}}_{L} \sigma ^{\mu \nu } e_R F_{\mu \nu } + \mathrm h.c.\,, \end{aligned}$$

(16)

which leads to

$$\begin{aligned} d_e=-\sqrt{2} \, \frac{v}{\Lambda ^2}\, \textrm{Im}\, [\mathcal {C}_{\underset{ee}{e\gamma }}^\prime ] \,, \end{aligned}$$

(17)

at tree level, where the small effect of running below the electroweak scale is neglected.

Inputting the experimental upper-bound of the electron EDM in Eq. (3) [17], we obtain the constraint of the Wilson coefficient:

$$\begin{aligned} \frac{1}{\Lambda ^2}{\textrm{Im}}\, [\mathcal {C}_{\underset{ee}{e\gamma }}^\prime ]<1.8\times 10^{-13}\, \mathrm {TeV^{-2}}. \end{aligned}$$

(18)

On the other hand, the experimental upper-bound of the muon EDM in Eq. (4) gives:

$$\begin{aligned} \frac{1}{\Lambda ^2}{\textrm{Im}}\, [\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime ]<7.9\times 10^{-3}\, \mathrm {TeV^{-2}}. \end{aligned}$$

(19)

Table 1 Relevant observables and the corresponding values of Wilson coefficients, which are presented in $1/\Lambda ^2\ (\textrm{TeV}^{-2})$ unit

The upper-bound of the tauon EDM in Eq. (6) also gives:

$$\begin{aligned} \frac{1}{\Lambda ^2}{\textrm{Im}}\, [\mathcal {C}_{\underset{\tau \tau }{e\gamma }}^\prime ]<8.2\times 10^{-1}\, \mathrm {TeV^{-2}}. \end{aligned}$$

(20)

Using these bounds of Wilson coefficients, we analyze the U(2) flavor model in the next section. These data are listed in Table 1.

3 U(2) flavor model

3.1 Flavor structure of Yukawa and dipole operator in charged leptons

In the lepton sector, we impose $U(2)_{L_L} \otimes U(2)_{E_R}$ flavor symmetry, which is the corresponding subgroup acting only on the first two light families. The minimal set of the breaking terms, which are so called spurions, are³

$$\begin{aligned} V_\ell \sim (\mathbf{2,\,1})\,,\qquad \Delta _e \sim (\textbf{2},\,\bar{\textbf{2}})\,. \end{aligned}$$

(21)

The two suprions can be parameterized by

$$\begin{aligned} V_\ell = \begin{pmatrix} 0\\ {\epsilon _{\ell }}\, \end{pmatrix} ,\qquad \Delta _e=O_e^T \ \begin{pmatrix} \delta '_e &{} 0\\ 0&{} \delta _e\\ \end{pmatrix}\,,\qquad O_e= \begin{pmatrix} c_e &{} s_e\\ -s_e&{} c_e\\ \end{pmatrix}\,, \end{aligned}$$

(22)

where $\delta '_e$, $\delta _e$ and $\epsilon _\ell$ are taken to be real without loss of generality, while $c_e$ and $s_e$ denote $\cos \theta _e$ and $\sin \theta _e$, respectively.

In this scheme, the flavor structure of the dipole operator has already discussed in Ref. [35]. The analysis was done in two family space with 1st-2nd- and 2nd-3rd-sector, separately. However, as will be discussed later, in the three family space, the third generation gives significant effects on the 1st-2nd sector. Discussing the flavor structure in three family space, we can present the systematic discussion of the interplay among the lepton $(g-2)_\ell$, EDMs and LFV decays. Especially, we can also discuss the EDM of the electron due to non-trivial CP phases.

Using the spurions in Eq. (22), the $3\times 3$ Yukawa coupling of leptons $Y_e$ is written in the left-right (LR) convention at order $\mathcal{O}(V_\ell ^2 \Delta _e)$ of spurion couplings:

$$\begin{aligned} Y_e= Y_{e0} \begin{pmatrix} C^y_{\Delta } (\Delta _e)_{\alpha \beta } + C^y_{VV\Delta } (V_\ell )_\alpha (V_\ell ^\dagger )_\gamma (\Delta _e)_{\gamma \beta } &{} C^y_{V} (V_\ell )_\alpha \\ C^y_{V\Delta } (V_\ell ^\dagger )_\alpha (\Delta _e)_{\alpha \beta } &{} C^y \end{pmatrix}_{LR} \, , \end{aligned}$$

(23)

where $\alpha ,\beta$ are the first or second component in Eq. (22). Next-to-leading-order spurion couplings as $C^y_{VVV}V_\ell V_\ell ^\dagger V_\ell$ and $C^y_{VV} V_\ell ^\dagger V_\ell$ can be added, but are not included here because they do not add any independent structure.

The coefficients $C^y$, $C^y_{\Delta }$, $C^y_{V}$, $C^y_{V\Delta }$ and $C^y_{VV\Delta }$

are complex parameters of order 1, and $Y_{e0}$ is a normalization factor to realize the observed tauon mass. Taking spurion parameters in Eq. (22), the Yukawa matrix is written explicitly as:

$$\begin{aligned} Y_e= Y_{e0} \begin{pmatrix} C^y_{\Delta } c_e \delta _e^\prime &{} -C^y_{\Delta } s_e \delta _e &{} 0 \\ s_e \delta _e^\prime (C^y_{\Delta }+C^n_{VV\Delta }\epsilon _\ell ^2) &{} c_e \delta _e (C^y_{\Delta }+C^y_{VV\Delta }\epsilon _\ell ^2) &{} C^y_{V} \epsilon _\ell \\ C^y_{V\Delta } (s_e \epsilon _\ell \delta _e^\prime ) &{} C^y_{V\Delta } (c_e \epsilon _\ell \delta _e) &{} C^y \end{pmatrix}_{LR} \,. \nonumber \\ \end{aligned}$$

(24)

The flavor structure of the leptonic dipole operator in Eq. (9) is given by $3\times 3$ matrix $X^{e\gamma }$. It is also given in terms of the spurion couplings like in Eq. (23) as follows:

$$\begin{aligned} X^{e\gamma }&= \begin{pmatrix} C^{e\gamma }_{\Delta } (\Delta _e)_{\alpha \beta } + C^{e\gamma }_{VV\Delta } (V_\ell )_\alpha (V_\ell ^\dagger )_\gamma (\Delta _e)_{\gamma \beta } &{}C^{e\gamma }_{V} (V_\ell )_\alpha \nonumber \\ C^{e\gamma }_{V\Delta } (V_\ell ^\dagger )_\alpha (\Delta _e)_{\alpha \beta }&{} C^{e\gamma } \end{pmatrix}_{LR} \, \nonumber \\&= \begin{pmatrix} C^{e\gamma }_{\Delta } c_e \delta _e^\prime &{} -C^{e\gamma }_{\Delta } s_e \delta _e &{} 0 \\ s_e \delta _e^\prime (C^{e\gamma }_{\Delta }+C^{e\gamma }_{VV\Delta }\epsilon _\ell ^2) &{} c_e \delta _e (C^{e\gamma }_{\Delta }+C^{e\gamma }_{VV\Delta }\epsilon _\ell ^2) &{} C^{e\gamma }_{V} \epsilon _\ell \\ C^{e\gamma }_{V\Delta } (s_e \epsilon _\ell \delta _e^\prime ) &{} C^{e\gamma }_{V\Delta } (c_e \epsilon _\ell \delta _e) &{} C^{e\gamma } \end{pmatrix}_{LR} \,, \nonumber \\ \end{aligned}$$

(25)

where $C^{e\gamma }$, $C^{e\gamma }_{\Delta }$, $C^{e\gamma }_{V}$, $C^{e\gamma }_{V\Delta }$ and $C^{e\gamma }_{VV\Delta }$ are also complex parameters of order 1. Since the Wilson coefficients in Eq. (9) are written in the mass-eigenstate basis of the charged leptons, the matrix $X^{e\gamma }$ in Eq. (25) should be transformed into the diagonal basis of Y in Eq. (24).

The eigenvalues of Yukawa matrix Y in Eq. (24) ($y_{e}\ll y_{\mu }\ll y_{\tau }$) are obtained by solving the eigenvalue equation. For the determinant and trace of $Y Y^\dagger$, one finds in the leading order:

$$\begin{aligned}&\textrm{Det}\,[Y Y^\dagger ]=y^2_{e}\, y^2_{\mu }\, y^2_{\tau } \simeq Y_{e0}^6\,|C^{y}_{\Delta }|^4 \,|C^y|^2\, c_e^4\, \delta _e^2\, { \delta '_e}^2 \,, \nonumber \\&\textrm{Tr}\,[Y Y^\dagger ]=y^2_{e}+y^2_{\mu }+y^2_{\tau } \simeq Y_{e0}^2\, |C^y|^2\,, \end{aligned}$$

(26)

where $\delta _e$ and $\delta '_e$ are much smaller than 1 to reproduce the charged lepton mass hierarchy. An expression for $y_{\mu }^2 y_{\tau }^2$ is given by the determinant of the 2-3 submatrix:

$$\begin{aligned} y_{\mu }^2\, y_{\tau }^2\simeq Y_{e0}^4\,|C^{y}_{\Delta }|^2 \,|C^y|^2\, c_e^2\, \delta _e^2\,. \end{aligned}$$

(27)

Then, one gets

$$\begin{aligned}&y_{\tau }^2\simeq Y_{e0}^2\,|C^y|^2 \,,\qquad y_{\mu }^2\simeq Y_{e0}^2\,|C^{y}_{\Delta }|^2 c_e^2\, \delta _e^2\,,\nonumber \\ {}&\qquad y_{e}^2\simeq Y_{e0}^2\,|C^{y}_{\Delta }|^2 c_e^2\, { \delta '_e}^2\,, \qquad \end{aligned}$$

(28)

which lead to

$$\begin{aligned} \frac{y_{e}^2}{y_{\mu }^2}\simeq \frac{ { \delta '_e}^2}{ \delta _e^2}\,, \qquad \frac{y_{\mu }^2}{y_{\tau }^2} \simeq \frac{ |C^{y}_{\Delta }|^2}{|C^{y}|^2}\,c_e^2\delta _e^2 \simeq \delta _e^2\,. \end{aligned}$$

(29)

These ratios indicate $\delta _e\gg \delta '_e$ to reproduce the Yukawa hierarchy of the charged leptons. Especially, ${y_{e}^2}/{y_{\mu }^2}$ is independent of other coefficients of order one.

While the magnitudes of $\delta _e$ and $\delta '_e$ can be constrained by the charged lepton Yukawa couplings, $s_e$ and $\epsilon _\ell$ cannot be determined directly.⁴ Since these parameters are the U(2) breaking ones, the most natural choice is [40, 42],

$$\begin{aligned} s_e\sim s_q\sim 0.01-0.1\,, \qquad \epsilon _\ell \sim \epsilon _q \sim 0.01-0.1\,, \end{aligned}$$

(30)

in the similar treatment of quark and lepton sectors, where $s_q$ and $\epsilon _q$ denote parameters of spurions of the quark sector.

The neutrino mass matrix was given in U(2) flavor model to reproduce observed large mixing angles of leptons in view of quark-lepton unification [61,62,63]. Also the large mixing angles have been discussed by introducing relevant spurions in U(2) and U(3) flavor model [40]. However, we do not address details of neutrino mass matrix in this work because its contribution to our result is negligibly small due to small neutrino masses.

3.2 Mass-eigenstate basis of the charged leptons

The Yukawa matrix Y in Eq. (24) is diagonalized by the unitary transformation $U_L^\dagger Y U_R$, where the unitary matrices are given in terms of $2\times 2$ orthogonal matrices and phase matrices:

$$\begin{aligned}&U_L=P_{L23} U_{L23} P_{L13} U_{L13} P_{L12} U_{L12}\,,\nonumber \\&U_R=P_{R23} U_{R23} P_{R13} U_{R13} P_{R12} U_{R12}\, . \end{aligned}$$

(31)

The rotation matrices are

$$\begin{aligned}&U_{12}= \begin{pmatrix} c_{12} &{} s_{12} &{}0\\ -s_{12}&{} c_{12}&{}0\\ 0&{}0&{}1\\ \end{pmatrix}\,, \qquad U_{13}= \begin{pmatrix} c_{13} &{}0&{} s_{13} \\ 0&{}1&{}0\\ -s_{13} &{}0&{} c_{13} \\ \end{pmatrix}\,,\nonumber \\&U_{23}= \begin{pmatrix} 1 &{}0&{} 0 \\ 0&{}c_{23} &{} s_{23} \\ 0&{}-s_{23} &{} c_{23} \\ \end{pmatrix}\,, \end{aligned}$$

(32)

and phase matrices are

$$\begin{aligned}&P_{12}= \begin{pmatrix} 1 &{} 0 &{}0\\ 0&{} e^{i \phi _{12}}&{}0\\ 0&{}0&{}1\\ \end{pmatrix}\,, \qquad P_{13}= \begin{pmatrix} 1 &{} 0 &{}0\\ 0&{} 1&{}0\\ 0&{}0&{}e^{i \phi _{13}}\\ \end{pmatrix}\,, \nonumber \\&P_{23}= \begin{pmatrix} 1 &{} 0 &{}0\\ 0&{} 1&{}0\\ 0&{}0&{}e^{i \phi _{23}}\\ \end{pmatrix}\, , \end{aligned}$$

(33)

where notations L and R are omitted. The $s_{ij}$ and $\phi _{ij}$ are obtained approximately from $Y Y^\dagger$ or $Y^\dagger Y$ in Appendix B for the left-handed or the right-handed sector.

In the following expression, we take $C^y_\Delta$ to be real positive and $C^y$, $C^y_{V}$, $C^y_{V \Delta }$ and $C^y_{VV\Delta }$ to be complex without loss of generality. The mixing angles $s_{Lij}$ and $s_{Rij}$ are obtained approximately (see Appendix B). The mixing angles $s_{L12}$ and $s_{R12}$ are:

$$\begin{aligned}&s_{L12}\simeq -\frac{s_e}{c_e} \left[ 1-\left| \frac{C^y_{VV\Delta }}{C^y_\Delta }\right| \epsilon _\ell ^2 \cos (\arg C^y_{VV\Delta }) \right] \,, \nonumber \\&s_{R12}\simeq 2\frac{s_e}{c_e} \frac{\delta '_e}{\delta _e} \left[ \cos (\arg C^y_{VV\Delta }) + \left| \frac{C^y_{VV\Delta }}{2C^y_\Delta }\right| \epsilon _\ell ^2 \right] \left| \frac{C^y_{VV\Delta }}{C^y_\Delta }\right| \epsilon _\ell ^2 \,, \end{aligned}$$

(34)

respectively. The phase $\phi _{L12}$ and $\phi _{R12}$ are:

$$\begin{aligned} \phi _{L12}\simeq -\left| \frac{C^y_{VV\Delta }}{C^y_\Delta }\right| \epsilon _\ell ^2 \sin (\arg C^y_{VV\Delta }) \,, \qquad \phi _{R12}\simeq 0\,, \end{aligned}$$

(35)

which are much smaller than 1. The mixing angles $s_{L23}$ and $s_{R23}$ are rather simple in the leading order as:

$$\begin{aligned} s_{L23}\simeq \left| \frac{C^y_{V}}{C^y} \right| \epsilon _\ell \,, \qquad s_{R23}\simeq \left| \frac{C^{y\,*}_\Delta C^y_V+C^{y\,*}_{V\Delta }C^y}{C^{y\, 2}} \right| c_e \delta _e \epsilon _\ell \,, \end{aligned}$$

(36)

respectively. The phase $\phi _{L12}$ and $\phi _{R12}$ are:

$$\begin{aligned}&\phi _{L23}\simeq \arg \frac{C^y_{V}}{C^y} \,, \nonumber \\&\phi _{R23}\simeq \arg \left[ \frac{C^{y\,*}_\Delta C^y_V+C^{y\,*}_{V\Delta }C^y}{|C^{y}|^2} \right] \,, \end{aligned}$$

(37)

which are of order 1.

The mixing angles $s_{L13}$ and $s_{R13}$ are also simple in the leading order as:

$$\begin{aligned}&s_{L13}\simeq \left| \frac{C^y_{\Delta }C^{y\,*}_{V\Delta }}{C^{y\,2}} \right| c_e s_e (\delta _e^2 -{\delta '_e}^2)\epsilon _\ell \,, \qquad \nonumber \\ {}&s_{R13}\simeq \left| \frac{C^{y\,*}_\Delta C^y_V+C^{y\,*}_{V\Delta }C^y}{C^{y\, 2}}\right| s_e \delta '_e \epsilon _\ell \,, \end{aligned}$$

(38)

respectively. The phase $\phi _{L13}$ and $\phi _{R13}$ are:

$$\begin{aligned} \phi _{L13}\simeq \arg \frac{C^y_{\Delta }C^{y\,*}_{V\Delta }}{|C^{y}|^2} \,, \qquad \qquad \phi _{R13}\simeq 0 \,. \end{aligned}$$

(39)

It is noticed that the (1, 3) and (2, 3) components of $(Y^\dagger Y)_{RR}$ have the same phase as seen in Eq. (65). Therefore, the phase matrix $P_{R23}$ removes phases of both (1, 3) and (2, 3) components, that is, $\phi _{R13}\simeq 0$ is derived.

In mass-eigenstate basis, the matrix $X^{e\gamma }$ in Eq. (25) is transformed by the unitary matrix of Eq. (31) as $U_L^\dagger X^{e\gamma } U_R$, whose elements correspond to the Wilson coefficients of Eq. (9):

$$\begin{aligned} \mathcal {C}_{\underset{ee}{e\gamma }}^\prime&= [ U_L^{ \dag } X^{e \gamma } U_R ]_{11}\nonumber \\&\simeq |C^{e\gamma }_\Delta | \delta _e' \left[ \frac{1}{c_e} +\frac{s_e^2}{c_e}\epsilon _{\ell }^2 \left( \frac{C^{e \gamma }_{VV\Delta }}{C^{e \gamma }_\Delta } - \frac{C^{y}_{VV\Delta }}{C^{y}_\Delta } \right) \right] \nonumber \\&\quad +\delta _e'\frac{s_e^2}{c_e}\epsilon _{\ell }^2 \, C_{ 3rd}\,, \nonumber \\ \mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime&=[U_L^{ \dag } X^{e \gamma } U_R ]_{22} \nonumber \\&\simeq |C^{e\gamma }_\Delta | \delta _e \left[ \frac{1}{c_e} + c_e \epsilon _{\ell }^2 \left( \left| \frac{C^{e \gamma }_{VV\Delta }}{C^{e \gamma }_\Delta }\right| \cos {(\arg {C^{e \gamma }_{VV\Delta }})} \right. \right. \nonumber \\&\quad \left. \left. - \left| \frac{C^{y}_{VV\Delta }}{C^{y}_\Delta }\right| \frac{s_e^2}{c_e^2}\cos {(\arg {C^y_{VV\Delta }})} \right) \right] \nonumber \\&\quad + i |C^{e\gamma }_\Delta | c_e \delta _e\epsilon _{\ell }^2 \left( \left| \frac{C^{e \gamma }_{VV\Delta }}{C^{e \gamma }_\Delta }\right| \sin {(\arg {C^{e \gamma }_{VV\Delta }})}\right. \nonumber \\&\quad \left. - \left| \frac{C^{y}_{VV\Delta }}{C^{y}_\Delta }\right| \sin {(\arg {C^y_{VV\Delta }})}\right) + c_e \delta _e\epsilon _{\ell }^2\, C_{3rd}\,, \nonumber \\ \mathcal {C}_{\underset{e\mu }{e\gamma }}^\prime&=[ U_L^{ \dag } X^{e \gamma } U_R ]_{12} \simeq |C^{e\gamma }_\Delta | s_e \delta _e \epsilon _{\ell }^2 \left( \frac{C^{e \gamma }_{VV\Delta }}{C^{e \gamma }_\Delta } - \frac{C^{y}_{VV\Delta }}{C^{y}_\Delta } \right) \nonumber \\&\quad + s_e \delta _e \epsilon _{\ell }^2 \, C_{3rd}\,,\nonumber \\&\mathcal {C}_{\underset{\mu e}{e\gamma }}^\prime =[ U_L^{ \dag } X^{e \gamma } U_R ]_{21} \simeq |C^{e\gamma }_\Delta | s_e \delta '_e \epsilon _{\ell }^2 \left( \frac{C^{e \gamma }_{VV\Delta }}{C^{e \gamma }_\Delta } - \frac{C^{y}_{VV\Delta }}{C^{y}_\Delta }\right) \nonumber \\&\quad \qquad +s_e \delta '_e \epsilon _{\ell }^2 \, C_{3rd}\,, \end{aligned}$$

(40)

where $C_{3rd}$ is given in terms of third-family parameters as:

$$\begin{aligned} C_{3rd}&=\frac{C^{y*}_\Delta C^y_V+C^{y*}_{V\Delta }C^y}{|C^y|^2} \left( \frac{C^{e\gamma }}{C^y}C^y_V -C^{e\gamma }_V\right) \nonumber \\&\quad + \frac{C^y_V}{C^y} \left( \frac{C^{e\gamma }_V}{C^y_V}C^y_{V\Delta } -C^{e\gamma }_{V\Delta } \right) \,. \end{aligned}$$

(41)

The contribution $C_{3rd}$ was not taken account in the analysis of Ref. [35]. It is found that the $C_{3rd}$ is of order 1 and does not vanish unless $C^{e\gamma }_V=C^y_V$, $C^{e\gamma }_{V\Delta }=C^y_{V\Delta }$ and $C^{e\gamma }=C^y$. It is remarked that the off-diagonal component of $\mathcal {C}_{\underset{e\mu (\mu e)}{e\gamma }}^\prime$ are not suppressed due to $C_{3rd}$ even if the alignment $C^{e\gamma }_{V\Delta }/C^{e\gamma }_\Delta =C^{y}_{V\Delta }/C^{y}_\Delta$ is imposed [35].

The third family contribution on the $\mu \rightarrow e\gamma$ decay is comparable to the one of the first- and second-family. It is also remarked that the non-vanishing electron EDM is realized from the third family even if there is no CP phase in first- and second-family as seen in the imaginary part of $\mathcal {C}_{\underset{e e}{e\gamma }}^\prime$ in Eq. (40).

The Wilson coefficients with respect to the third-family are given as:

$$\begin{aligned}&\mathcal {C}_{\underset{e\tau }{e\gamma }}^\prime = [ U_L^{ \dag } X^{e \gamma } U_R ]_{13} \simeq \left( {C^{e\gamma }_{V}- \frac{C^{e\gamma }}{C^{y}} C^{y}_{V}} \right) \frac{s_e}{c_e}\epsilon _{\ell } \,, \nonumber \\&\mathcal {C}_{\underset{\tau e}{e\gamma }}^\prime = [ U_L^{ \dag } X^{e \gamma } U_R ]_{31} \simeq \left( {C^{e\gamma }_{V\Delta }- \frac{C^{e\gamma }}{C^{y}} C^{y}_{V\Delta }} \right) s_e \delta '\epsilon _{\ell } \,, \nonumber \\&\mathcal {C}_{\underset{\mu \tau }{e\gamma }}^\prime = [ U_L^{ \dag } X^{e \gamma } U_R ]_{23} \simeq \left( {C^{e\gamma }_{V}- \frac{C^{e\gamma }}{C^{y}} C^{y}_{V}} \right) \epsilon _{\ell } \,, \nonumber \\&\mathcal {C}_{\underset{\tau \mu }{e\gamma }}^\prime = [ U_L^{ \dag } X^{e \gamma } U_R ]_{32} \simeq \left( {C^{e\gamma }_{V\Delta }- \frac{C^{e\gamma }}{C^{y}} C^{y}_{V\Delta }} \right) c_e \delta \epsilon _{\ell } \,, \nonumber \\&\mathcal {C}_{\underset{\tau \tau }{e\gamma }}^\prime = [ U_L^{ \dag } X^{e \gamma } U_R ]_{33} \simeq C^{e\gamma } + C^{e \gamma }_V \frac{C^y_V}{C^{y}} \epsilon _{\ell }^2 \,. \end{aligned}$$

(42)

As seen in Eq. (40), $\textrm{Im}\, \mathcal {C}_{\underset{ee}{e\gamma }}^\prime$, which gives the electron EDM, is suppressed by the factor of $s_e^2\epsilon _{\ell }^2\delta _e'/\delta _e$ while $\mu \rightarrow e\gamma$ ($| \mathcal {C}_{\underset{e\mu }{e\gamma }}^\prime |$) is suppressed by $s_e\epsilon _{\ell }^2$ compared with the muon $(g-2)_\mu$. It is noted that the $\tau _R \rightarrow e_L \gamma$ transition is not so suppressed due to the $e_L$-$\mu _L$ mixing angle $s_e=0.01-0.1$ as seen in Eq. (42) although $(X^{e \gamma })_{13}$ vanishes in the flavor basis as seen in Eq. (25)

In the next section, we show the numerical results without approximations. Indeed, it is found that the approximate Wilson coefficients in Eqs. (40) and (42) are agree with exact ones in accuracy of 10% numerically.

4 Numerical analyses

Let us discuss Wilson coefficients numerically in mass-eigenvalue basis. The parameters $\delta _e$ and $\delta _e'$ are determined according to the observed charged lepton mass ratios, $m_e/m_\mu$ and $m_\mu /m_\tau$ as in Eq. (29). On the other hand, we scan $s_e$ and $\epsilon _\ell$ in the region of Eq. (30), $[0.01-0.1]$ with equal weights, that is the random scan in the linear space. As seen in Eqs. (40) and (42), the leading terms of off-diagonal Wilson coefficients depend on these two parameters, while the leading terms of the diagonal ones do not. Therefore, the predictions of the LFV processes depend crucially on the scan range of these parameters. Since the imaginary parts of the diagonal Wilson coefficients also depend on these two parameters, the predictions of the EDM depend on the scan range of these parameters. The other parameters are $C^y$, $C^y_{\Delta }$, $C^y_{V}$, $C^y_{V\Delta }$ $C^y_{VV\Delta }$, $C^{e\gamma }$, $C^{e\gamma }_{\Delta }$, $C^{e\gamma }_{V}$, $C^{e\gamma }_{V\Delta }$ and $C^{e\gamma }_{VV\Delta }$ which are complex parameters of order 1. Since the relative phases contribute to the observables except for EDM, we take $C^y_{\Delta }$ and $C^{e\gamma }_{\Delta }$ to be real in order to predict the electron EDM properly removing unphysical CP phases. Those parameters are put in the normal distribution with an average 1 and standard deviation 0.25, which is given in the work of the flavor structure of quarks and leptons with reinforcement learning [64]. (We have checked that our numerical results are not so changed even if the standard deviation 0.5 is taken.) The phases are scanned to be random in $0\sim 2\pi$.

Then, we construct the matrices Eqs. (24) and (25) numerically. After diagonalizing Yukawa matrices in Eq.(24), we can obtain $\mathcal {C}_{\underset{\alpha \beta }{e\gamma }}^\prime$’s in the mass-eigenvalues basis. In the following analysis, we have only taken the regions where $\text {Re}\ [\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime ] =1.0 \times 10^{-5}$, corresponding to the $(g-2)_{\mu }$ anomaly, can be reproduced. It is noted that the U(2) flavor symmetry is supposed in the electroweak scale. Therefore, the contribution on the leptonic dipole operator of the renormalization group equations (RGEs) is neglected (see also the study in the subsection 4.3 of Ref. [43].).

4.1 Prediction of $(g-2)_{e}$ and $(g-2)_{\tau }$

The NP effect in $(g-2)_{\ell }$ is occurred by the diagonal components of the Wilson coefficient of the leptonic dipole operator at mass-eigenstate basis. We have the ratios of the diagonal coefficients from Eqs. (40) and (42) as:

$$\begin{aligned} \frac{ |\mathcal {C}_{\underset{e e}{e\gamma }}^\prime |}{|\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime |}\simeq & {} \frac{\delta _e'}{\delta _{e}} \simeq \frac{m_e}{m_\mu } \simeq 4.8\times 10^{-3} , \nonumber \\ \frac{ |\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime |}{ | \mathcal {C}_{\underset{\tau \tau }{e\gamma }}^\prime |}= & {} \frac{ |C^{e\gamma }_\Delta |}{| C^{e\gamma }|} \frac{1}{c_e}\delta _e \simeq \frac{m_\mu }{m_\tau }\simeq 5.9\times 10^{-2} , \end{aligned}$$

(43)

where the second equation is derived by taking account of $|C^{e\gamma }_\Delta |\sim | C^{e\gamma }|\sim 1$ and $c_e\sim 1$. Inputting the observed charged lepton masses with $3\,\sigma$ error-bar, we have obtained

$$\begin{aligned} \delta _e=(5.0-6.0)\times 10^{-2} \,,\qquad \quad \delta '_e=(2.3-3.0)\times 10^{-4}\,, \end{aligned}$$

(44)

in the numerical results.

Suppose that the leptonic dipole operator is responsible for the observed anomaly of $(g-2)_{\mu }$. Inputting the reference value of Eq. (2), we can estimate the magnitude of the electron $(g-2)_e$ by using the relation in Eq. (43) as:

$$\begin{aligned} \Delta a_{e}&= \frac{4 m_e}{e} \frac{v}{\sqrt{2}}\,\frac{1}{\Lambda ^2} \text {Re} \,[\mathcal {C}_{\underset{ee}{e\gamma }}^\prime ] \simeq 6.2\times 10^{-14}\,, \end{aligned}$$

(45)

where $v\approx 246$ GeV. It is easily seen that $\Delta a_{e}$ and $\Delta a_{\mu }$ are proportional to the lepton masses squared. This result is agreement with the naive scaling $\Delta a_\ell \propto m^2_\ell$ [65].

In the electron anomalous magnetic moment, the experiments [66] give

$$\begin{aligned} a_e^\textrm{Exp}=1\, 159\, 652\, 180.73(28)\times 10^{-12}\,, \end{aligned}$$

(46)

while the SM prediction crucially depends on the input value for the fine-structure constant $\alpha$. The two latest determinations [67, 68] based on Cesium and Rubidium atomic recoils differ by more than $5\sigma$. Those observations lead to the difference from the SM prediction

$$\begin{aligned}{} & {} \Delta a_e^{Cs}&= a_e^\textrm{Exp} - a_e^\textrm{SM,CS} = ({-8.8 \pm 3.6}) \times 10^{-13}~\,, \nonumber \\{} & {} \Delta a_e^{Rb}&= a_e^\textrm{Exp} - a_e^\textrm{SM,Rb} = ({4.8 \pm 3.0}) \times 10^{-13}~\,. \end{aligned}$$

(47)

Our predicted value is small of one order compared with the observed one at present. We wait for the precise determination of the fine structure constant to test our flavor model.

The tauon $(g-2)_\tau$ is also predicted by using the relation in Eq. (43) as:

$$\begin{aligned} \Delta a_{\tau }&= \frac{4 m_\tau }{e} \frac{v}{\sqrt{2}}\,\frac{1}{\Lambda ^2} \text {Re} \,[\mathcal {C}_{\underset{\tau \tau }{e\gamma }}^\prime ] \simeq 7.5\times 10^{-7}\,, \end{aligned}$$

(48)

which is also proportional to the lepton masses squared.

4.2 $(g-2)_{\mu }$ versus $\mu \rightarrow e\gamma$, $\tau \rightarrow \mu \gamma$ and $\tau \rightarrow e\gamma$

The NP in the LFV process is severely constrained by the experimental bound of the $\mu \rightarrow e\gamma$ decay in the MEG experiment [25]. It is also constrained by the $\tau \rightarrow \mu \gamma$ decay in the Belle experiment [27]. We can discuss the correlation between the anomaly of the muon $(g-2)_\mu$ and the LFV process $\mu \rightarrow e\gamma$ by using the Wilson coefficients in Eq. (40). The ratios are given as:

$$\begin{aligned} \left| \frac{ \mathcal {C}_{\underset{e \mu }{e\gamma }}^\prime }{\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime } \right| \simeq c_e s_e \epsilon _\ell ^2 \left| \frac{C^{e \gamma }_{VV\Delta }}{C^{e \gamma }_\Delta } - \frac{C^{y}_{VV\Delta }}{C^{y}_\Delta } + \frac{C_{3rd}}{C^{e \gamma }_\Delta } \right| , \end{aligned}$$

(49)

and

$$\begin{aligned} \left| \frac{ \mathcal {C}_{\underset{\mu e}{e\gamma }}^\prime }{\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime } \right| \simeq c_e s_e \frac{\delta '_e}{\delta _e}\epsilon _\ell ^2 \left| \frac{C^{e \gamma }_{VV\Delta }}{C^{e \gamma }_\Delta } - \frac{C^{y}_{VV\Delta }}{C^{y}_\Delta } + \frac{C_{3rd}}{C^{e \gamma }_\Delta } \right| . \end{aligned}$$

(50)

We also obtain ratios for $\tau \rightarrow \mu \gamma$ and $\tau \rightarrow e\gamma$ processes as:

$$\begin{aligned}{} & {} \left| \frac{ \mathcal {C}_{\underset{\mu \tau }{e\gamma }}^\prime }{\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime } \right| \simeq c_e \epsilon _\ell \frac{1}{\delta _e}\frac{1}{|C^{e\gamma }_\Delta |} \left| C^{e \gamma }_V - \frac{C^{e\gamma }}{C^{y}} C^y_V\right| , \nonumber \\{} & {} \left| \frac{ \mathcal {C}_{\underset{\tau \mu }{e\gamma }}^\prime }{\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime } \right| \simeq c_e^2 \epsilon _\ell \frac{1}{|C^{e\gamma }_\Delta |} \left| C^{e \gamma }_V - \frac{C^{e\gamma }}{C^{y}} C^y_V\right| , \end{aligned}$$

(51)

and

$$\begin{aligned}{} & {} \left| \frac{ \mathcal {C}_{\underset{e\tau }{e\gamma }}^\prime }{\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime } \right| \simeq s_e \epsilon _\ell \frac{1}{\delta _e}\frac{1}{|C^{e\gamma }_\Delta |} \left| C^{e \gamma }_V - \frac{C^{e\gamma }}{C^{y}} C^y_V\right| , \nonumber \\{} & {} \left| \frac{ \mathcal {C}_{\underset{\tau e}{e\gamma }}^\prime }{\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime } \right| \simeq c_e s_e \frac{\delta '_e}{\delta _e}\epsilon _\ell \frac{1}{|C^{e\gamma }_\Delta |} \left| C^{e \gamma }_V - \frac{C^{e\gamma }}{C^{y}} C^y_V\right| . \end{aligned}$$

(52)

For the $\tau _R\rightarrow \mu _L\gamma$ process, the ratio in Eq. (51) is proportional to $\epsilon _\ell /\delta _e$, which is expected to be of order 1. Since $\delta _e$ is fixed in Eq. (44), we have a strong constraint for $\epsilon _{\ell }$ from the experimental upper-bound of the Wilson coefficient in Eq. (14).

On the other hand, for the $\mu _R\rightarrow e_L\gamma$ process, the ratio in Eq. (49) is proportional to $s_e\epsilon _\ell ^2$. Therefore, $s_e$ is also constrained considerably as well as $\epsilon _{\ell }$.

In order to see the predicted range of $\mu \rightarrow e \gamma$, we plot the magnitude of $\mathcal {C}_{\underset{e\mu }{e\gamma }}^\prime$ versus $\epsilon _{\ell }$, which corresponds to $\mu _R\rightarrow e_L\gamma$ process, in Fig. 1. In this figure, $s_e=0.03$ is put as a benchmark. It is found that $\epsilon _{\ell }$ should be smaller than around 0.05 in order to obtain $\mathcal {C}_{\underset{e\mu }{e\gamma }}^\prime$ below the experimental upper-bound. The expected value of the branching ratio $\mathcal {B}({\mu \rightarrow e \gamma })$ will be discussed in Sect. 4.4.

We also show the magnitude of $\mathcal {C}_{\underset{\mu e}{e\gamma }}^\prime$ versus $\epsilon _{\ell }$ with $s_e=0.03$, which corresponds $\mu _L\rightarrow e_R\gamma$ process in Fig. 2. The magnitude of $\mathcal {C}_{\underset{\mu e}{e\gamma }}^\prime$ is suppressed compared with $\mathcal {C}_{\underset{e\mu }{e\gamma }}^\prime$. It is remarked that the NP signal of the $\mu \rightarrow e\gamma$ process mainly comes from the operator $\bar{e}_L \sigma _{\mu \nu }\mu _R$ in the U(2) flavor model. Indeed, the ratio is given as:

$$\begin{aligned} \left| \frac{ \mathcal {C}_{\underset{\mu e}{e\gamma }}^\prime }{\mathcal {C}_{\underset{e \mu }{e\gamma }}^\prime } \right| \simeq \frac{\delta _e'}{\delta _e}\simeq \frac{m_e}{m_\mu } . \end{aligned}$$

(53)

The angular distribution with respect to the muon polarization can distinguish between $\mu _R \rightarrow e_L\gamma$ and $\mu _L \rightarrow e_R\gamma$ [69].

Fig. 1

$|\mathcal {C}_{\underset{e \mu }{e\gamma }}^\prime |$ in $1/\Lambda ^2\ [\textrm{TeV}^{-2}]$ unit versus $\epsilon _{\ell }$, where $s_e=0.03$ is put and the grey region is excluded by the $\mu \rightarrow e\gamma$ experiment

Fig. 2

$|\mathcal {C}_{\underset{\mu e}{e\gamma }}^\prime |$ in $1/\Lambda ^2\ [\textrm{TeV}^{-2}]$ unit versus $\epsilon _{\ell }$, where $s_e=0.03$ is put and the grey region is excluded by the $\mu \rightarrow e\gamma$ experiment

Fig. 3

$|\mathcal {C}_{\underset{e \mu }{e\gamma }}^\prime |$ in $1/\Lambda ^2\ [\textrm{TeV}^{-2}]$ unit versus $\epsilon _{\ell }$ for case (a) (without third-family contribution), where $s_e=0.03$ is put and the grey region is excluded by the experiment of $\mu \rightarrow e\gamma$

Fig. 4

$|\mathcal {C}_{\underset{e \mu }{e\gamma }}^\prime |$ in $1/\Lambda ^2\ [\textrm{TeV}^{-2}]$ unit versus $\epsilon _{\ell }$ for case (b) (without first- and second-family contribution), where $s_e=0.03$ is put and the grey region is excluded by the experiment of $\mu \rightarrow e\gamma$

In order to see the contribution of the third-family to $\mathcal {C}_{\underset{e \mu }{e\gamma }}^\prime$, we show the magnitude of $\mathcal {C}_{\underset{e \mu }{e\gamma }}^\prime$ for both cases of alignment of coefficients (a) $C^{e\gamma }_V=C^y_V$, $C^{e\gamma }_{V\Delta }=C^y_{V\Delta }$, $C^{e\gamma }=C^y$ and (b) $C^{e\gamma }_{V\Delta }/C^{e\gamma }_\Delta =C^{y}_{V\Delta }/C^{y}_\Delta$. The case (a) corresponds to the case excluding the third-family contribution and (b) to the case excluding the first- and second-family contribution. The numerical results are presented in Fig. 3 for case (a) and Fig. 4 for case (b). Thus, the third-family contribution is comparable or rather large compared with the one from the first- and second-family.

The $\tau \rightarrow \mu \gamma$ decay is an interesting process in the U(2) flavor symmetry because it is suppressed by only $\epsilon _{\ell }$. [35]. The upper-bound of the branching ratio of $\tau \rightarrow \mu \gamma$ constrains the magnitude of $\epsilon _{\ell }$ as discussed below Eq. (52). We show the magnitude of $\mathcal {C}_{\underset{\mu \tau }{e\gamma }}^\prime$ versus $\epsilon _{\ell }$ in Fig. 5, where the predicted value is almost independent of $s_e$ as seen in Eq. (51). It is found that small $\epsilon _{\ell }$ (much less than 0.1) is favored by the experimental upper-bound of the $\tau \rightarrow \mu \gamma$ decay. On the other hand, $\mathcal {C}_{\underset{\tau \mu }{e\gamma }}^\prime$ is suppressed in more than one order by $\delta _e$. We omit a figure for this process.

Fig. 5

$|\mathcal {C}_{\underset{\mu \tau }{e\gamma }}^\prime |$ in $1/\Lambda ^2\ [\textrm{TeV}^{-2}]$ unit versus $\epsilon _{\ell }$, where the grey region is excluded by the $\tau \rightarrow \mu \gamma$ experiment

Fig. 6

Allowed region in the $\epsilon _{\ell }$-$s_e$ plane by the upper-bound of $\mu \rightarrow e\gamma$ and $\tau \rightarrow \mu \gamma$ branching ratios

As seen in Figs. 1 and 5, the substantial regions of predicted Wilson coefficients exceed the experimental upper-bounds. Imposing the upper-bounds of the branching ratios of $\mu \rightarrow e\gamma$ and $\tau \rightarrow \mu \gamma$ decays, we obtain the allowed region in $\epsilon _\ell -s_e$ plane in Fig. 6. It is found that $\epsilon _{\ell }$ is almost smaller than 0.05 while $s_e$ is allowed in rather wide range of $[0.01-0.1]$.

In order to see the correlation between $|\mathcal {C}_{\underset{e \mu }{e\gamma }}^\prime |$ and $|\mathcal {C}_{\underset{\mu \tau }{e\gamma }}^\prime |$, we plot their predictions in Fig. 7. It is found that the allowed region is restricted. In the next subsection, we discuss the expectation value of $\mu \rightarrow e\gamma$ and $\tau \rightarrow \mu \gamma$.

Fig. 7

$|\mathcal {C}_{\underset{\mu \tau }{e\gamma }}^\prime |$ in $1/\Lambda ^2\ [\textrm{TeV}^{-2}]$ unit versus $|\mathcal {C}_{\underset{e \mu }{e\gamma }}^\prime |$. The grey region is excluded by the experiments

Fig. 8

$|\mathcal {C}_{\underset{e \tau }{e\gamma }}^\prime |$ in $1/\Lambda ^2\ [\textrm{TeV}^{-2}]$ unit versus $|\mathcal {C}_{\underset{e \mu }{e\gamma }}^\prime |$. The grey region is excluded by the experiments

We also show the predicted region of $|\mathcal {C}_{\underset{e \tau }{e\gamma }}^\prime |$ versus $|\mathcal {C}_{\underset{\mu \tau }{e\gamma }}^\prime |$ in Fig. 8. The magnitude of $\mathcal {C}_{\underset{e \tau }{e\gamma }}^\prime$ is proportional to $|\mathcal {C}_{\underset{e \mu }{e\gamma }}^\prime |$ roughly. The prediction of $\mathcal {C}_{\underset{e \tau }{e\gamma }}^\prime$ is still low in one order compared with the experimental upper-bound. It is noted that $\mathcal {C}_{\underset{\tau e }{e\gamma }}^\prime$ is suppressed in $\delta '_e$ as seen in Eq. (42). We omit a figure for this process.

4.3 Predictions of EDM

In the allowed region of $\epsilon _\ell$ and $s_e$ in Fig. 6, we discuss the EDM of the charged leptons. The electron EDM comes from the imaginary part of $\mathcal {C}_{\underset{e e}{e\gamma }}^\prime$, and the magnitude is estimated approximately from Eq. (40). The ratio of $\textrm{Im}\ \mathcal {C}_{\underset{e e}{e\gamma }}^\prime$ and $\textrm{Re}\ \mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime$ is bounded by the observed constraints in Eqs. (11) and (18) as:

$$\begin{aligned} \left| \frac{ \textrm{Im}\ \mathcal {C}_{\underset{e e}{e\gamma }}^\prime }{\textrm{Re}\ \mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime } \right|\simeq & {} s_e^2 \frac{\delta '}{\delta } \epsilon _\ell ^2\, \textrm{Im} \, \left( \frac{C^{e \gamma }_{VV\Delta }}{C^{e \gamma }_\Delta } - \frac{C^{y}_{VV\Delta }}{C^{y}_\Delta }+ \frac{C_{3rd}}{|C^{e \gamma }_\Delta |} \right) \nonumber \\< & {} 1.8\times 10^{-8} . \end{aligned}$$

(54)

Putting $\epsilon _{\ell }=0.03$ and $s_e=0.03$ with $\delta '_e/\delta _e\simeq m_e/m_\mu$ in Eq. (53), the factor in front of the middle equation, $s_e^2 \epsilon _\ell ^2 \delta '/\delta$, is $4\times 10^{-9}$. Thus, the ratio is possibly predicted to be $\mathcal{O}(10^{-8})$, which corresponds to $|d_e|\sim 10^{-30}\, \mathrm{e\,cm}$. We expect it to be detectable in the near future.

Figure 9 shows a plot of $\textrm{Im}\ \mathcal {C}_{\underset{e e}{e\gamma }}^\prime$ versus $\mathcal {C}_{\underset{e \mu }{e\gamma }}^\prime$. These ratio can be expressed approximately as:

$$\begin{aligned} \frac{ \textrm{Im}\ \mathcal {C}_{\underset{e e}{e\gamma }}^\prime }{|\mathcal {C}_{\underset{e \mu }{e\gamma }}^\prime |} \simeq \frac{s_e}{c_e}\frac{\delta '}{\delta } \frac{ \textrm{Im} \, \left( \frac{C^{e \gamma }_{VV\Delta }}{C^{e \gamma }_\Delta } - \frac{C^{y}_{VV\Delta }}{C^{y}_\Delta }+ \frac{C_{3rd}}{|C^{e \gamma }_\Delta | } \right) }{\left| \frac{C^{e \gamma }_{VV\Delta }}{C^{e \gamma }_\Delta } - \frac{C^{y}_{VV\Delta }}{C^{y}_\Delta }+ \frac{C_{3rd}}{|C^{e \gamma }_\Delta | }\right| } , \end{aligned}$$

(55)

which is estimated to be $\mathcal{O}(10^{-4})$, as can be confirmed in Fig. 9. The predicted electron EDM is below the experimental upper-bound after taking account of the upper-bound of $\mathcal {B}({\mu \rightarrow e \gamma })$. In the next subsection, we discuss the expectation value of the electron EDM.

We also present the predicted region of EDMs of muon and tauon in Fig. 10. Those are still far from the present experimental upper-bounds, $|{d_\mu } |<1.8 \times 10^{-19} \, \mathrm e\,cm$ [21] and $|d_\tau |<1.85\times 10^{-17}\mathrm{e\,cm}$ [24] as seen in Eqs. (4) and (6).

Fig. 9

$\textrm{Im}\ \mathcal {C}_{\underset{e e}{e\gamma }}^\prime$ versus $|\mathcal {C}_{\underset{e \mu }{e\gamma }}^\prime |$ (electron EDM versus $\mu \rightarrow e\gamma$) in $1/\Lambda ^2\ [\textrm{TeV}^{-2}]$ unit. The grey region is excluded by the experiments

Fig. 10

Predicted EDMs of muon and tauon in $[\mathrm e\,cm]$ unit. The grey region is excluded by the experiments

4.4 Expectation of $\mu \rightarrow e\gamma$, $\tau \rightarrow \mu \gamma$, $\tau \rightarrow e\gamma$ and electron EDM

Since we have performed a random scan in the linear space of $s_e$ and $\epsilon _{\ell }$ in $[0.01-0.1]$ as given in Eq. (30), we can show the frequency distribution of the predicted LFV decays and the electron EDM. Indeed, the frequency distribution of the predicted $\mathcal {B}({\mu \rightarrow e \gamma })$ by imposing the constraints of the upper-bound on $\mathcal {B}(\tau \rightarrow \mu \gamma )$ and the electron EDM is shown in Fig. 11. The frequency is normalized so that the total sum is 1. The grey region has already been excluded by the experimental upper-bound on $\mathcal {B}({\mu \rightarrow e \gamma })$, and the maximal peak is almost entirely within the gray region. Since the future sensitivity at the MEG II experiment is $\mathcal {B}({\mu \rightarrow e \gamma })=6\times 10^{-14}$ [70], we expect the observation of $\mu \rightarrow e \gamma$ decay in the near future.

In Fig. 12, we plot the frequency distribution of the predicted $\mathcal {B}({\tau \rightarrow \mu \gamma })$ with imposing constraints of the upper-bound of $\mathcal {B}(\mu \rightarrow e\gamma )$ and the electron EDM. The peak is also within the grey region. We also expect to observe $\tau \rightarrow \mu \gamma$ decay in the near future.

In Fig. 13, we plot the frequency distribution of the predicted $\mathcal {B}({\tau \rightarrow e \gamma })$ with (without) imposing the upper-bounds of $\mu \rightarrow e\gamma$, $\tau \rightarrow \mu \gamma$ and the electron EDM with the color of orange I (blue II). Due to these constraints, the predicted $\mathcal {B}({\tau \rightarrow e\gamma })$ is far from the current experimental upper-bound and is smaller than three orders of magnitude.

Fig. 11

The frequency distribution of the predicted $\mathcal {B}({\mu \rightarrow e \gamma })$ with imposing the upper-bounds of $\tau \rightarrow \mu \gamma$ decay and the electron EDM. The grey region is excluded by the experimental data of $\mathcal {B}({\mu \rightarrow e \gamma })$

Fig. 12

The frequency distribution of the predicted $\mathcal {B}({\tau \rightarrow \mu \gamma })$ with imposing the upper-bound of the $\mu \rightarrow e\gamma$ decay and the electron EDM. The grey region is excluded by the experimental data of $\mathcal {B}({\tau \rightarrow \mu \gamma })$

Fig. 13

The orange I (blue II) frequency distribution of the predicted $\mathcal {B}({\tau \rightarrow e\gamma })$ with (without) imposing the upper-bounds of the $\mu \rightarrow e\gamma$ decay, $\tau \rightarrow \mu \gamma$ decay and the electron EDM. The grey region is excluded by the experimental data of $\mathcal {B}({\tau \rightarrow e\gamma })$

Fig. 14

The orange I (blue II) frequency distribution of the predicted electron EDM $[\mathrm e\,cm]$ with (without) imposing the $\mu \rightarrow e\gamma$ decay and $\tau \rightarrow \mu \gamma$ decay. The grey region is excluded by the experimental data of the electron EDM

Finally, the frequency distribution of the predicted electron EDM with (without) imposing the constrains of $\mu \rightarrow e\gamma$ and $\tau \rightarrow \mu \gamma$ is plotted in orange I (blue II) in Fig. 14. Due to these constraints, the peak appears around $|d_e|\simeq 3\times 10^{-31}$e cm. Since the future sensitivity at ACME $\mathrm I\hspace{-1.13791pt}I\hspace{-1.13791pt}I$ is expected to be $|d_e|<3\times 10^{-31}\,\text {e\,cm}$ [19, 20], the electron EDM will be possibly observed in the near future.

5 Summary and discussions

We have studied the interplay of NP among the lepton magnetic moments, LFV and the electron EDM in light of recent data of the muon $(g-2)_\mu$. The NP is discussed in the leptonic dipole operator with the $U(2)_{L_L} \otimes U(2)_{E_R}$ flavor symmetry of the charged leptons, where possible CP violating phases of the three family space are taken into account. It is remarked that the third-family contributes significantly to the $\mu \rightarrow e\gamma$ decay and the electron EDM. Indeed, the $\mu \rightarrow e\gamma$ process is not suppressed even if the contribution of the first- and second-family vanishes. The electron EDM is also predicted to be rather large due to the CP violating phase in the third-family even if the CP phase of the first- and second-family is zero.

In addition, the electron and tauon $(g-2)_{e,\tau }$ and the EDM of the muon are discussed, as well as LFV processes $\tau \rightarrow \mu \gamma$ and $\tau \rightarrow e \gamma$. In particular, the $\tau _R \rightarrow \mu _L \gamma$ process is predicted to be close to the experimental upper-bound due to the $\mu _L$-$\tau _L$ mixing of $\mathcal{O}(\epsilon _\ell )$. This decay will be possibly observed in Belle II experiment in the near future [71, 72]. The $\tau _R \rightarrow e_L \gamma$ decay is not so suppressed due to the $e_L$-$\mu _L$ mixing of $\mathcal{O}(s_e)$ together with the $\mu _L$-$\tau _L$ mixing. On the other hand, the $\mu _L \rightarrow e_R \gamma$, $\tau _L \rightarrow \mu _R \gamma$ and $\tau _L \rightarrow e_R \gamma$ decays are suppressed. The angular distribution with respect to the muon polarization can be distinguished between $\mu _R \rightarrow e_L\gamma$ and $\mu _L \rightarrow e_R\gamma$. The frequency distributions of the expected values of LFV decays and the electron EDM are presented. The electron EDM will be possibly observed as well as the $\mu \rightarrow e \gamma$ and $\tau \rightarrow \mu \gamma$ decays in the near future.

Commenting on the numerical results, the predictions for the LFV processes and EDM depend on the scan range of $s_\ell$ and $\epsilon _\ell$ in Eq. (30), which are the most natural choices for similar treatments of the quark and lepton sectors. The smaller the values of these two parameters, the smaller the predictions for the LFV process and the EDM. On the other hand, the NP effects of $(g-2)_\mu$ is almost independent of these two parameters.

In the numerical analyses, the NP effect is taken as $\Delta a_\mu = 249 \times 10^{-11}$. If $\Delta a_\mu$ is significantly lower, less than or of order $1\,\sigma$, we obtain somewhat different predictions for the interplay among the muon $(g-2)_\mu$, the electron EDM and the $\mu \rightarrow e\gamma$ decay. For example, if we take the input $\Delta a_\mu \simeq 50 \times 10^{-11}$, which is of order $1\,\sigma$, the predicted LFV branching ratios are reduced by 1/25 while predictions of $(g-2)_{e,\tau }$ and the predicted EDM are reduced by 1/5. To make the numerical results of the NP contribution to LFV and EDM reliable, the precise value of the SM prediction of HVP is needed.

Appendices

Appendix

Experimental constraints on the dipole operators

From the experimental data of the muon $(g-2)_\mu$ and ${\mu \rightarrow e\gamma }$, Ref.  [35] gave the constraints on the dipole operators. We summarize briefly them on the dipole operators in Eq. (9). Below the scale of electroweak symmetry breaking, the leptonic dipole operators are given as:

$$\begin{aligned} \mathcal {O}_{\underset{rs}{e\gamma }} = \frac{v }{\sqrt{2}} {\overline{e}}_{L_r} \sigma ^{\mu \nu } e_{R_s} F_{\mu \nu }\,, \end{aligned}$$

(56)

where $\{r,s\}$ are flavor indices $e,\mu ,\tau$ and $F_{\mu \nu }$ is the electromagnetic field strength tensor. The effective Lagrangian is

$$\begin{aligned} \mathcal {L}_{\textrm{dipole}}= \frac{1}{\Lambda ^2}\,\left( \mathcal {C}_{\underset{rs}{e\gamma }}^\prime \mathcal {O}_{\underset{rs}{e\gamma }} +\mathcal {C}_{\underset{rs}{e\gamma }}^\prime \mathcal {O}_{\underset{rs}{e\gamma }} \right) \,, \end{aligned}$$

(57)

where $\Lambda$ is a certain mass scale of NP in the effective theory. The corresponding Wilson coefficient $\mathcal {C}_{\underset{rs}{e\gamma }}^\prime$ is denoted in the mass-eigenstate basis of leptons.

The tree-level expression for $\Delta a_\mu$ in terms of the Wilson coefficient of the dipole operator is

$$\begin{aligned} \Delta a_{\mu }&= \frac{4 m_{\mu }}{e} \frac{v}{\sqrt{2}} \,\frac{1}{\Lambda ^2}\text {Re} \, [\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime ] \,, \end{aligned}$$

(58)

where $v\approx 246$ GeV. Let us input the value

$$\begin{aligned} \Delta a_\mu = 249 \times 10^{-11}\,, \end{aligned}$$

(59)

then, we obtain the Willson coefficient as:

$$\begin{aligned} \frac{1}{\Lambda ^2}\text {Re}\ [\mathcal {C}_{\underset{\mu \mu }{e\gamma }}^\prime ] = 1.0 \times 10^{-5} \, \textrm{TeV}^{-2} \,, \end{aligned}$$

(60)

where $e\simeq 0.3028$ is put in the natural unit.

The tree-level expression of a radiative LFV rate in terms of the Wilson coefficients is

$$\begin{aligned} \mathcal {B}(\ell _r \rightarrow \ell _s \gamma ) = \frac{m_{\ell _r}^3 v^2}{8 \pi \Gamma _{\ell _r}} \frac{1}{\Lambda ^4}\left( |\mathcal {C}_{\underset{rs}{e\gamma }}'|^2 + |\mathcal {C}_{\underset{sr}{e\gamma }}'|^2\right) \, . \end{aligned}$$

(61)

Taking the experimental bound $\mathcal {B}\!({\mu ^+ \rightarrow e^+ \gamma }) < 4.2 \times 10^{-13}$ (90% C.L.) obtained by the MEG experiment [25] in Eq. (7), we obtain the upper-bound of the Wilson coefficient as:

$$\begin{aligned} \frac{1}{\Lambda ^2}|\mathcal {C}_{\underset{e\mu (\mu e)}{e\gamma }}^\prime | < 2.1 \times 10^{-10} \, \textrm{TeV}^{-2} \, . \end{aligned}$$

(62)

On the other hand, by taking the following experimental upper-bound of the branching ratios, $\mathcal {B}\!({\tau \rightarrow \mu + \gamma }) < 4.2 \times 10^{-8}$ and $\mathcal {B}\!({\tau \rightarrow e \gamma }) < 3.3 \times 10^{-8}$ [26, 27], we obtain the upper-bound of the Wilson coefficient as:

$$\begin{aligned}&\frac{1}{\Lambda ^2}|\mathcal {C}_{\underset{\mu \tau (\tau \mu )}{e\gamma }}^\prime |< 2.65 \times 10^{-6} \, \textrm{TeV}^{-2} \,, \nonumber \\&\frac{1}{\Lambda ^2}|\mathcal {C}_{\underset{e\tau (\tau e)}{e\gamma }}^\prime | < 2.35 \times 10^{-6} \, \textrm{TeV}^{-2} \,, \end{aligned}$$

(63)

respectively.

Explicit forms of $3\times 3$ matrices for $YY^\dagger$ and $Y^\dagger Y$

Here, we present the $3\times 3$ matrices for $YY^\dagger$ and $Y^\dagger Y$ by using Eq. (24) explicitly. We can obtain the left (right)-handed mixing angles and phases by using these Hermitian matrices. The left-handed mixing is obtained by diagonalizing $YY^\dagger$, which is:

$$\begin{aligned}&YY^\dagger = Y_0^2 \, \times \nonumber \\&\begin{pmatrix} {C^y_{\Delta }}^2 (c_e^2 {\delta '_e}^2+s_e^2 \delta _e^2) &{} C^y_{\Delta }(C^{y\,*}_{\Delta }+C^{y\,*}_{VV\Delta }\epsilon ^2_{\ell }) ({\delta '_e}^2-{\delta _e}^2) c_es_e&{} C^{y}_{\Delta }C^{y\,*}_{V\Delta }({\delta '_e}^2-{\delta _e}^2) c_es_e\epsilon _{\ell }\\ C^{y\,*}_{\Delta }(C^{y}_{\Delta }+C^{y}_{VV\Delta }\epsilon ^2_{\ell }) ({\delta '_e}^2-{\delta _e}^2) c_es_e &{} |(C^{y}_{\Delta }+C^{y}_{VV\Delta }\epsilon ^2_{\ell })|^2 (s_e^2 {\delta '_e}^2+c_e^2 \delta _e^2)+|C^{y}_{V}|^2\epsilon ^2_{\ell } &{} [ C^{y\,*}_{V\Delta } (C^{y}_{\Delta }+C^{y}_{VV\Delta }\epsilon ^2_{\ell }) (s_e^2 {\delta '_e}^2+c_e^2 \delta _e^2)+C^{y}_V C^{{y\,*}}]\, \epsilon _{\ell } \\ C^{y\,*}_{\Delta }C^{y}_{V\Delta }({\delta '_e}^2-{\delta _e}^2) c_es_e\epsilon _{\ell }&{} [ C^{y}_{V\Delta } (C^{y\,*}_{\Delta }+C^{y\,*}_{VV\Delta }\epsilon ^2_{\ell }) (s_e^2 {\delta '_e}^2+c_e^2 \delta _e^2)+C^{y\,*}_V C^{y}]\, \epsilon _{\ell }&{} |C^y|^2+(s_e^2 {\delta '_e}^2+c_e^2 \delta _e^2)|C^{y}_{V\Delta }|^2 \end{pmatrix}. \end{aligned}$$

(64)

On the other hand, the right-handed mixing is obtained by diagonalizing $Y^\dagger Y$, which is:

$$\begin{aligned}&Y^\dagger Y= Y_0^2 \, \times \nonumber \\&\begin{pmatrix} [{C^y_{\Delta }}^2c_e^2+ (|C^{y}_{\Delta }+C^{y}_{VV\Delta }\epsilon ^2_{\ell }|^2+|C^{y}_{V\Delta }|^2\epsilon ^2_{\ell })s_e^2] {\delta '_e}^2 &{} (2\textrm{Re}{C^y_{\Delta }}+ |C^{y}_{VV\Delta }|^2\epsilon ^2_{\ell } +|C^{y}_{V\Delta }|^2) \delta '_e \delta _e \epsilon ^2_{\ell } c_e s_e &{} (C^{y\,*}_{\Delta }C^{y}_V+ C^{y\,*}_{V}C^{y}+C^{y\,*}_{VV\Delta }C^{y}_V\epsilon ^2_{\ell }) \delta '_e \epsilon _{\ell } s_e \\ (2\textrm{Re}{C^{y}_{\Delta }}+ |C^{y}_{VV\Delta }|^2\epsilon ^2_{\ell } +|C^{y}_{V\Delta }|^2) \delta '_e \delta _e \epsilon ^2_{\ell } c_e s_e&{} [{C^y_{\Delta }}^2 s_e^2+ (|C^{y}_{\Delta }+C^{y}_{VV\Delta }\epsilon ^2_{\ell }|^2+|C^{y}_{V\Delta }|^2\epsilon ^2_{\ell })c_e^2] {\delta _e}^2 &{} (C^{y\,*}_{\Delta }C^{y}_V+ C^{y\,*}_{V\Delta }C^{y}+C^{y\,*}_{VV\Delta }C^{y}_V\epsilon ^2_{\ell }) \delta _e \epsilon _{\ell } c_e \\ (C^{y}_{\Delta }C^{y\,*}_V+ C^{y}_{V}C^{y\,*}+C^{y}_{VV\Delta }C^{y\,*}_V\epsilon ^2_{\ell }) \delta '_e \epsilon _{\ell } s_e&{} (C^{y}_{\Delta }C^{y\,*}_V+ C^{y}_{V\Delta }C^{y\,*}+C^{y}_{VV\Delta }C^{y\,*}_V\epsilon ^2_{\ell }) \delta _e \epsilon _{\ell } c_e&{} |C^y|^2+|C^{y}_{V}|^2 \epsilon ^2_{\ell } \end{pmatrix}. \nonumber \\ \end{aligned}$$

(65)