Exact solutions based on Segre classification in the f(R) modified theory of gravity

Abstract

In this article, the Segre classification approach is used to obtain some new solutions for spherically symmetric static spacetime metric corresponding to Segre types [(1, 111)],  [1, (111)],  [(1, 1)(11)],  or [1, 1(11)]. The eigenvalue degeneracy in these situations correlates to timelike and spacelike eigenvectors and their primary null direction, which identify the kind of matter distribution in space and aid in the consideration of novel solutions for the corresponding energy momentum tensor. The isotropic Segre type [(1, 111)] in modified theory provides the Schwarzschild de-Sitter/anti-de-Sitter solutions, whereas in types [1, (111)] and [1, 1(11)] depending upon matter distribution new obtained solutions adhere all the physical conditions and present the viable trends of energy and causality conditions. Moreover, the profiles of the adiabatic index, surface, and gravitational redshift are observed along with the hydrostatic equilibrium using the Tolman–Oppenheimer–Volkoff equation. Additionally, for these types the solution is compared with observational data, and numerical values are calculated for central and surface densities and central pressure of compact star candidates $KS 1731-260$ and $PSR J1614-2230$. Segre type [(1, 1)(11)] relates to a non-null electromagnetic field that corresponds to models with anisotropy in dark energy, which is demonstrated by graphical analysis. Dark energy does not behave as an ordinary matter resulting in the violation of strong energy condition and the causality condition.

1 Introduction

General relativity (GR) is a fundamental physics theory that accurately predicts and explains universe processes. GR has been applied to understand galaxy origin, compact universe structures, black holes, gravitational wave spread, and universe expansion. The 1920s emergence of quantum mechanics and quantum field theory revealed flaws in GR, leading to the expansion of GR to reveal dark energy and dark matter, and the singularity theorem establishing a shared characteristic among all cosmological theories. Due to numerous shortcomings, scientists started studying alternative theories considering higher-order effects, to investigate dark energy and dark matter within the current cosmological paradigm.

Reference [1] solution, which predicts the existence of a black hole and explains the interior geometry of a fluid sphere with homogeneous energy density, was the first accurate vacuum solution in GR. Since then numerous studies have been conducted to find solutions for spherically symmetric and static spacetimes with and without charge, first in GR and currently in other theories of gravity. Researchers like [2,3,4,5,6,7,8,9] and many others have found solutions by considering the equations of state and different ansatz in GR. This particular research area is vastly explored in f(R) theory of gravity by many researchers, [10] studied spherically symmetric vacuum and perfect fluid solutions. In f(R) theory using the metric approach [11] found static plane-symmetric vacuum solutions and indicated their correspondence with well-known GR solutions. References [12, 13] in modified theory of gravity explained the mass radius relation and the causal maximum mass limit for the massive neutron star GW190814. The stability and dynamics of anisotropic compact stars using Krori and Barua metric potential is discovered by [14]. References [15, 16] in f(R) theory discussed the collapsing behavior of compact objects. A new rotating black hole solution in modified theory is obtained by [17] that exhibits stable thermodynamic features with two horizons, a significant singularity in comparison to Einstein’s GR, and asymptotic behavior towards AdS/dS spacetime. The physical features of the Schwarzschild black hole solution, including its declining gravity dominance in higher orders of f(R), are revealed through an exploration of its geodesics, stability requirements, and thermodynamic properties by [18]. Reference [19] obtained exact solutions for both the Ricci scalar dependent on the radial coordinate and the Ricci curvature scalar that is constant. Reference [20] also investigated spherically symmetric solutions using the Noether symmetry approach.

This paper aims to reduce arbitrariness in finding static spherically symmetric solutions of field equations in the modified theory of gravity. For this purpose, the Segre classification scheme is used, this scheme provides a systematic method for obtaining new solutions, limiting the need for ansatz in most cases. The only possible Segre types for spherically symmetric static spacetime are [(1,111)], [1,(111)], [(1,1)(11)] and [1,1(11)] as discussed earlier by [21]. The article is formatted as follows: In Sect. 2, field equations in the modified theory of gravity are explained briefly. Section 3 initially introduces the Segre classification scheme and solution of the Segre type [(1, 111)]. Further, in Sects. 3.1–3.3 solutions to $[1,(111)], [(1,1)(11)] \text {and} [1,1(11)]$ are explored in detail depending on their respective energy momentum tensor. Lastly, followed by the discussion in Sect. 4.

2 Field equation in the modified gravity

A key idea in general relativity that serves as the foundation for constructing the Einstein field equations is the Einstein–Hilbert action. The f(R) theory of gravity is essentially a generalization of general relativity. It is produced by replacing the Ricci scalar R in the Einstein–Hilbert action with an arbitrary function denoted by f(R). The action is given as

$$\begin{aligned} S=\frac{1}{16\pi }\int \sqrt{-g}\left( f(R)+L_M\right) d^4x, \end{aligned}$$

(1)

here g is the metrics determinant and $L_M$ stands for Lagrangian density for the matter Lagrangian. By varying the action with respect to $g_{ab}$, the relevant field equations are obtained as

$$\begin{aligned} f_RR_{ab}-\frac{f(R)}{2}g_{ab}+\left( g_{ab}\Box -\nabla _a\nabla _b\right) f_R=T_{ab}, \end{aligned}$$

(2)

where $f_R=\frac{\partial f}{\partial R}$, $\nabla _a$ represents the covariant derivative and $\Box$ is the d’Alembertian operator defined as $\Box =\frac{1}{\sqrt{-g}} \partial _a\left( \sqrt{-g}\partial ^a\right)$.

Here $T_{ab}$ is the energy momentum tensor for vacuum case we have $T_{ab}=0$ and the field equations are given as

$$\begin{aligned} f_RR_{ab}-\frac{f(R)}{2}g_{ab}+\left( g_{ab}\Box -\nabla _a\nabla _b\right) f_R=0. \end{aligned}$$

(3)

Let us consider the interior line element for static spherically symmetric spacetime given as

$$\begin{aligned} ds^2=-e^{\nu (r)} dt^2+e^{\lambda (r)} dr^2+r^2d\theta ^2+r^2sin^2\theta d\phi ^2, \end{aligned}$$

(4)

here the unknown metric potentials are denoted by $\lambda (r)$ and $\nu (r)$. The f(R) field equations corresponding to the spacetime metric (4) are given as

$$\begin{aligned}&f_R(e^{-\lambda })\left( \frac{\nu ^{\prime \prime }}{2}+\left( \nu ^\prime -\lambda ^\prime \right) \frac{\nu ^\prime }{4}+\frac{\nu ^\prime }{r}\right) +\frac{1}{2}f(R)\nonumber \\&\quad +e^{-\lambda }\left( f_R^{\ \prime }\left( \frac{\lambda ^\prime }{2}-\frac{2}{r}\right) -f_R^{\ \prime \prime }\right) =0, \end{aligned}$$

(5)

$$\begin{aligned}&f_R(e^{-\lambda })\left( \frac{-\nu ^{\prime \prime }}{2}-\frac{\nu ^\prime }{4}\left( \nu ^\prime -\lambda ^\prime \right) +\frac{\lambda ^\prime }{r}\right) -\frac{1}{2}f(R)\nonumber \\&\quad +e^{-\lambda }\left( f_R^{\ \prime }\left( \frac{\nu ^\prime }{2}+\frac{2}{r}\right) \right) =0, \end{aligned}$$

(6)

$$\begin{aligned}&\frac{f_R}{r^2}\left( 1+\frac{e^{-\lambda }}{2}\left( r\lambda ^\prime -r\nu ^\prime -2\right) \right) -\frac{1}{2}f(R)\nonumber \\&\quad +e^{-\lambda }\left[ f_R^{\ \prime }\left( \frac{\nu ^\prime }{2}-\frac{\lambda ^\prime }{2}+\frac{1}{r}\right) +f_R^{\ \prime \prime } \right] =0. \end{aligned}$$

(7)

The simplest type of function will be considered in this article; the quadratic gravity or inflationary model proposed by [22], expressed as

$$\begin{aligned} f(R)=R+\alpha R^2, \end{aligned}$$

(8)

where $\alpha$ is a positive constant and $f_{RR}\ge 0$. Further, [14] indicated that in stellar objects values of $\alpha$ vary from 0 to 6. It is significant to note that when $\alpha =0$, general relativity results are retrievable. The vacuum field equations corresponding to Eq. (8) are

$$\begin{aligned}&(1+2\alpha R)\left( \frac{1}{r^2}-\frac{1}{r^2}(re^{-\lambda })^\prime \right) -\frac{\alpha R^2}{2}\nonumber \\&\quad +2\alpha e^{-\lambda }\left[ R^\prime \left( \frac{\lambda ^\prime }{2}-\frac{2}{r}\right) -R^{\prime \prime }\right] =0, \end{aligned}$$

(9)

$$\begin{aligned}&(1+2\alpha R) \left( e^{-\lambda }\left( \frac{\nu ^\prime }{r}+\frac{1}{r^2}\right) -\frac{1}{r^2}\right) +\frac{\alpha R^2}{2}\nonumber \\&\quad +2\alpha R^\prime e^{-\lambda }\left( \frac{\nu ^\prime }{2}+\frac{2}{r}\right) =0, \end{aligned}$$

(10)

$$\begin{aligned}&e^{-\lambda }\left( 1+2\alpha R\right) \left( \frac{\nu ^{\prime \prime }}{2}+\frac{\nu ^\prime \left( \nu ^\prime -\lambda ^\prime \right) }{4}+\frac{\left( \nu ^\prime -\lambda ^\prime \right) }{2r}\right) +\frac{\alpha R^2}{2} \nonumber \\&\quad + 2\alpha e^{-\lambda }\left[ R^{\ \prime }\left( \frac{\nu ^\prime }{2}-\frac{\lambda ^\prime }{2}+\frac{1}{r}\right) +R^{\ \prime \prime } \right] =0. \end{aligned}$$

(11)

Here $R^\prime$ and $R^{\prime \prime }$ are the first and second order derivative of R, for the spacetime metric R is given as

$$\begin{aligned} R=e^{-\lambda }\left( -\nu ^{\prime \prime } -\frac{\nu ^\prime \left( \nu ^\prime -\lambda ^\prime \right) }{2}-\frac{2\nu ^\prime }{r}+\frac{2\lambda ^\prime }{r}-\frac{2}{r^2}+\frac{2e^\lambda }{r^2}\right) . \nonumber \\ \end{aligned}$$

(12)

3 Exact solution using segre classification

The Segre classification scheme is one of the most significant way for obtaining exact solutions. It helps to develop a systematic approach to obtain solutions, reducing the arbitrariness produced by a greater number of unknowns. This method was used by [21] to restrict ansatz for spherically symmetric static solutions of Einstein–Maxwell field equations (EMFEs). In the trace-free Ricci tensor context, the Segre types entail various combinations of eigenvalues and eigenvectors that lead to distinct algebraic patterns, aiding in understanding algebraic characteristics and symmetries of gravitational fields in specific spacetime areas and elucidating geometric and physical characteristics.

The trace-free Ricci tensor $S_{\alpha \beta }$ must first be defined in order to determine the classification of spacetime. It is given as [23]

$$\begin{aligned} S_{\alpha \beta }= R_{\alpha \beta }-\frac{1}{4}Rg_{\alpha \beta }, \end{aligned}$$

(13)

The Segre classification of $S_{\alpha \beta }$ is determined by splitting the matrix $S_{\alpha \beta }$ into Jordan canonical blocks, each of which stands for an eigenvalue. The number of eigenvalues in square brackets and the number of eigenvalues that recur in parentheses correlate to the size of Jordan blocks. The non-zero components of the symmetric matrix $\phi _{\alpha \beta }$ are used to compute the Segre type of matrix. Here, $\phi _{\alpha \beta }$ are the Ricci Newmann Penrose scalars that help in determining the nature of eigenvalues in different Segre types, defined as

$$\begin{aligned} \begin{aligned} \phi _{00}&= \frac{1}{2}S_{\alpha \beta }k^\alpha k^\beta , \hspace{2.82cm} \phi _{01} = \frac{1}{2}S_{\alpha \beta }k^\alpha m^\beta , \\&\quad \phi _{02} = \frac{1}{2}S_{\alpha \beta }m^\alpha m^\beta , \\ \phi _{11}&= \frac{1}{2}S_{\alpha \beta }\left( k^\alpha l^\beta +m^\alpha \overline{m}^\beta \right) , \hspace{1cm} \phi _{12}= \frac{1}{2}S_{\alpha \beta }l^\alpha m^\beta , \\&\quad \phi _{22}= \frac{1}{2}S_{\alpha \beta }l^\alpha l^\beta . \end{aligned} \nonumber \\ \end{aligned}$$

(14)

Here, $l^\alpha , k^\alpha , m^\alpha , {\overline{m}}^\alpha$ are the null tetrads components that must satisfy the following condition

$$\begin{aligned} k^\alpha k_\alpha =-1 \ \ \ m^\alpha {\overline{m}}_\alpha =1. \end{aligned}$$

(15)

For the metric (4), the only non-zero components of Ricci Newman Penrose scalars are

$$\begin{aligned} \phi _{00}&=\left( \frac{\nu ^\prime +\lambda ^\prime }{r}\right) \frac{e^{-\lambda }}{4}=\phi _{22}, \end{aligned}$$

(16)

$$\begin{aligned} \phi _{11}&=\left( \nu ^{\prime \prime }+\frac{\nu ^\prime \left( \nu ^\prime -\lambda ^\prime \right) }{2}-\frac{2}{r^2}+\frac{2e^\lambda }{r^2}\right) \frac{e^{-\lambda }}{8}. \end{aligned}$$

(17)

The relation between non zero scalars and different Segre types as given by [24] is

Table 1 A standard frame for Segre types of trace-free Ricci tensor

All non-zero scalars belong to distinct Segre types, and each type is physically interpreted and corresponds to a certain kind of energy momentum tensor. This interpretation is based on the algebraic features of the energy–momentum tensor and the solutions of general relativity field equations. In our case, we have three non-zero scalars and from Table 1, we write their relationship with various Segre types as:

• when $\phi _{00}=\phi _{22}=0$ and $\phi _{11}=0$ this refers to Segre Type [(1, 111)];

• when $\phi _{00}=\phi _{22}=2\phi _{11}\ne 0$ this refers to Segre Type [1, (111)];

• when $\phi _{00}=\phi _{22}=0$ and $\phi _{11}\ne 0$ this refers to Segre Type [(1, 1)(11)];

• when $\phi _{00}=\phi _{22}\ne 0$ and $\phi _{11}\ne 0$ this refers to Segre Type [1, 1(11)].

Based on the mathematical characteristics of the Ricci tensor, these classifications assist physicists in characterizing the source of gravity and other physical properties in a particular spacetime, whether generated by electromagnetic fields or a perfect fluid (isotropic/anisotropic). The first integer surrounded in square brackets represents the timelike eigenvalue, whereas the others are spacelike. The Segre type [(1, 111)] is entirely isotropic and gives the cosmological solution, since all the eigenvectors have similar eigenvalues. For Segre Type [(1, 111)] we obtained a comparable solution in f(R) theory of gravity to that established earlier by Iram et al in GR i.e.

$$\begin{aligned} ds^2= & {} -\left( 1-\frac{c_0}{r}-\frac{c_1r^2}{3}\right) dt^2+\left( 1-\frac{c_0}{r}-\frac{c_1r^2}{3}\right) dr^2\nonumber \\{} & {} +r^2d\theta ^2+r^2sin^2\theta d\phi ^2. \end{aligned}$$

(18)

For positive and negative values of $c_1$, respectively, it is an established Schwarzschild de-sitter/anti de-sitter solution. In the subsequent sections, we will go through the other novel solutions found by the remaining three Segre types in the f(R) theory of gravity.

3.1 Segre type [1, (111)]

In this case, the eigenvalue degeneracy refers to the three spacelike eigenvectors with equal eigenvalues, and the timelike eigenvector has a different eigenvalue. The fluids behavior is isotropic, with a unique timelike direction, but it is uniform in all spatial directions. Thus the energy–momentum tensor of Segre type [1, (111)] is considered to be perfect fluid given as

$$\begin{aligned} T^{\ \ (pf)}_{ab}=(\rho +p)u_au_b+pg_{ab}, \end{aligned}$$

(19)

here, $\rho$ is the energy density, p is the pressure, $u_a$ is the four velocity. Corresponding to the metric the components of energy momentum tensor become

$$\begin{aligned} T^{\ \ (pf)}_{ab}=(-\rho ,p,p,p). \end{aligned}$$

(20)

Now as $\phi _{00}=\phi _{22}=2\phi _{11}\ne 0$, this implies

$$\begin{aligned} \phi _{00}-2\phi _{11}= & {} \left( -\nu ^{\prime \prime }+\frac{\nu ^\prime }{r}+\frac{\lambda ^\prime }{r}+\frac{2}{r^2}\right. \nonumber \\{} & {} \quad \left. -\frac{2e^\lambda }{r^2}+\frac{\nu ^\prime \lambda ^\prime }{2}-\frac{\nu ^{\prime 2}}{2}\right) =0, \end{aligned}$$

(21)

along with two constraints given as

$$\begin{aligned}&\nu ^{\prime \prime }+\frac{\nu ^\prime \left( \nu ^\prime -\lambda ^\prime \right) }{2}-\frac{2}{r^2}+\frac{2e^\lambda }{r^2}\ne 0, \end{aligned}$$

(22)

$$\begin{aligned}&\frac{\nu ^\prime +\lambda ^\prime }{r}\ne 0. \end{aligned}$$

(23)

There is a system of two independent governing equations along with energy momentum tensor that specifies the existence of four unknowns $(e^\lambda ,e^\nu , \rho ,p)$. Segre classification yields a further Eq. (21) that decreases the arbitrariness by one degree. To ascertain the solution of the system in the Segre type [1, (111)] an assumption for one of the metric potentials is made. In our case we assume $\nu$, given as

$$\begin{aligned} \nu =ln\left( \frac{1+r^2}{4}\right) , \end{aligned}$$

(24)

using this $\nu$, differential equation (21) implies

$$\begin{aligned} \lambda =ln\left( -\frac{2r^2+1}{(a_2r^2-1)(r^2+1)}\right) . \end{aligned}$$

(25)

Fig. 1

Graph of metric potential for $\alpha =0.05$ and $a_2=0.2567$

Fig. 2

Graph of density, pressure and ratio of pressure-density for $\alpha =0.05$ and $a_2=0.2567$

Fig. 3

Graph of density and pressure gradient for $\alpha =0.05$ and $a_2=0.2567$

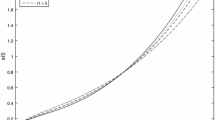
• By equation we get two metric potentials $e^{\lambda }$ and $e^{\nu }$ which are singularity free the most essential condition for a physically acceptable solution. The metric potential $e^\lambda$ is 1 at the center $(r=0)$ while $e^\nu$ at center is equivalent to some positive constant, both having increasing nature. The graph of the metric potential are plotted in Fig. 1 which satisfy the requisite conditions.

• The energy density and pressure expression in this case become

  $$\begin{aligned} \begin{aligned} \rho&=(1+2\alpha R)\left( \frac{1}{r^2}-\frac{1}{r^2}(re^{-\lambda })^\prime \right) -\frac{\alpha R^2}{2}\\&\quad +2\alpha e^{-\lambda }\left[ R^\prime \left( \frac{\lambda ^\prime }{2}-\frac{2}{r}\right) -R^{\prime \prime }\right] , \\ p&= \frac{\alpha R^2}{2}+ \left( \frac{e^{-\lambda }(1+2\alpha R)}{2}\right) \left( \frac{\nu ^{\prime \prime }}{2}+\frac{\nu ^\prime \left( \nu ^\prime -\lambda ^\prime \right) }{4}\right. \\&\quad \left. +\frac{3\nu ^\prime -\lambda ^\prime }{2r}+\frac{1-e^\lambda }{r^2}\right) \\&\quad +\alpha e^{-\lambda }\left( R^\prime \left( \nu ^\prime +\frac{3}{r}-\frac{\lambda ^\prime }{2}\right) +R^{\ \prime \prime }\right) . \end{aligned} \nonumber \\ \end{aligned}$$

  (26)

  Energy density and pressure must be free from central singularity. They should be decreasing with the variation in radial coordinate and pressure must vanish at boundary of the stellar object as illustrated in Fig. 2. Moreover, the pressure density ratio must be decreasing, continuous and less than one as in our case satisfying the requisite condition i.e. $\left( \frac{p}{\rho }\right) |_{r=0}\le 1$. Figure 3 depicts the decreasing nature of density gradient $\frac{d\rho }{dr}$ and pressure gradient $\frac{dp_r}{dr}$.

• Matching the interior solution at boundary $(r=R)$ to the Schwarzschild metric as

  $$\begin{aligned} e^{\lambda }=\left( 1-\frac{2M}{R}\right) ^{-1}, \end{aligned}$$

  (27)

  here, the total mass is given by M. The total mass at boundary in our case by using Eqs. (25) and (27) becomes

  $$\begin{aligned} \frac{2M}{R}= \frac{R^2}{2R^2+1}. \end{aligned}$$

  (28)

  The greatest allowable mass-to-radius ratio (M/R) for fluid spheres is $2M/R\le 8/9$, as stated by [25]. This is evident from Fig. 4, which illustrates the effective mass–radius relation for a static spherically symmetric perfect fluid star.

• The gravitational redshift occurs when leaving the gravitational well the photons or electromagnetic waves experience the energy loss, it is defined as

  $$\begin{aligned} z=e^{\frac{-\nu }{2}}-1. \end{aligned}$$

  (29)

  Whereas surface redshift refers to the entire mass and radius of the astronomical object. It is the most important component since no light will ever escape the event horizon, it is defined as

  $$\begin{aligned} z_s=e^{\frac{\lambda }{2}}-1. \end{aligned}$$

  (30)

  For our model the expressions become

  $$\begin{aligned} z&=\frac{2-\sqrt{2}\sqrt{r^2+1}}{\sqrt{2}\sqrt{r^2+1}},\end{aligned}$$

  (31)
  $$\begin{aligned} z_s&=\frac{\sqrt{-2r^2-1}}{\sqrt{(a_2r^2-1)(r^2+1)}}-1. \end{aligned}$$

  (32)

  The gravitational redshift is denser towards the center compared to the surface, as seen in Fig. 5. The surface redshift, however, is minimum at center and maximum at boundary.

• Energy conditions correspond to the following linear relationships between energy density and pressure, along with certain constraints.

  • 1. Weak Energy Condition (WEC):$\rho (r) \ge 0$,

  • 2. Null Energy Condition (NEC):$\rho (r)+p \ge 0$,

  • 3. Strong Energy Condition (SEC):$\rho (r)+3p \ge 0$,

  • 4. Dominant Energy Condition (DEC): $\rho (r) \ge |p|$.

  For this model Figs. 2 and 6 show that the energy criteria are fulfilled in the interior structure of the star.

• For stability of the compact object the causality condition inside the interior must be satisfied i.e. $0<v^2< 1$. It is defined as

  $$\begin{aligned} v^2= \frac{dp}{d\rho }, \end{aligned}$$

  (33)

  Figure 7 illustrates the required condition that is the speed of sound must be less than the speed of light $``c=1$” is satisfied making the system stable

• The adiabatic index is a thermodynamic parameter that in certain spacetime models discerns the effect of the matter and energy distribution with respect to specific heat capacity. In certain circumstances, it is a weak function of density while in some cases it has more intricate density dependence. For the stable configuration, the adiabatic index for pressure is given as the ratio of the specific heats, as explained by [26, 27]

  $$\begin{aligned} \Gamma =\left( \frac{\rho +p}{p}\right) \frac{dp}{d\rho }. \end{aligned}$$

  (34)

  If $\Gamma$ is greater than 4/3, as predicted by [28] then it is physically significant, as shown in Fig. 8.

• The TOV equations given by [29, 30] are the fundamental equation in astrophysics describing the equilibrium structure for static spherically symmetric spacetime modeling the gravitational balance and internal structure. Hydrostatic and gravitational forces are the two forces that are involved in this case, given as

  $$\begin{aligned} F_h= -\frac{dp}{dr}, \hspace{1cm}F_g= -(\rho +p)\nu '. \end{aligned}$$

  In the event of no net force acting, the stellar system remains in an equilibrium condition, implying that the following equation is satisfied

  $$\begin{aligned} F_h+F_g&=0,\end{aligned}$$

  (35)
  $$\begin{aligned} \frac{dp}{dr}+(\rho +p)\nu '&=0. \end{aligned}$$

  (36)

  Thus the sum of all forces, as shown in Fig. 9, is zero, with gravitational force acting as a counterbalance to the positive hydrostatic force.

Fig. 4

Graph of mass with radial coordinate for $\alpha =0.05$

Fig. 5

Graph of surface and gravitational redshifts for $\alpha =0.05$ and $a_2=0.2567$

Fig. 6

Graph of energy conditions for $\alpha =0.05$ and $a_2=0.2567$

Fig. 7

Graph of speed of sound for $\alpha =0.05$ and $a_2=0.2567$

Fig. 8

Graph of adiabatic index for $\alpha =0.05$ and $a_2=0.2567$

Fig. 9

Graph of forces for $\alpha =0.05$ and $a_2=0.2567$

3.2 Segre type [(1,1)(11)]

In this caes, the eigenvalue degeneracy corresponds to two eigenvectors with symmetry in the yz plane. The timelike eigenvector and the third eigenvector of spatial direction has a comparable eigenvalue to the timelike eigenvector. According to [23, 31], this type involves a non-null electromagnetic field. The fluid behavior of this Segre type will be anisotropic as a result of these principal null directions correlating to different eigenvalues. Therefore, non-null electromagnetic field with the anisotropic fluid distribution must be represented by a Segre-type energy–momentum tensor [(1,1)(11)] given as

$$\begin{aligned} T_{ab}=T^{\ \ (apf)}_{ab}+T^{\ \ (emt)}_{ab}, \end{aligned}$$

(37)

where $T^{\ \ (apf)}_{ab}$ and $T^{\ \ (emt)}_{ab}$ are given as

$$\begin{aligned} T^{\ \ (apf)}_{ab}=(\rho +p_t)u_au_b+p_tg_{ab}+(p_t-p_r)v_av_b, \end{aligned}$$

(38)

and

$$\begin{aligned} T^{\ \ (emt)}_{ab}=\frac{1}{4\pi }\left( F^{\ d}_aF_{bd}-\frac{1}{4}g_{ab}F_{cd}F^{cd}\right) . \end{aligned}$$

(39)

Here, E the electric field intensity, $p_r$ and $p_t$ are radial and tangential pressure, respectively, whereas $v^a$ denotes a unit space-like vector. Corresponding to the metric the component of energy momentum tensor become

$$\begin{aligned} T_{ab}= diag(-\rho -E^2,p_r-E^2,p_t +E^2,p_t +E^2). \end{aligned}$$

(40)

Reference [32] identified that anisotropy in dark energy is suggested by models like [(1, 1)(11)], with particular degeneracy complicating the behavior and having peculiar properties. In this type, we have $\phi _{00}=\phi _{22}=0$ and $\phi _{11}\ne 0$ that results in one constraint given by Eq. (22) and one additional equation, given as

$$\begin{aligned} \nu ^\prime +\lambda ^\prime =0. \end{aligned}$$

(41)

Due to the presence of anisotropy, electromagnetic field, and existence of system of three governing equations (9)–(11), there are a total of six unknowns $(e^\lambda , e^\nu , E^2, \rho , p_r, p_t)$ in this situation. So in order to find solution one needs to take three ansatz, but the presence of Segre type gives an additional equation (41) which reduces the arbitrariness to a choice of two. Thus assuming $E^2$ and $\lambda$, given as

$$\begin{aligned} E^2&= \frac{x}{2(1+x^2)}, \end{aligned}$$

(42)

$$\begin{aligned} \lambda&= ln\left( \frac{1+b_1r^2}{(1+b_2r^2)^2}\right) , \end{aligned}$$

(43)

where Eq. (41) implies

$$\begin{aligned} \nu = -ln\left( \frac{1+b_1r^2}{(1+b_2r^2)^2}\right) + a_3. \end{aligned}$$

(44)

• The metric potentials $e^\lambda$ and $e^\nu$ must be singularity free so our choice of $e^\lambda$ satisfies this condition and has an increasing nature. In this case, $e^\nu$ at center is equivalent to some positive constant and is decreasing when moving towards the boundary of compact object. The behavior of metric potential are shown in Fig. 10.

• The electric field intensity given by Eq. (42) satisfies the requisite condition of being zero at the center and then having an increasing nature when moving toward the boundary as depicted in Fig. 12.

• The energy density, radial and tangential pressure expression in this case become

  $$\begin{aligned} \begin{aligned} \rho&=(1+2\alpha R)\left( \frac{1}{r^2}-\frac{1}{r^2}(re^{-\lambda })^\prime \right) -\frac{\alpha R^2}{2}\\&\quad +2\alpha e^{-\lambda }\left[ R^\prime \left( \frac{\lambda ^\prime }{2}-\frac{2}{r}\right) -R^{\prime \prime }\right] -\frac{x}{2(1+x^2)},\\ p_r&=\frac{x}{2(1+x^2)}+(1+2\alpha R) \left( e^{-\lambda }\left( \frac{\nu ^\prime }{r}+\frac{1}{r^2}\right) -\frac{1}{r^2}\right) \\&\quad +\frac{\alpha R^2}{2}+2\alpha R^\prime e^{-\lambda }\left( \frac{\nu ^\prime }{2}+\frac{2}{r}\right) ,\\ p_t&=e^{-\lambda }\left( 1+2\alpha R\right) \left( \frac{\nu ^{\prime \prime }}{2}+\frac{\nu ^\prime \left( \nu ^\prime -\lambda ^\prime \right) }{4}+\frac{\left( \nu ^\prime -\lambda ^\prime \right) }{2r}\right) +\frac{\alpha R^2}{2} \\&\quad +2\alpha e^{-\lambda }\left[ R^{\ \prime }\left( \frac{\nu ^\prime }{2}-\frac{\lambda ^\prime }{2}+\frac{1}{r}\right) +R^{\ \prime \prime } \right] -\frac{x}{2(1+x^2)}. \end{aligned} \end{aligned}$$

  (45)

  Energy density and pressure must be free from central singularity. Here energy density at center ($\rho _c$) is equivalent to positive constant and is decreasing while moving towards the boundary of star. Both the tangential and radial pressure become negative that proves the presence of dark energy in models of Segre type [(1, 1)(11)]. $p_r$ is equivalent to $p_t$ at center and are increasing as moving further, whereas $p_r$ vanishes at boundary of star, as illustrated in Fig. 11.

• The difference between tangential and radial pressure i.e. ($\Delta$= $p_t$ − $p_r$) is defined as anisotropy where $p_r(0)=p_t(0)$ implies $\Delta _{r=0}$ is zero. It is essential for the compact object to have $\Delta$ > 0, which denotes that the anisotropic force is repellent in nature. This is feasible when ($p_t$ > $p_r$). Otherwise, if radial pressure is greater than tangential pressure ($p_r$ > $p_t$), then this indicates the existence of a new, attractive force. For this model the anisotropy is depicted in Fig. 12.

• Matching the interior solution at boundary to the Reissner Nordstrom metric as

  $$\begin{aligned} e^{\lambda }=\left( 1-\frac{2M}{R}+\frac{Q^2}{R^2}\right) ^{-1}, \end{aligned}$$

  (46)

  here, the total mass is given by M and charge by Q. The total mass at boundary in our case by using Eqs. (43) and (46) becomes

  $$\begin{aligned} \frac{2M}{R}= \frac{(1+aR^2)(1+E^2R^2)-(1+bR^2)^2}{1+aR^2}. \end{aligned}$$

  (47)

  The effective mass radius ratio as specified by [25] i.e. $2M/R\le 8/9$ is satisfied in this case as depicted in Fig. 13.

• The gravitational and surface redshift given by Eqs. (29) and (30) in this case become

  $$\begin{aligned} z&=\frac{(e^\frac{-a_3}{2})\sqrt{1+b_1r^2}-1-b_2r^2}{1+b_2r^2},\end{aligned}$$

  (48)
  $$\begin{aligned} z_s&=\frac{\sqrt{1+b_1r^2}-1-b_2r^2}{1+b_2r^2}. \end{aligned}$$

  (49)

  Graphically depicted in Fig. 14 where both profiles have increasing nature in the stellar interior.

• Energy conditions for anisotropic matter distribution correspond to the following linear relationships between energy density, radial and tangential pressure, along with certain constraints.

  • 1. WEC:         $\rho (r) \ge 0$,

  • 2. NEC:         $\rho (r)+p_r \ge 0$, $\rho (r)+p_t \ge 0$,

  • 3. SEC:         $\rho (r)+p_r+2p_t \ge 0$,

  • 4. DEC:          $\rho (r) \ge |p_i|$.

  Figures 11 and 15 show that the weak, dominant and null energy criteria are satisfied in this model. Regarding dark energy models, it is necessary to breach the strong energy condition, as shown in the profile, which is less than zero. Moreover, in these theories, the criteria for ordinary matter do not comply since dark energy is not an ordinary kind of matter or energy. The causality requirement is violated in addition to the violation of the strong energy condition. Since it affects the rate of expansion and the large-scale structure of cosmic objects, dark energy is essential to understanding the dynamics and development of the universe as a whole.

Fig. 10

Graph of metric potential with $\alpha =0.1$, $b_1=6$ and $a_3=-0.1$

Fig. 11

Graph of density, radial and tangential pressure with $\alpha =0.1$, $b_1=6$ and $a_3=-0.1$

Fig. 12

Graph of anisotropy with $\alpha =0.1$, $b_1=6$ and $a_3=-0.1$

Fig. 13

Graph of mass with radial coordinate for with $\alpha =0.1$, $b_1=6$ and $a_3=-0.1$ along with its upper bound

Fig. 14

Graph of surface and gravitational redshifts with $\alpha =0.1$, $b_1=6$ and $a_3=-0.1$

Fig. 15

Graph of energy conditions with $\alpha =0.1$, $b_1=6$ and $a_3=-0.1$

3.3 Segre type [1,1(11)]

In this case, the eigenvalue degeneracy refers to three spacelike eigenvectors, where there is a symmetry in the yz plane, while the other spacelike eigenvector indicates a different spatial direction from this symmetry plane. The one before the comma indicates the timelike eigenvector with a unique direction. As a result, the fluid behavior in this Segre type will be anisotropic, and the energy–momentum tensor for this Segre type [1, 1(11)] is considered to be an anisotropic perfect fluid, given by Eq. (38). Corresponding to the metric the component of energy momentum tensor become

$$\begin{aligned} T^{\ \ (apf)}_{ab}= (-\rho ,p_r,p_t,p_t). \end{aligned}$$

(50)

Now in this type, we have $\phi _{00}=\phi _{22}\ne 0$ and $\phi _{11}\ne 0$ which implies two constraints, one given by Eq. (22) and other given as

$$\begin{aligned} \left( -\nu ^{\prime \prime }+\frac{\nu ^\prime }{r}+\frac{\lambda ^\prime }{r}+\frac{2}{r^2}-\frac{2e^\lambda }{r^2}+\frac{\nu ^\prime \lambda ^\prime }{2}-\frac{\nu ^{\prime 2}}{2}\right) \ne 0, \end{aligned}$$

(51)

In this case, again for system of three governing Eqs. (9)–(11) and in presence of anisotropy there are five unknowns $(e^\lambda , e^\nu , E^2, \rho , p_r, p_t)$ along with the two constraints. This Segre type does not give any additional equation to reduce the arbitrariness, so we have to take two ansatz for finding the solution. So the Karmarkar criterion for class one spacetime is used to minimize the arbitrariness to take one ansatz. A 4-D curved space-time can be embedded within a 5-D pseudo-Euclidean space as discussed by [33]. The metric (4) can represent a class-I spacetime if satisfies the Karmarkar condition given as

$$\begin{aligned} R_{0101}R_{2323}=R_{0303}R_{1212}+R_{1220}+R_{1330}. \end{aligned}$$

(52)

The Riemann curvature tensor’s non-zero components for the metric (4) are given as

$$\begin{aligned} \begin{aligned} R_{0101}&= e^\nu \left( \frac{\nu ^{\prime \prime }}{2}+\frac{\nu ^{\prime 2}}{4}-\frac{\lambda ^\prime \nu ^\prime }{4}\right) ,\\ R_{0202}&=R_{0303}sin^2\theta =\frac{r\nu ^\prime }{2}, \\ R_{2323}&=r^2sin^2\theta (1-e^{-\lambda }), \\ R_{1212}&=R_{1313}sin^2\theta =\frac{r\lambda ^\prime }{2}, \end{aligned} \end{aligned}$$

(53)

where $R_{2323}\ne 0$. Thus the Karmarkar condition can be written as

$$\begin{aligned} \frac{\nu ''}{\nu '}=\frac{1}{2}\left[ \frac{\lambda 'e^\lambda }{e^\lambda -1}-\nu '\right] , \end{aligned}$$

(54)

by integrating Eq. (54), $\nu$ in terms of $\lambda$ is obtained as

$$\begin{aligned} e^\nu =\left( C_2\int \sqrt{e^\lambda -1}\,dr +C_1\right) ^2, \end{aligned}$$

(55)

where $C_1$ and $C_2$ are constants of integration. Consider the metric potential for the interior of anisotropic configuration as

$$\begin{aligned} e^\lambda =1+a_4r^2. \end{aligned}$$

(56)

By using Eq. (56) in Eq. (55) we get

$$\begin{aligned} e^\nu =\left( C_1+\frac{C_2\sqrt{a_4}r^2}{2} \right) ^2. \end{aligned}$$

(57)

Fig. 16

Graph of metric potential for $\alpha =0.1$, $C_1=0.56$, $C_2=0.62$ and $a_4=1.694$

Fig. 17

Graph of density for $\alpha =0.1$, $C_1=0.56$, $C_2=0.62$ and $a_4=1.694$

• The metric potential $e^\lambda$ and $e^\nu$ obtained in Eqs. (56) and (57) satisfy the necessary condition of being free from singularity, as shown in Fig. 16.

• The energy density, radial, and tangential pressure expression for this case are given as

  $$\begin{aligned} \rho&=(1+2\alpha R)\left( \frac{1}{r^2}-\frac{1}{r^2}(re^{-\lambda })^\prime \right) -\frac{\alpha R^2}{2}\nonumber \\&\quad +2\alpha e^{-\lambda }\left[ R^\prime \left( \frac{\lambda ^\prime }{2}-\frac{2}{r}\right) -R^{\prime \prime }\right] , \nonumber \\ p_r&=(1+2\alpha R) \left( e^{-\lambda }\left( \frac{\nu ^\prime }{r}+\frac{1}{r^2}\right) -\frac{1}{r^2}\right) \nonumber \\&\quad +\frac{\alpha R^2}{2}+2\alpha R^\prime e^{-\lambda }\left( \frac{\nu ^\prime }{2}+\frac{2}{r}\right) , \nonumber \\ p_t&=e^{-\lambda }\left( 1+2\alpha R\right) \left( \frac{\nu ^{\prime \prime }}{2}+\frac{\nu ^\prime \left( \nu ^\prime -\lambda ^\prime \right) }{4}+\frac{\left( \nu ^\prime -\lambda ^\prime \right) }{2r}\right) \nonumber \\&\quad +\frac{\alpha R^2}{2} + 2\alpha e^{-\lambda }\left[ R^{\ \prime }\left( \frac{\nu ^\prime }{2}-\frac{\lambda ^\prime }{2}+\frac{1}{r}\right) +R^{\ \prime \prime } \right] . \end{aligned}$$

  (58)

  The profiles given in Fig. 17 clearly exhibit the singularity free nature. Further, both the pressure are equivalent at the center, while radial pressure vanishes at the boundary. Due to $p_t>p_r$, Fig. 18 shows the positive anisotropy depicting the repellent nature of anisotropic force. This positive pressure satisfies the gradient condition i.e. $\frac{dp_r}{dr}$ and $\frac{dp_t}{dr}$ as displayed in Fig. 19. Moreover, In stellar interior Fig. 20 depicts the pressure density ratio is decreasing, continuous and less than one i.e $\left( \frac{p_r}{\rho }\right) |_{r=0}\le 1$ and $\left( \frac{p_t}{\rho }\right) |_{r=0}\le 1$.

• Now matching the interior solution at boundary to the Schwarzschild metric as done in Eq. (27), we get maximum mass at boundary. In this case, using the metric potential (56), we get

  $$\begin{aligned} \frac{2M}{R}= \frac{a_4R^2}{1+a_4R^2}. \end{aligned}$$

  (59)

  Figure 21 demonstrates that the maximum mass at the boundary is smaller than the upper bound 8/9 and that the effective mass-radius ratio is satisfied.

• In this case the expression for gravitational and surface redshift from Eqs.  (29) and (30) take the form as

  $$\begin{aligned} z&=\frac{2-2C_1-C_2\sqrt{a_4}r^2}{2C_1+C_2\sqrt{a_4}r^2},\end{aligned}$$

  (60)
  $$\begin{aligned} z_s&=\sqrt{(1+a_4r^2)}-1. \end{aligned}$$

  (61)

  The profiles are shown in Fig. 22, with the surface redshift increasing and the gravitational redshift decreasing within the compact object.

• The speed of sound in radial and transverse direction for anisotropic fluid distribution are obtained as

  $$\begin{aligned} v_r^2&= \frac{dp_r}{d\rho }=\left( \frac{dp_r/dr}{d\rho /dr}\right) , \end{aligned}$$

  (62)
  $$\begin{aligned} v_t^2&= \frac{dp_t}{d\rho }=\left( \frac{dp_t/dr}{d\rho /dr}\right) . \end{aligned}$$

  (63)

  For physical acceptance of solution both radially and transversely, the speed of sound must be less than the speed of light $``c=1''$ inside the stellar interior, as shown in Fig. 23. Reference [34] introduced the notion of ‘cracking’ for anisotropic matter dispersion. Later, [35] showed using the “cracking” notion that the region is possibly stable where $-1< v_t^2 -v_r^2 < 0$ and potentially unstable where $0< v_t^2 -v_r^2 < 1$ inside the anisotropic fluid sphere, implying $0<|v_t^2-v_r^2|<1$. From the graphical behavior shown in Fig. 24, it can be observed that this model satisfy causality conditions and the region inside the star is potentially stable.

• For this case, the energy conditions previously listed in Sect. 3.2 must be satisfied. From Figs. 17 and 18 one clearly observes that the dominant and weak energy criteria are fulfilled. Moreover, Fig. 25 shows profiles of the null, and strong energy conditions that abide by the necessary requirements.

• For stable configuration the adiabatic index for radial and tangential pressure is presented as the two specific heats ratio given as.

  $$\begin{aligned} \begin{aligned} \Gamma _r&=\left( \frac{\rho +p_r}{p_r}\right) \frac{dp_r}{d\rho },\\ \Gamma _t&=\left( \frac{\rho +p_t}{p_t}\right) \frac{dp_t}{d\rho }. \end{aligned} \end{aligned}$$

  (64)

  The model is physically relevant in this case as well when the value of $\Gamma _r$ and $\Gamma _t$ is greater than 4/3, as shown in Fig. 26.

• When anisotropy is taken into account, then hydrostatic, gravitational, and anisotropic forces are acting on the stellar configuration, given as

  $$\begin{aligned} F_h= -\frac{dp}{dr},\quad F_g= -(\rho +p)\nu ',\quad F_a=\frac{2}{r}(p_t-p_r), \end{aligned}$$

  The configuration remains in an equilibrium state if the net force acting is zero i.e.

  $$\begin{aligned}&F_h+F_g+F_a =0,\end{aligned}$$

  (65)
  $$\begin{aligned}&\frac{dp}{dr}+(\rho +p)\nu '-\frac{2}{r}(p_t-p_r)=0. \end{aligned}$$

  (66)

  The sum of all forces, as shown in Fig. 27 tends to zero, with gravitational force acting as a counterbalance to the positive hydrostatic and anisotropic force.

Fig. 18

Graph of radial and tangential pressure for $\alpha =0.1$, $C_1=0.56$, $C_2=0.62$ and $a_4=1.694$

Fig. 19

Graph of anisotropy for $\alpha =0.1$, $C_1=0.56$, $C_2=0.62$ and $a_4=1.694$

Fig. 20

Graph of pressure density gradients for$\alpha =0.1$, $C_1=0.56$, $C_2=0.62$ and $a_4=1.694$

Fig. 21

Graph of pressure density ratio for $\alpha =0.1$, $C_1=0.56$, $C_2=0.62$ and $a_4=1.694$

Fig. 22

Graph of mass with radial coordinate for $\alpha =0.1$, $C_1=0.56$, $C_2=0.62$ and $a_4=1.694$

Fig. 23

Graph of surface and gravitational redshifts for $\alpha =0.1$, $C_1=0.56$, $C_2=0.62$ and $a_4=1.694$

Fig. 24

Graph of speed of sound and stability factor for $\alpha =0.1$, $C_1=0.56$, $C_2=0.62$ and $a_4=1.694$

Fig. 25

Graph of energy conditions for $\alpha =0.1$, $C_1=0.56$, $C_2=0.62$ and $a_4=1.694$

Fig. 26

Graph of adiabatic index for $\alpha =0.1$, $C_1=0.56$, $C_2=0.62$ and $a_4=1.694$

Fig. 27

Graph of forces for $\alpha =0.1$, $C_1=0.56$, $C_2=0.62$ and $a_4=1.694$

4 Discussion

In literature, many attempts have been made to develop solutions for spherically symmetric and static spacetimes with and without charge, first in GR and currently in theories of gravity. In this article, some new solutions in the f(R) modified theory of gravity are presented using a systematic approach of Segre classification. By this systematic approach, the number of assumptions required to solve the complex system is reduced. Solution can only be of the Segre types [(1, 111)], [1, (111)], [(1, 1)(11)],  or [1, 1(11)] corresponding to the spacetime metric. The eigenvalue degeneracy in these situations correlates to timelike and spacelike eigenvectors and their primary null direction depending on which energy–momentum tensor for the respective Segre type tensor is considered. The entirely isotropic Segre type [(1, 111)] gives the cosmological solution as in our case we recover the Schwarzschild de-Sitter/anti-de-Sitter solutions in the modified theory of gravity. The type [1, (111)] can represent perfect fluid, with pressure isotropic in space, by considering this novel solution is obtained. In this case, the new solution satisfies all the physical and stability criteria. Each of the energy criteria is fulfilled along with the causality condition in which we have the speed of sound less than the speed of light. Moreover, the equilibrium condition is checked where the sum of all forces becomes zero making the model more stable and compact.

The type [(1, 1)(11)] represents a non-null electromagnetic field, for such type, the particular behavior is complex resulting in conventional dark energy models having anisotropy. Arbitrariness is decreased by one degree owing to the extra equation provided by the non-zero Ricci-Newmann Penrose scalars. The graphical analysis for this particular model is presented in Fig. 10, 11, 12, 13, 14 and 15. The resulting pressure is negative in this scenario which is associated with dark energy. Dark energy is not an ordinary form of matter, its repulsive nature counteracts the attractive gravitational forces caused by matter. The strong energy condition provides gravitational attraction due to positive curvature, but in this scenario repulsive nature of dark energy results in the violation of SEC as depicted in Figure. The causality criterion additionally fails in this instance since exotic substances do not always fit the prerequisites for ordinary matter. For such solutions, one can verify the existence of wormholes in the modified f(R) theory of gravity, as carried out by [36].

Table 2 Comparison of matter densities and central pressure for the stated compact object when $\alpha =0$ in the GR case and its deviation for $\alpha \ne 0$

Table 3 Comparison of matter densities and central pressure for fixed values of $C_1=1$ and $a_4=7.35\times 10^{-3}$ when $\alpha =0$ in the GR case and its deviation for $\alpha \ne 0$

The Segre type [1, 1(11)] refers to the anisotropic distribution of matter and energy. Here, we have two constraints, five unknowns, and a system of three governing equations. The Karmarkar condition with metric potential $e^\lambda =1+a_4r^2$ is used to further minimize the arbitrariness. The physical parameters $e^\lambda$, $e^\nu$, anisotropy, and mass increase when moving toward the boundary of the stellar interior, which is essential for a physically acceptable configuration. Furthermore, the viable trends of energy and causality conditions are presented. The profiles of the adiabatic index, pressure density ratio, surface and gravitational redshift are observed to satisfy the requisite criterion. The solution reflects a static and equilibrium configuration since the forces acting on the distribution of matter balance each other out. Now for different Segre types, we match the solution with the observational data of different compact objects. We specifically investigate two pulsars for type [1, (111)] and [1, 1(11)]: $KS 1731-260$, associated with thermonuclear bursts, and $PSR J1614-2230$, identified as a millisecond pulsar. The numerical values for constant are determined to performed a comparative analysis, ensuring that the results were consistent with observational limitations. Comprehensive numerical results are shown in Tables 2 and 3, which provide a thorough comparison of matter densities and central pressure under a modified gravity framework where $\alpha \ne 0$. These findings emphasize discrepancies from general relativity’s predictions. The tables also contain the outcomes of the special case where we return to GR i.e. $\alpha =0$. Such a comparison is earlier done by [37] by assuming a nuclear density of the order $10^{15}\mathrm{{g/cm}}^3$ for various pulsars. Our investigation further shows that the f(R) theory of gravity appears to be a suitable framework to explain the viability of a new classification. Furthermore, this study might be extended to other modified theories, enabling the identification of solutions via Segre classification that can be systematically compared with other astrophysical observations.