1 Introduction

The measurement of redshift and luminosity distance for type Ia supernovae events [1, 2], played a pivotal role in confirming the transition of the universe from a decelerated phase to its current accelerated phase during its late-time evolution. These findings are substantiated by the analysis of temperature anisotropies in the cosmic microwave background data from the WMAP mission [3, 4] and the detection of baryon acoustic oscillations [5]. The general theory of relativity posits that the accelerated expansion is driven by a hypothetical energy density component characterized by negative pressure, commonly referred to as dark energy. Investigating the origin and nature of dark energy responsible for the ongoing cosmic acceleration remains a prominent unsolved mystery in contemporary cosmology. The present-day cosmic acceleration cannot be accounted for by the standard equation of state, expressed as \(\omega = p/\rho \), where p and \(\rho \) represent the pressure and energy density of the conventional universe contents, such as radiation and matter. In fact, we need a ‘yet-to-be-identified’ component characterized by negative pressure, resulting in an equation of state \(\omega < -1/3\), to provide an explanation for the accelerated expansion.

Initially, Einstein introduced a cosmological constant term \(\Lambda g_{\mu \nu }\) into his field equations of general relativity to support his static universe theory. However, he later abandoned it in favor of Hubble’s observations of an expanding universe. Nevertheless, in the latter part of the last century, as late-time cosmic acceleration was discovered, the cosmological constant term regained attention due to its potential to offer a straightforward solution to Einstein’s field equations, resulting in an accelerated expansion. This gave rise to the \(\Lambda \)-CDM model, where ‘CDM’ refers to cold dark matter. Unfortunately, this model grapples with the coincidence problem [6] and the fine-tuning problem [7]. These issues drive the exploration of alternative models to account for dark energy.

One category of models involves field-theoretic approaches to dark energy, where modifications are made to the energy-momentum tensor in Einstein’s field equations due to the presence of a scalar field as an additional component in the universe, distinct from matter and radiation. These models encompass quintessence [8,9,10,11,12,13,14,15,16] as well as k-essence models [17,18,19,20,21,22,23,24,25,26,27,28,29]. Another class of models focuses on modifying the geometric aspects of Einstein’s equations, particularly the Einstein–Hilbert action, as a means to address late-time cosmic acceleration. These models include f(R) gravity models, scalar-tensor theories, Gauss–Bonnet gravity, and braneworld models of dark energy, as detailed in references [30,31,32,33,34,35,36]. In many of these scenarios, the universe is assumed to exhibit homogeneity and isotropy on large scales, described by the Friedmann–Lemaître–Robertson–Walker (FLRW) metric with a time-dependent scale factor denoted as a(t) and a curvature constant. Some approaches also consider an inhomogeneous universe, where a perturbed FLRW metric represents the background spacetime.

Dynamical systems techniques are powerful tools for exploring cosmic evolution in generic cosmological models, as well as for investigating specific cosmological solutions. Dynamical systems analysis has recently been employed to assess the stability of various scalar field dark energy models in comprehensive reviews [37,38,39,40,41], as well as in the context of f(R) gravity [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57]. A systematic and comprehensive exploration of dynamical systems within f(R) gravity theories has been carried out in a series of research endeavors documented in [58,59,60,61] and references therein. These studies aimed to identify and classify models that faithfully portray the correct cosmological evolution among a diverse set of f(R) gravity models. Consequently, they contributed to the construction and development of ‘cosmologically viable’ f(R) gravity models, characterized by trajectories in the dynamical system phase space that align with observed cosmic phenomena. These viable f(R) gravity models also conform to local gravity constraints, as extensively discussed with examples in references [42,43,44]. What makes these models appealing is their ability to provide cosmic acceleration without requiring a cosmological constant or the introduction of dark energy as an additional field component in the universe. Instead, dark energy is ‘curvature-driven’ - the dynamics described by the modified field equations incorporate the function f(R) of Ricci scalar (R), which possesses the potential to drive cosmic acceleration, even when facing stringent constraints from both local gravity tests and various observational limitations.

In this study, we explore a scenario in which curvature-driven dark energy interacts with (dark) matter, all within the framework of viable f(R) gravity models. We investigate whether the inclusion of these interactions in viable f(R) models has a significant impact on achieving accurate cosmological acceleration when compared to f(R) models that do not include matter-curvature interactions. In f(R)-gravity theories which maintain a minimal coupling to matter [30,31,32,33,34], the dynamics originate from an action composed of two components: a modified ‘geometric’ part obtained by replacing R with f(R) in the Einstein–Hilbert action, and a ‘matter’ component arising from the conventional constituents (matter and radiation) of the universe. The involvement of the metric \(g_{\mu \nu }\) in the matter component ensures minimal coupling with the geometry. The modified field equations can be restructured to assume the appearance of the standard field equations, expressed as \(G_{\mu \nu } = 8\pi G T^\mathrm{(tot)}_{\mu \nu }\), where \(G_{\mu \nu }\) is the Einstein tensor and \(T^\mathrm{(tot)}_{\mu \nu } \equiv T^\mathrm{(M)}_{\mu \nu } + T^\mathrm{(curv)}_{\mu \nu }\). The component \(T^\mathrm{(curv)}_{\mu \nu }\) is determined by f(R) and its derivatives, and vanishes for \(f(R) = R\) reducing to Einstein gravity. \(T^\mathrm{(M)}_{\mu \nu }\) is a modification obtained by scaling the usual energy-momentum tensor \(\tilde{T}_{\mu \nu }\) from Einstein’s equation by the factor \([df(R)/dR]^{-1}\). \(T^\mathrm{(curv)}_{\mu \nu }\) effectively serves as a representation of the stress–energy tensor, simulating a fluid-equivalent of the curvature function, while \(T^{\mu \nu }\) is the adjusted stress–energy tensor for ‘matter and radiation’ in the presence of gravity modifications arising from f(R). In FLRW spacetime background, the conservation of \(T^\mathrm{(tot)}_{\mu \nu }\) leads to a continuity equation that expresses the conservation in terms of the energy density and pressure for the comprehensive fluid, comprising radiation, matter, and curvature components. The continuity equation for each individual sector may allow for the inclusion of source terms, as long as the overall continuity equation for the comprehensive fluid remains valid without any source term. In this study, we considered radiation to be decoupled from matter and curvature and proposed that interactions between the matter and curvature components introduce a source term Q in their respective continuity equations, with opposite signs. The term Q serves as a measure of rate of energy exchange between the matter and curvature sectors owing to their interaction. In prior research [58], the expression for Q has been determined on the multiplicative function of matter density and Hubble parameter. In this subsequent analysis, we take a further step by formulating the interaction term as \(Q = \frac{\kappa ^2 \alpha }{3\,H}\tilde{\rho }_\textrm{m} \rho _\textrm{curv}\) where, \(\alpha \) signifies the strength of the coupling between matter and curvature with \(\tilde{\rho }_\textrm{m}\) and \(\rho _\textrm{curv}\) as their respective energy densities.

The incorporation of interactions between matter and curvature thus introduces the additional parameter \(\alpha \) in into the analytical framework. This coupling parameter, in conjunction with the parameters defining the function f(R), becomes intricately entwined within the evolution equations, playing a substantial role in shaping the evolutionary dynamics in the matter-curvature coupled scenario. We employed dynamical analysis technique as a method to explore this interacting curvature-matter scenario in the context of viable f(R)-gravity models. This process entailed setting up the representative autonomous equations in terms of appropriately defined dynamical variables describing the cosmic evolution in this context. The essential components of our study involved identifying the fixed points of the system and examining their stability using the technique of linear stability analysis. These are crucial for achieving a comprehensive understanding of critical aspects in cosmic evolution, particularly those influenced by the interactions between curvature and matter, as considered in the present framework of our study. In this investigation, we’ve opted for two specific f(R) models, namely, the generalised \(\Lambda \)-CDM model: \(f(R) = (R^b - \Lambda )^c,\quad c \geqslant 1, bc \approx 1 \) and the power law model: \(f(R) = R - \gamma R^n, \quad \gamma >0\), \(0<n<1\). Both models have the potential to drive cosmic acceleration while maintaining their cosmological viability. In general, the fixed points and characterisation of their stability are dependent on the parameters involved in the analysis, such as \(\alpha \), (b, c) or n. Additionally, values of the density parameters for various components and the equation of state for the overall fluid at these fixed points provide crucial insights into the distinctive critical phases associated with each point. We obtain the parameter limits within which a given fixed point may exhibit stable, unstable, or saddle-like behaviour. We also examine whether it can serve as an acceleration solution while staying within the boundaries of various cosmological constraints, as elaborated in subsequent sections.

Finally, we explore how curvature-driven dark energy influences various phases of cosmic evolution within the framework of matter-curvature interactions. To achieve this, we examined the evolution of matter-to-curvature energy density ratio (denoted as \(r_{mc}\) in the text), as well as two additional cosmographic parameters: deceleration (q) and jerk (j). The evolution of \(r_{mc}\) provides quantitative information about the dominance of curvature over matter at different stages of cosmic evolution. On the contrary, the deceleration parameter, along with the jerk, provides a detailed account of the kinematic aspects of evolution. These investigations shed light on the potential scenarios that may arise within the context of matter-curvature interactions. The observed evolution of the deceleration and jerk parameters suggests that all the mentioned models ultimately converge toward the \(\Lambda \)-CDM model in the distant future.

The paper is organised as follows: In Sect. 2, we establish a theoretical framework that addresses the interaction between the curvature and matter sectors within the context of a flat FLRW metric. Section 3 is dedicated to formulating the autonomous equations of the dynamical system, which incorporates the interaction between matter and curvature-driven dark energy within the framework of f(R) gravity. Within this section, we also discussed the two specific f(R) models considered for this study. We present the fixed points of the autonomous system for each model and discuss their stability characteristics. Within Sect. 4, we examine the influence of curvature-driven dark energy on different phases of cosmic evolution. We summarize our conclusions in Sect. 5.

2 Theoretical framework of interacting curvature–matter scenario in f(R) gravity

Within the framework of f(R) theory of gravity that incorporates minimal curvature-matter coupling, the action can be expressed as follows [30, 31]

$$\begin{aligned} \mathcal {S} = \frac{1}{2\kappa ^2}\int d^4x\sqrt{-g}f(R) + \int d^4x~\mathcal {L}_M(g_{\mu \nu },\phi _M), \end{aligned}$$
(1)

where \(\kappa ^2=8\pi G\), f(R) is an arbitrary function of the Ricci scalar R and \(\mathcal{L}_{M}\) commonly referred to as the ‘matter’ Lagrangian, represents the Lagrangian density associated with both the radiation and matter (baryonic and CDM) components of the universe. The symbol g represents the determinant of the space-time metric tensor \(g_{\mu \nu }\). In metric formalism, the variation of this action with respect to the field \(g_{\mu \nu }\) gives the corresponding modified field equation as

$$\begin{aligned}{} & {} F(R) R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }f(R) + g_{\mu \nu }\square F(R) - \nabla _{\mu }\nabla _{\nu } F(R) \nonumber \\{} & {} \quad = \kappa ^2 \tilde{T}_{\mu \nu }^{(\mathrm M)}. \end{aligned}$$
(2)

Here, \(F(R) \equiv df/dR\), and \(\tilde{T}_{\mu \nu }^{(\mathrm M)}\) is the stress–energy tensor corresponding to radiation and matter components given by

$$\begin{aligned} \tilde{T}_{\mu \nu }^{(\mathrm M)} \equiv -{2 \over \sqrt{-g}}{\delta (\sqrt{-g}\mathcal{L}_M)\over \delta (g^{\mu \nu })} . \end{aligned}$$
(3)

Equation (2) may be reconfigured as [30]

$$\begin{aligned} G_{\mu \nu } \equiv R_{\mu \nu }- \frac{1}{2}Rg_{\mu \nu } = \kappa ^2 \left( T_{\mu \nu }^{(\mathrm M)} + T_{\mu \nu }^{(\mathrm curv)}\right) \equiv \kappa ^2 T_{\mu \nu }^{(\mathrm tot)} ,\nonumber \\ \end{aligned}$$
(4)

where, \(G_{\mu \nu }\) is the Einstein tensor and

$$\begin{aligned} \kappa ^2 T_{\mu \nu }^{(\mathrm curv)}{} & {} \equiv \frac{1}{F} \left[ \frac{1}{2}(f-RF)g_{\mu \nu } +\left( \nabla _{\mu }\nabla _{\nu }- g_{\mu \nu }\square \right) F \right] \nonumber \\ \end{aligned}$$
(5)
$$\begin{aligned} \text{ and } \quad T_{\mu \nu }^{(\mathrm M)}{} & {} \equiv \frac{1}{F} \tilde{T}_{\mu \nu }^{(\mathrm M)} \end{aligned}$$
(6)

In its reformulated form, the modified field Eq. (4) describes a FLRW universe featuring a fluid with a comprehensive energy-momentum tensor denoted as \(T_{\mu \nu }^{(\mathrm tot)} \equiv T_{\mu \nu }^{(\mathrm M)} + T_{\mu \nu }^{(\mathrm curv)}\). The influence of the function f(R) is readily apparent in both of these distinct components \(T_{\mu \nu }^{(\mathrm curv)}\) and \(T_{\mu \nu }^{(\mathrm M)}\), which collectively constitute \(T_{\mu \nu }^{(\mathrm tot)}\). The component \(T_{\mu \nu }^{(\mathrm curv)}\) is exclusively determined by f(R) and its higher derivatives and it vanishes for \(f(R)=R\). This component effectively acts as a portrayal of the stress–energy tensor, mimicking a fluid-equivalent of the curvature function f(R). The component \(T_{\mu \nu }^{(\mathrm M)}\) is obtained by modifying \(\tilde{T}_{\mu \nu }^{(\mathrm M)}\) using a functional multiplier of 1/F (which equals 1 when \(f(R) = R)\). It serves as the revised stress–energy tensor for ‘matter and radiation’ in presence of gravity modifications resulting from f(R). In the context of a flat FLRW spacetime background, when we regard the matter and radiation content as a perfect fluid, the (unmodified) stress–energy tensor \(\tilde{T}_{\mu \nu }^{(\mathrm M)}\) becomes diagonal with entries being completely determined by the combined energy densities \((\tilde{\rho }_\textrm{m} + \tilde{\rho }_\textrm{r})\) of dark matter (\(\tilde{\rho }_m\)), radiation (\(\tilde{\rho }_\textrm{r}\)), and the radiation pressure (\(\tilde{P}_\textrm{r} = \tilde{\rho }_r/3\)). The matter component is considered to be non-relativistic pressureless dust. Consequently, the modified stress energy tensor \(T^{(M)}_{\mu \nu } = (1/F)\tilde{T}_{\mu \nu }^{(\mathrm M)}\) corresponds to a fluid with energy density \((\rho _\textrm{m} + \rho _\textrm{r})\) and pressure \(P_\textrm{r}\), where \((\rho _\textrm{r},\rho _\textrm{m}, P_\textrm{r}) \equiv (\tilde{\rho }_\textrm{r}/F, \tilde{\rho }_\textrm{m}/F, \tilde{P}_\textrm{r}/F)\). Note that, \(\rho _i, P_\textrm{r}\) (\(i=\textrm{r},\textrm{m}\)) are always positive because of the inherent positivity of (\(\tilde{\rho _i},\tilde{P_\textrm{r}}\)) and positivity of F as well—a necessary condition for any cosmologically viable f(R) model (discussed later in Sect. 3.2). However, under such considerations, the ‘00’ and ‘ii’ components of the modified field equation (4) respectively yield the following modified versions of the Friedmann equations;

$$\begin{aligned} \left( \frac{\dot{a}}{a}\right) ^2\equiv & {} H^2 = \frac{\kappa ^2 }{3}\Big [ \rho _\textrm{r} + \rho _\textrm{m} + \rho _\textrm{curv} \Big ], \end{aligned}$$
(7)
$$\begin{aligned} \frac{\ddot{a}}{a}= & {} \dot{H} + H^2 \nonumber \\= & {} - \frac{\kappa ^2}{6} \Big [ \rho _\textrm{r} + \rho _\textrm{m} + \rho _\textrm{curv} + 3(P_\textrm{r} + P_\textrm{curv})\Big ] , \end{aligned}$$
(8)

where a is the FLRW scale factor, \(H \equiv \dot{a}/a\) (the Hubble parameter) and dot \((\cdot )\) denotes derivative with respect to cosmic time. The quantities \( \rho _\textrm{curv}\) and \(P_\textrm{curv}\) are defined through the following equations

$$\begin{aligned} \kappa ^2 \rho _\textrm{curv}\equiv & {} \frac{1}{F}\left( \frac{RF-f}{2}-3H\dot{R}F'\right) \end{aligned}$$
(9)
$$\begin{aligned} \kappa ^2 P_\textrm{curv}\equiv & {} \frac{1}{F}\left( \dot{R}^2F'' + 2H\dot{R}F'+\ddot{R}F' +\frac{1}{2}(f-RF)\right) ,\nonumber \\ \end{aligned}$$
(10)

where \('\) denotes derivative with respect to R. It follows from Eq. (5) that, in a flat FLRW spacetime, the stress–energy tensor \(T_{\mu \nu }^\mathrm{{curv}}\) representing curvature-fluid can be equated with that of an ideal fluid with energy density and pressure given by \(\rho _\textrm{curv}\) and \(P_\textrm{curv}\) as provided in Eqs. (9) and (10). Also note that, we may express Eq. (7) as

$$\begin{aligned} \Omega _\textrm{m} + \Omega _\textrm{r} + \Omega _\textrm{curv}= & {} 1 \end{aligned}$$
(11)

where \(\Omega _\textrm{m}\), \(\Omega _{r}\) and \(\Omega _\textrm{curv}\) are modified form of density parameters defined by following equations:

$$\begin{aligned} \Omega _\textrm{m} \equiv \frac{\kappa ^2\rho _\textrm{m}}{3H^2}= & {} \frac{\kappa ^2\tilde{\rho }_\textrm{m}}{3FH^2},\nonumber \\ \Omega _\textrm{r} \equiv \frac{\kappa ^2 \rho _\textrm{r}}{3H^2}= & {} \frac{\kappa ^2\tilde{\rho }_\textrm{r}}{3FH^2},\nonumber \\ \Omega _\textrm{curv}\equiv & {} \frac{\kappa ^2\rho _\textrm{curv}}{3H^2} \end{aligned}$$
(12)

It’s also worth mentioning that the specific case of \(f(R) = R\) (\(F=1, F',F''=0\)) leads to \(\rho _{\textrm{curv}} = 0\), \(P_{\textrm{curv}} = 0\), \((\rho _i, P_{\textrm{r}}) =( \tilde{\rho }_i, \tilde{P}_{\textrm{r}} )\) implying reduction of modified Friedmann Eqs. (7) and (8) to conventional Friedmann equations.

Taking divergence of the both sides of Eq. (4) and use of Bianchi’s identity lead to the conservation equation of total stress–energy tensor \(T_{\mu \nu }^\textrm{tot} = T^{(M)}_{\mu \nu } + T^\textrm{curv}_{\mu \nu }\):

$$\begin{aligned} \nabla ^{\mu } T_{\mu \nu }^\textrm{tot}= & {} \nabla ^{\mu } \left( T_{\mu \nu }^{(\mathrm M)} + T_{\mu \nu }^{(\mathrm curv)}\right) =0 \end{aligned}$$
(13)

In FLRW spacetime, Eq. (13) takes the form of a continuity equation of the all-inclusive fluid with energy density \({\rho }_\textrm{tot} \equiv \rho _\textrm{r} + \rho _\textrm{m} + \rho _\textrm{curv} \) and pressure \(P_\textrm{tot} \equiv P_\textrm{r} + P_\textrm{curv}\) as

$$\begin{aligned} \dot{\rho }_\textrm{tot}+3H(\rho _\textrm{tot} +P_\textrm{tot}) = 0 \quad \text{ or } \quad \dot{\rho }_\textrm{tot}+3H{\rho }_\textrm{tot}(1 + \omega _\textrm{tot}) = 0, \nonumber \\ \end{aligned}$$
(14)

where \(\omega _\textrm{tot} \equiv P_\textrm{tot}/\rho _\textrm{tot}\) represents the ‘grand’ equation of state (EoS) parameter of the comprehensive (radiation+matter+curvature) fluid. Though the combined stress–energy tensor \(T^{(\mathrm tot)}_{\mu \nu }\) remains conserved, it is not necessary for its individual components: \(T^{(\mathrm curv)}_{\mu \nu }\) and \(T^{(M)}_{\mu \nu }\) (having radiation \(T^{(\mathrm r)}_{\mu \nu }\) and matter \(T^{(\mathrm m)}_{\mu \nu }\) as its further sub-components) to be separately conserved. This feature provides scope for incorporating ‘interactions’ between the matter and curvature sectors.

Considering the negligible contribution of the radiation component during the late time stages of cosmic evolution, we assume absence of interactions between radiation and combined matter-curvature sectors while simultaneously preserving the possibilities of interactions between matter and curvature sectors. With such considerations, we posit the conservation Eq. (13) as a system of equations: (I) \(\nabla ^{\mu } T_{\mu \nu }^{(\mathrm r)} = 0\) and (II) \(\nabla ^{\mu } T_{\mu \nu }^{(\mathrm m)} = -\nabla ^{\mu } T_{\mu \nu }^{(\mathrm curv)} \equiv - \mathcal {Q}{\nu } \ne 0\) which collectively, validate the overall conservation of the comprehensive tensor \(T^{(\mathrm tot)}_{\mu \nu }\). In FLRW spacetime, (I) implies \(\dot{\rho }_\textrm{r} +4H\rho _\textrm{r} = 0\) (\(\rho _\textrm{r} \sim a^{-4}\)) and equation set (II) corresponds to non-conservation equations of the form:

$$\begin{aligned} \dot{\rho }_\textrm{curv}+3H\left( \rho _\textrm{curv}+P_\textrm{curv}\right)= & {} Q \end{aligned}$$
(15)
$$\begin{aligned} \dot{\rho }_\textrm{m} +3H\rho _\textrm{m}= & {} -Q \end{aligned}$$
(16)

with a source term Q, which typically signifies a time-varying function characterizing the instantaneous rate of energy exchange between the curvature and matter sectors, reflecting their interactions. Interaction between dark matter and curvature-driven dark energy can either be introduced at the Lagrangian level, guided by field theoretic considerations, or at a phenomenological level by modelling the non-zero source term Q (in Eqs. (15),(16)) in temrs of suitable cosmological quantities. We adopt the latter approach, chosing a specific form of Q given by \(Q = \frac{\kappa ^2 \alpha }{3\,H}\tilde{\rho }_\textrm{m}\rho _\textrm{curv}\), where the coupling parameter \(\alpha \) is dimensionless maintaining the dimensional consistency in both Eqs. (15) and (16). In this context, we may mention that, in a previous study [58], the impact of interaction was explored using a functional form of the source term that exclusively depended on the energy density of the matter sector, Hubble parameter, and coupling constant in a multiplicative form. Expanding upon this framework, our chosen form of the source term involves the multiplication of the energy densities of both sectors capturing the instantaneous effects of both sectors on the source term with a dimensionless coupling constant. Our analysis reveals that such an interacting term also has the potential to address the coincidence problem, as discussed in the concluding section of the paper.

We imposed the constraint \(\rho _\textrm{curv} > 0\) in attributing the sense of ‘energy density’ (of the fluid-equivalent of the curvature) to \(\rho _\textrm{curv}\). This constraint restricts f(R) models to adhere to the condition \(RF - f>6H\dot{R}F'\) as evident from Eq. (9). It also constraints the coupling parameter \(\alpha \) as \(\rho _\textrm{curv}\) is interconnected with it through the source term Q as described by Eq. (15). Under such considerations, each of the modified density parameters \(\Omega _\textrm{r}\), \(\Omega _\textrm{m}\) and \(\Omega _\textrm{curv}\) remain positive and collectively subject to the constraint given by Eq. (11). This allows us to navigate and explore the parameter space relevant to the scenario of curvature-matter interaction by varying the parameter \(\Omega _\textrm{m}\) within the range \(0 \leqslant \Omega _\textrm{m} \leqslant 1\), eventually leading to obtaining constraints on the parameters of the model.

The acceleration phase (\(\ddot{a} > 0\)) corresponds to \(\omega _\textrm{tot} = P_\textrm{tot}/\rho _\textrm{tot} < -1/3\) as indicated by Eq. (8). F(R) and its derivatives are involved in \(\omega _\textrm{tot}\) through \(\rho _\textrm{curv}\) and \(P_\textrm{curv}\) which, in turn are linked to the coupling parameter \(\alpha \) via Equations (15) and (16). The values of the parameter \(\alpha \) and those involved in the parametrisation of F(R) that satisfy the condition \(\omega _\textrm{tot} < -1/3\) during the late-time phase of cosmic evolution corresponds a ‘Dark Energy’ scenario driven by matter-curvature interactions. Non-phantom dark energy scenarios adhere to the constraint \(-1< \omega _\textrm{tot} < -1/3\).

3 Dynamical analysis of f(R) models with curvature–matter interactions

3.1 Autonomous equations of dynamical system

We employ dynamical analysis as a tool to examine the curvature-matter interaction scenario within the framework of cosmologically viable f(R) gravity models. In this subsection we furnish the set of autonomous equations in terms of suitably constructed basic dynamical variables which serve to characterize the cosmological evolution within the context under consideration. This sets the ground for the application of techniques of dynamical analysis in our current context.

The basic dynamical variables are [44]

$$\begin{aligned} X_{1}= & {} - \frac{\dot{F}}{HF}, \quad X_{2}= - \frac{f}{6FH^2}, \quad X_{3}=\frac{R}{6H^2}, \nonumber \\ X_{4}= & {} \frac{\kappa ^2 \rho _\textrm{r} }{3H^2} = \frac{\kappa ^2 \tilde{\rho }_{r} }{3FH^2}=\Omega _{r} \end{aligned}$$
(17)

By introducing the dimensionless parameter denoted as \(N = \ln a\) to address temporal variations and applying the given definitions of dynamical variables (\(X_i\)’s), we can express Eqs. (9), (15), and (16) which capture the evolutionary dynamics within the curvature-matter interaction context, as the following set of 4 autonomous equations, forming a 4-D dynamical system:

$$\begin{aligned} \frac{dX_{1}}{dN}= & {} -1 - X_{1}X_{3}- X_{3} - 3X_{2} + X_{4} + X_{1}^2 \nonumber \\{} & {} +\ \alpha \left( 1- X_{1} - X_{2} - X_{3} - X_{4}\right) \left( X_{1} + X_{2} + X_{3}\right) \nonumber \\ \end{aligned}$$
(18)
$$\begin{aligned} \frac{dX_{2}}{dN}= & {} \frac{X_{1}X_{3}}{m}-X_{2}\left( 2X_{3}-4-X_{1}\right) \end{aligned}$$
(19)
$$\begin{aligned} \frac{dX_{3}}{dN}= & {} -\frac{X_{1}X_{3}}{m} - 2X_{3}\left( X_{3}-2\right) \end{aligned}$$
(20)
$$\begin{aligned} \frac{dX_{4}}{dN}= & {} - 2X_{3}X_{4} + X_{1}X_{4} , \end{aligned}$$
(21)

where

$$\begin{aligned} m\equiv & {} \frac{d \ln F}{d \ln R}= \frac{R F' }{F}, \end{aligned}$$
(22)

and in this context another parameter r is introduced as

$$\begin{aligned} r\equiv & {} -\frac{d \ln f}{d \ln R}= -\frac{R F}{f} = \frac{X_3}{X_2}. \end{aligned}$$
(23)

These dimensionless parameters m and r both depend on R through f(R), allowing us to write m as a function of r i.e. \(m = m(r)\). Each specific functional relation \(m = m(r)\) corresponds to a distinct class of f(R) models. When the coupling parameter \(\alpha \) is set to zero, the above set of equations reduces to the autonomous equations corresponding to the scenario that does not take into account interactions between the curvature and matter sectors. Also note that, if \(f(R)=R\), then the parameter m (as well as \(X_1\)) goes to zero, rendering the construction of the dynamical system infeasible.

By virtue of Eqs. (11) and (12) the dynamical variables in Eq. (17) are constrained by the equation

$$\begin{aligned} \Omega _\textrm{m} = 1 - X_{1} - X_{2} - X_{3} - X_{4} \end{aligned}$$
(24)

where \(\Omega _\textrm{m}\) is subject to the inequality \(0 \leqslant \Omega _\textrm{m} \leqslant 1\) and we can additionally write

$$\begin{aligned} \Omega _\textrm{curv} = 1 - \Omega _\textrm{m} - \Omega _{r} = X_{1} + X_{2} + X_{3}. \end{aligned}$$
(25)

Also, the ‘grand’ EoS parameter \(\omega _\textrm{tot}\) can be expressed as

$$\begin{aligned} \omega _\textrm{tot}= & {} -1 - \frac{2\dot{H}}{3H^2} = -\frac{1}{3}(2X_{3}-1) \end{aligned}$$
(26)

EoS parameter associated with the solo curvature sector [57] can be written as,

$$\begin{aligned} \omega _\textrm{curv}= & {} \frac{P_\textrm{curv}}{\rho _\textrm{curv}} = -\frac{(2X_{3}+X_{4}-1) }{3(X_{1}+X_{2}+X_{3})} \end{aligned}$$
(27)

The ratio of matter to curvature energy density, denoted as \(r_{mc} \equiv \Omega _\textrm{m}/\Omega _\textrm{curv}\), along with two additional cosmographic parameters - the deceleration \((q \equiv - a\ddot{a}/\dot{a}^2)\) and the jerk \((j \equiv \dddot{a}/aH^3)\)—serves as valuable indicators for evaluating various facets of cosmic dynamics. During late cosmic epochs, the ratio \(r_{mc}\), approximately reflects the ratio of ‘dark matter’ to ‘dark energy’ densities, as observations suggest baryonic contributions to be significantly smaller compared to dark matter contributions in the present-day universe. The parameter \(r_{mc}\) thus holds the potential to address the issue of the apparent coincidence between dark matter and dark energy densities in present-day universe (the cosmic coincidence problem). The deceleration (q) and jerk (j) parameters directly describe the ‘kinematic’ characteristics of cosmic evolution. A negative q signifies an accelerating universe, which is a hallmark of dark energy dominance. The constant \(q=-1\) value signifies presence of cosmological constant. A switchover from a positive to a negative value of q marks the transition point from a decelerating to an accelerating phase cosmic expansion. Furthermore, varying q values correspond to dynamical dark energy models, indicating the evolving nature of the universe’s acceleration. The jerk parameter, j is a measure of rate of change of acceleration (i.e. of q) and thus captures even finer temporal details of cosmic acceleration. Both q and j encapsulate kinematic aspects of cosmic evolution which leave distinct imprints on the large-scale structure of the universe. Consequently, these parameters have a crucial role to play in our endeavours to understand the impact of dark energy across the different stages of cosmic evolution. Furthermore, these parameters are instrumental in facilitating comparisons and distinctions among different ‘dark energy models’ that utilize various mechanisms to trigger cosmic acceleration.

In the context of the matter-curvature interaction scenario considered in this study, the expressions for the three parameters (\(r_{mc}, q, j\)) can be derived in terms of the dynamical variables (\(X_i\)’s) as

$$\begin{aligned} r_{mc}\equiv & {} \frac{\Omega _\textrm{m}}{\Omega _\textrm{curv}} = \frac{1 - X_1 - X_2 - X_3 - X_4}{X_1 + X_2 + X_3} \end{aligned}$$
(28)
$$\begin{aligned} q\equiv & {} - \frac{a\ddot{a}}{\dot{a}^2} = -1 - \frac{\dot{H}}{H^2} = 1 - X_3 \end{aligned}$$
(29)
$$\begin{aligned} j\equiv & {} \frac{\dddot{a}}{aH^3}= -\frac{X_1 X_3}{m}\nonumber \\{} & {} +2 (1 - X_3)^2+(1 - X_3)-2 X_3 (X_3-2) \end{aligned}$$
(30)

In Sect. 3.2 we have computed the temporal evolution of these three parameters for a FLRW universe.

The fixed points in the 4D dynamical system described above correspond to solutions for \(X_i\)’s of \(dX_i/dN = 0, (i=1,\cdots ,4)\)). These stationary solutions and the assessment of their stability are crucial for a comprehensive grasp of critical aspects in cosmic evolution driven by curvature-matter interactions, as explored within the scope of this study. To investigate the system’s behaviour around these critical points, we employ the linear stability analysis which involves performing a first-order Taylor expansion of the autonomous equations derived above, which have a generic expression of the form: \(d\textbf{X}/dN = \textbf{f}(\textbf{X})\), where \(\textbf{X} \equiv {X_1, \cdots , X_4}\) and \(\textbf{f} \equiv {f_1, \ldots , f_4}\) with \(f_i\)’s given by right hand side of the set of autonomous equations derived in Eqs. (18, 19, 20, 21). The Jacobian of the linear transformation \(\textbf{X} \rightarrow \textbf{f}\) is the \(4\times 4\) matrix

$$\begin{aligned} \mathcal {J}= & {} \vert \vert {\partial f_i}/{\partial x_j}\vert \vert . \end{aligned}$$
(31)

By examining the eigenvalues of \(\mathcal {J}\) computed at the critical points we may deduce the nature of the stability of the fixed points and classify them accordingly. When all the eigenvalues have negative (positive) real parts, the fixed point is classified as asymptotically stable (unstable). On the other hand, if any pair of eigenvalues occur with a relative opposite sign in their real parts, the corresponding fixed point is a saddle point. However, if any of the eigenvalues approaches zero at the fixed point, the linear stability theory proves inadequate, necessitating the application of center manifold theory for a more insightful exploration of the characteristics of these critical points. However, in our analysis detailed in later sections, we did not find any non-hyperbolic fixed points within the scope of the various f(R) models examined in this study. This suffices for adhering to linear stability analysis for the models considered here without necessitating an extended exploration using methods beyond linear stability analysis [47].

3.2 On the choice of f(R)-models

The main objective of this study is to investigate and analyze the dynamics of f(R)-driven dark energy models taking into account interactions between the curvature and matter sectors. To carry out this investigation, we have selected specific f(R) models that can induce cosmic acceleration while maintaining their cosmological viability. In the context of the metric formalism employed in this study, any f(R) function that is cosmologically viable must satisfy a set of stringent conditions which have been comprehensively discussed in [62, 63]. Below, we enumerate these conditions and provide the underlying rationale for each of them.

  1. (i)

    \(F>0\) for \(R\geqslant R_0 >0 \): Condition to avoid anti-gravity.

  2. (ii)

    \(F'>0\) for \(R\geqslant R_0 >0\): Condition to avoid Dolgov-Kawasaki instability (Alignment with local gravity tests).

  3. (iii)

    f(R) is close to (\(R-2\Lambda )\) for \(R \gg R_0\): Consistency with local gravity tests and presence of matter dominated era.

  4. (iv)

    \(0< \frac{RF'}{F} < 1\) at \(r = -\frac{RF}{f} = -2\): Stability of de-Sitter solution at late cosmic times.

Here \(R_0\) represents the value of the Ricci scalar at present epoch. The relationship \(m=m(r)\) between the dimensionless parameters m and r, as outlined in Eqs. (22) and (23), is determined by the choice of f(R). Conversely, a specific form of m(r) corresponds to a specific f(R). We investigate the autonomous system furnished in Sect. 3.1, focusing on two separate viable scenarios: The first scenario relates to a f(R) resulting in a constant m, while the second concerns a form of f(R) where m is a function of r, represented as m(r). We designate these scenarios as (A) and (B) and discuss their specifications below.

  1. (A)

    We understand that a scenario with a constant m can be achieved through the modified gravity model given by \(f(R) = (R^b - \Lambda )^c\) with \((c \geqslant 1, bc \approx 1)\). This model has been previously examined without taking into account matter-curvature interactions in [44, 61]. This was proposed with the aim of extending the \(\Lambda \)-CDM model to address local gravity constraints justifying it as a viable f(R) model. We will refer to this scenario as ‘generalised \(\Lambda \)-CDM model’ or sometimes simply as ‘model-A’ from here on. When constrained to \(c \geqslant 1\) and \(bc \approx 1\), this model converges to the \(\Lambda \)-CDM model with \(m=0\), ensuring a viable cosmological evolution. The m and r parameters for the model are given by \(m= \frac{(bc - 1)R^b - b\Lambda + \Lambda }{R^b - \Lambda }\), \(r=-\frac{bcR^b}{R^b-\Lambda }\) and consequently, the parameter m can be expressed as \(m(r)=\left( \frac{1-c}{c}\right) r+b-1\). A dynamical analysis (see [44, 61] for details) of this model indicates that at stable points \(r = -1 - m\), which results in \(m=-1+bc\), a constant value.

  2. (B)

    This scenario involves consideration of m as a specific function of r given by \(m(r) = \frac{n(1+r)}{r}\) which can be realised for the power law form \(f(R) = R - \gamma R^n\) with (\(\gamma >0\), \(0<n<1\)). We refer to this scenario in subsequent texts as ‘power law model’ and sometimes for convenience as ‘model-B’. As comprehensively discussed in [44, 64], the power law model correctly describes cosmic evolution within framework of non-interacting curvature-matter scenarios and satisfies the condition for cosmological viability as well for the above mentioned range of \(\gamma \) and n. This form of f(R) gives \(m=\frac{\gamma (n-1)nR^n}{R - \gamma n R^n}\) and \(r=\frac{R - \gamma n R^n}{R-\gamma R^n}\), the elimination of \(\gamma \) from which leads to the form \(m(r) = \frac{n(1+r)}{r}\).

In the context of our study, choice of the above two cases: (A) \(m=-1+bc=\) constant and (B) \(m = m(r) = \frac{n(1+r)}{r}\) are intended to explore implications of the two above mentioned f(R)-models in presence of matter-curvature interactions.

3.3 Stability analysis of fixed points in generalised \(\Lambda \)-CDM and power law models

In the context of model-A and model-B, we identify the fixed points of the autonomous system described in Sect. 3.1 representing curvature-matter interactions within the framework of f(R) gravity. The fixed points are obtained by solving the equations \(dX_k/dN = 0\) (\(k=1,2,3,4\)), where \(dX_k/dN\)’s are given by Eqs. (18,19,20,21) with \(m = -1+bc\) for model-A and \(m = m(r) = \frac{n(1+r)}{r} = \frac{n(X_2+X_3)}{X_3}\) for model-B. The fact that m is constant for model-A and r-dependent for model-B with \(r =\frac{X_3}{X_2}\) i.e. expressible completely in terms dynamical variables \(X_2\) and \(X_3\), enables us to formulate the system as a closed set of four autonomous equations involving four dynamical variables and the constant parameters (\(\alpha , b, c, n\)) without the necessity for additional dynamical variables.

The coupling parameter \(\alpha \) serves as a common parameter in the analytical framework across both models due to the consideration of matter-curvature coupling in our analysis. Moreover, the f(R) model includes distinct model parameters: (b, c) for model-A and (n) for model-B. We can also evaluate the values of density parameters (\(\Omega _\textrm{r}\), \(\Omega _\textrm{m}\), \(\Omega _\textrm{curv}\)), grand EoS parameter \(\omega _\textrm{tot}\) and EoS parameter associated with curvature sector \(\omega _\textrm{curv}\) at the fixed points using Eqs. (17), (24), (25), (26), (27). As per our considerations mentioned in Sect. 2 each of the modified density parameters are positive and subject to the constraint given by Eq. (11). Adherence to these constraints determines which fixed points hold cosmological significance. Therefore, providing a description of fixed points and their stability characteristics, which are dependent on model parameters, requires appropriate referencing of the relevant constraints within the model parameter space. Moreover, the density parameter values and the EoS parameter value at each fixed point provide crucial insights into characterizing the distinct critical phase associated with that point. If \(\omega _\textrm{tot} < -1/3\) for any fixed point, it represents cosmic acceleration. Specifically, if the value falls within the range of \(-1< \omega _\textrm{tot} < -1/3\), the fixed point corresponds to a ‘non-phantom’ acceleration and when \(\omega _\textrm{tot} = -1\), it corresponds to the de-Sitter acceleration solution. The density parameter values at any given fixed point provide indications of the predominant component during the cosmic phase represented by that specific fixed point.

A total of 10 (real) fixed points are identified in model-A, while model-B comprises 7 fixed points. To distinguish them within the text, we label them as follows:

$$\begin{aligned} \text{ For } \text{ scenario } \text{(A) }&:&\{P_1,P_2,P_3,P_4,P_{5A},\\ {}{} & {} P_{6A},P_{7A},P_{8A},P_{9A},P_{10A}\}\\ \text{ For } \text{ scenario } \text{(B) }&:&\{P_1,P_2,P_3,P_4,P_{5B},P_{6B},P_{7B}\} \end{aligned}$$

These fixed points, along with the corresponding values of \(\Omega _\textrm{m}\) and \(\omega _\textrm{tot}\) for both models, are displayed in Tables 1, 2, and 3. The arrangement of distributing the fixed points across three tables employs a classification scheme to facilitate a comparison of the characteristics attributed to the fixed points in both models.

Table 1 Common fixed points of model-A and model-B. The values of \(\Omega _\textrm{m}\), \(\omega _\textrm{tot}\) and \(\omega _\textrm{curv}\) at these fixed points are also presented
Full size table
Table 2 Fixed points of model-A that are independent of f(R) model parameters (b, c) but do not serve as fixed points of model-B. The values of \( \Omega _\textrm{m}\), \(\omega _\textrm{tot}\) and \(\omega _\textrm{curv}\) at these fixed points are also presented
Full size table

The 4 points (\(P_1, P_2, P_3, P_4\)) presented in Table 1 serve as common fixed points in both model-A and model-B and they are also independent of the parameters of their respective f(R)-model parameters. Notably, the first two points \(P_1\) and \(P_2\) are even independent of the coupling parameter \(\alpha \) implying that they would also persist as fixed points in the dynamical systems associated with non-interacting curvature-matter scenarios, regardless of any applied modifications to the gravity function f(R). Fixed points \(P_2\) and \(P_4\) correspond to \(\omega _\textrm{tot} = -1\), indicating an accelerating de-Sitter solution. The \(\alpha \)-dependence of the other two points (\(P_3\) and \(P_4\)) arises directly from the consideration of matter-curvature interaction in the analysis, and they would not serve as (finite) fixed points in scenarios that do not account for such interactions. This can be understood by observing that the values of \(X_2\) associated with these two points diverge as the matter-curvature coupling (\(\alpha \)) approaches zero. It is worth noting that for a critical value of \(\alpha = -3\), the points \(P_3\) and \(P_4\) converge to the points \(P_1\) and \(P_2\) respectively.

The 3 fixed points (\(P_{5A}, P_{6A}, P_{7A}\)) in model-A, listed in Table 2, appear to be independent of the corresponding f(R) model parameters (b, c) but do not function as fixed points in model-B, which pertains to a different f(R) model. The emergence of these points can be attributed to the constancy of the value of \(m=-1+bc\) within the dynamical equations for model-A, in contrast to the situation in model-B where \(m = \frac{n(X_2+X_3)}{X_3}\) itself enters as a function of the dynamical variables, as discussed earlier. It is worth noting that, the fixed point \(P_{7A}\) corresponds to a state characterized by complete radiation dominance (\(\Omega _\textrm{r} = 1, \omega _\textrm{tot} = 1/3\)) and none of the three points listed in Table 2 are representatives of cosmic acceleration.

The remaining fixed points (\(P_{8A}, P_{9A}, P_{10A}\)) in model-A, as well as (\(P_{5B}, P_{6B}, P_{7B}\)) in model-B, depend on the parameter(s) of their respective f(R) models. They are collectively presented in Table 3. Since the expressions for \(\omega _\textrm{tot}\) at these fixed points depend on their respective model parameters, they would correspond to non-phantom accelerating solutions only if appropriate parameter values exist for which the condition \(-1< \omega _\textrm{tot} < -1/3\) is satisfied.

Table 3 Fixed points in model-A and model-B that are dependent on parameters of corresponding f(R) models. The values of \( \Omega _\textrm{m} \), \(\omega _\textrm{tot}\) and \(\omega _\textrm{curv}\) at these fixed points are also presented
Full size table

Regarding the fixed points identified in our analysis, it’s worth noting that if we were to exclude matter-curvature interactions from our considerations by setting \(\alpha = 0\), the resulting dynamical system would consist of 8 fixed points model-A and 5 fixed points for model-B, as detailed below.

$$\begin{aligned} \text{ for } \text{ model-A }&:&\{P_1,P_2,P_{5A}^\star ,P_{6A},P_{7A},P_{8A},P_{9A}^\star ,P_{10A}\} \\ \text{ for } \text{ model-B }&:&\{P_1,P_2,P_{5B},{P_{6B}}^\star ,P_{7B} \} \end{aligned}$$

where the points \(P_{5A}^\star = (-1,0,0,0)\), \(P_{9A}^\star = \Bigg ( \frac{2 (1-bc) (3 b c)}{ -2 (bc)^2}, \frac{-3+4 b c }{ -2 (bc)^2}, \frac{b c (3-4 b c )}{ -2 (bc)^2},0\Bigg )\) and \({P_{6B}^\star } = \Bigg ( \frac{2 (-1+n) ( 3 n)}{ 2 n^2 },\frac{-3+4 n}{ -2 n^2 }, \frac{(3-4 n) n}{ -2 n^2 }, 0\Bigg )\) follow from the respective points \(P_{5A}, P_{9A}, P_{6B}\) (given in Tables 2 and 3) when we set \(\alpha =0\). However, point \(P_{5A}^\star \) would entail a value of \(\Omega _\textrm{m}=2\), falling outside the bound of \(0< \Omega _\textrm{m} < 1\).

Note that, here we have examined the stability properties of fixed points of the relevant autonomous system that occur with finite coordinate values. However, when dealing with scenarios involving non-compact phase spaces, it becomes crucial to explore the possibility of fixed points occurring at infinity and evaluate their stability criteria. The methodology for investigating features in the asymptotic regime is extensively discussed in [52, 53]. One may observe that all the dynamical variables of this system are bounded owing to the imposition of of the various energy density constraints \((0 \le \Omega _m, \Omega _r \le 1)\), \(-1< \omega _\textrm{tot} <1/3\) throughout the evolutionary era from radiation to dark energy domination and viable f(R) dark energy condition. This eliminates the necessity to explore fixed points at infinity. We examine the stability characteristics of the various fixed points using linear stability analysis, as outlined in Sect. 3.1. This entails an examination of the eigenvalues of the Jacobian matrix \(\mathcal {J}\) (Eq. (31)). The expression for these eigenvalues typically involves the coupling parameter \(\alpha \) and the parameters of the relevant f(R) model. Therefore, to explore the stability properties of the fixed points, it becomes essential to examine the eigenvalues of \(\mathcal {J}\) across the parameter space that is pertinent to the particular model being studied. Due to the substantial and intricate analytical expressions of most eigenvalues for arbitrary values of model parameters, we opt not to include their detailed expressions in the article. We perform a thorough scanning of the parameter space allowing for a wide range of values for \(\alpha \), (b, c), while concurrently enforcing the constraint \(0<n<1\), which is essential to uphold the cosmological viability of the power law model. We obtain the (i) parameter space limitations under which a given fixed point demonstrates stable / unstable or saddle-like behaviour. We also identify (ii) the parameter range within which the fixed point represents an acceleration solution of a specific kind - phantom/ non-phantom or de-Sitter. Simultaneously, we isolate (iii) the parameter constraints that ensure that \(\Omega _\textrm{m}\) remains within the range of \(0<\Omega _\textrm{m}< 1\).

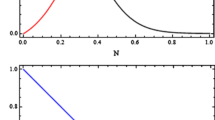
Table 4 Stability and cosmological features of the fixed points of model-A
Full size table

We perform a comprehensive scrutiny of the parameter constraints derived from the three schemes (i), (ii), and (iii) and offer a succinct overview of the stability characteristics and other cosmological aspects related to each of the fixed points. This summary, including description of relevant parameter ranges, is presented in Tables 4 and 5 for model-A and model-B respectively. Moreover, for visualization purposes, we specifically selected three fixed points, namely, \(P_{8A}\), \(P_{9A}\), and \(P_{6B}\), to illustrate the constraints within the parameter space. In Fig. 1, we present three distinct panels, each illustrating the permissible parameter ranges for individual points, wherein they separately (i) exhibit stability, (ii) demonstrate cosmic acceleration (\(-1< \omega _\textrm{tot} < -1/3\)), and (iii) satisfy the condition of \(0< \Omega _\textrm{m} < 1\). Note that, the condition \(0< \Omega _\textrm{m} < 1\) is not applicable for the case of point \(P_{8A}\) as it corresponds to an \(\Omega _\textrm{m}\) value that is independent of the model parameters (\(\Omega _\textrm{m} = 0\) for \(P_{8A}\), see Table 3). The areas of overlap between (i) and (ii) for point \(P_{8A}\) and among (i), (ii), and (iii) for point \(P_{9A}\) define the specific parameter domains for these two points within which ‘stable cosmic acceleration is achieved through curvature-driven (non-phantom) dark energy’. No intersection of the three domains corresponding to (i), (ii) and (iii) are found for point \(P_{6B}\).

It’s important to note that, within the framework of f(R)-gravity scenarios featuring curvature-matter interactions, the fixed points \(P_2\) and \(P_4\) (which are common to both model-A and model-B), as well as fixed point \(P_{8A}\) and \(P_{9A}\) in model-A, are the only fixed points that represent ‘stable acceleration solutions.’ These solutions remain stable within the specified range of \(\alpha \) values, as outlined in Tables 4 and 5. Specifically, \(P_2\) and \(P_4\) correspond to stable de-Sitter attractors, while \(P_{8A}\) and \(P_{9A}\) correspond to stable acceleration driven by non-phantom dark energy. It’s important to emphasize that there are no other points that exhibit both stability and acceleration while adhering to the constraint \(0< \Omega _\textrm{m} < 1\) for any combination of parameter values.

4 Evolutionary dynamics of curvature-matter coupled scenario in the context of cosmological and cosmographic variables

In the context of f(R) gravity models featuring matter-curvature interactions, we analyzed cosmic evolution across the entire timeline—from the radiation epoch to the matter epoch and finally to the late-time cosmological era. To comprehend the complete dynamics of the intertwined curvature-matter scenario, we introduced three cosmological parameters, namely the density parameters associated with curvature and matter (\(\Omega _i\)), the grand equation of state (EoS) parameter (\(\omega _\mathrm{tot.}\)), the ratio of matter density to curvature density (\(r_{mc}\)), and two crucial cosmographic parameters - deceleration (q) and jerk (j). These cosmographic parameters, previously introduced in Eqs. (28), (29), and (30), play a pivotal role in providing a quantitative characterization of the evolutionary progression.

Fig. 1
figure 1

Allowed region of the parameter space for which the critical points (a) \(P_{8A}\), (b) \(P_{9A}\), and (c) \(P_{6B}\) (i) exhibit stability, (ii) exhibit cosmic acceleration (\(-1< \omega _\textrm{tot} < -1/3\)), and (iii) satisfy the energy density condition \(0<\Omega _\textrm{m}<1\) are separately shown

Full size image
Table 5 Stability and cosmological features of the fixed points of model-B
Full size table

We numerically solve the system of autonomous Eqs. (18, 19, 20, 21) for the dynamical variables \(X_i\) in the two cases—one with a constant m corresponding to model-A and the other with \(m(r) = \frac{n(1+r)}{r}\), where \(r = X_3/X_2\) corresponding to model-B. Due to the non-linearity of the coupled autonomous equations, the solutions are highly sensitive to the initial conditions necessary for solving this set of equations. However, to visually illustrate the potential evolutionary dynamics in f(R)-gravity models with matter-curvature interactions, we establish specific valid boundary conditions that allow us to obtain solutions for \(X_i\) based on carefully selected parameter values. These obtained solutions are then employed in Eqs. (24), (25), and (26) to compute the temporal profiles of density parameters (\(\Omega _\textrm{m}\), \(\Omega _\textrm{curv}\)) and the equation of state parameter (\(\omega _\textrm{tot}\)). Additionally, we determine the temporal evolution of the triad of parameters (\(r_{mc}, q, j\)) using Eqs. (28), (29), and (30). The depicted outcomes in Fig. 2 model-A and Fig. 3 for model-B demonstrate the evolution of \(\Omega _\textrm{m}\), \(\Omega _\textrm{curv}\), \(\omega _\textrm{tot}\), and \(r_{mc}\) in the left panel, while showcasing the values of q and j in the right panel. This depiction covers a range of values for \(N = \ln a\), extending from 0.001 to 1000. The chosen parameter values (\(\alpha \), bc or n) for these representations are carefully selected to ensure that, they correspond to stable accelerating solutions and conform to the constraint \(0< \Omega _\textrm{m} < 1\). The specific parameter values are provided in the figure captions for their respective cases.

Fig. 2
figure 2

Evolution plots for generalised \(\Lambda \)-CDM model (scenario (A)). Left Panel: Plots of \(r_\textrm{mc}\), \(\Omega _\textrm{m}\), \(\Omega _\textrm{curv}\) and \(\omega _\textrm{tot}\) vs \(N (= \ln a)\) computed with \(bc = -3\) and \(\alpha =2\), Right panel: Plots of cosmographic parameters q and j computed with \(bc=1.5, \alpha =-2\)

Full size image
Fig. 3
figure 3

Evolution plots for power law model with \(m=m(r)=\frac{n(1+r)}{r}\) (scenario (B)). Left Panel: Plots of \(r_\textrm{mc}\), \(\Omega _\textrm{m}\), \(\Omega _\textrm{curv}\) and \(\omega _\textrm{tot}\) vs \(N (= \ln a)\) computed with \(n=0.9, \alpha =-5\), Right Panel: Plots of cosmographic parameters q and j computed with \(n=0.9, \alpha =-2\)

Full size image

The graphs of \(\Omega _\textrm{curv}\), \(\Omega _\textrm{m}\), and \(\omega _\textrm{tot}\) suggest the possibility of early cosmic phases where curvature energy density dominates over (dark) matter, yielding a positive \(\omega _\textrm{tot}\) (with the value of \(\frac{1}{3}\) for the cases presented in Figs. 2 and 3) and exhibiting a radiation-like EoS. As time progresses, curvature energy density diminishes while matter-energy density grows, and their values tend to converge. At the matter-dominated epoch (where, \(\omega _\mathrm{tot.}=0\)), the values of the two densities become equal, triggering a shift in the nature of their temporal behaviour, resulting in the rise of curvature energy density and the decline of matter energy density. It’s worth noting that curvature energy density consistently exceeds matter energy density throughout the depicted evolutionary phases in the left panel of Figs. 2 and 3. During moments when their values come together, the equation of state parameter \(\omega _\textrm{tot}\), which had remained constant and positive since the initial epochs experiences a rapid decline and swiftly falls below \(-\frac{1}{3}\). This indicates the onset of late-time cosmic acceleration. For model (A), \(\omega _\textrm{tot}\) parameter can’t cross the phantom barrier line, instead it saturates near the value of \(-0.8\). As this phase unfolds, the values of \(\Omega _\textrm{curv}\) and \(\Omega _\textrm{m}\) once again separate, with curvature density regaining dominance over matter energy density. This dynamic facet of cosmic evolution is common to both scenarios (A) and (B), as can be inferred from Figs. 2 and 3.

With a more in-depth comparison of Figs. 2 and 3, one may also recognize the distinctive impacts that the corresponding f(R) modifications in model-A and model-B exert on the generic features of cosmic evolution mentioned above. In model-A, as cosmic acceleration initiates, the rapid decline of \(\omega _\textrm{tot}\) does not cross the value of \(-1\), but rather gracefully saturates at a value slightly above \(-1\), indicating a non-phantom nature of curvature-driven dark energy. In contrast, in model-B, the sharp fall of \(\omega _\textrm{tot}\) takes it below \(-1\), but it subsequently rebounds and eventually settles at the value of \(-1\), never exceeding it. This feature implies that within the framework of the power-law model with matter-curvature interactions, the curvature-induced dark energy responsible for cosmic acceleration can exhibit characteristics of phantom dark-energy. Nevertheless, it’s important to note that such a scenario does not exhibit stability since \(\omega _\textrm{tot}\) eventually saturates -1 with the passage of time. Another notable distinction lies in the possibility for late-time cosmic acceleration to be purely curvature-dominated (\(\Omega _\textrm{curv}=1\)) in model-A. On the contrary, in model-B, cosmic acceleration can occur with both matter and curvature energy densities present in approximately equal proportions (on the order of \(\sim \) 1), with an edge towards curvature dominance over matter.

Furthermore in model-B, where f(R) follows a power law form indicated by \(m(r) = n(1+r)/r\), as the universe progresses into its late-time acceleration phase, the temporal profiles illustrating \(\Omega _\textrm{curv}\) and \(\Omega _\textrm{m}\) display intricate and non-trivial patterns, rather than a simple, monotonic progression, until they eventually stabilize in the distant future. In contrast, these traits are absent in the constant m scenario (model-A). This distinction can be attributed to the differences resulting from the specific forms of f(R) in each scenario.

Fig. 4
figure 4

Evolution plot of the parameter \(r_\textrm{mc}\) for different values of coupling strength \(\alpha \). Left Panel: For f(R) model with generalised \(\Lambda \)-CDM model with parameter \(bc=-3\). Right Panel: For power law form of f(R) with value of model parameter \(n=0.9\)

Full size image

The ratio of matter to curvature density \(r_\textrm{mc} \equiv \Omega _\textrm{m}/\Omega _\textrm{curv}\), serves as a gauge of the extent to which one component dominates over the other. The value \(r_\textrm{mc} = 0\) signifies complete curvature dominance, while \(r_\textrm{mc} \approx 1\) suggests a coincidence of matter and curvature energy densities in the universe. Therefore, the evolution of the parameter \(r_\textrm{mc}\), as depicted in Figs. 2 (model-A) and 3 (model-B), provides quantitative insights into the dominance of curvature over matter at different stages of cosmic evolution in the respective scenarios. The impact of the curvature-matter coupling strength on cosmic evolution becomes apparent when we compare the profiles of \(r_\textrm{mc}\) computed using different values of the interaction parameter \(\alpha \). According to Eqs. (15) and (16), a negative value of \(\alpha \) indicates energy transfer from the matter sector to the curvature sector, while a positive value of \(\alpha \) implies the opposite, with energy flowing from curvature to matter. In Fig. 4, we display the evolution of the parameter \(r_\textrm{mc}\) for different \(\alpha \)-values in model-A (left panel) and model-B (right panel). These computations use specific values of f(R)-model parameters, as mentioned in the caption of Fig. 4. Peaks in the \(r_\textrm{mc}\)-profiles signify the moments when the universe attains its highest matter density proportion. The trend of the peak height approaching unity for \(\alpha \sim -5\) or even more negative values implies the presence of epochs with almost perfect coincidence between curvature and matter energy densities for significantly negative \(\alpha \) values. For such negative \(\alpha \) values, the late-time and distant-future accelerated phase of the universe experiences the presence of both matter and curvature energy densities in comparable proportions. Scenarios within the framework of the power law model (right panel of Fig. 4) may emerge for significantly negative \(\alpha \) values where the matter energy density share may gradually rise as the universe progresses towards distant future epochs. However, the \(r_\textrm{mc}\) values consistently remain below one, indicating that curvature density consistently exceeds matter energy density, even if by a slightly smaller margin during epochs when matter density contribution is at its highest. At earlier epochs during the decelerated phase of the universe, the negative \(\alpha \) values result in very low \(r_\textrm{mc} \sim 0\) in both models, indicating curvature dominance over matter during this period. For the case of \(\alpha = 0\) representing the standard f(R) gravity framework without any additional matter-curvature interactions, the profile of \(r_\textrm{mc}\) exhibits a nearly symmetrical pattern centered around the epoch of maximum matter-energy density contribution, with the matter energy density remaining exceedingly minimal (\(r_\textrm{mc} \sim 0\)) during earlier as well as during distant future epochs. A positive \(\alpha \), on the other hand, results in a non-zero \(r_\textrm{mc}\) at early stages, which subsequently decreases over time, reaching a minimum before resuming its ascent to reach its highest point during the epoch when the universe maximizes its matter density share.

The right panels of Figs. 2 and 3 depict the evolution of deceleration and jerk parameters (q and j) for some benchmark values of the parameters corresponding to scenarios in model-A and model-B. These plots capture the kinematic aspects of cosmic evolution. During the early stages of evolution, they show positive values of both q and j, implying a decelerated phase with an increasing rate of deceleration. However, at a specific point, the deceleration parameter (q) rapidly declines, crosses the zero line, and becomes negative, signifying the onset of cosmic acceleration. It then sharply drops below the \(-1\) threshold, rebounds, and ultimately stabilizes at \(-1\) in the distant future. This decline of q and its eventual stabilization at \(q=-1\) in the distant future are further characterized by a significant increase in the jerk parameter j, reaching its peak. This signifies a growing rate of acceleration, culminating in its maximum value. Subsequently, the jerk parameter starts to decrease, indicating a reduction in the rate of acceleration, and eventually settles at a positive value of unity in both model-A and model-B. All these intricate features of cosmic evolution result from the complex interplay among the interacting components of matter and curvature within the framework of modified gravity.

5 Conclusion

In this work, we explored the possibility for accommodating interactions between curvature and matter within the framework of viable f(R) gravity models, all the while ensuring that these models retain their ability to achieve cosmic acceleration. At the action level, we consider minimal coupling between matter and curvature. The radiation component is considered to be decoupled from both matter and curvature, implying the conservation of its energy-momentum tensor. We incorporate interactions between the matter and curvature components by introducing a source term Q in their respective continuity equations with opposite signs. This ensures energy conservation within the combined matter-curvature sector, enabling the potential for a continuous exchange of energy between the two sectors at a rate determined by Q. A specific form of the interaction term Q is chosen to illustrate a dynamic connection between the curvature and matter sectors by incorporating their individual energy densities in a multiplicative manner within Q, along with a dimensionless parameter (\(\alpha \)) signifying the strength of coupling between the two sectors. The sign of \(\alpha \) dictates the direction of energy flow between the two sectors.

An essential component of this study is the establishment of a 4-D dynamical framework that portrays the dynamics of curvature-matter interacting scenario. The introduction of the interaction term Q leads to alterations in the autonomous equations that govern the dynamical system, distinguishing it from those resulting from f(R) theories that do not consider matter-curvature interactions. We identified the critical points of the dynamical system and analyzed their stability, separately in the context of two viable f(R) models viz. the generalized \(\Lambda \)-CDM model (model-A) and the Power-law model (model-B). The interaction parameter \(\alpha \) assumes a crucial role, significantly shaping the dynamics of the system. Its impact on the stability characteristics of various fixed points within the dynamical system, as well as on the evolutionary dynamics of the universe during different phases, have been thoroughly investigated.

The incorporation of the curvature-matter coupling (\(\alpha \ne 0\)) within the framework of f(R) gravity leads to an increase in the number of critical points, introducing new stable de-Sitter attractors. In both models, we notice the appearance of two stable de-Sitter attractors \(P_2\) and \(P_4\), in contrast to the scenario without interactions (\(\alpha = 0\)) where \(P_2\) exists as the only de Sitter point. An in-depth analysis of the stability traits of these fixed points across an extensive range of \(\alpha \)-values reveals intriguing patterns within the stability landscape of the matter-curvature interaction scenario. For \(\alpha = -3\), the stable de-sitter attractors \(P_2\) and \(P_4\) represents the same fixed point in both models. In model-A, for \(\alpha > -3\), \(P_2\) takes the role of stable de-Sitter attractor, whereas in the range of \(-18 < \alpha \le -3\), it is \(P_4\) that assumes this stabilizing role, provided the f(R)-model parameters b,c satisfy \(1< bc < 1.65\). On the other hand, in Model B, stable de-Sitter acceleration is achievable for \(\alpha > -3\), with \(P_2\) serving as the attractor and for \(\alpha \le -3\), \(P_4\) emerges as the stable de Sitter attractor, operating within the viable range of the f(R) model parameter \(0< n < 1\). As evident from the above discussion, a significant contrast between the two models is that, in Model B, the entire span of \(\alpha \) permits stability of de-Sitter acceleration solution, whereas in Model A, this range is notably more restricted. Shifting our focus to identifying fixed points that signify stable acceleration of non-phantom nature (\(-1<\omega _\textrm{tot} < -1/3\)), we observe that model-A presents two stable options, namely \(P_{8A}\) and \(P_{9A}\), with their stability demonstrated for \(\alpha > -4\) and \(\alpha \leqslant -4\) respectively. Notably, these conditions are dependent on the parameters (b,c) of model-A, as illustrated in Fig. 1a, b. In contrast, within the viable range of n in Model B, no stable fixed points with non-phantom acceleration have been found for any value of \(\alpha \).

The evolution of various cosmological and cosmographic parameters have been explored for a nuanced assessment of the influences of curvature-driven dark energy on various phases of cosmic evolution within the framework of matter-curvature interactions. Examining the evolution of modified energy densities and the EoS parameter, particularly the matter-to-curvature density ratio (\(r_\textrm{mc}\)), along with two cosmographic parameters - deceleration (q) and jerk (j), offers valuable insights into potential evolutionary scenarios within scenarios involving the interplay of matter and curvature. In model-A, we observed that in both the early and late stages, curvature energy density exhibits significant dominance over matter energy density. During the transitional phase between these two phases, curvature density decreases while matter density increases over time, eventually reaching its peak. Subsequently, there is a resurgence in curvature’s contribution and a decline in matter’s contribution, ultimately reestablishing the pronounced dominance of curvature in the later stages. During the transition from early to later phases, the EoS parameter swiftly drops below \(-1/3\), marking the onset of late-time cosmic acceleration and stabilizes around \(\sim -0.8\) in distant future, never reaching below \(-1\), affirming the non-phantom nature of curvature-driven dark energy. This stable acceleration phase in the distant future is achieved with prominent curvature dominance, indicated by \(r_\textrm{mc} \sim 0\). In model-B, while curvature density plays a dominant role in the early universe, matter density also becomes significant during the later phases, resulting in an order of magnitude around 1 (but always \(<1\)) for \(r_{mc}\) in the later stages. The EoS parameter drops from its positive value to values below \(-1/3\) as the universe enters its accelerated phase. The descent persists, surpassing the non-phantom threshold of \(-1\) before rebounding and stabilizing at this value in the later stages signifing the emergence of an unstable phantom region in model-B, albeit for a brief period. The evolution of parameters (q, j) remains consistent across both models. The positive jerk (j) and negative deceleration (q) observed during the late-time phase in both models confirm the presence of stable late-time cosmic acceleration in interacting curvature-matter scenario. We examined and illustrated (Fig. 4) the progression of \(r_{mc}\) at specific reference values of the coupling parameter \(\alpha \). The parameter \(r_{mc}\) is a measure of the extent to which matter dominates over the curvature component. In the absence of any interaction, the \(r_{mc}\) profile remains symmetric around the epoch of maximum energy density contribution of the matter component, with \(r_{mc}\) values tending to zero at both earlier and later time epochs in both models. When interactions are present (\(\alpha \ne 0\)), positive values of \(\alpha \) result in earlier epochs showing a notable contribution from the matter component. Conversely, with negative \(\alpha \) values, the later epochs display a substantial contribution from the (dark) matter component. Our study is able to address the issue of cosmological coincidence in the late-time epoch with a negative \(\alpha \).

The ratio of matter density to curvature density, denoted as \(r_\textrm{mc}\) and defined as \(\frac{\Omega _\textrm{m}}{\Omega _\textrm{curv}}\), serves as a measure of the dominance of one component over the other in the cosmic landscape. \(r_\textrm{mc} = 0\) indicates complete curvature dominance, while \(r_\textrm{mc} \approx 1\) suggests a coincidental balance between matter and curvature energy densities in the universe. The evolution of the parameter \(r_\textrm{mc}\) is illustrated in Figs. 2 (model-A) and 3 (model-B), providing quantitative insights into the dominance of curvature over matter at different stages of cosmic evolution in the respective scenarios. The impact of the curvature-matter coupling strength becomes evident when comparing \(r_\textrm{mc}\) profiles computed with different values of the interaction parameter \(\alpha \). Within the framework of equations (15) and (16), a negative \(\alpha \) implies energy transfer from matter to curvature, while a positive \(\alpha \) signifies the opposite, with energy flowing from curvature to matter. Figure 4 displays the evolution of \(r_\textrm{mc}\) for different \(\alpha \) values in model-A (left panel) and model-B (right panel), using specific values of f(R)-model parameters as mentioned in the caption of Fig. 4. Peaks in the \(r_\textrm{mc}\) profiles represent moments when the universe attains its highest matter density proportion. The trend of peak height approaching unity for \(\alpha \sim -5\) or more negative values indicates epochs with nearly perfect coincidence between curvature and matter energy densities. For significantly negative \(\alpha \) values, the late-time and distant-future accelerated phase of the universe experiences both matter and curvature energy densities in comparable proportions. However, \(r_\textrm{mc}\) values consistently remain below one, suggesting that curvature density consistently exceeds matter energy density, even during epochs with the highest matter density contribution. At earlier epochs during the decelerated phase of the universe, negative \(\alpha \) values result in very low \(r_\textrm{mc}\), indicating curvature dominance over matter. In the case of \(\alpha = 0\), representing the standard f(R) gravity framework without additional matter-curvature interactions, the \(r_\textrm{mc}\) profile exhibits a nearly symmetrical pattern centered around the epoch of maximum matter-energy density contribution. A positive \(\alpha \) results in a non-zero \(r_\textrm{mc}\) at early stages, decreasing over time and reaching a minimum before resuming its ascent to reach the highest point during the epoch when the universe maximizes its matter density share.

While numerous viable f(R) models exist to address the enigma of dark energy in cosmology, the qualitative insights from our study can form a foundation for more intricate examinations. These findings serve as supplementary constraints when assessing the viability of f(R) models, alongside the broader range of cosmological constraints applied to f(R) theories. Each f(R) gravity model leaves its distinct imprint on the evolution of cosmological perturbations. Specifically, the scrutiny of structure formation in the universe proves to be highly responsive to the nature of interaction between dark energy and dark matter within the framework of f(R) gravity. Notably, the interaction between curvature driven dark energy and dark matter in the early stages of the universe may potentially influence the epoch of matter-radiation equality. The manifestation of anisotropies resulting from this phenomenon can be quantitatively assessed in terms of the growth of structure formation within the curvature-matter interacting framework of f(R) gravity. Interestingly, the interaction between f(R)-dark energy and dark matter during the early phase of cosmological evolution may offer an explanation for the disparity in the Hubble tension parameter observed between local measurements and those derived from cosmic microwave background observations. Furthermore, the study of matter perturbations and the local gravity approximations of interacting dark energy in f(R) gravity holds promise for shedding light on the inconsistent predictions between non-interacting and interacting f(R) dark energy models. Additionally, exploring alternative models of interacting dark energy within the framework of f(R) gravity holds the potential to extract further physical implications and discern their cosmological consequences.

In summary, this research deepens our understanding of the intricate dynamics in modified f(R) gravity theories, particularly in the presence of interactions between curvature and matter. The emergence of stable de-Sitter attractors, nuanced stability characteristics, and distinctive evolutionary patterns in this scenario are instrumental in elucidating the various facets of the complex behavior of the system. The findings presented here not only enhance our understanding of the dynamics of these systems but also open up new avenues for further exploration in the field of cosmology, paving the way for gaining valuable insights into the fundamental dynamics of the universe.