1 Introduction

Dark compact objects, from a perspective of phenomenology, comprise a wide range of astronomical objects, such as white dwarfs, neutron stars, and BHs. Theoretically, scenarios incorporating particle physics outside the standard model and extended gravity theories might both contribute to the prediction of dark compact objects [1]. Gravitational waves detected by LIGO/Virgo observations recently demonstrated the occurrence of binary BH mergers [2, 3]. In addition, the event horizon telescope (EHT) confirmed the presence of supermassive BHs in the Milky Way and M87 galactic centres in [4,5,6]. Thus, it makes sense to expect that future developments in the area of gravitational wave astronomy and very long baseline interferometry is going to open the door to new compact object species. However, the investigation of dark compact objects from a mathematical perspective is intriguing since it helps us understand the mechanism at what limits an object tends to be a BH by increasing its compactness.

Although Albert Einstein’s general theory of relativity (GR) has made significant progress in interpreting observations and foretelling amazing events, it is still not a comprehensive theory that describes gravitational interaction and connecting cosmic events. Among the shortcomings of GR are the recurrence of the rotation curves of neighbouring galaxies [7, 8], mass profiles of galaxy clusters [9], inherent singularities at the core of black holes, etc. In addition, the positively accelerated expansion of the universe at late times cannot be explained by GR without the cosmological constant factor [10]. Restructuring the geometric component of general relativity (GR) using various methods is an intriguing method of reform. This can lead to the development of the referred to as modified gravity (MOG) theory, which is a scalar–tensor–vector (S–T–V) theory formulated by John W. Moffat that explains gravitational interaction [11]. The gravitational influences of spacetime in a MOG setup are expressed by a huge vector field in addition to three scalar fields: the mass of the vector field, the effective gravitational constant G, and the vector field coupling. In addition to being compatible with Planck 2018 data [12], the MOG theory has achieved various successes in explaining astrophysical phenomena. These include explaining the dynamics of galaxy clusters without dark matter and the rotation curves of many galaxies [13, 14]. Furthermore, within the framework of MOG theory, a number of BH solutions, such as rotating and non-rotating ones [15], even with additional dimensions [16], cosmological solutions [17,18,19], and non-stationary solutions for in homogeneity distributions of mass energy in spacetime [20], have been published recently. Additionally, a great deal of theoretical and observational work has been done to comprehend the aspects of the MOG theory and how it functions in various contexts [21,22,23,24,25]. Ref. [26] offers an interesting exploration of the solution characterizing the regular rotating and non-rotating MOG dark compact object.

Current astronomical discoveries provide compelling evidence of the universe’s accelerated expansion [27,28,29], suggesting the existence of an appealing scenario under negative pressure. There are two potential reasons for the negative pressure. First, there is the cosmological constant, and second, there is the termed quintessence, whose state equation is defined by the correlation between pressure \(p_q\) as well as energy density \(\rho _q\). This implies that at \(\omega \), \(\rho _q = \omega \) at \(\omega \) in the interval \(-1~<~ \omega ~<~-1/3\), which leads in acceleration. The cosmological constant term is explained by the border case of \(\omega = -1\) of the remarkable quintessence. The outer horizon, which prevents the emergence of the observable S-matrix with respect to asymptotic past and future states, provides an issue to the consistent theory of quantum gravity, as was noted [30,31,32]. The inner horizon of a BH, which possesses asymptotically flat space distant from the BH, is very different from the outer horizon of de Sitter space. In [30], the Robertson–Walker metric’s future horizon with the accelerating scale factor brought on by the quintessence was examined.

The early research on the temperature and entropy of the event horizon by Bekenstein and Hawking is referenced in the thermodynamic description of BHs [33, 34]. Basically, they established that the BH’s temperature and entropy are correlated with the event horizon’s area as well as surface gravity, respectively. We can study the first rule of thermodynamics in relation to the total energy (mass) of the BH by examining the conserved charge correlated with the time-translation symmetry, employing the same analogy as with standard systems. In a plausible scenario, we ought to examine the BH’s robustness to minor disturbances. In other words, we have to investigate both the dynamic as well as thermodynamic consistency of the solutions. The QNMs of the solutions can be employed to investigate thermodynamic stability, whereas the reaction of a system to fluctuations in temperature, energy, and various other thermodynamic parameters close to equilibrium might be used to evaluate dynamic stability. Through the utilization of micro-canonical, canonical, along with grand canonical ensembles, the thermodynamic viability of a BH might be probed via perturbative parameters. The prerequisites of thermal stability along with BH thermodynamics have been explored in the literature in recent times [35,36,37,38].

The initial step in viewing a typical BH as a thermodynamic system would be to search for thermodynamic parameters. The Smarr relationship to the scaling method, in addition to the fundamental principle of thermodynamics, can be useful in this context. In the referred to as extended phase space, one must modify the first rule of thermodynamics depending on the Smarr connection of BHs. There is a van der Waals-like phase transition involving AdS charged BHs and the extended phase space, in which the cosmological constant can be defined as a dynamical pressure. One of the fascinating techniques for studying the BH phase transition is geometrical thermodynamics. This approach enables one to describe a phase space via thermodynamical potentials and the related quantities. The divergence points of the Ricci scalar, that form the thermodynamic metric, provides significant details concerning a potential phase transition of the BH system. Weinhold and Ruppeiner thermodynamical metrics have been the most frequently utilized. The initial one is defined on the space of equilibrium state of thermodynamic structures which was introduced by Weinhold [39]. Following that, in 1979, Ruppeiner defined an additional the metric [40]. The drawbacks of both the Weinhold as well as Ruppeiner metrics stem from the fact that these metrics tend to not be invariant under Legendre transformation.

In this work we have discussed the QNMs and GF of MOG BH surrounded by quintessence along with the thermodynamic geometry. The organisation of this paper is as following. In Sect. 2, we write down the MOG BH solution in the presence of a quintessence field and briefly review this spacetime. Section 3 is devoted to investigate the scalar and electromagnetic perturbation and associated QNMs using 6th order WKB method. In Sect. 4, the QNM frequencies at the eikonal limit is calculated via circular null geodesics. Section 5, is reserved for the analysis of the greybody radiation. In Sect. 6, we study the thermodynamics of the regular MOG BH surrounded by a quintessence. Finally, we summarize our results and discuss some open issues in the conclusions section.

2 Regular MOG BH surrounded by a quintessence

2.1 A brief review of the spacetime

This section begins by describing the metric of a static BH in the S–V–T (MOG) gravity model with a quintessence scalar field, with the aim of analyzing its implications of this modified gravity theory on QNMs, GFs, and thermodynamics of massive astrophysical objects. The regular MOG, static spherically symmetric solution surrounded by quintessence can be written as [41,42,43]

$$\begin{aligned} ds^{2}=-f\left( r\right) dt^{2}+f^{-1}(r)dr^{2}+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}\right) \end{aligned}$$
(1)

where

$$\begin{aligned} f\left( r\right)&=1-\frac{2\left( 1+\alpha \right) Mr^{2}}{\left( r^{2}+\alpha \left( 1+\alpha \right) M^{2}\right) ^{3/2}}\nonumber \\ {}&\quad +\frac{\alpha \left( 1+\alpha \right) M^{2}r^{2}}{\left( r^{2}+\alpha \left( 1+\alpha \right) M^{2}\right) ^{2}} -\frac{c\left( 1+\alpha \right) }{r^{3\omega +1}}, \end{aligned}$$
(2)

in which, M is the mass parameter of the gravitating object, \(\alpha \) is the enhancement (MOG) parameter, c is a normalization factor and \(\omega \) is the state parameter of the quintessence which has the range \(-1< \omega < -1/3\). We will refer to the BH described by metric (1) as a MOG BHQ.

It is worth noting that Moffat [15] ignores the matter sector’s momentum tensor when building his MOG version of BHs. Under the assumptions of the S–T–V theory, the line element of the Schwarzschild-MOG BH solutions can be obtained using the action [11]:

$$\begin{aligned} S=\frac{1}{16\pi G_{N}\left( 1+\alpha \right) }\int d^{4}x\sqrt{-g}\left( R- \frac{1}{4}B^{\mu \nu }B_{\mu \nu }\right) , \end{aligned}$$
(3)

where \( G_{N}\) is the Newtonian constant. Variation of this action with respect to \(g^{\mu \nu }\) results in the following field equations [11]:

$$\begin{aligned} G_{\mu \nu }=8\pi G_{N}\left( 1+\alpha \right) T_{\mu \nu }, \end{aligned}$$
(4)

where the Einstein tensor \( G_{\mu \nu }=R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R\). In the Einstein field equation, the energy momentum tensor can be decomposed into two distinct components to obtain the metric of the MOG BH surrounded by quintessence [43]

$$\begin{aligned} T_{\mu \nu }=T_{\mu \nu }^{q}+T_{\mu \nu }^{\phi } \end{aligned}$$
(5)

where \(T_{\mu \nu }^{q}\) for the quintessence part and \(T_{\mu \nu }^{\phi }\) describes the vector field. Based on [43], the metric (1) (where we set \(G_{N} =1\)) of the regular MOG, static spherically symmetric solution surrounded by quintessence is obtained by introducing the matter sector as a quintessence scalar field.

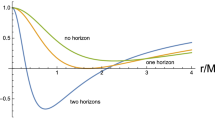
It is possible for such a static spherically symmetric MOG spacetime without quintessence to have two, one or no event horizon(s), depending on the parameter, \(\alpha \) [44]. Nevertheless, several authors have observed (such as [48, 49]) that cosmological horizons become apparent when the quintessence term is taken into account. Based on this, the spacetime of MOG BHQ (1) could have three horizons as shown in Fig. 1. Moreover, it shows how the number of the horizons in the MOG BHQ usually decreases from three to two or even to one as the parameter \(\alpha \) increases.

Fig. 1
figure 1

Metric function f(r) of MOG BHQ for different values of the MOG parameter \(\alpha \). Here \(\omega =-2/3\), \(c=0.02\) and \(M=1\)

Full size image

3 QNMs of MOG BH surrounded by a quintessence

Accordingly, the QNM ringing stage corresponds to the BH’s QNM, which typically exhibits damped oscillations represented by discrete complex frequencies, where the real part represents the frequency and the imaginary part represents the decay rate of the oscillation. Because QNMs are independent of the initial perturbation and are dependent only on the BH parameters, they are important tools for studying BHs and gravity theories. The BH can be perturbed by either adding test fields (Klein–Gordon or Dirac fields) to the background or by perturbing spacetime itself. In any case, the perturbation equation for a static and spherically symmetry line element can be reduced to the following like-Schrödinger equation [45]:

$$\begin{aligned} \frac{d^{2}U}{dr_{*}^{2}}+\left( k^{2}-V\right) U=0, \end{aligned}$$
(6)

where the tortoise coordinate \(r_{*}\) is defined as \(\frac{d}{dr_{*}} =f\frac{d}{dr}\), and V(r) is the effective potential given by:

$$\begin{aligned} V(r )=f\left( \frac{l\left( l+1\right) }{r^{2}}+f^{\prime }\frac{(1-s^{2})}{r}\right) \end{aligned}$$
(7)

where \(s = 0, 1, 2\) is the spin of the perturbing field. In this section, we shall consider \(s = 0\) for scalar field and \(s = 1\) for electromagnetic (EM) field.

Based on different values of MOG BHQ parameters, Figs. 2 and 3 show how the potentials (7) vary. Figure 2 demonstrates that as c increases, the potential curves of scalar field decrease significantly, indicating that quintessence has the effect of lowering the peaks of these potentials. Figure 3 depicts a similar trend in which potentials decrease as the parameter \(\alpha \) increases. According to this analysis, the effects of parameters c and \(\alpha \) on potential behaviour are comparable. As a result, they may have similar effects on QNMs. It worth to mention that the potentials in EM fields behave similarly to those in scalar fields.

Fig. 2
figure 2

Plot of effective potentials (7) for scalar field for specific choices of c (\(M=1\), \(\alpha =0.2\))

Full size image
Fig. 3
figure 3

Plot of effective potentials (7) for scalar field for specific choices of \(\alpha \) (\(M=1\), \(c=0.02\))

Full size image

To obtain QNM frequencies, there are several strategies that can be used. We will, however, apply the 6th WKB approximation [46] first presented in Ref. [47] to study scattering around BHs, for the sake of efficiency in computing the quasinormal frequencies. We focus on the fundamental mode with \(l = 2\) and \(n = 0,1\) due to its dominant ingredient of gravitational waves in order to study the influence of the parameters c and \(\alpha \) on the quasinormal frequencies. The complex frequency formula in the 6th order WKB approximation has the form [46]

$$\begin{aligned} i\frac{\left( \omega ^{2}-V_{0}\right) }{\sqrt{-2V_{0}^{\prime \prime }}} -\sum \limits _{i=2}^{6}\Lambda _{i}=n+\frac{1}{2} \end{aligned}$$
(8)

where \(V_{0}\) is the maximum of the effective potential V(r), \( V_{0}^{\prime \prime }=\left. \frac{d^{2}V(r_{*})}{dr_{*}^{2}} \right| _{r_{*}=r_{0}}\), \(r_{0}\) is the position of the peak value of the effective potential, and \(\Lambda _{i}\)’s are 2nd to 6th order WKB corrections that have been given in Refs. [46, 47].

The QNMs of the massless scalar and EM perturbation are presented in Table 1 with several values of c using the following model parameters: \(\alpha =0.2\), \(M=1\), \(l=2\), and overtone number \(n = 0, 1\). Similarly, Table 2 presents the QNMs of the massless scalar and EM perturbation with several values of \(\alpha \) using the following model parameters: \(c=0.02\), \(M=1\), \(l=2\), and overtone number \(n = 0, 1\). According to the Tables, all BH frequencies obtained have a negative imaginary part, indicating their stability. The real and imaginary QNMs have been explicitly plotted with respect to the model parameters in order to see how the model parameters affect the QNM spectrum. In Figs. 4 and 5, we show the variation of real and imaginary QNMs with respect to the model parameters c and \(\alpha \) for both massless scalar perturbation and EM perturbation respectively. It is observed that, with an increase in c and \(\alpha \), real QNMs or oscillation frequencies decrease significantly. However, the imaginary part of the quasinormal frequencies generally rises, with an increase in c and \(\alpha \), indicating a smaller damping rate. In Figs. 6 and 7 we plot the QNM frequencies in complex frequency plane. Figures show that increasing c and \(\alpha \) decreases both frequency and decay rate. In general, the system experiences weak oscillations and slow decays.

Table 1 The QNM of MOG BHQ for scalar and EM perturbations for specific choices of c. Here, \(M=1\), \(l=2\), \(\omega =-2/3\) and \(\alpha =0.2\)
Full size table
Table 2 The QNM of MOG BHQ for scalar and EM perturbations for specific choices of \(\alpha \). Here, \(M=1\), \(l=2\), \(\omega =-2/3\) and \(c=0.02\)
Full size table
Fig. 4
figure 4

Plot of QNM frequencies with real and imaginary parts (Table 1) versus the parameter c. Scalar perturbation (up), EM perturbation (down). Here, \(\omega =-2/3\), \(M=1\) and \(l=2\)

Full size image
Fig. 5
figure 5

Plot of QNM frequencies with real and imaginary parts (Table 2) versus the parameter \(\alpha \). Scalar perturbation (up), EM perturbation (down). Here, \(\omega =-2/3\), \(M=1\) and \(l=2\)

Full size image
Fig. 6
figure 6

Complex frequency plane for scalar perturbation showing the behavior of the quasinormal frequencies

Full size image
Fig. 7
figure 7

Complex frequency plane for EM perturbation showing the behavior of the quasinormal frequencies

Full size image

4 QNM frequencies at the eikonal limit calculated via circular null geodesics

Cardoso et al. [50] proposed the circular null geodesic method to calculate the QNM frequencies of a static spherically symmetric BH at the eikonal limit \(l\gg 1\). The formula for calculating the QNM frequencies through unstable null geodesics is [50]:

$$\begin{aligned} frequency =l\Omega -i\left( n+\frac{1}{2}\right) \left| \lambda \right| . \end{aligned}$$
(9)

The real and imaginary components of the QNM frequencies are determined by \(\Omega \) and \(\lambda \), which are respectively the angular velocity and Lyapunov exponent. The angular velocity is given by,

$$\begin{aligned} \Omega =\frac{\sqrt{f\left( r_{c}\right) }}{r_{c}}, \end{aligned}$$
(10)

and the Lyapunov exponent is

$$\begin{aligned} \lambda =\frac{1}{\sqrt{2}r_{c}}\sqrt{f\left( r_{c}\right) \left[ 2f\left( r_{c}\right) -r_{c}^{2}f^{\prime \prime }\left( r_{c}\right) \right] }, \end{aligned}$$
(11)

where \(r_{c}\) is the circular orbit of the unstable null geodesics where it is determined by:

$$\begin{aligned} 2f\left( r\right) -\left. r^{2}f^{\prime \prime }\left( r\right) \right| _{r=r_{c}}=0. \end{aligned}$$
(12)

By substituting Eqs. (2) into (10) and (11), graphs of \(\Omega \) and \(\lambda \) with respect to c and \(\alpha \) can be drawn. Figures 8 and 9 represent the angular velocity \(\Omega \) and the Lyapunov exponent \(\lambda \) with respect to the parameters c and \(\alpha \) respectively. There are notable similarities between Figs. 8, 9 and 4, 5. As a result, the Cardoso et al. [50] approach and the high-order WKB approximation produce results which correspond directly with those of the analysis of unstable null geodesics.

Fig. 8
figure 8

Graph of the angular velocity \(\Omega \) (left) and Lyapunov exponent \(\lambda \) (right) for different values of c. Here, \(\omega =-2/3\)

Full size image
Fig. 9
figure 9

Graph of the angular velocity \(\Omega \) (left) and Lyapunov exponent \(\lambda \) (right) for different values of \(\alpha \). Here, \(\omega =-2/3\)

Full size image

5 Greybody factors

In this section, we aim to analyse the transmission coefficient or the GF for the regular MOG BHQ. The GF describes how much radiation near a BH is trapped or reflected by the BH. The GF estimates the likelihood of an outwardly travelling wave reaching an observer at infinity without being absorbed, or the likelihood of an incoming wave being absorbed by the BH. In fact, many researchers have already studied reflection coefficients and transmission coefficients (GFs) in various scenarios [51,52,53,54,55,56,57,58,59,60,61,62,63]. To evaluate the GF, we will use the general semi-analytic bounds method. This method requires that GFs (or transfer coefficients) around a BH be greater or equal to the following formula: [58, 61, 64]

$$\begin{aligned} T\left( w\right) \ge \sec h^{2}\left( \frac{1}{2w} \int _{r_{h}}^{+\infty }V_{eff}dr_{*}\right) . \end{aligned}$$
(13)

To calculate the GF of massless scalar we will use potential given in Eq. (7). Hence

$$\begin{aligned} T\left( w\right) \ge \sec h^{2}\left( \frac{1}{2w } \int _{r_{h}}^{\infty }\left( \frac{l\left( l+1\right) }{r^{2}}+\frac{f^{\prime }}{r}\right) dr \right) . \end{aligned}$$
(14)

The analytical solution of Eq. (14) is

$$\begin{aligned} T\left( w\right)\ge & {} \sec h^{2}\left[ \frac{1}{w }\left( -\frac{l(l+1) }{r_{h}}\right. \right. \nonumber \\ {}{} & {} \quad \left. \left. -\frac{cr_{h}^{-2-3\omega }\left( 1+3\omega \right) \left( 1+\alpha \right) }{2+3\omega }\right. \right. \nonumber \\ {}{} & {} \left. \left. -\frac{\alpha M^{2}\left( 1+\alpha \right) r_{h}}{ \left( r_{h}^{2}+\alpha \left( 1+\alpha \right) M^{2}\right) ^{2}}\right) \right. \nonumber \\{} & {} -\frac{2r_{h}^{3}}{\alpha M\left( r_{h}^{2}+\alpha \left( 1+\alpha \right) M^{2}\right) ^{2/3}}\nonumber \\ {}{} & {} \quad +\frac{r_{h}}{2\left( r_{h}^{2}+\alpha \left( 1+\alpha \right) M^{2}\right) }\nonumber \\ {}{} & {} \quad -\frac{4r_{h}}{\alpha M\left( r_{h}^{2}+\alpha \left( 1+\alpha \right) M^{2}\right) ^{1/2}}.\nonumber \\{} & {} \left. -\frac{ArcTan\left( \frac{r_{h}}{M\sqrt{\alpha \left( 1+\alpha \right) }}\right) }{M+\sqrt{\alpha \left( 1+\alpha \right) }}-\frac{2}{ M\alpha }\right. \nonumber \\ {}{} & {} \quad \left. -\frac{\pi }{4M\sqrt{\alpha \left( 1+\alpha \right) }}\right] \end{aligned}$$
(15)

To illustrate the picture, we plot Eq. (15) for the choose \(\omega =-4/9\) in Fig. 10. As can be seen in the Figure, when the frequency of the wave is low, GF is zero, while when it is high, GF is one, which demonstrates that when its frequency is low, the wave can be entirely reflected, but at high frequencies it cannot. According to the Fig. 10, as the MOG parameter \(\alpha \) increases, GF also increases, and thus less scattering. The right panel Fig. 10 shows similar plot for varying the parameter c.

Fig. 10
figure 10

The greybody bound Eq. (15) of scalar massless field of MOG BHQ for several values of the parameters \(\alpha \) (left) and c (right)

Full size image

6 Thermodnamics of Regular MOG BH surrounded by a quintessence

Rao [65] gave the idea of informational geometry [66] and on the basis of it, Weinhold [67] generated the metric framework for a thermodynamic system. Weinhold has developed the thermodynamic function differentials as a vector space element and then explain an inner product. It is suggested that the metric components \(g_{ij}\) can be obtained through the second derivative of the internal energy concerning the extended parameter. The geometry in this formulation is based on the lowest energy principle for an isolated system, which indicates the tensor and Euclidean properties of \(g_{ij}\). Despite the fascinating features of this approach, which permits the geometric hypothesis to be applied to figure out the fundamental rules of equilibrium thermodynamics, it failed to yield any major findings.

Years later, Ruppeiner [68] was able to design a thermodynamic geometry with a precise physical interpretation by switching from the energy to the entropy representation. He stated the metric tensor as the Hessian of the entropy density and observed that the derived line element, i.e. the infinitesimal distance between adjacent equilibrium states, has an inversely proportional relationship with the classical theory’s fluctuation probability. In infinite-time thermodynamics, the increase in entropy caused by non-equilibrium facets can be related to the geodetic distance between a standard process’s end and beginning states [69]. Many exciting advancements emerged from the earlier concept of thermodynamic metric. Furthermore, Weinhold and Ruppeiner’s measures have been shown to be conformal [70] and to be limiting cases of Rao’s metric [71]. Jawad and Usman [72] have Studied the thermodynamic geometry of Einstein Gauss Bonnet BH. They have also tried to associate the thermodynamic geometry of BH with the deflection angle.

The metric function in asymptotic form can be written as

$$\begin{aligned} f(r)=-\frac{(\alpha +1) c}{r^{3 \omega +1}}+\frac{\alpha (\alpha +1) M^2}{r^2}-\frac{2 (\alpha +1) M}{r}+1.\nonumber \\ \end{aligned}$$
(16)

Hawking temperature palys a crucial rule in BH thermodynamics. To calculate the Hawking temperature we can use the given expression \(f'/4\pi \), which takes the form as

$$\begin{aligned} T=\frac{(\alpha +1) r^{-3 (\omega +1)} \left( c (3 r \omega +r)-2 M r^{3 \omega } (\alpha M-r)\right) }{4 \pi }.\nonumber \\ \end{aligned}$$
(17)

Another important aspect of BH thermodynamics is the thermodynamic features. As we know that due to absence of the cosmological constant so cannot use the expression of \(P=\frac{\Lambda }{8\pi }\). To derived the thermodynamic pressure for MoG BH, we can use the given relation

$$\begin{aligned} P=T\bigg (\frac{\partial {S_{bh}}}{\partial {V}}\bigg ), \end{aligned}$$
(18)

where V represents the volume of the BH and the volume of the BH is \(V=\frac{4}{3} \pi r^{3}\).

$$\begin{aligned} P=\frac{(\alpha +1) r^{-3 (\omega +1)-1} \left( c (3 r \omega +r)-2 M r^{3 \omega } (\alpha M-r)\right) }{8 \pi }.\nonumber \\ \end{aligned}$$
(19)

Bekenstein proposed in the early 1970s that the second principle of thermodynamics might be violated if BHs possesses no entropy. The entropy of a BH has been suggested as a monotone growing function of its area, because the area of a BH never decreases under classical theory [73]. The simplest monotone rising function of area is a proportional function and its expression given as,

$$\begin{aligned} S_{bh}= A/4, \end{aligned}$$
(20)

where \(A=~4 \pi r^{2}\) is the area of the BH at its event horizon. Entropy measures the level of uncertainty in a physical system. In general, more detail shows less uncertainty [74], which is often expressed clearly in a quantitative statement: Information exhibits a negative entropy. A system has less entropy or uncertainty the more information it possesses.

Thermal stability is quite fascinating topic in BH thermodynamics. Many scientist work in this direction to check the local and global stability of the BHs. To investigate the local stability we use heat capacity in which we have specific heat at constant volume, specific heat at constant pressure while the third one is the ratio between these two heat capacities. First, we investigate the specific heat at constant volume by using the following relation

$$\begin{aligned} C_{V}= & {} \bigg (2 \pi \alpha (\alpha +1) c r^2 (3 \omega -1)-4 \pi r^{3 \omega +3} (rY+1)\bigg )\nonumber \\ {}{} & {} \times \bigg (-\alpha (\alpha +1) c (9 \omega \nonumber \\ {}{} & {} \times (\omega +1)-4)+8 r^{3 \omega +2} Y+2 (\alpha +4) r^{3 \omega +1}\bigg )^{-1},\nonumber \\ \end{aligned}$$
(21)

where \(Y= \sqrt{\frac{(\alpha +1) (\alpha (\alpha +1) c r^{-3 \omega }+r)}{r^3}}\).

Fig. 11
figure 11

Plot of \(C_{V}\) of MoG BHQ versus r in Bekenstein entropy

Full size image

The behavior of \(C_{V}\) is clearly showed a negative behavior throughout the horizon radius which is observed in Fig. 11. It is also observed that the conduct of \(C_{V}\) of the MOG BH with respect to the horizon radius is unstable for the all the ranges. To discuss thermal stability more deeply, we now analyze the specific heat at constant pressure \(C_{P}\) and it is given as

$$\begin{aligned} C_{P}= & {} \bigg (4 \pi r^{3 \omega +2}(r Y+1)-2 \pi \alpha (\alpha +1) c r (3 \omega -1)\bigg )\\ {}{} & {} \times \bigg (\big (\big ((\alpha +1) (\alpha (\alpha +1)c r^{-3 \omega }+r)\big )\big (r^{-3}\big )\big )^{1/2} \\ {}{} & {} \times (-\alpha (\alpha +1) c (9 \omega (\omega +1)-4)+8 r^{3 \omega +2}\\ {}{} & {} +2 (\alpha +4) r^{3 \omega +1} Y)\bigg )^{-1}. \end{aligned}$$
Fig. 12
figure 12

Plot of \(C_{P}\) of MOG BHQ versus r in Bekenstein entropy

Full size image

The conduct of \(C_{P}\) shows a positive behavior throughout the horizon radius which is presented in Fig. 12. It is deduced from the Fig. 12 that the behavior of \(C_{V}\) of the MOG BH against the horizon radius is stable for the all the r. Now, we will discuss the heat capacity ration which can be observed from the ratio between the heat capacities and it is given as

$$\begin{aligned} \gamma= & {} -\frac{1}{r \sqrt{\frac{(\alpha +1) \left( \alpha (\alpha +1) c r^{-3 \omega }+r\right) }{r^3}}}. \end{aligned}$$
(22)
Fig. 13
figure 13

Plot of \(\gamma \) of MOG BHQ versus r in Bekenstein entropy

Full size image

Behavior of heat capacity ratio is very interesting and its trajectories showed negative behavior along the horizon radius that is presented in Fig. 13. One can notice that all the trajectories coincide at a common point which is at \(r=~1\) for all the values of \(\omega \) that is quite surprising. Overall, Behavior of the heat capacity ratio is unstable throughout the horizon radius.

Now, we will discuss the Gibss free energy (GFE) and also discuss its graphical representation. GFE of the MOG BH system is considered as its Global stability. GFE can be derived from the given expression

$$\begin{aligned} G=~M-~TS_{bh}+~PV, \end{aligned}$$
(23)

by inserting values in the Eq. (23), we have

$$\begin{aligned} G= & {} \bigg (12 \alpha (\alpha +1)\bigg )^{-1} \bigg (\alpha (\alpha +1)^2\nonumber \\ {}{} & {} \quad c (1-3 \omega ) r^{-3 \omega }+2 (\alpha +7) r^2 Y+14 (\alpha +1)r\bigg ).\nonumber \\ \end{aligned}$$
(24)
Fig. 14
figure 14

Plot of G of MOG BHQ versus r in Bekenstein entropy

Full size image

Examining the heat capacity’s positivity when a system’s equilibrium state corresponds to the global minimum of the GFE is one way to look into the local thermodynamic stability of a system. To determine a potential thermodynamic phase transition and its order, one must understand the behavior of GFE. Plotting the GFE allows one to examine the behavior of GFE with respect to horizon radius. Behavior of the GFE is decreasing but with positive behavior throughout the horizon radius that can be observed in Fig. 14. The positive behavior of the GFE indicates the stable behavior of MOG BH.

Helmholtz free energy (HFE) is another technique to examine the global stability of the BH. HFe can be calculated by using the given relation

$$\begin{aligned} F_{*}=~M-~TS_{bh}, \end{aligned}$$
(25)

by substituting the values of M,  T and \(S_{bh}\) in the Eqn. (25), then we have

$$\begin{aligned} F_{*}= & {} \bigg (\alpha (\alpha +1)^2 (-c) (3 \omega -1) r^{-3 \omega }+2 (\alpha +3) r^2 Y\nonumber \\ {}{} & {} \times +6 (\alpha +1) r\bigg ) \bigg (4\alpha (\alpha +1)\bigg )^{-1}. \end{aligned}$$
(26)
Fig. 15
figure 15

Plot of \(F_{*}\) of MOG BHQ versus r in Bekenstein entropy

Full size image

Plotting the HFE permits one to investigate the conduct of HFE in terms of the horizon radius. Behavior of the HFE is Increasing with positive behavior for all ranges of the horizon radius that can be observed in Fig. 15. The positive conduct of the HFE predicts the stable behavior of MOG BH.

6.1 Thermodynamic geometry

This section’s goal is to use the Bekenstein-Hawking entropy to examine the thermodynamic geometry of MOG BHQ. To do this, we use Eqs. 16 and 20 to compute the mass of the MOG BH in terms of entropy. This produces

$$\begin{aligned} M(S,~\alpha )= & {} (\sqrt{\pi } \alpha (\alpha +1))^{-1}(S\left( (\alpha +1) S^{\frac{1}{2}(-3) (\omega +1)} \right. \nonumber \\ {}{} & {} \left. \quad \times \left( \alpha (\alpha +1) c \pi ^{\frac{3 \omega }{2}+\frac{1}{2}}+S^{\frac{3 \omega }{2}+\frac{1}{2}}\right) \right) ^{1/2} \nonumber \\{} & {} +(\alpha +1)\times \sqrt{S}) \end{aligned}$$
(27)

In order to explain the quantum presence of gravity in Hawking radiation, BH thermodynamics is crucial [75]. Hawking highlighted the usual behavior of black bodies, which is emitting thermal radiation, in thermodynamic terms. Equation (28) provides the Hawking temperature in terms of Bekenstein–Hawking entropy.

$$\begin{aligned} T(S,~\alpha )= & {} \bigg (4 \sqrt{\pi } \alpha Y_S \bigg )^{-1}\bigg (S^{\frac{1}{2} (-3) (\omega +1)} \nonumber \\ {}{} & {} \times (2 S^{\frac{3 \omega }{2}} (S \big (Y_S+\sqrt{S})-\alpha (\alpha +1) c \pi ^{\frac{3 \omega }{2}+\frac{1}{2}}\nonumber \\{} & {} \times (3 \omega -1))\bigg ), \end{aligned}$$
(28)

where \(Y_S=\bigg ((\alpha +1) S^{\frac{1}{2} (-3) (\omega +1)} (\alpha (\alpha +1) c \pi ^{\frac{3 \omega }{2}+\frac{1}{2}}+S^{\frac{3 \omega }{2}+\frac{1}{2}})\bigg )^{1/2}\). To compute heat capacity in terms of entropy, use Eq. (28)

$$\begin{aligned} C(S,~\alpha )= & {} \bigg (4 S (\alpha (\alpha +1) c \pi ^{\frac{3 \omega }{2}+\frac{1}{2}}+S^{\frac{3 \omega }{2}+\frac{1}{2}}) (2 S^{\frac{3 \omega }{2}} \nonumber \\ {}{} & {} \times (S Y_S+\sqrt{S})-\alpha (\alpha +1) c \pi ^{\frac{3 \omega }{2}+\frac{1}{2}} (3 \omega -1))\bigg ) \nonumber \\{} & {} \times \bigg (3 \alpha ^2 (\alpha +1)^2 c^2 \pi ^{3 \omega +1} (\omega +1) (3 \omega -1)\nonumber \\ {}{} & {} -4 \alpha (\alpha +1) c \pi ^{\frac{3 \omega }{2}+\frac{1}{2}} S^{\frac{3 \omega }{2}+1} Y_S+6 \alpha (\alpha +1) c \nonumber \\ {}{} & {} \times \pi ^{\frac{3 \omega }{2}+\frac{1}{2}} (\omega +1) (3 \omega -1) S^{\frac{3 \omega }{2}+\frac{1}{2}}\nonumber \\ {}{} & {} -4 S^{3 \omega +\frac{3}{2}} Y_S-4 S^{3 \omega +1}\bigg )^{-1}. \end{aligned}$$
(29)

We now analyze the phase transition for MOG BHQ in light of the geometric structures addressed in the Weinhold and Ruppeiner formalism [67]. Weinhold constructs a purposed Riemannian metric in the form of the second derivative of internal energy and a geometrical basis for comprehending the thermodynamics of the BH [76]. Ruppeiner [68] created a Riemannian thermodynamic entropy metric in order to clarify thermodynamic fluctuation theory in the wake of Weinhold [67]’s groundbreaking work. He also found a structured method for determining the Ricci curvature R of the Ruppeiner metric. Weinhold’s and Ruppeiner’s thermodynamic metrics are not consistent under Legendre transformations, based on a relationship between phase space and metric structures of the space of equilibrium states. It has been found that there is an association between the type of inter-particle connection and the symbol of R. The weinhold geometry can be written as

$$\begin{aligned} g_{\beta \omega }^{W}=\partial _{\beta }\partial _{\omega } M(S,\alpha ), \end{aligned}$$
(30)

the line element of Weinhold metric for MOG BHQ is

$$\begin{aligned} dS^{2}_{W}=M_{SS}dS^{2}+M_{\alpha \alpha }d\alpha ^{2}+2M_{S\alpha }dSd\alpha , \end{aligned}$$
(31)

and the corresponding metric to this line element is given as

\(g^{W}=\left( \begin{array}{cc} M_{SS} &{} M_{S\alpha } \\ M_{\alpha S} &{} M_{\alpha \alpha } \\ \end{array}\right) \).

Ruppeiner geometry was employed in [77] for investigating the microscopic structure of BHs. The Ruppeiner metric’s curvature scalar can provide information about the type and strength of particle interactions as well as other aspects of the system’s microscopic behavior. Now, we study the Ruppeiner formalism which is proposed in the system of thermodynamics [78, 79] is

$$\begin{aligned} dS^{2}_{Rup}=1/T(dS^{2}_{Win}), \end{aligned}$$
(32)

and the corresponding metric is

\(g^{Rup}=\frac{1}{T}\left( \begin{array}{cc} M_{SS} &{} M_{S\alpha } \\ M_{\alpha S} &{} M_{\alpha \alpha } \\ \end{array}\right) \).

The curvature scalar which we obtained from Weinhold \(g^{W}\) and Ruppiener metric \(R^{W}\) cannot be presented in this paper due to their length. We are only going to show their graphical representation.

Fig. 16
figure 16

Plot of \(R^{W}\) of MOG BHQ versus r in Bekenstein entropy

Full size image
Fig. 17
figure 17

Plot of \(R^{Rup}\) of MOG BH versus r in Bekenstein entropy

Full size image

Heat capacity and curvature scalar obtained from Weinhold and Ruppiener metric is presented in Figs. 16 and 17. As one can observed that the trajectories for heat capacity depicted the negative behavior for all the values of the horizon which indicates the instable conduct of MOG BHQ. Curvature scalars depicted quite interesting behavior for different variations of the \(\omega \). For \(\omega =-1/3,~-2/3,~-1\), curvature scalar showed positive behavior which reflects the interaction between the particles of the MOG BHQ is repulsive which can be seen in Fig. 17. In case of ruppenier metric, Ricci scalar reflects the almost similar behavior for \(\omega =-1/3\) while for \(\omega =-2/3,~-1\) it showed negative behavior that can be observed in Fig. 17. The heat capacity’s divergence points and the Ricci scalars of the Weinhold and Weinhold metric in the Figs. 16 and 17 do not coincide.

7 Conclusion

In this paper we aimed to investigate the impact of the MOG field and the quintessence scalar field on the astrophysical observable surrounding a regular static spherically symmetric BH. To achieve this goal, we conducted extensive research on QNMs, GFs, and thermodynamics.

We first derived the master equations of scalar field and electromagnetic perturbations of MOG BHQ and calculated the QNM frequencies using the 6th order WKB approximation method. We draw the graphs of real and imaginary parts of quasinormal frequencies of the perturbations with respect to the parameters \(\alpha \) and c, respectively. In addition, we calculate the quasinormal modes at the eikonal limit using the null geodesic method. Finally, we arrive at the following conclusions: The imaginary part is negative in all of the obtained BH frequency modes, indicating their stability. Real QNMs or oscillation frequencies are observed to decrease significantly as c and \(\alpha \) increase. Gravitational wave damping or decay rates, on the other hand, increase as c and \(\alpha \) increase. Furthermore, c exhibits almost linear variation, whereas \(\alpha \) does not. We calculated the GFs associated with the BH metric and plotted transmission probability versus frequency for different model parameters. Our analysis revealed that as the MOG parameter \(\alpha \) increases, GF also increases, and thus less scattering. The impact of quintessence parameter c is same as MOG parameter. This is consistent with the effective potential.

We have also investigated the thermodynamic quantities and geometries for MOG BH with quintessence region. It is evident that MOG BH exhibits locally unstable behaviour, but globally displayed stable conduct, as shown in Figs. 11, 12, 13, 14, 15. Additionally, this work explored the MOG BH’s microscopic structure for variations in \(\omega \), resulting in some very intriguing results predicted. Employing the Hawking Bekenstein entropy, we have examined the thermodynamic geometry of the MOG BH. The conduct of the Ricci curvature scalars for MOG BH for \(-1/3 \le ~\omega \le ~-1\) is illustrated graphically in Figs. 16 and 17. We have noticed that the Weinhold’s curvature scalar exhibited positive behavior, demonstrating a repulsive interaction among the MOG BH particles. But in the instance of Ruppiener’s curvature scalar, we learned that it demonstrated negative for \(\omega =~-2/3,~-1\), revealing that particle interaction among the MOG BH molecules is attractive. Our results are intriguing because they suggests that, depending on how the quintessence parameter \(\omega \) fluctuates, the behavior of the two Ricci scalars will alter significantly. Future research could look into Dirac field perturbation and other thermodynamic geometric formalisms to study particle behaviour in the MOG BHQ, which would be fascinating.