1 Introduction

A jet refers to a spray of stable particles formed through the hadronization of an energetic quark or gluon. The W/Z/Higgs bosons and the top quark, the four most massive Standard Model (SM) particles, decay mainly into quarks and hadronize to jets [1]. Figure 1 illustrates a reconstructed \(e^+e^-\rightarrow Z\rightarrow c\bar{c}\) event with center-of-mass energy of 91.2 GeV. Efficient identification of the jet flavor could shed light on the properties of massive SM particles and is critical for experimental exploration at the high-energy frontier. Flavor tagging is used to distinguish jets which hadronize from quarks of different flavors or from gluons. To promote the development of future electron-positron Higgs factories, which is regarded as a high priority future collider [4], accurate performance analysis and optimization of both detectors and algorithms are essential. Jet flavor tagging and relevant benchmark analyses serve as good objectives.

The Circular Electron Positron Collider (CEPC) [5] is a large-scale collider facility that was proposed after the discovery of the Higgs boson in 2012. It is designed to have a circumference of 100 km with two interaction points. It will be able to operate at multiple center-of-mass energies, including 240 GeV as a Higgs factory, 160 GeV for a \(W^+W^-\) threshold scan, and 91 GeV as a Z factory. It also can be upgraded to 360 GeV for a \(t\bar{t}\) threshold scan. Table 1 summarizes its baseline operating scheme and the corresponding boson yield predictions [6]. One of the main scientific objectives of the CEPC is the precise measurement of properties of the Higgs boson. Additionally, trillions of \(Z\rightarrow q\bar{q}\) events can provide an excellent opportunity for studying flavor physics. In the future, the CEPC can be upgraded to a proton-proton collider to directly explore new physics at a center-of-mass energy of about 100 TeV.

Jet flavor tagging performance depends on the design of the experimental detector, particularly on the design of the vertex detector, as well as the utilization of reconstruction algorithms. In this study, we apply ParticleNet [7] to the CEPC and assess its flavor tagging performance in the measurement of \(\sigma (ZH)\cdot Br(Z\rightarrow \nu \bar{\nu }, H\rightarrow c\bar{c})\) and \(|V_{cb}|\) via W decay. Our results demonstrate that ParticleNet outperforms the baseline jet flavor tagging algorithm, LCFIPlus [8], by achieving a 36% and 75% improvement in the relative statistical accuracy of \(\sigma (ZH)\cdot Br(Z\rightarrow \nu \bar{\nu }, H\rightarrow c\bar{c})\) and \(|V_{cb}|\) measurement via W boson decay at the center-of-mass energy of 240 GeV with integrated luminosity of 5.6 ab\(^{-1}\). This improvement is likely attributed to the approach of viewing the jet as a particle cloud and the more effective utilization of local neighborhood information of particles in ParticleNet, as opposed to traditional multivariate methods based on observables motivated by QCD theory [7]. We also observe that both ParticleNet and LCFIPlus perform better in the barrel region when compared to the endcap region. By analyzing the dependence of flavor tagging performance on vertex detector configurations, we observe that the most sensitive vertex detector parameter is the inner radius, followed by the material budget and spatial resolution. This result is consistent with previous studies conducted using LCFIPlus.

Fig. 1
figure 1

The display of a reconstructed \(e^+e^-\rightarrow Z\rightarrow c\bar{c}\) event generated using Whizard 1.95 [2] and Pythia 6 [3], with a center-of-mass energy of 91.2 GeV. The event is simulated using CEPC baseline software. Different particles are depicted with different colors: red for \(e^{\pm }\), cyan for \(\mu ^{\pm }\), blue for \(\pi ^{\pm }\), orange for photons, and magenta for neutral hadrons

Full size image
Table 1 The operation scheme of the CEPC, including the center-of-mass energy, the instantaneous luminosity, the total integrated luminosity, and the event yields [6]
Full size table

This article is organized as follows. Section 2 introduces the CEPC detector, software, and the samples used in this analysis. Section 3 describes the jet flavor tagging algorithms (LCFIPlus and ParticleNet) and the method used to evaluate their performance. Section 4 quantifies the dependence of flavor tagging performance on the vertex detector configuration and compares the performance of ParticleNet and LCFIPlus. Finally, Sect. 5 provides a brief conclusion.

2 CEPC Detector, software, and samples

Fig. 2
figure 2

The CEPC baseline detector. From the innermost subdetector to outermost one, the detector is composed of a silicon pixel vertex detector, a silicon inner tracker, a TPC, a silicon external tracker, an ECAL, an HCAL, a solenoid magnet with a field strength of 3 Tesla, and a return yoke embedded with a muon detector. Five pairs of silicon tracking disks are installed in the forward regions to enlarge the tracking acceptance [6]

Full size image

At present, the two interaction points of the CEPC are designed with the same baseline detector [5], which is designed according to the Particle Flow Algorithm (PFA) principle [9] and emphasizes reconstructing visible final state particles in the most-suited detector subsystems. The structure of the CECP detector is shown in Fig. 2. From the innermost subdetector to outermost one, the baseline detector is composed of a silicon pixel vertex detector [10], a silicon inner tracker, a Time Projection Chamber (TPC) [11] surrounded by a silicon external tracker, a silicon-tungsten sampling Electromagnetic Calorimeter (ECAL) [12], a steel-glass Resistive Plate Chambers sampling Hadronic Calorimeter (HCAL) [5], a 3 Tesla superconducting solenoid magnet, and a flux return yoke embedded with a muon detector. For flavor tagging, the vertex detector is critical. At the CEPC, the vertex detector is designed with six concentric cylindrical layers of square silicon pixel sensors. The mechanical structure of the vertex detector consists of ladders, with each ladder supporting sensors on both sides. The detailed structure of the vertex detector is depicted in Fig. 3, and its specific parameters are listed in Table 2.

Fig. 3
figure 3

Schematic view of vertex detector. Two layers of silicon pixel sensors are mounted on both sides of each of the three ladders to provide six space points. The beam pipe is surrounded by the vertex detector [13]

Full size image
Table 2 The baseline design parameters of the CEPC vertex system [13]
Full size table
Fig. 4
figure 4

The information flow of the CEPC software chain [14]

Full size image

A baseline reconstruction software chain has been developed to quantify the scientific merit and guide the detector optimization of CEPC, see Fig. 4. The data flow of the CEPC baseline software starts from the event generators of Whizard 1.95 [2] and Pythia 6 [3]. The detector geometry is implemented into MokkaPlus [15], a GEANT4-based full simulation module. MokkaPlus calculates the energy deposition in the detector-sensitive volumes and creates simulated hits. The digitized tracker hits are reconstructed into tracks via Clupatra [16]. The Particle Flow algorithm, Arbor [17], reads the reconstructed tracks and the calorimeter hits to build reconstructed particles. High-level reconstruction algorithms reconstruct composite physics objects such as converted photons, jets, tau leptons, and so on, and identify the flavor of the jets.

We utilize hadronic events at Z-pole operation, including 1 million \(Z\rightarrow b\bar{b}\) events, 1 million \(Z\rightarrow c\bar{c}\) events, and 0.33 million each of \(Z\rightarrow u\bar{u}/d\bar{d}/s\bar{s}\) events. For ParticleNet, we divide the samples into three distinct sets: the training set for training the model, the validation set used to validate whether the model is overfitting or underfitting, and the testing set used to give flavor tagging results. The ratios of samples in these sets were set at 60%, 20%, and 20%, respectively. For LCFIPlus, we use the full event sample as the testing set, since the model is pre-trained with a separate, statistically independent Z-pole sample produced using the same software and identical simulation settings. Unless explicitly stated, the results presented in this paper are based on the aforementioned samples.

3 Flavor tagging algorithms and their performance

In this section, we introduce LCFIPlus and ParticleNet and compare their performance based on the CEPC detector and software. Both algorithms read the information of reconstructed jet candidates and calculate the jet likeness to b, c, and light categories.

The LCFIPlus package, a framework for jet analysis in linear collider studies, was originally developed for the International Linear Collider (ILC) [18], and has since been widely used for studies with the Compact Linear \(e^+e^-\) Collider (CLIC) [19], the Future Circular Collider \(e^+e^-\) (FCC-ee) [20], and the CEPC. The LCFIPlus package consists of vertex finding, jet clustering, vertex refinement, and flavor tagging. To perform flavor tagging, the jets are classified into four categories based on the number of reconstructed vertices and isolated leptons in the jet. A set of variables is then extracted for each category, which includes the number of tracks in each vertex, the vertex mass, the distance between the secondary vertex and the primary vertex, the vertex decay length, the track transverse momentum, and more. Further details can be found in [8]. In each category, two types of flavor tagging algorithms are trained using the Gradient Boosted Decision Tree (GBDT) method, one for the b-tagging algorithm and the other for the c-tagging algorithm.

Fig. 5
figure 5

The architecture of the ParticleNet (left) and the structure of the EdgeConv block (right) [7]

Full size image
Table 3 The input variables used in ParticleNet for jet flavor tagging at the CEPC
Full size table

The ParticleNet approach, based on a Graph Neural Network (GNN) [21], was first published in 2020 [7]. The architecture of ParticleNet is shown in the left panel of Fig. 5. It consists of three EdgeConv [22] blocks, one channel-wise global average pooling block, and two fully-connected blocks followed by a softmax function [23] to output the b/c/light-likeness for each jet. The core concept of ParticleNet is the EdgeConv operation, which is realized by applying feature aggregation for each particle and its k nearest particles in the jet. The specific process of each EdgeConv block is illustrated in the right panel of Fig. 5. It starts by finding the k-nearest neighbors for each particle within the jet. The edge between each particle and its k-nearest neighbors is determined using the input features of each particle. In the first EdgeConv block, the spatial coordinates (\(\mathrm \Delta \) \(\eta \), \(\mathrm \Delta \) \(\phi \)) of the particles in the pseudorapidity-azimuth space are used to compute the edge of each pair of particles, while the subsequent EdgeConv blocks use the learned feature vectors as coordinates. The input features for our task, listed in Table 3, include the kinematic variables constructed with the 4-momentum of each particle, the PID information, the charge, and the impact parameters, where the distance between the interaction point and the path of a track is defined as the impact parameter, and where the distance along the beam is called \(z_0\) and perpendicular to the beam is called \(d_0\).

Fig. 6
figure 6

The distribution of b/c-likeness for samples of \(e^+e^-\rightarrow Z\rightarrow b\bar{b}/c\bar{c}/\)light quarks with ParticleNet approach. The parallel lines divide the space spanned by the b/c-likeness into three regions

Full size image
Fig. 7
figure 7

The migration matrix of flavor tagging performance of ParticleNet (top) and LCFIPlus (bottom) at the CEPC

Full size image

Both flavor tagging algorithms assign three values to each jet: b-likeness, c-likeness, and light-likeness, with the constraint that their sum equals unity. The scatter plots in Fig. 6 show the distribution of b-likeness versus c-likeness for samples of \(e^+e^-\rightarrow Z\rightarrow b\bar{b}/c\bar{c}\)/light quarks with ParticleNet. In these plots, b-jets tend to concentrate in the region of larger b-likeness, c-jets in the region of larger c-likeness, and light-jets in the region of smaller b/c-likeness. Compared to that of ParticleNet, the bins that contain a larger number of counts tend to be more dispersed in LCFIPlus, which returns an overall broader distribution. The phase space spanned by the b/c-likeness is divided into three different regions corresponding to identified b, c, and light quarks. We then obtain the ratios of b-jets identified as b-jets, b-jets identified as c-jets, and so on. These ratios can be represented with a migration matrix, as shown in Fig. 7. The working point (phase space separation) can be optimized according to the specific analysis requirements. For general cases, we adopt the method using two orthogonal lines passing through the point (0.5, 0.5), as depicted by the two red lines in Fig. 6.

4 Performance analyses

The performance of jet flavor tagging can be characterized by the migration matrix, and this is reflected in the anticipated accuracy of benchmark measurements. The design of the vertex detector also plays an important role in the performance of jet flavor tagging.

4.1 Performance comparison and impact on benchmarks of \(\sigma (ZH)\cdot Br(Z\rightarrow \nu \bar{\nu }, H\rightarrow c\bar{c})\) and \(|V_{cb}|\)

Figure 7 displays the migration matrices obtained using LCFIPlus and ParticleNet, respectively. Compared to the performance of LCFIPlus, ParticleNet achieves a significant improvement in b/c-tagging efficiency, with an enhancement of 15% for b jets and 32% for c jets. The trace of the migration matrix, abbreviated as \({\textrm{Tr}}_{mig}\), is 3.0 for perfect jet flavor tagging performance, and it increases from 2.30 to 2.64 when switching from LCFIPlus to ParticleNet.

Fig. 8
figure 8

The top panel shows the correlation between jet flavor tagging performance, quantified using the trace of the flavor tagging performance matrix, and the jet polar angle. The bottom panel illustrates the performance improvement of ParticleNet relative to LCFIPlus at different jet polar angles. Two vertical lines mark the boundary between the barrel and endcap regions

Full size image

In the top panel of Fig. 8, we present the correlation between jet flavor tagging performance, described by \({\textrm{Tr}}_{mig}\), and jet polar angle, which is defined as the angle with respect to the beam line and represented by the angle \(\theta _\textrm{jet}\). The boundary between the barrel region and the endcap region is marked with two vertical orange dashed lines. Both LCFIPlus and ParticleNet exhibit better performance in the barrel region compared to the endcap region, due to the relatively lower resolution of transverse momentum (\(P_t\)) and impact parameters (\(d_0\) and \(z_0\)) in the endcap region. The value of ParticleNet performance divided by LCFIPlus performance can be used to describe the performance improvement of ParticleNet relative to LCFIPlus. The bottom panel of Fig. 8 shows the correlation between those ratio values and the jet polar angle. Compared to LCFIPlus, ParticleNet improves the trace of the migration matrix by more than 10% in the barrel region and more than 30% in the endcap regions, using the given selection criteria.

Fig. 9
figure 9

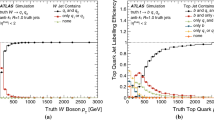
The dependence of relative statistical uncertainties for measurement of \(\sigma (ZH)\cdot Br(Z\rightarrow \nu \bar{\nu }, H\rightarrow c\bar{c})\) [24] (top) and \(|V_{cb}|\) [26] (bottom) on flavor tagging performance, which is represented with the trace of flavor tagging performance matrix. The larger green/orange marker corresponds to the result obtained by LCFIPlus/ParticleNet. When the vertex detector parameters, including the inner radius, material budget, and spatial resolution, are changed by a factor of 0.5/2 from the baseline design (the geometry used in this simulation), the \({\textrm{Tr}}_{mig}\) value changes accordingly. It shifts from 2.64 to 2.75/2.53 for ParticleNet and from 2.30 to 2.10/2.50 for LCFIPlus, as indicated by the four vertical lines

Full size image

The performance of both flavor tagging algorithms can also be compared in benchmark analyses. The first analysis we consider is the signal strength measurement of \(\sigma (ZH)\cdot Br(Z\rightarrow \nu \bar{\nu }, H\rightarrow c\bar{c})\). When CEPC operates as a Higgs factory at the center-of-mass energy of 240 GeV and collects an integrated luminosity of 5.6 ab\(^{-1}\), the top panel of Fig. 9, which uses the same analysis method as in Ref. [24], showcases the correlation between the trace of the migration matrix and the accuracy of the signal strength of \(\sigma (ZH)\cdot Br(Z\rightarrow \nu \bar{\nu }, H\rightarrow c\bar{c})\). Using LCFIPlus, the trace is 2.30, corresponding to an accuracy of 0.057, indicated by the green star. ParticleNet enhances the trace to 2.64, aligning with an accuracy of 0.042, represented by the orange star.

The second analysis we consider is the signal strength measurement of \(|V_{cb}|\), the magnitude of \(V_{cb}\). Accurate measurement of \(|V_{cb}|\) plays a pivotal role in the study of weak interactions within the SM [25]. When CEPC operates as a Higgs factory at the center-of-mass energy of 240 GeV and collects an integrated luminosity of 5.6 ab\(^{-1}\), ParticleNet can significantly improve the accuracy of signal strength by 75% in the measurement of \(|V_{cb}|\) through \(W^+W^-\rightarrow \mu \nu q\bar{q}\), as depicted in the bottom panel of Fig. 9 [26].

4.2 Comparison of vertex detector optimization

Jet flavor tagging performance depends on the detector design, especially that of the vertex detector. In this study, the vertex detector is characterized by three parameters: the material budget, the spatial resolution, and the inner radius. The CEPC vertex detector is designed with three concentric cylinders of double-sided layers, with parameters listed in Table 2.

In a previous study [13] using the LCFIPlus flavor tagging algorithm, the correlation between c-jet tagging efficiency multiplied by purity (\(\epsilon \cdot p\)) and the considered vertex detector parameters – the inner radius, the material budget, and the spatial resolution– was quantified for the CEPC. Furthermore, a study of Higgs\(\rightarrow b\bar{b}/c\bar{c}/gg\) at the CEPC [24] revealed a correlation between \({\textrm{Tr}}_{\textrm{mig}}\) and the c-jet tagging \(\epsilon \cdot p\). By combining these correlations – citing them from two previous studies rather than deriving them based on the samples used in this analysis – we obtain the correlation between \({\textrm{Tr}}_{mig}\) and relevant vertex detector parameters, as shown in the top panel of Fig. 10. This correlation is formulated in expression 1, where \({\textrm{R}}_{\textrm{radius}}^0\)/\({\textrm{R}}_{\textrm{resolution}}^0\)/\({\textrm{R}}^0_{\textrm{material}}\) represent the default design of the CEPC vertex detector and \({\textrm{R}}_{\textrm{radius}}\)/\({\textrm{R}}_{\textrm{resolution}}\)/\({\textrm{R}}_{\textrm{material}}\) represent the modified design. The coefficients of each term \({\textrm{log}}_2\frac{{\textrm{R}}^0}{\textrm{R}}\), extracted from fitting to each kind of colored point with a straight line, indicate the importance of the corresponding detector parameter on the flavor tagging performance. The results obtained from LCFIPlus demonstrate that the flavor tagging performance is most sensitive to the inner radius, followed by the material budget, and lastly the spatial resolution.

$$\begin{aligned}{} & {} \begin{aligned} {\textrm{Tr}}_{\textrm{mig}}&= 2.30 + 0.06\cdot {\textrm{log}}_2\frac{{\textrm{R}}^0_{material}}{{\textrm{R}}_{material}} \\&\quad + 0.04\cdot {\textrm{log}}_2\frac{{\textrm{R}}_{\textrm{resolution}}^0}{{\textrm{R}}_{\textrm{resolution}}} + 0.10\cdot {\textrm{log}}_2\frac{{\textrm{R}}_{\textrm{radius}}^0}{{\textrm{R}}_{\textrm{radius}}} \end{aligned} \nonumber \\ \end{aligned}$$
(1)
$$\begin{aligned}{} & {} \begin{aligned} {\textrm{Tr}}_{mig}&= 2.64 + 0.03\cdot {\textrm{log}}_2\frac{{\textrm{R}}^0_{\textrm{material}}}{{\textrm{R}}_{\textrm{material}}} \\&\quad + 0.02\cdot {\textrm{log}}_2\frac{{\textrm{R}}_{\textrm{resolution}}^0}{{\textrm{R}}_{\textrm{resolution}}} + 0.06\cdot {\textrm{log}}_2\frac{{\textrm{R}}_{\textrm{radius}}^0}{{\textrm{R}}_{\textrm{radius}}} \end{aligned}\nonumber \\ \end{aligned}$$
(2)
Fig. 10
figure 10

The correlation between the trace of a migration matrix and relative scanned parameters for LCFIPlus (top) and ParticleNet (bottom). It is important to note that the data for the top panel are cited from previous studies [13, 24]

Full size image

The same analysis was conducted using ParticleNet. The Z-pole samples are fully simulated based on different vertex detector configurations and fed to ParticleNet to train. The distribution of \({\textrm{Tr}}_{mig}\) at different vertex detector configurations is illustrated in the bottom panel of Fig. 10. The correlation between \({\textrm{Tr}}_{mig}\) and three vertex detector parameters – the inner radius, the material budget, and the spatial resolution – is expressed by Eq. (12). Compared to LCFIPlus, ParticleNet exhibits a larger \({\textrm{Tr}}_{mig}\) value (2.64 vs. 2.30), and its coefficients are roughly 50% of those of LCFIPlus. In other words, the ParticleNet demonstrates a lower dependence on the geometric parameters. However, both methods have the same order of impact for three different geometric parameters: both identify the inner radius as the most sensitive to flavor tagging performance and spatial resolution as the least sensitive.

Table 4 The accuracy of \(\nu \nu Hc\bar{c}\) and \(V_{cb}\) measurement is assessed under three scenarios: conservative, baseline, and optimal. In the conservative and optimal scenarios, three vertex detector parameters are adjusted to 2 and 0.5 times their values in the baseline design. The value of \(\frac{{\hbox {LCFIPlus}}}{{\hbox {ParticleNet}}}\) reflects the impact of the flavor tagging algorithm on benchmark measurements
Full size table

The influence of geometric modifications on benchmark analyses is assessed in Fig. 9 in Sect. 4.1. Consider two scenarios: one optimal with challenging technology and the other conservative with easily realized technology, where the values of three vertex detector parameters – the inner radius, the material budget, and the spatial resolution – are 0.5/2 times those of the baseline design. This adjustment leads to changes in \({\textrm{Tr}}_{mig}\) from 2.64 to 2.75/2.53 for ParticleNet and from 2.30 to 2.10/2.50 for LCFIPlus, as indicated by the vertical lines in Fig. 9. The accuracy of the measurement of \(\sigma (ZH)\cdot Br(Z\rightarrow \nu \bar{\nu }, H\rightarrow c\bar{c})\) and \(|V_{cb}|\) under these different scenarios using ParticleNet and LCFIPlus is presented in Table 4. Compared to LCFIPlus, ParticleNet significantly improves the accuracy of benchmark measurements. In the baseline scenario, the improvement is 36% and 75% for \(\sigma (ZH)\cdot Br(Z\rightarrow \nu \bar{\nu }, H\rightarrow c\bar{c})\) and \(V_{cb}\) measurement, respectively. While at the conservative scenario, the improvement can be enhanced to 58% for \(\sigma (ZH)\cdot Br(Z\rightarrow \nu \bar{\nu }, H\rightarrow c\bar{c})\) and nearly 3 times for \(V_{cb}\).

The values presented in Table 4 are contingent on the performance of flavor tagging, which, in turn, is influenced by various factors such as detector characteristics (including acceptance and stability), hadronic fragmentation modes, jet clustering algorithms, deep learning model architecture, and training settings (e.g., epoch size, batch size, learning rate, etc.). These factors introduce uncertainties in flavor tagging performance, subsequently impacting the values in the table. In certain analyses, jets with similar values of b-likeness, c-likeness, and light-likeness are often excluded to attain high-purity samples, thereby enhancing benchmark measurement performance. A comprehensive understanding and modeling of jet flavor tagging performance at the CEPC requires dedicated efforts. While we anticipate that experimental systematic uncertainties can be well-controlled with substantial statistics from di-jet events at the CEPC Z-pole operation, this study primarily aims to showcase the potential and drive innovation and development in deep learning within high-energy physics. Detailed exploration of these uncertainties is beyond the scope of this study.

The enhanced flavor tagging performance of ParticleNet contributes in two aspects [7]. Firstly, it adeptly treats the jet as a particle cloud, respecting the inherent property of permutation symmetry within jets. Secondly, the ParticleNet architecture leverages EdgeConv operations extensively—a convolution-like operation. The initial layers exploit local neighborhood information, while the deeper layers discern more global structures, akin to Convolutional Neural Networks. The success of ParticleNet has attracted attention from several future facilities to apply it in their studies [27] and achieve improved performance.

5 Conclusion

Flavor tagging, a methodology employed to discern the origins of jets, holds immense significance in the realm of experimental exploration at the High Energy Frontier. Jets originating from different quarks or gluons have key differences, represented in the multiplicity of different species of particles, the secondary vertices, the opening angle of jets, etc. The flavor tagging performance depends on both the flavor tagging algorithm and detector design. To pursue excellent discovery power and innovative design of the detector, intensive research into the design of the key detector technologies, especially that for vertex detectors, must be performed. Meanwhile, the development of innovative algorithms injects new momentum into this field.

In this paper, we analyze the performance of ParticleNet and LCFIPlus based on the preliminary CEPC baseline detector design. ParticleNet based on GNN has been intensively used at CMS [28,29,30] and for studies of a future FCC-ee [31]. LCFIPlus is a GBDT-based algorithm that has served as the baseline flavor tagging algorithm for CEPC and multiple future electron-positron Higgs factories. Using fully simulated hadronic events at a center-of-mass energy of 91.2 GeV at the CEPC baseline detector, we quantify the performance of both algorithms. We use a 3-dimensional migration matrix to describe the flavor tagging performance (representing the identification efficiency and misidentification rate), and the trace of the migration matrix is used as the key parameter to characterize flavor tagging.

Using the CEPC baseline detector geometry and general heavy-flavor jet selection criteria, we observe that ParticleNet offers improved performance over LCFIPlus. At the inclusive hadronic Z-pole sample, the trace of ParticleNet is larger than LCFIPlus by more than 14%. Consequently, the relative statistical accuracy of \(\sigma (ZH)\cdot Br(Z\rightarrow \nu \bar{\nu }, H\rightarrow c\bar{c})\) and \(|V_{cb}|\) measurement via W boson decay is improved by 36% and 75%, respectively, when CEPC operates as a Higgs factory at the center-of-mass energy of 240 GeV and collects an integrated luminosity of 5.6 ab\(^{-1}\). Reference [32] additionally shows that ParticleNet can improve the statistical uncertainty of \(R_C\) measurement by 60% at the CEPC. The flavor tagging performance of both ParticleNet and LCFIPlus, which is described by \({\textrm{Tr}}_{mig}\), depends on the polar angle at which the jet is produced. Both algorithms exhibit better performance in the barrel and smoothly degrade in the forward region. We also apply ParticleNet to different vertex detector geometries and observe that the flavor tagging performance is most sensitive to the inner radius, followed by the material budget and the spatial resolution. The result is consistent with that conducted by LCFIPlus. Benchmark performance in two scenarios, conservative and optimal, where the values of three vertex detector parameters – the inner radius, the material budget, and the spatial resolution – are 2 and 0.5 times those of the baseline design, reveals that ParticleNet can significantly enhance physics performance in the conservative scenario while showing less significant improvement with the optimal detector design.