1 Introduction

The existence of black holes (BHs) is a direct consequence of the equations of general relativity and plays a pivotal role in astrophysics today. The presence of astrophysical BH candidatesFootnote 1 is strongly supported by various factors. This support includes the discovery of gravitational waves generated by binary mergers [4,5,6,7,8,9] and the recent imaging of the “shadow” cast by the compact objects located at the centers of the M87 and Milky Way galaxies [10,11,12,13,14,15].

However, it is important to note that the imaging of a BH shadow alone cannot definitively rule out alternative models [16,17,18], including BH mimickers [19,20,21,22], and naked singularities [23,24,25,26,27,28,29,30,31]. This is due to the presence of degeneracy among competing models that fall within the range of observational error bars.

In addition, as spacetime curvature approaches and surpasses the Planck value, the concept of classical spacetime can become deceptive. The prevailing consensus is that singularities should be addressed within the framework of quantum gravity. This prompts the question of whether astrophysical BHs can be adequately characterized by the BH solutions established in general relativity, or if alternative models such as BH mimickers and non-singular BHs might offer better descriptions.

In this context, regular black holes (RBHs) emerge as exceptionally intriguing entities that defy the conditions laid out by singularity theorems while potentially embodying the characteristics of astrophysical black hole candidates. These RBHs, in both static and rotating forms, have been explored within a diverse range of scenarios [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57], with some models dynamically arising from gravitational collapse [58, 59]. As a result, it comes as no surprise that the investigation of their observable properties represents a thriving area of research [60,61,62,63,64,65,66,67,68]. Notably, recent studies have shed light on the effects of Bardeen [69] and Hayward [70] RBHs on the spectral luminosity of accretion disks, revealing deviations from the expected behavior observed with Kerr and Schwarzschild black holes [71].

Motivated by the considerations outlined above regarding RBHs, we envisage the possibility of distinguishing rotating RBHs from Kerr BHs through observations of the emission spectrum of accretion disks. To achieve this, we employ the approach pioneered by Novikov, Page, and Thorne [72, 73], to scrutinize the behavior of RBHs when surrounded by an accretion disk.

In this analysis, we build upon a fundamental conceptual model of the accretion disk. This model incorporates certain simplifications that allow us to efficiently predict various spectral and thermodynamic variables. Within this framework, we consider a thin accretion disk, characterized by a delta-like distribution of matter situated in the equatorial plane. We follow the assumption, as described in Ref. [74], that the mass of the disk is negligible compared to that of the central object. This assumption permits us to examine geodesic motion in the background geometry of the central object. We also assume that the particles within the disk lack charge and follow circular orbits. Consequently, we omit the consideration of the effects of dynamical friction, which would otherwise cause the particles to spiral inward.

Nevertheless, given a sufficiently short timescale, this effect can be neglected. We proceed to adopt a straightforward emission model for the disk particles, resulting in a black-body spectrum.

Based on the aforementioned assumptions, we conduct calculations involving the innermost stable circular orbit (ISCO), flux, differential luminosity, spectral luminosity, and the efficiency of mass-to-energy conversion within the accretion disk. Subsequently, we compare our results with their counterparts in the Kerr geometry.

The remainder of the paper is structured as follows: In Sect. 2, we provide a description of the key features pertaining to the class of rotating RBHs under consideration. We also provide a brief review of the formalism for test particle motion within accretion disks. Moving to Sect. 3, we review the thin accretion disk formalism, drawing from the Novikov–Thorne and Page–Thorne models, and applying it to the rotating RBH solution currently in focus. We then proceed to discuss and compare our findings with the corresponding results within the Kerr spacetime. Lastly, in Sect. 4, we explore the potential implications of our results for the observation of astrophysical black holes. Throughout this paper, we employ natural units, setting \(G=c=1.\)

2 Test particle motion around regular black holes

In this section, we examine a group of RBH solutions in a general form, which incorporates the cosmological constant [75], and derive the orbital parameters of neutral test particles on circular orbits in the equatorial plane.

The general solution considered here is built from a mass function of the type

$$\begin{aligned} m(r) = M\,\left[ 1 + \left( \frac{r_0}{r}\right) ^q \right] ^{-\frac{p}{q}}, \end{aligned}$$
(1)

which in the static case without cosmological constant guarantees an asymptotically flat spacetime for positive p and q. It has been shown that RBH static solutions of this kind can be obtained from gravity coupled to a theory of nonlinear electrodynamics [76,77,78]. Here, M and \(r_0\) are the mass and length parameters, respectively. The well-known Bardeen [69, 79] and Hayward [70] BHs correspond to the choices \(p=3,\) \(q=2\) and \(p=q=3,\) respectively, and the choice \(p\ge 3\) ensures that the geometry is regular at the center for the static RBHs.

The most general line element including rotation and the cosmological constant obtained from the above mass function is written in Boyer–Lindquist coordinates as

$$\begin{aligned} {\textrm{d}}s^{2}&=-\frac{1}{\Sigma }\left( \Delta _{r}-\Delta _{\theta }a^{2} \sin ^2\theta \right) {\textrm{d}}t^{2}+ \frac{\Sigma }{\Delta _{r}}{\textrm{d}}r^{2} + \frac{\Sigma }{\Delta _{\theta }}{\textrm{d}}\theta ^{2}\nonumber \\&\quad +\frac{1}{\Xi ^{2}\Sigma }\left[ (r^{2}+a^{2})^{2} \Delta _{\theta }-\Delta _{r}a^{2}\sin ^2\theta \right] \sin ^2\theta {\textrm{d}}\phi ^{2}\nonumber \\&\quad -\frac{2a}{\Xi \Sigma }\left[ (r^{2}+a^{2})\Delta _{\theta }-\Delta _{r}\right] \sin ^2\theta {\textrm{d}}t{\textrm{d}}\phi , \end{aligned}$$
(2)

where

$$\begin{aligned}&\Delta _{\theta }=1+\frac{\Lambda }{3}a^{2}\cos ^2\theta , \ \Sigma =r^{2}+a^{2}\cos ^2\theta , \end{aligned}$$
(3a)
$$\begin{aligned}&\Delta _{r}=\left( r^{2}+a^{2}\right) \left( 1-\frac{\Lambda }{3}r^{2}\right) -2rm, \quad \Xi =1+\frac{\Lambda }{3}a^{2}, \end{aligned}$$
(3b)

where a is the Kerr parameter related to the angular momentum of the source. For vanishing \(\Lambda \) and \(r_0\), the metric Eq. (2) reduces to the Kerr solution, which will be considered as a reference model to compare our RBH expectations.

Fig. 1
figure 1

Contour plots depicting the locations of the inner (left panel) and outer (right panel) horizons. These locations are presented as functions of the deformation parameter \(r_0^{*}=r_0/M\) and the spin parameter \(j=a/M\) for the rotating Hayward black hole. It is important to note that the shaded region represents the parameter values for which the horizons exist. The numerical values displayed on the contours indicate the corresponding horizon radius \(r_H/M.\) It should be observed that when \(r_0^{*}\ne 0,\) the values of the horizon radii satisfying the extremality condition may exceed 1

Full size image

2.1 Conditions on the metric

In the following, for the sake of simplicity, we consider the Hayward-like rotating RBH by setting \(p=q=3,\) without cosmological constant, i.e. \(\Lambda =0.\) The RBH obtained for \(p=q=3\) is also preferable because in the non-rotating case, it describes a simple model of a BH in general relativity coupled to a simple theory of nonlinear electrodynamics which can be obtained dynamically from a collapse scenario similarly to the classical Oppenheimer–Snyder model [58].

Similar to the Kerr solution, the rotating solution under consideration also has inner and an outer horizons, which are useful for characterizing the accretion disk properties. Specifically, the horizons of rotating Hayward BHs are calculated using the standard condition \(1/g_{rr}=0.\) Its solution contains five roots, only two of which are physical. The remaining three roots are complex and thus nonphysical. The largest of the two physical roots corresponds to the outer horizon and the smallest corresponds to the inner horizon, analogous to the Kerr metric. It should be noted that unlike the static case, where \(r_0\) can be only positive, for a rotating case, one can in principle allow for \(r_0\) to be negative. In the case of an RBH obtained from the theory of nonlinear electrodynamics, a negative \(r_0\) could then be interpreted as related to the sign of the magnetic charge. The values of the inner and outer horizons depending on the parameters \(r_0^*=r_0/M\) and \(j=a/M\) are plotted in Fig. 1.

It should be noted that for every given value of \(r_0^*,\) there exists a range of j values within which both horizons exist. However, there is a special extremal case where the two horizons coincide, resulting in a boundary beyond which the spacetime becomes horizonless. Furthermore, it is worth noting that in the Kerr case, where \(r_0^*=0,\) both the inner and outer horizons approach the limit \(r_H/M\rightarrow 1\) in the extremal scenario as \(j\rightarrow 1.\) However, when \(r_0^* \ne 0,\) the limiting value of \(r_H/M\) at which the two horizons coincide is larger than unity.

2.2 Circular orbits for the Kerr solution

As mentioned earlier, the line element for rotating RBHs, given by Eq. (2) in the absence of both cosmological and length parameters, reduces to the Kerr metric. Therefore, it is expedient to consider the Kerr metric first and then analyze circular geodesics in the gravitational field of rotating RBHs.

To facilitate a comparison of accretion disks surrounding rotating RBHs with the Kerr metric, we will now briefly review the relevant quantities for particles on circular orbits in the Kerr geometry, whose line element is [80]

$$\begin{aligned} {\textrm{d}}s^2= & {} -\left( 1-\frac{2Mr}{\Sigma }\right) {\textrm{d}}t^{2}+ \frac{\Sigma }{\Delta }{\textrm{d}}r^{2}+\Sigma {\textrm{d}}\theta ^{2}\nonumber \\{} & {} +\left( r^{2}+a^{2}+\frac{2Mra^{2}}{\Sigma }\sin ^2\theta \right) \sin ^2\theta {\textrm{d}}\phi ^{2}\nonumber \\{} & {} -\frac{4Mra}{\Sigma }\sin ^{2}\theta {\textrm{d}}\phi {\textrm{d}}t, \end{aligned}$$
(4)

where \(\Sigma =r^{2}+a^{2}\cos ^{2}\theta \) and \(\Delta =r^{2}-2Mr+a^{2}.\) The total gravitational mass of the source is given by M, ; its dimensionless angular momentum, namely the spin parameter, is \(j=a/M\), and so one can conclude that the Kerr metric is fully characterized by only two parameters. The Schwarzschild metric is recovered as \(a=0.\)

For circular orbits around the Kerr black hole in the equatorial plane we set \(\theta =\pi /2,\) with \(\dot{r}=\dot{\theta }=\ddot{r}=0.\) The expressions for the angular velocity, energy, and angular momentum of a test particle are

$$\begin{aligned} \Omega ^{2}&= \frac{M}{r^{3}\pm 2a r^{2}\sqrt{M/r} +a^{2}M}, \end{aligned}$$
(5a)
$$\begin{aligned} E^{2}&=\frac{\left( \sqrt{r}\left( r-2M \right) \pm a \sqrt{M} \right) ^{2}}{r^{2}\left( r\pm 2a\sqrt{M/r}-3M\right) }, \end{aligned}$$
(5b)
$$\begin{aligned} L^{2}&= \frac{M\left( r^{2}\mp 2a\sqrt{M/r}+a^{2}\right) ^{2}}{r^{2}\left( r\pm 2a\sqrt{M/r}-3M\right) }, \end{aligned}$$
(5c)

where the ± signs correspond to co-rotating and counter-rotating particles with respect to the direction of rotation of the BH, respectively [81].

In order to find \(r_{\textrm{ISCO}},\) we will simply use the \({\textrm{d}}L/{\textrm{d}}r={\textrm{d}}E/{\textrm{d}}r=0\) condition, which is equivalent to \({\textrm{d}}^2U_{\textrm{eff}}/{\textrm{d}}r^2=0,\) where \(U_{\textrm{eff}}\) is the effective potential of test particles in circular orbits. Hence, the radius of the ISCO for the Kerr metric is given by

$$\begin{aligned} \frac{r_{\textrm{ISCO}}^{\pm }}{M}=3+Z_2\pm \sqrt{(3-Z_1)(3+Z_1+2Z_2)}, \end{aligned}$$
(6)

with

$$\begin{aligned} Z_1&\equiv 1+\left( 1-j^2\right) ^{\frac{1}{3}}\left( \left( 1+j \right) ^{\frac{1}{3}}+\left( 1-j\right) ^{\frac{1}{3}}\right) , \end{aligned}$$
(7a)
$$\begin{aligned} Z_2&\equiv \left( 3 j^2+Z^2_1\right) ^{\frac{1}{2}}. \end{aligned}$$
(7b)

At this point, it is practical to introduce the BH efficiency, \(\eta ,\) in converting matter into radiation. Unlike the location of the ISCO, this quantity is coordinate-independent and can be measured, at least in principle. It is given by

$$\begin{aligned} \eta =[1-E(r_{\textrm{ISCO}})]\times 100\%, \end{aligned}$$
(8)

playing a prominent role in the physics of accretion disks.

Fig. 2
figure 2

Left panel: The ISCO radii as a function of the angular momentum j for the rotating RBH with different values of \(r_0^*.\) Right panel: The radiative efficiency \(\eta \) of rotating RBHs as a function of the angular momentum j for different values of the parameter \(r_0^*.\) The case \(r_0^*=0\) corresponds to the Kerr BH. The curves end at the values of j where the RBH horizon becomes extremal

Full size image
Fig. 3
figure 3

Left panel: The ISCO radii as a function of the parameter \(r_{0}^{*}\) for the rotating RBH (blue, red, green, and purple curves) and Hayward metric (black solid curve) for different values of the angular momentum j. Right panel: Radiative efficiency \(\eta \) as a function of the parameter \(r_{0}^{*}\) (blue, red, green, and purple curves) and Hayward metric (black solid curve) for different values of the angular momentum j. The curves end at the values of j, where the RBH horizon becomes extremal

Full size image

2.3 Circular orbits for rotating regular black holes

In analogy to the Kerr spacetime, we consider the orbital parameters of test particles in the field of rotating RBHs. For test particles moving in circular orbits in the equatorial plane, the angular velocity is given by

$$\begin{aligned} \Omega =\frac{aM\left( r^{3}-2r^{3}_{0}\right) - \sqrt{M\left( r^{3}-2r^{3}_{0}\right) }A}{a^{2}M\left( r^{3}- 2r^{3}_{0}\right) - A^{2}}, \end{aligned}$$
(9)

where \(A=A(r)=r^{3}+r^{3}_{0}\) and \(a>0\) \((a<0)\) corresponds to co-rotating (counter-rotating) particles with respect to the direction of rotation of the BH, respectively.

The energy per unit mass E and the angular momentum per unit mass L of test particles moving in circular orbits are then given by

$$\begin{aligned} {{E}}&=\frac{C_-+aB\Omega }{\sqrt{A\left( C_-+2aB\Omega - \left( Ar^{2}+a^{2}C_+\right) \Omega ^{2}\right) }}, \end{aligned}$$
(10a)
$$\begin{aligned} {{L}}&=\frac{\left( Ar^{2}+a^{2}C_+\right) \Omega -2aB}{\sqrt{A \left( C_-+2aB\Omega -\left( Ar^{2}+a^{2}C_+\right) \Omega ^{2}\right) }}, \end{aligned}$$
(10b)

where

$$\begin{aligned} B=2Mr^{2},\quad C_{\pm }=A\pm B. \end{aligned}$$
(11)

Unfortunately, the expression for \(r_{\textrm{ISCO}}\) in the field of rotating RBHs cannot be found analytically. Therefore, the value of \(r_{\textrm{ISCO}}\) has been calculated only numerically.

Thus, to carry out the numerical analysis and present results more explicitly, it is useful to introduce dimensionless quantities defined asFootnote 2\(\Omega ^*(r)=M\Omega (r),\) \(L^*(r)=L(r)/M,\) \(E^*(r)=E(r)\), and \(r_0^*=r/M.\) For comparison, the dependence of the angular velocity, angular momentum, and energy of neutral test particles on the radial coordinate in the Kerr and Hayward spacetimes is provided in the appendix.

In Fig. 2, we display the ISCO radius, \(r_{\textrm{ISCO}}\) (left panel), and the efficiency, \(\eta \) (right panel), of accretion disks as functions of the spin parameter j,  selecting different values of \(r_0^*.\) In Fig. 3, we display the ISCO radius, \(r_{\textrm{ISCO}}\) (left panel), and the efficiency, \(\eta \) (right panel), of accretion disks as functions of the parameter \(r_{0}^{*}\) for different values of j. As one may notice, in order to obtain smaller \(r_{\textrm{ISCO}}\) and correspondingly larger \(\eta ,\) the spin parameter j must increase and the parameter \(r_0^*\) must decrease. Eventually, one can obtain the smallest \(r_{\textrm{ISCO}}\) and largest \(\eta \) only when \(r_0^*=0\), i.e. \(j=1,\) which corresponds to the extreme Kerr black hole. However, for larger values of \(r_0^*\) and smaller values of j,  the rotating RBHs can have smaller \(r_{\textrm{ISCO}}\) and correspondingly larger \(\eta \) with respect to the Kerr black holes.

Recalling that the Kerr spacetime is obtained for \(r_0^*=0\) and the static Hayward BH is obtained for \(j=0,\) we note that the curves end at the values of j and \(r_0^*\) for which the RBH becomes extreme, consistently with what is shown in Fig. 1.

3 Spectra of thin accretion disks

To explore the luminosity and spectral properties of the accretion disk surrounding RBHs, we involve the simplest approach developed in [72, 73], where the radiative flux,Footnote 3\({\mathscr {F}},\) yields

$$\begin{aligned} {\mathscr {F}}(r)=-\frac{{\mathscr {K}}}{4\pi \sqrt{-g}} \frac{\Omega _{,r}}{\left( E-\Omega L\right) ^2 }\int ^r_{r_{\textrm{ISCO}}} \left( E-\Omega L\right) L_{,\tilde{r}}{\textrm{d}}\tilde{r},\nonumber \\ \end{aligned}$$
(12)

for a constant mass accretion rate, defined by \({\mathscr {K}}\equiv \dot{\textrm{m}},\) consequently computing the flux per unit accretion rate \({\mathscr {F}}/\dot{\textrm{m}}\) in lieu of the flux itself.

Spacetime geometry is clearly involved through the determinant of the metric of the three-dimensional subspace \((t,r,\varphi ),\) i.e. \(\sqrt{-g}=\sqrt{-g_{rr}(g_{tt}g_{\varphi \varphi }-g_{t\varphi }^2)}\) [82], where for the Kerr and rotating Hayward BH \(\sqrt{-g}=r\) when \(\theta =\pi /2.\) Thus, invoking thermodynamic equilibrium, the corresponding radiation appears emitted by virtue of a black body. Hence, radiation is modeled as isotropic, providing the Stefan–Boltzmann law for the emitted temperature

$$\begin{aligned} {\mathscr {F}}(r)=\sigma \,T^{*4}, \end{aligned}$$
(13)

where \(\sigma \) is the usual Stefan–Boltzmann constant and \({\mathscr {F}}(r)\) the radiative flux, function of the radial distance, whereas \(T^*\) the intrinsic temperature.

Fig. 4
figure 4

Radiative flux \({\mathscr {F}}^*\) multiplied by \(10^{5}\) of the accretion disk versus normalized radial distance r/M. Left panel: for rotating RBHs with \(r_{0}^{*}=0\) (Kerr). Right panel: for RBHs with \(j=0\) (Hayward)

Full size image

3.1 Observable quantities from accretion disks

Remarkably, it appears crucial to emphasize that the radiative flux \({\mathscr {F}}\) is not directly observable, as it is a quantity measured in the rest frame of the accretion disk.

From an observational perspective, the differential luminosity \({{\mathscr {L}}}_{\infty }\) appears more practical than radiative fluxes that, conversely, cannot be measured. Following Refs. [72, 73], we write the differential luminosity as

$$\begin{aligned} \frac{{\textrm{d}}{\mathscr {L}}_{\infty }}{{\textrm{d}}\ln {r}}=4\pi r \sqrt{-g}E {\mathscr {F}}(r), \end{aligned}$$
(14)

which clearly describes the radiation emitted by the accretion disk at a given distance.

From the differential luminosity, one can determine spectra and frequencies, i.e., the direct measurable quantities.

Defining the spectral luminosity distribution involves computing it as observed at infinity, following the procedure for modeling it as a black body, namely [83]

$$\begin{aligned} \nu {\mathscr {L}}_{\nu ,\infty }=\frac{60}{\pi ^3}\int ^{\infty }_{r_{\textrm{ISCO}}}\frac{\sqrt{-g }E}{M_T^2}\frac{(u^t y)^4}{\exp \left[ u^t y/{\mathscr {F}}^{*1/4}\right] -1}{\textrm{d}}r, \end{aligned}$$
(15)

where \({\mathscr {L}}_{\nu ,\infty }\) points out that observations are provided far from the source. In the above relation, \(y=h\nu /kT^*,\) h is the Planck constant, \(\nu \) is the emitted radiation frequency, and k is the Boltzmann constant.

Moreover, we have

$$\begin{aligned} u^t(r)=\frac{1}{\sqrt{-g_{tt}-2\Omega g_{t\varphi }-\Omega ^2 g_{\varphi \varphi }}}, \end{aligned}$$
(16)

where \(u^t\) is the contra-variant zero (time) component of the four-velocity.

The dimensionless argument implies normalized flux with respect to the total mass M. For our computations, the quantity \({\mathscr {F}}^{*}(r) = M^2 {\mathscr {F}}(r)\) yields a well-posed representation of the flux that we will display in our numerical findings.

Fig. 5
figure 5

Radiative flux \({\mathscr {F}}^*\) multiplied by \(10^{5}\) of the accretion disk versus normalized radial distance r/M. Left panel: for rotating RBHs with \(r_{0}^{*}=0.6.\) Right panel: for RBHs with \(j=0.4\)

Full size image
Fig. 6
figure 6

The temperature \(T^{*}\) of accretion disks versus normalized radial distance r/M. Left panel: Around the rotating RBHs with \(r^*_{0}=0.\) Right panel: Around the RBHs with \(j=0\)

Full size image
Fig. 7
figure 7

The temperature \(T^{*}\) of accretion disks versus normalized radial distance r/M. Left panel: Around the rotating RBHs with \(r^*_{0}=0.6.\) Right panel: Around the RBHs with \(j=0.4\)

Full size image
Fig. 8
figure 8

Differential luminosity multiplied by \(10^{2}\) of the accretion disk versus normalized radial distance r/M. Left panel: For rotating RBHs with \(r_{0}^{*}=0.\) Right panel: For RBHs with \(j=0\)

Full size image
Fig. 9
figure 9

Differential luminosity multiplied by \(10^{2}\) of the accretion disk versus normalized radial distance r/M. Left panel: For rotating RBHs with \(r_{0}^{*}=0.6.\) Right panel: For RBHs with \(j=0.4\)

Full size image

3.2 Theoretical analysis

In Fig. 4, we have plotted the radiative flux as a function of the normalized radial coordinate r/M for rotating RBHs with fixed \(r_0^{*}=0\) and different values of j,  corresponding to the Kerr metric (left panel), and for static RBHs with fixed \(j=0\) and different values of \(r_{0}^{*},\) corresponding to the Hayward metric (right panel). In the left panel, positive values of j result in a larger flux in all ranges of r compared to the Schwarzschild spacetime. Conversely, negative values of j lead to a smaller flux across all ranges of r compared to the Schwarzschild solution. In the right panel, the radiative flux in the Hayward spacetime with positive values of \(r_{0}^{*}\) consistently surpasses that in the Schwarzschild spacetime throughout the entire range of r.

In Fig. 5 we illustrate the radiative flux as a function of the normalized radial coordinate for rotating RBHs in analogy to Fig. 4, with one exception: we fixed \(r_{0}^{*} = 0.6\) and left j to be arbitrary (left panel), while in the right panel, we fixed \(j = 0.4\) and allowed \(r_{0}^{*}\) to vary. As can be seen in the left panel, the rotating Hayward black holes with the same values of j,  as in Fig. 4, will have larger radiative flux with respect to the Kerr black hole. In the right panel, the radiative flux for rotating Hayward BHs with fixed value of \(j=0.4\) and different values of \(r_{0}^{*}\) is larger than static Hayward BHs (see the right panel of Fig. 4).

In Fig. 6 we plot the dimensionless temperature \(T^{*}\) of accretion disks around the rotating RBHs with \(r_{0}^{*}=0,\) which as mentioned earlier correspond to the Kerr spacetime (left panel), and RBHs with \(j=0\) (right panel), correspond to the Hayward spacetime. In the left panel, the temperature for positive (negative) values of j is larger (smaller) than in the Schwarzschild spacetime (black solid curve). In the right panel, the temperature for all positive values \(r_{0}^{*}\) is always larger than in the Schwarzschild spacetime (black solid curve).

In Fig. 7 we present the dimensionless \(T^{*}\) of accretion disks around RBHs in analogy to Fig. 6, but with one exception: in the left panel, we fix \(r_{0}^{*}=0.6\) and vary j,  and in the right panel we fix \(j=0.4\) and vary \(r_{0}^{*}.\) Thus, the temperature in the accretion disk around rotating Hayward BHs is higher than that around Kerr BHs with identical \(j<1\) (left panel). In the right panel, the temperature of the disk around rotating Hayward BHs with fixed \(j=0.4\) and different \(r_{0}^{*}\) is higher than in the static Hayward metric with the same \(r_{0}^{*}.\)

In Fig. 8 we present the differential luminosity as a function of the normalized radial coordinate for rotating RBHs, where we fix \(r_{0}^{*}=0\) and vary j (left panel) and fix \(j=0\) and vary \(r_{0}^{*}\) (right panel). Here, the behavior of the differential luminosity is similar to that of the radiative flux shown in Fig. 4. This is because both quantities are related through Eq. (14). Therefore, everything observed in the flux automatically translates to the differential luminosity. The same description is true for Fig. 9, which is directly related to Fig. 5.

Fig. 10
figure 10

Spectral luminosity versus frequency of the emitted radiation for blackbody emission of the accretion disk. Left panel: For rotating RBHs with \(r_{0}^{*}=0.\) Right panel: For RBHs with \(j=0\)

Full size image
Fig. 11
figure 11

Spectral luminosity versus frequency of emitted radiation for black-body emission of the accretion disk. Left panel: For rotating RBHs with \(r_{0}^{*}=0.6.\) Right panel: For RBHs with \(j=0.4\)

Full size image

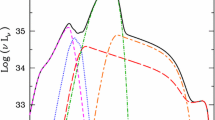
In Fig. 10, we depict the spectral luminosity \({\mathscr {L}}_{\nu ,\infty },\) defined by Eq. (15), as a function of the frequency of radiation emitted by the accretion disk. The left panel shows rotating RBHs with fixed \(r_{0}^{*}=0\) and arbitrary j,  corresponding to the Kerr metric, while the right panel represents RBHs with fixed \(j=0\) and arbitrary \(r_{0}^{*},\) corresponding to the Hayward metric, as mentioned above. Thus, for co-rotating (counter-rotating) orbits, the spectral luminosity of the accretion disk is larger (smaller) around the Kerr black hole compared to the Schwarzschild one (left panel). The spectral luminosity of the disk around the static Hayward black hole with \(r^*_0>0\) is always larger than around the Schwarzschild black hole. This fact is related to the value of \(r_{\textrm{ISCO}}.\) Unlike in the Schwarzschild spacetime, in the Hayward black hole with \(r^*_0>0\), circular orbits can be closer to the central object.

Furthermore, in Fig. 11, we observe behavior of the spectral luminosity similar to that presented in Fig. 10. However, the inclusion of \(r_0^*=0.6\) in the left panel and \(j=0.4\) in the right panel increases the values of the spectral luminosity in both panels. Thus, we confirm that in the field of rotating Hayward black holes with \(j<1\) and \(r^*_0>0,\) accretion disks can possess larger luminosity compared to the Kerr metric.

4 Final remarks

We have examined the spectral and thermodynamic properties of accretion disks surrounding rotating regular solutions. Our exploration of these characteristics is rooted in the idea that the luminosity of an accretion disk can serve as a discriminating factor in identifying the type of spacetime that represents a given BH or, more broadly, compact objects, BH mimickers, and the like.

As a result, we have delved into investigating the impact of a generic RBH solution, in the absence of a cosmological constant, on the physics of an accretion disk. In this endeavor, we have compared our findings with the corresponding singular scenario associated with the Kerr solution.

In doing so, we have also underscored the potential to differentiate between rotating RBHs and the expectations associated with Kerr black holes. Our objective was to distinguish the predicted outcomes of regular solutions from those of singular solutions, thereby highlighting the key disparities in both theoretical predictions and measurable effects.

Remarkably, we have extended our comparisons to include non-rotating RBHs, revealing the discrepancies one would anticipate when contrasting our solution with prior literature, particularly the Hayward RBH model.

To achieve this, we conducted a detailed analysis of the characteristics of accretion disks in the vicinity of rotating RBHs. Specifically, we investigated the behavior of neutral test particles moving along circular geodesics, which allowed us to determine crucial parameters such as the ISCO radius, radiative flux, differential luminosity, and spectral luminosity.

Furthermore, we quantified the efficiency of mass-to-energy conversion within the accretion disks, emphasizing the distinct deviations from the predictions of the Kerr solution.

For our accretion disk analysis, we employed the simplest standard model of a thin accretion disk, following the Novikov–Thorne–Page approach.

Remarkably, our results reveal a significant outcome: both the luminosity of the accretion disk and its efficiency are notably greater for rotating RBHs than the predictions of the Kerr metric. This distinction becomes particularly apparent when considering scenarios with fixed, small values of the spin parameter \((j<1).\) Similar disparities are observed in the spectra and thermodynamic properties, setting RBHs apart from the Kerr metric and non-rotating RBH solutions.

Fig. 12
figure 12

Angular velocity of test particles as a function of normalized radial distance r/M. Left Panel: For rotating regular black holes with \(r_{0}^{*}=0\) (Kerr). Right Panel: For regular black holes with \(j=0\) (Hayward)

Full size image

In view of our findings, future developments will explore alternative RBH configurations, incorporating additional components, such as the dark matter distribution (see, e.g., [84, 85]). Additionally, we will investigate alternatives to the Novikov–Thorne–Page scenario, including extra parameters that describe the accretion disk.