1 Introduction

In the standard model (SM) of particle physics, charged lepton flavour-violating (CLFV) processes are basically forbidden with only extremely small branching ratios (\({\sim 10^{-54}}\) [1]) when accounting for non-zero neutrino mass differences and mixing angles. Therefore, such decays are free from SM physics backgrounds and a positive signal would be unambiguous evidence for physics beyond the SM. Several SM extensions predict CLFV decays at measurable rates, and the channel \(\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma \) is particularly sensitive to new physics. Reviews of the theoretical expectations and experimental status are provided in [1, 2].

The MEG collaboration searched for the \(\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma \) decay at the Paul Scherrer Institut (PSI) in Switzerland in the period 2008–2013, improving the previous limit on the branching ratio by more than an order of magnitude, down to \({\mathcal {B}} (\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma ) < 4.2 \times 10^{-13}\) (90% CL) [3]. A detailed report of the MEG experiment’s motivation and design criteria is available in [4] and references therein.

In this paper, we report the first result of the MEG II experiment, an upgrade of MEG aiming to improve the sensitivity to the \(\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma \) branching ratio by one order of magnitude within the next few years.

2 Signal and background

The event signature is given by a \({\upgamma }\)-ray and a positron, forming a pair with the kinematic features of a two-body decay at rest. In particular, the positron and \({\upgamma }\)-ray are emitted at the same time \({t_\textrm{e}^+}= {t_{{\upgamma }}}\) \(({t_{\textrm{e}^+ \upgamma }}\equiv {t_{{\upgamma }}}- {t_\textrm{e}^+}= 0),\) and with the same energy, \({E_\textrm{e}^+}\ \approx E_{{\upgamma }}\ \approx \mathrm {m_\mu } \textrm{c}^2/2 \approx {52.83}\,\text {MeV}\) (the positron mass is negligible, given the detector resolutions), in opposite directions:

$$\begin{aligned} {\theta _{\textrm{e}^+ \upgamma }}\equiv & {} (\pi - {\theta _\textrm{e}^+}) - {\theta _{\upgamma }}= 0,\\ {\phi _{\textrm{e}^+ \upgamma }}\equiv & {} (\pi + {\phi _\textrm{e}^+}) - {\phi _{\upgamma }}= 0 \pmod {2\pi }, \end{aligned}$$

where \({\phi _\textrm{e}^+}\) and \({\theta _\textrm{e}^+}\) (\({\phi _{\upgamma }}\) and \({\theta _{\upgamma }}\)) are the azimuthal and polar angles of the positron (\({\upgamma }\)-ray).

The background has two components: one from the radiative muon decay (RMD) \(\upmu ^+ \rightarrow {\textrm{e}}+ \upnu \bar{\upnu }\upgamma \) and one from the accidental superposition of an energetic positrons from the standard muon Michel decay with a high energy \({\upgamma }\)-ray from RMD, positron–electron annihilation-in-flight or bremsstrahlung (ACC). For \(E_{{\upgamma }}> {51.5}\,\text {MeV}\), the \({\upgamma }\)-rays from annihilation-in-flight dominate. At the MEG II data taking rate in 2021, more than 90% of collected events with \(E_{{\upgamma }}> {48}\,\text {MeV}\) are from the ACC background.

The ACC background is characterised by wide distributions in \({E_\textrm{e}^+}\) and \(E_{{\upgamma }}\), dropping to zero at the kinematic endpoint at 52.83 MeV, and wide distributions in the relative angles, almost flat around \({\phi _{\textrm{e}^+ \upgamma }}= {\theta _{\textrm{e}^+ \upgamma }}= 0\). The distribution of \({t_{\textrm{e}^+ \upgamma }}\) is flat because the positron and the \({\upgamma }\)-ray originate from the decays of different muons.

The RMD background is characterised by an anticorrelated distribution of \({E_\textrm{e}^+}\) and \(E_{{\upgamma }}\), also dropping to zero at the kinematic endpoint. The angular distribution is peaked with positron and \({\upgamma }\)-ray aligned, while the back-to-back configuration is highly suppressed. The distribution of \({t_{\textrm{e}^+ \upgamma }}\) is peaked at zero.

3 The MEG II experiment

Fig. 1
figure 1

A sketch of the MEG II detector with a simulated \(\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma \) event

Full size image

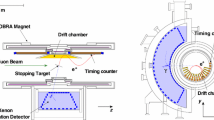
The MEG II detector, located at the \({\pi }\)E5 beam line at PSI, is designed to measure with high precision the positron and \({\upgamma }\)-ray kinematics and the relative production time of the two particles, coping with high \({\upmu ^+}\) stopping rates up to \(R_\mu = 5\times 10^{7}~{\textrm{s}}^{-1}\). A detailed description of the MEG II detector and its performance is in [5], and a sketch is shown in Fig. 1. A right-handed, Cartesian coordinate system is adopted, with the z axis along the beam direction and the y-axis vertical and pointing upward.

Briefly, a spectrometer is built inside a Constant Bending RAdius (COBRA) superconducting magnet, generating a gradient magnetic field with maximum intensity 1.27 T so as to contain the positrons emitted by \(\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma \) decays in a thin muon stopping target at the centre within the bore of the magnet and sweep them quickly outside.

The target is an elliptical foil (270 mm long and 66 mm high) with \((174\pm 20)\,\upmu \textrm{m}\) average thickness. The direction normal to The target foil normal lies on the (x, z) plane and forms an angle of \(({75.0 \pm 0.1})^{\circ }\) with respect to the beam axis (z-axis). This design maximise the muon stopping probability minimising the material crossed by the outgoing particles.

The spectrometer is instrumented with a single-volume, gaseous cylindrical drift chamber (CDCH) [6], and two sectors of scintillating tiles forming the pixelated timing counter (pTC) [7], all placed inside the bore of COBRA.

The CDCH is a 1.93 m-long, low-mass cylindrical volume, filled with a helium–isobutane gas mixture with the addition of small percentages of oxygen and isopropyl alcohol to avoid current spikes. It has nine concentric layers of gold-plated tungsten sense wires, arranged in a stereo configuration with two views. The drift cells, delimited by silver-plated aluminium wires, have a nearly square shape, with sides ranging from 5.8 mm in the central part of the innermost layer to 8.7 mm at the end plates of the outermost layer.

The pTC consists of two semicylindrically shaped sectors, one located upstream of the target and the other downstream, designed to provide precise measurements of the positron timing. Each sector consists of 256 scintillator tiles, each read out by two arrays of six SiPMs. A signal positron hits on average \(\sim \) 9 tiles, which provide independent measurements of the positron crossing timing with a resolution of \({\sim 100}\,{{\textrm{ps}}}\). The overall time resolution is \(\sigma _{{t_\textrm{e}^+},{\mathrm{{pTC}}}} = {43}\,{{\textrm{ps}}}\).

A liquid xenon detector (LXe), located outside of COBRA, consists of a homogeneous volume (900 L) of liquid xenon viewed by 4092 Multi-Pixel Photon Counters (MPPCs), located on the front face [8], and 668 UV-sensitive photomultiplier tubes (PMTs), all submerged in the liquid. This detector subtends the region \(\phi _{\upgamma }\in \left( \frac{2}{3} \pi , \frac{4}{3} \pi \right) \) and \(|\cos \theta _{\upgamma }| < 0.35\), corresponding to \(\sim 11\)% of the solid angle, determining the geometrical acceptance of MEG II for \(\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma \) decays. The efficiencies given below refer to this acceptance.

The radiative decay counter (RDC) is a novel detector, located downstream and centred on axis, designed to identify the ACC events with an RMD-originated high-energy \({\upgamma }\)-ray by tagging a low energy positron in coincidence. The RDC consists of a scintillating plastic detector to measure the positron timing and a LYSO crystal calorimeter to measure the energy.

The highly integrated trigger and data acquisition system called WaveDAQ [9] is based on WaveDREAM modules. They make use of the DRS4 chip to digitise the signals from the detectors at 1.4 GSPS (1.2 GSPS for CDCH) sampling speed. The waveforms are then analysed offline to extract time and amplitude information with high precision.

The trigger for \(\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma \) events is based on the online estimate of \(E_{{\upgamma }}\) with the LXe detector, on the relative time between the positron and the \({\upgamma }\)-ray \(T_{{\textrm{e}^+}{\upgamma }}\) measured by the LXe and the pTC and on the direction match measured by the same detectors. Trigger parameters had to be tuned during data taking. In addition, they depend on \(R_\mu \) and must be recalculated separately for each beam rate. The time needed to reach a satisfactory tuning limited the average trigger efficiency to \(\varepsilon _{\textrm{TRG}} = (80 \pm 1) \%\) in the analysis of the dataset presented here. On the basis of the past experience we expect for the following runs \(\varepsilon _{\textrm{TRG}}\) to be close to 95%.

The apparatus requires constant monitoring and calibrations. Dedicated instrumentation has been developed, such as: dedicated runs with a \(\pi ^-\) beam producing photons through the charge-exchange (CEX) reaction \(\pi ^- + p \rightarrow \pi ^0(\gamma \gamma ) + n\), a Cockroft–Walton accelerator (CW), a neutron generator, LED and \(\alpha \)-particles submerged in liquid xenon for LXe detector energy calibration; a laser system for pTC timing calibration; photo cameras for measuring precisely the target position [10,11,12,13,14].

For the LXe, a local system of curvilinear coordinates (u, v, w) is also used, where u and v are tangent to the cylindrical inner surface of the calorimeter (with u parallel to z) and w is the depth inside the liquid xenon fiducial volume.

4 Event reconstruction

In each event, positron and \({\upgamma }\)-ray candidates are described by five observables: \(E_{{\upgamma }}\), \({E_\textrm{e}^+}\), \({\phi _{\textrm{e}^+ \upgamma }}\), \({\theta _{\textrm{e}^+ \upgamma }}\) and \({t_{\textrm{e}^+ \upgamma }}\).

The positron kinematics is reconstructed by tracking the trajectory of the particle in the magnetic spectrometer and extrapolating it back to the muon stopping target [15].

Electronic waveforms are collected and digitised on both sides of the sense wires in the CDCH, digitally filtered to suppress the noise and analysed with both conventional and machine-learning techniques to extract the time and the induced charge of the ionisation signals (hits) [15].

Hits are combined into tracks by a track-following algorithm, which starts from clusters of near wires in the external layers of the chamber and propagates them through the detector, adding new hits with the help of a Kalman filter.

In parallel, scintillation signals in the tiles of the pTC are reconstructed from the SiPM waveforms and combined in clusters of close tiles, from which an estimate of the positron time is extracted. The combination of the CDCH hit times with the positron time in the pTC allows for precise determination of the drift distance of the ionisation electrons in the CDCH cell and hence the distance of closest approach (DOCA) of the positron trajectory to the wires. In this procedure, an innovative machine-learning procedure is used to extract the DOCA, using the full signal waveforms as inputs [16], instead of the drift times extracted with conventional approaches. The typical precision of the DOCA reconstruction is about 115 \(\upmu \textrm{m}\).

Once a track candidate is built and the DOCA of each hit has been precisely determined, a Kalman filter complemented by a deterministic annealing filter [17], including the effect of the positron interactions with the detector material, is used to fit the track. The track is finally extrapolated to the intermediate plane of the muon stopping target, where the positron position \((x_\textrm{e}^+, y_\textrm{e}^+, z_\textrm{e}^+)\) and momentum\(({p_\textrm{e}^+},{\theta _\textrm{e}^+},{\phi _\textrm{e}^+})\) are determined. It is also propagated to the corresponding pTC cluster, and the total trajectory length \(l_{{\textrm{e}^+}}\) from the target to pTC cluster is measured, with a resolution \(O({10}\,{\textrm{ps}})\). The positron time \({t_\textrm{e}^+}\) is determined as the pTC cluster time minus the positron time of flight \(l_{{\textrm{e}^+}}/{\textrm{c}}\).

The efficiency of the track reconstruction in the CDCH is \(\varepsilon _{{\textrm{e}^+},\textrm{CDCH}}= (74.0 \pm 1.5 \pm 4.0_{R_\mu })\% \) at \(R_\mu = 3 \times 10^{7} {\textrm{s}}^{-1},\) mainly limited by the pileup of multiple tracks in the same event and hence deteriorating with increasing beam rates. The second uncertainty is due to a systematic error on the measurement of \(R_\mu \) and is fully correlated among measurements of \(\varepsilon _{{\textrm{e}^+},\textrm{CDCH}}\) performed at different \(R_\mu \). Including the pTC acceptance and efficiency for signal positrons, \(\varepsilon _{{\textrm{e}^+},\mathrm{{pTC}}}= {(91 \pm 2)} \%,\) the positron reconstruction efficiency results \(\varepsilon _{{\textrm{e}^+}} = (67.0\pm 1.5 \pm 4.0_{R_\mu })\% \).

The tracking efficiency \(\varepsilon _{{\textrm{e}^+},\mathrm{{CDCH}}}\) decreases from \((77.0\pm 1.5 \pm 4.0_{R_\mu })\% \) to \((66.0\pm 1.5 \pm 4.0_{R_\mu })\% \) when \(R_\mu \) increases from \({2 \times 10^{7}}\, {\textrm{s}}^{-1}\) to \(5 \times 10^{7}\, {\textrm{s}}^{-1}\). This trend dominates the dependence of \(\varepsilon _{{\textrm{e}^+}}\) on \(R_\mu \).

The \({\upgamma }\)-rays are measured in the LXe detector from the combination of the individual MPPC and PMT signals. The digitised waveforms are filtered by subtracting average noise templates extracted from pedestal runs, where events are collected without beam on target and with a periodic trigger. Then, the charge collected in each sensor is measured by integrating the waveform in a 150 ns window around the expected signal time and converted into the number of scintillation photons by means of gains and quantum efficiencies (for PMTs) or photon detection efficiencies (for MPPCs) extracted from dedicated calibrations.

For the measurement of the first conversion position of the incident \({\upgamma }\)-ray (\(u_{\upgamma }\), \(v_{\upgamma }\), \(w_{\upgamma }\)), a \(\chi ^2\) is minimised, which compares the number of observed photons in the MPPCs to the number of expected photons for \({\upgamma }\)-ray’s converting in a given position. Similarly, once the position of the \({\upgamma }\)-ray conversion is known, the conversion time \(t_{\textrm{LXe}}\) is determined by minimising a \(\chi ^2\) based on the expected and observed arrival times of the scintillation photons to both PMTs and MPPCs. Finally, the energy of the \({\upgamma }\)-ray is determined by summing the number of photons in all sensors and converting it into an energy value by means of several correction factors. They account for the average light yield of the LXe, the position-dependent photosensor coverage and light detection efficiency, the evolution of the sensor response during the run, and residual non-uniformities in the response of the detector. The overall efficiency for signal \({\upgamma }\)-rays is \(\varepsilon _{\upgamma }= {(62 \pm 2)} \%\).

The direction of the \({\upgamma }\)-ray cannot be precisely measured in the LXe detector. Consequently, a direct reconstruction of the positron-\({\upgamma }\)-ray relative angles is not possible, and an indirect approach is used: the positron position \((x_{\textrm{e}^+}, y_{\textrm{e}^+}, z_{\textrm{e}^+})\) at the target is assumed to be the muon decay point and hence also the production point of the \({\upgamma }\)-ray for signal events. Therefore, the \({\upgamma }\)-ray direction \(({\theta _{\upgamma }},{\phi _{\upgamma }})\) is taken as the one joining the positron position at the target and the detection point in the LXe detector.

The time of flight from the supposed muon decay point to the \({\upgamma }\)-ray detection point is subtracted from the conversion time to determine the \({\upgamma }\)-ray production time \({t_{{\upgamma }}}\). The resolution on \({t_{\textrm{e}^+ \upgamma }}\) is dominated by the time resolution of the LXe detector \((\sigma _{t_{{\upgamma },\mathrm{{LXe}}}} = {65}\, {\textrm{ps}}).\)

The RDC measures the time \(t_{{\textrm{e}^+},\textrm{RDC}}\) and energy loss \(E_{{\textrm{e}^+},\textrm{RDC}}\) of a low-energy positron in coincidence with a high-energy \({\upgamma }\)-ray measured in the LXe detector. The distributions of \(t_{{\textrm{e}^+},\textrm{RDC}} - t_{{\upgamma },\textrm{LXe}}\) and \(E_{{\textrm{e}^+},\mathrm{{RDC}}}\) differ between signal (the former is flat and the latter is peaked at high energy) and ACC background with an RMD-originated \({\upgamma }\)-ray (the former is peaked around zero while the latter is peaked at low energy), providing additional discriminating power.

Details on the reconstruction algorithms and calibration procedures can be found in [5]. Table 1 shows the performance achieved on the 2021 dataset, in terms of resolutions and efficiencies.

Table 1 Resolutions (Gaussian \(\sigma \)) and efficiencies of the MEG II experiment, measured at \(R_\mu = 3 \times 10^{7}~{\textrm{s}}^{-1}\)
Full size table

5 Analysis

5.1 Overview

The data analysed in this work were collected in the year 2021 during the first, seven-week-long physics run of MEG II, with a total DAQ livetime of \(2.9 \times 10^{6}~{\textrm{s}}\). The data-taking was performed at four different beam intensities \((R_\mu = 2 \times 10^{7}, 3 \times 10^{7}, 4 \times 10^{7}, 5 \times 10^{7}~{\textrm{s}}^{-1}))\) in five different periods of time (in two of them, the beam intensity was \(R_\mu = 3 \times 10^{7}~{\textrm{s}}^{-1}\)) to study the beam rate dependence of the detector performance. A total of \(1.04 \times 10^{14}\) \({\upmu ^+}\) were stopped on the target. The fractions of the integrated \({\upmu ^+}\) on target for the above intensities are (0.13, 0.41, 0.20, 0.26), respectively. The \(\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma \) trigger rates went from \({\sim 4}\,{\textrm{Hz}}\) to \({\sim 20}\,{\textrm{Hz}}\). The size of the \(\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma \) trigger sample was \(\sim 2 \times 10^{7}\).

As in the MEG experiment [3], an unbinned maximum likelihood technique is applied in the analysis region defined by \({48}\,\text {MeV}< E_{{\upgamma }}< {58}\,\text {MeV}\), \({52.2}\,\text {MeV}< {E_\textrm{e}^+}< {53.5}\,\text {MeV}\), \(|{t_{\textrm{e}^+ \upgamma }}|< {0.5}\,{\textrm{ns}}\), \(|{\phi _{\textrm{e}^+ \upgamma }}|< {40}\,{\textrm{mrad}}\) and \(|{\theta _{\textrm{e}^+ \upgamma }}| < {40}\,{\textrm{mrad}}\).

This approach is adopted for a blind analysis: the events in a “blinding box” defined as \(48.0<E_{{\upgamma }}<{58.0}\,\text {MeV}\) and \(|{t_{\textrm{e}^+ \upgamma }}|<{1}\,{\textrm{ns}}\), which includes the analysis region, are initially hidden; only once the probability density functions (PDFs) of observables used to discriminate signal from background are ready to build a likelihood function \({{\mathcal {L}}}(N_\textrm{sig})\), the hidden data are released and used to extract a confidence interval for the expected number of signal events, \(N_\textrm{sig}\).

All necessary studies on the background, including the construction of the PDFs, are done in side-bands outside the analysis region. The regions defined by \({1}\, {\textrm{ns}}< |{t_{\textrm{e}^+ \upgamma }}| < {3}\,{\textrm{ns}}\) are called “time side-bands”, and are used to study the ACC background. The region defined by \({45}\,\text {MeV}< E_{{\upgamma }}< {48}\,\text {MeV}\) is called “\(E_{{\upgamma }}\) side-band”. It includes RMD events peaking at \({t_{\textrm{e}^+ \upgamma }}= 0\), and is used to extract the \({t_{\textrm{e}^+ \upgamma }}\) PDF for both RMD and signal events.

5.2 Confidence interval

The construction of the confidence interval for the number of signal \(N_\textrm{sig}\) events is based on the Feldman–Cousins prescription [18], with the profile likelihood ratio ordering [19]. The profile likelihood ratio \(\lambda _p\) is defined as

$$\begin{aligned} \lambda _{p}(N_\textrm{sig})= & {} \left\{ \begin{array}{ll} \frac{{{\mathcal {L}}}(N_\textrm{sig}, \hat{\hat{\varvec{\theta }}}(N_\textrm{sig}))}{{{\mathcal {L}}}(0 , \hat{\hat{\varvec{\theta }}}(0 ))} &{}\quad \text {if } \hat{N}_{\textrm{sig}} < 0\\ \frac{{{\mathcal {L}}}(N_\textrm{sig}, \hat{\hat{\varvec{\theta }}}(N_\textrm{sig}))}{\mathcal {L}(\hat{N}_{\textrm{sig}}, \hat{\varvec{\theta }} )} &{} \quad \text {if } \hat{N}_{\textrm{sig}} \ge 0, \end{array} \right. \end{aligned}$$

where \({\varvec{\theta }}\) is a vector of nuisance parameters; \(\hat{N}_{\textrm{sig}}\) and \(\hat{\varvec{\theta }}\) are the values of \(N_\textrm{sig}\) and \(\varvec{\theta }\) that maximise the likelihood; \(\hat{\hat{\varvec{\theta }}}(N_\textrm{sig})\) is the value of \(\varvec{\theta }\) which maximises the likelihood for the specified \(N_\textrm{sig}\).

The systematic uncertainties on the PDFs and the normalisation factor described in the next section are incorporated with two methods: either profiling them as nuisance parameters in the likelihood function or randomly fluctuating the PDFs according to the uncertainties. The profiling method is generally known to be more robust than the random fluctuation method, but it requires CPU-intensive calculations. It is, therefore, employed only for the uncertainty with the largest contribution, which is the detector misalignment, while the others are included by the random fluctuation method.

5.3 Likelihood function

The likelihood function is obtained by combining the PDFs for the observables discriminating between signal and background. Besides \({E_\textrm{e}^+}\), \(E_{{\upgamma }}\), \({t_{\textrm{e}^+ \upgamma }}\), \({\theta _{\textrm{e}^+ \upgamma }}\) and \({\phi _{\textrm{e}^+ \upgamma }}\), for events with RDC signals we also exploit the RDC observables \((t_{{\textrm{e}^+},{{\textrm{RDC}}}}-t_{{\upgamma },c}\), \(E_{{\textrm{e}^+},{{\textrm{RDC}}}}).\) Moreover, the \({t_{\textrm{e}^+ \upgamma }}\) resolution has a relevant dependence on the number of hits in the pTC cluster, \(n_{\textrm{pTC}}\). In order to take this into account, and considering that \(n_{\textrm{pTC}}\) has significantly different distributions in signal and background, this quantity is also included in the list of observables.

The extended likelihood function is hence defined as

$$\begin{aligned}&{\mathcal {L}}(N_\textrm{sig}, N_\textrm{RMD}, N_\textrm{ACC}, x_\textrm{T}) \nonumber \\&\quad = \frac{e^{-(N_\textrm{sig}+N_\textrm{RMD}+N_\textrm{ACC})}}{N_{\textrm{obs}}!} C(N_\textrm{RMD}, N_\textrm{ACC}, x_\textrm{T}) \nonumber \\&\qquad \times \prod _{i=1}^{N_{\textrm{obs}}} \bigl (N_\textrm{sig}S(\mathbf {x_i})+N_\textrm{RMD}R(\mathbf {x_i})+N_\textrm{ACC}A(\mathbf {x_i})\bigr ), \end{aligned}$$

where \(\mathbf {x_i} = ({E_\textrm{e}^+}, E_{{\upgamma }}, {t_{\textrm{e}^+ \upgamma }}, {\theta _{\textrm{e}^+ \upgamma }}, {\phi _{\textrm{e}^+ \upgamma }}, t_{{{\textrm{RDC}}}}-t_{\textrm{LXe}}, E_{{{\textrm{RDC}}}}, n_{\textrm{pTC}})\) is the set of the observables for the i-th event; S, R and A are the PDFs for the signal, RMD and ACC background, respectively; \(N_\textrm{sig}\), \(N_\textrm{RMD}\) and \(N_\textrm{ACC}\) are the expected numbers of signal, RMD and ACC background events in the analysis region; \(x_\textrm{T}\) is a parameter representing the misalignment of the muon stopping target; \(N_{\textrm{obs}}\) is the total number of events observed in the analysis region.

In the extraction of the confidence interval for \(N_\textrm{sig}\), the nuisance parameters are \({\varvec{\theta }} = (N_\textrm{RMD}, N_\textrm{ACC}, x_\textrm{T})\), with a constraint C applied to their values: \(N_\textrm{RMD}\) and \(N_\textrm{ACC}\) are Gaussian-constrained by the numbers evaluated in the side-bands and their uncertainties; \(x_\textrm{T}\) is Gaussian-constrained with its uncertainty.

Two independent likelihood analyses are performed for cross-checking the results with two different types of PDFs: “per-event PDFs” and “constant PDFs”.

5.3.1 Per-event PDF

The reconstruction performance depends on the detector conditions, on the position of the interaction in the detector, and other factors changing event by event, such as the occurrence of some specific interaction of the particles with the detector material. For the “per-event PDF” approach, the PDF parameters vary on an event-by-event basis to take into account these variations. This allows the exploitation of the detailed detector information to maximise the sensitivity. The PDFs are conditioned by observables that can reflect these variations.

For the \({\upgamma }\)-ray PDFs, the resolutions and the background spectrum are dependent on the \({\upgamma }\)-ray conversion position in the LXe detector. For the positron angle, vertex position and momentum, an event-by-event estimate of the track fit uncertainty can be extracted from the covariance matrix of the Kalman filter and used to build per-event PDFs. Correlations among the positron variables are also taken into account, although in this case, instead of extracting the parameters from the Kalman covariance matrix, an empirical analytic model of the average correlations is adopted, taking into account only their \({\phi _\textrm{e}^+}\) dependence.

For energies, angles and time, the signal PDFs are modelled as Gaussian functions reflecting the measured resolutions, with the possible addition of tails, according to the results of calibrations. The ACC \({E_\textrm{e}^+}\) PDF is the combination of the theoretical Michel spectrum with acceptance and resolution effects, fitted to data in the side-bands [15]. The ACC \(E_{{\upgamma }}\) PDF is taken from the Monte Carlo spectrum, with a Gaussian smearing and an additional cosmic-ray contribution to match the data distribution in the side-bands. The ACC angular PDFs are modelled with fourth-order polynomials fitted in the side-bands. The RMD PDFs are obtained by convolution of the theoretical spectra with the experimental resolutions.

The \(n_{\textrm{pTC}}\) PDFs are taken from the side-bands for the ACC background, and from the Monte Carlo for signal and RMD.

A special treatment is necessary for the RDC observables, because most of the events do not have RDC signals. The RDC PDFs are approximated with binned 2-dimensional distributions, with one additional bin reserved for events with no RDC signals. The ACC PDFs are extracted from the side-bands, the signal and RMD PDFs are extracted from a control sample made of events with signals in the RDC but not in time coincidence with the \({\upgamma }\)-ray in the LXe detector.

5.3.2 Constant PDF

Another approach for the PDFs’ construction uses “constant PDFs”, and is employed for cross-check purpose. The PDFs are constructed with constant parameters by averaging out the temporal variations, the position dependence of the detector response (with the only exception of the conversion depth inside the calorimeter, with different PDFs for \(w_{\upgamma }< {2} \,{\textrm{cm}}\) and \(w_{\upgamma }> {2}\,{\textrm{cm}}\)) and the correlations between the observables. The differences in performance at different beam rates are accounted. The relative angle \({\Theta _{\textrm{e}^+ \upgamma }}\) between the positron and the \({\upgamma }\)-ray, instead of the two separate projections, \({\phi _{\textrm{e}^+ \upgamma }}\) and \({\theta _{\textrm{e}^+ \upgamma }}\) is used. The RDC observables are not used in this analysis. It makes the analysis simpler and, given the small statistics of the 2021 dataset, does not deteriorate significantly the sensitivity.

This approach shows worse sensitivity compared to the per-event one, while it’s less prone to systematic uncertainties.

5.4 Normalisation

The estimated number of signal events is translated into the branching ratio as \( \mathcal{B} (\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma ) = N_\textrm{sig}/N_\mu \), where the normalisation factor \(N_\mu \) is the number of effectively measured muon decays in the experiment. \(N_\mu \) is evaluated with two independent methods: the number of Michel positrons counted with a dedicated trigger and the number of RMD events measured in the energy side-band [3]. In both methods, the normalisation dataset is collected in parallel with the physics data-taking, such to account possible variations of the detector condition and the instantaneous muon beam intensity. Both methods give consistent normalisation factors, yielding the combined result \(N_\mu = (2.64 \pm 0.12) \times 10^{12}\).

5.5 Results

The following results refer (unless otherwise specified) to the analysis based on the “per-event PDFs”, which is the one yielding the best sensitivity.

5.5.1 Sensitivity

The sensitivity \( \mathcal{S}_{90}\) is calculated as the median of the distribution of the 90% CL upper limits computed for an ensemble of pseudo-experiments with a null-signal hypothesis (Fig. 2). They are generated according to the PDFs constructed for RMD and ACC background and assuming the rates of the RMD and ACC events evaluated in the side-bands. The sensitivity is estimated to be \( \mathcal{S}_{90}= 8.8 \times 10^{-13}.\)

The limits include systematic uncertainties with dominant contribution from detector misalignment, \({\upgamma }\)-ray energy scales and normalisation.

Misalignment between detectors is calibrated using tracks of particles from muon decays or cosmic rays, crossing multiple detectors. The target position is determined from a combination of muon decay point reconstruction and a photogrammetric method exploiting the cameras installed inside the magnet bore. The \({\upgamma }\)-ray energy scale is calibrated with a combined analysis of CEX, CW, cosmic ray and side-band spectra. The worsening of the sensitivity due to the inclusion of systematic uncertainties is \({(5.0 \pm 3.7)} \%\).

5.5.2 Event distributions and likelihood fit in the analysis region

A total of 66 events were observed in the analysis region. The event distributions in the \(({E_\textrm{e}^+}, E_{{\upgamma }})\) and \((\cos {\Theta _{\textrm{e}^+ \upgamma }}, {t_{\textrm{e}^+ \upgamma }})\) planes are shown in Fig. 3, where even tighter selection requirements are applied to the discriminating variables to have a closer look around the signal region. The contours of the averaged signal PDFs are also shown for reference. No excess of events is observed in the region where the signal PDFs are peaking.

Fig. 2
figure 2

Distribution of the 90% CL upper limits computed for an ensemble of pseudo-experiments with a null-signal hypothesis. The sensitivity is calculated as the median of the distribution to be \( \mathcal{S}_{90}= 8.8 \times 10^{-13}.\) The sensitivity is indicated by a red dashed line while the upper limit observed in the analysis region with a solid arrow

Full size image
Fig. 3
figure 3

Event distributions on the \(({E_\textrm{e}^+}, E_{{\upgamma }})\)- and \((\cos {\Theta _{\textrm{e}^+ \upgamma }}, {t_{\textrm{e}^+ \upgamma }})\)-planes. Selections of \(\cos {\Theta _{\textrm{e}^+ \upgamma }}< -0.9995\) and \(|{t_{\textrm{e}^+ \upgamma }}| < {0.2}\,{\textrm{ns}}\), which have 97% signal efficiency for each observable, are applied for the \(({E_\textrm{e}^+}, E_{{\upgamma }})\)-plane, while selections of \({49.0}< E_{{\upgamma }}< {55.0}\,\text {MeV}\) and \(52.5< {E_\textrm{e}^+}< {53.2}\,\text {MeV}\), which have signal efficiencies of 93% and 97%, respectively, are applied for the \((\cos {\Theta _{\textrm{e}^+ \upgamma }}, {t_{\textrm{e}^+ \upgamma }})\)-plane. The signal PDF contours (\(1\sigma \), \(1.64\sigma \) and \(2\sigma \)) are also shown. The five highest-ranked events in terms of \(R_\textrm{sig}\) are indicated in the event distributions, if they satisfies the selection

Full size image
Fig. 4
figure 4

The projections of the best-fitted PDFs to the five main observables and \(R_\textrm{sig}\), together with the data distributions (black dots). The green dash and red dot-dash lines are individual components of the fitted PDFs of ACC and RMD, respectively. The blue solid line is the sum of the best-fitted PDFs. The cyan hatched histograms show the signal PDFs corresponding to four times magnified \(N_\textrm{sig}\) upper limit

Full size image

Figure 4 shows the projected data distribution for each of the observables \(({E_\textrm{e}^+}, E_{{\upgamma }}, {t_{\textrm{e}^+ \upgamma }}, {\theta _{\textrm{e}^+ \upgamma }}, {\phi _{\textrm{e}^+ \upgamma }})\), for all events in the analysis region, with the best-fitted PDFs. All data distributions are well-fitted by their background PDFs. Figure 4f shows the data distribution of the relative signal likelihood \(R_\textrm{sig}\), defined as

$$\begin{aligned} R_\textrm{sig}= \log _{10} \left( \frac{S(\varvec{x}_i)}{f_{\textrm{RMD}}R(\varvec{x}_i)+f_{\textrm{ACC}}A(\varvec{x}_i)} \right) , \end{aligned}$$

where \(f_{\textrm{RMD}}\) and \(f_{\textrm{ACC}}\) are the expected fractions of the RMD and ACC background events, which are estimated to be 0.02 and 0.98 in the side-bands, respectively. The data distribution for \(R_\textrm{sig}\) also shows a good agreement with the distribution expected from the likelihood fit result. The five highest-ranked events in terms of \(R_\textrm{sig}\) are indicated in the event distributions shown in Fig. 3.

Figure 5 shows the observed profile likelihood ratio as a function of the branching ratio. The computation of the confidence interval with the Feldman–Cousins prescription, which is performed with the profile likelihood ratios for positive \(N_\textrm{sig}\) only, is not affected by the behaviour of the curve at negative, nonphysical branching ratios. Nonetheless, for completeness, we also compute the likelihood ratio in the negative side, although we have to set the bound \(N_\textrm{sig}> {-0.004}\) \(( \mathcal{B} > -1.5 \times 10^{-15})\) (not distinguishable from zero in the figure) to ensure that the total PDF is always positive-valued all over the analysis region. The best estimate and the 90% CL upper limit of the branching ratio are estimated to be \( \mathcal{B}_\textrm{fit}= -1.1 \times 10^{-16}\) and \( \mathcal{B}_{90}= 7.5 \times 10^{-13},\) respectively. The obtained upper limit is consistent with the sensitivity calculated from the pseudo-experiments with a null-signal hypothesis (Fig. 2).

Fig. 5
figure 5

The negative log likelihood-ratio \((\lambda _{\textrm{p}})\) as a function of the branching ratio. The three curves correspond to the MEG II 2021 data, the MEG full dataset [3] and the combined result

Full size image

The limit includes the systematic uncertainties, the impact of which is an increase by 1.5%, consistent within statistical uncertainties with what is expected from pseudo-experiments.

5.5.3 Consistency checks

With the maximum likelihood analysis using the constant PDF approach, the 90% CL upper limit of the branching ratio, including systematic uncertainties, is \( \mathcal{B}_{90}= 1.31 \times 10^{-12}\). The consistency between the results of the two analyses is checked on a common ensemble of pseudo-experiments generated with a null-signal hypothesis. The comparison of the 90% CL upper limits obtained by the two analyses on the common pseudo-experiments is shown in Fig. 6, where systematic uncertainties are not included for simplicity, resulting in slightly smaller upper limits. The two results are strongly correlated, with the per-event PDFs’ analysis showing \({\sim 30}\%\) better sensitivity. The upper limits obtained in the analysis region and in the fictitious analysis regions in the time side-bands are also shown in Fig. 6, and are found to be in good agreement with the results of the pseudo-experiments.

To validate the techniques used to parameterise the signal PDFs, pseudo-experiments generated with a null-signal hypothesis were mixed with signal Monte Carlo samples coming from the Geant4 simulation of the full detector [5], assuming an expected signal yield of 10 events. A likelihood fit was performed, adopting the same techniques used on real data to parameterise the PDFs, including the correlations. We obtained a distribution of best-fit values with an average consistent with \(N_{\textrm{sig}} = 10\), we checked the correct coverage of the confidence intervals, and verified the consistency of the \(R_{\textrm{sig}}\) distributions with the ones obtained exclusively from pseudo-experiments.

The analysis was also applied to four fictitious analysis regions inside the time side-bands \((-3<{t_{\textrm{e}^+ \upgamma }}<{-2}\,{ \textrm{ns}}, -2<{t_{\textrm{e}^+ \upgamma }}<{-1}\,{\textrm{ns}}, 1<{t_{\textrm{e}^+ \upgamma }}<{2}\,{\textrm{ns}}, 2<{t_{\textrm{e}^+ \upgamma }}<{3}\,{\textrm{ns}}).\) The results are also shown in Fig. 6 and are consistent with the distribution of the 90% CL upper limits in the pseudo-experiments.

Finally, the likelihood fit in the analysis region was also performed without the constraints on \(N_\textrm{RMD}\) and \(N_\textrm{ACC}\). The best estimates of \(N_\textrm{RMD}={0\pm 3.9}\) and \(N_\textrm{ACC}={66\pm 8.1}\) are well consistent with the side-band estimates of \({1.2\pm 0.2}\) and \({68\pm 3.5}\), respectively.

Fig. 6
figure 6

Comparison of the branching ratio upper limits (without systematic uncertainties) extracted by the two likelihood analyses when run over a common ensemble of pseudo-experiments (red dots). The results obtained on real data are also shown, for the analysis region (black star) and four fictitious analysis regions in the time side-bands: \({-3}\,{\textrm{ns}}<{t_{\textrm{e}^+ \upgamma }}<{-2}\,{\textrm{ns}}\), \({-2}\,{\textrm{ns}}<{t_{\textrm{e}^+ \upgamma }}<{-1}\,{\textrm{ns}}\), \({1}\,{\textrm{ns}}<{t_{\textrm{e}^+ \upgamma }}<{2}\,{\textrm{ns}}\), \({2}\,{\textrm{ns}}<{t_{\textrm{e}^+ \upgamma }}<{3}\,{\textrm{ns}}\) (blue dots)

Full size image

5.5.4 Combination with the MEG result

The sensitivity of this analysis with the 2021 data is comparable to the one with the full MEG dataset [3] despite the much smaller dataset thanks to improvements in resolutions and efficiencies. The upper limit obtained in this analysis is combined with the MEG result. The two results are combined in a simplified manner, setting a threshold on the negative log likelihood-ratio curve instead of following the Feldman–Cousins approach. The negative log likelihood-ratio curves for the MEG full dataset and the MEG II 2021 data, including systematic uncertainties, are shown in Fig. 5, along with their combination, coming from the product of the two likelihood functions. The upper limit is determined as the branching ratio value at which the combined curve crosses a threshold of 1.6, which is conservatively chosen from pseudo-experiments, to match approximately the results of the Feldman–Cousins method. The systematic errors in MEG and MEG II are small and weakly correlated. The effect of neglecting the correlation has a negligible effect compared to the approximation implicit in the approach to combine the results. The combined upper limit at 90% CL is computed to be \( \mathcal{B}_{90}= 3.1 \times 10^{-13}\). It is consistent with the combined sensitivity of \( \mathcal{S}_{90}= 4.3 \times 10^{-13}\), which is estimated with the combined pseudo-experiments, with a 30% probability of having a more stringent upper limit.

6 Conclusions and perspectives

In 2021, the MEG II experiment was commissioned and started taking data with \(\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma \) trigger for seven weeks. A blind, maximum-likelihood analysis found no significant event excess compared to the expected background and established a 90% CL upper limit on the branching ratio \({\mathcal {B}} (\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma ) < {7.5 \times 10^{-13}}\).

When combined with the final result of MEG, we obtain the most stringent limit up to date, \({\mathcal {B}} (\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma ) < {3.1 \times 10^{-13}}\).

The MEG II collaboration has continued to take data during 2022 and 2023, with a projected statistic ten-fold larger than in 2021, and a more than twenty-fold increase in statistics is foreseen by 2026, with the goal of reaching a sensitivity to the \(\upmu ^+ \rightarrow {\textrm{e}}^+ \upgamma \) decay of \( \mathcal{S}_{90}{\sim 6.0 \times 10^{-14}}\).