1 Introduction

An elegant and straightforward scientific theory, the Einstein theory of general relativity (GR) is currently the most effective theory of gravity for explaining a wide range of observations, including the perihelion precession of mercury, light bending, and gravitational redshift of radiation from distant stars [1,2,3]. Recently, the Event Horizon Telescope’s astounding success has been furthered by the discovery of the black hole (BH) shadow in the Messier 87 (M87) image [4,5,6]. However, it is necessary to put GR through additional tests, as it is tainted with unresolved problems like singularities [7,8,9] and fails to adequately explain the nature of dark energy and dark matter [10,11,12,13,14]. In addition, the quantum nature of gravity is still unclear and elusive [15,16,17]. In light of all of this, the search for a more comprehensive theory of gravity becomes more compelling and eventually leads to GR in the low-energy limit. Numerous alternative models of gravity have been proposed to address the shortcomings in GR. A viable alternative gravity theory must not produce a fifth force in local physics, must be free of ghost modes and consistent with solar system-based tests, and must satisfactorily account for observations that GR theory does not address. The three categories of alternative gravity models that meet these criteria are as follows: (i) modified gravity models, such as f(R) gravity, where the gravity action is supplemented with higher curvature terms [18,19,20,21], or Lanczos–Lovelock models [22,23,24,25,26]; (ii) extra-dimensional models, which due to the bulk Weyl stresses and higher-order corrections to the stress tensor may alter the real four-dimensional gravitational field equations [27,28,29,30,31,32,33]; and (iii) gravitational scalar-tensor theories, such as the Brans–Dicke theory and the more general Horndeski models [34,35,36,37].

Among the various modified gravity model, physics researchers have long been interested in f(R) theories [18, 38,39,40,41], since these models use the simplest modification of the Einstein–Hilbert action while still demonstrating the ability to address a wide range of cosmological and astrophysical observations. The late time acceleration is one of these [41,42,43], along with the universe’s initial power-law inflation [41, 44], the rotation curves of spiral galaxies [45, 46], the four cosmological phases [19, 47], and the detection of the gravitational wave [48,49,50]. Although these models frequently suffer from ghost modes, some f(R) models, such as f(R) theory on a constant curvature hypersurface, can be demonstrated to be ghost-free [51,52,53,54]. Furthermore, they can outperform the solar system tests, which only place restrictions on \(f^{\prime \prime }(R)\) and consequently the model parameters [55,56,57].

Extra dimensions were proposed mainly as a way to combine gravity and electromagnetism into a single theoretical framework [58,59,60]. This later provided the foundation for string theory and M-theory, which aim to unify all forces of nature under one overarching theory [61,62,63]. The huge differences between the electroweak scale and the Planck scale led to many string-inspired brane world models [64,65,66,67,68]. Most of these models assume that the observable universe is restricted to a 3-brane, where the standard model particles and forces exist, while gravity can move into the extra dimensions [64,65,66,67,68,69,70]. These models have interesting and observable consequences [71,72,73,74,75,76], such as the production of mini-BHs that can be detected at colliders [77, 78]. On galactic scales, they offer an alternative to dark matter [45, 79,80,81,82], while in cosmology they provide implications for inflation and dark energy [31, 83,84,85,86,87,88,89,90,91,92,93,94,95]. Since we do not fully understand quantum gravity, deviations from Einstein’s theory of gravity could emerge at high energies through extra dimensions. The curvature of spacetime in the extra dimensions is expected to be near the Planck scale, so higher-order corrections to Einstein’s equations should become important at high energies.

While BH solutions in GR are also valid in many alternative gravity theories, including a broad class of f(R) gravity models [96], BH solutions that differ from those in GR can be used to distinguish between different modified gravity theories. They can also place constraints on model parameters using gravitational waves or BH shadows. As a result, finding exact BH solutions in f(R) gravity theories is important but difficult due to the complexity of the equations of motion, which contain higher-order terms.

Despite the difficulties, many precise and numerical solutions have been obtained using different methods, including the Lagrange multiplier [97] and the generator method [98]. First, the simplest case is a special class of f(R) gravity with constant curvature. The solutions of this class, such as Schwarzschild-like [96, 98,99,100,101], Reissner Nordström-like [102, 103], and Kerr-Newman-like solutions [104], differ from GR solutions only by a constant coefficient \(f'(R_0)\) that can be absorbed into Newton’s constant. Solutions with dynamic curvatures [96, 97, 105,106,107,108,109,110,111,112,113], however, have real differences from GR solutions. Static spherically symmetric solutions with perfect fluid [114], Yang–Mills field [115], nonlinear Yang–Mills field [102, 116], Maxwell field, and nonlinear electromagnetic field [117,118,119,120] have also been obtained. Using Noether symmetries, axially symmetric solutions can be derived from exact spherically symmetric solutions [121]. Interestingly, there is a correspondence between solutions in Einstein-conformally invariant Maxwell theory and solutions in f(R) gravity without matter in arbitrary dimensions [122, 123]. Furthermore, spherically symmetric vacuum solutions in f(R) gravity in higher dimensions have been studied. In summary, while exact solutions in f(R) gravity can be quite complex, methods have been developed to find many precise and numerical solutions that differ meaningfully from GR solutions in important ways [98, 124].

The remainder of the paper is organized as follows: In Sect. 2, we present the building block of the f(R) gravitational theory and obtain its field equations. In Sect. 3, we apply the field equations of f(R) gravity to a spacetime having spherically symmetric and unequal metric potentials. We present the nonlinear differential equations which are composed of four nonlinear differential equations having three unknown functions: one is the derivative \(f'(R)\) of f(R), and the other two are related to the metric potentials. We study special cases that yield a consistent BH solution derived in previous studies. Then, we study the general case and derive a new BH solution assuming that the derivative \(f'(R)=1-\frac{\alpha }{r^4}\). In Sect. 4, we study the physical properties of this new BH solution by giving the form of the metric potentials in asymptotic form and show that it is different from the GR metric potential of the Schwarzschild BH. This difference is due to the contribution of the nonlinear curvature scalar terms. We also study the scalars of the BH solution and show that its peculiarity is stronger than that of GR because of the contribution of the higher-order curvature. In Sect. 5, we study the geodesic of the extension of the Schwarzschild BH. In Sect. 6, we derive the trajectories of the test particles near the extension of the Schwarzschild BH. In Sect. 7, we study the radial motion and derive the conserved quantities momentum, \(h^2\), and energy, \(E^2\), of the extension of the Schwarzschild BH. In Sect. 7.3, we present the stability constraints of this BH solution by using geodesic deviation and investigate the regions of stability graphically. In Sect. 8, we evaluate the basic thermodynamic expressions, namely the Hawking temperature, entropy, quasi-local energy, heat capacity, and Gibbs free energy, related to our new BH solution and show that it is physically acceptable. In Sect. 8.2, we explain that the new BH solution fulfills the first law of thermodynamics. In the final section, we discuss our derived results.

2 f(R) gravity theory

The f(R) gravitational theory is different from GR when \(f(R)\ne R\), and when \(f(R)=R\) we recover GR. In the four-dimensional case, the action of f(R) gravity theory yields the form [18, 41, 125,126,127,128,129,130,131],

$$\begin{aligned} {{{S}}}:={\frac{1}{2\kappa } \int \textrm{d}^4x \sqrt{-g} f(R)}, \end{aligned}$$
(1)

where \(\kappa \) is the Newtonian gravitational constant and g is the determinant of the metric.

Using the variation principle of the action (1), we obtain the equations of motion of the f(R) gravitational theory in the form [132]

$$\begin{aligned} { R_{\mu \nu } f_R-\frac{1}{2}g_{\mu \nu }f(R) + \left[ g_{\mu \nu }\Box -\nabla _\mu \nabla _\nu \right] f_R =0}, \end{aligned}$$
(2)

where the symbol \(\Box \) refers to the d’Alembertian operator, and \(f_R\) is the derivative of the arbitrary function with respect to the Ricci scalar, i.e. \(f_R=\frac{\textrm{d}f}{\textrm{d}R}\). The trace of equations (2) yields the form

$$\begin{aligned} { 3\Box {f_R}+R{f_R}-2f(R)=0} . \end{aligned}$$
(3)

From Eq. (3) we get

$$\begin{aligned} {f(R)=\frac{1}{2}\left[ 3\Box f_{ {R}}+R{f_R} \right] }. \end{aligned}$$
(4)

The use of Eq. (3) in Eq (2) gives the field equations of f(R) as [133]

$$\begin{aligned} R_{\mu \nu } f_R-\frac{1}{4}g_{\mu \nu }Rf_R+\frac{1}{4}g_{\mu \nu }\Box f_R -\nabla _\mu \nabla _\nu f_R =0 . \end{aligned}$$
(5)

The field equations (5) reduce the order of derivatives from fourth order, which characterized the field equations (2), to third order. Thus, it is important to examine the field equations (5) to a spherically symmetric spacetime whose line element has two different unknown functions. This task will be discussed in the next section.

3 Construction of spherically symmetric BH solutions

Let us assume that the spherically symmetric line element has the form

$$\begin{aligned} ds^2= & {} -A(r)\textrm{d}t^2+\frac{\textrm{d}r^2}{A_1(r)}+\textrm{d}\Omega \, \qquad \qquad \text{ where } \qquad \qquad \textrm{d}\Omega \nonumber \\= & {} r^2 \left( \textrm{d}\theta ^2+\sin ^2\theta \textrm{d}\phi ^2 \right) , \end{aligned}$$
(6)

and A(r) and \(A_1(r)\) are two unknowns of r. The Ricci scalar of the spacetime (6) has the form

$$\begin{aligned} R(r)=\frac{r^2A_1{A'}^2-r^2AA'A'_1-2r^2AA_1A''_1-4rA \left[ A_1A'-AA'_1 \right] +4A^2(1-A_1)}{2r^2A^2}, \end{aligned}$$
(7)

with \(A\equiv A(r)\), \(A_1\equiv A_1(r)\), \(A'=\frac{\textrm{d}A}{\textrm{d}r}\), \(A''=\frac{\textrm{d}^2A}{\textrm{d}r^2}\), and \(A'_1=\frac{\textrm{d}A_1}{\textrm{d}r}\). Using Eqs. (3) and (5) with Eq. (6) and by using Eq. (7), we obtain the nonvanishing components of the field equations (5), i.e., the (t, t), (r, r), and \((\theta ,\theta )\) (or \((\phi ,\phi )\)), as

$$\begin{aligned} 0&=\frac{1}{8 A^{2}{r}^{2}}\left[ F A'^{2}A_1 {r}^{2}-F A' A'_1 A {r}^{2}-2\,F A_1 A''A {r}^{2}\right. \nonumber \\&\quad \left. -4\,F rA_1 A' A +4\,F r A'_1 \left( A \right) ^{2}-4\,F A^{2}+4\,F A^{2}A_1 \right. \nonumber \\&\quad \left. -3\,A {r}^{2} F'A_1 A' +2\, A^{2} {r}^{2} F''A_1+ A^{2}{r}^{2} F'A'_1 +4\,A^{2}r F'A_1\right] , \end{aligned}$$
(8)
$$\begin{aligned} 0&=\frac{1}{8 A^{2}{r}^{2}} \left[ F A'^{2}A_1{r}^{2}-2\,FA_1 A''A{r}^{2}-FA'A'_1A{r}^{2}\right. \nonumber \\&\quad \left. -4\,Fr A^{2}A'_1+4\,FrA_1 A' A-4\,F A^{2}+4\,F A^{2}A_1+A{r}^{2} F' A_1A'\right. \nonumber \\&\quad \left. -6A^{2}{ r}^{2} F''A_1-3\, A^{2}{r}^{2} F'A'_1+4A^{2}rF' A_1\right] , \end{aligned}$$
(9)
$$\begin{aligned} 0&=-\frac{1}{ 8A^{2}{r}^{2}}\left[ -4\,F A^{2}+4\,F A^{2}A_1-F A' A'_1 A {r}^{2}\right. \nonumber \\&\quad \left. -2\,FA_1A''A{r}^{2}+F A'^{2}A_1{r}^{2}-A{r}^{2} F' A_1A'\right. \nonumber \\&\quad \left. -2\, A^{2}{r}^{2}F''A_1{-} A^{2}{r}^{2} F' A'_1 {+}4\,A^{2}r F'A_1 \right] . \end{aligned}$$
(10)

The use of Eq. (3) gives the trace of the f(R) equation in the form

$$\begin{aligned} 0&=\frac{1}{2A^{2}{r}^{2}}\left[ 3\,A{r}^{2} F' A_1A'+6\,A^{2}{r}^{2} F''A_1+3\,A^{2}{r}^{2} F'A'_1\right. \nonumber \\&\quad \left. +12\,A^{2}r F'A_1-FA' A'_1A {r}^{2}-2 \,FA_1 A'' A{r}^{2}A'^{2}A_1{r}^{2}\right. \nonumber \\&\quad \left. -4\,FrA_1A' A -4\,F rA'_1A^{2}+4\,F A^{2}\right. \nonumber \\&\quad \left. -4\,FA^{2}A_1-4 \,f A^{2}{r}^{2} \right] , \end{aligned}$$
(11)

where \(F\equiv F(r)=\frac{\textrm{d}f(R(r))}{\textrm{d}R(r)}\), \(F'=\frac{\textrm{d}F(r)}{\textrm{d}r}\), \(F''=\frac{\textrm{d}^2F(r)}{\textrm{d}r^2}\), \(F'''=\frac{\textrm{d}^3F(r)}{\textrm{d}r^3}\), and f is an arbitrary function of the radial coordinate r. Now let us analyze the system of differential equations (8), (9), and (10) in detail.

Using Eqs. (8) and (9), i.e., (8) minus (9), we obtain

$$\begin{aligned} 0= & {} 2\,FA_1 A'-2\,F A'_1 A+ FA_1A' r\nonumber \\{} & {} -2\, F''AA_1r-F'A'_1Ar. \end{aligned}$$
(12)

Additionally, Eqs. (8) and (10), i.e., (8) plus (10), yield

$$\begin{aligned} 0= & {} 2\,FA_1 A'-2\,F A'_1A+ F'A_1A' r\nonumber \\{} & {} -2\, F'' AA_1r- F' AA'_1r . \end{aligned}$$
(13)

An in-depth examination of the above equations indicates that Eqs. (12) and (13) agree with each other. Thus we obtain two independent differential equations from Eqs. (8), (9), and (10). From the above discussion, it is clear that Eq. (8) is equivalent to Eq. (9) with a minus sign and equivalent to minus two times Eq. (10). Therefore, Eqs. (8) and (13) are two independent equations which contain all possible solutions. Now, we have three unknown functions A, \(A_1\), and F, which is the main reason we are unable to fix one function. To obtain specific solutions and to investigate the physical properties of the derived solutions indicating that Eqs. (8) and (13) involve all physically reasonable and natural solutions, we will assume the form of F in the following.

It was shown in previous studies that when \(A=A_1\), we obtain from Eq. (12)

$$\begin{aligned} F''=0, \quad \text{ which } \text{ leads } \text{ to } \quad F=F_1 + F_2 r. \end{aligned}$$
(14)

From Eqs. (14) and  (8) we obtain

$$\begin{aligned}&= - 2 r^2 \left( F_1 + F_2 r \right) A'' -2 r^2 F_2 A' + 4 \left( F_1 + 2 F_2 r \right) A \nonumber \\&\qquad - 4 \left( F_1 + F_2 r \right) \, . \end{aligned}$$
(15)

If we suppose that \(F_2=0\), then Eq. (15) gives

$$\begin{aligned} 0= F_1 [r^2 A''- 2A + 2]. \end{aligned}$$
(16)

From Eq. (16) we obtain

$$\begin{aligned} A= 1 + \frac{a_0}{r} + a_1 r^2, \qquad \qquad \text{ provided } \qquad \qquad F_1\ne 0, \end{aligned}$$
(17)

where \(a_0\) and \(a_1\) are constants of integration. Equation (17) is the well-known Schwarzschild-AdS spacetime.

If \(F_1=0\), then Eq. (15) yields

$$\begin{aligned} 0 =F_2[ r^2 A'' +2-4A+ r A']. \end{aligned}$$
(18)

The solution of Eq. (18) has the following form:

$$\begin{aligned} A= \frac{1}{2} + {{{\tilde{a}}}}_0 r^2 + \frac{{{{\tilde{a}}}}_1}{ r^{2}} . \end{aligned}$$
(19)

Here, \({{{\tilde{a}}}}_0\) and \({{{\tilde{a}}}}_1\) are constants of integration. Equation (19) is derived in [113, 134].

In previous studies [113, 134] we have assumed \(F=1+\frac{\alpha }{r^2}\) to solve the system of differential equations (11). In the present study, we will solve the system of differential equations (11) assuming thatFootnote 1

$$\begin{aligned} F=1-\frac{\alpha }{r^4}, \end{aligned}$$
(20)

where \(\alpha \) is a dimensional constant. The use of Eq. (20) in the system of equations (8), (9), and (10) gives

$$\begin{aligned} 0&=\frac{1 }{8{r}^{6} A^{2}}\left[ A_1 {r}^{2} \left( \alpha -{r}^{4} \right) A'^{2}-2\,A_1A{r}^{2} \left( \alpha -{r}^{4}\right) A''\right. \nonumber \\&\quad \left. - \left\{ r \left( \alpha -{r}^{4} \right) A'_1-4\,A_1\alpha \right\} rAA'\right. \nonumber \\&\quad \left. +4\, A^{2} \left\{ A'_1 \alpha r- \left( {r}^{4}+13\,\alpha \right) A_1+{r}^{4}-\alpha \right\} \right] , \end{aligned}$$
(21)
$$\begin{aligned} 0&=\frac{1}{8{r}^{6} A^{2 }}\left[ 2\,AA_1{r}^{2} \left( \alpha - {r}^{4}\right) A''-A_1 {r}^{2} \left( \alpha -{r}^{4} \right) A'^{2}\right. \nonumber \\&\quad \left. +rA \left[ r \left( \alpha -{r}^{4} \right) A'_1-4\,A_1 \left( {r}^{4}+2\alpha \right) \right] A'+4\left\{ A'_1 {r}^{5}\right. \right. \nonumber \\&\quad \left. \left. - \left( 7 \alpha -{r}^{4} \right) A_1 -{r}^{4}+\alpha \right\} A^{2}\right] , \end{aligned}$$
(22)
$$\begin{aligned} 0&=\frac{1}{8{r}^{6} A^{2 }}\left[ 2\,AA_1{r}^{2} \left( \alpha - {r}^{4}\right) A''-A_1 {r}^{2} \left( \alpha -{r}^{4} \right) A'^{2}\right. \nonumber \\&\quad \left. +r^2A \left[ \left( \alpha -{r}^{4} \right) A'_1+4\,A_1 {r}^{3} \right] A'-4\left\{ A'_1 r(2\alpha +{r}^{4})\right. \right. \nonumber \\&\quad \left. \left. - \left( 33 \alpha +{r}^{4} \right) A_1 +{r}^{4}-\alpha \right\} A^{2}\right] . \end{aligned}$$
(23)

We will try to solve the system of differential equations (21), (22), and (23) assuming some specific forms of the unknowns A and \(A_1\).

3.1 The case when \(A(r)=\left( 1-\frac{2M}{r}\right) \,X(r)\,Y(r)\) and \(A_1(r)=\left( 1-\frac{2M}{r}\right) \,Y(r)\)

Now we will assume the two unknowns A(r) and \(A_1(r)\) in the following form:

$$\begin{aligned} A(r)&=\left( 1-\frac{2M}{r}\right) \,X(r)\,Y(r), \qquad \text{ and } \qquad A_1(r)\nonumber \\&=\left( 1-\frac{2M}{r}\right) \,Y(r). \end{aligned}$$
(24)

The form of the unknown functions A and \(A_1\) given by Eq. (24) is a very important choice in the frame of f(R) gravitational theory because this choice is a natural extension of the Schwarzschild BH solution in f(R) gravitational theory. Here, X(r) and Y(r) are two unknown functions of the radial coordinate. Of course we can write the two unknown functions A and \(A_1\) in many different forms, such as \(A(r)=\left( 1-\frac{2M}{r}\right) \,X(r)\) and \(A_1(r)=\left( 1-\frac{2M}{r}\right) \,Y(r)\) but we chose the form given by Eq. (24) because it will reproduce a physical BH, as we will see below. Furthermore, if \(X(r)=1\) and \(Y(r)=1\), we naturally return to Einstein GR. Therefore, let us proceed and put the form of the unknowns A and \(A_1\) given by Eq. (24) in Eqs. (8), (9), and (10), and obtain

$$\begin{aligned} 0&=\frac{1}{8{r}^{7}X^{2}}\left[ {r}^{2}Y \left( \alpha -{r}^ {4}\right) \left( 2M -r\right) X'^{2}-2\,{r}^{2}Y X \left( \alpha -{r}^{4} \right) \right. \nonumber \\&\quad \times \left. \left( 2M -r \right) X'' -2\,{r}^{2} X^{2} \left( \alpha -{r}^{4}\right) \left( 2M -r \right) Y'' \right. \nonumber \\&\quad \left. -rX \left\{ 3r \left( \alpha -{r}^{4} \right) \left( 2M -r \right) Y' \right. \right. \nonumber \\&\quad \left. \left. -2Y \left( 2{r}^{5}-7M{r}^{ 4}+3M\alpha \right) \right\} X'\right. \nonumber \\&\quad \left. +4\,X^{2} \left\{ 2r \left( 3M\alpha -M{r}^{4}-r \alpha \right) Y' \right. \right. \nonumber \\&\quad \left. \left. + \left( {r}^{5}+ 33r\alpha -72\,M\alpha \right) Y+r \left( \alpha -{r}^{4} \right) \right\} \right] ,\nonumber \\ 0&=\frac{1}{8{r}^{7}X^{2}}\left[ 2{r}^{2}Y X \left( {r}^ {4}-\alpha \right) \left( 2M -r\right) X''\right. \nonumber \\&\quad \left. {+}2\,{r}^{2} X^2 \left( {r}^{4}{-}\alpha \right) \left( 2M {-}r \right) Y'' {-}{r}^{2} Y \left( {r}^{4}{-}\alpha \right) \left( 2M {-}r \right) X'^2 \right. \nonumber \\&\quad \left. -rX \left\{ 3r \left( \alpha -{r}^{4} \right) \left( 2M -r \right) Y' \right. \right. \nonumber \\&\quad \left. \left. -2Y \left( 2{r}^{5}-M{r}^{ 4}-11M\alpha +4r\alpha \right) \right\} X' \right. \nonumber \\&\quad \left. +4\,X^{2} \left\{ 2r \left( 3M\alpha -M{r}^{4}-r \alpha \right) Y' \right. \right. \nonumber \\&\quad \left. \left. + \left( {r}^{5}- 7r\alpha +8\,M\alpha \right) Y+r \left( \alpha -{r}^{4} \right) \right\} \right] ,\nonumber \\ 0&=\frac{1}{8{r}^{7}X^{2}}\left[ 2{r}^{2}Y X \left( \alpha -{r}^ {4}\right) \left( 2M -r\right) X''\right. \nonumber \\&\quad \left. {+}2\,{r}^{2} X^2 \left( \alpha {-}{r}^{4} \right) \left( 2M {-}r \right) Y'' {-}{r}^{2} Y \left( \alpha {-}{r}^{4} \right) \left( 2M {-}r \right) X'^2 \right. \nonumber \\&\quad \left. {+}rX \left\{ 3r \left( \alpha {-}{r}^{4} \right) \left( 2M {-}r \right) Y' {+}2Y \left( 2{r}\alpha {+}3M{r}^{ 4}{-}7M\alpha \right) \right\} X' \right. \nonumber \\&\quad \left. -4\,X^{2} \left\{ 2r \left( 3M\alpha -M{r}^{4}-r \alpha \right) Y' \right. \right. \nonumber \\&\quad \left. \left. + \left( {r}^{5}- 13r\alpha -32\,M\alpha \right) Y+r \left( \alpha -{r}^{4} \right) \right\} \right] . \end{aligned}$$
(25)

The analytical solution of the above system, given by Eq. (25), takes the following form:

$$\begin{aligned} X(r)&=c_1\left( 1+\frac{5\alpha }{r^4}+\frac{10\alpha ^2}{r^8}+\frac{10\alpha ^3}{r^{12}}+\frac{5\alpha ^4}{r^{16}}+\frac{\alpha ^5}{r^{20}}\right) ,\nonumber \\ Y(r)&= -\frac{r^2c_2}{F_3{}^5a(r)}+\frac{r^2c_3}{F_3{}^5a(r)}\int \frac{\sqrt{F_3{}^5}}{r^4F}\textrm{d}r+\frac{r^2}{F_3{}^5a(r)}\nonumber \\&\quad {\times } \left[ \int F\sqrt{F_3{}^5}\left( \int \frac{\sqrt{F_3{}^5}}{r^4F}\textrm{d}r\right) \textrm{d}r{+}\left( \int F\sqrt{F_3{}^5} \textrm{d}r\right) \right. \nonumber \\&\quad \times \left. \left( \int \frac{\sqrt{F_3{}^5}}{r^4F}\textrm{d}r\right) \right] , \end{aligned}$$
(26)

where \(F_3=1+\frac{\alpha }{r^4}\equiv F+\frac{2\alpha }{r^4}\), and \(a(r)=\left( 1-\frac{2M}{r}\right) \). Equation (26) shows that when the dimensional constant \(\alpha \) is vanishing, then \(F=F_3=1\), and in that case

$$\begin{aligned} X(r)=c_1, \qquad \text{ and } \qquad Y(r)=-\frac{3r^3c_2+c_3-3r}{3ra(r)}. \end{aligned}$$
(27)

For X(r) and Y(r) to have asymptotic flat spacetime, we must put \(c_1=1\) and \(c_2=0\) and \(c_3=-6M\).

Using Eq. (26) in (11), we derive the form of f(r) as follows:

$$\begin{aligned} f(r)&=\frac{2}{r^{3}F\sqrt{F_1{}^{13}}} \left\{ 3r^{3}F\sqrt{F_1}\left( 1+\frac{6\alpha }{r^4}-\frac{15\alpha ^2}{r^8}\right) \right. \nonumber \\&\quad \times \left. \left( \left[ 2\int F\sqrt{F_1{}^5} \textrm{d}r-c_3\right] \right. \right. \nonumber \\&\quad \times \left. \left. \int \frac{\sqrt{F_1{}^5}}{r^4F} \textrm{d}r-2\int F\sqrt{F_1{}^5}\left( \int \frac{\sqrt{F_1{}^5}}{r^4F}\textrm{d}r\right) \textrm{d}r\right) \right. \nonumber \\&\quad \left. +2F_1{}^4\left( 1-\frac{5\alpha }{r^4}\right) \int F\sqrt{F_1{}^5} \textrm{d}r+r\sqrt{F_1}F\right. \nonumber \\&\quad \times \left. \left( 1+3r^2c_2+\frac{18\alpha c_2}{r^2}+\frac{5\alpha }{r^4}+\frac{9\alpha ^2}{r^8}-\frac{45\alpha ^2c_2}{r^6}\right. \right. \nonumber \\&\quad \left. \left. +\frac{5\alpha ^3}{r^{12}}-\frac{5\alpha ^4}{r^{16}}-\frac{9\alpha ^5}{r^{20}}-\frac{5\alpha ^6}{r^{24}}\right. \right. \nonumber \\&\quad \left. \left. -\frac{\alpha ^7}{r^{28}}\right) -\left( 1-\frac{5\alpha }{r^4}\right) F_1{}^4c_3\right\} . \end{aligned}$$
(28)

Using Eq. (28) in Eq. (7), we obtain the Ricci scalar in the form

$$\begin{aligned} R&{=}\frac{4}{\sqrt{F_1{}^{13}}} \left\{ 3r^{16}F^2\sqrt{F_1}\left( 1{+}\frac{6\alpha }{r^4}\right) \left\{ \left[ 2\int F\sqrt{F_1{}^5} \textrm{d}r{-}c_3\right] \right. \right. \nonumber \\&\quad \left. \left. \times \int \frac{\sqrt{F_1{}^5}}{r^4F} \textrm{d}r - 2\int F\sqrt{F_1{}^5}\left( \int \frac{\sqrt{F_1{}^5}}{r^4F}\textrm{d}r\right) \textrm{d}r\right\} \right. \nonumber \\&\quad \left. -2r^{7}F_1{}^4\left( 1-\frac{2\alpha }{r^4}\right) \left[ \int F\sqrt{F_1{}^5} \textrm{d}r+r^{10}\sqrt{F_1}F^2\right. \right. \nonumber \\&\quad \times \left. \left. \left( \alpha ^6+6r^4\alpha ^5+15r^8\alpha ^4+20r^{12}\alpha ^3+15r^{16}\alpha ^2\right. \right. \right. \nonumber \\&\quad \left. \left. \left. +18r^{22}\alpha c_2+6r^{20}\alpha +r^{24}+3r^{26}c_2\right) \right] \right. \nonumber \\&\quad \left. -r^{7}\left( 1-\frac{2\alpha }{r^4}\right) F_1{}^4c_3\right\} , \end{aligned}$$
(29)

When \(\alpha =0\), we obtain

$$\begin{aligned} R=12r^{10}c_2, \end{aligned}$$
(30)

and when \(c_2=0\), we obtain a vanishing scalar Ricci which corresponds to the Schwarzschild BH.

Now we rewrite f(r) and R(r) at large r, i.e., as \(r\rightarrow \infty \), and small r, i.e., \(r\rightarrow 0\), and obtain

$$\begin{aligned}&f(r\rightarrow \infty )\approx 6c_2-\frac{36\alpha }{r^6}+\frac{16\alpha c_3}{r^7}-\frac{180\alpha ^2c_2}{r^8}+\frac{1152\alpha ^2}{r^{10}},\nonumber \\&f(r\rightarrow 0)\approx -\frac{12\alpha }{11r^6}+\frac{1024}{429r^2}-\frac{1280r^2}{1001\alpha }-\frac{6016r^6}{9009\alpha ^2},\nonumber \\&R(r\rightarrow \infty )\approx 12c_2{-}\frac{36\alpha }{r^6}{+}\frac{16\alpha c_3}{r^7}{-}\frac{180\alpha ^2c_2}{r^8}{+}\frac{1044\alpha ^2}{5r^{10}},\nonumber \\&R(r\rightarrow 0)\approx \frac{36\alpha ^2}{11}-\frac{3188\alpha r^4}{429}+\frac{46624r^8}{9009\alpha }. \end{aligned}$$
(31)

From Eq. (31) we obtain

$$\begin{aligned}&r(R)\approx \frac{1}{380}\sqrt{570\sqrt{20449R^2\alpha ^2+237120\alpha }-81510R\alpha },\nonumber \\&f(R)\approx \tilde{C_1}+\tilde{C_2} R+\tilde{C_3}R^2, \end{aligned}$$
(32)

where \(\tilde{C_1}\), \(\tilde{C_2}\), and \(\tilde{C_3}\) are constants structured by the constants \(c_1\), \(c_2\), and \(c_3\). Equation (32) shows that f(R) has ultraviolet terms.

In the next section, we will analyze the physical properties of the solution given by Eq. (24) using Eq. (26).

4 Intrinsic physical properties of the BH solutions given by Eq. (24)

Now we will extract the intrinsic physics of the BH solution given by Eq. (24) using Eq. (26). The asymptotic forms of the metric potentials given by Eq. (24) after using Eq. (26) take the following forms:

$$\begin{aligned} A(r)&\approx -r^2c_1c_2+c_1-\frac{c_1c_3}{3r}+\frac{\alpha c_1}{r^4}-\frac{\alpha c_1c_3}{2r^5}\nonumber \\&\quad +\frac{26\alpha ^2c_1}{r^8}-\frac{43\alpha ^2c_1c_3}{r^9},\nonumber \\ A_1(r)&\approx {-}r^2c_2{+}1{-}\frac{c_3}{3r}{+}\frac{5\alpha c_2}{r^2}{-}\frac{4\alpha }{r^4}{+}\frac{7\alpha c_3}{r^5}{-}\frac{15\alpha ^2 c_2}{r^6}\nonumber \\&\quad +\frac{376\alpha ^2}{35r^8}-\frac{15\alpha ^2 c_2}{r^6}-\frac{263\alpha ^2c_3}{88r^9}. \end{aligned}$$
(33)

Using Eq. (33) in Eq. (6), we rewrite the line element in the form

$$\begin{aligned} ds^2 \approx&-\left\{ -r^2\Lambda +1-\frac{2{\mathcal M}}{r}+\frac{\alpha }{r^4}-\frac{3{\mathcal M}\alpha }{r^5}+\frac{26\alpha ^2}{r^8}-\frac{258{\mathcal M}\alpha ^2}{r^9}\right\} \textrm{d}t^2\nonumber \\&+\frac{\textrm{d}r^2}{1-r^2\Lambda -\frac{2{\mathcal M}}{r}+\frac{5\alpha \Lambda }{r^2}-\frac{4\alpha }{r^4}+\frac{42\alpha {\mathcal M}}{r^5}-\frac{15\alpha ^2\Lambda }{r^6}+\frac{376\alpha ^2}{35r^8}-\frac{789\alpha ^2{\mathcal M}}{44r^9}} + \textrm{d}\Omega ^2, \end{aligned}$$
(34)

where we have put \(c_1=1\), \(c_2=\Lambda \), and \(c_3=6{{\mathcal {M}}}\).

Equation (34) shows that the line element expresses the asymptotic (A)dS spacetime when \(\Lambda >0\), and the dS spacetime when \(\Lambda <0\), and is not identical to the Schwarzschild spacetime due to the contribution of the extra terms of the higher-order curvature of f(R) gravity which come mainly from the dimensional constant \(\alpha \). Equation (34) ensures what we have stated in the introduction, that is, in f(R) gravity, one can derive a spacetime that is different from the Schwarzschild one, and when \(F_2=0\), we can recover the Schwarzschild (A)dS/dS metric [136] as usual. In conclusion, at a higher-order curvature, we can obtain a neutral spacetime that is unlike the Schwarzschild solution and coincides with the Schwarzschild (A)dS/dS at a lower order of \(f(R)= R+ \textrm{constant}\).

Now we will calculate the invariants of the solution given by Eq. (33) and obtain

$$\begin{aligned} R_{\mu \nu \rho \sigma } R ^{\mu \nu \rho \sigma }&= 24\Lambda ^2 +\frac{48{\mathcal M}^2-144\Lambda }{r^6}-\frac{384\Lambda \,\alpha {{\mathcal {M}}}}{r^7}\nonumber \\&\quad - \frac{120\Lambda ^2}{r^8}+\cdots \nonumber \\ R _{\mu \nu } R ^{\mu \nu }&= 36\Lambda ^2 {-}\frac{216\alpha \Lambda }{r^6}{+}\frac{576\Lambda \,\alpha {{\mathcal {M}}}}{r^7}- \frac{780\alpha ^2\Lambda ^2}{r^8}\nonumber \\&\quad {+}\cdots \nonumber \\ R&= -12\Lambda -\frac{36\alpha }{r^6}+\frac{96\alpha {{\mathcal {M}}}}{r^7}- \frac{180\alpha ^2\Lambda }{r^8}\nonumber \\ {}&\quad +\cdots , \end{aligned}$$
(35)

where \(\left\{ R, R _{\mu \nu } R ^{\mu \nu }, R _{\mu \nu \rho \sigma } R ^{\mu \nu \rho \sigma } \right\} \) are the Ricci scalar, the Ricci tensor square, and the Kretschmann scalar, respectively, and they all have a true singularity at \(r=0\). It must be noted that the dimensional constant \(\alpha \) is the source of the differentiation of the present study from the (A)dS Schwarzschild BH solution of GR whose invariants behave as \(\left( R _{\mu \nu \rho \sigma } R ^{\mu \nu \rho \sigma }, R _{\mu \nu } R ^{\mu \nu }, R \right) = \left( 24\Lambda ^2+\frac{48\,M^2}{r^6},36\Lambda ^2, 12\Lambda \right) \). Equation (35) shows that the leading order of the scalars \(\left( R _{\mu \nu \rho \sigma } R ^{\mu \nu \rho \sigma }, R _{\mu \nu } R ^{\mu \nu }, R \right) \) is \(\left( \frac{1}{r^{6}}, \frac{1}{r^{6}},\frac{1}{r^{6}} \right) \), which coincides with the form of the (A)dS Schwarzschild BH solution whose leading term of the Kretschmann is \(\left( \frac{1}{r^{6}}\right) \). Thus, Eq. (35) shows that the singularity of the Kretschmann coincides with the (A)dS Schwarzschild BH solution of GR.

5 Study of the geodesics

In this section, we will derive the geodesic equation for the BH given by Eq. (33) and also study the geodesic deviation equation to derive its stability condition.

5.1 Geodesics of the BH (33)

Because of the spherical symmetry of an improved Schwarzschild BH, we can study the motion of the test particles on the equatorial plane, i.e at \(\theta \) = \(\frac{\pi }{2}\). Therefore, we have three geodesic equations:

$$\begin{aligned}{} & {} \frac{\textrm{d}^2t}{\textrm{d}\varepsilon ^2}+\frac{A'(r)}{A(r)}\frac{\textrm{d}t}{\textrm{d}\varepsilon }\frac{\textrm{d}r}{\textrm{d}\varepsilon }=0, \end{aligned}$$
(36)
$$\begin{aligned}{} & {} \frac{\textrm{d}^2r}{\textrm{d}\varepsilon ^2}+\frac{1}{2}A_1(r)A'(r)\Big (\frac{\textrm{d}t}{\textrm{d}\varepsilon }\Big )^2-\frac{A'_1(r)}{2A_1(r)}\Big (\frac{\textrm{d}r}{\textrm{d}\varepsilon }\Big )^2\nonumber \\{} & {} \quad - rA_1(r)\Big (\frac{\textrm{d}\phi }{\textrm{d}\varepsilon }\Big )^2=0, \end{aligned}$$
(37)
$$\begin{aligned}{} & {} \frac{\textrm{d}^2\phi }{\textrm{d}\varepsilon ^2}+\frac{2}{r}\frac{\textrm{d}\phi }{\textrm{d}\varepsilon }\frac{\textrm{d}r}{\textrm{d}\varepsilon }=0, \end{aligned}$$
(38)

where A(r) and \(A_1(r)\) are given by Eq. (33).

To solve these geodesic equations we will consider two methods in the next section. One is the effective Newtonian potential method as studied in [137, 138], and the other is dynamical system analysis [139].

6 Effective Newtonian potential approach

The Lagrangian of a particle motion of the extended Schwarzschild BH is given by

$$\begin{aligned} 2\mathcal {L}= & {} -\left\{ -r^2\Lambda +1-\frac{2{\mathcal M}}{r}+\frac{\alpha }{r^4}-\frac{3{\mathcal M}\alpha }{r^5}+\frac{26\alpha ^2}{r^8}-\frac{258{\mathcal M}\alpha ^2}{r^9}\right\} \nonumber \\{} & {} \dot{t}^2+\frac{\dot{r}^2}{1-r^2\Lambda -\frac{2{\mathcal M}}{r}+\frac{5\alpha \Lambda }{r^2}-\frac{4\alpha }{r^4}+\frac{42\alpha {\mathcal M}}{r^5}}\nonumber \\{} & {} \quad +r^2({\dot{\theta }}^2+\sin ^2\theta {\dot{\phi }}^2), \end{aligned}$$
(39)

where the overdot refers to the differentiation with respect to the affine parameter \(\varepsilon \). Here, the Lagrangian \(\mathcal {L}\) is not explicitly dependent on the coordinates t and \(\phi \). Thus, because of these two cyclic coordinates, we obtain two conserved quantities, the energy E and the momentum h conjugate to \(\phi \).

Energy:

$$\begin{aligned} E=g_{tt}\frac{\textrm{d}t}{\textrm{d}\varepsilon }=A(r)\frac{\textrm{d}t}{\textrm{d}\varepsilon }. \end{aligned}$$
(40)

Momentum:

$$\begin{aligned} 2h=\frac{\partial {\mathcal {L}}}{\partial {{\dot{\phi }}}}=2r^2{\dot{\phi }}=constant, \end{aligned}$$
(41)

where h refers to the total angular momentum of the particles. Recalling the normalization condition

$$\begin{aligned} g_{\mu \nu }\frac{\textrm{d}x^{\mu }}{\textrm{d}\varepsilon }\frac{\textrm{d}x^{\nu }}{\textrm{d}\varepsilon }=-\epsilon , \end{aligned}$$
(42)

where \(\epsilon \) is a parameter whose value for timelike geodesics is \(\epsilon = 1\) and for null geodesics \(\epsilon = 0\) [139], we have on the equatorial plane

$$\begin{aligned} \Big (\frac{\textrm{d}r}{\textrm{d}\varepsilon }\Big )^2=E^2\left( \frac{A_1(r)}{A(r)}\right) -A_1(r)\Big (\frac{h^2}{r^2}+\epsilon \Big ). \end{aligned}$$
(43)

Therefore, Eqs. (40), (41), and (43) are the equations required to describe the dynamics of particle trajectories at the equatorial plane of the extension of the Schwarzschild BH.

Now we will rewrite Eq. (43) as

$$\begin{aligned} \frac{1}{2}\Big (\frac{\textrm{d}r}{\textrm{d}\varepsilon }\Big )^2&=E_{eff}-V_{eff}, \quad \text{ where } \quad E_{eff}=\frac{E^2}{2}\,\quad \text{ and }\nonumber \\ V_{eff}&\approx A_1\Big (\frac{h^2}{r^2}+\epsilon \Big )-\frac{5\mathcal {\alpha }}{r^4}+\frac{7\mathcal {C}_1}{r^7}-\frac{10\mathcal {C}_2}{r^8}+\frac{7\mathcal {C}_3}{r^9}\nonumber \\&\approx \Big (1-r^2\Lambda -\frac{2{\mathcal M}}{r}+\frac{5\alpha \Lambda }{r^2}-\frac{4\alpha }{r^4}+\frac{42\alpha {\mathcal M}}{r^5}\Big )\nonumber \\&\quad \Big (\frac{h^2}{r^2}+\epsilon \Big ) -\frac{5\mathcal {C}}{r^4}+\frac{7\mathcal {C}_1}{r^7}-\frac{10\mathcal {C}_2}{r^8}+\frac{7\mathcal {C}_3}{r^9}, \end{aligned}$$
(44)

where \(\mathcal {C}=\alpha E_{eff}\), \(\mathcal {C}_1=\alpha {\mathcal M}E_{eff}\), \(\mathcal {C}_2=\alpha ^2E_{eff}\), and \(\mathcal {C}_3=\alpha {\mathcal M}E_{eff}/\Lambda \). Therefore, Eq. (44) describes the equation of motion of a particle with a unit mass and an effective energy \(E_{eff}\) moving in a one-dimensional effective potential \(V_{eff}(r)\). Therefore, E describes the conserved energy of the particle per unit mass, \(V_{eff}(r)\) is the effective potential for the radial coordinate r, and \(E_{eff}\) is the effective energy. The physically acceptable regions are given by the values of those r for which \(E_{eff}>V_{eff}(r)\). Thus, Eq. (44) represents the energy equation for the radial coordinate r. This equation is necessary to study the radial free fall and the stability of the particle trajectories.

By imposing A(r), Eq. (43) takes the form

$$\begin{aligned} \Big (\frac{\textrm{d}r}{\textrm{d}\varepsilon }\Big )^2&\approx E^2-\epsilon +r^2\Lambda \epsilon +\frac{2{\mathcal M}\epsilon }{r}-\frac{5\alpha \Lambda \epsilon }{r^2}+\frac{4\alpha \epsilon }{r^4}\nonumber \\&\quad -\frac{42\alpha {\mathcal M}\epsilon }{r^5}-\frac{h^2}{r^2}+\Lambda h^2+\frac{2{\mathcal M}h^2}{r^3}-\frac{5\alpha \Lambda \,h^2}{r^4}\nonumber \\&\quad +\frac{4\alpha h^2}{r^6}-\frac{42\alpha {{\mathcal {M}}}h^2}{r^7}+\frac{5\mathcal {C}}{r^4}-\frac{7\mathcal {C}_1}{r^7}\nonumber \\&\quad +\frac{10\mathcal {C}_2}{r^8}-\frac{7\mathcal {C}_3}{r^9}. \end{aligned}$$
(45)

The geometry of the geodesics in the equatorial plane \(\theta \) = \(\frac{\pi }{2}\) can be determined by Eq. (45). To determine the shape of the trajectories, we use Eq. (41) to express \(\frac{\textrm{d}r}{\textrm{d}\varepsilon }\) as

$$\begin{aligned} \frac{\textrm{d}r}{\textrm{d}\varepsilon }=\frac{\textrm{d}r}{\textrm{d}\phi }\frac{\textrm{d}\phi }{\textrm{d}\varepsilon }=\frac{h}{r^2}\frac{\textrm{d}r}{\textrm{d}\phi }. \end{aligned}$$
(46)

Now, we introduce the transformation \(u = \frac{1}{r}\), which yields

$$\begin{aligned} \Big (\frac{\textrm{d}u}{\textrm{d}\varepsilon }\Big )^2=u^4\Big (\frac{\textrm{d}r}{\textrm{d}\varepsilon }\Big )^2. \end{aligned}$$
(47)

Using Eq.  (47) in Eq. (45), we obtain

$$\begin{aligned} \Big (\frac{\textrm{d}u}{\textrm{d}\varepsilon }\Big )^2&=-7\mathcal {C}_3u^{13}+10\mathcal {C}_2u^{12}+\mathcal {C}_4u^{11}+4Ch^2u^{10}\nonumber \\&\quad -42C{\mathcal M}\epsilon u^{9}+\mathcal {C}_5u^{8}+2{\mathcal M}h^2u^7+\mathcal {C}_6u^{6}\nonumber \\&\quad +2\mathcal {M}\epsilon u^{5} +(E^2-\epsilon +\Lambda h^2)u^4+\Lambda \epsilon u^2, \end{aligned}$$
(48)

where \(\mathcal {C}_4=-(7\mathcal {C}_1+42\mathcal {C}\mathcal {M}h^2)\),   \(\mathcal {C}_5=5{\mathcal C}(1-\Lambda h^2+4/5\epsilon )\),  and \(\mathcal {C}_6=-5{\mathcal C}\Lambda \epsilon -h^2\). Now, using Eqs. (46), (47), and (48), we obtain the expression \(\Big (\frac{\textrm{d}u}{\textrm{d}\phi }\Big )^2\) as follows:

$$\begin{aligned} \Big (\frac{\textrm{d}u}{\textrm{d}\phi }\Big )^2&=-\frac{7\mathcal {C}_3u^{9}}{h^2}+\frac{10\mathcal {C}_2u^{8}}{h^2}+\frac{\mathcal {C}_4u^{7}}{h^2}+\frac{4\mathcal {C}_5u^{10}}{h^2}\nonumber \\&\quad {-}\frac{42C{\mathcal M}\epsilon u^{5}}{h^2}{+}\frac{\mathcal {C}_6u^{4}}{h^2}{+}2{\mathcal M}u^3{+}\frac{\mathcal {C}_6u^{2}}{h^2}{+}\frac{2\mathcal {M}\epsilon u}{h^2}\nonumber \\&\quad +\frac{(E^2-\epsilon +\Lambda h^2)}{h^2}+\frac{\Lambda \epsilon }{ h^2 u^2}=S(u). \end{aligned}$$
(49)

Equation (49) describes the trajectories of the test particles near the extension of the Schwarzschild BH. From the physical viewpoint, the radial motion and the circular motion of the particles are two critical topics for studying the particle trajectories. Thus, in the next section we will study the particle trajectories for these two cases.

7 Radial motion

It is important to study the radial geodesics to investigate the ingredient properties of the spacetime for which the angular momentum becomes zero. Also, for the radial motion, \(\phi = constant\), in which Eq. (49) fails to provide us with the information about the radial trajectories because most of the terms blow up as \( h\rightarrow 0\). Additionally, to study the radial trajectories of the particles, we can consider Eq. (43), which becomes

$$\begin{aligned} \Big (\frac{\textrm{d}r}{\textrm{d}\varepsilon }\Big )^2=E^2\left( \frac{A_1(r)}{A(r)}\right) -A_1(r)\epsilon . \end{aligned}$$
(50)

7.1 Motion of massive particles

For massive particles, \(\epsilon \) = 1 and Eq. (50) yields

$$\begin{aligned} \Big (\frac{\textrm{d}r}{\textrm{d}\varepsilon }\Big )^2= & {} E^2-1+r^2\Lambda +\frac{2{\mathcal M}}{r}-\frac{5C\Lambda }{r^2}+\frac{4C}{r^4}-\frac{42C{\mathcal M}}{r^5}\nonumber \\{} & {} +\frac{5\mathcal {C}}{r^4}-\frac{7\mathcal {C}_1}{r^7}+\frac{10\mathcal {C}_2}{r^8}-\frac{7\mathcal {C}_3}{r^9}. \end{aligned}$$
(51)

By differentiating Eq. (51) with respect to \(\varepsilon \), we obtain

$$\begin{aligned}{} & {} \frac{\textrm{d}^2r}{\textrm{d}\varepsilon ^2}=-\Big (\frac{{\mathcal M}}{r^2}+\frac{10(C+5\mathcal {C}/4)}{r^5}+\frac{45{\mathcal C}_2}{r^{9}}\Big )\nonumber \\{} & {} \quad +\Big (r\Lambda +\frac{15C\Lambda }{2r^3}+\frac{126C{\mathcal M}}{r^6}+\frac{28\mathcal {C}_1}{r^8}+\frac{35\mathcal {C}_3}{r^{10}}\Big ). \end{aligned}$$
(52)

Since the trajectories of massive particles feature timelike geodesics, we suppose that along the path, the affine parameter proper time is \(\tau \) rather than \(\varepsilon \). Therefore, the motion of massive particles can be studied by the above equation, and the condition of attractive force per unit mass is given by

$$\begin{aligned}{} & {} \Big (\frac{{\mathcal M}}{r^2}+\frac{10(C+\mathcal {C}/4)}{r^5}+\frac{45{\mathcal C}_2}{r^{9}}\Big )\nonumber \\{} & {} \quad >\Big (r\Lambda +\frac{15C\Lambda }{2r^3}\frac{126C{\mathcal M}}{r^6}+\frac{28\mathcal {C}_1}{r^8}+\frac{35\mathcal {C}_3}{r^{10}}\Big ). \end{aligned}$$
(53)

The condition given by Eq. (53) is important because it gives the bound states of massive particles. The particle can gain kinetic energy during the gravitational interaction when it passes through the gravitational field of any BH. Then we can calculate the change in the potential energy of the particle in that gravitational field by considering the particle’s rest position, so that the radial coordinate r changes to R. Now, we are interested in describing the trajectories of the particle in the (t, r)-plane. With the help of Eqs. (40) and (51),

$$\begin{aligned} \Big (\frac{\textrm{d}r}{\textrm{d}t}\Big )^2=\Big [E^2\left( \frac{A_1(r)}{A(r)}\right) -A_1(r)\Big ]\frac{A^2(r)}{E^2}. \end{aligned}$$
(54)

It is clear that \(\frac{\textrm{d}r}{\textrm{d}t}\) = 0 for all points when \(E^2 = A(r)\). From Eq. (51) we can obtain the effective potential \(V_{eff}\) as followsFootnote 2

$$\begin{aligned} V_{eff}= & {} \frac{1}{2}\Bigg (1-r^2\Lambda -\frac{2{\mathcal M}}{r}+\frac{5C\Lambda }{r^2}-\frac{4C}{r^4}+\frac{42C{\mathcal M}}{r^5}\nonumber \\{} & {} -\frac{5\mathcal {C}}{r^4}+\frac{7\mathcal {C}_1}{r^7}-\frac{10\mathcal {C}_2}{r^8}+\frac{7\mathcal {C}_3}{r^9}\Bigg ). \end{aligned}$$
(55)
Fig. 1
figure 1

Plots: (a) the potential given by Eq. (55), (b) the momentum given by (61), and (c) the energy given by Eq.  (62). All these figures are depicted against the coordinate u of the BH (33)

Full size image

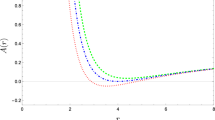
In Fig. 1, we show the behavior of the effective potential, \(V_{eff}\), with respect to the radius r of the orbits for three different values of the cosmological constant. From Fig. 1a it is clear that \(V_{eff}\) is an exponentially increasing function of the redial coordinate r but with negative values.

Now, from Eq. (54), we can write

$$\begin{aligned} \frac{\textrm{d}r}{\textrm{d}t}=\frac{A(r)}{E}\sqrt{E^2\left( \frac{A_1(r)}{A(r)}\right) -A_1(r)}. \end{aligned}$$
(56)

When \(\Lambda =0\), Eq. (54) will not be blow up for \(r\rightarrow \infty \). Hence, Eq. (56) will only be a function of the total energy E, and therefore if we can observe the behavior of the particle at infinite distance from the source, then it will behave like a free particle. However, \(\frac{\textrm{d}r}{\textrm{d}t}\) and E will be finite for a measurable distance from the source.

7.2 Motion of photons

For photon motion where \(\epsilon \) = 0, Eq. (50) yields

$$\begin{aligned} \Big (\frac{\textrm{d}r}{\textrm{d}\epsilon }\Big )^2=E^2\left( \frac{A_1(r)}{A(r)}\right) , \end{aligned}$$
(57)

where E is defined in Eq. (40). Also, defining \(\frac{\textrm{d}r}{\textrm{d}t}=\frac{\textrm{d}r}{\textrm{d}\varepsilon }\frac{\textrm{d}\varepsilon }{\textrm{d}t}\), we obtain

$$\begin{aligned} \frac{\textrm{d}r}{\textrm{d}t}=\pm E\sqrt{1+\frac{5\alpha }{r^4}+\frac{10\alpha ^2}{r^8}+\frac{10\alpha ^3}{r^{12}}+\frac{5\alpha ^4}{r^{16}}+\frac{\alpha ^5}{r^{20}}}. \end{aligned}$$
(58)

The solution of Eq. (58) is complicated, and thus it is difficult to prescribe the trajectories of the photons using this method.

Circular motion:

It is clear from Eq. (49) that at equilibrium position of circular orbits, \(u=constant\), so \(S(u) = 0\) and \(S'(u)\) = 0. From Eq. (49) we have

$$\begin{aligned} S(u)&=-\frac{7\mathcal {C}_3u^{9}}{h^2}+\frac{10\mathcal {C}_2u^{8}}{h^2}+\frac{\mathcal {C}_4u^{7}}{h^2}+\frac{4\mathcal {C}_5u^{10}}{h^2}\nonumber \\&\quad -\frac{42C{\mathcal M}\epsilon u^{5}}{h^2}+\frac{\mathcal {C}_6u^{4}}{h^2}+2{\mathcal M}u^3+\frac{\mathcal {C}_6u^{2}}{h^2}+\frac{2\mathcal {M}\epsilon u}{h^2}\nonumber \\&\quad +\frac{\Lambda \epsilon }{ h^2 u^2}+\frac{(E^2-\epsilon +\Lambda h^2)}{h^2}, \end{aligned}$$
(59)

and

$$\begin{aligned} S'(u)&=-\frac{63\mathcal {C}_3u^{8}}{h^2}+\frac{80\mathcal {C}_2u^{7}}{h^2}+\frac{7\mathcal {C}_4u^{6}}{h^2}+\frac{40\mathcal {C}_5u^{9}}{h^2}\nonumber \\&\quad -\frac{210C{\mathcal M}\epsilon u^{4}}{h^2}+\frac{4\mathcal {C}_6u^{3}}{h^2}+6{\mathcal M}u^2+\frac{2\mathcal {C}_6u}{h^2}\nonumber \\&\quad +\frac{2\mathcal {M}\epsilon }{h^2}-\frac{2\Lambda \epsilon }{ h^2 u^3}. \end{aligned}$$
(60)

Solving Eqs.  (59) and (60), we obtain an expression of angular momentum (h) and energy (E) of the particle obeying circular motion, respectively, as follows:

$$\begin{aligned} h^2={\frac{63\,\mathcal {C}_3\,r-80\,\mathcal {C}_2\,{r}^{2}-7\,\mathcal {C}_4\,{r}^{3 }-40\,\mathcal {C}_5+210\,\mathcal {C}{\mathcal M}{r}^{5}-4\,\mathcal {C}_6\,{r}^{6}-2\,\mathcal {C}_6\,{r}^{8 }-2\,{\mathcal M}{r}^{9}+2\,\Lambda \,{r}^{12}}{6{r}^{7}{{\mathcal {M}}}}}, \end{aligned}$$
(61)

and

$$\begin{aligned} E^2&{=}{-}\frac{1}{6M{r}^{10}}\bigg \{-6\,M{r}^{10}+8\,{M}^{2}{r}^{9}{+}2\,{\Lambda }^{2}{r}^{15} +84\,\mathcal {C}_3\,Mr\nonumber \\&\quad +63\,\Lambda \,\mathcal {C}_3\,{r}^{4}-100\,\mathcal {C}_2\,M{r}^{ 2}-80\,\Lambda \,\mathcal {C}_2\,{r}^{5}-8\,\mathcal {C}_4\,M{r}^{3}\nonumber \\&\quad -7\,\Lambda \,\mathcal {C}_4\,{r}^{6} -56\,\mathcal {C}_5\,M-40\,\Lambda \, \mathcal {C}_5\,{r}^{3}+168\,\mathcal {C} {M}^{2}{r}^{5}\nonumber \\&\quad -2\,\mathcal {C}_6\,{\mathcal M}{r}^{6}-4\,\Lambda \,\mathcal {C}_6\,{r}^{9}+2\, \mathcal {C}_6\,{\mathcal M}{r}^{8}-2\,\Lambda \,\mathcal {C}_6\,{r}^{11}\nonumber \\&\quad +8\,M\Lambda \,{r}^{12 }+210\,\mathcal {C}{{\mathcal {M}}}\Lambda \,{r}^{8}\bigg \}. \end{aligned}$$
(62)

The behavior of Eqs. (61) and (62) are shown in Fig. 1b, c.

7.3 Stability of the BH (33) using geodesic deviation

The geodesic equations have the following form: [136]:

$$\begin{aligned} \frac{\textrm{d}^2 x^\alpha }{\textrm{d}\varepsilon ^2} + \left\{ \begin{array}{c} \alpha \\ \beta \rho \end{array} \right\} \frac{d x^\beta }{\textrm{d}\varepsilon } \frac{\textrm{d} x^\rho }{\textrm{d}\varepsilon }=0, \end{aligned}$$
(63)

and the geodesic deviation equations take the form [140, 141]

$$\begin{aligned} \frac{\textrm{d}^2 \epsilon ^\sigma }{\textrm{d}\varepsilon ^2} + 2\left\{ \begin{array}{c} \sigma \\ \mu \nu \end{array} \right\} \frac{\textrm{d} x^\mu }{\textrm{d}\varepsilon } \frac{\textrm{d} \epsilon ^\nu }{\textrm{d}\varepsilon } + \left\{ \begin{array}{c} \sigma \\ \mu \nu \end{array} \right\} _{,\, \rho } \frac{\textrm{d} x^\mu }{\textrm{d}\varepsilon } \frac{\textrm{d} x^\nu }{\textrm{d}\varepsilon }\epsilon ^\rho =0,\nonumber \\ \end{aligned}$$
(64)

with \(\epsilon ^\rho \) being the four-vector deviation. Using Eqs. (63) and (64) in Eq. (6), we obtain

$$\begin{aligned} \frac{\textrm{d}^2 t}{\textrm{d}\varepsilon ^2}= & {} 0, \qquad \frac{1}{2} A'(r) \left( \frac{d t}{\textrm{d}\varepsilon }\right) ^2 - r\left( \frac{d \phi }{\textrm{d}\varepsilon }\right) ^2=0, \frac{\textrm{d}^2 \theta }{\textrm{d}\varepsilon ^2}{=}0,\qquad \nonumber \\ \frac{\textrm{d}^2 \phi }{\textrm{d}\varepsilon ^2}= & {} 0, \end{aligned}$$
(65)

and the form of the geodesic deviations using the line element (6) gives

$$\begin{aligned}&\frac{\textrm{d}^2 \epsilon ^1}{\textrm{d}\varepsilon ^2} +A_1(r)A'(r) \frac{\textrm{d}t}{\textrm{d}\varepsilon } \frac{\textrm{d} \epsilon ^0}{\textrm{d}\varepsilon } -2r A_1(r) \frac{\textrm{d} \phi }{\textrm{d}\varepsilon }\frac{\textrm{d} \epsilon ^3}{\textrm{d}\varepsilon } \nonumber \\&\qquad +\left[ \frac{1}{2} \left( A'(r)A'_1(r)+A_1(r) A''(r) \right) \left( \frac{\textrm{d}t}{\textrm{d}\varepsilon } \right) ^2\right. \nonumber \\&\qquad \left. -\left( A_1(r)+rA'_1(r) \right) \left( \frac{\textrm{d}\phi }{\textrm{d}\varepsilon }\right) ^2 \right] \epsilon ^1=0\, , \nonumber \\&\frac{\textrm{d}^2 \epsilon ^0}{\textrm{d}\varepsilon ^2} + \frac{A'_1(r)}{A(r)} \frac{\textrm{d}t}{\textrm{d}\varepsilon } \frac{d {\epsilon ^1}}{\textrm{d}\varepsilon }=0\, ,\quad \frac{\textrm{d}^2 \epsilon ^2}{\textrm{d}\varepsilon ^2} +\left( \frac{\textrm{d}\phi }{\textrm{d}\varepsilon }\right) ^2 \epsilon ^2 =0\, ,\nonumber \\&\quad \qquad \qquad \frac{\textrm{d}^2 \epsilon ^3}{\textrm{d}\varepsilon ^2} + \frac{2}{r} \frac{\textrm{d}\phi }{\textrm{d}\varepsilon } \frac{\textrm{d} \epsilon ^1}{\textrm{d}\tau }=0\, , \end{aligned}$$
(66)

where A(r) and \(A_1(r)\) are given by Eq. (33), and the prime, i.e. “\('\)”, is the derivative with respect to the radial coordinate r. From the condition of a circular orbit, we obtain

$$\begin{aligned} \theta = \frac{\pi }{2}, \qquad \qquad \frac{\textrm{d}\theta }{\textrm{d}\varepsilon }=0, \qquad \qquad \frac{d r}{\textrm{d}\varepsilon }=0. \end{aligned}$$
(67)

Using Eq. (67) in Eq. (65), we obtain

$$\begin{aligned}{} & {} \left( \frac{\textrm{d}\phi }{\textrm{d}\varepsilon }\right) ^2= \frac{A'(r)}{r \left[ 2A(r)-rA'(r) \right] }, \qquad \qquad \nonumber \\{} & {} \left( \frac{\textrm{d}t}{\textrm{d}\varepsilon }\right) ^2= \frac{2}{2A(r)-rA'(r)}. \end{aligned}$$
(68)

We can rewrite Eq. (66) as

$$\begin{aligned}&\frac{\textrm{d}^2 \epsilon ^1}{\textrm{d}\phi ^2} +A(r)A'(r) \frac{\textrm{d}t}{\textrm{d}\phi } \frac{d \epsilon ^0}{\textrm{d}\phi } -2r A_1(r) \frac{\textrm{d} \epsilon ^3}{\textrm{d}\phi } \nonumber \\&\quad +\left[ \frac{1}{2} \left[ A'(r)^2+A(r) A''(r) \right] \left( \frac{\textrm{d}t}{\textrm{d}\phi }\right) ^2\right. \nonumber \\&\quad \left. -\left[ A(r)+rA'(r) \right] \right] \zeta ^1=0\, , \nonumber \\&\frac{\textrm{d}^2 \epsilon ^2}{\textrm{d}\phi ^2}+\epsilon ^2=0\, , \qquad \qquad \frac{\textrm{d}^2 \epsilon ^0}{\textrm{d}\phi ^2} + \frac{A'(r)}{A(r)} \frac{\textrm{d}t}{\textrm{d}\phi } \frac{\textrm{d} \epsilon ^1}{\textrm{d}\phi }=0\, , \qquad \qquad \nonumber \\&\frac{\textrm{d}^2 \epsilon ^3}{\textrm{d}\phi ^2} + \frac{2}{r} \frac{\textrm{d} \epsilon ^1}{\textrm{d}\phi }=0\, . \end{aligned}$$
(69)

From the second equation of Eq. (69), we can show that we have a simple harmonic motion, which is the stability condition of the plane \(\theta =\pi /2\). The remaining equations of (69) assume the following solutions:

$$\begin{aligned} \epsilon ^0 = \zeta _1 \textrm{e}^{i \sigma \phi }, \quad \epsilon ^1= \zeta _2\textrm{e}^{i \sigma \phi }, \quad \text{ and } \qquad \epsilon ^3 = \zeta _3 \textrm{e}^{i \sigma \phi }, \end{aligned}$$
(70)

where \(\zeta _1, \zeta _2\), and \(\zeta _3\) are constants and \(\sigma \) is an unknown function. Using the values of \(\epsilon ^1\) and \(\epsilon ^3\) given by Eq. (70) in the fourth equation of Eq. (69), we obtain

$$\begin{aligned} \zeta _2=-\frac{\zeta _3\sigma \,r}{2}. \end{aligned}$$
(71)

Then, substituting the values of \(\epsilon ^0\) and \(\epsilon ^1\) given by Eq. (70) into the third equation of Eq. (69) and using Eq. (71), we obtain

$$\begin{aligned} \zeta _1=\frac{\zeta _3\sqrt{2A'\,r^3}}{2A}. \end{aligned}$$
(72)

Substituting Eq. (70), after using Eqs. (71) and (72), into the first equation of Eq. (69), we obtain the stability condition as

$$\begin{aligned} \frac{3A A_1 A'-\sigma ^2 A A'-2rA_1{A'}^{2}+rAA_1 A'' }{AA'}>0. \end{aligned}$$
(73)

We show Eq. (73) in Fig. 2 using specific values of the model. This figure exhibits the unshaded and shaded zones where the BH is stable and unstable, respectively.

Fig. 2
figure 2

Plots of Eq. (73) against the radial coordinate r for the BH (33) which indicate the region of stability and non-stability for different values of M, \(\alpha \), and \(\Lambda \)

Full size image

8 Thermodynamics of the BH solution (33)

In this section, we will investigate the thermodynamic properties of the BH solution (33) without/with the cosmological constant, i.e., \(\Lambda \). The Hawking temperature of a BH is defined as [142,143,144,145,146,147,148]

$$\begin{aligned} T =\frac{1}{4\pi }\lim \limits _{g_{tt}\rightarrow 0} \left( g'_{tt}\sqrt{g^{tt}g^{rr}}\right) \underline{}. \end{aligned}$$
(74)

The Hawking entropy of the horizons is defined as

$$\begin{aligned} S =\frac{1}{4}A\,f_R, \end{aligned}$$
(75)

where A is the area of the horizons. The quasi-local energy is defined as [142,143,144,145, 149, 150]

$$\begin{aligned} E =\frac{1}{4}\int \left[ 2f_R~r+r^2 \left\{ F_0 \left( R \left( r \right) \right) - R \left( r\right) f_R~r\right\} \right] \textrm{d}r. \end{aligned}$$
(76)

Finally, the Gibbs free energy is defined as [150, 151]

$$\begin{aligned} G= E- TS. \end{aligned}$$
(77)

8.1 Thermodynamics of the BH (33)

In this subsection, we will study the thermodynamics of the BH (33) without/with the cosmological constant. We will now discuss the case \(\Lambda =0\) for the BH solution (33) taking into account the BH up to \(O\left( \frac{1}{r^4}\right) \). The BH (33) is characterized by the mass of the BH \({\mathcal M}\) and the dimensional parameter \(\alpha \). The metric potentials when \(\Lambda \ne 0\) take the following form:

$$\begin{aligned} A(r)\approx & {} -\Lambda r^2+1-\frac{2{\mathcal M}}{r}-\frac{\alpha }{r^4}, \qquad A_1(r)\approx -\Lambda r^2+1\nonumber \\{} & {} -\frac{2{\mathcal M}}{r}+\frac{\alpha }{r^4}. \end{aligned}$$
(78)

The metric potentials of the BH (78) are calculated in Fig. 3a when \(\Lambda =0\).

From Fig. 3a we can easily see the two horizons of the metric potential A(r). To find the horizons of this BH, given by Eq. (78), we put \(A(r)=0\) in Eq. (78) when \(\Lambda =0\) [147]. This gives four roots, of which two are real and the others are imaginary. These real roots, inner and outer, are given respectively as

$$\begin{aligned}{} & {} r_-=\frac{1}{72\root 6 \of {\gamma }\root 4 \of {{{\mathcal M}} ^{2}{2}^{2/3}\root 3 \of {3}\root 3 \of {\gamma }+12\,\root 3 \of {\alpha }\root 3 \of {2 }{3}^{2/3}{\gamma }^{2/3}+288\,{\alpha }^{2/3}}} \left( 6\,{\mathcal M}\,\root 6 \of {\gamma }\root 4 \of {{{\mathcal M}}^{2}{2}^{2/3}\root 3 \of {3}\root 3 \of {\gamma }+12\,\root 3 \of {\alpha } \root 3 \of {2}{3}^{2/3}{\gamma }^{2/3}+288\,{\alpha }^{2/3}}\right. \nonumber \\{} & {} \quad \left. +{3}^{5/6} \left( { {\mathcal M}}^{2}{2}^{2/3}\root 3 \of {3}\root 3 \of {\gamma }+12\,\root 3 \of {\alpha } \root 3 \of {2}{3}^{2/3}{\gamma }^{2/3}+288\,{\alpha }^{2/3} \right) ^{3/4}{2}^{ 2/3}+{2}^{4/3}{3}^{1/2}\left\{ \left( {{\mathcal M}}^{2}\root 3 \of {2}\root 6 \of { 3}\root 3 \of {\gamma }-6\,\root 3 \of {\alpha }\sqrt{3}{\gamma }^{2/3}\right. \right. \right. \nonumber \\{} & {} \quad \left. \left. \left. -24\,{\alpha }^{ 2/3}{3}^{5/6}{2}^{2/3} \right) \sqrt{{{\mathcal M}}^{2}{2}^{2/3}\root 3 \of {3}\root 3 \of {\gamma }+12\,\root 3 \of {\alpha }\root 3 \of {2}{3}^{2/3}{\gamma }^{ 2/3}+288\,{\alpha }^{2/3}}+{{\mathcal M}}^{3}{2}^{2/3}\root 3 \of {3}\sqrt{ \gamma }\right\} ^{1/2}{3}^{{\frac{5}{12}}}\right) ,\nonumber \\{} & {} r_+=\frac{1}{72\root 6 \of {\gamma }\root 4 \of {{{\mathcal M}} ^{2}{2}^{2/3}\root 3 \of {3}\root 3 \of {\gamma }+12\,\root 3 \of {\alpha }\root 3 \of {2 }{3}^{2/3}{\gamma }^{2/3}+288\,{\alpha }^{2/3}}}\left( 6\,{\mathcal M}\,\root 6 \of {\gamma }\root 4 \of {{{\mathcal M}}^{2}{2}^{2/3}\root 3 \of {3}\root 3 \of {\gamma }+12\,\root 3 \of {\alpha } \root 3 \of {2}{3}^{2/3}{\gamma }^{2/3}+288\,{\alpha }^{2/3}}\right. \nonumber \\{} & {} \left. +{3}^{5/6} \left( { {\mathcal M}}^{2}{2}^{2/3}\root 3 \of {3}\root 3 \of {\gamma }+12\,\root 3 \of {\alpha } \root 3 \of {2}{3}^{2/3}{\gamma }^{2/3}+288\,{\alpha }^{2/3} \right) ^{3/4}{2}^{ 2/3}-{2}^{4/3}{3}^{1/2}\left\{ \left( {{\mathcal M}}^{2}\root 3 \of {2}\root 6 \of { 3}\root 3 \of {\gamma }-6\,\root 3 \of {\alpha }\sqrt{3}{\gamma }^{2/3}\right. \right. \right. \nonumber \\{} & {} \quad \left. \left. \left. -24\,{\alpha }^{ 2/3}{3}^{5/6}{2}^{2/3} \right) \sqrt{{{\mathcal M}}^{2}{2}^{2/3}\root 3 \of {3}\root 3 \of {\gamma }+12\,\root 3 \of {\alpha }\root 3 \of {2}{3}^{2/3}{\gamma }^{ 2/3}+288\,{\alpha }^{2/3}}+{{\mathcal M}}^{3}{2}^{2/3}\root 3 \of {3}\sqrt{ \gamma }\right\} ^{1/2}{3}^{{\frac{5}{12}}}\right) , \end{aligned}$$
(79)

where \(\gamma ={\mathcal M}^2+\sqrt{{\mathcal M}^2-768\alpha }\) and \({\mathcal M}^2>768\alpha \). It is easy to check that the degenerate horizon for the metric potential A(r) given by Eq. (78) occurs for specific values of \((\alpha ,{\mathcal M},r)\equiv (2,66,2.9)\), respectively, which correspond to the Nariai BH. The degenerate behavior is shown in Fig. 3c, and Fig. 3c shows that the horizon \(r_-\) decreases with r while \(r_+\) increases.

The degenerate behavior is indicated in Fig. 3c, which shows that \(r_-<r_d\). As we observe from Fig. 3c, as \(\alpha \) increases, we enter a parameter region where no horizon exists, and thus the central singularity is a naked singularity.

Now we will discuss the case when \(\Lambda \ne 0\) where we obtain six roots, three of which are real and the others are imaginary. The explicit forms of these roots are very lengthy, but their behavior is shown in Fig. 3b. Figure 3b clearly shows the three real roots, where we have two inner and outer roots, as usual for any BH, and the third horizon corresponding to the cosmological constant.

Fig. 3
figure 3figure 3

Plots of thermodynamic quantities of the BH solution given by Eq. (33): (a) the behavior of the metric potentials A and \(A_1\) for \(\Lambda =0\) when \({\mathcal M}=66\) and \(\alpha =0.3\); (b) typical behavior of the metric potentials A and \(A_1\) for \(\Lambda =0.001\) when \({\mathcal M}=12\) and \(\alpha =0.1\); (c) typical behavior of the horizons for \(\Lambda =0\) when \({\mathcal M}=66\) and \(\alpha =2\); (d) typical behavior of the horizons for \(\Lambda =0.1\) when \({\mathcal M}=12\) and \(\alpha =0.001\); (e) typical behavior of the entropy for \(\Lambda =0\) and \(\alpha =0.3\); (f) typical behavior of the horizons for \(\Lambda =0.01\) and \(\alpha =10000\); (g) typical behavior of the Hawking temperature for \(\Lambda =0\) and \(\alpha =0.3\); (h) typical behavior of the Hawking temperature for \(\Lambda =0.01\) and \(\alpha =10000\); (i) typical behavior of the quasi-local energy for \(\Lambda =0\) and \(\alpha =0.3\); (j) typical behavior of the quasi-local energy for \(\Lambda =0.01\) and \(\alpha =10000\); (k) typical behavior of the Gibbs free energy for \(\Lambda =0\) and \(\alpha =0.3\); (l) typical behavior of the Gibbs free energy for \(\Lambda =0.01\) and \(\alpha =10000\)

Full size image

From Eq. (75), the entropy of the BH (33) takes the form

$$\begin{aligned} S_+\approx \pi \, r_{+}{}^2\left( 1-\frac{\alpha }{r_{+}{}^4}\right) . \end{aligned}$$
(80)

Plots of the entropy (1) when \(\Lambda =0\) and \(\Lambda \ne 0\) are drawn in Fig. 3e, f, which indicate an increasing value for \(S_+\) when \(\Lambda =0\) and \(\Lambda \ne 0\).

From Eq. (74), the Hawking temperature of the BH (33) is calculated and we obtain

$$\begin{aligned} T_+\approx \frac{(3\Lambda r^6-r^4+3\alpha )(5\alpha -2r_+{}^4)}{8\pi r_+{}^9}. \end{aligned}$$
(81)

Plots of the entropy (81) when \(\Lambda =0\) and \(\Lambda \ne 0\) are drawn in Fig. 3g, h, which indicate a decreasing value for \(T_+\) when \(\Lambda =0\) and \(\Lambda \ne 0\).

From Eq. (76) we evaluate the local energy of BH (33) and obtain

$$\begin{aligned} E_{+}\approx \frac{21{r_{+}}^9+7\alpha {r_{+}}^5-21\Lambda {r_{+}}^{11}-126\alpha \Lambda {r_{+}}^7+378\Lambda \alpha ^2{r_{+}}^3+54\alpha ^2{r_{+}}-21\alpha ^2 {\mathcal M} }{42{r_{+}}^8}. \end{aligned}$$
(82)

Equation (82) shows that when \(\Lambda =\alpha =0\), we obtain \(E_{+}=\frac{r_{+}}{2}\), which is the energy of a spherically symmetric spacetime. Plots of Eq. (82) when \(\Lambda =0\) and \(\Lambda \ne 0\) are drawn in Fig. 3i, j, which also indicates positive increasing values for \(E_{+}\).

Finally, using Eqs. (74), (80), and (82) in (77), we evaluate Gibbs free energy as

$$\begin{aligned} G_{+}\approx \frac{42{r_{+}}^{12}+301\alpha {r_{+}}^8+42\Lambda {r_{+}}^{14}-84\alpha ^2{\mathcal M}{r_{+}}^3-330\alpha ^2{r_{+}}^4-945\alpha \Lambda {r_{+}}^{10}+1827\alpha ^2 \Lambda {r_{+}}^{6}+315\alpha ^3 }{168{r_{+}}^{11}}. \end{aligned}$$
(83)

The plots of these energy values are drawn in Fig. 3k, l when \(\Lambda =0\) and \(\Lambda \ne 0\), which indicate a positive increasing value for \(G_{+}\).

8.2 First law of thermodynamics of the BH solutions (33)

An important step for any BH solution is to check its validity for the first law of thermodynamics. Therefore, for the BH given by Eq. (33) the Smarr formula and the differential form for the first law of thermodynamics in the frame of f(R) gravity can be expressed as [150, 152]

$$\begin{aligned} M=2 \left( TS-PV \right) , \qquad \qquad \qquad \textrm{d}E=T\textrm{d}S+P\textrm{d}V, \end{aligned}$$
(84)

where S is the Hawking entropy, T is the Hawking temperature, P is the radial component of the stress-energy tensor that is used as thermodynamic pressure, i.e. \(P=T_r{}^r\mid _{\pm }\), and V is the geometric volume. The pressure, in the context of f(R) gravity, is determined as [150]

$$\begin{aligned} P=-\frac{1}{8\pi }\left\{ \frac{F}{{r_{+}}^2} +\frac{1}{2} \left( f(R)-RF \right) \right\} +\frac{1}{4}\left( \frac{2F}{r_{+}}+F'\right) T. \nonumber \\ \end{aligned}$$
(85)

Using Eq. (78), when \(\Lambda =0\), we obtain

$$\begin{aligned} M\approx \frac{1}{2}\left( r_{+}+\frac{\alpha }{3r_{+}{}^3}\right) . \end{aligned}$$
(86)

By calculating the necessary components of Eq. (84), we obtain

$$\begin{aligned} P_{+}&\approx -\frac{3}{16\pi \,r_{+}{}^2}\left( 1+\frac{14\alpha }{9r_{+}{}^4}\right) ,\qquad \qquad T_{+}\approx \frac{{r_{+}}^4-3\,\alpha }{4\pi {r_{+}}^5},\nonumber \\ S_{+}&\approx \frac{\pi \left[ {r_{+}}^4-\alpha \right] }{{r_{+}}^2},\qquad V=\frac{4}{3}\pi {r_{+}}^3. \end{aligned}$$
(87)

Using Eq. (87) in Eq. (84), we can prove that the first law of the BH (33) is verified when \(\Lambda =0\) and \(\alpha ^2=0\).

9 Discussion and conclusions

In this study, we focus on deriving an extension of the Schwarzschild BH solution in the framework of the f(R) amended gravitational theory. This so-called f(R) gravitational theory is a fourth-order derivative theory, and thus deriving an analytical solution in the realm of this theory is very difficult. To overcome this issue, we employed the trace equation of f(R) theory and solved it with respect to the arbitrary function f(R). By using this solution, we write the field equations of f(R) theory and apply them to a spherically symmetric spacetime that has unequal metric potentials and is of a radial coordinate, i.e., \(g_{tt}\ne g_{rr}\). The output differential equations are solved assuming the ansatzes as \(g_{tt}=\left( 1-\frac{2M}{r}\right) \,X(r)\,Y(r)\) and \(g_{rr}=\left( 1-\frac{2M}{r}\right) \,Y(r)\), where X(r) and Y(r) are two unknown functions of the radial coordinate. To be able to close the system, we assume the derivative of the \(F(r)=\frac{\textrm{d}f(R(r))}{\textrm{d}R(r)}=1-\frac{\alpha }{r^4}\), where \(\alpha \) is a dimensional constant. It is obvious from the assumption of F(r) that when \(\alpha =0\), we obtain \(F(r)=1\), which is the case of GR, and in that case we obtain \(X(r)=1\) and \(Y(r)=1\), and in turn we obtain the Schwarzschild solution, i.e., \(g_{tt}=g_{rr}=\left( 1-\frac{2M}{r}\right) \). In the general case, i.e., when \(F(r)=1-\frac{\alpha }{r^4}\), we solved the equations of motion of f(R) theory and derived the exact form of the metric potentials, that is, we derived the form of the two functions X(r) and Y(r).

To delve deep into the physics of this solution, we derive the asymptotic forms of \(g_{tt}\) and \(g_{rr}\). From this asymptote, we explicitly note that the BH solution of this study is completely different from the GR BH solution and coincides only when \(F=1\), i.e., \(\alpha =0\). Moreover, we write the line element of this BH and investigate whether it asymptotically behaves as (A)dS/dS spacetime. We calculate the asymptotic form of f(R) and show that it contains ultraviolet terms. We evaluate the invariants of such BH and investigate whether there is a true singularity as \(r\rightarrow 0\). Also, we show from these invariants that we have a strong BH compared with the Schwarzschild BH, and the source of this strength is the dimensional constant \(\alpha \). Also, we study the geodesic of this BH and derive the potential and the conserved quantities of energy and momentum. We reveal the behavior of these quantities as shown in Fig. 1. Additionally, we evaluate the geodesic deviations of this BH and obtain the condition of stability mathematically and graphically, as shown in Fig. 2.

Further checking the physics of this BH is carried out through the study of the thermodynamics of this BH by calculating its physical quantities of entropy, Hawking temperature, quasi-local energy, and Gibbs free energy, and derive their forms mathematically and draw them graphically. Additionally, we check the first law of thermodynamics and note that this BH verifies the first law. Finally, if we follow the procedure for odd perturbation discussed in [134], we can show that this BH is stable.

In summary, this research has brought to light a significant discovery: the expansion of the Schwarzschild BH is influenced primarily by the existence of higher-order gravity terms rather than because of a point mass at its center. The Schwarzschild BH is restored when the impact of these higher-order curvature terms diminishes.

To summarize our study, we derived a new BH solution in the frame of f(R) gravity and showed that its Ricci scalar is not constant. This BH is new, and its originality comes from the dimensional constant that involves \(\alpha \), which comes from our assumption of the first derivative of f(R), i.e., \(F(r)=\frac{\textrm{d}f(R(r))}{\textrm{d}R(r)}=1-\frac{\alpha }{r^4}\). We stress that the source of the gravitational field of this BH is not the gravitational mass of the Schwarzschild BH, but the contributions of the higher order of f(R). This means that the gravitational field reproduced from the higher-order f(R) gravitational theory is dominant in the Schwarzschild BH solution for the BH reproduced from f(R). Finally, can the procedure applied in this study be used to derive for the first time an extension of the Kerr solution in f(R) gravitational theory? This case needs further study and will be considered elsewhere.