Lepton $g-2$ and W-boson mass anomalies in the DFSZ axion model

Abstract

With regard to the leptonic magnetic dipole moment anomaly as well as the W-boson mass excess, we study the DFSZ axion model. Considering theoretical and experimental constraints, we show that the muon and electron $g-2$ anomalies can be explained within the parameter space of the model for extra Higgs bosons with mass spectra around the electroweak scale and for an almost equivalent contribution of one-and two-loop diagrams. A negative electron $g-2$ could be achieved by introducing heavy neutrinos. Furthermore, the W-boson mass excess can be consistently addressed within the mass range of the matter content testable at collider experiments.

1 Introduction

QCD axion models are well-motivated solutions to the strong CP problem of the Standard Model (SM) [1,2,3]. The axion appears as a pseudo-Nambu Goldstone boson from the spontaneous symmetry breaking of the $U(1)_{\textrm{PQ}}$ Peccei–Quinn (PQ) symmetry at high temperatures and gains a mass at lower scales around the QCD phase transition [4, 5]. The axion being neutral and long-lived, it is a viable candidate for cold dark matter. It could have been produced in the early universe by the misalignment mechanism or by decays of topological defects [6,7,8,9]. A review of different axion models and their cosmological implications can be found in Refs. [10, 11].

Although high-energy experiments have not reported so far any significant deviation from the SM, a set of experiments focusing on precision measurements may indicate anomalies in the SM requiring new physics. One of these high-precision experiments in particle physics measures the muon magnetic moment, $a_\mu \equiv (g_\mu -2)/2,$ where $g_\mu$ is the spin g factor of the muon. Fermi National Accelerator Laboratory (FNAL) has recently reported a large deviation from the SM prediction on $a_\mu$ [12], consistent with the previous measurement of Brookhaven National Laboratory (BNL) in 2006 [13]. The result of combining these measurements is

$$\begin{aligned} \Delta a_\mu \equiv a_\mu ^{\text {EXP}}-a_\mu ^{\text {SM}}=(251\pm 59)\times 10^{-11}, \end{aligned}$$

(1.1)

which shows a $4.2 \sigma$ discrepancy with the SM prediction [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34].

Moreover, improved measurements of the fine-structure constant $\alpha$ allow us to extract a value for the electron magnetic moment, $a_e,$ which shows a discrepancy with the SM prediction. Interestingly, there are two experiments whose results on $a_e$ are set in opposite directions. Based on the recoil frequency of $^{133}$Cs atoms at Berkeley [35], one has

$$\begin{aligned} \Delta a_e^{\text {B}}\equiv a_e^{\text {EXP}}-a_e^{\text {SM}}=(-87\pm 36)\times 10^{-14}, \end{aligned}$$

(1.2)

which features a $2.4\sigma$ discrepancy with the SM prediction [36, 37], while with $^{87}$Rb atoms, the result of the Laboratoire Kastler Brossel (LKB) [38] is

$$\begin{aligned} \Delta a_e^{\text {LBK}}\equiv a_e^{\text {EXP}}-a_e^{\text {SM}}=(48\pm 30)\times 10^{-14}, \end{aligned}$$

(1.3)

with a $1.6 \sigma$ deviation. We emphasize that even if both experiments show tension with respect to the SM in opposite directions, new physics may be required.

Additionally, another precise measured observable is the W-boson mass. Recently, the CDF-II experiment at Fermilab reported a new measurement of the W-boson mass, using data collected from 2002 to 2011 [39]

$$\begin{aligned} m_{W}^{\text {CDF-II}}=80.4335\pm 0.0094~\text {GeV}, \end{aligned}$$

(1.4)

which is in tension with the SM prediction $m_W^{{\textrm{SM}}} = 80.357 \pm 0.006$ GeV [40] about $7 \sigma$ and also differs from the previous average of PDG $m_{W}^{\textrm{PDG}} = 80.379 \pm 0.0012$ GeV [40]. Once again, if such a deviation is confirmed, new physics is required.¹

So far, a large number of different scenarios beyond the SM have been proposed to address the anomalies mentioned above (see, for example, Refs. [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66]). Here, alternatively, we employ the Dine–Fischler–Srednicki–Zhitnitsky (DFSZ) axion model [67, 68], which is an attractive framework that not only addresses the strong CP problem but also provides a viable dark matter candidate. The field content of the model, invariant under the global $U(1)_{\textrm{PQ}},$ includes a Peccei–Quinn complex scalar field and one additional Higgs doublet. We explore possible explanations for anomalous measurements and their phenomenological implications, restricting the parameter space of the model. Considering vacuum stability and perturbativity conditions as well as collider bounds on the mass of extra Higgs bosons [69, 70], we show that for Higgs fields with masses at the electroweak (EW) scale, the CDF-II W-boson mass anomaly and the anomalous muon magnetic moment can be explained. Furthermore, the measurement of the anomalous electron magnetic moment can be fitted in the case of a positive contribution. In the case of a negative $g_e-2,$ taking into account the bounds on charged lepton flavor decay processes such as $\mu \rightarrow e\, \gamma ,$ extra degrees of freedom (d.o.f.) are required; for example, a heavy neutrino contribution can be added, without spoiling the solutions to the W mass or $g_\mu -2.$

As we discussed, QCD axion is motivated as a solution to the strong CP problem and can be a candidate for dark matter. These are the low-energy phenomenological consequences of QCD axion models. Depending on the axion model, it can have different kinds of phenomenology at high energies. Here, our focus is on the DFSZ axion model to verify phenomenological effects imposed by possible explanations of the electron and muon magnetic moment and W-boson mass anomaly on the model.

In the next section, we introduce the model and discuss the physical d.o.f. and the mass spectrum. In Sect. 4, we discuss the oblique parameters, particularly the ${\mathcal {T}}$ parameter, and its impact on the W mass. Section 5 is devoted to the one- and two-loop-level contributions to the lepton magnetic moment. We conclude in Sect. 6.

2 The model

Regarding the smallness of the experimentally bounded CP-violating $\theta$ term in strong interactions, i.e. the strong CP problem, several QCD axion models, all based on a $U(1)_{{\textrm{PQ}}}$ symmetry, have been proposed. Different QCD axion models correspond to diverse realizations of the PQ symmetry under which the SM is not invariant. In particular, to absorb the $\theta$ term, independent chiral transformations of the u and d quarks are required [3]. The model can therefore be enlarged with a second Higgs doublet coupled to only the u- or to the d-quark types via Yukawa interactions [4, 5].

Moreover, the PQ symmetry could be spontaneously broken at an energy scale much higher than the EW scale, leading to the generation of a pseudo-Goldstone boson, the axion. By imposing astrophysical constraints, the symmetry-breaking scale is bounded to $10^8~{{\textrm{GeV}}}\lesssim f_a \lesssim 10^{17}$ GeV [11, 71, 72], where $f_a$ stands for the axion decay constant. This decoupling between the electroweak and PQ symmetry-breaking scales naturally occurs in the presence of a SM-singlet scalar field $\Phi .$ This kind of QCD axion model, which has such a field content, is called the DFSZ model.²

The Lagrangian of the model is given by

$$\begin{aligned}{} & {} {\mathcal {L}} \supset \frac{1}{2} \left| \partial _\mu \Phi \right| ^2 + \left( D_\mu H_d\right) ^{\dag } D^\mu H_d \nonumber \\{} & {} \qquad + \left( D_\mu H_u\right) ^\dag D^{\mu } H_u - V(\Phi , H_u, H_d), \end{aligned}$$

(2.1)

where $\Phi$ is the PQ scalar field, $H_u$ and $H_d$ denote the two Higgses, doublets under $SU(2)_L.$ The covariant derivative is defined as

$$\begin{aligned} D_\mu H_{d,u} \equiv \partial _\mu H_{d,u} - i\, g\, \tau \cdot W_\mu \, H_{d,u} -i\, g'\, Y\, B_\mu \, H_{d,u} ,\nonumber \\ \end{aligned}$$

(2.2)

where $W_\mu ^a$ and $B_\mu$ are the $SU(2)_L$ and $U(1)_Y$ gauge fields, respectively, whose coupling constants are denoted by g and $g',$ and $\tau _i$ correspond to the Pauli matrices. The scalar potential is given by

$$\begin{aligned}&V(\Phi , H_u, H_d) = \lambda _{\phi } \left( |\Phi |^{2} -V_{\phi }^{2}/2\right) ^{2} + \left| H_{d}\right| ^{2} \left( \kappa _{d}\, |\Phi |^{2} -\mu _{d}^{2}\right) \nonumber \\&\qquad + \left| H_{u}\right| ^{2} \left( \kappa _{u}\, |\Phi |^{2} - \mu _{u}^{2}\right) \nonumber \\&\qquad -\left( \kappa \, \Phi H_{u}^{\dagger }\, H_{d} + \text {H.c.}\right) + \lambda _{d} \left| H_{d}\right| ^{4} + \lambda _{u} \left| H_{u}\right| ^{4} \nonumber \\&\qquad + \lambda \left( \left| H_{u}\right| ^{2}\left| H_{d}\right| ^2-\left| H_{u}^{\dagger } H_{d}\right| ^{2} \right) . \end{aligned}$$

(2.3)

Finally, the Yukawa interactions are

$$\begin{aligned} y_u^{H_u}\, {\overline{Q}}_L\, {\widetilde{H}}_u\, u_R + y_d^{H_d}\, {\overline{Q}}_L\, H_d\, d_R + y_l^{H_d}\, {\overline{\Psi }}_{L_l}\, H_d\, l_R + \text {H.c.}\nonumber \\ \end{aligned}$$

(2.4)

where ${\widetilde{H}}_u \equiv -i\, \tau _2\, H^*_u.$ The model is invariant under the SM gauge symmetry group $SU(3)_C \otimes SU(2)_L \otimes U(1)_Y$ and under the $U(1)_{{\textrm{PQ}}},$ and therefore the PQ charges of the fields in this model can be obtained accordingly [75]. In fact, from the $\kappa$ term of Eq. (2.3) and the orthogonality between PQ and corresponding hypercharge currents [11], we obtain PQ charges of scalar fields as $X_{H_u}=\cos ^2\beta ,$ $X_{H_d}=-\sin ^2\beta ,$ and $X_{\Phi }=1.$ Moreover, supposing that left-handed fermions have no PQ charges, $X_{u_R}=X_{H_u},$ and $X_{d_R}=X_{l_R}=-X_{H_d}.$

The Higgs doublets can be expanded as [76]

$$\begin{aligned} H_{d} = \left( \begin{array}{l} \alpha _{+} \\ \alpha _{0} \end{array} \right) \quad \text {and}\quad H_{u}=\left( \begin{array}{l} \beta _{+} \\ \beta _{0} \end{array}\right) , \end{aligned}$$

(2.5)

and their vacuum expectation values (VEV) are given by $\langle \alpha _+\rangle = \langle \beta _+\rangle = 0,$ $\langle \alpha _0\rangle = v_d,$ $\langle \beta _0\rangle = v_u,$ with $v^2 \equiv v_d^2 + v_u^2,$ where $v \simeq 246$ GeV is the EW VEV. Furthermore, $\langle \Phi \rangle = v_\phi \sim f_a$ [11].

Using the minimization of the potential, three parameters $\mu _d,$ $\mu _u,$ and $V_{\phi },$ can be fixed (see Appendix A); therefore, in the scalar sector, the free parameters are $\lambda _{\phi },$ $\tan \beta = t_\beta \equiv v_u/v_d,$ $\kappa ,$ $\kappa _{d},$ $\kappa _{u},$ $\lambda _{u},$ $\lambda ,$ and $v_{\phi }.$ Finally, we note that $\lambda _d$ is fixed by imposing that one of the Higgs bosons has a mass of 125 GeV, as the SM Higgs.

2.1 Physical degrees of freedom in the scalar sector

In this section, we determine the mass spectrum of the scalar sector. From two complex doublets and a complex singlet, there are 10 d.o.f. Three combined Goldstone components are related to gauge bosons and are eliminated by gauge transformations, corresponding to longitudinal parts of the three massive gauge bosons [76, 77]. After rotating the interaction eigenstates (details of the transformation can be found in Appendix B), the mass eigenstates can be identified. The spectrum counts a pair of charged scalars $H^\pm ,$ a pseudoscalar A,  three CP-even scalars $h_i,$ and the axion field a.

First, the mass of the pseudoscalar Higgs A is given by

$$\begin{aligned} m_{A}^{2} = 8\, \frac{\kappa }{v_{\phi }}\left( s_{2 \beta }\, v^{2}+\frac{v_{\phi }^{2}}{s_{2 \beta }}\right) . \end{aligned}$$

(2.6)

From Eq. (2.3), the mass of the charged Higgs fields $H^\pm$ is

$$\begin{aligned} m_{H^{\pm }}^{2}=8\left( \lambda \, v^{2} + \frac{\kappa \, v_{\phi }}{s_{2 \beta }}\right) . \end{aligned}$$

(2.7)

Furthermore, there are three neutral scalar states, H,  S,  and $\varrho ,$ which are not mass eigenstates and should be expressed in the mass basis where the mass matrix can be diagonalized by a rotation matrix (Appendix C)

$$\begin{aligned} H=\sum _{i=1}^{3} R_{H i} h_{i}, \quad S=\sum _{i=1}^{3} R_{S i} h_{i}, \quad \varrho =\sum _{i=1}^{3} R_{\rho i} h_{i} , \end{aligned}$$

(2.8)

where $h_i$ are mass eigenstates and the rotation matrix, R,  and its components are expressed in Appendix C. The mass spectrum of these scalar fields, up to ${\mathcal {O}}(v^2/v_{\phi }^2),$ is

$$\begin{aligned} m_{h_{1}}^{2}&\simeq 32\, v^{2} \left( \lambda _{d}\, c_{\beta }^{4} + \lambda _{u}\, s_{\beta }^{4}\right) - \frac{16\, v^{2}}{\lambda _{\phi }} \left( \kappa _{d}\, c_{\beta }^{2}\right. \nonumber \\&\quad \left. + \kappa _{u}\, s_{\beta }^{2} - \frac{\kappa }{v_{\phi }}\, s_{2 \beta }\right) ^2, \nonumber \\ m_{h_{2}}^{2}&\simeq \frac{8\, \kappa }{s_{2 \beta }} v_{\phi } + 8\, v^{2}\, s_{2 \beta }^{2}\left( \lambda _{d} + \lambda _{u}\right) \nonumber \\&\quad - 4\, v^{2}\, \frac{\left[ (\kappa _{d} - \kappa _{u})\, s_{2 \beta } + 2\, \kappa \, c_{2 \beta } / v_{\phi }\right] ^{2}}{\lambda _{\phi }- 2\, \kappa /(v_{\phi }\, s_{2 \beta })} ,\nonumber \\ m_{h_{3}}^{2}&\simeq 4 \lambda _{\phi } v_{\phi }^{2} + 4 v^{2} \frac{\left[ (\kappa _{d}-\kappa _{u}) s_{2 \beta }+2 \kappa c_{2 \beta }/v_{\phi }\right] ^{2}}{\lambda _{\phi }-2 \kappa /(v_{\phi } s_{2 \beta })} \nonumber \\&\quad + \frac{16 v^{2}}{\lambda _{\phi }} \left( \kappa _{d} c_{\beta }^{2}+\kappa _{u} s_{\beta }^{2}-\kappa s_{2 \beta }/v_{\phi }\right) ^{2}. \end{aligned}$$

(2.9)

The lighter state $h_1$ is identified with the SM-like Higgs boson, while $h_2$ and $h_3$ are extra heavy neutral CP-even Higgs bosons.

We do not consider cases where the mass spectrum is decoupled from the EW energy scale, but cases that can address the aforementioned anomalous problems and lead to rather light masses for the Higgs fields, phenomenologically interesting for collider physics. In this sense, after fixing $t_{\beta },$ the mass spectrum of the Higgs fields depends mainly on $\kappa ,$ $\lambda ,$ and $\lambda _{\phi }.$ We consider $m_{h_1}$ as the SM Higgs and also fix $\lambda _{\phi } = 0.01$ that affects $m_{h_3}$ so that the very massive scalar field can be determined close to $v_\phi$ due to $v_\phi \gg v.$³ The case with $\lambda _\phi \rightarrow 0$ can lead to masses lighter than the SM Higgs mass. SM-like interactions of the Higgs, $h_1,$ with SM particles can also consistently be obtained, due to the relevant coefficient, a combination of $R_{H 1}\sim 1$ and $R_{S 1}$ proportional to $v^2/v_{\phi }^2,$ multiplied to SM Higgs couplings. For more details see Ref. [76].

3 Collider constraints

Constraints on the mass spectrum of extra Higgs fields in the framework of the Minimal Supersymmetric Standard Model (MSSM) [78] and two-Higgs-doublet models (2HDMs) [77] are extensively studied [40]. Regarding the mass of the charged Higgs boson, very light masses, $m_{H^{\pm }}\lesssim 80\,{\textrm{GeV}}$ have been excluded by LEP [79] and Tevatron [80]. Moreover, for $m_{H^{\pm }}<m_t$ (the top quark mass), the experimental lower bound from direct searches is $m_{H^{\pm }}>155\,{\textrm{GeV}}$ [40]. For mass ranges $m_{H^{\pm }}\sim 155{-}170\,{\textrm{GeV}},$ firm experimental analysis does not exist [81] and a reliable perturbative calculation of the charged Higgs boson production cross section must be performed. For $m_{H^{\pm }}>m_t,$ ATLAS and CMS have also been excluded regions of the parameter space of MSSM, $m_{H^{\pm }}< 180 (1100)\,{\textrm{GeV}},$ for $t_{\beta }=10 (60),$ with a certain luminosity [40]. This search is sensitive to the modeling of the top pair production background with extra partons and especially b-quarks.

Also, there have been numerous experimental searches at the LHC for a pseudo-scalar boson, excluding light pseudoscalar Higgs bosons $m_{A}\lesssim m_{h_1}/2$ [70]. In addition, in the context of MSSM, for heavy neutral/pseudo-scalar Higgs bosons in the $\tau \tau$ final state, the exclusion region is $m_A\lesssim 390 (1600)\,{\textrm{GeV}}$ for $t_{\beta }=10 (60)$ [40]. However, in the diphoton channel a slight excess has been observed by CMS at a mass of $95.3\,{\textrm{GeV}},$ consistent with the observed excess at LEP, with a local significance of $2.8\sigma$ and could not be ruled out by ATLAS at $95\%$ CL [40].

Experimental searches including extra Higgs production crucially depend on accurate theoretical predictions for inclusive cross sections. (For instance see Ref. [82] for precise predictions of pseudo-scalar inclusive cross section specially for the moderate mass range.) According to the matter content of our model and its parameter space, given additional decay channels, for instance $H^{\pm }\rightarrow aW^{\pm } ,$ $A\rightarrow a h_1 ,$ $h_2\rightarrow aa ,$ and $h_2\rightarrow aZ ,$ the bounds may somehow change.⁴ Here, aside from the exclusion region independent from $t_{\beta },$ i.e., $m_{H^{\pm }}\lesssim 155\,{\textrm{GeV}}$ and $m_{A}\lesssim m_{h_1}/2,$ we consider other mass values, provided that the model parameter $t_{\beta }$ is in the viable, allowed range. In the following calculations, we show that the anomalies may simultaneously be explained for $t_{\beta }>100.$

4 W-boson mass

In this section, we study the effects of new physics on the recently reported W-boson mass excess by analyzing the oblique parameters of this model [83, 84]. Some studies have already considered the impact of having a second Higgs doublet in the W-mass anomaly; see, e.g. Refs. [42, 43, 46, 48, 50, 51, 53,54,55,56,57,58, 60, 85]. The leading correction to the W-boson mass can be approximated as

$$\begin{aligned} \Delta m_W^2 \simeq \alpha \, \frac{c_W^4}{c_W^2-s_W^2}\, m_Z^2\, \Delta {\mathcal {T}}, \end{aligned}$$

(4.1)

where $\Delta {\mathcal {T}}$ is one of the Peskin–Takeuchi parameters, obtained by the following procedure. The one-loop corrected masses of the gauge bosons are given by

$$\begin{aligned} m_{W}^{2}&\simeq \frac{g^{2}\, v^{2}}{2}+\Pi _{W W}(0), \end{aligned}$$

(4.2)

$$\begin{aligned} m_{Z}^{2}&\simeq \left( g^{2} + {g'}^2\right) \frac{v^{2}}{2}+\Pi _{Z Z}(0), \end{aligned}$$

(4.3)

where $\Pi _{WW}(0)$ and $\Pi _{ZZ}(0)$ are the two-point functions of the gauge fields at zero-momentum transfer [76]. The deviation from the custodial symmetry can be parameterized as

$$\begin{aligned}{} & {} \rho \equiv \frac{m_{W}^{2}}{m_{Z}^{2}\, c_{W}^{2}} = \frac{m_{W(\text {tree})}^{2} + \Pi _{W W}(0)}{m_{Z(\text {tree})}^{2}\, c_{W}^{2} + \Pi _{Z Z}(0)\, c_{W}^{2}}\nonumber \\{} & {} \quad \simeq 1 + \frac{\Pi _{W W}(0)}{m_{W(\text {tree})}^{2}} - \frac{\Pi _{ZZ}(0)}{m_{Z(\text {tree})}^{2}}, \end{aligned}$$

(4.4)

where $m_{V (\text {tree})}^{2}$ is the mass at tree level of the gauge boson V,  and

$$\begin{aligned} \Delta \rho \equiv \frac{\Pi _{W W}(0)}{m_{W(\text {tree})}^{2}} - \frac{\Pi _{ZZ}(0)}{m_{Z(\text {tree})}^{2}}. \end{aligned}$$

(4.5)

Thus, $\Delta {\mathcal {T}} = \Delta \rho /\alpha$ is [76]

$$\begin{aligned} \Delta {\mathcal {T}}&= \frac{1}{16 \pi s_W^2m_W^2}\left[ m_{H^{\pm }}^{2}-\frac{v_{\phi }^{2}}{v_{\phi }^{2}+v^{2} s_{2 \beta }^{2}} f\left( m_{H^{\pm }}^{2}, m_A^2\right) \right. \nonumber \\&\quad \left. +\sum _{i=1}^{3} R_{S i}^{2}\left( \frac{v_{\phi }^{2}}{v_{\phi }^{2}+v^{2} s_{2 \beta }^{2}} f\left( m_A^{2}, m_{h_{i}}^{2}\right) -f\left( m_{H^{\pm }}^{2}, m_{h_{i}}^{2}\right) \right) \right] \nonumber \\&\simeq \frac{1}{16 \pi s_W^2m_W^2}\left[ m_{H^{\pm }}^{2}- f\left( m_{H^{\pm }}^{2}, m_A^2\right) \right. \nonumber \\&\quad \left. +\sum _{i=1}^{3} R_{S i}^{2}\left( f\left( m_A^{2}, m_{h_{i}}^{2}\right) -f\left( m_{H^{\pm }}^{2}, m_{h_{i}}^{2}\right) \right) \right] , \end{aligned}$$

(4.6)

where $R_{Si}$ is given in Appendix C, $f(x, y) \equiv x\, y\, \ln (x/y)/(x-y)$ and $f(x, x) = x.$ As a result, a positive value of $\Delta {\mathcal {T}}$ can explain the W-boson mass excess. We calculate the W-boson mass excess as a function of $m_{H^{\pm }},$ fixing all other parameters and masses. For a given value of $m_{A}$ and $m_{h_2} ,$ the excess, including the CDF-II measurement, can be justified within $m_{H^{\pm }}/m_{A}\gtrsim 1$ or in some regions for $m_{H^{\pm }}/m_{A}\lesssim 1,$ except for $m_{H^{\pm }}=m_{A},$ $m_{h_2}$ where $\Delta {\mathcal {T}}=0 .$ Note that within the considered parameter space the $h_3$ contribution is negligible. In this case, the low-energy effective theory would be a 2HDM model that has the advantage of avoiding the strong CP problem thanks to the QCD axion. To relate the parameters of the DFSZ potential to those of a 2HDM, see Ref. [76]. Also, in the whole studied problems, we also subtract the SM-like Higgs contribution in the calculation.

As we shall discuss in the following sections, the region of the parameter space that fits the lepton $g_l-2$ anomalies corresponds to small values of $\kappa ,$ $\kappa _{d}$ and $\kappa _{u},$ therefore, we fix $\kappa _{d} = \kappa _{u} = v^2 /v_\phi ^2$ and $\kappa = {\tilde{\kappa }}\, v^2 / v_\phi$ with ${\tilde{\kappa }} < 1.$⁵ Furthermore, considering vacuum stability conditions (Appendix A), we impose perturbativity criteria as $\lambda ,\, \lambda _{d,u}\lesssim 4\pi .$ Therefore, in Fig. 1, we set other parameters as follows. Taking into account $m_{h_1}=125$ GeV, we can find $\lambda _{d,u} ,$ fixing $t_{\beta }$ and $\lambda _{d}-\lambda _{u}.$ In this sense, since we obtain $\lambda _{d}-\lambda _{u}\approx \lambda _{d},$ we can fix $\lambda _{d}-\lambda _{u}< 4\pi .$ In our calculations, we take $\lambda _{d}-\lambda _{u}=5.$ Within the considered parameter values, we can approximately express the mass terms of scalar fields, Eq. (2.9), with their first term for each relation.

Additionally, based on the perturbativity constraints from the Yukawa sector Eq. (2.4), we consider a conservative upper bound $t_{\beta }\le 300.$ According to the mass relation of the scalar fields, $m_{h_3},$ $m_{h_2},$ and $m_{A}$ are also determined by fixing $\lambda _{\phi },$ and then $\kappa .$ Thus, we can plot $m_{W}$ as a function of $m_{H^{\pm }}.$ We consider $m_{H^{\pm }}$ as a variable, although its different values can be obtained by fixing $\lambda$ and ${\tilde{\kappa }}.$ As shown in Fig. 1, we can obtain the W-boson mass excess within the parameter space of the theory, showing by three different benchmarks for $\kappa _{d} = \kappa _{u} = v^2 /v_\phi ^2,$ $m_{h_1}=125$ GeV, $\lambda _{d}-\lambda _{u}=5,$ $\lambda _{\phi }=0.01,$ $v_{\phi }=10^9$ GeV and three different values of $t_{\beta }=10, 200, 300$ and ${\tilde{\kappa }}=0.032, 0.00035, 0.0007$ respectively, which are corresponded to $\{m_{A}=280$ GeV, $m_{h_2}=417$ GeV, $m_{h_3}=0.2 v_{\phi }\},$ $\{m_{A}=130$ GeV, $m_{h_2}=131$ GeV, $m_{h_3}=0.2 v_{\phi }\},$ and $\{m_{A}=226$ GeV, $m_{h_2}=226$ GeV, $m_{h_3}=0.2 v_{\phi }\}.$

Fig. 1

The W-boson mass $m_{W}$ is shown as a function of $m_{H^{\pm }},$ for $\kappa _{d} = \kappa _{u} = v^2 /v_\phi ^2,$ $m_{h_1}=125$ GeV, $\lambda _{d}-\lambda _{u}=5,$ $\lambda _{\phi }=0.01,$ $v_{\phi }=10^9$ GeV and three different values of $t_{\beta }=10, 200, 300$ and ${\tilde{\kappa }}=0.032, 0.00035, 0.001$ respectively. The relevant W-boson mass excess explanation with larger $m_{H^{\pm }}$ can be found with larger ${\tilde{\kappa }}$

5 Lepton $g_l - 2$ anomalies

In this section, we first compute and discuss the analytical expressions for the lepton $g_l - 2$ anomalies, and then we proceed to calculate the magnetic moment of the muon and electron. On the basis of Lorentz covariance and gauge symmetry, the vertex of the QED interaction of a lepton can be expressed as

$$\begin{aligned} {\bar{l}}\left( p'\right) \, \Gamma ^\mu \, l\left( p\right) = {\bar{l}}\left( p'\right) \left[ \gamma ^\mu \, F_1\left( q^2\right) + \frac{i\, \sigma ^{\mu \nu }\, q_\nu \, F_2\left( q^2\right) }{2\, m_l}\right] l\left( p\right) ,\nonumber \\ \end{aligned}$$

(5.1)

where $F_1(q^2)$ is related to the electric charge, and the lepton magnetic moment is defined as $a_l = F_2(0).$ Here, we calculate different $\Delta a_l$ contributions from the model.

Regarding the Yukawa couplings, using a unitary transformation on the charged leptons, these Yukawa coupling matrices can be diagonalized, ${\tilde{y}}_l ,$ so that from Eqs. (2.4) and (B.4), the Yukawa interactions of the leptonic sector, contributing to $a_{l},$ at one-loop level, can be expressed as

$$\begin{aligned} -{\mathcal {L}}_{Y}^{l}\supset -\frac{m_{l}}{v}\left( H\, {\bar{l}}\, l - t_{\beta }\, S\, {\bar{l}}\, l - i\, t_{\beta }\, \tilde{A}\, {\bar{l}}\, \gamma _{5}\, l\right) . \end{aligned}$$

(5.2)

Therefore, from Eqs. (B.7) and (2.8C.10) for mass eigenstates we obtain the one-loop amplitude, Fig. 2, as follows (checked by using Package-X [87])

$$\begin{aligned} \Delta a_{l}^{1L}= & {} \frac{m_{l}^2}{16 \pi ^{2}\, v^2} \left[ \sum _{i=1}^3 \left( R^2_{H_i} + t_{\beta }^{2}\, R^2_{S_i}\right) \, F(x_{h_i}) \right. \nonumber \\{} & {} \left. + \frac{t_{\beta }^{2}\, v_{\phi }^{2}}{v_{\phi }^{2} + v^{2}\, s_{2 \beta }^{2}}\, F(x_{A})\right] , \end{aligned}$$

(5.3)

where $x_{h_i}=m_{l}/m_{h_i},$ and $x_{A}=m_{l}/m_{A}.$⁶ The loop functions obtained, F(x) and $F_{H^{\pm }}(x, z)$ are given in Appendix D.

Fig. 2

One-loop Feynman diagrams contributing to $g_l - 2$ from Higgs fields

According to Eq. (2.4), the so-called Barr-Zee two-loop amplitudes can be obtained [89,90,91], where the dominant contribution, Fig. 3, is given by

$$\begin{aligned} \Delta a_{l}^{2L}= & {} \sum _{f} \frac{\alpha \, m_l^2}{4 \pi ^3\, v^2}\, N_C^f\, Q_f^2 \left[ \sum _{i=1}^3 \left( R^2_{H_i}\, \zeta _{f,l}^H + R^2_{S_i}\, \zeta _{f,l}^S\right) {\mathcal {F}}\left( \omega _{h_i}\right) \right. \nonumber \\{} & {} \left. + \frac{\zeta _f^A\, v_\phi ^2}{v_\phi ^2 + v^2\, s_{2 \beta }^2} \tilde{{\mathcal {F}}}\left( \omega _A\right) \right] , \end{aligned}$$

(5.4)

where $N_C^f$ is the number of colors and $Q_f$ is the electric charge. Note that the two-loop contribution is at the $\alpha$ and $\tilde{y}_l^2$ level. We consider the dominant contribution from the t and b quarks, and therefore $\zeta _{t,l}^H=\zeta _{b,l}^H=1,$ $\zeta _{t,l}^{S,A}=-1,$ $\zeta _{b,l}^{S,A}=t_{\beta }^{2}.$ Also, $\omega _{h_i}=m_f^2/m_{h_i}^2,$ $\omega _{h_i}=m_f^2/m_{A}^2.$ The functions ${\mathcal {F}}(\omega )$ and $\tilde{{\mathcal {F}}}(\omega )$ are defined in Appendix D.

Fig. 3

The Barr-Zee two-loop diagram contributing to $g_l - 2$

5.1 Muon $g_\mu - 2$ anomaly

Having obtained analytical formulas for $g_l - 2,$ we investigate possible solutions to the anomalous magnetic moment of the muon and for the recently measured $\Delta a_\mu$ in Eq. (1.1). We show that the observed $\Delta a_\mu$ can be obtained for a range of $t_{\beta }$ and small values of $\kappa ,$ $\kappa _{d},$ and $\kappa _{u},$ which is also consistent with the expansion of the scalar field mass spectra in terms of $v/v_\phi .$ In Fig. 4, we fix $\kappa _{d}=\kappa _{u}=v^2/v_\phi ^2,$ $m_{h_1}=125$ GeV, $\lambda _{\phi }=0.01,$ $\lambda _{d}-\lambda _{u}=5,$ $v_{\phi }=10^9$ GeV and obtain $\Delta a_\mu$ for a range of $\kappa$ and some representative values of $t_{\beta }$ that simultaneously determine the value of $m_{h_3},$ $m_{h_2}$ and $m_{A},$ showing in terms of $m_{A}.$

As it can be seen in Fig. 4, we can find the observed anomaly for a range of $t_{\beta }$ values. Taking into account the bounds from colliders on $m_{A}\gtrsim m_{h_1}/2$ [70], in addition to the small $t_{\beta },$ we can find the observed $\Delta a_\mu$ for $t_{\beta }\gtrsim 100.$⁷ It should be noted that for $1\lesssim t_{\beta }\lesssim 5$ the two-loop Barr-Zee contribution is dominated, whereas for other values of $t_{\beta }$ the one- and two-loop contributions, which are at the same order in $\tilde{y}_l,$ are almost equivalent. Additionally, in the small values of $t_{\beta },$ the top quark in the two-loop diagram contributes predominantly, while in the large values of $t_{\beta },$ the dominant contribution comes from the bottom quark. Furthermore, with $\lambda _{d}-\lambda _{u}\lesssim 0.2,$ the result of interest is obtained only for large $t_{\beta }.$

Fig. 4

For $\kappa _{d}=\kappa _{u}=v^2/v_\phi ^2,$ $m_{h_1}=125$ GeV, $\lambda _{d}-\lambda _{u}=5,$ $\lambda _{\phi }=0.01,$ $v_{\phi }=10^9$ GeV, and different values of $t_{\beta },$ we show that the observed $\Delta a_\mu$ can be obtained, plotting as a function of $m_{A}.$ The gray area shows the excluded region based on the bound $m_{A}\gtrsim m_{h_1}/2$ [70]

5.2 Electron $g_e - 2$ anomaly

As already mentioned, due to the discrepancy in the measurement of $\alpha$ of Berkeley and LKB experiments, two different values have been reported for $\Delta a_e,$ with opposite signs. Although results of the two experiments are rather inconsistent, we also study the averaged value case, combing the two results [94]

$$\begin{aligned} \Delta a_e^{\text {Avg}}=(-2\pm 2.2)\times 10^{-13}. \end{aligned}$$

(5.5)

We first try to explore possible explanations for $\Delta a_e^{\text {LBK}}$ and $\Delta a_e^{\text {Avg}}.$ We then study the physics which leads to the explanation of $\Delta a_e^{\text {B}},$ considering the constraints imposed by charged lepton flavor violation decays.

5.2.1 $\Delta a_e^{\text {LBK}}$

According to the LKB experiment and its result, Eq. (1.3), and because of the muon and electron mass difference, $m_e/m_{\mu }\sim 5\times 10^{-3},$ it is expected to obtain positive $\Delta a_e$ with the similar benchmark chosen for the case $\Delta a_\mu .$ Therefore, as shown in Fig. 5, we can find that $\Delta a_e^{\text {LBK}}$ can be obtained as a function of $m_A$ and $t_{\beta }.$ It is shown that $\Delta a_e^{\text {LBK}}$ can be explained for $1\lesssim t_{\beta }\lesssim 3$ where the two-loop Barr-Zee contribution is dominated, while for large $t_{\beta },$ this is fulfilled for $t_{\beta }\gtrsim 500.$ In these regions of the parameter space, based on our previous discussion, both the W-boson mass and $\Delta a_\mu$ anomalies can be explained. However, as can be seen from Figs. 4 and 5, the range of $m_A$ values explaining $\Delta a_e^{\text {LBK}}$ and $\Delta a_\mu$ is different and thus both cannot be simultaneously explained.

Fig. 5

Similar to values chosen for parameters in the Fig. 4, for different values of $t_{\beta },$ we show that the observed $\Delta a_e^{\text {LBK}}$ can be obtained with respect to $m_{A}$

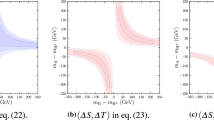
As shown in Fig. 6, we also find that $\Delta a_e^{\text {Avg}}$ can be obtained within the parameter space of the model. Interestingly, given the averaged value measured for the electron magnetic moment, in addition to the electron magnetic moment, the W-boson mass, and muon magnetic moment anomalies can be simultaneously explained for $t_{\beta }\gtrsim 120.$ For instance with the following benchmark, for $\kappa _{d} = \kappa _{u} = v^2 /v_\phi ^2,$ $m_{h_1}=125$ GeV, $\lambda _{d}-\lambda _{u}=5,$ $\lambda _{\phi }=0.01,$ $v_{\phi }=10^9$ GeV, $\lambda =0.048,$ ${\tilde{\kappa }}=0.00035$ and $t_{\beta }=200,$ one can obtain $m_W\simeq 80.44$ GeV, $\Delta a_\mu \simeq 2.34\times 10^{-9},$ and $\Delta a_e^{\text {Avg}}\simeq 0.17\times 10^{-13}.$ Also, as another example with the same parameters except for $\tan \beta =300$ and ${\tilde{\kappa }}= 0.0007,$ we find $m_W\simeq 80.43$ GeV, $\Delta a_\mu \simeq 2.08\times 10^{-9},$ and $\Delta a_e^{\text {Avg}}\simeq 0.16\times 10^{-13}.$ These benchmark points are shown in Fig. 7 with red and green color, respectively.

Fig. 6

Similar to values chosen for parameters in the Fig. 4, for different values of $t_{\beta },$ we show that $\Delta a_e^{\text {Avg}}$ can be obtained, plotting as a function of $m_{A}.$ The whole range of $\Delta a_e^{\text {Avg}}$ axis in this plot is allowed based on the average experimental bound. Because of the obtained positive results, negative values of Eq. (5.5) in the $\Delta a_e^{\text {Avg}}$ axis are not shown

Fig. 7

Benchmark points, associated with $t_{\beta }=200$ (red) and $t_{\beta }=300$ (green), are represented, satisfying different experimental bounds for $M_{\textrm{W}},$ $\Delta a_{\mu }$ and $\Delta a_e^{\text {Avg}}$ discussed in previous sections. Also, different experimental constraints are shown in three panels

5.2.2 $\Delta a_e^{\text {B}}$

As we discussed in the previous section, the parameter space of the model in which the W-boson mass and $\Delta a_\mu$ anomalies can be explained gives rise to a positive electron $g-2.$ Therefore, to explain the case of negative electron magnetic moment, Eq. (1.2), the mentioned model should be extended. Here we consider the model supplemented with heavy RH neutrinos, which are PQ charged and SM singlet, and study their contribution to the lepton $g_l - 2.$

The Lagrangian for right-handed neutrinos is given by

$$\begin{aligned} {\mathcal {L}}_{\mathcal {N}}{} & {} = {\overline{N}}_{R_{\alpha }}i\partial _\mu N_{R_{\alpha }}-m_{N_{R_{\alpha }}}{\overline{N}}_{R_{\alpha }} N_{R_{\alpha }}^c- y_{N_{\alpha }}^l{\overline{\Psi }}_{L_l} {\widetilde{H}}_d N_{R_{\alpha }}\nonumber \\{} & {} \quad +\text {H.c.} , \end{aligned}$$

(5.6)

where $N_{R_{\alpha }}$ are RH neutrinos. Then, the Yukawa interaction of the charged Higgs and RH neutrinos can be expressed as⁸

$$\begin{aligned} \sqrt{2}\, t_{\beta }\, y_{N_{\alpha }}^l\, H_{+}\, {\overline{l}}\, P_{R}\, N_{\alpha }+ \text {H.c.} \end{aligned}$$

(5.7)

Fig. 8

One-loop Feynman diagrams contributing to $(g_l-2)$ from charged Higgs fields and heavy neutrinos

Therefore, according to the relevant Feynman diagram, Fig. 8, an additional one-loop amplitude should be calculated and (checked by using Package-X [87]) the result would be as follows

$$\begin{aligned} \Delta a_{l}^{1L} = \sum _{\alpha =1}^{n_R} \frac{t_{\beta }^{2}\,\left( y_{N_{\alpha }}^l\right) ^{2}}{8\pi ^{2}}F_{H^{\pm }}(x_{H^{\pm }},z_{H^{\pm }}), \end{aligned}$$

(5.8)

where $x_{H^{\pm }}=m_{l}/m_{H^{\pm }},$ $z_{H^{\pm }}=m_{N_{R_{\alpha }}}/m_{H^{\pm }},$ and $n_R$ is the number of RH neutrinos. In our calculations, we assume $n_R=3$ and the same properties for all generations.

Since this additional contribution, Eq. (5.8), is negative, its effect on the muon magnetic moment should also be noted. For very heavy RH neutrinos, the contribution of this term is negligible. However, as shown in Fig. 9, for $y_N^{\mu }\gtrsim 0.01$ and sufficiently light RH neutrinos, $\Delta a_\mu$ can be negative, and hence we consider it $y_N^{\mu }< 0.01$ in the calculations.

Fig. 9

For $\kappa _{d}=\kappa _{u}=v^2/v_\phi ^2,$ $m_{h_1}=125$ GeV, $\lambda _{\phi }=0.01,$ $\lambda _{d}-\lambda _{u}=5,$ $v_{\phi }=10^9$ GeV, $t_{\beta }= 200,$ $m_{A}=130$ GeV and $y_N^{\mu }= 0.01,$ we find $\Delta a_\mu$ as a function of $m_{N_{R}}$ and $m_{H^{\pm }}.$ The colored regions show different values of the muon magnetic moment which could be even negative for small values of $m_{N_{R}}$ with $y_N^{\mu }= 0.01.$ For $y_N^{\mu }< 0.01$ the negative contribution, Eq. (5.8), to $\Delta a_\mu$ would be negligible. The region on the left of dashed grey line is excluded by the PDG $(g-2)_{\mu }$ bound

Before proceeding to calculate the electron magnetic moment for this case, we first discuss another constraint. Charged lepton flavor violations are highly constrained and the bound on the branching ratio of the decay $\mu \rightarrow e\gamma$ is more severe [95]

$$\begin{aligned} {{\textrm{Br}}}(\mu \rightarrow e\gamma )<4.2\times 10^{-13}. \end{aligned}$$

(5.9)

Thus, we can constrain the model as follows

$$\begin{aligned} {\textrm{Br}}(\mu \rightarrow e\gamma )\sim \frac{96\pi ^3\alpha \, v^4}{m_\mu ^4}a_{\mu e}^2, \end{aligned}$$

(5.10)

where

$$\begin{aligned} a_{\mu e}=\sum _{\alpha =1}^{n_R} \frac{t_{\beta }^{2}\,y_{N_{\alpha }}^{\mu }y_{N_{\alpha }}^e}{8\pi ^{2}}{\mathcal {F}}_{H^{\pm }}, \end{aligned}$$

(5.11)

and the function obtained ${\mathcal {F}}_{H^{\pm }}$ is given in Appendix D.⁹ According to Eq. (5.9), we should have $|a_{\mu e}|<2.5\times 10^{-14}.$ To pass the flavor violation decay bound, based on the previous estimation on $y_N^{\mu }< 0.01,$ with calculating $a_{\mu e},$ the hierarchy $y_N^{\mu }\ll y_N^{e}$ can be imposed, taking $y_N^{e}< 4\pi .$ For example, in Fig. 10, we show that $|a_{\mu e}|<2.5\times 10^{-14}$ can be obtained for $y_N^{e}\le 0.2$ and $y_N^{\mu }= 10^{-7}.$

Fig. 10

For $\kappa _{d}=\kappa _{u}=v^2/v_\phi ^2,$ $m_{h_1}=125$ GeV, $\lambda _{\phi }=0.01,$ $\lambda _{d}-\lambda _{u}=5,$ $v_{\phi }=10^9$ GeV, $t_{\beta }= 200,$ $m_{A}=130$ GeV, $m_{H^{\pm }}=160$ GeV, and $y_N^{\mu }= 10^{-7},$ we show that $|a_{\mu e}|<2.5\times 10^{-14}$ can be obtained, plotting as a function of $m_{N_R}$ and $y_N^{e}.$ All colored regions are consistent with the bound

Considering such bounds on the parameters, we obtain the electron magnetic moment and if $\Delta a_e^{\text {B}}$ is the case, we find that taking $y_N^{e}<4\pi ,$ the measured quantity can be obtained for $m_{N_R}\lesssim 200$ TeV. In Fig. 11, we show the result for $y_N^{e}\le 0.2.$

Fig. 11

For $\kappa _{d}=\kappa _{u}=v^2/v_\phi ^2,$ $m_{h_1}=125$ GeV, $\lambda _{\phi }=0.01,$ $\lambda _{d}-\lambda _{u}=5,$ $v_{\phi }=10^9$ GeV, $t_{\beta }= 200,$ $m_{A}=130$ GeV, and $m_{H^{\pm }}=160$ GeV, $\Delta a_e^{\text {B}}$ as a function of $m_{N_{R}}$ and $y_{N}^{e}$ is shown. The colored regions show different negative values of the electron magnetic moment

6 Conclusion

Recent measurements of the muon magnetic moment, the W-boson mass, and their deviation from the SM prediction can imply new physics beyond the SM. In this paper, in light of these observations we have studied a QCD axion model, enjoying the PQ symmetry, as an attractive framework that can address other SM shortcomings including the strong CP and the DM problem.

We considered the DFSZ axion model and calculated loop-level diagrams that contribute to the muon and the electron magnetic moment, and W-boson mass. Considering the lower bound on the mass of charged Higgs, we have shown that the CDF-II W boson mass excess can be addressed within the parameter space of the model, except for the case $m_{H^{\pm }}= m_A,$ $m_{h_2} .$ We have also shown that the positive muon magnetic moment $\Delta a_\mu$ can be obtained for a range of $t_{\beta }$ values with a mass range of extra Higgs bosons at the EW scale, respecting the direct collider bound on the pseudoscalar field and also theoretical constraints.

Regarding the electron $g-2,$ there are Berkeley and LKB experiments whose measurements are set in opposite directions. We showed that $\Delta a_e^{\text {LBK}}$ can be explained within a different region of the parameter space allowed for $\Delta a_\mu .$ However, we found that considering the averaged value of the two experiments, the three anomalies can be simultaneously explained. The electron magnetic moment measured by another experiment at Berkeley, $\Delta a_e^{\text {B}},$ is of a different sign and the physics that explains $\Delta a_\mu$ and the W-boson mass excess leads to a positive electron $g-2.$ To address $\Delta a_\mu ,$ $\Delta a_e^{\text {B}},$ and the W-boson mass anomalies simultaneously, we extended the model with heavy RH neutrinos. Taking into account the flavor violation decay bounds, we found that heavy neutrino-charged Higgs interactions contributing to one-loop diagrams that can be responsible for the negative $\Delta a_e$ with heavy neutrinos masses up to 200 TeV.

Appendices

Appendix A: Minimization and vacuum stability conditions

We can use the minimization of the potential, Eq. (2.3), and remove three parameters $\mu _{d} ,$ $\mu _{u}$ and $V_{\phi } ,$ expressing in terms of free parameters as follows

$$\begin{aligned}&2\lambda _{d} v^{2} c_{\beta }^{2}-\mu _{d}^{2}+\frac{v_{\phi }^{2}}{2}\left( \kappa _{d}-\frac{\kappa \tan \beta }{v_{\phi }}\right) =0, \end{aligned}$$

(A.1)

$$\begin{aligned}&2\lambda _{u} v^{2} s_{\beta }^{2}-\mu _{u}^{2}+\frac{v_{\phi }^{2}}{2}\left( \kappa _{u}-\frac{\kappa }{v_{\phi }\tan \beta }\right) =0, \end{aligned}$$

(A.2)

$$\begin{aligned}&\lambda _{\phi }\left( v_{\phi }^{2}-V_{\phi }^{2}\right) +2 v^{2}\left( \kappa _{d} c_{\beta }^{2}+\kappa _{u} s_{\beta }^{2}-\frac{\kappa s_{2 \beta }}{v_{\phi }}\right) =0 . \end{aligned}$$

(A.3)

Assuming that $\kappa _{d},$ $\kappa _{u}$ and $\kappa$ are sufficiently small and do not affect the vacuum stability conditions obtained from other quartic terms of the potential, we have

$$\begin{aligned}{} & {} \lambda _{\phi }>0, \quad \lambda _{d}>0, \quad \lambda _{u}>0 ,\nonumber \\{} & {} \lambda +2\sqrt{\lambda _{d}\lambda _{u}}>0 . \end{aligned}$$

(A.4)

Appendix B: Rotations for the Higgs fields

With the following rotated Higgs doublets, one can find the direction by which unphysical components are removed

$$\begin{aligned}{} & {} H_d' = c_\beta H_{d}+s_{\beta } H_{u} \nonumber \\{} & {} \quad = \frac{1}{\sqrt{2}} \left( \begin{array}{c} c_{\beta }\, \alpha ^{+} + s_{\beta }\, \beta ^{+} \\ c_{\beta } {\text {Re}} \left[ \alpha _{0}\right] + s_{\beta } {\text {Re}}\left[ \beta _{0}\right] + i \left( c_{\beta } {\text {Im}}\left[ \alpha _{0}\right] + s_{\beta } {\text {Im}}\left[ \beta _{0}\right] \right) \end{array} \right) ,\nonumber \\ \end{aligned}$$

(B.1)

where $c_{\beta } \equiv \cos \beta$ and $s_{\beta } \equiv \sin \beta .$ The upper components are combinations absorbed by $W^\pm$ and the real part is the component with non-zero vev, thus $H_d'$ has the structure of SM doublet so that

$$\begin{aligned} \langle c_{\beta } {\text {Re}}\left[ \alpha _{0}\right] +s_{\beta } {\text {Re}}\left[ \beta _{0}\right] \rangle =c_{\beta }v_d+s_{\beta }v_u=v \end{aligned}$$

(B.2)

and $\langle H+v\rangle =v.$ Also, the other rotated doublet would be

$$\begin{aligned}{} & {} H_u' = -s_{\beta } H_{d}+c_{\beta } H_{u}\nonumber \\{} & {} \quad =\frac{1}{\sqrt{2}}\left( \begin{array}{c} -s_{\beta } \alpha ^{+}+c_{\beta } \beta ^{+} \\ -s_{\beta } {\text {Re}}\left[ \alpha _{0}\right] +c_{\beta } {\text {Re}}\left[ \beta _{0}\right] +i\left( -s_{\beta } {\text {Im}}\left[ \alpha _{0}\right] +c_{\beta } {\text {Im}}\left[ \beta _{0}\right] \right) \end{array}\right) ,\nonumber \\ \end{aligned}$$

(B.3)

whose charged components denote the charged Higgs $H^{\pm }$ and the real neutral component is a scalar Higgs S such that $\langle S\rangle =\langle -s_{\beta } {\text {Re}}\left[ \alpha _{0}\right] +c_{\beta } {\text {Re}}\left[ \beta _{0}\right] \rangle =0.$ Therefore, the gauge-redefined doublets can be expressed as

$$\begin{aligned} H_{d}&=c_{\beta } H_{d}^{\prime }-s_{\beta } H_{u}^{\prime }=\frac{1}{\sqrt{2}}\left( \begin{array}{c} -\sqrt{2} s_{\beta } H^{+} \\ \left( v+H\right) c_{\beta }-s_{\beta }\left( S+i \tilde{A}\right) \end{array}\right) ,\end{aligned}$$

(B.4)

$$\begin{aligned} H_{u}&=s_{\beta } H_{d}^{\prime }+c_{\beta } H_{u}^{\prime }=\frac{1}{\sqrt{2}}\left( \begin{array}{c} \sqrt{2} c_{\beta } H^{+} \\ \left( v+H\right) s_{\beta }+c_{\beta }\left( S+i \tilde{A}\right) \end{array}\right) . \end{aligned}$$

(B.5)

Although $\tilde{A}$ remains after gauge redefinition, the field is not yet physical. Moreover, from $\phi =v_{\phi }+\varrho +i\tilde{G},$ $\tilde{G}$ is another non-physical d.o.f. whose combination with $\tilde{A}$ identifies the physical one in the pseudoscalar sector [76]. In addition to the massless eigenstate, the axion resulting from the PQ current is

$$\begin{aligned} a=\frac{ v_{\phi } \tilde{G}+v s_{2\beta } \tilde{A}}{\sqrt{ v_{\phi }^{2}+v^{2} s_{2\beta }^2}} . \end{aligned}$$

(B.6)

There is also a massive pseudoscalar eigenstate, evident from the cubic term in the potential, as

$$\begin{aligned} A=\frac{ v_{\phi } \tilde{A}-v s_{2\beta } \tilde{G}}{\sqrt{ v_{\phi }^{2}+v^{2} s_{2\beta }^2}}. \end{aligned}$$

(B.7)

Appendix C: The mass matrix of neutral scalar fields

The mass matrix of the neutral CP-even scalar fields is given by

$$\begin{aligned} M=\left( \begin{array}{ccc} 32 v^2\left( \lambda _d c_\beta ^4+\lambda _u s_\beta ^4\right) &{} M_{12} &{} M_{13} \\ M_{21} &{} \frac{8 \kappa v_\phi }{s_{2 \beta }}+8 v^2\left( \lambda _d+\lambda _u\right) s_{2 \beta }^2 &{} M_{23} \\ M_{31} &{} M_{32} &{} 4\lambda _\phi v_\phi ^2 \end{array}\right) ,\nonumber \\ \end{aligned}$$

(C.1)

where

$$\begin{aligned} M_{12}= & {} M_{21}=16 v^2\left( -\lambda _d c_\beta ^2+\lambda _u s_\beta ^2\right) s_{2 \beta }, \end{aligned}$$

(C.2)

$$\begin{aligned} M_{13}= & {} M_{31}=8 v v_\phi \left( \kappa _{d} c_\beta ^2+\kappa _{u} s_\beta ^2-\kappa s_{2 \beta }/v_\phi \right) , \end{aligned}$$

(C.3)

$$\begin{aligned} M_{23}= & {} M_{32}=-4v v_\phi \left[ (\kappa _{d}-\kappa _{u}) s_{2 \beta }+2 \kappa c_{2 \beta }/v_\phi \right] . \end{aligned}$$

(C.4)

The rotation matrix can be written as [76]

$$\begin{aligned} R=\exp \left( \frac{v}{v_{\phi }} {\mathcal {A}}+\frac{v^{2}}{v_{\phi }^{2}} {\mathcal {B}}\right) , \quad {\mathcal {A}}^{T}=-{\mathcal {A}}, \quad {\mathcal {B}}^{T}=-{\mathcal {B}} ,\nonumber \\ \end{aligned}$$

(C.5)

so that

$$\begin{aligned} R=\left( \begin{array}{ccc} 1-\frac{v^{2}}{v_{\phi }^{2}} \frac{{\mathcal {A}}_{13}^{2}}{2} &{} \frac{v^{2}}{v_{\phi }^{2}} \frac{{\mathcal {A}}_{13} {\mathcal {A}}_{23}+2 {\mathcal {B}}_{12}}{2} &{} \frac{v}{v_{\phi }} {\mathcal {A}}_{13} \\ -\frac{v^{2}}{v_{\phi }^{2}} \frac{{\mathcal {A}}_{13} {\mathcal {A}}_{23}+2 {\mathcal {B}}_{12}}{2} &{} 1-\frac{v^{2}}{v_{\phi }^{2}} \frac{{\mathcal {A}}_{23}^{2}}{2} &{} \frac{v}{v_{\phi }} {\mathcal {A}}_{23} \\ -\frac{v}{v_{\phi }} {\mathcal {A}}_{13} &{} -\frac{v}{v_{\phi }} {\mathcal {A}}_{23} &{} 1-\frac{v^{2}}{v_{\phi }^{2}} \frac{{\mathcal {A}}_{13}^{2}+{\mathcal {A}}_{23}^{2}}{2} \end{array} \right) ,\nonumber \\ \end{aligned}$$

(C.6)

where

$$\begin{aligned} {\mathcal {A}}_{13}= & {} \frac{2}{\lambda _{\phi }}\left( \kappa _{d} c_{\beta }^{2}+\kappa _{u} s_{\beta }^{2}-\kappa s_{2 \beta }/v_{\phi }\right) ,\quad \nonumber \\ {\mathcal {A}}_{23}{} & {} =\frac{(\kappa _{d}-\kappa _{u}) s_{2 \beta }+2 \kappa c_{2 \beta }/v_{\phi }}{\frac{2 \kappa }{v_{\phi }s_{2 \beta }}-\lambda _{\phi }}, \end{aligned}$$

(C.7)

$$\begin{aligned} {\mathcal {B}}_{12}= & {} -\frac{2v_{\phi }}{\kappa } s_{2 \beta }^{2}\left( \lambda _{d} c_{\beta }^{2}-\lambda _{u} s_{\beta }^{2}\right) \nonumber \\{} & {} +\frac{v_{\phi }s_{2 \beta }}{\lambda _{\phi } \kappa } \frac{\kappa -v_{\phi }\lambda _{\phi } s_{2 \beta }}{2 \kappa -v_{\phi }\lambda _{\phi } s_{2 \beta }}\left( \kappa _{d} c_{\beta }^{2}+\kappa _{u} s_{\beta }^{2}-\frac{\kappa s_{2 \beta }}{v_{\phi }}\right) \nonumber \\{} & {} \times \left[ (\kappa _{d}-\kappa _{u}) s_{2 \beta }+\frac{2 \kappa c_{2 \beta }}{v_{\phi }}\right] , \end{aligned}$$

(C.8)

and up to second order in $v/v_{\phi },$ ${\mathcal {A}}_{12}={\mathcal {B}}_{13}={\mathcal {B}}_{23}=0.$ Thus, the scalar states are related to the mass eigenstates $h_i,$ as

$$\begin{aligned} \left( \begin{array}{c} H \\ S \\ \varrho \end{array}\right) =R\left( \begin{array}{l} h_{1} \\ h_{2} \\ h_{3} \end{array}\right) . \end{aligned}$$

(C.9)

so that

$$\begin{aligned} H=\sum _{i=1}^{3} R_{H i} h_{i}, \quad S=\sum _{i=1}^{3} R_{S i} h_{i}, \quad \varrho =\sum _{i=1}^{3} R_{\rho i} h_{i} . \end{aligned}$$

(C.10)

Appendix D: Loop functions

Loop functions of one-loop calculations used in Sect. 5 are given as follows

$$\begin{aligned}&F(x) =\frac{\left( 3 x^2-2\right) x^2+\left( 3 x^2-1\right) \ln \left( x^2\right) +2 \left( x^2-1\right) \sqrt{1-4 x^2} \ln \left( \frac{1+\sqrt{1-4 x^2}}{2 x}\right) }{x^4}, \end{aligned}$$

(D.1)

$$\begin{aligned}&F_{H^{\pm }}(x,z) = \frac{x^2+2 z^2-2}{2 x^2}+\frac{\left( x^2-\left( z^2-1\right) ^2\right) \log \left( z^2\right) }{2 x^4}\nonumber \\&\quad -\frac{\left( x^4+x^2 \left( z^4+z^2-2\right) -\left( z^2-1\right) ^3\right) \log \left( \frac{\left( -x^2+z^2+1\right) +\sqrt{-2 \left( x^2+1\right) z^2+\left( x^2-1\right) ^2+z^4}}{2 z}\right) }{x^4 \sqrt{x^4-2 x^2 \left( z^2+1\right) +\left( z^2-1\right) ^2}}, \end{aligned}$$

(D.2)

and functions of the two-loop amplitude can be computed by

$$\begin{aligned}{} & {} {\mathcal {F}}\left( \omega \right) =\frac{\omega }{2}\int _0^1 d x\, \frac{2 x(1-x)-1}{x(1-x)-\omega } \log \frac{x(1-x)}{\omega }, \end{aligned}$$

(D.3)

$$\begin{aligned}{} & {} \tilde{{\mathcal {F}}}\left( \omega \right) =\frac{\omega }{2}\int _0^1 d x\, \frac{1}{x(1-x)-\omega } \log \frac{x(1-x)}{\omega }. \end{aligned}$$

(D.4)

Moreover, the function associated with the calculation of the lepton flavor violation process is obtained as

$$\begin{aligned}&{\mathcal {F}}_{H^{\pm }}=\frac{\left( m_\mu m_e^2-m_\mu m_{H^{\pm }}^2+m_\mu m_N^2-2 m_e m_{H^{\pm }}^2+2 m_e m_N^2\right) \Lambda \left( m_e^2,m_{H^{\pm }},m_N\right) }{4 m_e \left( m_\mu ^2-m_e^2\right) } \nonumber \\&\quad -\frac{\left( m_\mu ^2 m_e-2 m_\mu m_{H^{\pm }}^2+2 m_\mu m_N^2-m_e m_{H^{\pm }}^2+m_e m_N^2\right) \Lambda \left( m_\mu ^2,m_{H^{\pm }},m_N\right) }{4 m_\mu \left( m_\mu ^2-m_e^2\right) } \nonumber \\&\quad +\frac{1}{2} m_{H^{\pm }}^2 C_{0} \left( 0,m_\mu ^2,m_e^2,m_{H^{\pm }},m_{H^{\pm }},m_N\right) +\frac{m_\mu m_e-m_{H^{\pm }}^2+m_N^2}{4 m_\mu m_e} \nonumber \\&\quad -\frac{\log \left( \frac{m_{H^{\pm }}^2}{m_N^2}\right) \left( 2 m_\mu ^2 m_e^2 m_{H^{\pm }}^2-m_\mu ^2 m_{H^{\pm }}^4+2 m_\mu ^2 m_{H^{\pm }}^2 m_N^2-m_\mu ^2 m_N^4-2 m_\mu m_e m_{H^{\pm }}^4\right) }{8 m_\mu ^3 m_e^3} \nonumber \\&\quad -\frac{\log \left( \frac{m_{H^{\pm }}^2}{m_N^2}\right) \left( 4 m_\mu m_e m_{H^{\pm }}^2 m_N^2-2 m_\mu m_e m_N^4-m_e^2 m_{H^{\pm }}^4+2 m_e^2 m_{H^{\pm }}^2 m_N^2-m_e^2 m_N^4\right) }{8 m_\mu ^3 m_e^3}, \end{aligned}$$

(D.5)

where $\Lambda$ (DiscB) and $C_{0}$ (ScalarC0) are Veltman–Passarino functions that are also defined in the Package-X program.