Sensitivity to triple Higgs couplings via di-Higgs production in the 2HDM at the (HL-)LHC

Abstract

An important task of the LHC is the investigation of the Higgs-boson sector. Of particular interest is the reconstruction of the Higgs potential, i.e. the measurement of the Higgs self-couplings. Based on previous analyses, within the 2-Higgs-Doublet Model (2HDM) type I, we analyze several two-dimensional benchmark planes that are over large parts in agreement with all theoretical and experimental constraints. For these planes we evaluate di-Higgs production cross sections at the (HL-)LHC with a center-of-mass energy of $14 \,\, \textrm{TeV}$ at next-to-leading order in the heavy top-quark limit with the code HPAIR. We investigate in particular the process $gg \rightarrow hh$, with h being the Higgs boson discovered at the LHC with a mass of about $125 \,\, \textrm{GeV}$. The top box diagram of the loop-mediated gluon fusion process into Higgs pairs interferes with the s-channel exchange of the two ${\mathcal{C}\mathcal{P}}$-even 2HDM Higgs bosons h and H. The latter two involve the triple Higgs couplings (THCs) $\lambda _{hhh}$ and $\lambda _{hhH}$, respectively, possibly making them accessible at the HL-LHC. Depending on the size of the involved top-Yukawa and THCs as well as on the mass of H, the contribution of the s-channel H diagram can be dominating or be highly suppressed. We find regions of the allowed parameter space in which the di-Higgs production cross section can differ by many standard deviations from its SM prediction, indicating possible access to deviations in $\lambda _{hhh}$ from the SM value $\lambda _{\textrm{SM}}$ and/or contributions involving $\lambda _{hhH}$. The sensitivity to the beyond-the-SM (BSM) THC $\lambda _{hhH}$ is further analyzed employing the $m_{hh}$ distributions. We demonstrate how a possible measurement of $\lambda _{hhH}$ depends on the various experimental uncertainties. Depending on the underlying parameter space, the HL-LHC may have the option not only to detect BSM THCs, but also to provide a first rough measurement of their sizes.

1 Introduction

The discovery of a new scalar particle with a mass of $\sim 125\,\, \textrm{GeV}$ by ATLAS and CMS [1,2,3] – within the experimental and theoretical uncertainties – is in agreement with the properties of the Standard Model (SM) Higgs boson. On the other hand, no conclusive sign of Higgs bosons beyond the SM (BSM) has been observed so far. However, the experimental results about the state at $\sim 125 \,\, \textrm{GeV}$, whose couplings are known up to now to an experimental precision of roughly $\sim$ 10–20%, leave ample room for interpretations in BSM models. Many BSM models feature extended Higgs-boson sectors with correspondingly extended Higgs potentials. Consequently, one of the main tasks of present and future colliders will be to determine whether the observed scalar boson forms part of the Higgs sector of an extended model, or not.

In contrast to the Higgs couplings to the SM 3rd generation fermions and gauge bosons, the trilinear Higgs self-coupling $\lambda _{hhh}$ remains to be determined. So far it has been constrained by ATLAS [4] to be inside the range $-0.4< \lambda _{hhh}/\lambda _{\textrm{SM}}< 6.3$ at the 95% CL and $-1.24< \lambda _{hhh}/\lambda _{\textrm{SM}}< 6.49$ at the 95% CL by CMS [5], both assuming a SM-like top-Yukawa coupling of the light Higgs. Many BSM models can still induce significant deviations in the trilinear coupling $\lambda _{hhh}$ of the SM-like Higgs boson with respect to the SM value, see, e.g., Ref. [6] for an up-to-date investigation. For recent reviews on the measurement of the triple Higgs couplings at future colliders see for instance Refs. [7, 8]. In case a BSM Higgs sector manifests itself, it will be a prime task to measure also the BSM trilinear Higgs self-couplings. Despite the relevance of the topic, the prospects of measuring BSM values of $\lambda _{hhh}$ and possibly other BSM triple Higgs couplings (THCs), taking into account the experimental environment of the (HL-)LHC have not been investigated in the literature so far.

One of the simplest extensions of the SM Higgs sector is the 2-Higgs-Doublet Model (2HDM) [9,10,11,12], where a second Higgs doublet is added to the SM Higgs sector, leading to five physical Higgs bosons. To avoid flavor-changing neutral currents at tree level, a $\mathbb {Z}_2$ symmetry is imposed [13] Depending on how this symmetry is extended to the fermion sector, four types of the 2HDM can be realized , we only analyze Type I, in which only one of the doublets couples to all the fermions and gauge bosons.

In Ref. [14] an analysis was presented of the possible size of THCs in the 2HDM type I and II taking into account all relevant experimental and theoretical constraints.¹  For that analysis it was assumed that the lightest $\mathcal{C}\mathcal{P}$-even Higgs-boson h is SM-like with a mass of $m_h\sim 125 \,\, \textrm{GeV}$. All other Higgs bosons were assumed to be heavier. (An update and extension to type III and IV was presented in Ref. [15].) Future $e^+e^-$ linear colliders, like the ILC [16] and CLIC [17], will play a key role for the measurement of the Higgs potential and in detecting possible deviations from the SM with high precision [7, 8, 18,19,20,21].²  Employing the results of Ref. [14], in Ref. [22] the sensitivity of the ILC and CLIC to various 2HDM THCs (including BSM THCs) was analyzed. Further analyses of THCs at $e^+e^-$ colliders were presented in Refs. [23, 24]. Corresponding analyses of the (HL-)LHC sensitivity to BSM THCs, however, are missing so far. Recent reviews on triple Higgs couplings at $e^+e^-$ colliders can be found in Refs. [7, 8, 20, 21].

In this paper, based on the results of Ref. [14], we complement the above results with an analysis of the sensitivity to BSM triple Higgs couplings at the LHC, and in particular its high-luminosity phase, the HL-LHC. Further analyzes involving BSM triple Higgs couplings can be found in Refs. [6, 8, 25,26,27]. However, while these papers took the effects of BSM THCs into account, to our knowledge no analysis for the (HL-)LHC exists attempting the investigation presented in this paper: to quantify the potential sensitivity to BSM triple Higgs couplings.

The main Higgs pair production process at the LHC is gluon fusion into Higgs pairs [28]. Here we investigate in particular $gg \rightarrow hh$ in the 2HDM type I, with h corresponding to the state discovered at the LHC at $\sim 125 \,\, \textrm{GeV}$. The process is loop-mediated already at leading order and consists of a triangle and a box top-loop contribution. In the SM, the box diagram interferes destructively with the triangle contribution. In the 2HDM, an exchange of both h and H in the s-channel are possible. A resonantly produced H with subsequent decay into hh can lead to a significantly enhanced cross section. For our analysis, we take into account the next-to-leading order QCD corrections to the process in the heavy top-quark limit [29] by making use of the accordingly modified [6, 30] program HPAIR. In the first part of our analysis, focusing on the effects of THCs on the total di-Higgs production cross section, we find regions of the allowed parameter space in which the di-Higgs production cross section can differ by several standard deviations from its SM prediction, indicating possible access to deviations in $\lambda _{hhh}$ from $\lambda _{\textrm{SM}}$ and/or contributions involving $\lambda _{hhH}$. This demonstrates the general possibility to have sensitivity to $\lambda _{hhh}$ and $\lambda _{hhH}$ at the HL-LHC. In the second step of our analysis, the sensitivity to $\lambda _{hhH}$ is further analyzed employing the $m_{hh}$ distributions in the $gg \rightarrow hh$ production cross section. We investigate for the first time how a possible measurement of $\lambda _{hhH}$ depends on the assumed experimental uncertainties in $m_{hh}$, such as smearing, bin width, as well as on the position of the bins. Our findings clearly indicate where experimental analyses should be improved to gain access to BSM THCs. We demonstrate that, depending on the underlying parameter space, the HL-LHC may have the potential not only to detect BSM triple Higgs couplings, but also to provide a first rough measurement of their size.

Our paper is organized as follows. In Sect. 2 we briefly review the 2HDM, fix our notation, define the benchmark planes (representing the phenomenological variations of the 2HDM parameter space) used later for our investigation and summarize the constraints that we apply (which are the same as in Refs. [14, 15]). As a requisite for our analysis, the di-Higgs production cross sections in the benchmark planes are presented in Sect. 3 and analyzed w.r.t. their dependence on the triple Higgs couplings in the contribution from the s-channel H exchange. In the first step of our analysis, in Sect. 3.3 we analyze a possible sensitivity of the di-Higgs production cross section at the (HL-)LHC to $\lambda _{hhh}$ and in particular to $\lambda _{hhH}$. Finally, as the second step in our analysis in Sect. 4 we present the possible HL-LHC sensitivity to $\lambda _{hhH}$ via the $m_{hh}$ distribution, and in Sect. 5 also assess its dependence on smearing, bin width and position of the bins. Our conclusions are given in Sect. 6.

2 The model and the constraints

In this section we give a short description of the 2HDM to fix our notation. We briefly review the theoretical and experimental constraints, which are taken over from Refs. [14, 15]. Finally we will define the benchmark planes for our analysis of the $gg \rightarrow hh$ production cross section.

2.1 The 2HDM

We assume the ${\mathcal{C}\mathcal{P}}$-conserving 2HDM [9,10,11,12], where the potential can be written as,

$$\begin{aligned} V= & {} m_{11}^2 (\Phi _1^\dagger \Phi _1) + m_{22}^2 (\Phi _2^\dagger \Phi _2) - m_{12}^{2}(\Phi _1^\dagger \Phi _2 + \Phi _2^\dagger \Phi _1) \nonumber \\{} & {} + \frac{\lambda _1}{2} (\Phi _1^\dagger \Phi _1)^2 + \frac{\lambda _2}{2} (\Phi _2^\dagger \Phi _2)^2 \nonumber \\{} & {} + \lambda _3 (\Phi _1^\dagger \Phi _1) (\Phi _2^\dagger \Phi _2) + \lambda _4 (\Phi _1^\dagger \Phi _2) (\Phi _2^\dagger \Phi _1)\nonumber \\{} & {} + \frac{\lambda _5}{2} [(\Phi _1^\dagger \Phi _2)^2 +(\Phi _2^\dagger \Phi _1)^2] . \end{aligned}$$

(1)

After electroweak symmetry breaking (EWSB) the two $SU(2)_L$ doublets $\Phi _1$ and $\Phi _2$ can be expanded around their two vacuum expectation values (vevs) $v_1$ and $v_2$, respectively, as

$$\begin{aligned} \Phi _1= & {} \left( \begin{array}{c} \phi _1^+ \\ \frac{1}{\sqrt{2}} (v_1 + \rho _1 + i \eta _1) \end{array} \right) ,\nonumber \\ \Phi _2= & {} \left( \begin{array}{c} \phi _2^+ \\ \frac{1}{\sqrt{2}} (v_2 + \rho _2 + i \eta _2) \end{array} \right) , \end{aligned}$$

(2)

with the vev ratio given by $\tan \beta \equiv v_2/v_1$. The vevs satisfy the relation $v = \sqrt{(v_1^2 +v_2^2)}$ where $v\simeq 246\,\, \textrm{GeV}$ is the SM vev. The eight (scalar) degrees of freedom, $\phi _{1,2}^\pm$, $\rho _{1,2}$ and $\eta _{1,2}$, give rise to three Goldstone bosons, $G^0$ and $G^\pm$, and five physical scalar fields, two ${\mathcal{C}\mathcal{P}}$-even scalar fields, h and H, where by convention $m_h < m_H$, one ${\mathcal{C}\mathcal{P}}$-odd field, A, and one charged Higgs pair, $H^\pm$. The mixing angles $\alpha$ and $\beta$ diagonalize the $\mathcal{C}\mathcal{P}$-even and ${\mathcal{C}\mathcal{P}}$-odd/charged Higgs mass matrices, respectively.

The occurrence of tree-level flavor-changing neutral currents (FCNC) is avoided by imposing a $\mathbb {Z}_2$ symmetry, only softly broken by the $m_{12}^{2}$ term in the Lagrangian. The extension of the $\mathbb {Z}_2$ symmetry to the Yukawa sector prohibits tree-level FCNCs. This results in four variants of the 2HDM, depending on the $\mathbb {Z}_2$ parities of the fermion types. In this article we focus on the Yukawa type I, where all the fermions couple only to $\Phi _2$.

Here we work in the physical basis of the 2HDM, where most of the free parameters in Eq. (1) are expressed in terms of a set of “physical” parameters given by

$$\begin{aligned}{} & {} c_{\beta -\alpha }, \quad \tan \beta , \quad v, \quad m_h, \quad m_H,\nonumber \\{} & {} \quad \quad m_A, \quad m_{H^\pm }, \quad m_{12}^{2}, \end{aligned}$$

(3)

where we use the short-hand notation $s_x = \sin (x)$, $c_x = \cos (x)$. In our analysis we will identify the lightest ${\mathcal{C}\mathcal{P}}$-even Higgs boson, h, with the one observed at the LHC at $\sim 125 \,\, \textrm{GeV}$.

The couplings of the Higgs bosons to SM particles are modified w.r.t. the SM Higgs-coupling predictions because of the mixing in the Higgs-boson sector. The couplings of the CP-even neutral Higgs bosons to fermions and to gauge bosons are given by,

$$\begin{aligned} \mathcal {L}= & {} -\sum _{f=u,d,l}\frac{m_f}{v}\left[ \xi _h^f\bar{f}fh + \xi _H^f\bar{f}fH \right] \nonumber \\{} & {} +\sum _{h_i=h,H} \left[ g m_W \xi _{h_i}^W W_\mu W^\mu h_i + \frac{1}{2} g m_Z \xi _{h_i}^Z Z_\mu Z^\mu h_i\right] .\nonumber \\ \end{aligned}$$

(4)

Here $m_f$, $m_W$ and $m_Z$ are the fermion, W boson and Z boson masses, respectively. The modification factors in the couplings to fermions and gauge bosons, $\xi _{h,H}^f$ and $\xi _{h,H}^V$, for the 2HDM of type I are given in Table 1.

Table 1 Factors appearing in the couplings of the neutral Higgs bosons to fermions, $\xi _{h,H}^f$, and to gauge bosons, $\xi _{h,H}^V$, in the 2HDM of type I

The generic triple Higgs coupling $\lambda _{h h_i h_j}$ involving at least one SM-like Higgs boson h is defined such that the Feynman rules are given by

where n is the number of identical particles in the vertex. Relevant for our analysis here are $\lambda _{hhh}$ and $\lambda _{hhH}$. We adopt this convention in Eq. (5) so that the light Higgs triple coupling $\lambda _{hhh}$ has the same normalisation as $\lambda _{\textrm{SM}}$ in the SM, which is given by $-6iv\lambda _{\textrm{SM}}$ with $\lambda _{\textrm{SM}}=m_h^2/2v^2\simeq 0.13$. We furthermore define $\kappa _{\lambda }\equiv \lambda _{hhh}/\lambda _{\textrm{SM}}$.

The explicit expressions of the two triple Higgs couplings are given by

$$\begin{aligned} \lambda _{hhh}&= -\frac{1}{2} \Big \{ \lambda _1c_{\beta } s_{\alpha }^3-\lambda _2 c_{\alpha }^3 s_{\beta } +\left( \lambda _3+\lambda _4+\lambda _5\right) \nonumber \\&\quad \times \left( c_{\alpha }^2 c_{\beta } s_{\alpha }-c_{\alpha } s_{\alpha }^2 s_{\beta } \right) \Big \} \nonumber \\&= \frac{1}{2v^2} \bigg \{ m_h^2 s_{\beta -\alpha }^3 +\left( 3 m_h^2-2 \bar{m}^2\right) c_{\beta -\alpha }^2 s_{\beta -\alpha } \nonumber \\&\quad \times +2 \cot 2 \beta \left( m_h^2-\bar{m}^2\right) c_{\beta -\alpha }^3\bigg \}, \end{aligned}$$

(6)

$$\begin{aligned} \lambda _{hhH}&= \frac{1}{2} \Big \{ 3 \lambda _1 c_{\alpha } c_{\beta } s_{\alpha }^2 + 3 \lambda _2 c_{\alpha }^2 s_{\alpha } s_{\beta } \nonumber \\&\quad +\left( \lambda _3+\lambda _4+\lambda _5\right) \left( c_{\alpha }^3 c_{\beta }\right. \nonumber \\&\left. \quad -2 c_{\alpha }^2 s_{\alpha } s_{\beta }-2 c_{\alpha } c_{\beta } s_{\alpha }^2+s_{\alpha }^3 s_{\beta }\right) \Big \} \nonumber \\&= -\frac{c_{\beta - \alpha }}{2v^2} \bigg \{ \left( 2m_h^2+m_H^2-4\bar{m}^2\right) s_{\beta - \alpha }^2 \nonumber \\&\quad +2\cot {2\beta }\left( 2m_h^2+m_H^2-3\bar{m}^2\right) s_{\beta - \alpha }c_{\beta - \alpha }\nonumber \\&\quad -\left( 2m_h^2+m_H^2-2\bar{m}^2\right) c_{\beta - \alpha }^2 \bigg \}, \end{aligned}$$

(7)

where $\bar{m}^2$, derived from $m_{12}^{2}$, is given by:

$$\begin{aligned} \bar{m}^2= & {} \frac{m_{12}^{2}}{\sin \beta \cos \beta } . \end{aligned}$$

(8)

The triple Higgs couplings depend on $c_{\beta - \alpha }$. In particular, in the “alignment limit”, $c_{\beta - \alpha }\rightarrow 0$, where the light ${\mathcal{C}\mathcal{P}}$-even Higgs couplings to the SM particles recover SM values, the triple Higgs couplings approach the values $\lambda _{hhh}= \lambda _{\textrm{SM}}$ and $\lambda _{hhH}= 0$, respectively.

2.2 Theoretical and experimental constraints

In this subsection we briefly summarize the various theoretical and experimental constraints considered in our analysis (more details can be found in Refs. [14, 15]). Note, that we did not check for constraints arising from di-Higgs measurements at the LHC. The analysis performed in [6] showed that non-resonant and resonant di-Higgs searches start to cut in the parameter spaces of extended Higgs sector models. However, the parameter spaces of the ${\mathcal{C}\mathcal{P}}$-conserving 2HDM investigated here are not affected yet.

• Theoretical constraints

  The important theoretical constraints come from tree-level perturbartive unitarity and stability of the electroweak vacuum. They are ensured by an explicit test of the underlying Lagrangian parameters (details of our approach can be found in Ref. [14]). The parameter space allowed by these two constraints can be enlarged, if we allow for a mass term breaking the imposed $\mathbb {Z}_2$ symmetry softly, i.e. we choose a non-zero $m_{12}^2$. In some of the sample scenarios that we will investigate later, we chose $m_{12}^2$ as

  $$\begin{aligned} m_{12}^{2}= \frac{m_H^2\cos ^2\alpha }{\tan \beta }~. \end{aligned}$$

  (9)

  This choice prevents $\lambda _1$ to receive large corrections for large $\tan \beta$ and ensures a larger allowed region by theoretical constraints when close to the alignment limit [31].

• Constraints from electroweak precision data

  For SM extensions based solely on extensions of the Higgs sector the constraints from the electroweak precision observables (EWPO) can be expressed in terms of the oblique parameters S, T and U [32, 33]. Most constraining in the 2HDM is the T parameter, requiring either $m_{H^\pm }\approx m_A$ or $m_{H^\pm }\approx m_H$. In Ref. [14] three scenarios were defined to meet this constraint: (A)$\;m_{H^\pm }= m_A$, (B)$\;m_{H^\pm }= m_H$, and (C)$\;m_{H^\pm }= m_A= m_H$. Here it should be kept in mind that the EWPO used to set these constraints do not take into account the recent measurement of $m_W$ at CDF [34], which deviates from the SM prediction by $\sim 7\,\sigma$. After this result for $m_W$ was published, many articles appeared to describe the CDF value in BSM models, including analyses in the 2HDM, see Refs. [35,36,37] for the first papers. It was shown that the large $m_W$ value can be accommodated by introducing a certain amount of splitting between the masses of the heavy 2HDM Higgs bosons. This also holds (albeit with a smaller amount of splitting) if a possible new world average, see Ref. [38], is taken into account [39]. However, we will not include this possibility into our analysis.

• Constraints from direct Higgs-boson searches at colliders

  The exclusion limits at the 95% confidence level of all relevant BSM Higgs boson searches (including Run 2 data from the LHC) are included in the public code HiggsBounds v.5.9 [40,41,42,43,44].³  For a parameter point in a particular model, HiggsBounds determines on the basis of expected limits which is the most sensitive channel to test each BSM Higgs boson. Then, based on this most sensitive channel, HiggsBounds determines whether the point is allowed or not at the 95% CL. As input HiggsBounds requires some specific predictions from the model, like branching ratios or Higgs couplings, that were computed with the code 2HDMC-1.8.0 [46].⁴

• Constraints from the properties of the ${{\sim \,125\,{\,\, \textrm{GeV}}}}$ Higgs boson

  Any model beyond the SM has to accommodate a Higgs boson with mass and signal strengths as they were measured at the LHC. In the parameter points used the compatibility of the ${\mathcal{C}\mathcal{P}}$-even scalar h with a mass of $125.09\,\, \textrm{GeV}$, $h_{125}$, with the measurements of signal strengths at the LHC is tested with the code HiggsSignals v.2.6 [50,51,52]. The code provides a statistical $\chi ^2$ analysis of the $h_{125}$ predictions of a certain model compared to the measurement of Higgs-boson signal rates and masses from the LHC. As for the BSM Higgs boson searches, the predictions of the 2HDM have been obtained with 2HDMC [46]. For a 2HDM parameter point to be allowed it was required [15] that the corresponding $\chi ^2$ is within $2\,\sigma$ ($\Delta \chi ^2 = 6.18$) from the SM fit: $\chi _\textrm{SM}^2=84.73$ with 107 observables.⁵

• Constraints from flavor physics

  Constraints from flavor physics can be significant in the 2HDM, in particular because of the presence of the charged Higgs boson. Flavor observables like rare B decays, mixing parameters of B mesons, and LEP constraints on Z decay partial widths etc. are sensitive to charged Higgs boson contributions [53, 54]. To test the parameter space, taking into account the most constraining decays $B \rightarrow X_s \gamma$ and $B_s \rightarrow \mu ^+ \mu ^-$, the code SuperIso [55, 56] was used, again with the model input given by 2HDMC (see Ref. [14] for more details).

2.3 Benchmark planes

As a starting point for our study we take the analysis performed in Ref. [14], where the goal was to look for large deviations of BSM THCs in the 2HDM that are in agreement with present theoretical and experimental constraints. The analysis in this reference was done by performing a larger scan allowing the variations of all relevant free parameters in the 2HDM. The chosen benchmarks exhibit the largest deviations found in the THCs, which we expect can have an impact on the di-Higgs cross section, and therefore large deviations from the SM predictions can be found. Therefore, we define four benchmark planes that presumably exhibit an interesting phenomenology w.r.t. the di-Higgs production cross sections in the gluon fusion channel, $gg \rightarrow hh$. The planes furthermore exhibit certain specific aspects of the 2HDM phenomenology of di-Higgs production. The Yukawa type does not play an important role in the process $gg \rightarrow hh$, since the top Yukawa couplings, which are most relevant, are identical in the four types. On the other hand, it is desirable to be away from the alignment limits, to allow for a sizable $\lambda _{hhH}$, which can have an important impact via the resonant H exchange in the s-channel (see also the discussion in the next section). Consequently, the the four planes are all chosen to be in the 2HDM Yukawa type I, as this type allows for larger deviations from the alignment limit taking into account the experimental constraints. The parameters are chosen as:

• 1. $m_{H^\pm }= m_H= m_A= 1000 \,\, \textrm{GeV}$, $m_{12}^{2}$ fixed via Eq. (9),

  free parameters: $c_{\beta - \alpha }$, $\tan \beta$

  Expected features: small H contribution, variation of top Yukawa couplings and of $\lambda _{hhh}$ and $\lambda _{hhH}$.

• 2. $m_{H^\pm }= m_H= m_A= 650 \,\, \textrm{GeV}$, $\tan \beta = 7.5$,

  free parameters: $c_{\beta - \alpha }$, $m_{12}^{2}$

  Expected features: possibly relevant H contribution, variation of top Yukawa couplings and of $\lambda _{hhh}$ and $\lambda _{hhH}$.

• 3. $\tan \beta = 10$, $m_{12}^{2}$ fixed via Eq. (9),

  free parameters: $c_{\beta - \alpha }$, $m_{H^\pm }= m_H= m_A$

  Expected features: variation of the relevance of the H exchange contribution, variation of top Yukawa couplings and $\lambda _{hhH}$, including the alignment limit for $c_{\beta - \alpha }\rightarrow 0$.

• 4. $\tan \beta = 10$, $c_{\beta - \alpha }= 0.2$, $m_{12}^{2}$ fixed via Eq. (9)

  free parameters: $m_H$, $m_A=m_{H^\pm }$

  Expected features: variation of the relevance of the H exchange contribution, variation of top Yukawa couplings and $\lambda _{hhH}$, always away from the alignment limit.

3 Cross section results

In this section we start our numerical analysis with the evaluation of the di-Higgs production cross sections in the benchmark planes defined in Sect. 2.3. We first discuss details of the calculation and then present the results, where we analyze the impact of a possible heavy Higgs, H, in the s-channel. We perform this analysis in all benchmark planes listed above to give a broad overview about the possible phenomenology of di-Higgs production in the 2HDM. In the following sections we will discuss selected planes and points to further examine the effects of the various triple Higgs couplings and the properties of the heavy ${\mathcal{C}\mathcal{P}}$-even Higgs boson.

Fig. 1

Leading-order diagrams to SM-like Higgs pair production in gluon fusion processes at hadron colliders. The red dot shows the triple Higgs coupling, and $h_i=h,H$

3.1 Calculation of $gg \rightarrow hh$

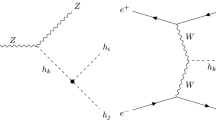
The main di-Higgs production process at the LHC is given by gluon fusion. The diagrams contributing at leading order are shown in Fig. 1. They both involve a heavy quark loop (top or bottom), where for small $\tan \beta$ the bottom-quark loop only plays a minor role. In the SM the triangle diagram, Fig. 1a, gives access to the trilinear Higgs coupling, $\lambda _{hhh}$, with the SM Higgs exchange in the s-channel. The box diagram, Fig. 1b, interferes destructively with the triangle diagram, resulting in a small cross section. In BSM theories additional diagrams can contribute. In particular in the case of the 2HDM the second ${\mathcal{C}\mathcal{P}}$-even Higgs can be exchanged in the s-channel, involving $\lambda _{hhH}$. This diagram will usually be referred to as the “resonant diagram”,⁶ whereas the SM-like contributions will be referred to as “the continuum”. Note that the Yukawa coupling and the trilinear Higgs self-coupling $\lambda _{hhh}$ of the SM-like Higgs boson h can deviate from the SM values so that the observed destructive interference between the triangle and box diagram in the SM may not be effective.

For our numerical evaluation we use the code HPAIR [6, 29, 30, 57], adapted to the 2HDM. The original code evaluates the cross section of the production of two neutral Higgs bosons through gluon fusion at the LHC for the SM and the MSSM. The calculation is done at leading order (LO, see Fig. 1), and includes next-to-leading order (NLO) QCD corrections in the heavy top-mass limit. In this limit, it is assumed that the contribution of the bottom quark is negligible (it would introduce modifications of less than 1% in the SM) and then the top mass is taken to infinity. This assumption becomes less accurate at high values of $\tan \beta$ because the bottom quark loop contribution gets larger.

At LO the calculation includes top- and bottom-quark loops with full mass dependence. It is equivalent to the calculation done in the Minimal Supersymmetric Standard Model (MSSM) since its Higgs sector is equivalent to the 2HDM Type II. The only changes that are implemented in the case of the 2HDM are the modifications of the Yukawa couplings of the MSSM according to Table 1, for the corresponding type and the change of the triple Higgs couplings.⁷  As the QCD corrections in the heavy top-quark limit only involve couplings between coloured particles, they can straightforwardly be taken over from the MSSM to the 2HDM. For further details, we refer to Refs. [6, 29, 30, 57].

Whenever we present NLO results in the following, these are based on the evaluation with the modified HPAIR code, i.e. in the heavy top-mass, $m_t \rightarrow \infty$, limit (HTL). This is the most accurate prediction that can be used for the 2HDM case with the publicly available tools. For the SM the NLO QCD corrections have been provided including the full top quark mass dependence [58,59,60,61,62]. The next-to-next-to-leading order (NNLO) corrections have been obtained in the large $m_t$ limit [63, 64], the results at next-to-next-to-leading logarithmic accuracy (NNLL) became available in [65, 66], and the corrections up to next-to-next-to-next-to leading order (N$^3$LO) were presented in [67,68,69,70] for the heavy top-mass limit.⁸ From the NLO results including the full top-mass dependence [58,59,60,61,62] it is known, that the top-mass effects reduce the Born-improved HTL result (i.e. the cross section including the full top-mass dependence at LO and the NLO result in the HTL) by about 15%. This is worse for distributions, where it was found that the top mass effects result in a total modification of the differential cross section of up to $-30$% compared to the Born-improved HTL at large invariant mass values, for a c.m. energy of 14 TeV. An assessment of the theory uncertainties originating from the scheme and scale choice of the virtual top mass was provided in [62] and found to be significant. Combined with the factorization scale uncertainties they range between $+6$% and $-23$% for the total cross section at 14 TeV center of mass energy.

Fig. 2

Plane 1. 2HDM type I, $\tan \beta$ versus $c_{\beta - \alpha }$. Upper left: Cross section prediction for di-Higgs production in 2HDM normalized to the SM value, both evaluated at NLO QCD in the heavy top-quark limit. Allowed area inside the black contour. Red lines indicate the values at with the ratio is 1 (i.e. $\sigma = \sigma _\textrm{SM}$). The color coding indicates the size of this ratio. Upper right: K-factor, defined as the ratio of the NLO and LO cross sections. Lower left: Total decay width of the heavy Higgs H. Lower right: Ratio of the cross section with and without resonant enhancement, both evaluated at LO

Recently, for the 2HDM the full NLO QCD corrections have been provided for the production of a mixed Higgs pair Hh and for a pair of pseudoscalars, AA, respectively, [73], with similar findings for the distributions, which increase with large invariant mass reaching $-30$% ($-20$%) in hH (AA) production at an invariant mass of 1.5 TeV. The mass effects hence not only change the absolute value of the cross section but also the shape of the distribution, so that the heavy top-mass approximation does not work as good as for the inclusive cross section (see also [74]). So far, however, there is no public code available that allows to compute the top-quark mass effects on the distributions for 2HDM Higgs pair production, in particular not for the interesting case of intermediate resonant heavy Higgs production, which we investigate here. In view of a missing code, we take the best prediction availabe at the moment and resort to the NLO QCD corrections in the heavy-top limit with the here mentioned caveats.⁹ Since we will investigate several distinct benchmark cases and analyze what issues in general can arise in the measurement of trilinear Higgs self-couplings, this will still give us new insights despite the used approximations. The overall conclusions will remain the same: They will represent the best case scenario, assuming the distributions are changed uniformly at NLO. In this way, they show what at least can be expected.

3.2 Analysis of the cross section predictions

In Figs. 2, 3, 4 and 5 we show the results for the di-Higgs production cross section in the 2HDM normalized to the SM value calculated at NLO QCD in the Born-improved HTL for the gluon fusion process. The SM prediction was obtained with HPAIR assuming the alignment limit and coincides with the values given in Ref. [6],¹⁰

$$\begin{aligned}{} & {} \sigma ^\textrm{LO}_\textrm{SM}\; (pp \rightarrow hh) = 19.76\; \textrm{fb}\,,\nonumber \\{} & {} \sigma ^\textrm{NLO}_\textrm{SM}\; (pp \rightarrow hh) = 38.24\; \textrm{fb}\,, \end{aligned}$$

(10)

Fig. 3

Plane 2. 2HDM, type I, $m_{12}^2$ versus $c_{\beta - \alpha }$. Otherwise plots as in Fig. 2

Fig. 4

Plane 3. 2HDM type I, $m_H=m_A=m_{H^\pm }$ versus $c_{\beta - \alpha }$. Otherwise plots as in Fig. 2

Fig. 5

Plane 4. 2HDM type I, $m_H$ versus $m_A = m_{H^\pm }$. Otherwise plots as in Fig. 2

The results for all the benchmark planes are shown as follows. In the upper left plot of each figure, we present the NLO 2HDM cross sections normalized to the NLO SM value, as indicated by the color coding. The red line shows where the ratio is one, and the inner part of the solid black line is allowed by all theoretical and experimental constraints (as evaluated in Refs. [14, 15]), see Sect. 2.2. The results away from the allowed region are also shown in order to see the general trends of the observables, but large deviations away from the allowed region signal deviations from the perturbative regime and should not be further analyzed. The upper right plot shows the K-factor, $K = \sigma _\textrm{NLO}/\sigma _\textrm{LO}$ of the 2HDM hh cross sections. It should be noted that for the determination of the K-factor we consistently evaluated the LO cross section with LO PDFs and the strong coupling $\alpha _s$ at LO, and the NLO cross section with NLO PDFs and $\alpha _s$  at NLO, we used CT14lo (for LO) and CT14nlo (for NLO) PDF sets [75,76,77]. The lower left plot indicates the total width of the heavy ${\mathcal{C}\mathcal{P}}$-even Higgs boson, which contributes via the s-channel diagram (Fig. 1a with $h_i = H$). This quantity will be relevant for the discussion of the dependence of the cross section on the underlying parameter space. In some parts of the shown parameter space the ratio $\Gamma _H/m_H$ reaches values . However, this happens far outside the allowed region, as indicated by the black solid line and thus does not have phenomenological consequences. Finally, the lower right plot shows the ratio of the full cross section, divided by the cross section obtained omitting the diagram with H in the s-channel, both evaluated at leading order. Large deviations from unity indicate an important contribution from the resonant H diagram.

The analysis for the benchmark plane 1 is presented in Fig. 2, where $\tan \beta$ is plotted against $c_{\beta - \alpha }$ for the four quantities described in the previous paragraph. In this scenario the heavy ${\mathcal{C}\mathcal{P}}$-even Higgs mass is set to $m_H= 1000 \,\, \textrm{GeV}$.¹¹ We observe that the maximum deviation from the SM prediction within the allowed area occurs precisely at the “tip” that is furthest away from the alignment limit $c_{\beta - \alpha }=0$ (see upper left plot). Here the enhancement factor in the cross section is $\sim 3$. This corresponds to the minimum size of the triple Higgs coupling $\lambda _{hhh}$ that was obtained in the allowed region of this benchmark plane ($\kappa _{\lambda }\sim -0.4$). If a deviation between the SM prediction and experiment is observed, this could point to a deviation of the $\kappa _{\lambda }$ coupling. The dark blue region in this plot indicates that the production cross section is smaller than the SM prediction, as the ratio drops to $\sigma /\sigma _\textrm{SM} \lesssim 1$. The decrease here is of order 1% due to minor changes in the top Yukawa coupling in the 2HDM. The K-factor in this benchmark plane results in a factor close to 2, more specifically in the allowed region of $\sim 1.92$ to $\sim 1.97$ (upper right plot). One can see that the decay width of H in this region can amount to $\sim 25 \,\, \textrm{GeV}$ (lower left plot). A large total width $\Gamma ^{\text {tot}}_H$ has a suppressing effect on the H contribution to the cross section due to its appearance in the denominator of the s-channel propagator, as will be discussed below. We see that the H contribution has no enhancing effect on hh production within the allowed area given by the black lines (lower right plot). Including the resonance either slightly suppresses the cross section or leaves it unchanged (we find the ratio 1 exactly at the “tip”, where the hh cross section is maximal within the allowed region). In conclusion, in this plane the maximum enhancement of the cross section is precisely due to the deviation of the triple Higgs coupling from the expected SM value.

In the case of the benchmark plane 2, shown in Fig. 3, where we now plot $m_{12}^2$ versus $c_{\beta - \alpha }$, it can be observed that the cross section does not have a significant enhancement in the allowed region, as it does not even reach a factor of $\sim 2$ times the SM value. Also for this benchmark plane we observe that the largest value of the cross section falls in the region of the minimum value of $\kappa _{\lambda }$, i.e. where the destructive interference between box diagram and h exchange is minimal. The K factor in the allowed region is roughly $\sim 1.91$ to $\sim 1.95$, again close to 2. In the evaluation of the effect of the heavy Higgs H, we observe that neither the decay widths nor the resonant enhancement are significant in the allowed region. The H contribution almost has no effect on the hh production cross section.

In the benchmark plane 3, shown in Fig. 4, where we plot $m_H=m_A=m_{H^\pm }$ against $c_{\beta - \alpha }$, we allow for a variation of the heavier Higgs masses by fixing the value of $\tan \beta$ and the mass $m_{12}^2$ according to the Eq. (9). Concerning the normalized NLO cross section there is no enhancement below $250 \,\, \textrm{GeV}$ since the heavy Higgs is not produced on-shell. Above this threshold there is resonant enhancement due to the contribution of the heavy Higgs in the s-channel. In particular, the cross section is enhanced by up to a factor of $\sim 8$ in the “tail” at $c_{\beta - \alpha }$ $\sim -0.1$. In this region one finds $\kappa _{\lambda }$ close to 1, so that the enhancement of the cross section w.r.t. the SM is given by the diagram with H in the s-channel that resonantly decays into hh. This can also be seen in the lower right plot of Fig. 4, where a ratio of resonant over non-resonant cross section of up to $\sim 8$ is found. In this case there are two distinct regions of a suppression of the production cross section w.r.t. the SM. In particular, for values of $m_H< 250 \,\, \textrm{GeV}$, the decay $H \rightarrow hh$ is kinematically disallowed and the production cross section is small. The second region is found for values of $c_{\beta - \alpha }\sim 0.2$ and large $m_H$ and is due to an enhanced prediction for $\kappa _{\lambda }$Ẇhen resonant production is suppressed, as starts to happen for higher values of $m_H$, the cross section is more sensitive to deviations in $\kappa _{\lambda }$Ṫhe dependence of the cross section on the value of $\kappa _{\lambda }$ is quadratic and reaches a minimum for $\kappa _{\lambda }$ $\sim$ 2.5 located within the dark blue region. This trend is well known in literature and is the underlying explanation of the suppression in this parameter region. The K-factor in the maximally enhanced region is slightly above 2 (up to $\sim 2.06$).

Since in this plane we allow for a variation of the mass of the heavy Higgs in the propagator one can observe the enhancement of the cross section around $m_H\sim 350-400 \,\, \textrm{GeV}$ that is expected from single Higgs production above the di-top threshold, $m_H\sim 2 m_t$. This feature will be noted several times further in the text whenever $m_H$ is a free parameter as well as for $m_{hh}$ distributions. In this benchmark plane the enhancement due to the di-top production threshold is clearly visible in the lower right plot of Fig. 4 (particularly for negative $c_{\beta - \alpha }$ within the allowed region).

The final plane we investigate in detail is plane 4 as shown in Fig. 5. Here the two free parameters, that we plot against each other, are $m_H$ and $m_A= m_{H^\pm }$. Correspondingly, one expects a large enhancement of the 2HDM cross section for $m_H\sim 400 \,\, \textrm{GeV}$ where $m_H > 2 m_h$ and above the di-top threshold. Exactly this can be observed in the upper left plot (total cross section) and the lower right plot (relative enhancement from the resonant diagram). The cross section can be up to 60% larger than the SM di-Higgs production cross section, with a K factor again close to 2. The total width of the heavy ${\mathcal{C}\mathcal{P}}$-even Higgs ranges from very small values up to larger than $200 \,\, \textrm{GeV}$ within the allowed region (found for low $m_A= m_{H^\pm }$ and large $m_H$). For large total widths the resonance enhancement is not effective. The largest enhancements of the cross section are found for relatively small values of .

3.3 Dependence on triple Higgs couplings

In this subsection we analyze the cross section with respect to the triple Higgs couplings involved in the di-Higgs production process. In particular, we will show in which part of the parameter space the total di-Higgs production cross section has a relevant dependence on $\lambda _{hhh}$ and/or $\lambda _{hhH}$.

Here we focus on a statistical treatment of the errors of the total cross section measurement, which is assumed to be Gaussian, neglecting systematic uncertainties. It was found in Refs. [8, 78] that the statistical uncertainty of the total di-Higgs cross section measurement, assuming SM values, will reach a level of $4.5\,\sigma$ at the end of the HL-LHC, combining ATLAS and CMS. (Taking into account systematic effects could lower this value to $\sim 4\,\sigma$.) Consequently, we will approximate the corresponding error in the measurement as $\delta \textbf{xs} = \textbf{xs} / 4.5$.¹²  The significance of the deviation of the (to be measured) 2HDM cross section w.r.t. the SM value can then be expressed as

$$\begin{aligned} \Delta \sigma _\textrm{SM} \equiv \frac{\textbf{xs}_\textrm{2HDM} - \textbf{xs}_\textrm{SM}}{\delta \textbf{xs}}. \end{aligned}$$

(11)

It should be noted that this approximation becomes worse for larger deviations of $\textbf{xs}_\textrm{2HDM}$ from $\textbf{xs}_\textrm{SM}$, since the precision of the measurements, $\delta \textbf{xs}$, has been evaluated assuming the SM value. For higher cross sections a more precise measurement can be expected. A more precise analysis is not possible because of the lack of corresponding experimental analyses.

Fig. 6

Plane 1. Upper line: triple Higgs coupling predictions in the 2HDM and value of the normalized cross section (w.r.t. the SM value) evaluated at NLO QCD in the same parameter space. Red (blue) dots show the maximum (minimum) value of the trilinears that is realized in the allowed region. Lower left: points realized in the couplings plane, the red area around $\kappa _{\lambda }= 1$ and $\lambda _{hhH}= 0$ represents the points that fall into the allowed region, indicated by a red arrow. Lower middle: zoom into the previous plot, color code indicates the normalized cross section within the allowed region for different values of triple Higgs couplings. Black dots indicate the existent scan parameter points in the $\kappa _{\lambda }$-$\lambda _{hhH}$ plane within and outside the allowed region that was obtained from the figures in the upper row. The red star indicates the SM limit ($\kappa _{\lambda }= 1$ and $\lambda _{hhH}= 0$). Lower right: expected sensitivity to the deviation of the cross section from the SM value. Red star indicates the SM

Fig. 7

Plane 2. 2HDM, type I, $m_{12}^2$ versus $c_{\beta - \alpha }$. Otherwise plots as in Fig. 6

We present our results within the four benchmark planes discussed above in Figs. 6, 7, 8, 9 and 10. For each plane in the upper left and middle plot we will show the predictions of $\kappa _{\lambda }$ and $\lambda _{hhH}$, as obtained in Refs. [14, 15]. The upper right plot, for better comparison, repeats the results of $\sigma _\textrm{2HDM}/\sigma _\textrm{SM}$ at NLO QCD as presented in the upper left plots in Figs. 2, 3, 4 and 5, where we here also show the maximum (minimum) value of the coupling that is realized within the allowed region as red (blue) dots. The three upper plots are always given in the plane of the two free parameters involved in the respective benchmark choice. The lower left plot shows which combinations of $\kappa _{\lambda }$ and $\lambda _{hhH}$ can be reached in each plane, where the points inside the area allowed by theoretical and experimental constraints are marked in red (and indicated with a red arrow). The lower middle plot, focusing on the allowed region in the $\kappa _{\lambda }$-$\lambda _{hhH}$ plane, presents the values of $\sigma _\textrm{2HDM}/\sigma _\textrm{SM}$ at NLO QCD in this plane (with the SM point $\kappa _{\lambda }= 1$, $\lambda _{hhH}= 0$ marked by a red star). This indicates the dependence of the total 2HDM di-Higgs production cross section on the two involved triple Higgs couplings. The black points represent the values of the THCs that are reached in this plane. The lower right plot shows the same area in the $\kappa _{\lambda }$-$\lambda _{hhH}$ plane, now indicating the expected number of $\Delta \sigma _\textrm{SM}$, see Eq. (11), that the (to be measured) 2HDM result differs from the SM prediction, i.e. with which significance such a deviation can be measured experimentally.

In benchmark plane 1, Fig. 6, one can observe from the comparison of the upper left and right plots that within the allowed range, as discussed above, the smallest $\kappa _{\lambda }$ value gives rise to the largest value of $\sigma _\textrm{2HDM}$. As can be inferred from the lower middle plot, in this benchmark plane the cross section depends strongly on $\kappa _{\lambda }$, but effectively not on $\lambda _{hhH}$. This is due to the fact, as discussed above, that the heavy ${\mathcal{C}\mathcal{P}}$-even Higgs is too heavy to give a sizable s-channel contribution. Overall, one can observe that for the smallest allowed $\kappa _{\lambda }$ values, $\kappa _{\lambda }\sim -0.4$, a cross section enhancement of up to $\sim 3$ can be found.

Finally, we see from the lower right plot that for the smallest $\kappa _{\lambda }$, corresponding to the largest $\sigma _\textrm{2HDM}$, a deviation of up to $\Delta \sigma _\textrm{SM} \sim 9$ can be expected. This indicates that within this 2HDM benchmark plane a clear distinction between the 2HDM and the SM via the di-Higgs production cross section can be possible. Deviations of more than $2\sigma$ can be expected for .

In benchmark plane 2 a similar result as in plane 1 can be observed, as shown in Fig. 7. The largest cross sections are found for the smallest $\kappa _{\lambda }$ values, and the predicted 2HDM di-Higgs cross section depends only mildly on $\lambda _{hhH}$. The latter can again be understood because of the relatively large value of $m_H= 650 \,\, \textrm{GeV}$ in this benchmark plane. The maximum significance of the 2HDM deviation w.r.t. the SM value is less than for plane 1 with a value of at most $3.5\,\sigma$, reached for $\kappa _{\lambda }\sim 0.9$ and $\lambda _{hhH}\sim -0.5$.

The situation is more involved in plane 3, which we show in Fig. 8. As discussed in the previous subsection, very large enhancements can be reached in this parameter plane, and larger allowed regions are found for both signs of $c_{\beta - \alpha }$. The lower middle plot, showing the cross section enhancement w.r.t. the SM seems to show a relatively small enhancement of up to $\sim 3$. The larger effects that actually occur (enhancements of up to $\sim 8$) are found in comparably small regions and are thus not well visible in this figure (but will be shown clearly below). The lower right plot shows the $\Delta \sigma _\textrm{SM}$, and for large parts of the parameter space we find the same feature as in the two benchmark planes above: the largest deviations are found for the smallest $\kappa _{\lambda }$ values, and independent of $\lambda _{hhH}$, reaching about $5\,\sigma$. However, some “overlaid” structure is visible around $\kappa _{\lambda }\sim 1$. Here the same combinations of $\kappa _{\lambda }$ and $\lambda _{hhH}$ are reached for different points in the parameter space, in particular for both signs of $c_{\beta - \alpha }$. To analyze this scenario in more detail we split up the plots for positive and negative $c_{\beta - \alpha }$.

Fig. 8

Plane 3. 2HDM type I, $m_H=m_A=m_{H^\pm }$ versus $c_{\beta - \alpha }$. Otherwise plots as in Fig. 6

Fig. 9

Plane 3. Split for negative (left) and positive (right) values of $c_{\beta - \alpha }$. Upper line: allowed region. Middle line: total di-Higgs production cross section at NLO QCD w.r.t the SM. Lower line: expected sensitivity to the cross section deviation (zoomed into the interesting region)

In Fig. 9 we present the results where we have divided the allowed region of benchmark plane 3 and the obtained cross sections and their sensitivity in the couplings plane in positive and negative values of $c_{\beta - \alpha }$. The left (right) column in Fig. 9 shows the results for $c_{\beta - \alpha }$ negative (positive). The upper row indicates the combination of $\kappa _{\lambda }$ and $\lambda _{hhH}$ that can be reached in the full benchmark plane. The middle row shows $\sigma _\textrm{2HDM}/\sigma _\textrm{SM}$, whereas the lower row indicates the level of $\Delta \sigma _\textrm{SM}$ that can be reached, where we have zoomed further into the interesting region. The middle left plot demonstrates that for $\kappa _{\lambda }$ close to 1 the cross section can be strongly enhanced with the enhancement strongly depending on the BSM THC $\lambda _{hhH}$. This behavior can be traced back to the H contribution in the s-channel for relatively small values of $m_H$, as discussed in the previous subsections. Looking into the (zoomed in) result for $\Delta \sigma _\textrm{SM}$ (lower left plot) one can observe that for the smallest values of $\lambda _{hhH}\sim -0.2$ a deviation from the SM by up to $35\,\sigma$ can be expected. More importantly, the size of the deviation may give an indication of the value of $\lambda _{hhH}$. Going to positive values of $c_{\beta - \alpha }$ as presented in the right column, one can observe that for large parts of the parameter space a dependence solely on $\kappa _{\lambda }$ is found, as in the previous benchmark planes. However, again for $\kappa _{\lambda }\sim 1$ strong enhancements are found due to the presence of the heavy ${\mathcal{C}\mathcal{P}}$-even Higgs in the resonance. This is better visible in the lower right plot (the “gap-like” structures originate from BSM Higgs-boson search limits, due to under-fluctuations for that mass in the experimental data), demonstrating that for small, but positive values of $\lambda _{hhH}$ deviations of up to $6\,\sigma$ can be seen, whereas for negative values of $\lambda _{hhH}\sim -0.2$ even deviations of up to $9\,\sigma$ can be found. Finally, we also see that in some parameter regions, namely when $\sigma /\sigma _\textrm{SM} < 1$, the sensitivity to the THC worsens w.r.t the SM and the variable $\Delta \sigma _\textrm{SM}$ drops below 1. This means that we would need more statistics to measure the cross section and infer the values of the THC than expected in the SM. Here it should be kept in mind that this analysis only demonstrates the possible dependencies and effects of the THCs on the di-Higgs production cross section. As will be discussed below, an actual possibility for a determination of $\lambda _{hhH}$ (or $\kappa _{\lambda }$ ) is not implied, as it depends on the precise knowledge of the other (free) parameters.

Our final analysis in this section is done for benchmark plane 4, as shown in Fig. 10. In this $m_A= m_{H^\pm }$-$m_H$ plane the value of $\kappa _{\lambda }$ is always close to 1, varying only by about $\sim 10\%$, so that large variations of the di-Higgs production cross section can only be produced by resonant enhancement. The coupling $\lambda _{hhH}$ varies between 0 to $\sim -1.5$ in the allowed region (and even down to $\sim -4.5$ for the largest $m_H$ values). The cross section, as discussed already in the previous subsection shows an interesting enhancement of up to $\sim 60\%$, where the heavy Higgs is resonant and not too heavy, $m_H\sim 400 \,\, \textrm{GeV}$. We will use the behavior of $\sigma _\textrm{2HDM}$ in this benchmark plane for a more detailed analysis of the invariant $m_{hh}$ distribution in the next section.

The projection into the $\kappa _{\lambda }$-$\lambda _{hhH}$ plane shows only a line, which can be understood as follows. Looking at Eqs. (6) and (7) and discarding all the terms proportional to constants (the angles $\alpha$ and $\beta$) we find the following relations:

$$\begin{aligned} \kappa _{\lambda }= & {} c_1 + c_2 \bar{m}^2,\nonumber \\ \lambda _{hhH}= & {} c_3 + c_4 \bar{m}^2, \end{aligned}$$

(12)

where the $c_{1,2,3,4}$ are constant terms, and it is taken into account that according to Eq. (9) $\bar{m}^2 \propto m_{12}^{2}\propto m_H^2$. Consequently, one finds

$$\begin{aligned} \lambda _{hhH}= c_3 - \frac{c_1 \,c_4}{c_2} + \frac{c_4}{c_2}\kappa _{\lambda }~, \end{aligned}$$

(13)

resulting in the linear dependence that is observed in the lower plots of Fig. 10.

Now we proceed to analyze the values of the cross section that are possible for the different values of the THCs, even though we do not have a truly 2-dimensional plot in these cases. For the benchmark plane 4, in the lower middle plot of Fig. 10 the cross section is badly defined in the sense that more than one value of the cross section corresponds to a particular value of the THCs. This happens when we allow for a change in the masses but fix the angles, as discussed above. The THCs change in a coherent way for different masses $m_H$ (see upper left and middle plots in Fig. 10), while the cross section has different possible values. As an example, for $m_H$ in the range $\sim 220 \,\, \textrm{GeV}$ to $\sim 800 \,\, \textrm{GeV}$ it can vary within $\sim (0.8-1.6) \times \sigma _\textrm{SM}$, as can be seen in the upper right plot. Therefore, in the lower middle plot we represented the mean value of the cross section as a circle for a particular combination of ($\kappa _{\lambda }, \lambda _{hhH}$). We show maximum (upper triangle “slightly displaced above the circles”) and minimum (lower triangle “slightly displaced below the circles”) values of the normalized cross section for this same combination of ($\kappa _{\lambda }, \lambda _{hhH}$). One can observe that the highest cross section is realized for a $\kappa _{\lambda }\sim 0.985$ and $\lambda _{hhH}\sim -0.2$. In this point the value of the cross section varies roughly from 1 to 1.6 and the sensitivity that can be reached in the most optimistic scenario (i.e. the largest deviation from the SM that is realized) is almost 2.5 $\sigma$, as can be seen in the lower right plot. This enhancement is relatively small, but it demonstrates that in this plane the relevant role of the coupling $\lambda _{hhH}$ is more significant than $\kappa _{\lambda }$, which is very close to 1, where these effects are found. The size of the deviation clearly depends on $\lambda _{hhH}$ in this case.

Fig. 10

Plane 4. 2HDM type I, $m_H$ versus $m_A = m_{H^\pm }$. Otherwise plots as in Fig. 6

Let us add a final word on the theory uncertainties. We outlined above that we have to rely on the NLO QCD corrections in the heavy-top limit. The higher-order corrections can, however, also change the shape of the distributions. Without an available calculation taking into account the NLO top-mass effects on the distributions, which is missing for the 2HDM case with resonant Higgs production, it is difficult and highly speculative to try to do an estimate, as can be seen from the at present available discussions on the theory uncertainties [62]. While a missing theory uncertainty estimate limits the interpretation of our results, they are still useful in the following sense. By investigating several benchmark points we get an overall picture that may also represent to some extent the impact of a changed shape. The latter would lead to a modified relation between the observation and the input parameters. Furthermore, our results represent the best case by assuming a constant K-factor for the distributions and hence give us insights on what can in the best case be expected.

3.4 Conclusion from the cross section analysis

The four benchmark planes have been chosen to map out the different phenomenology that can be expected from the 2HDM in di-Higgs production, $gg \rightarrow hh$. This refers to the variation of the relevance of the H exchange contribution, as well as to the variation of the involved Yukawa couplings and in particular of the two relevant THCs, $\lambda _{hhh}$ and $\lambda _{hhH}$.

It was demonstrated that the 2HDM cross section for $gg \rightarrow hh$ can differ substantially from the corresponding SM result. In most of the cases the deviation was found at the level of up to $3\,\sigma$, but also $10\,\sigma$ or more can be found in extreme cases. Smaller variations arise from the deviations from $\kappa _{\lambda }= 1$. The largest deviations, however, were shown to arise from the H exchange contribution. For this analysis particularly the mapping of our parameter space onto the $\kappa _{\lambda }$–$\lambda _{hhH}$ plane proved to be useful. The results are corroborated by the comparison of the calculation of the cross section including all diagrams in comparison with the calculation leaving out the H resonance contribution.

Furthermore, it could be observed (in agreement with Ref. [14]) that in the most extreme cases values of $\kappa _{\lambda }= [-0.5, 1.1]$ are found, where the lower range of these values would lead to an observable deviation at the HL-LHC.¹³

Fig. 11

Left: Partial result $\sigma _\textrm{interf}$ Eq. (15) for three different decay widths. Right: Effect of $\Gamma _H^\textrm{tot}$ on the the invariant mass distribution for one benchmark point and three values of $\Gamma _H^\textrm{tot}$ (see text)

4 Analysis of $m_{hh}$

In the next step of our analysis we will study the influence of the THCs on the di-Higgs production cross sections by evaluating the di-Higgs invariant mass distribution, $m_{hh}$. We first demonstrate in a toy example the effect of the characteristic properties of the resonant Higgs boson: its mass, its width, and the sign of the coupling combination $(\lambda _{hhH}\times \xi _H^t)$. Subsequently, the analysis will be performed for several benchmark points located in the planes discussed in the previous section, where the effects of the characteristics of the resonance will be demonstrated in a real model.

The invariant mass distributions, $d\sigma /dm_{hh}$, are also obtained with the code HPAIR. We will use a grid of values for the invariant mass $m_{hh}$ that range from $250 \,\, \textrm{GeV}$ to $1250 \,\, \textrm{GeV}$. As a default value we will use a bin size of $20 \,\, \textrm{GeV}$ (where experimentally a bin size of $\sim 50 \,\, \textrm{GeV}$ appears more realistic, see the discussion below). This bin size is used for demonstrative purposes. In a later step we will analyze the effect of different bin sizes and other experimental effects to obtain a more realistic picture of $m_{hh}$ distributions.

4.1 General analysis of the effects

In this subsection we will analyze a toy model for the resonance to demonstrate the effects of the mass, width and couplings of the resonant Higgs boson in the s-channel exchange.

The effect of the total decay width of the heavy Higgs boson, $\Gamma _H^\textrm{tot}$, is important whenever the resonant diagram gains significance in the calculation of the cross section. This happens close to the resonance at $m_H\sim m_{hh}$, as discussed in the previous section. For a correct treatment close to the resonance the total width has to be included into the propagator,

$$\begin{aligned} \frac{1}{Q^2-m_H^2} \rightarrow \frac{1}{Q^2-m_H^2 + im_H\Gamma _H^\textrm{tot}}. \end{aligned}$$

(14)

From this expression one can clearly see that the dominant effect of $\Gamma _H^\textrm{tot}$ appears when the intermediate Higgs boson mass is equal to the (reduced) center of mass energy $Q^2$. In the Higgs pair production process, the total decay width of the heavy Higgs becomes relevant near the resonant region where the behavior of the cross section can be dominated by the interference between the resonant and the non-resonant contributions, which is proportional to

$$\begin{aligned} {\sigma _\textrm{interf} =} \frac{Q^2-m_H^2}{(Q^2-m_H^2)^2+m_H^2{\Gamma ^\textrm{tot}_H}^2}\,. \end{aligned}$$

(15)

We use this expression to investigate the resonant behavior of the $m_{hh}$ distribution. In Fig. 11 (left) we show $\sigma _\textrm{interf}$ as a function of $m_{hh}= Q$. We have chosen $m_H= 300 \,\, \textrm{GeV}$ and three exemplary values of $\Gamma _H^\textrm{tot}$: $0.1 \,\, \textrm{GeV}$ (red), $10 \,\, \textrm{GeV}$ (dark blue) and $50 \,\, \textrm{GeV}$ (light blue). In all cases $\sigma _\textrm{interf}$ shows a peak-dip structure, with the change exactly at $m_{hh}= m_H$, as expected from Eq. (15). Furthermore, one observes that the highest (smallest) peak-dip structure is obtained for the smallest (highest) value of $\Gamma _H^\textrm{tot}$, following the analytical behavior of Eq. (15). We furthermore observe that the “total width of the effect”, given by the width of the peak at half of its maximum value, increases with increasing $\Gamma _H^\textrm{tot}$, as expected.

Fig. 12

Left: couplings involved in the resonant diagram (top Yukawa, $\xi _H^t$, and BSM triple Higgs coupling, $\lambda _{hhH}$). Right: invariant mass distributions for different signs of ($\lambda _{hhH}\times \xi _H^t$)

Table 2 Selected points in benchmark plane 3 with large di-Higgs production cross section

The features observed for $\sigma _\textrm{interf}$ are also found in the calculation of the $m_{hh}$ distribution of the complete cross section, i.e. the result from taking into account the complete resonant and the non-resonant contributions, as shown in the right plot of Fig. 11. Here we depict $d\sigma /dm_{hh}$ as a function of $m_{hh}$ for one benchmark point of benchmark plane 4 with $m_A= m_{H^\pm }= 544.72 \,\, \textrm{GeV}$ and $m_H= 515.5 \,\, \textrm{GeV}$.¹⁴  For the total width of H we find $\Gamma _H^\textrm{tot}\sim 3 \,\, \textrm{GeV}$, resulting in the red curve. In order to illustrate the effects of the size of $\Gamma _H^\textrm{tot}$, as seen in the left plot, we also show the results for ad-hoc set values of $\Gamma _H^\textrm{tot}= 10 \,\, \textrm{GeV}$ (dark blue) and $50 \,\, \textrm{GeV}$ (light blue). The main features of $\Gamma _H^\textrm{tot}$ (height of the peak-dip structure and the “width of the effect”) are found in the full calculation exactly as in $\sigma _\textrm{interf}$.

However, there is one important difference between the results for $\sigma _\textrm{interf}$ and the full invariant mass distribution results which can be observed in Fig. 11. While for $\sigma _\textrm{interf}$ a peak-dip structure is found, in the full calculation for our chosen benchmark point a dip-peak structure can be observed. This difference can be traced back to the sign of ($\lambda _{hhH}\times \xi _H^t$), which enters as prefactor in the the resonant diagram. In the left plot of Fig. 12 the resonant H diagram is shown with the two coupling factors entering the amplitude: the top-Yukawa coupling modification factor $\xi _H^t$ of the heavy Higgs H and the THC $\lambda _{hhH}$. The right plot in Fig. 12 demonstrates the effect of sign($\lambda _{hhH}\times \xi _H^t$). The red curve is identical to the red curve in the right plot of Fig. 11, as obtained for the value of $\lambda _{hhH}= -0.3975$, with $\lambda _{hhH}\times \xi _H^t < 0$. The blue curve shows the $m_{hh}$ distribution for the (ad hoc) flipped sign, i.e. with $\lambda _{hhH}= +0.3975$ (normalized to the corresponding value of the full cross section obtained for this trilinear Higgs coupling). As can be expected, the flip of the sign($\lambda _{hhH}\times \xi _H^t$) also flips the dip-peak structure to a peak-dip structure ($\sigma _\textrm{interf}$ shown above corresponds to a positive sign). The question arises whether an experimental analysis can be sensitive to the difference between peak-dip and dip-peak, and thus provide a handle on the sign of ($\lambda _{hhH}\times \xi _H^t$). This question will be analyzed below.

Fig. 13

Analysis of points with large di-Higgs production cross sections in the benchmark plane 3. Left: location of the benchmark points in the total production cross section plot. Middle: invariant mass distribution for selected points (with a bin size of $5 \,\, \textrm{GeV}$). The colors of the points in the two figures are matching. The values of $\sigma _\textrm{tot}$ in the legend indicate the LO inclusive cross section prediction for each point. Right: zoom in the region of interest in the $m_{hh}$ distribution

4.2 Model based analysis: benchmark plane 3

We start our model based $m_{hh}$ analysis for several points given in the benchmark plane 3. This choice is based on the fact that in this plane $m_H$ is a free parameter, and a large variation of $\lambda _{hhH}$ has been found, see the previous section. This allows for a detailed analysis of the effects of the resonant H contribution. First we will investigate the points that present the largest enhancement of the cross section w.r.t. the SM within the allowed region, as listed in Table 2. Second we will look at points with $c_{\beta - \alpha }\sim 0.1$, as listed in Table 4. Finally we will analyze points with $c_{\beta - \alpha }$ $\sim 0.2$, i.e. a relatively large deviation from the alignment limit, as listed in Table 5. The aim of this study is to extract the general behavior and the influence of specific parameters on the experimental measurement of the cross section. This will allow us to track variations of the parameters that we are mostly interested in ($m_H,\; \Gamma _{H}^\textrm{tot}$ and $\lambda _{hhH}$).

4.2.1 Benchmark plane 3: large di-Higgs production cross sections

We first analyze three points in benchmark plane 3 with large enhancements of the di-Higgs production cross section w.r.t. the SM. They are located close to the alignment limit and can be seen in the left part of Fig. 13 as red, blue and black dots. In the first step of the analyses we choose a bin size of $5 \,\, \textrm{GeV}$ to make the large resonant enhancement, which is very narrow, clearly visible. The values of the parameters of each point are listed in Table 2.

The di-Higgs production process is kinematically forbidden for $m_{hh}< 250 \,\, \textrm{GeV}= 2 \,m_h$. Once this threshold is surpassed, one can observe a resonant enhancement for $m_{hh}\sim m_H$. This is clearly seen at the location of the resonant peaks in the invariant mass distribution in Fig. 13 (middle). For the red and the black points the resonant peak is found around $\sim 265 \,\, \textrm{GeV}$, while for the blue point it is located at $\sim 292 \,\, \textrm{GeV}$, corresponding to the respective $m_H$ value. The “height” and “width” of the peaks is related to the total decay width $\Gamma _H^\textrm{tot}$ of the heavy Higgs boson, which is largest for the red point ($\sigma /\sigma _\textrm{SM} \sim 8$) and smallest for the black point ($\sigma /\sigma _\textrm{SM} \sim 2.5$), as shown in Table 2. Furthermore, the resonant heavy Higgs contribution yields the already observed typical pattern, a peak-dip or dip-peak structure, depending on the parameter point. The peak-dip structure is observed in the blue and red points, whereas in the case of the black point one can only see the peak, see the discussion below. This pattern is clear when looking at the zoom in the low $m_{hh}$ region in the right plot of Fig. 13. Moreover, we observe for all three points an enhancement at an invariant mass of 350–400 $\,\, \textrm{GeV}$, which is related to the top pair production threshold in the resonant diagram.¹⁵

The three points have different values of $c_{\beta - \alpha }$, which change the Yukawa coupling of the top quark according to the expression:

$$\begin{aligned} \xi _H^t = c_{\beta - \alpha }-s_{\beta - \alpha }\cot \beta , \end{aligned}$$

(16)

resulting in a positive (negative) sign of $(\lambda _{hhH}\times \xi _H^t)$ for the red and blue (black) points, as shown in Table 1. This in turn results in a peak-dip (dip-peak) structure, cf. Table 3. The pattern of the differential distribution changes according to the sign of $(\lambda _{hhH}\times \xi _H^t)$. For the black curve only a peak is visible, because the dip before it cannot be produced for masses below $250 \,\, \textrm{GeV}$.

Table 3 Structure of the resonance

A more detailed analysis of the three points is presented in Fig. 14, where we analyze the contribution of individual (groups of) diagrams. In the upper left plot we show the total, i.e. including all diagrams, distribution for the three points (as in the right plot of Fig. 13) but changing the bin size to 20 GeV in order to represent a more realistic experimental set up. One can observe already in the example of the black point that the bin size (and location) is important for the observation of the phenomenological features, as the closeness to the kinematic threshold can prevent the dip-peak structure to develop fully in the observed distribution.

In the upper right, and lower row of Fig. 14 we disentangle the contributions of the individual diagrams for the red, black and blue points, respectively. We have calculated the total differential distribution including all three diagrams for di-Higgs production (red), the SM-like cross section, called continuum, – including only the box and the SM-like Higgs boson in the s-channel diagrams – (black), the contribution of the diagram with no triple Higgs couplings involved, i.e. the box diagram (yellow), the contribution of the two diagrams with the triple Higgs couplings, which includes the h and H in the s-channel (purple), and the contribution with only h (light blue) and with only H (dark blue), respectively, in the ${s\mathrm{- channel}}$. For all three points the same pattern can be observed. The 2HDM cross section (red) follows largely the SM-like distribution (black), apart from the strong resonant enhancement at $m_{hh}\sim m_H$. This is caused by the H s-channel contribution (blue), potentially providing sensitivity to $\lambda _{hhH}$. Furthermore, the destructive interference of the box-diagram (yellow) and the SM-like h-exchange contribution (light blue) is clearly visible in the continuum, i.e. SM-like, contribution of the distribution (black).

Fig. 14

$m_{hh}$ distributions for selected points in plane 3. Upper left: total $m_{hh}$ distributions for the points of Table 2; upper right (red), lower left (blue), lower right (black): individual contributions to the $m_{hh}$ distribution for the three points: total cross section (red), continuum cross section (black), $m_{hh}$ involving only $\lambda _{hhh}$ ($\lambda _{hhH}$) in light (dark) blue, $m_{hh}$ involving both (no) THCs in purple (yellow)

4.2.2 Plane 3: $c_{\beta - \alpha }\sim$ 0.1

Next we proceed to study a set of points that are all located at the same value of $c_{\beta - \alpha }\sim 0.1$. The exact value of $c_{\beta - \alpha }= 0.1015$ results from the grid used to scan this plane. In this case the only change between the benchmark points, as listed in Table 4, is the common mass $m_H$ of the heavy Higgses, with correspondingly modified couplings and decay widths.

Table 4 Selected points in benchmark plane 3 for $c_{\beta - \alpha }$ $\sim$ 0.1

The points are also shown as orange, yellow, purple, garnet and green dots (in ascending mass order) in the upper left plot of Fig. 15 (repeating the upper left plot of Fig. 8). The upper right plot of Fig. 15 (repeating the middle right plot of Fig. 9) indicates the location of these points in the $\kappa _{\lambda }$-$\lambda _{hhH}$ plane. One can observe that with increasing $m_H$ the points are decreasing in $\kappa _{\lambda }$(from $\kappa _{\lambda }\sim 1$ down to zero) and are increasing in $\lambda _{hhH}$ (from $\lambda _{hhH}$ close to zero to $\lambda _{hhH}\sim 1$).

Fig. 15

Sensitivity to triple Higgs couplings for points with $c_{\beta - \alpha }= 0.1015$ in benchmark plane 3. Upper left: the common mass $m \equiv m_H= m_A= m_{H^\pm }$ and correspondingly $m_{12}^{2}$ change, as marked with orange, yellow, purple, garnet and green dots (in ascending mass order, color coding indicating $\sigma /\sigma _\textrm{SM}$). Upper right: location of the benchmark points in the $\kappa _{\lambda }$-$\lambda _{hhH}$ plane (color coding indicating $\sigma /\sigma _\textrm{SM}$). Lower plot: $m_{hh}$ distribution for the five benchmark points with a $5 \,\, \textrm{GeV}$ bin size. The colors indicate $m_H$, the red arrows show the location of the “resonant peak”

The $m_{hh}$ distributions for the five benchmark points are presented in the lower plot or Fig. 15, with a bin size of $5 \,\, \textrm{GeV}$. The color indicates the value of $m_H$ (as defined in the upper plots). The red arrows indicate the location of the “resonant peaks” (for $m_H > 250 \,\, \textrm{GeV}$). The resonant enhancement is found to be tiny, despite the non-negligible values of $\lambda _{hhH}$. The reason for the unrealistically small bin size of $5 \,\, \textrm{GeV}$ is to see any peak at all. It is clear that for these points the enhancement of $\sigma _\textrm{2HDM}$ w.r.t. $\sigma _\textrm{SM}$ is caused purely by the reduced $\kappa _{\lambda }$ values which alleviates the destructive interference between triangle and box contributions present in the SM. The resonant H exchange hardly contributes to the total cross section. The structure of the enhancement in this case is hard to infer from the plot, but looking closely one can see a peak-dip structure. The reason for this small resonant contribution can be found in the top Yukawa coupling value of the heavy ${\mathcal{C}\mathcal{P}}$-even Higgs. Following Eq. (16) we obtain a value of $\xi _H^t = 5 \times 10^{-4} >0$, thus rendering the resonant contribution negligible. The triple Higgs couplings $\lambda _{hhH}$ listed in Table 4 are all positive, so that the overall sign for the coupling factor of the triangle contribution is positive and the (hardly visible) structure is a peak-dip one as expected. Furthermore, we have seen in Fig. 14 that the largest contribution in the lower mass spectrum comes from the diagram with a light Higgs h exchange, i.e. from the diagram involving $\kappa _{\lambda }$. This diagram hence drives the behavior of the distribution. In the lower plot of Fig. 15 this trend is clearly visible in the lower part of the spectrum, . The smaller the value of $\kappa _{\lambda }$ for a particular point (as seen in upper right plot), the larger the enhancement in the invariant mass distribution at lower $m_{hh}$. The most extreme point is the green one, for which $\kappa _{\lambda }$ is close to zero, and the $m_{hh}$ spectrum shows a clear bump at $m_{hh}\sim 350 \,\, \textrm{GeV}$. It should be recalled that the gluon fusion di-Higgs production cross section has a minimum for $\kappa _{\lambda }\sim 2.5$ and is higher for small (or very large values) of $\kappa _{\lambda }$.

4.2.3 Plane 3: $c_{\beta - \alpha }\sim$ 0.2

We finish our analysis of benchmark points in plane 3 with five points with a relatively large value of $c_{\beta - \alpha }\sim 0.2$, i.e. relatively far away from the alignment limit, as given in Table 5. As above, the exact value of $c_{\beta - \alpha }= 0.203$ is given by the scanned grid. The points are shown in the upper left and upper right plot of Fig. 16 as colored dots in orange, yellow, purple, garnet and green dots (in ascending mass order), color coding indicating $\sigma /\sigma _\textrm{SM}$ in the $c_{\beta - \alpha }$-$m_H$ and $\kappa _{\lambda }$-$\lambda _{hhH}$ plane in the upper left and right plot, respectively. As can be observed in the upper right plot, all points have $\kappa _{\lambda }\sim 1$, i.e. no relevant change in the cross section can be expected from the contribution of the h-exchange diagram, so the lower part of the $m_{hh}$ spectrum is very similar for all the points. On the other hand, the values of $\lambda _{hhH}$ decrease from around zero down to $\lambda _{hhH}\sim -0.5$. However, as can be seen in the two upper plots of Fig. 16, the variation of the total cross section is relatively small. The largest cross sections are found for $m_H= 312.0 \,\, \textrm{GeV}$ (yellow) and $m_H= 399.75 \,\, \textrm{GeV}$ (purple), i.e. around $\sim 350 \,\, \textrm{GeV}$, see the discussion in Sect. 4.2.1. In the lower plot of Fig. 16 we show the $m_{hh}$ distribution for the five points. For four of them with $m_H> 2 m_h$ a clear resonance dip-peak structure can be observed at $m_H\sim m_{hh}$, as expected.

Table 5 Selected points in benchmark plane 3 for $c_{\beta - \alpha }$ $\sim 0.2$

Fig. 16

Sensitivity to triple Higgs couplings for points with $c_{\beta - \alpha }= 0.203$ in benchmark plane 3. Upper left $m \equiv m_H= m_A= m_{H^\pm }$ and correspondingly $m_{12}^{2}$ changes, as marked with orange, yellow, purple, garnet and green dots (in ascending mass order, color coding indicating $\sigma /\sigma _\textrm{SM}$). Upper right: location of the benchmark points in the $\kappa _{\lambda }$-$\lambda _{hhH}$ plane (color coding indicating $\sigma /\sigma _\textrm{SM}$). Lower plot: $m_{hh}$ distribution for the five benchmark points. The colors indicate $m_H$

Fig. 17

$m_{hh}$ distributions for selected points in plane 3 with $c_{\beta - \alpha }\sim 0.2$. Upper left: total $m_{hh}$ distributions for the points of Table 5; upper middle, left and lower left, middle and right: individual contributions to the $m_{hh}$ distribution for the five points: total SM-like cross section in black, total cross section in red, $m_{hh}$ involving only $\lambda _{hhh}$ ($\lambda _{hhH}$) in light (dark) blue, $m_{hh}$ involving both (no) THCs in purple (yellow)

In Fig. 17 we present a more detailed analysis of the sensitivity to the triple Higgs couplings in the invariant mass distribution following the same notation as in Fig. 14. We show the invariant mass distribution from all the diagrams in the upper right plot and then split the individual contributions for each particular mass point in the rest of the plots. The first one for $m_H= 244.5 \,\, \textrm{GeV}$ is shown in the upper middle plot, which has $m_H$ below the di-Higgs production threshold. Consequently, no enhancement due to the diagram containing $\lambda _{hhH}$ can be observed, and the total cross section is almost indistinguishable from the SM-like result in this case. For the other masses we find a similar result as in Fig. 14. One can observe that the s-channel contribution involving the heavy Higgs with its trilinear coupling $\lambda _{hhH}$ is responsible for the enhancement close to the mass of the intermediate Higgs boson, while the effect of the $\kappa _{\lambda }$ is mostly significant in the low mass region of the plot. The contribution of the diagrams involving THCs (purple) interferes with the continuum (box diagram) shown in yellow and creates the dip-peak structure that can be observed in the total distributions, see Fig. 17 (upper left).

The top Yukawa coupling for this value of $c_{\beta - \alpha }$ is $\xi _H^t = 0.1020 > 0$, and thus the sign of $(\lambda _{hhH}\times \xi _H^t)$ is negative, resulting in the dip-peak structure observed. In principle, this type of distributions can yield a handle on the size and sign of $\lambda _{hhH}$, as will be discussed in more detail below.

Fig. 18

Interference contributions for the benchmark points in plane 3 with $c_{\beta - \alpha }$ = 0.203. Left: interference of the two triangle diagrams. Middle: interference of the SM-like diagrams. Right: interference between the box and the resonant diagram. Solid lines indicate that the interference is positive and dashed lines indicate that it is negative

Table 6 Selected points in benchmark plane 4 for $m_A= m_{H^\pm }\sim 545 \,\, \textrm{GeV}$

In Fig. 18 we further analyze the interference contributions of the s-channel diagrams in Fig. 1. In the left plot we show the interference term of the diagram with the s-channel h exchange (A) and diagram with the s-channel H exchange (B). The interference term in this case is defined as $|A+B|^2-|A|^2-|B|^2$. The solid (dashed) lines indicate positive (negative) interference. One can observe a similar behavior to the above discussed interference between resonant and box contributions, i.e. that these two diagrams interfere constructively up to $m_{hh}\le m_H$, and destructively for larger $m_{hh}$ values, i.e. the interference term changes its sign. The diagram A and the box diagram (C) interfere negatively accross the whole invariant mass range as shown in the middle plot of Fig. 18. This behavior corresponds to the result found for the SM di-Higgs production, where only these two diagrams are present Finally, the interference of B and C, shown in the right plot of Fig. 18, has two sign changes. Up to $m_{hh}\le m_H$ the interference is negative, leading to the dip in the total $m_{hh}$ distribution. For larger values it turns positive, leading the subsequent peak in the total distribution, see the discussion in Sect. 4.1. The second sign change happens because the interference approaches zero at an $m_{hh}$ value not related to $m_H$. In the plot the interference lines in principle go down to zero, which, however, is not visible due to the log scale and the finite bin width.

4.3 Model based analysis: benchmark plane 4

To complete our $m_{hh}$ analysis we investigate benchmark points in plane 4. In this plane the heavy Higgs boson masses, as in plane 3, are free parameters and are in agreement with the applied constraints over a relatively large interval, i.e. the effects of a mass variation (as well as a variation of $\lambda _{hhH}$) can be readily analyzed. In contrast to plane 3, however, we are always far away from the alignment limit by fixing $c_{\beta - \alpha }= 0.2$. Furthermore, the effects of a variation of $m_H$ can be better isolated by defining this mass independent of the other heavy BSM Higgs-boson masses. The selected points are listed in Table 6. They are all located at the same mass of $m_A= m_{H^\pm }= 544.75 \,\, \textrm{GeV}$. As was demonstrated in Sect. 3.3, $\kappa _{\lambda }$ and $\lambda _{hhH}$ are proportional to each other, and allowed values of $\lambda _{hhh}$ are within $\sim 2\%$ of $\kappa _{\lambda }= 1$, whereas $\lambda _{hhH}$ is found for our benchmark points in the interval $[\sim 0, -0.7]$. Similarly, also $\Gamma _H^\textrm{tot}$ grows with increasing $m_H$. All corresponding numerical values can be found in Table 6.

Fig. 19

Sensitivity to triple Higgs couplings for points within benchmark plane 4. Upper left: the points have fixed $m_A= m_{H^\pm }= 544.75 \,\, \textrm{GeV}$, $c_{\beta - \alpha }= 0.2$, whereas $m_H$ and correspondingly $m_{12}^{2}$ change, as marked with purple, orange, blue, light blue, green, yellow and garnet dots (in ascending mass order, color coding indicating $\sigma /\sigma _\textrm{SM}$). Upper right: location of the benchmark points in the $\kappa _{\lambda }$-$\lambda _{hhH}$ plane. Lower line: $m_{hh}$ distribution for the seven benchmark points with a bin size of $5 \, (20) \,\, \textrm{GeV}$ in the left (right) plot. The colors indicate $m_H$

The location of the points in the benchmark plane is shown in the upper left plot of Fig. 19, and in the $\kappa _{\lambda }$-$\lambda _{hhH}$ plane in the upper right plot. The lower row shows the corresponding $m_{hh}$ distributions with the color indicating the $m_H$ value. In the left plot, for better visibility, we show the idealized case of a bin size of $5 \,\, \textrm{GeV}$, whereas the right plot shows the more realistic case of $20 \,\, \textrm{GeV}$.

One can observe that the resonant structure in this case is dip-peak since (as in the previous case) the top Yukawa coupling is positive and the BSM THC is negative. For the purple point no enhancement can be observed, since its mass is below the di-Higgs production threshold, $m_H^\textrm{purple} = 222.5 \,\, \textrm{GeV}$. The remaining points show a resonant enhancement as the invariant mass approaches the mass of the heavy Higgs, i.e. one expects to have the highest sensitivity to the THC $\lambda _{hhH}$ in this region. The difference between the heights of the peaks is found to be largest for small $m_H$, but naturally also decreases with increasing bin size, which will be further discussed below. The increasing bin size, in particular, decreases the visibility of the dip, an effect that is in particular visible for low $m_H$. This demonstrates the relevance of the bin size in a realistic experimental analysis (and will also be further discussed below).

5 Impact of experimental uncertainties

In this section we will analyze the impact of experimental uncertainties on the possible sensitivity to $\lambda _{hhH}$. These effects are the experimental smearing, i.e. the uncertainty in the $m_{hh}$ measurement, the experimental resolution, i.e. the size of the bin width, as well as the arbitrary location of the bin. We will also demonstrate how the experimental results for $\lambda _{hhH}$ change with a variation of sign$(\lambda _{hhH}\times \xi _H^t)$. We neglect any “background” from other SM processes. This would be subject to an dedicated experimental analysis that is far beyond the scope of our paper.

In order to estimate the sensitivity to the BSM coupling $\lambda _{hhH}$, following Ref. [22], we define a theoretical quantity that aims to quantify the “sensitivity to $\lambda _{hhH}$” (but is not meant as a determination of its precision, which requires a detailed experimental analysis, which is beyond the scope of our paper). We define

$$\begin{aligned} R := \frac{\sum _i |N_i^R - N_i^C|}{\sqrt{\sum _i N_i^C}}, \end{aligned}$$

(17)

where $N^{R}$ is the number of events of the resonant contribution, and $N^C$ is the number of events of the continuum. The window in which the events are counted is defined by

$$\begin{aligned} |N^R - N^C|&> \mathrm{bin\;size} \times 20 \,\, \textrm{GeV}~. \end{aligned}$$

(18)

The sum over i in Eq. (17) runs over all the bins that fulfill this condition. The chosen condition in Eq. (18) starts with a minimum of 1000 excess events due to the resonance when the bin size is 50 GeV and 200 events when the bin size is $10 \,\, \textrm{GeV}$, i.e. smaller bin sizes are not “punished”. Using the absolute value in the definition of R in Eq. (17), as well as in the definition of the window in Eq. (18) effectively makes use of both the dip and the peak of the smeared distribution. This constitutes a simplified theory definition, where in a realistic experimental analysis the dip-peak structure would be taken into account via a template fitting, see e.g. the analysis in Ref. [80]. The numbers of events are in turn obtained using the relation between the cross section and the integrated luminosity of the collider,

$$\begin{aligned} N = \sigma \cdot \mathcal {L}, \end{aligned}$$

(19)

where we have used $\mathcal {L} = 6000\; \mathrm{fb^{-1}}$, i.e. the sum of the anticipated luminosity of ATLAS and CMS combined at the end of the HL-LHC run. This constitutes the most optimistic case.

5.1 Smearing

Differential cross section measurements are affected by the finite resolution of the detectors. This translates into a blurred or “smeared” spectrum that can be observed in such experiments. We try to mimic this effect by artificially smearing the theoretical prediction for the invariant mass distributions of the chosen benchmark points. To do this we introduce a statistical error to our prediction of the invariant mass. We apply the uncertainties in $m_{hh}$ by allowing the value of an event to shift to the left or to the right in the spectrum according to a Gaussian probability distribution. The amount of smearing is defined in terms of a percentage of smearing p that indicates that the predicted value x should stay within the interval $[(1-p) \cdot x, (1+p) \cdot x]$ with a 78% probability, which corresponds to the definition of the full width half maximum of the Gaussian distribution (as given for the experimental analyses).

Fig. 20

Theoretical (blue) and smeared (red) invariant mass distributions for the selected benchmark point (see text). Solid (dashed) lines show the contribution of the total (continuum) differential cross section. Left (right) plot has a 10% (15%) smearing

Fig. 21

Different bin sizes for a 10% smeared distribution in the example benchmark point (10, 20, 40 and 50 $\,\, \textrm{GeV}$). The red lines correspond to the true (smeared and binned) prediction of the $m_{hh}$ distribution. The other color indicates the corresponding binned, but unsmeared distribution. Solid (dashed) lines represent the total (continuum) contribution to the cross section. The grey region represents the region that falls into the window defined to compute the variable R. The black vertical line indicates the value of the resonant mass, i.e. $512.5 \,\, \textrm{GeV}$

Fig. 22

Same as Fig. 21 but for 15% smearing

We illustrate this effect in Fig. 20 for one particular example of a benchmark point taken from the benchmark plane 4 with the masses fixed to $m_A= m_{H^\pm }= 544.72 \,\, \textrm{GeV}$ and $m_H= 515.5 \,\, \textrm{GeV}$.¹⁶ In this figure we show in blue the $m_{hh}$ distribution without smearing (the ideal case). The solid line depicts the full distribution, whereas the dashed line shows the result for the continuum (non-resonant) diagrams. The red lines demonstrate the effect of applying a 10% (left plot) and 15% (right plot) smearing on the theoretical prediction of the $m_{hh}$ distributions, where the solid (dashed) lines indicates the full (continuum) result. While a 15% smearing was given as a realistic future estimate, the 10% smearing indicates a potential optimistic improvement. One can observe that from the original dip-peak structure as seen in the solid blue line effectively only a peak or bump around the original peak remains. The original dip is visible only as a very small reduction of the unsmeared distribution, as the relative weight of the points below the continuum is smaller than those above the continuum (note the logarithmic scale). Furthermore it should be noted that on the edges of the $m_{hh}$ values there is a slight bump in the smeared distribution. This is an artifact of the method that we used for the smearing and should be neglected. Since we do not generate the number of events but rather a theoretical prediction for a specific value of $d\sigma /dm_{hh}$, we cannot redistribute the events according to some uncertainty. What we do is an approach that is independent of the number of events but should be equivalent. We generate a Gaussian probability distribution function centered at each of the predicted points and a standard deviation according to the percentage of smearing as explained above. Afterwards at each point in $m_{hh}$ the gaussians of the full distribution are summed and finally normalized to the original value of the integrated total cross section. This corresponds to taking the limit of the number of events N $\rightarrow \infty$. At the edges only events from one side contribute to the sum of the gaussians and are not lowered by a smaller counterpart on the other side. If the distribution would continue down to infinite values, there would be no bumps at the edges.

5.2 Bin width

As a further step in the evaluation of the experimental challenges, we analyze the effect of the bin width. The binning means that the data in a particular interval in $m_{hh}$ is presented as the mean value of the differential cross section of all the points that fall in that interval. Assuming that at least one of the Higgs bosons analyzed will decay in a $b\bar{b}$ pair,¹⁷ the bin size will eventually be determined by the b-jet mass resolution from the reconstruction of the $h \rightarrow b\bar{b}$ decay mode. This affects the visualization of the results in a realistic experimental set up, but also the counting of events for the evaluation of the experimental sensitivity, see Eq. (17). The binning is applied after the smearing discussed in the previous subsection.

The analysis is performed for the same benchmark point as in Sect. 5.1. In Figs. 21 and 22 we show the same spectrum but for a different bin size in the $m_{hh}$ variable: $10 \,\, \textrm{GeV}$ (upper left), $20 \,\, \textrm{GeV}$ (upper right), $40 \,\, \textrm{GeV}$ (lower left) and $50 \,\, \textrm{GeV}$ (lower right). Figure 21 assumes a 10% smearing, whereas in Fig. 22 we show the more realistic result with 15% smearing. The red lines show the true (smeared and binned) prediction, whereas the other colors indicate the unsmeared, but binned results for comparison. One can observe that the effect of the smearing becomes less significant in the region of resonant production for a larger bin size. The resonance is already partially diluted by the smearing, and the effect of the binning becomes less visible, as can be observed best in the lower right plots of Figs. 21 and 22. The effect of the binning is less important once the smearing of the experimental data is taken into account. After the binning the “dip” is effectively indistinguishable from the continuum contribution. The peak is still persistent and for larger bin size approaches the same height as the bump at $\sim 400 \,\, \textrm{GeV}$ before binning.

Table 7 Values of the variable R for the significance of the signal for different bin sizes for a 10% and 15% smeared distribution, see Figs. 21 and 22

Fig. 23

Invariant mass distributions for different bin locations assuming a bin size of 50 GeV and a smearing of 10$\%$ (left) and 15$\%$ (right). Solid (dashed) curves show the full (continuum) result

In the most conservative result the expected experimental resolution should have a bin size of $50 \,\, \textrm{GeV}$ and a smearing of $\sim 15\%$. The expected results in this case would possibly give access to the location of the resonance (the mass of the ${\mathcal{C}\mathcal{P}}$-even H should be know via single production by the time the di-Higgs cross section is measured) and partially to the height, and thus possibly to the size of $\lambda _{hhH}$. In order to make a quantitative estimate of the sensitivity of the signal produced by the resonant diagram we have calculated the value of the variable R defined in Eq. (17) that is obtained from Figs. 21 and 22, shown in Table 7. The grey region represents the region that falls into the window defined to compute the variable R. Overall, one can see that the values of R are significant, i.e. the signal could possibly be distinguished at the HL-LHC if our assumptions on the experimental uncertainties are met. It should be noted that we are not taking into account the efficiency of the particle detectors, which could reduce significantly the estimate of R. Comparing the two columns in Table 7 one observes R is roughly 10% worse as the assumed percentage of smearing increases by 5%. However, R is is somewhat more stable w.r.t. the bin size, where deviations within $\sim$ 5% are found. This would constitute a rather positive feature for an experimental set-up.

5.3 Bin location

The next part of the analysis concerns the arbitrary choice of the location of the bin. This choice can also affect the pattern of the invariant mass distribution. The concrete value of $m_{hh}^{\min }$ (the value of $m_{hh}$ at the bin start) and $m_{hh}^{\max }$ (the value of $m_{hh}$ at the bin end) affects the number of events that fall into that bin and thus can have an impact on the evaluation of the sensitivity R. For the previously used benchmark point we change the location of the bin for a 10% and 15% smeared distribution and a $50 \,\, \textrm{GeV}$ bin size.

In Fig. 23 we show the difference in the invariant mass distribution created by a change in the location of the first bin by 10 or $20 \,\, \textrm{GeV}$, i.e. we start the distribution at $251, 261, 271 \,\, \textrm{GeV}$ as orange, yellow and purple lines, respectively. In both plots we show the difference between the total differential cross section (solid lines) and the continuum contribution (dashed lines). The left (right) plot uses a smearing of 10% (15%). One can observe that for all three choices of bin locations the peak structure remains similarly visible (the dip is strongly diluted from the smearing and the binning as discussed in the previous subsections). To quantitatively evaluate the significance of the signal of the resonant enhancement we list the values of R for the two plots discussed above in Table 8.

In Table 8 one can observe that the variation in R stays within 5% when we modify the location of the bins. That means that the uncertainties associated to the location of the bin are smaller than the ones associated to the smearing and about the same as for the bin size. Therefore, overall we find that the experimental resolution of the particle detector, which we tried to mimic by smearing the data, has a larger impact on the resonance, and the width and location of the binning has a smaller effect in diluting the resonance.

Table 8 Values of the variable R for the sensitivity of the signal for different bin locations for a 10% and 15% smeared distribution and a bin size of $50 \,\, \textrm{GeV}$

5.4 Effect of sign($\lambda _{hhH}\times \xi _H^t$)

Finally, taking into account the above discussed experimental uncertainties, we analyze the possibility to access experimentally the relative sign of the involved couplings in the resonant diagram. For this analysis we will use the same benchmark point as above, where the effect of an ad-hoc change of sign($\lambda _{hhH}\times \xi _H^t$) has been shown already in the right plot of Fig. 12 and is reproduced for completeness of this analysis in Fig. 24. On this “ideal” result we will apply a smearing and a binning in order to see whether the difference in the peak-dip vs. dip-peak structure, and thus in the sign($\lambda _{hhH}\times \xi _H^t$), persists in the experimental analysis. This will demonstrate whether the access to this parameter is a realistic goal at the HL-LHC.

Fig. 24

Invariant mass distributions for different signs of ($\lambda _{hhH}\times \xi _H^t$) (see the right plot of Fig. 12)

Fig. 25

Invariant mass distributions for different signs of ($\lambda _{hhH}\times \xi _H^t$) with a 10% (left) and 15% (right) smearing applied. The black line shows the continuum distribution

The invariant mass distribution of the benchmark point is shown in red for the original value of $\lambda _{hhH}= -0.3975$ and a positive sign of ($\lambda _{hhH}\times \xi _H^t$), whereas the blue line gives the result for an ad-hoc changed sign of $\lambda _{hhH}= +0.3975$ and a negative sign of ($\lambda _{hhH}\times \xi _H^t$). Both distributions are normalized to the corresponding value of the total cross section, which is indicated in the legend of Fig. 24. The change in the structure is clearly visible in this plot. We remind that the value of the top Yukawa coefficient in this case was, as obtained from Eq. (16), $\xi _H^t = 0.104 > 0$. Therefore we see that for an overall minus (plus) sign the imprinted structure of the resonance in the $m_{hh}$ spectrum is a peak-dip (dip-peak) one.

Fig. 26

Invariant mass distributions for different signs of ($\lambda _{hhH}\times \xi _H^t$) with a 15% smearing applied. Results for different bin sizes: $10 \,\, \textrm{GeV}$ (upper left), $20 \,\, \textrm{GeV}$ (upper right), $40 \,\, \textrm{GeV}$ (lower left) and $50 \,\, \textrm{GeV}$ (lower right)

We now impose the various experimental uncertainties on the “ideal” result shown in Fig. 24. We start with the application of smearing as presented in Fig. 25. In the left (right) plot a 10% (15%) smearing is applied. The red and blue curves correspond, as before, to the negative and positive sign of $\lambda _{hhH}$. The black curves indicate the continuum distribution. One can observe that the blue curve is above (below) the red one right before (after) the bump. However, the overall structure cannot be resolved once the data is smeared.

The final step is the application of binning on top of a 15% smearing, which is the most realistic experimental set up. The results are shown in Fig. 26. One can conclude that effectively the dip-peak vs. peak-dip structure becomes unresolvable once both smearing and binning is applied.

6 Conclusions

In this work we have analyzed the impact of BSM triple Higgs couplings on the production cross section of two $\sim 125 \,\, \textrm{GeV}$ Higgs bosons at the HL-LHC, where the 2HDM has been chosen as an example framework. The first goal was to analyze the impact of $\lambda _{hhh}$ (with a focus on deviations from its SM value) and $\lambda _{hhH}$ on the di-Higgs production cross section and in particular to investigate the possibility of experimental sensitivity. In a second step we analyzed the potential sensitivity of the HL-LHC on the BSM THC $\lambda _{hhH}$ employing the $m_{hh}$ distributions. This sensitivity has been analyzed w.r.t. various experimental uncertainties. While it is crucial to determine all THCs of the Higgs sector realized in nature, no analyses for BSM Higgs-boson couplings at the HL-LHC is available so far. Consequently, here we explore for the first time the potential sensitivity to BSM THCs, as well as corresponding experimental effects at the HL-LHC.

We have chosen several observables that allow us to trace the impact of the THCs. The first one is the Higgs pair production cross section that is affected by the diagrams containing these couplings. Using the code HPAIR we have evaluated the cross sections of di-Higgs production including NLO QCD corrections (in the heavy top limit) in the specific benchmark planes that were selected to represent the various phenomenological situations that can occur in the 2HDM. We have analyzed the numerical impact of the THCs, and in particular the contribution of the heavy Higgs boson in the propagator and its decay width.

Differences of the di-Higgs production cross sections can originate from a changed value of $\lambda _{hhh}$, as well as from additional “resonant” contributions, given by the s-channel exchange of the heavy ${\mathcal{C}\mathcal{P}}$-even Higgs boson, H. In the analyzed benchmark planes we have found both types of effects, which can yield a strong enhancement of the di-Higgs production cross section w.r.t. its SM result. Using the projection for the experimental resolution of the di-Higgs production cross section at the HL-LHC we found effects in the few $\sigma$ range, but also ranging up to $10\,\sigma$, or higher. While these results indicate that the effect of the resonant s-channel H contribution may be visible, from the cross section alone it is not possible to disentangle the two sources.

In order to gain more direct access to $\lambda _{hhH}$ we analyzed the invariant di-Higgs mass distributions, $d\sigma /dm_{hh}$ as a function of $m_{hh}$. To our knowledge, this is the first analysis in this direction. The investigated effects are so far not taken into account in the searches for resonant contributions in the di-Higgs boson searches. Consequently, we expect that our findings support and facilitate the search for BSM Higgs bosons in the resonant di-Higgs measurements. Furthermore, they lay the ground work for the extraction of BSM THCs from the di-Higgs searches.

Starting with a toy example we analyzed the interference of the resonant H exchange with the non-resonant (continuum) diagrams. The interference term changes sign for $Q = m_{hh}= m_H$, resulting in a peak-dip (or dip-peak) structure of the $m_{hh}$ distribution (where often in the experimental search for resonant di-Higgs production only a simplified peak structure is assumed). We demonstrated that the interference effect becomes smaller with the total decay width of the H and that the “total width of the effect”, given by the width of the peak at half of its maximum value, increases with increasing $\Gamma _H^\textrm{tot}$. Furthermore, the structure of the interference (peak-dip vs. dip-peak) depends on the sign of ($\lambda _{hhH}\times \xi _H^t$), which enters as a prefactor of the interference contribution ($\xi _H^t$ denotes the top Yukawa coupling of the heavy ${\mathcal{C}\mathcal{P}}$-even Higgs boson).

The effects in the toy example were reproduced for the complete $m_{hh}$ distribution for several points in the before chosen benchmark planes. We demonstrated the dependencies of the size of the interference effects on $\lambda _{hhH}$ and $\xi _H^t$ for large di-Higgs production cross sections, as well as for selected points closer to the alignment limit ($c_{\beta - \alpha }\sim 0.1$) and further away from the alignment limit ($c_{\beta - \alpha }\sim 0.2$). These results indicate that the HL-LHC may have sensitivity to see effects of the BSM THC $\lambda _{hhH}$. As a theoretical variable quantifying the relative sensitivity to $\lambda _{hhH}$, the variable R was defined, see Eq. (17). However, it is not meant as a determination of the experimental $\lambda _{hhH}$ precision that requires a detailed experimental analysis, which is beyond the scope of our paper

In order to further analyze a possible sensitivity, we applied various experimental uncertainties on R. The first one is the smearing due to the detector resolution, which realistically can go down to $\sim 15\%$, but we also analyzed a potential (optimistic) improvement down to 10%. It is found that from the dip-peak structure mostly a bump survives, with a very small reduction due to the dip w.r.t. the unsmeared result. The next effect is the binning of the result, mostly given by the b-jet mass resolution from the reconstruction of the $h \rightarrow b\bar{b}$ decay of one of the Higgs bosons. A realistic value of a $50 \,\, \textrm{GeV}$ bin size was compared to more optimistic sizes down to $10 \,\, \textrm{GeV}$. While the smearing has a visible effect on R, the binning hardly reduces its value. Similarly, the location of the bin, which is partially arbitrary, has a smaller impact on R once we take into account the finite resolution of the detector (smearing). As a last step we showed that the sign($\lambda _{hhH}\times \xi _H^t$) does not leave any measurable imprint on the $m_{hh}$ distributions, once the experimental uncertainties are taken into account.

We conclude that, depending on the values of the underlying Lagrangian parameters, a sizable resonant H contribution to the di-Higgs production cross section can leave possibly visible effects in the $m_{hh}$ distribution. This would pave the way for a first determination of a BSM THC, a step that is crucial for the reconstruction of the Higgs potential of the underlying BSM model. We leave a detailed analysis in which for parts of the parameter space such a determination will be possible for future work.