1 Introduction

The AdS/CFT correspondence as a concrete realization of holographic principle identifies that the theory of quantum gravity in Anti-de-Sitter space-time (AdS) is equivalent to a dual conformal quantum field theory (CFT) [1]. And, the famous example is the correspondence that between the type IIB string theory on \(AdS_5 \times S^5\) and the maximally supersymmetric gauge theory in four dimensions, i.e., \({\mathcal {N}}=4\) super-Yang–Mills (SYM) [2, 3]. Since then, the holographic property of gravity has been widely accepted and applied to various fields of physics. At present, this correspondence is always regarded as a useful tool to study some problems in the strong coupling systems. For instance, some QCD-like models have been constructed with the help of AdS/CFT duality in low energy quantum chromodynamics (QCD). And, many properties of the strong coupling region of QCD are studied by using these holographic QCD models, such as the constrained phase transition, chiral phase transition, QCD vacuum, and so on [4]. In addition, the application of AdS/CFT correspondence in condensed matter physics has also attracted much attention [5], especially in superfluidity, superconductivity, non Fermi liquids and Fermi liquids [6,7,8,9]. Also, in spirit of AdS/CFT, some other holographic correspondences have also been extensively studied, such as dS/CFT correspondence and Kerr/CFT correspondence [10, 11]. So far, the holographic principle has been more and more important, and become an effective tool to study various physical topics in the background of modified gravity [12,13,14,15,16,17,18,19,20,21,22,23,24,25].

Black hole, predicted by general relativity (GR), is one of the most interesting celestial body in our universe. Recently, it has been proved to be existed by the astronomical observation experiments. For instance, the gravitational wave detection results provided by the Laser Interferometer Gravitational Wave Observatory (LIGO) have become the first strong evidence of the existence of black hole [26]. In 2019, the image of a supermassive black hole in the center of the giant elliptical galaxy M87 released by the international collaboration of Event Horizon Telescope (EHT) further provided a direct evidence for black hole [27,28,29,30,31,32]. According to black hole image obtained by EHT, there is a dark area inside the bright ring, which is the black hole shadow, where the bright ring is called as the photon sphere. The light ray came from the accretion materials will be absorbed by black hole due to its strong gravitational field, so that it cannot reach to the distant observer. Therefore, this resulting into the black hole shadow directly [33]. In 1966, Synge proposed the theoretical condition that the photon can escape from the strong gravitational field of black hole [34], which indicated that the shadow contour of a static spherically symmetric black hole is a standard circle [35,36,37]. After that, Bardeen found that the radius of Schwarzschild black hole is \(r=5.2M\), in which M is black hole mass [38]. And interestingly, the shadow for a rotating black hole can evolve into a D-shaped shape when the spin parameter is very big [39,40,41,42,43] for a equatorial-plane observer. More importantly, by considering the fact that there are some different accretion models around black hole, one has also studied the shadow and observational appearances of black hole, and obtained many interesting results [44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59].

The shadow of black hole contains a lot of information, which does not only enable us to comprehend the geometric structure of spacetime, but also help us to comprehend various gravity models more deeply. However, the above research on black hole shadow is based on the geometric optics, i.e., the famous ray-tracing method. Recently, in the framework of the wave optics, one has employed the AdS/CFT correspondence to carefully study the holographic image of AdS black hole, where the wave source located at the AdS boundary [60, 61]. With the aid of a optical system, the Einstein ring is clearly observed at a screen. The results show that the size of ring in this case is consistent with the size of black hole photon sphere obtained from geometric optics. Later, the Einstein ring structure of the lens response of the complex scalar field has been studied in the background of a charged AdS black hole, and the results implied that the radius of Einstein ring does not change with the chemical potential, but is closely related to black hole temperature [62]. In addition, the asymptotically AdS black hole dual to a superconductor was also imaged in [63], where the effect of the charged scalar condensate on the image have been investigated. In a word, the holographic images of black holes can be used as an effective method to test the existence of gravitational dual for given materials, and allow us to comprehend the configuration of the AdS black hole.

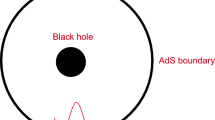
It is well known that, the Gauss–Bonnet gravity is a well-modified gravity model, and the equation of motion has no higher derivative than the second order. In four-dimensional spacetime, the Gauss–Bonnet term in the Lagrangian is topologically invariant and thus does not contribute to the dynamics. However, it can contribute to the dynamics of gravitational field in high-dimensional (\(d>4\)) cases [64]. Recently, Glavan and Lin proposed a Gauss–Bonnet black hole in four dimension with the Gauss–Bonnet (GB) coupling constant \(\alpha \rightarrow \alpha / (d-4)\), where d take the limit \(d \rightarrow 4\) [65]. However, their work does not lead to a well-defined way with the initial regularization scheme [66, 67]. To overcome this problem, Aoki found a well defined and consistent theory by breaking the temporal diffeomorphism property of the curved spacetime in [68]. Then, in four dimension case, the influence of Gauss–Bonnet constant on black hole shadow and photon sphere were studied in detail in [69, 70]. Obviously, It is worth noting that the work [69, 70] are all based on the method of geometrical optics. In this paper, we intend to employ the AdS/CFT correspondence to carefully study the image of the Gauss–Bonnet AdS black hole in the frame of the wave optics. Following the idea of [60, 61], we will take an oscillatory Gaussian wave source \({\mathcal {J}}_o\) on one side of the AdS boundary, and then let it’s scalar wave generated by the source propagate in the bulk(please see Fig. 1). After the wave reach to the other side of AdS boundary, we will detect it and study the corresponding response function. By using a special optical system, we will further convert the extracted response function \(\langle {\mathcal {O}} \rangle \) into the image that can be seen on a screen.

Fig. 1
figure 1

The schematic of imaging a dual black hole

Full size image

The remainders of the present paper are outlined as follows. In Sect. 2, we shall briefly introduce the Gauss–Bonnet gravity, and extract the response function at the north pole when the source located at the south pole of the AdS boundary. In Sect. 3, we will introduce a special optical system which is consist of a convex lens and a spherical screen. By using this system, the holographic image of Gauss–Bonnet AdS black hole is obtained through the response function. In this way, we further study the effects of various parameters on the holographic image of Gauss–Bonnet AdS black hole. Section 4 ends up with a brief discussion and conclusion.

2 Scalar field and response function in a Gauss–Bonnet AdS black hole

Firstly, we will introduce the Gauss–Bonnet AdS black hole. In general, for a d-dimensional spacetime with a negative cosmological constant, the action in Gauss–Bonnet gravity reads

$$\begin{aligned} {\mathcal {S}} = \frac{1}{16 \pi } \int d^d x \left( R+\frac{(d-1)(d-2)}{l^2} +\frac{\alpha }{d-4} L_{GB} -F_{\mu \nu }F^{\mu \nu } \right) , \end{aligned}$$
(1)

and

$$\begin{aligned} L_{GB}= R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }-4R_{\mu \nu }R^{\mu \nu }+R^2, \end{aligned}$$
(2)

where l is the AdS radius which is related to the cosmological constant, \(F_{\mu \nu }\) and \(\alpha \) are the Maxwell tensor and the Gauss–Bonnet coupling parameter, respectively. By rescaling the Gauss–Bonnet coupling parameter \(\alpha \rightarrow \alpha /(d-4)\) and taking the limit \(d-4\), one can obtain a 4-dimensional nontrivial black hole solution, which is

$$\begin{aligned} ds^2= -F(r)dt^2 + \frac{1}{F(r)} dr^2 + r^2 d\theta ^2 +r^2 {\sin \theta }^2 d\varphi ^2, \end{aligned}$$
(3)

with

$$\begin{aligned} F(r)= r^2 f(r) = 1 + \frac{r^2}{2\alpha }\left( 1- \sqrt{1+4\alpha \left( \frac{2M}{r^3} -\frac{1}{l^2} \right) } \right) . \end{aligned}$$
(4)

By using a new definition \(u=1/r\) and the coordinate, \(v = t+u_* = t- \int \frac{du}{f(u)}\), the metric function can be rewritten as following, which is

$$\begin{aligned} ds^2= \frac{1}{u^2}\left( -f(u)dv^2 -2dudv + d\theta ^2 + {\sin \theta }^2 d\varphi ^2 \right) , \end{aligned}$$
(5)

where

$$\begin{aligned} f(u)&= 1 + \frac{1}{2\alpha u^2}\nonumber \\&\quad \times \left( 1 - \sqrt{1-\alpha \left( 4 - 4 u^2 u_h\left( \frac{1}{u_h^4} +\frac{1}{u_h^2} + \alpha \right) \right) } \right) , \end{aligned}$$
(6)

where \(u_h = 1/r_h\), \(r_h\) is the event horizon of black hole which can be obtained with \(f(r)=0\). And, the gauge symmetry has been considered. For a massless particle in the scalar field, the Klein–Gordon equation is

$$\begin{aligned} \Box \Phi (v,u,\theta ,\varphi )=0. \end{aligned}$$
(7)

For the spacetime (5), we have

$$\begin{aligned}&u^2 f(u)\partial _u \partial _u \Phi + \left[ u^2 f'(u) - 2u f(u) \right] \partial _u \Phi -2 u^2\partial _v \partial _u \Phi \nonumber \\&\quad + 2u \partial _v\Phi + u^2 D^2_S \Phi =0, \end{aligned}$$
(8)

where \(f'(u)=\partial _u f(u)\). The asymptotic solution of Eq. (8) near the AdS boundary(\(z\rightarrow 0\)) reads [62]

$$\begin{aligned} \Phi (v,u,\theta ,\varphi )&= {\mathcal {J}}_{O}(v,\theta ,\varphi ) + u \partial _v {\mathcal {J}}_O(v,\theta ,\varphi ) \nonumber \\&\quad +\frac{1}{2} u^2 D_S^2{\mathcal {J}}_O(v,\theta ,\varphi )+ u^3 \langle O \rangle + {\mathcal {O}} (u^4). \end{aligned}$$
(9)

Here, \(D_S^2\) represents the scalar Laplacian on unit \(S^2\). According to the AdS/CFT dictionary, it is obvious that the \({\mathcal {J}}_{O}(v,\theta ,\varphi )\) and \(\langle O \rangle \) are the external scalar source and corresponding response function in the dual CFT, respectively. In this paper, we employ the monochromatic and axissymmetric Gussian wave packet source as the external scalar source, and fixed it at the south pole of the AdS boundary. In this sense, we have,

$$\begin{aligned}&{\mathcal {J}}_O(v,\theta ) = e^{i \omega v} \cdot \frac{1}{2 \pi \sigma ^2 } \cdot \exp \nonumber \\&\quad \times \left[ -\frac{(\pi - \theta )^2}{2 \sigma ^2} \right] = e^{i \omega v} \cdot \sum _{l=0}^{\infty } C_{l0} Y_{l0}(\theta ), \end{aligned}$$
(10)

with

$$\begin{aligned} C_{l0} = (-1)^l \sqrt{\frac{l+1/2}{2 \pi }} \exp \left[ -\frac{1}{2} (l+1/2)^2 \sigma ^2 \right] . \end{aligned}$$
(11)

In which \(C_{l0}\), \(\sigma \) and \(Y_{l0}\) denote the Gussian source feature and the spherical harmonics function, respectively. And, we only consider the case \(\sigma \ll \pi \) because the tiny value of Gaussian tail can be neglected. Considering the symmetry of Eq. (3), one can further decompose the function \(\Phi (v,z,\theta ,\varphi )\) into

$$\begin{aligned} \Phi (v,u,\theta ,\varphi ) = e^{i \omega v} \cdot \sum _{l=0}^{\infty } \sum _{m=-l}^{l} c_{l0} U_l(u) Y_{l0}(\theta ,\varphi ). \end{aligned}$$
(12)

And, the response function reads

$$\begin{aligned} \langle O \rangle = e^{i \omega v} \sum _{l} \langle O \rangle _l Y_{l0}(\theta ). \end{aligned}$$
(13)

With the aid of Eq. (12), we have

$$\begin{aligned} u^2 f(u) U''_l&+\left[ u^2 f'(u) -2 u f(u) + 2 i \omega u^2 \right] U'_l \nonumber \\&\quad + \left[ - 2 i \omega u - l(l+1) u^2 \right] U_l =0. \end{aligned}$$
(14)

And the asymptotic behaviour of \(U_l\) can be written as

$$\begin{aligned} \lim _{z \rightarrow 0} U_l{=} 1 {-} i \omega u {+} \frac{1}{2}\left[ -l(l+1) \right] u^2 {+}{\langle O \rangle _l} u^3 {+} {\mathcal {O}} (u^4).\nonumber \\ \end{aligned}$$
(15)

For Eq. (12), it is obvious that there are two boundary conditions for \(U_l\). One is the horizon boundary condition, which is

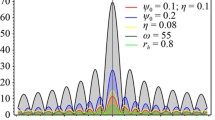
$$\begin{aligned} \left[ u_h^2 f'(u_h) + i 2 \omega u_h^2 \right] U'_l - \left[ 2 i\omega u_h +l(l+1)u_h^2 \right] U_l=0,\nonumber \\ \end{aligned}$$
(16)

at the event horizon \(u=u_h\). And, another one is AdS boundary condition, which is \(U_l(0)=1\) at the AdS boundary. Combined with two conditions, one can solve Eq. (14) and obtained the function \(U_l\) by employing the psuedo-spectral method [62]. Then, the total response function \(\langle O \rangle \) can be obtained with the aid of Eqs. (15) and (13). Here, we take some proper values of black hole and lens parameters as examples to clearly show the absolute amplitude of \(\langle O \rangle \), which can be seen in Fig. 2. In Fig. 2a, the values of Gauss–Bonnet coupling parameter changes while the values of other relevant state parameters do not change, where \(M=1\), \(r_h=1\), \(\sigma =0.05\), and \(\omega =75\). In Fig. 2b, the value of Gauss–Bonnet coupling parameter is fixed to \(\alpha =0.15\), while the value of other relevant state parameters changes, in which \(r_h=0.6, \sigma =0.05,\omega =75\) (the gray dashed), \(r_h=0.8, \sigma =0.05,\omega =75\) (the blue dashed), \(r_h=0.6, \sigma =0.06,\omega =75\) (the black dashed) and \(r_h=0.6, \sigma =0.05,\omega =80\) (the green dashed).

Fig. 2
figure 2

The absolute amplitude of total response function for different values of black hole and lens parameters

Full size image

From Fig. 2, one can obviously observe the diffraction pattern as the scalar wave propagates in the bulk. More importantly, it shows that the absolute amplitude of total response function increases with the decrease of Gauss–Bonnet coupling parameter \(\alpha \) and event horizon of black hole \(r_h\). In addition, we find that Gaussian source parameters(\(\sigma \) and \(\omega \)) also diminished the absolute amplitude. In other words, the total response function depends closely on the Gaussian source and the spacetime geometry. Therefore, if this response function can be transformed as the observed image, it can be regarded as a useful tool to reflect the feature of the spacetime geometry.

3 Holographic rings of Gauss–Bonnet AdS black hole

Fig. 3
figure 3

a The observed region on the boundary; b the structure of optical system

Full size image

After obtaining the response function, we will use it to directly observe the black hole images in this section. Here, we need to use a special optical system which is composed of an extremely thin convex lens and spherical screen, and consider that the observation area on the AdS boundary is a very small range, where the observation center is (\(\theta _{obs}, 0\)). The detail can be seen in Fig. 3a. As we can see, the convex lens is placed at the position \(\vec {x}=(x, y, 0)\), thereby the coordinates of spherical screen is \(\vec {x}_S=(x_S, y_S, z_S )\). And, the focal length f of the infinitely thin lens is much larger than the size of it, i.e., \(f\gg d\). For a wave source \(\Psi _p(\vec {x})\), it will be converted as the transmitted wave \(\Psi _s(\vec {x})\) after it transmits the convert lens according to the wave optics. This wave as the spherical wave will further convert to the observed wave \(\Psi _{sc}(\vec {x}_s)\) on the screen, which is shown in Fig. 3b. In this case, we have

$$\begin{aligned} \Psi _{sc}(\vec {x}_s)= & {} \int _{|\vec {x}|<d} dx^2 \Psi _s(\vec {x}) e^{- i \omega L} \nonumber \\= & {} \int _{|\vec {x}|<d} dx^2 e^{- i \omega \frac{|\vec {x}|^2}{2f}} \Psi _p(\vec {x}) e^{- i \omega L}, \end{aligned}$$
(17)

where \(f^2 = x_S^2 + y_S^2+ z_S^2 \), and the symbol L is the distance between \(\vec {x}\) and \(\vec {x}_S\). By considering \(L = \sqrt{(x_s-x)^2+(y_s-y)+z_s^2}\simeq f - \frac{\vec {x}_s \cdot \vec {x}}{f} + \frac{|\vec {x}|^2}{2f}\) and the Fresnel approximation \(f\gg |\vec {x}|\), one can get

$$\begin{aligned} \Psi _{sc}(\vec {x}_s) \propto \int _{|\vec {x}|<d} dx^2 \Psi _p(\vec {x}) \varpi (\vec {x}) e^{-\frac{i \omega }{f} \vec {x}\cdot \vec {x}_s}, \end{aligned}$$
(18)

with the window function reads

$$\begin{aligned} { \varpi (\vec {x})}\equiv {\left\{ \begin{array}{ll} \text {1}, \quad \quad 0 \le \mid \vec {x}\mid \le d\\ \text {0}, \quad \quad \mid \vec {x}\mid > d \end{array}\right. }. \end{aligned}$$
(19)

To find Eq. (18), we have used the Taylor expansion and some proper approximations. From Eq. (18), we find that the observed wave on the screen is connected with the incident wave by the Fourier transformation. As \(\Psi _p\) is identified as the respond function \(\langle O \rangle \), we will capture the images of the AdS black hole on the screen by using Eq. (18). When the observer located at different positions of AdS boundary, the holographic Einstein images for different parameters will be obtained, which have been presented in Figs. 4 and  5. Here, the vertical coordinate is \(y_S/f\), and horizontal coordinate is \(x_S/f\), which changes in the region \((-1.5,1.5)\).

Fig. 4
figure 4

The holographic images for \(d=0.6, \sigma =0.05, \omega =75\)

Full size image

When the observer located at the position \(\theta =0^\circ \), i.e., the observer located at the north pole of the AdS boundary, it can be seen that a series of axisymmetric concentric rings appear in the image, and one of them is particularly bright. At the center of the rings, there is a bright spot which called as the Poisson−like spot. For the case \(\theta =30^\circ \), the bright ring changed into a luminosity-deformed ring, which instead of a strict axisymmetric ring. And for \(\theta =60^\circ \), two bright light arcs appeared, rather than a ring. In particular, this ring evolved into two light points finally for the case \(\theta =90^\circ \) in Fig. 4, which correspond to the clockwise and anticlockwise light rays respectively from the viewpoint of geometrical optics.

With the change of Gauss–Bonnet coupling constant \(\alpha \), the holographic images are different. For instance, one can find that the size of ring decreases with the parameter \(\alpha \).Footnote 1 At other observed positions, with the increase of \(\alpha \), the observed brightness of the left area in the image will decrease rapidly, while decrease relatively slowly in the right area. For example, when the observation angle is \(\theta =60^\circ \), the brightness of the bright light arcs in the right area are significantly stronger than that obtained in the left area, which can be clearly seen for \(\alpha =0.1\) in Fig. 4c. Combined with above facts, we can conclude that the feature of holographic images can be regarded as an effective tool for revealing the geometric characteristics of black hole.

Fig. 5
figure 5

The holographic images for \(\alpha = 0.05\), and other corresponding parameters

Full size image

In addition, we also consider whether the wave source and optical system will affect the characteristics of the holographic Einstein image, which are shown in Fig. 5. From Figs. 4 and 5, we find that with the increase of the horizon \(r_h\), the size of the holographic ring seems a little bigger, and the concentric striped patterns is more clear. In addition, the results also show that the width of holographic ring becomes larger for a lower value of frequency of Gussian wave packet source \(\omega \) and the lens parameter d. Also, it can be found that the radius of it seems hardly changed for \(\omega \), but decreased with the decrease of d. And, it is true that the concentric striped patterns as well as holographic images are more indistinct for \(\omega \) and d. More importantly, we find from the subfigure (c) of Fig. 5 that the luminosity of ring deformed more quickly in the case \(\theta _{obs}=30^\circ \) by comparing with the subfigure (a) of Fig. 4. In addition, at the position \(\theta _{obs}=90^\circ \), one may also observed two light points in the subfigures (a) and (b) of Fig. 5, rather than only one light point which is shown in the subfigure (c) of Fig. 4. In view of this, one can see that the holographic images of AdS black hole can not only characterize the geometric of black hole, but also closely related to the properties of lens and wave packet source.

Next, we will investigate the photon ring from the perspective of optical geometry. Therefore, we will focus on the trajectory of light ray in the four-dimensional Gauss–Bonnet AdS black hole. It is well known that the Hamilton-Jacobi equation of null geodesic in general curved spacetime can be given by the massless Klein–Gordon equation through the the eikonal approximation. In this system, the Lagrangian \({\mathcal {L}}\) of the photon is

$$\begin{aligned} 2 {\mathcal {L}} = g_{\mu \nu } {\dot{x}}^{\mu } {\dot{x}}^{\nu }, \end{aligned}$$
(20)

in which the term of \({\dot{x}}^{\mu }\) is the four-velocity of photon. By considering the general spherically symmetric spacetime, we can restrict our discussion to the equatorial plane, i.e., \(\theta =\frac{1}{2} \pi \). For the metric coefficients in Eq. (3), it is not rely on the time t and azimuthal angle \(\phi \). Hence, one can obtain two constants of motion \({\hat{e}}\) and \(\ell \) which are related to the energy and angular momentum, which are

$$\begin{aligned} {\hat{e}}=F (r) {\dot{t}} = constant, \quad \ell =r^2 {\dot{\phi }} = constant. \end{aligned}$$
(21)

Based on the null geodesic \(g_{\mu \nu } {\dot{x}}^{\mu } {\dot{x}}^{\nu }=0\), and by introducing the affine parameter \(\lambda =\lambda /\ell \), we further have

$$\begin{aligned} {\dot{r}}^2=\frac{1}{b^2}-V_{eff}. \end{aligned}$$
(22)

In the above equation, \(b=\frac{\ell }{{\hat{e}}}\) is called the impact parameter. The behavior of the geodesic lines closely depends on its impact parameter b. In addition, the term of \(V_{eff}\) is the effective potential, which can be expressed as

$$\begin{aligned} V_{eff}=\frac{F(r)}{r^2}. \end{aligned}$$
(23)

We have plotted the effective potential \(V_{eff}\) as a function of radius r in Fig. 6, where \(M = 1\). The photon sphere conditions are \({\dot{r}}=0\) and \(\ddot{r}=0\), which means that the effective potential need to satisfy

$$\begin{aligned} V_{eff}(r_{ph})=\frac{1}{b_{ph}^2},\quad V'_{eff}(r_{ph})=0. \end{aligned}$$
(24)

Therefore, the maximum effective potential \(V_{max}\) corresponds to the position of photon sphere \(r_{ph}\). In this sense, the impact parameter is

$$\begin{aligned} b_{ph}=\frac{1}{\sqrt{V_m}}. \end{aligned}$$
(25)

If the observer on one side of the AdS boundary wants to capture the photon emitted from the other side of the boundary, the impact parameter need to satisfy condition \(b>b_{ph}\). Otherwise, the photon will fall directly into black hole in the case of \(b<b_{ph}\). Because the limiting factor \( \lim _{r\rightarrow \infty }V(r) =1\),Footnote 2 the photons that can be captured by the observer belong to the A region, i.e., \(1<\frac{1}{b^2}<V_{max} \), which is shown in Fig. 6. In particular, at the position of photon sphere \(b=b_{ph}\), the photon will neither escape from black hole nor fall into it, but rather in a state of constant rotation around the black hole. Hence, the closer to the value of impact parameter \(b_{ph}\), the more times of photon rotates around black hole. In Fig. 7, we show the schematic diagram of photons, which started from the south pole, and then rotating around black hole one time, and finally arriving at the north pole.

Fig. 6
figure 6

The effective potential for \(l=10\)

Full size image
Fig. 7
figure 7

a Schematic diagram of the orbit of the incident photon rotating once around black hole; b the relation between \(\theta _{hr}\) and \(x_{ring}\)

Full size image

It is evident that the incident angle between the photon orbit and radial direction is equal to the emitted angle \(\theta _{in}=\theta _{out}\), and one can get [65]

$$\begin{aligned} \sin \theta _{in}=\frac{\ell }{\hat{e}}. \end{aligned}$$
(26)

Therefore, due to the axisymmetry, it is obvious that the observer can clearly see a bright ring with its radius is closely related to \(r_{ph}\) from the geometrical optics. Meanwhile, we can also defined an angle to characterize the radius of holographic ring obtained in Fig. 7b, which reads

$$\begin{aligned} \sin \theta _\textrm{hr} = \frac{x_{ring}}{f}, \end{aligned}$$
(27)

By carrying out the similar approach in [65], one can also employ the spherical harmonics \(Y_{lm}(\theta ,\varphi )\) in Eq. (18) to find the position of peak of image, which is \(\frac{\ell }{\hat{e}}=\frac{x_{ring}}{f}\). So, this means that the position of photon ring obtained from the geometrical optics is full inconsistence with that of the holographic ring.

Fig. 8
figure 8

Comparison of ring angle \(\theta _{hr}\) and angle of photon sphere \(\theta _{in}\) in Gauss–Bonnet AdS black hole for \(\omega = 75\)

Full size image

To illustrate relationship \(\sin \theta _{in} = \sin \theta _{hr}\), we take two cases (i.e., \(\alpha = 0.01\) and \(r_h = 0.75\).) as examples to numerically present the evolution of the ring angle \(\theta _{in}\) and the angle of photon sphere \(\theta _{hr}\) as a function of \(r_h\) (Fig. 8a) and \(\alpha \) (Fig. 8b) in the Gauss–Bonnet AdS black hole. Here, the red dot represents the radius of holographic ring \(\theta _{hr}\) and the blue line is the location of the photon sphere. From Fig. 8, one can see that the ring angle increases with the event horizon radius and decreases with the Gauss–Bonnet parameter \(\alpha \), which hold for both the blue line or red dots. More importantly, it is clear from both subfigures, (a) and (b), that the red dots are always located around the blue line. This confirms that the location of photon ring obtained by the geometrical optics is consistent with that obtained by holography.

4 Conclusions and discussions

In the framework of Gauss–Bonnet gravity, we have studied the holography images of an AdS black hole. By considering the oscillating Gaussian source produced on the boundary, we have computed the response function based on the AdS/CFT dictionary. The result shows that there always exists the diffraction pattern of total response function after the scalar wave passes through black hole. And, the absolute amplitude of it does not only closely depend on the spacetime geometry, i.e., the Gauss–Bonnet coupling parameter \(\alpha \) of black hole, but also the properties of source, i.e., the frequency \(\omega \) of wave. In particular, as parameters \(\alpha \), \(\omega \) and \(r_h\) increase, the strength of the absolute amplitude of total response function decrease.

After performed the Fourier transformation to response function, we further obtained the Einstein image of the Gauss–Bonnet AdS black hole with an optical system, which is consist of a lens and a screen. It turns out that when the observer and source located at the north and south poles respectively, the image of AdS black hole called as the holographic Einstein ring can be captured. This ring surrounded with a series of concentric stripes, which corresponds to the diffraction pattern of total response function. At the center of ring, there is a bright spot which is called as the Poisson-like spot caused by the diffraction of scalar wave. By analyzing the images of Gauss–Bonnet AdS black hole, we found that the size and width of the ring are closely related to the parameters of black hole, optical system and wave source. Specifically, the size of holographic Einstein ring decreases with the increase of Gauss–Bonnet coupling parameter \(\alpha \) and d, but hardly changes for \(\omega \). For the width, it seems hardly influenced by the parameter \(\alpha \), but will become larger for a lower value of \(\omega \) and d. When the observer is not in the north pole, we found that the bright ring gradually evolve into two bright light arcs and finally form two light spots with the increase of observation angle. In a word, we will observe different holographic images of black hole for different values of parameters of black hole, optical system and wave source, and observation angles. The holographic images thus can be used as an effective tool to distinguish different types of black holes for the fixed wave source and optical system.