Charged particle dynamics in black hole split monopole magnetosphere

Abstract

This article examines particle dynamics and acceleration in the magnetic Penrose process (MPP) around Kerr black hole (BH) in a split monopole magnetic field. The characteristics of charged particle motion around magnetized BHs reveal four differen feasible regimes of ionized Keplerian disk behaviour: survival in regular epicyclic motion; changing into a chaotic toroidal state; collapse due to escaping along magnetic field lines and collapse due to falling into the BHs. By making use of the effective potential, we have investigated the position of stable circular orbits for both in- and off-equatorial planes. We observed that the positive magnetic field ${{\mathcal {P}}}>0$ increases the stability of effective potential, whereas ${{\mathcal {P}}}<0$ diminishes its stability. We show that ultra-efficient energy extraction from spinning supermassive BH controlled by the MPP can pay the bill. We anticipate neutral particle ionization, such as neutron beta-decay, edging closer to the BH horizon, charging protons to more than $10^{20}$eV for a supermassive BH of mass $10^9M_{\odot }$ and a magnetic field of strength $10^4$G.

1 Introduction

Active Galactic Nuclei, Gamma-ray bursts, and X-ray binaries are considered to be the most fascinating, as well as powerful systems of our Universe. It is believed that their power arises from a principal mechanism comprised of a magnetized, spinning entity just like BHs or neutron stars [1] or from an encircling accretion disk [2, 3]. Blandford and Znajek [4] observed that electromagnetic fields around BHs are force-free, as they decouple from other degrees of freedom. Hence, the force-free electrodynamics (FFE) equations can be expressed as

$$\begin{aligned}&F_{\mu \nu }=\partial _\mu A_\nu -\partial _\nu A_\mu , \quad D_\mu F^{\mu \nu }=-J^\nu , \nonumber \\&F_{\mu \nu } J^\nu =0,\quad J^\mu \ne 0. \end{aligned}$$

(1)

Where $A_\mu$ and $F_{\mu \nu }$, respectively represent the gauge potential and the strength of the electromagnetic field, while $J^\mu$ denotes current. In fact, they are classical equations of Maxwell’s with the conserved electromagnetic energy-momentum tensor and non-vanishing current. The Blandford–Znajek mechanism also known as the magnetized Penrose mechanism permits the process of energy extraction from rotating BHs [5, 6]. A systematic interpretation of the above mechanism was inaugurated by Blandford and Znajek to find the perturbative solution of the FFE equations 1 near a Kerr BH. The simplest form of such solution is termed the Blandford–Znajek monopole, which one can straightforwardly switch into the split monopole solution having a magnetic source near BHs. In the case of Kerr BH, Blandford–Znajek monopole can be expressed as a perturbation in the spinning parameter $a=J/GM^2$, where M and J respectively denote the mass and angular momentum [7]. Whereas, the magnetic monopole becomes static when $a=0$.

The presence of magnetic fields around BHs has essential consequences on the process of accretion, as well as charged matter. It is found that BHs possess an accretion disk generated by conducting plasma and its motion could constitute a regular magnetic field. A recent finding shows that the presence of a strong magnetic field near a supermassive BH in the Galaxy center has no association with the accretion disk [8]. Thus, BHs could be immersed in an external magnetic field having composite formation near the horizon of a BH, while its nature will be simple and adjacent to a homogeneous magnetic field at a larger finite distance [9]. Kovar et al. [10] observed that BH on the equatorial plane of a magnetar could be immersed in the homogeneous magnetic field provided that the magnetar is placed at a far distance. The equations of electrically charged particle dynamics outlined by the Reissner–Nordström or Kerr–Newman spacetime can easily be separated and integrated [11]. Such dynamical motion of particles has been studied in various articles [12,13,14,15,16,17,18,19]. Konoplya [20] by examining the particle dynamics around a magnetized BH deduced that the tidal charge has a vigorous influence on the motion of both massive and massless particles. While an abundant and detailed investigation of the charged particle motion in magnetized BH spacetimes can be found in [21,22,23,24,25,26,27,28,29,30]. Particle collisions inside the ergoregion and the motion of particles are respectively examined in the braneworld Kerr and Kerr–Newman–Kasuya BHs in [31,32,33].

The weak magnetic field has minor influences on the dynamics of neutral particles or background geometry. Nevertheless, the magnetic fields have enough strong influence on the dynamics of charged test particles. As a result, charged test particles of mass m and charge q revolve around a BH of mass M immersed in a magnetic field of strength B. Thus, one can inaugurate a dimensionless quantity $qB GM/mc^4$ that could be defined as the relative Lorenz force [34, 35]. This quantity could also have a large value in case of weak magnetic fields due to the larger value of specific charge q/m. In the current work, we consider that “charged particle” can denote any kind of matter ranging from electron to some charged inhomogeneity revolving in the innermost region of an accretion disk [36].

In this article, our aim is to investigate rotating BH’s magnetosphere previously studied as a split monopole solution [4]. Komissarov [37] found that radial investigation of the split monopole magnetic field can be admissible for the originating magnetic fields from thin accretion disk near BHs or for the originating magnetosphere from the accretion layout of another BH near the BH horizon [38]. To make our calculations simple, we will use $G=c=1$ throughout the current article.

2 Black hole magnetosphere

2.1 Kerr black hole

The spacetime geometry of a rotating Kerr BH in Boyer-Linquist coordinates ($t,r, \theta , \phi$), can be expressed as

$$\begin{aligned} \textrm{d}s^2 = g_{tt}\textrm{d}{t}^2 + g_{rr}\textrm{d}{r}^2 + g_{\theta \theta }\textrm{d}\theta ^2 + g_{\phi \phi }\textrm{d}\phi ^2 +2g_{t\phi }\textrm{d}{t}\textrm{d}\phi , \end{aligned}$$

(2)

with

$$\begin{aligned}{} & {} g_{tt} = -\left( 1-\frac{2Mr}{\rho ^2}\right) , \quad g_{t\phi }=-\frac{2Mra\sin ^{2}\theta }{\rho ^2},\nonumber \\{} & {} g_{\phi \phi } = \left( r^{2}+a^{2}+ \frac{2Mra^2 \sin ^{2}\theta }{\rho ^2} \right) \sin ^{2}\theta ,\nonumber \\{} & {} g_{rr} = \frac{\rho ^2}{\varDelta }, \quad g_{\theta \theta } = \rho ^2, \end{aligned}$$

(3)

where

$$\begin{aligned} \varDelta = r^2 - 2Mr + a^2, \quad \rho ^2 = r^2 + a^2 \cos ^2\theta . \end{aligned}$$

(4)

In the above expressions, M and a, respectively represent the mass and spin parameters of the BH. The metric 2, reduces to the Schwarzschild BH if $a=0$. Horizons of metric 2, can be obtained from $\varDelta =0$ as

$$\begin{aligned} r_{\pm }=M\pm \sqrt{M^2-a^2}, \end{aligned}$$

(5)

provided that $0 \le a^2 \le M^2$. In the above equation, $r_+$ and $r_-$, respectively represents the event and Cauchy horizons. For the maximal rotation, $a^2=M^2$ and nonmaximal rotation $a^2 < M^2$, respectively corresponds to the extremal and subextremal Kerr BH. In Boyer-Linquist coordinates the spacetime metric 2 becomes singular at $r=r_+$, while the angular velocity of the horizon can be expressed as

$$\begin{aligned} \varOmega _+=\frac{a}{r_+^2+a^2}. \end{aligned}$$

(6)

2.2 Split monopole magnetic field

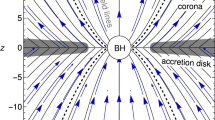
While gravity is given by the elegant Kerr BH spacetime solution (2), the external magnetic field in the premises of BH’s horizon may be very complex. The general relativistic magnetohydrodynamical (GRMHD) simulations of magnetized toroidal structures [39] show complex and highly dynamic magnetic fields in the tori, but the external magnetic field closer to the axis of rotation of the structure, in which the jets may be established relates to a split monopole or parabolic magnetic field independently on the original configuration of the magnetic field [40], “parabolic solution for large scale jet formation” [41] – magnetic monopole close to the BH [5] both parabolic and monopole magnetic field solutions are very similar. This regular parabolic magnetic field solution is indistinguishable from a split monopole magnetic field solution.

For these reasons, it is very relevant to explore the split monopole BH magnetosphere model using one charged test particle dynamics and used in several significant investigations of astrophysical processes. It is critical to note that even in this scenario, the $A_{t}$ factor stays non-zero, which may end up in a highly powerful acceleration process for sufficiently massive BHs and strong magnetic fields.

In general, if the magnetic field contains a non-zero poloidal element, every observer within the ergosphere will perceive a non-zero electric field [42, 43]. Non-zero electric field should lead to charged particle selective accretion and hence induced electric charge, giving the electrostatic energy for particle acceleration. As shown in [44] this electric field should not be screened by plasma [45]. The electric field could be screened if the following conditions

$$\begin{aligned} \vec {B}.\vec {E} = 0, \quad \text {and} \quad E^2 - B^2 < 0, \end{aligned}$$

(7)

are satisfied concurrently, whereas $\vec {B}$ and $\vec {E}$ represent the vectors of magnetic and electric fields recorded in LNRFs. It could be demonstrated [44] that $E^2-B^2$ is negative beyond the ergosphere while positive within it. As a result, the induced electric field created by the combined effect of the BH rotation and split monopole magnetic field does not undergo screening inside the ergosphere and can function as an effective charged particle accelerator.

In principle, magnetic monopoles do not exist in the theory of electromagnetism, thus in the case of the magnetic field, we get

$$\begin{aligned} \textrm{div}{} \textbf{B}=0. \end{aligned}$$

(8)

The origin of the split monopole magnetic field is considered to be an electric current traveling around the coordinate system found in an infinitesimally thin disk in the equatorial plane. We assume the magnetosphere of BH in the shape of split monopole solution [4], which could be expressed with the help of electromagnetic 4-vector potential as

$$\begin{aligned} \mathcal {A}_\mu = (\mathcal {A}_t,0,0,\mathcal {A}_\phi ). \end{aligned}$$

Thus, its non-vanishing terms can be described as

$$\begin{aligned} \mathcal {A}_t= & {} -{a{B} \cos \theta }/{\rho ^2}, \\ \mathcal {A}_{\phi }= & {} {(r^2+a^2) {B} \cos \theta }/{\rho ^2}. \end{aligned}$$

Here B is the intensity of the magnetic field. The split monopole magnetic field is considered to have the same symmetries as that of Kerr BH metric given in Eq. (2). By making use of the coordinate transformation, the Cartesian coordinates take the form

$$\begin{aligned} x=r\sin {\theta }\cos {\phi },\quad y=r\sin {\theta }\sin {\phi }, \quad z=r\cos {\theta }. \end{aligned}$$

(9)

3 Charged particle dynamics

This section aims to explore the characteristics of the motion of charged particles (with mass m and electric charge q) around Kerr BH, with the condition of $p^{\mu }p_{\mu }=-m^2$. Henceforth, by applying the technique of separation of variables, the corresponding geodesics motion of metric given in Eq. (2), could be expressed by the Hamilton-Jacobi equation as

$$\begin{aligned} \mathcal {H} = -\frac{\partial S}{\partial \tau }= \frac{1}{2}g_{\mu \nu }(P_\mu -q\mathcal {A}_\mu )(P_\nu -q\mathcal {A}_\nu )+\frac{1}{2}m^2, \end{aligned}$$

(10)

in Eq. (10), $\mathcal {H}$ and S, respectively, denote the Hamiltonian and Jacobi action. Moreover, $p_\mu ={\partial S}/{\partial {x}^{\mu }}$, is the four-momentum of particles. The spacetime symmetry allows us to define the corresponding conserved energy and angular momentum in terms of metric coefficient (3) as

$$\begin{aligned} -\mathcal {E}= & {} \frac{p_{t}}{m}=g_{tt}\dot{t}+g_{t\phi } \dot{\phi }+\frac{q}{m} \mathcal {A}_t, \end{aligned}$$

(11)

$$\begin{aligned} L= & {} \frac{ p_{\phi }}{m}=g_{t\phi }\dot{t}+g_{\phi \phi }\dot{\phi }+\frac{q}{m}\mathcal {A}_\phi . \end{aligned}$$

(12)

Here dot means derivative with respect to the proper time $\tau$. In the case of charged particle motion, the specific charge $\bar{q}=q/m$ and the magnetic field can be defined as ${{\mathcal {P}}}=B\bar{q}$. Hence, by making use of $\mathcal {E}$, L the Hamiltonian in Eq. (10) modifies to

$$\begin{aligned} \mathcal {H}=\frac{1}{2}g^{rr}p_r^2+\frac{1}{2}g^{\theta \theta }p_\theta ^2+\mathcal {H}_p(r,\theta ), \end{aligned}$$

(13)

with

Fig. 1

Off-equatorial $(\theta =\pi /3)$ graphical description of the effective potential at different values of the BH’s parameters

$$\begin{aligned} \mathcal {H}_p(r,\theta )= & {} \frac{1}{2}[g^{tt}(\mathcal {E}+\bar{q} \mathcal {A}_t)^2-2g^{t\phi }(\mathcal {E}+\bar{q} \mathcal {A}_t)(L-\bar{q} \mathcal {A}_\phi ) \nonumber \\{} & {} +g^{\phi \phi }(L-\bar{q} \mathcal {A}_\phi )^2+1]. \end{aligned}$$

(14)

In the above expression, $\mathcal {H}_p(r,\theta )$ represents the potential part of the Hamiltonian. Utilizing the Eqs. (11) and (12), the value of $\dot{t}$ and $\dot{\phi }$ can be obtained as

$$\begin{aligned} \dot{t}=-\frac{g_{t\phi }(L-\bar{q} \mathcal {A}_\phi )+g_{\phi \phi }(\mathcal {E}+\bar{q} \mathcal {A}_t)}{g_{tt}g_{\phi \phi }-g_{t\phi }^2}, \end{aligned}$$

(15)

$$\begin{aligned} \dot{\phi }=-\frac{g_{tt}(L-\bar{q} \mathcal {A}_\phi )+g_{t\phi }(\mathcal {E}+\bar{q} \mathcal {A}_t)}{g_{tt}g_{\phi \phi }-g_{t\phi }^2}. \end{aligned}$$

(16)

The motion of the charged test particle can be restricted with the energetic boundaries imposed by the constraints of $\mathcal {H}=0$. By making use of the energy condition, the effective potential can be related to the specific energy as $\mathcal {E}=V_{eff}(r, \theta )$ and in the case of Kerr BH takes the form [46]

$$\begin{aligned} V_{eff}(r, \theta )=\frac{-\beta +\sqrt{\beta ^2-4\delta \gamma }}{2\delta }, \end{aligned}$$

(17)

here

$$\begin{aligned} \delta= & {} -g^{tt}, \quad \beta =-2[g^{tt}\bar{q}\mathcal {A}_t)-g^{t\phi }(L-\bar{q}\mathcal {A}_\phi )],\\ \gamma= & {} -g^{tt}(\bar{q}\mathcal {A}_t)^2+2g^{t\phi }\bar{q}\mathcal {A}_t (L-\bar{q}\mathcal {A}_\phi )\\{} & {} - g^{\phi \phi }(L-\bar{q}\mathcal {A}_\phi )^2-1. \end{aligned}$$

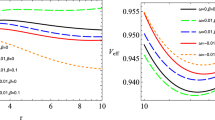
The presence of a magnetic field around BHs produces chaotic behavior in the charged particle dynamics, except for the particle dynamics on the equatorial plane. On the equatorial plane, the minima and maxima of the effective potential $V_{eff}$, which are respectively corresponding to the stable and unstable circular orbits. The circular orbits of Kerr BH can be distinguished into four different classes: namely the prograde anti-Larmor orbits (PALO) with $L>0, {{\mathcal {P}}}>0$; Retrograde Larmor orbits (RLO) with ${L}<0, {{\mathcal {P}}}>0$; Prograde Larmor orbits (PLO) with ${L}>0, {{\mathcal {P}}}<0$; Retrograde anti-Larmor orbits (RALO) with ${L}<0, {{\mathcal {P}}}<0$ for detail see [35]. Here ${L}>0$ and ${L}<0$, respectively denotes the co-and counter-rotating particles, while ${{\mathcal {P}}}>0$, ${{\mathcal {P}}}<0$, respectively defines the repulsive and attractive Lorenz forces.

Fig. 2

The locations of off-equatorial stable circular orbits at different values of the magnetic parameter ${{\mathcal {P}}}$, while the gray disk represents the outer horizon of the BH

Charged particle dynamics can be bounded by the boundaries of energetic

$$\begin{aligned} \mathcal {E}^2= V_{\textrm{eff}}(r, \theta , {{\mathcal {P}}}, L). \end{aligned}$$

(18)

To properly explore the properties of effective potential (17), we have plotted its behaviour against different parametric values in Fig. 1. We observed that ${{\mathcal {P}}}>0$ increases the stability of effective potential, whereas ${{\mathcal {P}}}<0$ diminishes its stability. The incoming particle from infinity with a larger value of both a and L required more energy to climb $V_{eff}$ in compression with a smaller value of a and L. Thus, a particle with smaller angular momentum L has a greater possibility to fall into the BH. The angular momentum L is accountable for two types of motion, i.e., $L>0$ represents prograde particle motion while $L<0$ defines retrograde particle motion. Figure 1, shows that prograde particle moves closer to the BH in comparison with retrograde particle motion, which shows a good agreement with the investigation of [47]. The existence of charged particles and their dynamics in the field is a potential justification for why the sign of the magnetic field may affect stability. Charged particles’ behaviour may vary depending on whether the field is either positive or negative, resulting in particular interactions between the BH and its neighboring matters. As a result, such interactions could have an impact on the BH system’s stability.

3.1 Charged particle trajectories

The trajectories of circular orbits near a BH could be generated by the Keplerian accretion disk, while the innermost stable circular orbit (ISCO) determines its lower boundary. On investigating the properties of effective potential $V_{eff}(r, \theta )$, one can obtain the boundaries of particle dynamics. Hence, charged test particle’s circular orbits could be acquired using stationary positions of the effective potential as

$$\begin{aligned} \partial _r V_{\textrm{eff}}(r, \theta )=0, \quad \partial _\theta V_{\textrm{eff}}(r, \theta )=0. \end{aligned}$$

(19)

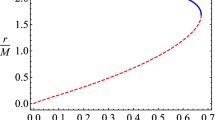
In the case of Schwarzschild BH, the local extrema of the effective potential $V_{eff}(r, \theta )$ is situated only on the equatorial plane, whereas in our case (Kerr BH) the local extrema on the off-equatorial plane can also determine the circular orbits [48]. We consider ${{\mathcal {P}}}>0$ and solve the system (19) of extreme conditions for the off-equatorial plane minima of the effective potential. For the Kerr BH case ($a\ne 0$), it is a little difficult to obtain the analytical expression for the position of off-equatorial plane minima, thus we have calculated it numerically. While for the case of $a=0$, the position where off-equatorial stable circular orbits are located can be recovered as [36]

$$\begin{aligned} r_{\textrm{min}}= & {} \frac{1}{2} \bigg (L^2 -{{\mathcal {P}}}^2 \nonumber \\{} & {} +\sqrt{ 12{{\mathcal {P}}}^2 +{{\mathcal {P}}}^4 -12 L^2 -2{{\mathcal {P}}}^2 L^2 +L^4} \bigg ), \end{aligned}$$

(20)

$$\begin{aligned} \theta _{\textrm{min}}= & {} \arctan \left( \frac{\sqrt{ L^2 -{{\mathcal {P}}}^2 }}{{{\mathcal {P}}}} \right) . \end{aligned}$$

(21)

In the case of Schwarzschild BH, the off-equatorial innermost stable circular orbit $r_{\mathrm{off\,ISCO}}$ is located at $r_{\mathrm{off\,ISCO}}=6\,M$, while in our case (at $a=0.5$ and $a=0.99$) $r_{\mathrm{off\,ISCO}} \approx 9\,M$ and $r_{\mathrm{off\,ISCO}} \approx 10.2M$ respectively, see Fig. 2. In principle, charged particle motion near a BH immersed in a uniform external magnetic field has chaotic behaviour. Although, charged particle trajectories near the stable circular orbits are still possessed a structured nature [22]. It has been observed that particles have structural trajectories on the equatorial plane as well, while their nature becomes chaotic as the angle of inclination varies from the equatorial plane. Since in our case, the monopole magnetic fields have the same symmetry as that of Kerr spacetime geometry and thus have no chaotic trajectories.

Fig. 3

Charged test particle trajectories (solid curves) around Kerr BH (shaded circle). The fourth column corresponds to the 3D particle trajectories, whereas the first and second columns describe its 2D sections. By making use of the conservation of energy and angular momentum, we can describe the 4D configuration space (t, x, y, z) in a 2D graph (third column), in which the boundary of the motion is plotted via the effective potential (dotted-dashed curves)

Fig. 4

Various kinds of charged particles, including those captured by the Kerr BH with split monopole magnetosphere, for details description, see Fig. 3

Fig. 5

Charged particle trajectories capture and escape from Kerr BH with a split monopole magnetosphere, for details description, see Fig. 3

The characteristic of effective potential can lead us to various kinds of energetic boundaries. Graphical behaviour of the test particle trajectories in the background of Kerr BH is shown in Fig. 3 equatorial plane, while in Figs. 4 and 5 off-equatorial plane. The difference between charged particle trajectories in the Schwarzschild and slowly rotating Kerr BH can be observed from the first and second rows of Fig. 3. The dotted-dashed red curves in the third column correspond to various kinds of energetic boundaries. The first kind may be referred to the existence of both outer and inner boundaries, in which the test particle is trapped in some region around BH generating a toroidal shape outside BH’s horizon (see Fig. 3 and the first and second row of Fig. 4). The second kind represents the case with an outer boundary in which BH captures the charged particle (see the third row of Fig. 4). The third kind corresponds to the situation where both inner and outer boundary does not exist, while the BH may capture the particle or it may escape to infinity. The last kind represents the case with an inner boundary, in which the particle instead of falling into the BH, escapes to infinity (see the last row of Fig. 5).

The consideration of magnetic parameters $|{{\mathcal {P}}}| \sim 1$ is necessary for a better understanding of the interaction between magnetic Lorentz force and BH’s gravitational attraction, which in general, leads to highly non-linear and chaotic motion. We notice regular and epicyclic motion owing to the response of repelling (${{\mathcal {P}}}> 0$) Lorentz forces, resulting in particle stability on circular orbits. Such an analogous conclusion for the repellent Lorentz force was previously discovered for BHs in the uniform [49] as well as parabolic magnetic field cases [50]. But in radiating charged particles this scenario operates differently than the uniform case as its circular parking orbits are not stable, and the particle spirals down to the BH gradually [50].

The neutral test particle dynamics around Schwarzschild BH are widely known to be regular and completely integrable. Whereas the motion of charged particle near magnetic BHs are often chaotic [51]. Due to the monopole’s spherical symmetry, the motion of charged particles is only regular (integrable) for split monopole magnetic field arrangement [36]. In the case of parabolic and uniform magnetic fields, strongly non-linear and chaotic trajectories can be seen. Trajectories with even little epicyclic oscillations around circular orbits are regular in our instance [9]. Such nearly circular trajectories are particularly significant in astrophysics, as they regulate thin (Keplerian) disks of accretion and toroidal fluid configurations. Our findings show chaotic scattering confirming the spherical symmetry of the monopole.

4 Particle acceleration in the magnetic Penrose process

Ionization of particles from a neutral accretion disk can be realized in many different ways, for example as atom ionization or particle decay. Another feasible hypothesis is that the accretion disk is a quasi-neutral mixture of charged particles, ions (protons), and electrons encircling the BH in circular orbits. When the matter in the disk is thick enough, the charged particles’ primary free route is very short with respect to the length of the circular orbits, and the charged particles travel together as a neutral body. Around the disk’s inner border, the plasma density drops significantly, and the charged particles are no longer inhibited by their neighbors and begin to travel freely, completely impacted by the electromagnetic field.

The presented particle ionization model was introduced in [52] and later studied also in [30, 53,54,55] and corresponds naturally to the magnetic Penrose process (MPP) [56, 57] with the original neutral particle being split into two charged particles. This simple ionization model can be used to study the fate of ionized Keplerian disks [54, 58] and if the magnetic influence is weak it could be used to generate small oscillations of the particle on circular orbits [59, 60].

Particle charge and canonical momentum are conserved in the ionization process [30]

$$\begin{aligned} 0 = q_2 + q_3 , \quad P_{\alpha (1)} = P_{\alpha (2)} + P_{\alpha (3)}. \end{aligned}$$

(22)

It can be demonstrated that kinetic momentum is preserved at the time of ionization

$$\begin{aligned} p_{\alpha (1)} = p_{\alpha (2)} + p_{\alpha (3)}, \end{aligned}$$

(23)

as the electromagnetic contributions cancel each other [52, 54]. In realistic scenarios one of the created charged particles could be much more massive than the other one, for example in the case of atom ionization the ion is much more massive than the electron. The progressively more massive charged product absorbs nearly every last of the kinetic momentum of its predecessor’s neutral particle, and the lighter charged product’s dynamical effect may be ignored

$$\begin{aligned} p_{\alpha (1)} \approx p_{\alpha (2)} \gg p_{\alpha (3)}. \end{aligned}$$

(24)

After the ionization, the neutral particle will be separated into two charged products and while their total mechanical momentum remains conserved, the charged particle will feel the influence of the electromagnetic field through Lorentz force and their trajectories will quite be different from the neutral one, see Fig. 6.

We assumed the ionization event will take place close to the Kerr BH equatorial plane, but with some small perturbation $\theta _{0}\sim \pi /2$ enabling the particle to move also in the vertical direction. The neutral parent particle will be located on the spherical orbit with initial position $x^\alpha$ and four-velocity $u_\alpha$

$$\begin{aligned} x^\alpha= & {} (t,r,\theta ,\phi )=(0,r_0,\theta _0,0), \end{aligned}$$

(25)

$$\begin{aligned} u_\alpha= & {} (u_t,u_r,u_\theta ,u_\phi )=({{\mathcal {E}}},0,0,{{\mathcal {L}}}), \end{aligned}$$

(26)

the motion constants of the particle are governed by the specific energy ${{\mathcal {E}}}$ and specific angular momentum ${{\mathcal {L}}}$ of the electrically neutral particles following circular orbits

$$\begin{aligned} {{\mathcal {E}}}= & {} \frac{ a r^{-3/2} -2 r^{-1} +1 }{\sqrt{ 2 a r^{-3/2} -3r^{-1} +1}}, \end{aligned}$$

(27)

$$\begin{aligned} {{\mathcal {L}}}= & {} \frac{ a^2 r^{-3/2} -2 a r^{-1} + \sqrt{r} }{\sqrt{ 2 a r^{-3/2} - 3 r^{-1} +1 } }. \end{aligned}$$

(28)

The inner edge of the Keplerian disks is located at the innermost stable circular orbit (ISCO) with a radius implicitly given by

$$\begin{aligned}{} & {} \left[ 2 a r \sqrt{r} -4 r^2+(r+1) r^2\right] \bigg [r^2 \bigg (r^2 \left( a^2-3 r^2\right) + 4 r^2 \nonumber \\{} & {} \quad \left( a^2+r^2\right) \bigg )-2 r^2 r^2 \left( a^2+r^2\right) -4 a r^3 r^{3/2}\bigg ]+\bigg [4 r^2 r^2\nonumber \\{} & {} \quad -r^4\bigg ] \left[ r-a\sqrt{r} \right] \left[ r \left( a^2+r^2\right) -2 a r^{3/2} \right] = 0, \end{aligned}$$

(29)

Fig. 6

Particle acceleration near a magnetized spinning BH: 1st neutral particle (neutron, black curves) lies along the inner edge of the accretion disk, and starts to fall into the BH, decomposing into two charged particles; the second (proton, blue curves) and the third (electron, red curves). The third (red) particle falls into the BH with a large quantity of negative energy, whereas the second (blue) particle is trapped in circular orbits around the BH with an excessive amount of energy

Fig. 7

Identical scenario to that of Fig. 6, however this time with comparatively smaller values of the magnetic field parameter ${{\mathcal {P}}}$

The MPP is a regional mechanism, consequently, its energy balance can only be estimated using the electromagnetic field’s local value. The neutral particle (neutron) orbiting central BH in a thin Keplerian disk or thick torus is in a bound state and its energy is slightly smaller than one $E_1<1$, the value $E_1=1$ reserved for a particle at rest located in infinity. The energy of the second particle (proton) $E_2 = p_{t2} + qA_t$ can be thus very large, while the energy of the third particle $E_3 = p_{t3} - qA_t$ can be negative with very large magnitude. Due to the chaotic motion with the combined gravitational and magnetic field the 2nd charged particle trajectory [52] and particle’s circular motion will be transmuted into the linear motion along the magnetic field lines, but in our case (in the absence of chaotic motion) the 2nd particle is trapped in circular orbits around BH due to its higher energy. This flow of charged particles can serve as a simple model of relativistic jets (or particle winds) observed in many active galactic nuclei and quasars. The third particle with large negative energy is immediately captured by the BH, as demonstrated in Figs. 6 and 7.

An identical MPP process of the accelerated charged particle is depicted in Figs. 6 and 7, at various discrete values of the magnetic field parameter ${{\mathcal {P}}}$. It can clearly be observed that in the case of a smaller magnetic field parameter ${{\mathcal {P}}}$ particle trajectories change their position frequently (see Fig. 6), whereas, in the case of larger magnetic field parameter values, the positions of trapped particles in circular orbits are more stable (see Fig. 7).

5 Astrophysical relevance

A realistic magnetic field is too weak to influence background spacetime

$$\begin{aligned} B<< B_{\textrm{G}}=\frac{c^4}{G^{3/2} M_{\odot }} \left( \frac{{M}_{\odot }}{M}\right) \sim 10^{19}{ \frac{{M}_{\odot }}{M} }\,\textrm{Gauss}\, . \end{aligned}$$

(30)

However, it might be extremely strong in terms of its impact on the charged particle motion. The interaction of the electromagnetic Lorentz force and gravitation exerted on the charged matter, symbolized by the particular charge q/m, could be mirrored by a dimensionless “magnetic parameter” ${{\mathcal {P}}}$ as

$$\begin{aligned} {{\mathcal {P}}}= \frac{q}{2m} \frac{G M}{c^4} B . \end{aligned}$$

(31)

where P is split monopole magnetic field magnitude in Gauss units. Charged test particles may symbolize protons, electrons, ions, and massive charged discrepancies like charged dust or plasma objects with specific charges q/m ranging from the electron maximum to zero. Due to the considerable magnitude of its particular charge q/m, the magnetic field parameter ${{\mathcal {P}}}$ for protons, ions, and mainly electrons could be enormous regardless of comparatively weak magnetic fields, establishing a significant impact of the electromagnetic Lorentz force on its dynamic regardless of the weak magnetic fields. Table 1 reveals a comparable analysis that includes protons and ions.

Table 1 Intensity of the magnetic field B corresponding to the magnetic parameter ${{\mathcal {P}}}=0.1$ for various types of charged particles moving in the vicinity of the BH with mass $M_{\textrm{BH}}\sim {}10~M_{\odot }$

If the MPP is associated with ionized Keplerian disks together with the chaotic dispersing procedure, one could deduce that in the case of magnetized revolving BHs, it could result in the producing jets departing to infinity at extremely high velocities owing to the extraction of rotational energy of the BHs due to capturing electrons with significant negative energy; this being thereby a basic process for a more complicated Blandford–Znajek mechanism [57].

If the ionized disk revolves around a non-spinning BH (or a slowly spinning BH encircled by a weak magnetic field), the MPP mechanism produces winds that do not escape to infinity, with energy earned from the circling matter’s rotational energy (which symbolizes the Payne-Blandford procedure [61]). The transformation of the rotational energy of the matter formerly circling in the Keplerian disk resulted in the creation of jets caused by the chaotic scattering procedure, however, the energy associated with this transformation of circular motion energy to translational dynamic energy is smaller as compared to the ones associated with electromagnetic field acceleration.

5.1 Ultra-high energy cosmic rays as products of MPP in the extreme regime

Cosmic rays are identified with a considerable expansion of particle energy. They are often composed of high-energy ions or protons; the noticed isotropic dispersion suggests an extra-Galactic origin, and the explanation of their formation has long been debated. Observations of Ultra-High-Energy Cosmic Rays (UHECRs) corresponding to particles with energy $E > 10^{18}$ eV-occasionally, particles with energy $E > 10^{21}$ eV are found, surpassing the GZK limit of $10^{19}$ eV owing to interaction with the cosmic microwave background-are of particular interest [30]. The investigation of particles having energies greater than the GZK limit implies stringent distance constraints on the source of such energetic particles.

The extreme acceleration of particles with energy $E > 10^{21}$ eV is challenging to explain. Still, we can suggest a straightforward approach centered on the ultra-efficient regime of the MPP if it acts near a supermassive BH encircled by a strong enough magnetic field. In an extremely efficient regime, the energy of a charged particle produced by the MPP can be represented as

$$\begin{aligned} {E_{MPP}= 1.3 \times 10^{21} eV \frac{q}{e} \frac{m_p}{m}\frac{B}{10^4 G}\frac{M}{10^{10} M_{\odot }}\frac{a}{0.4}.} \end{aligned}$$

(32)

In the above expression, q and m are, respectively, the charge and mass of the test particle, while e and $m_p$ represent the charge and mass of the proton. Protons having energies $E > 10^{21}$ eV may be produced even when $a=0.8$, the supermassive BH with mass $M = 10^{10} M_{\odot }$ is enclosed in a magnetic field of strength ${{\mathcal {P}}}= 10^4 G$ is slightly spinning.

It is worth mentioning that the energy of a photon can be obtained concerning the supermassive BH SgrA$^*$ and the associated magnetic field seen in the Galaxy’s center is given by

$$\begin{aligned} E_{p}^{\text {SgrA}^*}=10^{15.6} eV \frac{q}{e} \frac{m_p}{m}{\frac{a}{0.5}} \frac{B}{10^2 G}\frac{M}{4.14\times 10^{6} M_{\odot }}. \end{aligned}$$

(33)

It is extremely appealing that this quantity corresponds to the well-known knee of the energy range in the collected data, which lies at $E_{knee} \sim 10^{15.6}$ eV, where the total amount of discovered particle flux is substantially diminished, suggesting the presence of an extremely powerful only source situated at a somewhat close distance. The MPP implemented on the SgrA$^*$ advises that the model be linked to the UHECR data knee at $E \sim 10^{15.6}$ eV.

6 Concluding remarks

Since the GRMHD simulations show that the actual magnetic field around BH could possess a relatively complex nature [37, 38]. In the current work, we utilized a split-monopole magnetic field as an elementary model for the massive-scale BH’s magnetosphere with radial nature.

By making use of the effective potential, we have investigated the position of stable circular orbits for both in-and off-equatorial planes. On considering charged particle trajectories, we have numerically solved the equation of motion and graphically demonstrated its behaviour under the effect of different parametric values. Moreover, we have observed that ${{\mathcal {P}}}>0$ increases the stability of effective potential, whereas ${{\mathcal {P}}}<0$ diminishes its stability. The particle entering from infinity with a larger value of both a and L required more energy to climb $V_{eff}$ compared to a smaller value of a and L. Thus, a particle with smaller angular momentum L has a greater possibility of falling into BH. Figure 1 shows that the prograde particle ($L>0$) moves closer to the BH compared to the retrograde particle ($L<0$) motion, which is in good agreement with the investigation of [47].

It has been observed that charged particles also have structural trajectories in the equatorial plane, while their nature becomes chaotic as the angle of inclination varies from the equatorial plane, in an off-equatorial plane. In principle, charged particle dynamics around magnetized BHs reveal four different feasible regimes of ionized Keplerian disk behaviour: (i) survival in regular epicyclic motion, (ii) changing into a chaotic toroidal-like state, (iii) collapse due to escaping along magnetic field lines (causing to originate wind and/or most probably jet-like current that may provide the matter to escape the BH environment on the perpendicular direction) and (iv) collapse of accreting matter due to falling into the BH. The discovery of high-frequency quasiperiodic oscillations could be attributed to the region of epicyclic motion driven by an extremely weak magnetic field. In this regime, the combined effects of the external (electro)magnetic field and gravitational effects of BH rotation may generate an area of stable orbits in certain conditions. Magnetic fields may have a confining effect on particles, which aids in their regular motion. When magnetic fields get twisted or warped, they can cause chaotic activity disrupting any regular patterns in particle trajectories. This might happen due to the complex nature of the magnetic field structure in curved spacetime geometry, (locally) non-axisymmetric structures, or environmental disturbances. In the third scenario, tremendously energetic charged particles may escape due to the MPP. Since in our case, the split-monopole magnetic fields have identical symmetry as that of rotating Kerr BH spacetime, thus may have no chaotic (regular) trajectories like [55] for details, see Figs. 3, 4 and 5. The features of these regimes are currently being studied and may vary based on the BH’s and its accretion disk’s parameters.

We suggest an approach for supermassive BHs to be responsible for the production of ultra-high-energy cosmic rays. Using a unique, ultra-efficient regime of MPP and ionization of neutral particles, including neutron-beta decaying at the horizon of a rotating BH. Charged particles from ionized Keplerian disks can be accelerated near Kerr BHs with an MPP efficiency of more than $10^{10}$, allowing protons to be accelerated to energy:

$\bullet$ $10^{21}$ eV in the vicinity of a supermassive BH of mass $M = 10^{10}M_{\odot }$ and ${{\mathcal {P}}}= 10^{4}$G; $\bullet$ $10^{19}$ eV in the vicinity of M87, a supermassive BH of mass $M = 7\times 10^{9}M_{\odot }$ and ${{\mathcal {P}}}= 10^{2}$ G; and $\bullet$ $10^{15.6}$ eV in the vicinity of SgrA$^*$, a supermassive BH of mass $M = 4\times 10^{6}M_{\odot }$ and ${{\mathcal {P}}}= 10$ G.

The following is the model’s primary benefits:

• Supermassive BHs are predicted to be the source of the highest-energy cosmic rays

• processes under feasible astrophysical settings for supermassive BH in its vicinity, with modest spin and usual magnetic field intensity

• is not dependent on an expanded acceleration zone for particles to achieve ultra-high energy, nor does it necessitate fine-tuning of accreting matter parameters (for details see [55]).

Furthermore, understanding the impact of strong gravity and particle interactions and behaviour may be gained by researching energy extraction processes around rotating black holes. Frame dragging, gravitational time dilation and the effect of spacetime curvature on particle trajectories are examples of such phenomena.

In principle, the presented approach may be used for neutron stars with small masses compensated by enormous magnetic fields. However, this type of investigation will be left for future research. Because relativistic electrons lose synchrotron radiation $10^{10}$ times quicker than protons, heavier elements of UHECRs appear more likely in this scenario.

Predicting the candidate supermassive BHs within the suggested framework necessitates magnetic field data at the event horizon scale. There are few such exact measurements at present, but forthcoming global VLBI observations should increase this number. We think that the proposed model of supermassive BH as a UHECR power engine opens up novel possibilities for understanding this unique high-energy phenomenon and its applicability in various high-energy contexts.