1 Introduction

Raised by Einstein et al. [1] in discussions on the incompleteness of quantum mechanics in 1935, quantum nonlocality [2] has been extensively studied and played significant roles in a variety of quantum tasks [3]. Recent studies have shown that quantum nonlocality is also a unique quantum resource for some device-independent quantum tasks such as the key distribution [4], random expansion [5], random amplification [6] and the related experiments [7,8,9]. In particular, in 1987 a special kind of nonlocality called genuine tripartite nonlocality (GTN) was introduced by Svetlichny for tripartite systems [10]. Such multipartite nonlocal correlations have not only foundational implications [11] but also novel applications in quantum communication and quantum computation [12,13,14,15], as well as in phase transitions and criticality in many-body systems [14]. GTN can be detected by the violation of Svetlichny inequality. Let \(A_i=\vec {a}_i\cdot \vec {\sigma }\), \(B_i=\vec {b}_i\cdot \vec {\sigma }\) and \(C_i=\vec {c}_i\cdot \vec {\sigma }\), \(i=0,1\), be the measurement observables associated with the first, second and third qubit, respectively, with \(\vec {a}_i\), \(\vec {b}_i\) and \(\vec {c}_i\) the real unit vectors, \(\vec {\sigma }=(\sigma _1,\sigma _2,\sigma _3)\) the vector given by the standard Pauli matrices. The Svetlichny operator is defined by

$$\begin{aligned} {\mathbb {S}}{} & {} =A_0(B_0+B_1)C_0+A_0(B_0-B_1)C_1\nonumber \\{} & {} \quad +A_1(B_0-B_1)C_0-A_1(B_0+B_1)C_1. \end{aligned}$$
(1)

If a state \(\rho \) admits bi-local hidden variable model, then the expectation value of the Svetlichny operator satisfies the following Svetlichny’s inequality,

$$\begin{aligned} {\mathbb {S}}(\rho )=|Tr({\mathbb {S}}\rho )|\le 4. \end{aligned}$$
(2)

If the inequality (2) is violated, \(\rho \) must be a genuine three-qubit nonlocally correlated state.

In 1974, Hawking discovered black hole evaporation caused by thermal radiation emitted by the black hole [16]. Soon after, Unruh in 1976 proposed a very important prediction based on the effect of Hawking radiation, which says that a vacuum state observed by an observer who stays in flat Minkowski spacetime would be detected as a thermal state from another observer who hovers near the event horizon of the black hole with uniform acceleration [17, 18]. In recent years, as the intersection of classical informatics, quantum mechanics, special and general relativity and quantum field theory, the problem of quantum information in non-inertial system and curved spacetime has become a new hotspot in the research of quantum information science [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45]. Undoubtedly, the study of quantum information under the framework of relativity, especially in the non-inertial frame and curved spacetime, not only is of great significance to the development and perfectness of quantum information theory, but also plays a positive role in understanding the entropy and information paradox in black holes. For examples, Fuentes et al. [19] show that the entanglement in noninertial frames is characterized by the observer-dependent property. Martín-Martínez et al. [22] studied the entanglement degradation affected by the Hawking effect of Schwarzschild black hole. Mann et al. [30] pointed out that incorporating concepts from quantum theory into relativity can yield novel and interesting effects. More recently, Wu et al. [43] studied the GTN and the genuine tripartite entanglement (GTE) of Dirac fields in the background of a Schwarzschild black hole. Li et al. [44] explored the tripartite entropic uncertainty and genuine tripartite quantum coherence of Dirac fields in the background of the Garfinkle-Horowitz-Strominger (GHS) dilation space-time.

Much attention has been paid to the multipartite Greenberger–Horne–Zeilinger (GHZ) state \(|GHZ\rangle =\frac{1}{\sqrt{2}}(|000\rangle +|111\rangle )\) or the generalized GHZ states under the Hawking radiation. It is recently found in Refs. [43] and [44] that the GTN is not redistributable, but GTE can be redistributed through Hawking effect. With the growth of the Hawking temperature, the physically accessible GTN decreases, but physically inaccessible GTN is not generated. The GTE however behaves differently: with the loss of the physically accessible GTE, the physically inaccessible GTE is generated continually through Hawking effect. This is inconsistent with intuition since quantum entanglement and quantum nonlocality are in consistent for pure states [46,47,48]. On the other hand, previous studies have shown that for some three-qubit pure states (GGHZ state, MS state and so on), it has been observed only that the GTN decreases [49, 50]. But the measurement-induced-nonlocality of two-qubit mixed states can increase via the Unruh effect or near a black hole [51, 52]. To clarify such problems, in this article we study the GTN of multipartite mixed states for Dirac fields in the background of a Schwarzschild black hole. The paper is organized as follows. In Sect. 2, we briefly recall the quantization of Dirac fields in the background of Schwarzschild black hole, and the GTN, GTE and quantum coherence for three-qubit X-states. In Sect. 3, we calculate and analyze the GTN of a detailed mixed state after one or bipartite acceleration. A novel phenomenon that is basically different from that of pure states is illustrated: the Hawking effect may not only degrades the physically accessible GTN, but also enhances the physically inaccessible GTN. The “sudden death” of physically accessible GTN takes place at some critical Hawking temperature, while “sudden birth” happens to the physically inaccessible GTN. We show that such phenomenon may be not observed for other mixed states. In Sect. 4, we consider the quantum correlation GTE and quantum coherence. Analytical tradeoff relations among the distributions of GTE and coherence are derived. Section 5 is the conclusions and discussions.

2 Quantization of Dirac fields in a Schwarzschild black hole

We first recall the evolution process of vacuum state of Dirac fields in a Schwarzschild black hole [43, 44]. The Dirac equation under a general background spacetime can be written as [53],

$$\begin{aligned} {[}\gamma ^ae_a^{\mu }(\partial _{\mu +\Gamma _{\mu }})]\Phi =0, \end{aligned}$$
(3)

where\(\gamma ^a\) are the Dirac matrices, \(e_a^{\mu }\) is the inverse of the tetrad \(e_{\mu }^a\), \(\Gamma _{\mu }=\frac{1}{8}[\gamma ^a,\gamma ^b]e_a^{\nu }e_{b\nu ;\mu }\) are the spin connection coefficients. The metric of the Schwarzschild black hole can be written as [24, 54, 55]

$$\begin{aligned} ds^2= & {} -\left( \frac{r-2M}{r-2D}\right) dt^2+\left( \frac{r-2M}{r-2D}\right) ^{-1}dr^2\nonumber \\{} & {} + r(r-2D)(d\theta ^2+\sin ^2\theta d\phi ^2), \end{aligned}$$
(4)

where M denotes the mass of the black hole, and D denotes the parameter of the dilation field. The Hawking temperature is given by \(T=\frac{1}{8\pi (M-D)}\). The thermal Fermi-Dirac distribution of particles with Hawking temperature T was observed in Refs. [56,57,58].

Solving the Dirac equation (3) near the event horizon of black hole, one gets a set of positive frequency outgoing solutions for the inside and outside regions of the event horizon, [22, 23]

$$\begin{aligned} \phi _k^{I+}=\xi e^{-i\omega \mu }, \ \ \phi _k^{II+}=\xi e^{i\omega \mu }, \end{aligned}$$
(5)

where k represents the field mode, \(\xi \) denotes four-component Dirac spinor, \(\omega \) is a monochromatic frequency and \(\mu =t-r_{*}\), where the tortoise coordinate \(r_{*}=r+2M\ln \frac{r-2M}{2M}\). \(\phi _k^{I+}\) and \(\phi _k^{II+}\) are usually called Schwarzschild modes. Particles and antiparticles are classified according to future-directed timelike Killing vector under each region.

An analytic continuation of (5) [44] gives rise to a complete basis of positive energy modes, i.e., the Kruskal modes [58]. Then one can use the Schwarzschild mode and the Kruskal mode to expand the Dirac field, respectively, leading to the Bogoliubov transformations between annihilation operator and creation operator under the Schwarzschild and Kruskal coordinates [42]. After properly normalizing the state vector, the vacuum state and excited state of the Kruskal particle in the single-mode approximation are given by

$$\begin{aligned}{} & {} |0\rangle =\cos \beta |0\rangle _{I}^{+}|0\rangle _{II}^{-} +\sin \beta |1\rangle _{I}^{+}|1\rangle _{II}^{-}, \end{aligned}$$
(6)
$$\begin{aligned}{} & {} |1\rangle =|1\rangle _{I}^{+}|0\rangle _{II}^{-}, \end{aligned}$$
(7)

where \(|n\rangle _{I}\) and \(|n\rangle _{II}\) are the number states for the particle outside the region (physically accessible) and the antiparticle inside the region of the event horizon (physically inaccessible), respectively, the superscripts \(+\) and − indicate the particle and antiparticle, respectively, \(\cos \beta =(e^{-\frac{\omega }{T}})^{-\frac{1}{2}}\) and \(\sin \beta =(e^{\frac{\omega }{T}})^{-\frac{1}{2}}\).

In the following we will consider three-qubit X-state give by density matrix,

$$\begin{aligned} \rho _X=\left( \begin{array}{cccccccc} d_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} f_1 \\ 0 &{} d_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} f_2 &{} 0 \\ 0 &{} 0 &{} d_3 &{} 0 &{} 0 &{} f_3 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} d_4 &{} f_4 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} f_4^{*} &{} e_4 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} f_3^{*} &{} 0 &{} 0 &{} e_3 &{} 0 &{} 0 \\ 0 &{} f_2^{*} &{} 0 &{} 0 &{} 0 &{} 0 &{} e_2 &{} 0 \\ f_1^{*} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} e_1 \end{array}\right) \end{aligned}$$

in the orthogonal basis \(\{ |000\rangle ,|001\rangle ,\ldots ,|111\rangle \}\). The GTN (Svetlichny value) of \(\rho _X\) is simply given by [59, 60]

$$\begin{aligned} S(\rho _X)=\max \{8\sqrt{2}|f_i|,4|N|\}, \end{aligned}$$
(8)

where \(N=d_1-d_2-d_3+d_4-e_4+e_3+e_2-e_1\). The GTE of \(\rho _X\) is given by [61, 62]

$$\begin{aligned} E(\rho _X)=2\max \{0,|f_i|-m_i\}, i=1,2,3,4, \end{aligned}$$
(9)

where \(m_i=\sum _{j\ne i}^4\sqrt{d_je_j}\). The quantum coherence of \(\rho _X\) is given by [63,64,65]

$$\begin{aligned} C(\rho _X)=C_{l_1}(\rho _X)=\sum _{i\ne j}|\rho _{ij}|=2\sum _{i=1}^4|f_i|. \end{aligned}$$
(10)

3 Evolution of GTN for mixed states in Schwarzschild black hole

We first consider the initial tripartite mixed state \(\rho _1=p| GHZ\rangle \langle GHZ|+(1-p)| 000\rangle \langle 000|\) of the dirac fields shared by Alice, Bob and Charlie in the asymptotically flat region, where \(p\in [0,1]\).

Case(1): Alice and Bob stay at an asymptotically flat region, while Charlie hovers outside the event horizon of the black hole. Applying the transformation of Eqs. (6) and (7) for detector C, we obtain a 4-partite state \(\rho _{ABC_IC_{II}}\) associated with subsystems A, B and \(C_I\) observed by Alice, Bob and Charlie outside the event horizon of black hole, respectively, and the subsystem \(C_{II}\) observed by anti-Charlie inside the event horizon. Since the interior region of black hole is causally disconnected from the exterior region, Alice, Bob and Charlie cannot access the modes inside the event horizon. The mode \(C_I\) outside the event horizon is called the accessible modes, and the mode \(C_{II}\) inside the event horizon the inaccessible modes. By tracing over the inaccessible mode on \(\rho _{ABC_IC_{II}}\), we obtain the reduced density matrix,

$$\begin{aligned}{} & {} \rho _{ABC_I} \\ {}{} & {} =\left( \begin{array}{cccccccc} (\frac{2-p}{2})\cos ^2 r_c &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{p}{2}\cos r_c \\ 0 &{} (\frac{2-p}{2})\sin ^2 r_c &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{p}{2}\cos r_c &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{p}{2} \end{array}\right) , \end{aligned}$$

where \(\cos r_c=(e^{-\frac{\omega }{T_c}})^{-\frac{1}{2}}\) and \(\sin r_c=(e^{\frac{\omega }{T_c}})^{-\frac{1}{2}}\) are functions of the Hawking temperature \(T_c\). For simplicity, we set \(\omega =1\) and instead of \(T_c\), we use \(r_c\) in the following analysis.

From Eq. (8), we obtain the GTN of the state \(\rho _{ABC_I}\),

$$\begin{aligned} S(\rho _{ABC_I})\!=\!\max \!\left\{ 8\sqrt{2}\left| \frac{p}{2}\!\cos r_c \right| ,\!4\left| \left( 1\!-\!\frac{p}{2}\right) \cos 2r_c\!-\!\frac{p}{2}\right| \right\} . \end{aligned}$$

In Fig. 1a we plot the Svetlichny value \(S(\rho _{ABC_I})\) as function of \(r_c\) (the Hawking temperature T) and p. We find that, with the increase of Hawking temperature T and the decreasing of parameter p from 1 to 0, \(S(\rho _{ABC_I})\) is larger than 4 at first and then smaller than 4. This implies two interesting aspects. One is that the thermal noise introduced by Hawking temperature destroys the physically accessible GTN between Alice, Bob and Charlie. And the “sudden death” takes place at a critical temperature \(T_c\). Another phenomenon is that with the decrease of the parameter p, the GTN transition from the maximally entangled initial state to the complete separable one is also influenced by Hawking effect.

Fig. 1
figure 1

Case(1): Alice and Bob stay at an asymptotically flat region, while Charlie hovers outside the event horizon of the black hole. a The Svetlichny value \(S(\rho _{ABC_I})\) as function of \(r_c\) (the Hawking temperature T) and p. b The Svetlichny value \(S(\rho _{ABC_{II}})\) as function of \(r_c\) and p

Full size image

Similarly, by tracing over the accessible mode \(C_I\) ins \(\rho _{ABC_IC_{II}}\) we get the reduced density matrix,

$$\begin{aligned}{} & {} \rho _{ABC_{II}} \\{} & {} \quad =\left( \begin{array}{cccccccc} (\frac{2-p}{2})\cos ^2 r_c &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} (\frac{2-p}{2})\sin ^2 r_c &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{p}{2}\sin r_c &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \frac{p}{2}\sin r_c &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{p}{2}&{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array}\right) \end{aligned}$$

and the GTN of the state \(\rho _{ABC_{II}}\),

$$\begin{aligned} S(\rho _{ABC_{II}})=\max \left\{ 8\sqrt{2}\left| \frac{p}{2}\sin r_c \right| ,4\left| \left( \frac{2-p}{2}\right) \cos 2r_c+\frac{p}{2}\right| \right\} . \end{aligned}$$

From Fig. 1b we see that \(S(\rho _{ABC_{II}})\) is always small than 4 for any \(r_c\) and p. Thus the physically inaccessible GTN between modes A, B and \(C_{II}\) cannot be produced.

Case(2): Alice still stays at an asymptotically flat region, while Bob and Charlie hover outside the event horizon of the black hole. Then in terms of the Kruskal modes for Alice and Schwarzschild modes for Bob and Charlie, the initial state \(\rho _1\) can be rewritten as a 5-partite entangled state \(\rho _{AB_{I}B_{II}C_{I}C_{II}}\) consisted by subsystem A observed by Alice, subsystems \(B_I\) and \(C_I\) observed by Bob and Charlie outside the event horizon of black hole, and subsystems \(B_{II}\) and \(C_{II}\) observed by anti-Bob and anti-Charlie inside the event horizon, respectively. We call the modes \(B_I\) and \(C_I\) outside the event horizon the accessible modes, and the modes \(B_{II}\) and \(C_{II}\) inside the event horizon the inaccessible modes. Tracing over the inaccessible modes in state \(\rho _{AB_{I}B_{II}C_{I}C_{II}}\), we obtain the reduced density operator,

$$\begin{aligned}{} & {} \rho _{AB_IC_{I}} = \left( \begin{array}{cccccccc} d_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} f_1\\ 0 &{} d_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} d_3 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} d_4 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ f_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{p}{2} \end{array}\right) , \end{aligned}$$

where \(d_1=(\frac{2-p}{2})\cos ^2 r_b \cos ^2 r_c,\) \(d_2=(\frac{2-p}{2})\cos ^2 r_b \sin ^2 r_c,\) \(d_3=(\frac{2-p}{2})\sin ^2 r_b \cos ^2 r_c,\) \(d_4=(\frac{2-p}{2})\sin ^2 r_b \sin ^2 r_c\) and \(f_1=\frac{p}{2}\cos r_b \cos r_c.\) Here, \(\cos r_b=(e^{-\frac{\omega }{T_b}})^{-\frac{1}{2}}\) and \(\sin r_b=(e^{\frac{\omega }{T_b}})^{-\frac{1}{2}}\) are functions of the Hawking temperature \(T_b\). We obtain the GTN for \(\rho _{AB_IC_{I}}\),

$$\begin{aligned} S(\rho _{AB_IC_{I}}){} & {} =\max \Bigg \{4\sqrt{2}p|\cos r_b\cos r_c|, \\{} & {} \quad 4\left| \left( \frac{2-p}{2}\right) \cos 2r_b\cos 2r_c-\frac{p}{2}\right| \Bigg \}. \end{aligned}$$

In Fig. 2, we plot the Svetlichny value \(S(\rho _{AB_IC_I})\) as function of \(r_b=r_c\) and p. I it shown that \(S(\rho _{AB_IC_I})\) is larger than 4 at first and then smaller than 4 with the increase of Hawking temperature T and the decrease of p. This implies that the thermal noise introduced by Hawking temperature destroys the physically accessible GTN between Alice, Bob and Charlie. The “sudden death” of such physically accessible GTN takes place at some critical temperature \(T_b\).

Fig. 2
figure 2

Case(2): The Svetlichny value \(S(\rho _{AB_IC_I})\) as a function of \(r_c=r_b\) and p for the case that Alice still stays at an asymptotically flat region, while Bob and Charlie hover outside the event horizon of the black hole

Full size image

The reduced density matrix \(\rho _{AB_IB_{II}}\) can be expressed as

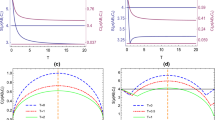
$$\begin{aligned}{} & {} \rho _{AB_IB_{II}} = \left( \begin{array}{cccccccc} d_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} f_1\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{p}{2} &{} 0 \\ f_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} e_1 \end{array}\right) , \end{aligned}$$

with the matrix elements give by \(d_1=(\frac{2-p}{2})\cos ^2 r_b,\) \(f_1=(\frac{2-p}{2})\cos r_b \sin r_b\) and \(e_1=(\frac{2-p}{2})\sin ^2 r_b\). In Fig. 3, we plot the Svetlichny value \(S(\rho _{AB_IB_{II}})\) as function of \(r_b=r_c\) and p. We find that \(S(\rho _{AB_IB_{II}})\) is smaller than 4 at first and then larger than 4 with the increase of Hawking temperature T and the decrease of p. This phenomenon is quite novel as the birth of the physically inaccessible GTN for \(\rho _{AB_IB_{II}}\) has never been observed in previous literature with pure initial states [43, 44]. To see this new phenomenon more clearly, we draw \(S(\rho _{AB_IB_{II}})\) corresponding to different values of p in Fig. 3b. We see that when \(p=1\), the birth of GTN does not show up. As the value of p becomes smaller, GTN becomes more than 4 when \(p=\frac{1}{2},\frac{1}{4}\) and so on. This result shows that the GTN can pass through the event horizon of black hole for the case of mixed states.

Additionally, we note that in Fig. 3b, the phenomenon of GTN can also be observed for \(p=0\), namely, the original state is separable. This is impossible in inertial fields, but it indeed happens in non-inertial fields with acceleration and rotation. Similar phenomenon has been observed for quantum entanglement [66, 67], where entangled states are successfully obtained under rotation effect when the initial state is separable. These facts also show the peculiarity of quantum information in the framework of relativity.

Fig. 3
figure 3

Case(2): Alice still stays at an asymptotically flat region, while Bob and Charlie hover outside the event horizon of the black hole. a The Svetlichny value \(S(\rho _{AB_IB_{II}})\) as function of \(r_b\) and p. b The Svetlichny value \(S(\rho _{AB_IB_{II}})\) as function of \(r_b\). The dotted red, the dashed blue, the dot-dashed gray and the solid green lines are for \(p=1,\frac{1}{2},\frac{1}{4},0\), respectively

Full size image

Due the symmetry under the interchange of Bob and Charlie, we have \(S(\rho _{AC_IC_{II}})=S(\rho _{AB_IB_{II}})\) and \(S(\rho _{AB_IC_{II}})=S(\rho _{AB_{II}C_I})\). Therefore, the GTN of \(\rho _{AC_IC_{II}}\) has similar properties to \(\rho _{AB_IB_{II}}\) under the influence of Hawking effect. We only need to consider the GTN for the rest two types of reduced states \(\rho _{AB_IC_{II}}\) and \(\rho _{AB_{II}C_{II}}\) of \(\rho _{AB_{I}B_{II}C_{I}C_{II}}\). By direct calculation, we have

$$\begin{aligned}{} & {} \rho _{AB_IC_{II}} = \left( \begin{array}{cccccccc} d_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} d_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} f_2 &{} 0 \\ 0 &{} 0 &{} d_3 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} d_4 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} f_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{p}{2} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array}\right) , \end{aligned}$$

where \(d_1=(\frac{2-p}{2})\cos ^2 r_b \cos ^2 r_c,\) \(d_2=(\frac{2-p}{2})\cos ^2 r_b \sin ^2 r_c,\) \(d_3=(\frac{2-p}{2})\sin ^2 r_b \cos ^2 r_c,\) \(d_4=(\frac{2-p}{2})\sin ^2 r_b \sin ^2 r_c\) and \(f_2=\frac{p}{2}\cos r_b \cos r_c\), and

$$\begin{aligned}{} & {} \rho _{AB_{II}C_{II}} = \left( \begin{array}{cccccccc} d_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} d_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} d_3 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} d_4 &{} f_4 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} f_4 &{} \frac{p}{2} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array}\right) , \end{aligned}$$

where \(d_1=(\frac{2-p}{2})\cos ^2 r_b \cos ^2 r_c,\) \(d_2=(\frac{2-p}{2})\cos ^2 r_b \sin ^2 r_c,\) \(d_3=(\frac{2-p}{2})\sin ^2 r_b \cos ^2 r_c,\) \(d_4=(\frac{2-p}{2})\sin ^2 r_b \sin ^2 r_c\) and \(f_4=\frac{p}{2}\sin r_b \sin r_c.\)

Using (8) we obtain \(S(\rho _{AB_IC_{II}})\) and \(S(\rho _{AB_{II}C_{II}})\), respectively. Figure 4 shows that the GTN cannot be generated between \(A, B_I \) and \(C_{II}\) or between \(A, B_{II}\) and \( C_{II}\).

Fig. 4
figure 4

Case(2): Alice still stays at an asymptotically flat region, while Bob and Charlie hover outside the event horizon of the black hole. a The Svetlichny value \(S(\rho _{AB_IC_{II}})\) as function of \(r_c=r_b\) and p. b The Svetlichny value \(S(\rho _{AB_{II}C_{I}})\) as function of \(r_c=r_b\) and p

Full size image

We have used the initial mixed state \(\rho _1=p| GHZ\rangle \langle GHZ| +(1-p)| 000\rangle \langle 000|\) to display the novel phenomenon of sudden birth of GTN. However, such phenomenon may not appear for other mixed states. Let us consider the mixed state \(\rho _2=p| GHZ\rangle \langle GHZ|+(1-p)| 111\rangle \langle 111|\). For \(\rho _2\) the GTN for other reduced states are similar to \(\rho _1\), except for \(S(\rho _{AB_IB_{II}})\) which is always less than 4, namely, no GTN is generated, see Fig. 5. The only difference between the states \(\rho _1\) and \(\rho _2\) is that the vector \(|000\rangle \) is replaced with \(|111\rangle \). Their different behaviors on the new generation of physically inaccessible GTN are due to that the evolution process of vacuum state of Dirac fields in a Schwarzschild black hole has different effects on \(|0\rangle \) and \(|1\rangle \).

Fig. 5
figure 5

Case (2): Alice still stays at an asymptotically flat region, while Bob and Charlie hover outside the event horizon of the black hole. The Svetlichny value \(S(\rho _{AB_IB_{II}})\) with respect to the initial state \(\rho _2\) as function of \(r_b\) and p

Full size image

4 Evolution of the GTE and quantum coherence in Schwarzschild black hole

In this section, we explore the GTE and quantum coherence under evolution of \(\rho _1\) after the acceleration effect for one or two accelerated detector(s) coupled to the vacuum field.

It is very coincidental that according to Eqs. (9) and (10), we find that for all the tripartite reduced states in the previous section, the GTE is equal to the quantum coherence. For the case (1), we have

$$\begin{aligned} \begin{array}{l} E(\rho _{ABC_I})=C(\rho _{ABC_I})=p\cos r_c,\\ E(\rho _{ABC_{II}})=C(\rho _{ABC_{II}})=p\sin r_c. \end{array} \end{aligned}$$

For the case (2), we obtain

$$\begin{aligned} \begin{array}{l} E(\rho _{AB_IC_I})=C(\rho _{AB_IC_I})=p|\cos r_b\cos r_c|,\\ E(\rho _{AB_IC_{II}})=C(\rho _{AB_IC_{II}})=p|\cos r_b\sin r_c|,\\ E(\rho _{AB_IB_{II}})=C(\rho _{AB_IB_{II}})=(2-p)|\cos r_b\sin r_b|,\\ E(\rho _{AB_{II}C_{II}})=C(\rho _{AB_{II}C_{II}})=p|\sin r_b\sin r_c|. \end{array} \end{aligned}$$

Due to the symmetry between Bob and Charlie, it is easy to find that

$$\begin{aligned} \begin{array}{l} E(\rho _{AC_{I}C_{II}})=E(\rho _{AB_{I}B_{II}})=(2-P)|\sin r_c\cos r_c|,\\ E(\rho _{AB_{II}C_{I}})=E(\rho _{AB_IC_{II}})=p|\cos r_c\sin r_b|. \end{array} \end{aligned}$$

The tradeoff relationship and the monogamy relations are important issues in characterizing the quantum correlations in quantum information theory, which are deeply related to quantum uncertainty and incompatibility principle. Noted that the acceleration of Bob and Charlie is completed under the same Hawking radiation. Hence, the corresponding changes of the Hawking temperatures \(T_b\) and \(T_c\) are the same. Therefore, the functions \(\cos r_b\) and \(\cos r_c\) corresponding to T are independent individually, namely, \(\cos r_b=\cos r_c\) and \(\sin r_b=\sin r_c\). Therefore, we have the following tradeoff relations between the physically accessible GTE (quantum coherence) and the physically inaccessible GTE (quantum coherence),

$$\begin{aligned}{} & {} E^2(\rho _{ABC_I})+E^2(\rho _{ABC_{II}})=p^2=E^2(\rho _1), \end{aligned}$$
(11)
$$\begin{aligned}{} & {} E(\rho _{AB_IC_I})+E(\rho _{AB_{II}C_{II}})=p=E(\rho _1), \end{aligned}$$
(12)
$$\begin{aligned}{} & {} E^2(\rho _{AB_IC_I})+E^2(\rho _{AB_{II}C_I})+E^2(\rho _{AB_IC_{II}})\nonumber \\{} & {} \quad +E^2(\rho _{AB_{II}C_{II}})=p^2. \end{aligned}$$
(13)

The above trade-off relations give restrictions on the redistribution of entanglement from physically accessible to physically inaccessible patterns. For instance, (12) shows that the total physically accessible GTE \(E(\rho _{AB_IC_I})\) and the physically inaccessible GTE \(E(\rho _{AB_{II}C_{II}})\) is equal to the initial GTE of \(\rho _1\). Therefore, under the time evolution how much the physically accessible GTE decreases implies how much the physically inaccessible GTE increases. The Eq. (13) poses a strong restrictive relationship among the four genuine tripartite entanglement. These tradeoff relations shed new lights on understanding the quantum information theory in the framework of relativity.

5 Conclusions and discussions

Quantum nonlocality is a distinctive feature of quantum mechanics. We have investigated the effect of Hawking radiation on GTN for Dirac fields in Schwarzschild spacetime. We first time show that the Hawking effect can not only degrades the physically accessible GTN, but also enhance the physically inaccessible GTN. The “sudden death” of the physically accessible GTN at certain critical Hawking temperature and the “sudden birth” of the physically inaccessible GTN imply that, with the loss of the physically accessible GTN, the physically inaccessible GTN is generated continually through Hawking effect. This phenomenon is observed first time for GTN. If we regard the redistribution of nonlocality as a kind of phenomenon of information tunnelling, this phenomenon shows that not only the flow of quantum entanglement can pass through the black hole perspective, but also the nonlocality can either. This phenomenon also enriches further understanding of relativistic quantum information.

We have also investigated the problem for quantum correlation GTE and quantum coherence. Interesting trade-off relations are derived among the GTEs and the quantum coherence, which restrict the distribution of GTE and coherence in the subsystems during the evolution. With regard to the related theories of entanglement measurement under the effect of Hawking radiation for Dirac fields in Schwarzschild spacetime, the previous literatures mainly focused on pure initial states. Based on initial mixed states, we have shown the new phenomenon that the physically inaccessible GTN is generated continually through Hawking effect. From the view of resource theory in quantum mechanics, the quantum correlations including entanglement and nonlocality, as well as the coherence may have universal redistribution properties. Our results may highlight new understanding of relativistic quantum information.