1 Introduction

The accelerated expansion of our universe, supported by various astronomical observations [1,2,3], has prompted the exploration of alternative gravity theories and exotic matter models. Among them, modifications to Einstein’s theory of gravity, such as f(R) gravity [4, 5], and the introduction of phantom energy with negative energy density [6, 7], have emerged as compelling explanations. Phantom AdS black holes, which encompass the effects of phantom fields within modified gravity theories, offer a unique avenue for investigating the interplay between gravity and exotic matter. By studying these solutions, obtained through the coupling of the electromagnetic field with a constant \(\eta \) [8], we can gain insights into the fundamental nature of gravity, the properties of phantom energy, and their implications for black hole thermodynamics.

Black hole thermodynamics has been a special and important topic in black hole physics for over two decades. Investigations of black holes in AdS spacetime has played a prominent role in advancing our understanding of this subject since the Hawking and Page demonstrated the existence of phase transition between thermodynamically stable large black hole and thermal radiation in the AdS spacetime [9]. This is particularly significant because these black holes admit a gauge-gravity duality description [10]. Subsequent developments have further enhanced our knowledge, as the thermodynamics of Reissner Nordström-AdS black holes revealed phase structures analogous to familiar thermodynamic systems [11, 12]. The study of AdS black hole thermodynamics has been extended to include the consideration of the cosmological constant as a thermodynamic pressure [13,14,15], and revealing several exciting results, such as P–V phase transitions (van der Waals type) [16,17,18,19,20,21,22,23,24], Hawking-Page-like phase transitions [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39], etc.Footnote 1

Motivated by the works, it would be interesting to investigate the thermodynamic properties of phantom AdS black holes. As far as we know, Ref. [8] obtained the basic quantities of phantom AdS black holes, such as the Hawking temperature, the entropy, the specific heat at constant charge and the free energy. Building upon these findings, subsequent studies [45, 46], expanded the investigation to the extended phase space in which the thermodynamic pressure defined by negative cosmological constant and treated as a variable,Footnote 2 and found there is no P–V (van der Waals type) phase transition.

In the present paper, we aim to examine the thermodynamic stability of phantom AdS black holes, focusing specifically on the Hawking-Page-like phase transition. To accomplish this, we employ the same methodology utilized in earlier works [11, 12] (for further related studies, refer to [49,50,51,52]). We calculate the temperature and free energy of AdS black holes with either a Maxwell field \((\eta =1)\) (where we revisit past studies) or a phantom field \((\eta =-1)\) in both the canonical and grand canonical ensembles. In the canonical ensemble, the black hole for \(\eta =1\) exhibits only a transition from a small to a large black hole phase, while for \(\eta =-1\), no transition is observed. It is worth noting that in the free energy-temperature diagram for the latter scenario, the branches representing small black holes reach and cross the T-axis as the temperature rises. We interpret this intriguing phenomenon as a direct consequence of the exotic characteristics exhibited by phantom black holes. In the grand canonical ensemble, we observe that the black holes with either a Maxwell field \((\eta =1)\) or a phantom field \((\eta =-1)\) exhibits a Hawking-Page-like phase transition between the thermal radiation of AdS spacetime and thermodynamically stable large black holes.

The paper is organized as follows. In Sec. 2, we will make a review of the basic thermodynamic quantities of spherically symmetric phantom AdS black holes. In Sec. 3, we calculate the temperature and free energy of phantom AdS black holes in both the canonical and grand canonical ensembles to investigate their thermodynamic stability and phase structures. Finally, we provide concise conclusions and discuss future research directions in Sect. 4. Throughout this paper, we will use the geometric units such that \(c=G=k_B=\hbar =1\).

2 Thermodynamics of phantom spherically symmetric AdS black holes

Black hole thermodynamics conceived as a discipline, was formulated with the development of quantum field theory in curved spacetime, which drew analogies between thermodynamic quantities such as mass, temperature, and entropy with the area of the black hole’s event horizon. In this section, we briefly review on thermodynamics of phantom spherically symmetric AdS black holes [8]. The corresponding action for the black hole is given by

$$\begin{aligned} S=\frac{1}{16\pi }\int d^{4}x\sqrt{-g}\Big (R+\frac{6}{L^2}+2\eta F_{\mu \nu } F^{\mu \nu } \Big ) , \end{aligned}$$
(1)

where R is the Ricci scalar which characterizes the Einstein-Hilbert action, L is the AdS radius which correspond to cosmological constant \(\Lambda =-3/L^2\), and the third term is represents to the electromagnetic field with constant \(\eta \). For \(\eta =1\), we obtain the classical Einstein-Maxwell theory, whereas the electromagnetic field is phantom for \(\eta =-1\). Consequently, the spherically symmetric solution for the action (1) is obtained by [8]

$$\begin{aligned} ds^{2}=-f(r)dt^{2}+\frac{dr^{2}}{f(r)}+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}\right) , \end{aligned}$$
(2)

with

$$\begin{aligned} f(r)= & {} 1-\frac{2M}{r}+ \frac{r^2}{L^2}+\eta \frac{Q^2}{r^2}, \end{aligned}$$
(3)

where M, Q denote the mass of the black hole and the electric charge of the source respectively. The metric is asymptotically flat for any finite values of the parameters M, Q, and \(\Lambda = 0\), while it becomes asymptotically AdS for \(\Lambda <0\). Additionally, when all the parameters vanish, it reduces to the Minkowski metric. Specifically, for \(\eta =1\), the metric corresponds to the Reissner–Nordstrom-AdS black hole in the Einstein-Maxwell-AdS theory, as discussed in [53, 54]. Figure 1 depicts the respective behaviors of f(r) with \(\eta =\pm 1\) as a function of r.

Fig. 1
figure 1

The behaviors of f(r) versus r for different example values of \(\eta \). Here we set \(Q=0.1, L=1\)

Full size image

The horizon of the black hole solution can be determined by finding the roots of the function

$$\begin{aligned} f(r)=0. \end{aligned}$$
(4)

There are two real roots, which are the external horizon \(r_+\) (events horizon), or internal horizon \(r_-\), where \(0< r_- < r_+\), for \(\eta =1\), and there is special case \(M=Q\) that a extremal case with degenerate horizon is \(f(r_{min})=f'(r_{min})=0\), thus one obtains \(r_{min}=r_{-}=r_{+}\), leads to \(T=0\), which is in contradiction to the third law of thermodynamics.Footnote 3 For the phantom AdS black hole (\(\eta =-1\)), there is a single positive root corresponding to the event horizon \(r_+\), and our focus is specifically on the determination of this horizon and its value.

From the Eq. (4) with (3), one can express the black hole mass in terms of \(r_+\) given by [8, 45]

$$\begin{aligned} M=\frac{r_+}{2}\left( 1+\frac{r_+^2}{L^2}+\eta \frac{Q^2}{r_+^2}\right) . \end{aligned}$$
(5)

Combining the above formula (5) with Eq. (3), the Hawking temperature for phantom AdS black holes is given by [8, 45]

$$\begin{aligned} T\equiv \left. \frac{f'(r)}{4\pi }\right| _{r=r_+}=\frac{1}{4\pi r_+}\left( 1+\frac{3 r_+^2}{L^2}-\eta \frac{Q^2}{r_+^2}\right) \,, \end{aligned}$$
(6)

and the entropy of the black hole associated with the event horizon radius is

$$\begin{aligned} S=\pi r_+^2 , \end{aligned}$$
(7)

which can be written as \(S = A/4\) with the area of the horizon \(A = 4\pi r^2_+\), which is the well-known Bekenstein–Hawking area formula [55].

3 Thermodynamic stability and phase structure of phantom AdS black holes

The thermodynamic behavior of black holes can be analyzed in either the canonical ensemble, where the charge is fixed, or the grand canonical ensemble, where the charge is allowed to vary. Previous studies, such as those by Chamblin et al. [11, 12], investigated the thermodynamics and phase structure of Reissner Nordström-AdS black holes in the context of Einstein-Maxwell-AdS theory (for \(\eta =1\)), establishing important frameworks and standards for discussing the thermodynamics of AdS black holes. In this work, we extend this analysis to examine the thermodynamic stability and phase structure of phantom spherically symmetric AdS black holes (for \(\eta =-1\)) in both the canonical and grand canonical ensembles.

3.1 In the canonical ensemble: with fixed charge

In the canonical ensemble, the thermodynamic properties of phantom spherically symmetric AdS black hole for \(\eta =-1\) is significantly different from \(\eta =1\). In this part, we revisit past studies, and present the thermodynamic stability and phase structure for the AdS black hole with the phantom field in the canonical ensemble.

3.1.1 The AdS black hole with a Maxwell field for \(\eta =1\)

When \(\eta =1\), from the Eqs. (5), (6) and (7), one can express the Hawking temperature and Helmholtz free energy as follows [11, 12]

$$\begin{aligned} T= & {} \frac{1}{4\pi r_+}\left( 1+\frac{3 r_+^2}{L^2}-\frac{Q^2}{r_+^2}\right) , \end{aligned}$$
(8)
$$\begin{aligned} F= & {} \frac{r_+}{4}\Big (1-\frac{r_+^2}{L^2}+\frac{3 Q^2}{r_+^2}\Big ). \end{aligned}$$
(9)

Inserting the temperature equation of state, i.e. \(T=T(r_+, L, Q)\) given in Eq. (8) to the following condition equations [11, 12]

$$\begin{aligned}{} & {} \frac{\partial T}{\partial r_+}=0, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \frac{\partial ^2 T}{\partial r_+^2}=0, \end{aligned}$$
(11)

the inflection point {\(r_c, Q_c, T_c\)} is obtained as

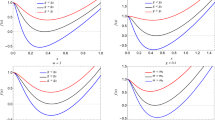
$$\begin{aligned} r_c=\frac{L}{\sqrt{6}},~~~~~~~~~~Q_c=\frac{L}{6},~~~~~~~~~~T_c=\sqrt{\frac{2}{3}}\frac{1}{\pi L}. \end{aligned}$$
(12)

Once the critical quantities obtained, it is useful to illustrate the temperature and Helmholtz free energy based on Eqs. (8) and (9), as shown in Fig. 2.

Fig. 2
figure 2

In the canonical ensemble: the figure show that for small charge (i.e., below \(Q<Q_c\)), there are three branches of black hole solutions, while for large charge (i.e., above \(Q > Q_c\)), there is only one branch of solutions that has not an interesting behavior

Full size image

In particular, we observe that there can be three branches of black hole solutions for \(Q<Q_c\). To better understanding the phase structure of the black hole, we discuss the particular situation in detail as our interest in the following. The corresponding phase diagram of Helmholtz free energy as a function of the temperature is illustrated in Fig. 3 based on Eqs. (6) and (9).

Fig. 3
figure 3

In the canonical ensemble: the Helmholtz free energy F of Reissner Nordström-AdS black hole (\(\eta =1\)) as function of T. Here we set \(L=1\). “SBH”, “IBH” and “LBH” represent the small, intermediate and large black holes, respectively

Full size image

From Fig. 3, we observe that the SBH/IBH black hole meet at the inflection point \(T_1\), the IBH/LBH meet at \(T_2\). Thus the LBH is the preferred state when \(T\in [T_0,T_1]\), and for \(T < T_0\), the preferred state is stable SBH. We see that the F–T diagram exhibits a characteristic “swallowtail” behaviour where the free energy of the black hole intersects with itself at \(T= T_0\) which is indicative of first-order phase transition between SBH and LBH [11, 12, 51]. This is analogous to the gas-liquid phase transition of van der Waals fluids. For \(T>T_2\), the intermediate black holes with higher free energy relatively unstable and the lower arm of large black hole curve eventually crosses [11, 12]

$$\begin{aligned} F=0 . \end{aligned}$$
(13)

In this respect, from the above criterion, a specific real positive solution of event horizon radius \(r_+\) for thermodynamically stableFootnote 4 large black hole obtained by

$$\begin{aligned} r_{s}=\frac{\sqrt{L(L+\sqrt{L^2+12 Q^2})}}{\sqrt{2}} . \end{aligned}$$
(14)

Substituting the solution into Eq. (8), we obtain the expression of specific temperature \(T_{s}\) as a functions of AdS radius L and charge Q given by

$$\begin{aligned} T_{s}=T_{r_+=r_{s}}=\frac{\sqrt{2} [L (L+\sqrt{L^2+12 Q^2})+4 Q^2]}{\pi [L (L+\sqrt{L^2+12 Q^2})]^{3/2}}. \end{aligned}$$
(15)

Obviously, when \(T < T_{s}\) the black hole has positive free energy. On the contrary, when \(T > T_{s}\) the black hole has negative free energy.

It is better presented in Fig. 4, as the inflection point on an isobaric T–\(r_+\) line plotted according to Eq. (8).

Fig. 4
figure 4

In the canonical ensemble: the behavior of temperature versus horizon radius for \(\eta =1\). The figure show that for small charge (i.e., below \(Q<Q_c\)), there can be three branches of black hole solutions. The middle branch is thermodynamically unstable while the branches with the smallest and largest radii is thermodynamically stable. Colored points represent the inflection points correspond to local minima and maxima of temperature

Full size image

As we can see from Fig. 4 that, the Hawking temperature for \(\eta =1\) decreases as \(r_+\) decreases. It reaches a local minimum \(T_2\) at horizon radius \(r_{+2}\) and then increases to a local maximum \(T_{1}\) at radius \(r_{+1}\) (\(r_{+1} < r_{+2}\)). Subsequently, it sharply drops to zero temperature at the critical radius \(r_{min}\). The local minimum and maximum of the black hole temperature T are determined by Eq. (10). For the temperature (8), the local maximum point (\(r_{+1}\), \(T_1\)) is

$$\begin{aligned} r_{+1}= & {} \sqrt{\frac{L(L-\sqrt{L^2-36 Q^2})}{6}}, \end{aligned}$$
(16)
$$\begin{aligned} T_{1}= & {} \frac{\sqrt{\frac{3}{2}}[L (L-\sqrt{L^2-36 Q^2})-12 Q^2]}{\pi [L(L-\sqrt{L^2-36 Q^2})]^{3/2}},~~~ \end{aligned}$$
(17)

and the local minimum point (\(r_{+2}\), \(T_{2}\)) is

$$\begin{aligned} r_{+2}= & {} \sqrt{\frac{L(L+\sqrt{L^2-36 Q^2})}{6}}, \end{aligned}$$
(18)
$$\begin{aligned} T_{2}= & {} \frac{\sqrt{\frac{3}{2}}[L (L+\sqrt{L^2-36 Q^2})-12 Q^2]}{\pi [L(L+\sqrt{L^2-36 Q^2})]^{3/2}}. \end{aligned}$$
(19)

Now, let us turn our attention to the relations between \(T_{s}\) and \(T_2\). Comparing Eq. (15) with (18), we obtain

$$\begin{aligned} \frac{T_{s}}{T_2}=\frac{2 [L (L+\sqrt{L^2-36 Q^2})]^{3/2} [L (L+\sqrt{L^2+12 Q^2})+4 Q^2]}{\sqrt{3} [L (L+\sqrt{L^2+12 Q^2})]^{3/2} [L (L+\sqrt{L^2-36 Q^2})-12 Q^2]}.\nonumber \\ \end{aligned}$$
(20)

3.1.2 The AdS black hole with a phantom field for \(\eta =-1\)

Using a similar method as in the previous part, we derive the temperature and Helmholtz free energy of the black hole in the canonical ensemble for \(\eta =-1\) by

$$\begin{aligned} T= & {} \frac{1}{4\pi r_+}\Big (1+\frac{3 r_+^2}{L^2}+\frac{Q^2}{r_+^2}\Big ) , \end{aligned}$$
(21)
$$\begin{aligned} F= & {} \frac{r_+}{4}\Big (1-\frac{r_+^2}{L^2}-\frac{3 Q^2}{r_+^2}\Big ). \end{aligned}$$
(22)

To gain a better understanding of the global stability and the phase structure of the black hole, we plot the Helmholtz free energy as a function of temperature using the equations (21) and (22), which is explicitly shown in Fig. 5.

Fig. 5
figure 5

In the canonical ensemble: the Helmholtz free energy F of AdS black hole with a phantom field (\(\eta =-1\)) as a function of T. Here we set \(Q=0.1\). The small and large black hole curves meet with a cusp at the temperature \(T_0\)

Full size image

We can see from Fig. 5 that, when \(T<T_0\), there is no black hole can exist, where \(T_0\) is the minimum temperature. When \(T>T_0\), there are two branches of black holes. The free energies of both small (upper branches) and large (lower branches) black holes decrease with increasing temperature T. Unlike most black hole systems, the branches of small black holes intersect the T-axis in this scenario. By solving \(F = 0\), the two specific real positive solutions of event horizon radius for the large and small black hole branches are obtained as

$$\begin{aligned} r_{s}(LBH)= & {} \frac{\sqrt{L (L+\sqrt{L^2-12 Q^2})}}{\sqrt{2}} \nonumber \\ r_{s}(SBH)= & {} \frac{\sqrt{L (L-\sqrt{L^2-12 Q^2})}}{\sqrt{2}},~~~ \end{aligned}$$
(23)

where obviously \(r_{s}(LBH) > r_{s}(SBH)\). Substituting these solutions into Eq. (21), we obtain the expressions of specific temperature for the large and small black hole branches as a functions of L and charge Q given by

$$\begin{aligned} T_{s}(LBH)= & {} \frac{\sqrt{2} [L (L+\sqrt{L^2-12 Q^2})-4 Q^2]}{\pi [L (L+\sqrt{L^2-12 Q^2})]^{3/2}}, \end{aligned}$$
(24)
$$\begin{aligned} T_{s}(SBH)= & {} \frac{\sqrt{2} [L (L-\sqrt{L^2-12 Q^2})-4 Q^2]}{\pi [L (L-\sqrt{L^2-12 Q^2})]^{3/2}}.~~~~~~~~~ \end{aligned}$$
(25)

In Fig. 5, it can be observed that the larger and smaller black holes intersect at the temperature \(T_0\), its additional checks are required based on the temperature function. Therefore, it is more appropriate to present this information in Fig. 6, which shows the minimum point on an isobaric T–\(r_+\) curve plotted using Eq. (21).

Fig. 6
figure 6

In the canonical ensemble: The behavior of temperature versus horizon radius for \(\eta =-1\). The colored points represent the local minima of the temperature. Here we set \(L=1.4\)

Full size image

The minimum \(T_0\) of Hawking temperature (21) obtained from the condition Eq. (10)

$$\begin{aligned} T_{0}= & {} \frac{\sqrt{\frac{3}{2}} [L (L+\sqrt{L^2+36q^2})+12 Q^2]}{\pi [L(L+\sqrt{L^2+36 Q^2})]^{3/2}}, \end{aligned}$$
(26)

with horizon radius

$$\begin{aligned} r_{0}=\sqrt{\frac{L(L+\sqrt{L^2+36 q^2})}{6}}. \end{aligned}$$
(27)

For \(T < T_0\), there is no black holes can exist. For \(T > T_0\), there exist small (\(0<r_+<r_0\)) and large (\(r_0<r_+\)) black hole branches.

Now, we turn our attention to the relation of specific temperature \(T_s\) for the large black hole and minimum temperature \(T_0\) branches with a phantom field in the canonical ensemble. Comparing Eq. (24) with (26), we obtain

$$\begin{aligned}{} & {} \frac{T_{s}(LBH)}{T_0}\nonumber \\{} & {} \quad = \frac{2 [L (L+\sqrt{L^2+36 Q^2})]^{3/2} [L (L+\sqrt{L^2-12 Q^2})-4 Q^2]}{\sqrt{3} [L (L+\sqrt{L^2-12 Q^2})]^{3/2} [L (L+\sqrt{L^2+36 Q^2})+12 Q^2]}.\nonumber \\ \end{aligned}$$
(28)

In summary, owing to the conservation of charge, a black hole in the canonical ensemble with a fixed charge can not undergo a Hawking-Page-like phase transition to the thermal AdS background that is electrically neutral. If \(Q=0\), the thermal AdS background with the global minimum of free energy is thermodynamically preferred, and thus the black holes can undergo a Hawking-Page-like phase transition, hence the results in Eqs. (20) and (28) are reduces to the relation

$$\begin{aligned} \frac{T_{HP}}{T_0}=\frac{2}{\sqrt{3}}, \end{aligned}$$
(29)

which is coincidence with the result of four dimensional Schwarzschild AdS black hole [9, 18, 29].

3.2 In the grand canonical ensemble: with fixed electric potential

In this part, we consider the black hole as a grand canonical ensemble system, in which the electric potential is held fixed as \(\Phi \equiv Q/r_+\), and the electric charge is thus allowed to vary [11, 12]. In this respect, the corresponding thermodynamic potential is the known Gibbs free energy, which is an appropriate state function to compare configurations in the canonical ensemble.

In the grand canonical ensemble, from Eqs. (30) and (31), the corresponding mass and temperature are obtained by

$$\begin{aligned} M= & {} \frac{r_+}{2}\Big (1+\frac{r_+^2}{L^2}+\eta \Phi ^2\Big ), \end{aligned}$$
(30)
$$\begin{aligned} T= & {} \frac{1}{4\pi r_+}\Big (1+\frac{3 r_+^2}{L^2}-\eta \Phi ^2\Big ). \end{aligned}$$
(31)

From Eq. (31), we can see that the temperature for \(\eta =1\) is lower compared to \(\eta =-1\) due to the influence of the electric potential \(\Phi \). Furthermore, by considering Eqs. (7), (30), and (31), one can suppose that the black hole obeys the first law of thermodynamics [8]

$$\begin{aligned} dM=TdS+\eta \Phi dQ. \end{aligned}$$
(32)

Then the corresponding free energy of phantom AdS black hole is given as the Gibbs free energy

$$\begin{aligned} G= & {} M-TS-\eta \Phi Q\nonumber \\= & {} \frac{r_+}{4}\Big (1-\frac{r_+^2}{L^2}- \eta \Phi ^2 \Big ). \end{aligned}$$
(33)

From this expression, it can be observed that the free energy for \(\eta =1\) shifts towards smaller values due to the contribution from the electric potential in the last term. This indicates that the presence of charge leads to a more negative free energy. Conversely, the free energy for \(\eta =-1\) shifts towards larger values due to the contribution from the electric potential in the last term. This implies that the charge contribution makes the free energy more positive. In order to gain a better understanding of the global stability and phase structure of the black hole, we utilize Eqs. (31) and (33) to illustrate the free energy landscapes in the G–T diagram as a function of temperature, as shown in Fig. 7.

Fig. 7
figure 7

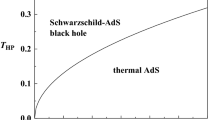
In the grand canonical ensemble: the Gibbs free energy G of phantom AdS black hole as functions of T. Here we set \(L=1\). The small and large black hole curves meet with a cusp at the temperature \(T_0\), below \(T<T_0\), there is no black hole can exist. a As \(\Phi \) decreases within the range \(\Phi <1\), \(T_{HP}\) shifts to the right, indicating an increase in \(T_{HP}\) for lower electric potentials, in agreement with Eq. (36) for \(\eta =1\). b Conversely, as \(\Phi \) increases, \(T_{HP}\) also moves to the right, indicating an increase in \(T_{HP}\) for higher electric potentials, consistent with Eq. (36) for \(\eta =-1\)

Full size image

We can see from Fig. 7 that, when \(T<T_0\), there is no black hole can exist, where \(T_0\) is the minimum temperature. Hence for that range of the temperature, the thermal radiation of AdS spacetime is preferred. When \(T>T_0\), there are two branches of black holes. The free energies of both small (upper branches) and large (lower branches) black holes decrease with increasing temperature T. Consequently, the thermal AdS spacetime is globally preferred as the thermodynamic state for \(T < T_{HP}\). Beyond this threshold, the large black hole exhibits a negative free energy, indicating its greater stability and thermodynamic preference. The horizon radius \(r_{HP}\) can be determined by solving the criterionFootnote 5 [11, 12]

$$\begin{aligned} G=0, \end{aligned}$$
(34)

at \(T = T_{HP}\). From these observations, one can see that there is a Hawking-Page-like phase transition between thermal radiation of AdS spacetime and stable large black holes. Thus, a real positive solution for the transition radius \(r_{HP}\) of the large black hole can be obtained from the criterion provided in Eq. (34), yieldingFootnote 6

$$\begin{aligned} r_{HP}= L \sqrt{1-\eta \Phi ^2} . \end{aligned}$$
(35)

Substituting the solution into Eq. (31), we obtain the corresponding expression of Hawking-Page-like phase transition temperature \(T_{HP}\) given by

$$\begin{aligned} T_{HP}= & {} \frac{\sqrt{1-\eta \Phi ^2}}{\pi L}. \, \end{aligned}$$
(36)

The Eq. (36) correctly yields \(T_{HP}={1/\pi L}\) in the Schwarzschild-AdS metric limit (i.e. \(\Phi =0\)) [9, 31, 35].

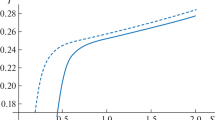
In Fig. 7, it can be observed that the larger and smaller black holes coincide at the temperature \(T_0\). In order to confirm the accessibility of the phase transition, additional checks are necessary, which are determined by the temperature function. For a clearer presentation, Fig. 8 depicts the minimum point on an isobaric T–\(r_+\) line obtained from Eq. (31), providing a more precise assessment of the phase transition.

Fig. 8
figure 8

In the grand canonical ensemble: the behavior of temperature versus event horizon radius, with colored points indicating local minima of temperature. The value of L is set to 1. a The temperature is plotted based on Eq. (31) for \(\eta =1\) within the range \(\Phi <1\), while panel b shows the temperature for \(\eta =-1\) with arbitrary \(\Phi \)

Full size image

For \(T < T_0\), there is no black holes can exist, except the vacuum phase. For \(T > T_0\), there exist small (\(0<r_+<r_0\)) and large (\(r_0<r_+\)) black hole horizon branches. Substituting the Eq. (31) into the condition Eq. (10), we obtain the minimum temperature

$$\begin{aligned} T_{0}=\frac{\sqrt{3(1-\eta \Phi ^2)}}{2\pi L}, \end{aligned}$$
(37)

with the corresponding minimum event horizon radius given by

$$\begin{aligned} r_{0}=\frac{L\sqrt{3(1-\eta \Phi ^2)}}{3}. \end{aligned}$$
(38)

We observe that for \(\eta =1\), the minimum temperature and event horizon radius decrease with increasing \(\Phi \) within the given range (\(\Phi <1\)). In contrast, for \(\eta =-1\), both the minimum temperature and event horizon radius increase. Now, we also turn our attention to the dual relations of \(T_{HP}\) and \(T_0\). Comparing the Eq. (36) with (37), we obtain

$$\begin{aligned} \frac{T_{HP}}{T_0}=\frac{2}{\sqrt{3}}. \end{aligned}$$
(39)

This result coincidence with the case of four dimensional Schwarzschild-AdS black hole [9, 18, 29].

4 Conclusions and discussion

In this paper, we have studied the thermodynamic stability and phase structures of phantom AdS black holes in both the canonical and grand canonical ensembles. Thermodynamical quantities such as temperature and free energy are discussed in detail to understand the thermodynamic properties of the black hole.

There are two different types of black holes for the values of \(\eta \) in the theory. As a result, the thermodynamical quantities and its behaviors differ considerably for \(\eta =1\) (Maxwell field) and \(\eta =-1\) (phantom field).

In the canonical ensemble, the thermodynamic characteristics of the AdS black hole for \(\eta =1\) is more complex. We have revisited the past studies, and the results indicate that the occurrence of a first-order phase transition between small and large black holes, as evidenced by the behavior of the free energy. For \(\eta =-1\), the black hole in AdS spacetime with a phantom field does not exhibit any noteworthy phase transition behaviors. Notably, as depicted in Fig. 5, we make the noteworthy observation that the branches of small black holes with a phantom field in the canonical ensemble cross the T-axis as the temperature increases. This behavior is rarely seen in previous studies, and we interpret this intriguing phenomenon as a consequence of the unique nature of phantom black holes.

In the grand canonical ensemble, upon examining the Gibbs free energy and temperature, we have observed that the AdS black holes with either a Maxwell field or a phantom field exhibit a Hawking-Page-like phase transition between thermal radiation in the AdS spacetime and thermodynamically stable large black holes. Furthermore, we have determined the key quantities such as the transition temperature \(T_{HP}\), the minimum temperature \(T_0\), and their interesting dual relations. It is evident that the quantities \(T_{HP}\) and \(T_0\) are greater for the latter case (black hole with \(\eta =-1\)) compared to the former (black hole with \(\eta =1\)).

Our research has shown that phantom fields have a profound influence on the thermodynamic properties of AdS black holes. In fact, some of the results presented here as a generalization of a result previously found on Schwarzschild-AdS black hole [9, 29]. Despite the findings of our study, further investigation into the microstructure and evaporation process of phantom black holes is necessary, as we believe they may differ from most other black hole systems. It is also unclear whether such an ensemble can be practically “prepared” for the black hole spacetimes, and this remains an open question.