Growth of matter perturbations in some parametrization of dark energy models

Abstract

In this work, we investigate the growth of matter perturbations in some known parameterizations of dark energy (DE) models i.e, CPL, JBP, BA, and a new parameterization of DE introduced in this study. We examine the growth of perturbations in the linear region by assuming the possibility of perturbations in DE. Then, we follow an overall likelihood analysis to put the same constraints on models using background and growth rate data, and we conclude that the reviewed DE parameterizations are compatible with the observational data at both background and perturbation levels. Furthermore, we find that DE parameterizations are comparable with each other, and with the $\Lambda$CDM model. In particular, we obtain the following significant results: (i) the growth rate of matter perturbations in the homogeneous DE case is smaller than its value in the clustered case for CPL and BA models, while it is the opposite for JBP and the new model. (ii) The growth rate of matter perturbations related to the CPL and BA models have very similar behavior for both homogeneous and clustered DE cases at all redshift z. This is also true for JBP and the new model. (iii) We show that the growth rate of matter perturbations relevant to the models is lower than its value in the $\Lambda$CDM model at low redshifts, and at high redshifts, the difference between them is insignificant. Finally, using AIC and BIC analysis, we conclude that the selection of a model that has better compatible with the observational data depends on the background and perturbation data.

1 Introduction

The accelerated expansion of the universe has been corroborated by the current independent observational data. These observations include: Supernovae type Ia ((SnIa) [1,2,3], Cosmic Microwave Background (CMB) [4,5,6,7], Baryon Acoustic Oscillations(BAO) [8,9,10,11,12], High redshift galaxy clusters [13, 14] and the observations of weak lensing surveys [15,16,17].

Since the finding of cosmic expansion until now, many attempts have been made to clarify the nature of this wonderful phenomenon, both theoretically and observationally. Overall, two entirely distinct approaches have been introduced to find out the nature of this phenomenon. The first approach is models based on the large distance modification of gravity. In this context, various models have been introduced. For example, $\textrm{f}( \textrm{R})$ gravity ($\textrm{f}$ is a function of the Ricci scalar $\textrm{R}$) [18, 19], Galileon gravity [20, 21], braneworld gravity (i.e, DGP braneworld model which modifies the action of Einstein–Hilbert by a term originating from large extra dimensions [22]), Gauss–Bonnet gravity [23, 24], and so on. One of the important aspects of these models is that cosmic acceleration can be explained by putting aside the dark energy component. In the second approach, the cosmic expansion can be well explained by considering an unknown cosmic fluid with adequate negative pressure and positive energy density, usually dubbed dark energy (hereafter DE). Both DE and MG (Modified Gravity) models introduce acceptable approaches to explain the late-time accelerated expansion of the Universe. Also, both kinds of models are consistent with background observational data and standard model $\Lambda$CDM (cosmological constant + Cold Dark Matter to explain the potential well of structure formation and galaxy rotation curves). Understanding the exotic nature of DE is one of the serious challenges in modern cosmology.

In this framework, many various models have been proposed to explain the origin of DE [25]. The cosmological constant with the equation of state, $\textrm{p}_{\Lambda }=-\uprho _{\Lambda }=\Lambda /8\pi \textrm{G}$ [26] is the first and simplest model of DE which arises from vacuum energy, and it seems that particle physics should be used to understand its nature. Although the $\Lambda \textrm{CDM}$ model is consistent with almost all of the current observational data, this model can not well explain the theoretical problems of fine-tuning and cosmic coincidence [25,26,27,28,29,30,31,32]. Accordingly, to obviate these Serious problems, cosmologists introduced various models of DE with time-varying energy density and negative pressure. These models are called dynamic DE models.

In the analysis of observational data, it is extensively considered that the DE equation of state (EoS) is independent of particular theoretical models and follows a given foreordained evolution. In these models, the EoS parameter evolves relative to redshift (z) or scale factor (a) [33,34,35,36,37,38].

In the last years, various parametric equations of state have been offered in the literature which contains some well-known parametrizations of DE, i.e: linear parametrization, [39, 40], Chevallier–Polarski–Linder parametrization (CPL), [41, 42], Jassal–Bagla–Padmanabhan parametrization (JBP), [43], Barboza–Alcaniz parametrization (BA), [44], Gerke and Efstathiou parametrization (GE), [45], Feng–Shen–Li–Li para metrizations (FSLL), [46], Ma–Zhang parametrization (MZ), [47] and so on. One can find other considerable works on the parameterizations of DE [47,48,49,50,51,52,53,54,55,56,57].

Dark energy has two essential roles in the evolution of the universe: (I) it accelerates the expansion of the universe, (II) it affects the formation of large-scale structures in the universe in different eras via varying the growth rate of matter perturbations [11, 58,59,60]. Furthermore, assuming the dynamical DE models and the possibility of perturbations in DE, the growth rate of cosmic structures changes [61,62,63,64,65,66,67,68].

To investigate the effect of dynamical DE models on the growth of matter perturbations in the linear regime, one can assume a universe with pressure-less dark matter (DM) and a DE component with a time-varying EoS parameter. Based on this, we consider three well-known EoS parameters i.e. CPL, JBP, BA, and a new parametrization introduced in this work. Many available parameterizations can be used in this work however we choose these parametrizations since these models are rival with each other, and their free parameters are the same. In this study, we investigate the effect of dark energy clustering on the growth of matter perturbations in the mentioned DE parametrizations.

In this study, we investigate the effect of dark energy clustering on the growth of matter perturbations in the aforementioned DE parametrizations. To this end, first we carry out a numerical Markov Chain Monte Carlo (MCMC) analysis to constrain the free parameters of the desired DE param etrizations.

The outline of the article is as follows: in Sect. 2, we obtain the required equations relevant to the background evolution of the universe. Also in this section, we introduce DE parametrizations which are investigated in this work. In Sect. 3, we explain briefly the current observational data sets at the background level and we carry out a numerical Markov Chain Monte Carlo (MCMC) analysis to constrain the free parameters of the DE parametrizations studied in this work. Afterward, we obtain the basic equations related to the DE and DM evolution in the linear regime and we investigate the growth rate of matter perturbations in Sect. 4. Also in this section, we add growth rate data to background data for more complete constraints on the free parameters of the models. In Sect. 5, using the best-fit values obtained from the likelihood analysis for the free parameters of the models, we compare them with each other and the $\Lambda$CDM model utilizing some important cosmological quantities. Finally, we express the conclusions in Sect. 6.

2 Evolution of background

The evolution of a spatially flat FRW universe with a homogeneous and isotropic background is usually governed by

$$\begin{aligned} H^{2}=\frac{8\pi \textrm{G}}{3}(\uprho _{\textrm{m}}+\uprho _{\textrm{de}}+\uprho _{\textrm{r}}) \end{aligned}$$

(1)

where $H=\dot{a}/a$ is the Hubble parameter and $\uprho _{\textrm{i}}$ stands for the energy density of the $\textrm{i}$-th fluid, where $\textrm{i}$ runs over dark matter ($\textrm{m}$), radiation ($\textrm{r}$), and DE fluid ($\textrm{de}$). Moreover, one can assume that all the components of fluids are minimally coupled to gravity and there is no interaction among the fluids, hence all the fluid components evolve independently. consequently, the energy density of fluids evolves with the following continuity equations:

$$\begin{aligned}&\dot{\uprho }_{\textrm{m}}+3H{\uprho }_{\textrm{m}}=0 \end{aligned}$$

(2)

$$\begin{aligned}&\dot{\uprho }_{\textrm{r}}+4H{\uprho }_{\textrm{r}}=0 \end{aligned}$$

(3)

$$\begin{aligned}&\dot{\uprho }_{\textrm{d}}+3H(1+w_{\textrm{d}}){\uprho }_{\textrm{d}}=0 \end{aligned}$$

(4)

where dot gives the meaning of derivative relative to cosmic time t. Using Eqs. (2–4), one can obtain ${\uprho }_{\textrm{m}}={\uprho }_{\textrm{0m}} \textrm{a}^{-3}$, ${\uprho }_{\textrm{r}}={\uprho }_{\textrm{0r}} \textrm{a}^{-4}$, and ${\uprho }_{\textrm{d}}={\uprho }_{\textrm{0d}}{g(a)}$, and g(a) is defined as follows:

$$\begin{aligned} {g(a)}&=\textrm{exp}\Bigg [-3\displaystyle \int _{1}^{{a}}\dfrac{1+w_{{d}}({a} ^{\prime })}{a^{\prime }}da^{\prime }\Bigg ] \end{aligned}$$

(5)

hence, considering the definitions $\Omega _{\textrm{i}}=\frac{8\pi \textrm{G}\uprho _{\textrm{i}}}{3\,H^{2}}$ and normalized Hubble parameter (${E(a)}={H(a)}/{H(a=1)}$), Eq. (1) can be written as follows:

$$\begin{aligned} {\textrm{E}}^{2}({a})&=[\Omega _{{\textrm{m0}}}a^{-3}+\Omega _{{\textrm{d0}}} {g(a)}+\Omega _{{\textrm{r0}}}\textrm{a} ^{-4}] \end{aligned}$$

(6)

Now, to obtain $\textrm{E}({a})$ related to the parameterizations considered in this work, ${w_{{d}}}({a})$ of these parameterizations can be replaced in Eq. (5), and finally one can insert the result in Eq. (6).

In the present work, we investigate three well-known DE parametrizations and a new parametrization of DE which is proposed in this work. These DE parametrizations are as follows:

Model I: The well-known CPL parametrization of DE is defined as follows:

$$\begin{aligned} w_{d}=w_{0}+w_{1}(1-a) \end{aligned}$$

(7)

This DE parametrization was individually raised by Chevallier and Polarski [41] and then by Linder [42]. The value of $w_{d}$ is $w_{0}$ at present time and $w_{d}\rightarrow w_{0}+w_{1}$ when $a\rightarrow 0$. Furthermore, the parameter $w_{1}$ indicates the rate of variation of the EoS parameter at present time, that is, $w_{1}=\frac{\textrm{d}w_{d}(a)}{\textrm{d}a}\mid _{a\rightarrow 1}$. CPL parametrization can be considered a linear expansion relative to the scale factor around its current value a=1.

Model II: This model which is known as JBP parametrization has been proposed by Jassal-Bagla-Padmanabhan in [43], and has the following evolution law:

$$\begin{aligned} {w}_{{d}}={w}_{0}+{w}_{1}a(1-a) \end{aligned}$$

(8)

In this case, we can see that the value of $w_{d}$ for both limit cases $a\rightarrow 1$, and $a\rightarrow 0$ is equal to $w_{0}$.

Model III: This model has been introduced by Barboza and Alcaniz [44] and hence it is named BA parametrization. This parametrization is expressed as follows:

$$\begin{aligned} {w}_{{d}}={w}_{0}+{w}_{1}\frac{(1-a)}{1-2a+2a^{2}} \end{aligned}$$

(9)

for this EoS parameterization, the value of $w_{d}$ is $w_{0}$ at present time, and when $a\rightarrow 0$, $w_{d}$ is equal to $w_{0}+w_{1}$.

Model IV: Phenomenologically, it is customary to probe some feasible time-dependent parameterizations to be eligible for the dark energy EoS. According to this view, we introduce a new EoS parameterization of this series with the following function:

$$\begin{aligned} w_{{d}}=w_{0}+a w_{1}\ln (2-a) \end{aligned}$$

(10)

we observe that the value of $w_{d}$ for both limit cases $a\rightarrow 1$, and $a\rightarrow 0$ is equal to $w_{0}$. Hence, considering the above DE parametrizations, The value of g(a) in Eq. (5) can be obtained as follow:

$$\begin{aligned} g(a)=\left\{ \begin{array}{ll} a^{-3(1+w_{0}+w_{1})} e^{-3(1-a)w_{1}}; &{}\ \text { Model I;}\\ a^{-3(1+w_{0})}e^{\frac{3(a-1)^{2}}{2}w_{1}};&{}\text { Model II;}\\ a^{-3(1+w_{0}+w_{1})}(1-2a+2a^{2})^{\frac{3w_{1}}{2}}; &{} \text { Model III;}\\ (2-a)^{-3(a-2)w_{1}}a^{-3(1+w_{0})} &{} \text {Model IV;}\\ e^{-3(1-a)w_{1}};&{}\\ \end{array}\right. \end{aligned}$$

In the next section, we examine the observational constraints on the models at the background level.

3 Observational constraints on the models: background level

Here, we study the performance of the EoS parameters of DE models considered in this work by utilizing the Markov Chain Monte Carlo ($\textrm{MCMC}$) analysis and the latest available observational data. We investigate a complete analysis of the $\Lambda \textrm{CDM}$ (as a concordance model), $\textrm{CPL}$, $\textrm{JBP}$, and $\textrm{BA}$ and a new parametrization of DE models. Based on this, the background parameters, i.e ($\Omega _{{b}}h^{2}$, $\Omega _{{c}}h^{2}$ ${H}_{0}$, ${w}_{0}$, ${w}_{1}$) related to each model can be constrained. Where $\Omega _{{b}}h^{2}$ and $\Omega _{{c}}h^{2}$ are the physical baryon and cold dark matter densities relative to the critical density.

Two analyses can be considered for constraining the free parameters of models. In the first analysis, we use 86 observational data points relevant to the background. These data points include $\textrm{SnIa}$ (1048 data points), $\textrm{CMB}$ (3 data points), $\textrm{BAO}$ (11 data points), $\mathrm {H(z)}$ (36 data points), and $\textrm{BBN}$ (1 data point).

Firstly, we review the basic equations and statistical implements for observational data in the $\textrm{SnIa}$, $\textrm{BAO}$, $\textrm{CMB}$, $\mathrm {H(z)}$, and $\textrm{BBN}$. In the following, we determine the best-fit values of free parameters of models as well as their uncertainties and argue about the results. The total likelihood within the background level using $\chi ^{2}_{\textrm{min}}= -2\textrm{ln}\mathcal {L}_{\textrm{max}}$ is given by:

$$\begin{aligned} \chi ^{2}_{\textrm{bac}}({\textbf {p}})=\chi ^{2}_{\textrm{H}}({\textbf {p}})+\chi ^{2}_{\textrm{bao}}({\textbf {p}}) +\chi ^{2}_{\textrm{sn}}({\textbf {p}})+\chi ^{2}_{\textrm{cmb}}({\textbf {p}})+ \chi ^{2}_{\textrm{bbn}}({\textbf {p}})\nonumber \\ \end{aligned}$$

(11)

where the statistical vector p = $\lbrace \Omega _{b}h^2, \Omega _{c}h^2, H_{0}, w_{0}, w_{1}\rbrace$ denotes the free parameters of the models.

In the second analysis, we also consider the growth rate data, particularly 22 independent redshift spatial distortion (RSD) data listed in Table 4. Hence in this analysis, $\chi ^{2}_{\textrm{tot}}$ (background+growth rate) can be written as follows:

$$\begin{aligned} \chi ^{2}_{\textrm{tot}}({\textbf {q}})=\chi ^{2}_{\textrm{bac}}({\textbf {p}})+\chi ^{2}_{\textrm{growth}} \end{aligned}$$

(12)

in this case, the statistical vector, q = $\lbrace {\textbf {p}}, \sigma _{8,0}\rbrace$ signifies the free parameters of the models at both background and perturbation levels. The $\chi ^{2}_{\textrm{growth}}$ is explained in Sect. 4.1.

In the following, the data sets used in this study are briefly explained.

3.1 SnIa data

Type Ia Supernovae are one of the most important research subjects in the dynamic background due to their standard nature, and still set the best constraints for DE models. SnIa dataset is simply the difference between the apparent magnitude and absolute magnitude of the observed SnIa, which is called the distance modulus and theoretically is specified by

$$\begin{aligned} \mu _{th}(z)=5\log _{10}{d_{L}(z)}+\mu _{0} \end{aligned}$$

(13)

where $\mu _{0}=42.384-5\log _{10}\textrm{h}$, and $d_{L}(z)$ is the luminosity distance, which is defined as follows:

$$\begin{aligned} d_{L}(z)=(1+z)\int _{0}^{z}\frac{dz^{\prime }}{H(z^{\prime })} \end{aligned}$$

(14)

Here we use the SnIa dataset which consists of 1048 data points sample [69]. Also, the corresponding $\chi ^{2}_{\textrm{sn}}$ is obtained as follows

$$\begin{aligned} \chi ^{2}_{\textrm{sn}}({\textbf {p}})=\sum _{i=1}^{n}\frac{[\mu _{th}({\textbf {p}}, z_{i})-\mu _{obs}(z_{i})]^{2}}{\sigma _{\mu , i}^{2}} \end{aligned}$$

(15)

where $\mu _{th}({\textbf {p}}, z_{i})$ is the theoretical prediction of distance modulus at the redshift $z_{i}$, and $\mu _{obs}(z_{i})$ is the distance modulus which is measured via observations. As well as, $\sigma _{\mu , i}$ is the uncertainty of the observational data.

3.2 BAO joint data

In recent years, investigations of BAO have shown that it can be a useful geometric probe of dark energy. The peak location of the BAO in the CMB power spectrum depends indeed on the proportion of $D_{V}(z)$ to the comoving sound horizon size ($r_{s}(z)$) at the drag epoch, $z_{d}$, at which baryons were liberated from photons. Komatsu et al. in [70] have indicated that the drag epoch is a little later than the photon decoupling epoch, $z_{d}< z_{*}$. Since the baryons are affected by the gravitational potential well. Because of this, the sound horizon size in the drag era is a little larger than that of the photon decoupling era.

Various researchers report their measurements of the BAO feature using different observable quantities. Some measurements included constraints on the ratio $r_{s}(z_{d})/D_{V}(z)$ or its inverse. The comoving sound horizon $r_{s}(z_{d})$ is given by

$$\begin{aligned} r_{s}(z_{d})=\frac{c}{H_{0}}\int ^{\infty }_{z_{d}}\frac{dz}{E(z)\sqrt{{3}[1+\frac{3\Omega _{b0}}{4(1+z)\Omega _{\gamma 0}}]}} \end{aligned}$$

(16)

where E(z) is given by Eq. (6). We use an approximated function for $\textrm{z}_{\textrm{d}}$ that is stated in [71]. Also, we set $\Omega _{\gamma 0}=2.469\times 10^{-5}h^{-2}$ (for $T_{\textrm{cmb}}$ = 2.725 K) [77]. Besides, $D_{V}(z)$ is the angular diameter distance and takes the following form [78].

$$\begin{aligned} D_{V}(z)=\frac{c}{H_{0}}\Bigg [(1+z)^{2}D_{A}^{2}(z)\frac{z}{E(z)}\Bigg ]^{\frac{1}{3}} \end{aligned}$$

(17)

We use two data sets in the old format Table 1 and the new format Table 2. Because the data points listed in the Tables 1 and 2 are uncorrelated, hence the $\chi ^{2}_{\textrm{bao,I}}$ in the first case obtained as follows

$$\begin{aligned} \chi ^{2}_{\textrm{bao,I}}=\sum _{i=1}^{4}\frac{[d_{z}(z_{i})|_{th}-(d_{z,i})|_{obs}]^{2}}{\sigma _{i}^{2}} \end{aligned}$$

(18)

where the theoretical prediction is given by $d_{z}(z)=\frac{r_{s}(z_{d})}{D_{V}(z_{\textrm{eff}})}$ and for the second case

$$\begin{aligned} \chi ^{2}_{\textrm{bao,II}}=\sum _{i=1}^{4}\frac{[\beta ^{*}(z_{i})|_{th}-\beta ^{*}_{z,i}|_{obs}]^{2}}{\sigma _{i}^{2}} \end{aligned}$$

(19)

where in this case the theoretical prediction is given by $\beta ^{*}(z)=\frac{D_{V}(z_{\textrm{eff}})}{r_{s}(z_{d})}r_{s}^{\textrm{fid}}$. Therefore $\chi ^{2}_{\textrm{bao}}=\chi ^{2}_{\textrm{bao,I}}+\chi ^{2}_{\textrm{bao,II}}$.

Table 1 The $\textrm{BAO }$ data points in old format with their survey and references

Table 2 The $\textrm{BAO }$ data points in new format with their survey and references

3.3 CMB data

Using the location of the CMB acoustic peak is useful to constrain DE models since this position depends on the dynamical DE models via angular diameter distance. The position of this peak in the power spectrum of the temperature anisotropy of the CMB is specified by ($l_{a}$, R, $\Omega _{b}h^{2}$). Where R is the scale distance or shift parameter at the decoupling time which is given as follows [79].

$$\begin{aligned} R(z_{*})=\frac{1}{c}\sqrt{\Omega _{m0}}H_{0}(1+z_{*})D_{A}(z_{*}) \end{aligned}$$

(20)

where $z_{*}$ implies the redshift at the decoupling time and we use the fitting formula stated in [80] for it. Also $D_{A}(z_{*})$ is the physical angular diameter distance [70]:

$$\begin{aligned} D_{A}(z_{*})=\frac{c}{H_{0}}\frac{\textrm{sinn}\Big [H_{0}\sqrt{\mid \Omega _{K}\mid }\int _{0}^{z_{*}}\frac{dz}{H(z)} \Big ]}{(1+z)\sqrt{\mid \Omega _{K}\mid }} \end{aligned}$$

(21)

where $\textrm{sinn}[x]=\sin (x), x,$ and $\sinh (x)$ for $\Omega _{K}< 0$ ($k=1$), $\Omega _{K}=0$ ($k=0$), and $\Omega _{K}>0$ ($k=-1$) respectively, which in the case of ($\Omega _{K}=0$) is defined by $D_{A}(z_{*})=\frac{c}{H_{0}(1+z)}\int _{0}^{z_{*}}\frac{dz}{E(z)}$. As well as, $l_{a}$ is the angular scale of the sound horizon at the decoupling time which is determined by:

$$\begin{aligned} l_{a}=(1+z_{*})\frac{\pi D_{A}(z_{*})}{r_{s}(z_{*})} \end{aligned}$$

(22)

where the coefficient of (1 + $z_{*}$) is due since $D_{A}(z_{*})$ is the physical angular diameter distance in Eq. (21), whilst $r_{s}(z_{*})$ is the comoving sound horizon at $z_{*}$ (Eq. 16).

Chen et al. in [81], have compared the full CMB power spectrum analysis with the distance prior method by constraining several DE models and have illustrated that the resultants of both methods are entirely in compliance. Hence in the current work, we use the combined CMB likelihood (Planck 2018 TT, TE, EE + lowE) concerning $X^{\textrm{obs}}_{i}= \lbrace R, l_{a}, \Omega _{b}h^{2}\rbrace = \lbrace 1.7493, 301.462, 0.02239\rbrace$, which has been obtained by Chen et al in [81]. The $\chi ^{2}_{\textrm{cmb}}$ is expressed as follows:

$$\begin{aligned} \chi ^{2}_{\textrm{cmb}}=\Delta X_{i}\Sigma _{ij}^{-1}\Delta X_{i}^{T} \end{aligned}$$

(23)

where $\Delta X_{i}=\lbrace X^{\textrm{th}}_{i}-X_{i}^{\textrm{obs}}\rbrace$ and $\Sigma _{ij}^{-1}$ is the inverse of the covariance matrix concerning $\Delta X_{i}$.

$$\begin{aligned} \Sigma _{ij}^{-1} =\left( \begin{matrix} 94392.3971 &{} - 1360.4913 &{}1664517.2916 \\ - 1360.4913 &{} 161.4349 &{} 3671.6180 \\ 1664517.2916&{}3671.6180&{} 79719182.5162 \end{matrix} \right) \end{aligned}$$

3.4 Hubble data

Here we use 36 data points of H(z) given in Table 3, which are in the redshift interval ${0.07\leqslant z\leqslant 2.34}$. Since the data points of H(z) are uncorrelated, hence the $\chi ^{2}_{H}$ statistics can be written as follows:

$$\begin{aligned} \chi ^{2}_{H}({\textbf {p}})=\sum _{i=1}^{{36}}\frac{[H_{th}({\textbf {p}}, z_{i})-H_{obs}(z_{i})]^{2}}{\sigma ^{2}_{i}} \end{aligned}$$

(24)

where $H_{th}({\textbf {p}}, z_{i})$ demonstrates the predictions of the models at redshift $z_{i}$, and $H_{obs}(z_{i})$ and $\sigma _{i}$ are the main values and the Gaussian errors of the measurements concerning data points shown in Table 3.

Table 3 The H(z) data used in the current analysis (in units of $\mathrm {km\; s^{-1}Mpc^{-1}}$). This compilation is partly based on those of Ref. [89]

3.5 BBN data point

To constrain the baryon density, one can use the abundance of one of the primary elements, i.e deuterium, and the radiative absorption of protons by it to $\mathrm {^{3}He}$ production [83] The empirical amount for the reaction rate is evaluated in [84], constraining the baryon density to $\Omega _{b0}h^2=0.02235\pm 0.016$, hence we accept this amount of $\Omega _{b0}h^2$ in our analyses. Based on this the $\chi ^{2}_{bbn}$ is given by

$$\begin{aligned} \chi ^{2}_{\textrm{bbn}}({\textbf {p}})=\frac{[\Omega _{b0}h^{2}-0.02235]^{2}}{0.016^{2}} \end{aligned}$$

(25)

4 Evolution of DE and DM: perturbations level

The perturbed FRW metric in the conformal Newtonian gauge is expressed as:

$$\begin{aligned} \textrm{d}\textrm{s}^2 =\textrm{a}(\eta )^{2}[ - (1+2\psi ) + (1-2\phi )\delta _{\textrm{ij}} \textrm{dx}^\textrm{i} \textrm{dx}^\textrm{j}], \end{aligned}$$

(26)

where $\psi$ and $\phi$ are scalar potentials and $\eta$ is the conformal time. Also, in the absence of anisotropic stresses, the equations of Einstein requires that $\phi =\psi$. However for models of modified gravity this is not valid generally. Conservation of the stress-energy tensor ($T^{\mu \nu }\;_{;\nu }=0$) of a perfect fluid gives the following equations [60, 94, 95]

$$\begin{aligned}&\dot{\delta }+3\mathcal {H}\left( \frac{\delta p}{\delta \uprho }-w\right) \delta +\left( 1+w\right) \theta =3\left( 1+w\right) \dot{\phi }, \end{aligned}$$

(27)

$$\begin{aligned}&\dot{\theta }+\mathcal {H}\left( 1-3c_{a}^{2}\right) \theta -\frac{\delta p}{\delta \uprho }\frac{k^{2}\delta }{\left( 1+w\right) }=k^{2}\phi . \end{aligned}$$

(28)

where dot denotes derivative with respect to the conformal time $\eta$ ($a\;d\eta =dt$). Also, k is wavenumber, $\mathcal {H}=\dot{a}/a$ is the conformal Hubble parameter, $\delta \equiv \delta \uprho /\uprho$ is the density contrast, $\theta$ is the divergence of the peculiar velocity, $p=w \uprho$ (for dust $w = 0$ and for dark energy $w=w_{d}$), and $c_{a}^{2}$ is the squared adiabatic sound speed of DE perturbations which is defined as follows:

$$\begin{aligned} c^{2}_{\textrm{a}}=w_{\textrm{d}}-\frac{\dot{w_{\textrm{d}}}}{3\mathcal {H}\left( 1+w_{\textrm{d}}\right) } \end{aligned}$$

(29)

We remind that Eqs. (27 and 28) can be used separately for each of the components, i.e. matter or dark energy. Also to study perturbations of DE, it is useful to define an effective sound speed of DE perturbations, $c_{\textrm{eff}}$, as follows [96]:

$$\begin{aligned} \frac{\delta p}{\delta \uprho }=c_{\textrm{eff}}^{2} +3\mathcal {H}\left( 1+w\right) \left( c_{\textrm{eff}}^{2}-c^{2}_{\textrm{a}}\right) \dfrac{\theta }{\delta }\frac{1}{k^{2}} \end{aligned}$$

(30)

In addition, In this context the Poisson equation is expressed by [97]

$$\begin{aligned} k^{2}\phi =- 4\pi G a^{2}(\delta \uprho +3\delta p), \end{aligned}$$

(31)

where $\delta \uprho = \delta \uprho _{m}+\delta \uprho _{d}$ and $\delta p = \delta p_{m}+\delta p_{d}$. After that, using quantities $\delta p_{m}=0$, $\delta p_{d}= c^2_{\textrm{eff}}\delta \uprho _{d}$, $\delta \uprho _{d}=\uprho _{d}\delta _{d}$, $\delta \uprho _{m}=\uprho _{m}\delta _{m}$ in Eq. (31), the Poisson equation can be written as follows:

$$\begin{aligned} - k^{2}\phi =\frac{3}{2}\mathcal {H}^{2}[\Omega _{m}\delta _{m}+(1+3c_{\textrm{eff}}^2)\Omega _{d}\delta _{d}], \end{aligned}$$

(32)

Now, we consider a matter-dominated universe with a small DE component. This is true because most structures are observed, most of them formed within the matter-dominated era. In this case, in the linear perturbation regime, and in sub-horizon scales $(k^{2}\gg \mathcal {H}^{2} )$, one can assume $\phi \simeq {\textrm{const}}$ [60]. Eliminating $\theta$ from Eqs. (27 and 28), one can obtain two second order coupled differential equations relevant to the evolution of DM and DE perturbations. Moreover, using $\frac{d}{d\eta }=a \mathcal {H}\frac{d}{da}$ and $\frac{d^{2}}{d\eta ^{2}}=(a\mathcal {H}^{2}+a\mathcal {\dot{H}}) \frac{d}{da} +a^{2}\mathcal {H}^{2} \frac{d^{2}}{da^{2}}$ these equations can be expressed in terms of the scale factor a. Hence we have

$$\begin{aligned}&\delta ^{\prime \prime }_{\textrm{m}}+\frac{1}{a}\Bigg (2+\frac{{\mathcal {H}^\prime }}{\mathcal {H}^{2}}\Bigg )\delta ^{\prime }_{\textrm{m}}= -\frac{k^{2}}{a^{2}\mathcal {H}^2}\phi \end{aligned}$$

(33)

$$\begin{aligned}&\delta ^{\prime \prime }_{\textrm{d}}+\frac{1}{a}\Bigg [2+\frac{{\mathcal {H}^\prime }}{\mathcal {H}^{2}}+3c_{\textrm{a}}^2-6w_{\textrm{d}}\Bigg ]\delta ^{\prime }_{\textrm{d}}\nonumber \\&\qquad +\frac{1}{a^2}\Bigg [-aw^{\prime }-w_{\textrm{d}}\Bigg (1+\frac{{\mathcal {H}}^\prime }{\mathcal {H}^2} -3w_{\textrm{d}}+3c^2_{\textrm{a}}\Bigg )\Bigg ]\delta _{\textrm{d}} \nonumber \\&\quad =-(1+w_{\textrm{d}})\frac{k^{2}}{a^{2}\mathcal {H}^2}\phi \end{aligned}$$

(34)

where $\mathcal {H}^\prime /\mathcal {H}^2$, is a function of scale factor and using Friedmann equations, we can write this quantity as follows:

$$\begin{aligned} \frac{\mathcal {H}^\prime }{\mathcal {H}^2}=-\frac{1}{2}\frac{\Omega _{\textrm{m}} +\Omega _{\textrm{d}}(1+3w_{\textrm{d}})}{\Omega _{\textrm{m}}+\Omega _{\textrm{d}}} =-\frac{1}{2}(1+3w_{\textrm{d}}\Omega _{\textrm{d}}) \end{aligned}$$

(35)

Finally, using Eqs. (29), (32) and (35), we can obtain Eqs. (33 and 34) as follows (see also [60, 98]):

$$\begin{aligned}&\delta ^{\prime \prime }_{\textrm{m}}+\frac{3}{2a}\left( 1-w_{\textrm{d}}\Omega _{\textrm{d}}\right) \delta ^{\prime }_{\textrm{m}}= \frac{3}{2a^{2}} \Bigg [\Omega _{\mathrm {\textrm{m}}}\delta _{\mathrm {\textrm{m}}}+\Omega _{\mathrm {\textrm{d}}}\delta _{\mathrm {\textrm{d}}}\left( 1+3c_{\textrm{eff}}^{2}\right) \Bigg ] \end{aligned}$$

(36)

$$\begin{aligned}&\delta ^{\prime \prime }_{\textrm{d}}+\frac{3}{2a}\Bigg [-2w_{\textrm{d}}-\frac{2}{3}\frac{aw^{\prime }_{\textrm{d}}}{(1+w_{\textrm{d}})}+\left( 1-w_{\textrm{d}}\Omega _{\textrm{d}}\right) \Bigg ]\delta ^{\prime }_{\textrm{d}}\nonumber \\&\qquad +\frac{1}{2a^2}\Bigg [-\frac{2aw^{\prime }_{\textrm{d}}}{1+w_{\textrm{d}}}-w_{\textrm{d}}\left( 1-3w_{\textrm{d}}\Omega _{\textrm{d}}\right) \Bigg ]\delta _{\textrm{d}}\nonumber \\&\quad =\frac{3}{2a^{2}} \left( 1+w_{\textrm{d}}\right) \Bigg [\Omega _{\textrm{m}}\delta _{\textrm{m}}+\Omega _{\textrm{d}}\delta _{\textrm{d}}\left( 1+3c_{\textrm{eff}}^{2}\right) \Bigg ] \end{aligned}$$

(37)

where $\Omega _{\textrm{m}}=\frac{\Omega _{\textrm{m,0}}\textrm{a}^{-3}}{E^{2}(\textrm{a})}$ and $\Omega _{\textrm{d}}=\frac{\Omega _{\textrm{d,0}}\mathrm {f(a)}}{E^{2}(\textrm{a})}$ are dimensionless density parameters of the DM and DE, respectively

We remind that Eqs. (36 and 37) are both valid in PN (Pseudo-Newtonian) and GR(General Relativity) formalism [99]. Based on the Eqs. (36 and 37), utilizing EoS parameterizations considered in this work, it is possible to investigate the effect of both clustered ($\textrm{c}_{\textrm{eff}}\simeq 0$) and non-clustered ($\textrm{c}_{\textrm{eff}}\simeq 1$) of DE on the growth of DM perturbations. As well as, for the non-clustered or homogenous DE, we can set $\delta _{\textrm{d}}=0$ in these equations. Now, to obtain the density contrast of DM and DE ($\delta _{\textrm{m}}$ and $\delta _{\textrm{d}}$), one can integrate the coupled system of Eqs. (36 and 37) numerically from $\textrm{a}_{\textrm{i}}=10^{-3}$ up to the present time (a = 1). To this end, the following initial conditions can be used [60, 66].

$$\begin{aligned} \delta _{\textrm{mi}}&=1.4\times 10^{-4} ,\quad \delta ^{\prime }_{\textrm{mi}}=\frac{\delta _{\textrm{mi}}}{\textrm{a}_{i}}. \end{aligned}$$

(38)

$$\begin{aligned} \delta _{\textrm{di}}&=\frac{1+\textrm{w}_{\textrm{di}}}{1-3\textrm{w}_{\textrm{di}}}\delta _{\textrm{mi}}.\end{aligned}$$

(39)

$$\begin{aligned} \delta ^{\prime }_{\textrm{di}}&=\frac{4\textrm{w}^{\prime }_{\textrm{di}}}{(1-3\textrm{w}_{\textrm{di}})^2}\delta _{\textrm{mi}}+\frac{1+\textrm{w}_{\textrm{di}}}{1-3\textrm{w}_{\textrm{di}}}\delta ^{\prime }_{\textrm{mi}}. \end{aligned}$$

(40)

where $w_{\textrm{di}}$ means the value of $w_{\textrm{d}}$ at $a_{\textrm{i}}$. Here, to make sure that the matter perturbations are in the linear regime, we set initial fluctuations of DM, $\delta _{\textrm{mi}}=1.4\times 10^{-4}$.

Table 4 The $f\sigma _{8}(z)$ data points and their references

4.1 Growth of matter perturbations

To evaluate the obtained results from solving Eqs. (36, 37) one can use observational data. Hence, we need to calculate $f(z)\sigma _{8}(z)$ where f(z) is the linear growth rate of matter perturbations, which is defined as follows [114, 115]

$$\begin{aligned} f=\dfrac{d\ln \delta _{m}}{d\ln a}\equiv -(1+z)\frac{\delta ^{\prime }_{m}(z)}{\delta _{m}(z)} \end{aligned}$$

(41)

where ($^{ \prime }$) denotes derivative relative to the redshift. Also, in the linear regime $\sigma _{8}(z)=\sigma _{8}(z=0)\frac{\delta _{m}(z)}{\delta _{m}(z=0)}$ is the redshift-dependent parameter which measures the growth of root-mean-square mass fluctuations in spheres with radius $8 \mathrm {Mpc/h}$ [116]. Moreover, $\sigma _{8,0}$ can be rescaled as $\sigma _{8,0}=\frac{\delta _{m}(z=0)}{\delta _{m,\Lambda }(z=0)}\sigma _{8,\Lambda }$ to obtain appropriate parameters for evaluating DE models. We remind that $f(z)\sigma _{8}(z)$ can be measured directly from the ratio of the monopole to the quadrupole of the redshift-space power spectrum. Briefly, through these observations, one can measure the perturbations of the galaxy density $\delta _{g}$, which can be related to DM perturbations via the bias factor $b=\delta _{g}/\delta _{m}$. Song and Percival in [104] have shown that $f(z)\sigma _{8}(z)$ is independent of the bias factor. Indeed, this quantity can be a useful discriminator of DE models.

The growth rate data sets shown in Table 4 are based on the “Gold-2017” gathered from [117], including 18 independent measurements of $f\sigma _{8}(z)$. These data sets have been obtained based on Redshift Space Distortion (RSD) measurements from various observations of the Large Scale Structure (LSS). In addition, we added 4 recent measurements from [112] to the ”Gold-2017” compilation. Eventually, we solve Eqs. (36) and (37) numerically to find $f\sigma _{8}(z)$ and calculate $\chi ^{2}_{\textrm{growth}}$ as follows

$$\begin{aligned} \chi ^{2}_{\textrm{growth}}=\sum _{i=1}^{22}\frac{[f\sigma _{8}(z_{i})-(f\sigma _{8,i})_{\textrm{ob}}]^{2}}{\sigma _{i}^{2}} \end{aligned}$$

(42)

5 Results of data analysis on models

In this section, we survey the DE parameterizations considered in this work in two steps.

In the first step, we carry out an $\textrm{MCMC}$ analysis to constrain the free parameters of the models utilizing the latest available background data (see Sect. 3 and Eq. (11)). Accordingly, we have summarized the results of our data analysis relevant to the DE parametrizations in the Table 8. As well, the confidence levels for $1\sigma$ and $2\sigma$ constraints on the DE parameterizations using background datasets have been shown in the Fig. 6. These three-angle plots are significant in the sense that they can demonstrate the correlations between each pair of free parameters of the models.

In the following, to compare the models with each other we investigate the main quantities, i.e. EoS parameter, Hubble parameter, deceleration parameter, and age of the universe by considering the best-fit values of free parameters listed in Table 8. To this end, we have shown the evolution of these quantities as a function of redshift z in Figs. 1 and 2.

Fig. 1

Upper panel: Evolution of the EoS parameter for the different DE parametrization models as a function of redshift z investigated in this work. Middle panel: Evolution of the f(z) of models as a function of redshift z. Lower panel: $\Delta \textrm{E}$ of models compared to the $\Lambda \textrm{CDM}$ model in terms of redshift z (see Eq. 43). The various DE models have been specified by different colors and line styles in the inner panels of the figure

Fig. 2

Upper panel: The Relative difference of the universe age relevant to the models compared to its value in the standard $\Lambda \textrm{CDM}$ model, using the best-fit values listed in Table 8 for the DE parametrizations. Lower panel: The evolution of the deceleration parameter for various models as a function of z (see Eq. 44)

In the upper panel of Fig. 1, the evolution of $w_{d}$ of models is plotted relative to the redshift z. As we observe, all models cross the phantom line ($w_{d}=-1$) around ${ z\sim {0.34}\; -\sim {0.54}}$ from the phantom region $(w_{d} < -1)$ into the quintessence regime $(-1< w_{d}< -\frac{1}{3})$. Also, models I and III evolve in the phantom region for all redshift z before crossing the phantom line, while models II and IV first evolve in the quintessence region, then enter the phantom region at ${z\sim 2.31}$ and ${ z\sim 1.42}$, respectively. Finally, a notable point is that models II and IV have the same behavior in all redshift z with a little difference. The EoS of DE parametrizations considered in this work can be written as, $w_{d}=w_{0}+w_{1}f(z)$. The errors in $w_{1}$ depend on the behavior of the given function f(z) . In other words, errors in $w_{1}$ are sensitive to the f(z) function. That is, if f(z) increases quickly with redshift z, then the errors in $w_{1}$ are smaller, and vice versa [113]. To compare the sensitivity of the models to $w_{1}$, we have shown the f(z) function of the models I–IV in terms of redshift z in the middle panel of Fig. 1. Below $z \sim 0.25$, one can observe that the sensitivity of the models to the $w_{1}$ is almost the same and their slight difference can be ignored. Finally, bigger than $z\sim 0.25$, the order of sensitivity to $w_{1}$, we expect that the outperforms are followed in order by model III, model I, model II, and model IV.

As we know, the Hubble parameter is one of the quantities that can describe the background evolution of the universe. Furthermore, the evolution of the Hubble parameter can affect the growth of matter perturbations, hence it is significant to investigate the behavior of the Hubble parameter in DE parametrizations. Based on this, we show in the lower panel of the Fig. 1 the evolution of the percentage deviance of the normalized Hubble parameter E(z) of the models relative to the concordance $\Lambda \textrm{CDM}$ model, i.e.

$$\begin{aligned} \Delta E(\%)= 100\times \Bigg [\frac{E(z)_{\textrm{model}}}{E(z)_{\Lambda \textrm{CDM}}}-1\Bigg ] \end{aligned}$$

(43)

We see that the value of quantity $\Delta E$ at ${z\sim 0.32}$ for models I, II, and IV, is ${\sim 2.92\% }$, ${ \sim 3.02\%}$, and ${ \sim 3.21\%}$ respectively. Also at ${z\sim 0.39}$, it is ${\sim 3.85\%}$ for model III. As well as, the value of $\Delta E(\%)$ is positive for models II and IV for all redshift, and $\Delta E(\%)$ at ${z\gtrsim 1.15}$ and ${z\gtrsim 1.48 }$ is negative for Models I and III, respectively. Finally, the considerable point is that model IV has the same behavior as model II in all redshift z with a little difference. Being positive (negative) value of quantity $\Delta \textrm{E}$ relative to the $\Lambda \textrm{CDM}$ model means that the cosmic expansion in the corresponding model is larger (smaller) compared to the $\Lambda \textrm{CDM}$ model. As well, in the right panel of the Fig. 4, we compare the theoretical evolution of the Hubble parameter of models, H(z) , in terms of redshift z, plus 36 cosmic chronometer data points given in Table 3.

Here we investigate the deceleration parameter quantity which is commonly used to evaluate DE parametrizations. This quantity is defined as follows

$$\begin{aligned} q(z)=-\frac{\ddot{a}}{aH^{2}}=\frac{1}{H(z)}\frac{dH(z)}{dz}(1+z)-1 \end{aligned}$$

(44)

Fig. 3

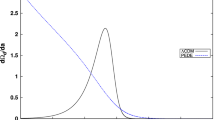
Upper panel: Evolution of the linear growth rate of matter perturbations (Eq. 41) for the various DE parametrizations in terms of the redshift z. Middle panel: $\Delta f(\%)$ of models compared to standard $\Lambda \textrm{CDM}$ model as a function of redshift z (Eq. 47). Lower panel: The evolution of the growth function for various models as a function of z. H and C in the explanations inside the panels mean the Homogeneous and Clustered case of the DE parametrizations, respectively

Using Eq. (44), It is possible to determine the transition time ($z_{t}$) of the universe from decelerated expansion phase ($q>0$) to the accelerated expansion phase ($q<0$) of the universe. This time is obtained by setting $q=0$ or $\ddot{a}=0$. In the lower panel of the Fig. 2, we have shown the evolution of the deceleration parameter in terms of redshift z. The transition redshift, $z_{t}$, for Models I, II, III, IV, and the $\Lambda \textrm{CDM}$ model is 0.827, 0.761, 0.835, 0.757, and 0.692, respectively. As can be observed, in the early times, due to the universe being matter-dominant, the value of q tends to $\frac{1}{2}$. Also, we see that the transition redshift related to models I and III are nearly the same. Also, the transition redshifts related to models II and IV are nearly equal. On the other hand, models I and III have the same behavior for all redshifts. This is also true for the models II and IV. These results are in consent with the values obtained in [118].

The age of the universe is another quantity that can be used to compare model of DE parametrizations. We can calculate the age of the universe using the best-fitting values listed in the Table 8 and the following relation

$$\begin{aligned} t_{U}=\frac{1}{H_{0}}\int _{0}^{\infty }\frac{dz}{(1+z)E(z)} \end{aligned}$$

(45)

which E(z) is given by Eq. (6). We obtained the following results for the age of the universe in the models studied in this work. The $t_{U}$ for Models I, II, III, and IV are ${13.581\; \textrm{Gyr}}$, ${13.562 \; \textrm{Gyr}}$, ${13.573 \; \textrm{Gyr}}$, and ${ 13.556\; \textrm{Gyr}}$, respectively. Also, $t_{U}$ for $\Lambda \textrm{CDM}$ is ${13.642 \;\textrm{Gyr}}$. We remind that the age of the universe based on the Planck (2018) results is $13.78 \textrm{Gyr}$ [7]. As well, upper panel of Fig. 2 shows the percentage of the relative difference of the universe age in the models compared to its value in the standard $\Lambda {\textrm{CDM}}$ model. This quantity is defined as follows:

$$\begin{aligned} \Delta T(\%)=100\times \Bigg [\frac{{{(t_{U})}_{\textrm{model}}}}{{{(t_{U})}_{\Lambda \textrm{CDM}}}}-1\Bigg ] \end{aligned}$$

(46)

In upper panel of Fig. 2, we observe that the $\Delta {T}(\%)$ for models I, II, III, and IV are ${\sim -0.38 \%}$, ${ \sim -0.52\%}$, ${ \sim -0.45\% }$, and ${\sim -0.60\%}$, respectively.

Fig. 4

Left panel: comparison of the observational growth rate data points (Table 4) and theoretical prediction of the growth rate $f\sigma _{8}(z)$(see Eq. (41) and explanations after it ) as a function of redshift z for both homogeneous (H) and clustered (C) cases of models. Right panel: comparison of the 32 cosmic chronometer data points given in [82] and the theoretical evolution of the Hubble parameter in terms of the redshift z

Fig. 5

The confidence levels for $1\sigma$ and $2\sigma$ constraints to the DE parameterizations using the just background data (blue) and combined background+growth rate data for clustered DE (red), and homogeneous DE (green) parameterizations. The upper left (upper right) panel displays the results for Model I ( Model II) parameterization. As well, the lower left (lower right) panel displays the results for Model III (Model IV) parameterization

In the second step, we investigate the growth of matter perturbations by solving Eqs. (36 and 37) in both homogeneous and clustered cases of DE parameterizations. Then we use a joint statistical analysis that included background and growth rate data obtained from RSD (see Eq. 12 and Sect. 4.1) to constrain $\sigma _{8}$ and other free parameters of DE parametrizations. The results of our data analysis, in this case, are given in Table 9. Using the best-fit values listed in Table 9, we study the evolution of the growth rate of matter perturbations, f(z) , $\Delta f(\%)$ relative to the $\Lambda \textrm{CDM}$, $D_{\textrm{m}}^{+}(a)$ for the DE parametrizations in both homogeneous and clustered cases.

Table 5 Numerical results of model selection using the background data for homogeneous DE (see Eq. (11) and Table 8)

Table 6 Numerical results of model selection using the background and growth rate data for homogeneous DE (see Eq. (12))

Table 7 Numerical results of model selection using the background and growth rate data for clustered DE (see Eq. (12))

In the top panel of the Fig. 3, we show the evolution of the linear growth rate of matter perturbations (see Eq. 41) related to models as a function of redshift z. The line $f=1$ indeed means the Einstein–de Sitter (EdS) universe ($\Omega _{\textrm{m}} =1$). We observe that the evolution of the linear growth rate of matter perturbations related to all models in high redshifts converge to the fixed line of EdS. In addition, the growth rate of the models has a slight deviation compared to the growth rate of the $\Lambda \textrm{CDM}$ model.

As well, The percentage of the relative difference in the growth rate of the models compared to its value in the $\Lambda \textrm{CDM}$ model is given as follows.

$$\begin{aligned} \Delta f (\%)=100\times \Bigg [\frac{f_{\textrm{model}}}{f_{\mathrm {\Lambda CDM}}}-1\Bigg ] \end{aligned}$$

(47)

The middle panel in Fig. 3 shows the $\Delta {{f}}(\%)$ based on the best-fit values of the free parameters in the Table 9 as a function of redshift z. Being positive (negative) value of quantity $\Delta {{f}}$ relative to the $\Lambda \textrm{CDM}$ model means that the linear growth rate of matter perturbations in the corresponding model is larger (smaller) compared to the $\Lambda \textrm{CDM}$ model. We obtained the following results for $\Delta {{f}}(\%)$ corresponding to the models for both homogeneous and clustered DE in the interval $0 \le z \le 3$.

$$\begin{aligned}{} & {} \Delta f\left( \%\right) \\{} & {} \quad = {\left\{ \begin{array}{ll} \;\;\;\;\;\ \text {Homogenous}\;\;\;\;\;\;\;\;\;\; \text {Clustered}\\ \sim \left[ +0.52, +1.02\right] ; \sim \left[ -1.32, +0.72\right] &{} \text { Model I;}\\ \sim \left[ -0.51,-0.29\right] ; \sim \left[ -0.33, +0.40\right] &{} \text { Model II;}\\ \sim \left[ - 0.18, +0.37\right] ;\sim \left[ +0.23, +1.77\right] &{} \text { Model III;}\\ \sim \left[ -0.97, -0.81\right] ;\sim \left[ -0.73, -0.43\right] &{}\; \text {Model IV;} \end{array}\right. } \end{aligned}$$

Comparing the lower panel of the Fig. 1 with the middle panel of the Fig. 3, we see that when the $\Delta {{E}}$ of the models is positive, the corresponding $\Delta {f}$ of the models becomes negative. This is because the evolution of $\Delta {E}$ and $\Delta {{f}}$ is not independent. In the other words, increasing $\Delta {{E}}$ leads to a decrease in the value of $\Delta {{f}}$ and vice versa. It is clear that when $\Delta {{E}}$ is maximum, the value of $\Delta {{f}}$ is minimum. Also, we see that the value of $\Delta {{f}}$ for homogeneous DE is smaller than its value in clustered case for models I and III. While for models II and IV, the value of $\Delta {{f}}$ related to the homogeneous DE is larger than its value in the clustered case. Another Significant result is that for both homogeneous and clustered DE cases, models I and III have very similar behavior for all redshifts z. This is also true for models II and IV. Finally, we observe that the growth rate corresponding to the models is lower than its value in the $\Lambda$CDM model at low redshifts, and at high redshifts, the differences between the growth rate of the models and the standard $\Lambda$CDM model are insignificant.

As well as, in the left panel of the Fig. 4, we compare the observational growth rate data points listed in Table 4 and theoretical prediction of the growth rate of matter perturbations, $f\sigma _{8}(z)$, (see Eq. (41) and explanations after it ) for both homogeneous and clustered cases of models. As can be seen, all the models are compatible with the growth rate data.

Table 8 Numerical results of parameter fitting with 1$\sigma$ confidence level in the models considered in this work from the combination of the dataset using Eq. (11) for the background data, $\mathrm {BAO + SnIa + CMB + H + BBN}$

Table 9 Numerical results of parameter fitting with 1$\sigma$ confidence level in the models investigated in this work assuming Homogeneous (H) and Clustered (C) DE from combining the data set using Eq. (12) for background and growth rate data, $\mathrm {BAO+SnIa+CMB +H+BBN+RSD}$

For a better comparison of the DE parametrization models investigated in this work, we plot the evolution of $D^{+}_{\textrm{m}}(a)/a$, as a function of redshift z in the bottom panel of the Fig. 3. The quantity $D^{+}_{\textrm{m}}(a)$ is known as the growth function and it is defined as $D^{+}_{\textrm{m}}(a)=\delta _{m}(a)/\delta _{m}(a=1)$. We observe that the formation of the structure in each of the models takes a different evolutionary path compared to the $\Lambda \textrm{CDM}$ model. Based on this, the studied models predict different rates of structure formation and meanwhile are comparable with the $\Lambda \textrm{CDM}$ model. Finally, Fig. 5 shows the effect of background and growth rate data on the free parameters of each model for both homogeneous and clustered DE cases.

5.1 Model selection

When the number of degrees of freedom of the models is equal, $\chi ^{2}_{\textrm{min}}$ can be used to compare the models. In this case, a smaller $\chi ^{2}_{\textrm{min}}$ means that the model in question has a better fit with the observational data. If the number of degrees of freedom of the model is not equal, the quantity $\chi ^{2}_{\textrm{red}}=\chi ^{2}_{\textrm{min}}/(N-k )$ can be used. Where k and N are the numbers of model free parameters and the total number of data points, respectively. In this case, if the value of $\chi ^{2}_{\textrm{red}}$ is around 1, it means that the model has a better fit with the observational data. Otherwise ($\chi ^{2}_{\textrm{red}}\ll 1$, $\chi ^{2}_{\textrm{red}}\gg 1$), the model is not desirable and should be discarded. In addition to using $\chi ^{2}_{\textrm{min}}$, Akaike information criterion (AIC) [119] and Bayesian information criterion (BIC) [120] can also be used to identify the most appropriate model that is compatible with observational data. These two criteria are defined as follows

$$\begin{aligned} \textrm{AIC}&=-2\ln \mathcal {L}_{\textrm{max}} +2k\nonumber \\ \textrm{BIC}&=-2\ln \mathcal {L}_{\textrm{max}} +k\ln \textrm{N} \end{aligned}$$

(48)

where N and k indicate the total number of data points and the number of free parameters of models, respectively. In our analysis, we used 1048 data points from the Pantheon set, 8 BAO points, 3 CMB points, 36 H(z) points, 1 BBN point, and 22 growth-rate data for a total of N = 1118 data points obtained from independent cosmological surveys. Also, $\mathcal {L}_{\textrm{max}}$ is the maximum value of the likelihood, which is related to $\chi ^{2}_{\textrm{min}}$ via $\chi ^{2}_{\textrm{min}}= -2\textrm{ln}\mathcal {L}_{\textrm{max}}$. We calculate the difference between $\textrm{AIC}$ and $\textrm{BIC}$ of models with respect to the $\Lambda \textrm{CDM}$ model as the best reference model, since this model has the best accordance with almost all cosmological data [121, 122].

$$\begin{aligned} \Delta \textrm{AIC}&=\textrm{AIC}_{\textrm{model}}-\textrm{AIC}_{\Lambda \textrm{CDM}}= \Delta \chi ^{2}_{\textrm{min}}+2\Delta k\nonumber \\ \Delta \textrm{BIC}&=\textrm{BIC}_{\textrm{model}}-\textrm{BIC}_{\Lambda \textrm{CDM}}= \Delta \chi ^{2}_{\textrm{min}}+\Delta k(\ln \textrm{N}) \end{aligned}$$

(49)

According to the interpretations related to these criteria in [121], (1) if $|\Delta \textrm{AIC}|\in (0,2]$, the considered model is substantially supported by the observational data, that is, that model can be appropriate, (2) if $|\Delta \textrm{AIC}|\in [4,7]$, we conclude that observational data considerably less support the model, (3) if $|\Delta \textrm{AIC}|>10$, the model is essentially not appropriate and should be discarded. Likewise, the following cases can be considered for $\Delta \textrm{BIC}$. For $|\Delta \textrm{BIC}|\in (0,2]$, $|\Delta \textrm{BIC}|\in [2,6]$, $|\Delta \textrm{BIC}|\in [6,10]$, and $|\Delta \textrm{BIC}|>10$ means that evidence against the model is weak, positive, strong, and very strong, respectively. Hence, in this case, the larger value of $\Delta \textrm{BIC}$ means that the model in question is more consistent with the observational data.

We have shown the results of these calculations in Tables 5, 6 and 7, using the numerical values of Tables 8 and 9, by assuming the homogenous and clustered DE parametrizations investigated in this study. By evaluating the results obtained from the AIC and BIC analysis, it can be concluded that the DE models and the standard $\Lambda$CDM model are all in agreement with the latest cosmological data. Clearly, a smaller value of AIC implies a better fit to the data. while, if we want to compare different models then we need to use the model pair difference, i.e. $\Delta \textrm{AIC}$.

Finally, using AIC and BIC analysis, we conclude that the selection of a model that has better compatible with the observational data, in addition to the background and growth rate data used, also depends on the homogeneity or clustering of the dark energy. For example, if we use AIC analysis and the background data are considered, we conclude that models III, I, II, and IV respectively, have a better fit with the observational data (see Table 5). We remind that in this case, the difference between the results for both clustered and homogeneous DE is negligible. Also, if we use the background and growth rate data jointly, in this case, for homogeneous DE the AIC analysis shows that models III, I, II, and IV have a better fit with the observational data, respectively. (see Table 6). Whereas if the clustered DE is considered, we conclude that models III, II, I, and IV, respectively, have a better fit with the data (see Table 7). Therefore, when we use both sets of data (background+growth) jointly, the homogeneous DE or clustered DE affects the fitting of the models with the data.

6 Conclusions

In this work, we investigated three well-known DE parametri zations (CPL, JBP, and BA) as well as a new parameterization of dark energy. All studied DE parametrizations have the same number of free parameters but different dependence on redshift z. In addition to the mentioned models, we used the $\Lambda \textrm{CDM}$ (as a concordance model) to compare the models with it. Considering these DE parameterizations, we surveyed the models in two steps.

Fig. 6

The confidence levels for $1\sigma$ and $2\sigma$ constraints to the models studied in this research for homogeneous DE, using background data (see Eq. (11) and Table 8 for numerical values)

Fig. 7

The confidence levels for $1\sigma$ and $2\sigma$ constraints to the models studied in this research for homogeneous ( left panel) and clustered DE (right panel), using both background and growth rate data (see Eq. (12) and Table 9 for numerical values)

In the first step, we carried out an $\textrm{MCMC}$ analysis to constrain the free parameters of the models utilizing the latest available background data such as SnIa, BAO, $\mathrm {H(z)}$(cosmic chronometers), CMB, BBN (see Sect. 3). The results of our data analysis relevant to the DE parametrizations considered in this work can be seen in Table 8. As well as, the confidence levels for $1\sigma$ and $2\sigma$ constraints on the DE parameterizations for homogeneous DE, using background data have been shown in the Fig. 6. After that, using the best-fit values obtained from the data analysis, we studied some important background quantities (such as $w_{d}$, $\Delta E$, q, and $\Delta T$) to compare the models with each other and $\Lambda \textrm{CDM}$ model.

Based on the results obtained we found out that, all models cross the phantom line around ${ z\sim {0.34}\;-\sim {0.54}}$ from the phantom region into the quintessence regime. Also, models I and III evolve in the phantom region for all redshift z before crossing the phantom line, while models II and IV first evolve in the quintessence region, then enter the phantom region at $z=2.31$ and $z=1.42$, respectively. Finally, a notable point is that models II and IV have the same behavior in all redshifts z with a little difference (see the upper panel of Fig. 1). Concerning the Hubble parameter, we concluded that the value of quantity $\Delta E$ at ${z\sim 0.32}$ for models I, II, and IV, is ${\sim 2.92\% }$, ${ \sim 3.02\%}$, and ${ \sim 3.21\%}$ respectively. Also at ${z\sim 0.39}$, it is ${\sim 3.85\%}$ for model III. As well as, we found that the value of $\Delta E(\%)$ is positive for models II and IV for all redshift, and $\Delta E(\%)$ at ${z\gtrsim 1.15}$ and ${z\gtrsim 1.48 }$ is negative for Models I and III, respectively. Finally, the considerable point is that model IV has the same behavior as model II in all redshifts z with a little difference. This is also true for models I and III (see lower panel of Fig. 1).

In addition, the value we obtained for the transition time from the decelerated expansion phase ($q>0$) to the accelerated expansion phase ($q<0$) corresponding to the models, is comparable to its value in the $\Lambda \textrm{CDM}$ model (see lower panel of Fig. 2). Furthermore to the aforementioned quantities, we calculated the age of the universe in each of the models. And we found that the age of the universe in each of the models is comparable to its value in the standard $\Lambda \textrm{CDM}$ model.

In the second step, we investigated the growth of matter perturbations by solving Eqs. (36 and 37) in both homogeneous and clustered cases of DE parameterizations. Then we used a joint statistical analysis that included background and growth rate data obtained from RSD (see Eq. 12 and Sect. 4.1) to constrain $\sigma _{8}$ and other free parameters of DE parametrizations. The results of our data analysis, in this case, are given in Table 9. Furthermore, the confidence levels for 1$\sigma$ and 2$\sigma$ constraints on the DE parameterizations for both homogeneous and clustered DE, using background and growth rate data have been shown in the panels of Fig. 7. Using the best-fit values obtained for the free parameters of models, we investigated the evolution of the growth rate, f(z) , $\Delta f(\%)$ relative to the $\Lambda \textrm{CDM}$, $D_{\textrm{m}}^{+}(a)$ for the DE parametrizations in both homogeneous and clustered cases. Accordingly, we concluded that the value of $\Delta {{f}}$ for homogeneous DE is smaller than its clustered case for models I and III. While for models II and IV, the value of $\Delta {{f}}$ related to the homogeneous DE is larger than its clustered case (see middle panel of Fig. 3. The significant result concerning the growth rate of models is that for both homogeneous and clustered DE cases, models I and III have very similar behavior for all redshift z. This is also true for models II and IV. Moreover, we concluded that the growth rate corresponding to DE parametrizations is lower than its value in the $\Lambda$CDM model at low redshifts, and at high redshifts, the differences between the growth rate of the models are insignificant. Based on this, we showed that the studied models predict different rates of structure formation and meanwhile are comparable with the $\Lambda$CDM model. Also, a notable point is that the new model is comparable to the other models and its behavior in all redshifts is very close to that of model II with a little difference. Afterward, we compared the growth rate data (Table 4) and the theoretical prediction of the growth rate, $f \sigma _{8}(z)$, and we found that the new DE parameterization like other models is in good agreement with the growth rate data (see left panel of Fig. 4). Eventually, we evaluated the results obtained from the AIC and BIC analysis and we concluded that DE parametrizations such as the standard $\Lambda$CDM model are all compatible with the latest cosmological data concerning both background and growth rate data. Finally, using AIC and BIC analysis, we found that the selection of a model that has better compatible with the observational data depends on the background and growth rate data. For example, if background data are considered, we found that models III, I, II, and IV respectively, have better compatibility with the observational data (see Table 5). We remind that in this case, the difference between the results for both clustered and homogeneous DE is negligible. Also, if we use the background and growth rate data jointly, in this case, for homogeneous DE the AIC analysis showed that models III, I, II, and IV respectively, have a better fit with the observational data. (see Table 6). On the other hand, assuming clustered DE, we concluded that models III, II, I, and IV respectively have better compatibility with the observational data (see Table 7). Therefore, when we used both sets of data (background + growth) jointly, we concluded that the homogeneity or clustering of dark energy affects the compatibility of the models with the data.