Loop enhancement of direct detection cross section in a fermionic dark matter model

Abstract

We investigate the effect of one loop quantum corrections on the elastic scattering of dark matter off the nucleon in a fermionic dark matter model. The model introduces two new singlet fermions and a singlet scalar. The fermions communicate with the SM particles through a Higgs portal. It is found that some viable regions in the parameter space respecting the bounds from the observed relic density, the Higgs invisible decay width, and direct detection experiment, will be shrunk significantly when one loop effects are taken into account. The regions already resided below the neutrino floor, partly may come into regions which are testable by the current or future direct detection experiments. In addition, some regions being viable at tree level, may be excluded when quantum corrections are included.

1 Introduction

The thermal production of weakly interacting massive particles (WIMPs) as dark matter (DM) candidates is a quite natural and ubiquitous mechanism [1,2,3,4,5,6]. The particle nature of dark matter will be demystified if its direct interaction with ordinary matter shows up in the so called direct detection (DD) experiments. On the theory side, the DM interaction with atoms may be so weak that it lies below the neutrino floor (NF) or not being detectable in the current DD experiments. The point is that when we present theoretical prediction of the DM-nucleon interaction, it is fare to know how much the computations are accurate in the perturbation theory.

There are models with dark matter candidates which may evade strong bounds from DD experiments. These models can be classified into two types. The first type occurs when the scattering amplitude at tree level and at zero momentum transfer vanishes by virtue of a symmetry breaking pattern. An example is the complex scalar DM model, wherein the DM candidate is a pseudo-Goldstone boson after a softly broken symmetry [7,8,9]. In the same category, it is demonstrated that via a scale symmetry breaking in a model with scalar dark matter, tree level DD cross section decreases significantly [10]. The second type contains models in which the scattering cross section of DM off nucleons is velocity or momentum suppressed, thus, escaping the DD bounds. Some instances are thermal DM candidates having a pseudo-scalar type interaction with nucleons [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. When DM-nucleon scattering cross section is suppressed at tree-level, it deems reasonable to include loop corrections. This may bring regions below the neutrino floor within reach of the present or future DD experiments. Works in this direction have been growing and the present findings generally show that the quantum corrections modify the viable parameter space significantly, see references [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42].

There may be other situations that loop effects of DM-nucleon scattering become salient. This is when the coupling involving in the DM-nucleon scattering cross section has small effect on the DM annihilation cross section, and in fact a second coupling mainly controls the size of the relic density. These types of models may be extensions to the simplest simplified DM models which are excluded almost entirely by the current direct detection experiments. The focus in this work is on a fermionic DM model with two fermion WIMPs, one of which playing the role of DM. As shown in [43], a large viable parameter space is available in this model satisfying the observed relic abundance and respecting the DD bounds. Working at tree level DM-nucleon scattering, it is found that parts of the parameter space are below the neutrino floor, and there are regions which respect the latest DD bounds. Now, by incorporating one loop effects, the arising question is that how the regions placing below the neutrino floor or the regions which are allowed by DD upper limits, will change to become regions above the neutrino floor or excluded regions, respectively.

The paper has the following structure. The dark matter model including two fermionic WIMPs which communicate with the SM particles via scalar-Higgs portal are introduced in Sect. 2. A brief discussion is given in Sect. 3 about the annihilation cross section and the tree level DD cross section of the DM particle. The invisible decay of the SM Higgs is introduced in Sect. 4. In Sect. 5, by imposing constraints from observed relic abundance and upper limits from DD experiments we show the viable parameter space by considering only tree level DD cross. We introduce in Sect. 6 the renormalization program for the present model, and find expressions for the counter terms needed to cancel the relevant divergences at one loop level. We collect the formulas representing different loop contributions to the DD cross section at one loop order in Sect. 7. In Sect. 8 our results are presented. The conclusion is given in Sect. 9.

2 Model

We describe here a renormalizable extension to the SM with two extra Dirac fermion fields $\chi _1$ and $\chi _2$, which are singlet under gauge symmetry of the SM. The new fermions communicate with the SM particles via a real singlet scalar $\varphi$. The scalar potential of the model accommodating the singlet scalar and the SM Higgs reads

$$\begin{aligned} V(\varphi , H)&=\mu _{H}^2 H^\dagger H + \lambda _H (H^\dagger H)^2 + \lambda _1 \varphi H^\dagger H \nonumber \\&\quad + \lambda _2 \varphi ^2 H^\dagger H+ \frac{1}{2} m^2 \varphi ^2 + \lambda _0 \varphi + \lambda _3 \varphi ^3 + \lambda \varphi ^4, \end{aligned}$$

(1)

The singlet scalar field gets a zero vacuum expectation value (vev), and the Higgs doublet in the unitary gauge is parameterized around its vacuum as

$$\begin{aligned} H=\begin{pmatrix} 0 \\ \frac{{{v}_{H}}+{h}^{\prime }}{\sqrt{2}} \\ \end{pmatrix}, \end{aligned}$$

(2)

where ${{v}_{H}}$ is the vacuum expectation value of the Higgs field with ${v}_{H}=246$ GeV. We choose $\mu _{H}$ and $\lambda _0$ such that at tree level the tadpole terms for the fields, s and $h^\prime$, become zero; i.e., $t_{\varphi } = t_{H} = 0$. The fermion fields $\chi _1$ and $\chi _2$ transform under ${\mathbb {Z}}_{2}$ symmetry as $\chi _i \rightarrow -\chi _i$. The particles of the standard model interact with the DM only through the Higgs portal. In this work we set $\lambda =\lambda _3 = 0$. The renormalizable Lagrangian containing the interactions of the new fermions with the singlet scalar is as follows

$$\begin{aligned} {\mathcal {L}}_{\textrm{Dark}}= \kappa _1 \varphi \bar{\chi }_1 \chi _1 +\kappa _2 \varphi \bar{\chi }_2 \chi _2 + (\kappa _{12} \varphi \bar{\chi }_1 \chi _2 + h.c ). \end{aligned}$$

(3)

The mass matrix of the scalars is not diagonal, so in the following we obtain the physical masses and eigenstates. By taking double derivative of the potential with respect to ${h}^{\prime }$ and $\varphi$, the elements of the mass matrix are obtained

$$\begin{aligned} {{M}^{2}}=\left( \begin{matrix} m_{\varphi }^2 = m^2 + \frac{1}{2} \lambda _2 v_H^2 &{} m_{\varphi h^\prime }^2 = \lambda _1 v_H \\ m_{\varphi h^\prime }^2 = \lambda _1 v_H &{} m_{h^\prime }^2 = \frac{1}{2} \lambda _H v_H^2 \\ \end{matrix} \right) . \end{aligned}$$

(4)

The mass eigenstates that diagonalize the mass matrix are defined

$$\begin{aligned} h= s_\omega \varphi + c_\omega h^\prime , ~~~ s= c_\omega \varphi - s_\omega h^\prime , \end{aligned}$$

(5)

where $s_\omega = \sin \omega$ and $c_\omega = \cos \omega$, and the mixing angle, $\omega$, is given by

$$\begin{aligned} \tan \,2\omega =\frac{2m_{\varphi h^\prime }^2}{m_{h^\prime }^2 -m_{\varphi }^2}. \end{aligned}$$

(6)

The mass eigenvalues are obtained as

$$\begin{aligned} m_{h,s}^{2}=\frac{m_{\varphi }^2 + m_{h^\prime }^2}{2} \pm \frac{1}{2} (m_{\varphi }^2-m_{h^\prime }^2) \sec 2\omega . \end{aligned}$$

(7)

In our numerical computations we take $m_h= 125$ GeV as the SM Higgs mass, and $m_s$ is the physical mass of the singlet scalar being a free parameter in our model. The couplings $\lambda _H$ and $\lambda _1$ are obtained in terms of the mixing angle and the physical masses of the scalars,

$$\begin{aligned} \lambda _H = \frac{m_s^2 \sin ^2 \omega + m_h^2 \cos ^2 \omega }{2 v_H^2}, ~~~ \lambda _1 = \frac{m_s^2-m_h^2}{2v_H} \sin 2\omega . \end{aligned}$$

(8)

A set of independent free parameters in our model is: $m_1, m_2, m_s, \lambda _2, \kappa _1, \kappa _2, \kappa _{12}, \omega$. We may define the mass difference between the two fermions as $\Delta = m_2 - m_1$, assuming that the light fermion is $\chi _1$, being our dark matter candidate with mass $m_{\textrm{DM}}$. Without lose of generality, we can take $\kappa _2 \sim 0$. The size of its one loop correction is then $\delta \kappa _2 \sim \kappa _{12}^2/(16\pi ^2)$, which is still quite small for $\kappa _{12} \sim {\mathcal {O}}(1)$. This will simplify our calculations. We end up having seven independent free parameters: $m_1, m_2, m_s, \lambda _2, \kappa _1, \kappa _{12}, \omega$. We will use $m_1 = m_{\textrm{DM}}$ interchangeably. The quartic couplings of the potential are constrained theoretically by requiring the stability of the potential. The stability conditions are $\lambda _H > 0$, $\lambda > 0$, and in case $\lambda _2 < 0$, then $\lambda \lambda _H > \lambda ^2_2/4$.

3 Annihilation cross section vs DD cross section

A detailed discussion is laid out on the relic density calculations and the tree-level DD cross section in [43] for the present model. Here we provide a short recap. There are two ways through which fermion DM can annihilate. (1) Through s-channel; by mediating h or s scalars, where DM may annihilate to the SM particles, a pair of Higgs, and a pair of singlet scalars. (2) Through t/u-channel; by mediating $\chi _1$ or $\chi _2$, where DM may annihilate to a pair of Higgs or a pair of singlet scalars. The annihilation cross section formulas are provided in Appendix A.

The condition where $\kappa _{12} = 0$, reduces the model to the simplest scenario. In this case, the annihilation cross section is a combination of terms each of which is proportional to $\kappa _1^2, \kappa _1^3$ or $\kappa _1^4$. On the other hand, the elastic scattering cross section is proportional to $\kappa _1^2$. Therefore, in order to get the relic density right, large coupling $\kappa _1$ is required, and this will give rise to quite a large direct detection cross section. As demonstrated in [43], unless the mixing angle is quite small, the entire parameter space of the simplest fermionic model (other than a resonance region with $m_{\textrm{DM}} \sim m_s/2$) is excluded by DD experiments.

For a given mixing angle, when $\kappa _{12} \ne 0$ then the DM annihilation cross section finds some new contributions as a function of $\kappa _{12}^4, \kappa _{12}^2 \kappa _1^2$, and so on. However, the DD cross section at tree level in this case remains intact, being proportional to $\kappa _1^2$. Now it is possible for the two cross sections to move in opposite directions. To evade DD bounds (demanding small DD cross section), small $\kappa _1$ is required, and at the same time to have large enough annihilation cross section, terms proportional to $\kappa _{12}^4$ will dominate when sizable $\kappa _{12}$ of ${\mathcal {O}}$(1) is picked out.

4 Invisible Higgs decay

In this model, if kinematically allowed, the SM Higgs may decay invisibly as: $h \rightarrow ss$, $h\rightarrow \chi _1 \chi _1$, and $h\rightarrow \chi _1 \chi _2$. These new decay channels will alter the theoretical decay width of the Higgs,

$$\begin{aligned} \Gamma ^{\textrm{tot}}_{h}&= \cos ^2(\omega )~\Gamma ^{\textrm{SM}}_{h} + \Theta (m_h -2m_s) \Gamma (h\rightarrow ss) \nonumber \\&\quad + \Theta (m_h -2m_{\chi _1}) \Gamma (h\rightarrow \chi _1 \chi _1) \nonumber \\&\quad + \Theta (m_h -m_{\chi _1}-m_{\chi _2}) \Gamma (h\rightarrow \chi _1 \chi _2), \end{aligned}$$

(9)

where $\Theta$ is the step function, and $\Gamma ^{\textrm{SM}}_{h}$ is the Higgs decay width computed within the SM. The Higgs decay to a pair of singlet scalars has the width

$$\begin{aligned} \Gamma (h\rightarrow s s) = \frac{{\mathcal {A}}^2}{128\pi m_h} \sqrt{1-4m^2_s/m^2_h}, \end{aligned}$$

(10)

where, the coupling ${\mathcal {A}}$ is given by

$$\begin{aligned} {\mathcal {A}}&= (2\sin \omega -3 \sin ^2 \omega ) \lambda _1 + (6 \sin ^2 \omega - 2 \cos \omega ) v_H \lambda _2\nonumber \\&\quad - 6 \sin ^2 \omega \cos \omega ~v_H \lambda _H. \end{aligned}$$

(11)

The decay width for the Higgs decay to two identical fermions is

$$\begin{aligned} \Gamma (h \rightarrow \chi _1 \chi _1) = \frac{\kappa ^2_1 m_h \sin ^2 \omega }{8 \pi } (1-4 m^2_{\chi _1}/m^2_h)^{3/2}. \end{aligned}$$

(12)

When the Higgs particle decays to $\chi _1 \chi _2$, its decay width reads

$$\begin{aligned} \Gamma (h\rightarrow \chi _1 \chi _2)&= \frac{\kappa _{12}^2 \sin ^2 \omega }{8\pi m^3_h}[m^2_h-(m_{\chi _1}+m_{\chi _2})^2]^{3/2} \nonumber \\&\quad \times [m^2_h -(m_{\chi _1}-m_{\chi _2})^2]^{1/2}. \end{aligned}$$

(13)

There is an experimental upper limit on the branching ratio of the invisible Higgs decay at the 95% CL, as $Br(h \rightarrow \text {invisible}) \lesssim 0.18$ [44]. The mass of the Higgs is measured to be $\sim 125$ GeV, and its total decay width is $\Gamma _{\textrm{Higgs}} = 3.2^{+2.8}_{-2.2}$ MeV [45]. The constraint from the invisible Higgs decay becomes more effective for small mass of the singlet scalar and fermions, as well as, for large mixing angle.

5 DD cross section at tree level

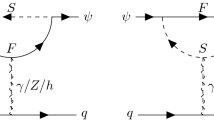
In this section we present our results concerning the DD cross section at tree level in perturbation theory. The following constraints are considered in the present and next sections: The upper limit from XENON1T experiment [46], and projected limit from XENONnT (20 ty) at 90% CL are imposed [47]. The lower bounds on the DM-nucleon scattering cross section is set by the neutrino floor [48]. The neutrino floor is a bound below which the detection of DM is very difficult. The predicted relic abundance by the model for each point in the parameter space is subject to the observed value $\Omega h^2 \sim 0.12$ [49]. The DD cross section at tree level is spin-independent (SI) in this model. The relevant Feynman diagram for this process is shown in Fig. 1. As mentioned in the previous section, the DD cross section at tree level depends only on one coupling, $\kappa _1$. At the limit of zero momentum transfer we arrive at the following formula for the the scattering amplitude as

$$\begin{aligned} {\mathcal {M}}^{LO}_{\chi _1 \chi _1} = {\mathcal {C}} \bar{\chi }_1 \chi _1 \bar{q} q, \end{aligned}$$

(14)

where the effective coupling ${\mathcal {C}}$ is

$$\begin{aligned} {\mathcal {C}} = \kappa _1 \sin (2\omega ) \frac{m_q}{2 v_H} \left( \frac{1}{m_h^2}-\frac{1}{m_s^2}\right) . \end{aligned}$$

(15)

The elastic scattering cross section of DM-proton is described by this formula

$$\begin{aligned} \sigma ^p = \frac{m_p^4 m_{\textrm{DM}}^2 \kappa _1^2 \sin ^2(2\omega )}{\pi (m_p + m_{\textrm{DM}})^2 v_H^2} \left( \frac{1}{m_h^2}-\frac{1}{m_s^2}\right) ^2 f^2, \end{aligned}$$

(16)

where $m_p$ stands for the proton mass, and $f \sim 0.28$ is the hadronic form factor. Let us take a numerical look at the tree-level DM-nucleon scattering cross section. The range of the parameters used in our scan over the parameter space are, 10 GeV $< m_{\textrm{DM}}<$ 2 TeV, $0.001< \kappa _1 < 1$, and $0.001< \kappa _{12} < 1$. The rest of the free parameters in the scan are fixed as, $\lambda _2 = 0.5$ and $\sin \omega = 0.1$. The results are shown in Fig. 2 and Fig. 3 for the DM-proton cross section as a function of DM mass for $m_s = 50$ GeV and $m_s = 250$ GeV, respectively. In both cases the mass difference between the two fermions is, $\Delta = 20$ GeV.

Fig. 1

Feynman diagram for DM-quark elastic scattering at tree level

Fig. 2

Tree-level DD cross section is shown as a function of DM mass for $m_s = 50$ GeV and $\Delta = 20$ GeV. In the left (right) panel, $\kappa _1$ ($\kappa _{12}$) is shown in the vertical color spectrum. All the points respect the observed relic density and invisible Higgs decay bound. Upper limits from XENON1t and projected XENONnT are placed. The neutrino floor is also shown

Fig. 3

The same as in Fig. 2, with $m_s = 250$ GeV

In both figures, it is evident that there are points with small DD cross section which reside below the XENONnT bound and the neutrino floor. When $m_s = 50$ GeV, a broader range of viable DM candidates are found with respect to the case when $m_s = 250$ GeV. The reason is that when $m_s$ is smaller, then annihilation of DM to a pair of singlet scalars is possible with smaller DM candidates and this will affect the range of the viable parameter space. As expected, the lower DD cross section, the smaller coupling $\kappa _1$ is picked out. The other involved coupling, $\kappa _{12}$, is quite large in the low DD cross section regions. This latter coupling has to be large in order to control the size of the theoretical relic density in such a way to satisfy the observed density.

Next, we redo our scan with 50 GeV $< m_s < 250$ GeV, and let the couplings $\kappa _1$ and $\kappa _{12}$ take smaller values in the range, $0.0001< \kappa _1 < 1$ and $0.0001< \kappa _1 < 1$. The other parameters are kept the same as before. It is expected that by taking smaller $\kappa _1$, smaller DD cross section is achieved which goes well below the neutrino floor. This is demonstrated in Fig. 4, wherein the cross section of DM-proton scattering is shown as a function of the DM mass. There, we notice that a large portion of the parameter space is below the neutrino floor.

Fig. 4

The same as in Fig. 2, with 50 GeV $< m_s < 250$ GeV

So, the main point that motivates the computations of the DD cross section at one loop order, is the existence of one loop Feynman diagrams for DM-nucleon scattering with purely $\kappa _{12}$ coupling which will enhance the DD cross section significantly in the regions with small DD cross section. It is also numerically checked that by varying the couplings $\lambda _2$ and the mass difference $\Delta$, the overall picture at tree level remains almost the same.

6 Renormalization of the model

We describe the renormalization program at one-loop order in this section. There are seven independent parameters in our model which need renormalization, namely, $m_1, m_2, m_s, \lambda _2, \kappa _1$,$\kappa _{12}$, $\omega$. In the following section we describe how to pursue the program.

6.1 One-point and two-point functions

Since we have mixing in the scalar sector at tree level, then the renormalization procedure needs a careful treatment. Note that here we will apply the on-shell scheme in the renormalization. Let us begin with the two scalar tadpoles; $t_\varphi$ and $t_H$. The relations between the tadpole counter terms in the two bases are

$$\begin{aligned}&\delta t_\varphi = c_\omega ~\delta t_s - s_\omega ~\delta t_h, \nonumber \\&\delta t_H = s_\omega ~\delta t_s + c_\omega ~\delta t_h, \end{aligned}$$

(17)

where $c_\omega = \cos (\omega )$ and $s_\omega = \sin (\omega )$. The wave function renormalization of the fields, h and s, in the present of mixing can be formulated in the following way, as introduced in [38, 50],

$$\begin{aligned} \begin{pmatrix} h \\ s \end{pmatrix} \rightarrow \begin{pmatrix} 1+ \frac{1}{2} \delta Z_{hh} &{}\quad \delta c_{hs} + \delta \alpha \\ \delta c_{sh}-\delta \alpha &{}\quad 1+ \frac{1}{2} \delta Z_{ss} \end{pmatrix} \begin{pmatrix} h \\ s \end{pmatrix}, \end{aligned}$$

(18)

where $\delta c_{hs}$ and $\delta c_{sh}$ are the counter terms of the off-diagonal mass terms. Let us begin by the renormalized one-point functions for the physical scalar fields, h and s, that we write them in terms of the 1PI diagrams $\Gamma ^{\textrm{1PI}}_h$ and $\Gamma ^{\textrm{1PI}}_s$: $t^r_h = \delta t_h + \Gamma ^{\textrm{1PI}}_h$, $t^r_s = \delta t_s + \Gamma ^{\textrm{1PI}}_s$. At one loop level, we impose the renormalization condition for the two scalar tadpoles: $t^r_s = t^r_h = 0$. This results in $\delta t_s = - \Gamma ^{\textrm{1PI}}_s$ and $\delta t_h = - \Gamma ^{\textrm{1PI}}_h$. It is worth mentioning that when the renormalized tadepoles vanish at one loop, it implies no shift of the vacuum state of the potential. Next, we express relations for the renormalized two-point functions of the scalar fields,

$$\begin{aligned} \Pi ^{r}_{ss}(p^2)&= \Pi ^{\textrm{1PI}}_{ss}(p^2) +\frac{s_\omega ^2 \delta t_H}{v_H} + \Big [(p^2- m_s^2) \delta Z_{ss} -\delta m_s^2 \Big ], \nonumber \\ \Pi ^{r}_{hh}(p^2)&= \Pi ^{\textrm{1PI}}_{hh}(p^2) +\frac{c_\omega ^2 \delta t_H}{v_H} + \Big [(p^2- m_h^2) \delta Z_{hh} -\delta m_h^2 \Big ], \nonumber \\ \Pi ^{r}_{sh}(p^2)&= \Pi ^{\textrm{1PI}}_{sh}(p^2) +\frac{s_\omega c_\omega \delta t_H}{v_H}\nonumber \\&\quad + p^2(\delta c_{hs} + \delta c_{sh}) + m_h^2 (\delta \omega - \delta c_{hs})\nonumber \\&\quad - m_s^2 (\delta \omega + \delta c_{sh}). \end{aligned}$$

(19)

We choose the one-shell renormalization conditions for the two-point functions as follow,

$$\begin{aligned} \Pi ^{r}_{ss}(m_s^2)&= \Pi ^{r}_{hh}(m_h^2) = 0, ~~\frac{d}{dp^2}\Pi ^{r}_{ss}(p^2)|_{p^2=m_s^2}\nonumber \\&= \frac{d}{dp^2}\Pi ^{r}_{hh}(p^2)|_{p^2=m_h^2} = 0, \end{aligned}$$

(20)

and from these relations four counter terms are determined,

$$\begin{aligned} \delta m_s^2&= \Pi ^{\textrm{1PI}}_{ss}(m_s^2) +\frac{s_\omega ^2 \delta t_H}{v_H}, ~~ \delta m_h^2 = \Pi ^{\textrm{1PI}}_{hh}(m_h^2) +\frac{c_\omega ^2 \delta t_H}{v_H} \nonumber \\ ~~\delta Z_{ss}&= -\frac{d}{dp^2} \Pi ^{\textrm{1PI}}_{ss}(p^2)|_{p^2=m_s^2}, ~~ \delta Z_{hh} \nonumber \\&= -\frac{d}{dp^2} \Pi ^{\textrm{1PI}}_{hh}(p^2)|_{p^2=m_h^2}. \end{aligned}$$

(21)

We can fix three counter terms, $\delta c_{hs}$, $\delta c_{sh}$ and $\delta \omega$ by imposing the conditions

$$\begin{aligned} \Pi ^r_{sh}(m_h^2) = \Pi ^r_{sh}(m_s^2) = 0, ~~ \delta c_{sh} = \delta c_{hs}, \end{aligned}$$

(22)

to find

$$\begin{aligned} \delta \omega&= \frac{1}{2(m_s^2- m_h^2)} \Big [ \Pi ^{\textrm{1PI}}_{sh}(m_h^2) +\Pi ^{\textrm{1PI}}_{sh}(m_s^2) +\frac{s_{2\omega } \delta t_H}{v_H} \Big ] \nonumber \\ \delta c_{hs}&= \frac{1}{2(m_s^2- m_h^2)} \Big [ \Pi ^{\textrm{1PI}}_{sh}(m_h^2) -\Pi ^{\textrm{1PI}}_{sh}(m_s^2) \Big ]. \end{aligned}$$

(23)

Now we consider the renormalized two point function of the two fermions, $\chi _1$ and $\chi _2$

(24)

With the renormalization conditions,

(25)

We can then obtain the two parameters,

(26)

A comment is appropriate to mention here. It is turned out in [51] that the mixing angle, $\omega$, remains gauge dependence in the on-shell renormalization scheme. A suggested in [52] to get gauge-independent definition for $\delta \omega$, one may define it in a physical process, like the decay $h \rightarrow \tau \tau$. We have checked this in our numerical results and it is found out that the gauge dependence of the one-shell renormalization at one loop order is up to about $1 \%$.

6.2 Renormalization of the couplings $\kappa _1$ and $\kappa _{12}$

Since the ultra-violet divergences are universal we opt for the minimal subtraction scheme. We will look at two vertices $h\chi _1 \chi _1$ and $h\chi _1 \chi _{12}$ to find the relevant counter terms. We begin by the vertex $h\chi _1 \chi _1$ and write,

$$\begin{aligned} \Gamma ^{\textrm{NLO}}_{h \chi _1 \chi _1} = \Gamma ^{\textrm{LO}}_{h \chi _1 \chi _1} + \Gamma ^{\textrm{1PI}}_{h\chi _1 \chi _1} +\Gamma ^{\textrm{CT}}_{h\chi _1 \chi _1}, \end{aligned}$$

(27)

where $\Gamma ^{\textrm{1PI}}_{h\chi _1 \chi _1}$ indicates the loop correction to the triple vertex, and the vertex counter terms are collected in $\Gamma ^{\textrm{CT}}_{h\chi _1 \chi _1}$. Combining the mixing effects and wave function renormalization the full expression for $\Gamma ^{\textrm{CT}}_{h\chi _1 \chi _1}$ reads

$$\begin{aligned} \Gamma ^{\textrm{CT}}_{h\chi _1 \chi _1}&= \frac{1}{2} \lambda _{h\chi _1 \chi _1} \delta Z_{hh} + \lambda _{h\chi _1 \chi _1} \delta Z_{\chi _1 \chi _1}\nonumber \\&\quad + \lambda _{s\chi _1 \chi _1} (\delta c_{hs} -\delta \omega )\nonumber \\&\quad +\lambda _{h\chi _1 \chi _2} \frac{\Pi ^{\textrm{1PI}}_{\chi _1 \chi _2}(m_1)}{m_2- m_1} + \frac{\partial \lambda _{h\chi _1 \chi _1}}{\partial \kappa _1} \delta \kappa _1, \end{aligned}$$

(28)

where for the couplings we have

$$\begin{aligned}&\lambda _{h\chi _1 \chi _1} = -\sin (\omega ) \kappa _1, ~~ \lambda _{s\chi _1 \chi _1} = -\cos (\omega ) \kappa _1,\nonumber \\&\lambda _{h\chi _1 \chi _2} = -\sin (\omega ) \kappa _{12}. \end{aligned}$$

(29)

The divergent part of $\delta \kappa _1$ is found as

$$\begin{aligned} \delta \kappa _1|_{\textrm{div}} = \frac{1}{\sin (\omega )} \Big (\Gamma ^{\textrm{1PI}}_{h\chi _1 \chi _1} +\Gamma ^{\textrm{CT}}_{h\chi _1 \chi _1}|_{\delta \kappa _1} \Big )|_{\textrm{div}}. \end{aligned}$$

(30)

The relevant Feynman diagrams as triple vertex corrections are shown in Fig. 5. Following the same approach the divergent part of $\delta \kappa _{12}$ cab be found. The counter term of this triple vertex is

$$\begin{aligned} \Gamma ^{\textrm{CT}}_{h\chi _1 \chi _2}&= \frac{1}{2} \lambda _{h\chi _1 \chi _2} \delta Z_{hh} + \lambda _{h\chi _1 \chi _2} \delta Z_{\chi _2 \chi _2}\nonumber \\&+ \lambda _{s\chi _1 \chi _2} (\delta c_{hs} -\delta \omega )\nonumber \\&\quad +\frac{1}{2} \lambda _{h\chi _2 \chi _2} \frac{\Pi ^{\textrm{1PI}}_{\chi _1 \chi _2}(m_1)}{m_2- m_1}\nonumber \\&\quad +\frac{1}{2} \lambda _{h\chi _1 \chi _1} \frac{\Pi ^{\textrm{1PI}}_{\chi _1 \chi _2}(m_2)}{m_1- m_2} + \frac{\partial \lambda _{h\chi _1 \chi _2}}{\partial \kappa _{12}} \delta \kappa _{12}, \end{aligned}$$

(31)

where, $\lambda _{s\chi _1 \chi _2} = -\cos (\omega ) \kappa _{12}$, and $\lambda _{h\chi _2 \chi _2} = 0$, since $\kappa _{2} = 0$ as discussed in Sect. 2. Finally, we can get the divergent part of $\delta \kappa _{12}$ by

$$\begin{aligned} \delta \kappa _{12}|_{\textrm{div}} = \frac{1}{\sin (\omega )} \Big (\Gamma ^{\textrm{1PI}}_{h\chi _1 \chi _2} +\Gamma ^{\textrm{CT}}_{h\chi _1 \chi _2}|_{\delta \kappa _{12}} \Big )|_{\textrm{div}}. \end{aligned}$$

(32)

Fig. 5

Triangle diagrams contributing to $\Gamma ^{\textrm{1PI}}_{h\chi _1 \chi _1}$ and $\Gamma ^{\textrm{1PI}}_{s\chi _1 \chi _1}$. S stands for the two scalars h and s, and $\chi _i = \chi _1, \chi _2$

7 DD cross section at one loop

In this section we present the amplitude for DM-quark scattering at one loop level or next to leading order (NLO). The structure of the one loop corrections to the DM scattering off the nucleons are shown as Feynman diagrams in Fig. 6. The diagrams entail one-loop contributions as triple vertex corrections, internal propagator corrections, and Box diagrams, respectively. The scattering amplitude can then be written as

$$\begin{aligned} {\mathcal {M}}^{\textrm{NLO}} = {\mathcal {M}}^{\textrm{LO}} + {\mathcal {M}}^{\textrm{VC}} + {\mathcal {M}}^{\textrm{PC}} + {\mathcal {M}}^{\textrm{Box}}, \end{aligned}$$

(33)

Fig. 6

One-loop Feynman diagrams including all types of corrections to the DM scattering off the quarks. The left diagram indicates vertex corrections, the diagram in the middle stands for propagator corrections, and the last diagrams shows box corrections. The scalar, $h_i$, indicates scalar s or h

where ${\mathcal {M}}^{\textrm{VC}}$, ${\mathcal {M}}^{\textrm{PC}}$ and ${\mathcal {M}}^{\textrm{Box}}$ stand for vertex correction of $\chi _1 \chi _1 h_i$, propagator correction and Box correction, respectively. We begin with the vertex correction. There are two types of corrections for the vertex $\chi _1 \chi _1 h_i$, as already shown in Fig. 5. Including these vertex corrections, it is possible to find an effective scattering amplitude. Let’s begin with the vertex correction where only one scalar runs in the loop. The corresponding scattering amplitude is

(34)

where $h_i = s, h$, and $\alpha _h = (-m_q/v_H) c_\omega$, and $\alpha _s = (m_q/v_H) s_\omega$. At zero momentum transfer we get the following relation for the effective scattering amplitude. Note that the amplitude is obtained in the minimal subtraction scheme,

$$\begin{aligned} {\mathcal {M}}^{\textrm{VC}}_{(a)}&= \frac{m_q \kappa _{1}^3}{16\pi ^2 v_H} \Bigg [ \frac{4}{\bar{\epsilon }} + \frac{c_\omega s_\omega ^3}{m_h^2} F(m_1,m_h) +\frac{s_\omega c_\omega ^3}{m_h^2} F(m_1,m_s)\nonumber \\&\quad -\frac{s_\omega c_\omega ^3}{m_s^2} F(m_1,m_s) -\frac{c_\omega s_\omega ^3}{m_s^2} F(m_1,m_h) \Bigg ] \nonumber \\&\quad \times \bar{q} q~\bar{\chi }_1 \chi _1 + \frac{m_q \kappa _1 \kappa _{12}^2}{16\pi ^2 v_H}\nonumber \\&\quad \times \Bigg [ \frac{4}{\bar{\epsilon }} +\frac{c_\omega s_\omega ^3}{m_h^2} F(m_1,m_2,m_h) +\frac{s_\omega c_\omega ^3}{m_h^2} F(m_1,m_2,m_s) \nonumber \\&\quad - \frac{s_\omega c_\omega ^3}{m_s^2} F(m_1,m_2,m_s) - \frac{c_\omega s_\omega ^3}{m_s^2} F(m_1,m_2,m_h) \Bigg ] \bar{q} q~\bar{\chi }_1 \chi _1, \end{aligned}$$

(35)

where in the above expression, $F(m_1,m_i) = F(m_1,m_1,m_i)$, and $1/\bar{\epsilon } =1/\epsilon -\gamma _E + \log (4\pi )$, $\gamma _E$ being the Euler–Mascheroni constant. These functions are defined in Appendix B.

The second diagram with vertex corrections in the scattering process involves two scalars ruining in the loop. The resulting scattering amplitude is found as

(36)

where the indices i, j, k stand for the scalars h and s. In the formula above, $\alpha _k$ takes the same definition as before. The integration will be performed at the limit of zero momentum transfer. The effective amplitude is obtained by taking into account all the possible triple scalar couplings in the triangle loop. The final result is finite and follows as

$$\begin{aligned} {\mathcal {M}}^{\textrm{VC}}_{(b)}&= \frac{m_q m_1 \kappa _1^2}{16\pi ^2 v_H} \Bigg [ \frac{c_\omega s_\omega ^2}{m_h^2} c_{hhh} G(m_h,m_1) + \frac{s_\omega c_\omega ^2}{m_h^2} c_{shh} G(m_h,m_s,m_1)\nonumber \\&\quad + \frac{c_\omega ^3}{m_h^2} c_{hss} G(m_s,m_1) -\frac{s_\omega ^3}{m_s^2} c_{shh} G(m_h,m_1)\nonumber \\&\quad -\frac{c_\omega s_\omega ^2}{m_s^2} c_{hss} G(m_h,m_s,m_1) - \frac{s_\omega c_\omega ^2}{m_s^2} c_{sss} G(m_s,m_1) \Bigg ]\nonumber \\&\quad \times \bar{q} q~\bar{\chi }_1 \chi _1 + \kappa _{12}^2 (m_1 \rightarrow m_2), \end{aligned}$$

(37)

where $G(m_i,m_1) = G(m_i,m_i,m_1)$, and G functions are given in Appendix B. As well, the scalar couplings, $c_{ijk}$, are given in Appendix B.

Another type of corrections to the scattering amplitude are due to propagator corrections as shown in Fig. 6 (the diagram in the middle). These corrections come in as self-energy correction to the scalar propagators s and h. At zero momentum transfer the amplitude reads

$$\begin{aligned} {\mathcal {M}}^{\textrm{PC}} = \sum _{i,j=h,s} f_i g_j \frac{\Pi ^{r}_{ij}(p^2=0)}{m^2_{h_i} m^2_{h_j}} \frac{m_q \kappa _1}{v_H} \bar{q} q~\bar{\chi }_1 \chi _1, \end{aligned}$$

(38)

where $f_s = -\cos \omega$, $f_h = -\sin \omega$, and $g_s = \sin \omega$, $g_h = \cos \omega$. The renormalized two-point functions are defined in Eq. (19), $\Pi ^{r}_{ij} = \Pi ^{r}_{hh},\Pi ^{r}_{ss},\Pi ^{r}_{sh}$.

Fig. 7

Shown are the ratio of DD cross section at one-loop to DD cross section at tree level as a function of the coupling $\kappa _1$. In all plots, the mixing angle is such that $\sin \omega = 0.1$. Two values are chosen for the mass difference between the fermions, $\Delta = 1, 100$ GeV. The coupling $\kappa _{12} = 1,2$. The constraint from the observed relic density is not imposed

Fig. 8

The same as in Fig. 7, with the mixing angle such that $\sin \omega = 0.05$

The last contributions to the amplitude are those from box diagrams, see the right diagram in Fig. 6. Including both t-channel and u-channel, the amplitude at zero momentum transfer is written

(39)

where $m_{h_j} = m_h, m_s$, and $m_{\chi _i} = m_{\chi _1}, m_{\chi _2}$. The parameter, $c_{ijk}$, is the multiplication of couplings coming from vertices involving $\chi _i$ and $h_i$, and the coupling $d_{jk}$ presents couplings which come from vertices with quarks. $c_{ijk}$ parameters are, $c_{\chi _1 hh} = \kappa ^2_1 \sin ^2 \omega$, $c_{\chi _1 ss} = \kappa ^2_1 \cos ^2 \omega$, $c_{\chi _1 hs} = \kappa ^2_1 \sin \omega \cos \omega$, $c_{\chi _2 hh} =\kappa ^2_{12} \sin ^2 \omega$, $c_{\chi _2 ss} = \kappa ^2_{12} \cos ^2 \omega$, $c_{\chi _2 hs} = \kappa ^2_{12} \sin \omega \cos \omega$, and $d_{jk}$ parameters are, $d_{hh} = \cos ^2 \omega$, $d_{ss} = \sin ^2 \omega$, $d_{sh} = \cos \omega \sin \omega$. To compute the effective scattering amplitude, we set the quark mass to zero in the denominator and when contracting the fermion lines in the numerator, will omit terms which generate momentum suppressed operators. Thus, what remains in the end is the spin-independent operator $\bar{q} q \chi _1 \chi _1$. Taking into account these approximations, the effective scattering amplitude reads

$$\begin{aligned} {\mathcal {M}}^{\textrm{Box}}&= \left( \frac{m_q}{v_H}\right) ^2 c_{ijk} d_{jk} \nonumber \\&\quad \times \Big [H_1(m_{\chi _1},m_{\chi _i},m_{h_j},m_{h_k}) - H_2(m_{\chi _1},m_{\chi _i},m_{h_j},m_{h_k}) \Big ]\nonumber \\&\quad \times m_q \bar{q} q~\bar{\chi }_1 \chi _1, \end{aligned}$$

(40)

where the functions, $H_{1,2}(m_{\chi _1},m_{\chi _i},m_{h_j},m_{h_k})$, is defined in Appendix B. We expect that the Box corrections be a subleading contribution to the cross section, because of the small extra factor, $m_q/v_H$, arising from the second scalar-quark vertex in the loop diagram. A consistency check of our calculation is the cancellation of the divergences in the scattering amplitude at one loop order. This is done by using the Mathematica tool Package-X [53], also cross checking our results obtained independently.

8 Results

Here, we present our numerical results for the DD cross section at one loop level. First, we look at the ratio $\sigma ^{\textrm{NLO}}/\sigma ^{\textrm{LO}}$ as a function of the coupling $\kappa _1$, while relaxing the bound from the observed relic density. The result for the mass splitting $\Delta =1, 100$ GeV, and the mixing angle $\sin \omega = 0.1$, are shown in Fig. 7. We also decrease the mixing angle as $\sin \omega = 0.05$ and present the results in Fig. 8. A general trend in all the figures is that the ratio is approaching unity with increasing the coupling $\kappa _1$ from 0.01 to 1, for the given values of the coupling $\kappa _{12}= 1,2$. This result is expected. The DD cross section at one loop depends on both $\kappa _1$ and $\kappa _{12}$, while it only depends on the coupling $\kappa _1$ at tree level. For instance, when $\kappa _1 \sim {\mathcal {O}}(10^{-2})$ and $\kappa _{12} \sim {\mathcal {O}}(1)$ then $\sigma ^{\textrm{NLO}}/\sigma ^{\textrm{LO}} \propto \kappa _{12}^2/\kappa _{1}^2$. Now by increasing $\kappa _1$, the cross section at tree level starts increasing, such that when $\kappa _{1} \sim {\mathcal {O}}(1)$, then we approach the limit $\sigma ^{\textrm{NLO}} \sim \sigma ^{\textrm{LO}}$.

Another observation is that by decreasing the mixing angle, the ratio increases slightly. The reason is that the cross section at tree level only depends on $\sin \omega$, while the cross section at one loop includes terms depending on $\cos \omega$ as well.

Next, we continue our computations to find the regions respecting the observed relic abundance, and bounds from direct detection experiments. First, we keep the same values for the free parameters as those in our computations at tree level; $\lambda _2 = 0.5$ and $\sin (\omega ) = 0.1$. The singlet scalar masses are fixed at two distinct values, $m_s =50, 150$ GeV. The range of the other free parameters in our scan are, $0.001< \kappa _1,\kappa _{12} < 1$ and $10~\text {GeV}< m_{\textrm{DM}} < 2$ TeV. We show the DD cross section at one loop in terms of the DM mass. The results with $\Delta = 1$ GeV and $m_s = 50$ GeV are presented in Fig. 9, with $\Delta = 1$ GeV and $m_s = 150$ in Fig. 10, with $\Delta = 100$ GeV and $m_s = 50$ in Fig. 11, and with $\Delta = 100$ GeV and $m_s = 150$ in Fig. 12. In all the figures, as it was anticipated, we notice an enhancement on the DD cross section in the regions with both small $\kappa _1$ and large $\kappa _{12}$. It is such that the regions below the neutrino floor shift to the regions which are respected by XENONnT bounds. In the case with $\Delta = 1$ GeV and $m_s = 50$, a small region around $m_{\textrm{DM}} \sim 60$ GeV still remains below the neutrino floor. Another observation is that the regions with DD cross section above the neutrino floor get smaller loop corrections. The reason is that in these regions the ratio, $\sigma ^{\textrm{NLO}}/\sigma ^{\textrm{LO}}$, decreases since $\kappa _1$ grows eventually and one loop and tree level cross sections are almost comparable in size.

Moreover, we scan regions in the parameter space where the mixing angle is quite small, for instance, $\sin \omega = 0.001$. In this case, we pick out the single scalar mass as $m_s= 50$ GeV, and the mass splitting parameter as $\Delta = 1$ GeV. The results presented in Fig. 13 for this quite smaller mixing angle, show that the entire viable parameter space shifts downward and resides below the XENON1T bound. When $\kappa _{12} \sim 0$, it is evident that the viable points lie slightly above XENONnT bounds, while there are regions below the neutrino floor at tree level if one chooses non zero value for $\kappa _{12}$. Again, including the one loop corrections to the DD cross section push a large portion of the viable region above the neutrino floor.

We also consider a case where the singlet scalar mass is quite large, $m_s = 500$ GeV, and $\sin \omega = 0.01$. In this case we take a wider range for the couplings as, $0< \kappa _1, \kappa _{12} < 2$. As shown in Fig. 14, in this case the viable parameter space is a resonance region around $m_{\textrm{DM}} \sim 250$ GeV and a region with $m_{\textrm{DM}} \gtrsim 500$ GeV. Now in the plots with the one loop corrections added, we see that viable regions below the neutrino floor go up and reside well above the neutrino floor.

Fig. 9

DD cross section at one loop is shown as a function of DM mass for $m_s = 50$ GeV and $\Delta =1$ GeV. All the points respect the observed relic density. Upper limits from XENON1t and projected XENONnT are placed. As such, the neutrino floor is shown

Fig. 10

The same as in Fig. 9, with $m_s = 150$ GeV

Fig. 11

DD cross section at one loop is shown as a function of DM mass for $m_s = 50$ GeV and $\Delta =100$ GeV. All the points respect the observed relic density. Upper limits from XENON1t and projected XENONnT are placed. As such, the neutrino floor is shown

Fig. 12

The same as in Fig. 11, with $m_s = 150$ GeV

Fig. 13

The same as in Fig. 9 with the mixing angle as $\sin \omega = 0.001$

Fig. 14

DD cross section at one loop is shown as a function of DM mass for $m_s = 500$ GeV and $\Delta =1$ GeV. Here the mixing angle is $\sin \omega = 0.01$. All the points respect the observed relic density. Upper limits from XENON1t and projected XENONnT are placed. As such, the neutrino floor is shown

9 Conclusion

In this work we have considered a DM model with two fermionic WIMPs, where the light one is the DM candidate. The interactions between fermions and the SM particles are possible through a scalar-Higgs portal. This model is motivated given that a large portion of the parameter space in the simplest scenario with only one fermion is excluded by the current DD experiments. Adding the second fermion to the minimal model, opens up larger viable parameter space respecting bounds from the observed relic density and DD experiments.

The main goal in this work has been to compute the one loop corrections to the DM-nucleon scattering cross section. It is found that by including these quantum corrections the allowed parameter space at tree level will change. More significantly, it happens for the regions below the limit of the neutrino floor on the DD cross section, where the coupling $\kappa _1$ is relatively smaller. This feature comes out as result of a characteristic in this model we explain here. The only coupling which determines the magnitude of the DD cross section at tree level is $\kappa _1$. The other coupling, $\kappa _{12}$, saturates the annihilation cross section when $\kappa _1$ is much smaller. Now, at one loop, the DD cross section incorporates some extra terms with pure $\kappa _{12}$ coupling. Thus, It becomes feasible to get a very large loop corrections in the regions with very small $\kappa _1$ and at the same time with large $\kappa _{12}$.

In conclusion, when studying the viable parameter space, there are situations that the regions with quite small direction detection cross section lying below the neutrino floor might be sensitive to one loop corrections, making the quantum correction indispensable in these cases.

Appendices

Appendix A

In this section we present the dark matter annihilation cross section formulas. The co-annihilation processes are included in our analysis but their cross sections are not given here. The s-channel annihilation cross section with the SM fermions, Z-boson and W-boson in the final state are

$$\begin{aligned}&\sigma v_{rel} (\bar{\chi }_1 \chi _1 \rightarrow \bar{f} f) = \frac{N_c m^2_f \kappa ^2_1 \sin ^2 2\omega }{8\pi s v^2_H}\nonumber \\&\quad \times \left[ (p_1.p_2)^2-2(p_1.p_2) m^2_f +2m^2_f m^2_1 -m^4_1\right] \nonumber \\&\quad \times \Bigg |\frac{1}{s-m^2_s+im_s \Gamma _s} -\frac{1}{s-m^2_h+im_h \Gamma _h}\Bigg |^2, \end{aligned}$$

(41)

$$\begin{aligned}&\sigma v_{rel} (\bar{\chi }_1 \chi _1 \rightarrow ZZ) = \frac{\kappa ^2_1 \sin ^2 2\omega }{16\pi s v^2_H}\nonumber \\&\quad \times \Big [ (p_1.p_2)^3-2(p_1.p_2)^2 m^2_Z +(p_1.p_2)^2 m^2_1 + 2(p_1.p_2) \nonumber \\&\quad m^4_Z-(p_1.p_2)m^4_1 -3m^4_Z m^2_1 + 2m^2_Z m^4_1 -m^6_1\Big ] \nonumber \\&\quad \times \Bigg |\frac{1}{s-m^2_s+im_s \Gamma _s} -\frac{1}{s-m^2_h+im_h \Gamma _h}\Bigg |^2, \end{aligned}$$

(42)

$$\begin{aligned}&\sigma v_{rel} (\bar{\chi }_1 \chi _1 \rightarrow W^+ W^-)= \frac{\kappa ^2_1 \sin ^2 2\omega }{8\pi s v^2_H}\nonumber \\&\quad \times \Big [ (p_1.p_2)^3-2(p_1.p_2)^2 m^2_W +(p_1.p_2)^2 m^2_1 + 2(p_1.p_2) \nonumber \\&\quad m^4_W-(p_1.p_2)m^4_1 -3m^4_W m^2_1 + 2m^2_W m^4_1 -m^6_1\Big ] \nonumber \\&\quad \times \Bigg |\frac{1}{s-m^2_s+im_s \Gamma _s} -\frac{1}{s-m^2_h+im_h \Gamma _h}\Bigg |^2. \end{aligned}$$

(43)

The annihilation cross section with two singlet scalars in the final state is given by

$$\begin{aligned} \sigma v_{rel} (\bar{\chi }_1 \chi _1 \rightarrow s s)&= \frac{\sqrt{1-4m^2_h/s}}{32\pi ^2s} \int d\Omega \Bigg [\frac{1}{8} b^2_1 \frac{\kappa ^2_1 \sin ^2 \omega [p_1.p_2-m^2_1]}{(s-m^2_h)^2}+ \frac{3}{4} b b_1 \frac{\kappa ^2_1 \sin ^2 \omega \cos \omega [p_1.p_2-m^2_1]}{(s-m^2_s)(s-m^2_h)} \nonumber \\&\quad -3 b \frac{\kappa _1 \kappa ^2_{12} \sin \omega \cos ^3 \omega [2(p_1.p_3)m_1-(p_1.p_2)m_2 -2(p_1.p_2) m_1 +m_2m^2_1]}{(s-m^2_s)(u-m^2_2)} \nonumber \\&\quad + \frac{9}{8} b^2 \frac{\kappa ^2_1 \cos ^2\omega \sin ^2\omega [p_1.p_2-m^2_1]}{(s-m^2_s)^2}\nonumber \\&\quad + b_1 \frac{\kappa _1 \kappa ^2_{12} \sin \omega \cos ^2 \omega [2(p_1.p_3)m_1 +(p_1.p_2)m_2 -m_2 m^2_1 -2 m^3_1]}{(s-m^2_h)(t-m^2_2)} \nonumber \\&\quad + b_1 \frac{\kappa ^3_1 m_1 \sin \omega \cos ^2 \omega [2(p_1.p_3) +(p_1.p_2) -3 m^2_1]}{(s-m^2_h)(t-m^2_1)}\nonumber \\&\quad + 3 b \frac{\kappa ^3_1 m_1 \sin \omega \cos ^3 \omega [2(p_1.p_3) +(p_1.p_2) -3 m^2_1]}{(s-m^2_s)(t-m^2_1)} - \kappa ^4_1 \cos ^4 \omega \nonumber \\&\quad \times \frac{[2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2) -10(p_1.p_3)m^2_1 + (p_1.p_2)m^2_s + m^2_s m^2_1 +8m^4_1]}{(t-m^2_1)^2}+ \kappa ^4_1 \cos ^4 \omega \nonumber \\&\quad \times \frac{[2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2) -2(p_1.p_3)m^2_1 + (p_1.p_2)m^2_s +4(p_1.p_2)m^2_1 + m^2_s m^2_1 -4m^4_1]}{(t-m^2_1) (u-m^2_1)} \nonumber \\&\quad -2 \frac{\kappa ^2_1 \kappa ^2_{12} \cos ^4 \omega }{(t-m^2_1) (t-m^2_2)} [2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2) -2(p_1.p_3)m_1 m_2 \nonumber \\&\quad -8(p_1.p_3)m^2_1 + (p_1.p_2)m^2_s -(p_1.p_2)m_1 m_2 +(p_1.p_2)m^2_1 \nonumber \\&\quad + m^2_s m^2_1 +3m_2 m^3_1 + 5 m^4_1] +2 \frac{\kappa ^2_1 \kappa ^2_{12} \cos ^4 \omega }{(t-m^2_1) (u-m^2_2)} \nonumber \\&\quad \times [2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2) +2(p_1.p_3)m_1 m_2 \nonumber \\&\quad -4(p_1.p_3)m^2_1 + (p_1.p_2)m^2_s +(p_1.p_2)m_1 m_2 +3 (p_1.p_2)m^2_1 \nonumber \\&\quad + m^2_s m^2_1 -3 m_2 m^3_1 - m^4_1] - \frac{\kappa ^4_{12} \cos ^4 \omega }{(t-m^2_2)^2}\nonumber \\&\quad \times [2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2)-4(p_1.p_3)m_1 m_2 -6(p_1.p_3)m^2_1 \nonumber \\&\quad + (p_1.p_2)m^2_s -(p_1.p_2)m^2_2 + (p_1.p_2)m^2_1 + m^2_s m^2_1 + m^2_1 m^2_2 +4 m_2 m^3_1 +3 m^4_1]\nonumber \\&\quad + \frac{\kappa ^4_{12} \cos ^4 \omega }{(t-m^2_2)(u-m^2_2)} \times [2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2)-2(p_1.p_3)m^2_1 \nonumber \\&\quad + (p_1.p_2) m^2_s +(p_1.p_2)m^2_2 +2 (p_1.p_2)m_1 m_2 +(p_1.p_2)m^2_1 + m^2_s m^2_1 - m^2_1 m^2_2 -2 m_2 m^3_1 - m^4_1]\Bigg ], \end{aligned}$$

(44)

where

$$\begin{aligned} b= & {} \sin \omega \cos \omega \lambda _1 - 2 \cos ^2 \omega \lambda _2 v_H - \sin ^2 \omega \lambda _H v_H , \nonumber \\ b_1= & {} 3 \sin ^3 \omega \lambda _1 - 2 \sin \omega \lambda _1 -6 \cos \omega \sin ^2 \omega \lambda _2 v_H \nonumber \\{} & {} + 2 \cos \omega \lambda _2 v_H + 3 \cos \omega \sin ^2 \omega \lambda _H v_H . \end{aligned}$$

(45)

As such, the annihilation cross section with two Higgs particles in the final state is

$$\begin{aligned} \sigma v_{rel} (\bar{\chi }_1 \chi _1 \rightarrow h h)&= \frac{\sqrt{1-4m^2_h/s}}{32\pi ^2s} \int d\Omega \Bigg [\frac{1}{8} b^2_2 \frac{\kappa ^2_1 \cos ^2 \omega [p_1.p_2-m^2_1]}{(s-m^2_s)^2}-\frac{3}{4}b_3 b_2 \frac{\kappa ^2_1 \cos ^2 \omega \sin \omega [p_1.p_2-m^2_1]}{(s-m^2_s)(s-m^2_h)} \nonumber \\&\quad + b_2 m_1 \frac{\kappa ^3_1 \cos \omega \sin ^2 \omega [2p_1.p_3-3p_1.p_2 +m^2_1]}{(s-m^2_s)(u-m^2_1)} \nonumber \\&\quad + b_2 \frac{\kappa _1 \kappa ^2_{12} \cos \omega \sin ^2 \omega [2(p_1.p_3)m_1-(p_1.p_2)m_2 -2(p_1.p_2)m_1 +m_2m^2_1]}{(s-m^2_s)(u-m^2_2)}\nonumber \\&\quad + \frac{9}{8} b^2_3 \frac{\kappa ^2_1 \cos ^2\omega \sin ^2\omega [p_1.p_2-m^2_1]}{(s-m^2_h)^2}\nonumber \\&\quad -3 b_3 m_1 \frac{\kappa ^3_1 \cos \omega \sin ^3 \omega [2p_1.p_3-3p_1.p_2 +m^2_1]}{(s-m^2_h)(u-m^2_1)} \nonumber \\&\quad -3 b_3 \frac{\kappa _1 \kappa ^2_{12} \cos \omega \sin ^3 \omega [2(p_1.p_3)m_1-(p_1.p_2)m_2 -2(p_1.p_2)m_1 +m_2m^2_1]}{(s-m^2_h)(u-m^2_2)} - \kappa ^4_1 \sin ^4 \omega \nonumber \\&\quad \times \frac{[2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2) -10(p_1.p_3)m^2_1 + (p_1.p_2)m^2_h + m^2_h m^2_1 +8m^4_1]}{(t-m^2_1)^2} + \kappa ^4_1 \sin ^4 \omega \nonumber \\&\quad \times \frac{[2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2) -2(p_1.p_3)m^2_1 + (p_1.p_2)m^2_h +4(p_1.p_2)m^2_1 + m^2_h m^2_1 -4m^4_1]}{(t-m^2_1) (u-m^2_1)} \nonumber \\&\quad -2 \frac{\kappa ^2_1 \kappa ^2_{12} \sin ^4 \omega }{(t-m^2_1) (t-m^2_2)} [2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2) -2(p_1.p_3)m_1 m_2 \nonumber \\&\quad -8(p_1.p_3)m^2_1 + (p_1.p_2)m^2_h -(p_1.p_2)m_1 m_2 \nonumber \\&\quad +(p_1.p_2)m^2_1 + m^2_h m^2_1 +3m_2 m^3_1 + 5 m^4_1] \nonumber \\&\quad +2 \frac{\kappa ^2_1 \kappa ^2_{12} \sin ^4 \omega }{(t-m^2_1) (u-m^2_2)} [2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2) +2(p_1.p_3)m_1 m_2 \nonumber \\&\quad -4(p_1.p_3)m^2_1 + (p_1.p_2)m^2_h +(p_1.p_2)m_1 m_2 +3 (p_1.p_2)m^2_1 \nonumber \\&\quad + m^2_h m^2_1 -3 m_2 m^3_1 - m^4_1] - \frac{\kappa ^4_{12} \sin ^4 \omega }{(t-m^2_2)^2} \nonumber \\&\quad \times [2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2)-4(p_1.p_3)m_1 m_2 \nonumber \\&\quad -6(p_1.p_3)m^2_1 + (p_1.p_2)m^2_h -(p_1.p_2)m^2_2 + (p_1.p_2)m^2_1 + m^2_h m^2_1 \nonumber \\&\quad + m^2_1 m^2_2 +4 m_2 m^3_1 +3 m^4_1] + \frac{\kappa ^4_{12} \sin ^4 \omega }{(t-m^2_2)(u-m^2_2)} \nonumber \\&\quad \times [2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2)-2(p_1.p_3)m^2_1 \nonumber \\&\quad + (p_1.p_2)m^2_h +(p_1.p_2)m^2_2 +2 (p_1.p_2)m_1 m_2 +(p_1.p_2)m^2_1 \nonumber \\&\quad + m^2_h m^2_1 - m^2_1 m^2_2 -2 m_2 m^3_1 - m^4_1]\Bigg ], \end{aligned}$$

(46)

where

$$\begin{aligned} b_2= & {} 3 \lambda _1 \cos \omega \sin ^2 \omega - \lambda _1 \cos \omega + 6 \lambda _2 v_H \sin ^3 \omega \nonumber \\{} & {} -4 \lambda _2 v_H \sin \omega + 3 \lambda _H v_H \cos ^2 \omega \sin \omega , \nonumber \\ b_3= & {} \lambda _1 \cos \omega \sin \omega + 2 \lambda _2 v_H \sin ^2 \omega + \lambda _H v_H \cos ^2 \omega . \end{aligned}$$

(47)

And finally, when a singlet scalar and a Higgs particle are in the final state, the annihilation cross section reads

$$\begin{aligned}&\sigma v_{rel} (\bar{\chi }_1 \chi _1 \rightarrow h s)\nonumber \\ {}&= \frac{\sqrt{1-4m^2_h/s}}{32\pi ^2s} \int d\Omega \Bigg [\frac{1}{4} b^2_1 \frac{\kappa ^2_1 \cos ^2 \omega [p_1.p_2-m^2_1]}{(s-m^2_s)^2} + \frac{1}{4} b^2_2 \frac{\kappa ^2_1 \sin ^2\omega [p_1.p_2-m^2_1]}{(s-m^2_h)^2} \nonumber \\&\quad -\frac{1}{2}b_1 b_2 \frac{\kappa ^2_1 \cos \omega \sin \omega [p_1.p_2-m^2_1]}{(s-m^2_s)(s-m^2_h)}+ \frac{1}{2} b_1 m_1 \frac{\kappa ^3_1 \cos ^2 \omega \sin \omega [4 p_1.p_3 + 2 p_1.p_2 + m^2_h -6m^2_1 -m^2_s]}{(s-m^2_s)(t-m^2_1)} \nonumber \\&\quad - \frac{1}{2} b_2 m_1 \frac{\kappa ^3_1 \cos \omega \sin ^2 \omega [4 p_1.p_3 + 2 p_1.p_2 + m^2_h -6m^2_1 -m^2_s]}{(s-m^2_h)(t-m^2_1)}- \frac{1}{2} b_1 m_1 \frac{\kappa ^3_1 \cos ^2 \omega \sin \omega [4 p_1.p_3 - 6 p_1.p_2 + m^2_h +2 m^2_1 - m^2_s]}{(s-m^2_s)(u-m^2_1)} \nonumber \\&\quad + \frac{1}{2} b_2 m_1 \frac{\kappa ^3_1 \cos \omega \sin ^2 \omega [4 p_1.p_3 - 6 p_1.p_2 + m^2_h +2 m^2_1 - m^2_s]}{(s-m^2_h)(u-m^2_1)} \nonumber \\&\quad + \frac{1}{2} b_1 \frac{\kappa _1 \kappa ^2_{12} \cos ^2 \omega \sin \omega [4(p_1.p_3)m_1 +2(p_1.p_2) m_2 +m^2_h m_1 -2m^2_1 m_2 - 4 m^3_1 - m_1 m^2_s]}{(s-m^2_s)(t-m^2_2)} \nonumber \\&\quad - \frac{1}{2} b_2 \frac{\kappa _1 \kappa ^2_{12} \cos \omega \sin ^2 \omega [4(p_1.p_3)m_1 +2(p_1.p_2)m_2 +m^2_h m_1 -2m^2_1 m_2 - 4 m^3_1 -m_1 m^2_s]}{(s-m^2_h)(t-m^2_2)} \nonumber \\&\quad + \frac{1}{2} b_2 \frac{\kappa _1 \kappa ^2_{12} \cos \omega \sin ^2 \omega [4(p_1.p_3)m_1 -2(p_1.p_2)m_2 - 4 (p_1.p_2)m_1 + m^2_h m_1 +2m^2_1 m_2 -m_1 m^2_s]}{(s-m^2_h)(u-m^2_2)} \nonumber \\&\quad - \frac{\kappa ^4_{1} \sin ^2 \omega \cos ^2 \omega }{(t-m^2_1)^2} [2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2)-10(p_1.p_3)m^2_1 + (p_1.p_3)m^2_h -(p_1.p_3)m^2_s +(p_1.p_2)m^2_s\nonumber \\&\quad -2 m^2_h m^2_1 +8 m^4_1 + 3 m^2_1 m^2_s] - \frac{\kappa ^4_{1} \sin ^2 \omega \cos ^2 \omega }{(u-m^2_1)^2} [2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2) +6 (p_1.p_3)m^2_1 + (p_1.p_3)m^2_h \nonumber \\&\quad -(p_1.p_3)m^2_s +(p_1.p_2)m^2_s -8 (p_1.p_2)m^2_1 +2 m^2_h m^2_1 - m^2_1 m^2_s] + 2\frac{ \kappa ^4_{1} \sin ^2 \omega \cos ^2 \omega }{(t-m^2_1)(u-m^2_1)} [2(p_1.p_3)^2-2(p_1.p_3)(p_1.p_2) \nonumber \\&\quad -2 (p_1.p_3)m^2_1 + (p_1.p_3)m^2_h -(p_1.p_3)m^2_s +(p_1.p_2)m^2_s +4 (p_1.p_2)m^2_1 - 4 m^4_1 + m^2_1 m^2_s] \nonumber \\&\quad + \frac{ \kappa ^2_{1} \kappa ^2_{12} \sin ^2 \omega \cos ^2 \omega }{(t-m^2_2)(u-m^2_1)} [4(p_1.p_3)^2 -4(p_1.p_3)(p_1.p_2) -4 (p_1.p_3)m_1 m_2 + 2(p_1.p_3)m^2_h -2(p_1.p_3)m^2_s +2(p_1.p_2)m^2_s \nonumber \\&\quad +6 (p_1.p_2)m_1 m_2 +2 (p_1.p_2)m^2_1 - m^2_h m_1 m_2+ m^2_h m^2_1 - 2 m_2 m^3_1 + m_2 m_1 m^2_s - 6m^4_1 + m^2_1 m^2_s] - \frac{ \kappa ^2_{1} \kappa ^2_{12} \sin ^2 \omega \cos ^2 \omega }{(t-m^2_1)(t-m^2_2)} \nonumber \\&\quad [4(p_1.p_3)^2 -4(p_1.p_3)(p_1.p_2) -4 (p_1.p_3)m_1 m_2+ 2(p_1.p_3)m^2_h -16(p_1.p_3)m^2_1 -2(p_1.p_3)m^2_s -2 (p_1.p_2) m_1 m_2 \nonumber \\&\quad +2 (p_1.p_2)m^2_1 +2 (p_1.p_2)m^2_s - m^2_h m_1 m_2-3 m^2_h m^2_1 +6 m_2 m^3_1 + m_2 m_1 m^2_s +10 m^4_1 +5 m^2_1 m^2_s] \nonumber \\&\quad + \frac{ \kappa ^2_{1} \kappa ^2_{12} \sin ^2 \omega \cos ^2 \omega }{(t-m^2_1)(u-m^2_2)} [4(p_1.p_3)^2 -4(p_1.p_3)(p_1.p_2) +4 (p_1.p_3)m_1 m_2+ 2(p_1.p_3)m^2_h -8(p_1.p_3)m^2_1 -2(p_1.p_3)m^2_s \nonumber \\&\quad +2 (p_1.p_2) m_1 m_2 +6(p_1.p_2)m^2_1 +2 (p_1.p_2)m^2_s + m^2_h m_1 m_2 - m^2_h m^2_1 -6 m_2 m^3_1 - m_2 m_1 m^2_s -2 m^4_1 + 3 m^2_1 m^2_s] \nonumber \\&\quad - \frac{ \kappa ^2_{1} \kappa ^2_{12} \sin ^2 \omega \cos ^2 \omega }{(u-m^2_1)(u-m^2_2)} [4(p_1.p_3)^2 -4(p_1.p_3)(p_1.p_2) +4 (p_1.p_3)m_1 m_2 \nonumber \\&\quad + 2(p_1.p_3)m^2_h +8(p_1.p_3)m^2_1 -2(p_1.p_3)m^2_s-6 (p_1.p_2) m_1 m_2 -10(p_1.p_2) m^2_1 +2 (p_1.p_2)m^2_s \nonumber \\&\quad +m^2_h m_1 m_2 +3 m^2_h m^2_1 +2 m_2 m^3_1 - m_2 m_1 m^2_s -2 m^4_1 - m^2_1 m^2_s] - \frac{ \kappa ^4_{12} \sin ^2 \omega \cos ^2 \omega }{(t-m^2_2)^2} \nonumber \\&\quad \times [2(p_1.p_3)^2 -2(p_1.p_3)(p_1.p_2) - 4 (p_1.p_3)m_1 m_2 + (p_1.p_3)m^2_h -6 (p_1.p_3) m^2_1 - (p_1.p_3) m^2_s - (p_1.p_3)m^2_s \nonumber \\&\quad - (p_1.p_2)m^2_2 + (p_1.p_2)m^2_1 + (p_1.p_2)m^2_s - m^2_h m_1 m_2 - m^2_h m^2_1 + m^2_2 m^2_1 +4 m_2 m^3_1 + m_2 m_1 m^2_s +3 m^4_1 +2 m^2_1 m^2_s] \nonumber \\&\quad +2 \frac{ \kappa ^4_{12} \sin ^2 \omega \cos ^2 \omega }{(t-m^2_2)(u-m^2_2)} [2(p_1.p_3)^2 -2(p_1.p_3)(p_1.p_2) + (p_1.p_3)m^2_h-2 (p_1.p_3) m^2_1 - (p_1.p_3) m^2_s + (p_1.p_2)m^2_s \nonumber \\&\quad + (p_1.p_2) m^2_2 + (p_1.p_2) m^2_1 + 2(p_1.p_2) m_1 m_2 - m^2_2 m^2_1 -2 m_2 m^3_1 - m^4_1 + m^2_1 m^2_s] - \frac{ \kappa ^4_{12} \sin ^2 \omega \cos ^2 \omega }{(u-m^2_2)^2} \nonumber \\&\quad \times [2(p_1.p_3)^2 -2(p_1.p_3)(p_1.p_2) + 4 (p_1.p_3)m_1 m_2- 4 (p_1.p_2)m_1 m_2 + (p_1.p_3)m^2_h +2 (p_1.p_3) m^2_1 - (p_1.p_3) m^2_s \nonumber \\&\quad + (p_1.p_2)m^2_s - (p_1.p_2)m^2_2 -3 (p_1.p_2)m^2_1 + m^2_h m_1 m_2 + m^2_h m^2_1 + m^2_2 m^2_1 - m_2 m_1 m^2_s - m^4_1 ].\Bigg ] \end{aligned}$$

(48)

Appendix B

Here, we provide loop functions introduced in the previous sections. These results are obtained by using Package-X.

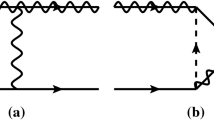
1.1 Loop functions for triangle diagrams

We have two types of triangle Feynman diagrams, each one brings in corresponding loop function. For type (a), we have the following functions

$$\begin{aligned} F(m_1,m_2,m_{h_i})&= \frac{\left( m_{h_i}^4-6 m_{h_i}^2 m_1^2 +2 m_1^4+4 m_1^3 m_2 \right) \log \left( \frac{m_{h_i}^2}{m_1^2}\right) }{4 m_1^3 (m_1-m_2)}\nonumber \\&\quad -\frac{\left( m_{h_i}^2-4 m_1^2\right) \sqrt{m_{h_i}^2 \left( m_{h_i}^2-4 m_1^2\right) } \log \left( \frac{\sqrt{m_{h_i}^2 \left( m_{h_i}^2-4 m_1^2\right) } +m_{h_i}^2}{2 m_{h_i} m_1}\right) }{2 m_1^3 (m_1-m_2)}\nonumber \\&\quad +\frac{\left( -m_{h_i}^4+2 m_{h_i}^2 m_1^2 +2 m_{h_i}^2 m_1 m_2+2 m_{h_i}^2 m_2^2- m_1^4-2 m_1^3 m_2-2 m_1 m_2^3-m_2^4\right) }{4 m_1^3 (m_1-m_2)} \nonumber \\&\quad \times \log \left( \frac{m_{h_i}^2}{m_2^2}\right) -\frac{\left( -m_{h_i}^2+m_1^2+2 m_1 m_2+ m_2^2 \right) \sqrt{\lambda \left( m_{h_i}^2, m_1^2, m_2^2\right) }}{2 m_1^3 (m_1-m_2)} \nonumber \\&\quad \times \log \left( \frac{\sqrt{\lambda \left( m_{h_i}^2, m_1^2, m_2^2 \right) } + m_{h_i}^2- m_1^2+ m_2^2}{2 m_{h_i} m_2}\right) + \frac{5 m_1+ m_2}{2m_1}, \end{aligned}$$

(49)

and in case $m_1 = m_2 = m$, we have

$$\begin{aligned}&F(m,m_{h_i}) \nonumber \\ {}&\quad = \frac{3 \sqrt{m_{h_i}^2 \left( m_{h_i}^2-4 m^2\right) } \log \left( \frac{\sqrt{m_{h_i}^2 \left( m_{h_i}^2-4 m^2\right) } +m_{h_i}^2}{2 m m_{h_i}}\right) }{m^2} \nonumber \\&\qquad -\frac{\left( 4 m^2-3 m_{h_i}^2\right) \log \left( \frac{m^2}{m_{h_i}^2}\right) }{2 m^2} + 4. \end{aligned}$$

(50)

For the triangle diagrams of type (b) we introduce the loop functions

$$\begin{aligned}&G(m_{h_i},m_{h_j},m_1)\nonumber \\&\quad = \frac{\left( 4 m_1^2-m_{h_i}^2\right) \sqrt{m_{h_i}^2 \left( m_{h_i}^2-4 m_1^2\right) } \log \left( \frac{\sqrt{m_{h_i}^2 \left( m_{h_i}^2 -4 m_1^2\right) }+m_{h_i}^2}{2 m_1 m_{h_i}}\right) }{2 m_1^4 \left( m_{h_i}^2-m_{h_j}^2\right) } \nonumber \\&\quad \times \frac{\left( 6 m_1^2-m_{h_i}^2-m_{h_j}^2\right) \log \left( \frac{m_1^2}{m_{h_j}^2}\right) }{4 m_1^4}\nonumber \\&\quad -\frac{m_{h_i}^2 \left( 6 m_1^2-m_{h_i}^2\right) \log \left( \frac{m_{h_i}^2}{m_{h_j}^2}\right) }{4 m_1^4 \left( m_{h_i}^2-m_{h_j}^2\right) } \nonumber \\&\quad +\frac{\left( 4 m_1^2-m_{h_j}^2\right) \sqrt{m_{h_j}^2 \left( m_{h_j}^2-4 m_1^2\right) } \log \left( \frac{\sqrt{m_{h_j}^2 \left( m_{h_j}^2 -4 m_1^2\right) }+m_{h_j}^2}{2 m_1 m_{h_j}}\right) }{2 m_1^4 \left( m_{h_j}^2-m_{h_i}^2\right) }\nonumber \\&\quad -\frac{1}{2 m_1^2}, \end{aligned}$$

(51)

and when $m_{h_i} =m_{h_j} = m$, we define $G(m,m,m_1) = G(m,m_1)$ and obtain

$$\begin{aligned}&G(m,m_1)\nonumber \\ {}&\quad = \frac{\left( m_1^2-m^2\right) \sqrt{m^2 \left( m^2-4 m_1^2\right) } \log \left( \frac{\sqrt{m^2 \left( m^2-4 m_1^2\right) }+m^2}{2 m_1 m}\right) }{m_1^4 \left( 4 m_1^2-m^2\right) }\nonumber \\&\quad \times \frac{1}{m_1^2} +\frac{\left( m_1^2+m^2\right) \log \left( \frac{m_1^2}{m^2}\right) }{2 m_1^4} \end{aligned}$$

(52)

1.2 Loop functions for box diagrams

When computing the scattering amplitude of box diagrams we encounter two loop functions, $H_1$ and $H_2$. Here we provide explicit expressions for these functions. The function $H_1$ is

$$\begin{aligned}&H_{1}(m_{\chi _1},m_{\chi _i},m_{h_j},m_{h_k}) \nonumber \\&\quad = \frac{\left( m_{\chi _1}^2+4 m_{\chi _1} m_{\chi _i} -5 m_{h_k}^2- m_{\chi _i}^2 \right) \sqrt{\lambda \left( m_{\chi _1}^2,m_{h_k}^2,m_{\chi _i}^2\right) } \log \left( \frac{\sqrt{\lambda \left( m_{\chi _1}^2,m_{h_k}^2, m_{\chi _i}^2\right) } -m_{\chi _1}^2+m_{h_k}^2+m_{\chi _i}^2}{2m_{h_k} m_{\chi _i}}\right) }{2 m_{\chi _1}^5 \left( m_{h_j}^2-m_{h_k}^2\right) } \nonumber \\&\qquad -\frac{ \left( m_{\chi _1}^2+4 m_{\chi _1} m_{\chi _i}-5 m_{h_j}^2 - m_{\chi _i}^2\right) \sqrt{\lambda \left( m_{\chi _1}^2,m_{h_j}^2, m_{\chi _i}^2\right) } \log \left( \frac{\sqrt{\lambda \left( m_{\chi _1}^2,m_{h_j}^2,m_{\chi _i}^2\right) } -m_{\chi _1}^2+m_{h_j}^2+m_{\chi _i}^2}{2 m_{h_j} m_{\chi _i}}\right) }{2 m_{\chi _1}^5 \left( m_{h_j}^2-m_{h_k}^2\right) }\nonumber \\&\qquad -\frac{\left( m_{\chi _1}^4+m_{\chi _1}^3 m_{\chi _i}+m_{\chi _1}^2 m_{\chi _i}^2+m_{\chi _1} m_{h_k}^2 m_{\chi _i}+m_{\chi _1} m_{\chi _i}^3 -m_{h_k}^4-2 m_{h_k}^2 m_{\chi _i}^2\right) C_0\left( 0,0,m_{\chi _1}^2,m_{\chi _i},0,m_{h_k}\right) }{m^3 \left( m_{h_j}^2-m_{h_k}^2\right) }\nonumber \\&\qquad +\frac{ \left( m_{\chi _1}^4+m_{\chi _1}^3 m_{\chi _i} +m_{\chi _1}^2 m_{\chi _i}^2+m_{\chi _1} m_{h_j}^2 m_{\chi _i} +m_{\chi _1} m_{\chi _i}^3-m_{h_j}^4-2 m_{h_j}^2 m_{\chi _i}^2\right) C_0 \left( 0,0,m_{\chi _1}^2,m_{\chi _i},0,m_{h_j}\right) }{m_{\chi _1}^3 \left( m_{h_j}^2-m_{h_k}^2\right) }\nonumber \\&\qquad +\frac{ \left( 3 m_{\chi _1}^4-2 m_{\chi _1}^2 m_{h_k}^2 +2 m_{\chi _1}^2 m_{\chi _i}^2-4 m_{\chi _1} m_{h_k}^2 m_{\chi _i} +4 m_{\chi _1} m_{\chi _i}^3+5 m_{h_k}^4-4 m_{h_k}^2 m_{\chi _i}^2 -m_{\chi _i}^4\right) \log \left( \frac{m_{h_k}^2}{m_{\chi _i}^2} \right) }{4 m_{\chi _1}^5 \left( m_{h_j}^2-m_{h_k}^2\right) }\nonumber \\&\qquad -\frac{\left( 3 m_{\chi _1}^4-2 m_{\chi _1}^2 m_{h_j}^2 +2 m_{\chi _1}^2 m_{\chi _i}^2-4 m_{\chi _1} m_{h_j}^2 m_{\chi _i} +4 m_{\chi _1} m_{\chi _i}^3+5 m_{h_j}^4-4 m_{h_j}^2 m_{\chi _i}^2 -m_{\chi _i}^4\right) \log \left( \frac{m_{h_j}^2}{m_{\chi _i}^2} \right) }{4 m^5 \left( m_{h_j}^2-m_{h_k}^2\right) }\nonumber \\&\qquad +\frac{5}{2 m_{\chi _1}^3}, \end{aligned}$$

(53)

where the Källén function is $\lambda (x,y,z) =x^2+y^2+z^2-2xy-2xz-2yz$. The scalar function, $C_0(0,0,x,y,0,z)$ is obtained as

$$\begin{aligned}&C_0(0,0,x,y,0,z) \nonumber \\&\quad = -\frac{\text {DiLog}\left( \frac{2 \left( x-y^2\right) }{-\sqrt{\lambda \left( x,y^2,z^2\right) } +x-y^2-z^2},x \left( x-y^2\right) \right) }{x}\nonumber \\&\qquad +\frac{\text {DiLog}\left( -\frac{2 y^2}{-\sqrt{\lambda \left( x,y^2,z^2\right) }+x-y^2-z^2},-x\right) }{x}\nonumber \\&\qquad +\frac{\text {DiLog} \left( -\frac{2 y^2}{\sqrt{\text {Kallen}\lambda \ \left( x,y^2,z^2\right) } +x-y^2-z^2},x\right) }{x} \nonumber \\&\qquad -\frac{\text {DiLog}\left( \frac{2 \left( x-y^2\right) }{\sqrt{\lambda \left( x,y^2,z^2\right) }+x-y^2-z^2},-x \left( x-y^2\right) \right) }{x}\nonumber \\&\qquad +\frac{\text {Li}_2 \left( \frac{y^2-x}{y^2}\right) }{x}-\frac{\pi ^2}{6 x}. \end{aligned}$$

(54)

And the function $H_2$ is obtained as

$$\begin{aligned}&H_{2}(m_{\chi _1},m_{\chi _i},m_{h_j},m_{h_k}) \nonumber \\&\quad = \frac{ \left( 9 m_{\chi _1}^2+4 m_{\chi _1} m_{\chi _i} +7 m_{h_k}^2-m_{\chi _i}^2\right) \sqrt{\lambda \left( m_{\chi _1}^2,m_{h_k}^2,m_{\chi _i}^2\right) } \log \left( \frac{\sqrt{\lambda \left( m_{\chi _1}^2, m_{h_k}^2,m_{\chi _i}^2\right) }-m_{\chi _1}^2+m_{h_k}^2 +m_{\chi _i}^2}{2 m_{h_k} m_{\chi _i}}\right) }{2 m_{\chi _1}^5 \left( m_{h_j}^2-m_{h_k}^2\right) }\nonumber \\&\qquad -\frac{ \left( 9 m_{\chi _1}^2+4 m_{\chi _1} m_{\chi _i}+7 m_{h_j}^2-m_{\chi _i}^2\right) \sqrt{\lambda \left( m_{\chi _1}^2,m_{h_j}^2, m_{\chi _i}^2\right) } \log \left( \frac{\sqrt{\lambda \left( m_{\chi _1}^2,m_{h_j}^2,m_{\chi _i}^2\right) } -m_{\chi _1}^2+m_{h_j}^2+m_{\chi _i}^2}{2 m_{h_j} m_{\chi _i}}\right) }{2 m_{\chi _1}^5 \left( m_{h_j}^2-m_{h_k}^2\right) } \nonumber \\&\qquad -\frac{ \left( 3 m_{\chi _1}^4+3 m_{\chi _1}^3 m_{\chi _i}+8 m_{\chi _1}^2 m_{h_k}^2-m^2 m_{\chi _i}^2 +3 m_{\chi _1} m_{h_k}^2 m_{\chi _i}-m_{\chi _1} m_{\chi _i}^3 +5 m_{h_k}^4-2 m_{h_k}^2 m_{\chi _i}^2\right) }{m_{\chi _1}^3 \left( m_{h_j}^2-m_{h_k}^2\right) } \nonumber \\&\qquad \times C_0 \left( 0,m_{\chi _1}^2,2 m_{\chi _1}^2,0, m_{h_k},m_{\chi _i}\right) \nonumber \\&\qquad +\frac{ \left( 3 m_{\chi _1}^4+3 m_{\chi _1}^3 m_{\chi _i}+8 m_{\chi _1}^2 m_{h_j}^2-m^2 m_{\chi _i}^2 +3 m_{\chi _1} m_{h_j}^2 m_{\chi _i}-m_{\chi _1} m_{\chi _i}^3+5 m_{h_j}^4-2 m_{h_j}^2 m_{\chi _i}^2\right) }{m_{\chi _1}^3 \left( m_{h_j}^2-m_{h_k}^2\right) }\nonumber \\&\qquad \times C_0 \left( 0,m_{\chi _1}^2,2 m^2,0,m_{h_j}, m_{\chi _i}\right) \nonumber \\&\qquad -\frac{ \left( 13 m_{\chi _1}^4+8 m_{\chi _1}^3 m_{\chi _i}+22 m_{\chi _1}^2 m_{h_k}^2-10 m_{\chi _1}^2 m_{\chi _i}^2+4 m_{\chi _1} m_{h_k}^2 m_{\chi _i}-4 m_{\chi _1} m_{\chi _i}^3+7 m_{h_k}^4-8 m_{h_k}^2 m_{\chi _i}^2+m_{\chi _i}^4\right) }{4 m_{\chi _1}^5 \left( m_{h_j}^2-m_{h_k}^2\right) } \nonumber \\&\qquad \times \log \left( \frac{m_{h_k}^2}{m_{\chi _i}^2}\right) \nonumber \\&\qquad +\frac{ \left( 13 m_{\chi _1}^4+8 m_{\chi _1}^3 m_{\chi _i}+22 m^2 m_{h_j}^2-10 m^2 m_{\chi _i}^2+4 m_{\chi _1} m_{h_j}^2 m_{\chi _i}-4 m_{\chi _1} m_{\chi _i}^3+7 m_{h_j}^4-8 m_{h_j}^2 m_{\chi _i}^2+m_{\chi _i}^4\right) }{4 m_{\chi _1}^5 \left( m_{h_j}^2-m_{h_k}^2\right) }\nonumber \\&\qquad \times \log \left( \frac{m_{h_j}^2}{m_{\chi _i}^2}\right) +\frac{3}{2 m^3}+\frac{5 \left( 2 m^2-m_{\chi _i}^2\right) \log \left( \frac{m_{\chi _i}^2}{m_{\chi _i}^2-2 m^2}\right) }{2 m^5} \end{aligned}$$

(55)

The scalar function, $C_0(0,x,2x,0,y,z)$ is obtained as

$$\begin{aligned}&C_0(0,x,2x,0,y,z) \nonumber \\&\quad = -\frac{\text {DiLog}\left( -\frac{2 x \left( x+2 y^2-z^2\right) }{x \sqrt{\lambda \left( x,y^2,z^2\right) }-x \left( x+3 y^2-z^2\right) },x \left( x+2 y^2-z^2\right) \right) }{x}\nonumber \\&\qquad +\frac{\text {DiLog}\left( -\frac{2 x \left( x+2 y^2-z^2\right) }{-x \sqrt{\lambda \left( x,y^2,z^2\right) }-x \left( x+3 y^2-z^2\right) }, -x \left( x+2 y^2-z^2\right) \right) }{x}\nonumber \\&\qquad -\frac{\text {DiLog}\left( -\frac{2 x \left( 2 y^2-z^2\right) }{x \sqrt{\lambda \left( x,y^2,z^2\right) }-x \left( x+3 y^2-z^2\right) },x \left( 2 y^2-z^2\right) \right) }{x}\nonumber \\&\qquad -\frac{\text {DiLog}\left( -\frac{2 x \left( 2 y^2-z^2\right) }{-x \sqrt{\lambda \left( x,y^2,z^2\right) }-x \left( x+3 y^2-z^2\right) },x \left( z^2-2 y^2\right) \right) }{x}\nonumber \\&\qquad +\frac{\text {Li}_2\left( \frac{2 y^2-z^2}{2 y^2}\right) }{x} +\frac{\text {Li}_2\left( \frac{2 y^2-z^2+2 x}{2 x-z^2}\right) }{x} +\frac{\text {Li}_2\left( \frac{2 y^2-z^2}{2 y^2-z^2+2 x}\right) }{x}\nonumber \\&\qquad -\frac{\text {Li}_2\left( \frac{2 y^2-z^2+x}{2 y^2-z^2+2 x}\right) }{x}+\frac{\log ^2\left( -\frac{2 y^2}{2 x-z^2}\right) }{2 x}. \end{aligned}$$

(56)

1.3 Scalar couplings

The triple scalar couplings defined in Sect. 7 are

$$\begin{aligned} c_{hhh}&= -3\cos (\omega ) \Bigg [ \cos (\omega ) \sin (\omega ) \lambda _1 \nonumber \\&\quad + 2 v_H \sin ^2(\omega ) \lambda _2 + 2 v_H \cos ^2(\omega ) \lambda _H \Bigg ]\nonumber \\ c_{hhs}&= 3 \cos (\omega ) \sin ^2(\omega ) \lambda _1 -\cos (\omega ) \lambda _1 +6 v_H \sin ^3(\omega ) \lambda _2\nonumber \\&\quad -4 v_H \sin (\omega ) \lambda _2 +6 v_H \cos ^2(\omega ) \sin (\omega ) \lambda _H \nonumber \\ c_{ssh}&= -3 \sin ^3(\omega ) \lambda _1 -2 \lambda _1 \sin (\omega ) -6 v_H \lambda _2 \cos (\omega ) \sin ^2(\omega )\nonumber \\&\quad +2 v_H \cos (\omega ) \lambda _2 +6 v_H \cos (\omega ) \sin ^2(\omega ) \lambda _H\nonumber \\ c_{sss}&= -3\sin (\omega ) \Bigg [ \cos (\omega ) \sin (\omega ) \lambda _1 \nonumber \\&\quad - 2 v_H \cos ^2(\omega ) -2 v_H \sin ^2(omega) \lambda _H \Bigg ] \end{aligned}$$

(57)