Possible molecular dibaryons with csssqq quarks and their baryon–antibaryon partners

Abstract

In this work, we systematically investigate the charmed–strange dibaryon systems with csssqq quarks and their baryon–antibaryon partners from the interactions $\varXi ^{(',*)}_{c}\varXi ^{(*)}$, $\varOmega ^{(*)}_c\varLambda$, $\varOmega ^{(*)}_c\varSigma ^{(*)}$, $\varLambda _c\varOmega$ and $\varSigma ^{(*)}_c\varOmega$ and their baryon–antibaryon partners from interactions $\varXi ^{(',*)}_{c}\bar{\varXi }^{(*)}$, $\varOmega ^{(*)}_c\bar{\varLambda }$, $\varOmega ^{(*)}_c\bar{\varSigma }^{(*)}$, $\varLambda _c\bar{\varOmega }$ and $\varSigma ^{(*)}_c\bar{\varOmega }$. The potential kernels are constructed with the help of effective Lagrangians under SU(3), heavy quark, and chiral symmetries to describe these interactions. To search for possible molecular states, the kernels are inserted into the quasipotential Bethe–Salpeter equation, which is solved to find poles from scattering amplitude. The results suggest that 36 and 24 bound states can be found in the baryon–baryon and baryon–antibaryon interactions, respectively. However, much large values of parameter $\alpha$ are required to produce the bound states from the baryon–antibaryon interactions, which questions the existence of these bound states. Possible coupled-channel effect are considered in the current work to estimate the couplings of the molecular states to the channels considered.

1 Introduction

As an important type of exotic hadrons, the dibaryons with baryon quantum number $B=2$ attract much attention from the hadron physics community. In fact, one type of the exotic hadrons proposed earliest in the literature is the dibaryons predicted by Dyson and Xuong in 1964 based on the SU(6) symmetry almost at the same time of the proposal of the quark model [1]. The WASA-at-COSY collaboration reported a new resonance $d^*(2380)$ with quantum number $I(J^P)=0(3^+)$, a mass of about 2370 MeV, and a width of about 70 MeV in the process $pp\rightarrow d\pi ^0\pi ^0$ at [2]. Soon after the observation of the $d^*(2380)$, it is related to the dibaryon predicted [3, 4] while there is still other interpretations, such as a triangle singularity in the last step of the reaction in a sequential single pion production process [5]. More experimental and theoretical works are still required to clarify its origin.

These early proposed dibaryons are exotic hadrons in the light flavor sector. In the past decades, many candidates of exotic states in charmed sector, such as hidden-charm tetraquarks and pentaquarks, have been observed in experiment, for example, the X(3872) and $Z_c(3900)$ [6,7,8,9,10], and a series of hidden-charm pentaquarks $P_c$ [11,12,13,14]. These states were observed near the thresholds of two charmed hadrons. Hence, it is natural to interpret them as the molecular states produced from interactions of a pair of charm and anticharm hadrons. Motivated by the observations of these states, theorists expect that there may exist dibaryon molecules composed of two heavy baryons. Due to large masses of the heavy baryons, the kinetic energy of a dibaryon system is reduced, which makes it easier to form a bound state. Possible hidden-charm and double-charm dibaryons were investigated in different approaches [15,16,17,18,19,20,21,22,23]. These results suggest that attraction may exist between a charmed baryon and an anticharmed or charmed baryon by light meson exchanges, which favors the existence of hidden-charm dibaryon molecular states and their double-charm partners.

In addition to the above hidden-charm and double-charm states, some charmed–strange states were also observed these years, and taken as the candidates of molecular states of a charmed meson and a strange meson in the literature. As early as 2003, the BaBar collaboration reported a narrow peak $D^{*}_{s0}(2317)$ near the DK threshold [24], and later confirmed at CLEO and BELLE [25, 26]. The CLEO collaboration also observed another narrow peak, the $D_{s1}(2460)$ near the $D^*K$ threshold [26]. These states can not be well put into the conventional quark model with a charmed and an antistrange quark. Since these charmed–strange states are very close to the threshold of a charmed meson and a strange meson, some authors interpreted them as the molecules of corresponding charmed and strange mesons [27,28,29,30,31,32,33,34]. Recently the LHCb collaboration reported the $X_0(2900)$ and $X_1(2900)$ near the $\bar{D}^{*}K^{*}$ threshold [35, 36]. Such states should be composed of four different quarks, and soon be explained as $\bar{D}^*K^*$ molecular state [37,38,39,40,41,42,43]. By adding an additional light quark to the above charmed–strange molecular states, the existence of charmed–strange pentaquark molecular states were also predicted in Refs. [44,45,46].

Following this way, if we continue to add light quark and convert all antiquarks to quarks, we will reach a charm-strange dibaryon systems. In Ref. [47], we systematically investigated the charmed–strange dibaryons with csqqqq quarks and their baryon–antibaryon partners from the interactions of a charmed baryon and a strange baryon $\varLambda _c\varLambda$, $\varLambda _c\varSigma ^{(*)}$, $\varSigma _c^{(*)}\varLambda$, and $\varSigma ^{(*)}_c\varSigma ^{(*)}$, and corresponding interactions of a charmed baryon and an antistrange baryon $\varLambda _c\bar{\varLambda }$, $\varLambda _c\bar{\varSigma }^{(*)}$, $\varSigma ^{(*)}_c\bar{\varLambda }$, and $\varSigma ^{(*)}_c\bar{\varSigma }^{(*)}$. The calculation suggests that attractions widely exist in charmed–strange dibaryon systems while few bound states are produced from the charmed–antistrange interactions. If one u/d quark in each constituent baryon is simultaneously replaced by a strange quark, we can reach charmed–strange dibaryon systems $\varXi ^{(',*)}_{c}\varXi ^{(*)}$, which are scarcely studied in the literature. In this work, we will study these systems together with the systems $\varOmega ^{(*)}_c\varLambda$, $\varOmega ^{(*)}_c\varSigma ^{(*)}$, $\varLambda _c\varOmega$ and $\varSigma ^{(*)}_c\varOmega$ with the same quark components, csssqq quarks, and their baryon–antibaryon partners $\varXi ^{(',*)}_{c}\bar{\varXi }^{(*)}$, $\varOmega ^{(*)}_c\bar{\varLambda }$, $\varOmega ^{(*)}_c\bar{\varSigma }^{(*)}$, $\varLambda _c\bar{\varOmega }$ and $\varSigma ^{(*)}_c\bar{\varOmega }$.

The work is organized as follows. After introduction, the potential kernels of systems considered are presented, which are obtained with the help of the effective Lagrangians with SU(3), heavy quark, and chiral symmetries. The quasipotential Bethe–Salpeter equation (qBSE) approach will also be introduced briefly. In Sect. 3, The bound states from all interactions will be searched with single-channel calculations. In Sect. 4, the bound states of the molecular states from full coupled-channel calculation will be presented. And the poles from two-channel calculations are also provided to estimate the strengths of the couplings between a molecular state and corresponding channels. In Sect. 5, discussion and summary are given.

2 Theoretical frame

In this work, we consider the possible molecular dibaryons from the interactions $\varXi ^{(',*)}_{c}\varXi ^{(*)}$, $\varOmega ^{(*)}_c\varLambda$, $\varOmega ^{(*)}_c\varSigma ^{(*)}$, $\varLambda _c\varOmega$ and $\varSigma ^{(*)}_c\varOmega$ and their baryon–antibaryon partners $\varXi ^{(',*)}_{c}\bar{\varXi }^{(*)}$, $\varOmega ^{(*)}_c\bar{\varLambda }$, $\varOmega ^{(*)}_c\bar{\varSigma }^{(*)}$, $\varLambda _c\bar{\varOmega }$ and $\varSigma ^{(*)}_c\bar{\varOmega }$. The coupling between different channels will also be included to make a coupled-channel calculation to obtain the scattering amplitude by solving the qBSE. To achieve this aim, the potential will be constructed by the light meson exchanges. The Lagrangians are required to obtain the vertices, and will be given below.

2.1 Relevant Lagrangians

For the couplings of strange baryons with light mesons, we consider the exchange of pseudoscalar mesons P ($\pi$, $\eta$, $\rho$), vector mesons V ($\omega$, $\phi$, K, $K^*$), and $\sigma$ mesons. For the former seven mesons, the vertices can be described by the effective Lagrangians with SU(3) and chiral symmetries [48, 49]. The explicit the effective Lagrangians reads,

$$\begin{aligned} \mathcal {L}_{BBP}= & {} -\frac{g_{BBP}}{m_P}\bar{B}\gamma ^{5}\gamma ^{\mu }\partial _{\mu }PB, \end{aligned}$$

(1)

$$\begin{aligned} \mathcal {L}_{BBV}= & {} -\bar{B}\left[ g_{BBV}\gamma ^{\mu }-\frac{f_{BBV}}{2m_{B}}\sigma ^{\mu \nu }\partial _{\nu }\right] V_{\mu }B, \end{aligned}$$

(2)

$$\begin{aligned} \mathcal {L}_{B^*B^*P}= & {} \frac{g_{B^*B^*P}}{m_P}\bar{B^*}_{\mu }\gamma ^{5} \gamma ^{\nu }B^{*\mu }\partial _{\nu }P, \end{aligned}$$

(3)

$$\begin{aligned} \mathcal {L}_{B^*B^*V}= & {} -\bar{B}^*_{\tau }\left[ g_{B^*B^*V}\gamma ^{\mu }-\frac{f_{B^*B^*V}}{2m_{B^*}}\sigma ^{\mu \nu }\partial _{\nu }\right] V_{\mu } B^{*\tau }, \end{aligned}$$

(4)

$$\begin{aligned} \mathcal {L}_{BB^*P}= & {} \frac{g_{BB^*P}}{m_{P}}\bar{B}^{*\mu } \partial _{\mu }PB\;+\; \text {h.c.}, \end{aligned}$$

(5)

$$\begin{aligned} \mathcal {L}_{BB^*V}= & {} -i \frac{g_{BB^*V}}{m_{V}}\bar{B}^{*\mu }\gamma ^5\gamma ^{\nu } V_{\mu \nu }B\;+\; \text {h.c.}, \end{aligned}$$

(6)

where $m_{p,V}$ is the mass of the pseudoscalar or vector meson. $B^{(*)}$ is the field of the strange baryon. $V_{\mu \nu }={\partial _{\mu }}{V}_{\nu }-{\partial _{\mu }}{V}_{\mu }$. The coupling constants can be determined by the SU(3) symmetry [48, 50,51,52] with the coupling constants for the nucleon and $\varDelta$. The SU(3) relations and the explicit values of coupling constants are calculated and listed in Table 1.

Table 1 The coupling constants in effective Lagrangians. Here, $g_{BBP}=g_{NN\pi }=0.989$, $g_{BBV}=g_{NN\rho }=3.25$, $g_{B^*B^*P}=\sqrt{60} g_{\varDelta \varDelta \pi }=13.78$, $g_{B^*B^*V}=\sqrt{60} g_{\varDelta \varDelta \rho }=59.41$, $g_{BB^*P}=\sqrt{20} g_{N\varDelta \pi }=9.48$, $g_{BB^*V}=\sqrt{20} g_{N\varDelta \rho }=71.69$, $\alpha _{P}=0.4$, $\alpha _{V}=1.15$, $f_{NN\rho }= g_{NN\rho }\kappa _{\rho }$, $f_{\varDelta \varDelta \rho }= g_{\varDelta \varDelta \rho }\kappa _{\rho }$ with $\kappa _{\rho }=6.1$, $f_{NN\omega }=0$ [48, 51, 52]

For the couplings of strange baryons with the scalar meson $\sigma$, the Lagrangians read [53]

$$\begin{aligned} \mathcal {L}_{BB\sigma }= & {} -g_{BB\sigma }\bar{B}\sigma B, \end{aligned}$$

(7)

$$\begin{aligned} \mathcal {L}_{B^*B^*\sigma }= & {} g_{B^*B^*\sigma }\bar{B}^{*\mu }\sigma B^*_{\mu }. \end{aligned}$$

(8)

The different choices of the mass of $\sigma$ meson from 400 to 550 MeV affects the result a little, which can be smeared by a small variation of the cutoff in the calculation. In this work, we adopt a $\sigma$ mass of 500 MeV. In general, we choose the coupling constants $g_{BB\sigma }$ and $g_{B^*B^*\sigma }$ as the same value as $g_{BB\sigma }=g_{B^*B^*\sigma }=6.59$ [53].

For the couplings of charmed baryons with light mesons, the Lagrangians can be constructed under the heavy quark and chiral symmetries [54,55,56,57]. The explicit forms of the Lagrangians can be written as,

$$\begin{aligned} \mathcal{L}_{BB\mathbb {P}}= & {} -\frac{3g_1}{4f_\pi \sqrt{m_{\bar{B}}m_{B}}}~\epsilon ^{\mu \nu \lambda \kappa }\partial _\nu \mathbb {P}~ \sum _{i=0,1}\bar{B}_{i\mu } \overleftrightarrow {\partial }_\kappa B_{j\lambda },\nonumber \\ \mathcal{L}_{BB\mathbb {V}}= & {} -i\frac{\beta _S g_V}{2\sqrt{2m_{\bar{B}}m_{B}}}\mathbb {V}^\nu \sum _{i=0,1}\bar{B}_i^\mu \overleftrightarrow {\partial }_\nu B_{j\mu }\nonumber \\{} & {} - i\frac{\lambda _S g_V}{\sqrt{2}}(\partial _\mu \mathbb {V}_\nu -\partial _\nu \mathbb {V}_\mu ) \sum _{i=0,1}\bar{B}_i^\mu B_j^\nu ,\nonumber \\ \mathcal{L}_{BB\sigma }= & {} \ell _S\sigma \sum _{i=0,1}\bar{B}_i^\mu B_{j\mu },\nonumber \\ \mathcal{L}_{B_{\bar{3}}B_{\bar{3}}\mathbb {V}}= & {} -i\frac{g_V\beta _B}{2\sqrt{2m_{\bar{B}_{\bar{3}}}m_{B_{\bar{3}}}} }\mathbb {V}^\mu \bar{B}_{\bar{3}}\overleftrightarrow {\partial }_\mu B_{\bar{3}},\nonumber \\ \mathcal{L}_{B_{\bar{3}}B_{\bar{3}}\sigma }= & {} \ell _B \sigma \bar{B}_{\bar{3}}B_{\bar{3}},\nonumber \\ \mathcal{L}_{BB_{\bar{3}}\mathbb {P}}= & {} -i\frac{g_4}{f_\pi } \sum _i\bar{B}_i^\mu \partial _\mu \mathbb {P} B_{\bar{3}}+\mathrm{H.c.},\nonumber \\ \mathcal{L}_{BB_{\bar{3}}\mathbb {V}}= & {} \frac{g_\mathbb {V}\lambda _I}{\sqrt{2 m_{\bar{B}}m_{B_{\bar{3}}}}}\epsilon ^{\mu \nu \lambda \kappa } \partial _\lambda \mathbb {V}_\kappa \nonumber \\{} & {} \quad \times \sum _i\bar{B}_{i\nu } \overleftrightarrow {\partial }_\mu B_{\bar{3}}+\mathrm{H.c.}, \end{aligned}$$

(9)

where $m_{\bar{B},B,\bar{B}_3,B_3}$ is the mass of the charmed baryon. $S^{\mu }_{ab}$ is composed of the Dirac spinor operators,

$$\begin{aligned} S^{ab}_{\mu }= & {} -\sqrt{\frac{1}{3}}(\gamma _{\mu }+v_{\mu }) \gamma ^{5}B^{ab}+B^{*ab}_{\mu }\equiv { B}^{ab}_{0\mu }+B^{ab}_{1\mu },\nonumber \\ \bar{S}^{ab}_{\mu }= & {} \sqrt{\frac{1}{3}}\bar{B}^{ab} \gamma ^{5}(\gamma _{\mu }+v_{\mu })+\bar{B}^{*ab}_{\mu }\equiv {\bar{B}}^{ab}_{0\mu }+\bar{B}^{ab}_{1\mu }, \end{aligned}$$

(10)

and the charmed baryon matrices are defined as,

$$\begin{aligned} B_{\bar{3}}&=\left( \begin{array}{ccc} 0&{}\varLambda ^+_c&{}\varXi _c^+\\ -\varLambda _c^+&{}0&{}\varXi _c^0\\ -\varXi ^+_c&{}-\varXi _c^0&{}0 \end{array}\right) ,\quad B=\left( \begin{array}{ccc} \varSigma _c^{++}&{}\frac{1}{\sqrt{2}}\varSigma ^+_c&{}\frac{1}{\sqrt{2}}\varXi '^+_c\\ \frac{1}{\sqrt{2}}\varSigma ^+_c&{}\varSigma _c^0&{}\frac{1}{\sqrt{2}}\varXi '^0_c\\ \frac{1}{\sqrt{2}}\varXi '^+_c&{}\frac{1}{\sqrt{2}}\varXi '^0_c&{}\varOmega ^0_c \end{array}\right) , \nonumber \\ B^*&=\left( \begin{array}{ccc} \varSigma _c^{*++}&{}\frac{1}{\sqrt{2}}\varSigma ^{*+}_c&{}\frac{1}{\sqrt{2}}\varXi ^{*+}_c\\ \frac{1}{\sqrt{2}}\varSigma ^{*+}_c&{}\varSigma _c^{*0}&{}\frac{1}{\sqrt{2}}\varXi ^{*0}_c\\ \frac{1}{\sqrt{2}}\varXi ^{*+}_c&{}\frac{1}{\sqrt{2}}\varXi ^{*0}_c&{}\varOmega ^{*0}_c \end{array}\right) . \end{aligned}$$

(11)

The ${\mathbb {P}}$ and ${\mathbb {V}}$ are the pseudoscalar and vector matrices as,

$$\begin{aligned} {{\mathbb {P}}}=\left( \begin{array}{ccc} \frac{\sqrt{3}\pi ^0+\eta }{\sqrt{6}}&{}\pi ^+&{}K^+\\ \pi ^-&{}\frac{-\sqrt{3}\pi ^0+\eta }{\sqrt{6}}&{}K^0\\ K^-&{}\bar{K}^0&{}-\frac{2\eta }{\sqrt{6}} \end{array}\right) , \mathbb {V}=\left( \begin{array}{ccc} \frac{\rho ^0+\omega }{\sqrt{2}}&{}\rho ^{+}&{}K^{*+}\\ \rho ^{-}&{}\frac{-\rho ^{0}+\omega }{\sqrt{2}}&{}K^{*0}\\ K^{*-}&{}\bar{K}^{*0}&{}\phi \end{array}\right) . \end{aligned}$$

The parameters in the above Lagrangians are listed in Table 2, which are cited from the literature [58,59,60,61].

Table 2 The parameters and coupling constants. The $\lambda$, $\lambda _{S,I}$ and $f_\pi$ are in the unit of GeV$^{-1}$. Others are in the unit of 1

2.2 Potential kernel of interactions

With the above Lagrangians for the vertices, the potential kernel can be constructed in the one-boson-exchange model with the help of the standard Feynman rule as in Refs. [62, 63]. The propagators of the exchanged light mesons are defined as,

$$\begin{aligned} P_\mathbb {P,\sigma }(q^2)= & {} \frac{i}{q^2-m_\mathbb {P,\sigma }^2}~f_i(q^2),\nonumber \\ P^{\mu \nu }_\mathbb {V}(q^2)= & {} i\frac{-g^{\mu \nu }+q^\mu q^\nu /m^2_{\mathbb {V}}}{q^2-m_\mathbb {V}^2}~f_i(q^2), \end{aligned}$$

(12)

where the form factor $f_i(q^2)$ is adopted to reflect the off-shell effect of exchanged meson, which is in form of $e^{-(m_e^2-q^2)^2/\varLambda _e^4}$ with $m_e$ and q being the mass and momentum of the exchanged mesons, respectively.

In this work, we still do not give the explicit form of the potential due to the large number of channels to be considered. Instead, we input the vertices $\varGamma$ obtained from the Lagrangians and the above propagators P into the code directly. The dibaryon systems potential can be constructed with the help of the standard Feynman rule as [62],

$$\begin{aligned} \mathcal{V}_{\mathbb {P},\sigma }=I_{\mathbb {P},\sigma }\varGamma _1\varGamma _2 P_{\mathbb {P},\sigma }(q^2),\quad \mathcal{V}_{\mathbb {V}}=I_{\mathbb {V}}\varGamma _{1\mu }\varGamma _{2\nu } P^{\mu \nu }_{\mathbb {V}}(q^2),\nonumber \\ \end{aligned}$$

(13)

where $I_{\mathbb {P},\mathbb {V},\sigma }$ is the flavor factors of the certain meson exchange, which are listed in Table 3. The interaction of their baryon–antibaryon partners interactions will be rewritten to the charmed–strange interactions by the well-known G-parity rule $V=\sum _{i}{\zeta _{i}V_{i}}$ [64, 65]. The G parities of the exchanged mesons i are left as a $\zeta _{i}$ factor. Since $\pi$, $\omega$ and $\phi$ mesons carry odd G parity, the $\zeta _{\pi }$, $\zeta _{\omega }$ and $\zeta _{\phi }$ should equal $-1$, and others equal 1.

Table 3 The flavor factors $I_e$ for charmed–strange interactions. The values for charmed–antistrange interactions can be obtained by G-parity rule from these of charmed–strange interactions. The $I_\sigma$ should be 0 for coupling between different channels

2.3 The qBSE approach

The Bethe–Salpeter equation is a 4-dimensional relativistic integral equation, which can be used to treat two body scattering. In order to reduce the 4-dimensional Bethe–Salpeter equation to a 3-dimensional integral equation, we adopt the covariant spectator approximation, which keeps the unitary and covariance of the equation [66]. In such treatment, one of the constituent particles, usually the heavier one, is put on shell, which leads to a reduced propagator for two constituent particles in the center-of-mass frame as [63, 67],

$$\begin{aligned} G_0= & {} \frac{\delta ^+(p''^{~2}_h-m_h^{2})}{p''^{~2}_l-m_l^{2}}\nonumber \\= & {} \frac{\delta ^+(p''^{0}_h-E_h(\textrm{p}''))}{2E_h(\mathrm{p''})[(W-E_h(\textrm{p}''))^2-E_l^{2}(\textrm{p}'')]}. \end{aligned}$$

(14)

As required by the spectator approximation adopted in the current work, the heavier particle (h represents the charmed baryons) satisfies $p''^0_h=E_{h}(\textrm{p}'')=(m_{h}^{~2}+\mathrm p''^2)^{1/2}$. The $p''^0_l$ for the lighter particle (remarked as l) is then $W-E_{h}(\textrm{p}'')$. Here and hereafter, the value of the momentum in center-of-mass frame is defined as $\textrm{p}=|{\varvec{p}}|$.

Then the 3-dimensional Bethe–Saltpeter equation can be reduced to a 1-dimensional integral equation with fixed spin-parity $J^P$ by partial wave decomposition [63],

$$\begin{aligned} i\mathcal{M}^{J^P}_{\lambda '\lambda }(\textrm{p}',\textrm{p})= & {} i\mathcal{V}^{J^P}_{\lambda ',\lambda }(\textrm{p}',\textrm{p})+\sum _{\lambda ''}\int \frac{\textrm{p}''^2d\textrm{p}''}{(2\pi )^3}\nonumber \\{} & {} \cdot i\mathcal{V}^{J^P}_{\lambda '\lambda ''}(\textrm{p}',\textrm{p}'') G_0(\textrm{p}'')i\mathcal{M}^{J^P}_{\lambda ''\lambda }(\textrm{p}'',\textrm{p}),\quad \quad \end{aligned}$$

(15)

where the sum extends only over nonnegative helicity $\lambda ''$. The partial wave potential in 1-dimensional equation is defined with the potential of the interaction obtained in the above as

$$\begin{aligned} \mathcal{V}_{\lambda '\lambda }^{J^P}(\textrm{p}',\textrm{p})= & {} 2\pi \int d\cos \theta ~[d^{J}_{\lambda \lambda '}(\theta ) \mathcal{V}_{\lambda '\lambda }({\varvec{p}}',{\varvec{p}})\nonumber \\{} & {} + \eta d^{J}_{-\lambda \lambda '}(\theta ) \mathcal{V}_{\lambda '-\lambda }({\varvec{p}}',{\varvec{p}})], \end{aligned}$$

(16)

where $\eta =PP_1P_2(-1)^{J-J_1-J_2}$ with P and J being parity and spin for the system. The initial and final relative momenta are chosen as ${\varvec{p}}=(0,0,\textrm{p})$ and ${\varvec{p}}'=(\textrm{p}'\sin \theta ,0,\textrm{p}'\cos \theta )$. The $d^J_{\lambda \lambda '}(\theta )$ is the Wigner d-matrix. Here, a regularization is usually introduced to avoid divergence, when we treat an integral equation. In the qBSE approach, we usually adopt an exponential regularization by introducing a form factor into the propagator as $f(q^2)=e^{-(k_l^2-m_l^2)^2/\varLambda _r^4}$, where $k_l$ and $m_l$ are the momentum and mass of the lighter baryon. The cutoff $\varLambda _r$ here and $\varLambda _e$ adopted for the exchanges play analogous roles in the calculation of the binding energy. For simplification, we set $\varLambda _e=\varLambda _r=\varLambda$ in the calculations. In the current work, the relation of the cutoff $\varLambda = m + \alpha \varLambda _0$ with $\varLambda _0= 0.22$ GeV and m being the mass of the exchanged meson is also introduced into the regularization form factor as in those for the exchanged mesons.

The partial-wave qBSE is a one-dimensional integral equation, which can be solved by discretizing the momenta with the Gauss quadrature. It leads to a matrix equation of a form $M=V+VGM$ [63]. The molecular state corresponds to the pole of the amplitude, which can be obtained by varying z to satisfy $|1-V(z)G(z)|=0$ where $z=E_R-i\varGamma /2$ being the exact position of the bound state.

3 Single-channel results

With previous information, the explicit numerical calculations will be performed on the systems mentioned above. In the current model, we have the only one free parameter $\alpha$. In the following, we vary the free parameter in a range of 0–5 to find the S-wave bound states with binding energy smaller than 30 MeV. In this work, we consider all possible channels with csssqq quarks, that is, $\varXi ^{(',*)}_{c}\varXi ^{(*)}$, $\varOmega ^{(*)}_c\varLambda$, $\varOmega ^{(*)}_c\varSigma ^{(*)}$, $\varLambda _c\varOmega$ and $\varSigma ^{(*)}_c\varOmega$ and their baryon–antibaryon partners $\varXi ^{(',*)}_{c}\bar{\varXi }^{(*)}$, $\varOmega ^{(*)}_c\bar{\varLambda }$, $\varOmega ^{(*)}_c\bar{\varSigma }^{(*)}$, $\varLambda _c\bar{\varOmega }$ and $\varSigma ^{(*)}_c\bar{\varOmega }$. However, the $\varLambda _c\varOmega$, $\varSigma ^{(*)}_c\varOmega$ and their baryon–antibaryon partners can not be considered in single-channel calculations due to the lack of exchanges of light mesons in the one-boson-exchange model considered in the current work. However, these channels will be considered in the later couple-channel calculations. Based on the quark configurations in different hadron clusters, these single-channel interactions can be divided into two categories: the $\varXi _c^{(',*)}\varXi ^{(',*)}$ and $\varOmega ^{(*)}_c\varLambda$ or $\varOmega ^{(*)}_c\varSigma ^{(*)}$ and their baryon–antibaryon partners.

3.1 Molecular states from interactions $\varXi _c^{(',*)}\varXi ^{(',*)}$ and $\varXi _c^{(',*)}\bar{\varXi }^{(',*)}$

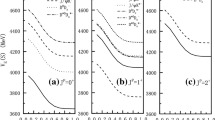
First, we consider the interactions $\varXi _c^{(',*)}\varXi ^{(*)}$ and $\varXi _c^{(',*)}\bar{\varXi }^{(*)}$ with quark configurations as [csq][ssq] and $[csq][\bar{s}\bar{s} \bar{q}]$, respectively. The single-channel results for the interactions $\varXi _c\varXi ^{(*)}$ and $\varXi _c\bar{\varXi }^{(*)}$, in which the charmed baryon belongs to the multiplet $B_{\bar{3}}$, are illustrated in Fig. 1. The results suggest that fourteen interactions produce bound states in considered range of parameter $\alpha$. All eight bound states from the $\varXi _c^{*}\varXi ^{(*)}$ interaction can appear at $\alpha$ values less than 1. The binding energies of the isovector $\varXi _c\varXi$ states with $(0,1)^+$ and the isoscalar and isovector $\varXi _c\varXi ^{*}$ states with $(1,2)^+$ both increase rapidly to 30 MeV at $\alpha$ values of about 1.5, which indicates the strong attraction. However, the binding energies of isoscalar bound states from the $\varXi _c\varXi$ interaction with $(1,2)^+$ increase slowly to 20 MeV at $\alpha$ values of about 5. The variation tendencies of the binding energies of the $\varXi _c\varXi ^{(*)}$ states with different spin parities are analogous. Almost all bound states from baryon–antibaryon interactions appear at the $\alpha$ values more than 3 and the isovector $\varXi _c\bar{\varXi }^{*}$ interaction with $(1,2)^-$ can no produce bound state. It suggests that the possibility of the existence of these baryon–antibaryon bound states is relatively low.

Fig. 1

Binding energies of bound states from the interactions $\varXi _c\varXi ^{(*)}$ (left) and $\varXi _c\bar{\varXi }^{(*)}$(right) with thresholds of 3787 (4002) MeV with the variation of $\alpha$ in single-channel calculation

In Fig. 2, the single-channel results about interactions $\varXi ^{'}_c\varXi ^{(*)}$ and $\varXi ^{'}_c\bar{\varXi }^{(*)}$ are presented. In these systems, the charmed baryon belongs to the multiplet $B_{6}$. The results suggest that twelve bound states can be produced from these interactions within considered range of parameter $\alpha$. All eight bound states from baryon–baryon interactions appear at $\alpha$ values less than 1. Among these bound states, the two isoscalar bound states from the $\varXi ^{'}_c\varXi$ interaction with $(0,1)^+$ are well distinguished and increase relatively slowly to 20 MeV at $\alpha$ values of about 3.5 and 5.0, respectively. Other six bound states increase rapidly to 30 MeV at $\alpha$ values of about 1.5, and the binding energies for states with different spins are almost the same. However, only four bound states can be produced from baryon–antibaryon interactions, which include the isoscalar and isovector $\varXi ^{'}_c\bar{\varXi }$ states with $1^{-}$, the isoscalar $\varXi ^{'}_c\bar{\varXi }^{(*)}$ state with $2^{-}$, and isovector $\varXi ^{'}_c\bar{\varXi }^{(*)}$ state with $1^{-}$. Again, one can still find that the states with the larger spin are easy to be produced for the isoscalar interactions, while the states with the smaller spin are easy to be produced for the isovector interactions. Still, these baryon–antibaryon states are produced at $\alpha$ values around or more than 3, which makes their coexistence less possible.

Fig. 2

Binding energies of bound states from the interactions $\varXi ^{'}_c\varXi ^{(*)}$(left) and $\varXi ^{'}_c\bar{\varXi }^{(*)}$(right) with thresholds of 3896 (4111) MeV with the variation of $\alpha$ in single-channel calculation

In the following Fig. 3, we present the results of the $\varXi ^{(*)}_c\varXi ^{(*)}$ and $\varXi ^{*}_c\bar{\varXi }^{(*)}$ systems, in which the charmed baryon belongs to the multiplet $B_{6}^*$. The results suggest that bound states can be produced from eighteen interactions. For the baryon–baryon systems, the bound states can be produced from all channels, and appear at $\alpha$ values below 1.5. The curves of two isoscalar $\varXi ^{*}_c\varXi$ states with $(0,1)^+$ are separated obviously, and their binding energies reach 5 MeV relative slowly at $\alpha$ values about 4.5 and 2, respectively. Besides the two states, other ten states increase with the parameter $\alpha$ to 30 MeV relatively rapidly at $\alpha$ values of about 2.5. Meanwhile, the interaction with the smaller spins have stronger attractions, which is reflected by the binding energies increasing faster with the variation of parameter. For their baryon–anibaryon partners, two isoscalar states from the $\varXi ^{*}_c\bar{\varXi }$ interaction with $2^-$ and interaction $\varXi ^{*}_c\bar{\varXi }^*$ with $3^-$, as well as four isovector states from the $\varXi ^{*}_c\bar{\varXi }$ interaction with $(1,2)^-$ and the $\varXi ^{*}_c\bar{\varXi }^*$ interaction with $(0,1)^-$, can be produced at the cutoff over 2.5.

Fig. 3

Binding energies of bound states from the interactions $\varXi ^{*}_c\varXi ^{(*)}$(left) and $\varXi ^{*}_c\bar{\varXi }^{(*)}$(right) with thresholds of 3963 (4178) MeV with the variation of $\alpha$ in single-channel calculation

3.2 Molecular states from interactions $\varOmega ^{(*)}_c\varLambda /\varOmega ^{(*)}_c\varSigma ^{(*)}$ and $\varOmega ^{(*)}_c\bar{\varLambda }/\varOmega ^{(*)}_c\bar{\varSigma }^{(*)}$

For the systems composed of [css][sqq] and $[css][\bar{s}\bar{q}\bar{q}]$, there exist interactions $\varOmega ^{(*)}_c\varLambda$, $\varOmega ^{(*)}_c\varSigma ^{(*)}$ and their baryon–antibaryon partners, interactions $\varOmega ^{(*)}_c\bar{\varLambda }$ and $\varOmega ^{(*)}_c\bar{\varSigma }^{(*)}$. In Fig. 4, we first give the results about the interactions $\varOmega _c\varLambda$, $\varOmega _c\varSigma ^{(*)}$, $\varOmega _c\bar{\varLambda }$ and $\varOmega _c\bar{\varSigma }^{(*)}$, in which the charmed baryons belong the multiplet $B_6$. Only seven states are produced from those interactions. For the $\varOmega _c\varLambda$ interaction and its baryon–antibaryon partner $\varOmega _c\bar{\varLambda }$ with isospin $I=0$, only the states that spin $J=1$ can be produced at the cutoff about 4.0 and 3.0, respectively. There is no bound state produced from the isovector interaction $\varOmega _c\varSigma$ with $(0,1)^+$ in the considered range of the parameter $\alpha$. Two bound states from the $\varOmega _c\bar{\varSigma }$ interaction with $(0,1)^-$ appear at $\alpha$ values of about 3.0 and 3.6, respectively. Two bound states from the isovector $\varOmega _c\varSigma ^*$ interaction with $(1,2)^+$ appear at $\alpha$ value of about 3.0 and 1.5, respectively, while only an isovector $\varOmega _c\bar{\varSigma }^*$ state with $1^-$ can be produced at $\alpha$ value of about 4.8. The states from the baryon–antibaryon interactions are still less likely to coexistence due to the large values of parameter $\alpha$ required to produce the bound states.

Fig. 4

Binding energies of bound states from the interactions $\varOmega _c\varLambda /\varOmega _c\varSigma ^{(*)}$(left) and $\varOmega _c\bar{\varLambda }/\varOmega _c\bar{\varSigma }^{(*)}$(right) with thresholds of 3810/3888 (4079) MeV with the variation of $\alpha$ in single-channel calculation

In Fig. 5, the results about the interactions $\varOmega ^{*}_c\varLambda$, $\varOmega ^{*}_c\varSigma ^{(*)}$, $\varOmega ^{*}_c\bar{\varLambda }$, and $\varOmega ^{*}_c\bar{\varSigma }^{(*)}$ are presented. Here, the charmed baryons are in the $B^*_6$ multiplet. The single-channel calculation suggests that nine bound states can be produced from sixteen interactions considered. The isoscalar $\varOmega ^{*}_c\varLambda$ state and its baryon–antibaryon partner $\varOmega ^{*}_c\bar{\varLambda }$ interaction with spin $J=2$ appear at $\alpha$ of about 3.5. As the $\varOmega _c\varSigma ^{*}$ interaction, the isovector $\varOmega ^{*}_c\varSigma$ systems with $(1,2)^+$ are unbound. The $\varOmega ^{*}_c\bar{\varSigma }$ state with $1^-$ is produced at $\alpha$ larger than 3.0. The isovector interactions $\varOmega ^{*}_c\varSigma ^{*}$ and $\varOmega ^{*}_c\bar{\varSigma }^{*}$ are found attractive, and four states with spin parities $(0,1,2,3)^+$ and two states with $(0,1)^-$ are produced, respectively. The $\varOmega ^{*}_ c\varSigma ^{*}$ states with $0^+$ appear at $\alpha$ value of about 3.5, while the $(1,2,3)^+$ states all appear at cutoff about 2.0. The two $\varOmega ^{*}_c\bar{\varSigma }^{*}$ with $(0,1)^-$ is produced at cutoff about 4.6.

Fig. 5

Binding energies of bound states from the $\varOmega ^*_c\varLambda /\varOmega ^*_c\varSigma ^{(*)}$(left) and $\varOmega ^*_c\bar{\varLambda }/\varOmega ^*_c\bar{\varSigma }^{(*)}$(right) with thresholds of 3882/3959 (4150) MeV with the variation of $\alpha$ in single-channel calculation

4 Coupled-channel results

In the previous single-channel calculations, many bound states are produced from the considered interactions within allowed range of parameter $\alpha$. To estimate the strength of the coupling between a molecular state and the corresponding decay channels, we will consider the couple-channel effects. In the coupled-channel calculations, the channels with the same quark components and the same quantum numbers can couple to each other, which will make the pole of the bound state deviate from the real axis to the complex energy plane and acquire an imaginary part. The imaginary part corresponds to the state of the width as $\varGamma =2\textrm{Im}z$. Here, we present the coupled-channel results of the position of bound state as $M_{th}-z$ instead of the origin position z of the pole, with the $M_{th}$ being the nearest threshold. In the above single-channel calculations, much larger $\alpha$ values are required to produce the bound states from the baryon–antibaryon interactions, which suggests that the possibility of the existence of these states are very low. Hence, in the following coupled-channel calculations, we only consider the baryon–baryon interactions. In the Table 4, we present the coupled-channel results of the isoscalar baryon–baryon interactions, which involve all possible couplings between the channels $\varXi ^{(',*)}_c\varXi ^{(*)}$, $\varLambda _c\varOmega$ and $\varOmega ^{(*)}_c\varLambda$. The poles of full coupled-channel interaction under the corresponding threshold with different $\alpha$ are given in the second and third columns.

Table 4 The masses and widths of isoscalar baryon–baryon molecular states at different values of $\alpha$. The “CC” means full coupled-channel calculation. The values of the complex position means mass of corresponding threshold subtracted by the position of a pole, $M_{th}-z$, in the unit of MeV. The two short line “–” means the coupling does not exist. The imaginary part shown as “0.0” means too small value under the current precision chosen

Glancing over the coupled-channel results of channels $\varXi ^{(',*)}_c\varXi ^{*}$, $\varXi ^{'}_c\varXi$ and $\varOmega ^{(*)}\varLambda$ in Table 4, we can find that the real parts of most poles from the coupled-channel calculation are similar to those from the single-channel calculations, and the small widths are acquired from the couplings with the channels considered. However, it has a great impact on the $\varXi ^{*}_c\varXi$ channel after including the full coupled-channel interactions as suggested by the variation in the mass and width. Compared with single-channel calculations, the masses change significantly, and the widths are much larger. Two-channel calculations are also performed, and the results are presented in the fourth to eleventh columns. For the states near the $\varXi ^{(',*)}_c\varXi ^{(*)}$ threshold with $(0,1,2,3)^+$, relatively obvious two-channel couplings can be found in the $\varXi ^{'}_c\varXi$ channel. For the states near the $\varXi ^{'}_c\varXi ^{*}$ threshold with $(1,2)^+$, the main two-channel couplings can be found in the $\varXi ^{'}_c\varXi$ channel. For two states near the $\varXi _{c}\varXi ^{*}$ threshold with $(1,2)^+$, the widths from two-channel couplings are both less than 1.0 MeV. For the states near the $\varXi ^{*}_c\varXi$ threshold with $(1,2)^+$, the main decay channel are $\varOmega ^{*}_c\varLambda$, which leads to a width of about a dozen of MeVs and large increase of binding energy. Similarly, the states near the $\varXi ^{'}_c\varXi$ threshold with $(0,1)^+$ have considerable large couplings with the $\varOmega _c\varLambda$ channel, which leads to obvious increase of mass. For the state near the $\varOmega ^{*}_c\varLambda$ threshold with $1^+$, the $\varXi _c\varXi$ channel is the dominant channel to produce their total widths. Since the $\varOmega _c\varLambda$ channel has the second lowest threshold, it can only couple to the $\varXi _c\varXi$ channel so that the only two-channel coupling width came from the $\varXi _c\varXi$ channel.

Table 5 The masses and widths of isovector charmed–strange molecular states at different values of $\alpha$. Other notations are the same as Table 4

The coupled-channel results of isovector baryon–baryon interactions are presented in Table  5. For the isovector states near the $\varXi ^{*}_c\varXi ^{*}$ threshold with $(0,1,2)^+$, large couplings can be found in the $\varOmega ^{*}_c\varSigma ^{*}$ channel and their binding energies also decrease a little compared with the single-channel results after including the two-channel couplings. Among the states near the $\varOmega ^{*}_c\varSigma ^{*}$ threshold with $(0,1,2,3)^+$, there exist some differences between different two-channel couplings. After including the two-channel couplings between the channel $\varOmega ^{*}_c\varSigma ^{*}$ and the channels $\varXi ^{'}_c\varXi ^*$, $\varXi _c\varXi ^*$ or $\varXi _c\varXi ^*$, the binding energy of the state with $0^+$ becomes obviously larger than the single-channel value together with considerable widths. The coupling to the $\varOmega _c^{*}\varSigma$ channel leads to a decrease of the binding energy. Other two-channel couplings affect a little on the single-channel results in mass and lead to small widths. For the state with $1^+$, large couplings can be found in the channels $\varXi ^{'}_c\varXi ^*$ and $\varOmega ^{*}_c\varSigma$ with large widths. However, when it couples to channels $\varOmega _c\varSigma ^{*}$, $\varXi ^{*}_c\varXi$ or $\varXi _c\varXi$, the bound state appears at a large $\alpha$ value of about 2.4. The state with $2^+$ strongly couples to channel $\varOmega ^{*}_c\varSigma$, and the couplings with channels $\varXi ^{'}_c\varXi ^{*}$, $\varXi _c\varXi ^{*}$, $\varXi ^{'}_c\varXi$ or $\varXi _c\varXi$ result in decreases of the binding energy. When the $(2,3)^+$ states couple to the channel $\varOmega ^{*}_c\varSigma$ at the parameters 2.9 and 2.8, respectively, the two “–” in table mean the binding energies beyond our coupled-channel calculation range with binding energy less than 50 MeV. For the isovector states near the $\varXi ^{'}_c\varXi ^{*}$ threshold with $(1,2)^+$, the coupling effects have no significant effect compared with the single-channel results as suggested by the almost unchanged masses and very small widths. However, the coupling effects decrease the binding energy and brings considerable widths when they couple to the $\varOmega _c\varSigma ^{*}$ channel. Hence, the two-channel results with the channel $\varOmega _c\varSigma ^{*}$, to some extent, affect the overall coupled-channel results a lot and give rise to the noticeable reduction in binding energies. For the states near $\varOmega _c\varSigma ^{*}$ threshold with $(1,2)^+$, the channels $\varXi _c\varXi ^{*}$ and $\varOmega _c\varSigma$ are dominant. In addition, the states with $(1,2)^+$ are not attractive enough to be produced within the range of parameter value considered after coupling to the $\varXi ^{'}_c\varXi$ channel. No obvious strongly coupled-channel effects can be found for the left states near the $\varXi _c\varXi ^{*}$, $\varXi ^{*}_c\varXi$ and $\varXi ^{'}_c\varXi$ thresholds, and the width from the two-channel couplings are all less than 1 MeV.

5 Summary and discussion

In this work, we systematically study the charmed–strange baryon systems composed of csssqq quarks and their baryon–antibaryon partners, in a qBSE approach. The potential kernels are constructed with the help of the effective Lagrangians with SU(3), chiral and heavy quark symmetries. The S-wave bound states are searched for as the pole of the scattering amplitudes. All S-wave charmed–strange dibaryon interactions $\varXi ^{(',*)}_{c}\varXi ^{(*)}$, $\varOmega ^{(*)}_c\varLambda$, $\varOmega ^{(*)}_c\varSigma ^{(*)}$, $\varLambda _c\varOmega$ and $\varSigma ^{(*)}_c\varOmega$ and their baryon–antibaryon partners $\varXi ^{(',*)}_{c}\bar{\varXi }^{(*)}$, $\varOmega ^{(*)}_c\bar{\varLambda }$, $\varOmega ^{(*)}_c\bar{\varSigma }^{(*)}$, $\varLambda _c\bar{\varOmega }$ and $\varSigma ^{(*)}_c\bar{\varOmega }$ are considered, which leads to 84 channels with different spin parities.

The single-channel calculations suggest that 36 and 24 bound states can be produced from the baryon–baryon and baryon–antibaryon interactions, respectively. Most bound states from baryon–antibaryon interactions are produced at much larger values of parameter $\alpha$, which suggests that these bound states are less possible to be found in future experiments than corresponding dibaryon states. Such results are consistent with our previous results [47] that fewer states can be produced in the charmed–antistrange interaction than charmed–strange interactions.

Furthermore, the coupling effects on the produced bound states in the single-channel calculations are studied. Since the states from the baryon–antibaryon interactions are less possible to exist, we do not consider these interactions in coupled-channel calculations. For the isoscalar interactions, the coupled-channel calculations hardly change the conclusion from the single-channel calculations, which means that the coupled-channel effects are not very significant. However, for the isovector interactions, the coupled-channel effects have obvious effects, which usually cause great variations of binding energy together with considerable widths. Compared with our previous coupled-channel calculations in Refs. [68, 69], the coupled-channel effect has obvious large influence on both the real part and imaginary part of poles. It may be related to the constituent hadrons considered in the current work. The systems studied in the current work are composed of a light hadron and a charmed hadron. Compared with the double-charmed or double-bottom systems, the systems containing light hadrons are usually more unstable.

Generally speaking, the charmed–strange dibaryon systems with csssqq quarks are usually attractive enough to produce bound states, while their baryon–antibaryon partners are less or hardly attractive. Both theoretical and experimental studies are suggested to give more valuable information.