Revisiting cosmography via Gaussian process

Abstract

In this paper, we revisit the kinematical state of our Universe via the cosmographic approach by using Gaussian process, where the minimum assumption is the cosmological principle, i.e. the Friedmann–Lemaître–Robertson–Walker metric. A obviously distinguished feature is that these cosmography parameters are free of any gravity theories and cosmological models. And Gaussian process is independent of any specific parameterized forms of function. Thus by transformations these generic cosmography parameters can be used to constrain a cosmological model and dark energy model directly at the kinematics level of our Universe. As a result, a series of cosmography parameters up to the fifth oder, i.e. the Hubble parameter H(z), the deceleration parameter q(z), the jerk parameter j(z), the snap parameter s(z) and the lerk parameter l(z), evolve with respect to the redshift z are reconstructed from the cosmic observations which include the recently released Pantheon+ SN Ia samples and the observational Hubble data H(z), also dubbed as cosmic chronometers. The result shows the transition redshift from a decelerated expansion to an accelerated expansion $z_t=0.652^{+0.054}_{-0.043}$ which is consistent with the previous results.

1 Introduction

In 1929 E. Hubble observed the galaxies are moving away from the Earth at speeds proportional to their distance [1]. This finding is the famous Hubble law, now also dubbed as Hubble–Lemaître law with memory of Lemaître [2]. From then on, the Hubble constant $H_0$ as a fundamental physical constant in cosmology is under measuring lasting about 100 years [3]. But the measured value of the Hubble constant $H_0$ varies from the first $H_0=500\mathrm \,km\,s^{-1}\,Mpc^{-1}$ to the present around $H_0\approx 70\mathrm \,km\,s^{-1}\,Mpc^{-1}$, a precise and consistent measurement still vanishes till to now. Eventually there is about $5\sigma$ discrepancy of $H_0$ values between the direct and model-independent local measurement $H_0=73.04\pm 1.04 \mathrm \,km\,s^{-1}\,Mpc^{-1}$ [4] from the recent release of the largest supernovae (SN) Ia sample called Pantheon+ [5, 6] and $H_0=67.4\pm 0.5\mathrm \,km\,s^{-1}\,Mpc^{-1}$ the Cosmic Microwave Background (CMB) measurement from Planck satellite (PLC18) [7] in the $\Lambda$CDM cosmology.

As a supplementary parameter, the deceleration parameter $q=-\ddot{a}/aH^2$, was introduced to describe the expansion state of our Universe, where a is the scale factor, $H\equiv \dot{a}/a$ is the Hubble parameter and the over dot denotes the derivative with respect to the cosmic time t. The minus sign in the definition of the deceleration parameter is added to have a positive dimensionless number to describe the possible slowing down expansion of our Universe due to attractive forces of matter and radiation. But two teams’ observation of type Ia supernovae reveals that our Universe is undergoing accelerated expansion [8, 9]. This unexpected finding demands a modification of general relativity (GR) at large scale or an addition of an extra exotic energy component dubbed as dark energy, see the monograph [10] and references therein, where specific modification to GR and parameterized dark energy models are proposed to match the cosmic observations, such as SN Ia and CMB etc, at the background and perturbation levels.

Instead of a specific modified gravity theory and parameterized dark energy model, investigating the kinematics of our Universe in a model-independent way is interesting and useful due to its potential ability to distinguish cosmological models. This is the main idea of the so-called cosmography. That is simple as a Taylor expansion of the scale factor a(t) in terms of the cosmic time t, a series of dimensionless parameters, such as q, j, s, l and so on, named the deceleration, jerk, snap and lerk parameters are defined respectively, for the detailed forms please see Eqs. (6, 7, 8, 9, 10) (see also Eqs. (18, 19, 20, 21, 22) in terms of the comoving distance and its derivatives) in the Sect. 2. For instance, the Hubble parameter H describes the expansion rate of our Universe, and a negative value of q means an accelerated expansion Universe. These cosmography parameters, which can be determined by the cosmic observations, describe the kinematics of Our universe. In the last few years, this kinematics approach has been studied extensively although in different names, for cosmography [11,12,13,14,15,16,17], cosmokinetics [18, 19], or Friedmannless cosmology [20, 21]. For recent progress, please see Refs. [22,23,24,25,26,27,28] for examples, but not for a complete list.

Without assuming a specific parameterized form, Gaussian process can reconstruct the function f(x) from data points $f(x_i)\pm \sigma _i$ via a point-to-point Gaussian distribution [29]. The Gaussian process was used extensively in cosmology study in the last few years [30,31,32,33,34,35,36,37,38,39,40,41,42,43], where the cosmography parameters, equation of state of dark energy are reconstructed by using the cosmic observational data points. In the Gaussian process method, the expected value $\mu$ and the variance $\sigma ^2$ of the function f(x) are given by

$$\begin{aligned} \mu (x)= & {} \sum _{i,j=1}^Nk(x,x_i)(M^{-1})_{ij}f(x_j), \end{aligned}$$

(1)

$$\begin{aligned} \sigma ^2(x)= & {} k(x,x)-\sum _{i,j=1}^Nk(x,x_i)(M^{-1})_{ij}k(x_j,x), \end{aligned}$$

(2)

where N is the number of data points. And $M_{ij}=k(x_i,x_j)+C_{ij}$ is the covariance matrix, where $C_{ij}$ is the covariance matrix of the data points, and $k(x, \tilde{x})$ is the covariance function or kernel between the points x and $\tilde{x}$, which is usually taken as the squared exponential covariance function in the form

$$\begin{aligned} k(x,\tilde{x}) = \sigma _f^2 \exp \left[ -\frac{(x - \tilde{x})^2}{2\ell ^2} \right] , \end{aligned}$$

(3)

where the ‘hyper-parameters’ $\sigma _f$ characterizes the ‘bumpiness’ of the function i.e. the typical change in the y-direction, and the length scale $\ell$ characterizes the distance traveling in x-direction to get a significant change in a function. These two ‘hyper-parameters’ $\sigma _f$ and $\ell$ can be determined in Gaussian process by maximizing the logarithmic marginalized likelihood function

$$\begin{aligned} \ln \mathcal {L}= & {} -\frac{1}{2}\sum _{i,j=1}^Nf(x_i) \left( M^{-1}\right) _{ij}f(x_j)\nonumber \\{} & {} -\frac{1}{2}\ln |M|-\frac{1}{2}N\ln 2\pi , \end{aligned}$$

(4)

where |M| is the determinant of $M_{ij}$. Fortunately, the above mentioned aspects were already realized in the GaPP code¹ [30].

Recently, the largest Supernovae Ia samples was released, dubbed as Pantheon+, which consists of 1701 light curves of 1550 spectroscopically confirmed SN Ia coming from 18 different sky surveys ranging in redshifts from $z=0.00122$ to 2.26137 [5, 6]. By using these SN Ia data points, one can reconstruct the distances and their derivatives at different orders with respect to the redshift, say the luminosity, comoving and physical distance, via Gaussian process. Meanwhile, the observed Hubble parameters at different redshifts, also named as cosmic chronometers, can reconstruct the first and higher order derivatives of the distances with respect to the redshift. Thus joining these two observations, one can obtain the ever acute reconstruction of distances and their derivatives with respect to the redshift, and by products the cosmography parameters. This is main purpose of this work.

This paper is organized as follows. In the next Sect. 2, we present the main cosmography parameters. The observational data points and main results are given in Sect. 3. In the Sect. 4, we present the conclusion.

2 Cosmography parameters

Assuming the cosmological principle, the geometry of our Universe is described by the Friedmann–Lemaître–Robertson–Walker (FLRW) metric

$$\begin{aligned} ds^2=-c^2dt^2+a^2(t)\left[ \frac{dr^2}{1-kr^2}+r^2(d{\theta }^2+\sin ^2{\theta }d{\phi }^2)\right] , \end{aligned}$$

(5)

where c is the speed of light, a(t) is the scale factor which is normalized to $a_0=1$ at present, t is the cosmic time, r is the comoving coordinate and $\theta$ and $\phi$ are the polar and azimuthal angles in spherical coordinates, the parameter $k=1,0,-1$ denotes three dimensional spatial curvature for closed, flat and open geometries respectively. In this work, we only consider the spatially flat case $k=0$.

In order to describe the kinematical state of our Universe, one defines the kinematics parameters or cosmography parameters as follows (named as Hubble, deceleration, jerk, snap and lerk parameters, respectively),

$$\begin{aligned} H\equiv & {} \frac{da(t)}{dt}\frac{1}{a(t)}\equiv \frac{\dot{a}(t)}{a(t)}, \end{aligned}$$

(6)

$$\begin{aligned} q\equiv & {} -\frac{1}{H^2}\frac{d^2a(t)}{dt^2}\frac{1}{a(t)}\equiv -\frac{1}{H^2}\frac{\ddot{a}(t)}{a(t)}, \end{aligned}$$

(7)

$$\begin{aligned} j\equiv & {} \frac{1}{H^3}\frac{d^3a(t)}{dt^3}\frac{1}{a(t)}\equiv \frac{1}{H^3}\frac{a^{(3)}(t)}{a(t)}, \end{aligned}$$

(8)

$$\begin{aligned} s\equiv & {} \frac{1}{H^4}\frac{d^4a(t)}{dt^4}\frac{1}{a(t)}\equiv \frac{1}{H^4}\frac{a^{(4)}(t)}{a(t)}, \end{aligned}$$

(9)

$$\begin{aligned} l\equiv & {} \frac{1}{H^5}\frac{d^5a(t)}{dt^5}\frac{1}{a(t)}\equiv \frac{1}{H^5}\frac{a^{(5)}(t)}{a(t)}. \end{aligned}$$

(10)

In term of the redshift $z=1/a(t)-1$, by using the relation

$$\begin{aligned} \frac{dt}{dz}=-\frac{1}{(1+z)H(z)}, \end{aligned}$$

(11)

the cosmography parameters can be rewritten as

$$\begin{aligned} q(z)\equiv & {} -1+(1+z)\frac{H'}{H}, \end{aligned}$$

(12)

$$\begin{aligned} j(z)\equiv & {} 1-2(1+z)\frac{H'}{H}+(1+z)^2\frac{H'^2}{H^2}+(1+z)^2\frac{H''}{H}, \end{aligned}$$

(13)

$$\begin{aligned} s(z)\equiv & {} 1-3(1+z)\frac{H'}{H}+3(1+z)^2\frac{H'^2}{H^2}-(1+z)^3\frac{ H'^3}{H^3} \nonumber \\{} & {} -4(1+z)^3\frac{H'H''}{H^2}+(1+z)^2\frac{H''}{H}-(1+z)^3\frac{H^{(3)}}{H},\end{aligned}$$

(14)

$$\begin{aligned} l(z)\equiv & {} 1-4(1+z)\frac{H'}{H}+6(1+z)^2\frac{H'^2}{H^2}-4(1+z)^3\frac{ H'^3}{H^3}\nonumber \\{} & {} +(1+z)^4\frac{ H'^4}{H^4}-(1+z)^3\frac{H'H''}{H^2} +7(1+z)^4\frac{H'H'''}{H^2} \nonumber \\{} & {} +11(1+z)^4\frac{H'^2H''}{H^3} +2(1+z)^2\frac{H''}{H}+4(1+z)^4\frac{H''^2}{H^2} \nonumber \\{} & {} +(1+z)^3\frac{H^{(3)}}{H}+(1+z)^4\frac{H^{(4)}}{H}, \end{aligned}$$

(15)

where the prime $'$ denotes the derivative with respect to the redshift z, and the $f^{(i)}$ denotes the i-th derivative of function f(z) with respect to the redshift z.

Fig. 1

The reconstructed cosmography parameters $D_C(z)$, $D'_C(z)$, $D''_C(z)$, $D'''_C(z)$, $D^{(4)}_C(z)$ and $D^{(5)}_C(z)$ (with $1\sigma$ error region) with the jointed CC+BAO and Pantheon+ SN Ia samples from the upper left panel to the lower right panel respectively

To reconstruct cosmography parameters, or investigate the kinematics of our Universe from cosmic observations, the comoving distances along the line of sight is needed

Fig. 2

The reconstructed Hubble parameter H(z) (with $1-3\sigma$ error regions) with the jointed CC+BAO and Pantheon+ SN Ia samples, where the Hubble parameter predicted from a spatially flat $\Lambda$CDM model is also plotted as for comparison

Fig. 3

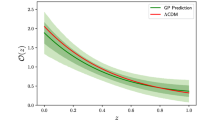
The reconstructed cosmography parameters q(z), j(z), s(z) and l(z) (with $1-3\sigma$ error curves) with the joint CC+BAO and Pantheon+ SN Ia samples from the upper left panel to the lower right panel respectively, where the corresponding cosmography parameters predicted from a spatially flat $\Lambda$CDM model are also plotted as for comparison. In the upper left q(z) panel, the horizon $q(z)=0$ line is for showing the transition redshift (at $z_t=0.652^{+0.054}_{-0.043}$ ) from a decelerated expansion to an accelerated expansion at the crossing point with the reconstructed q(z) red solid line

$$\begin{aligned} D_C(z)=c\int _0^{z}\frac{dz'}{H(z')}, \end{aligned}$$

(16)

and the luminosity distance $D_L(z)$, for a spatially flat Universe, is given as

$$\begin{aligned} D_L(z)=c(1+z)\int _0^{z}\frac{dz'}{H(z')}=(1+z)D_C(z). \end{aligned}$$

(17)

Thus, in terms of $D_C(z)$, the cosmography parameters can be rewritten as

$$\begin{aligned} H(z)\equiv & {} \frac{c}{D'_C},\end{aligned}$$

(18)

$$\begin{aligned} q(z)\equiv & {} -1-(1+z)\frac{ D_C''}{D_C'},\end{aligned}$$

(19)

$$\begin{aligned} j(z)\equiv & {} \frac{(1+z)^2}{D_C'}\left[ \frac{3 D_C''^2}{D_C'}+\frac{2D_C''}{(1+z)}-D_C'''\right] ,\end{aligned}$$

(20)

$$\begin{aligned} s(z)\equiv & {} 1+ \frac{(1+z)^3 D_C^{(4)}}{D_C'} - \frac{(1+z)^2 D_C^{(3)}}{D_C'} \nonumber \\{} & {} + \frac{3 (1+z)D_C''}{D_C'} - \frac{10 (1+z)^3 D_C^{(3)} D_C''}{D_C'^2} \nonumber \\{} & {} + \frac{15 (1+z)^3D_C''^3}{D_C'^3} +\frac{5 (1+z)^2 D_C''^2}{D_C'^2} \end{aligned}$$

(21)

$$\begin{aligned} l(z)\equiv & {} 1+ \frac{(1+z)^4 D_C^{(5)}}{D_C'} + \frac{(1+z)^3D_C^{(4)}}{D_C'} \nonumber \\{} & {} + \frac{2(1+z)^2D_C^{(3)}}{D_C'}-\frac{4(1+z) D_C''}{D_C'} \nonumber \\{} & {} +\frac{7(1+z)^4 D_C^{(4)}D_C''}{D_C'^2} +\frac{4(1+z)^4 D_C^{(3)2}}{D_C'^2} \nonumber \\{} & {} - \frac{(1+z)^3D_C^{(3)}D_C''}{D_C'^2} +\frac{(1+z)^4 D_C''^4}{D_C'^4} \nonumber \\{} & {} - \frac{4(1+z)^3D_C''^3}{D_C'^3} + \frac{11(1+z)^4 D_C^{(3)}D_C''^2}{D_C'^3} \nonumber \\{} & {} +\frac{6(1+z)^2D_C''^2}{D_C'^2}. \end{aligned}$$

(22)

It is clear that once the comoving distance and its derivatives are reconstructed via Gaussian process, the cosmography parameters and their uncertainties can be obtained consequently. Here, we would like warning the reader that the Hubble parameter H(z) obviously depends on the present Hubble parameter value $H_0$, but the other cosmography parameters q(z), j(z), s(z) and l(z) are dimensionless and $H_0$ free.

3 Reconstructed cosmography parameters via the Gaussian process

For a standard candle such as SN Ia, the luminosity distance $D_L(z)$ is related to the distance modulus $\mu =m-M=5\log _{10}D_L(\textrm{Mpc})+25$, where M is the absolute magnitude of SN Ia. Thus $D_L=(1+z)D_C$ can be expressed in terms of $\mu$ as

$$\begin{aligned} D_L=(1+z)D_C=10^{\frac{\mu -25}{5}}\textrm{Mpc}, \end{aligned}$$

(23)

where $\mu$ is the distance modulus of a SN Ia, and the absolute magnitude has been determined by the SH0ES Cepheid host distances for Pantheon+ samples [5, 6]. It corresponds to set $H_0=73.6 \pm 1.1$ km s$^{-1}$ Mpc$^{-1}$.

In order to reconstruct $D_C$ and its derivatives by using the Gaussian process code GaPP² [30], the covariance matrix for the new observable $D_C=D_L/(1+z)$, which can be derived by error propagation equation

$$\begin{aligned} C^\textrm{tot}_{ij} =\left[ \frac{D^i_L}{(1+z_i)^2}\right] ^2\sigma ^2_{z_{i}}\delta _{ij}+\frac{\ln 10 D^i_L}{5(1+z_i)} \tilde{C}^\textrm{tot}_{ij}\frac{\ln 10 D^j_L}{5(1+z_j)}, \end{aligned}$$

(24)

where $z_i$ and $D^i_L$ are the redshift and the observed luminosity distance of the i-th SN Ia respectively, and $\sigma _{z_{i}}$ is the $1\sigma$ error for $z_i$. And $\delta _{ij}$ is the standard Kronecker symbol. $\tilde{C}^\textrm{tot}_{ij}$ in the last term is total distance covariance matrix for Pantheon+ SN Ia samples³ [5, 6], and there is no Einstein’s summation convention. This variance $C^\textrm{tot}_{ij}$ will be added to the covariance matrix

$$\begin{aligned} {\varvec{y}} \sim \mathcal {N}\left( \varvec{\mu },K(\varvec{X},\varvec{X}) + C^\textrm{tot}\right) , \end{aligned}$$

(25)

where $[K(\varvec{X},\varvec{X})]_{ij}=k(x_i,x_j)$ is the covariance matrix for a set of input points $\varvec{X}=\{x_i\}$. Similarly, in order to reconstruct $D_C'$ from the observed Hubble data, the following covariance matrix is needed

$$\begin{aligned} C^\textrm{H}_{ij} = \left[ \frac{c}{H_i^2}\right] ^2\sigma ^2_{H_i} \delta _{ij}. \end{aligned}$$

(26)

In this paper, we will take the squared exponential covariance function Eq. (3) as the covariance function, which is infinitely differentiable and useful for reconstructing the derivative of a function.⁴ Meanwhile, in order to reconstruct l(z), we have modified the GaPP code to calculate the fifth order derivative of $D^{(5)}_C$.

The recent release of the Pantheon+ samples contains SN Ia ranging in redshifts from $z=0.00122$ to 2.26137, which consists of 1701 light curves of 1550 spectroscopically confirmed SN Ia coming from 18 different sky surveys. As pointed as in our previous study [17], due to the degeneracy between $H_0$ and the absolute magnitude M, the SN Ia cannot give any prediction of $H_0$ value without calibration. Therefore, in this work, we use $H_0$ from SH0ES to reconstruct H(z). In using the measurement of $H_0$ from SH0ES, and making it consistent and free of redundancy, some Pantheon+ SN Ia data points (marked as USED_IN_SH0ES_HF=1) are removed where they were already used in the Hubble flow dataset [4].

The observational Hubble data used in this work comes from the cosmic chronometers (CC) and from clustering measurements (BAO), see Tables A2 and A3 in Ref. [44] and references therein for examples, where the redshift ranges in $z\in [0.070, 2.360]$.

Implementing Gaussian process as described in the Sect. 1, the comoving distance and its derivatives up to the fifth oder with respect to the redshift are reconstructed as shown in Fig. 1, where $1\sigma$ errors are also plotted in shadow regions. It is seen that the error becomes larger with the increase of the oder of derivative with respect to the redshift z. On the contrary, the addition of CC+BAO data points gives an extra constraint to the first order derivative of $D_C(z)$, thus a relative narrow error region for the reconstructed functions can be obtained. Meanwhile, a large error is shown at high redshift due to the sparse data points at where.

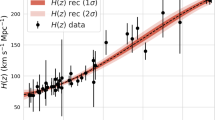
With the jointed CC+BAO and Pantheon+ SN Ia samples, the reconstructed Hubble parameter H(z) is shown in Fig. 2 including $1-3\sigma$ error curves, where the Hubble parameter H(z) predicted from a spatially flat $\Lambda$CDM cosmology, i.e. $H^2(z)=H^2_0[\Omega _{m0}(1+z)^3+\Omega _{\Lambda 0}]$ with $\Omega _{m0}=0.334$ ($\Omega _{\Lambda 0}=1-\Omega _{m0}$) from SH0ES [4] is also plotted as for comparison. The apparent bumps of error curves for H(z) at the redshift range $z\sim 1.0-2.0$ are mainly due to the sparse and large error bars of the data sets. If one takes the SH0ES $\Lambda$CDM cosmology as a benchmark, one can see that the reconstructed values of $H_0$ are larger (and lower) than that predicted by the $\Lambda$CDM cosmology at lower $z<0.1$ (and higher $z>1.5$) redshift ranges. And due to the luminosity distance is an integration in the whole redshift ranges, thus the see-saw like H(z) cancels out the losses and gains at the higher and lower redshifts respectively for a same luminosity distance.

Fig. 4

The same as Fig. 1 but with the Matérn ($\nu =9/2$) covariance function Eq. (27)

Fig. 5

The same as Fig. 2 but with the Matérn ($\nu =9/2$) covariance function Eq. (27)

The reconstructed cosmography parameters q(z), j(z), s(z) and l(z) are plotted in Fig. 3, where the corresponding cosmography parameters predicted from the spatially flat $\Lambda$CDM cosmology are also plotted as for comparison. The corresponding error is obtained by the error propagation equation, say for a function looks like $f=g^m/h^n$, the errors, after omitting the cross correlation between g and h, can be calculated as

$$\begin{aligned} \sigma ^2_f=\left[ \frac{ng^m}{h^{n+1}}\right] ^2\sigma ^2_h + \left[ \frac{mg^{m-1}}{h^n}\right] ^2\sigma ^2_g. \end{aligned}$$

(28)

Thus the corresponding calculation for $\sigma _q$ etc is quite easy, but the mathematical expression is long and ugly, so it is not shown in this paper. In the upper left q(z) panel of Fig. 3, the horizon $q(z)=0$ line is for showing the transition redshift (at $z_t=0.652^{+0.054}_{-0.043}$ ) from a decelerated expansion to an accelerated expansion at the crossing point with the reconstructed q(z) red solid line. It can be seen that the reconstructed cosmography parameters match the prediction ones from the $\Lambda$CDM cosmology almost well, with the exception of q(z) at the lower redshifts. It reflects the fact that the reconstructed q(z) favors smaller value of $\Omega _{m0}$. Thus if keeping a fixed $\Omega _{m}h^2=\Omega _{m0}\times (H_0/100)^2$ value, a larger value of $H_0=100h$ is arrived. From the q(z) panel of Fig. 3, one can also read another two accelerated phase transitions at higher redshifts $z= 1.694$ and $z= 2.260$ with larger errors. This comes from the fact that the reconstructed Hubble parameter H(z) increases slowly in the redshift range $z\sim 1.3-2.0$ as shown in Fig. 2, where the data points are really sparse and having larger error bars. Therefore, it is harder to give a promised prediction. This situation is expected to be improved with the addition of high quality and quantity redshift data sets in the future.

It would be useful to present the current values of the cosmography parameters as byproducts. Since we have already reconstructed the evolutions of cosmography parameters within $1-3\sigma$ regions with respect to the redshift ranging in $z\in [0,2.26137]$, one can read them as derived quantities from the reconstructed results with $1\sigma$ uncertainty easily: $q_0=-0.71\pm 0.04$, $j_0=1.26\pm 0.18$, $s_0=0.04\pm 0.59$ and $l_0=2.13\pm 1.14$.

4 Conclusion

We present the reconstructed results for the cosmography parameters up to the fifth order, or kinematical state of our Universe from the Pantheon+ SN Ia samples after removing the data points used in SH0ES via Gaussian process in Fig. 3. It is seen that the reconstructed cosmography parameters match the prediction ones from the spatially flat $\Lambda$CDM cosmology, i.e. $H^2(z)=H^2_0[\Omega _{m0}(1+z)^3+\Omega _{\Lambda 0}]$ with $\Omega _{m0}=0.334$ ($\Omega _{\Lambda 0}=1-\Omega _{m0}$) from SH0ES [4], almost well, with the exception of the deceleration parameter q(z) at the lower redshifts. It implies the reconstructed q(z) favors smaller value of $\Omega _{m0}$. As an effect for a fixed $\Omega _{m}h^2$, a larger value of $H_0=100h$ is expected. As a byproduct of the reconstruction, the transition redshift $z_t=0.652^{+0.054}_{-0.043}$ from a decelerated expansion to an accelerated expansion is also obtained. This result is consistent with the previous studies. However, one can also find another two accelerated phase transitions at higher redshifts $z= 1.694$ and $z= 2.260$ with larger errors in the q(z) panel of Fig. 3. These extra accelerated phase transitions are not consistent with the spatially flat $\Lambda$CDM cosmology prediction. But, the reader should not worry this consistency excessively, actually the reconstructed cosmography parameters cannot give a promised prediction at high redshift due to the sparse and larger error bars data points at where. And we expect the future high quality and quantity redshift data sets will improve this situation.

Appendix A: Reconstructed results for the Matérn (\(\nu =9/2\)) covariance function

Repeating the the analysis of the present work using this alternative Matérn ($\nu =9/2$) covariance function Eq. (27), we present the corresponding results for comparisons in Figs. 4, 5 and 6, where similar results are shown but having larger uncertainties at sparse data point regions with the squared exponential covariance function Eq. (3). With this Matérn ($\nu =9/2$) kernel, one has the derived quantities: $q_0=-0.67\pm 0.07$, $j_0=1.30\pm 0.50$, $s_0=1.55\pm 3.09$, $l_0=-0.58\pm 16.81$, and $z_t=0.66_{-0.06}^{+0.08}$.

Fig. 6

The same as Fig. 3 but with the Matérn ($\nu =9/2$) covariance function Eq. (27)