Experiments dedicated to the search for very rare events require very low background rates. The main background source above ground at almost every energy is the cosmic radiation, which consists of electrons, muons, gammas and neutrons produced by the interaction of primary cosmic rays with the Earth atmosphere. Cosmic radiation can be attenuated or completely absorbed by the rock overburden of a deep underground laboratory. In this case, main external sources of background for a hosted detector will be cosmic ray muons surviving up to the laboratory depth, and the products of local radioactivity. Additionally, high energy muons can interact with the rock surrounding the laboratory giving rise to showers of secondaries and, in some extreme cases, atmospheric and solar neutrinos can also be considered as background sources.

An accurate knowledge of the background characteristics of an underground laboratory, in terms of both energy spectra and related intensities, is essential to design the appropriate shielding of any experimental equipment to be hosted; moreover, a continuous monitoring of the time variations of the intensity of the background sources during data taking is recommended, see e.g. [1].

Among all the sources of background, neutrons play an exceptional role. In fact, due to their capability to mimic the searched signals, neutrons are the most important background source for a wide variety of underground experiments, such as those aimed to the search for Weakly Interacting Massive Particles (WIMPs) in which case the seasonal variation of the neutron rate could also simulate the expected modulation of the dark matter flux.

In general, the neutron flux in underground laboratories is orders of magnitude lower than that above ground [2]. Consequently, its measurement requires the use of detectors with high efficiency, high signal discrimination capability and long-term stability. The MOSCAB geyser-concept bubble-chamber, which has been in operation in Hall C of the INFN Gran Sasso National Laboratory (LNGS) during the period 2018–2021, has proven to have these characteristics [3].

The INFN Gran Sasso National Laboratory, located at the average depth of 3800 m w.e. under the Gran Sasso massif, a limestone mountain in the center of Italy, can ensure particularly low background conditions to the hosted experiments. Notably, the neutron flux at the LNGS underground laboratory has been measured in the past by several research groups, in different locations and employing different techniques [2, 4,5,6,7,8,9,10,11]. A discussion on the low energy component of the neutron flux at the Gran Sasso National Laboratory can be found in [12], according to which the flux is dominated by neutrons produced in the concrete layer covering the cavity surfaces, thus implying that, at least for fast neutrons, it is practically the same in the three halls of the laboratory, their differences being mainly due to differences in the environmental humidity. Fission and (\({\alpha , n}\)) reactions contribute more or less equally to the total production rates both in the rock and in the concrete, but, while the spontaneous fission of \(\mathrm {^{238}U}\), which dominates with respect to \(\mathrm {^{235}U}\) and \(\mathrm {^{232}Th}\), mainly gives rise to neutrons with energies below 4 MeV, (\({\alpha , n}\)) reactions are mainly responsible of the production of neutrons with higher energies, up to about 8 MeV. At higher energies the contribution of muon-induced neutrons becomes dominant, even if their flux is definitely lower.

A set of measurements carrying information about the neutron energy spectrum have been executed at different sites inside the LNGS underground laboratory as reported in Fig. 1. Within the estimated uncertainties, in the energy interval 1–20 MeV the different data sets are in fair agreement, identifying a single energy spectrum.

The differential neutron flux \({d \phi _n}/{dE}\) may be written as the product between the total neutron flux \({\varPhi _n}\) and the normalised energy distribution function \(\mathrm {g(E)}\) which describes the shape of the spectrum:

$$\begin{aligned} \frac{d \phi _n (E)}{dE}= \varPhi _n \cdot g(E) \quad with \quad \int _{0}^{\infty }{g(E)dE} = 1. \end{aligned}$$
(1)

With this notation, the experimental data were fitted by the function

$$\begin{aligned} \frac{d \phi _n (E)}{dE}= \varPhi _n\cdot \frac{e^{S_{3,k}(E)}}{E_0} \quad with \quad E_0=1\, \textrm{MeV} \end{aligned}$$
(2)

where \(S_{3,k}(E)\) is the cubic spline with k breaks (or knots) [13] obtained minimizing the Residual Sum of Squares between the experimental values of the flux (\(F_i\)) and the corresponding estimated values in the n energy intervals \([E_{i-1},~ E_i]\):

$$\begin{aligned} RSS_k= & {} \sum _{i=1}^{n} \left( \int _{E_{i-1}}^{E_i} \frac{d \phi _n (E)}{dE} dE-F_i \right) ^2 \nonumber \\= & {} \sum _{i=1}^{n} \left( \varPhi _n \cdot \int _{E_{i-1}}^{E_i} e^{S_{3,k}(E)}\frac{dE}{E_0}-F_i \right) ^2 \end{aligned}$$
(3)

The residual sum of squares tends to decrease with increasing the number of breaks, which, on the other hand, leads to an increase of the number of parameters (complexity) in the model. The trade-off between the goodness of fit and the simplicity of the model was performed applying the Akaike information criterion [14] which resulted in the optimal value of 3 knots. The uncertainties on the best fit function were calculated using the Monte Carlo method [15]. For each experimental value a log-normal probability density function was used for sampling the value of the neutron flux, and for each n-uple of sampled points the cubic spline was obtained. The resulting average continuous function and the relative 95% probability band are shown in Fig. 1.

Fig. 1
figure 1

Reconstructed neutron energy spectrum (\(E_n > 1 \, \textrm{MeV}\)) determined fitting results obtained by previous experiments. Different energy intervals are used by different authors, hence to make the comparison easier, each point in the figure shows the integral flux divided by the interval width. The result of the interpolation is shown in the figure as a dashed line, with the error band in grey

Full size image

In this paper we present the comparison between the expected event rate induced in the MOSCAB detector by the neutron energy spectrum shown in Fig. 1 and the experimental results obtained during a campaign of background measurement performed in Hall C of the Gran Sasso underground laboratory between 2020 and 2021.

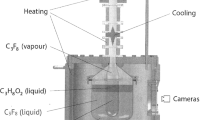
The MOSCAB geyser-concept bubble-chamber, exhaustively described in a previous study [16], consists of a bubble chamber operated just controlling the temperatures of \({C_3F_8}\) both in the metastable liquid phase and in the vapour phase. Its main strength is that it can be operated in such thermodynamic conditions to be insensitive to electron recoils, minimum ionizing particles and \(\alpha \) particles, maintaining its sensitivity to nuclear recoils. In fact, the production of a vapour bubble in a metastable liquid requires that a given amount of energy is released in a well defined volume, which results in two conditions that must be simultaneously met: an energy threshold represented by the critical energy, \(\mathrm {E_c}\), and a threshold in ionization power.

MOSCAB detector has been in operation in the LNGS underground laboratory from 2018 to 2021. During this period, thanks to the low background conditions existing inside the laboratory, we performed several calibration runs to validate the detector response functions computed for the detector operated in different conditions. Among them, the response function \(G(E_c, E)\) of the detector irradiated by an isotropic flux of neutrons, which we will use here, are reported in Fig. 2.

Fig. 2
figure 2

Response functions of the MOSCAB detector versus the neutron energy, calculated for a spherical (3 m diameter) isotropic neutron source surrounding the detector equipped with the 18 ls vessel filled with 13 ls of \(C_3F_8\) and different values of the critical energy \(E_c\)

Full size image

The bubble event rate due to the neutron background in the Gran Sasso Laboratory \(\dot{N}_{ev}\) may be computed by integrating the product between the response function \(G(E_c, E)\) and the differential neutron flux \(d \phi _n / dE\):

$$\begin{aligned} \dot{N}_{ev}(E_c)= & {} \int _o^{\infty }{G(E_c,E) \cdot \frac{d \phi _n}{dE} dE} \nonumber \\= & {} \varPhi _n \cdot \int _0^{\infty }{G(E_c,E) \cdot g(E) dE} = \varPhi _n \cdot G_B(E_c)\nonumber \\ \end{aligned}$$
(4)

where the function \({G_B(E_c) }\) evaluates the fraction of the neutron energy spectrum that can generate a bubble in the meta-stable liquid at the thermodynamic conditions corresponding to the critical energy \(E_c\).

The results of this calculation, conducted for \(\mathrm {E_c}\) ranging from 75 to 550 keV, are reported in Fig. 3 with the error band produced by the propagation of the errors of the neutron spectrum of Fig. 1 and the response functions of Fig. 2. In the same figure, the experimental results obtained during 16 runs of data taking, for a total of 2586 h, with the detector operated at critical energies ranging from 96 to 514 keV, are also reported for comparison purposes. The related details are listed in Table 1. Vertical error bars in Fig. 3 represent the standard deviation of the distributions or, when larger, the Poisson fluctuations. Horizontal bar visualizes the standard deviation of the corresponding critical energy distributions.

Fig. 3
figure 3

The background count rate of the MOSCAB detector placed in Hall C of the LNGS underground laboratory plotted versus the critical energy, \(E_c\) and compared with the count rate expected from the environmental fast neutron flux

Full size image
Table 1 Results of the background campaign in Hall C of the LNGS underground laboratory in the period August 2020 - October 2021
Full size table

It can be seen that less than 100 events have been detected during more than 100 days of live time of the detector, as in the cited range of critical energy the detector is sensitive only to neutron-induced recoils. The intrinsic background of the detector, which is dominated by the products of the \(\mathrm {^{222}Rn}\) decay chain, completely vanishes when the ionization power of the \(\alpha \) particle is not high enough to produce a bubble nucleation, even at the Bragg pick, and the energy of the daughter ions is lower than \(E_c\). Actually, at a critical energy \({E_c = 150}\) keV, \(\alpha \) particles certainly cannot give rise to vapour bubbles, while, on the other side, daughter ions in the \(\mathrm {^{222}Rn}\) decay chain, which surely have the necessary ionization power, are characterized by the following specific kinetic energies: 100.7 keV for \(\mathrm {^{218}Po}\), 112.2 keV for \(\mathrm {^{214}Pb}\) and 146.0 keV for \(\mathrm {^{210}Pb}\).

The experimental data in the range \(\mathrm {100~keV\le E_c \le } 150~\textrm{keV}\) shown by Fig. 3 support this interpretation and then, since we are aware that the background runs acquired at critical energies lower than about 150 keV are partly contaminated by signals due to the \(\mathrm {^{222}Rn}\) decay chain, in the analysis we introduced an additional energy cut at \(\mathrm {E_c=150 }\) keV, which corresponds to an energy threshold \(\mathrm {E_n ^{th}=1.9}\) MeV for neutrons scattering with Carbon and to an energy threshold \(\mathrm {E_n ^{th}=2.7}\) MeV for neutrons scattering with Fluorine [3].

The remaining 26 events collected during more than 95 days of life time of the detector operated at 11 different metastability conditions have allowed us to obtain a measurement of the neutron flux intensity. In this regard, by keeping unchanged the shape of the neutron energy spectrum described by the energy distribution function g(E) defined by Eq. 1, we computed the optimal value of the normalization parameter \( \varPhi _n\) as:

$$\begin{aligned} \varPhi _{n}^{opt}= & {} \arg \min _{\varPhi >0}~ [ \varPhi _n \cdot G_B(E_{c,i}) - O(E_{c,i})] \nonumber \\{} & {} for \quad E_{c,i}~\ge ~150~keV \end{aligned}$$
(5)

where \(O(E_{c,i})\) is the event rate of the i-th experimental run, while \(G_B(E_{c,i})\) is the value of function \(G_B(E_c)\) introduced in Eq. 4 calculated at \(E_{c,i}\).

According to our measurements, the neutron flux intensity integrated between 1 and 20 MeV turns out to be:

$$\begin{aligned} \int _{1\,\textrm{MeV}}^{20\,\textrm{MeV}}{\frac{d \phi _n}{dE} dE} = (0.38 ~\pm ~ 0.14) \cdot 10^{-6}~n \cdot \textrm{cm}^{-2} \cdot \textrm{s}^{-1} \end{aligned}$$

which is in excellent agreement with the results reported in [12], i.e., \(0.33 \pm 0.07 \le {\varPhi _n} \cdot 10^{6} \le 0.58 \pm 0.13~n \cdot \textrm{cm}^{-2} \cdot \textrm{s}^{-1} \).

Moreover, the integration between 2.5 and 20 MeV results in a total neutron flux:

$$\begin{aligned} \int _{2.5\,\textrm{MeV}}^{20\,\textrm{MeV}}{\frac{d \phi _n}{dE} dE} = (1.7 ~\pm ~ 0.5) \cdot 10^{-7}~n \cdot \textrm{cm}^{-2} \cdot \textrm{s}^{-1} \end{aligned}$$

which does not differ much from the neutron flux above 2.5 MeV of \({(0.9 \pm 0.6) \cdot 10^{-7} n \cdot \textrm{cm}^{-2} \cdot \textrm{s}^{-1}}\) measured by the GALLEX Collaboration [8] with a completely different technique.