Structural properties of anisotropic stars in modified teleparallel gravity: a brief study via an embedding approach

Abstract

In this paper, we attempt to construct the anisotropic solution for compact stellar configurations using the observed mass and radius of compact stars from the literature under the influence of Rastall Teleparallel gravity. To investigate the crucial elements of spherically symmetric metric space, we employed the embedding class one spacetime paradigm with Karmarkar’s condition. The field equations have been computed under the gravitational action of Rastall Teleparallel gravity. However, the unknown constants were evaluated via junction conditions using the Schwarzschild metric as the outer geometry. The compact stars analysis’s crucial physical and mathematical requirements are all admitted and shared by the model, which is physically viable and supports the emergence of novel realistic stellar configurations in Rastall Teleparallel gravity. We fix the parameters of our model to compare with three compact stars (LMC X-4, Cen X-3, and EXO 1785-248) and find that it can be regular, robust, and stable.

1 Introduction

The curvature imported from Riemannian geometry, which is characterized by the Ricci scalar R, is one of the cornerstones of general relativity (GR). The Ricci scalar R is switched out for some general function of R [1,2,3] in the modified f(R) gravity, which is a simple modification of GR. In addition, there are many alternatives to GR, such as the teleparallel equivalent of GR (TEGR), in which T-torsion is used for describing gravitational interactions. Contrary to the Weitzenbock connection in teleparallelism which is associated with torsion but zero curvature, the Levi-Civita connection in GR is associated with curvature but zero torsion. Meanwhile, one of the problems encountered by researchers in these two theories is the cosmological constant $\Lambda$ which serves as the negative pressure fluid $p_{\Lambda }=-\rho _{\Lambda }$. Only by including a scalar field as an additional term can GR handle the Universe’s present state of acceleration. Researchers refer to this topic as the “fine-tuning problem” since the observed value of $\Lambda$ significantly deviates from the expected value. Researchers believe that the only ways to solve this issue are to modify GR, add more scalar fields, or make modifications to the standard model of physics. According to some theories, GR modification can adequately explain the behavior of cosmic expansion in the late universe without the need for $\Lambda$. When discussing the early Universe, observations of fast expansion are referred to as the inflationary epoch. The cosmological constant $\Lambda$ cannot accommodate this rapid expansion. This problem can be improved by incorporating a scalar field, however, GR also doesn’t tell us anything about the origins or nature of inflation.

The inflationary era known as early-time expansion and the current dark energy era are both explained by modified gravity [4,5,6]. Moreover, the coincidence problem shows that the actual energy density of matter and eventual dark energy are identical. Some theorists believe that this is merely a coincidence and not a problem, although some GR modifications could be able to address this difficulty [6].

A modified theory of gravity known as Teleparallel Theory (TT), which was introduced many years after the original formulation of GR, is based on Einstein’s investigation of the new version of GR [7]. On the basis of the proposal described by the authors [8,9,10,11,12,13], the relationship between the original GR and TT has, nevertheless, once again been explained. From a GR perspective, the source’s curvature offers the best explanation for the gravitational effect induced by a gravitating source. In general, it is argued that space-time may possess both torsion and curvature (like Cartan space); one can distinguish between concepts that derive from the torsion of space-time, such as the Riemann tensor, relationship, etc. Consequently, the theory that proposes gravity based on the action of curvature of space-time (Riemann tensor) can be considered as a theory comprising just of torsion with no contribution from Riemann tensor without torsion [14].

In 1972 Rastall [15] suggested a generalization of Einstein’s general theory of relativity. The validity of the stress-energy tensor conservation law in curved space-time was also questioned by Rastall. Further, the covariant derivative of the stress-energy tensor is roughly related to the derivative of the Ricci scalar, i.e., $T^{\mu \nu }_{~~;\mu }=R^{,\nu }$ in this new gravitational theory. Rastall gravity [16] can be viewed in this light as a phenomenological application of certain quantum fluctuations in the background of curved space-time. Rastall gravity theory was applied to cosmology in recent years, and it has been providing some new and exciting findings at the cosmological level. It was also found to be in good agreement with diverse observational data in the cosmological background [17, 18]. On the other hand, the emergence of small DM fluctuations is identical to that of the Cold-DM model, while in Rastall theory, DE is huddled. This property causes inhomogeneities in dark matter evolvement in a non-linear area, which differs from the standard cold-DM model [19]. Furthermore, it has been debated whether Rastall gravity and Einstein gravity are equivalent or not. Some many years ago, the inequivalence between the two gravity theories was highlighted in Ref. [20]. Despite this, the equivalence has been recently claimed [21], however soon afterward the inequivalence survived [22] due to Rastall gravity being a more open gravity theory than Einstein gravity. The impacts of Rastall theory on stellar configurations simulated with both polytropic and non-relativistic equations of state (EoS) were evaluated in [23]. They came to the conclusion that only small GR deviations are coherent with stellar configuration restrictions, and that only values of the free-parameter $\lambda$ greater than those tested due to considerations of energy bounds.

By embedding the four-dimensional spherically symmetric space-time into the five-dimensional flat metric, a significant number of compact star models are constructed. If an embedding into a ($n+p$)-dimensional flat space-time is possible, then a Riemannian space-time with n-dimensions is of class p. Only embedded class-1 metrics are relevant to the Karmarkar condition. According to Pandey and Sharma [24], embedding class-1 space-time is a prerequisite for the implementation of Karmarkar condition. The Riemannian tensor, which joins the two gravitational potentials into a single differential equation, and geometry alone are the sole sources of the Karmarkar condition. Although many different methods might be accessible, Karmarkar condition offers a convenient and straightforward way to describe the model’s intricate gravitational behavior. One of the metric potentials’ components must be stated, and the other must be taken from Karmarkar condition by solving the differential equation. When modeling various compact objects using Karmarkar condition, attempts to generate stellar attributes like radius, mass, redshift, and compactness that are well-consistent with observational data have been remarkably successful, as shown in the Refs. [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52]. Ruderman [53] has looked into the effects of anisotropy. According to him, a star may exhibit anisotropic properties at very high energy densities, where nuclear interactions turn relativistic. Following that, Bowers and Liang [54] explored the generally populated, static, spherically symmetric, relativistic anisotropic matter dispersion’s limiting properties. Anisotropy is originally developed by relaxing the isotropic condition, i.e. $p_r \ne p_t$. Importantly, the general procedure described in [55,56,57,58,59,60,61,62,63,64,65,66] can be employed to derive any methodology for static isotropic, anisotropic, and charged anisotropic solutions of Einstein’s field equations based on spherically symmetric space-time.

It is broadly acknowledged that a variety of physical events that we would expect to appear in compact astrophysical objects (for a detailed discussion on this topic, see Refs. [58]) might cause deviations of the isotropy and fluctuations of the local anisotropy in pressures. Additionally, even if a system is initially thought to be isotropic, the existence of physical aspects such dissipative fluxes, energy density inhomogeneities, the appearance of shear in the fluid flow, and/or any of these will always tend to cause pressure anisotropy. Superfluids or type-A fluids, rotations, electromagnetic fields, pion and meson condensations, core formation, and other phenomena have all been mainly investigated in [58, 60,61,62,63,64,65], and they all contribute to the concept of anisotropy emerging in self-gravitational compact stars. This shows that the radial component ($p_r$) and the tangential component ($p_t$) are two different types of pressure components present in self-gravitational systems. In the study of self-gravitational fluids, local anisotropy is introduced as a consequence of the inequalities in radial and tangential pressures ($p_t \ne p_r$). In this regard, the implications of the Newtonian and general relativistic regimes in static anisotropic stars have been explored by Herrera et al. [66,67,68,69].

In this paper, we try to construct a new anisotropic solution for compact stellar configurations having observed mass and radius under the influence of Rastall Teleparallel gravity. For this purpose, we explore the key components of spherically symmetric metric space, using the embedding class one spacetime paradigm with Karmarkar’s condition. The paper is organized as follows. In Sect. 2, we briefly describe the fundamentals of Rastall teleparallel gravity. Using matching criteria, Sect. 3, calculates the unidentified parameters. We provide some significant discussion on the stellar properties in Sect. 4. The concluding remarks are given in Sect. 5.

2 Basic concepts of Rastall’s teleparallel gravity

To begin, we must introduce the notion of indices. For example, we use Greek alphabets ($\mu ,\; \nu ,\ldots =0,\;1,\;2,\;3$) to identify space-time indices and Latin alphabets ($i,\; j,\ldots =0,\;1,\;2,\;3$) to indicate tangent space indices. Tangent space is commonly defined as Minkowski space with the metric $\eta _{ij}=diag(1,\;-1,\;-1,\;-1)$. The tangential space indices are significantly raised and lowered along with the Minkowski metric $\eta _{ij}$. To achieve this raising and lowering of the space-time indices, the space-time indices Riemannian metric is employed, which is provided by,

$$\begin{aligned} g_{\mu \nu }=\eta _{ij}e^{i}{}_{\mu }e^{i}{}_{\nu }, \end{aligned}$$

(1)

here, tetrad fields are represented by the formula $e^{i}(x_{\mu })=e^{i}{}_{\mu }\partial ^{\mu }$. These nontrivial tetrad fields serve as the orthogonal basis of the tangential space, where $(e_{i}.e_{j})=\eta _{ij}$. According to (1), the aforementioned nontrivial tetrad fields attach to the gravitational field and leave a teleparallel structural imprint on space-time. Based on the following tetrad fields,

$$\begin{aligned} \Gamma ^{\alpha }{}_{\mu \nu }= e_{i}{}^{\alpha }\partial _{\nu }e^{i}{}_{\mu }=-e^{i}{}_{\mu }\partial _{\nu }e_{i}{}^{\alpha }, \end{aligned}$$

(2)

the Weitzenbock connection can be explained and their covariant derivative of such tetrad fields leads to zero, i.e.,

$$\begin{aligned} \nabla {\mu }e^{i}{}_{\nu }=\partial {\mu }e^{i}{}_{\nu }-\Gamma ^{\alpha }{}_{\mu \nu } e^{i}{}_{\alpha }=0. \end{aligned}$$

(3)

The general parallelism requirement is expressed in Eq. (3). Null curvature and non-vanishing torsion result from this connection, which is stated as,

$$\begin{aligned} T^{\alpha }{}_{\mu \nu }=\Gamma ^{\alpha }{}_{\nu \mu }-\Gamma ^{\alpha }{}_{\mu \nu }=e_{i}{}^{\alpha }(\partial _{\mu }e^{i}{}_{\nu }-\partial _{\nu }e^{i}{}_{\mu }). \end{aligned}$$

(4)

The Weitzenbock connection and the Levi-Civita connection are related by the expression,

$$\begin{aligned} {\hat{\Gamma }}^{\alpha }{}_{\mu \nu }=\Gamma ^{\alpha }{}_{\mu \nu }-K^{\alpha }{}_{\mu \nu }, \end{aligned}$$

(5)

where ${\hat{\Gamma }}^{\alpha }{}_{\mu \nu }$ is Levi-Civita connection and $K^{\alpha }{}_{\mu \nu }$ is the contorsion tensor explained as shown below,

$$\begin{aligned} K^{\alpha }{}_{\mu \nu }=\frac{1}{2}(T_{\mu }{}^{\alpha }{}_{\nu }+T_{\nu }{}^{\alpha }{}_{\mu }-T^{\alpha }{}_{\mu \nu }). \end{aligned}$$

(6)

The torsion scalar is defined as

$$\begin{aligned} T=S^{\alpha \mu \nu }T_{\alpha \mu \nu }, \end{aligned}$$

(7)

where $S^{\alpha \mu \nu }$ represents super-potential and is specified as,

$$\begin{aligned} S^{\alpha \mu \nu }=-S^{\alpha \nu \mu }=\frac{1}{2}(K^{\mu \nu \alpha }-g^{\alpha \nu }T^{\gamma \mu }{}_{\gamma }+g^{\alpha \mu }T^{\gamma \nu }{}_{\gamma }). \end{aligned}$$

(8)

The formulation of the Lagrangian, which defines the gravitational field in teleparallel gravity, reads

$$\begin{aligned} L_G=\frac{e}{16\pi }T, \end{aligned}$$

(9)

by considering the suppositions $c=G=1$ and $e=det(e^{i}{}_{\mu })$. The action [70] in teleparallel gravity can be expressed as follows for non-empty space-time,

$$\begin{aligned} S=-\int e\left( \frac{T}{16 \pi }+L_{m}\right) d^{4}x, \end{aligned}$$

(10)

where, $L_{m}$ is the matter Lagrangian notation. One can obtain the equation shown below by varying this action associated with the tetrad fields,

$$\begin{aligned} e^{-1}e^{i}{}_{\mu }\partial _{p}(ee_{i}{}^{\gamma }S_{\gamma }{}^{\nu p})+T^{\gamma }{}_{\lambda \mu }S_{\gamma }{}^{\nu \lambda }+\frac{1}{4}\delta ^{\nu }_{\mu }T=4\pi \Theta ^{\nu }_{\mu }, \end{aligned}$$

(11)

where $\Theta ^{\nu }_{\mu }$ notions the perfect fluid stress energy tensor. It’s proven that

$$\begin{aligned} D_{\nu }\left( e^{-1}e^{i}{}_{\mu }\partial _{p}(ee_{i}{}^{\gamma }S_{\gamma }{}^{\nu p})+T^{\gamma }{}_{\lambda \mu }S_{\gamma }{}^{\nu \lambda }+\frac{1}{4}\delta ^{\nu }_{\mu }T\right) =0.\nonumber \\ \end{aligned}$$

(12)

Here $D_{\nu }V^{\mu }$ is the teleparallel form of the covariant derivative, which is defined as

$$\begin{aligned} D_{\nu }V^{\mu }=\partial _{\nu }V^{\mu }+(\Gamma ^{\mu }{}_{\lambda \nu }-K^{\mu }{}_{\lambda \nu })V^{\lambda }. \end{aligned}$$

(13)

From Eq. (11) one may obtain

$$\begin{aligned} D_{\nu }\Theta _{\mu }{}^{\nu }=0. \end{aligned}$$

(14)

Since this work depends on anisotropic fluid material contents, the stress-energy tensor is stated as

$$\begin{aligned} \Theta _{\mu }{}^{\nu }=(\rho +p_t)u_{\mu }u^{\nu }-p_t \delta _{\mu }^{\nu }+(p_r -p_t)v_{\mu }v^{\nu }. \end{aligned}$$

(15)

For a space-like velocity vector, the notation $u_\mu$ can be used, where $u_0 u^0=1$. The unitary space-like vector along the radial direction is $v^\nu$, where $v_1v^1=-1$, and the radial and tangential pressure components are $p_r$ and $p_t$, respectively. It is crucial to note that $p_t-p_r\ne 0$, which specifies anisotropy, is justified by the surface tension within the stellar body. The most general form of static and spherically symmetric space-time is given by

$$\begin{aligned} ds^2=e^{a(r)}dt^2-e^{b(r)}dr^2-r^2(d \theta ^2+\sin ^2 \theta d\varphi ^2). \end{aligned}$$

(16)

Here a(r) and b(r) are arbitrary functions of the radial coordinate r. It is widely acknowledged that the Einstein theory of gravity is predicated on the supposition that $\Theta ^{\nu }{}_{\mu ;\nu }=0$. Rastall asserts, based on a few presumptions, that the relation $\Theta ^{\nu }{}_{\mu ;\nu }=0$ has been accepted and all of those presumptions are still up to criticism. According to his presumption $\Theta ^{\nu }{}_{\mu ;\nu }=a_{\mu }$, the function $a_\mu$ should vanish in flat space-time, as noted in [71]. As it is admitted that curvature space-time and gravitation are similar in nature, i.e., the gravitational field generated by the existence of matter generates curvature and vice versa. So, the factor $T_{\mu \nu }$ must be determined by the curvature. As an example, one may assume an elastic sphere of an elementary particle. So the existence of non-vanishing curvature tidal gravitational forces is produced which reshape the sphere by altering its rest mass and energy [71]. In light of the argument presented above, Rastall formulated the following relationship about energy conservation,

$$\begin{aligned} \Theta ^{\nu }{}_{\mu ;\nu }=\lambda R_{,\mu }, \end{aligned}$$

(17)

where, $\lambda$ notions the Rastall constant [71]. This Eq. (17) shows the relationship between matter and geometry, and how matter-geometry can be formed or destroyed. The stress-energy tensor $D_{\nu }\Theta _{\mu }{}^{\nu }$ in Eq. (11) is a function based on torsion that vanishes in flat space-time. Then, using Rastall formula in Eq. (17), we take

$$\begin{aligned} D_{\nu }\Theta _{\mu }{}^{\nu }=\frac{\lambda }{4}T_{,\mu }, \end{aligned}$$

(18)

where T denotes the torsion scalar and $\lambda$ is a real Rastall constant. The support of geometry’s torsion produces an alliance between matter and geometry. By incorporating Eqs. (15–16) into Eqs. (11) and (18), we get the field equations as follows,

$$\begin{aligned} \rho= & {} \frac{\frac{e^{-b(r)} \left( a'(r)+b'(r)\right) }{2 r}+\frac{1}{2 r^2}+\frac{1}{4} (\lambda -1) T(r)}{4 \pi }, \end{aligned}$$

(19)

$$\begin{aligned} p_r= & {} \frac{\frac{1}{4} (-(\lambda -1)) T(r)-\frac{1}{2 r^2}}{4 \pi }, \end{aligned}$$

(20)

$$\begin{aligned} p_t= & {} \frac{\frac{1}{2} e^{-b(r)} \left( \frac{a''(r)}{2}+\left( \frac{a'(r)}{4}+\frac{1}{2 r}\right) \left( a'(r)-b'(r)\right) \right) }{4 \pi } \nonumber \\{} & {} -\frac{\frac{1}{4} \lambda T(r)}{4 \pi }. \end{aligned}$$

(21)

The extraction of Eq. (7) gives the torsion written as

$$\begin{aligned} T(r)=\frac{\left( 2 e^{-b(r)}\right) \left( a'(r)+\frac{1}{r}\right) }{r}, \end{aligned}$$

(22)

where prime denotes the derivative with respect to r (radial coordinate).

To close the stellar system, we select two unknown viz., $e^{a(r)}$ and $e^{b(r)}$ using a well-known Karmarkar condition via an embedding approach provided as,

$$\begin{aligned} R_{1414}R_{2323}=R_{1212}R_{3434}+R_{1224}R_{1334}. \end{aligned}$$

(23)

Here $R_{2323}\ne 0$ (this is known as Pandey–Sharma constraint). It is worth noting that the space-time that agrees with this requirement is known as embedding space-time. By plugging the Ricci scalar values into Eq. (23), we get the differential equation (24) shown below,

$$\begin{aligned} \frac{b'(r)a'(r)}{1-e^{b(r)}}=-2\left( a''(r)+a^{'2}(r)\right) +a^{'2}(r){+}b'(r)a'(r).\nonumber \\ \end{aligned}$$

(24)

The following formula occurs from simplifying (24) in terms of $e^{b(r)}$,

$$\begin{aligned} e^{b(r)}=k_1+1+a^{'}(r)^2e^{a(r)}. \end{aligned}$$

(25)

For simplicity, we select the gravitational potential $e^{a(r)}$ as,

$$\begin{aligned} e^{a(r)}=\zeta _1 \left( \zeta _2 r^2+1\right) ^{\eta }. \end{aligned}$$

(26)

Term $\eta$ (an integer) is important to construct the physical solutions of stellar objects. For physical solutions, $\eta$ varies from 3 to $\infty$. $\eta <3$ does not contain any physical solutions. If $\eta \rightarrow \infty$, then the metric function $e^{a(r)}$ takes the form $e^{a(r)} = \zeta _1 e^{C_1 r^2}$, where $C_1=n\zeta _2$. In our study we discussed the the compact stars solution by variating $\eta$ from 3 to 20. By substituting the Eq. (26) into the Eq. (25), we obtain $e^{b(r)}$ as stated,

$$\begin{aligned} e^{b(r)}=\zeta _2 \zeta _3 r^2 \left( \zeta _2 r^2+1\right) ^{\eta -2}+1. \end{aligned}$$

(27)

Using Eqs. (26 and 27) in Eqs. (19–21), we obtain the following final formulations for $\rho$, $p_r$, and $p_t$,

$$\begin{aligned} \rho= & {} \frac{1}{8 r^2 \left( \pi \zeta _2 \zeta _3 r^2 \left( \zeta _2 r^2+1\right) ^{\eta -2}+\pi \right) }\nonumber \\{} & {} \times \Big [\lambda +\zeta _2 \zeta _3 r^2 \left( \zeta _2 r^2+1\right) ^{\eta -2}+\frac{2 \zeta _2 \eta \lambda r^2}{\zeta _2 r^2+1}\nonumber \\{} & {} +\frac{2 \zeta _2 \zeta _3 r^2 \left( \zeta _2 (\eta -1) r^2+1\right) \left( \zeta _2 r^2+1\right) ^{\eta -1}}{\zeta _2^2 r^4+\zeta _2 r^2 \left( \zeta _3 \left( \zeta _2 r^2+1\right) ^{\eta }+2\right) +1}\Big ],~ \end{aligned}$$

(28)

$$\begin{aligned} p_r= & {} -\frac{1}{8 r^2 \left( \pi \zeta _2 \zeta _3 r^2 \left( \zeta _2 r^2+1\right) ^{\eta -2}+\pi \right) }\nonumber \\{} & {} \times \Big [\lambda +\zeta _2 \zeta _3 r^2 \left( \zeta _2 r^2+1\right) ^{\eta -2}+\frac{2 \zeta _2 \eta (\lambda -1) r^2}{\zeta _2 r^2+1}\Big ], \end{aligned}$$

(29)

$$\begin{aligned} p_t= & {} -\frac{\left( \zeta _2 r^2+1\right) }{8 \pi \left( \zeta _2^2 r^5+\zeta _2 r^3 \left( \zeta _3 \left( \zeta _2 r^2+1\right) ^{\eta }+2\right) +r\right) ^2} \nonumber \\{} & {} \times \Big [\lambda +\zeta _2^3 r^6 \left( -\eta ^2+2 \eta \lambda +\lambda \right) \nonumber \\{} & {} +\zeta _2 r^2 \Big [2 \eta (\lambda -1)+3 \lambda +\zeta _3 (\lambda +1) \left( \zeta _2 r^2+1\right) ^{\eta }\Big ]\nonumber \\{} & {} -\zeta _2^2 r^4 \left( \eta ^2+\eta (2-4 \lambda )-3 \lambda \right. \nonumber \\{} & {} \left. -\zeta _3 (2 \eta \lambda +\lambda -1) \left( \zeta _2 r^2+1\right) ^{\eta }\right) \Big ]. \end{aligned}$$

(30)

3 Matching conditions

The measurement of the study’s metric function-related unknowns is a crucial step in the study of compact stars since it directly affects how exactly the findings can be relied upon. Here, we match the interior space-time expressed in (16) to the exterior Schwarzschild space-time given by,

$$\begin{aligned} ds^2= & {} \left( 1-\frac{2M}{R}\right) dt^2-\left( 1-\frac{2M}{R}\right) ^{-1}dr^2-r^2\nonumber \\{} & {} \quad \left( d\theta ^2+\sin ^2\theta d\phi ^2\right) . \end{aligned}$$

(31)

A wonderful way to compare internal and external space-time is supplied by the following system at boundary $r=R$,

$$\begin{aligned} \zeta _1 \left( \zeta _2 r^2+1\right) ^{\eta }= & {} 1-\frac{2 M}{R}, \end{aligned}$$

(32)

$$\begin{aligned} \zeta _2 \zeta _3 r^2 \left( \zeta _2 r^2+1\right) ^{\eta -2}+1= & {} \frac{1}{1-\frac{2 M}{R}}, \end{aligned}$$

(33)

$$\begin{aligned} \zeta _1 \zeta _2 \eta r \left( \zeta _2 r^2+1\right) ^{\eta -1}= & {} \frac{M}{R^2}. \end{aligned}$$

(34)

The following constant expressions are obtained at boundary $r=R$ by solving the set of equations represented by ((32) to (34)),

$$\begin{aligned} \zeta _1= & {} \frac{(R-2 M) \left( 1-\frac{M}{2 \eta M+M-\eta R}\right) ^{-\eta }}{R}, \end{aligned}$$

(35)

$$\begin{aligned} \zeta _2= & {} -\frac{M}{R^2 (2 \eta M+M-\eta R)}, \end{aligned}$$

(36)

$$\begin{aligned} \zeta _3= & {} \frac{2 \eta ^2 (2 M-R) \left( 1-\frac{M}{2 \eta M+M-\eta R}\right) ^{-\eta }}{2 \eta M+M-\eta R}. \end{aligned}$$

(37)

The values of these constants are calculated in Table 1 for compact stars LMC X-4, Cen X-3, EXO 1785-248 respectively.

Table 1 The values of model constants using mass and radius of Stars LMC X-4 [81], Cen X-3 [82] and EXO 1785-248 [83] for different values of $\eta$. Here we have fixed $\lambda =044416$

4 Physical analysis of the anisotropic solutions in Rastall’s teleparallel gravity

The fundamental focus of the study of compact stars is the discussion of the stellar system’s physical properties. In this section, we provide a detailed physical analysis of our solutions presented here for anisotropic stellar configurations generated by an embedding class one approach in Rastall’s teleparallel gravity. We will look at the graph’s trends for three different realistic compact stars, namely LMC X-4 [81], Cen X-3 [82], and EXO 1785-248 [83], to see how they stand up physically.

Fig. 1

Shows metric potentials of stars with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 2

Shows the energy density profile of stars ($\rho$ in [$km^{-2}$] vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 3

Shows the radial pressure profiles of stars ($p_r$ in [km$^{-2}]$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 4

Shows the tangential pressure profile of stars ($p_t$ in [km$^{-2}]$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 5

Shows the radial component of EoS of stars ($\frac{p_r}{\rho }$ dimensionless vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 6

Shows the tangential component of EoS of stars ($\frac{p_t}{\rho }$ dimensionless vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 7

Shows the gradient component of stars ($\frac{d\rho }{dr}$ in [km$^{-2}]$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 8

Shows the gradient component of stars ($\frac{d p_r}{dr}$ in [km$^{-2}]$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 9

Shows the gradient component of stars ($\frac{d p_t}{dr}$ in [km$^{-2}]$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 10

Shows the anisotropic profile of stars ($\Delta$ in [km$^{-2}]$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

4.1 Physical behavior of metric potentials, energy, pressure, Eos and gradients profiles

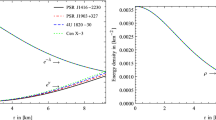
It is necessary for the gravitational pull responsible components of the metric space to exhibit regular and smooth behavior, such as $e^{a(r)}>0$ and $e^{b(r)}>0$. The behavior of three stars, LMC; X-4, Cen; X-3, EXO;1785-248, is shown in Fig. 1. It is clear that this behavior fits the desired behavior perfectly. An important quality that shows the stellar body’s physical existence is its energy profile. The energy density of a stellar body should, by definition, be positive and maximum at the center ($r\rightarrow 0$), and then show a smooth and coherent decrease towards the stellar surface ($r\rightarrow R$), where it should be minimum. The energy density behavior is perfectly consistent with the requirement, as shown by the graphs in Fig. 2. The physical existence of compact stellar objects can also be shown by pressure profiles like $p_r$ and $p_t$. These parameters, like energy density, have maximum values at the center and then smoothly fall to reach their minimum values at the stellar boundary ($p_t>p_r$ and $p_r|_{r=R}\rightarrow 0$ and $p_t|_{r=R}>0$). The findings of our solutions in this manuscript clearly show that they meet the necessary requirements for pressure profiles, as shown in Figs. 3 and 4. Nevertheless, the positive and negative behaviors of equation of state (EoS) are employed to determine the matter composition of a stellar body and whether it is made up of normal or dark matter. The behavior of EoS for a normal matter distribution should be positive and lie between 0 and 1 (like $0<w_r,w_t <1$). Otherwise, the matter composition is considered exotic if this criterion is not satisfied. The expression for EoS is,

$$\begin{aligned} w_r = \frac{p_r}{\rho }\;\;\;\;\text {and} \;\;\;\;w_t = \frac{p_t}{\rho }. \end{aligned}$$

(38)

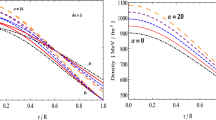
The behavior of graphs, as shown in Figs. 5 and 6, reflects the real distribution of matter. On the other hand, gradients profiles $\frac{d\rho }{dr}\;\frac{dp_r}{dr}\;\frac{dp_t}{dr}$ should be rising negatively starting at zero and moving toward the center such as $\frac{d\rho }{dr}|_{r=0}=\frac{dp_r}{dr}|_{r=0}=\frac{dp_t}{dr}|_{r=0}=0$, otherwise $\frac{d\rho }{dr},\frac{dp_r}{dr},\frac{dp_t}{dr}<0$ in the entire matter distribution. Figures 6, 7, 8 and 9 displays the graphs of gradient profiles. The behavior of $p_t$ is somewhat different since it propagates into negative behavior after starting at zero in the center and showing positive values near the center (for some values of $\eta$).

Fig. 11

Shows the energy limit profile of stars ($\rho -p_r$ in [km$^{-2}]$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 12

Shows the energy limit profile of stars ($\rho -p_t$ in [km$^{-2}]$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 13

Shows the energy limit profile of stars ($\rho +p_r+2p_t$ in [km$^{-2}]$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 14

Shows the velocity of sound profile of stars ($v_{r}^{2}$ in [km$^{-2}]$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 15

Shows the velocity of sound profile of stars ($v_{t}^{2}$ in [km$^{-2}]$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

4.2 Physical behavior of anisotropic profiles

By neutralizing the effect of gradients on the stellar system, anisotropy balancing is maintained. In this context, a positive anisotropic factor ($\Delta =p_t-p_r$ where $p_t>p_r$) acts as a repulsion force that balances the gradient attraction force and improves the system’s equilibrium and stability. Also, $\Delta \rightarrow 0$ when $r\rightarrow 0$ i.e., at the stellar body’s center, when $p_t$ and $p_r$ are both equal and hence the anisotropy is zero. Consequently, this phenomena allows for a more massive and compact formation. The graph of anisotropy in Fig. 10 is regular and increasing. It is evident that in our solutions for compact stellar systems, anisotropy propagates from negative to positive for one value of $\eta =3$ (Solid).

Fig. 16

Shows the casuality condition profile of stars ($v_{t}^{2}-v_{r}^{2}$ and $v_{r}^{2}-v_{t}^{2}$ in [km$^{-2}]$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 17

Shows the forces profile of stars ($F_i$ in [km$^{-2}]$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 18

Shows the adiabatic index profile of stars ($\Gamma _r$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

4.3 Physical behavior of energy conditions profiles

The behavior of energy constraints also ensures a physically plausible distribution. The stellar energy must be distributed evenly throughout the stellar mass and may admit some inequalities, which are famously known as Strong Energy Conditions (SEC), Null Energy Conditions (NEC), Weak Energy Conditions (WEC), and Dominant Energy Conditions (DEC) as seen below in the relations,

$$\begin{aligned} SEC&:&\rho +p_\gamma \ge 0,\rho +p_r+2p_t\ge 0, \end{aligned}$$

(39)

$$\begin{aligned} WEC&:&\rho \ge 0,\rho +p_\gamma \ge 0, \end{aligned}$$

(40)

$$\begin{aligned} NEC&:&\rho +p_\gamma \ge 0, \end{aligned}$$

(41)

$$\begin{aligned} DEC&:&\rho >|p_\gamma |. \end{aligned}$$

(42)

Figures 11, 12 and 13 shows the graphs of positive energy constraints in our stellar system.

4.4 Stability analysis via causality conditions and adiabatic index

The sound speeds $v^{2}_{sr}$ and $v^{2}_{st}$ are crucial indicators of the system’s stability. The following expressions represent sound speeds in mathematical form,

$$\begin{aligned} \begin{aligned} v^2_r=\frac{d p_r}{d\rho }\;\;\text {and}\;\; v^2_t=\frac{d p_t}{d\rho }. \end{aligned} \end{aligned}$$

(43)

The region for stability $v^2_r>v^2_t$ was specified by Abreu et al. [72], where there is no change of sign is observed in $v^2_r-v^2_t$. Andréasson [73] then floated the concept of no cracking and stability region to present a more generalized form of this requirement as $0<|v^2_t-v^2_r|<1$. The results of our stellar system are shown in Figs. 14, 15 and 16. For some values of $\eta$, our results in the center and very close to the center break the stability conditions followed by $v^2_t$. For all circumstances, the Abreu and Andréasson limits for stability are followed a little away from the center.

We keep focusing on the stability of our anisotropic stellar models generated by an embedding class one approach in Rastall’s teleparallel gravity. But this time, we do it employing the adiabatic index, which was first derived for isotropic pressure gradients by Chandrasekhar [76, 77].

Adiabatic index is a crucial factor for indicating the system’s stability. The adiabatic index predicts the solidity of the compact objects as a crucial component in the case study of spherically symmetric space-time. According to literature [78], the adiabatic index limit is $\Gamma >\frac{4}{3}$. If this limit of the adiabatic index inside the star’s radius is met, the stellar composition is stable. The expression represents the adiabatic index $\Gamma$ in its mathematical form,

$$\begin{aligned} \Gamma \equiv \Gamma _r =\frac{p_r + \rho }{p_r} v^{2}_r. \end{aligned}$$

(44)

It is clear from Fig. 18 that the adiabatic index profile’s stability and solidity limit are admissible in our case study of stellar systems.

4.5 Physical behavior of Tolman–Oppenheimer–Volkoff equilibrium

We provide the well-known Tolman–Oppenheimer–Volkoff (TOV) equation, which has been indicated as an equilibrium criteria for stellar systems [74, 75]. Their modified version for Rastall’s teleparallel gravity is turns out to be,

$$\begin{aligned}{} & {} \frac{d p_r}{dr}+\frac{\nu ^{'}(\rho +p_r)}{2}-\frac{2(p_t-p_r)}{r}\nonumber \\{} & {} \quad -\frac{\lambda }{4\lambda -1} \left( \frac{d\rho }{dr}-\frac{dp_r}{dr}-\frac{dp_t}{dr}\right) =0,~~ \end{aligned}$$

(45)

$$\begin{aligned}{} & {} F_g+F_h+F_a+F_r=0, \end{aligned}$$

(46)

where

$$\begin{aligned} F_g= & {} -\frac{\nu ^{'}(\rho +p_r)}{2}, \end{aligned}$$

(47)

$$\begin{aligned} F_h= & {} -\frac{d p_r}{dr}, \end{aligned}$$

(48)

$$\begin{aligned} F_a= & {} \frac{2(p_t-p_r)}{r}, \end{aligned}$$

(49)

$$\begin{aligned} F_r= & {} \frac{\lambda }{4\lambda -1}\left( \frac{d\rho }{dr}-\frac{dp_r}{dr}-\frac{dp_t}{dr}\right) . \end{aligned}$$

(50)

These forces ($F_g,\;F_h,\;F_a$ and $F_r$) balance each other to maintain the stellar body in equilibrium. The system is kept from collapsing to a point singularity by the balancing effect of TOV forces. The graphs of these regular and balanced forces are shown in Fig. 17.

4.6 Physical behavior of mass function, redshift and compactification profiles

The mass-to-radius ratio $\frac{m(R)}{R}$ and its relationship to the stellar system’s degree of compactification are both described. The mass function m(R) utilized in this ratio can be calculated using the formula,

$$\begin{aligned} m(R)= & {} 4\pi \int r^2 \rho dr. \end{aligned}$$

(51)

The compactness degree u is specified by the mass function m(R) in Eq. (51), which is then employed to compute the redshift function $z_s$.

$$\begin{aligned} u= & {} \frac{m(R)}{R}, \end{aligned}$$

(52)

$$\begin{aligned} z_s= & {} \left( 1-2u\right) ^{-\frac{1}{2}}-1. \end{aligned}$$

(53)

The aforementioned characteristics must satisfy some criterion available in literature on the study of compact objects. In the research [79], the peak value for the compactness factor was proposed as $u=\frac{m(R)}{R}<\frac{4}{9}$ for isotropic matter. Further this limit was generalized by Andréasson [73] for anisotropic matter. The maximum value for the redshift, according to Buchdhal’s findings [80], is $z_s\le 4.77$. The graphed mass function in Fig. 19 predicts a regular and smooth behavior that is very similar to the original masses of the stars selected for this current study. The compactness and redshift parameter graphs shown in Figs. 20 and 21 are both regular and perfectly meet the specified requirements.

Fig. 19

Shows the mass function profile of stars, (m(r) in $[M_{\odot }]$ vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 20

Shows the compactification profile of stars (u(r) vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

Fig. 21

Shows the redshift profile of stars (z(r) vs. radial coordinate, r in [km]), with $\eta =3\; (Solid)$, $\eta =5\; (Dotted)$, and $\eta =20\; (Dashed)$

5 Concluding remarks

In this study, we have successfully investigated a new anisotropic solution for compact stellar configurations having observed mass and radius under the influence of Rastall Teleparallel gravity. For this purpose, we explore the key components of spherically symmetric metric space, using the embedding class one spacetime paradigm with Karmarkar’s condition. Following that, we evaluated the unknown constants using well-known junction conditions taking Schwarzschild space-time as the exterior geometry. The major objective of our research is to construct a new realistic family of Rastall Teleparallel gravity solutions in the presence of anisotropic fluid. It is interesting to mention that the parameter $\eta$ has an important role in the current study. We have checked the effect of $\eta$ for larger values like $\eta =20$ and found that the small values of $\eta$ affect the results and larger values of $\eta$ have a minor effect on our investigations. So, we limited ourselves to the small values of $\eta$ like $\eta =3$, $\eta =5$, and $\eta =20$. The relevant findings are presented here.

Table 2 Summary of calculated results using observed values of stars LMC X-4 [81], Cen X-3 [82] and EXO 1785-248 [83]

Firstly, as can be shown in Fig. 1, the behavioral response of the metric potentials is regular, positive, and in accordance with the principles of the embedding class one spacetime paradigm with Karmarkar’s condition. Secondly, the behavioral propagation of energy density $\rho$ is positive, regular, and smoothly declines from maximum to minimum from center to the boundary as shown in Fig. 2. Similarly, pressure profiles are also positive and regular as shown in Figs. 3 and 4 such that $p_t>p_r$ and $p_r\rightarrow 0$ as $r\rightarrow 0$. Meanwhile, as shown in Figs. 5 and 6, $\frac{p_r}{\rho }$ and $\frac{p_r}{\rho }$ are regular, positive and express the essence of real matter by admitting $0\le \frac{p_r}{\rho },\frac{p_r}{\rho }<1$ as shown in Figs. 5 and 6. However, gradients profiles $\frac{\rho }{dr},\;\frac{p_r}{dr}$ and $\frac{p_t}{dr}$ are also regular and negatively propagating as can be seen in Figs. 7, 8 and 9. But $\frac{p_t}{dr}$ violates the condition $\frac{p_t}{dr}\le 0$ for some values of $\eta$, detail is given in Table 2. Furthermore, anisotropy is positive and regular, with an increasing trend along the radius r, indicating the stellar system’s equilibrium. But, for for $\eta =3$, anisotropy violates the principle by propagating from negative to positive, as seen in Fig. 10. According to Figs. 11, 12 and 13, the energy conditions are justified and represent the realistic matter distribution.

A stability analysis using adiabatic index and superluminal speeds reveals that the eventual models are stable. On the one hand, sound speeds $v_{t}^{2}$ and $v_{r}^{2}$are well within limits, indicating the system’s general stability. But near the center $v_{t}^{2}$ violates the stability criteria for some values of $\eta$ as shown in Table 2, before returning to the stability seen in Figs. 14 and 15. Stability by cracking concept limit is also supported, as graphed in Fig. 16. On the other hand, the plot in Fig. 18 shows that the adiabatic index, which follows the constraint $\Gamma _r>\frac{4}{3}$, predicts that our system of stellar objects is solid, anisotropic and completely stable. Additionally, TOV forces are balanced, ensuring the stellar system’s equilibrium as shown by Fig. 17. As observed in Figs. 19, 20 and 21, the graphic behavior of the mass function, compactification, and redshift function is regular and appropriate.

We have shown a comparative and interesting result with the one announced by Nashed and El Hanafy [84] in the Rastall theory of gravity. Further studies by Nashed and El Hanafy [84] provide a non-trivial class of anisotropic compact stellar models and reveal that the matter-geometry coupling in Rastall gravity allows a size slightly smaller than GR for a given mass. They showed that the mass of candidate stellar configurations increases with progressively increasing values of the surface densities and reached the maximum possible mass with stable configurations using strong energy condition (SEC) to set an upper limit on the compactness $u\approx 0.603$ (where the Rastall parameter goes to $-0.1$) less than Buchdahl compactness $u= 8/9$, which in our study is a captivating case because of the increasing estimates of the parameter $\eta$. Interestingly, Nashed and El Hanafy [84] found that in the context of Rastall gravity, the values of the physical quantity $z_s$ decrease accordingly as the Rastall parameter moves away from the GR, while in our case we find the same behavior in the context of Rastall teleparallel gravity, as the values of $\eta$ increase, the values of the physical quantity $z_s$ gradually decrease. It is therefore easy to compare the effects of Rastall gravity and Rastall teleparallel gravity by studying the physical quantity known as the redshift of the surface of compact stellar systems.

Finally, by getting witnessed from the foregoing arguments and also from the summarized results in Table 2 that our estimated results are, on the whole, acceptable, intriguing, and suitable for use in future research.