1 Introduction

Heavy quark system provides a unique window to understand the perturbative and nonperturbative nature of Quantum Chromodynamics (QCD) theory. The key quantity of the heavy quark system is the heavy quark mass with \(m_Q\gg \Lambda _{QCD}\), which is naturally employed to distinguish the perturbative and nonperturbative interactions. For the two heavy quark system such as heavy quarkonium and the threshold production of top quark pair, the non-relativistic QCD (NRQCD) effective theory is a very successful approach to separate the long-distance nonperturbative interactions and the short-distance perturbative interactions [1]. In this effective theory, the QCD observable can be further expanded into the NRQCD effective operator matrix elements with the corresponding matching coefficients. The matching coefficients can be calculated order by order and can be in series of two small parameters, i.e. the strong coupling constant \(\alpha _{s}\) and the quark relative velocity v.

Up to now, various matching coefficients for the two heavy quark currents, involving the \(b\bar{b}\), \(\bar{b}c \) and \(c\bar{c}\) systems, have been computed to higher-order accuracy within the NRQCD effective theory. Taking the double-heavy \(B_c^+ =\bar{b}c \) meson as an example, the next-to-leading order (NLO) matching coefficient for the axial-vector current was first obtained in 1995 [2]. Then, the NLO matching coefficient for the vector current was calculated in 1999 [3]. Later on, the NLO QCD corrections combined with the higher-order relativistic corrections for the axial-vector current and the vector current are investigated in Ref. [4]. The approximate result of the next-to-next-to-leading order (NNLO) QCD correction for the axial-vector current matching coefficient was first obtained in 2003 [5]. However, the complete analytical expression of the two-loop matching coefficient for the axial-vector current became available in 2015 [6]. Last year, the next-to-next-to-next-to-leading order ( NNNLO or N\(^3\)LO) QCD correction for the matching coefficient of the axial-vector current was first numerically calculated in Ref. [7]. Very recently, the two-loop matching coefficient of the vector current was evaluated by the authors of this work [8]. After that, the three-loop matching coefficient of the vector current was also achieved in Ref. [9].

For the case of heavy quark currents with equal masses, the matching coefficient has been evaluated within the NRQCD factorization frame at high order by various literature. For example, the NNLO QCD correction can be found in Ref. [10], and the N\(^3\)LO QCD correction can be found in Refs. [11, 12]. For more precision calculations about matching coefficients for doubly heavy quark systems, one can see the following literature  [11,12,13,14,15,16,17, 17,18,19,20,21,22,23,24,25,26,27,28,29].

However, the matching coefficient for the flavor-changing scalar current involving the heavy bottom and charm quark has not yet been found in previous works. Considering the state-of-the-art theoretical accuracy of the matching coefficients for other heavy quark currents, we will compute the matching coefficient for the flavor-changing heavy quark scalar current of the \(B_c\) meson family up to the three-loop QCD corrections within the NRQCD factorization frame. The novel calculation is helpful to analyze the threshold behaviours when two different heavy quarks such as the bottom and the charm quark are close to each other. In addition, the three-loop QCD matching procedure for the heavy flavor-changing scalar current of the \(B_c\) meson family provides a window to check the convergence of the perturbative series of the NRQCD effective theory.

The rest of the paper is arranged as follows. In Sect. 2, we introduce the matching formula between the full QCD theory and the NRQCD effective theory. We present the analytical results of the three-loop scalar current renormalization constant and the corresponding anomalous dimension in the NRQCD effective theory. We also discuss the matching and running equations for the strong coupling constant \(\alpha _{s}\). In Sect. 3, we give our calculation procedure and the projection for the heavy flavor-changing scalar current. In Sect. 4, we present our numeric results of the matching coefficient up to the three-loop order accuracy. Finally, we summarize in Sect. 5.

2 Matching formula  

The heavy flavor-changing scalar current involving \(\bar{b}\) and c quark in the full QCD can be written as \(j_s(y)=\bar{\Psi }_b(y) \Psi _c(y)\), which can be further expanded into the NRQCD effective scalar current

$$\begin{aligned} \tilde{j}_s(y)=-\frac{\chi ^\dag _b(y) \vec {p}\cdot \vec {\sigma }\psi _c(y)}{2m_\textrm{red}}, \end{aligned}$$
(1)

with the reduced heavy quark mass \(m_\textrm{red}=m_b m_c/(m_b+m_c)\) and the quark relative momentum p, at the leading order of quark relative velocity according to the definition as given in Ref. [10]. \(\psi \) is the two-component Pauli spinor field that annihilates a heavy quark, while \(\chi \) is the two-component Pauli spinor field that creates a heavy anitiquark. The matching coefficient can be determined through the conventional perturbative matching procedure. Namely, one performs renormalization for the on-shell vertex functions in both the perturbative QCD and the NRQCD sides, then solves the matching coefficient order by order in \(\alpha _s\).

The matching formula with renormalization procedure reads

$$\begin{aligned} \sqrt{Z_{2,b} Z_{2,c} } \,Z_s \, \Gamma _s^0= & {} {\mathcal {C}}_s(\mu _f,\mu ,m_b,m_c) \, \sqrt{\widetilde{Z}_{2,b} \widetilde{Z}_{2,c} } \, {\widetilde{Z}}_s^{-1} \, \widetilde{\Gamma }_s^0 \nonumber \\{} & {} + {\mathcal O}(v^2), \end{aligned}$$
(2)

where the left hand part of the equation represents the renormalization of the full QCD current while the right hand part represents the renormalization of the NRQCD current. The term \({\mathcal O}(v^2)\) denotes the higher order relativistic corrections in powers of the heavy quark relative velocity v between the bottom quark \(\bar{b}\) and the charm quark c. \(\Gamma _s^0\) (\(\widetilde{\Gamma }_s^0\)) denotes the on-shell unrenormalized heavy flavor-changing current vertex function in the QCD (NRQCD) theory, and the leading-order (LO) matching coefficient is normalized into 1. In this paper, we will consider higher-order QCD corrections up to \({\mathcal O}(\alpha _s^3)\) but at the lowest order in heavy quark relative velocity v [19, 29]. \(Z_s\) is the QCD current renormalization constant in on-shell (\(\textrm{OS}\)) scheme, i.e., \(Z_s=\frac{m_b Z_{m,b}+m_c Z_{m,c}}{m_b+m_c}\). And \(\tilde{Z}_s\) is the renormalization constant of the NRQCD effective current in the modified-minimal-subtraction (\(\mathrm {\overline{MS}}\)) scheme. \(Z_{2}\) and \(Z_{m}\) are QCD on-shell quark field and mass renormalization constants, respectively. The three-loop analytical results of the on-shell quark field and mass renormalization constants allowing for two different non-zero quark masses can be found in literature [30,31,32], which can be evaluated to high numerical precision with the package PolyLogTools [33]. The QCD coupling \(\mathrm {\overline{MS}}\) renormalization constant can be found in literature [34,35,36]. The NRQCD on-shell quark field renormalization constants \(\tilde{Z}_{2,b}=\tilde{Z}_{2,c}=1\), since all light particles in NRQCD are massless. The matching coefficient \({\mathcal {C}}_s(\mu _f,\mu ,m_b,m_c)\) depends on the NRQCD factorization scale \(\mu _f\) and the QCD renormalization scale \(\mu \) in a finite order QCD correction calculation.

After implementing the quark field, quark mass and the QCD coupling constant renormalization, the QCD vertex function gets rid of ultra-violet (UV) poles, while still contains uncancelled infra-red(IR) poles starting from order \(\alpha _s^2\). The remaining IR poles in QCD should be exactly cancelled by the UV divergences of \({\widetilde{Z}}_s\) in NRQCD, which renders the matching coefficient finite. With the aid of the obtained high-precision numerical results, combined with the features of the NRQCD current renormalization constants investigated in other known literature [7, 9, 12, 29], we have successfully reconstructed the exact analytical expression of the NRQCD renormalization constant for the flavor-changing heavy quark scalar current through numerical fitting recipes [33, 37, 38]. Here we directly present the final result as following

$$\begin{aligned} \widetilde{Z}_s\left( x, {\mu ^2_f\over m_b m_c } \right)= & {} 1+\left( \frac{\alpha _{s}^{\left( n_{l}\right) }\left( \mu _f\right) }{\pi }\right) ^{2} \widetilde{Z}_s^{(2)}(x)\nonumber \\{} & {} +\left( \frac{\alpha _{s}^{\left( n_{l}\right) }\left( \mu _f\right) }{\pi }\right) ^{3} \nonumber \\ {}{} & {} \widetilde{Z}_s^{(3)}\left( x,\frac{\mu ^2_f}{m_bm_c} \right) +{\mathcal {O}}(\alpha _s^4), \end{aligned}$$
(3)

where the coefficients \( \widetilde{Z}_s^{(2)}(x)\) and \(\widetilde{Z}_s^{(3)}\left( x,\frac{\mu ^2_f}{m_bm_c} \right) \) are of the following form

$$\begin{aligned} \widetilde{Z}_s^{(2)}(x)= & {} \pi ^{2}C_{F} \frac{1}{\epsilon }\left( \frac{3x^2+10x+3}{24\left( 1+x\right) ^2}C_{F}+\frac{1}{24}C_{A}\right) ,\nonumber \\ \end{aligned}$$
(4)
$$\begin{aligned} \widetilde{Z}_s^{(3)}\left( x,\frac{\mu ^2_f}{m_bm_c} \right)= & {} \pi ^{2}C_{F} \left\{ \frac{C_F^2}{\epsilon }\left( \frac{57x^2+146x+57}{216(x+1)^2}-\frac{\ln 2}{3}\right) \right. \nonumber \\{} & {} \left. -\frac{C_F C_A}{\epsilon ^2} \frac{11 x^2+41 x+11}{216 (x+1)^2 } \right. \nonumber \\{} & {} \left. + \frac{C_FC_A}{1296 \epsilon }\bigg [ \frac{379 x^2+1086x+379}{(x+1)^2}\right. \nonumber \\{} & {} \left. -72 \ln 2-\frac{9 (5 x+11) }{x+1}\ln x \right. \nonumber \\{} & {} \left. +144\nonumber \ln (x+1)\right. \nonumber \\{} & {} \left. +\frac{9 \left( 11 x^2+28 x+11\right) }{(x+1)^2}\ln \frac{\mu _f^2}{m_b m_c} \bigg ] \right. \nonumber \\{} & {} \left. + C_A^2\left[ \frac{-1}{48 \epsilon ^2}+\frac{1}{648 \epsilon }\Bigg (34+72 \ln 2 \right. \right. \nonumber \\{} & {} \left. \left. -9 \ln x+18 \ln (x+1)+9 \ln \frac{\mu _f^2}{m_b m_c}\Bigg )\right] \right. \nonumber \\{} & {} \left. + C_F T_F n_l\bigg [\frac{3 x^2+10x+3}{108\epsilon ^2 (x+1)^2 }\right. \nonumber \\{} & {} \left. -\frac{21 x^2+74 x+21}{324 \epsilon (x+1)^2 }\bigg ]\right. \nonumber \\{} & {} \left. +C_A T_F n_l \bigg [\frac{1}{108 \epsilon ^2}-\frac{53}{1296 \epsilon }\bigg ]\right\} , \end{aligned}$$
(5)

where \(C_F=4/3,C_A=3,T_F=1/2\), and the parameter \(x =m_c/m_b\) representing the ratio of the heavy charm and bottom quark mass.

The corresponding anomalous dimension \(\tilde{\gamma }_{s}\) for the NRQCD scalar current is related to \(\tilde{Z}_s\) by [22, 39,40,41,42,43]

$$\begin{aligned} \tilde{\gamma }_s\left( x, {\mu ^2_f\over m_b m_c } \right)\equiv & {} {d \ln \widetilde{Z}_s \over d \ln \mu _f } \equiv \frac{-2\,\partial {\tilde{Z}_s^{[1]}}}{\partial \ln \alpha _s^{(n_l)}(\mu _f)} \nonumber \\= & {} \left( \frac{\alpha _s^{(n_l)} \left( \mu _f\right) }{\pi }\right) ^2 \tilde{\gamma }_s^{(2)}(x )\nonumber \\{} & {} +\left( \frac{\alpha _s^{\left( n_l\right) } \left( \mu _f\right) }{\pi }\right) ^3 \nonumber \\{} & {} \tilde{\gamma }_s^{(3)}\left( x, {\mu ^2_f\over m_b m_c }\right) +{\mathcal {O}}(\alpha ^4_s), \end{aligned}$$
(6)

where \(\tilde{Z}_{s}^{[1]}\) denotes the coefficient of the \(\frac{1}{\epsilon }\) pole in \(\tilde{Z}_s\), and the NRQCD factorization scale \(\mu _f\) is used because both \(\tilde{Z}_{s}\) and \(\tilde{\gamma }_{s}\) are defined in the NRQCD effective theory. The explicit expressions of the coefficients \(\tilde{\gamma }_s^{(2)}(x )\) and \(\tilde{\gamma }_s^{(3)}\left( x, {\mu ^2_f\over m_b m_c }\right) \) in Eq. (6) are of the form of

$$\begin{aligned} \tilde{\gamma }_s^{(2)}(x )= & {} -\pi ^2C_F\left[ C_F \frac{3 x^2+10 x+3}{6(x+1)^2} +\frac{C_A}{6} \right] , \end{aligned}$$
(7)
$$\begin{aligned} \tilde{\gamma }_s^{(3)}\left( x, {\mu ^2_f\over m_b m_c }\right)= & {} \pi ^2C_F\left\{ C_F^2 \left[ -\frac{57 x^2+146 x+57}{36 (x+1)^2}+2\ln 2 \right] \right. \nonumber \\{} & {} \left. + C_A^2\left[ -\frac{17}{54}-\frac{2 }{3}\ln 2+\frac{1}{12}\ln x-\frac{1}{6} \ln (x+1)\right. \right. \nonumber \\{} & {} \left. \left. -\frac{1}{12} \ln \frac{\mu _f^2}{m_b m_c}\right] \right. \nonumber \\{} & {} \left. + C_F C_A \left[ -\frac{379 x^2+1086 x+379}{216 (x+1)^2}\right. \right. \nonumber \\{} & {} \left. +\frac{\ln 2 -2\ln (x+1)}{3} \right. \nonumber \\{} & {} \left. \left. +\frac{5 x+11 }{24 (x+1)}\ln x-\frac{11 x^2+28 x+11}{24 (x+1)^2}\ln \frac{\mu _f^2}{m_b m_c}\right] \right. \nonumber \\{} & {} \left. + C_F T_F n_l \frac{21 x^2+74 x+21}{54 (x+1)^2}+\frac{53}{216} C_A T_F n_l \right\} .\nonumber \\ \end{aligned}$$
(8)

From above expressions, one can see that both of \(\tilde{Z}_{s}\) and \(\tilde{\gamma }_{s}\) explicitly depend on the NRQCD factorization scale \(\mu _f\), which is a feature found in other NRQCD currents [7, 9, 12, 19, 29]. Note that the above three-loop expressions of \(\widetilde{Z}_{s}\) and \(\tilde{\gamma }_{s}\) for the flavor-changing scalar current involving the heavy charm and bottom quark are known for the first time. The obtained \(\widetilde{Z}_{s}\) and \(\tilde{\gamma }_{s}\) have been checked with several different values of \(m_b\) and \(m_c\). To verify the correction of our results, on the one hand, one can check that above \(\widetilde{Z}_s\left( \tilde{\gamma }_{s}\right) \) is symmetric under the combined exchange of \(m_b\leftrightarrow m_c\) and \(n_b\leftrightarrow n_c\). On the other hand, in the equal quark mass case of \(x=1\), our \(\widetilde{Z}_s\) and \(\tilde{\gamma }_{s}\) are in full agreement with the known results as given in Refs. [10,11,12].

In our calculation, we include the contributions from the loops of heavy charm and bottom quarks in the full QCD, which however are decoupled in the NRQCD. To match the QCD with the NRQCD, one need apply the decoupling relation [13, 43,44,45,46,47,48] of the coupling constant \(\alpha _s\). Conventionally, heavy flavours are decoupled one at a time, e.g., one first decouples bottom quark then decouples charm quark. Up to two-loop order, the iterative decoupling relation [13] reads:

$$\begin{aligned} \frac{\alpha _s^{(n_f+1)}(\mu )}{\alpha _s^{(n_f)}(\mu )}= & {} 1 + \frac{\alpha _s^{(n_f)}(\mu )}{\pi } T_F \bigg [ \frac{1}{3} L + \left( \frac{1}{6} L^2 + \frac{1}{36} \pi ^2 \right) \epsilon \nonumber \\{} & {} +\left( \frac{1}{18} L^3 + \frac{1}{36} \pi ^2 L - \frac{1}{9} \zeta _3 \right) \epsilon ^2 + {\mathcal {O}}{(\epsilon ^3)} \bigg ]\nonumber \\{} & {} +\left( \frac{\alpha _s^{(n_f)}(\mu )}{\pi } \right) ^2 T_F \left\{ \left( \frac{1}{4} L +\frac{15}{16} \right) C_F\right. \nonumber \\{} & {} \left. + \left( \frac{5}{12} L -\frac{2}{9} \right) C_A \right. \nonumber \\{} & {} \left. + \frac{1}{9} T_F L^2 + \bigg [ \left( \frac{1}{4} L^2 + \frac{15}{8} L + \frac{1}{48} \pi ^2 + \frac{31}{32} \right) C_F \right. \nonumber \\{} & {} \left. +\left( \frac{5}{12} L^2 -\frac{4}{9} L + \frac{5}{144} \pi ^2 + \frac{43}{108} \right) C_A \right. \nonumber \\{} & {} \left. +\left( \frac{1}{9} L^3 + \frac{1}{54} \pi ^2 L \right) T_F \bigg ] \epsilon \right. \nonumber \\{} & {} \left. + {\mathcal {O}}{(\epsilon ^2)} \right\} + {\mathcal {O}}{(\alpha _s^3)}, \end{aligned}$$
(9)

where \(L =\ln (\mu ^2/m_Q^2)\) and \(m_Q\) is the on-shell mass of the decoupled heavy quark. As described in Refs. [47, 48], equivalently, one can also decouple the bottom and charm quarks simultaneously in a single step. The iterative decoupling approach and the simultaneous decoupling approach are equivalent up to two-loop order, while the power-suppressed deviation terms \((m_c/m_b)^n\) arising from the three-loop order between the two approaches are very small in magnitude and can be neglected. We consider QCD where \(n_\ell \) light flavours, \(n_c\) flavours with heavy mass \(m_c\), and \(n_b\) flavours with heavy mass \(m_b\) possibly appear in the quark loops, then the coupling constants \(\alpha _s^{(n_l+n_c+n_b)}(\mu )\) in QCD with \(n_l+n_c+n_b\) flavours and \(\alpha _s^{(n_l)}(\mu )\) in the NRQCD with \(n_l\) light flavours are directly related by the following expressions:

$$\begin{aligned} \frac{\alpha _s^{(n_l+n_c+n_b)}(\mu )}{\alpha _s^{(n_l)}(\mu )}= & {} 1+\frac{\alpha _s^{(n_l)}(\mu )}{\pi } \left\{ n_b T_F \bigg [\frac{L_b}{3}+\frac{1}{36} \epsilon \left( 6 L_b^2+\pi ^2\right) \right. \nonumber \\{} & {} +\frac{1}{36} \epsilon ^2 \left( 2 L_b^3+\pi ^2 L_b-4 \zeta (3)\right) \bigg ] \nonumber \\{} & {} + n_c T_F\bigg [\frac{L_c}{3}+\frac{1}{36} \epsilon \left( 6 L_c^2+\pi ^2\right) \nonumber \\{} & {} \left. +\frac{1}{36} \epsilon ^2 \left( 2 L_c^3+\pi ^2 L_c-4 \zeta (3)\right) \bigg ]+ {\mathcal {O}}{(\epsilon ^3)}\right\} \nonumber \\{} & {} +\left( \frac{\alpha _s^{(n_l)}(\mu )}{\pi }\right) ^2 \left\{ n_b^2 T_F^2 \bigg [\frac{L_b^2}{9}+\frac{1}{54} \epsilon \left( 6 L_b^2 +\pi ^2\right) L_b\bigg ]\right. \nonumber \\{} & {} +n_c^2 T_F^2\bigg [\frac{L_c^2}{9}+\frac{1}{54} \epsilon \left( 6 L_c^2+\pi ^2\right) L_c\bigg ] \nonumber \\{} & {} + C_F n_b T_F \bigg [\frac{1}{16}\left( 4 L_b+15\right) +\frac{1}{96} \epsilon \left( 24 L_b^2 \right. \nonumber \\{} & {} +180 L_b \left. +2 \pi ^2+93\right) \bigg ] \nonumber \\{} & {} + C_F n_c T_F\bigg [\frac{1}{16} \left( 4 L_c+15\right) +\frac{1}{96} \epsilon \left( 24 L_c^2 \right. \nonumber \\{} & {} +180 L_c\nonumber \left. +2 \pi ^2+93\right) \bigg ] \nonumber \\{} & {} +C_A n_b T_F \bigg [\frac{5 L_b}{12}-\frac{2}{9}+\frac{1}{432} \epsilon \left( 180 L_b^2-192 L_b \right. \nonumber \\{} & {} \left. +15 \pi ^2+172\right) \bigg ] \nonumber \\{} & {} +C_A n_c T_F \bigg [\frac{5 L_c}{12}-\frac{2}{9}+\frac{1}{432} \epsilon \left( 180 L_c^2-192 L_c \right. \nonumber \\{} & {} \left. +15 \pi ^2+172\right) \bigg ] \nonumber \\{} & {} +n_b n_c T_F^2 \left[ \frac{2 L_b L_c}{9}+\frac{1}{54} \epsilon \left( L_b+L_c\right) \left( 6 L_b L_c \right. \right. \nonumber \\{} & {} \left. \left. \left. +\pi ^2\right) \right] + {\mathcal {O}}{(\epsilon ^2)} \right\} +{\mathcal {O}}{(\alpha _s^3)}, \end{aligned}$$
(10)

where \(L_b =\ln (\mu ^2/m_b^2)\) and \(L_c =\ln (\mu ^2/m_c^2)=L_b-2\ln x\) with \(x=m_c/m_b\).

Besides, we can evolve the strong coupling from the scale \(\mu _f\) to the scale \(\mu \) with renormalization group running equation [49] in \(D=4-2 \epsilon \) dimensions as following

$$\begin{aligned} \alpha _s^{(n_l)}\left( \mu _f\right)&= \alpha _s^{(n_l)}\left( \mu \right) \left( \frac{\mu }{\mu _f}\right) ^{2\epsilon }\nonumber \\&\quad \times \bigg [1+\frac{\alpha _s^{(n_l)}\left( \mu \right) }{\pi }\frac{\beta _0^{(n_l)}}{4\epsilon }\left( \left( \frac{\mu }{\mu _f}\right) ^{2\epsilon }-1\right) \bigg ] + {\mathcal {O}}{(\alpha _s^3)}. \end{aligned}$$
(11)

To calculate the values of the strong coupling, we also use the renormalization group running equation [50] in \(D=4\) dimensions as

$$\begin{aligned} \frac{\alpha _s^{(n_l)}\left( \mu \right) }{4\pi }&= \frac{1}{\beta _0^{(n_l)}L_{\Lambda }}\nonumber \\&\quad -\frac{b_1 \ln L_{\Lambda }}{\left( \beta _0^{(n_l)}L_{\Lambda }\right) ^2}+\frac{b_1^2(\ln ^2 L_{\Lambda }-\ln L_{\Lambda }-1)+b_2}{\left( \beta _0^{(n_l)}L_{\Lambda }\right) ^3}\nonumber \\&\quad +{\mathcal {O}}{\left( \left( \frac{1}{L_{\Lambda }}\right) ^4\right) }, \end{aligned}$$
(12)

where \(L_{\Lambda }=\ln \left( \mu ^2/{\Lambda _{QCD}^{(n_l)}}^2\right) \) and \(b_i=\beta _i^{(n_l)}/{\beta _0^{(n_l)}}\). At the one-, two- and three-loop level, the coefficients of the QCD \(\beta \) function are of the form of

$$\begin{aligned} \beta _0^{(n_l)}= & {} \frac{11}{3} C_A- \frac{4}{3} T_F n_l, \nonumber \\ \beta _1^{(n_l)}= & {} \frac{34}{3} C_A^2- \frac{20}{3} C_A T_F n_l - 4 C_F T_F n_l, \nonumber \\ \beta _2^{(n_l)}= & {} \frac{2857}{54} C_A^3- \left( \frac{1415}{27} C_A^2+\frac{205}{9} C_A C_F-2C_F^2\right) T_F n_l\nonumber \\{} & {} + \left( \frac{158}{27} C_A+\frac{44}{9} C_F \right) T_F^2 n_l^2. \end{aligned}$$
(13)

In our numerical evaluations, \(n_b=n_c=1\) and \(n_l=3\) are fixed through the decoupling region from \(\mu =1\,\textrm{GeV}\) to \(\mu =6.25\,\textrm{GeV}\), and the typical QCD scale \(\Lambda _{QCD}^{(n_l=3)}=0.3344\,\textrm{GeV}\) is determined using the three-loop formula with the aid of the package RunDec [50,51,52,53] by inputting the initial value \(\alpha _s^{(n_f=5)}\left( m_Z\right) =0.1179\) with \( m_Z=91.1876\,\textrm{GeV}\).

3 Calculation procedure 

Our high-order calculation consists of the following steps. First, we use FeynCalc [54] to obtain Feynman diagrams and corresponding Feynman amplitudes. By $Apart [55], we decompose every Feyman amplitude into several Feynman integral families. Second, we use FIRE [56]/Kira [57]/ FiniteFlow [58] based on Integration by Parts (IBP) [59] to reduce every Feynman integral family to master integral family. Third, based on symmetry among different integral families and using Kira+FIRE+Mathematica code, we can realize integral reduction among different integral families, and further on, the reduction from all of master integral families to the minimal set [60] of master integral families. Last, we use AMFlow [61], which is a proof-of-concept implementation of the auxiliary mass flow method [62], equipped with Kira [57]/FiniteFlow [58] to calculate the minimal set of master integral families.

In order to obtain the finite results of the high-order QCD corrections, one has to perform the conventional renormalization procedure [6, 10, 63, 64]. Equivalently, we can also use diagrammatic renormalization method [65] with the aid of the package FeynCalc [54], which at N\(^3\)LO sums contributions from three-loop diagrams and four kinds of counter-term diagrams, i.e., tree diagram inserted with one \(\alpha _s^3\)-order counter-term vertex, one-loop diagram inserted with one \(\alpha _s^2\)-order counter-term vertex, one-loop diagram inserted with two \(\alpha _s\)-order counter-term vertexes, two-loop diagrams inserted with one \(\alpha _s\)-order counter-term vertex. Our final finite results by these two renormalization methods are in agreement with each other.

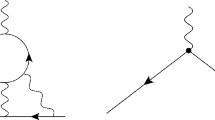
We want to mention that all contributions up to NNLO have been evaluated for general gauge parameter \(\xi \) and the NNLO results for the scalar current matching coefficient are all independent of \(\xi \), which constitutes an important check on our calculation. At N\(^3\)LO, we work in Feynman gauge. By FeynCalc, there are 1, 1, 13, 268 bare Feynman diagrams for the QCD vertex function with the flavor-changing heavy quark scalar current at tree, one-loop, two-loop, three-loop orders in \(\alpha _s\), respectively. Some representative Feynman diagrams up to three loops are displayed in Figs. 1 and 2. In the calculation of multi-loop diagrams, we have allowed for \(n_b\) bottom quarks with mass \(m_b\), \(n_c\) charm quarks with mass \(m_c\) and \(n_l\) massless quarks appearing in the quark loops. Physically, \(n_b=n_c=1\) and \(n_l=3\). To facilitate our calculation, we take full advantage of computing numerically. Namely, before generating amplitudes, \(m_b\) and \(m_c\) are chosen to be particular rational number values [66,67,68]. Following the literature [10], we employ the projector constructed for the flavor-changing heavy quark scalar current to obtain intended QCD amplitudes, which means one need extend the scalar current projector with equal heavy quark masses in Eq. (8) of Ref. [10] to the different heavy quark masses case. Adopting the same notation of Ref. [10], we choose \(q_1=\frac{m_c}{m_b+m_c}q+p\) and \(q_2=\frac{m_b}{m_b+m_c}q-p\) denoting the on-shell charm and bottom momentum, respectively, and present the projector for the flavor-changing heavy quark scalar current as

(14)

where the small momentum p refers to relative movement between the bottom and charm, q represents the total momentum of the bottom and charm, \(q_1^2=m_c^2\), \(q_2^2=m_b^2\), \(q^2=(m_b+m_c)^2+{\mathcal {O}}{(p^2)}\), \(q\cdot p=0\).

To match with the NRQCD, one need extract the contribution from the hard region in the full QCD amplitudes for the scalar current, which means one need first introduce the small relative momentum p to momenta in the amplitudes as above and then series expand propagator denominators with respect to p up to \({\mathcal {O}}{(p)}\) in the hard region of loop momenta [10]. As a result, the number and powers of propagators in Feynman integrals constituting the amplitudes for the scalar current will remarkably increase compared with the vector current case, the zeroth component of the axial-vector current and the pseudoscalar current case. In our practice, the total number of propagators in a three-loop Feynman integral family is 12. In our calculation, the most difficult thing is the reduction from Feynman integrals with rank 5, dot 4, and 12 propagators to the master integrals. By trial and error, we find it is more appropriate for Fire6 [56] to deal with this problem than Kira [57] or FiniteFlow [58]. After using Kira+FIRE+Mathematica code to achieve the minimal set of the master integral families based on symmetry among different integral families, the number of three-loop master integral families is reduced from 825 to 26, meanwhile the number of three-loop master integrals is reduced from 13,245 to 300.

Fig. 1
figure 1

Typical Feynman diagrams for the QCD vertex function with the \(\bar{b}c \) system up to two-loop order. The cross “\(\bigoplus \)” implies the insertion of the flavor-changing heavy quark scalar current

Full size image
Fig. 2
figure 2

Typical Feynman diagrams labelled with the corresponding color factor for the QCD vertex function with the flavor-changing heavy quark scalar current at three-loop order. The cross “\(\bigoplus \)” implies the insertion of the scalar current. The thickest solid closed circle represents the bottom quark loop, and the other solid closed circle represents the charm quark loop. The dotted closed circle represents the ghost loop

Full size image

4 Results 

Following Refs. [7, 9, 29], the dimensionless matching coefficient \({\mathcal {C}}_s\) for the flavor-changing scalar current involving the heavy bottom and charm quark can be decomposed as:

$$\begin{aligned}{} & {} {\mathcal {C}}_s(\mu _f,\mu ,m_b,m_c) =1+\frac{\alpha _s^{\left( n_l\right) }\left( \mu \right) }{\pi } {\mathcal {C}}^{(1)}(x)\nonumber \\{} & {} \quad +\left( \frac{\alpha _s^{\left( n_l\right) }\left( \mu \right) }{\pi }\right) ^2 \left( {\mathcal {C}}^{(1)}(x)\frac{\beta _0^{(n_l)}}{4}\text {ln}\frac{\mu ^2}{m_b m_c}+\frac{\tilde{\gamma }_s^{(2)}(x)}{2}\right. \nonumber \\{} & {} \quad \ln \frac{\mu _f^2}{m_b m_c}\left. +{\mathcal {C}}^{(2)}(x)\right) +\left( \frac{\alpha _s^{\left( n_l\right) }\left( \mu \right) }{\pi }\right) ^3\Bigg \{ \left( \frac{{\mathcal {C}}^{(1)}(x)}{16}\beta _1^{(n_l)}\right. \nonumber \\{} & {} \quad \left. +\frac{{\mathcal {C}}^{(2)}(x)}{2}\beta _0^{(n_l)}\right) \text {ln}\frac{\mu ^2}{m_b m_c} +\frac{{\mathcal {C}}^{(1)}(x)}{16}{\beta _0^{(n_l)}}^2\ln ^2 \frac{\mu ^2}{m_b m_c} \nonumber \\{} & {} \quad +\frac{1}{8}\left( \frac{d\tilde{\gamma }_s^{(3)}\left( x,\frac{\mu _f^2}{m_b m_c}\right) }{d \text {ln}\mu _f}-\beta _0^{(n_l)}\tilde{\gamma }_s^{(2)}(x)\right) \ln ^2\frac{\mu _f^2}{m_b m_c} \nonumber \\{} & {} \quad +\frac{1}{2}\left( {\mathcal {C}}^{(1)}(x) \tilde{\gamma }_s^{(2)}(x)+\tilde{\gamma }_s^{(3)}\left( x,1\right) \right) \ln \frac{\mu _f^2}{m_b m_c} \nonumber \\{} & {} \quad +\frac{\beta _{0}^{(n_l)}}{4}\tilde{\gamma }_s^{(2)}(x)\ln \frac{\mu _f^2}{m_b m_c}\,\text {ln}\frac{\mu ^2}{m_b m_c} + {\mathcal {C}}^{(3)}(x) \Bigg \} +{\mathcal {O}}\left( \alpha _s^4\right) , \nonumber \\ \end{aligned}$$
(15)

where the coefficients \(\tilde{\gamma }_s^{(2)}(x)\) and \( \tilde{\gamma }_s^{(3)}\left( x,\frac{\mu _f^2}{m_b m_c}\right) \) have been defined in Eqs. (6,7,8). The parameters \({\mathcal {C}}^{(i)}(x)(i=1,2,3)\) in above equation are independent of \(\ln \mu \) and \(\ln \mu _f\) and are the nontrivial parts of \({\mathcal {C}}_s\) at \({\mathcal {O}}\left( \alpha _s^i\right) \). It’s also well known that the coefficients \({\mathcal {C}}_s\) and \({\mathcal {C}}^{(i)}(x)\) satisfy the following symmetric replacements  [2,3,4,5,6,7, 9]:

$$\begin{aligned} {\mathcal {C}}_s(\mu _f,\mu ,m_b,m_c)= & {} {\mathcal {C}}_s(\mu _f,\mu ,m_c,m_b)|_{n_b\leftrightarrow n_c}, \end{aligned}$$
(16)
$$\begin{aligned} {\mathcal {C}}^{(i)}(x)= & {} {\mathcal {C}}^{(i)}\left( \frac{1}{x}\right) |_{n_b\leftrightarrow n_c}. \end{aligned}$$
(17)

The one-loop QCD correction to \({\mathcal {C}}_s\), denoted by \({\mathcal {C}}^{(1)}(x)\), can be analytically achieved as:

$$\begin{aligned} {\mathcal {C}}^{(1)}(x)=\frac{3}{4} C_F \left( \frac{x-1}{x+1}\,\ln x-\frac{2}{3}\right) . \end{aligned}$$
(18)

The two-loop and three-loop nontrivial coefficients in (15) are \({\mathcal {C}}^{(2)}(x)\) and \({\mathcal {C}}^{(3)}(x)\), which can be decomposed in terms of the different color/flavor structures by following the conventions as being used in Refs. [7, 9, 12, 19, 29, 69]:

$$\begin{aligned} {\mathcal {C}}^{(2)}(x)= & {} C_F^2 {\mathcal {C}}_{FF}(x)+C_F C_A {\mathcal {C}}_{FA}(x) +C_F T_F n_b {\mathcal {C}}_{FB}(x)\nonumber \\{} & {} +C_F T_F n_c {\mathcal {C}}_{FC}(x) +C_F T_F n_l {\mathcal {C}}_{FL}(x), \end{aligned}$$
(19)
$$\begin{aligned} {\mathcal {C}}^{(3)}(x)= & {} C^3_F \, {\mathcal {C}}_{FFF}(x)+C^2_F \,C_A \, {\mathcal {C}}_{FFA}(x)\nonumber \\{} & {} + C_A^2 C_F \, {\mathcal {C}}_{FAA}(x) + C^2_F T_F n_l\,{\mathcal {C}}_{FFL}(x) \nonumber \\{} & {} +C_A C_F T_F n_l\,{\mathcal {C}}_{FAL}(x) \nonumber \\{} & {} + C_F T^2_F n_l\, n_c \, {\mathcal {C}}_{FCL}(x) + C_FT^2_F \, n_l n_b \, {\mathcal {C}}_{FBL}(x)\nonumber \\{} & {} +C_F T^2_F \, n^2_l \, {\mathcal {C}}_{FLL}(x) + C_F T_F^2 \, n_b \,n_c \, {\mathcal {C}}_{FBC}(x) \nonumber \\{} & {} + C^2_F T_F n_c\,\, {\mathcal {C}}_{FFC}(x) + C_A C_F T_F \,n_c\, {\mathcal {C}}_{FAC}(x)\nonumber \\{} & {} +C_FT^2_F \, n_c^2 \, {\mathcal {C}}_{FCC}(x) + C^2_F T_F\,n_b\, {\mathcal {C}}_{FFB}(x)\nonumber \\{} & {} + C_AC_F T_F\,n_b\,{\mathcal {C}}_{FAB}(x)\nonumber \\{} & {} +C_FT^2_F \, n_b^2 \,{\mathcal {C}}_{FBB}(x). \end{aligned}$$
(20)

Because of the limited computing resources, we choose to calculate the matching coefficient \({\mathcal {C}}_s\) at five rational numerical points: (a) the physical point \(\{m_b=\frac{475}{100}\,\textrm{GeV}, m_c=\frac{150}{100}\,\textrm{GeV}\}\left( i.e.,x=x_0=\frac{150}{475}\right) \) and its check point \(x=1/x_0\); (b) the reference point \(\{m_b=\frac{498}{100}\,\textrm{GeV}, m_c=\frac{204}{100}\,\textrm{GeV}\}\left( i.e.,x=x_1=\frac{204}{498}\right) \) as being used in Refs. [7, 9] and its check point \(,x=1/{x_1}\); and (c) the equal mass point \(x=1\). The numerical values of \({\mathcal {C}}_s\) obtained at the physical point, the reference point and the two check points verify the symmetric features of \({\mathcal {C}}^{(i)}(x)\) as described in Eq. (17). The value of \({\mathcal {C}}_s(x=1)\) obtained at the equal mass point \(x=1\) are consistent with the known matching coefficient results \({\mathcal {C}}_s(x=1)\) as given in previous literatures [10,11,12].

To confirm our calculation, we have also applied the same calculation procedure to the evaluation of the three-loop matching coefficients \({\mathcal {C}}_v\), \({\mathcal {C}}_p\), \({\mathcal {C}}_{(a,0)}\) for the flavor-changing heavy quark vector current, the flavor-changing heavy quark pseudoscalar current, the zeroth component of the axial-vector current with the flavor-changing heavy quarks, respectively, where our results verify \({\mathcal {C}}_p\equiv {\mathcal {C}}_{(a,0)}\) and our results \({\mathcal {C}}_v\) and \({\mathcal {C}}_{(a,0)}\) agree with the known results at the reference point \(x=x_1=\frac{204}{498}\) and the equal mass point \(x=1\) in previous literature [7,8,9,10,11,12, 19].

Fig. 3
figure 3

The theoretical predictions of the two-loop coefficient \({\mathcal {C}}^{(2)}(x)\) with \(n_l=3,n_c=n_b=1\) and the five color-structure components as functions of the ratio x within the range of \(x=[0.05,1]\). The solid points on the curves show the results at the physics point \(x_0\)

Full size image

In the following, we will present the highly accurate numerical results of \({\mathcal {C}}^{(2)}(x)\) and \({\mathcal {C}}^{(3)}(x)\) at the two points \(x_0\) and \(x_1\) with about 30-digit precision. The various color-structure components of \(\mathcal{C}^{(2)}(x_i)\) read:

$$\begin{aligned} {\mathcal {C}}_{FF}(x_0)= & {} -6.96020737354849312657205418357, \nonumber \\ {\mathcal {C}}_{FF}(x_1)= & {} -7.04189123299345621723909527576, \nonumber \\ {\mathcal {C}}_{FA}(x_0)= & {} -4.12970820397051570036738297443,\nonumber \\ {\mathcal {C}}_{FA}(x_1)= & {} -4.21850920483664861878044456951,\nonumber \\ {\mathcal {C}}_{FB}(x_0)= & {} 0.048170796075386686136602545271, \nonumber \\ {\mathcal {C}}_{FB}(x_1)= & {} 0.04831339364011728369842997029092, \nonumber \\ {\mathcal {C}}_{FC}(x_0)= & {} 0.268781876466689639100436656736, \nonumber \\ {\mathcal {C}}_{FC}(x_1)= & {} 0.19607889785548892146634695477464, \nonumber \\ {\mathcal {C}}_{FL}(x_0)= & {} -0.363661393326874053432216153222. \nonumber \\ {\mathcal {C}}_{FL}(x_1)= & {} -0.2790540301576112932370509681006.\nonumber \\ \end{aligned}$$
(21)

While the various color-structure components of \(\mathcal{C}^{(3)}(x_i)\) read:

$$\begin{aligned} {\mathcal {C}}_{FFF}(x_0)= & {} -12.6512824902497489841790999287,\nonumber \\ {\mathcal {C}}_{FFF}(x_1)= & {} -12.0483722927091616912691626829,\nonumber \\ {\mathcal {C}}_{FFA}(x_0)= & {} -91.3076763843495687930187876995,\nonumber \\ {\mathcal {C}}_{FFA}(x_1)= & {} -88.0221499848013896554664472817,\nonumber \\ {\mathcal {C}}_{FAA}(x_0)= & {} -67.2034246352357623358462321068,\nonumber \\ {\mathcal {C}}_{FAA}(x_1)= & {} -67.1695173276489777616342429313,\nonumber \\ {\mathcal {C}}_{FFL}(x_0)= & {} 31.12323218543900065296825277243,\nonumber \\ {\mathcal {C}}_{FFL}(x_1)= & {} 30.68720372188183343269632427604, \nonumber \\ {\mathcal {C}}_{FAL}(x_0)= & {} 19.49987491622541782889333507621, \nonumber \\ {\mathcal {C}}_{FAL}(x_1)= & {} 20.21650152562553730982779532614, \nonumber \\ {\mathcal {C}}_{FCL}(x_0)= & {} -0.262383795777090819586462489511, \nonumber \\ {\mathcal {C}}_{FCL}(x_1)= & {} -0.2245258621166945887625691444034, \nonumber \\ {\mathcal {C}}_{FBL}(x_0)= & {} -0.0100054359359386271416783335057, \nonumber \\ {\mathcal {C}}_{FBL}(x_1)= & {} -0.028878464938238222688016298952333, \nonumber \\ {\mathcal {C}}_{FLL}(x_0)= & {} 0.3393017746199103339986949104357, \nonumber \\ {\mathcal {C}}_{FLL}(x_1)= & {} 0.15505258671412948142142209540887, \nonumber \\ {\mathcal {C}}_{FBC}(x_0)= & {} 0.0551829420149711792507691937024, \nonumber \\ {\mathcal {C}}_{FBC}(x_1)= & {} 0.039835889550135713463806218847457, \nonumber \\ {\mathcal {C}}_{FFC}(x_0)= & {} 4.4105666464862568415402096694718, \nonumber \\ {\mathcal {C}}_{FFC}(x_1)= & {} 3.5965832451050432778831172004519, \nonumber \\ {\mathcal {C}}_{FAC}(x_0)= & {} -0.6861454400278606762848799078670,\nonumber \\ {\mathcal {C}}_{FAC}(x_1)= & {} -0.59978497778001690299896961599382,\nonumber \\ {\mathcal {C}}_{FCC}(x_0)= & {} 0.09536045103106728669303211267177,\nonumber \\ {\mathcal {C}}_{FCC}(x_1)= & {} 0.054201663765338461641972843038436,\nonumber \\ {\mathcal {C}}_{FFB}(x_0)= & {} 1.1373781611175929139065523549900,\nonumber \\ {\mathcal {C}}_{FFB}(x_1)= & {} 1.2253534232464911597725316738417,\nonumber \\ {\mathcal {C}}_{FAB}(x_0)= & {} -0.318775996588438248091557753877,\nonumber \\ {\mathcal {C}}_{FAB}(x_1)= & {} -0.31106975116565799032232634094289,\nonumber \\ {\mathcal {C}}_{FBB}(x_0)= & {} 0.00994219408487397025982150577842.\nonumber \\ {\mathcal {C}}_{FBB}(x_1)= & {} 0.0084315690259692108776748520807028. \nonumber \\ \end{aligned}$$
(22)

From above numerical results one can see that the differences between the values for the same color-structure component at the point \(x_0\approx 0.316\) and \(x_1\approx 0.410\) are relatively small, which means a much weak x-dependence near physical region. One can also note that the dominant contributions in \({\mathcal {C}}^{(2)}(x_0)\) and \({\mathcal {C}}^{(3)}(x_0)\) come from the components corresponding to the color structures \(C_F^2\), \(C_FC_A\), \(C_F^2C_A\) and \(C_FC_A^2\) while the contributions from the heavy bottom and(or) charm quark loops are small.

In our high-order loop calculation process, the most dominant time-consuming work is the second step, i.e., reducing every Feynman integral family to master integral family, which will be optimized in our future research by mapping and merging symmetric and equivalent Feynman integral families into one family before IBP reduction. At present, calculating three-loop \({\mathcal {C}}_s\) at one point in x costs about two weeks with our 20-thread computer, so instead of fully investigating the three-loop results as functions of x, we will study the heavy quark mass dependence of the two-loop matching coefficients \({\mathcal {C}}^{(2)}(x)\) as an example.

Table 1 The values of the matching coefficient \({\mathcal {C}}_s\) for the flavor-changing heavy quark scalar current up to N\(^3\)LO
Full size table

In Fig. 3, we show the x-dependence of the two-loop coefficient \({\mathcal {C}}^{(2)}(x)\) with \(n_l=3,n_c=n_b=1\) and its various color-structure components \({\mathcal {C}}_{FF}(x),{\mathcal {C}}_{FA}(x),{\mathcal {C}}_{FB}(x),{\mathcal {C}}_{FC}(x),{\mathcal {C}}_{FL}(x)\) in the range of \(x=[0.05,1]\). The solid points on the curves in Fig. 3 show the results at the physics point \(x=x_0=150/475\). The numerical values for \(x>1\) can be obtained by the symmetric relation in Eq. (17). From Fig. 3, one can see that the coefficient \({\mathcal {C}}^{(2)}(x)\) and the five components have only a relatively weak x-dependence in the range of \(x=[0.05,1]\).

Fixing the renormalization scale \(\mu =m_b=4.75\,\textrm{GeV}\), \(m_c=1.5\,\textrm{GeV}\), and setting the factorization scale \(\mu _f=1\,\textrm{GeV}\), Eq. (15) then reduces to

$$\begin{aligned} {\mathcal {C}}_s(x_0)= & {} 1-0.06727332\left( \frac{\alpha _s^{\left( n_l=3\right) }(m_b)}{\pi }\right) \nonumber \\{} & {} -12.41489\left( \frac{\alpha _s^{\left( n_l=3\right) }(m_b)}{\pi }\right) ^2 \nonumber \\{} & {} -930.1229\left( \frac{\alpha _s^{\left( n_l=3\right) }(m_b)}{\pi }\right) ^3+{\mathcal {O}}(\alpha _s^4). \end{aligned}$$
(23)
Fig. 4
figure 4

The renormalization scale dependence of the matching coefficient \({\mathcal {C}}_s\) at the LO, NLO, NNLO and N\(^3\)LO accuracy. For details see the text

Full size image

With the values of \(\alpha _s^{\left( n_l=3\right) }(\mu )\) calculated by using the renormalization group running equation in Eq. (12), we show in Fig. 4 the renormalization scale \(\mu \)-dependence of the matching coefficient \({\mathcal {C}}_s\) for scalar current at the LO, NLO, NNLO and N\(^3\)LO accuracy, respectively. The central values of the matching coefficient \({\mathcal {C}}_s\) are calculated by using the physical values with \(\mu _f=1~\,\textrm{GeV}\), \(m_c=1.5\,\textrm{GeV}\) and \(m_b=4.75\,\textrm{GeV}\). The error bands come from the variation of \(\mu _f\) in the range of \(\mu _f= [0.4,1.5] \) GeV. We also present our precise numerical results of the matching coefficient \({\mathcal {C}}_s\) for scalar current at LO, NLO, NNLO and N\(^3\)LO in Table 1. The central values of the matching coefficient \({\mathcal {C}}_s\) are calculated by inputting the physical values with \(\mu _f=1~\textrm{GeV}\), \(\mu =4.75\,\textrm{GeV}\), \(m_b=4.75\,\textrm{GeV}\) and \(m_c=1.5\,\textrm{GeV}\). The errors are estimated by varying \(\mu _f\) from 0.4 to 1.5 GeV, \(\mu \) from 3 to 6.25 GeV, respectively.

From Fig. 4 and Table 1, one can find that the higher order QCD corrections have large influence compared with the NLO correction. Especially, the \(\mathcal{O}(\alpha _s^3)\) correction looks quite sizable, which confirms the breakdown of the convergence at \(\mathcal{O}(\alpha _s^3)\) for other heavy quark currents as being found in previous literature [7, 9, 12]. Note that, at each truncated perturbative order, the matching coefficient \({\mathcal {C}}_s\) is renormalization-group invariant [7, 9]. At N\(^3\)LO, for example, the coefficient \({\mathcal {C}}_s\) obeys the following renormalization-group running invariance:

$$\begin{aligned}&{\mathcal {C}}_s^\mathrm{N^3LO}(\mu _f,\mu ,m_b,m_c) ={\mathcal {C}}_s^\mathrm{N^3LO}(\mu _f,\mu _0,m_b,m_c) +{\mathcal {O}}(\alpha _s^4), \end{aligned}$$
(24)

where \({\mathcal {C}}_s^\mathrm{N^3LO}(\mu _f,\mu ,m_b,m_c)\) has dropped the \({\mathcal {O}}(\alpha _s^4)\) terms in Eq. (15). Namely the scale-dependence of the N\(^3\)LO matching coefficients rises from \({\mathcal {O}}(\alpha _s^4)\), which is suppressed compared to lower-order. However, the scale-independence coefficients of \(\alpha _s^4\) such as \({\mathcal {C}}^{(3)}(x)\) and \(\ln \mu _f\), which come from the \({\mathcal {O}}(\alpha _s^3)\) order in Eq. (15), are considerably large by aforementioned calculation within the framework of the NRQCD theory. These terms will lead to a significantly larger renormalization scale dependence at N\(^3\)LO. From Fig. 4, we also find the NRQCD factorization scale \(\mu _f\) has a large influence on the matching coefficient. When \(\mu _f\) decreases, both the convergence of \(\alpha _s\) expansion series and the independence of \(\mu \) will be improved. The understanding of the observed large N\(^3\)LO corrections in this paper and the previous literatures [7, 9, 12] is another important topic, which may be related to the higher order corrections to NRQCD long-distance matrix elements, higher order relativistic corrections and the resummation techniques. We will leave it in the future work.

5 Summary 

In this paper, we have performed the calculations of the \(\mathrm N^3LO\) QCD corrections to the matching coefficient for the flavor-changing heavy quark scalar current involving the bottom and charm quark within the framework of the NRQCD effective theory. For the first time, we obtain the analytical expressions of the three-loop renormalization constant and the corresponding three-loop anomalous dimension of the NRQCD scalar current with different heavy quark mass \(m_b\) and \(m_c\). Meanwhile, the three-loop matching coefficient \(C_s(\mu _f,\mu ,m_b,m_c)\) has also been obtained with high numerical accuracy, which is helpful to analyze the threshold behaviours when two different heavy quarks are close to each other. The obtained \(\mathrm N^3LO\) QCD corrections are considerably large compared with lower-order corrections, and exhibit stronger dependence on the QCD renormalization scale and the NRQCD factorization scale at higher order, which suggests that higher order QCD corrections should be combined with other techniques in order to get a reliable prediction within the NRQCD effective theory.