Abstract
In this work, the Standard Model (SM) is extended with two right-handed (RH) neutrinos and two singlet neutral fermions to yield active neutrino masses via (2,2) inverse see-saw mechanism. We first validate the multi-dimensional model parameter space with neutrino oscillation data, obeying the experimental bounds coming from the lepton flavor violating (LFV) decays: \(\mu \rightarrow e \gamma ,~ \tau \rightarrow e \gamma , ~ \tau \rightarrow \mu \gamma \). Besides we also search for the portion of the parameter space which yield the observed baryon asymmetry of the universe via resonant leptogenesis. Further, we pick up a few benchmark points from the aforementioned parameter space with TeV scale heavy neutrinos and perform an exhaustive collider analysis of the final states: \(2l + E_T \!\!\!\!\!\!/\;\,\) and \(1\,l + 2j + \not \! E_T \) in multi-TeV muon collider.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
While the Discovery of the Higgs boson at the Large Hadron Collider (LHC) [1, 2] completes the particle spectrum of the Standard Model (SM), this spin-zero boson also confirms the mass generation mechanism of the fermions and gauge bosons via spontaneous symmetry breaking. However, an exception of the aforesaid mechanism occurs for the neutrinos owing to the absence of the counterpart of the left-handed neutrinos in SM. On the contrary to this theoretical observation, the flavor oscillations of the neutrinos yield massive active neutrinos with an upper limit of \({\mathcal {O}}\) (0.1 eV) [3] coming from cosmological observations. This tiny neutrino mass can be generated via see-saw mechanism, which requires the extension of SM with additional fermionic or bosonic degrees of freedom. Depending on the nature and representations of the extended sector, various types of see-saw mechanisms like Type-I [4,5,6,7,8], Type-II [9,10,11,12,13,14,15,16,17,18,19,20], Type-III [21,22,23,24,25,26,27], have been studied in the literature. The requirement of tiny active neutrino masses pushes the masses of the additional beyond Standard Model (BSM) fields to higher end and also put a lower bound on the masses of the same. In most of the see-saw mechanisms, the BSM fields are too heavy to be produced and analysed in the present and future collider experiments. The inverse see-saw mechanism [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47] turns out to be very effective for addressing this problem as it can produce TeV scale heavy neutrinos which is well within the reach of future collider experiments. Heavy neutrinos have already been searched at LHC [48], LHeC and lepton colliders [49] previously. Signatures of heavy neutrinos originated from heavy \(Z'\)-boson has been analysed in [50].
Another shortcoming of SM causes lack of explanation of the observed baryon asymmetry of the universe. According to the current observation [3], the baryon asymmetry is:
Following the Sakharov conditions [51], baryon number, C and CP symmetry as well as thermal equilibrium should be violated to provide an explanation to the dynamic generation of this asymmetry. One of the most popular mechanisms to generate this asymmetry is leptogenesis [52,53,54,55,56,57,58,59,60,61,62,63,64,65,66], where the lepton asymmetry can originate from the out-of-equilibrium decay of heavy neutrinos. This asymmetry is further translated to baryon asymmetry via sphaleron transitions in SM [67,68,69], which are basically \(B-L\) conserving but \(B+L\) violating processes. One of the minimal models where leptogenesis can be realised by adding heavy right-handed neutrinos (with masses \(> 10^{9}\) GeV [70, 71]) to SM, can yield correct baryon asymmetry via Type-I thermal leptogenesis. Thus to probe interesting signatures involving the heavy neutrinos in various colliders, one needs to lower the masses of the heavy neutrinos at least to the TeV scale. A specific framework called inverse see-saw (ISS) serves the aforementioned purpose, where two of the mass eigenstates of the heavy neutrinos are almost mass degenerate, yielding the required baryon asymmetry via resonant leptogenesis [72,73,74,75,76,77,78,79].
In this paper, we consider a minimal inverse see-saw scenario ISS(2,2) [34], where the SM is extended by two generations of right-handed neutrinos and two SM gauge singlet neutral fermions. The phenomenology of the model in light of neutrino oscillation data [80], lepton flavor violating decay [81] and leptogenesis, has been thoroughly studied by us in one of our previous works [82]. Here, we intend to explore the parameter space derived from our previous study from collider perspective and examine the prospect of some interesting signatures at the multi-TeV muon collider [83]. As we mentioned earlier, this particular framework provides with TeV scale heavy neutrinos which can produce the baryon asymmetry of the universe in the correct ballpark, as well as can be probed at present and future colliders. Here we aim to probe the signal involving the pair production of active neutrinos along with the heavy neutrinos (masses ranging from 3.28 TeV to 10.12 TeV), followed by the subsequent decay of the heavy neutrinos to \(W^\pm \) and charged leptons. Further we consider both leptonic and hadronic decay of \(W^\pm \), leading to \(2l+ E_T \!\!\!\!\!\!/\;\,\) and \(1l + 2j + \not \! E_T \) final state respectively. We would have been opted for LHC or ILC to search for the aforementioned signal. In the context of LHC, the signal significance turns out to be low due to the presence of huge SM background and tiny signal cross-section at 14 TeV. The significance might be improved in the proposed 100 TeV collider but still, the SM background cross-section is expected to be very large compare to the signal cross-section. Besides the similar signal involving TeV scale heavy neutrinos at the production level cannot be investigated at ILC, since the maximum achievable center of mass energy (COM) at ILC is 1 TeV.
Now the possibility of detecting TeV scale neutrino can be achieved in a leptonic collider with a sufficiently high COM energy. Recently, there is a growing interest in muon colliders with multi TeV COM energy. This can provide a clean environment with hugely achievable signal cross-section, enhancing the signal significance. For our analyses, we choose multi TeV COM energies (\(\sqrt{s} = 6~\textrm{TeV},14\) TeV) at the muon collider with integrated luminosity (\({\mathcal {L}}\)) varying as [84]:
With this motivation, we analyze the \(2l + E_T \!\!\!\!\!\!/\;\,\) and \(1l+ 2j\) \(+ \not \! E_T \) final states at multi-TeV muon collider with \( \sqrt{s} = 6 \) TeV and 14 TeV. We shall show how a high significance could be produced by applying suitable cuts on the relevant kinematic variables to suppress the SM backgrounds using traditional cut-based analysis. We shall also compare the performances of the two aforementioned channels at the end of the analysis.
This paper is organized as follows. In Sect. 2, we describe the framework and the mechanism of neutrino mass generation. Further, we study phenomenological constraints in the context of the model in Sect. 3. In Sect. 4, we perform cut-based analysis to analyze the collider signature of \(2l + E_T \!\!\!\!\!\!/\;\,\) and \(1l + 2j + E_T \!\!\!\!\!\!/\;\,\) channels at multi-TeV muon collider. Finally, we summarize and conclude in Sect. 5.
2 Model
In the present work, we will be operating in the framework of SM, minimally extended with two right-handed neutrinos \(N_{{R_1}}, N_{{R_2}}\) and two neutral singlet fermions \(S_1, S_2\) yielding tiny neutrino mass and mixing via inverse see-saw mechanism. Thus this model is termed as ISS(2,2) in short, where the two numbers in the first bracket denote the numbers of added heavy right-handed neutrinos and two neutral singlet fermions respectively. Table 1 shows the \(SU(3)_C, ~ SU(2)_L, ~ U(1)_Y\) quantum numbers assigned to the bosonic and fermionic fields of the model. Here the hyper-charge Y is calculated using: \(Q = T_3 + \frac{Y}{2}\), where \(T_3\) and Q are the weak isospin and electric charge of the field respectively. In Table 1, the SM Higgs doublet is denoted by \(\phi \). \(Q_{L_i}, L_{L_i}\) are the left-handed SM quark and lepton doublets respectively, whereas \(u_{R_i}, d_{R_i}, \ell _{R_i}\) are right-handed up-type, down-type quark and lepton singlets respectively with \(i=3\).
The Yukawa Lagrangian signifying the inverse see-saw mechanism is:
where \(\alpha \) represents the flavor of leptons. Here \(y_{i \alpha }\) denotes the Yukawa coupling matrix with complex entries and C is the charge conjugation operator. The aforementioned Lagrangian contains both lepton number conserving Dirac mass term, as well as lepton number violating Majorana mass terms.
In the flavor basis \((\nu _L^i, N_{R_j}^c, S_k)^T\) (with \(i=3,~ j,k=2\)), following Eq. (3), the neutrino mass matrix can be written as:
Here each and every matrix element of \(M_\nu \) is considered to be complex to generalise the analysis, and thus the elements can be decomposed into real and imaginary parts as:
We can write down the neutrino mass matrix \(M_\nu \) in a compact form as:
with \(M_D = y_{i\alpha } \frac{v}{\sqrt{2}}\). With three generations of active neutrinos, two generations of \(N_{R_j}\) and \(S_j\)s, \(M_\nu \) is \(7\times 7\) dimensional. The individual dimensions of \(M_D, M_R, M_S\) and \(\mu \) are \(3 \times 2, ~ 2 \times 2, ~ 2 \times 2, ~ 2 \times 2\) respectively.
Following the mass hierarchy \(\mu , M_R \ll M_D \ll M_S\), with the see-saw approximation in the inverse see-saw mechanism, the effective neutrino mass matrix looks like: [85],
Thus one can neglect \(M_R\) in Eq. (7) and approximate the active neutrino mass matrix as:
From Eq. (8), it is evident that, with \(M_R = 0\),Footnote 1 double suppression by the mass scale \(M_S\) along with small \(\mu \), yield tiny active neutrino mass.
Upon diagonalising \(m_\nu \) in Eq. (8) the light neutrino masses are generated via the transformation:
where \(m_1, m_2, m_3\) are three light active neutrino masses, \(U_{\textrm{PMNS}}\) is the Pontecorvo–Maki–Nakagawa–Sakata matrix (PMNS matrix).Footnote 2
3 Constraints
In this subsection, we shall briefly describe relevant constraints imposed on the model parameter space. For details of the constraints, we refer to [82].
3.1 Neutrino data fitting
Following Eq. (8), \(\mu \) can be expressed in terms of the matrices \( m_\nu , M_R, M_D, M_S\) as:
Here \(m_\nu \) can be expressed in terms of \(U_{\textrm{PMNS}}, \hat{m_\nu }\) from Eq. (9), where the elements of the \(U_{\textrm{PMNS}}\) matrix in Eq. (10) are already constrained from neutrino oscillation data [80]. Thus the model parameter space which we consider in the present analysis becomes compatible with the neutrino oscillation data.Footnote 3 The texture of \(M_\nu \) in Eq. (6) yields one massless active neutrino, which is an unavoidable feature of the (2,2) inverse see-saw realising framework. Thus we set the lightest active neutrino mass \(m_1\) to be zero, satisfying \( (m_1 + m_2 + m_3) \le 0.12\) eV [3, 86].Footnote 4
3.2 Lepton flavor violation
Through the diagonalisation of mass matrix \(M_\nu \) in Eq. (6) by a \(7 \times 7\) unitary matrix U, one can obtain seven mass eigenstates \(\nu _1', \nu _2', \nu _3', \tilde{\Psi _1},\tilde{\Psi _2},\tilde{\Psi _3},\tilde{\Psi _4}\) with masses \(m_1,m_2,m_3,M_{\tilde{\Psi _1}},M_{\tilde{\Psi _2}},M_{\tilde{\Psi _3}},M_{\tilde{\Psi _4}}\) respectively. Following the mass hierarchy (\(\mu \ll M_D \ll M_S\)) in the inverse see-saw framework, the mass difference: \(|M_{{\tilde{\Psi }}_{1(3)}}-M_{{\tilde{\Psi }}_{2(4)}}| \sim \mu \). Thus the corresponding pairs having such a tiny mass difference become mass degenerate.
Thus the lepton flavor violating (LFV) decays like \(l_i \rightarrow \ l_j \gamma \) obtain additional contributions coming from the heavy neutrinos \(\tilde{\Psi _1},\tilde{\Psi _2},\tilde{\Psi _3},\tilde{\Psi _4}\) [82]. Among all LFV decays the most stringent bound comes from \(\mu \rightarrow e \gamma \) [81]. As we shall see later, in presence of the TeV scale heavy neutrinos, all these bounds are satisfied automatically.
3.3 Leptogenesis and baryon asymmetry
In this subsection, we briefly discuss the generation of baryon asymmetry via leptogenesis. For an exhaustive description of the mechanism, we refer to reference [82]. Considering the mass degeneracy of the pair of heavy neutrinos, the required CP-asymmetry will be generated through the out of equilibrium decay of the lightest mass degenerate pair (say \(\tilde{\Psi _{1}}, \tilde{\Psi _{2}}\)) via resonant leptogenesis. The diagrammatic representation of the aforementioned processes can be found in Fig. 1.
Assuming \(M_R=0\), \(M_\nu \) becomes block diagonalisable. While computing CP-asymmetry, the preferred choice of basis is that where the lower block of the \(M_\nu \) (4 \(\times \) 4 complex symmetric sub-matrix \({\mathcal {M}}\)Footnote 5) is diagonal. In this preferred basis, the Lagrangian in Eq. (3) can be rewritten as,
The relations connecting Yukawa couplings in the diagonal mass basis (\(h_{i \alpha }\)) and the Yukawa couplings in the flavor basis (\(y_{i \alpha }\)) can be found in [82]. The total CP-asymmetry \(\epsilon _j\) in the decay of \(\tilde{\Psi _j}\) into \(\ell _\alpha \phi ~ (\bar{\ell _\alpha } \phi ^\dag )\) can be calculated by summing over the SM flavor \(\beta \) as follows:
Since we are operating in the regime of resonant leptogenesis, the dominant contribution to \(f_{ij}\) comes from self energy correction, i.e. \(f_{ij} \sim f_{ij}^{\textrm{self}}\), where \(f_{ij}^{\textrm{self}} = \frac{(M_i^2 - M_j^2) M_i M_j}{(M_i^2 - M_j^2)^2 + R_{ij}^2}\).Footnote 6
Here we have assumed that \(\tilde{\Psi _{1}}, \tilde{\Psi _{2}}\) are almost mass degenerate and lighter than other two states \(\tilde{\Psi _{3}}, \tilde{\Psi _{4}}\). Here it is considered that the lightest mass degenerate states \(\tilde{\Psi _{1}}, \tilde{\Psi _{2}}\) decay into each other to generate the lepton asymmetry \(\epsilon _1\) and \(\epsilon _2\) as shown in Fig. 1. To be more specific, Fig. 1a–c represent the diagrams which contribute to the computation of \(\epsilon _1\) and \(\epsilon _2\). These lepton asymmetries enter into the coupled Bolzmann equations. By solving three coupled Boltzmann equations simultaneously, one can obtain co-moving densities \(Y_{\tilde{\Psi _{1}}}, Y_{\tilde{\Psi _{2}}}\) and \(Y_{B-L}\) of \(\tilde{\Psi _{1}}, \tilde{\Psi _{2}}\) and \(B-L\) asymmetry respectively. The co-moving density is denoted as the ratio of actual number densityFootnote 7 and the entropy density \({\bar{s}}\) of the universe.Footnote 8 The detailed presentation and discussion of the Boltzmann equations are relegated to Appendix A. The lepton asymmetry is converted into baryon asymmetry \(Y_B\) via sphelaron process [87] as:
where \(Y_{B-L} (z_{\textrm{sph}})\) is the solution of Boltzmann equations at \(z = z_{\textrm{sph}} = \frac{M_{\tilde{\Psi _1}}}{T_{\textrm{sph}}}\). Here \(N_f\) and \(N_H\) denote the number of generations of fermion families and number of Higgs doublets respectively. In our framework, \(N_f = 3\) and \(N_H =1\). In Eq. (1), we have quoted the observed baryon asymmetry \(\eta _B\)Footnote 9 at present days.
4 Collider studies
Before proceeding to perform the collider analysis, let us discuss some of the salient features of the model parameter space in light of various constraints described in Sect. 3. In Sect. 2, we already have mentioned that with the inverse see-saw hierarchy, one can ascertain tiny active neutrino masses by setting \(M_R = 0\). We have also verified that this assumption hardly alters the results with respect to the scenario with \(M_R \ne 0\). Thus we set \(M_R =0\) throughout this analysis, which in turn introduces a resemblance with the original inverse see-saw model. In addition, all the entries of \(M_\nu \) (except \(M_R\)) are considered as complex to make the analysis a general one. While fitting the neutrino oscillation data, we adopt normal hierarchy among the light active neutrinos and also set the mass of the lightest active neutrino to be zero (\(m_1 = 0\)), which arises as an artifact of the present framework. For the collider analysis, we shall restrict ourselves to a particular mass region, where the mass of the lightest heavy neutrino (\(M_{\tilde{\Psi _1}} \simeq M_{\tilde{\Psi _2}} \)) is less than or almost equal to 10 TeV. Now, the ranges for input parameters for the aforementioned range of \(M_{\tilde{\Psi _1}} \) are: \( M_{D_{i,j}}^{R,I} \in [10^7~\textrm{eV}: 10^8~\textrm{eV}]\), \(M_{S_{i,j}}^{R,I} \in [10^{10}~\textrm{eV}: 10^{13}~\textrm{eV}]\). From Eq. (11) one can solve \(\mu \) and express it in terms of the input parameters \(M_D, M_S\) ( with \(M_R = 0\) ) and neutrino oscillation parameters. In addition, it has been verified that in presence of the TeV scale heavy neutrinos, the most stringent bound coming from the LFV decay \(\mu \rightarrow e \gamma \) [81], can be easily evaded for all points in the parameter space. Next by solving the Boltzmann equations (given in Appendix A), one can compute the baryon asymmetry of the universe at each and every point of the parameter space. In Fig. 2a (Fig. 2b) (taken from one of our previous studies [82]), we have plotted Br(\(\mu \rightarrow e \gamma \)) vs. \(M_{\tilde{\Psi _1}}~(M_{\tilde{\Psi _3}}) \). The blue, red and green points are compatible with neutrino oscillation data only, neutrino oscillation data + LFV decay and neutrino oscillation data + LFV decay + current baryon asymmetry of the universe respectively. Here we have considered a 1\(\sigma \) deviation around the central value of observed baryon asymmetry.
In one of our previous studies [82], we have shown that there exists a stringent lower bound of \(\sim \) 3.2 TeV on \(M_{\tilde{\Psi _1}}\) to satisfy the current baryon asymmetry data. Thus one can anticipate that due to the presence of these TeV scale heavy neutrinos, our present framework becomes very attractive from the collider perspective.
In this paper, we are interested to probe the pair production of the heavy neutrinos \({\tilde{\Psi }}_{1,2,3,4}\)) along with SM active neutrinos (\(\nu _l\)) via s-channel and t-channel processes, followed by subsequent decays of the heavy neutrinos to \(W^+\) and an SM lepton (\(l^{\pm }\)Footnote 10). Further decays of unstable \(W^+\) into leptonic (\(W^{\pm } \rightarrow l^{\pm } \nu _l({\bar{\nu }}_l\)) and hadronic (\(W^\pm \rightarrow j j\)) modes, give rise to \(2l + E_T \!\!\!\!\!\!/\;\,\) and \(1l + 2j + E_T \!\!\!\!\!\!/\;\,\) final states respectively as shown in Figs. 3a, b and 4a, b respectively. Details of decay chain of the respective processes leading to the final states will be described in the following subsections.
For performing collider analysis of the aforementioned channels, we shall choose eight benchmark points (BP1, BP2, BP3, BP4, BP5, BP6, BP7, BP8) from the model parameter space, which lie well within the correct baryon asymmetry band. Thus the chosen benchmark points are compatible with the experimental data coming from neutrino oscillation, LFV decays and current baryon asymmetry of the universe. These benchmark points are characterised by low, medium and high lightest heavy neutrino masses (\(M_{\tilde{\Psi _1}}\)), spanning a wide range, from 3.2 TeV to 10.12 TeV. The eight benchmarks are tabulated in Table 2 along with \(M_{{\tilde{\Psi }}_{1(2)}}\), \(M_{{\tilde{\Psi }}_{3(4)}}\) and corresponding baryon asymmetry yield. To probe the benchmark points, we perform the collider analysis at two different center of mass (COM) energies (\(\sqrt{s}\)), i.e. \(\sqrt{s} = 6\) TeV (for BP1, BP2, BP3), 14 TeV (for BP4, BP5, BP6, BP7, BP8) at the muon collider.
In the next subsections we shall perform back to back collider analyses of the \(2l + E_T \!\!\!\!\!\!/\;\,\) and \(1l + 2j + E_T \!\!\!\!\!\!/\;\,\) final states, which turn out to be promising at aforementioned COM energies. Owing to small signal cross section and large background, even with high luminosity, this signal turns out to be non-promising at LHC. Besides, this signal involving TeV scale heavy neutrinos in the final state cannot be probed at ILC since the maximum achievable COM energy at ILC is 1 TeV. The leading order (LO) signal and background cross sections for the channels are generated via MG5aMC@NLO [88]. Further decays of the unstable particles are emulated through Pythia8 [89]. The detector effects are included in the analysis by passing both the signal and the backgrounds through Delphes\(-\)3.5.0 [90]. We use the default muon collider simulation card [91] for this purpose. We shall comment about the jet clustering algorithm later in Sect. 4.2. Following acceptance cuts are used for the aforementioned channels:
Here \(p_{T_{j(l)}}\) and \(|\eta _{j(l)}|\) are the transverse momentum and pseudo-rapidity of jets (leptons) respectively. The separation between the final state i-th and j-th particles can be defined as:
where \(\eta _{i}\) and \(\phi _i\) are the pseudo rapidity and azimuthal angle of i-th particle. Since traditional cut-based analysis is enough to yield high significances for all benchmarks, we shall only present the results generated from it. The signal significance has been computed using \({\mathcal {S}} = \sqrt{2\Big [(S + B) \log \Big (\frac{S + B}{B}\Big )- S\Big ]}\) [92], where S(B) denote the number of signal (background) events surviving the cuts applied on relevant kinematic variables.
4.1 \(2l + E_T \!\!\!\!\!\!/\;\,\) final state
In muon collider, heavy neutrinos can be produced along with active neutrinos via t-channel \(W^\pm \) mediation and s-channel Z mediation. In this analysis, we aim to probe the following signal containing two opposite sign (OS) same/different flavor leptons plus missing energy in the final state:
Here, the heavy neutrino can decay to \(W^{\pm }\) via charged current interaction which is further accompanied by the leptonic decay of \(W^{\pm }\). The dominant background for this signal originates from the \(\mu ^+ \mu ^- \rightarrow l^+ l^- + \not \! E_T \) final state, which receives dominant contributions from the following sub-processesFootnote 11:
-
\(\mu ^{+}\mu ^{-}\rightarrow l^{-} l^{+*} \rightarrow l^{-} W^{+*} {\bar{\nu }}_l \rightarrow l^{-} l^{+} \nu _l {{\bar{\nu }}}_l\),
-
\(\mu ^{+}\mu ^{-}\rightarrow l^{-} l^{+*} \rightarrow l^{-} Z^{*} l^+ \rightarrow l^{-} l^{+} \nu _l {\bar{\nu }}_l\),
-
\(\mu ^{+}\mu ^{-}\rightarrow \nu _l^{*} \nu _l\rightarrow \nu _l Z^{*} {\bar{\nu }}_l \rightarrow \nu _l {\bar{\nu }}_l l^+ l^{-}\),
-
\(\mu ^{+}\mu ^{-}\rightarrow \nu _l^{*} {\bar{\nu }}_l\rightarrow {\bar{\nu }}_l W^{+*} l^- \rightarrow \nu _l {\bar{\nu }}_l l^+ l^{-}\),
-
\(\mu ^+ \mu ^- \rightarrow W^+ W^-\); \(W^+ \rightarrow l^+ ~\nu _l, ~ W^- \rightarrow l^- ~{\bar{\nu }}_l\),
-
\(\mu ^+ \mu ^- \rightarrow ZZ\); \(Z \rightarrow l^+ l^-, ~ Z \rightarrow \nu _l ~{\bar{\nu }}_l\),
-
\(\mu ^+ \mu ^- \rightarrow W^+ W^- Z\); \(W^+ \rightarrow l^+ ~\nu _l, ~ W^- \rightarrow l^- ~{\bar{\nu }}_l, ~ Z \rightarrow \nu _l ~{\bar{\nu }}_l\),
-
\(\mu ^+ \mu ^- \rightarrow ZZZ\); \(Z \rightarrow l^+ l^-, ~ Z \rightarrow \nu _l ~{\bar{\nu }}_l, ~ Z \rightarrow \nu _l ~{\bar{\nu }}_l\).
The LO cross sections of the signals (for all benchmarks) and SM backgrounds are tabulated in Table 3.Footnote 12 To reduce the background with respect to signal, we choose a set of cuts on some of the kinematic variables. We denote the cuts on the kinematic variables for benchmarks BP1- BP3 at 6 TeV COM energy as \(B_i~(i:1-7)\) and for the rest of the benchmarks (BP4–BP8) at \(\sqrt{s}=14\) TeV, the cuts are defined as \(C_j~(j:1-7)\). For brevity, and also to avoid repetition, we discuss the cuts for two different COM energies together. All the names of the cuts or numbers within the bracket below will correspond to the analysis at 14 TeV. Following are the depiction of cuts chosen to enhance significance:
-
\({B_1~(C_1):}\) We demand two opposite sign, same or different flavored charged leptons l in the final state. As mentioned previously, here l denotes only electron and/or muon.
-
\({B_2~(C_2):}\) The normalized distributions of the transverse momentum of the leading lepton (\(p_{T_{l_1}}\)) for signalFootnote 13 and background are shown in Fig. 5a (Fig. 6a) for COM energy 6 TeV (14 TeV). Here the leading lepton gets larger boost in \(p_T\) for the signal, since it is generated directly via pair production. In contrary, for the background, the leading lepton is produced from subsequent decays of pair produced particles. Thus \(p_{T_{l_1}}\) for the signal peaks at a larger value with respect to the SM background. Thus putting a large lower cut on the transverse momentum, i.e. \(p_{T_{l_1}}> 400\) GeV (200 GeV) for 6 TeV (14 TeV) can be suitable to enhance the signal significance.
-
\(B_3\): We show the normalized distributions of the transverse momentum of the next to leading lepton (\(p_{T_{l_2}}\)) for signal and backgrounds in Fig. 5b. As can be seen from the distributions, the SM background peaks around \(p_T\sim 0\), because the major fraction of the transverse momentum is taken away by the leading lepton. The signal distribution starts dominating the background distribution after 200 GeV. Therefore, we put a lower cut of \(p_{T_{l_2}}>200\) GeV at 6 TeV to maximise the significance.
-
\( C_3:\) We depict the normalized distributions of scalar sum of the transverse momenta of two leptons in the final state in Fig. 6b. The nature of the distributions of the signal and background can be explained following the descriptions of the distributions of \(p_{T_{l_1}}\) and \(p_{T_{l_2}} \) in previously defined cuts B2 (C2) and B3. A suitable lower cut: \(p_T^{l_1,l_2}>2\) TeV helps magnifying the significance drastically for \(\sqrt{s} = 14\) TeV.
-
\(B_4~(C_4):\) In Fig. 5c (Fig. 6c), we plot the normalised distributions of the magnitude of the vector sum of the transverse momenta of two leptons in the final state for signal and background for \(\sqrt{s} \) = 6 TeV (14 TeV). It is defined as:
$$\begin{aligned} p^{vect}_{T_{l_1,l_2}} {\equiv }\sqrt{(p_{{T x}_{l_1}}{+}p_{{T x}_{l_2}})^2{+}(p_{{T y}_{l_1}}{+}p_{{T y}_{l_2}})^2{+}(p_{{T z}_{l_1}}{+}p_{{T z}_{l_2}})^2} \end{aligned}$$Table 4 The cut-flow for signal and backgrounds along with the required integrated luminosity to achieve 5\(\sigma \) significance for the \( \mu ^+ \mu ^- \rightarrow 2l+E_T \!\!\!\!\!\!/\;\,\) channel for BP1, BP2 and BP3 at 6 TeV Muon collider Here, \(p_{{T x}_{l_i}}, p_{{T y}_{l_i}}\) and \(p_{{T z}_{l_i}}\) are the x, y, z-components of the transverse momentum vector for \(i=1,2\) respectively. We choose \(p^{vect}_{T_{l_1,l_2}}>600\) GeV (2 TeV) to suppress SM background for \(\sqrt{s} = 6 \) TeV ( 14 TeV ).
-
\(B_5:\) We define a kinematic variable \(M_{eff}\), i.e. effective mass as the scalar sum of the transverse momenta of the final state leptons and missing transverse energy. The normalized distributions of \(M_{eff}\) both for signal and background are shown in Fig. 5d. The distributions mimic the distributions for individual transverse momentum of the final state leptons as expected. Since the signal distributions for almost all benchmarks start overshadowing the SM background distribution for \(M_{eff}>2\) TeV, to achieve large significance, we apply a 2 TeV lower cut on \(M_{eff}\).
-
\(B_6~(C_5)\): We portray the normalized distribution of \(\Delta R_{l_1 l_2}\) for signals and backgrounds in Fig. 5e (Fig. 6d) at COM energy 6 TeV (14 TeV). For the signal, the distribution of \(\Delta R_{l_1 l_2}\) peaks at higher values, which is expected. According to the signal topology in the \(2l + E_T \!\!\!\!\!\!/\;\,\) channel, one of the final state charged leptons is produced along with the W-boson from the decay of the heavy neutrino, whereas the second lepton is produced from the decay of the W-boson itself. Thus the two opposite sign same or opposite flavoured leptons do not originate from the same mother particle. Therefore the normalized distribution of \(\Delta R_{l_1 l_2}\) peaks at comparatively higher value for the signal benchmarks. While generating the background sample, we have included all possible backgrounds leading to the final state \(2l + E_T \!\!\!\!\!\!/\;\,\). Thus the distribution of the aforesaid variable is smeared spanning a wide range. Besides, one of the dominant contributions in \(2l + E_T \!\!\!\!\!\!/\;\,\) background comes from ZZ process. This process will mimic the \(2l + E_T \!\!\!\!\!\!/\;\,\) final state if one of the Z-bosons decays to two opposite sign same flavoured leptons, while the other Z decays into two neutrinos. In this case the leptons being originated from a single mother particle, they will be collimated enough to keep \(\Delta R_{l_1 l_2}\) small. In addition, if we consider the contribution coming from \(W^+ W^-\) process to the background, two leptons in the final state originate from two different W-bosons, thus they will be widely separated making \(\Delta R_{l_1 l_2}\) large. That is why the distribution of \(\Delta R_{l_1 l_2}\) for background does not peak at some particular value, rather it has a spread spanning low as well as high values. It is evident from the distributions of the signal and background, a proper cut of \(\Delta R_{l_1 l_2}>3.0(3.0)\) has been chosen to distinguish the signal from the background.
-
\(B_7~(C_6)\): We compute the magnitude of azimuthal angular separation of two final state leptons as:
$$\begin{aligned} \Delta \phi _{l_1 l_2}= & {} |\phi _{l_1}-\phi _{l_2}| \text { for }\Delta \phi _{l_1 l_2}<\pi \\ \Delta \phi _{l_1 l_2}= & {} 2\pi -|\phi _{l_1}-\phi _{l_2}|, \text { otherwise} \end{aligned}$$The normalized distributions of \( \Delta \phi _{l_1 l_2}\) are presented for signal and backgrounds in Fig. 5f (Fig. 6e) for \(\sqrt{s} =\) 6 TeV (14 TeV). The nature of the distributions of \( \Delta \phi _{l_1 l_2}\) for signal and backgrounds can be explained following the same logic provided to describe the distributions for \(\Delta R_{l_1 l_2}\) previously. We choose \(\Delta \phi _{l_1 l_2}>3.0~ (3.1)\), for the survival of the signal over background for two aforementioned COM energies.
-
\(C_7:\) We define the azimuthal angular separation between direction of the leading lepton \(l_1\) and missing energy vector
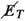 as
as  and present the normalized distributions of the same in Fig. 6f for COM energy 14 TeV. To differentiate the signal from the background, most optimal cut on the aforementioned variable is
and present the normalized distributions of the same in Fig. 6f for COM energy 14 TeV. To differentiate the signal from the background, most optimal cut on the aforementioned variable is  .
.
We summarize the results obtained after each cut, i.e. \((B_1- B_7)\) for \(\sqrt{s}=6\) TeV and \((C_1- C_7)\) for \(\sqrt{s}=14\) TeV in two tables. The cut-flow of the first three benchmarks along with the SM background for COM 6 TeV are presented in Table 4. The number of signal and background events after applying each cut are quoted at integrated luminosity 100 fb\(^{-1}\). It is evident from the table that the cuts are very effective to wipe out the background compare to the signal. At \(\sqrt{s} = 6\) TeV and \({\mathcal {L}} = 100\) fb\(^{-1}\), we are left with only 192 background events. Whereas the signal events remains almost steady after applying the same cuts. In the last column of the table, we compute the required integrated luminosity to achieve the 5\(\sigma \) significance. For BP1, 0.17 \(\textrm{fb}^{-1}\) luminosity is enough to achieve \(5\sigma \) significance while a benchmark with higher heavy neutrino mass 5.11 TeV (BP3) would require 14.19 \(\textrm{fb}^{-1}\). This happens owing to the decrease in signal cross section with increasing \(M_{{\tilde{\Psi }}_{1}}\).
Next in Table 5, we present the cut flow for benchmarks BP4–BP8 for COM energy 14 TeV with integrated luminosity 1600 \(\textrm{fb}^{-1}\). SM background events are reduced to 237 after employing all the chosen cuts. Whereas the number of the signal events surviving after imposing all cuts for BP4, BP5, BP6, BP7, BP8 are 25809, 4698, 1323, 430, and 98 respectively. In addition, we derive the integrated luminosity needed to attain \(5\sigma \) significance. For BP4–BP8, 1.56 \(\textrm{fb}^{-1}\), 8.94 \(\textrm{fb}^{-1}\), 35.66 \(\textrm{fb}^{-1}\), 144.05 \(\textrm{fb}^{-1}\) and 1380.55 \(\textrm{fb}^{-1}\) integrated luminosities are required to achieve 5\(\sigma \) discovery. Thus one can conclude that the benchmark with larger cross section and hence with smaller value of \(M_{{\tilde{\Psi }}_{1}}\), is more promising than others to probe at the muon collider in light of \(2l + E_T \!\!\!\!\!\!/\;\,\) final state.
4.2 \(1l + 2j + E_T \!\!\!\!\!\!/\;\,\) final state
In this subsection we shall analyse the aforementioned channel featuring the hadronic decay of W-boson (Fig. 4a, b). We consider corresponding SM backgrounds with the same final state. Before we start analysing the channel, let us make brief comment on the jet clustering algorithm, which we have used here. Here the jet clustering occurs via Valencia (VLC) jet clustering algorithm [93, 94], which is well suited at high energy lepton colliders. Using this algorithm, the events are clustered into two jets with \(R = 0.5\) in our case. The dominant background for this signal originates from the \(\mu ^+ \mu ^- \rightarrow 1l + 2j + \not \! E_T \) final state, which receives contributions from the following sub-processes:
-
\(\mu ^{+} \mu ^{-} {\rightarrow } W^{+} W^{-}\); \(W^{+} (W^-) {\rightarrow } l^{+}(l^-) ~\nu _\ell (~{\bar{\nu }}_\ell ), ~W^-(W^+) \) \( {\rightarrow } jj,\)
-
\(\mu ^+ \mu ^- \rightarrow ZZ\); \(Z \rightarrow l^+ l^-, ~ Z \rightarrow jj\), (one of the leptons is missed)
-
\(\mu ^+ \mu ^- \rightarrow W^+ W^- Z\);
-
1.
\(W^+ \rightarrow l^+ ~\nu _l, ~ W^- \rightarrow l^- ~{\bar{\nu }}_l, ~ Z \rightarrow jj\), (one of the leptons is missed)
-
2.
\(W^+ \rightarrow l^+ ~\nu _l, ~ W^- \rightarrow jj, ~ Z \rightarrow \nu _l ~{\bar{\nu }}_l\),
-
3.
\(W^+ \rightarrow jj, ~ W^- \rightarrow l^- ~{\bar{\nu }}_l, ~ Z \rightarrow \nu _l ~{\bar{\nu }}_l\),
-
1.
-
\(\mu ^+ \mu ^- \rightarrow ZZZ\); \(Z \rightarrow l^+ l^-, ~ Z \rightarrow jj, ~ Z \rightarrow \nu _l ~{\bar{\nu }}_l\), (one of the leptons is missed)
-
\(\mu ^+ \mu ^- \rightarrow Z ~ h\);
-
1.
\(Z \rightarrow l^+ l^-, ~h \rightarrow jj, \) (one of the leptons is missed)
-
2.
\(Z \rightarrow jj, ~h \rightarrow l^+ l^- \). (one of the leptons is missed)
-
1.
We follow the same procedure as the previous channel for analysing this signal. We shall refrain ourselves from discussing the details of generating the signal and backgrounds to avoid repetition. Similar to the previous analysis, we divide the study in two parts: for the first three benchmarks BP1–BP3, the COM energy of muon collider is taken to be 6 TeV and for the rest of the benchmarks BP4–BP8, the COM energy is assumed to be 14 TeV.
We compute the leading order cross-sections for signal (for all the benchmarks) and SM backgrounds and presented them in the Table 6. In Table 6, the top half of the table presents LO cross-sections for BP1–BP3 and corresponding backgrounds for \(\sqrt{s}=6\) TeV. The lower half contains cross-sections for BP4–BP8 and SM backgrounds at \(\sqrt{s}=\) 14 TeV. As can be seen from Table 6, the most significant contribution in backgrounds comes from \(W^+ W^{-}\) owing to its high cross-section. With the change of \(\sqrt{s}\) from 6 to 14 TeV, the dominant SM background cross-section decreases significantly from 40.92 fb to 9.25 fb. Same feature is observed for \(W^+ W^- Z\) background, i.e. cross-section decreases with increase in \(\sqrt{s}\). The cross-sections for BP1 and BP4 are quite large compare to the dominant SM background \(W^+ W^-\). However for BP3 and BP6–BP8, the signal cross-sections are lower than the cross-section of the dominant background.
We have drawn the normalized distributions of some relevant kinematic variables for both signal and backgrounds. like the previous subsection, following the same logic, we have presented the distributions for BP1,BP3 (BP4,BP6,BP8) and dominant backgrounds \(W^+ W^-\) and \(W^+ W^- Z\) for 6 TeV (14 TeV). Further, we imposed cuts on some kinematic variables to enhance the signal significance. We choose cuts \(D_i\)’s (for BP1–BP3 at 6 TeV) and \(E_i\)s (for BP4–BP8 at 14 TeV) which are described below:
-
\(D_1~(E_1):\) Particularly we select those events in which the number of jets are \(\ge 2\) and there is one charged lepton \(l=e\) or \(\mu \).
-
\(D_2:\) We plot normalized distributions of the transverse momentum of the leading jet (\(p_{T_{j_{1}}}\)) for signal and backgrounds in Fig. 7a. For signal, the mother particle of two jets (\(W^+\)) is originated from the decay of a heavy TeV scale neutrino. Thus the distributions of \(p_{T_{j_1}}\) for BP1,BP3 peak at higher values. Since the distributions of BP1,BP3 start dominating for \(p_{T_{j_1}}>800\) GeV, we apply lower cut of 800 GeV on \(p_{T_{j_{1}}}\) to maximize the signal significance.
-
\(D_3:\) Next we depict the normalized distributions of the transverse momentum of the second leading jet (\(p_{T_{j_2}}\)) in Fig. 7b. Most of the transverse momentum being carried away by the leading jet, the corresponding distribution of \(p_{T_{j_2}}\) for the background peaks around zero transverse momentum. The distributions of \(p_{T_{j_2}}\) for BP1,BP3 peak at higher values due to the aforementioned reason. Thus a cut: \(p_{T_{j_2}}>400\) GeV is chosen which significantly improve the signal significance.
-
\(E_2:\) The normalized distributions of the pseudo rapidity of leading jet (\(\eta _{j_1}\)) for signal and backgrounds are shown in Fig. 8b. For signal, the jets originate from the decay of W-boson, which is previously produced from the decay of the heavy neutrino. Thus the distributions of \(\eta _{j_1}\) for signals are centrally peaked. A suitable cut \(\eta _{j_1}<0.6\) is chosen to wipe out the backgrounds.
We summarize the results of the analysis and present the cut-flow for all the signal benchmarks and backgrounds in Tables 7 and 8 for \(\sqrt{s} =\) 6 TeV and 14 TeV respectively. We apply all the cuts mentioned above and the number of events surviving after each cut are quoted in the aforementioned tables. The upper half of Table 7, presents cut-flow for dominant backgrounds \(W^+ W^-\) and \(W^+ W^- Z\) at integrated luminosity 100 fb\(^{-1}\). In the bottom half of the same table, we show the cut-flow of the signal benchmarks BP1–BP3 at \(\sqrt{s}=6\) TeV. After incorporating all three cuts (\(D_1, D_2, D_3\)), only 187 and 103 events survive from \(W^{+} W^{-}\) and \(W^{+} W^{-}Z\) backgrounds respectively at integrated luminosity 100 fb\(^{-1}\). While remaining signal events for BP1, BP2 and BP3 are 27545, 3962 and 541 respectively at the same luminosity. Therefore, it is observed that the combination of cuts have efficiently reduced the SM backgrounds. We also compute the required luminosity to achieve \(5\sigma \) significance (\({\mathcal {L}}_{5 \sigma }\)) and quote them in Table 7. For BP1,BP2 and BP3, 0.09 fb\(^{-1}\), 0.68 fb\(^{-1}\) and 7.12 fb\(^{-1}\) are required respectively to claim discovery.
We summarize the results for benchmarks BP4–BP8 at 14 TeV in the Table 8. The first half of the table show the surviving events of two dominating backgrounds after imposing each of the aforementioned cuts (\(E_1-E_2\)). The background events for \(W^+ W^-\) drops from 2275 to 1301 events and for \(W^+ W^- Z\) it reduces from 1426 to 864 events after applying all the cuts at integrated luminosity 1600 fb\(^{-1}\). In the bottom half part of the table, we provide the number of signal events for benchmarks BP4–BP8 after applying the same cuts. One can infer that the combination of two cuts \(E_1\) and \(E_2\) efficiently kills the backgrounds and helps to enhance the signal significance. Finally, in the same table, we provide the luminosity needed to achieve 5\(\sigma \) significance, which increases from BP4 to BP8 owing to monotonically decreasing signal cross-sections.
Before concluding this section, let us present a comparative study between two signal channels which have been analysed in this paper. Comparing the integrated luminosities required to achieve \(5 \sigma \) significances for the two channels, \(1l + 2j + \not \! E_T \) channel turns out to be the most promising channel among the two. For example to probe BP1 (BP4) in \(2l + \not \! E_T \) channel, 0.17 fb\(^{-1}\) (1.56 fb\(^{-1}\)) is required at \(\sqrt{s} = 6\) TeV (14 TeV). Whereas, for \(1l + 2j + \not \! E_T \) channel, the corresponding luminosity is 0.09 fb\(^{-1}\) (0.32 fb\(^{-1}\)) at \(\sqrt{s} = 6\) TeV (14 TeV). This holds for other benchmarks too. The signal cross sections (at a given COM energy) are larger in the hadronic final state and corresponding background cross sections are smaller than the same in the leptonic final state. Putting these all together, the ratio of the signal cross section over the background cross section before any selection cut is much larger for the \(1l+2j+E_T \!\!\!\!\!\!/\;\,\) channel than the \(2l + E_T \!\!\!\!\!\!/\;\,\) channel. Basically this is one of the reasons for which a leptonic collider is preferred over a hadronic one to probe the hadronic final states. Since we cannot produce this signal at ILC, muon collider turns out to be useful to probe such hadronic final states. Thus at muon collider, the second channel containing jets in the final state turns out to be the most promising. It is also expected as a consequence of a clean, jet-free environment of a leptonic collider compare to LHC.
5 Summary and conclusion
In this present paper, we have focused on a framework popularly known as ISS(2,2), i.e. (2,2) inverse see-saw realisation, where the SM is accompanied with two singlet right handed neutrinos and two singlet neutral fermions. From the name of the model itself, it is evident that the neutrino mass generation in this scenario occurs via inverse see-saw mechanism. To make the analysis a robust one, we have considered the most general structure of the \(7 \times 7\) neutrino mass matrix \(M_\nu \) with complex entries. Further by regulating the input model parameters and assuming normal mass hierarchy between the active neutrinos, we can segregate the portion of the parameter space, which becomes compatible with the neutrino oscillation data. Upon diagonalising the mass matrix \(M_\nu \), we are left with three active neutrino and four heavy neutrino mass eigenstates (\(\tilde{\Psi _1}, \tilde{\Psi _2}, \tilde{\Psi _3}, \tilde{\Psi _4}\)). The interesting feature of these heavy neutrino mass eigenstates is the pairwise mass degeneracy of the same, i.e. \(M_{\tilde{\Psi _1}} \simeq M_{\tilde{\Psi _2}}\) and \(M_{\tilde{\Psi _3}} \simeq M_{\tilde{\Psi _4}}\). In addition, we have checked that the former parameter space also obeys the bounds coming from the LFV decays including \(\mu \rightarrow e \gamma \). Next at each and every point in the parameter space satisfying neutrino oscillation data and the bounds coming from the LFV decays, the baryon asymmetry is computed. Thus we can obtain a subset of the larger parameter space, which is compatible with (i) neutrino oscillation data, (ii) constraints coming from LFV decay and (iii) observed baryon asymmetry data. One can conclude that the baryon asymmetry constraint itself has put a lower bound on the lightest heavy neutrino state i.e. \(M_{\tilde{\Psi _1}} > 3.2\) TeV.
Next we aim to analyse some promising collider signatures of the TeV scale heavy neutrinos at multi-TeV muon collider. First we choose some benchmark points from the previously derived parameter space, depending on \(M_{\tilde{\Psi _1}}\). For collider study, we intend to analyse those benchmarks which satisfy the observed baryon asymmetry of the universe. Accordingly, we have picked up different benchmarks where \(M_{\tilde{\Psi _1}}\) ranges between 3.2 TeV to 10.12 TeV (BP1–BP8). The range of heavy neutrino masses which we are talking about, cannot be produced at ILC. The signal contains pair production of active neutrino and a heavy neutrino, followed by the decay of the heavy neutrino into \(W^\pm \) and a charged lepton (e, \(\mu \)). Further if we consider the leptonic decay of the generated \(W^\pm \), it will lead to a di-lepton plus missing energy state. For analysis, we choose \(\sqrt{s} = 6\) TeV for BP1, BP2 and BP3 and \(\sqrt{s} = 14\) TeV for the rest of the benchmarks (BP4–BP8). We have not considered conventional LHC or ILC for purpose. The cross-section of the same process at LHC is much smaller than what we obtained in muon-collider. In addition, the large LHC backgrounds would be sufficient to kill the signal. The disadvantage of ILC lies in the maximal achievable COM energy (1 TeV). The dominant background for this signal is \(2l + E_T \!\!\!\!\!\!/\;\,\), arising from the subprocesses like \(W^+ W^-, ~ZZ, ~ W^+ W^- Z, ~ ZZZ\). Here we impose cuts on a few relevant kinematic variables to achieve maximally enhanced signal significances, suppressing the backgrounds with respect to the signals. Among all benchmarks, BP1 (BP4) turns out to be most promising with respect to the analysed signal at \(\sqrt{s} =6\) TeV (14 TeV). To achieve 5\(\sigma \) significance one needs 0.17 fb\(^{-1}\), 1.28 fb\(^{-1}\) and 14.19 fb\(^{-1}\) integrated luminosity for BP1, BP2, BP3 respectively at COM energy 6 TeV. Besides the integrated luminosities required for 5\(\sigma \) significance are 1.56 fb\(^{-1}\), 8.94 fb\(^{-1}\), 35.66 fb\(^{-1}\), 144.05 fb\(^{-1}\), 1380.55 fb\(^{-1}\) respectively for BP4, BP5, BP6, BP7, BP8 at \(\sqrt{s}=14\) TeV. Though this particular channel provides encouraging results at muon collider, for completeness, we also consider the hadronic decay of \(W^\pm \) in the signal instead of leptonic decay, leading to \(1l + 2j + E_T \!\!\!\!\!\!/\;\,\) signature. Analysing this channel is very challenging due to the presence of large jetty SM backgrounds. In presence of the dominant background \(W^+ W^-\) and \(W^+ W^- Z\), the end result of analysing this channel is encouraging. Required luminosities to procure 5\(\sigma \) significance at \(\sqrt{s} =\) 6 TeV (14 TeV) for BP1–BP3 (BP4–BP8) are 0.09 fb\(^{-1}\), 0.68 fb\(^{-1}\) and 7.12 fb\(^{-1}\) (0.32 fb\(^{-1}\), 2.0 fb\(^{-1}\), 9.11 fb\(^{-1}\), 44.59 fb\(^{-1}\) and 563.06 fb\(^{-1}\)) respectively. By looking at the integrated luminosity required to achieve 5\(\sigma \) significances for different benchmarks at \(\sqrt{s} = 6\) TeV and 14 TeV, one can conclude that \(1l+2j+\not \! E_T \) channel is indeed more promising than the previous one.
Feynman diagram representing a decay of lightest heavy RH-neutrino \(\tilde{\Psi _{1}}~(\tilde{\Psi _{2}})\) (contributes to \(\gamma _{D}^{(1)}, \gamma _{D}^{(2)}\)), b \(\Delta L = 2\), s-channel scattering via \(\tilde{\Psi _{1}}~(\tilde{\Psi _{2}})\) (contributes to \(\gamma _{{\tilde{\Psi }},s}\)), c \(\Delta L = 1\), s-channel scattering via Higgs (contributes to \(\gamma ^{1}_{\phi ,s}, \gamma ^{2}_{\phi ,s}\)), d, e \(\Delta L = 1\), t-channel scattering via Higgs (contributes to \(\gamma ^{1}_{\phi ,t}, \gamma ^{2}_{\phi ,t}\)), f \(\Delta L = 2\), t-channel scattering via \(\tilde{\Psi _{1}}~(\tilde{\Psi _{2}})\) (contributes to \(\gamma _{{\tilde{\Psi }},t}\))
Data Availability
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The data we used in our manuscript to compare with our model estimations are already public from the ATLAS, CMS and PLANCK experiments.]
Notes
In [82], we have shown that following the hierarchy \(\mu , M_R \ll M_D \ll M_S\), with a non-zero but tiny \(M_R\), all the numerical results hardly show any deviation with respect to what is obtained by setting \(M_R = 0\). Thus our assumption of taking a vanishing \(M_R\), for simplifying the analysis, is justified.
\(U_{\textrm{PMNS}}\) can be written as:

Here \(c_{ij} \equiv \cos \theta _{ij}, s_{ij} \equiv \sin \theta _{ij}\) and \(\delta _{CP}\) is the CP-violating phase.
Assuming normal hierarchy (NH) among the light neutrinos, the parameters are fixed at their central values:
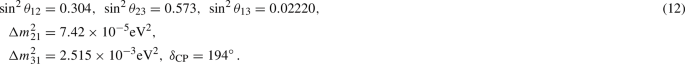
\(m_1, m_2, m_3 \) are the masses of three active neutrinos.
4 \(\times \) 4 complex symmetric sub-matrix \({\mathcal {M}}\) is defines as:

In the analysis we have considered \(R_{ij} = |M_i \Gamma _i + M_j \Gamma _j|\) [82] and \(\Gamma _j = \frac{(h h^\dag )_{ii} M_j}{8 \pi }\) is the total decay width of \(\tilde{\Psi _j}\). The logic behind choosing this particular form of \(R_{ij}\) can be found in one of our previous studies [82]. Thus we shall not present that here to avoid repetition.
The number densities of particles with mass M and temperature T can be written as:

g being the number of degrees of freedom of corresponding particles, \(K_2\) being second modified Bessel function of second kind.
Entropy density is computed as: \({\bar{s}} = \frac{2 \pi ^2}{45}~ g_{eff} T^3\). Here T is the temperature and \(g_{eff}\) is the number of degrees of freedom (D.O.F), which is computed in Appendix A.
\(\eta _B\) is related to \(Y_B\) via: \(Y_B \simeq \frac{\eta _B}{7,04}= (8.75 \pm 0.23) \times 10^{-11} \) [70].
Here we consider \(l = e, \mu \).
Here superscript \(``*''\) denotes the off-shell particle and \(\nu _l\) is the Standard Model neutrino with \(l = e, \mu \).
There exists a destructive interference between the amplitudes of different background sub-processes contributing to the final state \(2l + E_T \!\!\!\!\!\!/\;\,\). Thus obtaining the total background cross section by summing up the cross sections of individual sub-processes will be erroneous. Hence we directly generate the final state \(2\,l + E_T \!\!\!\!\!\!/\;\,\) through Madgraph and checked that all the aforementioned sub-processes are readily included in the background sample. Thus we have not provided the individual cross sections of the sub-processes, instead we have quoted the cross section of the entire process with \(2l + E_T \!\!\!\!\!\!/\;\,\) final state for two centre of mass energies.
To avoid clumsiness, we shall present the normalized distributions of the relevant kinematic variables for BP1, BP3 (BP4, BP6, BP8) at \(\sqrt{s} =\) 6 TeV (14 TeV).
Not to be confused with “s-channel” mentioned earlier.
References
ATLAS Collaboration, G. Aad et al., Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716, 1–29 (2012). https://doi.org/10.1016/j.physletb.2012.08.020. arXiv:1207.7214
CMS Collaboration, S. Chatrchyan et al., Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 716, 30–61 (2012). https://doi.org/10.1016/j.physletb.2012.08.021. arXiv:1207.7235
Planck Collaboration, N. Aghanim et al., Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 641, A6 (2020). https://doi.org/10.1051/0004-6361/201833910. arXiv:1807.06209
P. Minkowski, \(\mu \rightarrow e\gamma \) at a rate of one out of \(10^{9}\) muon decays? Phys. Lett. B 67, 421–428 (1977). https://doi.org/10.1016/0370-2693(77)90435-X
R.N. Mohapatra, G. Senjanovic, Neutrino mass and spontaneous parity nonconservation. Phys. Rev. Lett. 44, 912 (1980). https://doi.org/10.1103/PhysRevLett.44.912
J. Schechter, J.W.F. Valle, Neutrino masses in SU(2) \(\times \) U(1) theories. Phys. Rev. D 22, 2227 (1980). https://doi.org/10.1103/PhysRevD.22.2227
J. Schechter, J.W.F. Valle, Neutrino decay and spontaneous violation of lepton number. Phys. Rev. D 25, 774 (1982). https://doi.org/10.1103/PhysRevD.25.774
A. Das, N. Okada, Bounds on heavy Majorana neutrinos in type-I seesaw and implications for collider searches. Phys. Lett. B 774, 32–40 (2017). https://doi.org/10.1016/j.physletb.2017.09.042. arXiv:1702.04668
W. Konetschny, W. Kummer, Nonconservation of total lepton number with scalar bosons. Phys. Lett. B 70, 433–435 (1977). https://doi.org/10.1016/0370-2693(77)90407-5
T.P. Cheng, L.-F. Li, Neutrino masses, mixings and oscillations in SU(2) \(\times \) U(1) models of electroweak interactions. Phys. Rev. D 22, 2860 (1980). https://doi.org/10.1103/PhysRevD.22.2860
G. Lazarides, Q. Shafi, C. Wetterich, Proton lifetime and fermion masses in an SO(10) model. Nucl. Phys. B 181, 287–300 (1981). https://doi.org/10.1016/0550-3213(81)90354-0
R.N. Mohapatra, G. Senjanovic, Neutrino masses and mixings in gauge models with spontaneous parity violation. Phys. Rev. D 23, 165 (1981). https://doi.org/10.1103/PhysRevD.23.165
S. Antusch, Flavour-dependent type II leptogenesis. Phys. Rev. D 76, 023512 (2007). https://doi.org/10.1103/PhysRevD.76.023512. arXiv:0704.1591
R. Barbieri, D.V. Nanopoulos, G. Morchio, F. Strocchi, Neutrino masses in grand unified theories. Phys. Lett. B 90, 91–97 (1980). https://doi.org/10.1016/0370-2693(80)90058-1
M. Magg, C. Wetterich, Neutrino mass problem and gauge hierarchy. Phys. Lett. B 94, 61–64 (1980). https://doi.org/10.1016/0370-2693(80)90825-4
R. Gonzalez Felipe, F.R. Joaquim, H. Serodio, Flavoured CP asymmetries for type II seesaw leptogenesis. Int. J. Mod. Phys. A 28, 1350165 (2013). https://doi.org/10.1142/S0217751X13501650. arXiv:1301.0288
M. Chakraborty, M.K. Parida, B. Sahoo, Triplet leptogenesis, type-II Seesaw dominance, intrinsic dark matter, vacuum stability and proton decay in minimal SO(10) breakings. JCAP 01, 049 (2020). https://doi.org/10.1088/1475-7516/2020/01/049. arXiv:1906.05601
W. Rodejohann, Type II seesaw mechanism, deviations from bimaximal neutrino mixing and leptogenesis. Phys. Rev. D 70, 073010 (2004). https://doi.org/10.1103/PhysRevD.70.073010. arXiv:hep-ph/0403236
C.-S. Chen, C.-M. Lin, Type II seesaw Higgs triplet as the inflaton for chaotic inflation and leptogenesis. Phys. Lett. B 695, 9–12 (2011). https://doi.org/10.1016/j.physletb.2010.11.016. arXiv:1009.5727
M.K. Parida, M. Chakraborty, S.K. Nanda, R. Samantaray, Purely triplet seesaw and leptogenesis within cosmological bound, dark matter, and vacuum stability. Nucl. Phys. B 960, 115203 (2020). https://doi.org/10.1016/j.nuclphysb.2020.115203. arXiv:2005.12077
R. Foot, H. Lew, X.G. He, G.C. Joshi, Seesaw neutrino masses induced by a triplet of leptons. Z. Phys. C 44, 441 (1989). https://doi.org/10.1007/BF01415558
C.H. Albright, S.M. Barr, Leptogenesis in the type III seesaw mechanism. Phys. Rev. D 69, 073010 (2004). https://doi.org/10.1103/PhysRevD.69.073010. arXiv:hep-ph/0312224
D. Suematsu, Low scale leptogenesis in a hybrid model of the scotogenic type I and III seesaw models. Phys. Rev. D 100, 055008 (2019). https://doi.org/10.1103/PhysRevD.100.055008. arXiv:1906.12008
M.K. Parida, B.P. Nayak, Singlet fermion assisted dominant seesaw with lepton flavor and number violations and leptogenesis. Adv. High Energy Phys. 2017, 4023493 (2017). https://doi.org/10.1155/2017/4023493. arXiv:1607.07236
A. Biswas, D. Borah, D. Nanda, Type III seesaw for neutrino masses in U(1)\(_{B-L}\) model with multi-component dark matter. JHEP 12, 109 (2019). https://doi.org/10.1007/JHEP12(2019)109. arXiv:1908.04308
A. Das, S. Mandal, Bounds on the triplet fermions in type-III seesaw and implications for collider searches. Nucl. Phys. B 966, 115374 (2021). https://doi.org/10.1016/j.nuclphysb.2021.115374. arXiv:2006.04123
A. Das, S. Mandal, T. Modak, Testing triplet fermions at the electron–positron and electron–proton colliders using fat jet signatures. Phys. Rev. D 102, 033001 (2020). https://doi.org/10.1103/PhysRevD.102.033001. arXiv:2005.02267
R.N. Mohapatra, Mechanism for understanding small neutrino mass in superstring theories. Phys. Rev. Lett. 56, 561–563 (1986). https://doi.org/10.1103/PhysRevLett.56.561
R.N. Mohapatra, J.W.F. Valle, Neutrino mass and baryon number nonconservation in superstring models. Phys. Rev. D 34, 1642 (1986). https://doi.org/10.1103/PhysRevD.34.1642
J. Bernabeu, A. Santamaria, J. Vidal, A. Mendez, J.W.F. Valle, Lepton flavor nonconservation at high-energies in a superstring inspired standard model. Phys. Lett. B 187, 303–308 (1987). https://doi.org/10.1016/0370-2693(87)91100-2
M.B. Gavela, T. Hambye, D. Hernandez, P. Hernandez, Minimal flavour seesaw models. JHEP 09, 038 (2009). https://doi.org/10.1088/1126-6708/2009/09/038. arXiv:0906.1461
M.K. Parida, A. Raychaudhuri, Inverse see-saw, leptogenesis, observable proton decay and \(\Delta ^{\pm \pm }_{{\rm R}}\) in SUSY SO(10) with heavy W_R. Phys. Rev. D 82, 093017 (2010). https://doi.org/10.1103/PhysRevD.82.093017. arXiv:1007.5085
J. Garayoa, M.C. Gonzalez-Garcia, N. Rius, Soft leptogenesis in the inverse seesaw model. JHEP 02, 021 (2007). https://doi.org/10.1088/1126-6708/2007/02/021. arXiv:hep-ph/0611311
A. Abada, M. Lucente, Looking for the minimal inverse seesaw realisation. Nucl. Phys. B 885, 651–678 (2014). https://doi.org/10.1016/j.nuclphysb.2014.06.003. arXiv:1401.1507
S.S.C. Law, K.L. McDonald, Generalized inverse seesaw mechanisms. Phys. Rev. D 87, 113003 (2013). https://doi.org/10.1103/PhysRevD.87.113003. arXiv:1303.4887
T.P. Nguyen, T.T. Thuc, D.T. Si, T.T. Hong, L.T. Hue, Low energy phenomena of the lepton sector in an \(A_4\) symmetry model with heavy inverse seesaw neutrinos. arXiv:2011.12181
F. Deppisch, J.W.F. Valle, Enhanced lepton flavor violation in the supersymmetric inverse seesaw model. Phys. Rev. D 72, 036001 (2005). https://doi.org/10.1103/PhysRevD.72.036001. arXiv:hep-ph/0406040
C. Arina, F. Bazzocchi, N. Fornengo, J.C. Romao, J.W.F. Valle, Minimal supergravity sneutrino dark matter and inverse seesaw neutrino masses. Phys. Rev. Lett. 101, 161802 (2008). https://doi.org/10.1103/PhysRevLett.101.161802. arXiv:0806.3225
P.S.B. Dev, R.N. Mohapatra, TeV scale inverse seesaw in SO(10) and leptonic non-unitarity effects. Phys. Rev. D 81, 013001 (2010). https://doi.org/10.1103/PhysRevD.81.013001. arXiv:0910.3924
M. Malinsky, T. Ohlsson, Z.-Z. Xing, H. Zhang, Non-unitary neutrino mixing and CP violation in the minimal inverse seesaw model. Phys. Lett. B 679, 242–248 (2009). https://doi.org/10.1016/j.physletb.2009.07.038. arXiv:0905.2889
M. Hirsch, T. Kernreiter, J.C. Romao, A. Villanova del Moral, Minimal supersymmetric inverse seesaw: neutrino masses, lepton flavour violation and LHC phenomenology. JHEP 01, 103 (2010). https://doi.org/10.1007/JHEP01(2010)103. arXiv:0910.2435
S. Blanchet, P.S.B. Dev, R.N. Mohapatra, Leptogenesis with TeV scale inverse seesaw in SO(10). Phys. Rev. D 82, 115025 (2010). https://doi.org/10.1103/PhysRevD.82.115025. arXiv:1010.1471
A.G. Dias, C.A. de S. Pires, P.S. Rodrigues da Silva, A. Sampieri, A simple realization of the inverse seesaw mechanism. Phys. Rev. D 86, 035007 (2012). https://doi.org/10.1103/PhysRevD.86.035007. arXiv:1206.2590
K. Agashe, P. Du, M. Ekhterachian, C.S. Fong, S. Hong, L. Vecchi, Natural seesaw and leptogenesis from hybrid of high-scale type I and TeV-scale inverse. JHEP 04, 029 (2019). https://doi.org/10.1007/JHEP04(2019)029. arXiv:1812.08204
N. Gautam, M.K. Das, Neutrino mass, leptogenesis and sterile neutrino dark matter in inverse seesaw framework. arXiv:2001.00452
X. Zhang, S. Zhou, Inverse seesaw model with a modular \(S^{}_4\) symmetry: lepton flavor mixing and warm dark matter. arXiv:2106.03433
A. Das, N. Okada, Inverse seesaw neutrino signatures at the LHC and ILC. Phys. Rev. D 88, 113001 (2013). https://doi.org/10.1103/PhysRevD.88.113001. arXiv:1207.3734
A. Das, N. Okada, Improved bounds on the heavy neutrino productions at the LHC. Phys. Rev. D 93, 033003 (2016). https://doi.org/10.1103/PhysRevD.93.033003. arXiv:1510.04790
A. Das, S. Jana, S. Mandal, S. Nandi, Probing right handed neutrinos at the LHeC and lepton colliders using fat jet signatures. Phys. Rev. D 99, 055030 (2019). https://doi.org/10.1103/PhysRevD.99.055030. arXiv:1811.04291
W. Liu, K.-P. Xie, Z. Yi, Testing leptogenesis at the LHC and future muon colliders: a Z’ scenario. Phys. Rev. D 105, 095034 (2022). https://doi.org/10.1103/PhysRevD.105.095034. arXiv:2109.15087
A.D. Sakharov, Violation of CP invariance, c asymmetry, and baryon asymmetry of the universe. Pisma Zh. Eksp. Teor. Fiz. 5, 32–35 (1967). https://doi.org/10.1070/PU1991v034n05ABEH002497
M. Fukugita, T. Yanagida, Baryogenesis without grand unification. Phys. Lett. B 174, 45–47 (1986). https://doi.org/10.1016/0370-2693(86)91126-3
L. Covi, E. Roulet, F. Vissani, CP violating decays in leptogenesis scenarios. Phys. Lett. B 384, 169–174 (1996). https://doi.org/10.1016/0370-2693(96)00817-9. arXiv:hep-ph/9605319
E. Roulet, L. Covi, F. Vissani, On the CP asymmetries in Majorana neutrino decays. Phys. Lett. B 424, 101–105 (1998). https://doi.org/10.1016/S0370-2693(98)00135-X. arXiv:hep-ph/9712468
A. Pilaftsis, CP violation and baryogenesis due to heavy Majorana neutrinos. Phys. Rev. D 56, 5431–5451 (1997). https://doi.org/10.1103/PhysRevD.56.5431. arXiv:hep-ph/9707235
W. Buchmuller, R.D. Peccei, T. Yanagida, Leptogenesis as the origin of matter. Annu. Rev. Nucl. Part. Sci. 55, 311–355 (2005). https://doi.org/10.1146/annurev.nucl.55.090704.151558. arXiv:hep-ph/0502169
E.J. Chun, K. Turzynski, Quasi-degenerate neutrinos and leptogenesis from L(mu) - L(tau). Phys. Rev. D 76, 053008 (2007). https://doi.org/10.1103/PhysRevD.76.053008. arXiv:hep-ph/0703070
T. Kitabayashi, Remark on the minimal seesaw model and leptogenesis with tri/bi-maximal mixing. Phys. Rev. D 76, 033002 (2007). https://doi.org/10.1103/PhysRevD.76.033002. arXiv:hep-ph/0703303
C. Martinez-Prieto, D. Delepine, L.A. Urena-Lopez, Leptogenesis and reheating in complex hybrid inflation. Phys. Rev. D 81, 036001 (2010). https://doi.org/10.1103/PhysRevD.81.036001. arXiv:0908.2436
D. Suematsu, Thermal leptogenesis in a TeV scale model for neutrino masses. Eur. Phys. J. C 72, 1951 (2012). https://doi.org/10.1140/epjc/s10052-012-1951-z. arXiv:1103.0857
D. Aristizabal Sierra, F. Bazzocchi, I. ds Medeiros Varzielas, Leptogenesis in flavor models with type I and II seesaws. Nucl. Phys. B 858, 196–213 (2012). https://doi.org/10.1016/j.nuclphysb.2012.01.009. arXiv:1112.1843
T. Hambye, Leptogenesis: beyond the minimal type I seesaw scenario. New J. Phys. 14, 125014 (2012). https://doi.org/10.1088/1367-2630/14/12/125014. arXiv:1212.2888
S. Kashiwase, D. Suematsu, Leptogenesis and dark matter detection in a TeV scale neutrino mass model with inverted mass hierarchy. Eur. Phys. J. C 73, 2484 (2013). https://doi.org/10.1140/epjc/s10052-013-2484-9. arXiv:1301.2087
D. Borah, M.K. Das, Neutrino masses and leptogenesis in Type I and Type II seesaw models. Phys. Rev. D 90, 015006 (2014). https://doi.org/10.1103/PhysRevD.90.015006. arXiv:1303.1758
Y. Hamada, K. Kawana, Reheating-era leptogenesis. Phys. Lett. B 763, 388–392 (2016). https://doi.org/10.1016/j.physletb.2016.10.067. arXiv:1510.05186
Z.-H. Zhao, Renormalization group assisted leptogenesis in the minimal type-I seesaw model. arXiv:2003.00654
V.A. Rubakov, M.E. Shaposhnikov, Electroweak baryon number nonconservation in the early universe and in high-energy collisions. Usp. Fiz. Nauk 166, 493–537 (1996). https://doi.org/10.1070/PU1996v039n05ABEH000145. arXiv:hep-ph/9603208
F.R. Klinkhamer, N.S. Manton, A saddle-point solution in the Weinberg–Salam theory. Phys. Rev. D 30, 2212–2220 (1984). https://doi.org/10.1103/PhysRevD.30.2212
N.S. Manton, Topology in the Weinberg–Salam theory. Phys. Rev. D 28, 2019–2026 (1983). https://doi.org/10.1103/PhysRevD.28.2019
S. Davidson, E. Nardi, Y. Nir, Leptogenesis. Phys. Rep. 466, 105–177 (2008). https://doi.org/10.1016/j.physrep.2008.06.002. arXiv:0802.2962
S. Davidson, A. Ibarra, A Lower bound on the right-handed neutrino mass from leptogenesis. Phys. Lett. B 535, 25–32 (2002). https://doi.org/10.1016/S0370-2693(02)01735-5. arXiv:hep-ph/0202239
T. Hambye, Leptogenesis at the TeV scale. Nucl. Phys. B 633, 171–192 (2002). https://doi.org/10.1016/S0550-3213(02)00293-6. arXiv:hep-ph/0111089
T. Hambye, Leptogenesis at the TeV scale. Nucl. Phys. B 633, 171–192 (2002). https://doi.org/10.1016/s0550-3213(02)00293-6
A. Pilaftsis, T.E.J. Underwood, Resonant leptogenesis. Nucl. Phys. B 692, 303–345 (2004). https://doi.org/10.1016/j.nuclphysb.2004.05.029. arXiv:hep-ph/0309342
T. Hambye, J. March-Russell, S.M. West, Tev scale resonant leptogenesis from supersymmetry breaking. J. High Energy Phys. 2004, 070 (2004). https://doi.org/10.1088/1126-6708/2004/07/070
T. Hambye, J. March-Russell, S.M. West, TeV scale resonant leptogenesis from supersymmetry breaking. JHEP 07, 070 (2004). https://doi.org/10.1088/1126-6708/2004/07/070. arXiv:hep-ph/0403183
A. Pilaftsis, T.E.J. Underwood, Electroweak-scale resonant leptogenesis. Phys. Rev. D 72, 113001 (2005). https://doi.org/10.1103/PhysRevD.72.113001. arXiv:hep-ph/0506107
V. Cirigliano, G. Isidori, V. Porretti, CP violation and leptogenesis in models with minimal lepton flavour violation. Nucl. Phys. B 763, 228–246 (2007). https://doi.org/10.1016/j.nuclphysb.2006.11.015. arXiv:hep-ph/0607068
Z.-Z. Xing, S. Zhou, Tri-bimaximal neutrino mixing and flavor-dependent resonant leptogenesis. Phys. Lett. B 653, 278–287 (2007). https://doi.org/10.1016/j.physletb.2007.08.009. arXiv:hep-ph/0607302
I. Esteban, M.C. Gonzalez-Garcia, M. Maltoni, T. Schwetz, A. Zhou, The fate of hints: updated global analysis of three-flavor neutrino oscillations. JHEP 09, 178 (2020). https://doi.org/10.1007/JHEP09(2020)178. arXiv:2007.14792
MEG Collaboration, A.M. Baldini et al., Search for the lepton flavour violating decay \(\mu ^+ \rightarrow {\rm e}^+ \gamma \) with the full dataset of the MEG experiment. Eur. Phys. J. C 76, 434 (2016). https://doi.org/10.1140/epjc/s10052-016-4271-x. arXiv:1605.05081
I. Chakraborty, H. Roy, T. Srivastava, Resonant leptogenesis in (2,2) inverse see-saw realisation. Nucl. Phys. B 979, 115780 (2022). https://doi.org/10.1016/j.nuclphysb.2022.115780. arXiv:2106.08232
K. Long, D. Lucchesi, M. Palmer, N. Pastrone, D. Schulte, V. Shiltsev, Muon colliders to expand frontiers of particle physics. Nat. Phys. 17, 289–292 (2021). https://doi.org/10.1038/s41567-020-01130-x. arXiv:2007.15684
T. Han, S. Li, S. Su, W. Su, Y. Wu, Heavy Higgs bosons in 2HDM at a muon collider. Phys. Rev. D 104, 055029 (2021). https://doi.org/10.1103/PhysRevD.104.055029. arXiv:2102.08386
S. Centelles Chuliá, R. Srivastava, A. Vicente, The inverse seesaw family: Dirac and Majorana. JHEP 03, 248 (2021). https://doi.org/10.1007/JHEP03(2021)248. arXiv:2011.06609
S. Vagnozzi, E. Giusarma, O. Mena, K. Freese, M. Gerbino, S. Ho et al., Unveiling \(\nu \) secrets with cosmological data: neutrino masses and mass hierarchy. Phys. Rev. D 96, 123503 (2017). https://doi.org/10.1103/PhysRevD.96.123503. arXiv:1701.08172
Y. Burnier, M. Laine, M. Shaposhnikov, Baryon and lepton number violation rates across the electroweak crossover. JCAP 0602, 007 (2006). https://doi.org/10.1088/1475-7516/2006/02/007. arXiv:hep-ph/0511246
J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer et al., The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP 07, 079 (2014). https://doi.org/10.1007/JHEP07(2014)079. arXiv:1405.0301
T. Sjöstrand, S. Ask, J.R. Christiansen, R. Corke, N. Desai, P. Ilten et al., An introduction to PYTHIA 8.2. Comput. Phys. Commun. 191, 159–177 (2015). https://doi.org/10.1016/j.cpc.2015.01.024. arXiv:1410.3012
DELPHES 3 Collaboration, J. de Favereau, C. Delaere, P. Demin, A. Giammanco, V. Lemaître, A. Mertens et al., DELPHES 3, A modular framework for fast simulation of a generic collider experiment. JHEP 02, 057 (2014). https://doi.org/10.1007/JHEP02(2014)057. arXiv:1307.6346
M. Selvaggi, Talk at mdi studies meeting of the muon collider collaboration. https://indico.cern.ch/event/957299/contributions/4023467/attachments/2106044/3541874/delphes_card_mucol_mdi%20.pdf
G. Cowan, K. Cranmer, E. Gross, O. Vitells, Asymptotic formulae for likelihood-based tests of new physics. Eur. Phys. J. C 71, 1554 (2011). https://doi.org/10.1140/epjc/s10052-011-1554-0. arXiv:1007.1727
M. Boronat, J. Fuster, I. Garcia, E. Ros, M. Vos, A robust jet reconstruction algorithm for high-energy lepton colliders. Phys. Lett. B 750, 95–99 (2015). https://doi.org/10.1016/j.physletb.2015.08.055. arXiv:1404.4294
M. Boronat, J. Fuster, I. Garcia, P. Roloff, R. Simoniello, M. Vos, Jet reconstruction at high-energy electron–positron colliders. Eur. Phys. J. C 78, 144 (2018). https://doi.org/10.1140/epjc/s10052-018-5594-6. arXiv:1607.05039
M. Plumacher, Baryogenesis and lepton number violation. Z. Phys. C 74, 549–559 (1997). https://doi.org/10.1007/s002880050418. arXiv:hep-ph/9604229
Acknowledgements
The authors thank Aleksander Filip Zarnecki, Yongcheng Wu, Nabarun Chakrabarty and Gourab Saha for technical help and fruitful discussions. IC acknowledges support from DST, India, under grant number IFA18-PH214 (INSPIRE Faculty Award). HR is supported by the Science and Engineering Research Board, Government of India, under the agreement SERB/PHY/2016348 (Early Career Research Award). TS acknowledges the support from the Dr. D. S. Kothari Postdoctoral scheme No. PH/20-21/0163.
Author information
Authors and Affiliations
Corresponding author
Appendix A: Evolution of asymmetry
Appendix A: Evolution of asymmetry
Evolution of asymmetry can be calculated by solving the following Boltzmann equations: \(\tilde{\Psi _{1}}, \tilde{\Psi _{2}}\) and the \((B-L)\) asymmetry can be written as [95],
where \(z = \frac{M_{\tilde{\Psi _1}}}{T}\) and \(H(M_{\tilde{\Psi _1}})\) is the Hubble parameter at \(T = M_{\tilde{\Psi _1}}\) and \(H(T=M_{\tilde{\Psi _1}}) = 1.66 ~g_{eff}^{1/2} \frac{T^{2}}{M_{{\textrm{Pl}}}}|_{T=M_{\tilde{\Psi _1}}} \), \(M_{{\textrm{Pl}}} \sim 10^{19}\) GeV being Planck scale. \(Y_{\tilde{\Psi _{j}}}^{eq}, Y_l^{eq}\) are the comoving densities at equilibrium. We solve these three equations with initial conditions:
at \(T \gg M_{\tilde{\Psi _1}}\).
Contributions to \(\gamma ^{'}\)s are given by diagrams shown in Fig. 9. The lepton asymmetry is further can be translated into baryon asymmetry. This results in the final baryon number at \(T_{\textrm{sph}} \sim 150\) GeV (the freeze-out temperature of the sphelaron process) as [87]:
With \(Y_{B-L} (z_{\textrm{sph}})\) as the solution of Boltzmann equations at \(z = z_{\textrm{sph}} = \frac{M_{\tilde{\Psi _1}}}{T_{\textrm{sph}}}\).
Here \(N_f:\) the number of generations of fermion families and \(N_H:\) number of Higgs doublets. For our case, \(N_f = 3\) and \(N_H =1\). \(\gamma _{D}^{(i)}\) can be written as [95]:
\(N_{{\tilde{\Psi }}_i}^{eq}\) being the equilibrium number density of mass eigenstate \({\tilde{\Psi }}_i\). Here \(K_1\) and \(K_2\) are the first and second modified Bessel functions of second kind respectively and \(\Gamma _{{\tilde{\Psi }}_i}\) is the total decay width of \({\tilde{\Psi }}_i\).
Decay width of \({\tilde{\Psi }}_i\) at tree level,
with \(\alpha , \theta _W\) being the Fine structure constant and the Weinberg angle.
For two body scattering \( a + b \rightarrow i + j +\cdots \), \(\gamma _{eq}\) can be written as [95],
here sFootnote 14 is the square of center of mass energy and \({\hat{\sigma }}(s)\) is reduced cross section, which can be expressed in terms of actual cross section as [95]:
with \(p_k\) and \(M_k\) being three momentum and mass of particle k. Expressions for reduced cross-section (\({\hat{\sigma }}\)) for all the scattering processes shown in Fig. 9 are given in [82, 95].
For our model the total D.O.F turns out to be:
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Chakraborty, I., Roy, H. & Srivastava, T. Searches for heavy neutrinos at multi-TeV muon collider: a resonant leptogenesis perspective. Eur. Phys. J. C 83, 280 (2023). https://doi.org/10.1140/epjc/s10052-023-11406-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-023-11406-0









 (for signal and SM background) for
(for signal and SM background) for 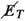 as
as  and present the normalized distributions of the same in Fig.
and present the normalized distributions of the same in Fig.  .
.