$\Lambda _b \rightarrow p, N^*(1535)$ form factors from QCD light-cone sum rules

Abstract

In this work, we calculate the transition form factors of $\Lambda _b$ decaying into proton and $N^*(1535)$ ($J^P={1/2}^+$ and ${1/2}^-$ respectively) within the framework of light-cone sum rules with the distribution amplitudes (DAs) of $\Lambda _b$-baryon. In the hadronic representation of the correlation function, we have isolated both the proton and the $N^*(1535)$ states so that the $\Lambda _b \rightarrow p, N^*(1535)$ form factors can be evaluated simultaneously. Due to the less known properties of the baryons, we investigate three interpolating currents of the light baryons and five parametrization models for DAs of $\Lambda _b$. Numerically, our predictions on the $\Lambda _b \rightarrow p$ form factors and the branching fractions of $\Lambda _b\rightarrow p\ell \nu$ from the Ioffe or the tensor currents are consistent with the Lattice simulation and the results from the light-baryon sum rules, as well as the experimental data of $Br(\Lambda _b^0\rightarrow p\mu ^-{{\bar{\nu }}})$. The predictions on the form factors of $\Lambda _b \rightarrow N^*(1535)$ are very sensitive to the choice of the interpolating currents so that the relevant measurement could be helpful to clarify the properties of baryons.

1 Introduction

Heavy hadron decays provide an ideal platform for precisely extracting the Cabibbo-Kobayashi-Maskawa (CKM) matrix matrix elements, understanding the QCD dynamics in the heavy hadron system, investigating the standard model (SM) description of the CP violation and searching for the signal of new physics beyond the SM. The essential problem in the heavy hadron decays is to evaluate the matrix element of the effective Hamiltonian. Both in the semi-leptonic and nonleptonic decays, the heavy-to-light form factors play a crucial role in evaluating the decay amplitudes. At leading power of the heavy quark expansion, the mesonic heavy-to-light form factors such as $B \rightarrow \pi$ form factor can be divided into two parts, the nonfactorizable soft form factor and the factorizable hard spectator scattering contribution. The latter is calculable but suppressed by the strong coupling constant. To study the soft form factor, the nonperturbative methods such as Lattice simulation and light-cone sum rules (LCSR) need to be employed. There exist two kinds of LCSRs, namely light-hadron LCSR [1, 2] and heavy-hadron LCSR [3,4,5], which are classed according to the hadron states (light hadron in the final state or heavy hadron in the initial state, respectively) entering the correlation function. In the LCSR framework, the soft form factors have been investigated using different correlation functions, and the QCD corrections as well as the resummation of large logarithmic terms have also been performed [6,7,8,9,10,11]. For the baryonic form factors, the power counting is different from the mesonic case. It was found that at the leading power, the baryonic heavy-to-light form factor is completely factorizable [12], but numerically suppressed compared with the power suppressed soft contribution due to the $\alpha _s^2$ suppression from hard gluon exchange. Therefore, one of the most important issues in the heavy baryon decays is to study the heavy-to-light form factors with non-perturbative method.

As more and more data of the heavy baryon decays are accumulated in the large hadron collider, it turns more important to precisely study the heavy baryon decays theoretically. The baryonic heavy-to-light form factors, such as $\Lambda _b \rightarrow \Lambda$ and $\Lambda _b \rightarrow p$, have been studied using Lattice QCD simulaltion, the LCSRs and the light-front quark model, etc. [13,14,15, 17,18,19,20,21, 36, 37]. The lattice simulation is based on the first principle of QCD and believed to be a reliable method, while it prefers to work in the small recoil region. The LCSR is applicable in the large recoil region, thus the LCSR predictions supplement to the Lattice result. The light-baryon LCSR has been employed to study the baryonic heavy-to-light transition form factors in [14, 16, 17], and the $\Lambda _b \rightarrow p$ form factors were studied with $\Lambda _b$-LCSR with the Chernyak-Zhitnitsky(CZ) current being adopt as the interpolating current for the proton [13], where the predictions of the $\Lambda _b \rightarrow p$ form factors are too small compared with the Lattice QCD and the LCSR with proton LCDAs [14, 37].

In this work, we will take advantage of the $\Lambda _b$-LCSR to revisit the $\Lambda _b \rightarrow p$ form factors and simultaneously study the $\Lambda _b \rightarrow N^*(1535)$ (in what follows we will use $N^*$ to denote $N^*(1535)$ for convenience) transition form factors where $N^*$ $(1/2^-)$ is the parity conjugate state of the proton $(1/2^+)$. Compared with the previous studies, we will make improvement in the following aspects:

• Since the interpolating current is not unique for the baryonic state, we will employ three different interpolating currents of the nucleon in the correlation functions, including the Ioffe current, the tensor current and the leading power (LP) current, so as to find out which one is the most appropriate choice in the $\Lambda _b$-LCSR by comparing our predictions with the experimental data or other theoretical results.

• We will isolate the proton state and $N^*$ state simultaneously in the hadronic representation of correlation functions. Thereby, there will be no redundant Lorentz structures in the partonic representation of the correlation function. We can then obtain all the $\Lambda _b \rightarrow p, N^*$ form factors without ambiguity by solving the equations of sum rules.

• The light-cone distribution amplitudes (LCDAs) of $\Lambda _b$-baryon is the most important input in the sum rules of the form factors, which are not well determined yet. We will take advantage of the complete set of the three-particle LCDAs of $\Lambda _b$-baryon up to twist-5 in our calculation, some of which have been omitted in the previous studies. In addition, we will employ five different models for the LCDAs of $\Lambda _b$-baryon for a comparison [45,46,47].

• We will obtain the leading power contribution of the universal $\Lambda _b \rightarrow p$ form factors by taking the SCET limit of the correlation function. By comparing the leading power contribution with the full result, we can estimate the size of the power suppressed contributions.

Except for the theoretical improvements, the form factors of $\Lambda _b\rightarrow N^*$ have some phenomenological significance. CP violation has never been established in the baryon systems. Multi-body $\Lambda _b$ decays are among the most important processes to search for CP violation in baryons, for example $\Lambda _b\rightarrow p\pi ^-\pi ^+\pi ^-$ [22]. The intermediate states such as $N^*$ would contribute to these multibody decays, especially for the strong phases. In the theoretical calculations, the transition form factors of $\Lambda _b\rightarrow N^*$ are important input quantities. This case is similar to the theoretical prediction on the discovery channel of double-charm baryons, $\Xi _{cc}^{++}\rightarrow \Lambda _c^+K^-\pi ^+\pi ^+$, where the form factors of intermediate states are firstly calculated [23, 24].

This paper is organized as follows. In the next section we start with the definition of the form factors and the symmetry relations in the heavy-quark/SCET limit, then the sum rules for the $\Lambda _b \rightarrow p, N^*(1535)$ form factors are obtained, and the investigation on the result from SCET limit is also given in this section. The details of the numerical analysis of the form factors are collected in Sect. 3, and we also give our predictions on some observables for the the exclusive semileptonic decays $\Lambda _b \rightarrow p(N^*)l^-\bar{\nu _l}$. The last section is reserved for the summary. The paper also contains two appendices where the expressions of the LCSR for the form factors (App. A) and the models of LCDAs of $\Lambda _b$ baryon are collected (App. B).

2 The LCSR of $\Lambda _b \rightarrow p, N^*(1535)$ form factors

2.1 $\Lambda _b \rightarrow {p, N^*}$ form factors

The heavy-to-light $\Lambda _b \rightarrow p$ and $\Lambda _b \rightarrow N^*$ form factors induced by $V-A$ current are defined as [25]

$$\begin{aligned}{} & {} \left\langle p(p,s')\left| {\bar{u}} \gamma ^{\mu } b\right| \Lambda _{b}(P,s)\right\rangle = {\bar{u}}\nonumber \\{} & {} \quad \left( p, s'\right) \left( f_{1} \gamma ^{\mu }+f_{2} i\sigma ^{\mu \nu }{\hat{q}}_\nu +f_{3} {\hat{q}}^\mu \right) u\left( P, s\right) , \nonumber \\{} & {} \left\langle p(p,s')\left| {\bar{u}} \gamma ^{\mu } \gamma _{5} b\right| \Lambda _{b}(P,s)\right\rangle = {\bar{u}}\nonumber \\{} & {} \quad \left( p, s'\right) \left( g_{1} \gamma ^{\mu }+g_{2} i \sigma ^{\mu \nu }{\hat{q}}_\nu +g_{3} {\hat{q}}^\mu \right) \gamma _5u\left( P, s\right) , \nonumber \\{} & {} \left\langle N^*(p,s')\left| {\bar{u}} \gamma ^{\mu } b\right| \Lambda _{b}(P,s)\right\rangle = {\bar{u}}\nonumber \\{} & {} \quad \left( p, s'\right) \left( F_{1} \gamma ^{\mu }+F_{2} i\sigma ^{\mu \nu }{\hat{q}}_\nu +F_{3} {\hat{q}}^\mu \right) \gamma _{5} u\left( P, s\right) , \nonumber \\{} & {} \left\langle N^*(p,s')\left| {\bar{u}} \gamma ^{\mu } \gamma _{5} b\right| \Lambda _{b}(P,s)\right\rangle = {\bar{u}}\nonumber \\{} & {} \quad \left( p, s'\right) \left( G_{1} \gamma ^{\mu }+G_{2}i\sigma ^{\mu \nu }{\hat{q}}_\nu +G_{3}{\hat{q}}^\mu \right) u\left( P, s\right) . \end{aligned}$$

(1)

where $\sigma _{\mu \nu }=i[\gamma _{\mu },\gamma _{\nu }]/2$, and $u(P,s) \ (u(p,s^{'}))$ is the spinor of the $\Lambda _b$ baryon (proton or $N^*$) with the momentum $P\ (p)$ and the spin $s\ (s^{'})$. The form factors $f_i\ (F_i)$ and $g_i\ (G_i)$ depend on the invariant mass squared of the lepton pair $q^2$ with $q_{\nu }=P_{\nu }-p_{\nu }$, and ${\hat{q}}_\nu =q_\nu /m_{\Lambda _b}$ so that all the form factors have the same mass dimension. In HQET, one can use the heavy-baryon velocity $v^{\mu }=P^{\mu } / m_{\Lambda _{b}}$ to project the b -quark field onto its large-spinor component $h_{v}^{(b)}={\not {v}} h_{v}^{(b)}$, then the form factors can be written as

$$\begin{aligned}{} & {} \langle N^{(*)}(p,s')|{{\bar{q}}} \Gamma b | \Lambda _{b}(P,s)\rangle \rightarrow \langle N^{(*)}(p,s')|{{\bar{q}}} \Gamma h^{(b)}_v | \Lambda _{b}(v,s)\rangle \nonumber \\{} & {} \quad ={\bar{u}}_{N^{(*)}}(p,s') \left[ \zeta _{1}(q^{2})+{\not {v}} \zeta _{2}(q^{2})\right] \nonumber \\{} & {} \qquad \times \Gamma u_{\Lambda _{b}}(v,s), \end{aligned}$$

(2)

where $N^{(*)}$ stands for proton or $N^{*}$, $\Gamma$ is any Dirac matrix, $|\Lambda _b(v,s)\rangle$ is the heavy-baryon state with the heavy-baryon spinor in HQET. Therefor, $\zeta _{1}(q^{2})$ and $\zeta _{2}(q^{2})$ are the only two form factors that should be present at leading order in $\alpha _{s}$ and $\Lambda / m_{b}$ according to HQET. Taking the heavy-quark limit (neglecting the contributions suppressed by $\Lambda / m_{b}$ and $m_{N^{(*)}} / m_{\Lambda _b}$) in the definition of the form factors yields:

$$\begin{aligned}{} & {} f_1=g_1=\zeta _1; \,\,\,\,\, f_2=g_2=f_3=g_3=\zeta _2; \nonumber \\{} & {} F_1=G_1=-\zeta _1; \,\,\,\,\, F_2=G_2=F_3=G_3=\zeta _2. \end{aligned}$$

(3)

In the heavy-to-light transitions, the light quark moves approximately along the light-cone, thus it must be regarded as a collinear quark in the soft-collinear effective theory(SCET). In SCET [26, 27], the collinear quark field is divided into the large component and small component, namely $q=\xi +\eta$ with and two light-like unit vectors ${\bar{n}}^2=n^2=0$, satisfying $(n^{\mu }+{\bar{n}}^{\mu })=2v^{\mu }$ and $n\cdot {\bar{n}}=2$. At leading power, the large component $\xi$, $h_v^{(b)}$ will take the place of the u quark field and b quark field respectively, then the weak current turns to

$$\begin{aligned} j_{\mu , V} ={{\bar{\xi }}} \, {\not {n}} \, h_v^{(b)}\frac{{{\bar{n}}}_{\mu }}{ 2},\ \ \ j_{\mu , A}={{\bar{\xi }}} \, {\not {n}} \gamma _5 \, h_v^{(b)}\frac{{{\bar{n}}}_{\mu }}{2}. \end{aligned}$$

(4)

The matrix element of the leading power current will result in one universal form factor due to the heavy quark symmetry and large recoil symmetry, i.e.,

(5)

2.2 Interpolating currents and correlation function

Following the standard strategy of heavy-hadron LCSR, we start with the two-point correlation function sandwiched between vacuum and the on-shell $\Lambda _b$-baryon state:

$$\begin{aligned}{} & {} \Pi _{\mu , a}(p,q)\nonumber \\{} & {} \quad = i \int d^4 x \, e^{i p \cdot x} \, \langle 0 |T \{\eta (x), j_{\mu , a}(0) \}| \Lambda _b(p+q) \rangle , \end{aligned}$$

(6)

where the local current $\eta$ is the interpolating current for the light baryons $N^{(*)}$ and the $j_{\mu , a}$ stands for the heavy-light weak transition current ${{\bar{u}}} \, \Gamma _{\mu , a} \, b$ with the index “a” indicating a certain Lorentz structure, i.e.,

$$\begin{aligned} j_{\mu , V} ={{\bar{u}}} \, \gamma _{\mu } \, b,&\qquad&j_{\mu , A}={{\bar{u}}} \, \gamma _{\mu }\, \gamma _5 \, b. \end{aligned}$$

(7)

For comparison, we adopt three types of the interpolating current for the $N^{(*)}$ baryon, namely the Ioffe current, the tensor current and the LP current respectively [28, 29], and they are listed below

$$\begin{aligned} \eta _{\textrm{IO}}(x)= & {} \varepsilon ^{a b c}\left[ u^{a T}(x) C \gamma ^{\rho } u^{b}(x)\right] \gamma _5 \gamma _{\rho } d^{c}(x)\nonumber , \\ \eta _{\textrm{TE}}(x)= & {} \varepsilon ^{a b c}\left[ u^{a T}(x) C \sigma ^{\rho \sigma } u^{b}(x)\right] \gamma _5 \sigma _{\rho \sigma } d^{c}(x)\nonumber , \\ \eta _{\textrm{LP}}(x)= & {} \varepsilon ^{a b c}\left[ u^{a T}(x) C {\not {n}} u^{b}(x)\right] \gamma _5 {\not {n}} d^{c}(x). \end{aligned}$$

(8)

where T represents the transposition, C is the charge conjugation matrix and the sum runs over the color indices a, b, c.

Following the usual procedure of LCSR, the correlation function is to be expressed in the hadronic representation as well as calculated by the operator product expansion in QCD. On the hadronic level, one inserts a complete set of states with the same quantum numbers of light baryon $N^{(*)}$ between the interpolating current $\eta _i$ and the transition current $j_{\mu , a}$. In order to obtain the $\Lambda _b \rightarrow p, N^{*}$ form factors without ambiguity, we isolate the contribution both from the lowest state p and its negative-parity partner $N^{*}$ in the hadrnoic dispersion relation. The results in two different representations of the correlation function are then matched by employing the quark-hadron duality assumption. Finally, one needs to perform the Borel-transformation to eliminate the possible subtraction terms which may appear in the dispersion relation and to suppress the contributions from the higher states.

At hadronic level, the correlation function can be expressed in terms of hadronic matrix elements as follows

$$\begin{aligned}{} & {} \Pi _{\mu ,a}(p,q)\nonumber \\{} & {} \quad = \frac{1}{m_{p}^2-p^{ 2}}\sum _{s'}\left\langle 0\left| \eta _i(0)\right| p\left( p,s'\right) \right\rangle \left\langle p\left( p,s'\right) \left| j_{\mu , a}(0)\right| \right. \nonumber \\{} & {} \qquad \times \left. \Lambda _b(p+q)\right\rangle +\frac{1}{m_{N^{*}}^2-p^{ 2}}\sum _{s'}\left\langle 0\left| \eta _i(0)\right| N^{*}\left( p,s'\right) \right\rangle \nonumber \\{} & {} \qquad \times \left\langle N^{*}\left( p,s'\right) \left| j_{\mu , a}(0)\right| \Lambda _b(p+q)\right\rangle +\cdots \, \nonumber \\ \end{aligned}$$

(9)

where the ellipsis stands for the contribution of excited and continuum states with the same quantum numbers as p and $N^*$. The couplings of the $p, N^*$ with the interpolating currents $\eta$ (the decay constants) are defined as

$$\begin{aligned}{} & {} \langle 0| \eta _{\textrm{IO}} | p(p,s')\rangle = \lambda _{1}^p m_p u\left( p,s'\right) ,\nonumber \\{} & {} \langle 0| \eta _{\textrm{IO}} | N^*(p,s')\rangle = \lambda ^{N^*}_{1} m_{N^*} \gamma _5u\left( p,s'\right) , \nonumber \\{} & {} \langle 0| \eta _{\textrm{TE}} | p(p,s')\rangle = \lambda ^{p}_{2} m_{p} u\left( p,s' \right) ,\,\nonumber \\{} & {} \langle 0| \eta _{\textrm{TE}} | N^*(p,s')\rangle = \lambda ^{N^*}_{2} m_{N^*} \gamma _5u\left( p,s'\right) , \nonumber \\{} & {} \langle 0| \eta _{\textrm{LP}} | p(p,s')\rangle = \lambda ^{p}_{3} {\not {n}} n\cdot p u\left( p,s'\right) ,\nonumber \\{} & {} \langle 0| \eta _{\textrm{LP}} | N^*(p,s')\rangle = \lambda ^{N^*}_{3} {\not {n}} n\cdot p \gamma _5u\left( p,s'\right) . \end{aligned}$$

(10)

By using the equation of motion, the correlation function can be decomposed into 12 independent, Lorentz invariant amplitudes. For the vector current $j_{\mu , V}$, we have:

$$\begin{aligned} \Pi ^{i}_{\mu ,V}(p,q){} & {} =\left( \Pi ^i_1p_{\mu }+\Pi ^i_2p_{\mu }{\not {q}}+\Pi ^i_3\gamma _{\mu } +\Pi ^i_4\gamma _{\mu }{\not {q}} \right. \nonumber \\{} & {} \quad \left. +\Pi ^i_5q_{\mu }+\Pi ^i_6q_{\mu }{\not {q}}\right) u_{\Lambda _b}(p+q), \end{aligned}$$

(11)

where the dependence of $\Pi ^i_{1-6}$ on $p^2, q^2$ is not shown specifically. A similar decomposition can be done for the axial-vector current $j_{\mu ,A}$:

$$\begin{aligned} \Pi ^{i}_{\mu ,A}(p,q){} & {} =\left( {{\tilde{\Pi }}}^i_1p_{\mu }+{{\tilde{\Pi }}}^i_2p_{\mu }{\not {q}} +{{\tilde{\Pi }}}^i_3\gamma _{\mu }+{{\tilde{\Pi }}}^i_4\gamma _{\mu }{\not {q}}+{{\tilde{\Pi }}}^i_5q_{\mu }\right. \nonumber \\{} & {} \quad \left. +{{\tilde{\Pi }}}^i_6q_{\mu }{\not {q}}\right) \gamma _5 u_{\Lambda _b}(p+q). \end{aligned}$$

(12)

Employing the definitions of the decay constants and the form factors, and summing over the spin of the p and $N^*$, we arrive at the hadronic expression for the correlation functions. For the vector current $j_{\mu , V}$, we have:

$$\begin{aligned} \Pi ^i_{\mu , V}= & {} \frac{\lambda ^p_im_p}{m^2_p-p^2}\Bigg \{2f_1(q^2)p_{\mu }-\frac{2 f_2(q^2)}{m_{\Lambda _b}}p_{\mu }{\not {q}} \nonumber \\{} & {} +(m_{\Lambda _b}-m_p)\Bigg [\frac{m_{\Lambda _b}+m_p}{m_{\Lambda _b}}f_2(q^2)-f_1(q^2)\Bigg ]\gamma _{\mu }\nonumber \\{} & {} +\Bigg [f_1(q^2)-\frac{m_{\Lambda _b}+m_p}{m_{\Lambda _b}}f_2(q^2)\Bigg ]\gamma _{\mu }{\not {q}} \nonumber \\{} & {} +\frac{m_{\Lambda _b}+m_p}{m_{\Lambda _b}}[f_2(q^2)+f_3(q^2)]q_{\mu }\nonumber \\{} & {} -\frac{f_2(q^2)+f_3(q^2)}{m_{\Lambda _b}}q_{\mu }{\not {q}}\Bigg \}u_{\Lambda _b}(p+q) \nonumber \\{} & {} +\frac{\lambda ^{N^*}_im_{N^*}}{m^2_{N^*}-p^2}\Bigg \{2F_1(q^2)p_{\mu } +\frac{2 F_2(q^2)}{m_{\Lambda _b}}p_{\mu }{\not {q}} \nonumber \\{} & {} -(m_{\Lambda _b}+m_{N^*})\Bigg [\frac{m_{\Lambda _b}-m_{N^*}}{m_{\Lambda _b}}F_2(q^2)+F_1(q^2)\Bigg ]\gamma _{\mu }\nonumber \\{} & {} +\Bigg [F_1(q^2)-\frac{m_{N^*}-m_{\Lambda _b}}{m_{\Lambda _b}}F_2(q^2)\Bigg ]\gamma _{\mu }{\not {q}} \nonumber \\{} & {} -\frac{m_{\Lambda _b}-m_{N^*}}{m_{\Lambda _b}}[F_2(q^2)+F_3(q^2)]q_{\mu }\nonumber \\{} & {} +\frac{F_2(q^2)+F_3(q^2)}{m_{\Lambda _b}}q_{\mu }{\not {q}}\Bigg \}u_{\Lambda _b}(p+q) \nonumber \\{} & {} +\int _{s_0^h}^{\infty } \frac{ds}{s-p^2}\Bigg (\rho _1^i(s,q^2)p_{\mu }+\rho _2^i(s,q^2)p_{\mu }{\not {q}} \nonumber \\ {}{} & {} + \rho _3^i(s,q^2)\gamma _{\mu }+\rho _4^i(s,q^2)\gamma _{\mu }{\not {q}}+\rho _5^i(s,q^2)q_{\mu }\nonumber \\{} & {} +\rho _6^i(s,q^2)q_{\mu }{\not {q}}\Bigg ). \end{aligned}$$

(13)

where i denotes the interpolating current, the contribution of the excited and continuum states is described by the spectral densities $\rho _j^i$ with $j=1,\ldots ,6$, and $s_0^h$ is the corresponding threshold parameter. From the above expression, the invariant amplitudes $\Pi ^i_{1,\ldots 6}$ can be directly related to the form factors which are then extracted after the $\Pi ^i_{1,..6}$ being calculated in QCD. The similar expression for the invariant amplitude ${{\tilde{\Pi }}}^{i}_{1,..,6}$ of the axial current $j_{\mu , A}$ can be obtained from Eq. (13) by replacing $f_i \rightarrow g_i, F_i\rightarrow G_i$, changing the sign of $m_{\Lambda _b}$ and adding the $\gamma _5$ before the spinor $u_{\Lambda _b}(p+q)$.

2.3 The light-cone sum rules for the form factors

Now we turn to compute the correlation function $\Pi _{i\mu , a}(p, q)$ form the partonic side. For the space-like interpolating momentum $|{{\bar{n}}} \cdot p| \sim {{\mathcal {O}}} (\Lambda )$ and $n \cdot p\sim m_{\Lambda _b}$, the product of the two currents can be expanded around the light-cone $x^2\simeq 0$. After contracting the u quark field and integrating out the coordinate, the correlation function at partonic level can be factorized into the convolution of the hard kernel and the LCDA of $\Lambda _b$ baryon, as shown in the diagram of Fig. 1.

$$\begin{aligned} \Pi ^\mathrm{}_{i\mu , a}(p, q)= & {} \int d \omega _1^{\prime } \int d \omega _2^{\prime } \, T^{(0),a}_{\alpha \beta \gamma \delta }\nonumber \\{} & {} (p, q, \omega _1^{\prime }, \omega _2^{\prime })\, \Phi _{\Lambda _b}^{ \, \alpha \beta \delta }(\omega _1^{\prime }, \omega _2^{\prime }), \end{aligned}$$

(14)

Fig. 1

Diagrammatical representation of the correlation function $\Pi _{\mu , a}(n \cdot p,{{\bar{n}}} \cdot p)$ at tree level, where the black square denotes the weak transition vertex, the black blob represents the Dirac structure of the $N^{(*)}$-baryon current and the pink internal line indicates the hard-collinear propagator of the u quark

where the superscript (0) indicates the tree-level approximation, $\omega '_{i}(i=1.2)$ are the energies of the $u-$ and $d-$quarks, the Lorenz index $\mu$ is not shown exactly, and $\alpha ,\beta , \gamma ,\delta$ are the Dirac indices.

Evaluating the diagram in Fig. 1 leads to the leading-order hard kernel

$$\begin{aligned} T^{(\mathrm IO,0)}_{\alpha \beta \gamma \delta }(p,q)= & {} -\left[ 2C\gamma ^\rho {{\not {k}}\over k^2}\gamma _\mu (I,\gamma _5)\right] _{\alpha \delta } (\gamma _5\gamma _\rho )_{\gamma \beta }, \nonumber \\ T^{(\mathrm Te,0)}_{\alpha \beta \gamma \delta }(p,q)= & {} -\left[ 2C\sigma ^{\rho \sigma }{{\not {k}}\over k^2}\gamma _\mu (I,\gamma _5)\right] _{\alpha \delta } (\gamma _5\sigma _{\rho \sigma })_{\gamma \beta },\nonumber \\ T^{(\mathrm LP,0)}_{\alpha \beta \gamma \delta }(p,q)= & {} -\left[ 2C{\not {n}}{{\not {k}}\over k^2}\gamma _\mu (I,\gamma _5)\right] _{\alpha \delta } (\gamma _5{\not { n}})_{\gamma \beta }, \end{aligned}$$

(15)

and the definition of the general light-cone hadronic matrix element in coordinate space [47] is given by

$$\begin{aligned} \Phi _{\Lambda _b}^{\alpha \beta \delta }(t_1, t_2)\equiv & {} \epsilon _{i j k} \, \langle 0 | \left[ u^{\textrm{T}}_{i} (t_1 {{\bar{n}}}) \right] _{\alpha } \, [0, t_1 {{\bar{n}}}] \, \left[ d_{j} (t_2 {{\bar{n}}}) \right] _{\beta } \, \nonumber \\{} & {} \times [0, t_2 {{\bar{n}}}] \, \left[ b_{k}(0)\right] _{\delta } | \Lambda _b(v) \rangle \nonumber \\= & {} \frac{1}{4 } \, \left\{ f_{\Lambda _b}^{(1)}(\mu ) \, \left[ {\tilde{M}}_1(v, t_1, t_2) \, \gamma _5 \, C^{T} \right] _{\beta \alpha }\right. \nonumber \\{} & {} \left. + f_{\Lambda _b}^{(2)}(\mu ) \, \left[ {\tilde{M}}_2(v, t_1, t_2) \, \gamma _5 \, C^{T} \right] _{\beta \alpha } \right\} \, \left[ \Lambda _b(v) \right] _{\delta }, \nonumber \\ \end{aligned}$$

(16)

where the b-quark field needs to be understood as an effective heavy field in HQET, $t_i$ are the real numbers which describe the location of the valance quarks inside the $\Lambda _b$ baryon on the light-cone. Performing the Fourier transformation, the momentum space light-cone projectors of the LCDAs of $\Lambda _b$ baryon in D dimensions read

(17)

(18)

where we have adjusted the notation of the $\Lambda _b$-baryon LCDA defined in [47]. Applying the equations of motion in the Wandzura-Wilczek approximation yields

$$\begin{aligned}{} & {} \psi _{\perp , 1}^{-+}(\omega _1^{\prime },\omega _2^{\prime })=\omega _1^{\prime } \, \psi _4(\omega _1^{\prime },\omega _2^{\prime }) \nonumber \\{} & {} \psi _{\perp , 2}^{+-}(\omega _1^{\prime },\omega _2^{\prime })=\omega _2^{\prime } \, \psi _4(\omega _1^{\prime },\omega _2^{\prime }). \end{aligned}$$

(19)

For convenience, we introduce two new parameters $\omega , u$ which satisfy $\omega =\omega _1'+\omega _2', u=\omega _1'/\omega$. Combining the projectors of the LCDAs of $\Lambda _b$ baryon and the hard kernels and simplifying the Lorentz structures, the invariant amplitudes at the partonic side can be obtained as

$$\begin{aligned} \Pi ^i_j(p^2, q^2)=\sum _{n=1,2}\int ^{\infty }_0d\omega \int ^1_0du\frac{w^{(i)}_{jn}(p^2, q^2)}{D^n}, \end{aligned}$$

(20)

with the denominator

$$\begin{aligned} D={\bar{\sigma }}p^2+\sigma q^2-\sigma {\bar{\sigma }}m^2_{\Lambda _b}, \end{aligned}$$

(21)

where $\sigma ={\omega }/{m_{\Lambda _b}},\ {\bar{\sigma }}=1-\sigma$. The functions $w^{(i)}_{jn}$ are distinguished by their indices: i=IO, TE, LP(the interpolating current), $j=1,\ldots ,6$ (the invariant amplitude) and $n=1,2$(the power of the denominator).

The invariant amplitudes in Eq. (20) can be expressed by the following dispersion integral

$$\begin{aligned} \Pi ^{i}_{j}(p^2, q^2)=\frac{1}{\pi } \int ^{\infty }_0 \frac{ds}{s-p^2} \textrm{Im}_s \Pi ^i_j(s,q^2), \end{aligned}$$

(22)

Compared with the hadronic dispersion integral involved the $p,N^*$ and higher states in Eq. (13), it can be employed to extract the form factors. Using the quark-hadron duality to approximate the contribution of the hadronic states above the threshold $s^h_0$:

$$\begin{aligned} \int ^{\infty }_{s^h_0}\frac{ds}{s-p^2}\rho ^i_j(s,q^2) \approx \frac{1}{\pi }\int ^{\infty }_{s_0}\frac{ds}{s-p^2}\textrm{Im}_s \Pi ^{i}_j(s,q^2),\qquad \end{aligned}$$

(23)

where $s_0$ is the effective threshold parameter. After performing the Borel transformation, we can get the sum rules for the form factors of the vector transition current $j_{\mu , V}$:

$$\begin{aligned} f_1(q^2)= & {} \frac{e^{m_p^2/M^2}}{2m_p(m_p+m_{N^*})\lambda _i^p}\frac{1}{\pi }\int ^{s_0}_0 ds e^{-s/M^2}\nonumber \\{} & {} \times \Big [(m_{\Lambda _b}+m_p)\Big (\textrm{Im}_s\Pi ^i_1(s,q^2) \nonumber \\{} & {} +(m_{\Lambda _b}-m_{N^*})\textrm{Im}_s\Pi ^i_2(s,q^2)\Big )+2\textrm{Im}_s\Pi ^i_3(s,q^2)\nonumber \\{} & {} +2(m_{N^*}-m_p)\textrm{Im}_s\Pi ^i_4(s,q^2)\Big ],\nonumber \\ f_2(q^2)= & {} \frac{m_{\Lambda _b}e^{m_p^2/M^2}}{2m_p(m_p+m_{N^*})\lambda _i^p}\frac{1}{\pi }\int ^{s_0}_0 ds e^{-s/M^2}\nonumber \\{} & {} \times \Big [\textrm{Im}_s\Pi ^i_1(s,q^2) +(m_{\Lambda _b}-m_{N^*})\textrm{Im}_s\Pi ^i_2(s,q^2)\nonumber \\{} & {} -2\textrm{Im}_s\Pi ^i_4(s,q^2)\Big ],\nonumber \\ f_3(q^2)= & {} -\frac{e^{m_p^2/M^2}}{2m_p(m_p+m_{N^*})\lambda _i^p}\frac{1}{\pi }\int ^{s_0}_0 ds e^{-s/M^2}\nonumber \\{} & {} \times \Big [\textrm{Im}_s\Pi ^i_1(s,q^2)+(m_{\Lambda _b}-m_{N^*})\textrm{Im}_s\Pi ^i_2(s,q^2) \nonumber \\{} & {} -2\textrm{Im}_s\Pi ^i_4(s,q^2)-2\textrm{Im}_s\Pi ^i_5(s,q^2)\nonumber \\{} & {} -2(m_{\Lambda _b}-m_{N^*})\textrm{Im}_s\Pi ^i_6(s,q^2)\Big ], \end{aligned}$$

(24)

$$\begin{aligned} F_1(q^2)= & {} -\frac{e^{m_{N^*}^2/M^2}}{2m_{N^*}(m_p+m_{N^*})\lambda _i^{N^*}}\frac{1}{\pi }\int ^{s_0}_0 ds e^{-s/M^2}\nonumber \\{} & {} \times \Big [(m_{\Lambda _b}-m_{N^*})\Big (\textrm{Im}_s\Pi ^i_1(s,q^2) \nonumber \\{} & {} +(m_{\Lambda _b}+m_{p})\textrm{Im}_s\Pi ^i_2(s,q^2)\Big )\nonumber \\{} & {} +2\textrm{Im}_s\Pi ^i_3(s,q^2)+2(m_{N^*}-m_p)\textrm{Im}_s\Pi ^i_4(s,q^2)\Big ],\nonumber \\ F_2(q^2)= & {} \frac{m_{\Lambda _b}e^{m_{N^*}^2/M^2}}{2m_{N^*}(m_p+m_{N^*})\lambda _i^{N^*}}\frac{1}{\pi }\int ^{s_0}_0 ds e^{-s/M^2}\nonumber \\{} & {} \times \Big [\textrm{Im}_s\Pi ^i_1(s,q^2) +(m_{\Lambda _b}+m_{p})Im_s\Pi ^i_2(s,q^2)\nonumber \\{} & {} -2\textrm{Im}_s\Pi ^i_4(s,q^2)\Big ],\nonumber \\ F_3(q^2)= & {} -\frac{e^{m_{N^*}^2/M^2}}{2m_{N^*}(m_p+m_{N^*})\lambda _i^{N^*}}\frac{1}{\pi }\int ^{s_0}_0 ds e^{-s/M^2}\nonumber \\{} & {} \times \Big [\textrm{Im}_s\Pi ^i_1(s,q^2)+(m_{\Lambda _b}+m_{p})\textrm{Im}_s\Pi ^i_2(s,q^2) \nonumber \\{} & {} -2\textrm{Im}_s\Pi ^i_4(s,q^2)-2Im_s\Pi ^i_5(s,q^2)\nonumber \\{} & {} -2(m_{\Lambda _b}+m_{N^*})\textrm{Im}_s\Pi ^i_6(s,q^2)\Big ], \end{aligned}$$

(25)

The sum rules for the form factors $g_i(q^2)$ and $G_i(q^2)$ of the axial-vector transition current $j_{\mu ,A}$ can be obtained from the above expressions for the form factors $f_i(q^2)$ and $F_i(q^2)$ by replacing $\textrm{Im}_s \Pi ^i_j(s,q^2)\rightarrow \textrm{Im}_s{{\tilde{\Pi }}}^i_j(s,q^2)$ respectively and changing the sign of $m_{\Lambda _b}$. In practice, to obtain the final result, we should integrate out the variable s. All of the three procedures, including the expression of the correlation function with the dispersion integral, subtraction of continuum states with quark-hadron duality and Borel transformation, can be realized with the following substitution rules

$$\begin{aligned}{} & {} \int d\omega \int du\frac{w(s, q^2)}{D}\rightarrow -m_{\Lambda _b} \int ^1_0 du\nonumber \\{} & {} \int ^{\sigma _0}_{0}\frac{d\sigma }{{\bar{\sigma }}}\omega (s,q^2)\exp \Big ({-\frac{s}{M^2}}\Big ),\nonumber \\{} & {} \int d\omega \int du\frac{w(s, q^2)}{D^2}\rightarrow \frac{m_{\Lambda _b}}{M^2} \int ^1_0 du\nonumber \\{} & {} \int ^{\sigma _0}_{0}\frac{d\sigma }{{\bar{\sigma }}^2}\omega (s,q^2)\exp \Big ({-\frac{s}{M^2}}\Big )\nonumber \\{} & {} \quad +\int ^1_0 du\frac{\omega (s_0,q^2)\eta (\sigma _0)e^{-s_0/M^2}}{{\bar{\sigma }}^2_0m_{\Lambda _b}}, \nonumber \\ \end{aligned}$$

(26)

where the transformed coefficient functions $\omega ^{(i)}_{jn}(s,q^2)$ are presented in Appendix A and the involved parameters are defined as:

$$\begin{aligned} s(\sigma )=\sigma m_{\Lambda _b}^2-{\sigma q^2\over {{\bar{\sigma }}}},\,\,\, \eta (\sigma )=\left( 1-{ q^2\over {{\bar{\sigma }}}^2m_{\Lambda _b}^2}\right) ^{-1}, \end{aligned}$$

(27)

and $\sigma _0$ is the positive solution of the corresponding quadratic equation for $s=s_0$:

$$\begin{aligned} \sigma _0=\frac{(s_0+m^2_{\Lambda _b}-q^2)-\sqrt{(s_0+m^2_{\Lambda _b}-q^2)^2-4m^2_{\Lambda _b}s_0}}{2m^2_{\Lambda _b}}.\nonumber \\ \end{aligned}$$

(28)

2.4 The SCET limit

In this section, we present a short discussion on the SCET limit of the $\Lambda _b \rightarrow p$ form factors. We have mentioned that in the SCET limit, the three $\Lambda _b \rightarrow p$ form factors reduce to a unique one. In order to obtain the unique form factor, the interpolating current should be fixed so that the power suppressed part is eliminated and it is easy to find that the LP current will give rise to the leading power contribution. At leading power, the quark fields in the LP current should be replaced by the large component of the collinear quark fields

$$\begin{aligned} \eta ^{\textrm{LP}}(x)=\varepsilon ^{a b c}\left[ \xi _u^{a T}(x) C {\not { n}} \xi _u^{b}(x)\right] \gamma _5{\not { n}} \xi _d^{c}(x), \end{aligned}$$

(29)

In addition, the weak current ${{\bar{u}}} \gamma _\mu (\gamma _5) b$ also should be changed into ${{\bar{\xi }}} {\not { n}}(\gamma _5) h_v^{(b)}$, then the leading power hard kernel for the vector current can be obtained as

$$\begin{aligned} T^{(0)}_{\alpha \beta \gamma \delta }(p,q)=-{1{{\bar{n}}}\cdot (p-k)} \left[ C{\not { n}}{{{\bar{n}}}2}{\not { n}}\right] _{\alpha \delta } (\gamma _5{\not { n}})_{\gamma \beta }, \end{aligned}$$

(30)

Note that an additional $\gamma _5$ will appear for the axial vector current. The correlation function is then expressed in terms of the convolution of the hard function and the LCDAs of $\Lambda _b$ baryon

$$\begin{aligned} \Pi ^{\textrm{par,LP}}_{\mu , a}(p, q)=f_{\Lambda _b}^{(2)}\int _0^\infty \omega d\omega {{{\bar{\psi }}}_4(\omega )\over {{\bar{n}}}\cdot p-\omega }{\not { n}}\Lambda _b(v,s), \end{aligned}$$

(31)

where ${{\bar{\psi }}}_4(\omega )=\omega \int _0^1 du\ \psi _4(u\omega ,{{\bar{u}}}\omega )$. On the hardonic side, we can insert a complete set of the baryonic states with the same quark structure with the interpolating current to the correlation function and isolate the proton state(note that we do not isolate the negative parity state here, since there is no redundant Lorentz structures on the partonic side). Combined with the hadronic representation of the correlation function, the LCSR for the leading power current can be obtained after taking advantage of the quark-hardon duality and performing the Borel transform, and the result reads

$$\begin{aligned} \xi (n\cdot p)= & {} {f_{\Lambda _b}^{(2)}\over \lambda _p^{(3)}n\cdot p}\textrm{Exp}\!\left( m_p^2 \over n\cdot p \omega _M\right) \!\int _0^{\omega _s}\! d\omega e^{-\omega / \omega _M}{{\bar{\psi }}}_4(\omega ).\nonumber \\ \end{aligned}$$

(32)

where $n\cdot p\simeq (m^2_{\Lambda _b}+m_p^2-q^2)/m_{\Lambda _b}$ at large hadronic recoil, $M^2\equiv n\cdot p\omega _M$ and $s_0\equiv n\cdot p\omega _s$. This result is quite similar to the $\Lambda _b\rightarrow \Lambda$ form factor obtained in [15], and only the LCDA $\psi _4(u,\omega )$ appears in the LCSRs, which makes it straightforward to perform the next-to-leading order corrections to the sum rules at leading power, which will be left for a future study.

3 Numerical analysis

3.1 The results for form factors

In this subsection, we present the numerical results of the form factors of $\Lambda _b\rightarrow p(N^*)$ transition with the LCDA models of $\Lambda _b$-baryon given in Appendix B. The masses of the involved baryons are taken from [30]: $m_{\Lambda _b}=5.620$ GeV, $m_p=0.938$ Gev, and $m_{N^*}=1.530$ GeV. The normalization parameters $\lambda ^{p(N^*)}_i$ of the $p, N^*$ with the interpolating currents $\eta _i$ have been calculated from lattice-QCD [31], and the couplings $f^{(1,2)}_{\Lambda _b}$ are taken from the NLO QCD sum rule analysis [32]:

$$\begin{aligned} \lambda ^p_1{} & {} =-(3.877\pm 0.189)\times 10^{-2}\ \text {GeV}^{2}, \nonumber \\ \lambda ^{N^*}_1{} & {} =(2.463\pm 0.110)\times 10^{-2}\ \text {GeV}^{2}, \nonumber \\ \lambda ^p_2{} & {} =(7.764\pm 0.375)\times 10^{-2}\ \text {GeV}^{2}, \nonumber \\ \lambda ^{N^*}_2{} & {} =(5.552\pm 0.278)\times 10^{-2}\ \text {GeV}^{2},\nonumber \\ \lambda ^p_3{} & {} =(3.071\pm 0.360)\times 10^{-3}\ \text {GeV}^2, \nonumber \\ \lambda ^{N^*}_3{} & {} =(0.757\pm 0.040)\times 10^{-3}\ \text {GeV}^2, \nonumber \\ f^{(2)}_{\Lambda _b}{} & {} =f^{(1)}_{\Lambda _b}=0.030\pm 0.005\ \text {GeV}^3, \end{aligned}$$

(33)

The sum rules for the form factors contain two additional auxiliary parameters: the Borel parameter $M^2$ and the effective threshold parameter $s_0$, and the results of the form factors should be actually independent on these parameters. Therefore, one should find appropriate regions where the form factors weakly depend on these parameters. In addition, the parameters $s_0$ and $M^2$ are adjusted in order to suppress the contributions of the continuum states and the high twist $\Lambda _b$-LCDAs. To fulfill these requirements, the allowed regions of the Borel parameter $M^2$ and the effective threshold parameters $s_0$ are chosen as

$$\begin{aligned}&M^2=(2.6\pm 0.4)\ \text {GeV}^{2},\ \ \ \ s_0=(2.56\pm 0.10)\ \text {GeV}^{2},\nonumber \\ \end{aligned}$$

(34)

where the obtained regions of $M^2$ and $s_0$ are approximately in agreement with that used in [13].

Inputting the values of the parameters given above into the analytic expression of the LCSR of the $\Lambda _b \rightarrow p$ and $\Lambda _b \rightarrow N^*$ form factors, the numerical results of these form factors at $q^2=0$ from LCSR are collected in Tables 1 and 2 respectively, where three kinds of the interpolating current, namely Ioffe current, Tensor current and LP current are adopted in the correlation functions for a comparison, and five different LCDA models of $\Lambda _b$-baryon (Gegenbauer-1, Gegenbauer-2, QCDSR, Exponential and Free-parton) are employed in the calculation of the correlation function in the partonic level in order that one has the chance to find out which one is the most preferable by comparing with the results of the experiment or the other studies. The uncertainties of the form factors arise from the variation of the thresholds parameter $s_0$, the Borel parameter $M^2$, the normalization constants for $p(N^*)$ and $\Lambda _b$-baryon and the parameters in the LCDA models of $\Lambda _b$-baryon. Some comments on the numerical results of the form factors obtained in Tables 1 and 2 are in order:

• From the Tables 1 and 2, we can see that both for the $\Lambda _b \rightarrow p$ and $\Lambda _b \rightarrow N^*$ form factors, the form factor relations from heavy quark symmetry in Eq. (3) hold. This result is natural in the LCSR with $\Lambda _b$-LCDAs, since we have taken the heavy quark limit in the definition of the $\Lambda _b$-LCDAs. To obtain the symmetry breaking effect, one must introduce the power suppressed contribution in HQET, which exceeds the scope of the present study.

• The results of the form factors based on QCDSR model, Exponential model, Free-parton model are consistent with each other, while the results of the form factors based on Gegenbauer-1 model and Gegenbauer-2 model are significantly larger. This may indicate that Gegenbauer expansion of the LCDAs of $\Lambda _b$-baryon is not applicable to the $\Lambda _b$-baryon decays, since the light-quarks inside the $\Lambda _b$ baryon are soft quarks, albeit that the evolution equation contains ERBL-like term. In our following calculations, we will not take advantage of the results from the Gegenbauer-1 model and Gegenbauer-2 model.

• The LP current can give rise to the unique leading power $\Lambda _b \rightarrow p$ form factor at SCET limit. The obtained results for the form factors $\xi (0)$ from various LCDAs-models of $\Lambda _b$ baryon read

  $$\begin{aligned} \xi (0)= & {} 0.223\pm 0.047\,\,\,\mathrm{(QCDSR\,\, model)},\,\,\,\nonumber \\ \xi (0)= & {} 0.277\pm 0.125 \,\,\,\mathrm{(Exponential \,\, model)},\nonumber \\ \,\,\,\xi (0)= & {} 0.285\pm 0.129\,\,\,\mathrm{(Free\,\, parton\,\, model)},\,\,\, \end{aligned}$$

  (35)

  and these results are close to the form factors shown in Table 1 where the quark field is not replaced by the SCET field. Compared with the results from the Ioffe and tensor current, the results from the LP current are much larger, which implies that the high power correction which has been picked up when the Ioffe current or tensor current being employed is of great importance. As for the $\Lambda _b \rightarrow N^*$ form factors, the results from the LP current are extraordinarily large because that the normalization constants $\lambda _3^{N^*}$ is about four times smaller than $\lambda _3^{p}$. It is worth noting that it is more difficult to identify the negative parity baryon $N^*$ on lattice than the nucleon. Therefore, the value of normalization constant $\lambda _3^{N^*}$ maybe is not as reliable as the proton normalization constant.

• The form factors for $\Lambda _b \rightarrow p$ from the Ioffe and tensor current are very close to each other once the contribution of the $N^*$ baryon is included in the hadronic dispersion relation. This conclusion is consistent with that in [14] where the $\Lambda _b \rightarrow p$ form factors calculated by using LCSR with the LCDAs of the nucleon with two different interpolating currents(the axial-vector and pseudoscalar currents) for the $\Lambda _b$ baryon are close to each other under the condition that the contribution of the negative-parity heavy $\Lambda _b^*$ baryon was included.

• The form factors for $\Lambda _b \rightarrow N^*$ from the Ioffe current are much smaller than that from the tensor current because of the large numerical cancellations between the different invariant amplitudes, i.e., the contribution from the invariant amplitude $\textrm{Im}_s \Pi ^{\textrm{IO}}_3$ is significantly cancelled by that from the invariant amplitudes $\textrm{Im}_s \Pi ^{\textrm{IO}}_4,\textrm{Im}_s \Pi ^{\textrm{IO}}_1, \textrm{Im}_s \Pi ^{\textrm{IO}}_2$ in Eq. (25), when the Ioffe current is employed to calculate the form factor $F_1$ for $\Lambda _b \rightarrow N^*$, and the result is very sensitive to the models of LCDA of $\Lambda _b$-baryon after the cancellation. The large discrepancy between the predictions from the Ioffe and tensor current indicates that the form factors for $\Lambda _b \rightarrow N^*$ are very sensitive to the interpolating currents.

• It was mentioned in [33] that the Ioffe current coupling to the lowest baryonic state(the proton) is stronger than to the higher state(the $N^*$), then the predicted results of the $\Lambda _b \rightarrow N^*$ form factors are probably less accurate than that of the $\Lambda _b \rightarrow p$ form factors. We hope the future experimental observables of the semi-leptonic decay $\Lambda _b\rightarrow N^*l\nu$ can help us to determine which kind of the interpolating current is more preferable.

Table 1 The results of form factors $f_i$ and $g_i$ for $\Lambda _b \rightarrow p$ at $q^2=0$ under three interpolating currents for the proton(Ioffe, Tensor and LP) with five different LCDA models of $\Lambda _{b}$ baryon(Gegenbauer-1, Gegenbauer-2, QCDSR, Exponential and Free-parton) in this work. The results for the form factor $f_2(0)$ and $f_3(0)$ are same, $f_2(0)=f_3(0)$, as well as for $g_2(0)$ and $g_3(0)$. For comparison, we also collect the results of the form factors from other works

Table 2 The results of form factors $f_i$ and $g_i$ for $\Lambda _b \rightarrow N^*$ at $q^2=0$ under three interpolating currents for the $N^*$(Ioffe, Tensor and LP) with five different LCDA models of $\Lambda _{b}$ baryon(Gegenbauer-1, Gegenbauer-2, QCDSR, Exponential and Free-parton) in this work. The results for the form factor $F_2(0)$ and $F_3(0)$ are same, $F_2(0)=F_3(0)$, as well as for $G_2(0)$ and $G_3(0)$. For comparison, we also collect the results of the form factors from other works

For comparison, we also collect the predictions on the $\Lambda _b \rightarrow p$ and $\Lambda _b \rightarrow N^*$ form factors in other researches in Tables 1 and 2 respectively. The $\Lambda _b \rightarrow p$ form factors was studied in [13] based on LCSR with $\Lambda _b$-LCDAs where the Gegenbauer-1 model of $\Lambda _b$-LCDAs was employed and the nucleon(without the negative-parity partner) was interpolated by the CZ current, and the predicted from factors $f_1(0)$ and $g_1(0)$ are about an order of magnitude smaller than our results. This difference arises from the different model of LCDAs, the different interpolating currents and the absence of the negative-parity partner of the nucleon. The results in [14] are consistent with our results, which implies that the results of light-hadron LCSR and heavy-hadron LCSR can give rise to the consistent results. In [17], the LCSR with the nucleon-distribution amplitudes was employed where the $\Lambda _b$ was also interpolated by CZ current and only the ground state was considered in the hadronic dispersion integral, and the results of the $\Lambda _b \rightarrow p$ form factors are also about an order of magnitude smaller than ours. The predictions of $\Lambda _b \rightarrow p$ form factors from the covariant constituent quark model [34], the relativistic quark model [35], the light-front quark model [36], and the lattice simulation [37] are also listed in Table 1. It can be seen that our results are consistent with these predictions by considering the theoretical uncertainty. The $\Lambda _b \rightarrow N^*$ form factors were studied in [38] where the LCSR with $N^*$-LCDA was employed. The interpolating current of $\Lambda _b$ baryon was adopted as the axial-vector current and two different models of the LCDAs of $N^*$ were used in the calculation. The results from these two models( called LCSR(1) and LCSR(2) respectively) have large discrepancy because of the different parameters of twist-4 LCDA in these two models. In [39], these form factors were revisited where the $\Lambda _b$ baryon was interpolated by the most general current with an arbitrary parameter $\beta$ for the mixing of different components and the contribution of negative-parity $\Lambda _b^*$ baryon was included, and the results still significantly depend on the models of the LCDAs, and they are not consistent with our predictions. Thus we hope our studies can provide useful hints on the LCDAs of the negative-parity states. Recently, a new study about the $\Lambda _b \rightarrow p$ form factors based on the perturbation QCD(PQCD) approach was presented in [40]. Different from the previous PQCD calculations [41, 42], this work includes the contribution from the higher twist LCDAs of $\Lambda _b$ baryon and proton, and the results indicate that the higher twist LCDAs give the dominant contributions since the important endpoint region of the convolution of the LCDAs and the hard kernels has been picked up. The renewed numerical result from the PQCD calculation can also be consistent with our predictions.

To guarantee the light-cone dominance, the LCSR predictions for the form factors are reliable up to a limited region of the momentum transfer, namely $q^2\le 10\mathrm{GeV^2}$. In order to extend the LCSR predictions to the whole physical region, we take advantage of the z-series parameterization in the BCL-version suggested in [43],

$$\begin{aligned} z(q^2,t_0)=\frac{\sqrt{t_+-q^2}-\sqrt{t_+-t_0}}{\sqrt{t_+-q^2}+\sqrt{t_+-t_0}}, \end{aligned}$$

(36)

where $t_{\pm }=(m_{\Lambda _b}\pm m_{p(N^*)})^2$, and $t_0=t_+-\sqrt{t_+-t_{-}}\sqrt{t_+-t_{min}}$ is chosen to reduce the interval of z after mapping $q^2$ to z with the interval $t_{min}<q^2<t_{-}$. In the numerical analysis, we adopt $t_{min}=-6\mathrm{GeV^2}$. To achieve the best parametrization of the form factors, we employ the following parametrization

$$\begin{aligned} f(q^2)=\frac{f_i(0)}{1-q^2/(m_{pole}^f)^2} \Big \{1+a_1(z(q^2,t_0)-z(0,t_0))\Big \},\nonumber \\ \end{aligned}$$

(37)

For the pole masses, we adopt $m_{pole}=m_{B^*}=5.325$ GeV for the from factors $f_1,f_2, F_1,F_2$; $m_{pole}=m_{B_1}=5.723$ GeV for the from factors $g_1,g_2, G_1,G_2$; $m_{pole}=m_{B_0}=5.749$ GeV for the from factors $f_3, F_3$; $m_{pole}=m_{B}=5.280$ GeV for the from factors $g_3, G_3$.

Table 3 The z-fit parameters, namely f(0) and $a_1$, as well as the correlation coefficient $\rho$ between them obtained from LCSR for $\Lambda _b \rightarrow p$ under two interpolating current (Ioffe and tensor) with QCDSR LCDA models of $\Lambda _b$ baryon

Table 4 The z-fit parameters, namely f(0) and $a_1$, as well as the correlation coefficient $\rho$ between them obtained from LCSR for $\Lambda _b \rightarrow N^*$ under two interpolating current (Ioffe and tensor) with three different LCDA models of $\Lambda _b$ baryon (QCDSR, Exponential and Free-parton)

To determine the central values, the uncertainties and the correlation coefficients of the z-fit parameters $f_i(0)$ and $a_{1i}$ for each $\Lambda _b\rightarrow p,N^*$ form factor, we first generate an ensemble of correlated LCSR data points of these form factors. The LCSR data pointss for each form factor are calculated at $q^2=\{-6,-3,0,3,6\}$ GeV$^2$ with N = 500 ensembles of the input parameter set (including $M^2$, $s_0$,and the parameters of LCDAs for $\Lambda _b$) where the value of the input parameters are randomly distributed according to a multivariate joint distribution [44]. Then we fit the z-series expansion to all the $\Lambda _b\rightarrow p,N^*$ form factors to get the z-fit parameters $f_i(0)$ and $a_{1i}$, as well as the correlation coefficients between them. The fitting results are given in Tables 3 and 4 respectively, and the resultant $q^2$ dependence of these form factors are shown in Figs. 2 and 3 respectively, where both the Ioffe current and tensor current are employed to interpolate the baryon states, and the QCDSR model, the Exponential model and the Free-parton model of $\Lambda _b$ baryon LCDA are all taken into account for comparison. In order to test whether the results from these interpolating currents and LCDAs models are consistent within uncertainties, we also display the error bands of the form factors under two different interpolating currents with Exponential LCDA model for $\Lambda _b$. From Fig. 2, we can see that the form factors of $\Lambda _b \rightarrow p$ are insensitive to the interpolating currents apparently and the results from the different interpolating currents and LCDAs models are consistent within the uncertainties. The predictions based on QCDSR model are very close to that based on Exponential model, and the Free-parton model give rise to little larger values of the form factors. As for the form factors for $\Lambda _b \rightarrow N^*$, the results are sensitive to the interpolating currents and the results from the different LCDAs models of $\Lambda$ are consistent within uncertainties. We note that the uncertainties of the fitted results are mainly from the LCDAs of the $\Lambda _b$ baryon. Therefore, it is an essential task to determine the most preferable model and to constrain the parameters of the LCDAs of $\Lambda _b$ baryon in the study on the heavy baryon decays.

3.2 Semi-leptonic decays of $\Lambda _b \rightarrow p(N^*)l^-\bar{\nu _l}$

Now, we can take advantage of the obtained $\Lambda _b \rightarrow p(N^*)$ form factors to calculate the branching ratios of the semileptonic decays, as well as different asymmetry parameters and the other observables. In doing this, we employ the Ioffe current and the tensor current and three suitable LCDA models of $\Lambda _{b}$-baryon which are QCDSR model, Exponential model and Free-parton model to evaluate the correlation function used in the LCSRs. We hope the future experiments will measure these observables so that it can help us to make certain which kind of the interpolating currents and which type of LCDA models of $\Lambda _b$ baryon are correct.

Fig. 2

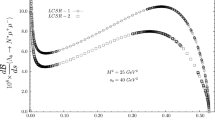
$\Lambda _b\rightarrow p$ transition form factor obtained from LCSR at $q^2\le 10$ GeV$^2$ and extrapolation to large $q^2$ using the z serizes-parametrization: the red(blue) solid line correspond to the Ioffe(tensor) current for proton with QCDSR-LCDA model for $\Lambda _b$, the red(blue) dashed line correspond to the Ioffe(tensor) current for pronto with Exponential LCDA model for $\Lambda _b$ and the red(blue) dot-dashed line correspond to the Ioffe(tensor) current for proton with Free-parton LCDA model for $\Lambda _b$. With the LCDA of $\Lambda _b$ being fixed as the Exponential model, the red (blue) band correspond to the range of the uncertainties of the form factors under the Ioffe(tensor) interpolating current

Fig. 3

Same as Fig. 2 but for $\Lambda _b\rightarrow N^*$ transition form factor

Table 5 The predictions for the branching fractions, the averaged leptonic forward-backward asymmetry$\langle A_{FB}\rangle$, the averaged final hadronic polarization $\langle P_{B}\rangle$ and the averaged lepton polarization $\langle P_{l}\rangle$ for $\Lambda _b\rightarrow pl^-{\bar{\nu }}_l$ under two interpolating current (Ioffe and Tensor) with three different LCDA models of $\Lambda _b$ baryon (QCDSR, exponential and free-parton). For comparison, we also collect the results of these observables from other works and the experiment

Table 6 The predictions for the branching fractions, the averaged leptonic forward-backward asymmetry$\langle A_{FB}\rangle$, the averaged final hadron polarization $\langle P_{B}\rangle$ and the averaged lepton polarization $\langle P_{l}\rangle$ for $\Lambda _b\rightarrow N^*l^-{\bar{\nu }}_l$ under two interpolating current(Ioffe and tensor) with three different LCDA models of $\Lambda _b$ baryon(QCDSR, Exponential and Free-parton)

In order to calculate these observables, it is convenient to introduce the helicity amplitudes [48, 49]. The helicity amplitudes can be defined by

$$\begin{aligned} H^{V,A}_{\lambda _{p(N^*)},\lambda _{W^-} }=\epsilon ^{\dagger \mu }(\lambda _{W^-})\langle p(N^*),\lambda _{p(N^*)}|V(A)|\Lambda _b, \lambda _{\Lambda _b}\rangle ,\nonumber \\ \end{aligned}$$

(38)

where the $\lambda _{\Lambda _b}, \lambda _{p(N^*)}, \lambda _{W^-}$ denote the helicity of the $\Lambda _b$ baryon, the proton($N^*$) and the off-shell $W^-$ respectively. The helicity amplitudes $H^{V,A}_{\lambda _{p(N^*)},\lambda _{W^-}}$ can be expressed as functions of the form factors [50, 51]

$$\begin{aligned}{} & {} H^{V}_{\frac{1}{2},0}(1/2^+\rightarrow 1/2^{\pm })=\frac{\sqrt{Q_{\mp }}}{\sqrt{q^2}}\nonumber \\{} & {} \quad \times \Big (M_{\pm }f(F)_1(q^2)\mp \frac{q^2}{m_{\Lambda _b}}f(F)_2(q^2)\Big ), \nonumber \\{} & {} H^{A}_{\frac{1}{2},0}(1/2^+\rightarrow 1/2^{\pm })=\frac{\sqrt{Q_{\pm }}}{\sqrt{q^2}}\nonumber \\{} & {} \quad \times \Big (M_{\mp }g(G)_1(q^2)\pm \frac{q^2}{m_{\Lambda _b}}g(G)_2(q^2)\Big ), \nonumber \\{} & {} H^{V}_{\frac{1}{2},1}(1/2^+\rightarrow 1/2^{\pm })=\sqrt{2Q_{\mp }}\nonumber \\{} & {} \quad \times \Big (f(F)_1(q^2)\mp \frac{M_{\pm }}{m_{\Lambda _b}}f(F)_2(q^2)\Big ), \nonumber \\{} & {} H^{A}_{\frac{1}{2},1}(1/2^+\rightarrow 1/2^{\pm })=\sqrt{2Q_{\pm }}\nonumber \\{} & {} \quad \times \Big (g(G)_1(q^2)\pm \frac{M_{\mp }}{m_{\Lambda _b}}g(G)_2(q^2)\Big ), \nonumber \\{} & {} H^{V}_{\frac{1}{2},t}(1/2^+\rightarrow 1/2^{\pm })=\frac{\sqrt{Q_{\pm }}}{\sqrt{q^2}}\nonumber \\{} & {} \quad \times \Big (M_{\mp }f(F)_1(q^2)\pm \frac{q^2}{m_{\Lambda _b}}f(F)_3(q^2)\Big ), \nonumber \\{} & {} H^{A}_{\frac{1}{2},t}(1/2^+\rightarrow 1/2^{\pm })=\frac{\sqrt{Q_{\mp }}}{\sqrt{q^2}} \nonumber \\{} & {} \quad \times \Big (M_{\pm }g(G)_1(q^2)\mp \frac{q^2}{m_{\Lambda _b}}g(G)_3(q^2)\Big ). \end{aligned}$$

(39)

where $Q_{\pm }$ is defined as $Q_{\pm }=(m_{\Lambda _b}\pm m_{p(N^*)})^2-q^2$ and $M_{\pm }=m_{\Lambda _b} \pm m_{p(N^*)}$. The negative helicity amplitudes for the involved final baryon with $J^P=1/2^+$ and $1/2^-$ can be obtained by using the relation

$$\begin{aligned}{} & {} H^V_{-\lambda _{p(N^*)},-\lambda _{W^-}}=\mathcal {P}^V H^V_{\lambda _{p(N^*)},\lambda _{W^-}}, \nonumber \\{} & {} H^A_{-\lambda _{p(N^*)},-\lambda _{W^-}}=\mathcal {P}^A H^A_{\lambda _{p(N^*)},\lambda _{W^-}}, \end{aligned}$$

(40)

with $(\mathcal {P}^V,\mathcal {P}^A)=(+,-)$ and $(\mathcal {P}^V,\mathcal {P}^A)=(-,+)$, respectively. The total helicity amplitudes for the $V-A$ current are given by

$$\begin{aligned} H_{\lambda _{p(N^*)},\lambda _{W^-}}=H^V_{\lambda _{p(N^*)},\lambda _{W^-}}-H^A_{\lambda _{p(N^*)},\lambda _{W^-}}, \end{aligned}$$

(41)

With the helicity amplitudes, the differential angular distribution for the decay $\Lambda _b \rightarrow p(N^*)l^-{\bar{\nu }}_l$ can be obtained

$$\begin{aligned} \frac{d\Gamma (\Lambda _b \rightarrow p(N^*)l^-{\bar{\nu }}_l)}{dq^2d\cos \theta _l}= & {} \frac{G_F^2|V_{ub}|^2q^2|\vec {p}_{p(N^*)}|}{512\pi ^3m^2_{\Lambda _b}}\Big (1-\frac{m^2_l}{q^2}\Big )^2 \nonumber \\{} & {} \times \Big [A_1+\frac{m_l^2}{q^2}A_2\Big ], \end{aligned}$$

(42)

where $G_F$ is the Fermi constant, $V_{ub}$ is the CKM matrix element, $m_l$ is the lepton mass($l=e,\mu ,\tau$), $\theta _l$ is the angle between the three-momentum of the final $p(N^*)$ baryon and the lepton in the $q^2$ rest frame and

$$\begin{aligned} A_1= & {} 2\sin ^2\theta _l(H^2_{1/2,0}+H^2_{-1/2,0})+(1-\cos \theta _l)^2H^2_{1/2,1}\nonumber \\{} & {} +(1+\cos \theta _l)^2H^2_{-1/2,-1},\nonumber \\ A_2= & {} 2\cos ^2\theta _l(H^2_{1/2,0}+H^2_{-1/2,0})+\sin ^2 \theta _l(H^2_{1/2,1}\nonumber \\{} & {} +H^2_{-1/2,-1})+2(H^2_{1/2,t}+H^2_{-1/2,t}) \nonumber \\{} & {} -4\cos \theta _l(H_{1/2,t}H_{1/2,0}+H_{-1/2,t}H_{-1/2,0}), \nonumber \\{} & {} |\vec {p}_{p(N^*)}|\nonumber \\= & {} \frac{\sqrt{m_{\Lambda _b}^4+m^4_{p(N^*)}+q^4-2(m^2_{\Lambda _b}m^2_{p(N^*)}+m^2_{p(N^*)}q^2+m^2_{\Lambda _b}q^2)}}{2m_{\Lambda _b}}, \nonumber \\ \end{aligned}$$

(43)

The differential decay rate can be obtained by integrating out cos$\theta _l$

$$\begin{aligned}{} & {} \frac{d\Gamma (\Lambda _b\rightarrow p(N^*)l^-{\bar{\nu }}_l)}{dq^2}\nonumber \\{} & {} \quad =\int ^1_{-1}\frac{d\Gamma (\Lambda _b \rightarrow p(N^*)l^-{\bar{\nu }}_l)}{dq^2d\cos \theta _l}d\cos \theta _l, \end{aligned}$$

(44)

Additionally, many other important physical observables, e.g., the leptonic forward-backward asymmetry ($A_{FB}$), the final hadron polarization($P_B$) and the lepton polarization($P_l$), can be expressed in terms of the helicity amplitudes. They are defined as

$$\begin{aligned} A_{FB}(q^2)= & {} \frac{\int ^1_0 \frac{d\Gamma }{dq^2d\cos \theta _l}d\cos \theta _l-\int ^0_{-1} \frac{d\Gamma }{dq^2d\cos \theta _l}d\cos \theta _l}{\int ^1_0 \frac{d\Gamma }{dq^2d\cos \theta _l}d\cos \theta _l+\int ^0_{-1} \frac{d\Gamma }{dq^2d\cos \theta _l}d\cos \theta _l}, \nonumber \\ \end{aligned}$$

(45)

$$\begin{aligned} P_B(q^2)= & {} \frac{d\Gamma ^{\lambda _{p(N^*)}=1/2}/dq^2-d\Gamma ^{\lambda _{p(N^*)}=-1/2}/dq^2}{d\Gamma /dq^2}, \end{aligned}$$

(46)

$$\begin{aligned} P_l(q^2)= & {} \frac{d\Gamma ^{\lambda _l=1/2}/dq^2-d\Gamma ^{\lambda _l=-1/2}/dq^2}{d\Gamma /dq^2}. \end{aligned}$$

(47)

respectively, where

$$\begin{aligned} \frac{d\Gamma ^{\lambda _{p(N^*)}=1/2}}{dq^2}= & {} \frac{4m^2_l}{3q^2}\Big (H^2_{1/2,1}+H^2_{1/2,0}+3H^2_{1/2,t}\Big )\nonumber \\{} & {} +\frac{8}{3}\Big (H^2_{1/2,0}+H^2_{1/2,1}\Big ), \end{aligned}$$

(48)

$$\begin{aligned} \frac{d\Gamma ^{\lambda _{p(N^*)}=-1/2}}{dq^2}= & {} \frac{4m^2_l}{3q^2}\Big (H^2_{-1/2,-1}+H^2_{-1/2,0}+3H^2_{-1/2,t}\Big )\nonumber \\{} & {} +\frac{8}{3}\Big (H^2_{-1/2,0}+H^2_{-1/2,-1}\Big ), \end{aligned}$$

(49)

$$\begin{aligned} \frac{d\Gamma ^{\lambda _l=1/2}}{dq^2}= & {} \frac{m^2_l}{q^2}\nonumber \\{} & {} \times \Big [\frac{4}{3}\Big (H^2_{1/2,1}+H^2_{1/2,0}+H^2_{-1/2,-1}+H^2_{-1/2,0}\Big )\nonumber \\{} & {} +4\Big (H^2_{1/2,t}+H^2_{-1/2,t}\Big )\Big ], \end{aligned}$$

(50)

$$\begin{aligned} \frac{d\Gamma ^{\lambda _l=-1/2}}{dq^2}= & {} \frac{8}{3}\Big (H^2_{1/2,1}+H^2_{1/2,0}+H^2_{-1/2,-1}+H^2_{-1/2,0}\Big ).\nonumber \\ \end{aligned}$$

(51)

Having the form factors in hand, we can obtain the predictions of the total branching fractions, the averaged forward-backward asymmetry $\langle A_{FB}\rangle$, the averaged final hadron polarization $\langle P_{B}\rangle$ and the averaged lepton polarization $\langle P_{l}\rangle$. The numerical results of the relevant observables in the semi-leptonic decays $\Lambda _b \rightarrow p(N^*)l^-\nu$ are presented in Tables 5 and 6 respectively. Similar to the prediction on the form factors, we list the results from the Ioffe current and the tensor current as well as three different models of $\Lambda _b$ baryon for comparison. The lepton masses used in this work are taken from PDG [30], the central value of the life times of $\Lambda _b$ and the CKM matrix element $|V_{ub}|$ are adopted as $\tau _{\Lambda _b}=1.470$ps and $|V_{ub}|=3.82\times 10^{-3}$ respectively. From the Table 5, we can see that these physical observables for the semi-leptonic decay $\Lambda _b \rightarrow pl^-\nu$ from two different interpolating currents and three LCDA models of $\Lambda _b$ baryon are consistent with each other. Our results are also consistent with the predictions from the relativistic quark model [35] and the lattice simulation [52], which is under expectation since the form factors are consistent as mentioned before. Our estimation of the branch fraction of $Br({\Lambda _b \rightarrow p\mu ^-\bar{\nu _{\mu }}})$ also agrees with the result reported by the LHCb Collaboration [53], and this channel provides a good platform to determine the CKM matrix element $|V_{ub}|$ if the uncertainties can be reduced.

As for the physical observables of the semi-leptonic decay $\Lambda _b \rightarrow N^*l{\bar{\nu }}$, we can see from the Table 6 that the results from the two different interpolating currents have large discrepancy. The branching ratio of $\Lambda _b \rightarrow N^*l{\bar{\nu }}$ decay from the tensor current is about seven times larger than that from the Ioffe current under the QCDSR and the Exponential models for the LCDA of $\Lambda _b-$baryon, and the ratio is even bigger when the Free-parton model is taken into account. For the averaged forward-backward asymmetry $\langle A_{FB}\rangle$ and the averaged final hadron polarization $\langle P_{B} \rangle$, the predictions from the Ioffe current also significantly deviate from the results from the tensor current, which is mainly due to the smaller value of the $\Lambda _b \rightarrow N^*$ transition form factors and the stronger LCDA-model dependency when the Ioffe current is adopted, see Table 2. Therefore, the physical observables of the semi-leptonic decay $\Lambda _b \rightarrow N^*l{\bar{\nu }}$ is very useful to figure out the properties of the baryon, such as the interpolating current of light-baryons, and the LCDAs of heavy-baryons can be better determined once the physical observables of heavy baryon semi-leptoinc decays are precisely measured.

4 Summary

We have calculated the form factors of $\Lambda _b \rightarrow p, N^*(1535)$ transition within the framework of LCSR with the LCDAs of $\Lambda _b$-baryon, and utilized the results to evaluate the experimental observables such as the branching ratios, the forward-backward asymmetries and final state polarizations of the semileptonic decays $\Lambda _b \rightarrow p, N^*(1535)\ell \nu$. Since the interpolating current of the baryon is not unique, we employed three kinds of the current, namely the Ioffe current, the tensor current and the leading power current for a comparison. Following a standard procedure of the calculation of heavy-to-light form factors by using LCSR approach, we can arrive at the sum rules of the $\Lambda _b \rightarrow p, N^*(1535)$ transition form factors. In the hadronic representation of the correlation function, we have isolated both proton state and the $N^*(1535)$ state so that the $\Lambda _b \rightarrow p, N^*(1535)$ form factors can be evaluated simultaneously. The LCDAs of $\Lambda _b$-baryon are not well determined so far, thus we employed five different models, i.e, the QCDSR model, the exponential model, the free-parton model and the Gagenbauer-(I,II) models in order to find out the most suitable models.

Taking advantage of the leading power current, we can obtain the unique $\Lambda _b \rightarrow p$ form factor at SCET limit, where only the LCDA $\psi _4$ of $\Lambda _b$-baryon appears in the sum rules. If we do not take the SCET limit, the numerical results will be only sightly changed. However, when the Ioffe current or tensor current are employed, we can obtain much smaller values of the $\Lambda _b \rightarrow p$ form factors, and the results from the two interpolating currents are consistent with each other after including the contribution of the negative-parity $N^*(1535)$ baryon in the hadronic dispersion relation. Since the correlation function defined in terms of these two current contains some power suppressed terms, the numerical results indicate that the power suppressed contributions play a very important role in the sum rules of the $\Lambda _b \rightarrow p$ form factors. In the numerical calculation, we have employed five different models for the LCDAs of $\Lambda _b$-baryon, and found that the results obtained from the models based on Gegenbauer polynomial expansion are too large and the results from the other three models are consistent with each other. Therefore, the Gegenbauer expansion of the $\Lambda _b$ LCDAs is not appropriate in the study on the $\Lambda _b$-baryon decays. Our predictions on the form factors for the $\Lambda _b \rightarrow p$ transition are consistent with the results of other theoretical works, especially those from the QCD-inspired approaches such as light-hadron LCSR and Lattice QCD simulations. As for the form factors of the $\Lambda _b \rightarrow N^*(1535)$ transition, the results are very sensitive to the choice of the interpolating currents and the uncertainties are very large. We only hope our predictions will provide some useful information on the parameters of the $N^*$-LCDAs once the experimental data is available.

We further obtained the predictions of the total branching fractions, the averaged forward-backward asymmetry $\langle A_{FB}\rangle$, the averaged final hadron polarization $\langle P_{B}\rangle$ and the averaged lepton polarization $\langle P_{l}\rangle$. Our results are consistent with the predictions from the relativistic quark model [35] and the lattice simulation [52], and the prediction on the the branch fraction of $Br({\Lambda _b \rightarrow p\mu ^-\bar{\nu _{\mu }}})$ also agrees with the measurement by the LHCb [53], and this channel provides a good platform to determine the CKM matrix element $|V_{ub}|$. It also should be mentioned that the errors of our results are sizable, mainly due to the large uncertainties of the parameters in the LCDAs of the $\Lambda _b$-baryon. Therefore, more studies on the $\Lambda _b$ baryon decays are required to constrain the parameters of the LCDAs of $\Lambda _b$ -baryon. Moreover, we only performed a tree-level calculation, and the QCD corrections to the hard kernel in the partonic expression of the correlation function are needed to increase the accuracy. In the literatures [15], the QCD corrections to the leading power form factors of $\Lambda _b \rightarrow \Lambda$ have been calculated, the method can be directly generalized to the $\Lambda _b \rightarrow p$ transition. The power suppressed contributions have been shown to be important, and a more careful treatment on the power corrections is of great importance. For example, since the LCDAs of $\Lambda _b$-baryon are defined in terms of the large component of the heavy quark field in HQET, we have not included the power suppressed contributions from the heavy quark expansion, which will lead to an important kind of power correction. The above mentions problems will be considered in the future work.

Appendices

Correlation function in the LCSR for $\Lambda _b\rightarrow p, N^*(1535)$ form factor

The invariant amplitudes $\Pi ^i_j(p^2,q^2)$ for the correlation function with the vector transition current $j_{\mu ,V}$ in Eq. (2.2) are given in form of Eq. (20), where the transformed coefficient functions $w^{(i)}_{jn}(s,q^2)$ with $i= \textrm{Ioffe, Tensor, LP}$ interpolating currents and $j=1,\ldots , 6$ (the invariant ampitude), $n=1,2$ (the power of the denominator D) are listed below:

• The Ioffe-type current

  $$\begin{aligned} w^{\textrm{Io}}_{11}{} & {} =4f^{(1)}_{\Lambda _b}m_{\Lambda _b}\sigma {\bar{\sigma }}\psi ^s_3\,\ \ \ \ \ w^{\textrm{Io}}_{12}=0, \\ w^{\textrm{Io}}_{21}{} & {} =w^{\textrm{Io}}_{61}=-\frac{2f^{(2)}_{\Lambda _b}}{{\bar{\sigma }}m^2_{\Lambda _b}}{{\tilde{\psi }}}_2, \\ w^{\textrm{Io}}_{22}{} & {} =w^{\textrm{Io}}_{62}=2f^{(2)}_{\Lambda _b}\frac{2m^2_{\Lambda _b}\sigma +q^2-m^2_{\Lambda _b}-s}{m^2_{\Lambda _b}}{{\tilde{\psi }}}_2\\{} & {} \qquad -\frac{2f^{(2)}_{\Lambda _b}}{m_{\Lambda _b}}{{\tilde{\Psi }}}^{-+}_{12},\\ w^{\textrm{Io}}_{31}{} & {} =-2f^{(1)}_{\Lambda _b}m^2_{\Lambda _b}\sigma {\bar{\sigma }}\psi ^s_3+f^{(2)}_{\Lambda _b}[{{\tilde{\psi }}}_4\\{} & {} \quad +m_{\Lambda _b}\sigma (\psi ^{+-}_1+\psi ^{+-}_2)] \\{} & {} \quad -f^{(2)}_{\Lambda _b}\Bigg [\frac{(2s-3m_{\Lambda _b}^2\sigma -2q^2+m_{\Lambda _b}^2)}{m_{\Lambda _b}^2{\bar{\sigma }}}{{\tilde{\psi }}}_2 \\{} & {} \quad -\frac{1}{m_{\Lambda _b}{\bar{\sigma }}}{{\tilde{\Psi }}}^{-+}_{12}\Bigg ], \\ w^{\textrm{Io}}_{32}{} & {} =f^{(2)}_{\Lambda _b}\Bigg [\frac{(2m^2_{\Lambda _b}\sigma +q^2-m^2_{\Lambda _b}-s)(s-m_{\Lambda _b}^2\sigma -q^2)}{m^2_{\Lambda _b}}{{\tilde{\psi }}}_2 \\{} & {} \quad -\frac{s-q^2-m_{\Lambda _b}^2\sigma }{m_{\Lambda _b}}{{\tilde{\Psi }}}^{-+}_{12}\Bigg ], \\ w^{\textrm{Io}}_{41}{} & {} =2f^{(1)}_{\Lambda _b}m_{\Lambda _b}\sigma \psi ^s_3-\frac{f^{(2)}_{\Lambda }}{m_{\Lambda _b}{\bar{\sigma }}}{{\tilde{\psi }}}_2,\\ w^{Io}_{42}{} & {} =f^{(2)}_{\Lambda _b}\Bigg [\frac{2m^2_{\Lambda _b}\sigma +q^2-m^2_{\Lambda _b}-s}{m_{\Lambda _b}}{{\tilde{\psi }}}_2 -{{\tilde{\Psi }}}^{-+}_{12}\Bigg ],\\ w^{\textrm{Io}}_{51}{} & {} =-4f^{(1)}_{\Lambda _b}m_{\Lambda _b}\sigma ^2\psi ^s_3+\frac{2f^{(2)}_{\Lambda }}{m_{\Lambda _b}{\bar{\sigma }}}{{\tilde{\psi }}}_2,\\ w^{Io}_{52}{} & {} =2f^{(2)}_{\Lambda _b}\Bigg [-\frac{(2m^2_{\Lambda _b}\sigma +q^2-m^2_{\Lambda _b}-s)}{m_{\Lambda _b}}{{\tilde{\psi }}}_2 +{{\tilde{\Psi }}}^{-+}_{12}\Bigg ], \end{aligned}$$

  where ${{\tilde{\Psi }}}^{-+}_{12}={{\tilde{\psi }}}^{-+}_1-{{\tilde{\psi }}}^{+-}_1+{{\tilde{\psi }}}^{-+}_2-{{\tilde{\psi }}}^{+-}_2$ and the functions ${{\tilde{\psi }}}(\omega ,u)$ are defined as:

  $$\begin{aligned} {{\tilde{\psi }}}(\omega , u)=\int ^{\omega }_0 d\tau \ \tau \psi (\tau ,u), \end{aligned}$$

  (52)

  originating from the partial integral in the variable $\omega$ in Eq. (20)

• The Tensor-type current

  $$\begin{aligned} w^{\textrm{Te}}_{11}{} & {} =-2f^{(1)}_{\Lambda _b}m_{\Lambda _b}\sigma \Big [{\bar{\sigma }}(\psi _3^{+-}+2\psi _3^{-+})\\{} & {} \quad +\frac{2}{m_{\Lambda _b}}(\psi ^2_{\perp ,3}-\psi ^1_{\perp ,3})\Big ], \\ w^{\textrm{Te}}_{12}{} & {} =8f^{(1)}_{\Lambda _b}{\bar{\sigma }}({{\tilde{\psi }}}^2_{\perp ,Y}-{{\tilde{\psi }}}^1_{\perp ,Y}), \\ w^{\textrm{Te}}_{21}{} & {} =w^{\textrm{Te}}_{61}=0,\ \ \ \ w^{\textrm{Te}}_{22}=w^{\textrm{Te}}_{62}=\frac{2f^{(1)}_{\Lambda _b}}{m_{\Lambda _b}}({{\tilde{\psi }}}^{+-}_{3}-{{\tilde{\psi }}}^{-+}_{3}), \\ w^{\textrm{Te}}_{31}{} & {} =-f^{(1)}_{\Lambda _b}m_{\Lambda _b}\sigma \Big [m_{\Lambda _b}{\bar{\sigma }}(\psi _3^{+-}+2\psi _3^{-+})\\{} & {} \quad +2(\psi ^2_{\perp ,3}-\psi ^1_{\perp ,3})\Big ]-\frac{f^{(1)}_{\Lambda _b}}{m_{\Lambda _b}{\bar{\sigma }}}({{\tilde{\psi }}}^{+-}_{3}-{{\tilde{\psi }}}^{-+}_{3}), \\ w^{\textrm{Te}}_{32}{} & {} =-f^{(1)}_{\Lambda _b}\Big [\frac{s-q^2-m^2_{\Lambda _b}\sigma }{m_{\Lambda _b}}({{\tilde{\psi }}}^{+-}_{3}-{{\tilde{\psi }}}^{-+}_{3})\\{} & {} \quad -4m_{\Lambda _b}{\bar{\sigma }}({{\tilde{\psi }}}^2_{\perp ,Y}-{{\tilde{\psi }}}^1_{\perp ,Y})\Big ], \\ w^{\textrm{Te}}_{41}{} & {} =-f^{(1)}_{\Lambda _b}m_{\Lambda _b}\sigma (\psi _3^{+-}+2\psi _3^{-+}), \\ w^{Te}_{42}{} & {} =f^{(1)}_{\Lambda _b}\Big [({{\tilde{\psi }}}^{+-}_{3}-{{\tilde{\psi }}}^{-+}_{3})+4\sigma ({{\tilde{\psi }}}^2_{\perp ,Y}-{{\tilde{\psi }}}^1_{\perp ,Y})\Big ],\nonumber \\ w^{\textrm{Te}}_{51}{} & {} =2f^{(1)}_{\Lambda _b}m_{\Lambda _b}\sigma \Big [\sigma (\psi _3^{+-}+2\psi _3^{-+})\\{} & {} \quad -\frac{2}{m_{\Lambda _b}}(\psi ^2_{\perp ,3}-\psi ^1_{\perp ,3})\Big ], \\ w^{Te}_{52}{} & {} =-2f^{(1)}_{\Lambda _b}\Big [({{\tilde{\psi }}}^{+-}_{3}-{{\tilde{\psi }}}^{-+}_{3})+4\sigma ({{\tilde{\psi }}}^2_{\perp ,Y}-{{\tilde{\psi }}}^1_{\perp ,Y})\Big ].\nonumber \end{aligned}$$

• The LP-type current

  $$\begin{aligned}{} & {} w^{LP}_{11}=-2f^{(2)}_{\Lambda _b}m_{\Lambda _b}\sigma {\bar{\sigma }}\psi _4 \nonumber \\{} & {} w^{LP}_{i2}(i=1-6)=0,\,\,\nonumber \\{} & {} w^{LP}_{21}=w^{LP}_{61}=0, \nonumber \\{} & {} w^{LP}_{31}=f^{(2)}_{\Lambda _b}m^2_{\Lambda _b}\sigma {\bar{\sigma }}\psi _4+f^{(1)}_{\Lambda _b}m_{\Lambda _b}\sigma (\psi ^2_{\perp , 3}-\psi ^1_{\perp , 3}\nonumber \\{} & {} \qquad \qquad \, +2(\psi ^2_{\perp , Y}-\psi ^1_{\perp , Y})), \ \ \ \nonumber \\{} & {} w^{LP}_{41}=-f^{(2)}_{\Lambda _b}m_{\Lambda _b}\sigma \psi _4,\,\, \ \ \ w^{LP}_{51}=2f^{(2)}_{\Lambda _b}m_{\Lambda _b}\sigma ^2\psi _4.\ \ \ \ \ \nonumber \\ \end{aligned}$$

  (53)

The transformed coefficient functions ${{\tilde{\omega }}}^{(i)}_{jn}(s, q^2)$ for the correlation function with axial vector transition current $j_{\mu ,A}$ can be obtained from $\omega ^{(i)}_{jn}(s,q^2)$ in the above expressions.

Table 7 Parameters for the LCDA of $\Lambda _b$ baryon

The LCDA models of $\Lambda _b$ baryon

Light-cone distribution amplitudes(LCDA) of the $\Lambda _b$ baryon are the fundamental ingredients for the LCSR of the $\Lambda _b \rightarrow p(N^*)$ form factors, but they have attracted less attention compared to the B-meson. So far, only few works [45,46,47] concerned about the LCDAs of the $\Lambda _b$ baryon, where different parameterization for the LCDAs of $\Lambda _b$ baryon have been proposed. In the present paper, we consider the following five different models:

• QCDSR model [45]

  $$\begin{aligned} \psi _2(\omega , u)= & {} \frac{15}{2\mathcal {N}}\omega ^2 u(1-u)\int ^{s^{\Lambda _b}_0}_{\omega /2}ds\ e^{-s/\tau } (s-\omega /2), \nonumber \\ \psi ^{+-}_{3}(\omega ,u)= & {} \frac{15}{\mathcal {N}}\omega u\int ^{s^{\Lambda _b}_0}_{\omega /2}ds\ e^{-s/\tau }(s-\omega /2)^2, \nonumber \\ \psi ^{-+}_{3}(\omega ,u)= & {} \frac{15}{\mathcal {N}}\omega (1-u)\int ^{s^{\Lambda _b}_0}_{\omega /2}ds\ e^{-s/\tau }(s-\omega /2)^2, \nonumber \\ \psi _4(\omega ,u)= & {} \frac{5}{\mathcal {N}}\int ^{s^{\Lambda _b}_0}_{\omega /2}ds\ e^{-s/\tau }(s-\omega /2)^3, \end{aligned}$$

  (54)

  with $\mathcal {N}=\int ^{s^{\Lambda _b}_0}_0ds\ s^5e^{-s/\tau }$. The $\tau$ is the Borel parameter which is taken to be in the interval $0.4<\tau <0.8$ GeV and ${s^{\Lambda _b}_0}=1.2$ GeV is the continuum threshold.

• Gegenbauer-1 model [45]

  $$\begin{aligned} \psi _{2}(\omega , u)= & {} \omega ^2u(1-u)\Bigg [\frac{1}{\epsilon ^4_0}e^{-\omega /\epsilon _0}\nonumber \\{} & {} +a_2C^{3/2}_{2}(2u-1)\frac{1}{\epsilon ^4_1}e^{-\omega /\epsilon _1}\Bigg ], \nonumber \\ \psi ^{+-}_{3}(\omega , u)= & {} \frac{2}{\epsilon ^3_3}\omega ue^{-\omega /\epsilon _3}, \nonumber \\ \psi ^{-+}_{3}(\omega , u)= & {} \frac{2}{\epsilon ^3_3}\omega (1-u)e^{-\omega /\epsilon _3}, \nonumber \\ \psi _4(\omega ,u)= & {} \frac{5}{\mathcal {N}}\int ^{s^{\Lambda _b}_0}_{\omega /2}ds\ e^{-s/\tau }(s-\omega /2)^3, \end{aligned}$$

  (55)

  with $C^{3/2}_2$ is Gegenbauer polynomial, and $\epsilon _0=200^{+130}_{-60}$ Mev, $\epsilon _1=650^{+650}_{-300}$ Mev, $a_2=0.333^{+0.250}_{-0.333}$ and $\epsilon _3=230\pm 60$ MeV.

• Gegenbauer-2 model [46]

  $$\begin{aligned} \psi _{2}(\omega , u)= & {} \omega ^2 u(1-u)\sum ^2_{n=0}\frac{a_n}{\epsilon ^{4}_{n}}\frac{C^{3/2}_{n}(2u-1)}{|C^{3/2}_n|^2}e^{-\omega /\epsilon _n}, \nonumber \\ \psi ^{\sigma ,s}_{3}(\omega , u)= & {} \frac{\omega }{2} \sum ^{2}_{n=0}\frac{a_n}{\epsilon ^3_n}\frac{C^{1/2}_n (2u-1)}{|C^{1/2}_n|^2}e^{-\omega /\epsilon _n},\nonumber \\ \psi _{4}(\omega , u)= & {} \sum ^2_{n=0}\frac{a_n}{\epsilon ^2_n}\frac{C^{1/2}_n (2u-1)}{|C^{1/2}_n|^2}e^{-\omega /\epsilon _n}, \end{aligned}$$

  (56)

  with $|C^{1/2}_{0}|^2=|C^{3/2}_{0}|^2=1,\ |C^{1/2}_1|^2=1/3,\ |C^{3/2}_1|^2=3,\ |C^{1/2}_2|^2=1/5$ and $|C^{3/2}_2|^2=6$. The parameters in the above are collected in Table 7 and $A=0.5\pm 0.1$. The twist-3 LCDAs $\psi ^{+-}_3, \psi ^{-+}_3$ are given by the combination of $\psi ^{\sigma ,s}_3$

  $$\begin{aligned} \psi ^{+-}_3(\omega , u)= & {} 2\psi ^{s}_3(\omega , u)+2\psi ^{\sigma }_3(\omega , u),\nonumber \\ \psi ^{-+}_3(\omega , u)= & {} 2\psi ^{s}_3(\omega , u)-2\psi ^{\sigma }_3(\omega , u), \end{aligned}$$

  (57)

• Exponential model [47]

  $$\begin{aligned} \psi _2(\omega ,u)= & {} \frac{\omega ^2 u(1-u)}{\omega ^4_0}e^{-\omega /\omega _0}, \nonumber \\ \psi ^{+-}_3(\omega , u)= & {} \frac{2\omega u}{\omega ^3_0}e^{-\omega /\omega _0},\nonumber \\ \psi ^{-+}_3(\omega , u)= & {} \frac{2\omega (1-u)}{\omega ^3_0}e^{-\omega /\omega _0},\nonumber \\ \psi _4(\omega , u)= & {} \frac{1}{\omega ^2_0}e^{-\omega /\omega _0}, \end{aligned}$$

  (58)

  where $\omega _0=0.4\pm 0.1$ GeV measures the average of the two light quarks inside the $\Lambda _b$ baryon.

• Free parton model [47]

  $$\begin{aligned} \psi _2(\omega , u)= & {} \frac{15\omega ^2 u(1-u)(2{\bar{\Lambda }}-\omega )}{4{\bar{\Lambda }}^5}\theta (2{\bar{\Lambda }}-\omega ), \nonumber \\ \psi ^{+-}_3(\omega , u)= & {} \frac{15\omega u (2{\bar{\Lambda }}-\omega )^2}{4{\bar{\Lambda }}^5}\theta (2{\bar{\Lambda }}-\omega ), \nonumber \\ \psi ^{-+}_3(\omega , u)= & {} \frac{15\omega (1-u) (2{\bar{\Lambda }}-\omega )^2}{4{\bar{\Lambda }}^5}\theta (2{\bar{\Lambda }}-\omega ), \nonumber \\ \psi _4(\omega , u)= & {} \frac{5(2{\bar{\Lambda }}-\omega )^3}{8{\bar{\Lambda }}^5}\theta (2{\bar{\Lambda }}-\omega ), \end{aligned}$$

  (59)

  where $\theta (2{\bar{\Lambda }}-\omega )$ is the step-function, and ${\bar{\Lambda }}=m_{\Lambda _b}-m_b\approx 0.8\pm 0.2$ GeV.

The LCDAs of the NLO term off the light-cone are given by:

$$\begin{aligned} \psi ^{+-}_{\perp , 1}(\omega , u)= & {} \psi ^{-+}_{\perp , 2}=\psi ^{(1)}_{\perp , 3}=\psi ^{(2)}_{\perp , 3}=\frac{\omega ^2 u(1-u)}{\omega _0^3} e^{-\omega /\omega _0},\nonumber \\ \psi ^{-+}_{\perp , 1}(\omega , u)= & {} \frac{\omega u}{\omega _0^2} e^{-\omega /\omega _0}, \nonumber \\ \psi ^{+-}_{\perp , 2}(\omega , u)= & {} \frac{\omega (1-u)}{\omega _0^2} e^{-\omega /\omega _0}, \nonumber \\ \psi ^{(1)}_{\perp , Y}(\omega , u)= & {} \frac{\omega u(\omega _0-\omega (1-u))}{2\omega _0^3}e^{-\omega /\omega _0},\nonumber \\ \psi ^{(2)}_{\perp , Y}(\omega , u)= & {} \frac{\omega (1-u)(\omega _0-\omega u)}{2\omega _0^3}e^{-\omega /\omega _0}. \end{aligned}$$

(60)

where $\omega _0=0.4\pm 0.1$ GeV.