Analytic solutions of scalar field cosmology, mathematical structures for early inflation and late time accelerated expansion

Abstract

We study the most general cosmological model with real scalar field which is minimally coupled to gravity. Our calculations are based on Friedmann–Lemaitre–Robertson–Walker (FLRW) background metric. Field equations consist of three differential equations. We switch independent variable from time to scale factor by change of variable ${\dot{a}}/a=H(a)$. Thus a new set of differential equations are analytically solvable with known methods. We formulate Hubble function, the scalar field, potential and energy density when one of them is given in the most general form. a(t) can be explicitly found as long as methods of integration techniques are available. We investigate the dynamics of the universe at early times as well as at late times in light of these formulas. We find mathematical machinery which turns on and turns off early accelerated expansion. On the other hand late time accelerated expansion is explained by cosmic domain walls. We have compared our results with recent observations of type Ia supernovae by considering the Hubble tension and absolute magnitude tension. Eighty-nine percent of present universe may consist of domain walls while rest is matter.

1 Introduction

The scalar field plays an important role in many parts of modern physics. Its usage in cosmology was seen firstly in Nordstrom’s studies after Newton’s gravity which has a scalar potential field. Although he introduced scalar theory of gravity [1,2,3,4] in 1912–1913, none of them have been verified by observation [5]. Then in 1916 Einstein’s theory of general gravity was established. This is a purely tensor theory. Seeds of some alternative theories which in cooperates a scalar field were conceived by Jordan [6] and Dirac [7].

The standard model of cosmology has the flatness problem, the horizon problem and the monopole problem. To solve these problems many inflationary models were proposed in the begining of 1980s. Curvature-driven inflation scenario which was introduced by Starobinsky is the first model of inflation in the early universe [8]. Then Guth and Linde established inflationary cosmology in which it has been shown that one or more scalar fields drive the early phase of accelerated expansion [9, 10]. Among these studies predictions of the celebrated Starobinsky model of inflation are in good agreement with Planck measurements of the Cosmic Microwave Background (CMB) radiation [11].

In 1998–2000 a wide variety of different astrophysical observations have shown that the expansion of the universe is accelerating [12,13,14]. According to standard cosmology this behaviour is explained by contribution of dark energy ($\sim 68\%$), dark matter ($\sim 27\%$) and baryonic matter ($\sim 5\%$) to the total density parameter. A Simple explanation of dark energy just as a cosmological constant in standard model of cosmology is problematic [15]. Hence to explain dark energy many different studies have been developed by using scalar fields similar to early inflationary theories. A detailed disccussion on both observational and theoretical aspects of a small cosmological $\Lambda$-term was presented in [16]. On the other hand in [17], particularly scalar field models such as quintessence, K-essence, tachyon, phantom and dilatonic models widely explained. The second main part of the universe consists of dark matter. This still keeps its secrets. It has not been explained properly yet. A scalar field is again a candidate to reveal its nature [18].

Domain walls differentiate among various candidates for dark energy. They supply the required accelerated expansion with negative pressure $p=-(2/3)\rho$. Altough cosmic fluids with a negative equation of state have an imaginary sound speed there have been several studies indicating that cosmic walls are not ruled out in cosmology [19,20,21,22,23,24]. To include them in cosmology is very appealing because they appear in a field theory which has spontaneously broken discrete symmetries [25].

The field equations which govern the universe are ordinary differential equations. To be able to solve them many different approcahes have been developed. One of them is the dynamical systems methods in which stabiliy analysis of systems of nonlinear differential equations are investigated. Detailed studies have been performed by this method in [26,27,28,29]. Other methods are based on assumptions or approximations. In the more general context of a bouncing cosmological model where the scalar field has a “slow climb” before the bounce and slow roll after it, the slow-roll approximation was first suggested by Starobinsky in 1978 [30]. In proceeding years the “slow-roll approximation” has become the most common one which is applied in scenarios of the inflationary universe [31, 32]. Lastly, the generating function method is proposed as a method which gives exact solution of the field equations in [33]. Some of the searches for exact solutions of the field equations where the scalar field is minimally cooupled to gravity have been presented in [34,35,36,37].

In this article we have three main purposes. The first is solving field equations analytically. The second is finding a mathematical machinery which causes to turn on and to turn off accelerated expansion in early universe. Last is explaining late time accelerated expansion without dark energy. In Sect. 2 we introduce a mathematical tool which is a change of variable. Thus the field equations are converted to a new set of differential equations. In Sect. 3 we exactly solve this new set of equations and present solutions in four different forms. In Sect. 4 we investigate single-component universes. In Sect. 5 we examine two-component universes and we find a new exotic matter which causes mathematical mechanisms which turns on and turns off accelerated expansion in an early universe. In Sect. 6 we show that a universe which contains matter and cosmic walls results in accelerated expansion. Furthermore we have compared our results with type Ia supernovae data. Results are quite satisfactory. Then we examined dark energy dominated universe with the same procedure. Our discussion is given in the conclusion.

2 Field equations

2.1 Original form

Action of general relativity with scalar field and the cosmological constant is given by

$$\begin{aligned} S=\int \sqrt{-g}\left[ \dfrac{1}{2\kappa }(R-2\Lambda )-\frac{1}{2}g^{\mu \nu }\partial _{\mu } \phi \partial _{\nu }\phi -V(\phi )+ {\mathcal {L}}_{M}\right] \end{aligned}$$

(1)

where R is the Ricci scalar and $\kappa =8\pi Gc^{-4}$. We will use FLWR metric with space dominant metric sign $(-,+,+,+)$ and units with $\hbar =1$, $c=1$

$$\begin{aligned} ds^{2}=-dt^{2}+a^{2}(t)\left[ \frac{dr^{2}}{1-k\dfrac{r^{2}}{L^{2}}}+r^{2}(d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2})\right] . \end{aligned}$$

(2)

where $k=-1,0,1$ and $a(t)=\dfrac{R(t)}{R(t_{0})}$ is normalized scale factor, with the convention $a(t_{0})=1$, $L=R(t_{0})$ and r has dimension of lenght.

Energy-momentum tensor for the field is defined as

$$\begin{aligned} T_{\mu \nu }=\dfrac{-2}{\sqrt{-g}}\dfrac{\delta S_{\phi }}{\delta g^{\mu \nu }} \end{aligned}$$

(3)

where $T^{\mu \nu }=\{\rho , p,p,p\}$.

In standard cosmology field equations have been found as

$$\begin{aligned} \dfrac{{\dot{a}}^{2}}{a^{2}}&=\dfrac{8\pi G}{3}\rho +\dfrac{\Lambda }{3}-\dfrac{k}{L^{2}a^{2}} , \end{aligned}$$

(4)

$$\begin{aligned} \dfrac{\ddot{a}}{a}&=-\dfrac{4\pi G}{3}(\rho +3p)+\dfrac{\Lambda }{3} \end{aligned}$$

(5)

where $\rho =\rho _{ord}+\rho _{\phi }$ and $p =p _{ord}+p _{\phi }$ are known as Einstein equations. ord stands for ordinary and represents matter-energy distribution placed in Einstein equations by hand as a function the scale size of the universe.

In addition, variation of the Lagrangian density with respect to the field $\phi$ gives another equation

$$\begin{aligned} \ddot{\phi }+3H{\dot{\phi }}+\dfrac{dV}{d\phi }=0. \end{aligned}$$

(6)

For scalar field dominated universe we have

$$\begin{aligned} \rho&=\dfrac{{\dot{\phi }}^{2}}{2}+V(\phi ) , \end{aligned}$$

(7)

$$\begin{aligned} p&=\dfrac{{\dot{\phi }}^{2}}{2}-V(\phi ) \end{aligned}$$

(8)

where we assume that $\phi$ is a function only of t. Then Eq. (6) is equivalent to continuity equation which is given by

$$\begin{aligned} {\dot{\rho }}+3\dfrac{{\dot{a}}}{a}(\rho +p)=0. \end{aligned}$$

(9)

We name our potential as an effective potential in the sense that it may reflect another more basic physical theory. We will call Eq. (4) as the first Einstein equation, Eq. (5) as the second Einstein equation and the Eq. (6) as the $\phi$ equation.

2.2 New form of field equations

If independent variable does not appear explicitly in the differential equation one can define a new variable in terms of dependent variables so that the order of the differential equation can be reduced by one [38]. In our field equations independent variable is “t”. We define our new dependent variable as Hubble function

$$\begin{aligned} H(a)=\dfrac{{\dot{a}}}{a} . \end{aligned}$$

(10)

Thus our new independent variable becomes the scale factor a. For this reason we write all other variables in terms of the new variable.

$$\begin{aligned} \phi =\phi (a) \quad \text {and} \quad V(\phi )=V(a) . \end{aligned}$$

(11)

Expressions for derivatives of a and $\phi$ with respect to time in terms of derivatives with respect to new independent variable a are given in appendix A. In addition $\Lambda$ can be included in $V(\phi )$ so we will not carry it anymore.

One can easily write the field equations, energy density of the scalar field and the pressure of the scalar field as

$$\begin{aligned}{} & {} H^{^2}=\dfrac{8\pi G}{3}\rho -\dfrac{k}{L^{2}a^{2}}, \end{aligned}$$

(12)

$$\begin{aligned}{} & {} H^{'}Ha+H^{2}=-\dfrac{4\pi G}{3}(\rho +3p), \end{aligned}$$

(13)

$$\begin{aligned}{} & {} \phi ^{''}a^{2}H^{2}+4\phi ^{'}aH^{2}+\phi ^{'}a^{2}HH^{'}+V^{'}\dfrac{1}{\phi ^{'}}=0 \end{aligned}$$

(14)

$$\begin{aligned}{} & {} \rho (a)=\dfrac{1}{2}(\phi ^{'}aH)^{2}+V(a), \end{aligned}$$

(15)

$$\begin{aligned}{} & {} p(a)=\dfrac{1}{2}(\phi ^{'}aH)^{2}-V(a) \end{aligned}$$

(16)

where prime denotes $\dfrac{d}{da}$.

When this set of differential equations is solved exactly we will obtain all unknown functions; H(a), $\phi (a)$, V(a), $\rho (a)$, p(a) and the deceleration parameter q(a) as a function of scale factor, a. Thus it will be possible to track the dynamical history of the universe backward and forward in time. Indeed in some cases it will be possible to formulate some of these functions as a function of time.

3 Solution for field equations

When solving this differential equation set one should be careful. By taking time derivative of first Einstein equation and using the continuity equation we reach the second Einstein equation. Thus by taking time derivative of first Einstein equation and using the second Einstein equation we reach the continuity equation. In addition by substitution $\rho (t)$ and p(t) in the continuity equation one can reach $\phi$ equation. One of the field equations can be derivable from other two of them. One can combine these 3 equations in 3 different pairs such that when their solutions are plugged in the remaining differential equation it will be satisfied automatically.

First combination is the easiest one. We take the first Einstein equation and the $\phi$ equation. Then we multiply the $\phi$ equation by $\phi ^{'}$ and obtain

$$\begin{aligned} a^{2}\phi ^{'}\phi ^{''}H^{2}+4a\phi ^{'2}H^{2}+a^{2}\phi ^{'2}HH^{'}+V^{'}(a)=0 . \end{aligned}$$

(17)

We define

$$\begin{aligned} \gamma (a)=\frac{\phi ^{'2}H^{2}a^{2}}{2} \end{aligned}$$

(18)

to be able to solve the last differential equation. Therefore this equation is converted to

$$\begin{aligned} \gamma ^{'}+\dfrac{6}{a}\gamma =-V^{'} . \end{aligned}$$

(19)

This is a first order linear differential equation and it’s solution can be found easily as

$$\begin{aligned} \gamma (a)=\dfrac{1}{a^{6}}\left[ \int _{a_{in}}^{a} (-{\tilde{a}}^{6}V^{'}({\tilde{a}}))d{\tilde{a}}+a^{6}_{in}\gamma (a_{in})\right] . \end{aligned}$$

(20)

Hence by rewriting Eq. (18) we obtain

$$\begin{aligned}{} & {} \dfrac{\phi ^{'2}H^{2}a^{2}}{2}=\gamma (a),\nonumber \\{} & {} \phi ^{'2}H^{2}a^{2}=\dfrac{2}{a^{6}}\left[ \int _{a_{in}}^{a} (-{\tilde{a}}^{6}V^{'}({\tilde{a}}))d{\tilde{a}}+a^{6}_{in}\gamma (a_{in})\right] . \end{aligned}$$

(21)

It is apparent that to be able to solve this field equation one needs the knowledge of one of the following functions; V(a), H(a), $\phi (a)$. There is one more function which can be used as a starting point of calculations. This is the energy density. The relation between $\rho (a)$ and Eq. (21) will be studied in Sect. 3.4.

We have gone further by plugging energy density into the first Einstein equation

$$\begin{aligned} H^{2}&=\frac{8\pi G}{3}\left[ \dfrac{1}{2}\phi ^{'2}H^{2}a^{2}+V(a)\right] -\dfrac{k}{L^{2}a^{2}} , \end{aligned}$$

(22)

$$\begin{aligned} H^{2}&=\dfrac{\dfrac{8\pi G}{3}V(a)-\dfrac{k}{L^{2}a^{2}}}{1-\dfrac{4\pi G}{3}\phi ^{'2}a^{2}} . \end{aligned}$$

(23)

We will refer the last equation as our Friedmann equation.

3.1 Solution for given V(a)

In this section we start our calculations by using our Friedmann equation. Substituting (23) in (21) we obtain

$$\begin{aligned} \phi ^{'2}\left[ \dfrac{\dfrac{8\pi G}{3}V(a)-\dfrac{k}{L^{2}a^{2}}}{1-\dfrac{4\pi G}{3}\phi ^{'2}a^{2}}\right] a^{2}=2\gamma (a) . \end{aligned}$$

(24)

Then one can reach the following results

$$\begin{aligned} \phi ^{'2}= & {} \dfrac{2\gamma (a)}{a^{2}\left[ \dfrac{8\pi G}{3}(V(a)+\gamma (a))-\dfrac{k}{L^{2}a^{2}}\right] }, \end{aligned}$$

(25)

$$\begin{aligned} \phi (a)= & {} \pm \int _{a_{in}}^{a} \sqrt{\dfrac{2\gamma ({\tilde{a}})}{{\tilde{a}}^{2}\Bigg [\dfrac{8\pi G}{3}(V({\tilde{a}})+\gamma ({\tilde{a}}))-\dfrac{k}{L^{2}{\tilde{a}}^{2}}}\Bigg ]}d{\tilde{a}}\nonumber \\{} & {} +\phi _{a_{in}}. \end{aligned}$$

(26)

One should decide to pick one of the ± sign in front of the right side of $\phi (a)$ such that the value of the scalar field increase or decrease as the universe expands. H(a) has been found by using the formula of the scalar field in our Friedmann equation.

$$\begin{aligned} H(a)=\sqrt{\dfrac{8\pi G}{3}(V(a)+\gamma (a))-\dfrac{k}{L^{2}a^{2}}} \end{aligned}$$

(27)

where

$$\begin{aligned} \gamma (a)=\dfrac{1}{a^{6}}\left[ \int _{a_{in}}^{a} (-{\tilde{a}}^{6}V^{'}({\tilde{a}}))d{\tilde{a}}+a^{6}_{in}\gamma (a_{in})\right] . \end{aligned}$$

(28)

It is apparent that knowledge of the potential energy function V(a) is sufficient to formulate the scalar field $\phi (a)$ and the Hubble function H(a) as an exact solution of the field equations.

We would like to mention that the results of this subsection are similar to results of [39]. They have reduced the differential equations to quadrature problems by writing V(a) in a complicated way. Then exponential potentials and hyperbolic potentials were focused in their examples.

3.2 Solution for given $\phi (a)$

In some cases one may need to solve the field equations for a specific scalar field. In this calculation V(a) becomes the unknown dependent variable in (24). To be able to go further first we write the solution of the $\phi$ equation as

$$\begin{aligned} \gamma (a)&=-V(a)+\dfrac{1}{a^{6}}\left[ 6\int _{a_{in}}^{a} V({\tilde{a}}){\tilde{a}}^{5}d{\tilde{a}}+a^{6}_{in}{\tilde{\gamma }}(a_{in})\right] ,\nonumber \\ {\tilde{\gamma }}_(a_{in})&=\gamma (a_{in})+V(a_{in}) \end{aligned}$$

(29)

where we have applied integration by parts to Eq. (20). Details of this calculation are given in the appendix.

3.2.1 Singular case

Firstly we will investigate the special form of the scalar field which causes this singularity in the denominator of right side of the equation. From (23) we have

$$\begin{aligned} 1-\dfrac{4\pi G}{3}\phi ^{'2}a^{2}=0. \end{aligned}$$

(30)

Therefore

$$\begin{aligned}{} & {} \int _{\phi _{in}}^{\phi }d\phi ^{'}=\pm \sqrt{\dfrac{3}{4\pi G}}\int _{a_{in}}^{a}\dfrac{d{\tilde{a}}}{{\tilde{a}}} \end{aligned}$$

(31)

$$\begin{aligned}{} & {} \phi = {\left\{ \begin{array}{ll} \sqrt{\dfrac{3}{4\pi G}}ln\Bigg (\dfrac{a}{a_{in}}\Bigg )+\phi _{in} , \\ -\sqrt{\dfrac{3}{4\pi G}}ln\Bigg (\dfrac{a}{a_{in}}\Bigg )+\phi _{in}. \end{array}\right. } \end{aligned}$$

(32)

Since $a_{in}\le a$, “$+$” sign indicates that the scalar field always increases. On the other hand minus sign implies that one will have positive and decreasing scalar field when $\phi _{in}$ big enough.

One easily obtains the potential by plugging the field into (22)

$$\begin{aligned} V(a)=\dfrac{3}{8\pi G}\left( \dfrac{k}{L^{2}a^{2}}\right) \end{aligned}$$

(33)

Then the Hubble function is formulated just by substitution of $\phi (a)$ and V(a) into the solution of the $\phi$ equation which is given by the (21)

$$\begin{aligned} H^{2}(a)= & {} \dfrac{2}{a^{6}}\left\{ \int _{a_{in}}^{a}\dfrac{k}{L^{2}}{\tilde{a}}^{3}d{\tilde{a}}+\dfrac{4\pi G}{3}a^{6}_{in}\gamma (a_{in})\right\} , \end{aligned}$$

(34)

$$\begin{aligned} H(a)= & {} \sqrt{\dfrac{k}{2L^{2}a^{2}}+\dfrac{8\pi G}{3}\dfrac{a^{6}_{in}{\tilde{\gamma }} (a_{in})}{a^{6}}}, \nonumber \\ \gamma (a_{in})= & {} \dfrac{3k}{16\pi GL^{2}a^{2}_{in}}+{\tilde{\gamma }} (a_{in}) \end{aligned}$$

(35)

At first sight one can say that the spatially flat universe is static by choosing ${\tilde{\gamma }}(a_{in})=0$. However this statement is incorrect because it is incomplete. Firstly we would like to remind that our choice at the change of variable $\dfrac{{\dot{a}}}{a}=H(a)$ works only for the dynamic universes where $H(a)\ne 0$. Secondly by using the first Einstein equation one can easily deduce that the static and spatially flat universe must be empty. Therefore complete and correct interpretation says that the spatially flat and dynamic universes have time varying energy density.

Considering the solution for $k=0$, it is seen from the Eq. (33), $V=0$ for spatially flat universe. Thus we jump back to Eq. (19) and it turns to

$$\begin{aligned}{} & {} \gamma ^{'}+\dfrac{6}{a}\gamma =0 \end{aligned}$$

(36)

$$\begin{aligned}{} & {} \int _{\gamma _{in}}^{\gamma }\dfrac{d{\tilde{\gamma }}}{{\tilde{\gamma }}}=-6\int _{a_{in}}^{a}\dfrac{d{\tilde{a}}}{{\tilde{a}}} \nonumber \\{} & {} ln\gamma -ln\gamma _{in}=-6(lna-lna_{in}) \nonumber \\{} & {} \gamma (a)=\dfrac{{\tilde{\gamma }}(a_{in})}{a^{6}} \quad \text {and} \quad {\tilde{\gamma }}(a_{in})=\gamma (a_{in})a^{6}_{in}. \end{aligned}$$

(37)

Hence by plugging $\gamma$ and $\phi$ in (18) we have obtained the Hubble function as

$$\begin{aligned} H=\sqrt{\dfrac{8\pi G}{3}\dfrac{{\tilde{\gamma }}(a_{in})}{a^{6}}} \end{aligned}$$

(38)

3.2.2 Nonsingular case

In this case we investigate general form of the scalar field where $\phi (a)\ne \sqrt{\dfrac{3}{4\pi G}}ln(a)$. We have started this case by using (29) in (25)

$$\begin{aligned} \phi ^{'2}=\dfrac{2\left\{ -V(a)+\dfrac{1}{a^{6}}[6\int _{a_{in}}^{a} V({\tilde{a}}){\tilde{a}}^{5}d{\tilde{a}}+a^{6}_{in}{\tilde{\gamma }}(a_{in})]\right\} }{a^{2}\left\{ \dfrac{8\pi G}{3a^{6}}[6\int _{a_{in}}^{a} V({\tilde{a}}){\tilde{a}}^{5}d{\tilde{a}}+a^{6}_{in}{\tilde{\gamma }}(a_{in})]-\dfrac{k}{L^{2}a^{2}}\right\} }. \end{aligned}$$

(39)

To be able to calculate the potential V(a), one should define a new function

$$\begin{aligned} \alpha (a)=6\int _{a_{in}}^{a} V({\tilde{a}}){\tilde{a}}^{5}d{\tilde{a}}+a^{6}_{in}{\tilde{\gamma }}(a_{in}) V(a)=\dfrac{\alpha ^{'}}{6a^{5}}, \end{aligned}$$

(40)

where $\alpha (a_{in})=a^{6}_{in}{\tilde{\gamma }}_{in}$. Then (39) turns into a first order linear differential equation which is obtained as

$$\begin{aligned} \alpha ^{'}+\left( 8\pi Ga\phi ^{'2}-\frac{6}{a}\right) \alpha =\left( \dfrac{3ka^{5}}{L^{2}}\right) \phi ^{'2} . \end{aligned}$$

(41)

The solution is found as

$$\begin{aligned} \alpha (a)&=exp\left[ \int _{a_{in}}^{a}\left( \dfrac{6}{{\tilde{a}}}-8\pi G{\tilde{a}}\phi ^{'2}\right) d{\tilde{a}}\right] \left\{ \alpha (a_{in})\right. \nonumber \\&\quad +\int _{a_{in}}^{a}exp\left[ \int _{a_{in}}^{{\tilde{a}}}\left( -\dfrac{6}{\tilde{{\tilde{a}}}}+8\pi G\tilde{{\tilde{a}}}\phi ^{'2}\right) d\tilde{{\tilde{a}}}\right] \nonumber \\&\quad \left. \times \left( \dfrac{3k{\tilde{a}}^{5}\phi ^{'2}}{L^{2}}\right) d{\tilde{a}}\right\} . \end{aligned}$$

(42)

Then according to relation (40) the potential V(a) is found as

$$\begin{aligned} V(a)= & {} \dfrac{\alpha ^{'}}{6a^{5}}, \nonumber \\ V(a)= & {} \left( 1-\dfrac{4\pi G}{3}a^{2}\phi ^{'2}\right) e^{\lambda (a)}\beta (a)+\dfrac{k\phi ^{'2}}{2L^{2}}, \end{aligned}$$

(43)

$$\begin{aligned} \lambda (a)= & {} -\int _{a_{in}}^{a}8\pi G{\tilde{a}}\phi ^{'2}d{\tilde{a}}, \end{aligned}$$

(44)

$$\begin{aligned} \beta (a)= & {} \alpha (a_{in})+\int _{a_{in}}^{a}e^{-\lambda ({\tilde{a}})}\dfrac{3ka^{6}_{in}\phi ^{'2}}{L^{2}{\tilde{a}}}d{\tilde{a}}\Bigg ]. \end{aligned}$$

(45)

H(a) has been found by substituting this potential and the specific scalar field into our Friedmann equation

$$\begin{aligned} H^{2}= & {} \dfrac{\dfrac{8\pi G}{3}V(a)-\dfrac{k}{L^{2}a^{2}}}{1-\dfrac{4\pi G}{3}\phi ^{'2}a^{2}}, \nonumber \\ H(a)= & {} \sqrt{\dfrac{8\pi G}{3a_{in}^{6}}e^{\lambda (a)}\beta (a)-\dfrac{k}{L^{2}a^{2}}} \end{aligned}$$

(46)

where $\lambda (a)$ and $\beta (a)$ are given by (44) and (45). Hence for a specific scalar field exact solution of the field equations are given by the last two equations

Both these two cases have a common physical result. If there is only scalar field without any kinds of matter except the dark energy this universe has dynamic behaviour as a result of it being curved by the scalar field.

For $k=0$ the solution changes. Equation (41) is solved as

$$\begin{aligned}{} & {} \alpha ^{'}=\left( \dfrac{6}{a}-8\pi Ga\phi ^{'2}\right) \alpha \end{aligned}$$

(47)

$$\begin{aligned}{} & {} \int _{\alpha _{in}}^{\alpha }\dfrac{d{\tilde{\alpha }}}{{\tilde{\alpha }}} =\int _{a_{in}}^{a}\left( \dfrac{6}{{\tilde{a}}}-8\pi G{\tilde{a}}\phi ^{'2}({\tilde{a}})\right) d{\tilde{a}} \nonumber \\{} & {} \quad ln\alpha -ln\alpha _{in}=(lna^{6}-lna^{6}_{in}) -\int _{a_{in}}^{a}8\pi G{\tilde{a}}\phi ^{'2}({\tilde{a}})d{\tilde{a}} \nonumber \\{} & {} \quad \dfrac{\alpha }{\alpha _{in}}=\dfrac{a^{6}}{a^{6}_{in}} exp\left[ -\int _{a_{in}}^{a}8\pi G{\tilde{a}}\phi ^{'2}({\tilde{a}})d{\tilde{a}}\right] \nonumber \\{} & {} \quad \alpha =\dfrac{\alpha _{in}a^{6}}{a^{6}_{in}} exp\left[ -\int _{a_{in}}^{a}8\pi G{\tilde{a}}\phi ^{'2}({\tilde{a}})d{\tilde{a}}\right] . \end{aligned}$$

(48)

Then we formulate the potential by using Eq. (40)

$$\begin{aligned} V(a)= & {} \dfrac{\alpha ^{'}}{6a^{5}} \nonumber \\ V(a)= & {} \dfrac{\alpha _{in}}{a^{6}_{in}}\left[ 1-\dfrac{4\pi G}{3}a^{2}\phi ^{'2}(a)\right] e^{\lambda (a)} \end{aligned}$$

(49)

where $\lambda (a)$ is given by Eq. (44). The Hubble function is found just by substuting the potential and the scalar field into our Friedmann equation

$$\begin{aligned} H(a)=\sqrt{\dfrac{8\pi G}{3}\dfrac{\alpha _{in}}{a_{in}^{6}}e^{\lambda (a)}}, \end{aligned}$$

(50)

where $\lambda (a)$ is given in (44).

3.3 Solution for given H(a)

In this section we will start our calculations by rewriting our Friedmann equation in the following form

$$\begin{aligned} H^{2}=\frac{8\pi G}{3}\left( \dfrac{1}{2}\phi ^{'2}H^{2}a^{2}+V(a)\right) -\dfrac{k}{L^{2}a^{2}} . \end{aligned}$$

This equation is easily converted to

$$\begin{aligned} \dfrac{\phi ^{'2}a^{2}H^{2}}{2}=\frac{3}{8\pi G}\Bigg (H^{2}+\dfrac{k}{L^{2}a^{2}}\Bigg )-V(a). \end{aligned}$$

(51)

Therefore one can recognize the first term on the left side of Eq. (51) as $\gamma (a)$ which is the variable found as a solution of the $\phi$ equation at the beginning of the Sect. 3. Hence (51) turns into the following form

$$\begin{aligned} \gamma (a)=\frac{3}{8\pi G}\Bigg (H^{2}+\dfrac{k}{L^{2}a^{2}}\Bigg )-V(a) . \end{aligned}$$

(52)

By using the last form of $\gamma (a)$ which is formulated in (29)

$$\begin{aligned} \gamma (a)=-V(a)+\dfrac{1}{a^{6}}\Bigg [6\int _{a_{in}}^{a} V({\tilde{a}}){\tilde{a}}^{5}d{\tilde{a}}+a^{6}_{in}{\tilde{\gamma }}(a_{in})\Bigg ]. \end{aligned}$$

So we have obtained

$$\begin{aligned}&-V(a)+\dfrac{1}{a^{6}}\Bigg [6\int _{a_{in}}^{a} V({\tilde{a}}){\tilde{a}}^{5}d{\tilde{a}}+a^{6}_{in}{\tilde{\gamma }}(a_{in})\Bigg ]\nonumber \\&\quad =\Bigg [\frac{3}{8\pi G}\Bigg (H^{2}+\dfrac{k}{L^{2}a^{2}}\Bigg )-V(a)\Bigg ] . \end{aligned}$$

(53)

As we have done in the previous section we now find the potential energy. The last equation can be easily solved so that $\alpha (a)$

$$\begin{aligned} \alpha (a)=6\int _{a_{in}}^{a} V({\tilde{a}}){\tilde{a}}^{5}d{\tilde{a}}+a^{6}_{in}{\tilde{\gamma }}(a_{in}) \; \text {so} \; V(a)=\dfrac{\alpha ^{'}}{6a^{5}} . \end{aligned}$$

Therefore $\alpha (a)$ is found algebraically from Eq. (53) as

$$\begin{aligned} \alpha (a)=\dfrac{3a^{6}}{8\pi G}\Bigg (H^{2}+\dfrac{k}{L^{2}a^{2}}\Bigg ) . \end{aligned}$$

(54)

As a result the potential energy is calculated as

$$\begin{aligned} V(a)=\dfrac{3}{8\pi G}\Bigg [\Bigg (H^{2}+\dfrac{k}{L^{2}a^{2}}\Bigg )+\dfrac{a}{3}\Bigg (HH^{'}-\dfrac{k}{L^{2}a^{3}}\Bigg )\Bigg ]. \end{aligned}$$

(55)

The scalar field is found by substituting the potential into Eq. (51) as

$$\begin{aligned} \phi (a)=\pm \int _{a_{in}}^{a} \sqrt{\dfrac{1}{4\pi G{\tilde{a}}H^{2}}\Bigg (-HH^{'}+\dfrac{k}{L^{2}{\tilde{a}}^{3}}\Bigg )} d{\tilde{a}}+\phi (a_{in}) . \end{aligned}$$

(56)

Therefore last equations can be used to construct the scalar field and the potential for a given Hubble function.

3.4 Solution for given $\rho (a)$

When one starts the calculations with one of the following functions V(a), $\phi (a)$, H(a) one can end up with some unusual forms of the energy density. To avoid this possibility one should start the calculations for desired energy density. It is written in terms of our new independent variable “a” as

$$\begin{aligned} \rho (a)=\dfrac{1}{2}(\phi ^{'}aH)^{2}+V(a) . \end{aligned}$$

One can recognize the first term on the right side of this equation as $\gamma (a)$. Hence we obtain

$$\begin{aligned} V(a)=\rho (a)-\gamma (a) \quad \text {and} \quad \gamma (a)=\dfrac{(\phi ^{'}aH)^{2}}{2} . \end{aligned}$$

(57)

Then we substitute this into the $\phi$ equation

$$\begin{aligned} \gamma ^{'}+\dfrac{6}{a}\gamma =-V^{'} \end{aligned}$$

and we obtain

$$\begin{aligned} \gamma (a)=- \dfrac{a}{6}\rho {'}. \end{aligned}$$

(58)

By using the definition of $\gamma (a)$ we also obtain

$$\begin{aligned} \phi ^{'2}=\dfrac{2\gamma (a)}{a^{2}H^{2}}. \end{aligned}$$

(59)

The Hubble function is known just by inserting the energy density into the original form of the first Einstein equation

$$\begin{aligned} H(a)=\sqrt{\dfrac{8\pi G}{3}\rho -\dfrac{k}{L^{2}a^{2}}} . \end{aligned}$$

(60)

Therefore the scalar field is formulated as

$$\begin{aligned} \phi (a)=\pm \int _{a_{in}}^{a} \sqrt{\dfrac{- \dfrac{{\tilde{a}}}{3}\rho {'}}{{\tilde{a}}^{2}\Bigg [\dfrac{8\pi G}{3}\rho -\dfrac{k}{L^{2}{\tilde{a}}^{2}}\Bigg ]}}d{\tilde{a}}+\phi (a_{in}) . \end{aligned}$$

(61)

The potential energy is written by substitution of (58) into (57) as

$$\begin{aligned} V(a)=\rho (a)+\dfrac{a}{6}\rho {'} . \end{aligned}$$

(62)

Exact solution of the field equations for a desired energy density are given by the formulas in (60–62).

4 Single component universes

We present some general solutions for a universe which has a single component. This purpose is easily achieved for a given $\rho (a)$ in Sect. (4.1) and for a given V(a) in Sect. (4.2). In addition we have performed calculations for both a curved universe and a spatially flat universe. Therefore one can see the effect of curvature term in dynamics of the universe.

4.1 General solution for $\rho (a)=\dfrac{\rho _{n}}{a^{n}}$

To satisfy the weak energy condition $\rho \ge 0$ and $\rho +p\ge 0$ one should start calculations with a given energy density.

4.1.1 $k\ne 0$

We begin this subsection by taking the energy density as in the form of perfect fluid

$$\begin{aligned} \rho =\dfrac{\rho _{n}}{a^{n}}. \end{aligned}$$

(63)

Then by applying the procedure which is explained in Sect. (3.4) we immediately obtain H(a), V(a), $\phi (a)$, p(a), q(a) as

$$\begin{aligned} H(a)= & {} \sqrt{\dfrac{8\pi G\rho _{n}}{3a^{n}}-\dfrac{k}{L^{2}a^{2}}}, \end{aligned}$$

(64)

$$\begin{aligned} V(a)= & {} \dfrac{(6-n)}{6}\dfrac{\rho _{n}}{a^{n}}, \end{aligned}$$

(65)

$$\begin{aligned} \phi (a)= & {} \pm \int _{a_{in}}^{a}\sqrt{\dfrac{\dfrac{n\rho _{n}}{3{\tilde{a}}^{n}}}{\dfrac{8\pi G\rho _{n}}{3{\tilde{a}}^{n-2}}-\dfrac{k}{L^{2}}}}d{\tilde{a}}+\phi (a_{in}), \end{aligned}$$

(66)

$$\begin{aligned} p(a)= & {} \Bigg (\dfrac{n-3}{3}\Bigg )\dfrac{\rho _{n}}{a^{n}}, \end{aligned}$$

(67)

$$\begin{aligned} q(a)= & {} \dfrac{4(n-2)\pi G\rho _{n}}{8\pi G\rho _{n}-\dfrac{3ka^{n -2}}{L^{2}}}. \end{aligned}$$

(68)

For $k=1$, the relation between the scalar field and the scale factor is found as,

$$\begin{aligned}{} & {} \mu (\phi -{\tilde{\phi }}_{in})= \pm ArcCosh(u), \end{aligned}$$

(69)

$$\begin{aligned}{} & {} \mu =(2-n)\sqrt{\dfrac{2\pi G}{n}}, u=\sqrt{\dfrac{8\pi G\rho _{n}L^{2}}{3}}a^{(2-n)/2}, \end{aligned}$$

(70)

$$\begin{aligned}{} & {} {\tilde{\phi }}_{in}= \mp ArcCosh(u_{in})+\phi (a_{in}). \end{aligned}$$

(71)

One can write potential as

$$\begin{aligned} V(\phi )= & {} \Bigg (\dfrac{6-n}{6}\Bigg )\rho _{n}\big \{\nu Cosh[\pm \mu (\phi -{\tilde{\phi }}_{in})]\big \}^{\dfrac{2n}{n-2}}, \nonumber \\ \nu= & {} \sqrt{\dfrac{3}{8\pi G\rho _{n}L^{2}}}. \end{aligned}$$

(72)

For $k=-1$ we obtain

$$\begin{aligned}{} & {} \mu (\phi -{\tilde{\phi }}_{in})=ArcSinh(u), \end{aligned}$$

(73)

$$\begin{aligned}{} & {} {\tilde{\phi }}_{in}=\mp \dfrac{1}{\mu }ArcSinh(u_{in})+\phi (a_{in}). \end{aligned}$$

(74)

where $\mu$ and u are given in (70). Therefore potential is written as

$$\begin{aligned} V(\phi )=\Bigg (\dfrac{6-n}{6}\Bigg )\rho _{n}\big \{\nu Sinh[\pm \mu (\phi -{\tilde{\phi }}_{in})]\big \}^{\dfrac{2n}{n-2}}, \end{aligned}$$

(75)

where $\nu$ is given by (72).

The relation between time and the scale factor is found as

$$\begin{aligned}{} & {} \int _{0}^{t}d{\tilde{t}}=\int _{a_{in}}^{a}\dfrac{d{\tilde{a}}}{{\tilde{a}}H({\tilde{a}})}, \end{aligned}$$

(76)

$$\begin{aligned}{} & {} t=\sqrt{\dfrac{3}{2\pi G\rho _{n}}}\Bigg \{\dfrac{{\tilde{a}}^{n/2}}{n}{}_{2}F_{1}\Bigg [\dfrac{1}{2},\dfrac{n}{2(n-2)};\dfrac{n}{2(n-2)}\nonumber \\{} & {} \quad \nonumber \\{} & {} \quad +1;\dfrac{3k{\tilde{a}}^{n-2}}{8\pi G\rho _{n}L^{2}}\Bigg ]\Bigg \}_{a_{in}}^{a}, \end{aligned}$$

(77)

where ${}_{2}F_{1}$ is the hypergeometric function

$$\begin{aligned} {}_{2}F_{1}(1/2,b;b+1;u)=\sum _{m=0}^{\infty }\dfrac{(1/2)_{m}(b)_{m}}{(b+1)_{m}}\dfrac{u^{m}}{m!}, \end{aligned}$$

(78)

where $(b)_{m}$ is the Pochhammer symbol which is defined as

$$\begin{aligned} (b)_{m}= {\left\{ \begin{array}{ll} 1 \quad \text {if} \; m=0, \\ b(b+1)(b+2)...(b+m-1),\quad \text {if} \; m>0. \end{array}\right. } \end{aligned}$$

(79)

Then, we interpret these formulas generally. When we apply the boundaries on equation of state $\nu =\dfrac{p}{\rho }$ we obtain

$$\begin{aligned} -1\le \nu \le 1, -1\le \dfrac{n-3}{3}\le 1,0\le n \le 6 \end{aligned}$$

(80)

Therefore all exotic fluids with energy density in the form of $\dfrac{\rho _{n}}{a^{n}}$ have $0\le n \le 6$. This condition also makes the potential non-negative. Then special cases pops up immediately for $n=0,2,6$.

Case $n=0$ corresponds to constant energy density $\rho =\rho _{0}$. One presents related functions for more comments,

$$\begin{aligned} H(a)= & {} \sqrt{\dfrac{8\pi G\rho _{0}}{3}-\dfrac{k}{L^{2}a^{2}}}, \end{aligned}$$

(81)

$$\begin{aligned} V(a)= & {} \rho _{0}, \end{aligned}$$

(82)

$$\begin{aligned} \phi (a)= & {} 0, \end{aligned}$$

(83)

$$\begin{aligned} p(a)= & {} -\rho _{0}, \end{aligned}$$

(84)

$$\begin{aligned} q(a)= & {} -1+\dfrac{3k}{3k-8\pi G\rho _{0}L^{2}a^{2}}. \end{aligned}$$

(85)

Furthermore a(t) can be formulated by the following steps

$$\begin{aligned} \int _{0}^{t}d{\tilde{t}}= & {} \int _{a_{in}}^{a}\dfrac{d{\tilde{a}}}{{\tilde{a}}H({\tilde{a}})}, \end{aligned}$$

(86)

$$\begin{aligned} a(t)= & {} \Bigg (\dfrac{a_{in}}{2}+\dfrac{\sqrt{\mu ^{2}a_{in}^{2}-k/L^{2}}}{2\mu }\Bigg )e^{\mu t}\nonumber \\{} & {} +\Bigg (\dfrac{a_{in}}{2}-\dfrac{\sqrt{\mu ^{2}a_{in}^{2}-k/L^{2}}}{2\mu }\Bigg )e^{-\mu t}, \nonumber \\{} & {} \quad \mu =\sqrt{\dfrac{8\pi G\rho _{0}}{3}}. \end{aligned}$$

(87)

Since the scalar field is zero in this case, our solutions reduce to solutions of standard cosmology with dark energy. According to results given in (81) and (87), to have a dynamic universe with real Hubble function and real scale factor cosmological constant must be big enough to overcome the smallness of the universe;

$$\begin{aligned} \dfrac{8\pi G\rho _{0}}{3} > \dfrac{k}{L^{2}a_{in}^{2}}. \end{aligned}$$

(88)

This is the mathematical reason which explains the big value of the cosmological constant in the early universe according to the standard model.

Case $n=2$ creates a singularity in (75) and in (77). Thus we have calculated $\phi (a)$ separately and we have found it as

$$\begin{aligned} \phi (a)=\pm \sqrt{\dfrac{2\rho _{2}}{8\pi G\rho _{2}-\dfrac{3k}{L^{2}}}}ln\Bigg (\dfrac{a}{a_{in}}\Bigg )+\phi (a_{in}). \end{aligned}$$

(89)

Then one can immediately write the potential as

$$\begin{aligned} V(\phi )&=\dfrac{2}{3}\rho _{2}a^{-2}_{in}exp[\mp 2\mu (\phi -\phi (a_{in}))], \nonumber \\ \mu&=\sqrt{\dfrac{8\pi G\rho _{2}-3k/L^{2}}{2\rho _{2}}}. \end{aligned}$$

(90)

Furthermore a(t) is

$$\begin{aligned} a(t)=\tau t+a_{in},\tau =\sqrt{\dfrac{8\pi G\rho _{2}}{3}-\dfrac{k}{L^{2}}} \end{aligned}$$

(91)

which is consistent with (68) which tells us that for $n=2$, the universe expands with constant speed.

Case $n=6$ requires special attention. Potential becomes $V=0$ and equation of state becomes $\nu =\dfrac{p}{\rho }=1$. This case corresponds to a massless scalar field.

4.1.2 $k=0$

When we study the spatially flat universe, nature of the scalar field changes. As a result of this change we can formulate the potential as a function of the scalar field.

$$\begin{aligned} \phi (a)=\pm \sqrt{\dfrac{n}{8\pi G}}ln\Bigg (\dfrac{a}{a_{in}}\Bigg )+\phi (a_{in}). \end{aligned}$$

(92)

Therefore one can formulate the scale factor and hence the potential as a function of the scalar field as

$$\begin{aligned} a= & {} a_{in}exp\Bigg [\pm \sqrt{\frac{8\pi G}{n}}(\phi -\phi (a_{in}))\Bigg ], \end{aligned}$$

(93)

$$\begin{aligned} V(\phi )= & {} \Bigg (\dfrac{6-n}{6}\Bigg )\dfrac{\rho _{n}}{a_{in}^{n}}exp\Bigg [\mp \sqrt{8\pi nG}(\phi -\phi (a_{in}))\Bigg ]. \end{aligned}$$

(94)

Furthermore we can find a(t) by

$$\begin{aligned} \int _{0}^{t}d{\tilde{t}}= & {} \int _{a_{in}}^{a}\dfrac{d{\tilde{a}}}{{\tilde{a}}H({\tilde{a}})},\nonumber \\ a(t)= & {} \Bigg (n\sqrt{\dfrac{2\pi G\rho _{n}}{3}}t+a_{in}^{n/2}\Bigg )^{2/n} \end{aligned}$$

(95)

where there is a singularity in the case $n=0$. This case corresponds to the standard model with cosmological constant. Hence

$$\begin{aligned} \int _{0}^{t}d{\tilde{t}}= & {} \int _{a_{in}}^{a}\dfrac{d{\tilde{a}}}{{\tilde{a}}H({\tilde{a}})},\nonumber \\ a(t)= & {} a_{in}e^{\mu t}, \mu =\sqrt{\dfrac{8\pi G\rho _{0}}{3}}. \end{aligned}$$

(96)

As it is seen there is no constraint on this constant energy density. It can be big as well as it can be small.

4.2 General solution for $V(a)=\dfrac{V_{n}}{a^{n}}$

To start calculations with given V(a) is more fundamental. After getting intuition about the form of the potential which is required for the perfect fluid, we continue our work by choosing the potential. Results are important because they are surprisingly different than Sect. (4.1).

4.2.1 $k\ne 0$

We have plugged in $V(a)=\dfrac{V_{n}}{a^{n}}$ in the formulas given by (26–28) and we have obtained

$$\begin{aligned} \gamma (a)= & {} \dfrac{1}{a^{6}}\Bigg [\dfrac{nV_{n}}{6-n}a^{6-n}+a^{6}_{in}{\tilde{\gamma }}(a_{in})\Bigg ], \nonumber \\ {\tilde{\gamma }}(a_{in})= & {} -\dfrac{nV_{n}}{6-n}a_{in}^{-n}+\gamma (a_{in}), \end{aligned}$$

(97)

$$\begin{aligned} H(a)= & {} \sqrt{\dfrac{16\pi GV_{n}}{(6-n)a^{n}}+\dfrac{8\pi Ga^{6}_{in}{\tilde{\gamma }} (a_{in})}{3a^{6}}-\dfrac{k}{L^{2}a^{2}}}, \end{aligned}$$

(98)

$$\begin{aligned} \phi (a)= & {} \pm \sqrt{6}\int _{a_{in}}^{a}\nonumber \\{} & {} \sqrt{\dfrac{nV_{n}{\tilde{a}}^{6}+(6-n)a^{6}_{in}{\tilde{\gamma }} (a_{in}){\tilde{a}}^{n}}{48\pi GV_{n}{\tilde{a}}^{8}+(n-6)(3k{\tilde{a}}^{4}/L^{2}-8\pi Ga^{6}_{in}{\tilde{\gamma }} (a_{in})){\tilde{a}}^{n+2}}}\nonumber \\{} & {} d{\tilde{a}}+\phi (a_{in}), \end{aligned}$$

(99)

$$\begin{aligned} \rho (a)= & {} \dfrac{6V_{n}}{(6-n)a^{n}}+\dfrac{a^{6}_{in}{\tilde{\gamma }} (a_{in})}{a^{6}}, \end{aligned}$$

(100)

$$\begin{aligned} p(a)= & {} \dfrac{2(n-3)V_{n}}{(6-n)a^{n}}+\dfrac{a^{6}_{in}{\tilde{\gamma }} (a_{in})}{a^{6}}, \end{aligned}$$

(101)

$$\begin{aligned} q(a)= & {} \dfrac{8\pi G[2(6-n)a^{6}_{in}{\tilde{\gamma }} (a_{in})a^{n}+3(n-2)V_{n}a^{6}]}{48\pi GV_{n}a^{6}+(n-6)(3ka^{4}/L^{2}-8\pi Ga^{6}_{in}{\tilde{\gamma }} (a_{in}))a^{n}}.\nonumber \\ \end{aligned}$$

(102)

For all n there is the term proportional to $a^{-6}$ in energy density. Therefore not only for zero potential but also for each potential, universe contains the stiff fluid.

Integration techniques are not adequate to evaluate the expression which is given in (99) explicitly. However the condition $a^{6}_{in}{\tilde{\gamma }} (a_{in})=0$ simplifies the expression. Then (99) becomes the same as (66) where $\rho _{n}$ is replaced with $\dfrac{6V_{n}}{6-n}$. Hence after applying this modification, the relation between the scalar field and the scale factor is given by (69–71) for $k=1$ and this relation is given by (73–74) for $k=-1$. The formula for $V(\phi )$ is given by (72) for $k=1$ and it is given by (75) for $k=-1$.

After replacement of $\rho _{n}$ with $\dfrac{6V_{n}}{6-n}$, the relation between the scale factor and time can be obtained by using the related formulas given in Sect. 4.1.1.

The case $n=6$ is the only exception where the simplification explained above does not work because formulas for Hubble function and $\phi (a)$ contains logarithmic terms. This case will be studied at the end of this subsection.

For case $n=0$ one should perform the calculations by starting from Eq. (19),

$$\begin{aligned}{} & {} \int _{\gamma (a_{in})}^{\gamma }\dfrac{d{\tilde{\gamma }}}{{\tilde{\gamma }}}=-\int _{a_{in}}^{a}\dfrac{6}{{\tilde{a}}}d{\tilde{a}}, \end{aligned}$$

(103)

$$\begin{aligned}{} & {} \gamma (a)=\dfrac{\gamma (a_{in})a_{in}^{6}}{a^{6}}, \end{aligned}$$

(104)

$$\begin{aligned}{} & {} H(a)=\sqrt{\dfrac{8\pi G}{3}\Bigg (\dfrac{\gamma (a_{in})a_{in}^{6}}{a^{6}}+V_{0}\Bigg )-\dfrac{k}{L^{2}a^{2}}}, \end{aligned}$$

(105)

$$\begin{aligned}{} & {} \phi (a)=\pm \sqrt{6}\int _{a_{in}}^{a}\sqrt{\dfrac{\gamma (a_{in})a_{in}^{6}}{8\pi G(\gamma (a_{in})a_{in}^{6}+V_{0}{\tilde{a}}^{6}){\tilde{a}}^{2}-3k{\tilde{a}}^{6}/L^{2}}}d{\tilde{a}}\nonumber \\{} & {} \quad +\phi (a_{in}), \end{aligned}$$

(106)

$$\begin{aligned}{} & {} \rho (a)=\dfrac{\gamma (a_{in})a_{in}^{6}}{a^{6}}+V_{0}, \end{aligned}$$

(107)

$$\begin{aligned}{} & {} p(a)=\dfrac{\gamma (a_{in})a_{in}^{6}}{a^{6}}-V_{0}, \end{aligned}$$

(108)

$$\begin{aligned}{} & {} q(a)=\dfrac{8\pi G[2\gamma (a_{in})a_{in}^{6}-V_{0}a^{6}]}{8\pi G[\gamma (a_{in})a_{in}^{6}+V_{0}a^{6}]-3ka^{4}/L^{2}}. \end{aligned}$$

(109)

In contrast to constant energy density case, constant potential differs from cosmological constant case.

As it is seen from formulas there is a singularity for $n=6$. Thus we have investigated this case separately:

$$\begin{aligned} \gamma (a)= & {} \dfrac{1}{a^{6}}\Bigg [6V_{6}ln\Bigg (\dfrac{a}{a_{in}}\Bigg )+a^{6}_{in}\gamma (a_{in})\Bigg ], \end{aligned}$$

(110)

$$\begin{aligned} H(a)= & {} \sqrt{\dfrac{8\pi G}{3}\Bigg [\dfrac{V_{6}+a^{6}_{in}\gamma (a_{in})}{a^{6}}+\dfrac{6V_{6}ln\Bigg (\dfrac{a}{a_{in}}\Bigg )}{a^{6}}\Bigg ]-\dfrac{k}{L^{2}a^{2}}},\nonumber \\ \end{aligned}$$

(111)

$$\begin{aligned}{} & {} \phi (a)= \pm \sqrt{6}\int _{a_{in}}^{a}\sqrt{\dfrac{a^{6}_{in}\gamma (a_{in})+6V_{6}ln\Bigg (\dfrac{{\tilde{a}}}{a_{in}}\Bigg )}{\Bigg [48\pi GV_{6}ln\Bigg (\dfrac{{\tilde{a}}}{a_{in}}\Bigg )+8\pi G(V_{6}+a^{6}_{in}\gamma (a_{in}))-3k{\tilde{a}}^{4}/L^{2}\Bigg ]{\tilde{a}}^{2}}}d{\tilde{a}}+\phi (a_{in}), \end{aligned}$$

(112)

$$\begin{aligned} \rho (a)= & {} \dfrac{a^{6}_{in}\gamma (a_{in})+V_{6}}{a^{6}}+\dfrac{6V_{6}ln\Bigg (\dfrac{a}{a_{in}}\Bigg )}{a^{6}}, \end{aligned}$$

(113)

$$\begin{aligned} p(a)= & {} \dfrac{a^{6}_{in}\gamma (a_{in})-V_{6}}{a^{6}}+\dfrac{6V_{6}ln\Bigg (\dfrac{a}{a_{in}}\Bigg )}{a^{6}}, \end{aligned}$$

(114)

$$\begin{aligned} q(a)= & {} \dfrac{8\pi G\Bigg [2a^{6}_{in}\gamma (a_{in})-V_{6}+12V_{6}ln\Bigg (\dfrac{a}{a_{in}}\Bigg )\Bigg ]}{48\pi GV_{6}ln\Bigg (\dfrac{a}{a_{in}}\Bigg )+8\pi G(a^{6}_{in}\gamma (a_{in})+V_{6})-3ka^{4}/L^{2}}.\nonumber \\ \end{aligned}$$

(115)

Energy density and pressure should be written in the following form

$$\begin{aligned} \rho (a)= & {} \rho _{1}(a)+\rho _{2}(a), \end{aligned}$$

(116)

$$\begin{aligned} \rho _{1}(a)= & {} \dfrac{a^{6}_{in}\gamma (a_{in})}{a^{6}} \rho _{2}(a)=\dfrac{V_{6}}{a^{6}}ln\Bigg [e\Bigg (\dfrac{a}{a_{in}}\Bigg )^{6}\Bigg ], \end{aligned}$$

(117)

$$\begin{aligned} p(a)= & {} p_{1}(a)+p_{2}(a), \end{aligned}$$

(118)

$$\begin{aligned} p_{1}(a)= & {} \dfrac{a^{6}_{in}\gamma (a_{in})}{a^{6}} p_{2}(a)=\dfrac{V_{6}}{a^{6}}ln\Bigg [\dfrac{1}{e}\Bigg (\dfrac{a}{a_{in}}\Bigg )^{6}\Bigg ]. \end{aligned}$$

(119)

Thus each component satisfies the continuity equation which is given by (9) according to perfect fluid theorem.

Furthermore investigation of equation of state for the second part of the fluid is important. First we write the pressure in the following form:

$$\begin{aligned} p_{2}(a)= & {} \dfrac{V_{6}}{a^{6}}ln\Bigg [\dfrac{1}{e}\Bigg (\dfrac{a_{in}}{a}\Bigg )^{6}\Bigg (\dfrac{a}{a_{in}}\Bigg )^{12}\Bigg ], \end{aligned}$$

(120)

$$\begin{aligned} p_{2}(a)= & {} \dfrac{V_{6}}{a^{6}}\Bigg \{ln\Bigg [\dfrac{1}{e}\Bigg (\dfrac{a_{in}}{a}\Bigg )^{6}\Bigg ]+ln\Bigg (\dfrac{a}{a_{in}}\Bigg )^{12}\Bigg \}. \end{aligned}$$

(121)

Then equation of state turns into

$$\begin{aligned} \nu _{2}&=\dfrac{p_{2}}{\rho _{2}}, \end{aligned}$$

(122)

$$\begin{aligned} \nu _{2}&=\dfrac{ln\Bigg [\dfrac{1}{e}\Bigg (\dfrac{a_{in}}{a}\Bigg )^{6}\Bigg ]+ln\Bigg (\dfrac{a}{a_{in}}\Bigg )^{12}}{ln\Bigg [e\Bigg (\dfrac{a}{a_{in}}\Bigg )^{6}\Bigg ]}, \end{aligned}$$

(123)

$$\begin{aligned} \nu _{2}&=-1+\dfrac{12ln\Bigg (\dfrac{a}{a_{in}}\Bigg )}{1+6ln\Bigg (\dfrac{a}{a_{in}}\Bigg )}. \end{aligned}$$

(124)

In addition

$$\begin{aligned} \lim _{a\rightarrow a_{in}} \nu _{2}=-1, \lim _{a\rightarrow \infty } \nu _{2}=1. \end{aligned}$$

(125)

This phenomenon says that at the beginning of the universe there was a negative pressure. This pressure was huge because it is proportional to $\dfrac{1}{a^{6}}$. As the universe expands this pressure and the related energy density becomes negligible since both of them proportional to $\dfrac{1}{a^{6}}$.

4.2.2 k=0

First simplification occurs in the relation between cosmological time and the scale factor of the universe as

$$\begin{aligned} t= & {} \int _{a_{in}}^{a}\dfrac{d{\tilde{a}}}{{\tilde{a}}H({\tilde{a}})}, \nonumber \\ t= & {} \int _{a_{in}}^{a}\dfrac{d{\tilde{a}}}{{\tilde{a}}\sqrt{\dfrac{8\pi G}{3}\Bigg (\dfrac{a_{in}^{6}{\tilde{\gamma }}(a_{in})}{{\tilde{a}}^{6}}+\dfrac{6v_{n}}{(6-n){\tilde{a}}^{n}}\Bigg )}}, \end{aligned}$$

(126)

$$\begin{aligned} t= & {} \sqrt{\dfrac{1}{24\pi Ga_{in}^{6}{\tilde{\gamma }}(a_{in})}}\Bigg [{\tilde{a}}^{3}{}_{2}F_{1}\Bigg (\dfrac{1}{2},\dfrac{3}{6-n};\dfrac{3}{6-n}\nonumber \\{} & {} +1;-\dfrac{6v_{n}}{(6-n)a_{in}^{6}{\tilde{\gamma }}(a_{in})}{\tilde{a}}^{(6-n)}\Bigg )\Bigg ]_{a_{in}}^{a}. \end{aligned}$$

(127)

where ${}_{2}F_{1}$ is the hypergeometric function which is introduced in (78). Our condition, $n<6$ for positivity of energy avoids the singularity of the hypergeometric function given in (127).

To carry out the calculation of the scalar field, we rewrite (99) in the following form with $k=0$

$$\begin{aligned}&\phi (a)=\pm \sqrt{\dfrac{3}{4\pi G}}\int _{a_{in}}^{a}\sqrt{\dfrac{\dfrac{nV_{n}{\tilde{a}}^{6}}{{\tilde{a}}^{n}}+(6-n)f}{\dfrac{6V_{n}{\tilde{a}}^{6}}{{\tilde{a}}^{n}}+(6-n)f}}\dfrac{d{\tilde{a}}}{{\tilde{a}}}+\phi (a_{in}),\nonumber \\&\quad f=a_{in}^{6}{\tilde{\gamma }}(a_{in}). \end{aligned}$$

(128)

For the cases $n=1,2,3,4,5$ we apply following change of variable

$$\begin{aligned} V=\dfrac{V_{n}}{a^{n}}\Rightarrow a=\Bigg (\dfrac{V_{n}}{V}\Bigg )^{1/n}, \dfrac{da}{a}=-\dfrac{dV}{nV}. \end{aligned}$$

(129)

Thus we have

$$\begin{aligned}&\phi (V)=\mp \sqrt{\dfrac{3}{4\pi G}}\dfrac{1}{n}\int _{V_{in}}^{V}\sqrt{\dfrac{nb{\tilde{V}}^{1-6/n}+(6-n)f}{6b{\tilde{V}}^{1-6/n}+(6-n)f}}\dfrac{d{\tilde{V}}}{{\tilde{V}}}\nonumber \\&\quad +\phi _{in}, b=V_{n}^{6/n}. \end{aligned}$$

(130)

For $n=1$;

$$\begin{aligned} \phi (V)= & {} \mp \dfrac{1}{10\sqrt{2\pi G}n}ln \nonumber \\{} & {} \Bigg [\dfrac{(\sqrt{b+5fV^{5}}+\sqrt{6b+5fV^{5}})^{2\sqrt{6}}}{(\sqrt{6(b+5fV^{5})}+\sqrt{6b+5fV^{5}})^{2}}V^{5}\Bigg ]+{\tilde{\phi }}_{in}, \end{aligned}$$

(131)

$$\begin{aligned} {\tilde{\phi }}_{in}= & {} \pm \dfrac{1}{10\sqrt{2\pi G}n}ln\nonumber \\{} & {} \Bigg [\dfrac{(\sqrt{b+5fV_{in}^{5}}+\sqrt{6b+5fV_{in}^{5}})^{2\sqrt{6}}}{(\sqrt{6(b+5fV_{in}^{5})}+\sqrt{6b+5fV_{in}^{5}})^{2}}V_{in}^{5}\Bigg ]+\phi _{in}.\nonumber \\ \end{aligned}$$

(132)

For $n=2$;

$$\begin{aligned} \phi (V)= & {} \mp \dfrac{1}{4\sqrt{\pi G}n}ln\nonumber \\{} & {} \Bigg [\dfrac{(\sqrt{b+2fV^{2}}+\sqrt{3b+2fV^{2}})^{2\sqrt{3}}}{(\sqrt{3(b+2fV^{2})}+\sqrt{3b+2fV^{2}})^{2}2^{\sqrt{3}-1}}V^{2}\Bigg ]\nonumber \\{} & {} +{\tilde{\phi }}_{in}, \end{aligned}$$

(133)

$$\begin{aligned} {\tilde{\phi }}_{in}= & {} \pm \dfrac{1}{4\sqrt{\pi G}n}ln \nonumber \\{} & {} \Bigg [\dfrac{(\sqrt{b+2fV_{in}^{2}}+\sqrt{3b+2fV_{in}^{2}})^{2\sqrt{3}}}{(\sqrt{3(b+2fV_{in}^{2})}+\sqrt{3b+2fV_{in}^{2}})^{2}2^{\sqrt{3}-1}}V_{in}^{2}\Bigg ]\nonumber \\{} & {} +\phi _{in}. \end{aligned}$$

(134)

For $n=3$;

$$\begin{aligned} \phi (V)= & {} \mp \dfrac{\sqrt{3}}{2\sqrt{2\pi G}n}ln\Bigg [\dfrac{(\sqrt{b+fV}+\sqrt{2b+fV})^{2\sqrt{2}}}{(\sqrt{2(b+fV)}+\sqrt{2b+fV})^{2}}V\Bigg ]\nonumber \\{} & {} +{\tilde{\phi }}_{in}, \end{aligned}$$

(135)

$$\begin{aligned} {\tilde{\phi }}_{in}= & {} \pm \dfrac{\sqrt{3}}{2\sqrt{2\pi G}n}ln\nonumber \\{} & {} \Bigg [\dfrac{(\sqrt{b+fV_{in}}+\sqrt{2b+fV_{in}})^{2\sqrt{2}}}{(\sqrt{2(b+fV_{in})}+\sqrt{2b+fV_{in}})^{2}}V_{in}\Bigg ]+\phi _{in}.\nonumber \\ \end{aligned}$$

(136)

For $n=4$;

$$\begin{aligned} \phi (V)= & {} \mp \dfrac{1}{\sqrt{2\pi G}n}ln\nonumber \\{} & {} \Bigg [\dfrac{(\sqrt{2b+f\sqrt{V}}+\sqrt{3b+f\sqrt{V}})^{2\sqrt{6}}}{(\sqrt{3(2b+f\sqrt{V})}+\sqrt{3b+f\sqrt{V}})^{4}}V\Bigg ]\nonumber \\{} & {} +{\tilde{\phi }}_{in}, \end{aligned}$$

(137)

$$\begin{aligned} {\tilde{\phi }}_{in}= & {} \pm \dfrac{1}{\sqrt{2\pi G}n}ln\nonumber \\{} & {} \Bigg [\dfrac{(\sqrt{2b+f\sqrt{V_{in}}}+\sqrt{3b+f\sqrt{V_{in}}})^{2\sqrt{6}}}{(\sqrt{3(2b+f\sqrt{V_{in}})}+\sqrt{3b+f\sqrt{V_{in}}})^{4}}V_{in}\Bigg ]+\phi _{in}.\nonumber \\ \end{aligned}$$

(138)

For $n=5$;

$$\begin{aligned}{} & {} \phi (V)=\mp \dfrac{\sqrt{5}}{2\sqrt{2\pi G}n}ln \nonumber \\{} & {} \quad \Bigg [\dfrac{(\sqrt{5b+fV^{1/5}}+\sqrt{6b+fV^{1/5}})^{2\sqrt{30}}}{(\sqrt{6(5b+fV^{1/5})}+\sqrt{5(6b+fV^{1/5}})^{10}}V\Bigg ]+{\tilde{\phi }}_{in}, \end{aligned}$$

(139)

$$\begin{aligned}{} & {} {\tilde{\phi }}_{in}=\pm \dfrac{\sqrt{5}}{2\sqrt{2\pi G}n}ln \nonumber \\{} & {} \quad \Bigg [\dfrac{(\sqrt{5b+fV_{in}^{1/5}}+\sqrt{6b+fV_{in}^{1/5}})^{2\sqrt{30}}}{(\sqrt{6(5b+fV_{in}^{1/5})}+\sqrt{5(6b+fV_{in}^{1/5}})^{10}}V_{in}\Bigg ]+\phi _{in}.\nonumber \\ \end{aligned}$$

(140)

The case $n=0$ corresponds to a constant potential and one can obtain explicit form of the scalar field as

$$\begin{aligned} \phi (u)= & {} \mp \dfrac{1}{\sqrt{12\pi G}}ArcSinh\Bigg [\dfrac{u}{\sqrt{V_{0}}}\Bigg ]+{\tilde{\phi }}_{in}, \end{aligned}$$

(141)

$$\begin{aligned} u= & {} \dfrac{\sqrt{f}}{a^{3}}, {\tilde{\phi }}_{in}=\pm \dfrac{1}{\sqrt{12\pi G}}ArcSinh\Bigg [\dfrac{u_{in}}{\sqrt{V_{0}}}\Bigg ]+\phi _{in}.\nonumber \\ \end{aligned}$$

(142)

Formulation of a(t) is also possible

$$\begin{aligned} t= & {} \int _{a_{in}}^{a}\dfrac{d{\tilde{a}}}{{\tilde{a}}\sqrt{\dfrac{8\pi G}{3}\Bigg (V_{0}+\dfrac{\gamma (a_{in})a_{in}^{6}}{{\tilde{a}}^{6}}\Bigg )}}, \end{aligned}$$

(143)

$$\begin{aligned} a(t)= & {} \Bigg [\dfrac{b^{2}V_{0}e^{2\mu t}-\gamma (a_{in})a_{in}^{6}e^{-2\mu t}}{2bV_{0}}\Bigg ]^{1/3}, \nonumber \\ b= & {} a_{in}^{3}+\sqrt{a_{in}^{6}+\dfrac{\gamma (a_{in})a_{in}^{6}}{V_{0}}} \quad \text {and} \quad \mu =\sqrt{6\pi GV_{0}}.\nonumber \\ \end{aligned}$$

(144)

This case will be investigated in more detail in Sect. 5.3.

The case $n=6$ has two simplification for a spatially flat universe. The scalar field has been found as

$$\begin{aligned} \phi (a)= & {} \pm \dfrac{1}{12}\sqrt{\dfrac{3}{\pi G}}\dfrac{1}{V_{6}}I(a)+\phi (a_{in}), \end{aligned}$$

(145)

$$\begin{aligned} I(a)= & {} x(a)\sqrt{1-\dfrac{V_{6}}{x(a)}}+\dfrac{V_{6}}{2}ln\Bigg [-\dfrac{2x(a)}{V_{6}}+1\nonumber \\{} & {} \quad +\dfrac{2x(a)}{V_{6}}\sqrt{1-\dfrac{V_{6}}{x(a)}}\Bigg ], \end{aligned}$$

(146)

$$\begin{aligned} x(a)= & {} a_{in}^{6}\gamma (a_{in})+V_{6}\Bigg [1+6ln\Bigg (\dfrac{a}{a_{in}}\Bigg )\Bigg ]. \end{aligned}$$

(147)

Expression of a(t) is

$$\begin{aligned}{} & {} a(t)=a_{in}exp\Bigg \{\dfrac{1}{6}\Bigg [2\Bigg (erfi^{-1}(\mu t+b)\Bigg )^{2}\nonumber \\{} & {} \quad -1-\dfrac{a_{in}^{6}\gamma (a_{in})}{V_{6}}\Bigg ]\Bigg \}, \end{aligned}$$

(148)

$$\begin{aligned}{} & {} \mu =\sqrt{\dfrac{8\pi G}{3}}\dfrac{1}{a_{in}^{3}}, b=erfi\Bigg [\dfrac{1}{2}\Big (1+\dfrac{a_{in}^{6}\gamma (a_{in})}{V_{6}}\Big )\Bigg ], \end{aligned}$$

(149)

$$\begin{aligned}{} & {} erfi(\theta )=\dfrac{2}{\sqrt{\pi }}\int _{0}^{\theta } exp(z^{2})dz, \end{aligned}$$

(150)

where $erfi(\theta )$ is the imaginary error function. When $\theta$ is real $erfi(\theta )$ is real [40]. Therefore it’s inverse function $erfi^{-1}(\theta )$ becomes real for real $\theta$.

One can go further by choosing initial condition $a_{in}^{6}{\tilde{\gamma }}(a_{in})=0$. Results are very similar to what we have obtained in Sect. 4.1.2. The scale factor is found as

$$\begin{aligned} a(t)=\Bigg (2n\sqrt{\dfrac{\pi Gv_{n}}{(6-n)}}t+a_{in}^{n/2}\Bigg )^{2/n}. \end{aligned}$$

(151)

Positivity condition $n<6$ for energy density makes a(t) real. The scalar field is found as

$$\begin{aligned} \phi (a)=\pm \sqrt{\dfrac{n}{8\pi G}}ln\Bigg (\dfrac{a}{a_{in}}\Bigg )+\phi (a_{in}). \end{aligned}$$

(152)

Then

$$\begin{aligned} a=a_{in}exp(\pm \mu \psi ), \psi =\phi (a)-\phi (a_{in})\; \text {and} \; \mu =2\sqrt{\dfrac{2\pi G}{n}}. \end{aligned}$$

(153)

Therefore

$$\begin{aligned}&V(\psi )=V_{n}a_{in}^{-n}exp(\mp n\mu \psi )\quad \text {or} \nonumber \\&V(\phi )=V_{n}a_{in}^{-n}exp\{\mp n\mu [\phi (a)-\phi (a_{in})]\}. \end{aligned}$$

(154)

5 Early epoch of the universe

There have been many studies which show that the early universe should expand with exponential expansion to be able to reach its size today. Thus our purpose in this section is to explore the mathematical turn on and turn of mechanism to start and to end up exponential expansion. For this reason we have studied three different combinations for curved and spatially flat universes.

5.1 Dark energy

We will search for the universe with energy density in the following form

$$\begin{aligned} \rho (a)=\dfrac{\rho _{n}}{a^{n}}+\rho _{0}. \end{aligned}$$

(155)

5.1.1 $k\ne 0$

Firstly we take nonzero curvature. We have found H(a), V(a), $\phi (a)$, p(a) and q(a) as

$$\begin{aligned} H(a)= & {} \sqrt{\dfrac{8\pi G}{3}\Bigg (\dfrac{\rho _{n}}{a^{n}}+\rho _{0}\Bigg )-\dfrac{k}{L^{2}a^{2}}}, \end{aligned}$$

(156)

$$\begin{aligned} V(a)= & {} \dfrac{(6-n)}{6}\dfrac{\rho _{n}}{a^{n}}+\rho _{0}, \end{aligned}$$

(157)

$$\begin{aligned} \phi (a)= & {} \pm \int _{a_{in}}^{a}\sqrt{\dfrac{n\rho _{n}}{8\pi G(\rho _{n}{\tilde{a}}^{2}+\rho _{0}{\tilde{a}}^{2+n})-3k{\tilde{a}}^{n}/L^{2}}}d{\tilde{a}}\nonumber \\{} & {} +\phi (a_{in}), \end{aligned}$$

(158)

$$\begin{aligned} p(a)= & {} \dfrac{(n-3)}{3}\dfrac{\rho _{n}}{a^{n}}-\rho _{0}, \end{aligned}$$

(159)

$$\begin{aligned} q(a)= & {} \dfrac{4\pi G[-2\rho _{0}a^{n}+(n-2)\rho _{n}]a^{2}}{8\pi G[\rho _{n}a^{2}+\rho _{0}a^{2+n}]-3ka^{n}/L^{2}}. \end{aligned}$$

(160)

An explicit form of the scale factor can be found for $n=1,2,4$ by using the formula

$$\begin{aligned} \int _{0}^{t}d{\tilde{t}}=\int _{a_{in}}^{a}\dfrac{d{\tilde{a}}}{{\tilde{a}}H({\tilde{a}})}. \end{aligned}$$

(161)

A case $n=1$ corresponds a universe which consists of domain walls and dark energy. Thus we have

$$\begin{aligned} a(t)= & {} \dfrac{e^{-\mu (t-b)}[6\pi Gk\rho _{0}/L^{2}+(e^{\mu (t-b)}-2\pi G\rho _{1})^{2}]}{8\pi G\rho _{0}}, \end{aligned}$$

(162)

$$\begin{aligned} \mu= & {} 2\sqrt{\dfrac{2\pi G\rho _{0}}{3}}, b=-\dfrac{1}{\mu }ln\Bigg \{2\pi G(2\rho _{0}a_{in}+\rho _{1})\nonumber \\{} & {} +\sqrt{2\pi G\rho _{0}[-3\dfrac{k}{L^{2}}+8\pi Ga_{in}(\rho _{0}a_{in}+\rho _{1})]}\Big \}. \end{aligned}$$

(163)

A case $n=2$ corresponds a universe which consists of cosmic strings and dark energy. Thus we have

$$\begin{aligned} a(t)= & {} \dfrac{1}{8}e^{-\mu (t-b)}\Bigg [\dfrac{6k}{L^{2}}-16\pi G\rho _{2}+\dfrac{e^{2\mu (t-b)}}{\pi G\rho _{0}}\Bigg ], \end{aligned}$$

(164)

$$\begin{aligned} \mu= & {} 2\sqrt{\dfrac{2\pi G\rho _{0}}{3}}, b=-\dfrac{1}{\mu }ln\Bigg \{4\pi G\rho _{0}a_{in}\nonumber \\{} & {} +\sqrt{2\pi G\rho _{0}[-\dfrac{3k}{L^{2}}+8\pi G(\rho _{0}a^{2}_{in}+\rho _{2})]}\Bigg \}. \end{aligned}$$

(165)

A case $n=4$ corresponds a universe which consists of radiation and dark energy. Thus we have

$$\begin{aligned} a(t)= & {} \dfrac{\sqrt{e^{-\mu (t-b)}[(e^{\mu (t-b)}+3k/L^{2})^{2}-256\pi ^{2}G^{2}\rho _{0}\rho _{4}]}}{4\sqrt{2\pi G\rho _{0}}}, \end{aligned}$$

(166)

$$\begin{aligned} \mu= & {} 4\sqrt{\dfrac{2\pi G\rho _{0}}{3}}, b=-\dfrac{1}{\mu }ln\Bigg \{-\dfrac{3k}{L^{2}}+16\pi G\rho _{0}a_{in}^{2}\nonumber \\{} & {} +4\sqrt{2\pi G\rho _{0}[-3ka_{in}^{2}+8\pi G(\rho _{0}a^{4}_{in}+\rho _{4})]}\Bigg \}. \end{aligned}$$

(167)

An explicit form of the $V(\phi )$ can be found for $n=2,4$ by using (158). For a universe which consists of cosmic strings and dark energy we have

$$\begin{aligned} \mu (\phi -{\tilde{\phi }}_{in})= & {} \pm ln\Bigg \{2\Bigg (-\sqrt{8\pi G\rho _{2}-\dfrac{3k}{L^{2}}}\nonumber \\{} & {} +\sqrt{8\pi G(\rho _{0}a^{2}+\rho _{2})-\dfrac{3k}{L^{2}}}\Bigg )\Bigg \}, \end{aligned}$$

(168)

$$\begin{aligned} \mu= & {} \sqrt{\dfrac{8\pi G\rho _{2}-3k/L^{2}}{2\rho _{2}}},\nonumber \\{} & {} {\tilde{\phi }}_{in}=\mp \dfrac{1}{\mu }ln\Bigg \{2\Bigg (-\sqrt{8\pi G\rho _{2}-\dfrac{3k}{L^{2}}}\nonumber \\{} & {} +\sqrt{8\pi G(\rho _{0}a_{in}^{2}+\rho _{2})-\dfrac{3k}{L^{2}}}\Bigg )\Bigg \}+\phi (a_{in}).\nonumber \\ \end{aligned}$$

(169)

Therefore the relation between potential and the scalar field is written as

$$\begin{aligned} V(\phi )= & {} \dfrac{2}{3}\dfrac{\rho _{2}}{a^{2}(\phi )}+\rho _{0}, \end{aligned}$$

(170)

$$\begin{aligned} a(\phi )= & {} \dfrac{\sqrt{e^{\pm \mu (\phi -{\tilde{\phi }}_{in})}(e^{\pm \mu (\phi -{\tilde{\phi }}_{in})}+4\sqrt{8\pi G\rho _{2}-3k/L^{2}})}}{4\sqrt{2\pi G\rho _{0}}}.\nonumber \\ \end{aligned}$$

(171)

For a universe which consists of radiation and dark energy we have

$$\begin{aligned}{} & {} \mu (\phi -{\tilde{\phi }}_{in}) = \mp ln\Bigg \{\dfrac{-3ka^{2}/L^{2}+16\pi G \rho _{4} +4\sqrt{2\pi G\rho _{4}[-3ka^{2}/L^{2}+8\pi G(\rho _{0}a^{4}+\rho _{4})]}}{a^{2}}\Bigg \}, \end{aligned}$$

(172)

$$\begin{aligned}{} & {} \mu =2\sqrt{2\pi G}, {\tilde{\phi }}_{in}=\pm ln\Bigg \{\dfrac{-3ka^{2}_{in}/L^{2}+16\pi G \rho _{4}+4\sqrt{2\pi G\rho _{4}[-3ka^{2}_{in}/L^{2}+8\pi G(\rho _{0}a^{4}_{in}+\rho _{4})]}}{a^{2}_{in}}\Bigg \}. \end{aligned}$$

(173)

Therefore the relation between potential and the scalar field is written as

$$\begin{aligned} V(\phi )= & {} \dfrac{1}{3}\dfrac{\rho _{4}}{a^{4}(\phi )}+\rho _{0}, \end{aligned}$$

(174)

$$\begin{aligned} a(\phi )= & {} \dfrac{4\sqrt{2\pi G\rho _{4}}e^{\pm \mu (\phi -{\tilde{\phi }}_{in})/2}}{\sqrt{\Bigg (1+\dfrac{3ke^{\pm \mu (\phi -{\tilde{\phi }}_{in})}}{L^{2}}\Bigg )^{2}-256\pi ^{2}G^{2}\rho _{0}\rho _{4}e^{\pm 2\mu (\phi -{\tilde{\phi }}_{in})}}}.\nonumber \\ \end{aligned}$$

(175)

We continue to investigate the dynamics of the early universe for small a as

$$\begin{aligned}{} & {} \lim _{a\rightarrow 0}q(a)=\dfrac{4\pi G[(n-2)\rho _{n}]a^{2}}{8\pi G\rho _{n}a^{2}-3ka^{n}/L^{2}}, \end{aligned}$$

(176)

$$\begin{aligned}{} & {} \lim _{a\rightarrow 0}q(a)= {\left\{ \begin{array}{ll} -1+\dfrac{n}{2} \quad \text {if} \; 2< n\le 6,\\ 0 \text {if} \; 0\le n\le 2. \end{array}\right. } \end{aligned}$$

(177)

One should check the roots of q(a). Since the denominator of the $q(a)\sim H^{2}(a)$ and $H^{2}(a)>0$ we are only interested in numerator of q(a).

$$\begin{aligned} q(a)=0 \Rightarrow a=\Bigg [\dfrac{(n-2)\rho _{n}}{2\rho _{0}}\Bigg ]^{1/n} \end{aligned}$$

(178)

where there is no real and positive root for $n\le 2$. Hence for $2<n\le 6$ the universe starts to expand with deceleration and then expansion turns to acceleration. For $0<n\le 2$ the universe starts with constant Hubble function and it immediately accelerates. In both cases although there are mathematical turn on mechanism to initiate acceleration there is no mathematical turn off mechanism to end acceleration in the this model.

5.1.2 $k=0$

For $k=0$, behaviour of the deceleration parameter changes as follows

$$\begin{aligned} \lim _{a\rightarrow 0}q(a)=-1+\dfrac{n}{2} \quad \text {if} \; 0\le n\le 6. \end{aligned}$$

(179)

Root of q(a) is still given by (178). The difference between spatially flat and curved universe occurs just at the beginning of the universe for $n<2$. The universe starts to expand with acceleration.

The scalar field can be simplified as

$$\begin{aligned} \phi (a)=\mp \dfrac{1}{\sqrt{2\pi Gn}}ln\Bigg [\dfrac{a^{-n/2}+\sqrt{a^{-n}+\dfrac{\rho _{0}}{\rho _{n}}}}{a_{in}^{-n/2}+\sqrt{a_{in}^{-n}+\dfrac{\rho _{0}}{\rho _{n}}}}\Bigg ]+\phi (a_{in}).\nonumber \\ \end{aligned}$$

(180)

Then one can derive $V(\phi )$ as follows

$$\begin{aligned}{} & {} \dfrac{a^{-n/2}+\sqrt{a^{-n}+\dfrac{\rho _{0}}{\rho _{n}}}}{a_{in}^{-n/2}+\sqrt{a_{in}^{-n}+\dfrac{\rho _{0}}{\rho _{n}}}}=exp(-\sqrt{n}\psi ),\nonumber \\{} & {} \quad \psi =\pm \sqrt{2\pi G}[\phi (a)-\phi (a_{in})]. \end{aligned}$$

(181)

Thus for some specific values of n one obtains

$$\begin{aligned} V(\psi )= & {} {\left\{ \begin{array}{ll} \rho _{0} \quad \text {if} \; n=6,\\ \dfrac{1}{3}\dfrac{\rho _{4}}{a^{4}(\psi )}+\rho _{0}\quad \text {if} \; n=4,\\ \dfrac{1}{2}\dfrac{\rho _{3}}{a^{3}(\psi )}+\rho _{0}\quad \text {if} \; n=3, \end{array}\right. } \end{aligned}$$

(182)

$$\begin{aligned} a(\psi )= & {} {\left\{ \begin{array}{ll} \sqrt{2}\Bigg \{\dfrac{-a_{in}^{2}e^{2\psi }\Bigg [1-\sqrt{1+a_{in}^{4}\dfrac{\rho _{0}}{\rho _{4}}}+\Bigg (1+\sqrt{1+a_{in}^{4}\dfrac{\rho _{0}}{\rho _{4}}}\Bigg )e^{4\psi }\Bigg ]}{a_{in}^{4}\dfrac{\rho _{0}}{\rho _{4}}(1+e^{8\psi })-2\Bigg (2+a_{in}^{4}\dfrac{\rho _{0}}{\rho _{4}}\Bigg )e^{4\psi }}\Bigg \}^{1/2}\quad \text {if} \; n=4,\\ 2^{2/3}\Bigg \{\dfrac{a_{in}^{3/2}e^{\sqrt{3}\psi }\Bigg [-1+\sqrt{1+a_{in}^{3}\dfrac{\rho _{0}}{\rho _{3}}}-\Bigg (1+\sqrt{1+a_{in}^{3}\dfrac{\rho _{0}}{\rho _{3}}}\Bigg )e^{2\sqrt{3}\psi }\Bigg ]}{a_{in}^{3}\dfrac{\rho _{0}}{\rho _{3}}(1+e^{4\sqrt{3}\psi })-2\Bigg (2+a_{in}^{3}\dfrac{\rho _{0}}{\rho _{3}}\Bigg )e^{2\sqrt{3}\psi }}\Bigg \}^{2/3}\quad \text {if} \; n=3. \end{array}\right. } \end{aligned}$$

(183)

]

Formulation of a(t) is possible for $k=0$ as

$$\begin{aligned} t= & {} \int _{a_{in}}^{a}\dfrac{d{\tilde{a}}}{{\tilde{a}}H({\tilde{a}})}, \end{aligned}$$

(184)

$$\begin{aligned} t= & {} \sqrt{\dfrac{3}{8\pi G\rho _{0}}}\dfrac{2}{n}ln\Bigg [\dfrac{a^{n/2}+\sqrt{a^{n}+\dfrac{\rho _{n}}{\rho _{0}}}}{a^{n/2}_{in}+\sqrt{a^{n}_{in}+\dfrac{\rho _{n}}{\rho _{0}}}}\Bigg ]. \end{aligned}$$

(185)

For some specific n

$$\begin{aligned} a(t)= & {} \Bigg [\dfrac{\Bigg (a_{in}^{3}+\sqrt{a_{in}^{6}+\dfrac{\rho _{n}}{\rho _{0}}}\Bigg )e^{3\mu t}+\Bigg (a_{in}^{3}-\sqrt{a_{in}^{6}+\dfrac{\rho _{n}}{\rho _{0}}}\Bigg )e^{-3\mu t}}{2}\Bigg ]^{1/3}, \nonumber \\{} & {} \quad \text {if} \; n=6, \end{aligned}$$

(186)

$$\begin{aligned} a(t)= & {} \Bigg [\dfrac{\Bigg (a_{in}^{2}+\sqrt{a_{in}^{4}+\dfrac{\rho _{n}}{\rho _{0}}}\Bigg )e^{2\mu t}+\Bigg (a_{in}^{2}-\sqrt{a_{in}^{4}+\dfrac{\rho _{n}}{\rho _{0}}}\Bigg )e^{-2\mu t}}{2}\Bigg ]^{1/2}, \nonumber \\{} & {} \quad \text {if} \; n=4, \end{aligned}$$

(187)

$$\begin{aligned} a(t)= & {} \Bigg [\dfrac{\Bigg (a_{in}^{3/2}+\sqrt{a_{in}^{3}+\dfrac{\rho _{n}}{\rho _{0}}}\Bigg )e^{3\mu t/2}+\Bigg (a_{in}^{3/2}-\sqrt{a_{in}^{3}+\dfrac{\rho _{n}}{\rho _{0}}}\Bigg )e^{-3\mu t/2}}{2}\Bigg ]^{2/3},\nonumber \\{} & {} \quad \text {if} \; n=3, \end{aligned}$$

(188)

where $\mu =\sqrt{\dfrac{8\pi G\rho _{0}}{3}}$. If one chooses $a_{in}=0$, for $t\ll 1$ a(t) can be approximately written as

$$\begin{aligned} a(t)=\Bigg \{ \begin{array}{ll} 3^{1/3}\Bigg (\dfrac{\rho _{6}}{\rho _{0}}\Bigg )^{1/6}(\mu t)^{1/3} &{} \text {if} \;n=6,\\ 2^{1/2}\Bigg (\dfrac{\rho _{4}}{\rho _{0}}\Bigg )^{1/4}(\mu t)^{1/2} &{} \text {if} \;n=4, \\ \Bigg (\dfrac{3}{2}\Bigg )^{2/3}\Bigg (\dfrac{\rho _{3}}{\rho _{0}}\Bigg )^{1/3}(\mu t)^{2/3} &{} \text {if} \;n=3. \end{array} \end{aligned}$$

(189)

5.2 Cosmic domain walls

Cosmic domain walls are known with their contribution to energy density with term $\rho \sim 1/a$. Their equation of state is given by $\mu =-2/3$. Dynamics of the universe with two components where one of them is a domain wall are very similar to dynamics of universes with two components where one of them is dark energy. We have taken the energy density in the following form

$$\begin{aligned} \rho (a)=\dfrac{\rho _{w}}{a}+\dfrac{\rho _{n}}{a^{n}}. \end{aligned}$$

(190)

5.2.1 $k \ne 0$

For a curved space results are found as

$$\begin{aligned} H(a)= & {} \sqrt{\dfrac{8\pi G}{3}\Bigg (\dfrac{\rho _{w}}{a}+\dfrac{\rho _{n}}{a^{n}}\Bigg )-\dfrac{k}{L^{2}a^{2}}}, \end{aligned}$$

(191)

$$\begin{aligned} V(a)= & {} \dfrac{5\rho _{w}}{6a}+\dfrac{(6-n)}{6}\dfrac{\rho _{n}}{a^{n}}, \end{aligned}$$

(192)

$$\begin{aligned} \phi (a)= & {} \pm \int _{a_{in}}^{a}\sqrt{\dfrac{n\rho _{n}{\tilde{a}}+\rho _{w}{\tilde{a}}^{n}}{8\pi G[\rho _{w}{\tilde{a}}^{2+n}+\rho _{n}{\tilde{a}}^{3}]-3k{\tilde{a}}^{1+n}/L^{2}}}d{\tilde{a}}\nonumber \\{} & {} +\phi (a_{in}), \end{aligned}$$

(193)

$$\begin{aligned} p(a)= & {} \dfrac{-2\rho _{w}}{3a}+\dfrac{(n-3)}{3}\dfrac{\rho _{n}}{a^{n}}, \end{aligned}$$

(194)

$$\begin{aligned} q(a)= & {} \dfrac{4\pi G[-\rho _{w}a^{n}+(n-2)\rho _{n}a]a}{8\pi G(\rho _{w}a^{n}+\rho _{n}a)a-3ka^{n}/L^{2}}. \end{aligned}$$

(195)

An explicit form of the scale factor can be found only for $n=0,2$ by using the formula

$$\begin{aligned} \int _{0}^{t}d{\tilde{t}}=\int _{a_{in}}^{a}\dfrac{d{\tilde{a}}}{{\tilde{a}}H({\tilde{a}})}. \end{aligned}$$

(196)

The case $n=0$ which corresponds to combination of domain walls and dark energy has been already studied in Sect. 5.1.1. For the case $n=2$ which corresponds to combination of domain walls and cosmic strings we obtain the following relation

$$\begin{aligned} a(t)= & {} \dfrac{2\pi G\rho _{w}}{3}(t-b)^{2}+\dfrac{1}{\rho _{w}}\Bigg (\dfrac{3k}{8\pi GL^{2}}-\rho _{2}\Bigg ), \end{aligned}$$

(197)

$$\begin{aligned} b= & {} \dfrac{\sqrt{3}}{4\pi G\rho _{w}}\sqrt{8\pi G(\rho _{2}+\rho _{w}a_{in})-\dfrac{3k}{L^{2}}}. \end{aligned}$$

(198)

The scalar field is found as

$$\begin{aligned} \phi (a)= & {} \mp c_{1}ln\Bigg \{\dfrac{\sqrt{(-3k/L^{2}+8\pi G\rho _{2})(2\rho _{2}+a\rho _{w})}+\sqrt{2\rho _{2}[-3k/L^{2}+8\pi G(\rho _{2}+a\rho _{w})]}}{\sqrt{a}}\Bigg \} \end{aligned}$$

(199)

$$\begin{aligned}{} & {} \pm c_{2}ln\Bigg \{2\sqrt{2\pi G(2\rho _{2}+a\rho _{w})} +\sqrt{-3k/L^{2}+8\pi G(\rho _{2}+a\rho _{w})]}\Bigg \}+{\tilde{\phi }}_{in}, \end{aligned}$$

(200)

$$\begin{aligned} c_{1}= & {} 2\sqrt{\dfrac{2\rho _{2}}{-\dfrac{3k}{L^{2}}+8\pi G\rho _{2}}} c_{2}=\dfrac{1}{\sqrt{2\pi G}}, \end{aligned}$$

(201)

$$\begin{aligned} {\tilde{\phi }}_{in}= & {} \pm c_{1}ln\Bigg \{\dfrac{\sqrt{(-3k/L^{2}+8\pi G\rho _{2})(2\rho _{2}+a_{in}\rho _{w})}+\sqrt{2\rho _{2}[-3k/L^{2}+8\pi G(\rho _{2}+a_{in}\rho _{w})]}}{\sqrt{a_{in}}}\Bigg \} \end{aligned}$$

(202)

$$\begin{aligned}{} & {} \mp c_{2}ln\Bigg \{2\sqrt{2\pi G(2\rho _{2}+a_{in}\rho _{w})}+\sqrt{-3k/L^{2}+8\pi G(\rho _{2}+a_{in}\rho _{w})]}\Bigg \}+\phi (a_{in}) \end{aligned}$$

(203)

Formulation of a(V) is found by using (192). Thus the implicit relation between the scalar field and the potential can be obtained by substituting the following formula in (199)

$$\begin{aligned} a(V)=\dfrac{5\rho _{w}+\sqrt{25\rho _{w}^{2}+96\rho _{2}V}}{12V}. \end{aligned}$$

(204)

Behaviour of the deceleration parameter at the beginning is obtained as

$$\begin{aligned} \lim _{a\rightarrow 0}q(a)= {\left\{ \begin{array}{ll} -1+\dfrac{n}{2} \quad \text {if} \; 2< n\le 6,\\ 0\quad \text {if} \; 0< n\le 2. \end{array}\right. } \end{aligned}$$

(205)

Furthermore since denominator of $q(a)\sim H^{2}(a)$ as stated before, numerator of q(a) determines dynamics of the universe. Roots of the deceleration parameter is found as

$$\begin{aligned} a=\Bigg [(n-2)\dfrac{\rho _{n}}{\rho _{w}}\Bigg ]^{1/(n-1)}. \end{aligned}$$

(206)

Therefore the universe start to expand with deceleration and then turns to accelerate for $2<n\le 6$. On the other hand for $0\le n\le 2$ at the beginning of universe H(a) was constant and thus the universe starts to its expansion with acceleration.

5.2.2 $k=0$

Behaviour of q(a) changes as

$$\begin{aligned} \lim _{a\rightarrow 0}q(a)= {\left\{ \begin{array}{ll} -1+\dfrac{n}{2} &{} \text {if} \; 1< n\le 6,\\ -\dfrac{1}{2} &{} \text {if} \; 0\le n\le 1. \end{array}\right. } \end{aligned}$$

(207)

Therefore the differences in dynamics of the universe when it is spatially flat is seen when $0\le n\le 2$. In this case at the beginning H(a) is not constant and the universe starts its expansion with acceleration.

$\phi (a)$ has been simplified for these cases: domain walls and stiff fluid, domain walls and radiation, domain walls and matter as

$$\begin{aligned} \phi (a)&=\pm \dfrac{1}{5\sqrt{2\pi G}}\Bigg \{-\sqrt{6}ln\Bigg [\dfrac{(\sqrt{6}\sqrt{\rho _{s}+\rho _{w}a^{5}}+\sqrt{6\rho _{s}+\rho _{w}a^{5}})a_{in}^{5/2}}{(\sqrt{6}\sqrt{\rho _{s}+\rho _{w}a_{in}^{5}}+\sqrt{6\rho _{s}+\rho _{w}a_{in}^{5}})a^{5/2}}\Bigg ]\Bigg \}\nonumber \\&\quad +ln\Bigg [\dfrac{\sqrt{\rho _{s}+\rho _{w}a^{5}}+\sqrt{6\rho _{s}+\rho _{w}a^{5}}}{\sqrt{\rho _{s}+\rho _{w}a_{in}^{5}}+\sqrt{6\rho _{s}+\rho _{w}a_{in}^{5}}}\Bigg ]\nonumber \\&\quad +\phi (a_{in}) \text {if}\;n=6, \end{aligned}$$

(208)

$$\begin{aligned} \phi (a)&=\pm \dfrac{1}{3\sqrt{2\pi G}}\Bigg \{-2ln\Bigg [\dfrac{(2\sqrt{\rho _{r}+\rho _{w}a^{3}}+\sqrt{4\rho _{r}+\rho _{w}a^{3}})a_{in}^{3/2}}{(2\sqrt{\rho _{r}+\rho _{w}a_{in}^{3}}+\sqrt{4\rho _{r}+\rho _{w}a_{in}^{3}})a^{3/2}}\Bigg ]\nonumber \\&\quad +ln\Bigg [\dfrac{\sqrt{\rho _{r}+\rho _{w}a^{3}}+\sqrt{4\rho _{r}+\rho _{w}a^{3}}}{\sqrt{\rho _{r}+\rho _{w}a_{in}^{3}}+\sqrt{4\rho _{r}+\rho _{w}a_{in}^{3}}}\Bigg ]\Bigg \}\nonumber \\&\quad +\phi (a_{in})\text {if}\;n=4, \end{aligned}$$

(209)

$$\begin{aligned} \phi (a)&=\pm \dfrac{1}{2\sqrt{2\pi G}}\Bigg \{-\sqrt{3}ln\Bigg [\dfrac{(\sqrt{3}\sqrt{\rho _{m}+\rho _{w}a^{2}}+\sqrt{3\rho _{m}+\rho _{w}a^{2}})a_{in}}{(\sqrt{3}\sqrt{\rho _{m}+\rho _{w}a_{in}^{2}}+\sqrt{3\rho _{m}+\rho _{w}a_{in}^{2}})a}\Bigg ]\nonumber \\&\quad +ln\Bigg [\dfrac{\sqrt{\rho _{m}+\rho _{w}a^{2}}+\sqrt{3\rho _{m}+\rho _{w}a^{2}}}{\sqrt{\rho _{m}+\rho _{w}a_{in}^{2}}+\sqrt{3\rho _{m}+\rho _{w}a_{in}^{2}}}\Bigg ]\Bigg \}\nonumber \\&\quad +\phi (a_{in})\text {if}\;n=3. \end{aligned}$$

(210)

After finding a(V) by using (192) the implicit relation between the scalar field and the potential can be obtained by substituting the a(V) in (208–210).

It is possible to simply the relation between time and the scale factor as

$$\begin{aligned} t= & {} \int _{a_{in}}^{a}\dfrac{d{\tilde{a}}}{{\tilde{a}}H({\tilde{a}})}, \nonumber \\ t= & {} \int _{a_{in}}^{a}\dfrac{d{\tilde{a}}}{{\tilde{a}}\sqrt{\dfrac{8\pi G}{3}\Bigg (\dfrac{\rho _{w}}{{\tilde{a}}}+\dfrac{\rho _{n}}{{\tilde{a}}^{n}}\Bigg )}}, \end{aligned}$$

(211)

$$\begin{aligned} t= & {} \sqrt{\dfrac{3}{2\pi G\rho _{w}}}\Bigg [\sqrt{{\tilde{a}}}{}_{2}F_{1}\Bigg (\dfrac{1}{2},\dfrac{1}{2-2n};\dfrac{1}{2-2n}\nonumber \\{} & {} +1;-\dfrac{\rho _{n}}{\rho _{w}}{\tilde{a}}^{(1-n)}\Bigg )\Bigg ]_{a_{in}}^{a} \end{aligned}$$

(212)

where ${}_{2}F_{1}$ is the hypergeometric function which was introduced in Sect. 4.1.1 Implication of (190) avoids singularity in (212) which occurs for $n=1$.

5.3 Dark Energy revisited

We have already examined the case $V=V_{0}$ in Sect. 4.2. For spatially flat universe we have obtained

$$\begin{aligned} a(t)= & {} \Bigg [\dfrac{b^{2}V_{0}e^{2\mu t}-\gamma (a_{in})a_{in}^{6}e^{-2\mu t}}{2bV_{0}}\Bigg ]^{1/3}, \\ b= & {} a_{in}^{3}+\sqrt{a_{in}^{6}+\dfrac{\gamma (a_{in})a_{in}^{6}}{V_{0}}} \quad \text {and} \quad \mu =\sqrt{6\pi GV_{0}}. \end{aligned}$$

Then we formulate the Hubble function and the deceleration parameter as a function of t as

$$\begin{aligned} H(t)= & {} \dfrac{2\mu }{3}(1-\dfrac{2f}{f-b^{2}V_{0}e^{4\mu t}}), f=\gamma (a_{in})a_{in}^{6}, \end{aligned}$$

(213)

$$\begin{aligned} q(t)= & {} -1+\dfrac{12b^{2}fV_{0}e^{4\mu t}}{(1+b^{2}V_{0}e^{4\mu t})^{2}}. \end{aligned}$$

(214)

First constraint on our parameters comes from positivity of the Hubble function

$$\begin{aligned} H(t)>0 \Rightarrow f<b^{2}V_{0}. \end{aligned}$$

(215)

On the other hand q(t) has only one real root

$$\begin{aligned} q(t)=0 \Rightarrow t=\dfrac{1}{4\mu }ln\Bigg [\dfrac{(5+2\sqrt{6})f}{b^{2}V_{0}}\Bigg ]. \end{aligned}$$

(216)

We choose

$$\begin{aligned} t>0 \Rightarrow f>\dfrac{b^{2}V_{0}}{\tau }, \tau =(5+2\sqrt{6}). \end{aligned}$$

(217)

One can write

$$\begin{aligned}&f=\Bigg (\dfrac{1}{\tau }+\varepsilon \Bigg )b^{2}V_{0}, \nonumber \\&0<\varepsilon<1-\dfrac{1}{\tau }\Rightarrow \dfrac{b^{2}V_{0}}{\tau }<f<b^{2}V_{0}. \end{aligned}$$

(218)

Now we will find the condition which results in acceleration at the beginning of the universe

$$\begin{aligned} \lim _{t->0}q(t)=-1+\dfrac{12b^{2}fV_{0}}{(f+b^{2}V_{0})^{2}} <0. \end{aligned}$$

(219)

Thus

$$\begin{aligned}&5-\dfrac{1}{\tau }-\sqrt{24}<\varepsilon <1-\dfrac{1}{\tau }, \end{aligned}$$

(220)

$$\begin{aligned}&4.3\times 10^{-16}<\varepsilon <0.90. \end{aligned}$$

(221)

With these initial conditions universe starts to expand with acceleration and then turns into deceleration.

5.4 Combination containing exotic matter

We have already explored the case of exotic matter in Sect. 4.2. Now we will study combination of this kind of matter and some ordinary matters in the early universe. We have taken the most general form of the potential as

$$\begin{aligned} V(a)=\dfrac{V_{s}}{a^{6}}+\dfrac{V_{n}}{a^{n}}. \end{aligned}$$

(222)

Related cosmological functions have been found as

$$\begin{aligned} \gamma (a)= & {} \dfrac{1}{a^{6}}\Bigg [\dfrac{nV_{n}}{6-n}a^{6-n}+6V_{s}ln\Bigg (\dfrac{a}{a_{in}}\Bigg )+a_{in}^{6}{\tilde{\gamma }}(a_{in})\Bigg ], {\tilde{\gamma }}(a_{in})=\gamma (a_{in})-\dfrac{nV_{n}}{(6-n)a_{in}^{n}} \end{aligned}$$

(223)

$$\begin{aligned} H(a)= & {} \sqrt{\dfrac{8\pi G}{3}\Bigg [\dfrac{6V_{n}}{(6-n)a^{n}}+\dfrac{a_{in}^{6}{\tilde{\gamma }}(a_{in})+V_{s}\Bigg [1+6ln\Bigg (\dfrac{a}{a_{in}}\Bigg )\Bigg ]}{a^{6}}\Bigg ]-\dfrac{k}{L^{2}a^{2}}}, \end{aligned}$$

(224)

$$\begin{aligned} \phi (a)= & {} \pm \sqrt{6}\int _{a_{in}}^{a}\sqrt{\dfrac{(6-n)\Bigg [a_{in}^{6}{\tilde{\gamma }}(a_{in})+6V_{s}ln\Bigg (\dfrac{{\tilde{a}}}{a_{in}}\Bigg )\Bigg ]+nV_{n}{\tilde{a}}^{6}}{(6-n)\{8\pi G\Bigg [a_{in}^{6}{\tilde{\gamma }}(a_{in})+V_{s}\Bigg (1+6ln\Bigg (\dfrac{{\tilde{a}}}{a_{in}}\Bigg )\Bigg )\Bigg ]-3k{\tilde{a}}^{4}/L^{2}\}{\tilde{a}}^{2+n}+48\pi GV_{n}{\tilde{a}}^{8}}}d{\tilde{a}}+\phi (a_{in}), \end{aligned}$$

(225)

$$\begin{aligned} \rho (a)= & {} \dfrac{6V_{n}}{(6-n)a^{n}}+\dfrac{V_{s}}{a^{6}}ln\Bigg [e\Bigg (\dfrac{a}{a_{in}}\Bigg )^{6}\Bigg ]+\dfrac{a_{in}^{6}{\tilde{\gamma }}(a_{in})}{a^{6}}, \end{aligned}$$

(226)

$$\begin{aligned} p(a)= & {} \dfrac{2(n-3)V_{n}}{(6-n)a^{n}}+\dfrac{V_{s}}{a^{6}}ln\Bigg [\dfrac{1}{e}\Bigg (\dfrac{a}{a_{in}}\Bigg )^{6}\Bigg ]+\dfrac{a_{in}^{6}{\tilde{\gamma }}(a_{in})}{a^{6}}, \end{aligned}$$

(227)

$$\begin{aligned} q(a)= & {} \dfrac{8\pi G\{(6-n)\Bigg [2a_{in}^{6}{\tilde{\gamma }}(a_{in})+V_{s}\Bigg (-1+12ln\Bigg (\dfrac{a}{a_{in}}\Bigg )\Bigg )\Bigg ]a^{n}+3(n-2)V_{n}a^{6}\}}{(6-n)\{8\pi G\Bigg [a_{in}^{6}{\tilde{\gamma }}(a_{in})+V_{s}\Bigg (1+6ln\Bigg (\dfrac{a}{a_{in}}\Bigg )\Bigg )\Bigg ]-3ka^{4}/L^{2}\}a^{n}+48\pi GV_{n}a^{6}}. \end{aligned}$$

(228)

5.4.1 Combination with radiation

When the exotic matter is accompanied with radiation its dynamics is governed by the following deceleration parameter

$$\begin{aligned}&q(a)=\dfrac{2a_{in}^{6}{\tilde{\gamma }}(a_{in})+V_{s}\Bigg [-1+12ln\Bigg (\dfrac{a}{a_{in}}\Bigg )\Bigg ]+3V_{r}a^{2}}{a_{in}^{6}{\tilde{\gamma }}(a_{in})+V_{s}\Bigg [1+6ln\Bigg (\dfrac{a}{a_{in}}\Bigg )\Bigg ]+3V_{r}a^{2}},\nonumber \\&\quad {\tilde{\gamma }}(a_{in})=\gamma (a_{in})-\dfrac{2V_{r}}{a_{in}^{4}}. \end{aligned}$$

(229)

One can trace its behaviour back into time as

$$\begin{aligned} q(a_{in})=\dfrac{2a_{in}^{6}\gamma (a_{in})-V_{r}a_{in}^{2}-V_{s}}{a_{in}^{6}\gamma (a_{in})+V_{r}a_{in}^{2}+V_{s}}. \end{aligned}$$

(230)

The following condition

$$\begin{aligned} V_{s}+V_{r}a_{in}^{2}>2a_{in}^{6}\gamma (a_{in}). \end{aligned}$$

(231)

causes accelerated beginning for the universe. Moreover this choice also results in negative total pressure in the beginning as

$$\begin{aligned} p(a_{in})=\dfrac{\gamma (a_{in})a_{in}^{6}-V_{r}a_{in}^{2}-V_{s}}{a_{in}^{6}}<0, \end{aligned}$$

(232)

while energy density remains positive. Thus negative pressure results in accelerated motion for a while. Then this behaviour changes as pressure becomes positive and the universe decelerates. Therefore this exotic matter and radiation with initial condition which satisfies (231) also has mathematical turn on and turn off mechanism for accelerated motion in the early universe.

5.4.2 Combination with domain walls

In spatially flat universe the deceleration parameter becomes

$$\begin{aligned} q(a)=\dfrac{10a_{in}^{6}{\tilde{\gamma }}(a_{in})-3v_{w}a^{5}+5v_{s}\Bigg [-1+12ln\Bigg (\dfrac{a}{a_{in}}\Bigg )\Bigg ]}{5a_{in}^{6}{\tilde{\gamma }}(a_{in})+6v_{w}a^{5}+5v_{s}\Bigg [1+6ln\Bigg (\dfrac{a}{a_{in}}\Bigg )\Bigg ]}. \end{aligned}$$

(233)

Although this universe may start to expand with acceleration or deceleration, after a while it will accelerate because the leading term $a^{5}$ in the numerator has a negative coefficient.

5.4.3 Combination with dark energy

In spatially flat universe the deceleration parameter becomes

$$\begin{aligned} q(a)=\dfrac{2a_{in}^{6}{\tilde{\gamma }}(a_{in})-v_{0}a^{6}+v_{s}\Bigg [-1+12ln\Bigg (\dfrac{a}{a_{in}}\Bigg )\Bigg ]}{a_{in}^{6}{\tilde{\gamma }}(a_{in})+v_{0}a^{6}+v_{s}\Bigg [1+6ln\Bigg (\dfrac{a}{a_{in}}\Bigg )\Bigg ]}. \end{aligned}$$

(234)

Although this universe may start to expand with acceleration or deceleration, after a while it will accelerate because the leading term $a^{6}$ in the numerator has a negative coefficient.

Here we would like to mention about two independent studies in which dynamical exotic fluids were studied [16, 39]. In [39] a universe is filed with a scalar field and a perfect fluid and in [16] only $\Lambda$-term is described by the scalar field. However we study the scalar field dominated universe. Thus our results are different than previous works. On the other hand in these studies authors succeeded to construct $V(\phi )$ corresponding to a power-law behaviour of V(a) in the case of the additional presence of dust-like matter and $k=0$.

6 Late time expansion of the universe

We try to understand the present era which is usually described by dark matter and dark energy. However we consider different forms of energy components. Thus in the first subsection we model a universe with domain walls and matter. After obtaining formulas for functions we compare our results with supernova type Ia data just by curve fitting. In the second subsection we study dark energy dominated universe with the same steps.

6.1 Cosmic walls

The hypothesis that the scalar field is the dark matter and the dark energy was investigated for flat universe in [41]. The results were compared with observations of type Ia supernovae which were available in 2000. In that study, matter part of the universe was neglected and it was found that $\rho _{\phi }\sim a^{-1.09}$ and $q_{0}=-0.45$. Different from them we include matter component of the universe and we solve field equations analytically. Then we compare our results with the type Ia supernovae data released in 2018 [42]. Furthermore in this comparision we extract the value of Hubble constant $H_{0}$ and the value of absolute magnitude M with cosmological density parameters.

Today our universe is believed to be almost flat and contribution of radiation to the energy density is very tiny. For this reason we investigate the case in which

$$\begin{aligned} \rho (a)=\dfrac{\rho _{m}}{a^{3}}+\dfrac{\rho _{w}}{a}. \end{aligned}$$

(235)

Domain wall dominated universes have been already studied in Sect. 5.2. Just plugging $n=3$ in Sect. 5.2.2 we obtain the Hubble function, the scalar field and the potential as

$$\begin{aligned} H(a)&=\sqrt{\dfrac{8\pi G}{3}\Bigg (\dfrac{\rho _{w}}{a}+\dfrac{\rho _{m}}{a^{3}}\Bigg )}, \end{aligned}$$

(236)

$$\begin{aligned} \phi (a)&=\pm \dfrac{1}{2\sqrt{2\pi G}}\left\{ -\sqrt{3}ln\right. \nonumber \\&\quad \left[ \dfrac{(\sqrt{3}\sqrt{\rho _{m}+\rho _{w}a^{2}}+\sqrt{3\rho _{m}+\rho _{w}a^{2}})a_{in}}{(\sqrt{3}\sqrt{\rho _{m}+\rho _{w}a_{in}^{2}}+\sqrt{3\rho _{m}+\rho _{w}a_{in}^{2}})a}\right] \nonumber \\&\quad +ln\left. \left[ \dfrac{\sqrt{\rho _{m}+\rho _{w}a^{2}}+\sqrt{3\rho _{m}+\rho _{w}a^{2}}}{\sqrt{\rho _{m}+\rho _{w}a_{in}^{2}}+\sqrt{3\rho _{m}+\rho _{w}a_{in}^{2}}}\right] \right\} \nonumber \\&\quad +\phi (a_{in}), \end{aligned}$$

(237)

$$\begin{aligned} V(a)&=\dfrac{5\rho _{w}}{6a}+\dfrac{\rho _{m}}{2a^{3}}, \end{aligned}$$

(238)

$$\begin{aligned} p(a)&=-\dfrac{2\rho _{w}}{3a}, \end{aligned}$$

(239)

$$\begin{aligned} q(a)&=-\dfrac{1}{2}+\dfrac{\rho _{m}}{\rho _{m}+\rho _{w}a^{2}}, \end{aligned}$$

(240)

$$\begin{aligned} t&=\sqrt{\dfrac{3}{2\pi G\rho _{w}}}\Bigg [\sqrt{{\tilde{a}}}{}_{2}F_{1}\Bigg (\dfrac{1}{2},-\dfrac{1}{4};\dfrac{3}{4};-\dfrac{\rho _{m}}{\rho _{w} {\tilde{a}}^{2}}\Bigg )\Bigg ]_{a_{in}}^{a}. \end{aligned}$$

(241)

Investigation of the deceleration parameter tells us

$$\begin{aligned}{} & {} \lim _{a\rightarrow 0}q(a)=\dfrac{1}{2}, \lim _{a\rightarrow \infty }q(a)=-\dfrac{1}{2}, \end{aligned}$$

(242)

$$\begin{aligned}{} & {} q(a)=0 \Rightarrow a=\sqrt{\dfrac{\rho _{m}}{\rho _{w}}}. \end{aligned}$$

(243)

Hence if $\rho _{m}<\rho _{w}$ this model of the universe accelerates.

To test the reliability of the theoretical model we will use supernovae data. Luminosity distance-redshift relation had been already constructed as [43]

$$\begin{aligned} d_{L}=(1+z)R_{0}S(\chi (z)). \end{aligned}$$

(244)

The comoving coordinate $\chi$ is given as

$$\begin{aligned} \chi (z)=\dfrac{c}{R_{0}}\int _{0}^{z}\dfrac{dz^{'}}{H(z^{'})}. \end{aligned}$$

(245)

The function $r=S(\chi )$ is given by

$$\begin{aligned} S(\chi )= {\left\{ \begin{array}{ll} Sin(\chi ) &{} \text {if } k=1, \\ \chi &{} \text {if } k=0, \\ Sinh(\chi )&{} \text {if } k=-1. \end{array}\right. } \end{aligned}$$

Thus

$$\begin{aligned} R_{0}S(\chi (z)) =\dfrac{c}{H_{0}} {\left\{ \begin{array}{ll} \left| \Omega _{k,0}\right| ^{-1/2}S(\sqrt{\left| \Omega _{k,0}\right| }E(z)) &{} \text {for } \Omega _{k}\ne 0, \\ E(z) &{} \text {for } \Omega _{k}=0 \end{array}\right. } \end{aligned}$$

where $E(z)=\dfrac{R_{0}H_{0}}{c}\chi (z)$.

For spatially flat universe with matter and domain walls it reduces to the following form

$$\begin{aligned} d_{L}=\dfrac{c(1+z)}{H_{0}}\int _{0}^{z} \frac{dz^{'}}{[\Omega _{m}(1+z^{'})^{3}+\Omega _{w}(1+z^{'})]^{1/2}} \end{aligned}$$

(246)

where $\Omega _{m}=1-\Omega _{w}$. The relation between observational measurements and the theory are established as

$$\begin{aligned} m=5log_{10}\Bigg (\dfrac{d_{L}}{1Mpc}\Bigg )+25+M \end{aligned}$$

(247)

where m and M are the apparent and the absolute magnitudes respectively. Then the distance modulus is defined as $\mu =m-M$.

Before going further we would like to remind the Hubble tension and supernova absolute magnitude tension. Both of them are fundamental cosmological parameters. Their values must be presented precisely.

To determine the value of $H_{0}$ different methods have been applied. According to the Planck measurement of the cosmic microwave background (CMB) anisotropies, assuming the base-$\Lambda$CDM model [44] $H_{0}=67.36\pm 0.54 \,\textrm{kms}^{-1}\textrm{Mpc}^{-1}$. On the other hand Hubble Space Telescope (HST) observations of Cepheids have been used to calibrate the measurements using type Ia supernovae in [45] and it has been declared $H_{0}=74.13\pm 1.42 \,\textrm{kms}^{-1}\textrm{Mpc}^{-1}$. On the other hand redshift evolution of $H_{0}(z)$ was investigated for flat $\Lambda$CDM model in [46]. In this work authors let the parameters $H_{0}$ and $\Omega _{m,0}$ vary simultaneously and they found $H_{0}=70.093\pm 0.102$.

In last years it has been pointed out that the absolute peak magnitude $M_{B}$ of Type Ia supernovae is converted into a value of $H_{0}$ [47,48,49,50]. It’s value has been stated as $M_{B}=-19.401\pm 0.027$ mag [51] in 2020 and $M_{B}=-19.244\pm 0.037$ mag [48] in 2021 by application of different methods. Furthermore in [52] the absolute magnitude was found as $M=-19.25$ for a fixed value of $H_{0}=73.5$.

The most recent data set for type Ia supernova observation which is called as Pantheon dataset was released in [42]. 1048 data points are presented as (m, z) pairs where $z<2.3$. Since there is a debate on values of $H_{0}$ and M we include their values as parameters which are to be derived from curve fitting. Therefore we have to extract values of $\rho _{w}$, $H_{0}$ and M from data. To be able to see effects of these numbers on each other separately we applied the curve fitting method for three combinations of two parameter sets.

Then we applied the $\chi ^{2}$ test to measure the goodness of these fits. $\chi ^{2}$ per degrees of freedom, $\chi _{\nu }^{2}$ is calculated according to following formula

$$\begin{aligned} \chi ^{2}= & {} \sum _{i}^{N}\dfrac{(\mu _{i}^{data}-\mu _{i}^{model})^{2}}{\sigma _{i}^{2}}, \end{aligned}$$

(248)

$$\begin{aligned} \chi ^{2}_{\nu }= & {} \dfrac{\chi ^{2}}{\nu }, \nu =N-k \end{aligned}$$

(249)

where k is the number of parameters that will be extracted from the N number of data points.

First, we assign trial number for $\Omega _{w}$ and results are shown in Table 1.

Table 1 Values of $H_{0}$ and M for given $\Omega _{w}$

The best fit which is obtained for $\Omega _{w}=0.90$ gives $H_{0}=72.1563\pm 0.0001$, $M=-19.269\pm 0.004$ and $\chi ^{2}/\nu =1.009$.

After getting intuition about parameters we perform curve fitting for trial $H_{0}$ values. Results are given in Table 2.

Table 2 Values of M and $\Omega _{w}$ for given $H_{0}$

Numbers in Table 2 tell us that the hundredths digit of M is sensitively depended on the ones digit of $H_{0}$. In addition, more accurate result for $\Omega _{w}$ is obtained. All of the results have the same $\chi ^{2}/\nu$ value. Thus we choose $3^{rd}$ line: $H=72$, $M=-19.270\pm 0.006$, $\Omega _{w}=0.888\pm 0.015$ and $\chi ^{2}/\nu =1.008$. These numbers are compatible with best fit of the Table 1.

Effect of trial values of M on $H_{0}$ and $\Omega _{w}$ are presented in Table 3.

Table 3 Values of $H_{0}$ and $\Omega _{w}$ for given M

It is apparent that the value of the ones digit of $H_{0}$ is sensitively depended on the hundredths digit of M. Our choice is the $5^{th}$ line: $M=-19.25$, $H_{0}=72.68\pm 0.21$, $\Omega _{w}=0.889 \pm 0.015$ and $\chi ^{2}/\nu =1.008$. These numbers are in agreement with best fit of the Table 1.

Assuming base $\Lambda$CDM cosmology, late universe parameters were found as $H_{0}=67.27\pm 0.60$, $\Omega _{m}=0.3166\pm 0.0084$ and $\Omega _{\Lambda }= 0.6834\pm 0.0084$ in [44]. It is known that $\Omega _{m}=\Omega _{bm}+\Omega _{dm}$ where $\Omega _{bm}\simeq 0.05$ and $\Omega _{dm}\simeq 0.27$. However our results indicate that late universe parameters as $H_{0}=72.68\pm 0.21$, $\Omega _{w}=0.889\pm 0.015$ and $\Omega _{m}=0.111\pm 0.015$. Since $\Omega _{bm}\simeq 0.05$, $\Omega _{dm}\simeq 0.06$. Therefore domain wall dominated universe is a candidate to explain 94 percentage of the structures in the present universe while still 6 percentage of the universe remains as unknown.

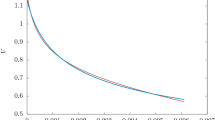
To compare our results with Pantheon-data graphically we draw distance modulus $\mu$ vs redshift z plot. In Fig. 1 we use results given in $5^{th}$ line of Table 3 where $M=-19.25$, $H_{0}=72.68\pm 0.21$, $\rho _{w}=0.889\pm 0.015$ and $\rho _{m}=0.111\pm 0.015$.

Fig. 1

Distance modulus vs redshift plot for domain wall dominated universe.Dots represent observation of Pantheon data while green line represents domain wall dominated universe

We obtain $q_{0}=-0.389$ by using values of cosmological density parameters in (240).

6.2 Dark energy

Now we will present exact solutions for energy density given as

$$\begin{aligned} \rho =\rho _{0}+\dfrac{\rho _{m}}{a^{3}}. \end{aligned}$$

(250)

Actually this case corresponds to $n=3$ in Sect. 5.1. For $k=0$ we have already obtained the scalar factor as

$$\begin{aligned} a(t)=\Bigg [\dfrac{(a_{in}^{3/2}+\sqrt{a_{in}^{3}+\dfrac{\rho _{m}}{\rho _{0}}})e^{3\mu t/2}+(a_{in}^{3/2}-\sqrt{a_{in}^{3}+\dfrac{\rho _{m}}{\rho _{0}}})e^{-3\mu t/2}}{2}\Bigg ]^{2/3}, \end{aligned}$$

(251)

where $\mu =\sqrt{\dfrac{8\pi G\rho _{0}}{3}}$. In addition potential is formulated as

$$\begin{aligned}&V(\psi )=\dfrac{1}{2}\dfrac{\rho _{m}}{a^{3}(\psi )}+\rho _{0}, \end{aligned}$$

(252)

$$\begin{aligned}&a(\psi )=2^{2/3}\nonumber \\&\quad \Bigg \{\dfrac{a_{in}^{3/2}e^{\sqrt{3}\psi }\Bigg [-1+\sqrt{1+a_{in}^{3}\dfrac{\rho _{0}}{\rho _{m}}}-\Bigg (1+\sqrt{1+a_{in}^{3}\dfrac{\rho _{0}}{\rho _{m}}}\Bigg )e^{2\sqrt{3}\psi }\Bigg ]}{a_{in}^{3}\dfrac{\rho _{0}}{\rho _{m}}(1+e^{4\sqrt{3}\psi })-2\Bigg (2+a_{in}^{3}\dfrac{\rho _{0}}{\rho _{m}}\Bigg )e^{2\sqrt{3}\psi }}\Bigg \}^{2/3}, \end{aligned}$$

(253)

$$\begin{aligned} \psi&=\pm \sqrt{2\pi G}[\phi (a)-\phi (a_{in})]. \end{aligned}$$

(254)

Behaviour of the deceleration parameter is shown by

$$\begin{aligned}{} & {} q(a)=\dfrac{-2\rho _{0}a^{3}+\rho _{m}}{2(\rho _{0}a^{3}+\rho _{m})}, \end{aligned}$$

(255)

$$\begin{aligned}{} & {} \lim _{a\rightarrow \infty }q(a)=-1. \end{aligned}$$

(256)

To extract cosmological parameters from Pantheon data we apply the procedure as explained in the previous subsection with modification

$$\begin{aligned} d_{L}=\dfrac{c(1+z)}{H_{0}}\int _{0}^{z} \frac{dz^{'}}{[\Omega _{m}(1+z^{'})^{3}+\Omega _{0}]^{1/2}} \end{aligned}$$

(257)

where $\Omega _{m}=1-\Omega _{0}$.

First, we perform curve fitting for trial values of $\Omega _{0}$. Results are shown in Table 4.

Table 4 Values of $H_{0}$ and M for given $\Omega _{0}$

The best fit occurs for $\Omega _{0}=0.70$. Thus $H_{0}=72.1749\pm 0.0001$, $M=-19.282\pm 0.004$ and $\chi ^{2}/\nu =0.992$.

Then we perform curve fitting for trial $H_{0}$ values. Results are given in Table 5.

Table 5 Values of M and $\Omega _{0}$ for given $H_{0}$

Results in the third line are compatible with the best fit of Table 4. $M= -19.294 \pm 0.007$, $\Omega _{0}=0.715\pm 0.012$ and $\chi ^{2}/\nu =0.990$ are obtained for a given $H_{0}=72$.

Finally we test the effect of M on $H_{0}$ and $\Omega _{0}$. Results are presented in Table 6.

Table 6 Values of $H_{0}$ and $\Omega _{w}$ for given M

Numbers in the fourth line are compatible with the best fit of Table 4. $H_{0}=71.80\pm 0.22$, $\Omega _{0}=0.715\pm 0.012$ and $\chi ^{2}/\nu =0.990$ are found for a given $M=-19.30$.

All the tables in this article have a common interpretation: The number in ones digit of the Hubble constant $H_{0}$ is sensitively depended on the number in the hundredths digit of the absolute magnitude M in both models. In addition as the value of $H_{0}$ increases, the value of M decreases. We will stop to dig more about this argument here since it is beyond the scope of our article. Cosmologists will continue to reveal the relation between $H_{0}$ and M more clearly on further studies.

Now we would like to compare our results for a domain wall dominated universe and a dark energy dominated universe in the same plot. However this goal can not be achieved accurately, because best fit values of M are different for both models. For this reason we plot two figures.

We draw our Fig. 2 by taking $M=-19.25$ for which one of the best fits of the domain wall dominated universe is obtained with parameters $H_{0}=72.68\pm 0.21$, $\Omega _{w}=0.889\pm 0.015$ and $\Omega _{m}=0.111\pm 0.015$. On the other hand we have obtained $H_{0}=73.47\pm 0.23$, $\Omega _{0}=0.715\pm 0.012$, $\Omega _{m}=0.285\pm 0.12$ and $\chi ^{2}/\nu =0.990$ for $M=-19.25$.

In Fig. 3 we choose one of the best fits of the dark energy dominated universe for which $M=-19.30$, $H_{0}=71.80\pm 0.22$, $\Omega _{0}=0.715\pm 0.012$ and $\Omega _{m}=0.285\pm 0.012$. In the first model we have obtained $H_{0}=71.03\pm 0.20$, $\Omega _{w}=0.889\pm 0.015$, $\Omega _{m}=0.111\pm 0.015$ and $\chi ^{2}/\nu =0.990=1.008$ for $M=-19.30$

Fig. 2

Distance modulus vs redshift plot for $M=-19.25$. Dots represent observations, green line represents domain wall dominated universe and red line represents dark energy dominated universe

Fig. 3

Distance modulus vs redshift plot for $M=-19.30$. Dots represent observations, green line represents domain wall dominated universe and red line represents dark energy dominated universe

Two figures are almost the same because $\chi ^{2}/\nu$ for both models are very close the 1. We need more data for bigger redshift values to decide whether one of the models is superior to the other one. We obtain $q_{0}=-0.572$ by using these values of cosmological parameters in (255).

7 Disccusion

Differential equations have deterministic solutions. To reach the reality and beauty of the nature scientists should improve mathematical methods. Thus we have chosen one of these mathematical tools and this is the change of independent variable.

Our main claim is that scale factor of the universe is a successful candidate to describe all dynamical functions. Data from observations are obtained in terms of redshift which is defined as

$$\begin{aligned} 1+z=\dfrac{a(t_{0})}{a(t_{e})}=\dfrac{1}{a(t_{e})}, \end{aligned}$$

(258)

where $a(t_{0})=1$. With a as their argument, this knowledge is sufficient to determine the numerical values of associated functions. Additionally, parametric graphs can be used to study the functions’ general behavior.

Dynamical functions take on distinct forms for each era of the cosmos in accordance with the energy-matter composition of the universe. For this reason the differential equations should be approached as an initial value problem. As a matter of course our solutions contain arbitrary integration constants, such as $a_{in}$, $\phi (a_{in})$, and $\gamma (a_{in})$, where subscript represents the start of the relevant epoch. Given that the universal rules cease to apply at smaller scales, to take $a_{in}=l_{Planck}$ is reasonable for the early epoch.

We would like to remind that $\phi$ equation which is given by (6) is a second order differential equation when time is an independent variable. It turns into a first order differential equation which is given by (19) for $\gamma (a)$ by defining $\gamma (a)=\dfrac{\phi ^{'2}H^{2}a^{2}}{2}$ when “a” is the independent variable. If we give V(a), solution of $\gamma (a)$ which is given by (28) can be obtained. Since at the same time we can write $\gamma =\frac{{\dot{\phi }}^{2}}{2}$, solution of $\phi (a)$ contains two arbitrary constants which are $\gamma (a_{in})=\dfrac{{\dot{\phi }}^{2}_{in}}{2}$ and $\phi (a_{in})$. On the other hand for a given $\rho (a)$ first order differential equation for $\gamma (a)$ collapses to an algebraic equation and we do not need the information of ${\dot{\phi }}_{in}$. Thus for this case solution of the scalar field contains one arbitrary integration constant. Furthermore if it ever becomes possible to quantize this approach the undetermined integration constant $\phi (a_{in})$ can be used in the renormalization to remove infinities.

For a given V(a) we always end up with a stiff fluid term in our energy density. This term has the following coefficient

$$\begin{aligned} a_{in}^{6}{\tilde{\gamma }}(a_{in}), \quad {\tilde{\gamma }}(a_{in})=-\dfrac{nV_{n}a_{in}^{-n}}{6-n}+\gamma (a_{in}), \quad \gamma (a_{in})=\dfrac{{\dot{\phi }}^{2}}{2},\nonumber \\ \end{aligned}$$

(259)

except for constant potential and for $V(a)=V_{6}/a^{6}$. For these cases coefficient of stiff fluid becomes $a_{in}^{6}\gamma (a_{in})$. Quantum fluctuations in the vacuum cause ${\dot{\phi }}^{2}/2$ ($=\gamma (a_{in})$) to take on non-zero values. Consequently, one could consider quantum fluctuations to be a source of stiff fluid [53].

Hubble function may take imaginary value for a universe with positive curvature parameter. Before performing detailed investigation of these cases we would like to remind that imaginary value of the Hubble function indicates imaginary time. There are some studies which explain physical menaing of imaginary time. For example in [54] it was shown that in the one-loop approximation, quantum metric fluctuations of empty Euclidean space produce an exact solution to the self-consistent equations of quantum gravity that is conceptualized as a de Sitter gravitational instanton in imaginary time. Analytical development of this solution results in a de Sitter expansion in the Lorentzian space of real time. Thus it is possible that tunneling from “nothing” produced a flat inflationary universe.

In Sect. 4 we have investigated behaviour of single component universe. We have taken $\rho (a)=\rho _{n}/a^{n}$ and $k\ne 0$ in Sect. 4.1.1. We would like to remind some basic formulas

$$\begin{aligned}{} & {} \Omega _{n}(t)\equiv \dfrac{8\pi G}{3H^{2}(t)}\rho _{n}(t), \rho _{n}(t)=\dfrac{\rho _{n,0}}{a^{n}(t)}, \nonumber \\{} & {} \rho _{\Lambda }= \rho _{\Lambda ,0}=\Lambda , \end{aligned}$$

(260)

$$\begin{aligned}{} & {} \Omega _{k}(t)=-\dfrac{k}{H^{2}(t)a^{2}(t)L^{2}}, \sum _{i=1}^{m}\Omega _{i}+\Omega _{k}=1, \end{aligned}$$

(261)

where 0 denotes today’s value of the related parameter. It is seen from (64) that there will be a period of time in which Hubble function takes imaginary values for positive curvature, $k=1$. For $n<2$, this period ends up for $a<1$. Thus it is reasonable to take $a_{in}=\Bigg (\dfrac{|\Omega _{k,0}|}{\Omega _{n,0}}\Bigg )^{1/(2-n)}$ for this kind of universe. As it is seen form deceleration expression which is given by (68), this kind of universe starts to expand by bouncing from negative infinite deceleration parameter. A cosmic string dominated universe where $n=2$ always expands with constant Hubble function. If $n>2$, the Hubble function will take imaginary values after the point where ${{a}}=\Big (\dfrac{\Omega _{n,0}}{|\Omega _{k,0}|}\Big )^{1/(n-2)}>1$. Ultimately this kind of universe will collapse with infinite positive deceleration parameter. On the other hand for $k=0$ and for $k=-1$ the universe expands with real Hubble function where the deceleration parameter is negative for $n<2$, the deceleration parameter is zero for $n=2$ and the deceleration parameter is positive for $n>2$.

As we pointed earlier, behaviour of the universe for a given V(a) is different from behaviour of the universe for a given $\rho (a)$ because of the stiff fluid term which stems from quantum fluctuations. In Sect. 4.2.1 we have taken $V(a)=V_{n}/a^{n}$ and $k\ne 0$. For the cases $n=1,3,4,5,6$ and $k=1$ the Hubble function will take imaginary values when $a>1$. The ultimate fate of these universes is to collapse with infinite positive deceleration parameter. If $n=2$ and $\Omega _{2}>|\Omega _{k}|$ a universe expands forever. If $\Omega _{2}<|\Omega _{k}|$, a universe will collapse. We would like to explain the case for $n=0$ by drawing plots since it is more complicated.

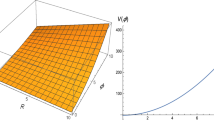
A universe can be approximately described by a single component at late times as well as at early times where the contribution of curvature parameter may be important. To investigate importance of value of $\Omega _{k}$ in the following three cases we will take it comparable with other density parameters. First, we will study the following chosen cosmological density parameters

$$\begin{aligned} \Omega _{\Lambda ,0}=1, \Omega _{s,0}=5, \Omega _{k}=-5, \end{aligned}$$

(262)

where s stands for stiff fluid and their sum is equal to 1. Behaviour of $H^{2}$ is shown in Fig. 4 while behaviour of the deceleration parameter is shown in Fig. 5.

Fig. 4

$H^{2}(a)$ vs “a” plot

Fig. 5

q(a) vs “a” plot

Second, we will study the case $n=0$ for the following chosen cosmological density parameters

$$\begin{aligned} \Omega _{\Lambda ,0}=1, \Omega _{s,0}=1, \Omega _{k}=-1, \end{aligned}$$

(263)

where s stands for stiff fluid and their sum is equal to 1. Behaviour of $H^{2}$ is shown in Fig. 6 while behaviour of the deceleration parameter is shown in Fig. 7.

Fig. 6

$H^{2}(a)$ vs “a” plot

Fig. 7

q(a) vs “a” plot

The Hubble function for the first choice of cosmological parameters becomes imaginary while the Hubble function for the second choice of cosmological parameters is always real. Differences between both cases stem from values of $\Omega _{s,0}$. In other words large value of quantum fluctuations with constant potential may cause the universe to collapse and it may cause the universe to reemerge by bouncing with negative infinite deceleration parameter.

Third, we will study the following chosen cosmological density parameters

$$\begin{aligned} \Omega _{\Lambda ,0}=10, \Omega _{s,0}=5, \Omega _{k}=-14, \end{aligned}$$

(264)

where s stands for stiff fluid and their sum is equal to 1. Behaviour of $H^{2}$ is shown in Fig. 8 while behaviour of the deceleration parameter is shown in Fig. 9.

Fig. 8

$H^{2}(a)$ vs “a” plot

Fig. 9

q(a) vs “a” plot

When we compare third case with first case the effect of constant potential (cosmological constant) is seen. When the value of $V_{0}$ is huge enough, Hubble function always takes real values.

Contrastingly, for a universe with small values of $\Omega _{k}$ we have found the following results. In the fourth case we take

$$\begin{aligned} \Omega _{\Lambda ,0}=1.2, \Omega _{s,0}=0.0001, \Omega _{k}=-0.2001, \end{aligned}$$

(265)

where s stands for stiff fluid and their sum is equal to 1. Behaviour of $H^{2}$ is shown in Fig. 10 while behaviour of the deceleration parameter is shown in Fig. 11.

Fig. 10

$H^{2}(a)$ vs “a” plot

Fig. 11

q(a) vs “a” plot

In the fifth case we will study the following chosen cosmological density parameters

$$\begin{aligned} \Omega _{\Lambda ,0}=1.2, \Omega _{s,0}=0.001, \Omega _{k}=-0.201, \end{aligned}$$

(266)

where s stands for stiff fluid and their sum is equal to 1. Behaviour of $H^{2}$ is shown in Fig. 12 while behaviour of the deceleration parameter is shown in Fig. 13.

Fig. 12

$H^{2}(a)$ vs “a” plot

Fig. 13

q(a) vs “a” plot

The Hubble function for the fourth choice of cosmological parameters becomes imaginary while the Hubble function for the fifth choice of cosmological parameters is always real. Differences between both cases stem from values of $\Omega _{s,0}$. In other words small value of quantum fluctuations with constant potential may cause the universe to collapse and it may cause the universe to reemerge by bouncing with negative infinite deceleration parameter.

In the sixth case, we will study the following chosen cosmological density parameters

$$\begin{aligned} \Omega _{\Lambda ,0}=1, \Omega _{s,0}=0.0001, \Omega _{k}=-0.0001, \end{aligned}$$

(267)

where s stands for stiff fluid and their sum is equal to 1. Behaviour of $H^{2}$ is shown in Fig. 14 while behaviour of the deceleration parameter is shown in Fig. 15.

Fig. 14

$H^{2}(a)$ vs “a” plot

Fig. 15

q(a) vs “a” plot

When we compare sixth case with fourth case the effect of constant potential (cosmological constant) is seen. When the value of $V_{0}$ is small enough, Hubble function always takes real values.

Effects of cosmological constant and quantum fluctuations on the dynamics of the universe depends on the value of $\Omega _{k}$ as we have shown for the previous six cases. These effects for small value of $\Omega _{k}$ are just opposite of effects of the same variables for large value of $\Omega _{k}$.

In Sect. 5.1 we have taken $\rho (a)=\rho _{n}/a^{n}+\rho _{0}$. We would like to explain affect of positive curvature. A universe which consists of domain walls and cosmological constant will have imaginary Hubble function for $a_{in}<1$. This kind of universe has a non-zero initial scale factor. When $n=2$ there are two possibilities. If $\Omega _{2}>|\Omega _{k}|$, the Hubble function is always real. If $\Omega _{2}<|\Omega _{k}|$, the Hubble function will take imaginary values for $a<1$ therefore this kind of universe has non-zero initial value for the scale factor. When $n>2$, if $|\Omega _{k}|$ is large enough from $\Omega _{n}$, a universe collapses and reemerges with infinite negative deceleration parameter. Otherwise universe always expands with real Hubble function.

In Sect. 5.2 we have taken $\rho (a)=\rho _{w}/a+\rho _{n}/a^{n}$. The case with $n=0$ has been already discussed in the previous paragraph. If $n=2$ and $\Omega _{2}>|\Omega _{k}|$, a universe expands forever. If $\Omega _{2}<|\Omega _{k}|$, the Hubble function will take imaginary values for $a<1$ therefore this kind of universe has non-zero initial value for the scale factor. When $n>2$, if $|\Omega _{k}|$ is large enough from $\Omega _{n}$, a universe collapses and reemerge with infinite negative deceleration parameter. Otherwise universe always expands with real Hubble function.

In Sect. 5.4 we have taken $V(a)=V_{s}/a^{6}+V_{n}/a^{n}$. It is seen that when the value of $|\Omega _{k}|$ is large enough the universe will collapse and reemerge with infinite deceleration parameter.

In Sect. 6.1 we have investigated a flat universe which consists of domain walls and ordinary matter. To compare our results with observation we have used type Ia supernova Pantheon data set. Our way of data analysis is different than what has been done in the literature. Thus we have investigated a universe which consists of dark energy and matter in the same manner. Then it is seen that the number in ones digit of the Hubble constant $H_{0}$ is sensitively dependent on the number in the hundredths digit of the absolute magnitude M in both models.

For domain wall dominated universe we have found that $\Omega _{w}=0.889\pm 0.015$, $\Omega _{m}=0.111\pm 0.015$ and $H_{0}=72.68\pm 0.21$ for $M=-19.25$. This universe accelerates with $q_{0}=-0.389$. Comparison of this model with CMB data is beyond the scope of this article. Careful and detailed analysis of CMB data will be one of our further studies.

On the other hand, in 1980s Modified Theories of Newtonian Dynamics or MOND, were proposed [55, 56]. This model mainly claims that observational aspects of galaxies can be understood without dark matter. Recent observational evidence for the external field effect in MOND which was proposed as an alternative to dark matter is presented in [57]. A new relativistic MOND theory [58] successfully reproduces cosmic microwave background power spectra. These theories may explain non-baryonic part of domain wall dominated universe which covers six percent of the energy-matter content of the universe.

8 Conclusion

We studied FLRW cosmology with real scalar field which is minimally coupled to gravity. Our main motivation in this article has been to assign the effective scalar field a source of all components of energy density. We applied a change of variable twice which is a more powerful method in the set of differential equations which represent dynamics of the universe. In the first one, we have replaced the independent variable “t” with “a”. In the second one, we have changed the dependent variable of the $\phi$ equation so that it became a first order linear differential equation. We presented exact solutions in four different forms; solutions for given V(a), solutions for given $\phi ^{'}(a)$, solutions for given H(a), and solutions for given $\rho (a)$.

Then we have examined single component universes and two component universes for a given energy density and for a given potential. In these solutions we have searched for mathematical mechanisms which create turn on and turn off for early inflationary expansion. We have explored mathematical structure of a new exotic matter. Equation of state for this component changes with the scale factor or equivalently changes with time. A universe which consists of radiation and this exotic matter, has mathematical machinery to turn on and to turn off inflationary expansion in early epoch.

We have investigated the present era of the universe. Domain wall dominated universe and dark energy dominated universe have been studied. We have extracted numerical values of cosmological parameters from the most recent type Ia supernova data by taking care of the Hubble tension and the absolute magnitude tension. For domain wall dominated universe we have found that $\Omega _{w}=0.889\pm 0.015$, $\Omega _{m}=0.111\pm 0.015$ and $H_{0}=72.68\pm 0.21$ for $M=-19.25$. This universe accelerates with $q_{0}=-0.389$.

On the other hand for dark energy dominated universe cosmological parameters have been found as $\Omega _{0}=0.715\pm 0.012$, $\Omega _{m}=0.285\pm 0.012$ and $H_{0}=71.80\pm 0.22$ for $M=-19.30$. Deceleration parameter of this universe is $q=-0.572$. Detailed analysis for the relation between distance modulus and redshift have shown that the number in ones digit of the Hubble constant $H_{0}$ is sensitively dependent on the number in the hundredths digit of the absolute magnitude M in both models.

These two analyses indicate that both models equivalently explains dynamics of late time accelerated expansion of the universe. The difference between these models most probably will be seen when bigger redshift data are available.

Appendix

1.1 Change of variable

$$\begin{aligned} H(a)=\dfrac{{\dot{a}}}{a} \end{aligned}$$

(A-1)

Therefore our new independent variable becomes a scale factor $'a'$. For this reason we write all other variables in terms of the new variable.

$$\begin{aligned} \phi =\phi (a) V(\phi )=V(a) {\dot{a}}=aH(a) \end{aligned}$$

(A-2)

As a result we obtain by change of variable

$$\begin{aligned} \dfrac{d\phi }{dt}= & {} \dfrac{d\phi (a)}{dt}\dfrac{da}{dt}=\phi ^{'}{\dot{a}}=\phi ^{'}aH \end{aligned}$$

(A-3)

$$\begin{aligned} {\dot{\phi }}= & {} \phi ^{'}aH \end{aligned}$$

(A-4)

$$\begin{aligned} \dfrac{d^{2}\phi }{dt^{2}}= & {} \dfrac{d}{dt}(\phi ^{'}aH)=\dfrac{d}{da}(\phi ^{'}aH)\dfrac{da}{dt} \end{aligned}$$

(A-5)

$$\begin{aligned} \ddot{\phi }= & {} \phi ^{''}a^{2}H^{2}+\phi ^{'}aH^{2}+\phi ^{'}a^{2}HH^{'} \end{aligned}$$

(A-6)

By the help of the chain rule

$$\begin{aligned} \dfrac{dV}{d\phi }&=\dfrac{dV}{da}\dfrac{da}{d\phi }=\dfrac{dV}{da}\dfrac{1}{\dfrac{d\phi }{da}} , \end{aligned}$$

(A-7)

$$\begin{aligned} \dfrac{dV}{d\phi }&=V^{'}\dfrac{1}{\phi ^{'}} . \end{aligned}$$

(A-8)

On the other hand by starting from our definition we get followings

$$\begin{aligned}{} & {} \dfrac{{\dot{a}}}{a}=H(a) \end{aligned}$$

(A-9)

$$\begin{aligned}{} & {} \dfrac{\ddot{a}}{a}-\dfrac{{\dot{a}}^{2}}{a^{2}}=\dfrac{dH}{da}\dfrac{da}{dt} \end{aligned}$$

(A-10)

$$\begin{aligned}{} & {} \dfrac{\ddot{a}}{a}=H^{'}aH+H^{2} \end{aligned}$$

(A-11)

1.2 Integration by parts

By using functions u and v a theorem integration by parts is written as

$$\begin{aligned} \int _{x_{0}}^{x} u(x)dv(x)=u(x)v(x)\Biggr |_{x_{0}}^{x}-\int _{x_{0}}^{x} v(x)du(x) \end{aligned}$$

(A-12)

When calculating the function $\gamma (a)$ we choose

$$\begin{aligned} u=-{\tilde{a}}^{6} dv=V^{'}d{\tilde{a}} \end{aligned}$$

(A-13)

thus

$$\begin{aligned} du=-6{\tilde{a}}^{5}d{\tilde{a}}, v=V({\tilde{a}}) \end{aligned}$$

(A-14)

results in

$$\begin{aligned} \int _{a_{in}}^{a} (-{\tilde{a}}^{6}V^{'})d{\tilde{a}}&=-{\tilde{a}}^{6}V({\tilde{a}})\Biggr |_{a_{in}}^{a}+6\int _{a_{in}}^{a} V({\tilde{a}}){\tilde{a}}^{5}d{\tilde{a}} \nonumber \\ \int _{a_{in}}^{a} (-{\tilde{a}}^{6}V^{'})d{\tilde{a}}&=-a^{6}V(a)+6\int _{a_{in}}^{a} V({\tilde{a}}){\tilde{a}}^{5}d{\tilde{a}}\nonumber \\&\quad +a_{in}^{6}V(a_{in}) \end{aligned}$$

(A-15)