1 Introduction

The Facility for Antiproton and Ion Research (FAIR) is an international accelerator facility under construction which will use antiprotons and ions to perform research in a lot of fields of physics. As part of the FAIR in the GSI Helmholtz Center for Heavy Ion Research it is planned to create a High Energy Storage Ring (HESR) for the accumulation of antiprotons in the range of kinetic energies from \(\approx \)1  to 14 GeV [1]. These antiprotons will be used for a future generation of strong interaction experiments. At the beginning of HESR, its main user will be the PANDA experiment. However, if it is possible to extract a part of the beam or a halo of the beam from the storage ring, it will allow in parallel with the main experiment to conduct a number of others, using antiprotons extracted from the ring in separate experimental channels [2]. The use of bent crystals to deflect antiprotons may allow such particle extraction, as there are several mechanisms for deflecting charged particles by means of bent crystals, and among them are those that are effective for deflecting not only positively but also negatively charged particles.

There are three main mechanisms for deflecting high-energy charged particles as they pass through a bent crystal: planar channeling [3, 4], which is particle motion in a potential well formed by the potential of neighboring crystal atomic planes, volume reflection [5], which is the reflection of particles from one or more bent atomic planes within the crystal, and stochastic deflection [6, 7], which is the scattering of particles on bent crystal atomic strings. Volume reflection does not allow the particles to be deflected at angles that would significantly exceed [8, 9] the critical angle of planar channeling in the crystal \(\theta _c = \sqrt{2 U_0 / p v}\) [10] (\(U_0\) is the depth of the potential well formed by neighboring atomic planes, p and v are the momentum and velocity of the particle, respectively) and this mechanism is much less effective for negatively charged particles, than for positively charged ones [9]. Because of this, the volume reflection is not considered as a mechanism by which antiprotons or other negatively charged particles could be removed from the storage ring. Instead, two other mechanisms allow [11,12,13,14,15,16,17] to deflect negatively charged particles at angles that significantly exceed the critical angle of planar channeling. Below we consider the deflection of a part of negatively charged particle beam by means of a bent crystal with a help of planar channeling and stochastic deflection.

2 Deflection of a beam with no angular divergence

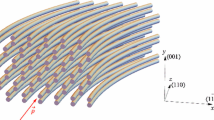
To compare the efficiency of planar channeling and stochastic deflection in a bent crystal to deflect high-energy negatively charged particles under the conditions which are being achievable at the FAIR, numerical simulation of the motion of antiprotons with a kinetic energy of 14 GeV in a bent silicon crystal has been carried out. Since silicon crystals have been selected for most of the CERN experimental tests (see e.g. [11, 14,15,16]), we have chosen this material for our investigation. This material has fewer defects than tungsten, and is much cheaper than germanium. Silicon has a face-centered diamond cubic crystal structure. The most densely packed directions in it are axes \(\left\langle 100 \right\rangle \), \(\left\langle 110 \right\rangle \), and \(\left\langle 111 \right\rangle \). In simulation of stochastic deflection we have chosen the axis \(\left\langle 110 \right\rangle \) to be parallel to the direction of momentum of the incident particles. The arrangement of atomic strings of silicon crystal aligned along the \(\left\langle 110 \right\rangle \) axis is schematically shown in Fig. 1. Black dots show atomic strings in a plane orthogonal to the \(\left\langle 110 \right\rangle \) axis. The lines show the boundaries of the unit cell. This orientation for a silicon crystal corresponds to the highest value of the potential of atomic strings. The simulation was based on the numerical solution of the two-dimensional equation of particle motion in the field of bent crystalline atomic strings. In the simulation, such incoherent effects as scattering by thermal vibrations of crystal atoms and scattering by the electronic subsystem of the crystal were taken into account. The energy losses of particles due to radiation and ionization of crystal atoms, as well as nuclear interactions, were not taken into account due to the small thickness of the crystal (the article considers a single passage of the beam particles through the crystal, and not multiple passage).

Fig. 1
figure 1

Location of atomic strings along the \(\left\langle 110 \right\rangle \) axis of a silicon crystal

Full size image

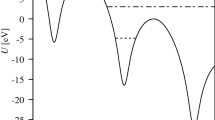
The crystal bending plane was chosen to be parallel to the (001) crystal planes. This choice of the bending plane leads to the fact that the planes \((1{\bar{1}}0)\) have the smallest radius of curvature in the crystal (see Fig. 2, which schematically shows the orientation of bent crystal atomic strings towards the initial particle momentum \(\textbf{p}\)). Therefore, when studying planar channeling of negatively charged particles in a bent crystal, the motion of particles in the field of \((1{\bar{1}}0)\) planes was considered. We have chosen \((1{\bar{1}}0)\) planes to analyze the efficiency of planar channeling for deflecting negatively charged particles because the potential well for this plane is much deeper (\(U_{0,(1{\bar{1}}0)} \approx 21\) eV) than for the (100) plane (\(U_{0,(100)} \approx 12\) eV), and almost as deep as for the plane (111) (\(U_{0,(111)} \approx 23\) eV). At the same time, the planes \((1{\bar{1}}0)\) are located at the same distance from each other, while for each of the planes (111) one of the neighboring planes is always significantly closer than the second. This leads to the fact that in the case of planar channeling of negatively charged particles, there are two planes at the center of the potential well, which leads to stronger incoherent scattering and dechanneling than in the case of \((1{\bar{1}}0)\) planes. As it is shown in Fig. 2 for our analysis we have chosen the coordinate system in which the x axis lies in the plane of bending of the crystal, and when particles enter the crystal the x axis coincides with the curvature vector of the crystal. Thus, the angle \(\theta _x\) between the particle momentum and the \((1{\bar{1}}0)\) plane is the deflection angle of the particle.

Fig. 2
figure 2

Orientation of a bent silicon crystal with respect to charged particles impinging on the crystal

Full size image

Thus, in the simulation, when particles impinged on the crystal having a small angle to the \(\left\langle 110 \right\rangle \) axis, the stochastic deflection took place. At the same time, if the angle between the momentum of each incident particle and the plane (001) many times exceeded the critical angle of axial channeling \(\psi _c = \sqrt{4 Z |q e|/pvd}\) [10] (Z|e| is the charge of atomic nucleus, q is the charge of the impinging particle, d is the distance between neighboring atoms in \(\left\langle 110 \right\rangle \) atomic strings), which for the considered energy is 118.8 \(\upmu \)rad, and the angle between the momentum of the incident particle and the plane \((1{\bar{1}}0)\) is less than the critical angle of planar channeling, the particles were captured in planar channeling mode in planar channels \((1{\bar{1}}0)\). In the simulation, in order to obtain the conditions under which planar channeling takes place, the angle between the momentum of the incident particles and the axis \(\left\langle 110 \right\rangle \) was taken equal to 2.376 mrad (20 values of the critical angle of axial channeling), which is a sufficient angle to observe planar channeling [18].

First of all, the dependence of the maximum deflection angle of the particles on the bending radius of the crystal for planar channeling was obtained. As shown in [19] the value of this angle depends on the value f of the fraction of beam particles that must be deflected by the bent crystal. The smaller is the given fraction of beam particles, the larger is the maximum deflection angle. We simulated the motion of \(5 \times 10^4\) antiprotons with a kinetic energy of 14 GeV through the bent crystal for different values of the bending radius of the crystal from 2 cm to 0.5 m. The simulation method is described in [20]. For each particle, we determined the thickness of the crystal at which the particle left planar channeling mode, passing into above-barrier mode. In order to obtain the angle of deflection of the particle, this thickness of the crystal must be divided by the bending radius of the crystal (the thickness of the crystal is much smaller than the bending radius of the crystal).

Figure 3 shows the dependence of the maximum deflection angle of antiprotons with a kinetic energy of 14 GeV on the bending radius of the crystal in case of planar channeling. The solid curve corresponds to \(f=5\%\), the dashed curve corresponds to \(f=10\%\), the dash-dotted line corresponds to \(f=15\%\), the dotted line corresponds to \(f=20\%\). The dashed horizontal line shows the value of the critical angle of axial channeling. We see that planar channeling allows to deflect a small part of the beam at an angle that is several times higher than \(\psi _c\). At the same time, as the fraction of particles to be deflected increases, the maximum deflection angle decreases rapidly, and for a fraction of 20% of the particles, this angle is less than \(\psi _c\).

Fig. 3
figure 3

Dependence of the maximum deflection angle of of antiprotons with a kinetic energy of 14 GeV on the bending radius of the crystal in case of planar channeling

Full size image

Similarly, we obtained the dependence of the deflection angle of the particles on the bending radius of the crystal in the case of stochastic deflection of particles. In this case, the bending radius of the crystal varied from 10 cm to 3 m. Particles whose angle between the momentum and the direction of the axis \(\left\langle 110 \right\rangle \) of the crystal became greater than 1.5\(\psi _c\) were considered to have left the stochastic deflection mode [21].

The simulation results are shown in Fig. 4. The solid curve corresponds to \(f=5\%\), the dashed curve corresponds to \(f=10\%\), the dash-dotted line corresponds to \(f=20\%\), the dash-dotted line with two dots corresponds to \(f=30\%\), the dash-dotted line with three dots corresponds to \(f=40\%\), the dotted line corresponds to \(f=50\%\). The dashed horizontal line shows the value of the critical angle of axial channeling. We see that for the same fraction of deflected particles the stochastic mechanism gives larger angles of deflection than planar channeling. In addition, even for a fraction of half of the beam particles, the deflection angle exceeds \(\psi _c\).

Fig. 4
figure 4

Dependence of the maximum deflection angle of of antiprotons with a kinetic energy of 14 GeV on the bending radius of the crystal in case of stochastic deflection

Full size image

3 Taking into account the influence of the initial angular divergence of the beam

Let us now investigate in more detail both mechanisms of deflection in the optimal conditions for each of them. For certainty, we will consider the optimal conditions for the deflection of 10% of the beam particles. By optimal conditions, we mean the choice of the bending radius, which corresponds to the maximum in the dependence of the deflection angle of a given fraction of the beam on the bending radius of the crystal. For planar channeling in this case, the optimal bending radius is 15.9 cm, and the angle of deflection is 212 \(\upmu \)rad. This corresponds to the crystal thickness of 33.7 \(\upmu \)m. Bent crystals of similar thickness and bending radius can be produced and have been used in experiments [22, 23].

Fig. 5
figure 5

Angular distributions of antiprotons after planar channeling in a bent crystal at optimal crystal parameters

Full size image

Figure 5 shows the angular distributions of antiprotons after passing through the bent crystal in the conditions of planar channeling at the optimal crystal parameters mentioned above. Figure 5a corresponds to the case of the beam without angular divergence, and Fig. 5b corresponds to the case of the beam with angular divergence of \(\Delta \psi _{in} = 2\psi _c\). Such angular divergence was chosen because in most CERN experiments on particle deflection using bent crystals, the beam divergence did not exceed two values of the critical axial channeling angle [11,12,13,14,15,16,17]. At the moment, it is difficult to say what will be the angular divergence of the antiproton beam at HESR, therefore, for a rough estimate of the influence of the angular divergence of the beam, we took the indicated value. In the figures we see that for the beam with no angular divergence the deflected part of the beam particles is well collimated and deflected by an angle that is approximately twice larger then \(\psi _c\). However, with increasing angular divergence of the beam, the fraction of deflected particles significantly decreases. This is due to the fact that particles with a large value of the angle between the crystal plane and the initial momentum of the particle are above-barrier with respect to planar channels and are not captured in the channeling mode.

Similar angular distributions were obtained also for the case of stochastic deflection of antiprotons. They are shown in Fig. 6a for the case of the initial beam without angular divergence and in Fig. 6b for the case of the initial beam with angular divergence of \(2\psi _c\). From Fig. 4 we see that at \(f=0.1\) the optimal bending radius of the crystal is 65 cm, and the maximum deflection angle is 540 \(\upmu \)rad. This corresponds to a crystal thickness of 351 \(\upmu \)m. The simulation was performed at these optimal parameters.

Fig. 6
figure 6

Angular distributions of antiprotons after stochastic deflection in a bent crystal at optimal crystal parameters

Full size image

In Fig. 6 we see that the angular distributions in the case of stochastic deflection are very different from the distributions in the case of planar channeling. This is due to the phenomenon of doughnut scattering of particles [24]. We also see that with increasing angular divergence of the beam, the fraction of deflected particles in the case of stochastic deflection decreases not as significantly as in the case of planar channeling.

4 Smaller energies of negatively charged particles

Let us apply the method of determining the optimal deflection conditions for the deflection of antiprotons with a kinetic energy of 1 GeV and 10 GeV. As in the previous two sections, numerical simulation was performed for the \(\left\langle 110 \right\rangle \) axial orientation of silicon crystal in the case of stochastic deflection and the \((1{\bar{1}}0)\) planar orientation of silicon crystal in the case of planar channeling. A characteristic angle in experiments on the deflection of charged particles using bent crystals is the critical angle of axial channeling. For the axial orientation \(\left\langle 110 \right\rangle \) the critical angle of axial channeling of antiprotons with a kinetic energy of 10 GeV is approximately 139 \(\upmu \)rad, and for antiprotons with a kinetic energy of 1 GeV \(\psi _c \approx 376\) \(\upmu \)rad.

Figure 7 shows the dependence of the angle at which a given part of the beam of antiprotons with a kinetic energy of 10 GeV can be deflected using planar channeling (a) and stochastic deflection (b) on the bending radius of the crystal. Numerical simulation was performed by solving a two-dimensional equation of motion for \( 5 \times 10^4\) antiprotons moving in the potential of bent atomic strings. The initial angular divergence of the beam was equal to zero. In the case of planar channeling (Fig. 7a) a solid thick line corresponds to the part of the beam \(f=0.02\), dashed line corresponds to \(f=0.05\), dotted line corresponds to \(f=0.1\), and dash-dotted line corresponds to \(f=0.15\). In the case of stochastic deflection (Fig. 7b), the solid thick line corresponds to the part of the beam \(f=0.02\), dashed line corresponds to \(f=0.05\), dotted line corresponds to \(f=0.1\), dash-dotted line corresponds to \(f=0.15\), dash-dotted line with two dots corresponds to \(f=0.25\), and dash-dotted line with three dots corresponds to \(f=0.5\). A thin solid horizontal line shows the value of \(\psi _c\).

Fig. 7
figure 7

Dependence of the angle at which a given part of a beam of antiprotons with a kinetic energy of 10 GeV can be deflected by means of planar channeling (a) and stochastic deflection (b)

Full size image

The simulation results presented in Fig. 7 showed that both mechanisms allow to deflect a certain part of the beam particles at an angle greater than the critical angle of axial channeling, and for each of mechanisms there is an optimal bending radius of the crystal. At the same time, in the case of planar channeling only less than 15% of the beam particles can be deflected to an angle greater than \(\psi _c\). The stochastic mechanism under the same conditions allows to deflect even half of the beam of antiprotons at a single passage through the bent crystal. The maximum deflection angles in the case of stochastic particle deflection are approximately twice as large as those obtained in the case of planar channeling.

Fig. 8
figure 8

Dependence of the angle at which a given part of a beam of antiprotons with a kinetic energy of 1 GeV can be deflected by means of planar channeling (a) and stochastic deflection (b)

Full size image

In [25, 26] it was shown that as the kinetic energy of particles decreases, the angle of their deflection increase. Let us consider the results of simulation of deflection of antiprotons with a kinetic energy of 1 GeV. Figure 8 shows the dependence of the angle at which a given part of the beam of antiprotons with a kinetic energy of 1 GeV can be deflected using planar channeling (a) and stochastic deflection (b). In the case of planar channeling (Fig. 8a) a solid thick line corresponds to the part of the beam \(f=0.02\), dashed line corresponds to \(f=0.05\), dotted line corresponds to \(f=0.1\). In the case of stochastic deflection (Fig. 8b), the solid thick line corresponds to the part of the beam \(f=0.02\), dashed line corresponds to \(f=0.05\), dotted line corresponds to \(f=0.1\), dash-dotted line corresponds to \(f=0.25\), dash-dotted line with two dots corresponds to \(f=0.5\). A thin solid horizontal line shows the value of the critical angle of axial channeling.

The simulation results presented in Fig. 8, show that the value of deflection angle actually increases as the kinetic energy of antiprotons decreases to 1 GeV. However, it should be noted that the increase in the value of the critical angle of axial channeling is faster than the increase in deflection angle in the case of planar channeling. Only 5% of the beam particles can be deflected at an angle greater than \(\psi _c\), instead of 15%, as in the case of the kinetic energy of 10 GeV antiprotons. Thus, this mechanism loses its efficiency with decrease of particle energy. This is due to the fact that with decreasing energy, the intensity of incoherent scattering on thermal oscillations of the crystal atoms increases. However, the stochastic deflection mechanism at \(E=1\) GeV remains as effective as at \(E=10\) GeV. The deflection angles of the stochastic deflection of antiprotons with a kinetic energy of 1 GeV are more than four times higher than those that can be obtained by planar channeling.

Thus, the comparative analysis showed that the optimal orientation of the bent crystal to obtain the most effective deflection of high-energy antiprotons is the axial orientation. Regarding the radius of curvature of the crystal, the results showed that for \(E=10\) GeV, the optimal radius of curvature of the crystal is about 50 cm, and for \(E=1\) GeV \(R_{opt} \approx 6\) cm. Thus, for energies of antiprotons that will be achievable at FAIR, the dependence of \(R_{opt}\) on E is close to linear. In addition, the exact value of \( R_{opt}\) depends on the choice of the value of f, but with increasing f the value of \( R_{opt} \) decreases rather slowly (see Figs. 7b,  8b).

Using numerical simulation, we also found the angular distribution of antiprotons after passing the bent crystal under optimal conditions for deflection, which were found above (axial orientation of the crystal, \(R_{opt} \approx 50\) cm at \(E = 10\) GeV and \(R_{opt} \approx 6\) cm at \(E = 1\) GeV). The density of these angular distributions along the x axis for antiprotons with a kinetic energy of 10 GeV and 1 GeV is shown in Fig. 9. For \(E = 10\) GeV solid curve corresponds to the thickness of the crystal \(L = 500\) \(\upmu \)m, dashed curve corresponds to \(L = 350\) \(\upmu \)m, dotted curve corresponds to \(L = 250\) \(\upmu \)m. For \(E = 1\) GeV solid curve corresponds to the thickness of the crystal \(L = 180\) \(\upmu \)m, dashed curve corresponds to \(L = 126\) \(\upmu \)m, dotted curve corresponds to \(L = 90\) \(\upmu \)m.

Fig. 9
figure 9

The density of the angular distributions of antiprotons after passing through a bent crystal in optimal conditions for deflection (axial alignment of the crystal with respect to the direction of beam incidence, \(R=R_{opt}\)). a \(E=10\) GeV, b \(E=1\) GeV. \(N_0\) is the total number of particles in the beam, \(N (\theta _x)\) is the number of particles whose angle between between the particle momentum and the \((1{\bar{1}}0)\) plane exceeds \(\theta _x\)

Full size image

Thus, we see that in the range of kinetic energies of antiprotons from 1  to 10 GeV, the stochastic deflection mechanism allows to deflect a significant fraction of beam particles at angles that noticeably exceed the critical angle of axial channeling.

5 Conclusions

To carry out experiments with a fixed target on cyclic accelerators at high energies, it is necessary to ensure the extraction of a part of the beam particles into a straight channel. Such extraction of particles can be carried out from the beam halo using bent crystals. The possibility of such an effect at high energies is due to the presence of correlations in the collisions of particles with bent crystal atomic planes when particles fall along one of the crystallographic planes of the crystal or with bent crystal atomic strings when particles fall along one of the crystallographic axes of the crystal.

In the first case, the beam particles trapped in the planar channeling regime then follow the bending of the crystal atomic planes [3, 4]. Due to this, particles are deflected from the initial direction of their motion by angles that can exceed the value of the critical angle of planar channeling. The account of incoherent effects in scattering leads to the dechanneling of particles from planar channels, which results in a limitation of the maximum values of particle deflection angles based on planar channeling.

In the second case, the beam deflection is due to the features of multiple scattering of particles by bent crystal atomic strings. Herewith, despite the periodicity of the arrangement of atomic strings in a crystal, the phenomenon of dynamic chaos during scattering is possible, in which collisions of a particle with different atomic strings can be considered as random [24, 27, 28]. This phenomenon takes place up to angles between the current direction of the momentum of particles and the current direction of the axis of bent atomic strings on the order of several values of the critical angle of axial channeling. In this case, the scattering of particles occurs mainly along the azimuthal angle in a plane orthogonal to the current direction of the axis of atomic strings. Given this, the particle seems to become entangled between atomic strings and, therefore, follows the bending of the axes of atomic strings, which leads to the deflection of the direction of particle motion by angles exceeding several values of the critical angle of axial channeling [6, 7]. Incoherent effects in scattering lead to the exit of particles from such a regime of their motion and, consequently, to limiting the maximum values of beam deflection angles based on such a stochastic mechanism of particle scattering in a bent crystal. It should be noted that, in order to implement the stochastic deflection mechanism, the crystal must be oriented along the axis with respect to the direction of particle incidence on the crystal, i.e. in contrast to planar channeling, for crystal alignment, it is necessary to use not single-axis, but two-axis goniometers. However, such an alignment of the crystal is possible and was realized, in particular, in experiments [11, 14].

Both mechanisms considered above are realized both for positively and negatively charged particles of high energy. At the same time, their efficiency significantly depends on many factors, such as the sign of the charge of particles, the magnitude of their energy, the thickness of the crystal, the rate of dechanneling and rechanneling of particles, etc. The case of negatively charged particles is of particular interest, since such particles are more likely to approach the thermal spread of the positions of atoms in the crystal lattice and, therefore, incoherent effects in scattering are more significant for such particles than for positively charged particles.

The above analysis showed that for antiprotons with an energy of 1–14 GeV, which are planned to be obtained within the framework of the FAIR project, the stochastic mechanism of particle deflection based on their multiple scattering by bent crystal atomic strings is much more favorable than the mechanism based on the phenomenon of planar channeling. In this case, beam deflection angles of the order of 1 mrad, at which particles can subsequently be extracted into a straight channel, can be achieved using bent silicon crystals with a thickness of about several hundred microns. The production of such crystals and the technique required for their bending have been developed in several laboratories around the world (see, in particular, [29]). Thus, the results obtained indicate the possibility of extracting the antiproton beam from cyclic accelerators into direct channels for conducting experiments on a fixed target within the framework of the FAIR project.