RGESolver: a C++ library to perform renormalization group evolution in the Standard Model Effective Theory

Abstract

Renormalization group evolution above the electroweak scale is a crucial ingredient in the phenomenology of the Standard Model Effective Theory. The RGESolver open-source C++ library performs the evolution at leading order for dimension-six operators in the most general flavour scenario (assuming lepton and baryon number conservation). Given its efficiency, RGESolver can be used to include the effects of renormalization group evolution in extensive phenomenological analyses in the framework of the Standard Model Effective Theory.

1 Introduction

The Standard Model (SM) is one of the biggest scientific successes of our time: it describes three (weak, strong and electromagnetic) of the four currently known elementary interactions in nature, closing a long path started between the nineteenth and the twentieth century. The particle content of the SM was completed in 2012 with the discovery of a Higgs-like boson with properties consistent with the SM within current experimental errors. In spite of its success, however, the SM leaves several phenomena unexplained. For example, neutrino masses, the origin of the baryon asymmetry in the universe and dark matter suggest the presence of physics beyond the SM. The absence of direct evidence of new particles at energies ${\mathcal {O}}\left( \textrm{TeV} \right)$ allows us to parametrize the effects of possible heavy New Physics (NP), lying beyond the reach of the LHC for direct production, with an effective field theory, known as the Standard Model Effective Field Theory (SMEFT) [1, 2]. The SMEFT Lagrangian contains the SM Lagrangian plus a complete set of independent higher-dimensional operators. Working in the framework of the SMEFT makes it possible to search for NP through its virtual effects in a general, model-independent way.

Going from the SM to the SMEFT entails dramatic phenomenological consequences, since the SM enjoys several accidental symmetries that are potentially broken by higher-dimensional operators, such as Baryon (B) and Lepton (L) number conservation, or the absence of tree-level Flavour Changing Neutral Currents (FCNC). Phenomenology requires the coefficients of those higher-dimensional operators that violate accidental symmetries of the SM to be tiny, implying in turn that any NP not too far from the electroweak (EW) scale must be at least approximately invariant under the accidental symmetries of the SM. However, while SM interactions will not generate B or L violation perturbatively if the corresponding operators in the SMEFT have vanishing coefficients, FCNC’s will always be generated, even if NP is invariant under the full $\mathrm {U(3)}^5$ flavour symmetry group of SM gauge interactions, due to the SM Yukawa couplings. Therefore, the flavour properties of the SMEFT Wilson coefficients must be specified at the NP scale, and then the coefficients must be evolved using Renormalization group equations (RGE’s) down to the scale relevant for the processes of interest in order to compute the NP contributions. Conversely, a phenomenological bound on low-scale Wilson coefficients can be turned into a bound on the coefficients at the NP scale, allowing to extract information on the viable values of SMEFT coefficients and, hopefully, on the symmetries of the NP models of interest.

Assuming B and L conservation but a general flavour structure, the SMEFT has 2499 independent operators, so that the full system of RGE’s involves more than 2500 parameters. At Leading Order (LO), the renormalization group (RG) evolution is dictated by the Anomalous Dimension Matrices (ADM’s) of the SMEFT operators, which in general receive contributions from scale-dependent gauge and Yukawa couplings, as well as from the Higgs self-coupling. Since the ADM contributions proportional to different couplings are in general non-commuting, an analytic resummation of logarithmic contributions cannot be achieved and the numerical solution of the full system of equations is the only possibility, in particular when the NP scale is much heavier than the EW one. RGESolver is an open-source C++ library that performs the RG evolution of the SMEFT Wilson coefficients in a fast and easy-to-use manner, as detailed below. RGESolver will be also integrated in HEPfit [3], a flexible open-source tool which, given the Standard Model or any of its extensions, allows to fit the model parameters to a given set of experimental observables and to obtain predictions for observables.

This paper is organized as follows: we briefly introduce the theoretical framework of the SMEFT in Sect. 2, presenting the notation used in RGESolver. In Sect. 3 we describe in more detail the structure of the library, with a specific focus on the handling of the flavour structure and on the implementation of the numerical solution of the RGE’s. Section 4 is devoted to describing the usage of RGESolver: we discuss the installation procedure and we describe how to use the basic functionalities of the library, together with a list of its most important methods. We discuss the efficiency of the library and the comparison with DSixTools [4, 5] in Sect. 5. We present our conclusions in Sect. 6.

2 Theoretical framework: the SMEFT

As discussed above, the absence of new particles at energies at or above the TeV scale allows us to parametrize the effects of physics beyond the SM with a tower of dimension ${\mathfrak {D}}>4$, Lorentz and gauge-invariant operators [1, 2]. The resulting effective field theory is the SMEFT. The SM gauge group is

$$\begin{aligned} {\mathcal {G}}_{\textrm{SM}}\equiv \mathrm {SU(3)}_{\textrm{C}} \otimes \mathrm {SU(2)}_{\textrm{W}}\otimes \mathrm {U(1)}_{\textrm{Y}}. \end{aligned}$$

(1)

The three factors represent color, weak isospin and hypercharge gauge group. The quantum numbers of SM fields under ${\mathcal {G}}_{\textrm{SM}}$ are listed in Table 1.

Table 1 $\mathrm {SU(3)}_{\textrm{C}} \otimes \mathrm {SU(2)}_{\textrm{W}}\otimes \mathrm {U(1)}_{\textrm{Y}}$ quantum numbers of SM fields. p is a flavour index

The Lagrangian of the Standard Model is (following the notation used in Refs. [6,7,8])

(2)

With this notation, when spontaneous symmetry breaking occurs, the physical Higgs boson acquires a mass given by $m^2_H = 2 \lambda v^2$, with $v = (\sqrt{2} G_F)^{-1/2}\sim 246$ GeV. The sum over $\psi$ is extended to all fermion fields in the SM, both left-handed (q, l) and right-handed (u, d, e). The gauge covariant derivative is $D_\mu = \partial _\mu$ $+ i g_1 {\textsf{y}}_{} B_\mu$ $+i g_2 t^I W_\mu ^I$ $+i g_3 T_{} ^{A}G_\mu ^A$, with $T_{} ^{A}$ and $t^I= \tau _{} ^{I}/2$¹ the generators in the fundamental representation of $\mathrm {SU(3)}$ and $\mathrm {SU(2)}$ respectively:

$$\begin{aligned}{}[ T_{} ^{A}, T_{} ^{B}] = i f^{ABC} T_{} ^{C}, \quad [t^{I},t^{J}] = i \varepsilon ^{IJK} t^K. \end{aligned}$$

(3)

Finally, ${\tilde{H}}$ and ${\tilde{X}}$ (with $X = B,W^I,G^A$) are defined via the totally antisymmetric Levi-Civita symbol, with $\varepsilon _{12}=1$ and $\varepsilon _{0123}=1$:

$$\begin{aligned} \tilde{H_j} = \varepsilon _{jk} H^{* k}, \quad {\tilde{X}}^{\mu \nu } = \frac{1}{2} \varepsilon ^{\mu \nu \rho \sigma } X_{\rho \sigma }. \end{aligned}$$

(4)

Fermions appear in $n_g = 3$ different generations, so every fermion field carries, together with the gauge indices, a generation (or flavour) index that runs from 1 to 3. We did not write explicitly neither of these indices in (2) for the sake of simplicity. Yukawa couplings $Y_\psi$ are thus complex matrices in flavour space.

Table 2 The 59 independent dimension-six operators built from SM fields which conserve baryon and lepton number. p, r, s, t are fermion flavour indices, j, k are indices in the fundamental representation of $\mathrm {SU(2)}_{\textrm{W}}$, I, J, K (A, B, C) are indices in the adjoint representation of $\mathrm {SU(2)}_{\textrm{W}}$ ($\mathrm {SU(3)}_{\textrm{C}}$) and greek letters ($\mu ,\nu \dots$) are Lorentz indices. Contraction of indices in the fundamental representation of $\mathrm {SU(3)}_{\textrm{C}}$ is implicit

At dimension six a complete basis of independent and gauge invariant operators that conserve B and L is given by the so-called Warsaw basis, defined in [2] and displayed in Table 2. Their independence means that no linear combination of them and their Hermitian conjugates vanishes due to the equations of motion (up to total derivatives). The equations of motion are used at ${\mathcal {O}}\left( 1/\Lambda ^2 \right)$ level, so they can be derived from ${\mathcal {L}}_{\textrm{SM}}$ alone.

The Warsaw basis consists of 59 operators, for a total of 2499 independent parameters in the generic flavour scenario (see Appendix A of Ref. [8]). The operators are divided in 8 classes, depending on their field content, which schematically are

$$\begin{aligned} \begin{array}{lll} 1: X^3, &{} 2:H^6, &{} 3: H^4 D^2, \\ 4:X^2 H^2, &{} 5:\psi ^2 H^3, &{} 6: \psi ^2 HX, \\ 7:\psi ^2 H^2 D, &{} 8: \psi ^4, &{} \end{array} \end{aligned}$$

(5)

where X stands for a gauge field-strength tensor (or its dual), $\psi$ for a fermion field, D for a derivative and H is the Higgs field.

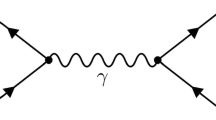
To conclude the discussion about the SMEFT we note that higher dimensional operators contribute to observables not only through their matrix element, but also through their contribution to the running of SM couplings. An example is given by the diagrams in Fig. 1. Coherently with the power counting, their effects in the running of $\lambda$ are suppressed by a factor of $m^2_H/\Lambda ^2$. The contributions to the running of the SM parameters due to SMEFT operators are available in Ref. [6].

Fig. 1

Two SMEFT diagrams that contribute to the running of the Higgs quartic coupling $\lambda$. The solid square denotes a SMEFT vertex and the dot denotes a SM vertex

2.1 Flavour basis and back-rotation

In the SM a unitary transformation for each fermion field in flavour space,

$$\begin{aligned} \psi = R_\psi ^\dagger \psi ^\prime , \qquad \psi = q,l,u,d,e, \end{aligned}$$

(6)

does not alter the structure of the Lagrangian, provided the Yukawa matrices are redefined as

$$\begin{aligned} {\left\{ \begin{array}{ll} {Y}_{u} = R_u^\dagger {Y}_{u}^\prime R_q,\\ {Y}_{d} = R_d^\dagger {Y}_{d}^\prime R_q,\\ {Y}_{e} = R_e^\dagger {Y}_{e}^\prime R_l. \end{array}\right. } \end{aligned}$$

(7)

This freedom allows to diagonalize simultaneously two out of the three matrices (${Y}_{e}$ and one between ${Y}_{u}$ and ${Y}_{d}$).² Denoting with ${\hat{{Y}_{}}}$ a diagonal Yukawa matrix we can define two reference bases: the down basis where ${{Y}_{e}}=$ ${\hat{{Y}_{e}}}$, ${{Y}_{d}}=$ ${\hat{{Y}_{d}}}$, ${{Y}_{u}}={\hat{{Y}_{u}}} V$ and the up basis where ${{Y}_{e}}= {\hat{{Y}_{e}}}$, ${{Y}_{u}}={\hat{{Y}_{u}}}$, ${{Y}_{d}}= {\hat{{Y}_{d}}} V^\dagger$, with V a unitary matrix. In the SM, V is the Cabibbo–Kobayashi–Maskawa matrix. In the SMEFT this is not true, since the mass matrices are not simply proportional to the Yukawa couplings due to the contributions from dimension-six operators. With a slight abuse of notation, in the following we still refer to the matrix V as the CKM matrix. It is worth noticing that the matrix V is not the one appearing in the interaction vertices between quarks and $W^{\pm }$ bosons, again due to effects from higher dimensional operators. A more detailed discussion is available in Section 2 of Ref. [9].

Notice that the up and down bases are not stable under renormalization group evolution, even in the SM. For example, the SM $\beta$ function for ${Y}_{d}$ (available in Ref. [10]) contains a term proportional to ${Y}_{d}({Y}_{d}^\dagger {Y}_{d}-{Y}_{u}^\dagger {Y}_{u} )$, which is always non-diagonal in flavour space. Starting from a diagonal ${Y}_{d}$ at the scale $\mu _{\textrm{I}}$ (down basis) leads to a non-diagonal ${Y}_{d}$ at a different scale $\mu _{\textrm{F}}$. To go back into the down basis, a further flavour rotation is thus required. Clearly, the same holds for the up basis.In the SMEFT the flavour transformations in Eq. (6) imply not only a redefinition of the Yukawa couplings, but also a rotation of the Wilson coefficients. For example, the coefficient ${\mathcal {C}}_{dH} ^{}$ of operator ${\mathcal {O}}_{dH} ^{}$ is redefined as ${\mathcal {C}}_{dH} ^{} = R_q^\dagger {\mathcal {C}}_{dH} ^{\prime } R_d$. It should be noticed that the flavour rotations are not uniquely determined by the singular value decomposition. The three Yukawa matrices are diagonalized via six unitary matrices:

$$\begin{aligned} {Y}_{\psi }= U_\psi {\hat{{Y}_{\psi }}} V^{\dagger }_\psi , \quad \psi = u,d,e. \end{aligned}$$

(8)

If $U_\psi ,\,V_\psi$ satisfy the relation (8), also $U_\psi \phi _\psi ,\,V_\psi \phi _\psi$ with $\phi _\psi = \text {diag}\left( e^{\alpha _1^\psi },e^{\alpha _2^\psi },e^{\alpha _3^\psi }\right)$ satisfy it. The phase matrices $\phi _u,\, \phi _d$ are determined unambiguosly once the phase convention for the CKM matrix is chosen, while, in the absence of right-handed neutrinos, the phase of the lepton matrices cannot be determined. A possibility to fix the phases would be using one of the SMEFT coefficients that involve leptons, but this would not be a general solution. In fact, the user may want to set that coefficient to 0, frustrating the choice of phase convention. To overcome this problem, we choose $\phi _e = \text {diag}\left( e^{-i \arg \left[ \left( U_e\right) _{11}\right] }, e^{-i \arg \left[ \left( U_e\right) _{22}\right] }, e^{-i \arg \left[ \left( U_e\right) _{33}\right] }\right)$. This choice ensures that an evolution between two energy scales close to each other produces a small change in the coefficients. The user is then free to perform the rotation in the lepton sector choosing any other convention.

To go into the up basis, the rotation matrix $R_q$ in (6) must be set equal to $V_u\phi _u$. To go into the down basis one must instead set $R_q = V_d\phi _d$. Obviously, in both bases one sets $R_u=U_u\phi _u$, $R_d=U_d\phi _u$, $R_l=V_e\phi _e$ and $R_e=U_e\phi _e$.

2.2 Solution of the renormalization group equations

The RGE for a parameter $x_i$, that in this context is a SMEFT coefficient ${\mathcal {C}}_{i} ^{}$ or a SM parameter, is

$$\begin{aligned} \mu \frac{d x_i}{d \mu } \equiv \beta _{i}\left( \{x_j\}\right) , \end{aligned}$$

(9)

that defines the $\beta$-function for the parameter. In general, when the theory has multiple parameters, the $\beta$-function for $x_i$ can contain terms proportional to integer powers of $x_i$, but also terms proportional to other parameters $x_j$, $i \ne j$. In this article we always consider the $\beta$-functions at one-loop level.

The $\beta$-functions of SMEFT coefficients (as well as SMEFT contributions to the running of SM parameters) are available in Refs. [6,7,8], the SM $\beta$-functions of gauge couplings can be found for example in Ref. [11] and the $\beta$-functions of Yukawa couplings, $m_H^2$ and $\lambda$ in Ref. [10].³

The $\beta$-function for SMEFT coefficients must be linear in the coefficients themselves by power counting. In fact, the product of two dimension-six SMEFT coefficients would be suppressed by a factor of $1/\Lambda ^4$, negligible at ${\mathcal {O}}\left( m^2_H/\Lambda ^2 \right)$. This allows to write the RGE’s for the ${\mathcal {C}}_{i} ^{}$s introducing the anomalous dimension matrix $\Gamma$ (ADM),

$$\begin{aligned} \mu \frac{ d {\mathcal {C}}_{i} ^{} }{d \mu } = \frac{1}{16 \pi ^2} \Gamma _{ij} {\mathcal {C}}_{j} ^{} . \end{aligned}$$

(10)

The indices i, j in the previous equation run on the whole set of independent coefficients: $\Gamma$ is a square $2499 \times 2499$ matrix. Clearly, the $\beta$-function for the i-th coefficient is $\beta _{{ {\mathcal {C}}_{i} ^{} }}=$ $\Gamma _{ij} {\mathcal {C}}_{j} ^{} /(16 \pi ^2)$.

A simple approximation consists in neglecting the $\mu$ dependence of the right-hand side of Eq. (10) and taking only linear order terms in $\ln \left( \mu _{\text {F}} / \mu _{\text {I}}\right)$, yielding

$$\begin{aligned} {\mathcal {C}}_{i} ^{} (\mu _{\text {F}}) = {\mathcal {C}}_{i} ^{} (\mu _{\text {I}}) + \Gamma _{ij}(\mu _{\text {I}}) {\mathcal {C}}_{j} ^{} (\mu _{\text {I}}) \frac{\ln {\left( \mu _{\text {F}} / \mu _{\text {I}}\right) }}{16 \pi ^2}. \end{aligned}$$

(11)

While this drastic simplification may be appropriate for cases in which the two energy scales are not too different, so that the second term in Eq. (11) is a small correction, in general the log on the right-hand side will become large, calling for a resummation of log-enhanced terms.

To provide a more accurate solution of the system of first-order differential equations in Eq. (10) is a non-trivial task since the anomalous dimension matrix depends on $\mu$ through the SM couplings, the running of which is in turn influenced by SMEFT operators. The anomalous dimension matrix can be written as

$$\begin{aligned} \Gamma _{ij} (\mu )= g_1^2 (\mu ) \Gamma _{ij} ^{(g_1^2)} + g_2^2(\mu ) \Gamma _{ij} ^{(g_2^2)} + \cdots , \end{aligned}$$

(12)

where the matrices on the right-hand side do not depend on the renormalization scale. In general the $\Gamma ^{(g_i)}$ matrices cannot be diagonalized simultaneously: an exact analytic solution of the system is then impossibile. One could proceed with an hybrid scheme as commonly done in the Effective Theory for Weak interactions (WET) below the EW scale, where QCD and QED corrections are implemented by resumming the logs generated by the strong coupling only. However, in the SMEFT the top Yukawa coupling is also large, calling for the resummation of both strong and Yukawa contributions.

Thus, a numerical approach is required to obtain precise results in the general case.⁴ More details about the implementation of this method are given in Sect. 3.2.

3 Description of the library

RGESolver is implemented in C++. We use the GNU Scientific Library for the integration of the RGE’s (more information about the numerical methods used are given below). The whole code (including input and output) handles separately real and imaginary parts of the parameters.

3.1 Flavour structure

Operators (or equivalently their coefficients) in the SMEFT can be divided in different categories according to their symmetry properties as in Table 3,⁵ where we partially modify the notation used in Table 14 of Ref. [5].

Table 3 Symmetry categories for operators in the SMEFT. nF indicates the number of flavour indices for each category

We work splitting real and imaginary part for each ${\mathcal {C}}_{i} ^{}$. For example, the real part of the coefficient of an Hermitian 2F operator is a (real) symmetric matrix, while the imaginary part is a (real) antisymmetric matrix. Also the real and imaginary part of symmetric 4F operators are in different categories. This is not the case for non-Hermitian operators: the real and imaginary parts of their coefficient do not have any constraints, and they belong to categories 1 (2F) and 5 (4F). Clearly it is convenient to store and evolve only the independent parameters, but for ease of use it is convenient to be able to access the coefficients with any combination of indices, not only the independent ones. We achieve this flexibility by defining specific symmetry-aware getters and setters for each category. For example, setting $\textrm{Re}[ {\mathcal {C}}_{Hl(1)} ^{1,2} ]=0.5$ via S.SetCoefficient(“CHl1R”,0.5,1,2) (where S is an instance of the RGESolver class) will lead to S.GetCoefficient(“CHl1R”,2,1) returning the value 0.5 due to Hermiticity.

3.2 Numerical implementation of renormalization group evolution

As already mentioned, we use the routines provided by the GNU Scientific Library (GSL, [13]) to perform the integration of the RGEs. Let $\vec {y}$ be the vector that contains all the independent parameters of the SMEFT. Introducing $t = \ln ( \mu / \text {GeV})$, the system in Eq. (9) can be rewritten as

$$\begin{aligned} \frac{d \vec {y}}{d t} = \vec {\textrm{f}}(\vec {y}), \end{aligned}$$

(13)

where the right-hand side of the equation depends on t only through $\vec {y}$. When all the symmetries of the operators are considered, the coefficients of operators at dimension-six level are completely determined through 2499 independent real parameters. The three gauge couplings $g_1$, $g_2$, $g_3$, the Higgs quartic coupling $\lambda$ and the mass $m_H$ of the Higgs boson are real scalars. Yukawa couplings ${Y}_{u}$, ${Y}_{d}$ and ${Y}_{e}$ are $3\times 3$ complex matrices, each of which has 18 parameters.⁶ This yelds 59 further parameters, raising the total number to 2558: this is the dimension of $\vec {y}$. The system in Eq. (9) is thus a 2558-dimensional system of first order coupled differential equations. We use an adaptive stepsize routine to solve the system: the stepsize h is changed throughout the integration in order to match the estimated local error $E_i$ with a user-defined error level, to obtain the maximum efficiency. The desired error level $D_i$ for each component is determined through four parameters $a_y$, $a_{dydt}$, $\epsilon _{\text {abs}}$ and $\epsilon _{\text {rel}}$ with the expression

$$\begin{aligned} D_i = \epsilon _{\text {abs}} + \epsilon _{\text {rel}} \left( a_y |{y_i}|+ h a_{dydt} \left| \frac{d y_i}{d t} \right| \right) \end{aligned}$$

(14)

The second term in brackets in the previous expression ensures a correct estimation also for situations where some components $y_i$ are very close to zero. The error is determined not only from the value $y_i$ but also from its increment. In particular, we use $a_y=$ $a_{dydt}=1$.

$E_i$ can be estimated with the step-doubling technique, that consists in advancing the solution from t to $t+2h$ in two different ways (performing two steps of length h or one step of length 2h) and taking the error as the difference between the two. A more sofisticated and efficient error estimate is possible for the embedded integration methods, where the same evaluations of the function $\vec {\text {f}}$ are used to compute two different values of the solution at $t+h$. The error is taken as the difference between the two values (see Section 16.2 of Ref. [14]).

If $E_i$ exceeds the desired error $D_i$ by more than $10 \%$ for any component, the stepsize is reduced according to

$$\begin{aligned} h \rightarrow h \times 0.9 \times \left( \frac{E}{D}\right) ^{-\frac{1}{q}}, \end{aligned}$$

(15)

where 0.9 is a safety factor (the error can only be estimated, not accurately determined), q is the consistency order of the method (i.e. the local error scales as $h^{q+1}$) and $E/D = \max _i \left( E_i / D_i \right)$ is the maximum ratio of estimated and desired error among the components.

If, instead, the estimated error is lower than the desired one (precisely, when E/D $<50 \%$) the stepsize is increased according to

$$\begin{aligned} h \rightarrow h \times 0.9 \times \left( \frac{E}{D}\right) ^{-\frac{1}{q+1}}. \end{aligned}$$

(16)

To avoid uncontrolled changes in the stepsize, the overall scaling factor is limited to the range (1/5, 5). In RGESolver the explicit embedded Runge–Kutta–Fehlberg method is used (with initial stepsize $h=\ln (\mu /\Lambda )/100$), for which $q=4$.

It should be stressed that Eq. (14) refers to a local error: there is no simple relation that connects the four parameters to an estimate of the global error affecting the final result. We tested the accuracy of the adaptive stepsize integration comparing it with a fixed-step integration with an high number of steps. Using $\mu _{\text {I}}= \Lambda = 1000\,$ TeV and $\mu _{\text {F}}=250$ GeV as energy scales, $\epsilon _{\text {abs}}=10^{-16}$ and $\epsilon _{\text {rel}}=10^{-4}$ for the adaptive integration and $N_{\text {FS}}=1000$ steps for the fixed stepsize integration we obtained percentual differences $\lesssim 10^{-5}$. The initial conditions for SM parameters at the high energy scale are obtained evolving them from $\mu \sim v$ to $\Lambda$ with the pure SM $\beta$-functions (namely neglecting SMEFT contributions). The initial conditions for SMEFT coefficients are ${\mathcal {O}}\left( 1/\Lambda ^2 \right)$, as prescribed by the power counting.

4 Using RGESolver

4.1 Installation

RGESolver is a free software released under the GNU General Public License. The download can be performed directly from the command line, typing in the terminal:

More details can be found on the dedicated $\texttt {GitHub}$ webpage. The extended documentation is also available here

4.1.1 Dependencies

The installation of RGESolver requires the availability of CMake in the system (version 3.1 or greater). A description of CMake and the instructions for its installation can be found in the $\texttt {CMake}$ website. We list below the dependencies that need to be satisfied to succesfully install RGESolver:

• GSL: The GNU Scientific Library (GSL) is a C library for numerical computations. More details can be found on the $\texttt {GSL}$ website.

• BOOST: BOOST is a set of libraries for the C++ programming language. RGESolver requires only the BOOST headers, not the full libraries, thus a header-only installation is sufficient. More details can be found on the $\texttt {BOOST}$ website.

• C++11: a C++ compiler supporting at least the C++11 standard.

If all dependencies are satisfied, the installation procedure is completed typing in a terminal session in the downloaded RGESolver directory:

The available options are:

• -DLOCAL_INSTALL=ON: to install RGESolver in the directory build/install (default: OFF).

• -DCMAKE_INSTALL_PREFIX=<RGESolverinstallation directory>: the directory in which RGESolver will be installed (default: /usr/local). This variable cannot be modified when -DLOCAL_ INSTALL=ON is set.

• -DDEBUG_MODE=ON: to enable the debug mode (default: OFF).

• -DBOOST_INCLUDE_DIR=<boost custom include path>/boost/ : CMake checks for BOOST headers availability in the system and fails if they are not installed. Thus, if BOOST is not installed in the predefined search path, the user can specify where it is with this option. The path must end with the boost/ directory which contains the headers.

• -DGSL_CONFIG_DIR=<path to gsl-config>: RGESolver uses gsl-config to get the GSL parameters. If this is not in the predefined search path, the user can specify it with this option.

If no <options> are specified, the default installation will be performed. Note that, depending on the setting of installation prefix, root privileges may be required (thus cmake --install . should be replaced with sudo cmake --install .). RGESolver can be uninstalled by typing in the build directory of the RGESolver library the command (sudo) cmake --build . --target uninstall.

4.2 Class methods

Here we briefly describe the most important methods available in RGESolver. The detailed documentation is available on $\texttt {GitHub}$.

4.2.1 Evolution

• void Evolve(std::string method, double muI, double muF): performs the one-loop renormalization group evolution from $\mu =$ muI to $\mu =$ muF (where muI and muF are expressed in GeV). The current values of the SMEFT parameters are taken as initial condition at $\mu =$ muI. After the evolution, they are updated with the new values at $\mu =$ muF. The available methods for the solution of the RGE’s are “Approximate” and “Numeric”. The first method is faster than the latter, but less accurate, as explained in Sect. 2.2.

• void EvolveSMOnly(std::string method, double muI, double muF): same as Evolve, but only for the SM parameters. The user should use this method instead of Evolve when interested in pure SM running. Using this function is the same of using Evolve with all the SMEFT coefficients set to 0, but it is faster since it computes only the evolution for the SM parameters.

• void EvolveToBasis(std::string method, double muI, double muF, std::string basis): same as Evolve, but performs in addition the flavour back-rotation described in Sect. 2.1 to go into the selected basis (“UP” or “DOWN”). After the evolution, the CKM matrix is computed.

• void GenerateSMInitialConditions(...): generates the initial conditions for Standard Model parameters ($g_1, g_2, g_3, \lambda , \, m_h^2,$ ${Y}_{u},\,{Y}_{d},\,{Y}_{e}$) at the scale muFin (in GeV), using one-loop pure SM beta functions. At such scale, the CKM matrix is computed.The generation can be done starting from user-defined low-energy input or using the default values summarized in Table 4 (the arguments to be passed to the function are different in the two cases, see the documentation for the details and Sect. 4.3 for an example). In case of user-defined input, this method should be used with usual fermion hierarchy (smallest mass for the 1st generation and greatest mass for the 3rd without mass degeneracy for all up and down quarks and for charged leptons).

Table 4 SM parameters used by default to generate SM initial conditions at an arbitrary scale. The scale at which these parameters are given is $\mu = 173.6$ GeV. We follow UTfit for what concerns the conventions for the CKM matrix

4.2.2 Input and output

Table 5 Standard Model parameters in RGESolver. The last 3 labels of this table must be used with the GetCKMAngle method. All the others must be used with the GetCoefficient method

Table 6 SMEFT coefficients without flavour indices in RGESolver

Table 7 SMEFT coefficients with two flavour indices in RGESolver

Table 8 SMEFT coefficients with four flavour indices in RGESolver

Getters and setters take as first argument a string (name), that identifies the corresponding parameter. The names that must be used to correctly invoke these functions are reported in Tables 5, 6, 7 and 8. The functions for non-scalar coefficients take as additional arguments the flavour indices (2 or 4), that must be in the interval [0:2].

• void SetCoefficient(std::string name, double val): setter function for the scalar parameters. Sets the parameter name equal to val.

• double GetCoefficient(std::string name): getter function for the scalar parameters. Returns the parameter name.

• void SetCoefficient(std::string name, double val, int i, int j): setter function for the parameters with two flavour indices. Sets the parameter name[i,j] equal to val.

• double GetCoefficient(std::string name, int i, int j): getter function for the parameters with two flavour indices. Returns the parameter name[i,j].

• void SetCoefficient(std::string name, double val, int i, int j, int k, int l): setter function for the parameters with four flavour indices. Sets the parameter name[i,j,k,l] equal to val.

• double GetCoefficient(std::string name, int i, int j, int k, int l): getter function for the parameters with four flavour indices. Returns the parameter name[i,j,k,l].

• double GetCKMAngle(std::string name), double GetCKMPhase(): getter methods to access CKM matrix parameters. These methods should be called only after methods that choose a specific flavour basis (as GenerateSM InitialConditions() or EvolveToBasis()), in which case the CKM matrix is updated.

• double GetCKMRealPart(int i, int j), double GetCKMImagPart(int i, int j): getter functions for the real and imaginary part of the (i, j) element of the CKM matrix. These methods should be called only after methods that choose a specific flavour basis (as GenerateSM InitialConditions() or EvolveToBasis()), in which case the CKM matrix is updated. The indices must be in the range [0:2].

• void SaveOutputFile(std::string filename, std::string format): saves the current values of the SMEFT parameters in the file filename. Currently, the only available format is Susy Les Houches Accord “SLHA” ( [15]).

4.2.3 Numerical integration parameters

Here we list the methods related to the parameters that control the numerical evolution, as described in Sect. 3.2:

• void Setepsrel(double epsrel): sets $\epsilon _{\text {rel}}$ equal to epsrel (the default value is $\epsilon _{\text {rel}}=5\times 10^{-3}$).

• double epsrel(): returns $\epsilon _{\text {rel}}$.

• void Setepsabs(double epsabs): sets $\epsilon _{\text {abs}}$ equal to epsabs (the default value is $\epsilon _{\text {abs}}=10^{-13}$).

• double epsabs(): returns $\epsilon _{\text {abs}}$.

4.2.4 General methods

4.3 Writing and compiling a program using the library

We discuss here the usage of the main methods of the class, in order to make the reader acquainted with RGESolver’s functionalities. The examples discussed in this section can be found in the $\texttt {Examples}$ directory repository. Let us start with the simplest case: the renormalization group evolution from an high-energy scale $\Lambda =10{,}000$ GeV to $\mu _{\textrm{Low}} = 250$ GeV with a single non-zero SMEFT coefficient at the starting scale, namely ${\mathcal {C}}_{HG} ^{}$. We do not report the whole program here, but we discuss just the crucial steps. This program is available under the name ExampleEvolution.cpp. The library must be included with

Inside the main, an instance of the class must be created:

We define the two energy scales (given in GeV) and we set the initial condition.

The (numeric) evolution is then performed using the line

At this point, the user can access the evolved coefficients via the GetCoefficient() methods (see Tables 5, 6, 7 and 8 for a list of all the names to be used). For example, this line prints on the terminal the evolved value of ${\mathcal {C}}_{HG} ^{}$.

The user should compile this program typing in the terminal⁷

If the RGESolver library is not in the predefined search path (as usually is the case for local installation), it may be necessary to specify the path needed for compilation and linking against RGESolver. A rgesolver-config script is available in the <CMAKE_INSTALL_PREFIX>/bin directory, which can be invoked with the following options:

• $-$ $-$cflags: to obtain the include path needed for compilation against RGESolver.

• $-$ $-$libs: to obtain the flags needed for linking against RGESolver.

A more advanced example can be found in ExampleBackRotation.cpp. The goal is to perform the evolution from $\Lambda =10{,}000$ GeV to $\mu _{\textrm{Low}}=250$ GeV and perform the back-rotation. The default initial conditions for the SM parameters in Table 4 are given at the scale $\mu =173.65$ GeV. It is possible to generate the initial conditions for the SM parameters at any scale, both evolving the default input or using a different set of values. We thus define our custom input, starting from the energy scale at which the input is given:

We then define the masses of the fermions (in GeV), the CKM parameters (the CKM phase must be expressed in radians), the gauge couplings, the quartic coupling and the Higgs’ mass squared (in $\textrm{GeV}^2$):

The initial conditions at the scale $\Lambda$ are thus generated in the down basis through the solution of the pure SM RGE’s (via numeric integration) simply using:

As anticipated, the user can also take advantage of the default low-energy input for the SM parameters via:

Having generated the initial conditions for the SM parameters, the user can thus set the values of the SMEFT coefficients at the scale $\Lambda$ and perform the evolution to $\mu _{\textrm{Low}}$, as done before. We don’t discuss this since the syntax is the same of the previous case.

The evolution and the back-rotation (in the down basis) are performed via:

Since this method computes also the CKM matrix, we can access its parameters or its elements using the dedicated getter functions. For example, the following lines print on-screen $\sin \theta _{12}$ at the scale muLow:

5 Execution times and comparison with DSixTools

We tested our code against DSixTools ( [4, 5]), a Mathematica package for the handling of the SMEFT (and the Low-energy Effective Field Theory, but we focus on the SMEFT part of the package). DSixTools solves the SMEFT RGE’s numerically and via the approximation described in Sect. 2.2, as RGESolver does. We performed an evolution from $\Lambda$ to $\mu _{\text {Low}}=250$ GeV with both codes to compare the values of the coefficients after the evolution. The initial conditions at the high energy scale $\Lambda$ for the SM parameters are obtained using pure SM RGE’s to run them up to such scale. We set ${\mathcal {O}}\left( 1/\Lambda ^2 \right)$ initial conditions for every SMEFT coefficient at $\mu =\Lambda$.⁸ The result of this comparison is displayed in Table 9.To compare the two results, we introduce $\Delta ^{\textrm{max}} = \max | {\mathcal {C}}_{i} ^{\texttt{R}} (\mu _{\textrm{Low}})- {\mathcal {C}}_{i} ^{\texttt{D}} (\mu _{\textrm{Low}})|/(1/\Lambda ^2)$, with ${\mathcal {C}}_{i} ^{\texttt{R}(\texttt{D})} (\mu _{\textrm{Low}})$ the evolved coefficient computed by RGESolver (DSixTools). We observe that the two codes produce the same results up to ${\mathcal {O}}\left( 10^{-5}/\Lambda ^2 \right)$ (${\mathcal {O}}\left( 10^{-6}/\Lambda ^2 \right)$) in the case of numeric solution (approximate solution). Clearly, the agreement is better for the simpler solution, namely the approximate one.

Table 9 Comparison between DSixTools and RGESolver. The first (last) three values refer to the approximate solution (numeric solution)

Let us briefly discuss RGESolver’s efficiency performances. We report in Table 10 the execution times that we measured (referring to a PC whose specifications are shown in Table 11). The execution times consider not only the evolution, but also the input/output (setting the initial conditions for the SMEFT parameters and accessing them after the evolution). These times should not be taken as exact, but as an order-of-magnitude estimate.

This result should be compared to the execution times of DSixTools, that can be up to ${\mathcal {O}}\left( 20 \,\textrm{s} \right)$ (${\mathcal {O}}\left( 10 \,\textrm{s} \right)$) for the numeric (approximate) solution. This package performs a consistency check on the input that affects heavily the execution time for large inputs. Such impact is $\sim 8\,$s for the input used in the comparison between the two programs.

Conversely, considering just 3 non vanishing independent operators at $\mu = \Lambda$, the execution time is ${\mathcal {O}}\left( 10\,\textrm{s} \right)$ (${\mathcal {O}}\left( 2 \,\textrm{s} \right)$) for the numeric (approximate) solution.

Table 10 Execution times of C++ programs that use RGESolver

Table 11 Technical specifications of the computer used for the test

6 Conclusions

RGESolver is an open-source C++ library that performs the renormalization group evolution in the context of the SMEFT at dimension-six level, in the most general flavour scenario. Only operators that preserve baryon and lepton number are considered. RGESolver was designed to be easy to use, highly efficient and suitable to perform extensive phenomenological analysis. To this aim, it will be included in HEPfit ( [3]), a multipurpose and flexible analysis framework that can be used for fitting models to experimental and theoretical constraints. RGESolver outperforms DSixTools in execution time by two orders of magnitude, while retaining an excellent accuracy. Further details and the full documentation can be found on $\texttt {GitHub}$.