1 Introduction

Modified gravity is one of the two main avenues that one can follow in order to describe the early and late phases of Universe’s acceleration [1, 2], and compared to the other alternative, namely the introduction of the inflaton/dark-energy concept [3,4,5], has the additional advantage of being closer to the quantum description of gravity [6]. Although the simplest way to build novel classes of gravitational theories is to start from the standard, curvature, formulation of gravity and extend it in various ways [7,8,9,10,11], one can equally well follow the alternative, torsional, formulation and extend it suitably. In particular, since the basic torsional theory, namely the teleparallel equivalent of general relativity (TEGR) [12, 13] uses the torsion scalar T as the Lagrangian, one can construct torsional modifications extending it such as in f(T) gravity [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40], in \(f(T,T_G)\) gravity [41, 42], in f(T, B) gravity[43], in scalar-torsion theories [44, 45], etc.

On the other hand, primordial black holes (PBHs), firstly introduced in the early ’70s [46,47,48], have rekindled the interest of the scientific community given the fact that they can solve a number of fundamental issues of modern cosmology. In particular, they may indeed constitute a viable candidate for dark matter [49, 50], and explain the large-scale structure formation process through the Poisson fluctuations they can seed [51, 52]. At the same time, depending on their mass they can give access to a wide variety of physical phenomena from the early universe up to late times [53].

PBHs are tightly connected with gravitational wave (GW) physics, and specifically through the GW signals they are associated with [54]. In particular, PBHs are connected with GW background signals from PBH merging events  [55,56,57,58,59,60] and from PBH Hawking radiated gravitons [61, 62], as well as with scalar induced gravitational waves, which are induced at second order in cosmological perturbation theory either from primordial curvature perturbations [63,64,65,66,67,68,69] (for a recent review see [70]) or from Poisson PBH energy density fluctuations [71,72,73]. All these signals have been mainly studied within the context of general relativity.

Hence, given the motivation behind modified gravity theories, one can use the aforementioned GW portal associated to PBHs in order to constrain them. Specifically, there have been some first attempts in  [74, 75], where the authors study the primordial scalar induced GWs within the context of Hordenski gravity and non-canonical Higgs inflation, as well as in  [76] where the scalar induced GWs from PBH Poisson fluctuations were studied within f(R) gravity theories and in particular within Starobinsky inflation.

In this manuscript, we focus on f(T) modified gravity, and we study the scalar induced GWs from Poisson fluctuations of ultralight PBHs (i.e. with \(m_\textrm{PBH}<10^{9}\textrm{g}\)), which evaporate before BBN and transiently dominate the energy content of the universe before their evaporation [59, 77,78,79]. Thus, the main goal of the work is to examine whether such an analysis will impose constraints on the various specific f(T) models, similarly to other observational investigations [80,81,82,83,84,85,86,87,88].

The plan of the work is as follows: in Sect. 2 we review the calculation of the PBH gravitational potential of Poisson distributed PBHs within general relativity, and in Sect. 3 we perform the extended analysis, extracting the PBH gravitational potential in the framework of f(T) gravity. In Sect. 4 we focus on three mono-parametric f(T) gravity models and we present the formalism for the computation of the relevant scalar induced gravitational wave signal. Then, in Sect. 5 we investigate the modifications of the GW signal within f(T) gravity by accounting for GW source and GW propagation effects, showing that f(T) theories of gravity safely pass the constraints imposed by the gravitational-wave signal induced from PBH Poisson fluctuations. Finally, Sect. 6 is devoted to conclusions.

2 The primordial black hole gravitational potential in general relativity

In this section, we briefly review the calculation of the PBH gravitational potential in the case of general relativity, following [71, 76]. We first present the background and perturbation equations, and then we extract the power spectrum of the PBH gravitational potential.

2.1 Background evolution and scalar perturbations

We consider a flat Friedmann–Lemaître–Robertson–Walker (FLRW) background geometry with metric

$$\begin{aligned} \textrm{d}s^{2}_\textrm{b}=-\textrm{d}t^{2}+a^{2}(t)\delta _{ij}\textrm{d}x^{i}\textrm{d}x^{j}\,, \end{aligned}$$
(2.1)

where a(t) is the scale factor. Additionally, we consider that the Universe is filled with hydrodynamic fluid matter described with energy–momentum tensor \(T^{\textrm{m}}_{\mu \nu } = \textrm{diag}( - \bar{\rho },\) \( \bar{p}, \bar{p}, \bar{p})\), where \(\bar{\rho }\) and \(\bar{p}\) are the total matter (i.e. including radiation, baryonic and dark matter) energy density and pressure. Thus, the Friedmann equations are

$$\begin{aligned} H^2&= \frac{8\pi G }{3} \bar{\rho }+ \frac{\Lambda }{3} \equiv \frac{8\pi G }{3} \bar{\rho }_{\textrm{tot}} \end{aligned}$$
(2.2)
$$\begin{aligned} \dot{H} + H^2&=-\frac{4\pi G }{3} \left( \bar{\rho }+ 3\bar{p}\right) {+} \frac{\Lambda }{3} \equiv -\frac{4\pi G }{3} \left( \bar{\rho }_{\textrm{tot}} + 3\bar{p}_{\textrm{tot}}\right) , \end{aligned}$$
(2.3)

where G is the Newton constant (throughout this paper we work in units where \(c=1\)), \(\Lambda \) is the cosmological constant, \(H=\dot{a}/a\) is the Hubble parameter and dots denote derivatives with respect to the cosmic time t. Note that we have introduced the total background energy density and pressure, \(\bar{\rho }_{\textrm{tot}}\) and \(\bar{p}_{\textrm{tot}}\), which include the total matter sector alongside with the cosmological constant.

In order to proceed to the investigation of the scalar perturbations it proves convenient to introduce the conformal time \(\eta \), defined as \(\textrm{d}t \equiv a \textrm{d}\eta \), and hence the conformal Hubble parameter reads as \(\mathcal {H}\equiv a'/a=aH\), where primes denote derivatives with respect to \(\eta \). Restricting ourselves to scalar perturbations in the Newtonian gauge, we can write the perturbed metric as

$$\begin{aligned} \textrm{d}s^2 = a^2(\eta )\left\{ -(1+2\Psi )\textrm{d}\eta ^2 + \left[ (1-2\Phi )\delta _{ij}\right] \textrm{d}x^i\textrm{d}x^j\right\} , \nonumber \\ \end{aligned}$$
(2.4)

where \(\Psi \) and \(\Phi \) are the two Bardeen potentials [89]. Additionally, we include perturbations around the background stress-energy tensor of the total matter content of the Universe (matter and radiation) which we express as follows:

$$\begin{aligned} T^{0}_{0}&= -(\bar{\rho }+ \delta \rho )\nonumber \\ T^{0}_{i}&= (\bar{\rho }+ \bar{p})\upsilon _{i} \, , \, \, \upsilon _{i} \equiv a \delta u_{i} \nonumber \\ T^{i}_{j}&= \bar{p}( \delta ^{i}_{j} + \Pi ^{i}_{j}), \end{aligned}$$
(2.5)

where \(\delta \equiv \delta \rho / \bar{\rho }\)   is the relative energy density perturbation, \(\delta u_i \equiv \upsilon _i/a \) is the velocity perturbation and \(\Pi ^i_j\) is the (dimensionless) anisotropic stress. In this context, one obtains the following perturbed equations for \(\Phi \) and \(\Psi \) [90]:

$$\begin{aligned}&3\mathcal {H}(\Phi ' + \mathcal {H}\Psi ) -\nabla ^2\Phi = -4\pi G a^2 \, \delta \rho \end{aligned}$$
(2.6)
$$\begin{aligned}&(\Phi ' + \mathcal {H}\Psi )_{,i} = 4\pi G a^2 (\bar{\rho }+ \bar{p}) \upsilon _{i} \end{aligned}$$
(2.7)
$$\begin{aligned}&\Phi '' + \mathcal {H}(\Phi ' + 2\Psi ') + (\mathcal {H}^2 + 2\mathcal {H}')\Phi \nonumber \\&\quad + \nabla ^2(\Phi - \Psi ) /3 = 4\pi G a^2 \delta p \end{aligned}$$
(2.8)
$$\begin{aligned}&\Phi - \Psi = 8\pi G a^2 \bar{p}\Pi . \end{aligned}$$
(2.9)

In the time period that we focus on, \(\Pi ^i_j\) is negligible and therefore \(\Phi \approx \Psi \), which we consider to be the case from now on. Elaborating on the above equations, and using also the (total) conservation equation \(\bar{\rho } ' = - 3\mathcal {H}(\bar{\rho } + \bar{p})\), one obtains

$$\begin{aligned}{} & {} \Phi '' + 3\mathcal {H}\left( 1+c^2_\textrm{s}\right) \Phi ' - c^2_\textrm{s}\nabla ^2\Phi + 3\left( c^2_\textrm{s} - w \right) \mathcal {H}^2\Phi \nonumber \\{} & {} \quad = - \frac{9}{2}c^2_\textrm{s} (1+ w) \mathcal {H}^3\left( \frac{\delta p}{\bar{p}'} - \frac{\delta \rho }{\bar{\rho }'} \right) , \end{aligned}$$
(2.10)

with \(w \equiv \bar{p}/ \bar{\rho }\) being the equation-of-state parameter and \( c^2_\textrm{s}\equiv \bar{p}' / \bar{\rho }' \) the sound speed square of the total matter content sector. Hence, during the period of PBH domination, \(\Phi \) is the potential arising from the PBH distribution.

2.2 The PBH gravitational potential power spectrum

In order to proceed we assume conventionally that PBHs are formed in the radiation-dominated era. Considering that PBHs are randomly distributed, their energy density is inhomogeneous while the total background energy density is homogeneous, and thus their energy density perturbations can be viewed as isocurvature Poisson fluctuations with the associated Poissonian power spectrum for the PBH density contrast being read as [71]

$$\begin{aligned} \mathcal {P}_\delta (k) = \frac{k^3}{2\pi ^2}P_\delta (k)= \frac{2}{3\pi } \left( \frac{k}{k_{\textrm{UV}}}\right) ^3 \Theta (k_\textrm{UV}-k), \end{aligned}$$
(2.11)

where we have assumed monochromatic PBH mass function [91]. Additionally, \(k_{\textrm{UV}}\equiv a/\bar{r}\) is the Ultraviolet (UV) cut-off scale, which is related to the mean PBH separation scale, since at smaller scales the PBH fluid description is not valid. Introducing then the density parameter for the PBH fluid as \(\Omega _\textrm{PBH}\equiv \frac{\rho _\textrm{PBH}}{\rho _\textrm{tot}}\) we can find that during the radiation-dominated era, \(\Omega _\textrm{PBH} \propto a\), and therefore if the initial PBH abundance is sufficiently large then PBHs can dominate. Hence, the isocurvature PBH perturbations in the radiation-dominated era will be converted to adiabatic curvature perturbations in the subsequent PBH dominated era [92, 93].

In order to relate \(\Phi \) and \(\delta _\textrm{PBH}\), we introduce the uniform-energy density curvature perturbation of each fluid, \(\zeta _i\) [94]. At super-horizon scales, \(\zeta _\textrm{r}\) and \(\zeta _\textrm{PBH}\) are separately conserved, hence at the PBH formation time we can neglect the adiabatic contribution associated to the radiation fluid on the scales we are interested in and obtain

$$\begin{aligned} \zeta \simeq \frac{1}{3} \delta _\textrm{PBH}(t_\textrm{f})\quad \textrm{for}\quad k\ll \mathcal {H}\,. \end{aligned}$$
(2.12)

Thus, during the PBH-matter dominated era, where \(w=0\) and \(\Phi \) is constant in time [95] using the fact that on super-horizon scales \(\zeta \simeq - \mathcal {R}\) [94], where \(\mathcal {R}\) is the comoving curvature perturbation, as well as the relation between \(\mathcal {R}\) and \(\Phi \) in GR [95], we finally obtain that [71, 76]

$$\begin{aligned} \Phi \simeq -\frac{1}{5} \delta _\textrm{PBH}(t_\textrm{f})\quad \textrm{for}\quad k\ll \mathcal {H}\,. \end{aligned}$$
(2.13)

On the other hand, at sub-horizon scales one can determine the evolution of \(\delta _ \textrm{PBH}\) by solving the evolution equation for the matter density perturbations

$$\begin{aligned} \delta ^{\prime \prime }_\textrm{m}+\mathcal {H}\delta ^\prime _\textrm{m}-4\pi G a^2\bar{\rho }_\textrm{m}\delta _\textrm{m} = 0 , \end{aligned}$$
(2.14)

which, in the case of a Universe with radiation and PBH-matter, takes the form of the so-called Mészaros growth equation [96]:

$$\begin{aligned} \frac{\textrm{d}^2 \delta _\textrm{PBH}}{\textrm{d}s^2}+\frac{2+3s}{2s(s+1)}\frac{\textrm{d}\delta _\textrm{PBH}}{\textrm{d}s}-\frac{3}{2s (s+1)} \delta _\textrm{PBH}=0\,. \end{aligned}$$
(2.15)

By solving the Mészaros growth equation we deduce that the dominant solution deep in the PBH-dominated era is  [71, 76]

$$\begin{aligned} \delta _\textrm{PBH}\simeq \frac{3s}{2} \delta _\textrm{PBH}(t_\textrm{f}). \end{aligned}$$
(2.16)

Since the Bardeen potential is related to the density contrast through the Poisson equation, one gets that in the matter-dominated era

$$\begin{aligned} \delta _\textrm{PBH} = -\frac{2}{3} \left( \frac{k}{\mathcal {H}}\right) ^2\Phi , \end{aligned}$$
(2.17)

and thus inserting into Eq. (2.16) we find

$$\begin{aligned} \Phi \simeq -\frac{9}{4}\left( \frac{\mathcal {H}_{\textrm{d}}}{k}\right) ^2\, \delta _\textrm{PBH}(t_\textrm{f}) \quad \textrm{for}\quad k\gg {\mathcal {H}}_{\textrm{d}}\, , \end{aligned}$$
(2.18)

with \({\mathcal {H}}_{\textrm{d}}\) being the conformal Hubble parameter at the PBH domination time. At the end, interpolating between (2.18) and (2.13), and using (2.11), we obtain that

$$\begin{aligned} \mathcal {P}_\Phi (k) \equiv \frac{k^3}{2\pi ^2}P_\Phi (k)= \frac{2}{3\pi }\left( \frac{k}{k_\textrm{UV}}\right) ^3 \left( 5+\frac{4}{9}\frac{k^2}{k_{\textrm{d}}^2}\right) ^{-2}, \end{aligned}$$
(2.19)

with \(k_\textrm{d}\equiv \mathcal {H}_\textrm{d}\) being the comoving scale exiting the Hubble radius at PBH domination time.

3 The primordial black hole gravitational potential in f(T) gravity

In this section we perform the calculation of the PBH gravitational potential in the framework of f(T) gravity. We first review the relevant background and perturbation equations and then we proceed to calculate the associated power spectrum.

3.1 Background evolution and scalar perturbations

In the torsional formulation of gravity one uses the tetrad or vierbein fields \({\textbf{e}_A(x^\mu )}\) as the dynamical variables instead of the metric tensor. They form an orthonormal basis for the tangent space at each point \(x^\mu \) of the manifold, that is \( e_A\cdot e_B = \eta _{AB}\), where Greek and Latin indices run in coordinate and tangent space respectively and \(\eta _{AB}=\textrm{diag} (-1,1,1,1)\) is the Minkowski metric for the (flat) tangent space. One can express them in the coordinate basis \(\textbf{e}_A=e^\mu _A\partial _\mu \) and thus construct the metric as

$$\begin{aligned} g_{\mu \nu }(x)=\eta _{AB}\, e^A_\mu (x)\, e^B_\nu (x). \end{aligned}$$
(3.1)

In teleparallel gravity one describes gravity using the torsion of spacetime instead of its curvature. In this spirit, instead of the familiar Christoffel connection, which is the unique connection whose torsion vanishes, one can introduce the Weitzenböck connection \(\overset{\textbf{w}}{\Gamma }^\lambda _{\nu \mu }\equiv e^\lambda _A\, \partial _\mu e^A_\nu \), which is a connection whose curvature vanishes [12]. The torsion tensor is given by

$$\begin{aligned} {T}^\lambda _{\,\mu \nu }\equiv \overset{\textbf{w}}{\Gamma }^\lambda _{ \nu \mu }- \overset{\textbf{w}}{\Gamma }^\lambda _{\mu \nu } =e^\lambda _A\,(\partial _\mu e^A_\nu -\partial _\nu e^A_\mu ), \end{aligned}$$
(3.2)

and its contraction provides the torsion scalar as

$$\begin{aligned} T\equiv \frac{1}{4} T^{\rho \mu \nu } T_{\rho \mu \nu } +\frac{1}{2}T^{\rho \mu \nu }T_{\nu \mu \rho } -T_{\rho \mu }^{\ \ \rho }T_{\ \ \ \nu }^{\nu \mu }. \end{aligned}$$
(3.3)

Using T as a Lagrangian gives rise to the teleparallel equivalent of general relativity (TEGR), since variation in terms of the tetrads leads to the same field equations with general relativity [12].

One then can generalize TEGR by extending T to an arbitrary function of T as the Lagrangian, resulting to f(T) gravity, whose action is [14]

$$\begin{aligned} S = \frac{1}{16\pi G} \int \textrm{d}^4x \, |e| \, f(T) + \int \textrm{d}^4x \, |e| \, \mathcal {L}_\textrm{m} , \end{aligned}$$
(3.4)

with \(|e| = \textrm{det}(e^{A}_{\mu }) = \sqrt{-g}\), and where we have included the total matter Lagrangian \(L_m\) for completeness. Variation of the action (3.4) with respect to the tetrad \(e^{A}_{\mu }\) yields the following field equations:

$$\begin{aligned}{} & {} e^{-1}\partial _{\mu }(ee_A^{\rho }S_{\rho }{}^{\mu \nu })f_{T} + e_A^{\rho }S_{\rho }{}^{\mu \nu }\partial _{\mu }({T})f_{TT} {-}f_{T}e_{A}^{\lambda }T^{\rho }{}_{\mu \lambda }S_{\rho }{}^{\nu \mu }\nonumber \\{} & {} \quad +\frac{1}{4} e_ {A } ^ { \nu }f({T}) = 4\pi Ge_{A}^{\rho }\overset{\textbf{em}}{T}_{\rho }{}^{\nu }, \end{aligned}$$
(3.5)

with \(f_{T}\equiv \partial f/\partial T\), \(f_{TT}\equiv \partial ^{2} f/\partial T^{2}\) and where \(\overset{\textbf{em}}{T}_{\rho }{}^{\nu }\) denotes the total matter energy–momentum tensor. Note that for convenience we have introduced the super-potential tensor \( S_\rho ^{\,\,\,\mu \nu }\equiv \frac{1}{2}\Big (K^{\mu \nu }_{\,\,\,\,\rho } +\delta ^\mu _\rho \,T^{\alpha \nu }_{\,\,\,\,\alpha }-\delta ^\nu _\rho \, T^{\alpha \mu }_{\,\,\,\,\alpha }\Big )\), with \(K^{\mu \nu }_{\,\,\,\,\rho }\equiv -\frac{1}{2}\Big (T^{\mu \nu }_{ \,\,\,\,\rho } -T^{\nu \mu }_{\,\,\,\,\rho }-T_{\rho }^{\,\,\,\,\mu \nu }\Big )\) being the contorsion tensor.

Applying f(T) gravity in a cosmological framework we impose the FLRW metric (2.1), which in turn arises from the tetrad \(e_{\mu }^A=\textrm{diag}(1,a,a,a)\). Inserting this ansatz into (3.5) one obtains the familiar Friedmann equations

$$\begin{aligned} H^2&= \frac{8\pi G }{3}\left( \bar{\rho }+\rho _{\mathrm {f(T)}}\right) \equiv \frac{8\pi G }{3} \bar{\rho }_{\textrm{tot}} \end{aligned}$$
(3.6)
$$\begin{aligned} \dot{H} + H^2&=-\frac{4\pi G }{3} \left( \bar{\rho }+ 3\bar{p}+\rho _{\mathrm {f(T)}} +3p_{\mathrm {f(T)}} \right) \nonumber \\&\quad \equiv -\frac{4\pi G }{3} \left( \bar{\rho }_{\textrm{tot}} + 3\bar{p}_{\textrm{tot}}\right) , \end{aligned}$$
(3.7)

where we have defined the effective energy density and pressure due to the f(T) modification as [14]

$$\begin{aligned}{} & {} \rho _{\mathrm {f(T)}}\equiv \frac{3}{8\pi G}\left[ -\frac{f}{6}+\frac{Tf_T}{3}-\frac{T}{6}\right] , \end{aligned}$$
(3.8)
$$\begin{aligned}{} & {} p_{\mathrm {f(T)}}\equiv \frac{1}{16\pi G}\left[ \frac{f-f_{T} T +2T^2f_{TT}}{ f_{T}+2Tf_{TT}}\right] , \end{aligned}$$
(3.9)

with equation-of-state parameter given by

$$\begin{aligned}{} & {} w_{\mathrm {f(T)}}\equiv \frac{p_{\mathrm {f(T)}}}{\rho _{\mathrm {f(T)}}}= \frac{f-f_{T} T +2T^2f_{TT}}{ (f_{T}+2Tf_{TT})(-f+2 Tf_T- T)} . \nonumber \\ \end{aligned}$$
(3.10)

Thus, \(\bar{\rho }_{\textrm{tot}}\equiv \bar{\rho }+ \rho _{\mathrm {f(T)}} \) and \(\bar{p}_{\textrm{tot}}\equiv \bar{p}+ p_{\mathrm {f(T)}} \). Lastly, note that in FLRW geometry according to (3.3) the torsion scalar becomes simply \(T=6H^2\).

Proceeding to the perturbation level and focusing on scalar perturbations, one can write the perturbed tetrad fields as follows:

$$\begin{aligned} e_{\mu }^A = \bar{e}_{\mu }^A + {\mathbb {E}}_{\mu }^A ~, \end{aligned}$$
(3.11)

where the symbols \({e}_{\mu }^A\) and \(\bar{e}_{\mu }^A\) are used for the perturbed and the unperturbed tetrad fields correspondingly. Then, one can impose the following ansatz for the scalar contributions of the perturbed tetrad fields:

$$\begin{aligned} \bar{e}_{\mu }^0 = \delta _{\mu }^0, \,\,\,\,\, \bar{e}_{\mu }^a = \delta _{\mu }^aa, \,\,\,\,\, \bar{e}^{\mu }_0 = \delta ^{\mu }_0, \,\,\,\,\, \bar{e}^{\mu }_a = \frac{\delta ^{\mu }_a}{a} ~, \end{aligned}$$
(3.12)

and

$$\begin{aligned} {\mathbb {E}}_{\mu }^0 = \delta _{\mu }^0\Psi , \,\,\, {\mathbb {E}}_{\mu }^a =-\delta _{\mu }^a a\Phi , \, \,\, {\mathbb {E}}^{\mu }_0 = -\delta _{0}^{\mu }\Psi , \,\,\, {\mathbb {E}}^{\mu }_a = \frac{\delta ^{\mu }_ a}{a}\Phi .\nonumber \\ \end{aligned}$$
(3.13)

In the above expressions, the scalar perturbations \(\Phi \) and \(\Psi \) are introduced, which are functions of space \(\textbf{x}\) and time t. With such a choice, one can match the tetrad perturbations with a perturbed metric in the Newtonian gauge [17, 97], namely

$$\begin{aligned} \textrm{d}s^2 = -(1 + 2\Psi ) \textrm{d}t^2 +a^2(1-2\Phi )\delta _{ij} \textrm{d}x^i \textrm{d}x^j. \end{aligned}$$
(3.14)

Following then [14], and writing \(f(T)= T+ F(T)\), one can expand the gravitational equations of motion (3.5) to linear order and obtain the (00), (0i), (ij) and (ii) component perturbation equations, which read as follows:

$$\begin{aligned}&\left( 1+F_{T} \right) \frac{\nabla ^2}{a^2}\Psi -3(1+F_{T})H\dot{\Psi }-3(1+F_{T})H^2\Phi \nonumber \\&\quad +36F_{TT}H^3(\dot{\Psi }+H\Phi ) = 4{\pi }G ~ \delta \rho ~, \end{aligned}$$
(3.15)
$$\begin{aligned}&(1+F_{T}-12H^2F_{TT}) (\dot{\Psi }+H\Phi ) = 4{\pi }G (\bar{\rho } + \bar{p})\upsilon ~, \end{aligned}$$
(3.16)
$$\begin{aligned}&(1+F_{T})(\Psi -\Phi ) = 8{\pi }G ~\bar{p}\Pi ~, \end{aligned}$$
(3.17)

and

$$\begin{aligned}&(1+F_{T}-12H^2F_{TT})\ddot{\Psi }+H(1+F_{T}-12H^2F_{TT})\dot{\Phi }\nonumber \\&\quad +3H(1+F_{T} -12H^2F_{TT} \nonumber \\&\quad -12\dot{H}F_{TT}+48H^2\dot{H}F_{TTT})\dot{\Psi }\nonumber \\&\quad +\left[ 3H^2(1+F_{T}-12H^2F_{TT}) +2\dot{H}\right. \nonumber \\&\quad \times \left. (1+F_{T}-30H^2F_{TT} +72H^4F_{TTT})\right] \Phi \nonumber \\&\quad +\frac{1+F_{T}}{3a^2}\nabla ^2(\Psi -\Phi ) = 4{\pi }G ~\delta {p} ~, \end{aligned}$$
(3.18)

where the total matter content of the Universe is expressed as in (2.5).

In the context of this work, all the models of f(T) gravity that we are going to investigate (see Sect. 5) are the viable ones, characterised by \(F_T\ll 1\), \(F_{TT}\ll 1\) and \(F_{TTT}\ll 1\) [82]. Furthermore, as we already mentioned in the previous section, the anisotropic stress can be neglected, and therefore by virtue of (3.17) one obtains that \(\Phi \sim \Psi \). Therefore, under these conditions it is straightforward to show that from the form of the aforementioned equations one can use for the evolution of \(\Phi \) the GR equation (2.10), namely:

$$\begin{aligned}{} & {} \Phi '' + 3\mathcal {H}\left( 1+c^2_\textrm{s}\right) \Phi ' - c^2_\textrm{s}\nabla ^2\Phi + 3\left( c^2_\textrm{s} - w \right) \mathcal {H}^2\Phi \nonumber \\{} & {} \quad = - \frac{9}{2}c^2_\textrm{s} (1+ w) \mathcal {H}^3\left( \frac{\delta p}{\bar{p}'} - \frac{\delta \rho }{\bar{\rho }'} \right) . \end{aligned}$$
(3.19)

On the other hand, we stress out that the effect of f(T) gravity will be taken into account at the level of the evolution of the matter density contrast, as we will show in the next subsection, as well as at the level of the tensor perturbations (see Sect. 4).

Regarding the evolution of the matter density contrast, it is given via the growth equation, which is derived from (3.15) and (3.16) at subhorizon scales, and assuming matter domination it is given by [82, 98]

$$\begin{aligned} \delta ^{\prime \prime }_\textrm{m}+\mathcal {H}\delta ^\prime _\textrm{m}-4\pi G_\textrm{eff} a^2\bar{\rho }_\textrm{m}\delta _\textrm{m} = 0. \end{aligned}$$
(3.20)

In this expression the quantity

$$\begin{aligned} G_\textrm{eff}\equiv \frac{{G}}{f_{T}} \end{aligned}$$
(3.21)

is the effective Newton’s constant and primes denote derivatives with respect to the conformal time. Thus, comparing (2.14) and (3.20), one can see that the effect of f(T) gravity at the level of the matter perturbations at sub-horizon scales is essentially captured by the modification of the Newton’s constant, which is related to the modification of the gravitational field. As we can see, in the limit \(F(T)\rightarrow const.=-2\Lambda \) all the above equations recover the ones of \(\Lambda \)CDM cosmology.

3.2 The power spectrum of the PBH gravitational potential in f(T) gravity

We shall now repeat the procedure of Sect. 2.2 but in the context of f(T) gravity. Once again, we will use the uniform-energy density curvature perturbation of each fluid, \(\zeta _i\), in order to relate \(\Phi \) and \(\delta _\textrm{PBH}\). For \(\zeta \) we will use the usual definition [94]:

$$\begin{aligned} \zeta \equiv -\Phi - \mathcal {H}\frac{\delta \rho }{\bar{\rho }'} . \end{aligned}$$
(3.22)

The relevant fluids for our analysis are the radiation and the PBH-matter ones. Their corresponding energy–momentum tensors are both conserved, i.e. the (background) continuity equation \(\bar{\rho }_{i} ' = - 3\mathcal {H}(\bar{\rho }_{i} + \bar{p}_{i})\) holds for each fluid, and thus \(\zeta _{i}\) is expressed as:

$$\begin{aligned} \zeta _{i} \equiv -\Phi + \frac{\delta _{i}}{3(1+w_{i})}. \end{aligned}$$
(3.23)

By substituting the equation of state \(w_{i}\) for each fluid we obtain:

$$\begin{aligned}{} & {} \zeta _\textrm{r}=-\Phi +\frac{1}{4} \delta _\textrm{r}, \end{aligned}$$
(3.24)
$$\begin{aligned}{} & {} \zeta _\textrm{PBH}=-\Phi +\frac{1}{3} \delta _\textrm{PBH}. \end{aligned}$$
(3.25)

Moreover, we introduce the isocurvature perturbation defined as:

$$\begin{aligned} S = 3\left( \zeta _\textrm{PBH}-\zeta _\textrm{r}\right) =\delta _\textrm{PBH} - \frac{3}{4} \delta _\textrm{r} \,. \end{aligned}$$
(3.26)

On superhorizon scales, \(\zeta _\textrm{r}\) and \(\zeta _\textrm{PBH}\) are conserved separately  [94], like the isocurvature perturbation S. Thus, in the PBH-dominated era, \(\zeta \simeq \zeta _\textrm{PBH} = \zeta _{\textrm{r}}+S/3 \simeq S/3\). Since S is conserved, it can be calculated at formation time \(t_\textrm{f}\). Consequently, neglecting the adiabatic contribution associated to the radiation fluid at the PBH formation time, since it does not play any role at the scales considered here, from Eq. (3.26) we obtain that \(S=\delta _\textrm{PBH}(t_\textrm{f})\). Hence, as in the case of GR we find that

$$\begin{aligned} \zeta \simeq \frac{1}{3} \delta _\textrm{PBH}(t_\textrm{f})\quad \textrm{if}\quad k\ll \mathcal {H}\,. \end{aligned}$$
(3.27)

Further, as we show explicitly in Appendix A, in the context of f(T) gravity the property \(\zeta \simeq -\mathcal {R}\) is valid too at super-horizon scales as it does in GR (see e.g. [94]), by requiring that \(F_T\ll 1\), with \(\mathcal {R}\) being the comoving curvature perturbation defined in the usual way

$$\begin{aligned} \mathcal {R} \equiv \frac{2}{3}\frac{{\Phi }^\prime /\mathcal {H}+\Phi }{1+w }+\Phi . \end{aligned}$$
(3.28)

During a matter-dominated era, such as the one driven by PBHs, \(\Phi ^\prime \) can be neglected since it is proportional to the decaying mode, thus we obtain \(\mathcal {R}=-\zeta =(5/3)\Phi \). Therefore, combining with (2.12), we deduce that

$$\begin{aligned} \Phi \simeq -\frac{1}{5} \delta _\textrm{PBH}(t_\textrm{f})\quad \textrm{if}\quad k\ll \mathcal {H}\,. \end{aligned}$$
(3.29)

Let us now focus on sub-Hubble scales. We can determine the evolution of \(\delta _ \textrm{PBH}\) by solving the evolution equation of the matter density perturbations in f(T) gravity (3.20). At the background level, the Friedmann equation (2.2) can be expressed as \( \mathcal {H}^2 = \frac{8\pi Ga^2}{3}\left[ \bar{\rho }_\textrm{PBH}+\bar{\rho }_\textrm{r}+ \rho _\mathrm {f(T)}\right] \) where \(\bar{\rho }^\mathrm {f(T)}\) is given by (3.8). Since at the epochs we focus on, namely before Big Bang Nucleosynthesis (BBN), we expect that deviations from \(\Lambda \)CDM are negligible, we can neglect the effective fluid contribution, writing the Friedmann equation as

$$\begin{aligned} \mathcal {H}^2 \simeq \mathcal {H}^2_\textrm{f}\Omega ^2_\textrm{PBH,f}\left( \frac{1}{s}+\frac{1}{s^2}\right) . \end{aligned}$$
(3.30)

In this equation, \(s\equiv a/a_\textrm{d}\) and \(a_\textrm{d}\) denotes the time at the transition from the radiation to the PBH domination era, while we have assumed that \(\Omega _\textrm{r,f}=1\) since PBHs are considered to be formed in the radiation era [71]. Note that the scale factor is normalised at one at formation time, i.e. \(a_\textrm{f}=1\).

At the perturbation level, we can treat the gas of PBHs as a matter fluid, and by using s as the time variable, the growth equation (3.20) can be recast in the following form:

$$\begin{aligned} \frac{\textrm{d}^2 \delta _\textrm{PBH}}{\textrm{d}s^2}+\frac{2+3s}{2s(s+1)}\frac{\textrm{d}\delta _\textrm{PBH}}{\textrm{d}s}-\frac{3}{2s (s+1)} \frac{1}{ f_T} \delta _\textrm{PBH}=0\,. \nonumber \\ \end{aligned}$$
(3.31)

We proceed by relating our solution for \(\delta _\textrm{PBH}\) from (3.31) with \(\Phi \), via the sub-Hubble scale approximation of the time-time field equation in f(T) gravity for the PBH dominated era (Eq. (3.15)), which is:

$$\begin{aligned} \delta _\textrm{PBH} = -\frac{2}{3} \left( \frac{k}{\mathcal {H}}\right) ^2 f_T\Phi . \end{aligned}$$
(3.32)

Hence, making an interpolation between Eqs. (3.29) and  (3.32), as in the case of GR, and using the expression for the PBH matter power spectrum in Eq. (2.11), we straightforwardly extract the following PBH gravitational potential power spectrum:

$$\begin{aligned} \mathcal {P}_\Phi (k) \equiv \frac{k^3}{2\pi ^2}P_\Phi (k)= & {} \frac{2}{3\pi }\left( \frac{k}{k_\textrm{UV}}\right) ^3\nonumber \\{} & {} \left[ 5+\frac{2}{3} \left( \frac{k}{\mathcal {H}}\right) ^2 \frac{f_T}{\xi (a)}\right] ^{-2}. \end{aligned}$$
(3.33)

In the above expression, \(\xi (a)\) is defined as

$$\begin{aligned} \xi (a)\equiv \frac{\delta _\textrm{PBH}(a)}{\delta _\textrm{PBH}(a_\textrm{f})}, \end{aligned}$$
(3.34)

where \(\delta _\textrm{PBH}(a)\) is the solution of Eq. (3.31). As verified numerically, \(\xi (a)\) has a mild dependence on the comoving scale k, and thus for practical reasons we will consider \(\xi (a)\) as k independent.

4 Scalar induced gravitational waves in f(T) gravity

Since we have calculated the power spectrum of the gravitational potential of the initially Poisson-distributed PBHs, we can now proceed to the extraction of the stochastic gravitational wave background induced from the PBH Poisson fluctuations.

4.1 Tensor perturbations

The perturbed metric in the Newtonian gauge, assuming as mentioned above zero anisotropic stress, can be recast as

$$\begin{aligned} \textrm{d}s^2= & {} a^2(\eta )\left\{ -(1+2\Phi )\textrm{d}\eta ^2 + \left[ (1-2\Phi )\delta _{ij}\right. \right. \nonumber \\{} & {} \quad \left. \left. + \frac{h_{ij}}{2}\right] \textrm{d}x^i\textrm{d}x^j\right\} , \end{aligned}$$
(4.1)

where we have multiplied by a factor 1/2 the second-order tensor perturbation as it is standard in the literature. Then, by Fourier transforming the tensor perturbations and taking into account the two polarization modes of the GWs in f(T) gravity [99], namely the \(\times \) and the \(+\) as in GR case, the equation of motion for the tensor modes \(h_{\varvec{k}}\) reads as

$$\begin{aligned} h_{\varvec{k}}^{s,\prime \prime } + 2\mathcal {H} (1-\gamma _T) h_{\varvec{k}}^{s,\prime } + k^{2} h^s_{\varvec{k}} = 4 S^s_{\varvec{k}}\, , \end{aligned}$$
(4.2)

with \(s = (+), (\times )\). In this equation the modified dispersion due to the f(T) effects is quantified by the term [100]

$$\begin{aligned} \gamma _T \equiv -\frac{f_T'}{2\mathcal {H} f_T}, \end{aligned}$$
(4.3)

while the source function \(S^s_{\varvec{k}}\) is given by

$$\begin{aligned} S^s_{\varvec{k}}{} & {} = \int \frac{\textrm{d}^3 {\varvec{q}}}{(2\pi )^{3/2}}e^s_{ij}({\varvec{k}})q_iq_j\nonumber \\{} & {} \quad \times \left[ 2\Phi _{\varvec{q}}\Phi _{\varvec{k-q}} + \frac{4}{3(1+w_\textrm{tot})}(\mathcal {H}^{-1}\Phi _{\varvec{q}} ^{\prime }\right. \nonumber \\{} & {} \quad \left. +\Phi _{\varvec{q}})(\mathcal {H}^{-1}\Phi _{\varvec{k-q}} ^{\prime }+\Phi _{\varvec{k-q}}) \right] , \end{aligned}$$
(4.4)

where the polarization tensors \(e^{s}_{ij}(k)\) are defined as [2]

$$\begin{aligned} e^{(+)}_{ij}({\varvec{k}}) = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix}, \quad e^{(\times )}_{ij}({\varvec{k}}) = \frac{1}{\sqrt{2}} \begin{pmatrix} 0 &{} 1 &{} 0\\ 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix}.\nonumber \\ \end{aligned}$$
(4.5)

As we have mentioned above, since we focus on second-order effects, in this work we assume that the background evolution is close to that of the \(\Lambda \textrm{CDM}\) scenario – note that we consider PBH domination eras before BBN time. Considering also the fact that in the time period that we investigate the Universe is matter (i.e. PBH) dominated, we have \(c^2_\textrm{tot} \approx w_\textrm{tot} \simeq w_\textrm{PBH}= 0\). Hence, for the time evolution of the potential \(\Phi \) given by Eq. (3.19), we obtain

$$\begin{aligned} \Phi _{\varvec{k}}^{\prime \prime } + \frac{6(1+w_\textrm{tot})}{1+3w_\textrm{tot}}\frac{1}{\eta }\Phi _{\varvec{ k}}^{\prime } + w_\textrm{tot}k^2\Phi _{\varvec{k}} =0. \end{aligned}$$
(4.6)

The solution of the above equation is a superposition of a constant and a decaying mode. In the late-time limit, one can neglect the decaying mode, and write the solution for the Fourier transform of \(\Phi \) as \(\Phi _{\varvec{k}}(\eta ) = T_\Phi (\eta ) \phi _{\varvec{k}}\), where \(\phi _{\varvec{k}}\) is the value of the gravitational potential at some reference time (which here we consider to be the time at which PBHs dominate the energy budget of the Universe, \(x_\textrm{d}\)) and \(T_\Phi (\eta )\) is a transfer function, defined as the ratio of the dominant mode between the times x and \(x_\textrm{d}\). Consequently, Eq. (4.4) can be written in a more compact form as

$$\begin{aligned} S^s_{\varvec{k}} = \int \frac{\textrm{d}^3 q}{(2\pi )^{3/2}}e^{s}({\varvec{k}},{\varvec{q}})F({\varvec{q}} ,{\varvec{k-q}},\eta )\phi _{\varvec{q}}\phi _{\varvec{k-q}}\, , \end{aligned}$$
(4.7)

where

$$\begin{aligned}{} & {} F({\varvec{q}},{\varvec{k-q}},\eta ) \equiv 2T_\Phi (q\eta )T_\Phi \left( |{\varvec{k}}-{\varvec{q}}|\eta \right) \nonumber \\{} & {} + \frac{4}{3(1+w)}\left[ \mathcal {H}^{-1}qT_\Phi ^{\prime } (q\eta )+T_\Phi (q\eta )\right] \nonumber \\{} & {} \cdot \left[ \mathcal {H}^{-1}\vert {\varvec{k}}-{\varvec{q}}\vert T_\Phi ^{\prime }\left( |{\varvec{k}}-{\varvec{q}} |\eta \right) +T_\Phi \left( |{\varvec{k}}-{\varvec{q}} |\eta \right) \right] , \end{aligned}$$
(4.8)

and the contraction \(e^s_{ij}({\varvec{k}})q_iq_j \equiv e^s({\varvec{k}},{\varvec{q}})\) can be expressed in terms of the spherical coordinates \((q,\theta ,\varphi )\) of the vector \(\varvec{q}\) as

$$\begin{aligned} e^s({\varvec{k}},{\varvec{q}})= {\left\{ \begin{array}{ll} \frac{1}{\sqrt{2}}q^2\sin ^2\theta \cos 2\varphi \mathrm {\;for\;} s= (+)\\ \frac{1}{\sqrt{2}}q^2\sin ^2\theta \sin 2\varphi \mathrm {\;for\;} s= (\times ) \end{array}\right. } . \end{aligned}$$
(4.9)

Finally, the solution of Eq. (4.2) for the tensor modes \(h^s_{\varvec{k}}\) can be obtained using the Green’s function formalism where one can write for \(h^s_{\varvec{k}}\) that

$$\begin{aligned} a(\eta )h^s_{\varvec{k}} (\eta ) =4 \int ^{\eta }_{\eta _\textrm{d}}\textrm{d}\bar{\eta }\, G^s_{\varvec{k}}(\eta ,\bar{\eta })a(\bar{\eta })S^s_{\varvec{k}}(\bar{ \eta }), \end{aligned}$$
(4.10)

and where the Green’s function \(G^s_{\varvec{k}}(\eta ,\bar{\eta })\) is the solution of the homogeneous equation

$$\begin{aligned}{} & {} G_{\varvec{k}}^{s,\prime \prime }(\eta ,\bar{\eta }) - 2\mathcal {H}\gamma _T G_{\varvec{k}}^{s,\prime }(\eta ,\bar{\eta }) \nonumber \\{} & {} \quad + \left( k^{2} -\frac{a^{\prime \prime }}{a}+ 2 \mathcal {H}^2 \gamma _T \right) G^s_{\varvec{k}}(\eta ,\bar{\eta }) = \delta \left( \eta -\bar{\eta }\right) , \end{aligned}$$
(4.11)

with the boundary conditions \(\lim _{\eta \rightarrow \bar{\eta }}G^s_{\varvec{k}}(\eta ,\bar{\eta }) = 0\) and \( \lim _{\eta \rightarrow \bar{\eta }}G^{s,\prime }_{\varvec{k}}(\eta ,\bar{\eta })=1\).

Having extracted above the tensor perturbations, the next step is to derive the tensor power spectrum, \(\mathcal {P}_{h}(\eta ,k)\), for the different polarization modes, which is defined as the equal-time correlator of the tensor perturbations through the following relation:

$$\begin{aligned} \langle h^r_{{\varvec{k}}}(\eta )h^{s,*}_{{\varvec{k}}^\prime }(\eta )\rangle \equiv \delta ^{(3)}({\varvec{k}} - {\varvec{k}}^\prime ) \delta ^{rs} \frac{2\pi ^2}{k^3}\mathcal {P}^s_{h}(\eta ,k), \end{aligned}$$
(4.12)

where \(s=(\times )\) or \((+)\). Finally, after a long but straightforward calculation one acquires that \(\mathcal {P}_{h}(\eta ,k)\) for the \((\times )\) and \((+)\) polarization states can be recast as  [101,102,103,104]

$$\begin{aligned}{} & {} \mathcal {P}^{(\times )\;\textrm{or}\; (+)}_h(\eta ,k) \nonumber \\{} & {} \quad = 4\int _{0}^{\infty } \textrm{d}v\int _{|1-v|}^{1+v}\textrm{d}u \left[ \frac{4v^2 - (1+v^2-u^2)^2}{4uv}\right] ^{2}\nonumber \\{} & {} \qquad I^2(u,v,x)\mathcal {P}_\Phi (kv)\mathcal {P} _\Phi (ku)\,. \end{aligned}$$
(4.13)

The two auxiliary variables u and v are defined as \(u \equiv |{\varvec{k}} - {\varvec{q}}|/k\) and \(v \equiv q/k\) and the kernel function I(u, v, x) is given by

$$\begin{aligned} I(u,v,x) = \int _{x_\textrm{d}}^{x} \textrm{d}\bar{x}\, \frac{a(\bar{x})}{a(x)}\, k\, G^s_{k}(x,\bar{x}) F_k(u,v,\bar{x}). \end{aligned}$$
(4.14)

In the above expressions \(x=k\eta \), and we use the notation \(F_{k}(u,v,\eta )\equiv F(k ,|{\varvec{k}}-{\varvec{q}}|,\eta )\) since the function \(F({\varvec{q}},{\varvec{k-q}},\eta )\) depends only on the modulus of its first two arguments.

4.2 The gravitational-wave energy-density spectrum

In this subsection we calculate the energy density associated to the scalar induced GWs, focusing only on subhorizon scales. Consequently, after a lengthy but straightforward calculation the GW energy density can be recast as [105]

$$\begin{aligned} \rho _{\textrm{GW}}(\eta ,{\varvec{x}}) = \frac{M_{\scriptscriptstyle {\textrm{Pl}}}^2}{32 a^2}\, \overline{\left( \partial _\eta h_\mathrm {\alpha \beta }\partial _\eta h^\mathrm {\alpha \beta } + \partial _{i} h_\mathrm {\alpha \beta }\partial ^{i}h^\mathrm {\alpha \beta } \right) }\, , \end{aligned}$$
(4.15)

which is simply the sum of a kinetic term and a gradient term. The overall bar denotes an oscillation averaging on sub-horizon scales, performed to deduce the envelope of the gravitational-wave spectrum. The GW spectral abundance is just the GW energy density per logarithmic comoving scale, i.e.

$$\begin{aligned} \Omega _\textrm{GW}(\eta ,k) = \frac{1}{\bar{\rho }_\textrm{tot}}\frac{\textrm{d}\rho _\textrm{GW}(\eta ,k)}{ \textrm{d}\ln k}. \end{aligned}$$
(4.16)

Considering a matter-dominated era driven by PBHs, where \(w=0\), the transfer function \(T_\mathrm {\Phi }\) is constant in time (see the discussion after Eq. (4.6)) , and we normalise it to one at PBH domination time, namely \(T_\mathrm {\Phi }(x_\textrm{d})=1\). This forces the source term \(S^s_{\varvec{k}}\) to be constant in time and consequently at sub-horizon scales, where \(k\gg \mathcal {H}\), from Eq. (4.2) we obtain that \(h^s_{\varvec{k}}\simeq \frac{4S^s_{\varvec{k}}}{k^2}\). Finally, the tensor modes have a mild dependence on time and therefore the kinetic term in the expression for the GW energy density (4.15) can be neglected. Therefore, we straightforwardly obtain that

$$\begin{aligned} \left\langle \rho _{\textrm{GW}}(\eta ,{\varvec{x}}) \right\rangle\simeq & {} \left\langle \rho _{\textrm{GW,grad}} (\eta ,{\varvec{x}}) \right\rangle {=} \sum _{s=+,\times }\frac{M_{\scriptscriptstyle {\textrm{Pl}}}^2}{32a^2}\overline{ \left\langle \left( \nabla h^{s}_\mathrm {\alpha \beta }\right) ^2\right\rangle } \nonumber \\ {}= & {} \frac{M_{\scriptscriptstyle {\textrm{Pl}}}^2}{32a^2 \left( 2\pi \right) ^3} \sum _{s=+,\times } \int \textrm{d}^3{\varvec{k}}_1\nonumber \\{} & {} \times \int \textrm{d}^3{\varvec{k}}_2\, k_1 k_2 \overline{ \left\langle h^{s}_{{\varvec{k}}_1}(\eta )h^{s,*}_{{\varvec{k}}_2} (\eta )\right\rangle } e^{i({\varvec{k}}_1-{\varvec{k}}_2)\cdot {\varvec{x}}},\nonumber \\ \end{aligned}$$
(4.17)

where the brackets stand for an ensemble average. At the end, by combining Eqs. (4.17),  (4.16) and  (4.12) and taking into account from Eq. (4.13) that the \((\times )\) and \((+)\) polarization modes give an equal contribution, we find that

$$\begin{aligned} \Omega _\textrm{GW}(\eta ,k)\simeq & {} \frac{1}{\bar{\rho }_\textrm{tot}}\frac{\textrm{d}\rho _\textrm{GW,grad}(\eta ,k)}{ \textrm{d}\ln k}\nonumber \\= & {} \frac{1}{48}\left( \frac{k}{\mathcal {H}(\eta )}\right) ^{2}\overline{\mathcal {P}^{ (\times )}_h(\eta ,k)}. \end{aligned}$$
(4.18)

In order to compute the contribution of the induced GWs to the energy budget of the Universe at the present epoch, one should evolve \(\Omega _\textrm{GW}(\eta ,k)\) from a reference conformal time \(\eta _\mathrm {*}\) up to today. To do so, one has that

$$\begin{aligned} \Omega _{\textrm{GW}}(\eta _0,k)= & {} \frac{\rho _{\textrm{GW}}(\eta _0,k)}{\rho _\textrm{c}(\eta _0)} = \frac{\rho _{\textrm{GW}}(\eta _\mathrm {*},k)}{\rho _\textrm{c}(\eta _\mathrm {*})}\left( \frac{ a_\mathrm {*}}{a_\textrm{0}}\right) ^4 \frac{\rho _\textrm{c}(\eta _\mathrm {*})}{\rho _\textrm{c}(\eta _0)} \nonumber \\= & {} \Omega _{\textrm{GW}}(\eta _\mathrm {*},k)\Omega ^{(0)}_\textrm{r}\frac{\rho _\mathrm {r,*} a^4_\mathrm {*}}{\rho _\textrm{r,0}a^4_0}, \end{aligned}$$
(4.19)

where we have taken into account that \(\Omega _\textrm{GW}\sim a^{-4}\), and where the index 0 refers to the present time. Then, taking into account that the energy density of radiation can be recast as \(\rho _r = \frac{\pi ^2}{15}g_{*\mathrm {\rho }}T_\textrm{r}^4\) and that the temperature of the radiation bath, \(T_\textrm{r}\), scales as \(T_\textrm{r}\propto g^{-1/3}_{*\textrm{S}}a^{-1}\), one finds that

$$\begin{aligned} \Omega _\textrm{GW}(\eta _0,k) = \Omega ^{(0)}_r\frac{g_{*\mathrm {\rho },\mathrm {*}}}{g_{*\mathrm {\rho },0}} \left( \frac{g_{*\textrm{S},\textrm{0}}}{g_{*\textrm{S},\mathrm {*}}}\right) ^{4/3} \Omega _{\textrm{GW}}(\eta _\mathrm {*},k), \end{aligned}$$
(4.20)

where \(g_{*\mathrm {\rho }}\) and \(g_{*\textrm{S}}\) stand for the energy and entropy relativistic degrees of freedom.

5 Constraints on f(T) gravity

In this section we use the portal of the scalar induced GWs from PBH Poisson fluctuations presented above, in order to derive constraints on f(T) gravity.

5.1 Mono-parametric f(T) Models

Since we will perform specific calculations we have to specify the form of the function f(T). In particular, we consider the following three f(T) gravity models depending on one free parameter, denoted here as \(\beta \).

  1. 1.

    The power-law model [15] (hereafter \(f_{1}\) model), in which

    $$\begin{aligned} f(T)=T+\alpha (-T)^{\beta }, \end{aligned}$$
    (5.1)

    with

    $$\begin{aligned} \alpha =(6H_0^2)^{1-\beta }\frac{\Omega _{F0}}{2\beta -1}, \end{aligned}$$
    (5.2)

    where \(\Omega _{F0}=1-\Omega _{m0}-\Omega _{r0}\). According to observational constraints for \(\beta \) one has that \(-0.3<\beta <0.3\) [82, 98, 106]. Note that GR is recovered for \(\beta \rightarrow 0\).

  2. 2.

    The square-root exponential model (hereafter \(f_{2}\)) [16]

    $$\begin{aligned} f(T)=T+\alpha T_{0}(1-e^{-\frac{1}{\beta }\sqrt{T/T_{0}}}), \end{aligned}$$
    (5.3)

    with

    $$\begin{aligned} \alpha =\frac{\Omega _{F0}}{1-(1+\frac{1}{\beta })e^{-\frac{1}{\beta }}}. \end{aligned}$$
    (5.4)

    The \(\beta \) parameter is observationally constrained within the range \(0.05<\beta <0.4\) [82, 98, 106] and GR is recovered for \(\beta \rightarrow 0^+\).

  3. 3.

    The exponential model (hereafter \(f_{3}\)) [82]:

    $$\begin{aligned} f(T)=T+\alpha T_{0}[1-e^{-T/(\beta T_{0})}], \end{aligned}$$
    (5.5)

    with

    $$\begin{aligned} \alpha =\frac{\Omega _{F0}}{1-\big (1+\frac{2}{\beta }\big )e^{-\frac{1}{\beta }}}. \end{aligned}$$
    (5.6)

    The \(\beta \) parameter is observationally constrained within the range \(0.02<\beta <0.2\) [82, 98, 106] and GR is recovered for \(\beta \rightarrow 0^+\).

5.2 Theoretical parameters

In this subsection we discuss the theoretical parameters that are involved in the analysis. These parameters include the mass of the PBH \(m_\textrm{PBH}\), the initial PBH abundance at formation time \(\Omega _\textrm{PBH,f}\), and of course the parameter \(\beta \) of the mono-parametric f(T) model at hand.

For the PBH mass range we consider that the PBHs are formed after the end of inflationary era and evaporate before the BBN time. In particular, one can derive an upper bound on the PBH mass by accounting for the current Planck upper bound on the tensor-to-scalar ratio for single-field slow-roll models of inflation, which gives \(\rho ^{1/4}_\textrm{inf}<10^{16}\textrm{GeV}\)  [107]. On the other hand one can extract a conservative lower bound on the reheating energy scale, i.e. \(\rho ^{1/4}_\textrm{reh}> 4\textrm{MeV}\), derived by taking into account the thermalization of neutrino background and the hadron scatterings emitted from PBHs as discussed in [108]. Hence, one can show that the relevant PBH mass range is given by  [71]

$$\begin{aligned} 10 \textrm{g}< m_\textrm{PBH}< 10^{9} \textrm{g}. \end{aligned}$$
(5.7)

We proceed to the range of \(\Omega _\textrm{PBH,f}\). In order to have a transient PBH domination era, we can set it by requiring that the PBH evaporation time \(t_\textrm{evap}\) is larger than the PBH domination time \(t_\textrm{d}\). Consequently, knowing that during a radiation dominated era we have \(\Omega _\textrm{PBH}=\rho _\textrm{PBH}/\rho _\textrm{d} \propto a^{-3}/a^{-4}\propto a\) and demanding that \(t_\textrm{evap}>t_\textrm{d}\), we obtain that

$$\begin{aligned} \Omega _\textrm{PBH,f} > 10^{-15} \sqrt{\frac{g_\textrm{eff}}{100}} \frac{10^9\textrm{g}}{m_\textrm{PBH}}. \end{aligned}$$
(5.8)

Lastly, concerning the parameter \(\beta \), according to observational constraints mentioned above from [82, 98, 106], its value should roughly vary within the following range:

$$\begin{aligned} -0.4 \le \beta \le 0.4\, , \end{aligned}$$
(5.9)

depending on the f(T) model at hand.

5.3 Gravitational waves from an early primordial black hole dominated era

We have now all the necessary material in order to investigate the relevant GW signal created in the early PBH dominated era, in the context of f(T) gravity. Let us mention here that one should discriminate between two decisive effects which introduce deviations from standard GR gravity, namely a) the effect of the source of the induced GWs, which is actually encapsulated within the power spectrum of the PBH gravitational potential \(\mathcal {P}_\Phi \), and b) the effect of the GW propagation, which is encoded within the time evolution of the Green function \(G_k(\eta ,\bar{\eta })\), which can be viewed as the propagator of the tensor perturbations as it can be seen by Eq. (4.10).

5.3.1 The effect of the gravitational-wave source

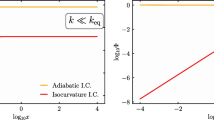
After solving numerically the Meszaros equation (3.31) for the PBH energy density perturbations, we proceed to the calculation of the PBH gravitational potential power spectrum \(\mathcal {P}_\Phi \), as dictated by Eq. (3.33), by accounting for the three mono-parametric f(T) models presented in Sect. 5.1. The power spectrum \(\mathcal {P}_\Phi \) is actually the source of the induced GWs as it can be seen from Eq. (4.13).

Fig. 1
figure 1

The power spectrum of the PBH gravitational potential at PBH domination time, for the three mono-parametric f(T) models, by choosing different values of the initial PBH abundance \(\Omega _\textrm{PBH,f}\). In all graphs we have used \(\beta =0.1\) and \(m_\textrm{PBH,f}=10^{5}\textrm{g}\). The dashed curves correspond to the GR results

Full size image
Fig. 2
figure 2

The power spectrum of the PBH gravitational potential at PBH domination time, for the three mono-parametric f(T) models, by choosing different values of the PBH mass \(m_\textrm{PBH}\). In all graphs we have used \(\beta =0.1\) and \(\Omega _\textrm{PBH,f}=10^{-3}\). The dashed curves correspond to the GR results

Full size image
Fig. 3
figure 3

The power spectrum of the PBH gravitational potential at PBH domination time, for the three mono-parametric f(T) models, by choosing different values of the parameter \(\beta \) within its observationally allowed range. In all graphs we have used \(m_\textrm{PBH}=10^5\textrm{g}\) and \(\Omega _\textrm{PBH,f}=10^{-3}\). The dashed curves correspond to the GR results

Full size image

In Figs. 1, 2 and 3 we depict the power spectrum of the PBH gravitational potential at PBH domination time, for the three f(T) models, for various choices of the initial PBH abundance \(\Omega _\textrm{PBH,f}\), of the PBH mass \(m_\textrm{PBH}\), and of the model-parameter \(\beta \). As it can be clearly seen from Fig. 1, the amplitude of the PBH gravitational potential power spectrum increases with the initial PBH abundance, whereas from Fig. 2 we can notice that the position of the peak of \(\mathcal {P}_\Phi \) depends on the PBH mass. Finally, from Fig. 3, where \(\mathcal {P}_\Phi \) is plotted for different values of the modified gravity parameter \(\beta \), one can clearly infer that the deviation from GR is practically indistinguishable. As it was verified numerically for all the monoparametric f(T) models considered here, the relative change of the gravitational potential power spectrum with respect to the one of GR around the peak of the power spectrum, i.e. at \(k\sim k_\textrm{d}\), is of the order \(10^{-2}\), namely

$$\begin{aligned} \left| \frac{\mathcal {P}^{f(T)}_\Phi (k_\textrm{d}) -\mathcal {P}^{GR}_\Phi (k_\textrm{d}) }{\mathcal {P}^{GR}_\Phi (k_\textrm{d})}\right| \sim 10^{-2}. \end{aligned}$$
(5.10)

In summary, we conclude that the effect of f(T) gravity on the source of gravitational waves, is very small, and practically indistinguishable from GR for realistic f(T) model-parameter values.

5.3.2 The effect of the gravitational-wave propagation

We now come to the effect of the GW propagation. One should extract the behavior of \(G_k(\eta ,\bar{\eta })\) by solving Eq. (4.11) and investigate possible deviations from GR. During the time evolution of the GW spectrum one should take into account the fact that during a sudden transition from the PBH dominated era to the subsequent radiation era, in the case of a monochromatic PBH mass function as the one considered here, the GW is enhanced due a very rapid increase of the time derivative of the gravitational potential \(\Phi \) which is present in the source term (see Eq. (4.7)) as noted in  [109, 110]. Then, during the radiation-dominated era, the source term is decaying on subhorizon scales and therefore \(\Omega _\textrm{GW}\) stops growing after the moment when the source term has sufficiently decayed. After this point, the scalar induced GWs are propagating as free waves, with their present energy density spectrum given by Eq. (4.20) and \(\eta _{*}\) being a reference time during the radiation-dominated era when GWs start to propagate as free waves.

Having these in mind let us focus on Eq. (4.11), namely

$$\begin{aligned}{} & {} G_{\varvec{k}}^{s,\prime \prime }(\eta ,\bar{\eta }) - 2\mathcal {H}\gamma _T G_{\varvec{k}}^{s,\prime }(\eta ,\bar{\eta }) \nonumber \\{} & {} \quad + \left( k^{2} -\frac{a^{\prime \prime }}{a}+ 2 \mathcal {H}^2 \gamma _T \right) G^s_{\varvec{k}}(\eta ,\bar{\eta }) = \delta \left( \eta -\bar{\eta }\right) . \end{aligned}$$
(5.11)

One can identify the dominant terms of the above equation by taking the ratios between the GR terms and the new f(T) terms multiplied by the \(\gamma _T\) function. In this procedure, we should take into consideration the fact that the \(\gamma _T\) function, as it was checked numerically for all the three mono-parametric models studied here, is a negative decreasing function of time, which implies that its absolute value increases with time. Therefore, in order to find the maximum deviation from GR we compute the ratios between the GR and f(T) terms at a time during radiation domination when the \(\gamma _T\) function acquires its maximum value. Being quite conservative we set this time to be the standard matter-radiation equality time at redshift \(z_\textrm{eq}=3387\).

At this point, we should stress that in the comparison of the different terms in Eq. (5.11) one should compute the derivative terms \(G^\prime _k(\eta ,\bar{\eta })\) and \(G^{\prime \prime }_k(\eta ,\bar{\eta })\). To achieve this we take into account the fact that the solutions of Eq. (5.11) are expected to be trigonometric functions (sines and cosines), in particular Bessel functions in the case of GR. One then expects that \(G^\prime _k(\eta ,\bar{\eta })\), \(G_k(\eta ,\bar{\eta })\) and \(G^{\prime \prime }_k(\eta ,\bar{\eta })\) should differ by a phase difference, and this was indeed verified numerically. Consequently, one expects in general that \(\left| G^\prime _k(\eta ,\bar{\eta })/G_k(\eta ,\bar{\eta })\right| _{\eta =\eta _\textrm{ eq}}\sim O(1)\) and \(\left| G^{\prime \prime }_k(\eta ,\bar{\eta })/G_k(\eta ,\bar{\eta })\right| _{ \eta =\eta _\textrm{eq}}\sim O(1)\), when comparing the different terms of Eq. (5.11).

Thus, taking the above discussion into account, let us start the identification of the dominant terms by comparing the first two terms in Eq. (5.11), namely the second derivative term \(G_{\varvec{k}}^{s,\prime \prime }(\eta ,\bar{\eta })\) and the friction term \(2\mathcal {H}\gamma _T G_{\varvec{k}}^{s,\prime }(\eta ,\bar{\eta })\), and in particular let us consider their ratio \(G_{\varvec{k}}^{s,\prime \prime }(\eta ,\bar{\eta })/[2\mathcal {H}\gamma _T G_{\varvec{k}}^{s,\prime }(\eta ,\bar{\eta })]\). Eventually, we find that for the power-law f(T) model and for \(m_\textrm{PBH}=10^{5}\textrm{g}\), \(\Omega _\textrm{PBH,f}=10^{-3}\) and \(\beta =0.1\), we acquire

$$\begin{aligned} \left| \frac{G_{\varvec{k}}^{\prime \prime }(\eta ,\bar{\eta })}{2\mathcal {H}\gamma _T G_{\varvec{k}}^{\prime }(\eta ,\bar{\eta })}\right| \simeq \left. \frac{1}{2\mathcal {H}\gamma _T}\right| _{\eta =\eta _\textrm{eq}} \simeq 10^{46}\gg 1. \end{aligned}$$
(5.12)

Similar results are obtained for the square-root exponential and the exponential f(T) models, and by varying the parameters \(m_\textrm{PBH}\), \(\Omega _\textrm{PBH,f}\) and \(\beta \) too.

With the same reasoning we can additionally examine the ratio between the \(k^2\) and \(2\mathcal {H}^2\gamma _T\) terms inside the parenthesis of Eq. (5.11). Choosing again \(\eta =\eta _\textrm{eq}\) in order to find the maximum deviation from GR, we straightforwardly find that

$$\begin{aligned} \left. \frac{k^2}{2\mathcal {H}^2 \gamma _T }\right| _{k=k_\textrm{evap},\eta =\eta _\textrm{eq}} \simeq 10^{83}\gg 1, \end{aligned}$$
(5.13)

where \(k=k_\textrm{evap}\) is the comoving scale exiting the Hubble radius at PBH evaporation time and as a consequence it is the largest scale considered here.

In summary, we can safely argue that the f(T) modifications at the level of the propagation equation (5.11) can be neglected and consequently one obtains that

$$\begin{aligned} G_{\varvec{k}}^{f(T)} (\eta ,\bar{\eta })\simeq G_{\varvec{k}}^{\textrm{GR}} (\eta , {\bar{\eta }}). \end{aligned}$$
(5.14)

Hence, we conclude that the effect of f(T) gravity on the propagation of gravitational waves, is very small, and practically indistinguishable from GR for realistic f(T) model-parameter values. We mention that this behavior is different than the case of f(R) gravity, in which the corresponding effect is small but still distinguishable from GR [76], which reveals the different nature and effects of the two gravitational modifications.

6 Conclusions

Primordial black holes (PBH) can address a number of issues of modern cosmology since they may account for a part or all of the dark matter contribution, they can seed the large-scale structure formation through Poisson fluctuations, and they may constitute the progenitors of the black-hole merging events recently detected by LIGO-VIRGO. Interestingly, PBHs are tightly associated with gravitational wave (GW) signals, providing us the possibility to gain information of the physics of different cosmic epochs, from the very early universe up to later times, depending on the GW production mechanism. Since their formation and effects are determined by the underlying gravitational theory, one can use them as a novel tool in order to test general relativity and investigate possible modified gravity deviations.

In this work we focused on the primordial scalar induced gravitational waves, generated at second order in cosmological perturbation theory, from PBH Poisson fluctuations, in the framework of f(T) modified gravity. In particular, we desired to use it as a novel probe to extract constraints on the involved model-parameters. We considered three viable mono-parametric f(T) models, and we investigated the induced modifications at the level of the gravitational-wave source, which are encoded in terms of the power spectrum of the PBH gravitational potential \(\mathcal {P}_\Phi \), as well as at the level of their propagation, described in terms of the Green function \(G_{\varvec{k}}(\eta ,\bar{\eta })\) which can be considered as the propagator of the tensor perturbations.

Our detailed analysis showed that within the observationally allowed range of the parameters of the f(T) models at hand, the obtained deviations from GR, both at the level of source, as well as at the level of propagation, are practically indistinguishable. Indicatively, regarding the PBH gravitational potential power spectrum we found that the deviation from GR is of the order of \(10^{-2}\) for all the monoparametric f(T) models considered here. This behavior is different than the case of other modified gravity theories, such as f(R) gravity, in which the corresponding effect is small but still distinguishable from GR [76]. Hence, we conclude that realistic and viable f(T) theories of gravity can safely pass the primordial black hole constraints, which may offer an additional argument in their favor.

Finally, one should stress that one can extend our analysis to other modified teleparallel theories of gravity, such as f(T, B) gravity and scalar-torsion theories, whose polarization numbers have been calculated in [111]. Especially in the cases where extra polarization modes do appear, one expects to find significant differences, as it was found in [76]. This interesting and necessary investigation will be performed in a separate paper.