Light-cone sum rule analysis of semileptonic decays $\varLambda _b^0 \rightarrow \varLambda _c^+ \ell ^- {\overline{\nu }}_\ell$

Abstract

In this work, we analyze the semileptonic decay processes of $\varLambda _b \rightarrow \varLambda _c$ in the light-cone sum rule approach. In order to calculate the form factors of the $\varLambda _b$ baryon transition matrix element, we use the light-cone distribution amplitudes of $\varLambda _b$ obtained from the QCD sum rule in the heavy quark effective field theory framework. With the calculation of the six form factors of the $\varLambda _b \rightarrow \varLambda _c$ transition matrix element, the differential decay widths of $\varLambda _b^0 \rightarrow \varLambda _c^+ \ell ^- {\overline{\nu }}_\ell (\ell = e, ~\mu , ~\tau )$ and their absolute branching fractions are obtained. Additionally, the ratio of $R(\varLambda _c^+) \equiv {\mathcal {B}}r(\varLambda _b^0 \rightarrow \varLambda _c^+ \tau ^- {\overline{\nu }}_\tau )/{\mathcal {B}}r(\varLambda _b^0 \rightarrow \varLambda _c^+ \mu ^- {\overline{\nu }}_\mu )$ is also obtained in this work. Our results are in accord with the newest experimental result and other theoretical calculations and predictions.

1 Introduction

Semileptonic decays of $\varLambda _b$ to $\varLambda _c$ baryons provide a good way to study and determine the CKM matrix element $|V_{cb}|$. In most cases, the CKM matrix element $|V_{cb}|$ is extracted from the B to D meson semileptonic decay processes. Compared with different methods and models, there is a small difference in the value of $|V_{cb}|$. Meanwhile, theoretical analysis and experimental measurements of the ratio ${\mathcal {R}}(\varLambda _c^+) \equiv {\mathcal {B}}r(\varLambda _b^0 \rightarrow \varLambda _c^+ \tau ^- {\overline{\nu }}_\tau )/{\mathcal {B}}r(\varLambda _b^0 \rightarrow \varLambda _c^+ \mu ^- {\overline{\nu }}_\mu )$ also give a good test of the Standard Model and lepton universality.

Experimentally, LHCb reported their measurement of the branching fractions of semileptonic decay $\varLambda _b$ to $\varLambda _c$ with tau lepton final state with a significance of $6.1\sigma$ recently [1]. They gave the branching fraction of the semi-tauonic decay $\varLambda _b^0\rightarrow \varLambda _c^+\tau ^-{\overline{\nu }}_\tau$, ${\mathcal {B}}r(\varLambda _b^0\rightarrow \varLambda _c^+\tau ^-{\overline{\nu }}_\tau )=(1.50\pm 0.16_{stat}\pm 0.25_{syst}\pm 0.23)\%$. At the same time, the experimental test also gave the ratio of branching fractions of the processes $\varLambda _b^0\rightarrow \varLambda _c^+\tau ^-{\overline{\nu }}_\tau$ and $\varLambda _b^0\rightarrow \varLambda _c^+\mu ^-{\overline{\nu }}_\mu$, which is ${\mathcal {R}}(\varLambda _c^+) \equiv {\mathcal {B}}r(\varLambda _b^0\rightarrow \varLambda _c^+\tau ^-{\overline{\nu }}_\tau )/{\mathcal {B}}r(\varLambda _b^0\rightarrow \varLambda _c^+\mu ^-{\overline{\nu }}_\mu )=(0.242\pm 0.026\pm 0.040\pm 0.059)$, with the last uncertainty coming from the errors of measurement of $\varLambda _b^0\rightarrow \varLambda _c^+\mu ^-{\overline{\nu }}_\mu$ branching fraction. In the early experiments, the DELPHI and CDF collaborations reported the branching fractions of the semileptonic decay $\varLambda _b^0\rightarrow \varLambda _c^+\ell ^-{\overline{\nu }}_\ell$ ($\ell$ stands for electron and muon) ${\mathcal {B}}r(\varLambda _b^0\rightarrow \varLambda _c^+\ell ^-{\overline{\nu }}_\ell )=5.0\%$ and ${\mathcal {B}}r(\varLambda _b^0\rightarrow \varLambda _c^+\ell ^-{\overline{\nu }}_\ell )/{\mathcal {B}}r(\varLambda _b^0\rightarrow \varLambda _c^+\pi ^-)=16.6$, respectively [2, 3]. With the ratio ${\mathcal {R}}(\varLambda _c^+)$ analyzed within the Standard Model, the early measurement of semileptonic decay of $\varLambda _b^0$ to $\varLambda _c^+$ with electron and muon final states gave the branching fraction of $\varLambda _b^0\rightarrow \varLambda _c^+\tau ^-{\overline{\nu }}_\tau$ around two percent. Because of the poor experimental data of these processes, the newest observation and measurement also provided the material for testing the Standard Model by the ratio ${\mathcal {R}}(\varLambda _c^+)$.

Theoretically, some methods have been used to calculate and analyze the processes $\varLambda _b^0\rightarrow \varLambda _c^+\ell ^-{\overline{\nu }}_\ell$, such as QCD sum rules [4,5,6], light-front quark model [7,8,9,10], lattice QCD [11, 12], heavy quark effective theory [5, 13, 14], relativistic quark model [15], covariant confined quark model [16, 17], Hypercentral constituent quark model [18] and the analysis in searching for new physics [19, 20] etc.. They calculated the branching fractions at some regions, and the results were consistent with experimental values. But with the analysis of tau lepton’s final state semileptonic decay, some references gave bigger results than the newest experiment or gave a large error. Besides, the Standard Model also gave a prediction of the ratio of branching fractions ${\mathcal {R}}(\varLambda _c^+)$, and the difference between experimental results and the values of the Standard Model predicted can be used to test the Standard Model or discover new physics beyond the Standard Model [21,22,23,24,25]. Based on these considerations, the reanalysis of the processes $\varLambda _b^0\rightarrow \varLambda _c^+\ell ^-{\overline{\nu }}_\ell$ is needed and important.

With the light-cone distribution amplitudes of $\varLambda _b$ developed from B-meson light-cone distribution amplitudes [26,27,28], the light-cone sum rule approach is used in this article to calculate the correlation function of heavy baryon transition and study the properties of hadronic decay. Light-cone sum rule is a fruitful hybrid of the SVZ technique [29,30,31] and the theory of hard exclusive process [32, 33]. The basic idea of this approach is to expand the time-ordered products of hadrons and weak currents near the light-cone $x^2=0$. The method provides a powerful tool in the calculation of baryon transition form factors. With form factors calculated by the light-cone sum rule method, one can obtain the decay properties of hadrons. In this work, the method is used to calculate the form factors of the $\varLambda _b \rightarrow \varLambda _c$ transition. In the procedure to obtain the decay width and branching fractions of semileptonic decay $\varLambda _b^0 \rightarrow \varLambda _c^+ \ell ^- {\overline{\nu }}_\ell (\ell =e,~\mu ,~\tau )$ processes, we combine these form factors and the helicity form of differential decay width to obtain the decay properties of these processes. In order to compare the ratio of branching fractions ${\mathcal {R}}(\varLambda _c^+)={\mathcal {B}}r(\varLambda _b^0 \rightarrow \varLambda _c^+\tau ^- {\overline{\nu }}_\tau )/{\mathcal {B}}r(\varLambda _b^0 \rightarrow \varLambda _c^+ \mu ^- {\overline{\nu }}_\mu )$ predicted by the Standard Model and measured by experiments, ${\mathcal {R}}(\varLambda _c^+)$ is also given in this work.

The article is arranged as follows: Sect. 2 is the basic framework of the light-cone sum rule of the semileptonic decay $\varLambda _b^0 \rightarrow \varLambda _c^+ \ell ^- {\overline{\nu }}_\ell$, in which the light-cone distribution amplitudes of bottom baryon $\varLambda _b$ are listed and the six form factors of weak transition $\varLambda _b \rightarrow \varLambda _c$ are given by the light-cone sum rule. Numerical analysis and the physical results of the $\varLambda _b \rightarrow \varLambda _c$ processes with two types of interpolating currents of $\varLambda _c$ states are given in Sect. 3. Section 4 are the conclusions and discussions.

2 Light-cone sum rules of $\varLambda _b \rightarrow \varLambda _c$ semileptonic decays

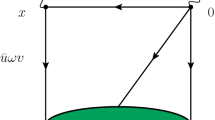
Before the theoretical analysis, one should convince oneself that the light-cone sum rule approach is valid for the physical process of bottom baryon for charm baryon decay. Similar to the light-cone sum rule analysis of $B\rightarrow D^{(*)}$ transition form factors, one expands the correlation function near the light-cone with the finite charm quark mass and with the light-cone dominance region of the interpolating charm baryon states momentum p and momentum transfer q. With the same discussion as that in reference [34] and the applications in references [35,36,37,38,39,40], the light-cone sum rule approach is used in this work to calculate the $\varLambda _b^0\rightarrow \varLambda _c^+\ell ^-{\overline{\nu }}_\ell$ processes. This approach employs a vacuum to an on-shell state correlation function and it is different from the conventional SVZ sum rule which is vacuum-to-vacuum. The other difference is that, in light-cone sum rule one expands the field operator product near the light-cone $x^2=0$ with a series of light-cone distribution amplitudes, while in the conventional SVZ sum rule one expands the field operator product near the position $x=0$ with a series of vacuum condensate operators. It gives us an easy way to calculate the form factors that appear in the three-point correlation function in the QCD sum rule method.

2.1 The basic framework of the semileptonic decay processes

The light-cone sum rule starts with the hadronic correlation function sandwiching the time-ordered product of the final hadronic current and weak current between vacuum and hadronic state, and the correlation function can be expressed as

$$\begin{aligned} T_\mu (p,q)=i\int d^4x e^{ip\cdot x} \langle 0|{\mathcal {T}}\{j_{\varLambda _c}(x),j_\mu (0)\}|\varLambda _b(p+q)\rangle , \end{aligned}$$

(1)

where p is the four-momentum of $\varLambda _c$ and q is the momentum transfer. The interpolating current of heavy baryon $\varLambda _Q$ had been discussed in [41,42,43,44,45]. There are two types of interpolating currents of $\varLambda _c$ in QCD sum rules, and they are given by

$$\begin{aligned} j_{\varLambda _c}^1(x)=\epsilon _{ijk}[u^{iT}(x)C\gamma _5 d^j(x)]c^k(x), \end{aligned}$$

(2)

and

$$\begin{aligned} j_{\varLambda _c}^2(x)=\epsilon _{ijk}[u^{iT}(x)C\gamma _5\gamma _\nu d^j(x)]\gamma ^\nu c^k(x). \end{aligned}$$

(3)

Both two choices of interpolating current can construct the light-cone sum rules of baryon decay. In the main text, we take the current type $j_{\varLambda _c}^1$ as an example to construct the light-cone sum rules of $\varLambda _b^0 \rightarrow \varLambda _c^+ \ell ^- {\overline{\nu }}_{\ell }$ processes. The alternative interpolating current version $j_{\varLambda _c}^2$ can be obtained through the same procedures, and they are given in the appendix. The weak decay current of $b \rightarrow c$ is

$$\begin{aligned} j_\mu (0)={\overline{c}}(0)\gamma _\mu (1-\gamma _5)b(0). \end{aligned}$$

(4)

In the light-cone sum rule approach, the correlation function can be derived at the hadronic and quark levels respectively. On the hadronic level, the correlation function can be parameterized by inserting a complete series of hadronic states with the same quantum number as the $\varLambda _c$ state,

$$\begin{aligned} \int d^4p\sum _i|\varLambda _c^i(p)\rangle \langle \varLambda _c^i(p)|=1. \end{aligned}$$

(5)

where the index i contains all states with the same quantum numbers of $\varLambda _c$.

On the hadronic level, the correlation function can be represented as

$$\begin{aligned} T_\mu (p,q)&=\frac{\langle 0|j_{\varLambda _c}^i|\varLambda _c(p)\rangle \langle \varLambda _c(p)|j_{\mu }|\varLambda _b(p+q)}{M_{\varLambda _c}^2-p^2}\nonumber \\&\quad +\frac{\langle 0|j_{\varLambda _c^*}^i|\varLambda _c^*(p)\rangle \langle \varLambda _c^*(p)|j_{\mu }|\varLambda _b(p+q)}{M_{\varLambda _c^*}^2-p^2} \nonumber \\&\quad +\cdots . \end{aligned}$$

(6)

$i=1,2$ corresponds to two types of interpolating current $j_{\varLambda _c}^1$ and $j_{\varLambda _c}^2$. The correlation function on the hadronic level contains both the contributions of positive and negative parity interpolating states $\varLambda _c$ and $\varLambda _c^*$ baryons. $\langle 0|j_{\varLambda _c}|\varLambda _c(p)\rangle =f_{\varLambda _c}u_{\varLambda _c}(p)$ is the transition matrix element for the quantum number $(1/2)^+$ $\varLambda _c$ baryon, and $\langle 0|j_{\varLambda _c^*}|\varLambda _c^*(p)\rangle =f_{\varLambda _c^*}\gamma _5 u_{\varLambda _c^*}(p)$ is for the quantum number $(1/2)^-$ $\varLambda _c^*$ baryon. $f_{\varLambda _c}$ and $f_{\varLambda _c^*}$ are the decay constants, $u_{\varLambda _c}(p)$ and $u_{\varLambda _c^*}$ are the spinors of $\varLambda _c$ and $\varLambda _c^*$, respectively. The ellipsis in the righthand side of the correlation function represents all the contributions of excited and continuum states with the same quantum number of $\varLambda _c$. The transition matrix element $\langle \varLambda _c(p)|j_\mu |\varLambda _b(p+q)\rangle$ can be parameterized by six form factors dependent on momentum transfer square $q^2$, and it’s given by

$$\begin{aligned}&\langle \varLambda _c^{(*)}(p,s_1)|j_\mu |\varLambda _b(p+q,s_2)\rangle \nonumber \\&\quad = {\overline{u}}_{\varLambda _c^{(*)}}(p,s_1)\left[ \gamma _\mu f_1^{(*)} (q^2)+i\frac{f_2^{(*)}(q^2)}{M_{\varLambda _b}}\sigma _{\mu \nu }q^{\nu } \right. \nonumber \\&\qquad \left. +\, \frac{f_3^{(*)}(q^2)}{M_{\varLambda _b}}q_\mu \right] u_{\varLambda _b}(p+q,s_2)\nonumber \\&\qquad -{\overline{u}}_{\varLambda _c^{(*)}}(p,s_1)\left[ \gamma _\mu g_1^{(*)} (q^2)+i\frac{g_2^{(*)}(q^2)}{M_{\varLambda _b}}\sigma _{\mu \nu }q^{\nu }\right. \nonumber \\&\qquad \left. +\frac{g_3^{(*)}(q^2)}{M_{\varLambda _b}}q_\mu \right] \gamma _5 u_{\varLambda _b}(p+q,s_2). \end{aligned}$$

(7)

On the QCD level, by contracting the charm quark, the correlation function can be written as

$$\begin{aligned} T_\mu (p,q)&=i\int d^4 x e^{ip\cdot x}\langle 0|{\mathcal {T}}\{j_{\varLambda _c}(x),j_\mu (0)\}|\varLambda _b(p+q) \nonumber \\&=i\int d^4xe^{ip\cdot x}(C\gamma _5)_{\alpha \beta }S_{\sigma \tau }(x)[\gamma _\mu (1-\gamma _5)]_{\tau \gamma } \nonumber \\&\quad \times \langle 0|\epsilon _{ijk}u_\alpha ^{iT}(x)d_\beta ^j(x)b_\gamma ^k(0)|\varLambda _b(p+q)\rangle . \end{aligned}$$

(8)

where C is the charge conjugation matrix, and S(x) is the free charm quark propagator.

The light-cone distribution amplitude of $\varLambda _b$ baryon has been investigated in [26] and used in the analysis of heavy baryon decay in [46,47,48]. We should notice that the light-cone distribution amplitudes are obtained in the heavy quark effective theory framework. And in reference [26], the light-cone distribution amplitude $\langle 0|\epsilon _{abc}u^{aT}_\alpha (x)d^b_\beta (x)b^c_\gamma (0)|\varLambda _b(p+q)\rangle$ is represented by $\langle 0|\epsilon _{abc}u^{aT}_\alpha (x)d^b_\beta (x)b^c_\gamma (0)|\varLambda _b(v)\rangle$. Considering the heavy quark effective theory on both the hadronic and QCD level, the direct replacement $|\varLambda _b(p+q)\rangle \rightarrow |\varLambda _b(v)\rangle$ can be made safely. Therefore, the four-momentum of $\varLambda _b$ will be $p+q=M_{\varLambda _b}v$ with the on-shell condition.

At the quark level of the correlation function, the transition matrix element $\epsilon _{ijk}\langle 0|u_\alpha ^{iT}(x)d_\beta ^j(x)b_\gamma ^k(0)|\varLambda _b(v)\rangle$ is

(9)

where $n_\mu$, ${\overline{n}}_\mu$, and $\sigma _{{\overline{n}}n}$ are

$$\begin{aligned} n_\mu =\frac{x_\mu }{v\cdot x},\quad {\overline{n}}_\mu =2v_\mu -\frac{x_\mu }{v\cdot x}, \quad \sigma _{{\overline{n}}n}=\sigma _{\mu \nu }{\overline{n}}^{\mu }n^{\nu }. \end{aligned}$$

The distribution amplitudes which have been given in [26] are

$$\begin{aligned} \varPsi _i(t_1,t_2)=\int _{0}^{\infty }\omega d\omega \int _{0}^{1}due^{-i\omega (t_1u+t_2{\overline{u}})}{\tilde{\psi }}_i(\omega ,u), \end{aligned}$$

(10)

with ${\overline{u}}=1-u$, $t_in=x_i$, and

$$\begin{aligned} {\tilde{\psi }}_2(\omega ,u)&=\omega ^2u(1-u)[\frac{1}{\epsilon _0^4}e^{-\omega /\epsilon _0}\nonumber \\&\quad +a_2C_2^{3/2}(2u-1)\frac{1}{\epsilon _1^4}e^{-\omega /\epsilon _1}],\end{aligned}$$

(11)

$$\begin{aligned} {\tilde{\psi }}_3^s(\omega ,u)&=\frac{\omega }{2\epsilon _3^3}e^{-\omega /\epsilon _3}, \end{aligned}$$

(12)

$$\begin{aligned} {\tilde{\psi }}_3^\sigma (\omega ,u)&=\frac{\omega }{2\epsilon _3^3}(2u-1)e^{-\omega /\epsilon _3},\end{aligned}$$

(13)

$$\begin{aligned} {\tilde{\psi }}_4(\omega ,u)&=5{\mathcal {N}}^{-1}\int _{\omega /2}^{s_0^{\varLambda _b}}dse^{-s/\tau }(s-\omega /2)^3. \end{aligned}$$

(14)

These parameters in the four light-cone distribution amplitudes are $\epsilon _0=200^{+130}_{-60}$ $\textrm{MeV}, \epsilon _1=650^{+650}_{-300}$ $\textrm{MeV}, \epsilon _3=230$ $\textrm{MeV}$ and $a_2=0.333^{+0.250}_{-0.333}$. $C_2^{3/2}(2u-1)$ is the Gegenbauer polynomial. Other parameters and expressions and reliable regions, such as $s_0^{\varLambda _b}$ and $\tau$ can be found in reference [26]. The ${\mathcal {N}}$ in ${\tilde{\psi }}_4(\omega ,u)$ is

$$\begin{aligned} {\mathcal {N}}=\int _0^{s_0} ds s^5 e^{-s/\tau }. \end{aligned}$$

(15)

Except for the above four light-cone distribution amplitudes, another definition will be useful in the following light-cone sum rules calculation in the $j_{\varLambda _c}^2$ interpolating current framework,

$$\begin{aligned} {\overline{\psi }}_i(\omega ,u)=\int _0^{\omega }d\tau \tau {\tilde{\psi }}_i(\tau , u). \end{aligned}$$

(16)

where ${\tilde{\psi }}_i(\tau , u)$ correspond to light-cone distribution amplitudes (11)–(14).

2.2 Form factors of $\varLambda _b \rightarrow \varLambda _c$ transition

In order to calculate the decay widths and branching ratios of semileptonic decay $\varLambda _b^0 \rightarrow \varLambda _c^+ \ell ^- {\overline{\nu }}_\ell$, the information of six form factors $f_i$ and $g_i$ $(i=1,2,3)$ should be known. It is known that the QCD sum rule method contains both the positive and negative parity contribution of ground states $\varLambda _c$ baryons with spin-1/2. To avoid the hidden uncertainty from the contribution of negative parity baryon $\varLambda _c^*$, the scheme developed in [49] which was used in QCD sum rules for nucleon and applied to light-cone sum rules for heavy baryon in [50] is taken into account. By substituting $\varLambda _c$ decay matrix element and $\varLambda _b \rightarrow \varLambda _c$ transition matrix elements (7) of both positive and negative parity baryon $\varLambda _c$ and $\varLambda _c^*$ to Eq. (6), and using the relations , the representation of correlation function on the hadronic level with the contribution both $\varLambda _c$ and $\varLambda _c^*$ can be expressed as

(17)

Substituting the light-cone distribution amplitudes of $\varLambda _b$ Eq. (9) into the correlation function Eq. (8), the expression on the QCD level is obtained as

(18)

Comparing with the same coeffecients of Lorentz structures and $\varGamma \gamma _5$ on both the hadronic and QCD levels, one can substract and eliminate the contributions of negative parity baryon $\varLambda _c^*(\frac{1}{2})^-$ in the light-cone sum rules by solving the linear equations of form factors. Thereafter, one can make a standard light-cone sum rule calculation, and a Borel transformation to suppress both the higher twist and continuum contributions

$$\begin{aligned} \int _{0}^{\infty }d\sigma \frac{\rho _i(\sigma )}{(p-\omega v)^2-m_c^2} \rightarrow -\int _{0}^{\sigma _0}d\sigma \frac{\rho _i(\sigma )e^{-s/M_B^2}}{{\overline{\sigma }}}, \end{aligned}$$

(19)

where $\sigma =\omega /M_{\varLambda _b}$ and ${\overline{\sigma }}=1-\sigma$. We should also notice that in the heavy quark effective theory the decay constant of $\varLambda _b$ and $\varLambda _c$ has no difference, which has been discussed in reference [5]. With the quark-hadron duality assumption, after making the light-cone sum rule calculation procedure, and excluding the negative paity $\varLambda _c^*$ contribution, one has the relations of form factors $f_1(q^2)=g_1(q^2)$ and $f_2(q^2)=f_3(q^2)=g_2(q^2)=g_3(q^2)$. Form factors $f_1(q^2)$ and $f_2(q^2)$ can be expressed as

$$\begin{aligned} f_1(q^2)&=\int _0^1 du \int _0^{\sigma _0} d\sigma \frac{\sigma M_{\varLambda _b}^2(m_c-\sigma M_{\varLambda _c}+M_{\varLambda _c^*})}{{\overline{\sigma }}(M_{\varLambda _c}+M_{\varLambda _c^*})} \times \nonumber \\&\quad \times \psi _3^s(\omega ,u)e^{(M_{\varLambda _c}^2-s)/M_B^2}, \end{aligned}$$

(20)

$$\begin{aligned} f_2(q^2)&=-\int _0^1 du \int _0^{\sigma _0} d\sigma \frac{\sigma ^2 M_{\varLambda _b}^3\psi _3^s(\omega ,u)}{{\overline{\sigma }}(M_{\varLambda _c}+M_{\varLambda _c^*})}e^{(M_{\varLambda _c}^2-s)/M_B^2}. \end{aligned}$$

(21)

The parameter $M_B$ is the Borel mass and the extra parameters introduced in the above equations are defined as

$$\begin{aligned}&s=\sigma M_{\varLambda _b}^2+\frac{m_c^2-\sigma q^2}{{\overline{\sigma }}}, \end{aligned}$$

(22)

$$\begin{aligned}&\sigma _0=\frac{(s_0+M_{\varLambda _b}^2-q^2)}{2M_{\varLambda _b}^2} \nonumber \\&\qquad \qquad -\frac{\sqrt{(s_0+M_{\varLambda _b}^2-q^2)^2-4M_{\varLambda _b}^2(s_0-m_c^2)}}{2M_{\varLambda _b}^2}, \nonumber \\ \end{aligned}$$

(23)

here $s_0$ is the threshold of $\varLambda _c$ baryon. One can notice that the mass of $\varLambda _c^*$ enters the sum rules through the practice of eliminating the contribution of negative parity baryon $\varLambda _c^*$.

3 Numerical analysis

The input parameters in the numerical analysis, such as the mass of heavy baryons and leptons, are adopted from PDG [51] and listed in Table 1. The heavy charm quark mass $m_c$ adopted in this work is the pole mass. Since the pole mass is a gauge-invariant, infrared finite, and renormalization-scheme-independent quantity [52]. The pole mass of charm quark $m_c=(1.67\pm 0.07)$ $\textrm{GeV}$ corresponds to the ${\overline{MS}}$ mass ${\overline{m}}_c=(1.27\pm 0.02)$ $\textrm{GeV}$ in PDG, and the relations between ${\overline{MS}}$ and pole mass can be found in [51, 53].

Table 1 Masses of heavy baryons, quarks and leptons

Fig. 1

The form factors of $f_1(q^2)$ and $f_2(q^2)$ depend on the momentum transfer $q^2$ with the values $m_c=1.67~\textrm{GeV},~s_0=(M_{\varLambda _c}+0.4)^2~\mathrm {GeV^2}$ at $M_B^2=6$ $\mathrm {GeV^2}$, $M_B^2=8$ $\mathrm {GeV^2}$ and $M_B^2=10$ $\mathrm {GeV^2}$ with each form factor of the current type $j_{\varLambda _c}^1$

With these parameters and equations of form factors, one can calculate the semileptonic decay process. One considers the threshold $s_0$ of $\varLambda _c$ set to be larger than the ground states baryon $\varLambda _c$ and $\varLambda _c^*$ mass, but lower than the excited states baryon $\varLambda _c$ mass. So, we set $s_0=(M_{\varLambda _c}+\varDelta )^2$, $\varDelta =(0.40\pm 0.05)$ $\textrm{GeV}$. The Borel parameter $M_B$ is set to the interval where the form factors have a stable region with $M_B^2$, and should also suppress the contribution of excited and continuum states of final baryon $\varLambda _c$ and the higher twist of the initial baryon $\varLambda _b$ light-cone distribution amplitudes. With these requirements, the Borel parameter $M_B$ is chosen as $M_B^2=(8\pm 2)$ $\mathrm {GeV^2}$. The form factors relying on the momentum transfer square $q^2$ are calculated with the current $j_{\varLambda _c}^1$ and $j_{\varLambda _c}^2$ respectively based on the above considerations. With the threshold $(M_{\varLambda _c}+0.35)^2~\mathrm {GeV^2} \le s_0 \le (M_{\varLambda _c}+0.45)^2~\textrm{GeV}^2$, and Borel parameters $M_B^2$ $6~\mathrm {GeV^2} \le M_B^2 \le 10~\mathrm {GeV^2}$ respectively, form factors $F_i(q^2)$ with the interpolating current $j_{\varLambda _c}^1$ at $q^2=0$ $\mathrm {GeV^2}$ are $f_1(0)=g_1(0)=0.534^{+0.060}_{-0.074}$, $f_2(0)=f_3(0)=g_2(0)=g_3(0)=-(0.054^{+0.013}_{-0.011})$, the errors come from the uncertainties of input parameters and the regions of Borel parameters $M_B$ and threshold $s_0$.

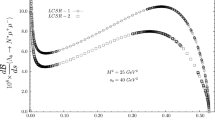
As discussed in reference [54] and our numerical analysis, the light-cone sum rule is not applicable to the whole physical region $m_\ell ^2\le q^2 \le (M_{\varLambda _b}-M_{\varLambda _c})^2$. In this work, the only applicable region of $q^2$ is 0 $\textrm{GeV}^2\le q^2 \le 2.5$ $\textrm{GeV}^2$, as shown in Fig. 1. For the whole physical regions, we should extrapolate the form factors obtained by the light-cone sum rule from the light-cone sum rule applicable region to the whole physical region through a fitting formula. In this work, the following general “z-expansion” formula is used to fit the form factors and extrapolate them to the whole physical region [55].

$$\begin{aligned} F_i(q^2)&=\frac{F_i(0)}{1-\frac{q^2}{M_{B_c}^2}}\{1+b_1[z(q^2,t_0)-z(0,t_0)]\nonumber \\&\quad +b_2[z(q^2,t_0)^2-z(0,t_0)^2]\}, \end{aligned}$$

(24)

where

$$\begin{aligned} z(q^2,t_0)=\frac{\sqrt{t_+-q^2}-\sqrt{t_+-t_0}}{\sqrt{t_+-q^2}+\sqrt{t_+-t_0}}, \end{aligned}$$

(25)

and

$$\begin{aligned} t_+&=(M_{\varLambda _b}+M_{\varLambda _c})^2, \nonumber \\ t_0&=(M_{\varLambda _b}+M_{\varLambda _c})\cdot (\sqrt{M_{\varLambda _b}}-\sqrt{M_{\varLambda _c}})^2. \end{aligned}$$

(26)

$M_{B_c}=6.27447~\textrm{GeV}$ is the mass of $B_c$ meson [51]. $F_i(0)$ is the form factor at $q^2=0~\mathrm {GeV^2}$.

With the fitting formula and the data of form factors at $q^2=0$ $\mathrm {GeV^2}$ and the interval $0\le q^2\le 2.5$ $\mathrm {GeV^2}$, the fitting parameters of form factors $F_i(q^2)$ with the interpolating current type $j_{\varLambda _c}^1$ can be obtained and are listed in Table 2.

To obtain the branching fractions of semileptonic decays of $\varLambda _b^0$ to $\varLambda _c^+$, one should know the lifetime or partial decay width of $\varLambda _b^0$. The lifetime of $\varLambda _b$ baryon is adopted from PDG, with $\tau _{\varLambda _b}=(1.471\pm 0.009)$ $\textrm{ps}$. The helicity amplitude forms of semileptonic decay widths are used in these processes [56]. One has the following equation of differential decay width written as two polarized decay widths

$$\begin{aligned} \frac{d\varGamma }{dq^2}=\frac{d\varGamma _L}{dq^2}+\frac{d\varGamma _T}{dq^2}. \end{aligned}$$

(27)

where $\varGamma _L$ and $\varGamma _T$ are longitudinally and transversely polarized decay widths, respectively. The total decay width is

$$\begin{aligned} \varGamma =\int _{m_l^2}^{(M_{\varLambda _b}-M_{\varLambda _c})^2}dq^2\frac{d\varGamma }{dq^2}, \end{aligned}$$

(28)

where

$$\begin{aligned} \frac{d\varGamma _L}{dq^2}&=\frac{G_F^2|V_{cb}|^2 q^2 p(1-{\hat{m}}_l^2)^2}{384\pi ^3 M_{\varLambda _b}^2}\left[ (2+{\hat{m}}_l^2)(|H_{\frac{1}{2},0}|^2 \right. \nonumber \\&\quad \left. +|H_{-\frac{1}{2},0}|^2)+3{\hat{m}}_l^2(|H_{\frac{1}{2},t}|^2+|H_{-\frac{1}{2},t}|^2)\right] , \end{aligned}$$

(29)

$$\begin{aligned} \frac{d\varGamma _T}{dq^2}&=\frac{G_F^2|V_{cb}|^2 q^2 p(1-{\hat{m}}_l^2)^2(2+{\hat{m}}_l^2)}{384\pi ^3 M_{\varLambda _b}^2}\left( |H_{\frac{1}{2},1}|^2 \right. \nonumber \\&\quad \left. +|H_{-\frac{1}{2},-1}|^2\right) . \end{aligned}$$

(30)

In the above equations, $p=\sqrt{Q_+Q_-}/2M_{\varLambda _b}, Q_\pm =(M_{\varLambda _b}\pm M_{\varLambda _c})^2-q^2$, and ${\hat{m}}_l\equiv m_l/\sqrt{q^2}$, in which $m_l$ is the mass of lepton ($e,~\mu$ or $\tau$). The relevant expressions of the helicity connected with form factors are given by

$$\begin{aligned} H_{\frac{1}{2},0}^V&=-i\frac{\sqrt{Q_-}}{\sqrt{q^2}}\left[ (M_{\varLambda _b} +M_{\varLambda _c})f_1(q^2)-\frac{q^2}{M_{\varLambda _b}}f_2(q^2)\right] , \end{aligned}$$

(31)

$$\begin{aligned} H_{\frac{1}{2},1}^V&=i\sqrt{2Q_-}\left[ -f_1(q^2) +\frac{M_{\varLambda _b}+M_{\varLambda _c}}{M_{\varLambda _b}}f_2(q^2)\right] , \end{aligned}$$

(32)

$$\begin{aligned} H_{\frac{1}{2},0}^A&=-i\frac{\sqrt{Q_+}}{\sqrt{q^2}} \left[ (M_{\varLambda _b}-M_{\varLambda _c})g_1(q^2)+\frac{q^2}{M_{\varLambda _b}}g_2(q^2)\right] , \end{aligned}$$

(33)

$$\begin{aligned} H_{\frac{1}{2},1}^A&=i\sqrt{2Q_+}\left[ -g_1(q^2) -\frac{M_{\varLambda _b}-M_{\varLambda _c}}{M_{\varLambda _b}}g_2(q^2)\right] , \end{aligned}$$

(34)

$$\begin{aligned} H_{\frac{1}{2},t}^V&=-i\frac{\sqrt{Q_+}}{q^2}\left[ (M_{\varLambda _b} -M_{\varLambda _c})f_1(q^2)+\frac{q^2}{M_{\varLambda _b}}f_3(q^2)\right] , \end{aligned}$$

(35)

$$\begin{aligned} H_{\frac{1}{2},t}^A&=-i\frac{Q_-}{\sqrt{q^2}}\left[ (M_{\varLambda _b} +M_{\varLambda _c})g_1(q^2)-\frac{q^2}{M_{\varLambda _b}}g_3(q^2)\right] . \end{aligned}$$

(36)

The negative helicity amplitudes can be obtained through the positive helicity amplitudes as

$$\begin{aligned} H_{-\lambda ,-\lambda _W}^V= & {} H_{\lambda ,\lambda _W}^V, \nonumber \\ H_{-\lambda ,-\lambda _W}^A= & {} -H_{\lambda ,\lambda _W}^A. \end{aligned}$$

(37)

$\lambda$ and $\lambda _W$ are the polarizations of the final $\varLambda _c$ baryon and W-Boson, respectively.

With the $V-A$ current, the total helicity amplitudes are expressed as

$$\begin{aligned} H_{\lambda ,\lambda _W}=H_{\lambda ,\lambda _W}^V-H_{\lambda ,\lambda _W}^A. \end{aligned}$$

(38)

Table 2 Fitting parameters of form factors $F_i(q^2)$ with the interpolating current type $j_{\varLambda _c}^1$, with the errors coming from the uncertainties of input parameters, Borel parameters $M_B$ and threshold $s_0$

Table 3 The decay widths $\varGamma (\varLambda _b^0 \rightarrow \varLambda _c^+ \ell ^- {\overline{\nu }}_\ell )$, branching fractions ${\mathcal {B}}r(\varLambda _b^0\rightarrow \varLambda _c^+\ell ^-{\overline{\nu }}_\ell )$ and ratios $\varGamma _L/\varGamma _T$ of current type $j_{\varLambda _c}^1$

Table 4 The decay widths and branching fractions compared with other models. The first and second values in the $\varGamma$ and ${\mathcal {B}}r$ columns of $\varLambda _b^0 \rightarrow \varLambda _c^+ \ell ^-{\overline{\nu }}_\ell$ stand for the $\varLambda _b^0 \rightarrow \varLambda _c^+ e^- {\overline{\nu }}_e$ and $\varLambda _b^0 \rightarrow \varLambda _c^+ \mu ^- {\overline{\nu }}_\mu$, respectively. All the data listed are the central values

One substitutes the form factors of weak decay $\varLambda _b \rightarrow \varLambda _c$ into the helicity form of decay widths, uses these basic parameters provided by PDG, and considers the CKM matrix element $|V_{cb}|=(41.0\pm 1.4)\times 10^{-3}$ [51], then integrates the momentum transfer square $q^2$ on the whole physical region. Therefore, the information on decay widths $\varGamma (\varLambda _b^0\rightarrow \varLambda _c^+\ell ^-{\overline{\nu }}_\ell )$ and the ratios $\varGamma _L/\varGamma _T$ can be known. The absolute branching ratios ${\mathcal {B}}r(\varLambda _b^0\rightarrow \varLambda _c^+\ell ^-{\overline{\nu }}_\ell )$ can be calculated with the lifetime of $\varLambda _b$ baryon and results are listed in Table 3. To compare our results with other works, the unit second inverse is used and listed in Table 4. The pictures of differential decay widths of $\varLambda _b^0\rightarrow \varLambda _c^+\ell ^-{\overline{\nu }}_\ell$ with current $j_{\varLambda _c}^1$ at central values of parameters are shown in Fig. 2.

Fig. 2

Differential decay widths of the current type $j_{\varLambda _c}^1$ of lepton final state with electron (left), muon (middle), and tau (right) respectively. The figures are plotted at the central values $m_c=1.67~\mathrm {GeV^2}$, $s_0=(M_{\varLambda _c}+0.4)^2~\mathrm {GeV^2}$ and $M_B^2=8~\mathrm {GeV^2}$

Turn to another case of $\varLambda _c$ interpolating current $j_{\varLambda _c}^2(x)=\epsilon _{ijk}[u^{iT}(x)C\gamma _5\gamma _\nu d^j(x)]\gamma ^\nu c^k(x)$. By using the same procedures as those for the current type $j_{\varLambda _c}^1$ with the same parameters as those in the above analysis, and then obtains the same relations of form factors $f_1(q^2)=g_1(q^2)$, $f_2(q^2)=f_3(q^2)=g_2(q^2)=g_3(q^2)$ as well as that in the case of $j_{\varLambda _c}^1$. Setting the same threshold $s_0$ and the Borel mass $M_B^2$ as in the case of $j_{\varLambda _c}^1$, form factors with the interpolating current type $j_{\varLambda _c}^2$ at $q^2=0$ $\textrm{GeV}^2$ give the values $f_1(0)=g_1(0)=0.644^{+0.175}_{-0.352}$, $f_2(0)=f_3(0)=g_2(0)=g_3(0)=-0.100^{+0.061}_{-0.039}$, where the uncertainties contain the errors of input parameters, thresholds, and Borel parameters. Using the helicity amplitudes form of decay width, the decay widths $\varGamma (\varLambda _b^0\rightarrow \varLambda _c^+\ell ^-{\overline{\nu }}_\ell )$, branching fractions ${\mathcal {B}}r(\varLambda _b^0\rightarrow \varLambda _c^+\ell ^-{\overline{\nu }}_\ell )$, and the ratios $\varGamma _L/\varGamma _T$ within the interpolating current $j_{\varLambda _c}^2$ can be obtained and they are shown in Table 5.

Table 5 The decay widths $\varGamma (\varLambda _b^0 \rightarrow \varLambda _c^+ \ell ^- {\overline{\nu }}_\ell )$, branching fractions ${\mathcal {B}}r(\varLambda _b^0\rightarrow \varLambda _c^+\ell ^-{\overline{\nu }}_\ell )$ and ratios $\varGamma _L/\varGamma _T$ of current type $j_{\varLambda _c}^2$

Table 6 Ratios of branching fractions ${\mathcal {R}}(\varLambda _c^+)$ compared with others’ work with the central values

The ratio of semileptonic decay branching fractions with tau lepton final states and light lepton final states ${\mathcal {R}}(H_c)$ (H stands for hadron), in the early experimental measurement was only reported in the $B\rightarrow D(D^*)$ weak decay. BaBar collaboration gave their evidence ${\mathcal {R}}(D)=(0.440\pm 0.058)$ and ${\mathcal {R}}(D^*)=(0.332\pm 0.024)$ [65]. Meanwhile the Standard Model gave the prediction ${\mathcal {R}}(D)=(0.297\pm 0.017)$ and ${\mathcal {R}}(D^*)=(0.252\pm 0.003)$ [66]. It shows that there is a larger value in the experiment than the Standard Model prediction, which is ${\mathcal {R}}(D^*)$ puzzle. The recent experiment LHCb reported ${\mathcal {R}}(\varLambda _c^+)=(0.242\pm 0.026\pm 0.040\pm 0.059)$, with the last uncertainty from the measurement of branching fraction uncertainty of the channel $\varLambda _b^0\rightarrow \varLambda _c^+\mu ^-{\overline{\nu }}_\mu$, and what they reported in their experiment agrees with the prediction of the Standard Model. In this work, the values of ${\mathcal {R}}(\varLambda _c^+)$ that we calculate are ${\mathcal {R}}(\varLambda _c^+)=(0.274^{+0.009}_{-0.005})$ with the $\varLambda _c$ interpolating current type $j_{\varLambda _c}^1$, and ${\mathcal {R}}(\varLambda _c^+)=0.239^{+0.070}_{-0.021}$ with the $\varLambda _c$ interpolating current type $j_{\varLambda _c}^2$, which are also consistent with the recent experimental report and the prediction of the Standard Model. The comparison of the results in our works with other models and experiments’ is displayed in Table 6.

4 Conclusions and discussions

In the light-cone sum rules approach, the six transition form factors of $\varLambda _b\rightarrow \varLambda _c$ weak decay are calculated with the $\varLambda _b$ baryon light-cone distribution amplitudes. In the calculations, we use two types of $\varLambda _c$ interpolating currents $j_{\varLambda _c}^1$ and $j_{\varLambda _c}^2$, and give the relations of these form factors $f_1(q^2)=g_1(q^2)$, $f_2(q^2)=f_3(q^2)=g_2(q^2)=g_3(q^2)$ for both types of $\varLambda _c$ interpolating current $j_{\varLambda _c}^1$ and $j_{\varLambda _c}^2$. The values of six form factors at $q^2=0$ $\mathrm {GeV^2}$ obtained by the light-cone sum rule with $\varLambda _b$ baryon distribution amplitudes give that $f_1(0)=g_1(0)=0.533^{+0.060}_{-0.074}$, $f_2(0)=f_3(0)=g_2(0)=g_3(0)=(-0.054^{+0.013}_{-0.011})$ with interpolating current $j_{\varLambda _c}^1$ and $f_1(0)=g_1(0)=0.644^{+0.175}_{-0.352}$, $f_2(0)=f_3(0)=g_2(0)=g_3(0)=-0.100^{+0.061}_{-0.039}$ with interpolating current $j_{\varLambda _c}^2$, which are all in accordance with the results in other methods and models’ and have similar results to heavy quark effective theory analysis [13]. When these form factors are combined with the helicity amplitudes to calculate the differential decay widths and branching fractions of heavy baryon semileptonic decay $\varLambda _b^0\rightarrow \varLambda _c^+\ell ^-{\overline{\nu }}_\ell$, the results in our work are in agreement with those in other theoretical models and experimental reports.

The uncertainties of form factors and decay rates with interpolating current $j_{\varLambda _c}^1$ are small, they present a good accuracy result of $\varLambda _b$ decay. However, considering the $j_{\varLambda _c}^2$ type interpolating current, the uncertainties become larger. This is because the uncertainty of the input parameter of $\varLambda _b$ baryon light-cone distribution amplitudes $\epsilon _0$ has a big influence on the form factors while the other input parameters only have a small influence on the form factors and the decay properties of $\varLambda _b^0 \rightarrow \varLambda _c^+ \ell ^- {\overline{\nu }}_{\ell }$. Taking the large uncertainties caused by the interpolating current type $j_{\varLambda _c}^2$ in the branching fractions and the comparision with form factors calculated in other models introduced in the introduction into consideration, choosing $j_{\varLambda _c}^1$ type interpolating current may be preferable.

Testing the ratio of branching fractions ${\mathcal {R}}(\varLambda _c^+)$ of tau lepton and light lepton final states, provides an excellent way to test the Standard Model. The difference between the experiment and the Standard Model may imply that new physics beyond the Standard Model can be found. However, there are still some uncertainties about the semileptonic decay processes $\varLambda _b \rightarrow \varLambda _c \ell {\overline{\nu }}_\ell$. Fortunately, the recent LHCb result is consistent with the Standard Model under the uncertainty of the measurement of branching fraction ${\mathcal {B}}r(\varLambda _b^0\rightarrow \varLambda _c^+\mu ^-{\overline{\nu }}_\mu )$. Even so, more precise experiments and theoretical analysis should be conducted to explore whether there is new physics beyond Standard Model.

Appendix

Light-cone QCD sum rules of $\varLambda _b \rightarrow \varLambda _c \ell \nu _{\ell }$ within the $\varLambda _c$ baryon current type $j_{\varLambda _c}^2=\epsilon _{ijk}[u^{iT}(x)C\gamma _5\gamma _\nu d^j(x)]\gamma ^\nu c^k(x)$.

QCD representation of correlation function with current type $j_{\varLambda _c}^2$

(1)

As the same procrdure in the current $j_{\varLambda _c}^1(x)$, and extracting the contribution of negative parity baryon $\varLambda _c^*$, we have the relations of form factors $f_1(q^2)=g_1(q^2), f_2(q^2)=f_3(q^2)=g_2(q^2)=g_3(q^2)$.

Form factors $f_1(q^2)$ and $f_2(q^2)$ with the current type $j_{\varLambda _c}^2$ are

$$\begin{aligned} f_1(q^2)&=-\frac{M_{\varLambda _b}}{M_{\varLambda _c}+M_{\varLambda _c^*}} \int _0^1 du \int _0^{\sigma _0}\frac{d\sigma }{{\overline{\sigma }}} \{\sigma [M_{\varLambda _c}(M_{\varLambda _c^*} \nonumber \\ {}&\quad -M_{\varLambda _c} -m_c)-{\overline{\sigma }}M_{\varLambda _b}^2 +q^2]\psi _2(\omega ,u) +2[{\overline{\psi }}_2(\omega ,u) \nonumber \\ {}&\quad -{\overline{\psi }}_4(\omega ,u)]\}e^{(M_{\varLambda _c}^2-s)/M_B^2} \nonumber \\ {}&\quad +\frac{M_{\varLambda _b}}{(M_{\varLambda _c}+M_{\varLambda _c^*})M_B^2}\int _0^1 du \int _0^{\sigma _0}\frac{d\sigma }{{\overline{\sigma }}^2}[(\sigma M_{\varLambda _c} \nonumber \\ {}&\quad -M_{\varLambda _c^*})m_c +\sigma ({\overline{\sigma }}M_{\varLambda _b}^2-q^2)-{\overline{\sigma }}M_{\varLambda _c}^2][{\overline{\psi }}_2(\omega ,u) \nonumber \\ {}&\quad -{\overline{\psi }}_4(\omega ,u)] e^{(M_{\varLambda _c}^2-s)/M_B^2} \nonumber \\ {}&\quad +\frac{M_{\varLambda _b}}{M_{\varLambda _c}+M_{\varLambda _c^*}}\int _0^1 du \frac{\eta (\sigma _0,q^2)}{{\overline{\sigma }}_0}[(\sigma _0 M_{\varLambda _c}-M_{\varLambda _c^*})m_c \nonumber \\ {}&\quad +\sigma _0({\overline{\sigma }}_0 M_{\varLambda _b}^2-q^2)-{\overline{\sigma }}_0 M_{\varLambda _c}^2][{\overline{\psi }}_2(\omega _0,u) \nonumber \\ {}&\quad -{\overline{\psi }}_4(\omega _0,u)] e^{(M_{\varLambda _c}^2-s_0)/M_B^2}, \end{aligned}$$

(2)

$$\begin{aligned} f_2(q^2)&=-\frac{M_{\varLambda _b}^2}{M_{\varLambda _c}+M_{\varLambda _c^*}}\int _0^1 du \int _0^{\sigma _0}\frac{d\sigma }{{\overline{\sigma }}}\sigma (M_{\varLambda _c^*} \nonumber \\ {}&\quad -m_c){\tilde{\psi }}_2(\omega ,u) e^{(M_{\varLambda _c}^2-s)/M_B^2} \nonumber \\ {}&\quad +\frac{M_{\varLambda _b}^2}{(M_{\varLambda _c}+M_{\varLambda _c^*})M_B^2}\int _0^1 du \int _0^{\sigma _0} \frac{d\sigma }{{\overline{\sigma }}^2}\sigma M_{\varLambda _b}^2m_c[{\overline{\psi }}_2(\omega ,u) \nonumber \\ {}&\quad -{\overline{\psi }}_4(\omega ,u)]e^{(M_{\varLambda _c}^2-s)/M_B^2} \nonumber \\ {}&\quad +\frac{M_{\varLambda _b}^2}{M_{\varLambda _c}+M_{\varLambda _c^*}}\int _0^1 du \frac{\eta (\sigma _0,q^2)}{{\overline{\sigma }}_0^2}\sigma _0 M_{\varLambda _b}^2m_c[{\overline{\psi }}_2(\omega _0,u) \nonumber \\ {}&\quad -{\overline{\psi }}_4(\omega _0,u)]e^{(M_{\varLambda _c}^2-s_0)/M_B^2} \end{aligned}$$

(3)

The Borel transformation

$$\begin{aligned} \int _{0}^{\infty }d\sigma \frac{\rho _i(\sigma )}{[(p-\omega v)^2-m_c^2]^2}&\rightarrow \int _{0}^{\sigma _0}d\sigma \frac{1}{{\overline{\sigma }}^2}\frac{\rho _i(\sigma )}{M_B^2}e^{-s/M_B^2} \nonumber \\ {}&\quad +\frac{1}{{\overline{\sigma }}_0^2}\eta (\sigma _0)\rho _i(\sigma _0)e^{-s_0/M_B^2} \end{aligned}$$

(4)

is used in the above equations, where

$$\begin{aligned} \eta (\sigma )=\frac{d\sigma }{ds}=\frac{{\overline{\sigma }}^2}{{\overline{\sigma }}^2M_{\varLambda _b}+m_c^2-q^2} \end{aligned}$$

(5)

and $\omega _0=\sigma _0 M_{\varLambda _b}$.