1 Introduction

The existence of a region known as the Swampland, where inconsistent semi-classical effective field theories inhabit, is directly related to the de Sitter vacua problem. It is an indication that in a consistent quantum theory of gravity the de Sitter vacuum does not exist. Moreover, the existence of the Swampland is a logically justified consequence relying on the fact that in the string Landscape (low energy effective field theories inhabit there) Minkowski and Anti-de Sitter solutions could be obtained easily. In other words, the existence of the Swampland (even vaster than the Landscape) is a statement pointing towards where a set of consistently-looking effective quantum field theories coupled to gravity, inconsistent with a quantum theory of gravity, should be inhibited. The boundaries or parameter values required to estimate where a theory inhabits is an important issue. Therefore, attempts to estimate the boundaries between these two regions have led to several conjectures.

In this regard, two Swampland criteria have recently been proposed, which determine what are the constraints to embed an effective field theory into quantum gravity [1,2,3]. In a short time, a good number of works have appeared in the literature discussing their cosmological implications. Studies for a dark-energy dominated low-redshift Universe and an inflating early Universe have been issued, providing interesting conclusions and consequences. In particular, in several papers, it has been shown that, if we argue in favor of string theory as the ultimate quantum gravity theory, then there are pieces of evidence that exact de Sitter solutions (with a positive cosmological constant), cannot actually describe the late-time evolution of the Universe.

The generic algorithm in these studies essentially consists in choosing explicit forms for the scalar field potential (known also as the Swampland potential) and for the dark-energy model. The last has been used to obtain observational constraints, which eventually allow to estimate of the parameter of the Swampland potential and to check whether the Swampland criteria for a dark-energy dominated Universe will be satisfied or not. Let us also remind the reader of the fact that this approach has been accepted assuming that GR with the standard matter fields in the presence of a quintessence field \(\phi \) will be the effective field theory. It is clear that the adopted strategy provides a highly model-dependent analysis, and that it would be desirable to perform the estimations using a model-independent method. Some of the above mentioned results can be found in [4,5,6,7,8,9,10,11,12,13,14,15,16,17].

However, shortly after these publications, a study of the Swampland criteria in a dark-energy-model independent way, for a dark-energy dominated Universe, appeared, providing a hint that the Swampland criteria in the form discussed in the literature needed to be reconsidered [4]. In the mentioned analysis, the authors adopted GPs and used the expansion rate data to rewrite the form of the potential and the field in terms of the Hubble parameter and its higher-order derivatives. In this way they could prove that, using a GP and H(z) data in a (dark energy) model-independent way it was possible to estimate the upper bounds on the two Swampland criteria. In this regard, the study of Ref. [4] is unique and provides hints for when the Swampland criteria is valid, in the scope of the measured and available H(z) data points.

The study of the accelerated expansion of the low-redshift Universe and the relatively good low-redshift observational data provide an ideal frame to further explore the Swampland criteria from the viewpoint of their cosmological implications. Despite significantly improved low-redshift data, several problems remain without a clear answer; and this could be alleviated if one could eventually decide whether the recent conditions of the Universe actually reflect the existence of dark energy or, on the contrary, they can be explained through a necessary modification of GR. In modern cosmology, the interest in dark energy comes from the possibility to generate a negative pressure, able to accelerate the expansion of the Universe. The goal of this paper does not go in the direction of dark energy and thus, correspondingly, we will suppress any further discussion of it, referring the readers to [18,19,20,21,22,23,24,25,26,27,28,29,30] and to the references at the end of this paper, for more information.

Recently our attention was captured by a study where it has been found that specific f(R) models can naturally satisfy the Swampland criteria [31]. However, we would like to point out that, besides the form of f(R) gravity, these authors also used an explicitly given model for dark energy. Following the discussion in [31], we noticed that, by using a GP, we are able to extend it, removing the need to involve a dark energy model in the analysis. In this way, any bias that could be induced by the specific choice of dark energy model would be suppressed; even then, good constraints similar to those of [4] could be obtained.

The goal of the present paper is to develop an intuition about the Swampland criteria and f(R) gravity without incorporating in the analysis any dark energy model. Later, we will see that in this case also the Swampland criteria can be expressed in terms of the H(z) Hubble function and its higher order derivatives, and the GP allows to obtain them directly from the expansion rate data. At the same time, we will constrain the parameters for each f(R) model considered. Moreover, we will provide the constraints on the model parameters leading to an alleviation of the \(H_{0}\) tension. This is mainly due to the structure of the data points used during the reconstruction of the H(z) Hubble function and its higher-order derivatives by GPs. This also means that our approach to the problem is different from that of previous studies. It should be stressed too, that from the discussion in the next section it will become clear that, owing to the structure of the problem considered, only one component – either the dark energy model or the form of f(R) – can be replaced. This is what prevents us to get a truly model-independent analysis of the problem, in a strict sense.

To end this introduction, we recall the Einstein field equations for f(R) gravity that will be used to constrain the models. The Einstein field equations can be written as [31,32,33,34,35]

$$\begin{aligned} G_{\alpha \beta } = R_{\alpha \beta } - \frac{1}{2}g_{\alpha \beta }R = T^{R}_{\alpha \beta } + T^{m}_{\alpha }{\beta }, \end{aligned}$$
(1)

where

$$\begin{aligned} T^{R}_{\alpha \beta }= & {} \frac{1}{2f_{R}(R)}g_{\alpha \beta } [f(R) - R f_{R}(R)] \nonumber \\&+ \frac{f^{;\alpha \beta }_{R}(R)}{f_{R}(R)}(g {\alpha \mu }g_{\beta \nu } - g_{\alpha \beta }g_{\mu \nu }), \end{aligned}$$
(2)

and

$$\begin{aligned} T^{m}_{\alpha \beta } = \frac{1}{f_{R}(R)} {\hat{T}}^{m}_{\alpha \beta }, \end{aligned}$$
(3)

is the stress-energy tensor of matter, taking into account the non-trivial coupling to geometry. The standard perfect fluid stress energy is

$$\begin{aligned} {\hat{T}}^{m}_{\alpha \beta } = (\rho _{m} + P_{m})u_{\alpha \beta } - P_{m}g_{\alpha \beta }, \end{aligned}$$
(4)

where \(\rho _{m}\) and \(P_{m}\) are the matter-energy density and pressure, respectively. On the other hand, we can define the curvature pressure

$$\begin{aligned}&P_{R} = \frac{1}{f_{R}(R)} \left( 2 H {\dot{R}} f_{RR}(R) + {\ddot{R}} f_{RR}(R) \right) \nonumber \\&\quad + \frac{1}{f_{R}(R)} \left( {\dot{R}}^{2} f_{RRR}(R) - \frac{1}{2} [f(R) - R f_{R}(R)] \right) , \end{aligned}$$
(5)

and the curvature density

$$\begin{aligned} \rho _{R} = \frac{1}{f_{R}(R)} \left( \frac{1}{2} [f(R) - R f_{R}(R) ]- 3 H {\dot{R}} f_{RR}(R) \right) , \end{aligned}$$
(6)

from the curvature–stress–energy tensor assuming a Friedmann–Robertson–Walker (FRW) metric, where we have imposed a null spatial curvature \(k=0\) and that \(8\pi G = c = 1\). In the above equations, R is the Ricci scalar,

$$\begin{aligned} R = -6 \left( \frac{\ddot{a}}{a} + \left( \frac{{\dot{a}}}{a}\right) ^{2} \right) , \end{aligned}$$
(7)

while \(f_{R}\), \(f_{RR}\) and \(f_{RRR}\) are the first, second and third order R-derivatives obtained from f(R). It is well known that thanks to adopted notifications, we can write any f(R) cosmology in GR form, with

$$\begin{aligned} \left( \frac{{\dot{a}}}{a} \right) ^{2} = \frac{1}{3} \rho _{tot}, \end{aligned}$$
(8)

and

$$\begin{aligned} \frac{\ddot{a}}{a} = -\frac{1}{6} (\rho _{tot} + P_{tot}), \end{aligned}$$
(9)

where \(P_{tot} = P_{R} + P_{m}\) and \(\rho _{tot} = \rho _{R} + \rho _{m}\) with \(P_{m}\) and \(\rho _{m}\) the pressure and the energy density for the usual matter fields, respectively. It is clear that using expansion rate data, the GP allows, from Eq. (7), to reconstruct the functional form of R.

This paper is organized as follows. In Sect. 2 we discuss how to reshape f(R) gravity to be able to perform the Swampland criteria analysis. Moreover, towards the end, we give some basic information about GPs. In Sect. 3 we discuss the results obtained for two 41-points H(z) data sets with very specific f(R) models. The discussion includes the constraints on the model parameters, too. Section 4 is devoted to the conclusions we have drawn from our analysis, and indications are given on further directions along which the work may be extended.

2 Swampland criteria and Gaussian processes

To start, we shall recall the formulation of the two Swampland criteria proposed. They can be expressed as:

  1. 1.

    SC1: The scalar field net excursion in reduced Planck units should satisfy the bound [1]

    $$\begin{aligned} \frac{|\Delta \phi |}{M_{P}} < \Delta \sim O(1), \end{aligned}$$
    (10)
  2. 2.

    SC2: The gradient of the scalar field potential is bounded by [2, 3]

    $$\begin{aligned} M_{P}\frac{|V^{\prime }|}{V} > {\hat{c}} \sim O(1), \end{aligned}$$
    (11)

    or

    $$\begin{aligned} M^{2}_{P} \frac{V^{\prime \prime }}{V} < - {\hat{c}} \sim O(1). \end{aligned}$$
    (12)

Both \(\Delta \) and \({\hat{c}}\) are here positive constants of order one. On the other hand, the prime denotes derivative with respect to the scalar field \(\phi \), and \(M_{P} = 1/\sqrt{8\pi G}\) is the reduced Planck mass. The Swampland criteria above give us a clear understanding on what to demand from the field. In particular, we see that the field should traverse a larger distance so that CS2 can be fulfilled in order to have the domain of validity of the effective field theory. Now, if we assume that GR with the standard matter field in the presence of a quintessence field \(\phi \) is the effective theory, then the Swampland criteria can be expressed in terms of the H(z) Hubble function and its higher-order derivatives, which can be reconstructed using the GPs. This allows to estimate \(|V^{\prime }|/V\) (or \(|V^{\prime \prime }|/V\)) directly.

This way of proceeding is completely model-independent, because of the fact that (1) we do not involve any form of the potential in the analysis, and (2) no extra dark energy model needs to be used to constrain the quintessence potential. However, an interesting aspect that still needs to be considered is the form of the kernel used in the GP reconstruction process (for more details see [4]). To this point, we will come back towards the end of this section.

Let us now see how the situation changes if we have f(R) gravity with

$$\begin{aligned} L = \int d^{4} x \sqrt{-g} [f(R) + L_{m}], \end{aligned}$$
(13)

where f(R) is a function of the Ricci scalar R and \(L_{m}\) is the standard matter Lagrangian density, to be the effective field theory. If we take into account the conformal transformations and recast the theory from the Jordan to the Einstein frame, the theory, Eq. (13), can be expressed in terms of the effective field with [31]

$$\begin{aligned} \phi = \frac{1}{2 {\hat{k}}}\ln (f_{R}), \end{aligned}$$
(14)

and the effective potential related to the conformal field as

$$\begin{aligned} V = -\frac{1}{2} \left( \frac{f - R f_{R} }{f^{2}_{R}}\right) , \end{aligned}$$
(15)

where \({\hat{k}}\) is a generic constant. On the other hand, if we calculate \(\partial {V}/\partial {\phi }\), then we can express Eqs. (10) and (11) (and Eq. (12)) in terms of f(R), \(f_{R}\) etc. In particular, for Eq. (11) – which will be studied in this paper for the dark energy-dominated Universe – we obtainFootnote 1

$$\begin{aligned} \frac{|\nabla _{\phi } V|}{V}= & {} \left| \left( \frac{4{\hat{k}}}{f(R) - R f_{R}(r) } \right) \left[ -f(R) + \frac{R f_{R}(R)}{2} \right. \right. \nonumber \\&\left. \left. + \frac{f_{R}(R)}{2} \left( \frac{\partial f(R)}{\partial f_{R}(R)} \right) - \frac{f^{2}_{R}(R)}{2} \left( \frac{\partial R}{\partial f_{R}(R)}\right) \right] \right| .\nonumber \\ \end{aligned}$$
(16)

Now, from Eq. (16) we see that, when the form of f(R) gravity is given, then Eq. (16) can be expressed in terms of the H(z) function and its higher-order derivatives, what allows to estimate \(|V^{\prime }| /V\), because of the Ricci scalar form.

Therefore, we need to understand what GPs are and what tools to use to achieve the final goal. It is well known that GPs are Bayesian state-of-the-art tools and the kernel is their key ingredient. The assumption that a GP prior can govern the set of possible latent functions and the likelihood of the latent function with observations shape this prior is a key one. Given this, GPs should be understood as distributions over functions, characterized by a mean function and a covariance matrix providing a full conditional statistical description of the predictions. In other words, GPs provide posterior probabilistic estimates and, for given observations, this can infer the relation between independent and dependent variables. However, there are several drawbacks that is important to understand, for a correct interpretation of the obtained results.

To start, we should understand that GPs are Machine Learning (ML) tools. This is important, namely that, similar to other ML techniques, they have advantages and disadvantages that one should not neglect. In general, the goal of ML is to learn about underlying latent distribution in the data at hand. Then, the learned latent distribution can be used to do classification, prediction, and generation of new distributions (among other possibilities). However, it should be understood that the learning process is strongly affected by the given data and, most likely, the algorithm can fail when meeting unforeseen situations or data. Unfortunately, this is one of the biggest disadvantages of ML and one that significantly reduces its applications in everyday life.

However, recently we have witnessed significant progress in this direction. Intensive research to increase ML robustness and safeness and make it less data hungry are on the way. We should be very careful when choosing a specific ML approach, having in mind that mainly the human experience stands for the algorithm success expressed either in terms of labeled data or as an agent in Reinforcement Learning and its various extensions and modifications. It is also highly recommended to avoid the well-known over-learning/under-learning problem. It can affect the learned latent distribution seriously. The point here is that the general goal of ML (and GPs too) is to learn general features and not to visit each single data point to understand why it is there. In other words, the goal of ML is to learn a logic explaining why the majority of the data is there, to be used later. This is of course a very general and rather philosophical description of the situation. Anyhow, with these considerations we wish to stress the fact that it is not surprising that GPs are not able to deal with unseen situations, giving sometimes wrong predictions. No surprise, then, that some situations are predicted with some probability \(Prob < 100 \%\). Moreover, another disadvantage of the method is that the choice of the kernel is not a standard process. Only expert experience-based exploration can allow us to estimate which kernel works better and make sure that the results have not just been got by chance.Footnote 2 One should be warned, that not treating this aspect very seriously can lead to misleading results, with bad consequences. In Cosmology, however, one can significantly reduce the kernel numbers to be considered, because one deals with relatively small datasets, contrary to robotics or autonomous driving research. We have to limit our discussion on philosophical aspects to the above paragraphs, but we do hope they were enough to get a proper message about the topic.

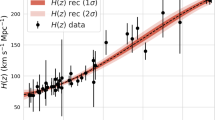
Table 1 H(z) and its uncertainty \(\sigma _{H}\) are in units of km s\(^{-1}\) Mpc\(^{-1}\). The upper panel depicts 30 samples deduced from the differential age method. The lower panel, 10 samples obtained from the radial BAO method. The table is built according to [4] (see also references therein for details)
Full size table

The expansion rate data presented in Table 1 is here depicted, consisting of 30-point samples of H(z) values deduced from the differential age method in addition to 10-point samples obtained from the radial BAO method. During the reconstruction, we have considered two different cases: (1) \(H_{0}\) is taken from the Planck mission and the forms of H(z), \(H^{\prime }(z)\), \(H^{\prime \prime }(z)\) and \(H^{\prime \prime \prime }(z)\) are reconstructed, and (2) \(H_{0}\) is taken from the Hubble mission and then the forms of H(z), \(H^{\prime }(z)\), \(H^{\prime \prime }(z)\) and \(H^{\prime \prime \prime }(z)\) are reconstructed. The reason for this is to see whether or not it is possible to find ways to solve, or at least to alleviate, the \(H_{0}\) tension problem.Footnote 3 In this way, already the reconstruction and the constraints obtained on the model parameters will allow seeing when is it possible to alleviate the \(H_{0}\) tension problem for a specifically given f(R).

We should stress again that the analysis presented here is based on one type of data set and that further study will be required, involving more observational data sets. However, even in this case, we can already see that what we now have on hand gives both reliable and thigh constraints on the model parameters, allowing to study the Swampland criteria in a quite accurate way. In the next section, the constraints obtained on the model parameters, and related consequences, will be discussed. The analysis here presented is related to the background dynamics described by Eqs. (8) and (9), with the assumption that \(P_{m} = 0\), while \(P_{R}\) and \(\rho _{R}\) are given by Eqs. (5) and (6), respectively. However, despite our previous discussion, we had to restrict ourselves by considering only one kernel and various f(R) models.

In particular, during the reconstruction the squared exponential function

$$\begin{aligned} k(x,x^{\prime }) = \sigma ^{2}_{f}\exp \left( -\frac{(x-x^{\prime })^{2}}{2l^{2}} \right) , \end{aligned}$$
(17)

has been chosenFootnote 4 But the material presented here is self-consistent and contains all details allowing the interested readers to extend the present work in either direction. We start our discussion from the case when an explicitly given f(R) model is considered.

To end this section, we invite the readers to check the following references, in order to see how GPs can be used in Cosmology and learn the necessary mathematics behind the method allowing the learning of non-parametric statistical representation from a given dataset [42,43,44,45,46,47,48,49,50,51,52].

3 Models with explicitly given f(R)

In the literature, different forms of f(R) gravity had been studied but, up to our knowledge, none of them has been constrained using GPs. In this regard, the present work attempts to fill this gap. We cannot analyze all possibilities here; instead, we will try to keep some balance between the models available and the problems under consideration. Our choice and analysis does not mean at all that we consider the role of the other f(R) models to be less important (see [31, 53,54,55,56,57,58,59,60,61,62,63] and references therein for more details about the past and recent status of f(R) gravity). We need to stress that the well-known Starabinsky model will not be reanalysed here, as this has been already done in [31]. On the other hand, our analysis of the \(f(R) = \sum {R^{n}}\) models, restricted to \(n>0\) (or \(n<0\)) shows that they can be used to explain just the very low-redshift evolution of the Universe, what is in principle a problem. However, our study in this direction with GPs will show that some models that combine positive and negative powers of R have the necessary flexibility to cover redshift ranges interesting for cosmological applications. Of the many possibilities to craft such models, we had to limit ourselves and consider only a few of them.

3.1 Swampland with \(f(R) = C + R + \alpha R^{-1} + \beta R^{-2} + \gamma R^{-3}\)

One of the toy models we will discuss in some detail is the following:

$$\begin{aligned} f(R)= C + R + \alpha R^{-1} + \beta R^{-2} + \gamma R^{-3}, \end{aligned}$$
(18)

where C, \(\alpha \), \(\beta \) and \(\gamma \) are constants. This model has 4 parameters to be constrained using GPs and given expansion rate data. Working with this model, it was not hard to see that, after some simple algebra for \(|\nabla _{\phi } V|/V\), Eq. (16), one gets

$$\begin{aligned} \frac{|\nabla _{\phi } V|}{V} = \sqrt{\frac{2}{3}} \left| \frac{5 \gamma + R^4 + 2 C R^3+3 \alpha R^2+4 \beta R}{4 \gamma +C R^3+2 \alpha R^2+3 \beta R} \right| . \end{aligned}$$
(19)

This is a function of R which can be reconstructed from the expansion rate data using GPs, too. Thus we see that we do not need additional information to study the Swampland criteria in this case. Concerning to the analysis of this model we have found the constraints on the model parameters to be: \(\alpha = 0.21 \pm 0.04\), \(\beta = 0.12\pm 0.04\), \(\gamma = 0.14\pm 0.03\), and \(C = 2.32\pm 0.02\), when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\) has been merged with the expansion rate data used in the GP. On the other hand, when \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\) Mpc\(^{-1}\) is merged instead, we obtain that \(\alpha = 0.09 \pm 0.045\), \(\beta = 0.11\pm 0.04\), \(\gamma = 0.11\pm 0.03\) and \(C = 2.02\pm 0.03\), respectively. The reconstructed behavior of the functions \(\omega _{R}\) and \(\Omega _{R} = \frac{\rho _{R}}{3H^{2}}\), which allow to infer the above mentioned constraints, can be found in Fig. 1. To be more constructive, and trying to grasp the possible consequences of our analysis, let us discuss what is inferred about \(\omega _{R}\) and \(\Omega _{R}\). This is a minimal step, needed to clarify from where the above-mentioned constraints do come.

Fig. 1
figure 1

The GP reconstruction of \(\omega _{R}\) and \(\Omega _{R}\), for the 30 H(z) samples deduced from the differential age method with 10 additional samples obtained from the radial BAO method (Table 1), is presented on the upper panel, when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\) has been merged to the expansion rate data used in the GP. The bottom panel corresponds to the GP reconstruction of \(\omega _{R}\) and \(\Omega _{R}\), when \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\) Mpc\(^{-1}\) has been merged to the expansion rate data used in the GP. The reconstruction is obtained for the f(R) model given by Eq. (18). The solid line is the mean of the reconstruction and the shaded blue regions are the \(68\%\) and \(95\%\) C.L. of the reconstruction, respectively. From the reconstruction of \(\Omega _{R} = \frac{\rho _{R}}{3H^{2}}\), the constraints on \(\alpha \), \(\beta \), \(\gamma \) and C are found to be \(\alpha = 0.21 \pm 0.04\), \(\beta = 0.12\pm 0.04\), \(\gamma = 0.14\pm 0.03\) and \(C = 2.32\pm 0.02\), when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\). On the other hand, when \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\) Mpc\(^{-1}\), then the constraints are found to be \(\alpha = 0.09 \pm 0.045\), \(\beta = 0.11\pm 0.04\), \(\gamma = 0.11\pm 0.03\) and \(C = 2.02\pm 0.03\)

Full size image
  1. 1.

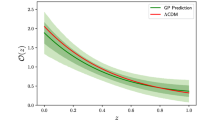
    In particular, the results in the case when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\) have been merged to the expansion rate data and have been used in the GP, can be found on the upper panel of Fig. 1. From where we see that the model in Eq. (18), can correspond to a model of the Universe where dark energy would be a cosmological constant, but which evolution may cross the phantom divide and, eventually, at low redshifts it can mimic again the cosmological constant. On the other hand, there is a hint that at high redshifts the model can mimic phantom dark energy, through its evolution it can start mimicking a quintessence behavior, while at low redshifts will again mimic the cosmological constant. It is not excluded that mimicking phantom behavior at high redshifts it will continue mimicking phantom behavior and only at very low redshift ranges will start to mimic the cosmological constant. In other words, we see that the model allows realizing different scenarios where the nature of dark energy can actually change; however, we see that at low redshifts it will always mimic the cosmological constant (see the left plot of the upper panel of Fig. 1). Moreover, the estimation for \(\omega _{R}\) for \(z=0\) is \(\omega _{R} \in [-1.002, -0.997]\), with \(\omega _{R} = -1.0\) as mean, indicating very tight constraints on it, and that this model at low redshift can recover the \(\Lambda \)CDM model. The reconstruction of \(\Omega _{R}\), presented on the right plot on the upper panel of Fig. 1 indicates that \(\Omega _{R} \in [0.64, 0.76]\), with \(\Omega _{R} \approx 0.7\) as mean. From the same plot, we see that during its evolution \(\Omega _{R}\) has smoothly increased in our Universe.

  2. 2.

    On the other hand, when \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\) Mpc\(^{-1}\), the GPs reconstruction shows that \(\omega _{R}\) will mimic either quintessence or a dark energy model with \(\omega _{R} \approx -1.0\). In other words, this model is also able to reproduce the \(\Lambda \)CDM model and we should note that the model cannot mimic the phantom dark energy behavior. Moreover, the analysis of \(\Omega _{R}\), the reconstruction of which can be found on the right-hand side of the bottom panel of Fig. 1, shows that \(\Omega _{R} \in [0.705, 0.769]\), with the reconstruction, mean being \(\Omega _{R} = 0.737\).

Table 2 Form of the f(R) theory and constraints obtained for the model parameters when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\) has been merged to the expansion rate data used in the GP. The constraints are for the three models given in Eqs. (18), (20) and (21), respectively
Full size table
Table 3 Form of the f(R) theory and obtained constraints for the model parameters when \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\) Mpc\(^{-1}\) has been merged to the expansion rate data used in the GP. The constraints are for the three models given in Eqs. (18), (20) and (21), respectively
Full size table

Another model we have constrained is the following:

$$\begin{aligned} f(R)= C+R + \alpha R^{2}+ \beta R^{-2}, \end{aligned}$$
(20)

where we learned the constraints to be \(\alpha = -0.000017 \pm 0.000005\), \(\beta = 1.12 \pm 0.04\), \(C = 2.18 \pm 0.04\) when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\). In this case, we see that dark energy at \(z=2.4\) will have only quintessence nature. Then, during its evolution two scenarios are possible. In particular, according to one of them we can have a transition from a quintessence phase to a phantom phase, and then a transition to a phase where \(\omega _{R} = -1.0\). According to the second scenario, we can have a transition from a quintessence phase to the phase where \(\omega _{R} > 0\) (allowing to recover even stiff matter behavior) and then a transition to a phase where \(\omega _{R} = -1.0\). Moreover, we can see that the oscillating behavior of \(\omega _{R}\) allows having quintessence – phantom – quintessence transitions, to end in the cosmological constant phase (see Fig. 5 for more details covering also the case when \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\) Mpc\(^{-1}\)). The performed analysis already shows how, on one side, GPs with expansion rate data are able to impose tight constraints on the model parameters and, on the other, allow to infer deep details about the model dynamics indicating how the models actually differ from each other.

Fig. 2
figure 2

The GP reconstruction of \(|V^{\prime }|/V\), Eq. (19), for the 30 H(z) samples deduced from the differential age method with 10 additional samples obtained from the radial BAO method (Table 1) is depicted on the left hand side plot, when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\) has been merged to the expansion rate data used in the GP. The right hand side plot represents the GP reconstruction of \(|V^{\prime }|/V\), Eq. (19), when \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\) Mpc\(^{-1}\) has been merged to the expansion rate data used in the GP. The reconstruction obtained is for the f(R) model given by Eq. (18). The solid line corresponds to the mean of the reconstruction, and the shaded blue regions to the \(68\%\) and \(95\%\) C.L. of the reconstruction, respectively

Full size image
Fig. 3
figure 3

The GP reconstruction of \(\omega _{R}\) and \(\Omega _{R}\) for the 30 H(z) samples deduced from the differential age method, with 10,additional samples obtained from the radial BAO method (Table 1) is presented on the upper panel, when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\) has been merged to the expansion rate data used in the GP. The bottom panel corresponds to the GP reconstruction of the functions \(\omega _{R}\) and \(\Omega _{R}\), when \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\) Mpc\(^{-1}\) has been merged to the expansion rate data used in the GP. The reconstruction here obtained is for the f(R) model given by Eq. (22). The solid line is the mean of the reconstruction and the shaded blue regions correspond to the \(68\%\) and \(95\%\) C.L. of the reconstruction, respectively. From the reconstruction of \(\Omega _{R} = \frac{\rho _{R}}{3H^{2}}\) the constraints on \(\alpha \) and \(\beta \) have been found to be \(\alpha = -1.19 \pm 0.01\) and \(\beta = -0.81 \pm 0.02\), when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\). On the other hand, for \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\) Mpc\(^{-1}\), then the constraints are found to be \(\alpha = -0.94 \pm 0.005\) and \(\beta = -1.03 \pm 0.005\)

Full size image
Fig. 4
figure 4

The GP reconstruction of \(|V^{\prime }|/V\), Eq. (23), for the 30 H(z) samples deduced from the differential age method with 10 additional samples obtained from the radial BAO method (Table 1) is depicted on the left hand side plot, when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\) has been merged to the expansion rate data used in the GP. The right hand side plot corresponds to the GP reconstruction of \(|V^{\prime }|/V\), Eq. (23), when \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\) Mpc\(^{-1}\) has been merged to the expansion rate data used in the GP. The reconstruction thus obtained is for the f(R) model given by Eq. (22). The solid line depicts the mean of the reconstruction and the shaded blue regions the \(68\%\) and \(95\%\) C.L. of the reconstruction, respectively

Full size image

Finally, we have considered the model:

$$\begin{aligned} f(R)= C+R + \alpha R^{2}+ \beta R^{-2} + \gamma R^{-1}. \end{aligned}$$
(21)

Combining together all the results obtained so far, we have found a strong hint that the \(H_{0}\) tension problem actually indicates that a change in the background dynamics and in the dark energy EoS evolution could have occurred, which may be crucial for understanding how this particular problem can be solved within f(R) gravity. More details about the \(\Omega _{R}\) and \(\omega _{R}\) reconstructions for the model in Eq. (21), can be found in Fig. 5, while Tables 2 and 3 summarize the constraints on the model parameters for the 3 models presented here. They clearly indicate how the constraints on the model parameters can change, and also the best regions in parameter space to look for, in order to alleviate or try to solve the \(H_{0}\) tension problem.

We now address the issue of the Swampland criteria. More precisely, the question is whether the swampland criteria for the given f(R) model will be satisfied. Our analysis shows that the first criteria, Eq. (10), will most likely be; however, with the second criteria, Eq. (11), the situation is not so clear. It does seem that the second criteria will be fulfilled at higher-redshift ranges, but for low redshifts (e.g., for a dark-energy dominated Universe) it cannot be satisfied. The GPs related reconstruction and inferring here derived can be found in Figs. 2, 6, and 8, respectively. Additionally, from the corresponding figures representing the second criteria, Eq. (11), for two \(H_{0}\) values we have found a strong hint that crafting the \(H_{0}\) tension problem solutions from the Swampland criteria in f(R) gravity would be practically impossible. And we should stress that the analysis of the models in the second part of this section will make this hint even stronger.

Table 4 Forms of the f(R) theory and constraints obtained for the model parameters, when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\) has been merged to the expansion rate data used in the GP. The constraints correspond to the models given by Eqs. (22), (24) and (26), respectively
Full size table
Table 5 Forms of f(R) theory and constraints obtained for the model parameters when \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\) Mpc\(^{-1}\) has been merged to the expansion rate data used in the GP. The constraints correspond to the models given by Eqs. (22), (24) and (26), respectively
Full size table

3.2 Swampland with \(f(R) = R - 2 \alpha (1 - e^ {-\beta R})\)

The model to be considered in this section is a two-parameter model given by the following f(R)

$$\begin{aligned} f(R)= R-2 \alpha (1 - e^ {-\beta R}), \end{aligned}$$
(22)

where \(\alpha \) and \(\beta \) are the parameters to be constrained by the GPs. We have found that \(\alpha = -1.19 \pm 0.01\) and \(\beta = -0.81 \pm 0.02\), when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\). On the other hand, for \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\), \(\alpha = -0.94 \pm 0.005\) and \(\beta = -1.03 \pm 0.005\). Moreover, after some simple algebra, we got

$$\begin{aligned} \frac{|\nabla _{\phi } V|}{V} = \frac{1}{\sqrt{6}} \left| \frac{2 \alpha (\beta R+2)+e^{\beta R} (R-4 \alpha )}{\alpha \left( -\beta R+e^{\beta R}-1\right) } \right| . \end{aligned}$$
(23)

The reconstruction of \(\omega _{R}\) and \(\Omega _{R}\) can be found in Fig. 3, From both panels, representing reconstructions for the two values assigned to \(H_{0}\), we see that, at low redshift, the evolution of \(\omega _{R}\) clearly indicates the possibility to mimic the cosmological constant. However, we would like to stress that the second Swampland criteria, Eq. (16) is not so easy to tackle down. In particular, we see that, when \(H_{0} = 67.40 \pm 0.5\) km s\(^{-1}\) Mpc\(^{-1}\), the GPs reconstruction of Eq. (23) shows that the second Swampland criteria, Eq. (11), for a dark energy dominated Universe, will not be satisfied. The same conclusion has been obtained for the case when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\). However, for this same case, we found a hint that at higher redshift this conclusion may change. For more details, we refer the reader to Fig. 4, where the recently discussed Swampland challenging issue (which definitely requires future and detailed analysis) is clearly exhibited.

We have considered another model, with

$$\begin{aligned} f(R)= R -2 \alpha (1- e^{-\beta R})+\gamma R^{2}, \end{aligned}$$
(24)

and

$$\begin{aligned} \frac{|\nabla _{\phi } V|}{V} = 2 \sqrt{\frac{2}{3}} \left| \frac{(R-4 \alpha ) e^{\beta R}+2 \alpha (\beta R+2)}{2 e^{\beta R} \left( 2 \alpha +\gamma R^2\right) -4 \alpha (\beta R+1)} \right| . \end{aligned}$$
(25)

The constraints we obtained are: (1) \(\alpha = -1.15 \pm 0.02\) and \(\beta = -1.05 \pm 0.01\) and \(\gamma = -0.00003 \pm 0.00001\), when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\), and (2) \(\alpha = -0.93 \pm 0.01\) and \(\beta = -1.03 \pm 0.01\) and \(\gamma = -0.00002 \pm 0.00001\), when \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\). The results of the reconstruction can be seen in Figs. 9 and 10, respectively. We notice the absence of the Swampland second criteria challenging issue, for high redshift ranges. It should be observed that the second Swampland criteria for a dark-energy dominated Universe is not satisfied.

Finally, the last toy model we have considered is

$$\begin{aligned} f(R)= R -2 \alpha (1- e^{-\beta R})+\gamma R^{-2}. \end{aligned}$$
(26)

From Eq. (16) and after some algebra, we have got that

$$\begin{aligned} \frac{|\nabla _{\phi } V|}{V} = 2 \sqrt{\frac{2}{3}} \left| \frac{(R-4 \alpha ) e^{\beta R}+2 \alpha (\beta R+2)}{2 e^{\beta R} \left( 2 \alpha +\gamma R^2\right) -4 \alpha (\beta R+1)} \right| , \end{aligned}$$
(27)

should be used in order to estimate possible bounds on \(|\nabla _{\phi } V|/V\). The reconstruction results of \(\omega _{R}\) and \(\Omega _{R}\) can be found in Fig. 11, which allows to infer that: (1) \(\alpha = -1.11 \pm 0.03\) and \(\beta = -0.87 \pm 0.04\) and \(\gamma = 1.67 \pm 0.03\), when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\), and (2) \(\alpha = -0.94 \pm 0.01\), \(\beta = -0.82 \pm 0.02\) and \(\gamma = 1.55 \pm 0.03\), when \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\). The top panel of Fig. 11 represents the reconstructed behavior when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\), while the bottom panel corresponds to the case when \(H_{0} =67.40 \pm 0.5\) km s\(^{-1}\). We see from the top panel, in particular, that with \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\), the model mimics the cosmological constant of the recent Universe. Moreover, it could have started its evolution from the phase where dark energy either mimics the cosmological constant (according to the mean of the reconstruction) or mimics a quintessence behavior. However, before entering the low redshift phase of the evolution, there appear to be several quintessence – phantom – quintessence transitions, and, according to the mean of the reconstruction this behavior has a periodic nature. Following the same logic, we can interpret the bottom panel of Fig. 11. In this case, we also see that the second Swampland criteria for a dark-energy dominated Universe is not satisfied (see Fig. 12).

To end this section, we would like to refer the readers to Tables 4 and  5 where a summary of the constraints obtained for the models given by Eqs. (22), (24) and (26), respectively, is depicted. It also provides a hint on how the \(H_{0}\) tension issue can affect the constraints on the model parameters. In all cases considered we have learned that for the corresponding models the \(H_{0}\) tension problem cannot be uniquely inferred from the Swampland criteria.

4 Conclusions

The study of the Swampland criteria for a dark-energy-dominated Universe has attracted a lot of attention in the recent literature. Generally speaking, two types of studies have appeared. One of them is based on the use of a specific dark-energy model in order to constrain the underlying background dynamics and then estimate possible bounds on the Swampland criteria. In contrast, in the second case, GPs and the available observational data are used to constrain the background dynamics and, at the same time – without the need to involve any specific dark energy model – to estimate possible bounds on the Swampland criteria.

Modifications of GR constitute an attractive alternative to the dark energy problem and have received huge attention, too. The study of the Swampland criteria for modified theories of gravity is also an important task. We do not want to come back to the question of why the Swampland criteria study is important and what is the origin of this development. The provided reference list (and the references therein) will cover this point sufficiently. Moreover, a short discussion has been included in the main text of the paper about such issues. What we need to explain here is what have we learned when we have taken advantage of the expansion rate data and of GP techniques with the aim to study the Swampland criteria in f(R) gravity.

As we have already mentioned, the only issue is that the form of the f(R) theory must be given; which forces us to impose some sort of limitations on the main conclusions obtained. In particular, we have to limit the number of models considered, which is just a mechanical issue (if one wants) and does not mean, at all, that we prefer some kind of models over others. Anyhow, following this strategy, we have considered 6 different models and, in the first step, we were able to obtain the constraints on the model parameters in each case. That allowed us to directly infer where, on the parameter space, we needed to look preferably, so as to be able to solve or alleviate the \(H_{0}\) tension problem.

Moreover, and in parallel, we have been able to check the validity of the second Swampland criterion, indicating that, in all cases corresponding to the dark energy Universe, the criteria will not be satisfied. However, we could claim that, at high-redshift ranges, the second Swampland criteria will be fulfilled. And, there has been one interesting situation which has captured our attention. Namely, when we have considered the model with \(f(R) = R - 2 \alpha (1 - e^ {-\beta R})\) we have got a hint that, even at high redshift ranges, the second Swampland criteria cannot be satisfied here, when \(H_{0} =73.52 \pm 1.62\) km s\(^{-1}\) Mpc\(^{-1}\). This is a deviation from the pattern that we learned during this analysis and has required future study to understand what is the reason for this kind of anomaly. We need to stress also that, so far, we have not found a hint signaling that the \(H_{0}\) tension solution can be inferred from the Swampland criteria and expansion rate data in f(R) theories. Another interesting result was that for \(f(R)=\sum _{n}R^{n}\) and considering the possibility of having both positive and negative n’s, it is still possible to craft f(R) models that are interesting for cosmological applications.

We would like to stress again that GPs are ML algorithms, and that the generic goal is to learn the logic explaining why the given observational data are what they are, in a model-independent way. In general, to answer (and, previously, to pose) this question, a kernel is required; which helps to learn a non-parametric logic answering why certain observations are there. For instance, in the case of the expansion rate data used in this paper, GPs allow learning a non-parametric form of the H(z) function that explains its behavior in the best possible way. It is obvious that it would be better to consider different kernels to additionally infer what is the impact of its choice on our gained knowledge. Here, for lack of space, we have considered one kernel, only, but it is clear that the present discussion marks the path to be followed in order to extend the analysis by involving other kernels, and then check if and how the learned results change.

Finally, we should also remark that, as ML tools, GPs can fail when they do not see or are not trained with the data/scenario previously; which can also happen for the \(H_{0}\) value estimation and error estimations, as well. Moreover, similar to other ML tools, there are situations where they cannot do a very great job, also for some of the cases that have already been considered. This is not surprising, and one should always keep an eye on this, having it in mind when one applies these methods. Contrasting with other analysis is advisable, before taking the results at face value. Their physical feasibility and interpretation should be checked. We have kept this in mind, when applying to Cosmology some inferring processes, like in the present study, that has been guided by expert experience. In particular, in obtaining the model parameter constraints, we used our recent knowledge about the \(\omega _{R}\) EoS and \(\Omega _{R}\) fraction of the dark energy, respectively.

Various questions have been left to be studied, including how to obtain a model-independent reconstruction of f(R) gravity, which hopefully will be discussed in a forthcoming paper. Another interesting direction that we need to look at is the one of learning the kernel itself, instead of inserting it by hand. However, this is a deep, more ML-related issue; anyhow, the unique data available from Cosmology and Astrophysics could probably help to advance towards this goal and to point out some drawbacks, what for earth-based data maybe not be so easy.