1 Introduction

How to construct the realistic string models which are consistent with the low energy phenomenology is a great challenge question. Among various string models, the Pati–Salam model building in Type IIA theory on \(T^6/(\mathbb {Z}_2\times \mathbb {Z}_2)\) orientifold with intersecting D6-branes [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27] is very interesting, although the absence of gauge coupling unification at the string scale might be a generic problem. Recently, some concrete supersymmetric Pati–Salam models have been constructed [28, 29], and such D-brane models have been investigated with more powerful reinforcement machine learning methods and genetic algorithms as shown in [30, 31].

In [33], we propose a systematic method for such kind of model building and for the first time construct all the three-family \({\mathcal N}=1\) supersymmetric Pati–Salam models from intersecting D6-branes where the gauge symmetry can be broken down to the Standard Model (SM) gauge symmetry via the D-brane splitting and supersymmetry (SUSY) preserving Higgs mechanism. We find that there are 202752 models in total, and show that there are only 33 independent models with different gauge coupling relations at string scale after moduloing the equivalent relations. Thus, for the string landscape study, we would like to emphasize that it is very important to consider the equivalent relations. However, one and only one model has traditional gauge coupling unification at string scale. We also find that the largest absolute value of wrapping number is 5.

In [16], additional vector-like matter was introduced to push GUT scale unification up to Planck scale for SU(5) and SO(10) GUT theories. Instead of studying pushing up the unification scale, we will study the methods to achieve string scale gauge unification from \({\mathcal N}=1\) supersymmetric Pati–Salam models without GUT scale unification. Taking models with largest wrapping number 5 and approximate gauge coupling unification as an examples, we show that the additional exotic particles can be decoupled and its gauge coupling relation can be realized at string scale via two-loop renormalization group equation running by introducing seven pairs of vector-like particles from \({\mathcal N}=2\) sector. Therefore, although most of these Pati–Salam models do not directly have gauge coupling unification at string scale, their gauge coupling unification may indeed be achieved at string scale by introducing the vector-like particles from \({\mathcal N}=2\) sector. And then we solve the gauge coupling unification problem in the generic D-brane models. Moreover, one can explain the SM fermion masses and mixings via the three-point and four point functions [32]. Furthermore, it seems to us that this brand new systematic method can be applied to the other intersecting D-brane model building as well.

2 Review of model building

First, we briefly review the basics of constructing supersymmetric Pati–Salam models on Type IIA \(T^6/(\mathbb {Z}_2\times \mathbb {Z}_2)\) orientifolds with D6-branes intersecting at generic angles as discussed in [15, 17]. Consider the six-torus \(T^{6}\) factorized as three two-tori \(T^{6} = T^{2} \times T^{2} \times T^{2}\). Let \(z_i\), \(i=1,\; 2,\; 3\) be respectively the complex coordinates for the i-th two-torus. For the orbifold group \(\mathbb {Z}_{2} \times \mathbb {Z}_{2}\), the generators \(\theta \) and \(\omega \) are associated with the twist vectors \((1/2,-1/2,0)\) and \((0,1/2,-1/2)\) respectively. They act on the complex coordinates \(z_i\) as

$$\begin{aligned} \theta : (z_1,z_2,z_3)\mapsto & {} (-z_1,-z_2,z_3), \nonumber \\ \omega : (z_1,z_2,z_3)\mapsto & {} (z_1,-z_2,-z_3). \end{aligned}$$
(2.1)

The orientifold projection is implemented by gauging the \(\Omega R\) symmetry, where \(\Omega \) is world-sheet parity and R acts on the complex coordinates as

$$\begin{aligned} R: (z_1,z_2,z_3) \mapsto ({\overline{z}}_1,{\overline{z}}_2,{\overline{z}}_3). \end{aligned}$$
(2.2)

In total, we have four kinds of orientifold 6-planes (O6-planes) for the actions of \(\Omega R\), \(\Omega R\theta \), \(\Omega R\omega \), and \(\Omega R\theta \omega \) respectively [14, 15, 17, 27]. Moreover, three stacks of \(N_a\) D6-branes wrapping on the factorized three-cycles are introduced to cancel the RR charges of these O6-planes.

Table 1 General massless particle spectrum for intersecting D6-branes at generic angles
Full size table
Table 2 The wrapping numbers for four O6-planes
Full size table

There are two kinds of complex structures: rectangular and tilted, consistent with the orientifold projection. The homology classes of these three cycles wrapped by the D6-brane stack are of the form \(n_a^i[a_i]+m_a^i[b_i]\) for a rectangular torus and \(n_a^i[a'_i]+m_a^i[b_i]\) for a tilted torus, where \([a_i']=[a_i]+\frac{1}{2}[b_i]\). A generic one cycle can be labeled by \((n_a^i,l_a^i)\) in terms of these wrapping numbers, with \(l_{a}^{i}\equiv m_{a}^{i}\) and \(l_{a}^{i}\equiv 2\tilde{m}_{a}^{i}=2m_{a}^{i}+n_{a}^{i}\) for a rectangular and tilted two-torus respectively. Note that \(l_a^i-n_a^i\) is an even number for tilted two-tori. We denote the wrapping number for stack a of D6-branes along the cycle to be \((n_a^i,l_a^i)\), and their \(\Omega R\) images \({a'}\) stack of \(N_a\) D6-branes are with wrapping numbers \((n_a^i,-l_a^i)\). The homology three-cycles for stack a of D6-branes and its orientifold image \(a'\) can be expressed as

$$\begin{aligned}{}[\Pi _a]= & {} \prod _{i=1}^{3}\left( n_{a}^{i}[a_i]+2^{-\beta _i}l_{a}^{i}[b_i]\right) , \end{aligned}$$
(2.3)
$$\begin{aligned}= & {} \prod _{i=1}^{3} \left( n_{a}^{i}[a_i]-2^{-\beta _i}l_{a}^{i}[b_i]\right) , \end{aligned}$$
(2.4)

where \(\beta _i=0\) if the i-th two-torus is rectangular and \(\beta _i=1\) otherwise. The homology three-cycles wrapped by the four O6-planes take the forms of

$$\begin{aligned} \Omega R: [\Pi _{\Omega R}]= & {} 2^3 [a_1]\times [a_2]\times [a_3],\nonumber \\ \Omega R\omega : [\Pi _{\Omega R\omega }]= & {} -2^{3-\beta _2-\beta _3}[a_1]\times [b_2]\times [b_3],\nonumber \\ \Omega R\theta \omega : [\Pi _{\Omega R\theta \omega }]= & {} -2^{3-\beta _1-\beta _3}[b_1]\times [a_2]\times [b_3],\nonumber \\ \Omega R\theta : [\Pi _{\Omega R}]= & {} -2^{3-\beta _1-\beta _2}[b_1]\times [b_2]\times [a_3]. \end{aligned}$$
(2.5)

The intersection numbers can be expressed in terms of the wrapping numbers as

$$\begin{aligned} I_{ab}= & {} [\Pi _a][\Pi _b]=2^{-k}\prod _{i=1}^3(n_a^il_b^i-n_b^il_a^i),\nonumber \\ I_{ab'}= & {} [\Pi _a][\Pi _{b'}]=-2^{-k}\prod _{i=1}^3(n_{a}^il_b^i+n_b^il_a^i),\nonumber \\ I_{aa'}= & {} [\Pi _a][\Pi _{a'}]=-2^{3-k}\prod _{i=1}^3(n_a^il_a^i),\nonumber \\ I_{aO6}= & {} [\Pi _a][\Pi _{O6}]\nonumber \\= & {} 2^{3-k}(-l_a^1l_a^2l_a^3 +l_a^1n_a^2n_a^3+n_a^1l_a^2n_a^3+n_a^1n_a^2l_a^3) \end{aligned}$$
(2.6)

where \(k=\beta _1+\beta _2+\beta _3\) is the total number of tilted two-tori, while \([\Pi _{O6}]=[\Pi _{\Omega R}]+[\Pi _{\Omega R\omega }]+[\Pi _{\Omega R\theta \omega }]+[\Pi _{\Omega R\theta }]\) is the sum of the four O6-plane homology three-cycles.

The massless particle spectrum obtained from intersecting D6-branes at general angles can be expressed in terms of these intersection numbers as in Table 1. Here, the representations refer to \(U(N_a/2)\), e.g. when the intersecting D6-branes are of number \(N_a=8, N_b=4, N_c=4\), this gives \(U(N_x/2)\) gauge groups for \(x=a, b, c\). The gauge symmetry results from \(\mathbb Z_2\times \mathbb Z_2\) orbifold projection, as discussed in [15]. The chiral supermultiplets contain both scalars and fermions in this supersymmetric constructions, while the positive intersection numbers refer to the left-handed chiral supermultiplets. To have three families of the SM fermions with quantum numbers are under \(SU(4)_C\times SU(2)_L\times SU(2)_R\) gauge symmetries, we require the intersection numbers to satisfy

$$\begin{aligned}&I_{ab} + I_{ab'}=3,~\nonumber \\&I_{ac} =-3,\,\, I_{ac'} =0, \end{aligned}$$
(2.7)

or with c and \(c'\) exchange. And then we can break the Pati–Salam gauge symmetry down to the SM gauge symmetry via the D-brane splitting and supersymmetry preserving Higgs mechanism [18].

In addition to the three generation conditions Eq. (2.7), there are two other main constraints on the four-dimensional \(N=1\) supersymmetric model building, namely, the RR tadpole cancellation conditions and the \(N=1\) supersymmetry preservation in four dimension [11, 12, 15]. In the brane constructions, D6-branes and the orientifold O6-planes are the sources of RR fields and restricted by the Gauss law in a compact space. Due to the conservations of the RR field flux lines, the RR charges from D6-branes must cancel with it from the O6-planes, which results in the RR tadpole cancellations conditions

$$\begin{aligned} \sum _a N_a [\Pi _a]+\sum _a N_a \left[ \Pi _{a'}\right] -4[\Pi _{O6}]=0, \end{aligned}$$
(2.8)

where the last term arises from the O6-planes are with \(-4\) RR charges in D6-brane charge unit. To simplify the discussion on tadpole cancellation condition in the next section, we define

$$\begin{aligned} \begin{array}{rrrr} A_a \equiv -n_a^1n_a^2n_a^3,\,B_a \equiv n_a^1l_a^2l_a^3,\, C_a \equiv l_a^1n_a^2l_a^3,\, D_a \equiv l_a^1l_a^2n_a^3, \\ \tilde{A}_a \equiv -l_a^1l_a^2l_a^3,\, \tilde{B}_a \equiv l_a^1n_a^2n_a^3, \,\tilde{C}_a \equiv n_a^1l_a^2n_a^3,\, \tilde{D}_a \equiv n_a^1n_a^2l_a^3. \end{array}\nonumber \\ \end{aligned}$$
(2.9)

In order to cancel the RR tadpoles, we introduce D6-branes wrapping cycles along the orientifold planes as the so-called “filler branes”. They contributes to the RR tadpole cancellation conditions, and trivially satisfy the four-dimensional \(N=1\) supersymmetry conditions. They are chosen such that the tadpole conditions satisfy

$$\begin{aligned} -2^k N^{(1)}+\sum _a N_a A_a= & {} -2^k N^{(2)}+\sum _a N_a B_a \nonumber \\ =-2^k N^{(3)}+\sum _a N_a C_a= & {} -2^k N^{(4)}+\sum _a N_a D_a=-16,\nonumber \\ \end{aligned}$$
(2.10)

where \(2 N^{(i)}\) is the number of filler branes wrapping along the i-th O6-plane. Moreover, these filler branes represent the USp group and carry the wrapping numbers with one of the O6-planes as shown in Table 2.

Furthermore, the four-dimensional \(N=1\) supersymmetry can be preserved with the orientation projection iff the rotation angle of any D6-brane with respect to the orientifold plane is an element of SU(3), as shown in [35]. It follows that \(\theta _1+\theta _2+\theta _3=0 \) mod \(2\pi \), where \(\theta _i\) is the angle between the D6-brane and the orientifold-plane in the i-th two-torus. The 4-dimensional N = 1 supersymmetry automatically survive the \(\mathbb Z_2\times \mathbb Z_2\) orbifold projection [17], and the SUSY conditions result in the equality and inequality conditions

$$\begin{aligned}&x_A\tilde{A}_a+x_B\tilde{B}_a+x_C\tilde{C}_a+x_D\tilde{D}_a=0,\nonumber \\&A_a/x_A+B_a/x_B+C_a/x_C+D_a/x_D<0, \end{aligned}$$
(2.11)

where \(x_A=\lambda \), \(x_B=\lambda ~2^{\beta _2+\beta 3}/\chi _2\chi _3\),  \(x_C=\lambda ~2^{\beta _1+\beta 3}/\chi _1\chi _3,\)  \(x_D=\lambda ~2^{\beta _1+\beta 2}/\chi _1\chi _2\), while \(\chi _i=R^2_i/R^1_i\) represent the complex structure moduli for the i-th two-torus. The positive parameter \(\lambda \) is introduced to put all the variables \(A,\,B,\,C,\,D\) at equal footing.

3 Search method for supersymmetric Pati–Salam models

From a mathematical point of view, the search for wrapping numbers satisfying all the conditions described in the last section is equivalent to solving a Diophantine equation. In general, there does not exist any algorithm to solve such equation, as implied by the negative solution of Hilbert’s tenth problem. However, we devise an algorithm specially adapted to the form of our equations for Supersymmetric Pati–Salam Models [33].

Now we describe the main strategy of our algorithm. First step: we enumerate all the possible combinations of the signs of the twelve wrapping number products \(A_a,B_a,\dotsc ,C_c,D_c\). As observed previously in [17], because of the SUSY condition, \((A_a,B_a,C_a,D_a)\) contains three negative numbers and one positive number, or two negative numbers and two zeroes, or with one negative and three zeros. The same applies to the stack b and the stack c.

Second step: for each possibility listed in the first step, we append the twelve corresponding inequalities to the our system and try to solve the new system. Inside the system, we look for the following kinds of equations or subsystems

  1. 1.

    Equation with only one non constant monome.

  2. 2.

    A system of linear equations of full rank.

  3. 3.

    A system of linear inequalities which has finitely many integer solutions.

When we find inside our system equations or subsystems of these kinds, we can solve them with respect to the variables appearing in them. After the resolution, the total number of unknown variables decreases. This might lead to branching into subcases because the solution might not be unique. But there are only finitely many subcases because we specifically looked for subsystems admitting finite integer solution sets. Then, we repeat the procedure for each subcase.

Third step: we repeat the procedure described in the second step until there are no subsystem of the three kinds. At this stage, each subcase either gives a solution or still has some unsolved variables (wrapping numbers). Now we make use of inequalities of degree larger than 1, such as those given by Eq. (2.11). By enumerating all the possible signs of the remaining variables, we can determine whether Eq. (2.11) can be achieved.

Implementing this algorithm with the help of a computer program, we find that in total there are 202752 models. Because each equivalent class has 6144 models, we obtain that there are only 33 independent models with different gauge coupling relations at string scale after moduloing the equivalent relations. Thus, for the string landscape study, it is very important to consider the equivalent relations.

4 Supersymmetric Pati–Salam models

As presented with details in [33], the full list of supersymmetric Pati–Salam models have 33 different gauge coupling relations.

First, there is one and only one inequivalent model with gauge coupling unification, i.e., the strong, weak and hypercharge gauge couplings \(g^2_a, g^2_b\) and \(\frac{5}{3}g^2_Y\) satisfy \(g^2_a=g^2_b=g^2_c=(\frac{5}{3}g^2_Y)=4\sqrt{\frac{2}{3}} \pi e^{\phi ^4}\), where \(\phi ^4\) is the dilaton field. Also, there are four confining USp(2) gauge groups, and then we might stabilize the moduli and break SUSY via gaugino condensation.

Second, let us present three representative models for the following discussions of gauge coupling relations in the next Section: Model 1 in Table 3 is a representative model with gauge coupling unification at GUT scale; Model 2 in Table 4 and Model 3 in Table 5 are two kinds of models with the largest possible wrapping number 5, which are related to each other by exchanging \(b-\) an \(c-\)stacks of D6-branes up to equivalent relations. The gauge symmetry groups in Model 1 has four USp(2) groups with negative \(\beta \) functions, so their moduli may be stabilized and supersymmetry might be broken via gaugino condensations. However, Models 2 and 3 contain two USp(2) groups, and only one USp(2) group has negative \(\beta \) function.

In Model 1, similar to [26], the additional exotic particles can be decoupled. In Models 2 and 3, similar to [26], we can decouple the additional exotic particles except the four chiral multiplets under \(SU(4)_C\) anti-symmetric representation. And these four chiral multiplets can be decoupled via instanton effects in principle [36,37,38], which we will discuss in [34].

Table 3 D6-brane configurations and intersection numbers of Model 1, with its gauge coupling relation is \(g^2_a=g^2_b=g^2_c=(\frac{5}{3}g^2_Y)=4 \sqrt{\frac{2}{3}} \pi e^{\phi ^4}\)
Full size table
Table 4 D6-brane configurations and intersection numbers of Model 2, with its gauge coupling relation is \(g^2_a=\frac{7}{6}g^2_b=\frac{5}{6}g^2_c=\frac{25}{28}(\frac{5}{3}g^2_Y)=\frac{8}{27} 5^{3/4} \sqrt{7} \pi e^{\phi ^4}\)
Full size table
Table 5 D6-brane configurations and intersection numbers of Model 3, with its gauge coupling relation is \(g^2_a=\frac{5}{6}g^2_b=\frac{7}{6}g^2_c=\frac{35}{32}(\frac{5}{3}g^2_Y)=\frac{8}{27} 5^{3/4} \sqrt{7} \pi e^{\phi ^4}\)
Full size table

5 String-scale gauge coupling unification

Once we obtain the full list of supersymmetric Pati–Salam models, we can discuss the gauge coupling relations at the string scale. As shown in Table 3, Model 1 has exact gauge coupling unification at GUT scale from brane construction, while the other models do not.

Using the current precision electroweak data and setting \(M_{\text {SUSY}}=3\) TeV, we study the gauge coupling relations at string scale (around \(5\times 10^{17}\) GeV ) by solving two-loop renormalization group equations (RGEs) [39, 40], i.e., \(M_U\simeq M_{\text {string}}\). The generic gauge coupling relations at string scale for intersecting D6-brane models can be written as \(g_a^2=k_2\,g_b^2=k_Y\,g_Y^2=g_{U}^2\), where \(k_Y\) and \(k_2\) are constants for each model. For simplicity, we call these gauge coupling relations as gauge coupling unification by redefining \(\alpha _1 \equiv k_Yg_Y^2/4\pi \), \(\alpha _2 \equiv k_2g_b^2/4\pi \), and \(\alpha _3 \equiv g_a^2/4\pi \). To define the unification scale, we choose the evolution under the conditions \(\alpha _{U}^{-1}\equiv \alpha _1^{-1}=(\alpha _2^{-1}+\alpha _3^{-1})/2\) and \(\Delta =|\alpha _1^{-1}-\alpha _2^{-1}|/\alpha _1^{-1}\) as in [40, 41]. In our study, the difference between \(\alpha _U^{-1}\) and \(\alpha _2^{-1}\) or \(\alpha _3^{-1}\) is limited to be less than \(1.0\%\).

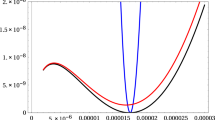
For Model 1, the canonical hypercharge normalization \(k_Y=5/3\) and \(k_2=1\). Utilizing two-loop RGEs method, we obtain that the gauge coupling unification can be achieved at \(1.39\times 10^{16}\) GeV which is just the supersymmetric GUT scale value as shown in Fig. 1. Note that this unification scale is about one order magnitude smaller than string scale \(5\times 10^{17}\) GeV.

In [16], it was presented that additional vector-like matter can push the unification at GUT scale up to Planck scale for SU(5) and SO(10) GUT theories. Instead of studying pushing up the unification scale with additional vector-like matter, we will study the feature while introducing vector like particle to the models without GUT scale unification, such as Model 2 and 3. To achieve canonical gauge coupling unification, we first introduce the vector-like particles whose quantum numbers are the same as those of the SM fermions and their Hermitian conjugate, see [40] and references therein. Their quantum numbers under \(SU(3)_C \times SU(2)_L \times U(1)_Y\) and their contributions to one-loop beta functions, \(\Delta b \equiv (\Delta b_1, \Delta b_2, \Delta b_3)\) as complete supermultiplets are

$$\begin{aligned}&XQ + {\overline{XQ}} = {\mathbf {\left( 3, 2, {1\over 6}\right) + \left( {\mathbf {3}}, 2, -{1\over 6}\right) }}, \Delta b =\left( {1\over 5}, 3, 2\right) ; \end{aligned}$$
(5.1)
$$\begin{aligned}&XU + {\overline{XU}} = {\mathbf { \left( {3},1, {2\over 3}\right) + \left( {\mathbf {3}}, 1, -{2\over 3}\right) }}, \quad \Delta b =\left( {8\over 5}, 0, 1\right) ;\ \end{aligned}$$
(5.2)
$$\begin{aligned}&XD + {\overline{XD}} = {\mathbf { \left( {3},1, -{1\over 3}\right) + \left( {\mathbf {3}}, 1, {1\over 3}\right) }}, \quad \Delta b =\left( {2\over 5}, 0, 1\right) ; \end{aligned}$$
(5.3)
$$\begin{aligned}&XL + {\overline{XL}} = {\mathbf {\left( 1, 2, {1\over 2}\right) + \left( {1}, 2,-{1\over 2}\right) }}, \quad \Delta b = \left( {3\over 5}, 1, 0\right) ; \end{aligned}$$
(5.4)
$$\begin{aligned}&XE + {\overline{XE}} = {\mathbf {({1}, 1, {1}) + ({1}, 1,-{1})}}, \quad \Delta b = \left( {6\over 5}, 0, 0\right) ; \end{aligned}$$
(5.5)
$$\begin{aligned}&XG = {\mathbf {({8}, 1, 0)}}, \quad \Delta b = (0, 0, 3); \end{aligned}$$
(5.6)
$$\begin{aligned}&XW = {\mathbf {({1}, 3, 0)}}, \quad \Delta b = (0, 2, 0); \end{aligned}$$
(5.7)
$$\begin{aligned}&XT + {\overline{XT}} = {\mathbf {(1, 3, 1) + (1, 3, -1)}}, \quad \Delta b =\left( {{18}\over 5}, 4, 0\right) ; \end{aligned}$$
(5.8)
$$\begin{aligned}&XS + {\overline{XS}} = {\mathbf {\left( 6, 1, -{2\over 3}\right) + \left( {\mathbf {6}}, 1, {2\over 3}\right) }}, \quad \Delta b = \left( {16\over 5}, 0, 5\right) ; \end{aligned}$$
(5.9)
$$\begin{aligned}&XY + {\overline{XY}} = {\mathbf {\left( 3, 2, -{5\over 6}\right) + \left( {\mathbf {3}}, 2, {5\over 6}\right) }}, \quad \Delta b =(5, 3, 2). \end{aligned}$$
(5.10)

For Models 2 as shown in Table 4, the gauge coupling relation at GUT scale is \(g^2_a=\frac{7}{6}\,g^2_b=\frac{5}{6}\, g^2_c=\frac{25}{28}\,(\frac{5}{3}g^2_Y)=\frac{8}{27}\, 5^{3/4} \sqrt{7} \pi e^{\phi ^4}\), without gauge coupling unification from brane construction. By introducing additional pairs vector-like particles (XD, \(\overline{XD}\)) for Model 2 with \(k_Y=125/84,~k_2=7/6\) with \(\Delta b = ({2\over 5}, 0, 1)\), it would be possible to “bend” the values of \(\alpha _1^{-1}, \alpha _3^{-1}\) to achieve gauge coupling as shown in Fig. 2. Here the number of additional particles is important as it determines the slope of bending and, as follows, the energy scale of the gauge unification. We speculate the number given by brane intersection might lead to string scale gauge coupling unification. Recall the quantum numbers of (XD, \(\overline{XD}\)) under \(SU(3)_C\times SU(2)_L \times U(1)_Y\) are \(XD=(3,1,-1/3)\), \(\overline{XD}=(\bar{3},1,1/3)\). It is obvious that these vector-like particles arise from a and c stack of brane intersection, representing \(SU(3)_C\) and \(U(1)_Y\) respectively.

Read off the wrapping numbers \((n_x^i, l_x^i)\) for a and c stack of the from Table 4, we note that \((n_a^3, l_a^3)\) and \((n_c^3, l_c^3)\) has the same value yet with opposite sign. This indicates the D6-branes wrapping on the third torus are parallel to each other. Therefore there is no intersection on the third torus, but only on the first and second torus. Following Eq. (2.6), we have intersection number \(I_{ac}=2^{-k}\prod _{i=1}^2(n_a^i\,l_c^i-n_c^i\,l_a^i)= 7\). This indicates there are 7 number of such vector-like particles naturally arise from brane construction. By introducing 7 pairs of vector-like particle (XD, \(\overline{XD}\)) for Model 2 with \(k_Y=125/84,~k_2=7/6\), via two-loop RGEs method, we indeed obtain string scale gauge coupling unification at around \(7.22\times 10^{17}\) GeV presented in Fig. 2.

Fig. 1
figure 1

Gauge coupling unification at \(1.39\times 10^{16}\) GeV for Model 1

Full size image
Fig. 2
figure 2

Gauge coupling unification at \(7.22\times 10^{17}\) GeV for Model 2

Full size image

For Models 3 as shown in Table 5, the gauge coupling relation at GUT scale is \(g^2_a=\frac{5}{6}\,g^2_b=\frac{7}{6}\,g^2_c=\frac{35}{32}\,(\frac{5}{3}g^2_Y)=\frac{8}{27}\, 5^{3/4} \,\sqrt{7} \pi e^{\phi ^4}\), again without gauge coupling unification from brane construction. Similar as for Model 2, we find vector-like particle (XQ, \(\overline{XQ}\)) with quantum number \(XQ=(3,2,1/6)\) and \(\overline{XQ}=(\bar{3},2,-1/6)\) are nature candidate to realize string scale gauge coupling unification. These particles are realized from a and b stacks of brane intersection, with intersection number \(I_{ab}=2^{-k}\prod _{i=1}^2(n_a^i\,l_b^i-n_b^i\,l_a^i)= 7\).

Thus, by introducing 7 pairs of vector-like particle (XQ, \(\overline{XQ}\)) in Model 3 with \(k_Y=175/96,~k_2=5/6\), we achieve gauge coupling unification at around string scale \(1.09\times 10^{17}\) GeV, which we show in Fig. 3.

Fig. 3
figure 3

Gauge coupling unification at \(1.09\times 10^{17}\) GeV for Model 3

Full size image

The masses of the extra vector-like particles for Model 2 and Model 3 are also presented in Figs. 2 and 3, respectively. The right-side kinked points on the plots indicate masses of the extra vector-like particles on the x-axis.

One may ask the reason why only these type of vector-like particle are turned on, but not the other type of vector-like particles. This is realized by setting the minimal distance squared \(Z^2_{(ac')}\) (in \(1/M_s\) units) between parallel D6-branes along the third torus is small, i.e., the minimal length squared of the stretched string is small. Therefore, we have the light scalars with squared-masses \(Z^2_{(ab')}/(4\pi ^2 \alpha ')\) from the NS sector, and the light fermions with the same masses from the R sector [11, 12]. These scalars and fermions form the 4-dimensional \(N=2\) hypermultiplets, so, e.g. for Model 2 we obtain the \(I_{ac}\) (the intersection numbers for a and c stacks on the first two two-tori) vector-pairs of (XD, \(\overline{XD}\)) under \(SU(3)_C\times SU(2)_L \times U(1)_Y\) with quantum number \(XD=(3,1,-1/3)\), \(\overline{XD}=(\bar{3},1,1/3)\). This setting applies to Model 3 with \({\mathcal N}=2\) vector-like particles (XQ, \(\overline{XQ}\)) also.

6 Conclusions

In [33], we obtain all the three-family \({\mathcal N}=1\) supersymmetric Pati–Salam models from intersecting D6-branes through systematic method. The gauge symmetry can be broken down to the SM via the D6-brane splitting and supersymmetry preserving Higgs mechanism. There are only 33 independent models with different gauge coupling relations at string scale in total after modding out the equivalent relations. In particular, one and only one model has natural gauge coupling unification at GUT scale through brane construction.

In this paper, we study the gauge coupling unification at string scale for the models without direct gauge unification at GUT scale from brane construction. Taking models with approximate gauge coupling unification at GUT scale as example, we showed that gauge coupling unification can be realized at string scale by introducing pairs of vector-like particles from \({\mathcal N}=2\) sector. In particular, to achieve the gauge unification as string scale, we propose that the number of these introduced vector-like particles are fully determined by the brane intersection numbers while there are two D6-brane parallel to each other along one two-torus. Intriguingly, with two-loop RGEs method, we explicitly showed for Model 2 and 3 that gauge coupling unified at string-scale \(10^{17}\) GeV by introducing 7 pairs vector-like particles (XD, \(\overline{XD}\)) and (XQ, \(\overline{XQ}\)) with their masses given respectively.

We expect that by introducing pairs of vector-like particles from \({\mathcal N}=2\) sector for intersecting brane models, gauge coupling unification at string scale can be achieved for generic D-brane models. In particular, the number of vector-like particles are fully determined by brane intersection numbers.