1 Introduction

Quantum metrology [1] studies the employment of quantum resources (such as entanglement [2] and discord [3]) on the enhancement of measurement accuracy [4]. The problem of quantum metrology can be reduced to find optimal scheme for the estimation of parameters that are encoded in a probe system undergoing parameter-dependent evolutions. Taking into account the laws of quantum mechanics, quantum resources are capable to improve the precision of the gravitational wave detection [5,6,7], distributed quantum sensing [8, 9], quantum imaging [10, 11], and clock synchronization [12,13,14]. In recent years, quantum metrological technique has been employed to enhance the accuracy of estimation for relativistic effects and spacetime parameters, which gives birth to relativistic quantum metrology [15,16,17,18,19,20,21,22,23,24,25]. These studies are nontrivial because the estimated parameters govern some key phenomena in which both quantum and spacetime effects are relevant [26,27,28]. Previous researches on the relativistic quantum metrology include the estimation of Unruh-Hawking effect for free modes [15,16,17], moving cavities [18, 19], and accelerated detectors [20, 21], the metrology of cosmological parameters [22, 23], and precise measurement of spacetime parameters of the Earth [24, 25], among others.

The advantage of optical quantum metrological settings has been experimentally verified by the detection of gravitational via squeezed light [5,6,7] and the quantum-enhanced clock synchronization [14]. For a customary optical quantum metrology, the generator of parameter is known as a priori, then tailored quantum resources such as squeezed and entangled states can be exploited to improve the precision of phase estimation. In 2014, Girolami et al. proposed a framework for the black-box quantum parameter estimation [29], which can be applied to the case where the generator of the estimated parameter in the probe state is not known a priori. The interferometric power was introduced to quantify the precision for the estimation of encoded parameters in a worst-case scenario [29], and has been proved that it is equivalent to a computable measure of discord-type quantum correlations for the probe state. Adesso [30] generalized the research on interferometric power to continuous-variable and proposed a closed formula of the Gaussian interferometric power (GIP) for continuous-variable quantum systems. There are two reasons for the study of relativistic quantum metrology for the de Sitter space.

In this paper, we suggest a black-box parameter estimating strategy for the spacetime parameters and study the dynamics of the GIP for the de Sitter space [31]. There are two reasons for the study of relativistic quantum metrology in the de Sitter space. On the one hand, according to the current observations and expansion theories, in the distant past and future, our universe spacetime metric is likely to be described by the asymptotic de Sitter spacetime metric. Therefore, it is meaningful for the development of relativistic quantum metrology method for the de Sitter space because the spacetime parameter of the de Sitter space do not correspond to a quantum observable. On the other hand, Gibbons and Hawking have shown that the horizon of de Sitter space emits radiation [32], which is similar to the event horizon of a black hole and the causal horizon of accelerated observers. However, like the Unruh radiation, the Gibbons-Hawking effect is too weak to be directly detected in the near future. Therefore, it is necessary to develop a relativistic parameter estimating strategy in order to obtain a precision estimation for the spacetime information rather than directly detect the Gibbons-Hawking effect.

The black-box estimation strategy is required because the spacetime effect of the de Sitter space is a two-mode squeezing transformation acting on the causally disconnected regions [31,32,33,34]. Therefore, it is impossible to perform a customary metrological process where the generator of parameter is known as a priori. In the present work, an optical Mach-Zender interferometer is involved to estimate the expanding parameter for the de Sitter space. Such a setup can be theoretically modeled as a dual-arm channel, where the estimated parameter is encoded to one arm only, and the identity operation is applied to the other arm. We assume that a subsystem of the initial state is observed by the global observer Alice who moves along geodesics, the other subsystem is described by the observer Bob who is restricted to one region in the de Sitter space, which is causally disconnected from the other region [33, 34]. Under the spacetime effect of the de Sitter space, the parameters of the two-mode squeezing transformation are encoded into the black-box device. The information of the spacetime is obtained when the measurements are completed at the output side of the interferometer. We find that the role of the probe state between different open charts is quite distinct for the black-box parameter estimation. In addition, the quantum discord of probe states serves as a promising resource for the black-box quantum parameter estimation when there is no entanglement between the initially uncorrelated probe states in the de Sitter space.

The organization of the paper is as follows. In Sect. 2 we review the solutions of mode functions and Bogoliubov transformations in the de Sitter space. In Sect. 3 we introduce the scheme of the black-box optical interferometer and the role of the GIP. In Sect. 4 we study the black-box estimation of spacetime parameters and the behavior of the GIP in the de Sitter space. In the final section, we summarize our results.

2 The behavior of scalar field in the de Sitter space

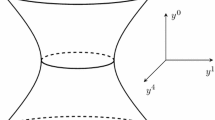
We consider a free scalar field \(\phi \) with mass m which is initially described by two experimenters, Alice and Bob, in the Bunch-Davies vacuum of the de Sitter space. The coordinate frames of the open charts in the de Sitter space can be obtained by analytic continuation from the Euclidean metric. As shown in Fig. 1, the spacetime geometry of the de Sitter space is divided into three open charts, which are denoted by R, L and C, respectively. We assume that a subsystem of the initial state is observed by the global observer Alice moving along geodesics, the other subsystem is described by the observer Bob restricted to the region R in the de Sitter space, and the region R is causally disconnected from the region L. The metrics for the two causally disconnected open charts R and L in the de Sitter space are given by [31]

$$\begin{aligned} ds^2_R= & {} H^{-2}\left[ -dt^2_R+\sinh ^2t_R\left( dr^2_R+\sinh ^2r_R\,d\Omega ^2\right) \right] ,\nonumber \\ ds^2_L= & {} H^{-2}\left[ -dt^2_L+\sinh ^2t_L\left( dr^2_L+\sinh ^2r_L\,d\Omega ^2\right) \right] , \nonumber \\ \end{aligned}$$
(1)

where \(d\Omega ^2\) is the metric on the two-sphere and \(H^{-1}\) is the Hubble radius.

The solutions of the Klein–Gordon equation in different regions are found to be

$$\begin{aligned}&u_{\sigma p\ell m}(t_{R(L)},r_{R(L)},\Omega )\nonumber \\&\quad \sim \frac{H}{\sinh t_{R(L)}}\, \chi _{p,\sigma }(t_{R(L)})\,Y_{p\ell m} (r_{R(L)},\Omega ),\qquad \nonumber \\&\quad -\mathrm{\mathbf{L}^2}Y_{p\ell m}=\left( 1+p^2\right) Y_{p\ell m}, \end{aligned}$$
(2)

where \(Y_{p\ell m}\) are harmonic functions on the three-dimensional hyperbolic space. In Eq. (2), \(\chi _{p,\sigma }(t_{R(L)})\) are positive frequency mode functions supporting on the R and L regions [31]

$$\begin{aligned} \chi _{p,\sigma }(t_{R(L)})=\left\{ \begin{array}{l} \frac{e^{\pi p}-i\sigma e^{-i\pi \nu }}{\Gamma (\nu +ip+\frac{1}{2})}P_{\nu -\frac{1}{2}}^{ip}(\cosh t_R) -\frac{e^{-\pi p}-i\sigma e^{-i\pi \nu }}{\Gamma (\nu -ip+\frac{1}{2})}P_{\nu -\frac{1}{2}}^{-ip}(\cosh t_R),\\ \\ \frac{\sigma e^{\pi p}-i\,e^{-i\pi \nu }}{\Gamma (\nu +ip+\frac{1}{2})}P_{\nu -\frac{1}{2}}^{ip}(\cosh t_L) -\frac{\sigma e^{-\pi p}-i\,e^{-i\pi \nu }}{\Gamma (\nu -ip+\frac{1}{2})}P_{\nu -\frac{1}{2}}^{-ip}(\cosh t_L), \end{array} \right. \end{aligned}$$
(3)

where \(\sigma =\pm 1\) distinguish the independent solutions for each open chart and \(P^{\pm ip}_{\nu -\frac{1}{2}}\) are the associated Legendre functions. The above solutions can be normalized by the factor \( N_{p}=\frac{4\sinh \pi p\,\sqrt{\cosh \pi p-\sigma \sin \pi \nu }}{\sqrt{\pi }\,|\Gamma (\nu +ip+\frac{1}{2})|}, \) where p is a positive real parameter normalized by H. The mass parameter \(\nu \) is defined by \( \nu =\sqrt{\frac{9}{4}-\frac{m^2}{H^2}}\, \). The mass parameter of the calar field in de Sitter space depends on the ratio of the two scales, which are the Hubble radius \(H^{-1}\) and the Compton wavelength \(m^{-1}\). Here we only focus on the case \(m^2/H^2<9/4\) to make the discussion clear. The mass parameter \(\nu \) has two special values: \(\nu =1/2\) (\(m^2=2H^2\)) for the conformally coupled massless scalar field, and \(\nu =3/2\) for the minimally coupled massless scalar field. Note that the curvature effect starts to appear around \(p\sim 1\) in three-dimensional hyperbolic space [31,32,33,34, 36, 37], and the effect of the curvature becomes stronger when p is less than 1. Therefore, p can be considered as the curvature parameter of the de Sitter space.

The scalar field can be expanded in accordance with the creation and annihilation operators

$$\begin{aligned} {\hat{\phi }}(t,r,\Omega ) =\frac{H}{\sinh t}\int dp \sum _{\ell ,m}\phi _{p\ell m}(t)Y_{p\ell m}(r,\Omega ), \end{aligned}$$
(4)

where \(a_{\sigma p\ell m}|0\rangle _{\mathrm{BD}}=0\) is the annihilation operator of the Bunch-Davies vacuum, and the Fourier mode field operator \( \phi _{p\ell m}(t)\equiv \sum _\sigma \left[ \,a_{\sigma p\ell m}\,\chi _{p,\sigma }(t) +a_{\sigma p\ell -m}^\dagger \,\chi ^*_{p,\sigma }(t)\right] \) has been introduced. For brevity, the indices p, \(\ell \), m of \(\phi _{p\ell m}\) of the operators and mode functions will be omitted below.

Since the Fourier mode field operator should be the same under the change of mode functions, we can relate the operators \((a_\sigma ,a_\sigma ^\dag )\) and \((b_q,b_q^\dag )\) by a Bogoliubov transformation [31, 34, 38]

$$\begin{aligned} \phi (t)=a_\sigma \,\chi ^\sigma +a_\sigma ^\dag \,\chi ^\sigma {}^* =b_q\,\varphi ^q+b_q^\dag \,\varphi ^q{}^*, \end{aligned}$$
(5)

where the creation and annihilation operators (\(b_q,b_q^\dag \)) in different regions are introduced to ensure \(b_q|0\rangle _{q}=0\). To facilitate the calculation of degrees of freedom in L space, the Bunch-Davies vacuum is expressed as

$$\begin{aligned} |0\rangle _{\mathrm{BD}} = N_{\gamma _p}^{-1} \exp \left( \gamma _p\,c_R^\dagger \,c_L^\dagger \,\right) |0\rangle _{R'}|0\rangle _{L'}. \end{aligned}$$
(6)

In Eq. (6) we have introduced new operators \(c_q=(c_R,c_L)\) that satisfy [33, 34]

$$\begin{aligned} c_R = u\,b_R + v\,b_R^\dagger ,\qquad c_L = u^*\,b_L + v^*\,b_L^\dagger . \end{aligned}$$
(7)

The normalization factor \(N_{\gamma _p}\) in Eq. (6) is given by

$$\begin{aligned} N_{\gamma _p}^2 =\left| \exp \left( \gamma _p\,c_R^\dagger \,c_L^\dagger \,\right) |0\rangle _{R'}|0\rangle _{L'} \right| ^2 =\frac{1}{1-|\gamma _p|^2}. \end{aligned}$$
(8)

Considering the definition of \(c_R\) and \(c_L\) in Eq. (7) and the consistency relations from Eq. (6), it is demanded that \(c_R|0\rangle _\mathrm{BD}=\gamma _p\,c_L^\dag |0\rangle _{\mathrm{BD}}\), \(c_L|0\rangle _\mathrm{BD}=\gamma _p\,c_R^\dag |0\rangle _{\mathrm{BD}}\). Then we obtain

$$\begin{aligned} \gamma _p = i\frac{\sqrt{2}}{\sqrt{\cosh 2\pi p + \cos 2\pi \nu } + \sqrt{\cosh 2\pi p + \cos 2\pi \nu +2 }}. \nonumber \\ \end{aligned}$$
(9)

For the conformally coupled massless scalar field (\(\nu =1/2\)) and the minimally coupled massless scalar (\(\nu =3/2\)), \(\gamma _p\) simplifies to \(|\gamma _p|=e^{-\pi p}\).

3 Black-box optical parameter estimation and the GIP

Fig. 1
figure 1

Schematic diagram for the black-box optical quantum parameter estimation in the de Sitter space

Full size image

Our black-box parameter estimation setup is modeled as a dual-arm channel, where the estimated parameter \(\gamma _p\) is encoded to the upper arm. As shown in Fig. 1, the proposal of black-box quantum parameter estimation includes the following steps. Initially, Alice and Bob share a two-mode squeezed state \(\rho _{AB}\) in the Bunch-Davies vacuum, which plays as the probe state at the “in” side. Then the mode B in the upper arm of the channel passes through the de Sitter space region, which acts as the black-box device. As shown in [33, 34], under the influence of the de Sitter spacetime, the mode B undergoes a two-mode squeezing transformation \( S_{B,{\bar{B}}}(\gamma _p)\), which encodes the expanding parameter \(\gamma _p\) that we want to estimate. The other mode A in the lower arm of the channel is not subjected to the spacetime. Finally, we get the output state \(\rho _{AB}^{\gamma _p,S_{B,{\bar{B}}}(\gamma _p)}\) at the “out” side by tracing over the mode \({\bar{B}}\), and one can perform a measurement on the output state \(\rho _{AB}^{\gamma _p,S_{B,{\bar{B}}}(\gamma _p)}\) to construct an estimator \({\gamma _p}_{\mathrm{est}}\) for the parameter \({\gamma _p}\). If the measurements are performed independently on the transformed state N times, the uncertainty of the parameter will be constrained by the Cramér-Rao bound [4, 39]

$$\begin{aligned} N\Delta \gamma _p^2 \ge \frac{1}{\mathcal{F}\left( \rho _{AB}^{\gamma _p,S_{B,{\bar{B}}}(\gamma _p)}\right) }, \end{aligned}$$
(10)

where the variance of the parameter \(\gamma _p\) is defined as \(\Delta \gamma _p^2 \equiv \langle ({\gamma _p}_{\mathrm{est}} - \gamma _p)^2\rangle \). The quantity \({\mathcal {F}}\) at the denominator is known as the quantum Fisher information [4, 40].

On the other hand, one can define the vector of field quadratures (position and momentum) operators as \({\hat{R}}=({\hat{x}}_{A},{\hat{p}}_{A},{\hat{x}}_{B},{\hat{p}}_{B})\) for a two-mode continuous-variable quantum system, which are related to the annihilation \({\hat{a}}_{i}\) and creation \({\hat{a}}_{i}^{\dag }\) operators for each mode, by the relations \({\hat{x}}_{i}=\frac{({\hat{a}}_{i}+{\hat{a}}_{i}^{\dag })}{\sqrt{2}}\) and \({\hat{p}}_{i}=\frac{({\hat{a}}_{i}-{\hat{a}}_{i}^{\dag })}{\sqrt{2}i}\). The vector operator satisfies the commutation relationship: \([{{{{{\hat{R}}}}_i},{{{{\hat{R}}}}_j}} ] = i{\Omega _{ij}}\), with \(\Omega = \bigoplus _1^{n+m} {{\ 0\ \ 1}\atopwithdelims (){-1\ 0}}\) being symplectic form [41, 42]. It is known that, the first and second moments of a two-mode Gaussian state \({\rho _{AB}}\) can completely describe all of the properties. For the bipartite state \(\rho _{AB}\), its covariance matrix (second moments) has the form [43]

$$\begin{aligned} \varvec{\sigma }_{AB}=\left( \begin{array}{cc} \mathcal {A}&{}\quad \mathcal {C} \\ \mathcal {C}^\mathsf{T} &{}\quad \mathcal {B} \end{array}\right) , \end{aligned}$$
(11)

which can be transformed to a standard form with all diagonal \(2 \times 2\) subblocks, \(\mathcal {A}=\text {diag}(a,a)\), \(\mathcal {B}=\text {diag}(b,b)\), \(\mathcal {C}=\text {diag}(c,d)\), where \(a,b \ge 1, c \ge |d| \ge 0\). The GIP of a two-mode Gaussian probe state with the covariance matrix \(\varvec{\sigma }_{AB}\) is defined as [30]

$$\begin{aligned} {{\mathcal {P}}}^B(\varvec{\sigma }_{AB}) = \frac{1}{4} \inf _{S_{B,{\bar{B}}}(\gamma _p)}\mathcal{F}(\varvec{\sigma }_{AB}^{\gamma _p,S_{B,{\bar{B}}}(\gamma _p)}), \end{aligned}$$
(12)

where \(\frac{1}{4}\) is the normalization factor. The GIP \(\mathcal{P}^B(\varvec{\sigma }_{AB})\) represents the worst-case precision that can be obtained among all possible local dynamic choices if \(\rho _{AB}\) is used as a probe state. It is a precision index that can be applied to any two-mode Gaussian state [30]. In practice, a probe state \(\rho _{AB}\) with the higher GIP reflects a more reliable metering resource, which ensures that the variance for the estimation of \(\gamma _p\) is smaller.

A closed formula for the GIP of two-mode Gaussian states can be obtained by introducing Eq. (11) into Eq. (12) [30]

$$\begin{aligned} {{\mathcal {P}}}^B_G(\varvec{\sigma }_{AB})=\frac{X+\sqrt{X^2+Y Z}}{2Y}, \end{aligned}$$
(13)

where

$$\begin{aligned} X= & {} (I_{\mathcal {A}}+I_{\mathcal {C}})(1+I_{\mathcal {B}}+I_{\mathcal {C}}-I)-I^2, \\ Y= & {} (I-1)(1+I_{\mathcal {A}}+I_{\mathcal {B}}+2I_{\mathcal {C}}+I), \\ Z= & {} (I_{\mathcal {A}}+I)(I_{\mathcal {A}}I_{\mathcal {B}}-I)+I_{\mathcal {C}}(2I_{\mathcal {A}}+I_{\mathcal {C}})(1+I_{\mathcal {B}}). \end{aligned}$$

In Eq. (13), we have employed \(I_{\mathcal {A}}=\det \mathcal {A}\), \(I_{\mathcal {B}}=\det \mathcal {B}\), \(I_{\mathcal {C}}=\det \mathcal {C}\), and \(I=\det \varvec{\sigma }_{AB}\). Here the symplectic eigenvalues are given by \(2\nu _{\pm }^2 = \Delta \pm \sqrt{\Delta ^2-4I}\) with \(\Delta = I_{\mathcal {A}}+I_{\mathcal {B}}+2I_{\mathcal {C}}\).

As one of the most important resources in quantum information tasks, quantum entanglement plays a significant role in quantum metrology. To better explore how to obtain higher parameter estimation accuracy, we calculate the logarithmic negativity [2] to measure entanglement

$$\begin{aligned} {\mathbf {E}}_{{\mathcal {N}}}(\varvec{\sigma }_{AB}) = \max \{0,\, -\ln {{\tilde{\nu }}_{-}}\}, \end{aligned}$$
(14)

and explore the relationship between entanglement and the GIP. In Eq. (14), the logarithmic negativity is defined in terms of the minimum symplectic eigenvalue of the partially transposed state. Under the partial transposition, the invariant \(\Delta \) is changed into \({\tilde{\Delta }}=I_{\mathcal {A}}+I_{\mathcal {B}}-2I_{\mathcal {C}}\) for a bipartite quantum state. The symplectic eigenvalues are given by \(2{\tilde{\nu }}_{\pm }^2 = {\tilde{\Delta }}\pm \sqrt{{\tilde{\Delta }}^2-4I}\).

4 Black-box estimation of spacetime parameters and the GIP

4.1 The worst-case precision for Black-box metrology for the initially correlated probe state

We assume that the mode in the black-box is observed by Bob who resides in the open chart region R. Initially, Bob and the global observer Alice share a two-mode squeezed state in the Bunch-Davies vacuum, which can be described by the covariance matrix

$$\begin{aligned} \sigma ^{\mathrm{(G)}}_{AB}(s)= \left( \!\!\begin{array}{cccc} \cosh (2s)I_2&{}\quad \sinh (2s)Z_2\\ \sinh (2s)Z_2&{}\quad \cosh (2s)I_2\\ \end{array}\!\!\right) , \end{aligned}$$
(15)

where s is the squeezing of the initial state and \(I_2= {{\ 1\ \ 0}\atopwithdelims (){\ 0\ \ 1}},\) \(Z_2= {{\ 1\ \ 0}\atopwithdelims (){\ 0 \ -1}}\). As showed in [33], the Bunch-Davies vacuum for a global observer can be expressed as the squeezed state of the R and L vacua

$$\begin{aligned} |0\rangle _{\mathrm{BD}}=\sqrt{1-|\gamma _p|^2}\,\sum _{n=0}^\infty \gamma _p ^n|n\rangle _L|n\rangle _R, \end{aligned}$$

where \(\gamma _B\) is the squeezing parameter given in Eq. (9). In the phase space, we use a symplectic operator \( S_{B,{\bar{B}}}(\gamma _p)\) to express such transformation, which is

$$\begin{aligned} S_{B,{\bar{B}}}(\gamma _p)= \frac{1}{\sqrt{1-|\gamma _p|^2}}\left( \!\!\begin{array}{cccc} 1&{}\quad 0&{}\quad |\gamma _p|&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad -|\gamma _p|\\ |\gamma _p|&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad -|\gamma _p|&{}\quad 0&{}\quad 1 \end{array}\!\!\right) , \nonumber \\ \end{aligned}$$
(16)

where \( S_{B,{\bar{B}}}(\gamma _p)\) denotes that the squeezing transformation is performed to the bipartite state shared between Bob and anti-Bob (\({\bar{B}}\)).

Bob’s observed mode is mapped into two open charts under this transformation. That is to say, an extra set of modes \(\bar{B}\) is relevant from the perspective of a observer in the open charts. Then we can calculate the covariance matrix of the entire state [44], which is

$$\begin{aligned} \sigma ^{\mathrm{}}_{AB {\bar{B}}}(s,\gamma _p)= & {} \left( \begin{array}{ccc} \mathcal {\sigma }_{A} &{}\quad \mathcal {E}_{AB} &{}\quad \mathcal {E}_{A{\bar{B}}} \\ \mathcal {E}^\mathsf{T}_{AB} &{}\quad \mathcal {\sigma }_{B} &{}\quad \mathcal {E}_{B{\bar{B}}} \\ \mathcal {E}^\mathsf{T}_{A{\bar{B}}} &{}\quad \mathcal {E}^\mathsf{T}_{B{\bar{B}}} &{}\quad \mathcal {\sigma }_{{\bar{B}}} \\ \end{array} \right) , \end{aligned}$$
(17)

where \(\sigma ^{\mathrm{(G)}}_{AB}(s) \oplus I_{{\bar{B}}}\) is the initial covariance matrix for the entire system. In the above expression, the diagonal elements are given by

$$\begin{aligned} \mathcal {\sigma }_{A}= & {} \cosh (2s)I_2, \end{aligned}$$
(18)
$$\begin{aligned} \mathcal {\sigma }_{B}= & {} \frac{|\gamma _p|^2+\cosh (2s)}{1-|\gamma _p|^2}I_2, \end{aligned}$$
(19)

and

$$\begin{aligned} \mathcal {\sigma }_{\bar{B}}=\frac{1+|\gamma _p|^2\cosh (2s)}{1-|\gamma _p|^2}I_2. \end{aligned}$$
(20)

Similarly, we find that the non-diagonal elements are \(\mathcal {E}_{AB}=\frac{\sinh (2s)}{\sqrt{1-|\gamma _p|^2}}Z_2\), \(\mathcal {E}_{B\bar{B}}=\frac{|\gamma _p|(\cosh (2s)+1)}{1-|\gamma _p|^2}Z_2\) and \(\mathcal {E}_{A\bar{B}}=\frac{|\gamma _p|\sinh (2s)}{\sqrt{1-|\gamma _p|^2}}I_2\).

Because Bob in chart R has no access to the modes in the causally disconnected region L, we must trace over the inaccessible modes. Then one obtains covariance matrix \(\sigma _{AB}\) for Alice and Bob

$$\begin{aligned}&\varvec{\sigma }_{AB}(s,\gamma _p)\nonumber \\&\qquad = \left( \!\!\begin{array}{cccc} \cosh (2s)&{}\quad 0&{}\quad \frac{\sinh (2s)}{\sqrt{1-|\gamma _p|^2}}&{}\quad 0\\ 0&{}\quad \cosh (2s)&{}\quad 0&{}\quad -\frac{\sinh (2s)}{\sqrt{1-|\gamma _p|^2}}\\ \frac{\sinh (2s)}{\sqrt{1-|\gamma _p|^2}}&{}\quad 0&{}\quad \frac{|\gamma _p|^2+\cosh (2s)}{1-|\gamma _p|^2}&{}\quad 0\\ 0&{}\quad -\frac{\sinh (2s)}{\sqrt{1-|\gamma _p|^2}}&{}\quad 0&{}\quad -\frac{|\gamma _p|^2+\cosh (2s)}{-1+|\gamma _p|^2} \end{array}\!\!\right) .\nonumber \\ \end{aligned}$$
(21)

From Eq. (21), we obtain \(\Delta ^{(AB)}=1+\frac{(1+|\gamma _p|^2\cosh (2s))^2}{(1-|\gamma _p|^2)^2}\). The GIP and entanglement of this state can be calculated via Eq. (13) and Eq. (14).

Fig. 2
figure 2

a The GIP and quantum entanglement between Alice and Bob versus the mass parameter \(\nu \). b The evolution of the GIP and quantum entanglement versus the space curvature parameter p. The initial squeezing parameter is fixed as \(s=1\)

Full size image

In Fig. 2a, b, we demonstrate the function images of the GIP and quantum entanglement for the state \(\varvec{\sigma }_{AB}(s,\gamma _p)\) as a function of the mass parameter \(\nu \) and the space curvature parameter p, respectively. It can be seen in Fig. 2a that the variation trend of the GIP and entanglement is basically the same, which verifies the fact that quantum entanglement is the resource of parameter estimation. As mentioned above, the GIP quantifies the precision for the estimation of encoded parameters in a worst-case scenario. A probe state with the higher GIP reflects more reliable metering resources, which ensures the variance for the estimated parameter is smaller. Therefore, we can conclude that the precision of the black-box quantum metrology depends on the abundance of the quantum entanglement in the de Sitter space.

It is interesting to find that, either the precision of the black-box parameter estimation or the resource of entanglement is unaffected by the mass parameter \(\nu \) in the flat space limit (\(p=1\)). However, the mass parameter of the field has remarkable effects on the GIP as well as the accuracy of black-box metrology in the curved de Sitter space. This is because the survivability of quantum resources (quantum entanglement and quantum discord) depends on the mass of the scalar field. It has been shown that the behavior of decoherence in de Sitter space depends on the mass scales of the field very much [35]. In particular, the vacuum fluctuations of low-mass fields appears decoherence behavior (\(m^2<9 H^2/4\)), while those of heavy fields do not (\(m^2>9 H^2/4\)). In addition, the mass of the scalar field has been found to have a remarkable influence on the quantum coherence and quantum correlations in the de Sitter space [36, 37]. Here we apply the quantum metrological technique to estimate the spacetime feature of the de Sitter space by employing the two-mode squeezed state state as the probe of quantum vacuum. In the present model, the mass dependence of quantum metrology is because the quantum resource in the estimation depends on the mass scales of the the scalar field [35,36,37]. In other words, the precision of the black-box parameter estimation depends on the abundant of quantum resources, which are found to be greatly influenced by the mass of the field [36, 37]. Therefore, the accuracy of the black-box quantum parameter estimation depends on the mass scales in the de Sitter space.

In Fig. 2b, we can see that both the GIP and entanglement are monotone increasing functions of the curvature parameter p. Considering that the effect of the curvature becomes stronger when p becomes less and less from 1 to 0 [31,32,33,34, 36, 37], this in fact demonstrates that the lower the space curvature, the higher the accuracy of parameter estimation. It is worth noting that the values of the GIP and entanglement are more sensitive to the spacetime curvature in the massless scalar limit \(\nu =3/2\). Conversely, more quantum entanglement is reserved and higher precision can be attained for the case \(\nu =0\).

4.2 The dynamics of GIP between initially unrelated modes

We also are interested in whether the bipartite state between the initially uncorrelated modes can be employed as probe state for the black-box estimation. To this end we study the behavior of the quantum parameter estimation between all the bipartite pairs in the de Sitter spacetime. The covariance matrix \(\sigma _{A{\bar{B}}}\) between the observer Alice and the other observer anti-Bob in the region L is obtained by tracing over the modes B

$$\begin{aligned}&\sigma _{A{\bar{B}}}(s,\gamma _p)\nonumber \\&\qquad = \left( \!\!\begin{array}{cccc} \cosh (2s)&{}\quad 0&{}\quad \frac{|\gamma _p| \sinh (2s)}{\sqrt{1-|\gamma _p|^2}}&{}\quad 0\\ 0&{}\quad \cosh (2s)&{}\quad 0&{}\quad \frac{|\gamma _p| \sinh (2s)}{\sqrt{1-|\gamma _p|^2}}\\ \frac{|\gamma _p|\sinh (2s)}{\sqrt{1-|\gamma _p|^2}}&{}\quad 0&{}\quad \frac{1+|\gamma _p|^2\cosh (2s)}{1-|\gamma _p|^2}&{}\quad 0\\ 0&{}\quad \frac{|\gamma _p|\sinh (2s)}{\sqrt{1-|\gamma _p|^2}}&{}\quad 0&{}\quad \frac{1+|\gamma _p|^2\cosh (2s)}{1-|\gamma _p|^2} \end{array}\!\!\right) .\nonumber \\ \end{aligned}$$
(22)

The GIP and entanglement of state \(\sigma _{A{\bar{B}}}\) can be obtained by using this covariance matrix and have been plotted in Fig. 3.

Fig. 3
figure 3

a Plots of the GIP (\(\mathcal {P}\)) and the quantum entanglement (\({\mathbf {E}}_{{\mathcal {N}}}\)) for the probe state \(\rho _{A{\bar{B}}}\) as a function of the mass parameter \(\nu \). b Quantum entanglement and the GIP vs. the variation of the space curvature parameter p. The initial squeezing parameter is fixed as \(s=1\)

Full size image

In Fig. 3, we can see that the quantum entanglement between Alice and anti-Bob is zero for any different mass and curvature parameters. That is to say, the curvature of the de Sitter spacetime does not generate quantum entanglement between Alice and anti-Bob [36]. It is shown from Fig. 3a that the mass of the scalar field remarkably affects the accuracy of the black-box parameter estimation in the de Sitter space, which is quite different from the flat space case (\(p=1\)) where the mass parameter does not influence the precision of estimation. If the space curvature parameter is less than 1, the GIP is generated by the curvature effect of the de Sitter space. This means the advantage of quantum metrology is ensured in the curved spacetime even the entanglement is zero. In addition, the GIP reaches its maximum when the mass parameters are \(\nu =1/2\) (conformal scalar limit) and \(\nu =3/2\) (massless scalar limit). In Fig. 3b, it is shown that for the probe state \(\rho _{A{\bar{B}}}\), the GIP increases with the increase of curvature effect. Again, we find that the GIP always maintains a non-zero value if the space curvature parameter is less than 1. This means the precision of the black-box estimation is enhanced under the influence of the de Sitter curvature. In other words, the role of quantum resources for the black-box estimation is played by a non-entanglement quantum correlation. The spacetime effect of the expanding universe may generate some non-entanglement quantum resources between Alice and Bob.

The discord-type quantum correlation [45] is believed to be more practical than entanglement to describe the quantum resources in certain quantum systems. As seen in Refs. [46], although there is no entanglement, quantum information processing tasks can also be done efficiently. We wonder if quantum discord is generated by spacetime effects of the de Sitter space. To this end, we introduce the Gaussian quantum discord [29] to explore the relationship between the GIP and the discord-type quantum correlation . For the two-mode Gaussian state \(\rho _{AB}\), the Rényi-2 measure of quantum discord \({{\mathcal {D}}}_2(\rho _{A|B})\) admits the following expression [42, 47]

$$\begin{aligned} {{\mathcal {D}}}_2(\rho _{A|B})= & {} \ln b - \frac{1}{2} \ln \big (\det {\varvec{\sigma }_{AB}}\big ) + \frac{1}{2} \ln \left( \inf _{\lambda ,\varphi }{\det \tilde{\varvec{\sigma }}^{\Pi _{\lambda ,\varphi }}_A}\right) . \nonumber \\ \end{aligned}$$
(23)

In particular, for the form covariance matrix given in Eq. (11), one obtains

$$\begin{aligned}&\inf _{\lambda ,\varphi }\det \tilde{\varvec{\sigma }}^{\Pi _{\lambda ,\varphi }}_A = \left\{ \begin{array}{l} a \left( a-\frac{c_+^2}{b}\right) , \\ \text {if}\ {\scriptstyle {\left( a b^2 c_-^2-c_+^2 \left( a+b c_-^2\right) \right) \left( a b^2 c_+^2-c_-^2 \left( a+b c_+^2\right) \right) <0}}\, \text{; } \\ \quad \\ \scriptscriptstyle {\frac{2 \left| c_- c_+\right| \sqrt{\left( a \left( b^2-1\right) -b c_-^2\right) \left( a \left( b^2-1\right) -b c_+^2\right) }+\left( a \left( b^2-1\right) -b c_-^2\right) \left( a \left( b^2-1\right) -b c_+^2\right) +c_-^2 c_+^2}{\left( b^2-1\right) ^2}}, \\ \text {otherwise.} \end{array} \right. \end{aligned}$$
(24)

Inserting Eq. (24) into Eq. (23), we can compute the discord of the two-mode Gaussian state.

Fig. 4
figure 4

The variation functions of quantum discord (blue solid line), the GIP (orange dotted line) and entanglement (green dotted line) between Alice and anti-Bob vs. the mass parameter of the field. Other parameters are fixed as \(s = 1\) and \(p=0.3\)

Full size image

In Fig. 4, we plot the quantum discord, the GIP as well as the entanglement between Alice and anti-Bob as a function of the mass parameter. It is shown that the quantum-enhance parameter is ensured for the probe state \(\rho _{A{\bar{B}}}\) because the GIP is always nonzero. The variation trend of the GIP is in accord with the quantum discord. This means the quantum discord in the probe state provides quantum resources for the black-box quantum parameter estimation. It is interesting to note that the bipartite state between Alice and anti-Bob can also be employed as the probe state for the black-box estimation in the expanding de Sitter spacetime even if there is no entanglement generated between them. Therefore, the discord-type quantum correlation for the input probe is the key resource for black-box estimation in the de Sitter space, which ensures the advantage of quantum metrology.

We are also interested in the behavior of the GIP between Bob and anti-Bob, which are separated by the event horizon of the de Sitter space. We get the covariance matrix \(\sigma _{B{\bar{B}}}\) by tracing off the mode A

$$\begin{aligned}&\sigma _{B{\bar{B}}}(s,\gamma _p)\nonumber \\&\quad = \left( \!\!\begin{array}{cccc} \frac{|\gamma _p|^2+\cosh (2s)}{1-|\gamma _p|^2}&{}\quad 0&{}\quad \frac{2|\gamma _p|\cosh ^2(s)}{1-|\gamma _p|^2}&{}\quad 0\\ 0&{}\quad \frac{|\gamma _p|^2+\cosh (2s)}{1-|\gamma _p|^2}&{}\quad 0&{}\quad -\frac{2|\gamma _p|\cosh ^2(s)}{1-|\gamma _p|^2}\\ \frac{2|\gamma _p|\cosh ^2(s)}{1-|\gamma _p|^2} &{}\quad 0&{}\quad \frac{1+|\gamma _p|^2\cosh (2s)}{1-|\gamma _p|^2}&{}\quad 0\\ 0&{}\quad -\frac{2|\gamma _p|\cosh ^2(s)}{1-|\gamma _p|^2} &{}\quad 0&{}\quad \frac{1+|\gamma _p|^2\cosh (2s)}{1-|\gamma _p|^2} \end{array}\!\!\right) .\nonumber \\ \end{aligned}$$
(25)

Similarly, the entanglement and the GIP of Bob and anti-Bob can be calculated by employing the measurement introduced above.

Fig. 5
figure 5

a Plots of the GIP (\(\mathcal {P}\)) and the quantum entanglement (\({\mathbf {E}}_{{\mathcal {N}}}\)) for the probe state \(\rho _{B{\bar{B}}}\) as a function of the mass parameter \(\nu \) of the field. b Plots of the GIP (\(\mathcal {P}\)) and the quantum entanglement (\({\mathbf {E}}_{{\mathcal {N}}}\)) as a function of the space curvature parameter p. The initial squeezing parameter is fixed as \(s=1\)

Full size image

In Fig. 5, we plot the behavior of the GIP and the entanglement between Bob and anti-Bob. It is shown that the GIP increases significantly when the curvature parameter \(p\rightarrow 0\), i.e., the effect of curvature gets stronger. In fact, this indicates space curvature in the de Sitter space enhances the precision of quantum parameter estimation if \(\rho _{B{\bar{B}}}\) is employed as the probe state. This is nontrivial because the open charts R and L are causally disconnected in the de Sitter spacetime and classical information can not be exchanged between the causally disconnected regions according to the general relativity. Here we find that quantum precision measurements are achieved between causally disconnected areas in the de Sitter space, and a more accurate experimental result can be performed in a more curved spacetime. Unlike the initial correlation system Alice and Bob, the GIP and entanglement are maximized for the mass parameters \(\nu =1/2\) (conformal) and \(\nu =3/2\) (massless). This is because the curvature effect of the de Sitter space damages the entanglement and the GIP for the probe state \(\rho _{AB}\), while it generates entanglement for the probe state \(\rho _{B{\bar{B}}}\).

5 Conclusions

We have proposed a black-box quantum parameter estimation scheme for the expanding parameter and discussed the behavior of the GIP for the de Sitter space. It is found that under the curvature effect of the de Sitter space, the changes of the GIP for the probe states \(\rho _{AB}\) and \(\rho _{B {\bar{B}}}\) are consistent with the changes of entanglement. This verifies the fact that quantum resources provide a guarantee for obtaining the higher GIP, and the probe state with the higher GIP ensures a smaller variance for the estimation of expanding parameter. It is demonstrated that the change of the mass parameter does not affect the minimum accuracy of black-box parameter estimation in flat space, but has remarkable effects on the GIP of the black-box parameter estimation in the curved space. Interestingly, the state between separated open charts can be employed as the probe state for the black-box quantum metrology. It is worth noting that the quantum discord of probe states serves as a promising resource for the black-box quantum parameter estimation when there is no entanglement between the initially uncorrelated open charts. The behavior of the probe state for the black-box estimation is quite different because the curvature effect of the de Sitter space damages the entanglement and the GIP for the initially correlated probe state, while it generates quantum resources for initially uncorrelated probe states.